Reconstruction of Piecewise Smooth Functions Based on Fourier Extension

Abstract

This paper proposes a hierarchical Fourier extension framework for the accurate reconstruction of piecewise smooth functions with mixed-order singularities. To address key challenges in spectral approximation–namely boundary-induced artifacts, instability in edge detection, and loss of accuracy near discontinuities–the method integrates three main components: (1) boundary-focused Fourier extensions that isolate endpoint effects while preserving internal structures; (2) a multi-stage edge detection strategy combining spectral mollifiers and coordinate transformations to identify discontinuities in function values and their derivatives; (3) adaptive domain partitioning followed by localized Fourier extensions to retain spectral accuracy on smooth segments. Numerical results demonstrate near machine-precision accuracy (∼10⁻¹⁴–10⁻¹⁵) with significantly improved stability and performance over traditional global methods.

1. Introduction

The reconstruction of piecewise smooth functions, characterized by their composition of multiple smooth segments, which are separated by discontinuities or singularities, is a critical challenge in computational mathematics and engineering. These functions frequently arise in diverse applications such as solutions to nonlinear hyperbolic partial differential equations (e.g., shock waves), physical fields with abrupt transitions (e.g., temperature or stress discontinuities), and signal processing [1,2,3]. The inherent non-smoothness of such functions poses significant hurdles for traditional global approximation methods like polynomial expansions or Fourier series. Classical results, such as Bernstein’s theorem, highlight the limitations of polynomial approximations for non-smooth functions, where convergence rates degrade near singularities [4]. Furthermore, the Gibbs phenomenon–persistent oscillations near discontinuities–compromises both numerical stability and accuracy, necessitating advanced techniques tailored to address these challenges [5].

Recent developments in approximation theory have sought to address these challenges through innovative localized and nonlinear approaches. Early foundational work by Gelb and Gottlieb [6] proposed mitigating Gibbs phenomena by strategically “stitching” analytic functions across non-overlapping subdomains while leveraging Fourier coefficients for approximation, though their approach left room for enhanced oscillation suppression. Subsequent progress emerged through Geer and Banerjee’s [7] introduction of a periodic basis function family with embedded discontinuities, which is theoretically proven to achieve exponential convergence rates in the maximum norm for approximating piecewise smooth functions. This framework demonstrated how tailored basis systems could fundamentally improve reconstruction accuracy near singularities. Another innovative direction involves piecewise polynomial approximations, such as Treffthen’s recursive detection of singularities to construct segmented Chebyshev interpolants, which avoid global oscillations by adaptively partitioning the domain [8]. Similarly, Eckhoff’s algebraic method identifies jump discontinuities by solving linear systems to recover both the locations and magnitudes of singularities [9]. Akansha’s recent breakthrough [10] introduced the Piecewise Padé-Chebyshev (PiPC) method: a nonlinear rational approximation technique that partitions the domain $I:=[a,b]$ into N subintervals, each independently approximated through localized Padé-Chebyshev interpolants. Crucially, PiPC eliminates the need for explicit singularity localization while maintaining spectral accuracy, as its adaptive partitioning inherently captures discontinuities through rational function flexibility.

Fourier extension has emerged as a pivotal technique in computational mathematics for approximating non-periodic functions while mitigating the Gibbs phenomenon. The core idea of Fourier extension lies in artificially extending a non-periodic function defined on an interval $[-1,1]$ to a larger periodic domain $[-T,T](T>1)$, thereby enabling efficient Fourier-based approximation [11]. This approach transforms the problem into a frame approximation, where the extended function is represented as a truncated Fourier series on the enlarged domain. However, this formulation introduces significant challenges, primarily due to the ill-conditioned nature of the associated least-squares systems and oscillations in the extended region [12]. Early advancements in Fourier extension focused on stabilizing these ill-posed systems through regularization techniques. Boyd’s introduction of Truncated Singular Value Decomposition (TSVD) marked a critical step that enabled stable solutions by discarding singular vectors corresponding to negligible singular values [13]. Since then, many researchers have achieved significant results in the field of Fourier extension [14,15,16]. A persistent issue in Fourier extension has been the emergence of oscillations in the extended region. Recent work by Zhao et al. addresses this through a weighted generalized inverse framework. By reformulating the extension as a compact operator equation and introducing weighted norms to enforce coefficient decay, the method shifts the approximation target from minimizing the Euclidean norm of coefficients to a smoother, oscillation-reducing solution [17].

Edge detection in Fourier data is a well-established challenge in spectral methods [18,19]. A fundamental limitation of existing Fourier-based edge detection techniques lies in the inherent discontinuity of domain boundaries within Fourier representations. This discontinuity introduces spurious “edges” and obstructs the precise identification of internal singularities genuinely associated with derivatives. Crucially, even low-order derivative discontinuities significantly degrade the approximation accuracy of piecewise functions. While a Fourier extension appears intuitively promising for mitigating boundary singularities, its direct application to non-smooth function data proves problematic: the intrinsic singularities amplify the Fourier extension coefficients dramatically [20]. From the perspective of compact operator equations, this phenomenon arises from substantial data “errors” [17]. Consequently, global extension approaches analogous to [11] fail to reliably extract accurate edge information through Fourier coefficients.

In prior work [21], one of the present authors developed a boundary-driven Fourier extension method that circumvents internal singularity interference by computing extensions using data near the two endpoints of the interval. This paper adapts this methodology to the approximation of piecewise smooth functions. The proposed framework proceeds hierarchically:

• Initial Extension: Compute boundary extensions for the global interval using data near the two endpoints.
• Singularity Identification: Detect intrinsic function discontinuities via Fourier-coefficient-based edge detection.
• Domain Partitioning: Subdivide the interval at identified non-smooth points, yielding sub-intervals with at least first-order differentiability.
• Recursive Refinement: For each sub-interval, repeat boundary-driven extensions and employ Fourier-transform differentiation properties to detect first-order derivative edges. Iteratively apply this process to resolve second-order derivative edges.

This hierarchical approach systematically disentangles boundary artifacts from true derivative singularities, enabling progressive recovery of edge information across multiple differentiation orders. The core innovation of this approach lies in its recursive boundary-driven structure and localized processing strategy, which–when combined–offer a novel paradigm not previously realized in the spectral methods literature. Traditional Fourier-based techniques rely heavily on global information, making them susceptible to instability and loss of accuracy when dealing with localized non-smooth behavior [6,17]. In contrast, the present method confines Fourier extensions to data near the endpoints and recursively applies this process on adaptively partitioned subdomains, enabling precise isolation and recovery of singular features at multiple derivative levels.

Compared to classical global extension or filtering strategies, the proposed framework offers several distinctive advantages:

• Decoupling of boundary and interior singularities: By restricting initial extensions to the domain boundaries, the method prevents interior discontinuities from contaminating the Fourier coefficients, thereby cleanly separating boundary-induced artifacts from true edges.
• Hierarchical recovery of derivative discontinuities: Leveraging the analytic differentiation properties of the Fourier transform, the method systematically detects discontinuities in successive derivatives, enabling a structured and complete characterization of non-smooth behavior.
• Simultaneous stability and accuracy: By limiting the region of Fourier extension and employing local reconstruction, the method significantly reduces the amplification of singularities in the spectral coefficients, ensuring numerical stability and high approximation accuracy.

This framework not only provides a new direction for handling non-smooth functions in Fourier spectral methods but also establishes a foundation for the accurate and stable numerical solution of differential equations with discontinuous or singular data. The combination of spectral accuracy with localized refinement opens new possibilities for robust edge-aware spectral algorithms across a broad range of applications.

The remainder of this paper is organized as follows. In Section 2, we reformulate the Fourier extension problem, analyze the properties of piecewise smooth functions in the Sobolev space, and provide a preliminary estimate of the error. In Section 3, we discuss the method for piecewise smooth reconstruction based on uniform sampling. Section 4 verifies the effectiveness of the proposed method through numerical experiments. Finally, in Section 5, we summarize the research content of this paper and propose further discussions.

2. Fourier Extension Method Based on Boundary Interval Data

In this section, we review the Fourier extension algorithm using boundary interval data initially presented in [21]. To address the sensitivity of edge detection to extension area smoothness, we incorporate the weighted generalized inverse matrix from [17] into our boundary extension computation. This integration introduces key modifications to the original formulation in [21].

Let $f:[0,1]\to \mathbb{R}$ be a function sampled at equidistant nodes:

$$t_{\mathsf{\ell }}={\displaystyle \frac{\mathsf{\ell }}{M}},\mathsf{\ell }=0,1,\dots ,M.$$

For boundary extension, we first let $m_{\mathrm{\Delta }}\in {\mathbb{N}}^{+}$ be the number of boundary interval nodes. Given an extension parameter $T_{\mathrm{\Delta }}>1$, define

$$L_{\mathrm{\Delta }}=2\times \lceil T_{\mathrm{\Delta }}\times (m_{\mathrm{\Delta }}-1)\rceil ,h={\displaystyle \frac{2\pi }{L_{\mathrm{\Delta }}}},s_j=(j-1)h,j=1,2,\dots ,L_{\mathrm{\Delta }},$$

where $\lceil ·\rceil$ is the rounding symbol. The extension function g is constructed through boundary value mapping:

$$g\left(s_j\right)=\left\{\begin{array}{cc}f\left(t_{M-m_{\mathrm{\Delta }}+j}\right),\hfill & j\in J_{\mathrm{\Delta },1},\hfill \\ f\left(t_{j-L_{\mathrm{\Delta }}/2-1}\right),\hfill & j\in J_{\mathrm{\Delta },2},\hfill \end{array}\right.$$

(1)

with index sets:

$$J_{\mathrm{\Delta },1}=\{1,2,\dots ,m_{\mathrm{\Delta }}\},J_{\mathrm{\Delta },2}=\{{\displaystyle \frac{L_{\mathrm{\Delta }}}{2}}+1,{\displaystyle \frac{L_{\mathrm{\Delta }}}{2}}+2,\dots ,{\displaystyle \frac{L_{\mathrm{\Delta }}}{2}}+m_{\mathrm{\Delta }}\}.$$

Let the sampling ratio $\gamma \ge 1$ determine the spectral resolution:

$$n_{\mathrm{\Delta }}=⌈{\displaystyle \frac{m_{\mathrm{\Delta }}}{\gamma }}⌉.$$

Define the weight function and basis functions:

$${\rho }_k=e^{{\displaystyle \frac{\left|k\right|}{4}}-{\displaystyle \frac{1}{2}}},{\varphi }_k\left(s\right)={\displaystyle \frac{1}{\sqrt{L_{\mathrm{\Delta }}}}}{e}^{\mathrm{i}ks},{\psi }_k\left(s\right)={\displaystyle \frac{1}{{\rho }_k}}{\varphi }_k\left(s\right),k=-n_{\mathrm{\Delta }},\dots ,n_{\mathrm{\Delta }}.$$

(2)

Construct the system matrix $\left({\tilde{\mathbf{F}}}_{\gamma ,N_{\mathrm{\Delta }}}^T\right)\in {\mathbb{C}}^{2m_{\mathrm{\Delta }}\times (2n_{\mathrm{\Delta }}+1)}$

$${\left({\tilde{\mathbf{F}}}_{\gamma ,N_{\mathrm{\Delta }}}^T\right)}_{\mathsf{\ell },k}=\left\{\begin{array}{cc}\hfill {\psi }_k\left(s_{\mathsf{\ell }}\right),& 1\le \mathsf{\ell }\le m_{\mathrm{\Delta }},\hfill \\ \hfill {\psi }_k(s_{{\displaystyle \frac{L_{\mathrm{\Delta }}}{2}}+\mathsf{\ell }-m_{\mathrm{\Delta }}}),& m_{\mathrm{\Delta }}<\mathsf{\ell }\le 2m_{\mathrm{\Delta }}\hfill \end{array}\right.$$

and the observation vector $\left(\mathbf{g}\right)\in {\mathbb{C}}^{2m_{\mathrm{\Delta }}\times 1}$

$${\left(\mathbf{g}\right)}_{\mathsf{\ell }}=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{1}{m_{\mathrm{\Delta }}}}g\left(s_{\mathsf{\ell }}\right),& 1\le \mathsf{\ell }\le m_{\mathrm{\Delta }},\hfill \\ \hfill {\displaystyle \frac{1}{m_{\mathrm{\Delta }}}}g\left(s_{\mathsf{\ell }-m_{\mathrm{\Delta }}+{\displaystyle \frac{L_{\mathrm{\Delta }}}{2}}}\right),& m_{\mathrm{\Delta }}<\mathsf{\ell }\le 2m_{\mathrm{\Delta }}.\hfill \end{array}\right.$$

The truncated singular value decomposition (TSVD) solves:

$${\tilde{\mathbf{F}}}_{\gamma ,N_{\mathrm{\Delta }}}^T\mathbf{c}=\mathbf{g},$$

(3)

yielding the regularized solution:

$${\mathbf{c}}^{ϵ}=\sum _{{\sigma }_i>ϵ}{\displaystyle \frac{{\mathbf{u}}_i^T\mathbf{g}}{{\sigma }_i}}{\mathbf{v}}_i,$$

(4)

where $ϵ$ serves as the regularization parameter and $\{{\sigma }_i,{\mathbf{u}}_i,{\mathbf{v}}_i\}$ denotes the singular system of matrix ${\tilde{\mathbf{F}}}_{\gamma ,N_{\mathrm{\Delta }}}^T$.

The extended function $g_c\left(s\right)$ is then obtained as follows:

$$g_c\left(s\right)=\sum _{k=-n_{\mathrm{\Delta }}}^{n_{\mathrm{\Delta }}}{\mathbf{c}}_k^{ϵ}{\psi }_k\left(s\right).$$

Finally, we construct the periodic extension $f_c$ with period $P=1+\lambda$, where

$$\lambda ={\displaystyle \frac{\lceil T_{\mathrm{\Delta }}-1\rceil \times (m_{\mathrm{\Delta }}-1)}{M}}$$

defined over $[0,P)$ by

$$f_c\left(t_{\mathsf{\ell }}\right)=\left\{\begin{array}{cc}\hfill f\left(t_{\mathsf{\ell }}\right),& 0\le \mathsf{\ell }\le M,\hfill \\ \hfill g_c\left(s_{m_{\mathrm{\Delta }}+\mathsf{\ell }-M}\right),& l>M.\hfill \end{array}\right.$$

Figure 1 illustrates the computational workflow for the non-smooth function $f\left(t\right)=|t-1/2|$, defined on the interval $[0,1]$. Notably, while the function contains a singularity at $1/2$, the boundary interval data utilized in constructing $g_c$ deliberately excludes this critical point. This strategic exclusion ensures numerically stable extension results, as evidenced by the computed solution. The incorporation of the weighting factor ${\rho }_k$ further guarantees a smooth extended profile in the reconstructed function. Leveraging the inherent differentiation properties of Fourier analysis combined with subsequent edge detection techniques, our method achieves precise localization of the singularity at $1/2$.

Remark 1.

Regarding the proposed algorithm, two critical implementation notes require emphasis:

• Weight Simplification: Given the intentionally limited spectral resolution ($n_{\mathrm{\Delta }}\ll M$) employed in our extension framework, the weighting coefficients ${\rho }_k$ can be unified through the standard form (2). This represents a significant simplification compared to the multi-stage weighting mechanism proposed in [17], while maintaining equivalent regularization effectiveness for small-scale systems.
• Parameter Selection: Reference [21] conducted a large amount of empirical research on the parameters involved and provided specific configuration recommendations. We adopt these parameters from [21] without revisiting the detailed analysis: $\gamma =1$, $m_{\mathrm{\Delta }}=25$, $T_{\mathrm{\Delta }}=6$.

3. Edge Detection of Functions and Their Derivatives

Let h be a piecewise smooth function defined on the interval $[0,1]$, which possesses a finite number of jump discontinuities located at points $a_k$, for $k=1,\dots ,K$. The associated jump function $\left[h\right]$ captures these discontinuities and is defined as

$$\left[h\right]\left(t\right):=h(t+)-h(t-),t\in [0,1],$$

(5)

where $h(t+)$ and $h(t-)$ denote the right and left limits of h at t, respectively.

Suppose that h admits a Fourier expansion of the form

$$h\left(t\right)=\sum _{k=-\infty }^{\infty }{\widehat{h}}_k{e}^{2\pi \mathrm{i}kt},$$

(6)

where ${\widehat{h}}_k$ are the Fourier coefficients. To detect edges (i.e., locations of discontinuities), we employ a mollified version of the derivative of the truncated Fourier series, as proposed in [22]:

$$\left(T_{N,{\sigma }_{\lambda }}h\right)\left(t\right)=2\pi \mathrm{i}\sum _{k=-N}^{N}k{\widehat{\omega }}_{\lambda }\left(k\right){\widehat{h}}_k{e}^{2\pi \mathrm{i}kt},$$

(7)

where the mollification is achieved by a smooth spectral filter defined through the Gaussian window

$${\omega }_{\lambda }\left(t\right):=\omega \left(\lambda t\right),\mathrm{with}\omega \left(t\right)=e^{-{\pi }^2{t}^2},$$

and the regularization parameter $\lambda ={\lambda }_N$ is set as $N/\sqrt{logN}$ to balance convergence and localization.

This operator $T_{N,{\sigma }_{\lambda }}$ possesses the key property of uniform convergence to the jump function:

$$\underset{N\to \infty }{lim}\left(T_{N,{\sigma }_{\lambda }}h\right)\left(t\right)=\left[h\right]\left(t\right),\mathrm{uniformly}\mathrm{on}[0,1].$$

While this methodology, particularly when combined with coordinate transformations, is effective for detecting edge information in functions defined on finite intervals, additional care must be taken in the non-periodic setting. Specifically, the endpoints of the interval $[0,1]$ introduce artificial discontinuities when the function is extended periodically. Consequently, if a derivative of the function contains a discontinuity within the interior of the interval, such an edge may be obscured or misidentified by direct application of the Fourier-based method. This limitation is illustrated in Figure 2.

Figure 3a presents the original piecewise-defined function

$$f\left(t\right)=\left\{\begin{array}{cc}-cos\left(\pi t\right),\hfill & 0\le t\le {\displaystyle \frac{1}{2}},\hfill \\ \pi t-{\displaystyle \frac{\pi }{2}},\hfill & {\displaystyle \frac{1}{2}}<t\le 1,\hfill \end{array}\right.$$

(8)

along with its direct periodic extension. Due to this extension, the endpoints $t=0$ and $t=1$ exhibit artificial zero-order jumps. In Figure 3b, we attempt to detect third-order edge features by directly substituting ${\widehat{h}}_k={\left(\mathrm{i}\xi \right)}^3{\widehat{f}}_k$ into Equation (7). The result indicates that the true third-order edge at $t=1/2$ is difficult to resolve due to the contamination by endpoint effects.

To overcome this limitation, we perform a Fourier continuation procedure to generate a smooth periodic extension $f_c\left(t\right)$, as shown in Figure 3c. This extension eliminates spurious discontinuities and permits the accurate application of spectral differentiation. Figure 3d displays the result of applying the edge detection operator to the third derivative $f_c^{\left(3\right)}\left(t\right)$, successfully isolating the true high-order discontinuity.

Based on the above analysis and demonstration, we propose the following systematic procedure for detecting discontinuities in the k-th derivative of a function defined on a finite interval:

• Fourier Extension: Construct a smooth periodic extension $h_c$ of the original function h using the method described in Section 2, thereby mitigating artificial endpoint effects.
• Spectral Differentiation: Compute the k-th derivative in the frequency domain via the Fourier differentiation property: $\widehat{h_c^{\left(k\right)}}={\left(2\pi \mathrm{i}k\right)}^k{\widehat{h}}_k$.
• Edge Detection: Apply the mollified edge detection operator in Equation (7) to the differentiated function, optionally combined with a coordinate transformation for better localization.

This framework enables robust and accurate identification of derivative discontinuities—often indicative of features such as curvature or inflection points—in a wide class of piecewise smooth, non-periodic functions.

4. Reconstruction of Piecewise Smooth Functions with k-Order Discontinuities

Let $F:[a,b]\to \mathbb{R}$ be a piecewise $C^r$-smooth function, meaning that on each subinterval of a partition, F is r-times continuously differentiable. We assume that the k-th derivatives of F (for $k=0,1,\dots ,r$) exhibit jump discontinuities at a set of points ${\left\{a_j\right\}}_{j=0}^J$, where $a=a_0<a_1<\cdots <a_J=b$.

Suppose we are given discrete samples of F on a uniform grid ${\left\{x_i\right\}}_{i=0}^N$ defined by

$$x_i=a+ih,\mathrm{with}h={\displaystyle \frac{b-a}{N}}.$$

Initially, we assume that the discontinuity locations $\left\{a_j\right\}$ align with the sampling grid, i.e., $\left\{a_j\right\}\subset \left\{x_i\right\}$. If this assumption does not hold, the edge positions can be iteratively refined via adaptive grid refinement around the initially detected discontinuities.

Our goal is to reconstruct F with high accuracy, particularly near discontinuities. The reconstruction begins by detecting the locations of the discontinuities $\left\{a_j\right\}$ using the following multi-stage procedure:

• Initialization: Set the initial edge set as $D=\{a,b\}$.
• For each derivative order $k=0,1,\dots ,r$, perform the following:
  • Local Approximation: On each subinterval defined by the current partition D, compute a Fourier extension of F using the method described in Section 2, incorporating coordinate transformations to handle non-periodic domains.
  • Edge Detection: Compute the k-th derivative of the extended function and apply the edge detection Formula (7) (with appropriate coordinate adjustments) to identify potential jump discontinuities in the k-th derivative.
  • Update: Incorporate the newly detected edges into D, ensuring that the list remains sorted.

After completing the edge detection process, the domain $[a,b]$ is partitioned into J subintervals $I_j=[a_{j-1},a_j]$ for $j=1,2,\dots ,J$. We define the restriction of F on each subinterval as follows:

$$F_j\left(x\right)=F\left(x\right),x\in I_j,j=1,2,\dots ,J.$$

To facilitate the use of Fourier extensions on each subinterval, we introduce a normalized variable $t\in [0,1]$ via the affine mapping:

$$f_j\left(t\right)=F_j(a_{j-1}+r_{j}t),\mathrm{where}{r}_j=a_j-a_{j-1}.$$

For each normalized function $f_j\left(t\right)$, we compute its Fourier extension approximation ${\left(f_j\right)}_c\left(t\right)$ using the techniques in Section 2. The global approximation ${\mathcal{Q}}_J^{ϵ}F$ of the function F is then assembled from the local approximations:

$$\left({\mathcal{Q}}_J^{ϵ}F\right)\left(x\right):={\left(f_j\right)}_c\left({\displaystyle \frac{x-a_{j-1}}{r_j}}\right),x\in I_j,j=1,2,\dots ,J.$$

As shown in Figure 2a, when Fourier extension is directly applied over the entire domain for approximation, the overall accuracy is compromised due to the presence of singularities, and the desired level of precision cannot be achieved (The regions where the error approaches machine precision correspond to the locations of the given data points). However, by accurately detecting the edge at $t=1/2$ and applying local Fourier extensions (Figure 2b), the reconstruction quality improves substantially. This demonstrates the effectiveness of incorporating edge information into the reconstruction pipeline.

5. Numerical Tests

To validate the effectiveness and versatility of the proposed reconstruction method, we first present three numerical experiments involving piecewise smooth functions with different types of singularities. Unless otherwise specified, all tests share the following settings:

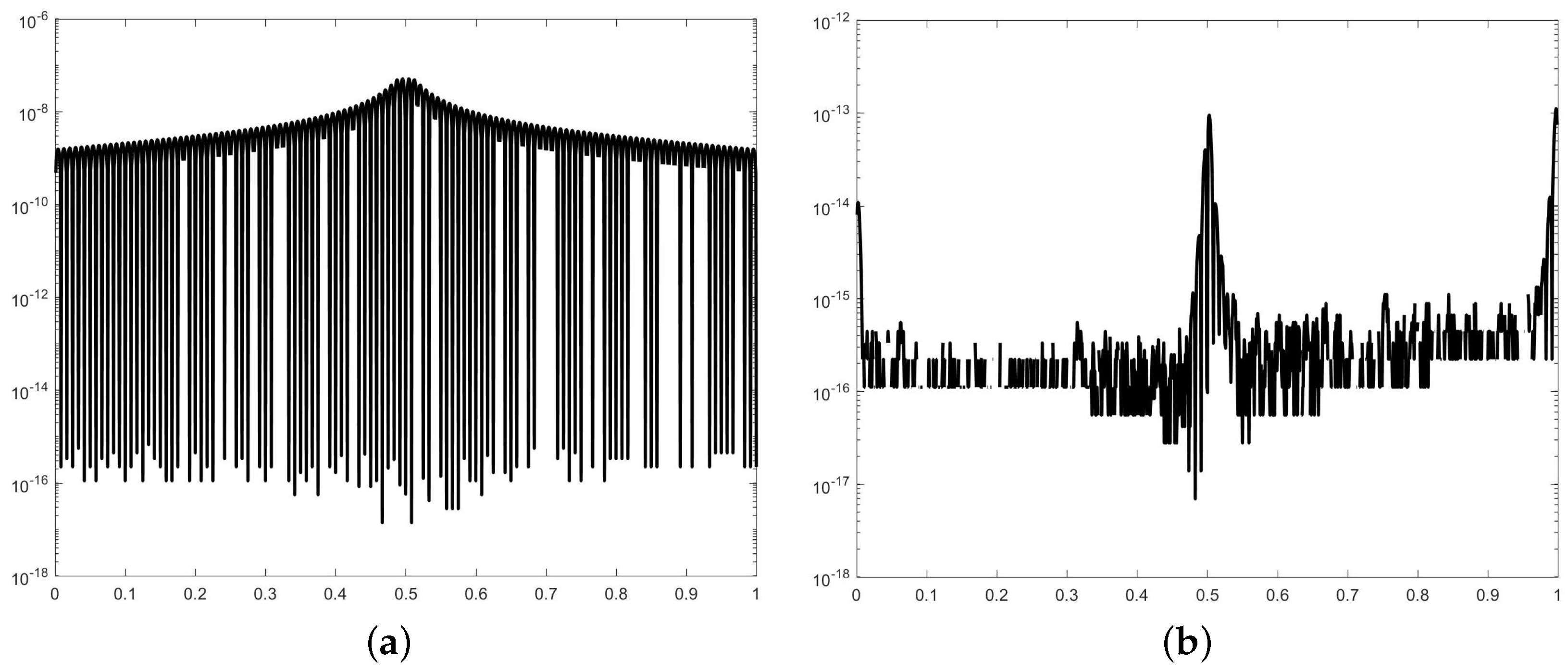
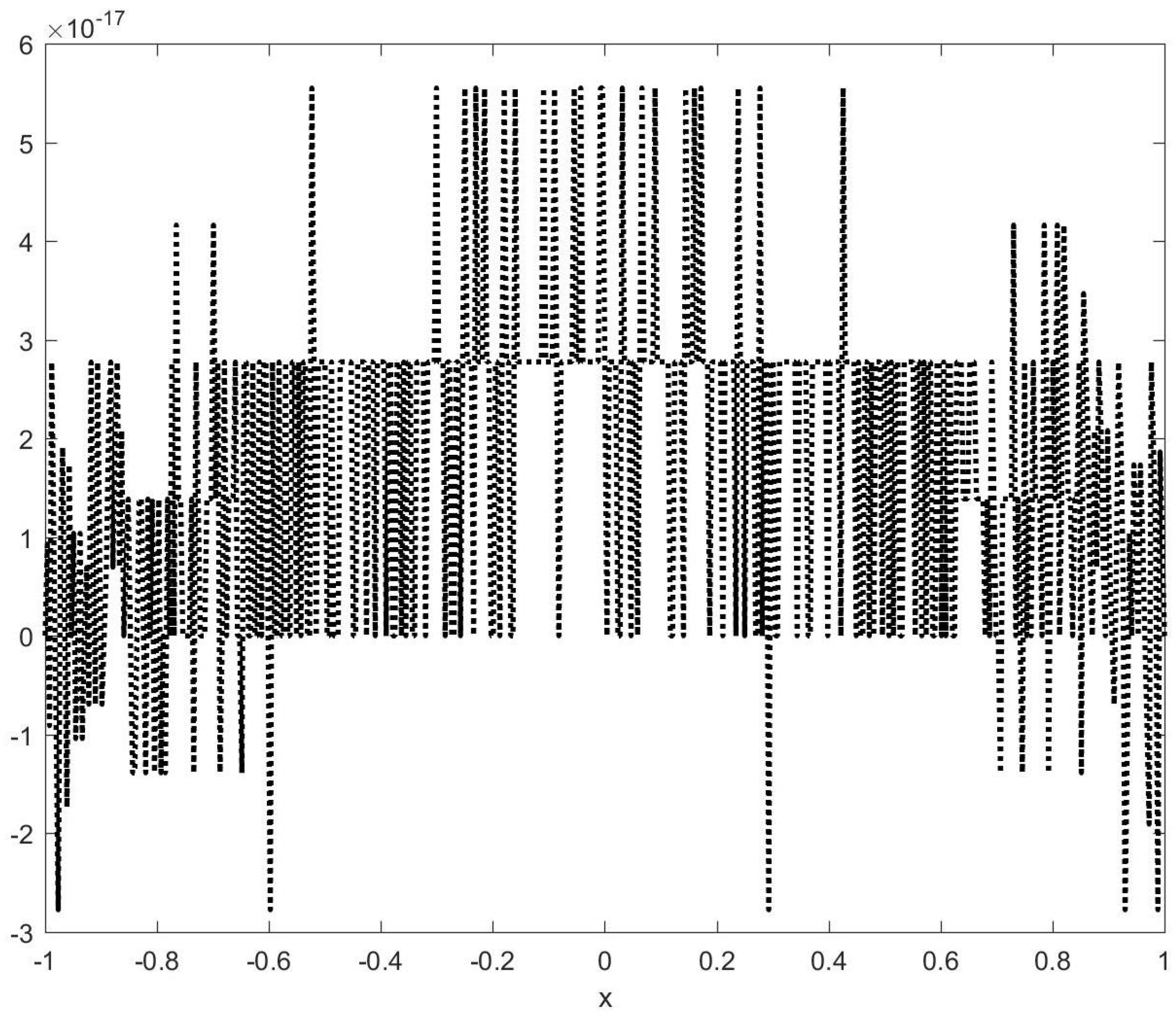
• Error metric: The approximation error is measured as the maximum pointwise difference on a refined evaluation grid, which is 10 times denser than the construction grid.
• Parameters: Regularization parameter $ϵ={10}^{-14}$; domain $[a,b]=[-1,1]$; initial sampling grid with $N=512$ points.

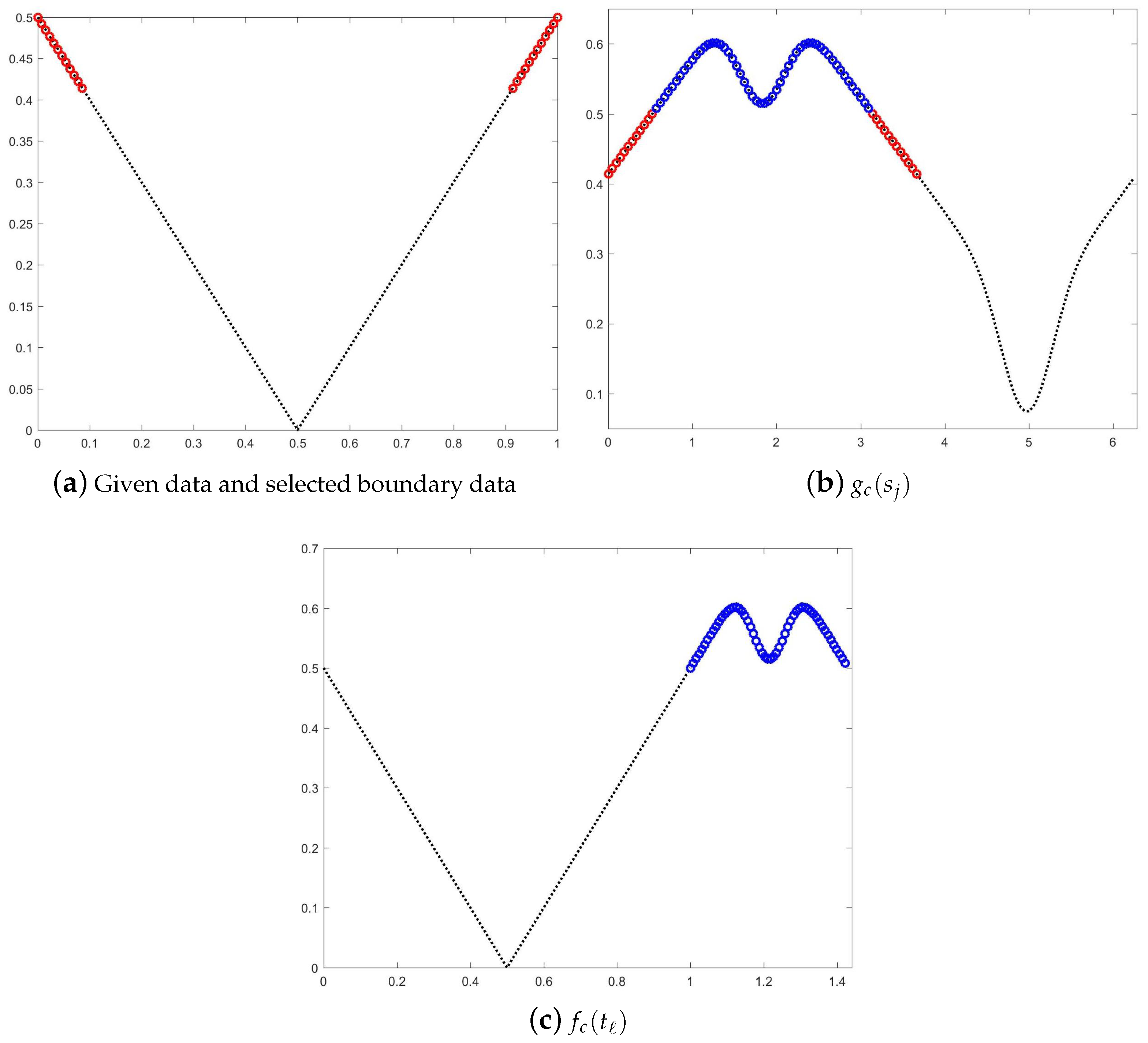
5.1. Example 1: First-Order Derivative Discontinuities

We consider a piecewise linear-quadratic function with discontinuities in the first derivative:

$$F\left(x\right)=\left\{\begin{array}{cc}2x+1,\hfill & -1\le x\le -0.5,\hfill \\ x+0.5,\hfill & -0.5<x\le 0,\hfill \\ 0.5,\hfill & 0<x\le 0.5,\hfill \\ 2x^2,\hfill & 0.5<x\le 1.\hfill \end{array}\right.$$

All internal discontinuities are of first-order (i.e., jumps in $F^{\prime }$). The reconstruction procedure proceeds as follows:

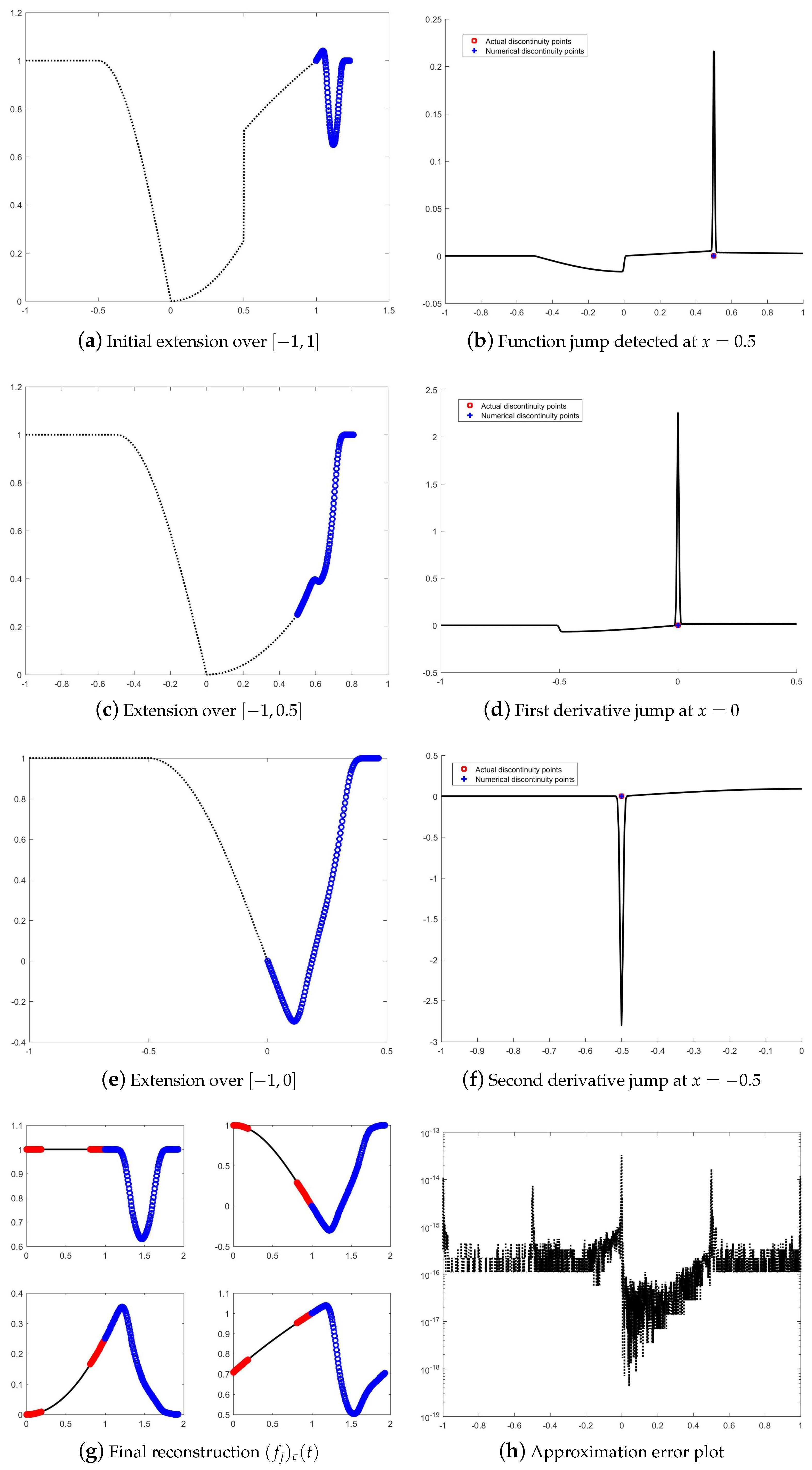
• Figure 4a displays the Fourier extension of F over the entire domain.
• Figure 4b shows the successful detection of all first-order derivative jumps.
• Figure 4c illustrates the reconstructed function on subintervals using localized Fourier extensions.
• Figure 4d confirms that the maximum error is close to machine precision (∼10⁻¹⁴).

Evaluation: This example demonstrates that the proposed method achieves high-accuracy reconstruction for functions with multiple first-order singularities. The precision is comparable to Fourier extension performance on globally smooth functions.

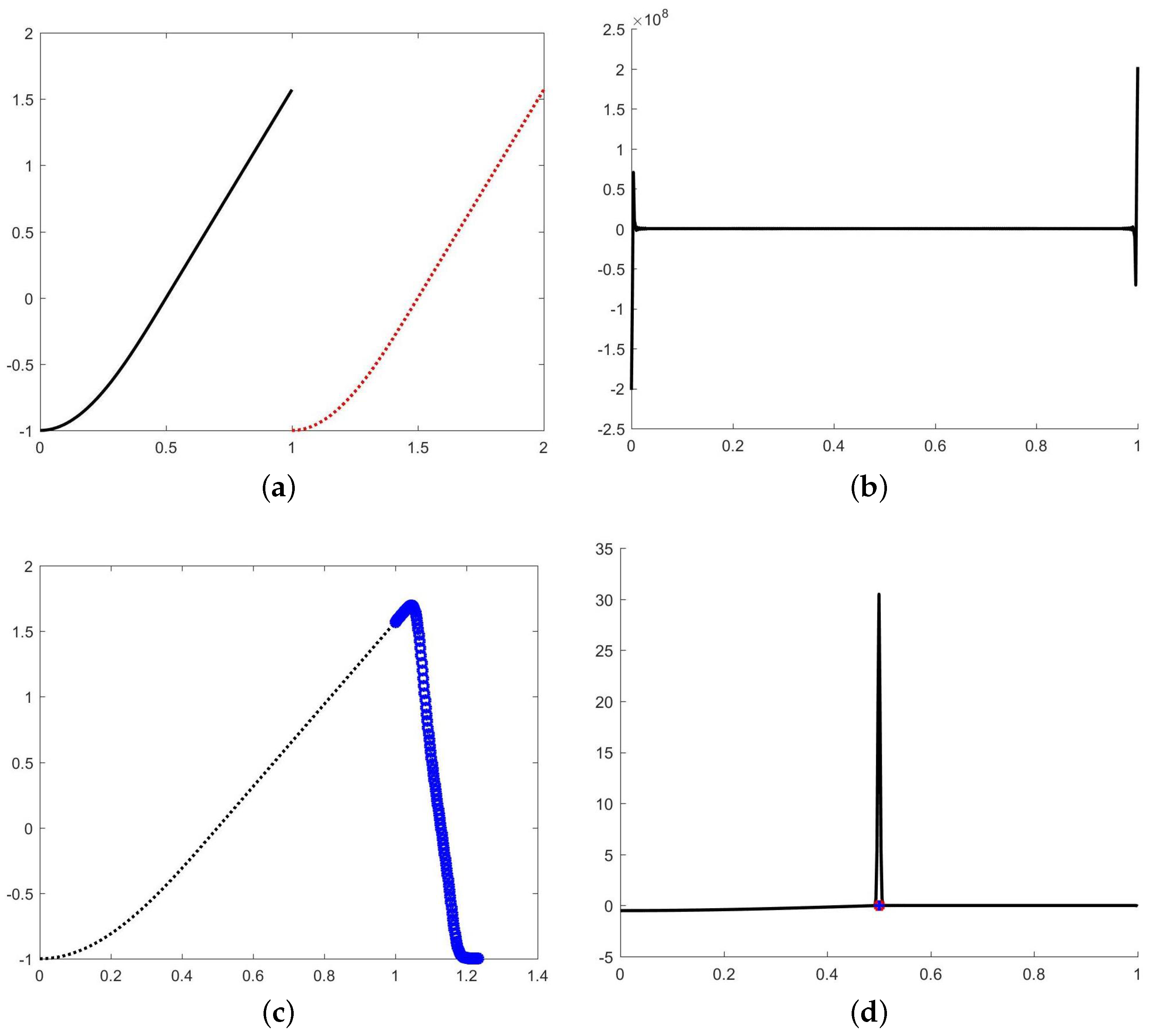
5.2. Example 2: Second-Order Derivative Discontinuities

Consider the function:

$$F\left(x\right)=\left\{\begin{array}{cc}sin\left(\pi x\right),\hfill & -1\le x\le -0.5,\hfill \\ -1,\hfill & -0.5<x\le 0.5,\hfill \\ 2x^3-1.5x-0.5,\hfill & 0.5<x\le 1.\hfill \end{array}\right.$$

Here, the discontinuities appear in the second derivative $F^{″}$. The reconstruction process is as follows:

• Figure 5a shows the global extension of F.
• Figure 5b illustrates successful detection of second-order singularities.
• Figure 5c shows the reconstruction based on segmented intervals.
• Figure 5d confirms a final reconstruction error near ${10}^{-14}$.

Evaluation: This test case demonstrates the method’s robustness in handling higher-order singularities. Even when discontinuities are not directly visible in the function but only appear in its second derivative, the algorithm accurately detects and localizes them, ensuring high-fidelity reconstruction.

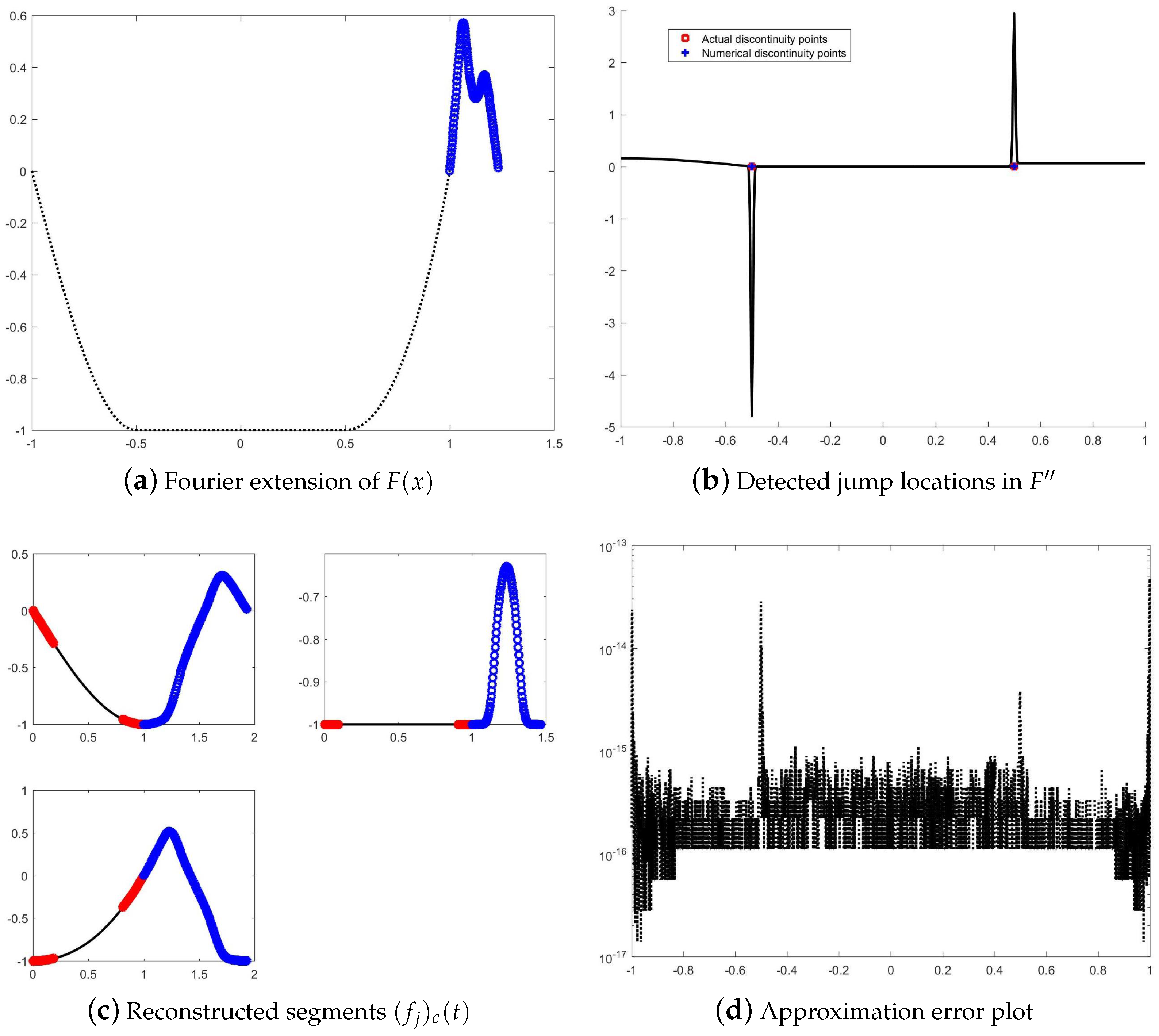
5.3. Example 3: Mixed-Type Singularities

In this example, we test the method on a function that combines singularities of different orders:

$$F\left(x\right)=\left\{\begin{array}{cc}1,\hfill & -1\le x\le -0.5,\hfill \\ sin(-\pi x),\hfill & -0.5<x\le 0,\hfill \\ x^2,\hfill & 0<x\le 0.5,\hfill \\ \sqrt{x},\hfill & 0.5<x\le 1.\hfill \end{array}\right.$$

The singularities are

• A function jump at $x=0.5$;
• A first-order derivative discontinuity at $x=0$;
• A second-order derivative discontinuity at $x=-0.5$.

Evaluation: This example highlights the strength of the proposed multi-stage edge-detection scheme. By successively isolating discontinuities of decreasing smoothness, the method successfully classifies and localizes mixed singularities, enabling accurate segmentation and near-machine-precision reconstruction across the domain (Figure 6).

5.4. Summary of Results

Across all three examples, the proposed method consistently delivers

• Accurate and automatic detection of edge locations at various smoothness levels;
• Efficient reconstruction using localized Fourier extensions with error bounded by $\mathcal{O}\left(ϵ\right)$;
• Robust performance for both isolated and compound singularity structures.

These experiments demonstrate that the method is well-suited for practical applications involving piecewise smooth signals, offering both high fidelity and computational stability.

Finally, we give a simple example of solving a differential equation to demonstrate the potential application value of the method when the problem contains singularities.

5.5. Example 4: Apply the Method to Solve Differential Equation

In this example we consider the following differential equation:

$$u_{xx}=\left|x\right|,-1<x<1,u(\pm 1)=0.$$

It is a Poisson equation, with solution

$$u={\displaystyle \frac{{\left|x\right|}^3-1}{6}}.$$

(9)

For the above differential equation, we can first construct the Fourier extension approximation of the source term $\left|x\right|$ and identify the singular point 0. Then, we can construct the approximate solution piecewise and use the corresponding relationship between the Fourier coefficients, the boundary condition $u(\pm 1)=0$, and the continuity conditions

$$u(0+)=u(0-),u^{\prime }(0+)=u^{\prime }(0-)$$

to determine the final solution. Figure 7 shows the approximation error of the numerical solution. It can be seen that for differential equations containing singular points, the new method can also achieve spectral accuracy.

6. Computational Complexity and Comparison with Gegenbauer Reconstruction

6.1. Computational Complexity of the Proposed Method

The proposed reconstruction method involves three main stages:

• Initial Fourier extension over the full domain.
• Iterative edge detection to identify discontinuity points and classify their orders.
• Segment-wise reconstruction via local Fourier extensions on smooth subintervals.

Let N denote the total number of sampling points, and let K be the number of detected singularities. The complexity of each component is estimated as follows:

• Fourier extension (global and local): For smooth intervals of size $N_j\approx N/K$, computing a Fourier extension using FFT-based methods costs $\mathcal{O}(N_{j}log{N}_j)$. Summing over all intervals yields $\mathcal{O}(Nlog(N/K\left)\right)$.
• Edge detection: Assuming d iterative detection stages (e.g., for jumps in F, $F^{\prime }$, and $F^{″}$), the detection cost is $\mathcal{O}(dNlogN)$, leveraging FFT-based derivative filters.
• Interval assembly: The segmentation and global reconstruction require $\mathcal{O}\left(N\right)$ operations.

Total computational cost is thus

$$\mathcal{O}(dNlogN),$$

assuming K and d remain small relative to N.

6.2. Comparison with Gegenbauer Reconstruction

Gegenbauer reconstruction is a classical method for recovering piecewise smooth functions from global spectral data by suppressing the Gibbs phenomenon. It generally consists of

• Edge detection (using Fourier-based indicators or concentration kernels);
• Gegenbauer polynomial expansion on smooth subintervals;
• Coefficient computation via projection or least-squares.

6.2.1. Complexity Comparison

The following applies in the Gegenbauer reconstruction:

• Edge detection: Similar to our method, typically $\mathcal{O}(NlogN)$.
• Expansion cost: Each interval requires computing M Gegenbauer coefficients, costing $\mathcal{O}\left(M^2\right)$. With K subintervals, the total cost is $\mathcal{O}\left(K{M}^2\right)$.
• Since M often grows with N to maintain accuracy, the overall complexity can approach $\mathcal{O}\left(N^2\right)$ in practice.

6.2.2. Qualitative Comparison

Both methods aim to achieve high-order or spectral accuracy for functions with discontinuities. The proposed method offers several practical advantages:

• It is highly adaptive, requiring minimal parameter tuning.
• The FFT-based implementation leads to quasi-linear computational complexity.
• It performs well even for functions with multiple and mixed-order singularities.

By contrast, while the Gegenbauer approach is theoretically elegant and achieves high accuracy when properly configured, it can be computationally expensive and sensitive to parameter choices (

Table 1. Comparison between the proposed method and Gegenbauer reconstruction.

Aspect	Proposed Fourier Extension Method	Gegenbauer Reconstruction
Edge detection	Iterative Fourier-based filters (multi-order)	Typically single-stage, Fourier-based
Basis for reconstruction	Local Fourier extensions on smooth subintervals	Gegenbauer polynomials
Computational complexity	$\mathcal{O}(NlogN)$	$\mathcal{O}\left(K{M}^2\right)$
Parameter tuning	Fully adaptive	Requires choice of M, $\lambda$
Handling mixed singularities	Robust via recursive detection	Limited; may require manual case handling
Accuracy	Spectral (∼10−14 observed)	Spectral if parameters are optimal
Ease of implementation	Moderate (FFT, segmentation)	More complex (special functions, tuning)

).

7. Conclusions

This paper introduces a novel Fourier extension-based framework for the high-accuracy reconstruction of piecewise smooth functions. Our approach addresses three core challenges in the spectral approximation of functions with discontinuities:

• Boundary Singularity Resolution. By constructing tailored Fourier extensions that span the domain boundaries, we effectively eliminate artificial discontinuities (i.e., “natural breakpoints”) at the endpoints. This preprocessing step is essential for the accurate spectral detection of internal derivative jumps.
• Stable Edge Detection. The extension process uses only data near the domain boundaries, isolating the edge treatment from internal irregularities. This localization ensures that edge information in the derivative spectra is accurately retained without interference, leading to numerically stable and reliable detection of singularities.
• Adaptive Segmentation and Local Reconstruction. After edge detection, the domain is adaptively partitioned into smooth subintervals. On each segment, high-fidelity Fourier extensions are computed independently. This strategy integrates precise singularity localization with the exponential convergence properties of spectral methods on smooth domains.

Comprehensive numerical experiments validate the proposed method’s ability to achieve machine-level accuracy (up to ${10}^{-14}$ to ${10}^{-15}$) even in the presence of mixed-order singularities, including jump discontinuities in the function itself and its first and second derivatives.

The method demonstrates robust performance in scenarios that require

• Simultaneous handling of multiple, heterogeneous discontinuities;
• High local resolution near singular points;
• Uniform accuracy across discontinuity scales and types.

Future research will focus on extending the method to higher-dimensional domains, with particular attention to given applications in the numerical solutions of partial differential equations involving moving or evolving discontinuities.