The Mean and the Variance as Dual Concepts in a Fundamental Duality
Abstract
1. Introduction: A Basic Duality in the Exact Sciences
2. Methods
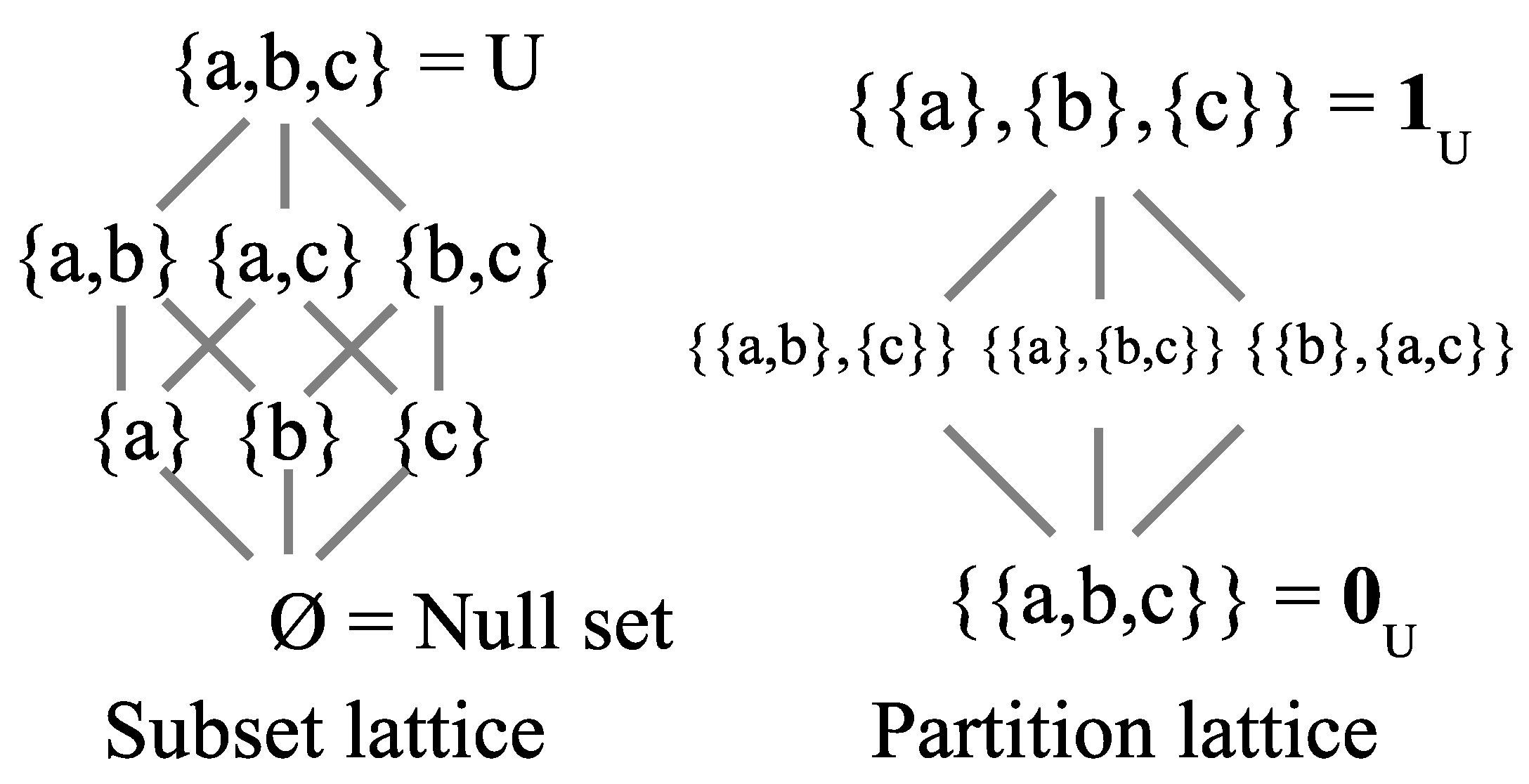
2.1. The Duality of Subsets and Partitions
Equivalence relations are so ubiquitous in everyday life that we often forget about their proactive existence. Much is still unknown about equivalence relations. Were this situation remedied, the theory of equivalence relations could initiate a chain reaction generating new insights and discoveries in many fields dependent upon it.
This paper springs from a simple acknowledgment: the only operations on the family of equivalence relations fully studied, understood and deployed are the binary join ∨ and meet ∧ operations. [12] (p. 445)
2.2. The Two Lattices of Subsets and of Partitions
2.3. Fundamental Status of the Two Lattices
- Subset creation story: “In the Beginning was the Void”, and then elements were created, fully propertied and distinguished from one another, until finally reaching all the elements of the universe set U.
- Partition creation story: “In the Beginning was Undifferentiated Substance (e.g., “Formless Chaos”), and then there was a “Big Bang” where the substance is was objectively informed by the making of distinctions (i.e., symmetry-breaking) until the final result was the fully distinguished (i.e., the equivalence classes are singletons) elements of the universe U.
2.4. Logical Entropy
2.4.1. A Little History of Information-as-Distinctions
For in the general we must note, that whatever is capable of a competent difference, perceptible to any sense, may be a sufficient means whereby to express the cogitations. It is more convenient, indeed, that these differences should be of as great variety as the letters of the alphabet; but it is sufficient if they be but twofold, because two alone may, with somewhat more labour and time, be well enough contrived to express all the rest. [18] (p. 67)
Thus any two letters or numbers, suppose A. B. being transposed through five places, will yield thirty-two differences, and so consequently will superabundantly serve for the four and twenty letters,…. [18] (pp. 67-68)
Any difference meant a binary choice. Any binary choice began the expressing of cogitations. Here, in this arcane and anonymous treatise of 1641, the essential idea of information theory poked to the surface of human thought, saw its shadow, and disappeared again for [three] hundred years. [20] (p. 161) (an old Pennsylvania Dutch superstition is that if on the second of February each year, a groundhog emerges from its den and sees its shadow, then it stays in its den for another six weeks).
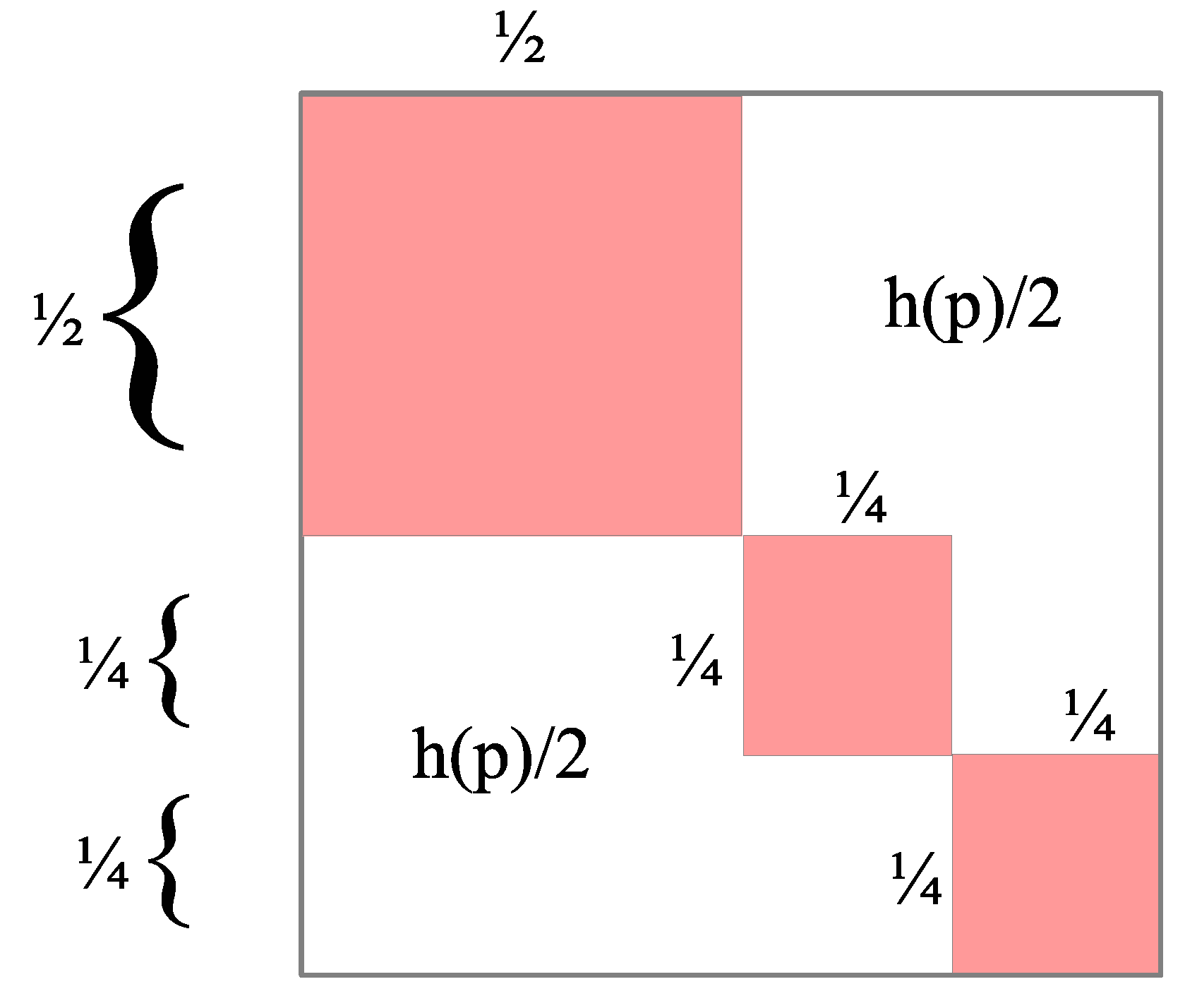
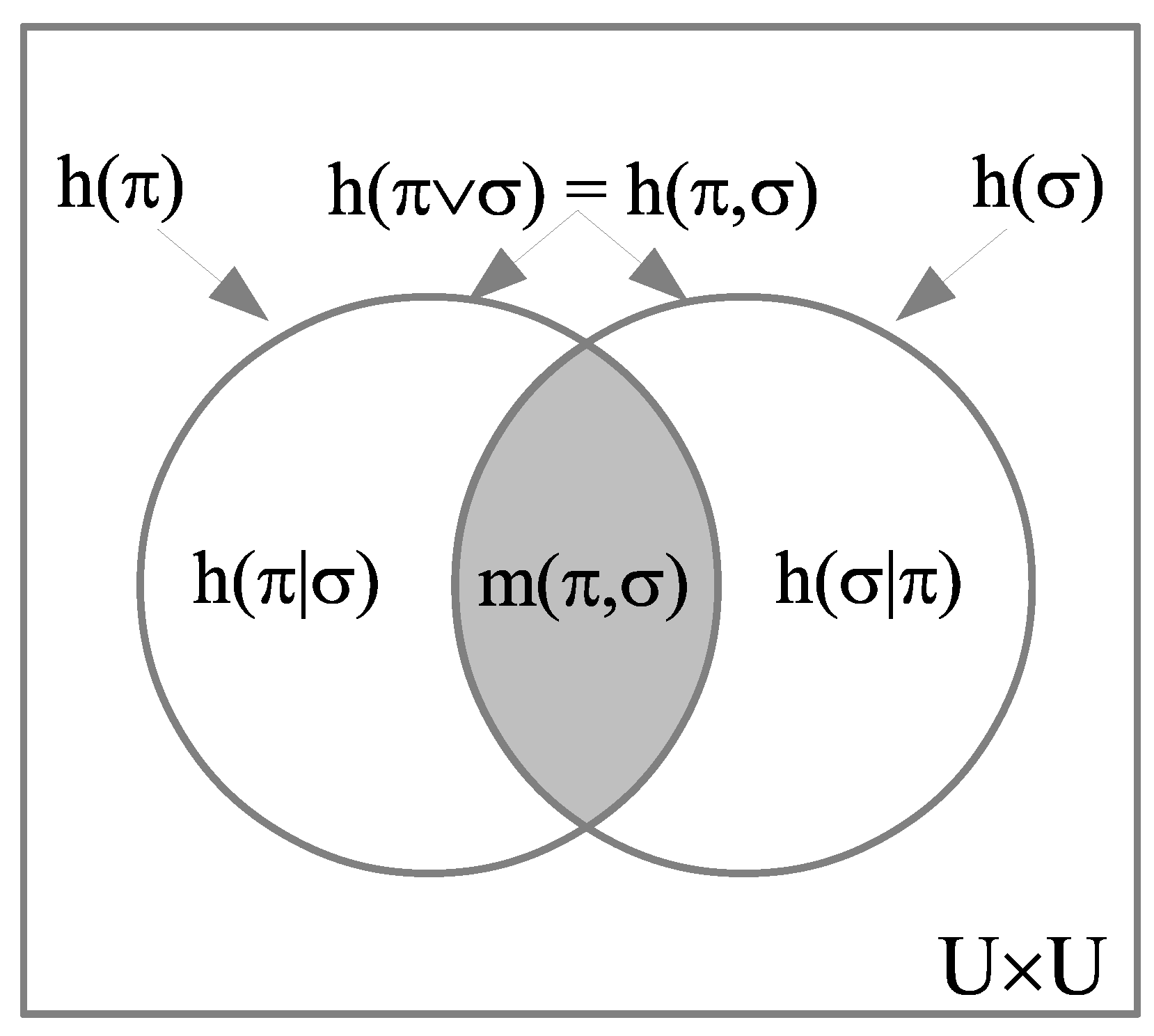
2.4.2. The Mathematics of Logical Entropy
2.4.3. The Relationship with Shannon Entropy
Information theory must precede probability theory, and not be based on it. By the very essence of this discipline, the foundations of information theory have a finite combinatorial character. [24] (p. 39)
2.4.4. Some History of the Logical Entropy Formula
3. Results: The Logical Basis for Variance and Covariance
- Given an element, the natural questions are “to be or not to be” in a subset, or existence versus non-existence, the questions of the Boolean logic of subsets.
- Given a pair of elements, the natural questions are identity or difference, distinct or indistinct, or equivalent or in-equivalent, the questions of the logic of partitions (or equivalence relations).
This interesting relation shows that the variance may in fact be defined as half the mean square of all possible variate differences, that is to say, without reference to deviations from a central value, the mean. [8] (p. 42)
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RST | reflexive–symmetric–transitive |
References
- Ellerman, D. The Logic of Partitions: Introduction to the Dual of the Logic of Subsets. Rev. Symb. Log. 2010, 3, 287–350. [Google Scholar] [CrossRef]
- Ellerman, D. An Introduction of Partition Logic. Log. J. IGPL 2014, 22, 94–125. [Google Scholar] [CrossRef]
- Ellerman, D. The Logic of Partitions: With Two Major Applications. Studies in Logic 101; College Publications: London, UK, 2023; Available online: https://www.collegepublications.co.uk/logic/?00052 (accessed on 13 June 2025).
- Ellerman, D. A Fundamental Duality in the Exact Sciences: The Application to Quantum Mechanics. Foundations 2024, 4, 175–204. [Google Scholar] [CrossRef]
- Boole, G. An Investigation of the Laws of Thought on Which Are Founded the Mathematical Theories of Logic and Probabilities; Macmillan and Co.: Cambridge, UK, 1854. [Google Scholar]
- Kung, J.P.S.; Rota, G.-C.; Catherine, H.Y. Combinatorics: The Rota Way; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Zhang, Y.; Wu, H.; Cheng, L. Some New Deformation Formulas about Variance and Covariance. In Proceedings of the 2012 International Conference on Modelling, Identification and Control (ICMIC2012), Wuhan, China, 24–26 June 2012; pp. 987–992. [Google Scholar]
- Kendall, M.G. Advanced Theory of Statistics Vol. I; Charles Griffin & Co.: London, UK, 1945. [Google Scholar]
- Eilenberg, S.; Lane, S.M. General Theory of Natural Equivalences. Trans. Am. Math. Soc. 1945, 58, 231–294. [Google Scholar] [CrossRef]
- Lawvere, F.W.; Rosebrugh, R. Sets for Mathematics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Finberg, D.; Mainetti, M.; Rota, G.-C. The Logic of Commuting Equivalence Relations. In Logic and Algebra; Ursini, A., Agliano, P., Eds.; Marcel Dekker: New York, NY, USA, 1996; pp. 69–96. [Google Scholar]
- Britz, T.; Mainetti, M.; Pezzoli, L. Some operations on the family of equivalence relations. In Algebraic Combinatorics and Computer Science: A Tribute to Gian-Carlo Rota; Crapo, H., Senato, D., Eds.; Springer: Milano, Italy, 2001; pp. 445–459. [Google Scholar]
- Birkhoff, G. Lattice Theory; American Mathematical Society: New York, NY, USA, 1948. [Google Scholar]
- Grätzer, G. General Lattice Theory, 2nd ed.; Birkhäuser Verlag: Boston, MA, USA, 2003. [Google Scholar]
- Ainsworth, T. Form vs. Matter. In The Stanford Encyclopedia of Philosophy (Spring 2016 Edition); Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2016; Available online: https://plato.stanford.edu/archives/spr2016/entries/form-matter/ (accessed on 13 June 2025).
- Bateson, G. Mind and Nature: A Necessary Unity; Dutton: New York, NY, USA, 1979. [Google Scholar]
- Bennett, C.H. Quantum Information: Qubits and Quantum Error Correction. Int. J. Theor. Phys. 2003, 42, 153–176. [Google Scholar] [CrossRef]
- Wilkins, J. Mercury: Or the Secret and Swift Messenger. In The Mathematical and Philosophical Works of the Right Rev. John Wilkins, Vol. II; C. Whittingham: London, UK, 1802; pp. 1–87. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gleick, J. The Information: A History, A Theory, A Flood; Pantheon: New York, NY, USA, 2011. [Google Scholar]
- Ellerman, D. New Foundations for Information Theory: Logical Entropy and Shannon Entropy; Springer Nature: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Manfredi, G. Logical Entropy—Special Issue. 4Open 2022, 5, E1. [Google Scholar] [CrossRef]
- Ellerman, D. A New Logical Measure for Quantum Information. Quantum Inf. Comput. 2025, 25, 81–95. [Google Scholar]
- Kolmogorov, A.N. Combinatorial Foundations of Information Theory and the Calculus of Probabilities. Russ. Math. Surv. 1983, 38, 29–40. [Google Scholar] [CrossRef]
- Gini, C. Variabilità e Mutabilità; Tipografia di Paolo Cuppini: Bologna, Italy, 1912. [Google Scholar]
- Good, I.J.A.M. Turing’s statistical work in World War II. Biometrika 1979, 66, 393–396. [Google Scholar] [CrossRef]
- Rejewski, M. How Polish Mathematicians Deciphered the Enigma. Ann. Hist. Comput. 1981, 3, 213–234. [Google Scholar] [CrossRef]
- Kullback, S. Statistical Methods in Cryptoanalysis; Aegean Park Press: Walnut Creek, CA, USA, 1976. [Google Scholar]
- Simpson, E.H. Measurement of Diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Rao, C.R. Gini-Simpson Index of Diversity: A Characterization, Generalization and Applications. Util. Math. B 1982, 21, 273–282. [Google Scholar]
- Good, I.J. Comment on Patil and Taillie: Diversity as a Concept and its Measurement. J. Am. Stat. Assoc. 1982, 77, 561–563. [Google Scholar]
- Rao, C.R. Diversity and Dissimilarity Coefficients: A Unified Approach. Theor. Popul. Biol. 1982, 21, 24–43. [Google Scholar] [CrossRef]
- Kendall, M.G. Review of Variabilita e Concentrazione. By Corrado Gini. J. R. Stat. Soc. Ser. A (Gen.) 1957, 120, 222–223. [Google Scholar] [CrossRef]
- Riečan, B.; Neubrunn, T. Integral, Measure, and Ordering; Springer Science + Business Media: Bratislava, Slovakia, 1997. [Google Scholar]
- Markechová, D.; Riečan, B. Logical Entropy of Fuzzy Dynamical Systems. Entropy 2016, 18, 157. [Google Scholar] [CrossRef]
- Mohammadi, U. The Concept of Logic Entropy on D-Posets. Algebr. Struct. Their Appl. 2016, 3, 53–61. [Google Scholar]
- Ebrahimzadeh, A. Logical Entropy of Quantum Dynamical Systems. Open Phys. 2016, 14, 1–5. [Google Scholar] [CrossRef]
- Markechová, D.; Riečan, B. Logical Entropy and Logical Mutual Information of Experiments in the Intuitionistic Fuzzy Case. Entropy 2017, 19, 429. [Google Scholar] [CrossRef]
- Ebrahimzadeh, A.; Jamalzadeh, J. Conditional Logical Entropy of Fuzzy σ-Algebras. J. Intell. Fuzzy Syst. 2017, 33, 1019–1026. [Google Scholar] [CrossRef]
- Giski, Z.E.; Ebrahimzadeh, A. An Introduction of Logical Entropy on Sequential Effect Algebra. Indag. Math. 2017, 28, 928–937. [Google Scholar] [CrossRef]
- Ebrahimzadeh, A.; Giski, Z.E.; Markechová, D. Logical Entropy of Dynamical Systems—A General Model. Entropy 2017, 5, 4. [Google Scholar] [CrossRef]
- Markechová, D.; Ebrahimzadeh, A.; Giski, Z.E. Logical Entropy of Dynamical Systems. Adv. Differ. Equ. 2018, 70, 1–17. [Google Scholar] [CrossRef]
- Markechová, D.; Mosapour, B.; Ebrahimzadeh, A. Logical Divergence, Logical Entropy, and Logical Mutual Information in Product MV-Algebras. Entropy 2018, 20, 129. [Google Scholar] [CrossRef]
- Birkhoff, G.; Neumann, J.V. The Logic of Quantum Mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
- Ellerman, D. The Quantum Logic of Direct-Sum Decompositions: The Dual to the Quantum Logic of Subspaces. Log. J. IGPL 2018, 26, 1–13. [Google Scholar] [CrossRef]
- Auletta, G.; Fortunato, M.; Parisi, G. Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]

| Dualities | Boolean Lattice of Subsets | Lattice of Partitions |
|---|---|---|
| “Its” or “Dits” | Elements of subsets | Distinctions of partitions |
| Partial order | ||
| Join | ||
| Top | Subset U with all elements | Partition with all distinctions |
| Bottom | Subset ∅ with no elements | Partition with no distinctions |
| Fundamental Duality | Subset or Element Side | Partition or Distinction Side |
|---|---|---|
| Its & Dits | Elements of subsets | Distinctions of partitions |
| Logic | Subset logic | Partition logic |
| “Creation stories” | Ex Nihilo | Big Bang |
| Quantitative versions | Probability | Logical entropy |
| Sampling | 1-draw | 2-draw (with replacement) |
| Random variable X | Mean | Variance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellerman, D. The Mean and the Variance as Dual Concepts in a Fundamental Duality. Axioms 2025, 14, 466. https://doi.org/10.3390/axioms14060466
Ellerman D. The Mean and the Variance as Dual Concepts in a Fundamental Duality. Axioms. 2025; 14(6):466. https://doi.org/10.3390/axioms14060466
Chicago/Turabian StyleEllerman, David. 2025. "The Mean and the Variance as Dual Concepts in a Fundamental Duality" Axioms 14, no. 6: 466. https://doi.org/10.3390/axioms14060466
APA StyleEllerman, D. (2025). The Mean and the Variance as Dual Concepts in a Fundamental Duality. Axioms, 14(6), 466. https://doi.org/10.3390/axioms14060466







