Stability of Weak Rescaled Pure Greedy Algorithms

Abstract

We study the stability of Weak Rescaled Pure Greedy Algorithms for convex optimization, WRPGA(co), in general Banach spaces. We obtain the convergence rates of WRPGA(co) with noise and errors under a weaker assumption for the modulus of smoothness of the objective function. The results show that the rate is almost the same as that of WRPGA(co) without noise and errors, which is optimal and independent of the spatial dimension. This makes WRPGA(co) more practically applicable and scalable for high-dimensional data. Furthermore, we apply WRPGA(co) with errors to the problem of m-term approximation and derive the optimal convergence rate. This indicates the flexibility of WRPGA(co) and its wide utility across machine learning and signal processing. Our numerical experiments verify the stability of WRPGA(co). Thus, WRPGA(co) is a desirable choice for practical implementation.

1. Introduction

It is well known that problems with m-term approximation arise naturally in image processing, statistical learning, artificial neural networks, numerical solutions of PDEs, and other fields. It is also well known that greedy-type algorithms can effectively generate such approximations. We provide an overview of some important results for greedy algorithms for m-term approximation.

Let H be a real Hilbert space with an inner product $\langle ·,·\rangle$. The norm induced by this inner product is ${\parallel x\parallel }_H={\langle x,x\rangle }^{1/2}$. A subset $\mathcal{D}$ of H is called a dictionary if ${\parallel \phi \parallel }_H=1$ for any $\phi \in \mathcal{D}$ and the closure of span of $\mathcal{D}$ is H. For any element $f\in H$, we define its best m-term approximation error by

$${\sigma }_m\left(f\right):=\underset{\#\mathsf{\Lambda }=m,c_k\in \mathbb{R},{\phi }_k\in \mathcal{D}}{inf}{∥f-\sum _{k\in \mathsf{\Lambda }}{c}_k{\phi }_k∥}_H.$$

(1)

We use greedy algorithms to obtain an m-term approximation. The core idea behind greedy algorithms is to reduce the problem of best m-term approximation to that of best one-term approximation. It is not difficult to see that the best one-term approximation of f is

$$\langle f,\phi \rangle \phi ,$$

where $\phi =arg{max}_{g\in \mathcal{D}}\langle f,g\rangle$. Then, by iterating the best one-term approximation m times, one can obtain an m-term approximation of f. This algorithm is called the Pure Greedy Algorithm (PGA), which was defined in [1] as follows:

• PGA$(H,\mathcal{D})$

• Step 0: Given $f\in H$, set $f_0=0$.
• Step m:

  -

  If $f=f_{m-1}$, then finish the algorithm and define $f_k=f_{m-1}=f$ for $k\ge m$.

  -

  If $f\ne f_{m-1}$, then choose an element ${\phi }_m\in \mathcal{D}$ such that

  $$|\langle f-f_{m-1},{\phi }_m\rangle |=\underset{\phi \in \mathcal{D}}{sup}|\langle f-f_{m-1},\phi \rangle |.$$

Define the next approximant to be

$$f_m=f_{m-1}+\langle f-f_{m-1},{\phi }_m\rangle {\phi }_m,$$

and proceed to Step $m+1$.

To obtain the convergence rate of the PGA, we always assume that the target element f belongs to some basic sparse classes; see [2]. Let $\mathcal{D}\subset H$ be a dictionary and M be a positive real number. We define the class

$${\mathcal{A}}_1^0(\mathcal{D},M):=\left\{f\in H:f=\sum _{k\in \mathsf{\Lambda }}{c}_k{\phi }_k,{\phi }_k\in \mathcal{D},\#\left(\mathsf{\Lambda }\right)<\infty ,\sum _{k\in \mathsf{\Lambda }}|c_k|\le M\right\}$$

and define ${\mathcal{A}}_1(\mathcal{D},M)$ to be its closure in H. Let

$${\mathcal{A}}_1\left(\mathcal{D}\right)=\bigcup _{M>0}{\mathcal{A}}_1(\mathcal{D},M).$$

For $f\in {\mathcal{A}}_1\left(\mathcal{D}\right)$, we define its norm by ${\parallel f\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}:=inf\left\{M:f\in {\mathcal{A}}_1(\mathcal{D},M)\right\}$.

It is known from [1] that the optimal convergence rate of the best m-term approximation on ${\mathcal{A}}_1\left(\mathcal{D}\right)$ for all dictionaries $\mathcal{D}\subset H$ is $O\left(m^{-1/2}\right)$. Livshitz and Temlyakov in [3] proved that there is a dictionary $\mathcal{D}\subset H$, a constant $c>0$, and an element $f\in {\mathcal{A}}_1(\mathcal{D},1)$ such that

$$\parallel f-f_m^{\mathrm{PGA}}{\parallel }_H\ge c{m}^{-0.27},m=1,2,\dots .$$

Thus, the PGA fails to reach the optimal convergence rate $O\left(m^{-1/2}\right)$ on ${\mathcal{A}}_1(\mathcal{D},1)$ for all dictionaries $\mathcal{D}$. This leads to various modifications of the PGA. Among others, the Orthogonal Greedy Algorithm (OGA) and the Rescaled Pure Greedy Algorithm (RPGA) were shown to achieve the optimal convergence rate $O\left(m^{-1/2}\right)$.

We first recall the OGA from [1].

• OGA$(H,\mathcal{D})$

• Step 0: Given $f\in H$, set $f_0=0$.
• Step m:

  -

  If $f=f_{m-1}$, then finish the algorithm and define $f_k=f_{m-1}=f$ for $k\ge m$.

  -

  If $f\ne f_{m-1}$, then choose an element ${\phi }_m\in \mathcal{D}$ such that

  $$|\langle f-f_{m-1},{\phi }_m\rangle |=\underset{\phi \in \mathcal{D}}{sup}|\langle f-f_{m-1},\phi \rangle |.$$

Denote $H_m:=\mathrm{span}\{{\phi }_1,{\phi }_2,···,{\phi }_m\}.$ Define the next approximant to be

$$f_m=P_{m}f,$$

where $P_{m}f$ is the orthogonal projection of f on $H_m$, and proceed to Step $m+1$.

Clearly, $f_m^{\mathrm{OGA}}$ is the best approximation of f on $H_m$. DeVore and Temlyakov in [1] obtained the following convergence rate of the OGA for $f\in {\mathcal{A}}_1\left(\mathcal{D}\right)$:

$$\parallel f-f_m^{\mathrm{OGA}}{\parallel }_H\le {\parallel f\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{m}^{-1/2},m=1,2,\dots .$$

Then, we recall from [4] another modification of the PGA, which is called the Rescaled Pure Greedy Algorithm (RPGA).

• RPGA$(H,\mathcal{D})$

• Step 0: Given $f\in H$, set $f_0=0$.
• Step m:

  -

  If $f=f_{m-1}$, then finish the algorithm and define $f_k=f_{m-1}=f$ for $k\ge m$.

  -

  If $f\ne f_{m-1}$, then choose an element ${\phi }_m\in \mathcal{D}$ such that

  $$|\langle f-f_{m-1},{\phi }_m\rangle |=\underset{\phi \in \mathcal{D}}{sup}|\langle f-f_{m-1},\phi \rangle |.$$

With

$${\lambda }_m:=\langle f-f_{m-1},{\phi }_m\rangle ,{\widehat{f}}_m:=f_{m-1}+{\lambda }_m{\phi }_m,s_m:={\displaystyle \frac{\langle f,{\widehat{f}}_m\rangle }{\parallel {\widehat{f}}_m{\parallel }_H^2}},$$

define the next approximant to be

$$f_m:=s_m{\widehat{f}}_m$$

and proceed to Step $m+1$.

Note that if the output at each Step m was ${\widehat{f}}_m$ and not $f_m=s_m{\widehat{f}}_m$, this would be the PGA. However, the RPGA does not use ${\widehat{f}}_m$ but the best approximation of f from the one-dimensional space $\mathrm{span}\left\{{\widehat{f}}_m\right\}$, that is, $s_m{\widehat{f}}_m$. It is clear that the RPGA is simpler than the OGA. At Step m, the OGA needs to solve the m-dimensional optimization problem, while the RPGA only needs to solve the one-dimensional optimization problem. This implies that the RPGA has less computational complexity.

Moreover, Petrova in [4] derived the following convergence rate of the RPGA$(H,\mathcal{D})$:

Theorem 1 

([4]). If $f\in {\mathcal{A}}_1\left(\mathcal{D}\right)\subset H$, then the output ${\left\{f_m\right\}}_{m\ge 0}$ of the RPGA$(H,\mathcal{D})$ satisfies

$$\parallel f-f_m{\parallel }_H\le {\parallel f\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{(m+1)}^{-1/2},m=0,1,\dots .$$

Theorem 1 shows that the RPGA can achieve the optimal convergence rate on ${\mathcal{A}}_1\left(\mathcal{D}\right)$. Based on these advantages, the RPGA has been successfully applied to machine learning and signal processing, see [5,6,7,8,9]. Moreover, a generalization of RPGA can be used to solve the convex optimization problem; see [10].

Note that when selecting ${\phi }_m$ in the above algorithms, the supremum in the equality

$$|\langle f-f_{m-1},{\phi }_m\rangle |=\underset{\phi \in \mathcal{D}}{sup}|\langle f-f_{m-1},\phi \rangle |$$

(2)

may not be attainable. Thus, we replace the greedy condition by a weaker condition:

$$|\langle f-f_{m-1},{\phi }_m\rangle |\ge t_m\underset{\phi \in \mathcal{D}}{sup}|\langle f-f_{m-1},\phi \rangle |,$$

where $0<t_m\le 1$. Greedy algorithms that use this weak condition are called weak greedy algorithms. In this way, we can obtain the Weak Rescaled Pure Greedy Algorithm (WRPGA).

The following convergence rate of the WRPGA$(H,\mathcal{D})$ was obtained in [4]:

Theorem 2 

([4]). If $f\in {\mathcal{A}}_1\left(\mathcal{D}\right)\subset H$, then the output ${\left\{f_m\right\}}_{m\ge 0}$ of the WRPGA$(H,\mathcal{D})$ satisfies the inequality

$$\parallel f-f_m{\parallel }_H\le {\parallel f\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{\left(\sum _{k=1}^m{t}_k^2\right)}^{-1/2},m\ge 1.$$

Some greedy algorithms have been extended to the setting of Banach spaces. Let X be a real Banach space with norm ${\parallel ·\parallel }_X$. A set $\mathcal{D}\subset X$ is called a dictionary if each $\phi \in \mathcal{D}$ has norm ${\parallel \phi \parallel }_X=1$, and the closure of $span$$\mathcal{D}$ is X. Let $X^{*}$ denote the set of all continuous linear functionals on X. It is known from the Hahn–Banach theorem that for every non-zero $x\in X$, there exists $F_x\in X^{*}$ such that

$$\parallel F_x\parallel =1\mathrm{and}{F}_x\left(x\right)={\parallel x\parallel }_X.$$

(3)

The functional $F_x$ is called the norming functional of x. The modulus of smoothness of X is defined as

$$\rho \left(u\right):=\underset{x,y\in {X,\parallel x\parallel }_X={\parallel y\parallel }_X=1}{sup}\left({\displaystyle \frac{{\parallel x+uy\parallel }_X+{\parallel x-uy\parallel }_X}{2}}-1\right),u>0.$$

(4)

If $\underset{u\to 0}{lim}{\displaystyle \frac{\rho \left(u\right)}{u}}=0$, then the Banach space X is called uniformly smooth. We say that the modulus of smoothness $\rho \left(u\right)$ is of power type $1<q\le 2$ if $\rho \left(u\right)\le \gamma u^q$ with some $\gamma >0$. The sparse class ${\mathcal{A}}_1\left(\mathcal{D}\right)$ in Banach space X is defined in the same way as in Hilbert space H.

We recall from [4] the definition of the WRPGA in the setting of Banach spaces.

• WRPGA$(X,\mathcal{D})$

• Step 0: Given $f\in H$, set $f_0=0$.
• Step m:

  -

  If $f=f_{m-1}$, then finish the algorithm and define $f_k=f_{m-1}=f$ for $k\ge m$.

  -

  If $f\ne f_{m-1}$, then choose an element ${\phi }_m\in \mathcal{D}$ such that

  $$F_{f-f_{m-1}}\left({\phi }_m\right)\ge t_m\underset{\phi \in \mathcal{D}}{sup}|F_{f-f_{m-1}}\left(\phi \right)|.$$

With

$${\lambda }_m:=\mathrm{sign}\left\{F_{f-f_{m-1}}\left({\phi }_m\right)\right\}\parallel f-f_{m-1}{\parallel }_X{\left(2\gamma q\right)}^{{\displaystyle \frac{1}{1-q}}}{|F_{f-f_{m-1}}\left({\phi }_m\right)|}^{{\displaystyle \frac{1}{q-1}}},{\widehat{f}}_m:=f_{m-1}+{\lambda }_m{\phi }_m,$$

choose $s_m$ such that

$$\parallel f-s_m{\widehat{f}}_m{\parallel }_X:=\underset{s\in \mathbb{R}}{min}{\parallel f-s{\widehat{f}}_m\parallel }_X.$$

Define the next approximant to be

$$f_m:=s_m{\widehat{f}}_m$$

and proceed to Step $m+1$.

Petrova in [4] derived the following convergence rate of the WRPGA$(X,\mathcal{D})$:

Theorem 3 

([4]). Let X be a Banach space with $\rho \left(u\right)\le \gamma u^q$, $1<q\le 2$. If $f\in {\mathcal{A}}_1\left(\mathcal{D}\right)\subset X$, then the output ${\left\{f_m\right\}}_{m\ge 0}$ of the WRPGA$(X,\mathcal{D})$ satisfies

$$\parallel f-f_m{\parallel }_X\le c{\parallel f\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{\left(\sum _{k=1}^m{t}_k^{{\displaystyle \frac{q}{q-1}}}\right)}^{1/q-1}.$$

Observe that the best m-term approximation problem with respect to a given dictionary $\mathcal{D}$ is essentially an optimization problem for a norm function $E\left(x\right):={\parallel f-x\parallel }_X$. In fact, the norming functional $F_{f-f_{m-1}}$ used in the selection of ${\phi }_m$ in the greedy algorithms is closely related to the function $E\left(x\right):={\parallel f-x\parallel }_X$. Their relationship is given in Section 3. Naturally, one can use a similar technique, such as a greedy strategy used in m-term approximation, to handle optimization problems, especially convex optimization problems.

Now, we turn to the problem of convex optimization. Convex optimization occurs in many fields of modern science and engineering, such as automatic control systems, data analysis and modeling, statistical estimation and learning, and communications and networks; see [11,12,13,14,15,16] and the references therein. The problem of convex optimization can be formulated as follows:

Let X be a Banach space and $\mathsf{\Omega }$ be a bounded convex subset of X. Let E be a function on X satisfying

$$E(\alpha x+\beta y)\le \alpha E\left(x\right)+\beta E\left(y\right),x,y\in \mathsf{\Omega },\alpha ,\beta \ge 0,\mathrm{and}\alpha +\beta =1.$$

We aim to find an approximate solution to the problem

$$\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right).$$

(5)

Usually, the domain X of the objective function E in classical convex optimization is finite-dimensional, while some applications of convex optimization require that X has a large dimension, even an infinite dimension, which may require that the rate of convergence of a numerical algorithm to be independent of the dimension of X. Otherwise, it may suffer from the curse of dimensionality. It is well known that the convergence rates of greedy-type algorithms are independent of the dimension of X. Thus, greedy-type algorithms are increasingly used in solving (5); see [17,18,19]. The main idea is that the algorithm outputs $x_m$ after m iterations such that $E\left(x_m\right)$ is a good approximation of

$$\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right).$$

Generally, $x_m$ is a linear combination of m elements from a dictionary of X. These algorithms usually choose $x_0=0$ as an initial approximant and select $\mathsf{\Omega }$ as

$$\mathsf{\Omega }:=\left\{x\in X:E\left(x\right)\le E\left(0\right)=E\left(x_0\right)\right\}.$$

Some greedy-type convex optimization algorithms, such as the Weak Chebychev Greedy Algorithm (WCGA(co)), the Weak Greedy Algorithm with Free Relaxation (WGAFR(co)), and the Relaxed Weak Relaxed Greedy Algorithm (RWRGA(co)), have been successfully used to solve convex optimization problems; see [17,20,21,22]. Furthermore, Gao and Petrova in [10] proposed the Weak Rescaled Pure Greedy Algorithm (WRPGA(co)) for convex optimization in Banach space X. This algorithm is a generation of WRPGA$(X,\mathcal{D})$ for m-term approximation. To give the definition of the WRPGA(co), we first recall some concepts and notations.

We assume that the function E is Fréchet-differentiable at any $x\in X$. That is, there is a continuous linear functional $E^{\prime }\left(x\right)$ in Banach space X such that

$$\underset{h\to 0}{lim}{\displaystyle \frac{|E(x+h)-E\left(x\right)-\langle E^{\prime }\left(x\right),h\rangle |}{{\parallel h\parallel }_X}}=0,$$

where $\langle E^{\prime }\left(x\right),h\rangle :=E^{\prime }\left(h\right)$. We call the functional $E^{\prime }\left(x\right)$ the Fréchet derivative of E. Under the assumptions that E is convex and Fréchet-differentiable, it is well known that the minimizer of E exists and is attainable; see [17]. Throughout this article, we assume that the minimizer of E belongs to the basic sparse class ${\mathcal{A}}_1\left(\mathcal{D}\right)$.

We call the convex function $E:X\to \mathbb{R}$ satisfying Condition 0 if E has a Fréchet derivative $E^{\prime }\left(x\right)$ at every $x\in \mathsf{\Omega }$, and $\parallel E^{\prime }\left(x\right)\parallel \le M_0.$

If there exist constants $\alpha >0,M_1>0$, and $1<q\le 2$, such that for all $x,x^{\prime }$ with $\parallel x-x^{\prime }{\parallel }_X\le M_1,$ and $x\in \mathsf{\Omega },$

$$E\left(x^{\prime }\right)-E\left(x\right)-\langle E^{\prime }\left(x\right),x^{\prime }-x\rangle \le \alpha {\parallel x^{\prime }-x\parallel }_X^q,$$

(6)

then we say that E satisfies the Uniform Smoothness (US) condition on $\mathsf{\Omega }$.

The Weak Rescaled Pure Greedy Algorithm with a weakness sequence ${\left\{t_m\right\}}_{m=1}^{\infty },0<t_m\le 1$, and a parameter sequence ${\left\{{\mu }_m\right\}}_{m=1}^{\infty }$ satisfying

$${\mu }_m>max\{1,{\alpha }^{-1}{M}_0{M}_1^{1-q}\},m=1,\dots ,$$

is defined as follows:

• Weak Rescaled Pure Greedy Algorithm (WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$)

• Step 0:

• Define $x_0^w:=0$. If $E^{\prime }\left(x_0^w\right)=0$, then finish the algorithm and define $x_k^w:=x_0^w,k\ge 1$.

• Step m:

• Assume $x_{m-1}^w$ has been defined and $E^{\prime }\left(x_{m-1}^w\right)\ne 0$. Perform the following steps:

  -

  Choose an element ${\phi }_m\in \mathcal{D}$ such that

  $$|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |\ge t_m\underset{\phi \in \mathcal{D}}{sup}|\langle E^{\prime }\left(x_{m-1}^w\right),\phi \rangle |.$$

  -

  Compute ${\lambda }_m$, given by the formula

  $${\lambda }_m:=\mathrm{sign}\left\{\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle \right\}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{1}{q-1}}}.$$

  -

  Compute

  $${\widehat{x}}_m^w:=x_{m-1}^w-{\lambda }_m{\phi }_m,b_m:=arg\underset{b\in \mathbb{R}}{min}E\left(b{\widehat{x}}_m^w\right).$$

  -

  Define the next approximant as

  $$x_m^w=b_m{\widehat{x}}_m^w.$$

• If $E^{\prime }\left(x_m^w\right)=0$, then finish the algorithm and define $x_k^w:=x_m^w,$ for $k>m$.
• If $E^{\prime }\left(x_m^w\right)\ne 0$, then proceed to Step $m+1$.

The following convergence rate of the WRPGA(co) was also obtained in [10]:

Theorem 4 

([10]). Let E be a convex function defined on X. It satisfies Condition 0 and the US condition. Moreover, we assume its minimizer $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)$. Then, the output of the WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ with ${\mu }_m>max\{1,{\alpha }^{-1}{M}_0{M}_1^{1-q}\}$ satisfies the following inequality:

$$E\left(x_m^w\right)-E\left(\overline{x}\right)\le \alpha {\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q{\left(C_1(q,\alpha ,E)+\sum _{j=1}^m({\mu }_j-1){\left({\displaystyle \frac{t_j}{{\mu }_j}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q},m\ge 1,$$

(7)

where $C_1(q,\alpha ,E)={\left({\displaystyle \frac{\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q}{E\left(x_0^w\right)-E\left(\overline{x}\right)}}\right)}^{{\displaystyle \frac{1}{q-1}}}$.

It follows from the definition of the WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ and Theorem 4 that the weakness sequence ${\left\{t_m\right\}}_{m\ge 1}$ and the parameter sequence ${\left\{{\mu }_m\right\}}_{m\ge 1}$ are important for the algorithm. The weakness sequence ${\left\{t_m\right\}}_{m\ge 1}$ allows us to have more freedom to choose element ${\phi }_m$ in the dictionary $\mathcal{D}$. The parameter sequence $\left\{{\mu }_m\right\}$ gives more choice in how much to advance along the selected element ${\phi }_m$. We remark that the function

$$f\left(\mu \right)=(\mu -1){\mu }^{{\displaystyle \frac{q}{q-1}}}$$

is increasing on $(1,q)$ and decreasing on $(q,\infty )$, with a global maximum at $\mu =q$. Thus, if we set $t_k=1$ and ${\mu }_k=q$ for $k=1,\dots ,m$, then WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ satisfies the error

$$E\left(x_m^w\right)-E\left(\overline{x}\right)\le C{q}^q{(q-1)}^{1-q}{m}^{1-q},$$

where C is a constant. This setting of $t_k$ and ${\mu }_k$ ensures that the value on the right-hand side of inequality (7) is minimized. For any particular target function E, we can optimize some constants related to parameter ${\mu }_m$ to obtain the optimal convergence results in terms of optimal constants. For example, the authors in [23] selected $\mu =q$ in Hilbert space as an example.

Very often, noise and errors are inevitable during the algorithm implementation. Thus, taking them into account and exploring their dependence on algorithms are of great importance. If the convergence rate of an algorithm changes relatively little when influenced by noise and errors, then we say that this algorithm exhibits a certain level of stability, which allows us to portray and analyze the behavior of the algorithm in a certain way, providing a theoretical basis for the design and improvement of the algorithm. The study of the stability of greedy algorithms for m-term approximation in Banach spaces began in [24] and was further developed in [25]. In [17,20,22], the stability of WCGA(co) and some relaxed-type greedy algorithms for convex optimization was studied, where computational inaccuracies were allowed in the process of error reduction and biorthogonality.

To the best of our knowledge, no relevant results exist concerning the numerical stability of the WRPGA(co). In the present article, we study the stability of the WRPGA(co). We consider the perturbation value $f^{\epsilon }$ such that

$$E\left(f^{\epsilon }\right)\le \underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)+\epsilon$$

instead of $arg{min}_{x\in \mathsf{\Omega }}E\left(x\right).$ Then, we investigate the dependence of WRPGA(co) on the error in the computation of ${\lambda }_m$ in the second step of the algorithm. We obtain the convergence rates of WRPGA(co) with noise and errors. The results show that WRPGA(co) is stable in some sense, and the associated convergence rates remain independent of the spatial dimension. This addresses real-world scenarios where exact computations are rare, making the algorithm more practically applicable, especially for high-dimensional applications. We verify this conclusion through numerical experiments. Furthermore, we apply WRPGA(co) with errors to the problem of m-term approximation and derive the optimal convergence rate, which indicates its flexibility and wide utility across applied mathematics and signal processing. Notably, the condition we use diverges from that used in [10]. We just use one condition: that $\rho (E,\mathsf{\Omega },u)$ has the power type $1<q\le 2$. However in [10], the authors need to use not only the US condition but also additional conditions to ensure that the US condition still holds for the sequence generated from WRPGA(co). This is also one of the strengths of our article.

We organize the article as follows: In Section 2, we state the results for the convergence rates of WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ with noise and errors. In Section 3, we apply WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ with errors to m-term approximation. In Section 4, we provide two numerical examples to illustrate the stability of WRPGA(co). In Section 5, we make some concluding remarks and discuss future work.

2. Convergence Rate of WRPGA(co) with Noise and Error

In this section, we will discuss the performance of WRPGA(co) in the presence of noise and computational errors. We first recall some notions. The modulus of smoothness, $\rho (E,\mathsf{\Omega },u)$, of E on the set $\mathsf{\Omega }$ is defined as

$$\rho (E,\mathsf{\Omega },u):={\displaystyle \frac{1}{2}}\underset{x\in {\mathsf{\Omega },\parallel y\parallel }_X=1}{sup}|E(x+uy)+E(x-uy)-2E\left(x\right)|.$$

Clearly, $\rho (E,\mathsf{\Omega },u)$ is an even function with respect to u. If $\rho (E,\mathsf{\Omega },u)=o\left(u\right)$ as $u\to 0$, then we call E uniformly smooth on $\mathsf{\Omega }$. It is known from [23] that the condition that

$$\rho (E,\mathsf{\Omega },u)\le \alpha u^q,1<q\le 2,$$

(8)

is closely related to the US condition (6). However, the US condition on the set $\mathsf{\Omega }$ is not sufficient to derive the convergent result. It also requires Condition 0 so that the output sequence $\left\{x_m^w\right\}$ of the algorithm remains in $\mathsf{\Omega }$, where the US condition holds. Thus, we use condition (8).

Now, we discuss the performance of WRPGA(co) with data noise. Suppose that $arg\underset{x\in \mathsf{\Omega }}{min}E\left(x\right)$ is influenced by noise. That is, in the implementation of the algorithm, we consider the perturbation value $f^{\epsilon }$ such that

$$E\left(f^{\epsilon }\right)\le \underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)+\epsilon ,\epsilon \ge 0.$$

We obtain the following convergence rates of WRPGA(co) in that case:

Theorem 5. 

Let $E:X\to \mathbb{R}$ be a uniformly smooth Fréchet-differentiable convex function with $\rho (E,\mathsf{\Omega },u)\le \alpha u^q$, $1<q\le 2$. Take $\epsilon \ge 0$ and $f^{\epsilon }\in \mathsf{\Omega }$ such that

$$E\left(f^{\epsilon }\right)\le \underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)+\epsilon ,f^{\epsilon }/A\in {\mathcal{A}}_1(\mathcal{D},1),$$

with some number $A>0$. Then, for WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ with ${\mu }_m>2$, we have

$$E\left(x_m^w\right)-\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)\le max\left\{2\epsilon ,\alpha A^q{\left(\sum _{k=1}^m({\mu }_k-2){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q}\right\}.$$

(9)

Taking $t_k=t$ and ${\mu }_k=\mu$ for $k=1,\dots ,m$ in Theorem 5, we obtain

$$E\left(x_m^w\right)-\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)\le max\left\{2\epsilon ,\alpha A^q{t}^{-q}{\mu }^q{(\mu -2)}^{1-q}{m}^{1-q}\right\}.$$

(10)

It is clear that the function

$$g\left(\mu \right)={\mu }^q{(\mu -2)}^{1-q}$$

is decreasing on $(2,2q)$ and increasing on $(2q,\infty )$, with a global minimum at $\mu =2q$. Thus, if we set $t_k=1$ and ${\mu }_k=2q$ for $k=1,\dots ,m$, WRPGA(co) satisfies

$$E\left(x_m^w\right)-\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)\le max\left\{2\epsilon ,2\alpha A^q{q}^q{(q-1)}^{1-q}{m}^{1-q}\right\}.$$

This setting of $t_k$ and ${\mu }_k$ ensures that the value on the right-hand side of inequality (9) is minimized.

Theorem 5 implies the following result for the noiseless case ($\epsilon =0$):

Corollary 1. 

Let the convex function $E:X\to \mathbb{R}$ be uniformly smooth and Fréchet-differentiable with $\rho (E,\mathsf{\Omega },u)\le \alpha u^q$, $1<q\le 2$. If $arg\underset{x\in \mathsf{\Omega }}{min}E\left(x\right)\in {\mathcal{A}}_1(\mathcal{D},1)$, then for WRPGA(co) $(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ with ${\mu }_m>2$, the following inequality holds:

$$E\left(x_m^w\right)-\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)\le \alpha {\left(\sum _{k=1}^m({\mu }_k-2){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q}.$$

Corollary 1 gives the convergence rate of WRPGA(co) with noiseless data, which is different from the result in Theorem 4. It is known from [23] that the US Condition is equivalent to the condition $\rho (E,\mathsf{\Omega },u)\le \alpha u^q$ in Hilbert spaces. Theorem 5 and Corollary 1 do not require Condition 0. From this point of view, our assumption is weaker than that of Theorem 4 for general Banach spaces. By choosing an appropriate ${\mu }_k$, we can achieve the same error as Theorem 4.

To prove Theorem 5, we first recall some lemmas.

Lemma 1 

([18]). Let E be a convex function on X. Assume that it is Fréchet-differentiable. Then, for every $x\in \mathsf{\Omega },y\in X$, and $u\in \mathbb{R}$,

$$0\le E(x+uy)-E\left(x\right)-u\langle E^{\prime }\left(x\right),y\rangle \le {2\rho (E,\mathsf{\Omega },u\parallel y\parallel }_X).$$

Lemma 2 

([2]). For any $F\in X^{*}$ and any dictionary $\mathcal{D}$ of X, we have

$$\underset{\phi \in \mathcal{D}}{sup}\langle F,\phi \rangle =\underset{\varphi \in {\mathcal{A}}_1(\mathcal{D},1)}{sup}\langle F,\varphi \rangle .$$

Lemma 3 

([18]). Let E be a convex function on X. Assume that it is Fréchet-differentiable at every point in Ω. Then, for each $x\in \mathsf{\Omega }$ and $x^{\prime }\in X$,

$$\langle E^{\prime }\left(x\right),x-x^{\prime }\rangle \ge E\left(x\right)-E\left(x^{\prime }\right).$$

Lemma 4 

([4]). Let $B>0,r>0,$ and $\ell >0$ and let $\left\{a_m\right\}$ and $\left\{r_m\right\}$ be sequences of positive numbers satisfying

$$a_J\le B,a_m\le a_{m-1}\left(1-{\displaystyle \frac{r_m}{r}}{a}_{m-1}^{\ell }\right),m=J+1,J+2,\dots .$$

Then, the following inequality holds:

$$a_m\le max\{1,{\ell }^{-1/\ell }\}{r}^{1/\ell }{\left(r{B}^{-\ell }+\sum _{k=J+1}^m{r}_k\right)}^{-1/\ell },m=J+1,J+2,\dots .$$

The following lemma was stated in [21] without proof. Moreover, we have not found the proof of this lemma in other studies. For convenience, we provide a proof here.

Lemma 5. 

Let E be a uniformly smooth, Fréchet-differentiable convex function on X. Let L be a subspace of X with finite dimension. If $x^{*}\in \mathsf{\Omega }$ satisfies

$$E\left(x^{*}\right)=\underset{y\in L}{min}E\left(y\right),$$

then, for all $y\in L$, we have $\langle E^{\prime }\left(x^{*}\right),y\rangle =0.$

Proof. 

We prove the lemma by contradiction. Suppose that there exists a $y\in L$ such that ${\parallel y\parallel }_X=1$ and $\langle E^{\prime }\left(x^{*}\right),y\rangle =\beta >0$. Note that $x^{*}\in \mathsf{\Omega }$. Then, applying Lemma 1 to y and $-u$ with $u>0$, we have

$$E(x^{*}-uy)-E\left(x^{*}\right)+u\langle E^{\prime }\left(x^{*}\right),y\rangle \le 2\rho (E,\mathsf{\Omega },u),$$

which implies

$$E\left(x^{*}\right)\ge E(x^{*}-uy)+u\langle E^{\prime }\left(x^{*}\right),y\rangle -2\rho (E,\mathsf{\Omega },u)=E(x^{*}-uy)+u\beta -2\rho (E,\mathsf{\Omega },u).$$

Since $\rho (E,\mathsf{\Omega },u)=o\left(u\right)$, we can find $\tilde{u}>0$ such that $\tilde{u}\beta -2\rho (E,\mathsf{\Omega },\tilde{u})>0$. Then, we have

$$E\left(x^{*}\right)>E(x^{*}-\tilde{u}y).$$

This inequality contradicts the assumption that E reaches its minimum at $x^{*}$ in space L. Thus, the proof of this lemma is finished. □

Proof of Theorem 5. 

It is known from the definition of WRPGA(co)$(\left\{t_m\right\},\left\{{\mu }_m\right\},\mathcal{D})$ that

$$E\left(x_m^w\right)\le E\left({\widehat{x}}_m^w\right)=E(x_{m-1}^w-{\lambda }_m{\phi }_m),m\ge 1.$$

(11)

Then, applying Lemma 1 to (11) with $x=x_{m-1}^w,u=|{\lambda }_m|,$ and $y=-\mathrm{sign}\left\{{\lambda }_m\right\}{\phi }_m$, we obtain

$$\begin{array}{ccc}\hfill E(x_{m-1}^w-{\lambda }_m{\phi }_m)& \le & E\left(x_{m-1}^w\right)+|{\lambda }_m|\langle E^{\prime }\left(x_{m-1}^w\right),-\mathrm{sign}\left\{{\lambda }_m\right\}{\phi }_m\rangle +2\rho \left(E,\mathsf{\Omega },|{\lambda }_m|\parallel {\phi }_m{\parallel }_X\right)\hfill \\ & \le & E\left(x_{m-1}^w\right)-{\lambda }_m\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle +2\alpha {|{\lambda }_m|}^q,\hfill \end{array}$$

where we have used the fact that $\parallel {\phi }_m{\parallel }_X=1$. Substituting

$${\lambda }_m=\mathrm{sign}\left\{\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle \right\}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{1}{q-1}}}$$

into

$$E\left(x_{m-1}^w\right)-{\lambda }_m\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle +2\alpha {|{\lambda }_m|}^q,$$

after a simple calculation, we obtain

$$E(x_{m-1}^w-{\lambda }_m{\phi }_m)\le E\left(x_{m-1}^w\right)-{\displaystyle \frac{{\mu }_m-2}{{\mu }_m}}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{q}{q-1}}}.$$

(12)

Combining (11) with (12), we have

$$E\left(x_m^w\right)\le E\left(x_{m-1}^w\right)-{\displaystyle \frac{{\mu }_m-2}{{\mu }_m}}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{q}{q-1}}}.$$

(13)

Thus, the sequence ${\left\{E\left(x_m^w\right)\right\}}_{m=0}^{\infty }$ is decreasing. If $E\left(x_{m-1}^w\right)-E\left(f^{\epsilon }\right)\le 0$, then from the monotonicity of $\left\{E\left(x_m^w\right)\right\}$, we have $E\left(x_m^w\right)-E\left(f^{\epsilon }\right)\le 0$, and hence inequality (9) holds.

We proceed to the case that $E\left(x_{m-1}^w\right)-E\left(f^{\epsilon }\right)>0$. We first estimate the lower bound of $|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |$. From the choice of ${\phi }_m$ and Lemma 2, we have

$$\begin{array}{ccc}\hfill |\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |& \ge & t_m\underset{\phi \in \mathcal{D}}{sup}|\langle E^{\prime }\left(x_{m-1}^w\right),\phi \rangle |\hfill \\ & =& t_m\underset{\varphi \in {\mathcal{A}}_1(\mathcal{D},1)}{sup}|\langle E^{\prime }\left(x_{m-1}^w\right),\varphi \rangle |\hfill \\ \hfill & \ge & t_m{A}^{-1}|\langle E^{\prime }\left(x_{m-1}^w\right),f^{\epsilon }\rangle |.\hfill \end{array}$$

(14)

Applying Lemma 5 to $x_{m-1}^w$ with $L=\mathrm{span}\left\{{\widehat{x}}_{m-1}^w\right\}$, we have $\langle E^{\prime }\left(x_{m-1}^w\right),x_{m-1}^w\rangle =0.$ Then, from Lemma 3, we have

$$\begin{array}{ccc}\hfill |\langle E^{\prime }\left(x_{m-1}^w\right),f^{\epsilon }\rangle |& =& |\langle E^{\prime }\left(x_{m-1}^w\right),f^{\epsilon }-x_{m-1}^w\rangle |\hfill \\ & \ge & E\left(x_{m-1}^w\right)-E\left(f^{\epsilon }\right).\hfill \end{array}$$

(15)

Combining (13) with (14) and (15), we obtain

$$E\left(x_m^w\right)\le E\left(x_{m-1}^w\right)-{\displaystyle \frac{{\mu }_m-2}{{\mu }_m}}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}{t}_m^{{\displaystyle \frac{q}{q-1}}}{A}^{-{\displaystyle \frac{q}{q-1}}}{\left(E\left(x_{m-1}^w\right)-E\left(f^{\epsilon }\right)\right)}^{{\displaystyle \frac{q}{q-1}}}.$$

(16)

Subtracting $E\left(f^{\epsilon }\right)$ from both sides of (16), we derive

$$E\left(x_m^w\right)-E\left(f^{\epsilon }\right)\le E\left(x_{m-1}^w\right)-E\left(f^{\epsilon }\right)-{\displaystyle \frac{{\mu }_m-2}{{\mu }_m}}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}{t}_m^{{\displaystyle \frac{q}{q-1}}}{A}^{-{\displaystyle \frac{q}{q-1}}}{\left(E\left(x_{m-1}^w\right)-E\left(f^{\epsilon }\right)\right)}^{{\displaystyle \frac{q}{q-1}}}.$$

For each $m\ge 0$, we define

$$a_m=E\left(x_m^w\right)-E\left(f^{\epsilon }\right).$$

Then, the sequence ${\left\{a_m\right\}}_{m=0}^{\infty }$ is decreasing and

$$\begin{array}{ccc}\hfill a_m& \le & a_{m-1}-{\displaystyle \frac{{\mu }_m-2}{{\mu }_m}}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}{t}_m^{{\displaystyle \frac{q}{q-1}}}{A}^{-{\displaystyle \frac{q}{q-1}}}{a}_{m-1}^{{\displaystyle \frac{q}{q-1}}}\hfill \\ & =& a_{m-1}\left(1-{\displaystyle \frac{{\mu }_m-2}{{\mu }_m}}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}{t}_m^{{\displaystyle \frac{q}{q-1}}}{A}^{-{\displaystyle \frac{q}{q-1}}}{a}_{m-1}^{{\displaystyle \frac{1}{q-1}}}\right).\hfill \end{array}$$

(17)

From the above discussion, it is sufficient to consider the case that $a_0>0$. The details are as follows:

Case 1: $0<a_0<\alpha {\mu }_1{A}^q{\left({\displaystyle \frac{{\mu }_1}{{\mu }_1-2}}\right)}^{q-1}{t}_1^{-q}$. It follows from the monotonicity of the sequence ${\left\{a_m\right\}}_{m=0}^{\infty }$ that either all elements of ${\left\{a_m\right\}}_{m=0}^{\infty }$ belong to $\left(0,\alpha {\mu }_1{A}^q{\left({\displaystyle \frac{{\mu }_1}{{\mu }_1-2}}\right)}^{q-1}{t}_1^{-q}\right)$, or for some $m^{*}\ge 1$, it holds that $a_{m^{*}}\le 0$. Then, for $m\ge m^{*}$, inequality (9) clearly holds.

Applying Lemma 4 to all positive numbers in ${\left\{a_m\right\}}_{m=0}^{\infty }$ with $J=1$, $\ell ={\displaystyle \frac{1}{q-1}}$, $r={\left(\alpha A^q\right)}^{{\displaystyle \frac{1}{q-1}}}$,

$$B=\alpha {\mu }_1{A}^q{\left({\displaystyle \frac{{\mu }_1}{{\mu }_1-2}}\right)}^{q-1}{t}_1^{-q}\mathrm{and}{r}_m=({\mu }_m-2){\left({\displaystyle \frac{t_m}{{\mu }_m}}\right)}^{{\displaystyle \frac{q}{q-1}}},$$

we have

$$a_m\le \alpha A^q{\left(\sum _{k=1}^m({\mu }_k-2){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q},$$

which implies that

$$E\left(x_m^w\right)-\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)\le \epsilon +\alpha A^q{\left(\sum _{k=1}^m({\mu }_k-2){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q}.$$

Hence, inequality (9) holds.

Case 2: $a_0\ge \alpha {\mu }_1{A}^q{\left({\displaystyle \frac{{\mu }_1}{{\mu }_1-2}}\right)}^{q-1}{t}_1^{-q}.$ Taking $m=1$ in inequality (17), we obtain

$$a_1\le a_0\left(1-{\displaystyle \frac{{\mu }_1-2}{{\mu }_1}}{\left(\alpha {\mu }_1\right)}^{-{\displaystyle \frac{1}{q-1}}}{t}_1^{{\displaystyle \frac{q}{q-1}}}{A}^{-{\displaystyle \frac{q}{q-1}}}{a}_0^{{\displaystyle \frac{1}{q-1}}}\right).$$

Hence, $a_1\le 0$. Combining this with the monotonicity of ${\left\{a_m\right\}}_{m=0}^{\infty }$ gives inequality (9). □

Proof of Corollary 1. 

If $arg\underset{x\in \mathsf{\Omega }}{min}E\left(x\right)\in {\mathcal{A}}_1(\mathcal{D},1)$, then $A=1$ and $\epsilon =0$. Thus, Corollary 1 follows from Theorem 5. □

Now, we compare the performance of WRPGA(co) with the Weak Chebyshev Greedy Algorithm with errors (WCGA($\Delta$,co)). Dereventsov and Temlyakov in [17] investigated the numerical stability of WCGA($\Delta$,co) and established the corresponding convergence rate with data noise. We recall the definition of WCGA($\Delta$,co). Let $\tau ={\left\{t_m\right\}}_{m=1}^{\infty },$$t_m\in (0,1]$ be a weakness sequence and $\Delta :={\{{\delta }_m,{\epsilon }_m\}}_{m=1}^{\infty }$ be an error sequence with ${\delta }_m\in [0,1]$ and ${\epsilon }_m\ge 0$ for $m=1,2,\dots .$ The WCGA($\Delta$,co) is defined as follows:

• Weak Chebyshev Greedy Algorithm with errors (WCGA($\Delta$,co))

• Set $x_0^c=0$, and for each $m\ge 1$, perform the following steps:

(1)

Select ${\phi }_m^c\in \mathcal{D}$ satisfying

$$\langle -E^{\prime }\left(x_{m-1}^c\right),{\phi }_m^c\rangle \ge t_m\underset{\phi \in \mathcal{D}}{sup}\langle -E^{\prime }\left(x_{m-1}^c\right),\phi \rangle .$$

(2)

Denote ${\mathsf{\Phi }}_m=\mathrm{span}{\left\{{\phi }_j^c\right\}}_{j=1}^m$ and define the next approximant $x_m^c$ from ${\mathsf{\Phi }}_m$ such that

$$E\left(x_m^c\right)\le \underset{x\in {\mathsf{\Phi }}_m}{inf}E\left(x\right)+{\delta }_m.$$

(3)

The approximant $x_m^c$ satisfies

$$|\langle E^{\prime }\left(x_m^c\right),x_m^c\rangle |\le {\epsilon }_m.$$

Note that in the definition of the WCGA($\Delta$,co), the dictionary $\mathcal{D}$ must be symmetric; that is, if $\phi \in \mathcal{D}$, then $-\phi \in \mathcal{D}$. It is well known that the WCGA(co) has the best approximation properties; see [26] for example. Let $C_0$ be a constant such that $E\left(x_m^c\right)\le E\left(0\right)+C_0.$ Assume that the set

$$\mathsf{\Omega }\subset {\mathsf{\Omega }}_1:=\{x\in X:E\left(x\right)\le E\left(0\right)+C_0\}\subset X$$

is bounded. Under this assumption, the authors in [17] obtained the following convergence rate of the WCGA($\Delta$,co):

Theorem 6 

([17]). Let E be a convex function with $\rho (E,\mathsf{\Omega },u)\le \alpha u^q$, $1<q\le 2$. Take an element $f^{\epsilon }\in \mathsf{\Omega }$ and a number $\epsilon \ge 0$ such that

$$E\left(f^{\epsilon }\right)\le \underset{x\in {\mathsf{\Omega }}_1}{inf}E\left(x\right)+\epsilon ,f^{\epsilon }/A\left(\epsilon \right)\in {\mathcal{A}}_1(\mathcal{D},1),$$

with some number $A\left(\epsilon \right)\ge 1$. Then, for the WCGA(Δ,co) with a constant weakness sequence $\tau =t\in (0,1]$ and an error sequence $\Delta ={\{{\delta }_m,{\epsilon }_m\}}_{m=1}^{\infty }$ with ${\delta }_m+{\epsilon }_m\le c{m}^{-q}$, $m=1,2,\dots$, we have

$$E\left(x_m^c\right)-\underset{x\in {\mathsf{\Omega }}_1}{inf}E\left(x\right)\le \epsilon +C(E,q,\alpha ,t,c)A^q{m}^{1-q}.$$

(18)

Notice that when ${\delta }_m={\epsilon }_m=0$ for all $m\ge 1$, the WCGA($\Delta$,co) reduces to the WCGA(co). Theorem 6 shows that the WCGA($\Delta$,co) maintains the optimal convergence rate $O\left(m^{1-q}\right)$ despite the presence of noise and computational errors.

Comparing (10) with (18), we see that the convergence rate of the WRPGA(co) with data noise is the same as that of the WCGA($\Delta$,co). We remark that the rate $m^{1-q}$ is independent of the dimension of the space X. Moreover, the WRPGA(co) has less computational complexity than the WCGA(co). It involves only one one-dimensional optimization problem rather than an m-dimensional optimization problem for the WCGA(co).

Next, we discuss the performance of the WRPGA(co) in the presence of computational errors. There are some results on the WRPGA for m-term approximation in this direction. In [4], Petrova investigated the WRPGA(H,$\mathcal{D}$) with some errors in the computation of the inner product $\langle f-f_{m-1},{\phi }_m\rangle$. That is, in Step m of the WRPGA$(H,\mathcal{D})$, the coefficient ${\lambda }_m$ is computed according to the following formula:

$${\lambda }_m:=(1+{\epsilon }_m)\langle f-f_{m-1},{\phi }_m\rangle ,|{\epsilon }_m|<1.$$

They obtained that for any $f\in {\mathcal{A}}_1\left(\mathcal{D}\right)$, the output ${\left\{f_m\right\}}_{m\ge 0}$ of the WRPGA$(H,\mathcal{D})$ with errors ${\left\{{\epsilon }_m\right\}}_{m\ge 1}$ satisfies

$$\parallel f-f_m{\parallel }_H\le {\parallel f\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{\left(\sum _{j=1}^m(1-{\epsilon }_j^2)t_j^2\right)}^{-1/2},m=1,2,\dots .$$

Jiang et al. in [27] studied the stability of the WRPGA$(X,\mathcal{D})$ for m-term approximation, which allows for computational inaccuracies in calculating the coefficient ${\lambda }_m$. That is, ${\lambda }_m$ is calculated based on

$${\lambda }_m:=(1+{\epsilon }_m)\mathrm{sign}\left\{F_{f-f_{m-1}}\left({\phi }_m\right)\right\}\parallel f-f_{m-1}{\parallel }_X{\left(2\gamma q\right)}^{{\displaystyle \frac{1}{1-q}}}|F_{f-f_{m-1}}\left({\phi }_m\right){|}^{{\displaystyle \frac{1}{q-1}}},|{\epsilon }_m|<1.$$

They called this algorithm the Approximate Weak Relaxed Pure Greedy Algorithm (AWRPGA$(X,\mathcal{D})$). Moreover, they derived the following convergence rate of the AWRPGA$(X,\mathcal{D})$.

Theorem 7 

([27]). Let X be a Banach space with $\rho \left(u\right)\le \gamma u^q$, $1<q\le 2$. For all $f\in {\mathcal{A}}_1\left(\mathcal{D}\right)$, the AWRPGA$(X,\mathcal{D})$ satisfies

$$\parallel f-f_m{\parallel }_X\le {\left(2\gamma q\right)}^{{\displaystyle \frac{1}{q}}}{\parallel f\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{\left(\sum _{k=1}^m{t}_k^{{\displaystyle \frac{q}{q-1}}}\left(1+{\epsilon }_k-{\displaystyle \frac{1}{q}}{(1+{\epsilon }_k)}^q\right)\right)}^{1/q-1},m=1,2,\dots .$$

More generally, we consider the dependence of the WRPGA(co) on the computational error in the second step of each iteration. We assume that in Step m of the algorithm, the coefficient ${\lambda }_m^{{\epsilon }_m}$ is calculated by using the following formula:

$${\lambda }_m^{{\epsilon }_m}:=(1+{\epsilon }_m)\mathrm{sign}\left\{\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle \right\}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{1}{q-1}}},|{\epsilon }_m|<1.$$

Such an algorithm is an approximate version of the WRPGA(co), denoted by AWRPGA(co). For simplicity, we use the notation $E\left(\overline{x}\right)=\underset{x\in X}{inf}E\left(x\right)=\underset{x\in \mathsf{\Omega }}{inf}E\left(x\right)$. We obtain the following error bound for the AWRPGA(co):

Theorem 8. 

Let the convex function $E:X\to \mathbb{R}$ be uniformly smooth and Fréchet-differentiable with minimizer $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)$ and $\rho (E,\mathsf{\Omega },u)\le \alpha u^q$, $1<q\le 2$. Assume that the error sequence ${\left\{{\epsilon }_m\right\}}_{m=1}^{\infty }$ satisfies $|{\epsilon }_m|<1$ for any $m\ge 1$. Then, for the AWRPGA(co) with

$${\mu }_m>max\{1,2{(1+{\epsilon }_m)}^{q-1}\},$$

it holds that

$$E\left(x_m^w\right)-E\left(\overline{x}\right)\le \alpha {\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q{\left(C(\alpha ,q,E)+\sum _{k=1}^m({\mu }_k-2{(1+{\epsilon }_k)}^{q-1})(1+{\epsilon }_k){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q},$$

where $C(\alpha ,q,E)={\left({\displaystyle \frac{\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q}{E\left(x_0^w\right)-E\left(\overline{x}\right)}}\right)}^{{\displaystyle \frac{1}{q-1}}}$.

Proof. 

Just like in the proof of inequality (13), we obtain

$$E\left(x_m^w\right)\le E\left(x_{m-1}^w\right)-\left(1-{\displaystyle \frac{2{(1+{\epsilon }_m)}^{q-1}}{{\mu }_m}}\right)(1+{\epsilon }_m){\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{q}{q-1}}}.$$

(19)

Note that ${\mu }_m>2{(1+{\epsilon }_m)}^{q-1}$. Thus,

$$0<\left(1-{\displaystyle \frac{2{(1+{\epsilon }_m)}^{q-1}}{{\mu }_m}}\right)(1+{\epsilon }_m)<1+{\epsilon }_m<2.$$

Then, we estimate the lower bound of $|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |$. Since $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)$, for any fixed $\epsilon >0$, $\overline{x}$ can be represented as $\overline{x}=\sum _{\phi \in \mathcal{D}}{c}_{\phi }\phi$, with

$$\sum _{\phi \in \mathcal{D}}|c_{\phi }|<\parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}+\epsilon .$$

Applying Lemma 5 to $x_{m-1}^w$ with $L=\mathrm{span}\left\{{\widehat{x}}_{m-1}^w\right\}$, we have $\langle E^{\prime }\left(x_{m-1}^w\right),x_{m-1}^w\rangle =0$. Therefore,

$$\begin{array}{ccc}\hfill \langle E^{\prime }\left(x_{m-1}^w\right),x_{m-1}^w-\overline{x}\rangle & =& -\langle E^{\prime }\left(x_{m-1}^w\right),\overline{x}\rangle \hfill \\ & =& -\sum _{\phi \in \mathcal{D}}{c}_{\phi }\langle E^{\prime }\left(x_{m-1}^w\right),\phi \rangle \hfill \\ & \le & t_m^{-1}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |\sum _{\phi \in \mathcal{D}}|c_{\phi }|\hfill \\ & <& t_m^{-1}(\parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}+\epsilon )|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |.\hfill \end{array}$$

Let $\epsilon \to 0$. We have

$$\langle E^{\prime }\left(x_{m-1}^w\right),x_{m-1}^w-\overline{x}\rangle \le t_m^{-1}\parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |.$$

Then, by using Lemma 3, we obtain

$$E\left(x_{m-1}^w\right)-E\left(\overline{x}\right)\le \langle E^{\prime }\left(x_{m-1}^w\right),x_{m-1}^w-\overline{x}\rangle \le t_m^{-1}\parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |,$$

and hence

$$|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle |\ge t_m{\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^{-1}\left(E\left(x_{m-1}^w\right)-E\left(\overline{x}\right)\right).$$

(20)

Combining (19) with (20), we derive

$$E\left(x_m^w\right)\le E\left(x_{m-1}^w\right)-{\displaystyle \frac{{\mu }_m-2{(1+{\epsilon }_m)}^{q-1}}{{\left(\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q\right)}^{\frac{1}{q-1}}}}(1+{\epsilon }_m){\left({\displaystyle \frac{t_m}{{\mu }_m}}\right)}^{{\displaystyle \frac{q}{q-1}}}{\left(E\left(x_{m-1}^w\right)-E\left(\overline{x}\right)\right)}^{{\displaystyle \frac{q}{q-1}}}.$$

Thus, it holds that

$$\begin{array}{cc}\hfill E\left(x_m^w\right)-E\left(\overline{x}\right)& \le (E\left(x_{m-1}^w\right)-E\left(\overline{x}\right))(1-{\displaystyle \frac{{\mu }_m-2{(1+{\epsilon }_m)}^{q-1}}{{\left(\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q\right)}^{\frac{1}{q-1}}}}\hfill \\ \hfill & \times (1+{\epsilon }_m){\left({\displaystyle \frac{t_m}{{\mu }_m}}\right)}^{{\displaystyle \frac{q}{q-1}}}{(E\left(x_{m-1}^w\right)-E\left(\overline{x}\right))}^{{\displaystyle \frac{1}{q-1}}}).\hfill \end{array}$$

Applying Lemma 4 to the sequence ${\{E\left(x_m^w\right)-E\left(\overline{x}\right)\}}_{m=0}^{\infty }$ with $J=0,B=E\left(x_0^w\right)-E\left(\overline{x}\right),\ell ={\displaystyle \frac{1}{q-1}}$,

$$r_m=({\mu }_m-2{(1+{\epsilon }_m)}^{q-1})(1+{\epsilon }_m){\left({\displaystyle \frac{t_m}{{\mu }_m}}\right)}^{{\displaystyle \frac{q}{q-1}}}\mathrm{and}r={\left(\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q\right)}^{{\displaystyle \frac{1}{q-1}}},$$

we obtain

$$\begin{array}{cc}\hfill E\left(x_m^w\right)-E\left(\overline{x}\right)& \le \alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q({\left({\displaystyle \frac{\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q}{E\left(x_0^w\right)-E\left(\overline{x}\right)}}\right)}^{{\displaystyle \frac{1}{q-1}}}\hfill \\ \hfill & +\sum _{k=1}^m({\mu }_k-2{(1+{\epsilon }_k)}^{q-1})(1+{\epsilon }_k){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}{)}^{1-q}.\hfill \end{array}$$

Thus, the proof is completed. □

By limiting the error ${\epsilon }_m$ to a certain range $[a,b]\subset (-1,1)$, we derive the following corollary from Theorem 8:

Corollary 2. 

Let the convex function $E:X\to \mathbb{R}$ be uniformly smooth and Fréchet-differentiable with minimizer $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)$ and $\rho (E,\mathsf{\Omega },u)\le \alpha u^q$, $1<q\le 2$. For any $a,b\in (-1,1)$, let ${\epsilon }_m\in [a,b]\subset (-1,1)$ for all $m\ge 1$. Then, for the AWRPGA(co) with ${\mu }_m>max\{1,2q{(1+{\epsilon }_m)}^{q-1}\}$, it holds that

$$E\left(x_m^w\right)-E\left(\overline{x}\right)\le \alpha ·c_1^{1-q}{\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q{\left(C(\alpha ,q,E)+\sum _{k=1}^m({\mu }_k-2{(1+a)}^{q-1}){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q},$$

where $c_1=min\left\{1,1+a\right\}$ and $C(\alpha ,q,E)={\left({\displaystyle \frac{\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q}{E\left(x_0^w\right)-E\left(\overline{x}\right)}}\right)}^{{\displaystyle \frac{1}{q-1}}}$.

Proof. 

Since ${\epsilon }_k\in [a,b]\subset (-1,1)$ and ${\mu }_k>max\{1,2q{(1+{\epsilon }_k)}^{q-1}\}$, we have ${\mu }_k>2q{(1+b)}^{q-1}$. It is easy to check that the minimum of the function

$$\psi \left(x\right)={\mu }_{k}x-2x^q,x\in [1+a,1+b]$$

is $\psi (1+a)$. Taking $x=1+{\epsilon }_k$, we have

$${\mu }_k(1+{\epsilon }_k)-2{(1+{\epsilon }_k)}^q\ge {\mu }_k(1+a)-2{(1+a)}^q.$$

Then, from Theorem 8, we have

$$E\left(x_m^w\right)-E\left(\overline{x}\right)\le \alpha ·c_1^{1-q}{\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q{\left(C(\alpha ,q,E)+\sum _{k=1}^m({\mu }_k-2{(1+a)}^{q-1}){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q},$$

where $c_1=min\left\{1,1+a\right\}$ and $C(\alpha ,q,E)={\left({\displaystyle \frac{\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q}{E\left(x_0^w\right)-E\left(\overline{x}\right)}}\right)}^{{\displaystyle \frac{1}{q-1}}}$, which completes the proof of Corollary 2. □

Observe that the above rate of convergence of the AWRPGA(co) is independent of the dimension of the space X. Comparing the convergence rates in Theorem 4 with those in Corollary 2, we can see that when the noise amplitude changes relatively little, the WRPGA(co) is stable.

We remark that when the US condition (6) holds on the whole domain X, Condition 0 in Theorem 4 is not necessary. In that case, we obtain the following theorem:

Theorem 9. 

Let the convex function $E:X\to \mathbb{R}$ be uniformly smooth and Fréchet-differentiable with minimizer $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)$. Assume that there are constants $\alpha >0$ and $1<q\le 2$ such that for all $x,x^{\prime }\in X$,

$$E\left(x^{\prime }\right)-E\left(x\right)-\langle E^{\prime }\left(x\right),x^{\prime }-x\rangle \le \alpha {\parallel x^{\prime }-x\parallel }_X^q.$$

(21)

Given an error sequence ${\left\{{\epsilon }_m\right\}}_{m=1}^{\infty }$ that satisfies $|{\epsilon }_m|<1$ for any $m\ge 1$, for the AWRPGA(co) with ${\mu }_m>max\{1,{(1+{\epsilon }_m)}^{q-1}\}$, the inequality

$$E\left(x_m^w\right)-E\left(\overline{x}\right)\le \alpha {\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q{\left(C(\alpha ,q,E)+\sum _{k=1}^m({\mu }_k-{(1+{\epsilon }_k)}^{q-1})(1+{\epsilon }_k){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{1-q}$$

holds with $C(\alpha ,q,E)={\left({\displaystyle \frac{\alpha \parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}^q}{E\left(x_0^w\right)-E\left(\overline{x}\right)}}\right)}^{{\displaystyle \frac{1}{q-1}}}$.

Proof. 

Taking $x^{\prime }=x_{m-1}^w-{\lambda }_m^{{\epsilon }_m}{\phi }_m$ and $x=x_{m-1}^w$ in (21), we have

$$\begin{array}{ccc}\hfill E\left({\widehat{x}}_m^w\right)& =& E(x_{m-1}^w-{\lambda }_m^{{\epsilon }_m}{\phi }_m)\le E\left(x_{m-1}^w\right)-{\lambda }_m^{{\epsilon }_m}\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle +\alpha {|{\lambda }_m^{{\epsilon }_m}|}^q\hfill \\ & =& E\left(x_{m-1}^w\right)-\left(1-{\displaystyle \frac{{(1+{\epsilon }_m)}^{q-1}}{{\mu }_m}}\right)(1+{\epsilon }_m){\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{q}{q-1}}},\hfill \end{array}$$

(22)

where we have used the definition of ${\lambda }_m^{{\epsilon }_m}$ and the assumption $\parallel {\phi }_m{\parallel }_X=1$.

Note that $E\left(x_m^w\right)\le E\left({\widehat{x}}_m^w\right)$. Thus, using (22), we derive

$$E\left(x_m^w\right)\le E\left(x_{m-1}^w\right)-\left(1-{\displaystyle \frac{{(1+{\epsilon }_m)}^{q-1}}{{\mu }_m}}\right)(1+{\epsilon }_m){\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}|\langle E^{\prime }\left(x_{m-1}^w\right),{\phi }_m\rangle {|}^{{\displaystyle \frac{q}{q-1}}}.$$

The remaining part of the proof of this theorem is similar to that of Theorem 8. Here, we omit it. □

Note that when ${\epsilon }_m=0$, the above convergence rate is consistent with that of Theorem 4. Moreover, the parameter $\left\{{\mu }_m\right\}$ just satisfies ${\mu }_m>1$ instead of

$${\mu }_m>max\{1,{\alpha }^{-1}{M}_0{M}_1^{1-q}\}.$$

It follows from Theorems 5, 8, and 9 and Corollaries 1 and 2 that the convergence rates of the WRPGA(co) do not change significantly despite the presence of noise and computational errors. This assertion is crucial for the practical implementation of the algorithm, which implies that the WRPGA(co) has certain robustness against noise and errors.

3. Convergence Rate of the AWRPGA$(\left\{{\mathit{\mu }}_{\mathit{m}}\right\},\mathit{X})$

In this section, we will apply the AWRPGA(co) to solve the problem of m-term approximation with respect to dictionaries in Banach spaces. Let X be a Banach space and $\overline{x}$ be a fixed element in X. If we set $E\left(x\right):=\parallel \overline{x}{-x\parallel }_X$ in convex optimization problem (5), then problem (5) reduces to an m-term approximation problem. Similarly, the discussion about the stability of the greedy-type convex optimization algorithms reduces to that of the greedy algorithm for m-term approximation. Since the function $E\left(x\right):=\parallel \overline{x}{-x\parallel }_X$ is not a uniformly smooth function in the sense of the smoothness of a convex function, we consider $E(x,q):=\parallel \overline{x}{-x\parallel }_X^q$ with $1<q\le 2$. Recall that the authors in [28] pointed out that if the modulus of smoothness, $\rho \left(u\right)$, of X defined as (4) satisfies $\rho \left(u\right)\le \gamma u^q$, $1<q\le 2$, then $E(x,q)$ is uniformly smooth and satisfies $\rho (E(·,q),\mathsf{\Omega },u)\le \alpha u^q$. It is known from [2] that the functional $F_x$ defined as (3) is the derivative of the norming function $E\left(x\right):={\parallel x\parallel }_X$. Then,

$$E^{\prime }(x,q)=-q{\parallel \overline{x}-x\parallel }_X^{q-1}{F}_{\overline{x}-x}.$$

Thus, the conditions of Theorem 8 are satisfied.

In this case, the AWRPGA(co) is reduced to the AWRPGA$(\left\{{\mu }_m\right\},X)$, which is defined as follows.

• AWRPGA$(\left\{{\mu }_m\right\},X)$

• Step 0:

• Define $x_0^w:=0$. If $\overline{x}=0$, then finish the algorithm and define $x_k^w:=x_0^w=\overline{x},k\ge 1$.

• Step m:

• Assume $x_{m-1}^w$ has been defined and $x_{m-1}^w\ne \overline{x}$. Perform the following steps:

  -

  Choose an element ${\phi }_m\in \mathcal{D}$ such that

  $$|F_{\overline{x}-x_{m-1}^w}\left({\phi }_m\right)|\ge t_m\underset{\phi \in \mathcal{D}}{sup}|F_{\overline{x}-x_{m-1}^w}\left(\phi \right)|.$$

  -

  Compute ${\lambda }_m$, given by the formula

  $${\lambda }_m:=(1+{\epsilon }_m)\mathrm{sign}\left\{-F_{\overline{x}-x_{m-1}^w}\left({\phi }_m\right)\right\}{\left(\alpha {\mu }_m\right)}^{-{\displaystyle \frac{1}{q-1}}}{q}^{{\displaystyle \frac{1}{q-1}}}{\parallel \overline{x}-x_{m-1}^w\parallel }_X|F_{\overline{x}-x_{m-1}^w}\left({\phi }_m\right){|}^{{\displaystyle \frac{1}{q-1}}}.$$

  -

  Compute

  $${\widehat{x}}_m^w:=x_{m-1}^w-{\lambda }_m{\phi }_m.$$

  -

  Choose $b_m$ such that

  $$\parallel \overline{x}-b_m{\widehat{x}}_m^w{\parallel }_X^q=\underset{b\in \mathbb{R}}{min}{\parallel \overline{x}-b{\widehat{x}}_m^w\parallel }_X^q$$

  and define the next approximant as

  $$x_m^w=b_m{\widehat{x}}_m^w.$$

• If $x_m^w=\overline{x}$, then finish the algorithm and define $x_k^w:=x_m^w=\overline{x},$ for $k>m$.
• If $x_m^w\ne \overline{x}$, then proceed to Step $m+1$.

It is clear that the AWRPGA generates an m-term approximation of $\overline{x}$ after m iterations. Applying Theorem 8 to $E(x,q)$, we obtain the following convergence rate of this new algorithm.

Theorem 10. 

Let $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)\subset X$ and, for suitable γ, $\rho \left(u\right)$ satisfy $\rho \left(u\right)\le \gamma u^q$, $1<q\le 2$. Assume that the error sequence ${\left\{{\epsilon }_m\right\}}_{m=1}^{\infty }$ satisfies $|{\epsilon }_m|<1$ for any $m\ge 1$. Then, for the AWRPGA$(\left\{{\mu }_m\right\},X)$ with ${\mu }_m>max\{1,2{(1+{\epsilon }_m)}^{q-1}\}$, it holds that

$$\parallel \overline{x}-x_m^w{\parallel }_X\le {\alpha }^{1/q}{\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{\left({\alpha }^{{\displaystyle \frac{1}{q-1}}}+\sum _{k=1}^m({\mu }_k-2{(1+{\epsilon }_k)}^{q-1})(1+{\epsilon }_k){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^{{\displaystyle \frac{q}{q-1}}}\right)}^{{\displaystyle \frac{1}{q}}-1}.$$

When $t_m=1$ for all $m\ge 1$, the AWRPGA$(\left\{{\mu }_m\right\},X)$ reduces to the ARPGA$(\left\{{\mu }_m\right\},X)$. Taking $t_m=1$, ${\mu }_m=\mu$, ${\epsilon }_m={\epsilon }_0$, and $m=1,2,\dots ,$ we obtain the following convergence rate of the ARPGA$(\mu ,X)$ with error ${\epsilon }_0$.

Theorem 11. 

Let $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)\subset X$ and, for suitable γ, $\rho \left(u\right)$ satisfy $\rho \left(u\right)\le \gamma u^q$, $1<q\le 2$. Assume that the error sequence ${\left\{{\epsilon }_m\right\}}_{m=1}^{\infty }$ satisfies ${\epsilon }_m={\epsilon }_0$ for all $m\ge 1$ with $|{\epsilon }_0|<1$. Then, for the ARPGA$(\mu ,X)$ with $\mu >max\{1,2{(1+{\epsilon }_0)}^{q-1}\}$, it holds that

$$\begin{array}{ccc}\hfill \parallel \overline{x}-x_m^w{\parallel }_X& \le & {\alpha }^{1/q}{\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{\left({\alpha }^{{\displaystyle \frac{1}{q-1}}}+(\mu -2{(1+{\epsilon }_0)}^{q-1})(1+{\epsilon }_0){\mu }^{-{\displaystyle \frac{q}{q-1}}}m\right)}^{{\displaystyle \frac{1}{q}}-1}.\hfill \\ & \le & C·\parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{m}^{1/q-1}.\hfill \end{array}$$

We proceed to remark that the rate of Theorem 11 is sharp. We take Lebesgue spaces as examples. Let $(O,\mathcal{M},\nu )$ be a measure space; that is, $\nu$ is a measure on the $\sigma$-algebra $\mathcal{M}$ of subsets of O. For $1<p<\infty$, define the Lebesgue space $L_p(O,\mathcal{M},\nu )$ as

$$L_p(O,\mathcal{M},\nu ):=\left\{{f\mathrm{is}\mathrm{measurable}:\parallel f\parallel }_p={\left({\int }_O{|f|}^{p}d\nu \right)}^{1/p}\right\}.$$

It is known from [29] that the modulus of smoothness of $L_p(O,\mathcal{M},\nu )$ satisfies

$$\begin{array}{c}\hfill \rho \left(u\right)\le \left\{\begin{array}{cc}{\displaystyle \frac{u^p}{p}},\hfill & 1<p\le 2,\hfill \\ {\displaystyle \frac{(p-1)u^2}{2}},\hfill & 2<p<\infty .\hfill \end{array}\right.\end{array}$$

Applying Theorem 11 to $L_p(O,\mathcal{M},\nu )$, we obtain the following theorem.

Theorem 12. 

Let $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)\subset L_p(O,\mathcal{M},\nu ),1<p<\infty$. Assume that the error sequence ${\left\{{\epsilon }_m\right\}}_{m=1}^{\infty }$ satisfies ${\epsilon }_m={\epsilon }_0$ for all $m\ge 1$ with $|{\epsilon }_0|<1$. Then, for the ARPGA$(\mu ,L_p(O,\mathcal{M},\nu ))$ with $\mu >max\{1,2{(1+{\epsilon }_0)}^{min\{p,2\}-1}\}$, it holds that

$$\begin{array}{cc}\hfill \parallel \overline{x}-x_m^w{\parallel }_p& \le {\alpha }^{1/min\{p,2\}}{\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}({\alpha }^{{\displaystyle \frac{1}{min\{p,2\}-1}}}+(\mu -2{(1+{\epsilon }_0)}^{min\{p,2\}-1})\hfill \\ \hfill & \times (1+{\epsilon }_0){\mu }^{-{\displaystyle \frac{min\{p,2\}}{min\{p,2\}-1}}}m{)}^{{\displaystyle \frac{1}{min\{p,2\}}}-1}\hfill \\ \hfill & \le C\parallel \overline{x}{\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{m}^{{\displaystyle \frac{1}{min\{p,2\}}}-1}.\hfill \end{array}$$

Jiang et al. in [27] have shown that the rate $m^{{\displaystyle \frac{1}{min\{p,2\}}}-1}$ is sharp.

Now, we apply the ARPGA$(\left\{{\mu }_m\right\},X)$ to Hilbert spaces. When $X=H$, a Hilbert space H with the inner product $\langle ·,·\rangle$ and the norm ${\parallel ·\parallel }_H={\langle ·,·\rangle }^{1/2}$, the AWRPGA$(\left\{{\mu }_m\right\},H)$ takes the following form:

• Step 0:

• Define $x_0^w:=0$. If $\overline{x}=0$, then finish the algorithm and define $x_k^w:=x_0^w=\overline{x},k\ge 1$.

• Step m:

• Assume $x_{m-1}^w$ has been defined and $x_{m-1}^w\ne \overline{x}$. Perform the following steps:

  -

  Choose an element ${\phi }_m\in \mathcal{D}$ such that

  $$|\langle x_{m-1}^w-\overline{x},{\phi }_m\rangle |\ge t_m\underset{\phi \in \mathcal{D}}{sup}|\langle x_{m-1}^w-\overline{x},\phi \rangle |.$$

  -

  Compute ${\lambda }_m^{{\epsilon }_m}$, given by the formula

  $${\lambda }_m^{{\epsilon }_m}:={\displaystyle \frac{2}{{\mu }_m}}(1+{\epsilon }_m)\langle x_{m-1}^w-\overline{x},{\phi }_m\rangle .$$

  -

  Compute

  $${\widehat{x}}_m^w:=x_{m-1}^w-{\lambda }_m^{{\epsilon }_m}{\phi }_m,b_m:={\displaystyle \frac{\langle \overline{x},{\widehat{x}}_m^w\rangle }{\parallel {\widehat{x}}_m^w{\parallel }_H^2}}.$$

  -

  Define the next approximant as

  $$x_m^w=b_m{\widehat{x}}_m^w.$$

• If $x_m^w=\overline{x}$, then finish the algorithm and define $x_k^w:=x_m^w=\overline{x},$ for $k>m$.
• If $x_m^w\ne \overline{x}$, then proceed to Step $m+1$.

For the AWRPGA$(\left\{{\mu }_m\right\},H)$, we obtain the following corollary from Theorem 9:

Corollary 3. 

Let $\overline{x}\in {\mathcal{A}}_1\left(\mathcal{D}\right)\subset H$. Assume that the error sequence ${\left\{{\epsilon }_m\right\}}_{m=1}^{\infty }$ satisfies $|{\epsilon }_m|<1$ for any $m\ge 1$. Then, the output of the AWRPGA$(\left\{{\mu }_m\right\},H)$ with

$${\mu }_m>max\{1,1+{\epsilon }_m\}$$

satisfies the following inequality:

$$\parallel x_m^w-\overline{x}{\parallel }_H\le {\parallel \overline{x}\parallel }_{{\mathcal{A}}_1\left(\mathcal{D}\right)}{\left(1+\sum _{k=1}^m({\mu }_k-(1+{\epsilon }_k))(1+{\epsilon }_k){\left({\displaystyle \frac{t_k}{{\mu }_k}}\right)}^2\right)}^{-1/2}.$$

Proof. 

It is well known that $E(x,2)$ is Fréchet-differentiable on Hilbert space H. Moreover, its Fréchet derivative $E^{\prime }\left(x\right)$ acts on $h\in H$ as $\langle E^{\prime }\left(x\right),h\rangle =2\langle x-\overline{x},h\rangle$; see [10] for instance. Therefore, we obtain

$$\begin{array}{ccc}\hfill E\left(x^{\prime }\right)-E\left(x\right)-\langle E^{\prime }\left(x\right),x^{\prime }-x\rangle & =& \parallel x^{\prime }-\overline{x}{\parallel }_H^2-{\parallel x-\overline{x}\parallel }_H^2-2\langle x-\overline{x},x^{\prime }-x\rangle \hfill \\ & =& \parallel x^{\prime }{-x\parallel }_H^2.\hfill \end{array}$$

Thus, $E(x,2)$ satisfies the conditions of Theorem 9 with $\alpha =1$ and $q=2$. Then, Corollary 3 follows from Theorem 9. □

We remark that the result of Corollary 3 for ${\mu }_m=2$, $m\ge 1$, was obtained in [4,27].

4. Examples and Numerical Results

Observe that the convergence results of the WRPGA(co) in Banach spaces apply to any dictionary, including those in infinite-dimensional Banach spaces. In this case, dictionaries contain infinitely many elements. This is a somewhat surprising result, which shows the power of the WRPGA(co). On the other hand, in practice, we deal with optimization problems in finite high-dimensional spaces. A typical example is sparse signal recovery in compressive sensing. Let $X={\mathbb{R}}^N$, and for any $\mathbf{x}\in X$, define its norm by

$${\parallel \mathbf{x}\parallel }_2={\left(\sum _{j=1}^N{|x_j|}^2\right)}^{1/2}.$$

Let $\mathbf{x}$ be a d-dimensional compressible vector and $\mathsf{\Phi }\in {\mathbb{R}}^{N\times d}$ be the measurement matrix with $d\gg N$. Our goal is to find the best approximation of the unknown $\mathbf{x}$ by utilizing $\mathsf{\Phi }$ and the given data $f=\mathsf{\Phi }\mathbf{x}$. It is well known that this problem is equivalent to solving the following convex optimization problem on ${\mathbb{R}}^d$:

$$\underset{{\widehat{x}}_1,\dots ,{\widehat{x}}_d\in \mathbb{R}}{min}{∥f-\sum _{i=1}^d{\widehat{x}}_i{\phi }_i∥}_2,$$

(23)

where ${\phi }_1,\dots ,{\phi }_d$ denote the columns of $\mathsf{\Phi }$. Note that the dimension d is larger than N, which means that the column vectors of the measurement matrix $\mathsf{\Phi }$ are linearly dependent. Thus, the column vectors of $\mathsf{\Phi }$ can be considered a dictionary of ${\mathbb{R}}^N$. Notably, when $d\gg N$, solving problem (23) is difficult. Observe that problem (23) can also be considered an approximation problem with a dictionary in space X. Naturally, one can adapt greedy approximation algorithms to handle this problem. It turns out that greedy algorithms are powerful tools for solving problem (23); see [7,30,31,32].

Next, we will present two numerical examples to illustrate the stability of the WRPGA(co) with noise and errors, which are discussed in Section 2 and Section 3. We begin with the first example to verify Theorems 5 and 8 (see Figure 1, Figure 2 and Figure 3). We will randomly generate a Banach space $X={\ell }_p^{\dim }$ and a dictionary $\mathcal{D}$ based on a given distribution of parameter p. We will choose a suitable target functional $E:X\to \mathbb{R}$ and then apply the WRPGA(co) to solve the convex optimization problem (5); that is, we seek to find a sparse minimizer to approximate

$$\overline{x}=arg\underset{x\in X}{min}E\left(x\right)=arg\underset{x\in \mathsf{\Omega }}{min}E\left(x\right).$$

In this process, we assume that the WRPGA(co) is affected by noise and error. We evaluate the performance of the WRPGA(co) using

$${\displaystyle \frac{E\left(\overline{x}\right)-{inf}_{x\in X}E\left(x\right)}{E\left(0\right)-{inf}_{x\in X}E\left(x\right)}}\in [0,1].$$

(24)

Now, we give the details of this example. Let $p\sim \mathcal{U}(1,10)$ and $X={\ell }_p^{1000}$. We consider a dictionary with size 10,000, where every element is the normalized linear combination of the standard basis, ${\left\{e_i\right\}}_{i=1}^{1000}$, of X and coefficients follow a normal distribution, that is, $\mathcal{D}={\left\{{\phi }_j\right\}}_{j=1}^{10000},$ where

$${\phi }_j={\displaystyle \frac{{\sum }_{i=1}^{1000}{c}_j^i{e}_i}{{\left({\sum }_{i=1}^{1000}{|c_j^i|}^p\right)}^{1/p}}},c_j^i\sim \mathcal{N}(0,1).$$

We choose the target functional $E:X\to \mathbb{R}$ as

$$E\left(x\right)={\parallel x-f\parallel }_2^2,$$

where $f\in X$ is randomly generated in the form of

$$f=\sum _{k=1}^{K_f}{a}_k{\phi }_{\sigma \left(k\right)},{\phi }_{\sigma \left(k\right)}\in \mathcal{D}$$

with $a_k\sim \mathcal{N}(0,1)$, where $\sigma$ is a permutation of {1, …, 10,000} and $K_f\sim \mathcal{U}(100,300)$. Although the example is simple, it is a classical problem in compressed sensing and has many practical backgrounds. We will use the WRPGA(co) to derive an approximate minimizer with a sparsity of 100. The following results are based on 100 simulations.

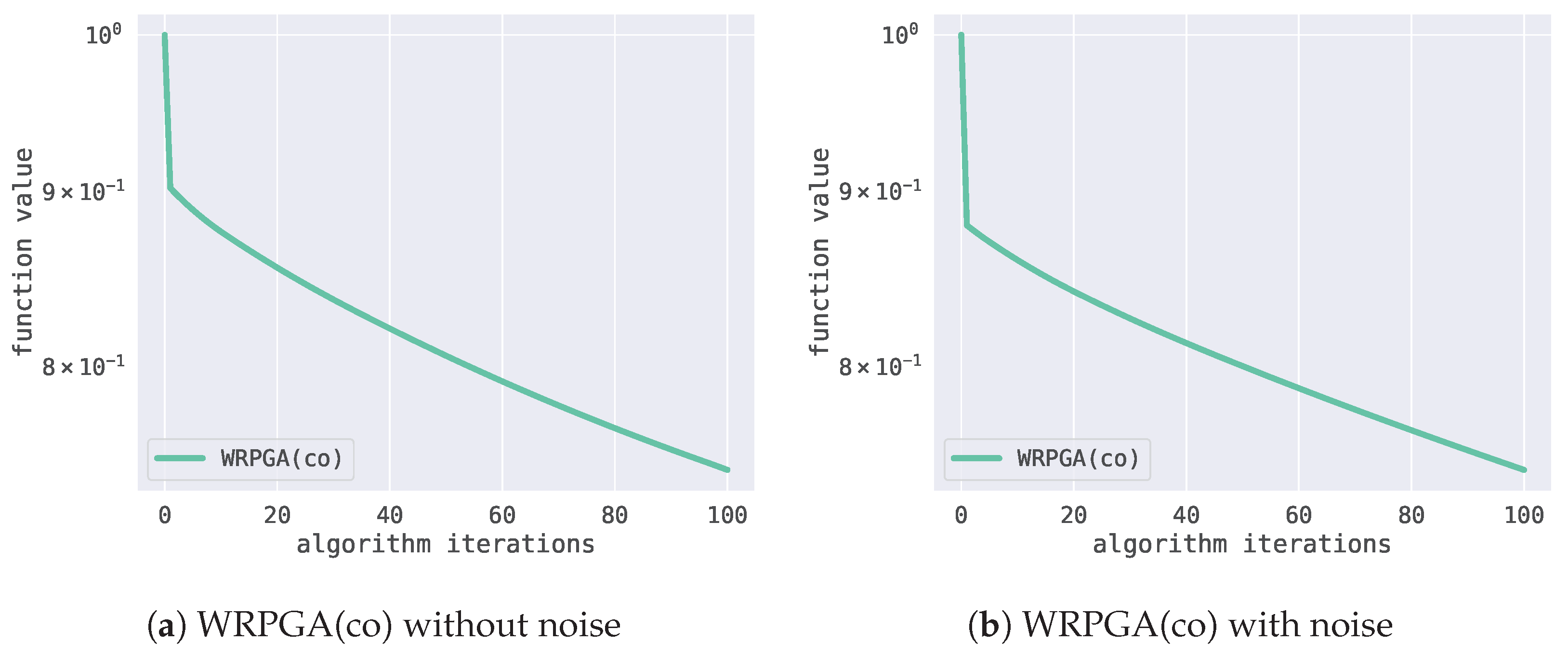
Figure 1 demonstrates the relationship between the number of iterations of the WRPGA(co) and the function value (24) in data noise and noiseless cases, which verifies Theorem 5. Here, the noise is randomly generated with small amplitude values. In both cases, we randomly choose a parameter ${\mu }_m$ slightly larger than 2 for simplicity. It shows that the function value (24) does not change greatly under this noise, which implies that the WRPGA(co) is stable in a sense and will perform well in practice.

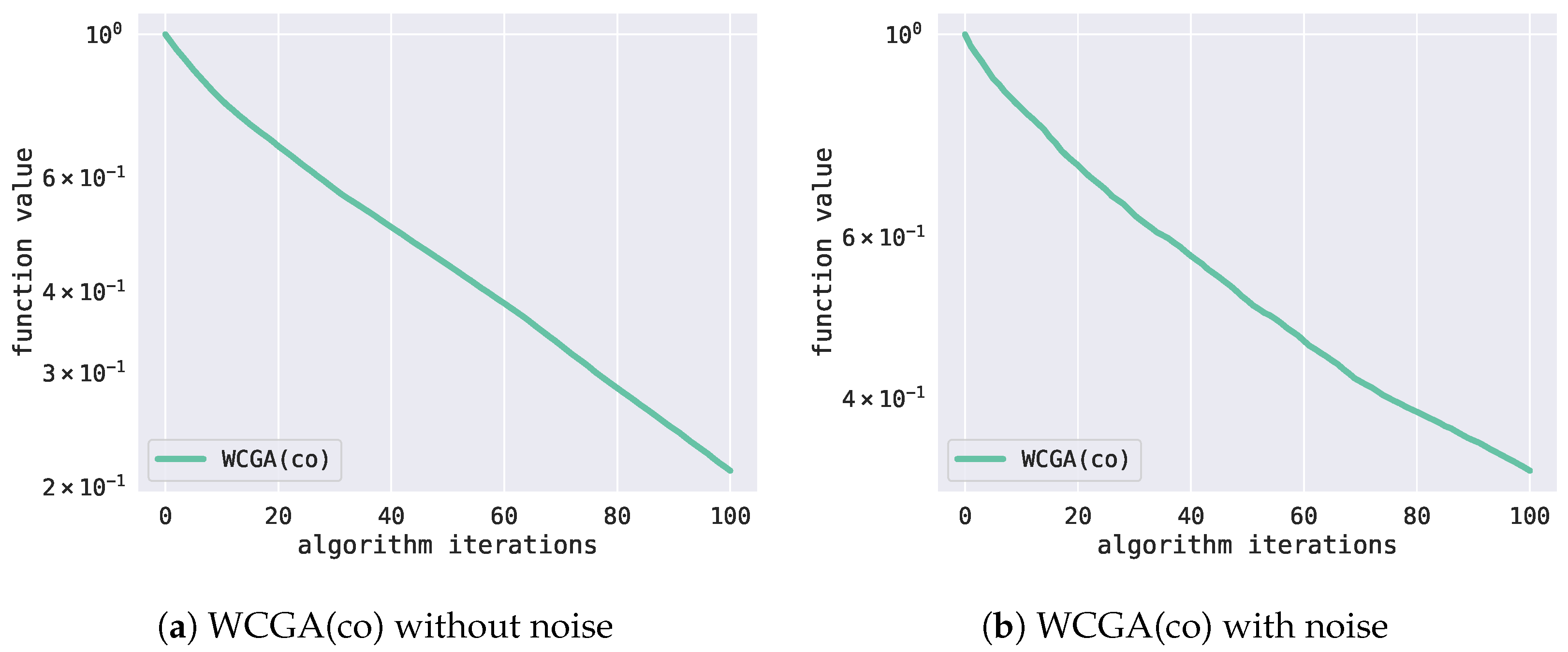
Furthermore, we use the WCGA(co) to obtain an approximate minimizer with a sparsity of 100 for the above problem. The corresponding setting is the same as that of the WRPGA(co). In the field of signal processing, the WCGA(co) is known as the Orthogonal Matching Pursuit (OMP). After 100 simulations, we obtained the relationship between the number of iterations of the WCGA(co) and the function value with data noise and that without noise, as shown in Figure 2. Here, the choice of noise is the same as that of the WRPGA(co).

It follows from Figure 1 and Figure 2 that the approximation performance of the WCGA(co) is better than that of the WRPGA(co) even in the presence of noise. However, unlike the WCGA(co), the difference in the function value of the WRPGA(co) with data noise is not huge. This means that the WRPGA(co) is not sensitive to the noise, showing its stability. There is a trade-off between computational complexity and approximation performance.

Figure 3 reveals the relationship between the number of iterations of the AWRPGA(co) and the function value (24) in the presence of computational error and the ideal case, which verifies Theorem 8. Here, the computational error, ${\epsilon }_m$, is randomly selected from $(-1,1)$. From Figure 3, we know that in the error case, the function value fluctuates but does not change significantly, which indicates that the WRPGA(co) with errors is weakly stable.

Now, we consider the stability of the special AWRPGA$(\left\{{\mu }_m\right\},H)$ with $t_m=1$ and ${\mu }_m=2$ for all $m\ge 1$, that is, the RPGA with computational error ${\left\{{\epsilon }_m\right\}}_{m\ge 1},$ $|{\epsilon }_m|<1$. We will illustrate Corollary 3 with the following numerical experiment on regression learning. One can also refer to [8] for more details about the Rescaled Pure Greedy Algorithms in learning problems.

Let $f\left(x\right)=cos\left(\pi x\right)$, $x\in [-1,1]$. We uniformly select 500 sample points from this function. Set $x_0=-1$. Let

$$\mathcal{X}:=\left\{x_i:x_i={\displaystyle \frac{i-1}{200}},0\le i<200\right\}$$

be a set of 200 equally spaced points in $[-1,1]$. We choose $\{e^{-\parallel x-x_i{\parallel }^2}:i=0,1,\dots ,100\}$ as a dictionary. We seek to approximate $f\left(x\right)$ by using the RPGA based on the sampling points ${\left\{\widetilde{x_j}\right\}}_{j=1}^{500}$. In the implementation of the algorithm, Gaussian noise from $\mathcal{N}(o,{\delta }^2)$ with ${\delta }^2=0.2$ is allowed. The function values with noise are used as inputs to the regression. To measure the performance of the algorithm, we use the mean square error (MSE) of f on the unlabeled samples $\mathbf{x}={\left\{{\tilde{x}}_j\right\}}_{j=1}^{500}$, which is defined as

$$\mathrm{MSE}={\displaystyle \frac{1}{500}}\sum _{j=1}^{500}{(f\left({\tilde{x}}_j\right)-f_{\rho }\left({\tilde{x}}_j\right))}^2.$$

To make the performance of the RPGA clear, we also discuss the performance of the OGA. Moreover, we add computational inaccuracies in the implementation of the RPGA. By repeating the test 100 times, we obtain the following

Table 1. The average MSE, running time, and relative error of the OGA and the RPGA with computation error ${\epsilon }_m$ on noisy data.

Algorithms	Average MSE	Average Running Time (s)	Relative Error
OGA	3.0705 × 10−4	0.4074	0.0001
RPGA with $|{ϵ}_m|=0$	0.0122	0.2809	0.0016
RPGA with $|{ϵ}_m|<1$	0.0296	0.1322	0.0030

and Figure 4.

Figure 4 demonstrates that the performance of the OGA on noisy data and noiseless data outperforms that of the RPGA with computational error $\left\{{\epsilon }_m\right\}$ in the regression learning problem. However, according to the running time in Table 1, we observe that the RPGA runs more quickly than the OGA even in the noise case. This is related to the design of the algorithm. The OGA updates the approximant by solving an m-term optimization problem. On the other hand, the RPGA only needs to solve a one-dimensional optimization problem.

It is well known that the above two numerical examples can also be solved by the Least Absolute Shrinkage and Selection Operator (LASSO). The LASSO algorithm introduces sparsity through $L_1$-regularization; see [33]. When the design matrix X satisfies certain conditions and the regularization parameter $\lambda$ is appropriately chosen, the solution is guaranteed to be unique. However, its robustness to noise in practice critically depends on the proper selection of $\lambda$. In contrast, greedy algorithms (e.g., OGA) iteratively build sparse solutions with low per-step complexity. While they converge quickly in low-noise scenarios, their inability to revise earlier decisions makes them prone to error accumulation and less robust to noise compared to LASSO; see [34,35].

5. Conclusions and Discussions

It is well-known that the Weak Rescaled Pure Greedy Algorithm for convex optimization (WRPGA(co)) is simpler than other greedy-type convex optimization algorithms, such as the Weak Chebychev Greedy Algorithm (WCGA(co)), the Weak Greedy Algorithm with Free Relaxation (WGAFR(co)), and the Rescaled Weak Relaxed Greedy Algorithm (RWRGA(co)), and has the same approximation properties as them. The rate of convergence of all these algorithms is of the optimal order $m^{1-q}$, which is independent of the spatial dimension; see [10,17,21]. In this article, we study the stability of the WRPGA(co) in real Banach spaces and obtain the corresponding convergence rates with noise and error. We use the condition that $\rho (E,\mathsf{\Omega },u)$ has power type $1<q\le 2$ instead of the US condition since the US condition of E on $\mathsf{\Omega }$ is restrictive and requires additional conditions to ensure that the US condition still holds for the sequence generated from the WRPGA(co). Our results show that the WRPGA(co) is stable in the sense that the rate of the convergence of the WRPGA(co) is basically unchanged, which demonstrates that the WRPGA(co) maintains desirable properties even in imperfect computation scenarios. Moreover, we apply the WRPGA(co) with error to the problem of m-term approximation and derive the optimal convergence rate. This indicates that the WRPGA(co) is flexible and can be widely utilized in applied mathematics and signal processing. The numerical simulation results have also verified our theoretical results. The stability of the WRPGA(co), allowing for noise and error, is crucial for practical implementation, which may produce predictable results and guarantee the consistency of the results when the algorithm is implemented repeatedly. This advantage, as well as the advantages in computational complexity and convergence rates, indicate that the WRPGA(co) is efficient in solving high-dimensional and even infinity-dimensional convex optimization problems.

In summary, the novelty of our work is as follows:

• Under weaker conditions, $\rho (E,\mathsf{\Omega },u)\le \alpha u^q,1<q\le 2$, we show that the WRPGA(co) with noise has the same convergence rate as that of the WRPGA(co) without noise.
• We introduce and study a new algorithm—the Approximate Weak Rescaled Pure Greedy Algorithm for convex optimization (AWRPGA(co)). We show that the AWRPGA(co) has almost the same convergence rate as that of the WRPGA(co).
• We apply, for the first time, the WRPGA(co) with error to m-term approximation problems in Banach spaces. The convergence rate we obtained is optimal.
• We compare the efficiency of the WRPGA(co) with that of the WCGA(co) through numerical experiments. The results show that the WCGA(co) has better approximation performance but higher computational cost than the WRPGA(co).

Next, we discuss some future work. The introduction of the weakness sequence ${\left\{t_m\right\}}_{m\ge 1}$, $0<t_m\le 1$, into the algorithm allows for controlled relaxation in selecting elements from the dictionary, which increases the flexibility of the algorithm. Observe that when $t_m=1$ for all $m\ge 1$, the algorithm can achieve the optimal error, which is sharp as a general result. However, the supremum of greedy condition (2) may not be attainable. Our results provide the same rate of convergence for the weak versions (in the case $t_m=t$) as for the strong versions ($t_m=1$) of the algorithms. Thus, taking $t_m=t$ may be a good choice. However, there is no general answer to the question of how to choose the optimal t, which relies on the specific convex optimization problem. Recently, some researchers have used some strategies, such as utilizing the a posteriori information gained from previous iterations of the algorithm, to improve the convergence rate of the algorithm; see [36,37]. This inspires us to use this strategy to improve our results. In addition, it is known from [26,38] that research on the WCGA and the WGAFR for m-term approximation in real Banach spaces has been extended to complex Banach spaces. Thus, it would be interesting to extend our study to the setting of complex Banach spaces.

Above all, we will concentrate on the following problems in our future work:

• For a given convex optimization problem, we will explore the optimal selection of the parameter t.
• In the implementation of the WRPGA(co), we will take the a posterior information into account to further improve our convergence rates and numerical results.
• We will investigate the performance of greedy-type algorithms in complex Banach spaces for m-term approximation or convex optimization.