Numerical Method for Band Gap Structure and Dirac Point of Photonic Crystals Based on Recurrent Neural Network
Abstract
1. Introduction
2. Method
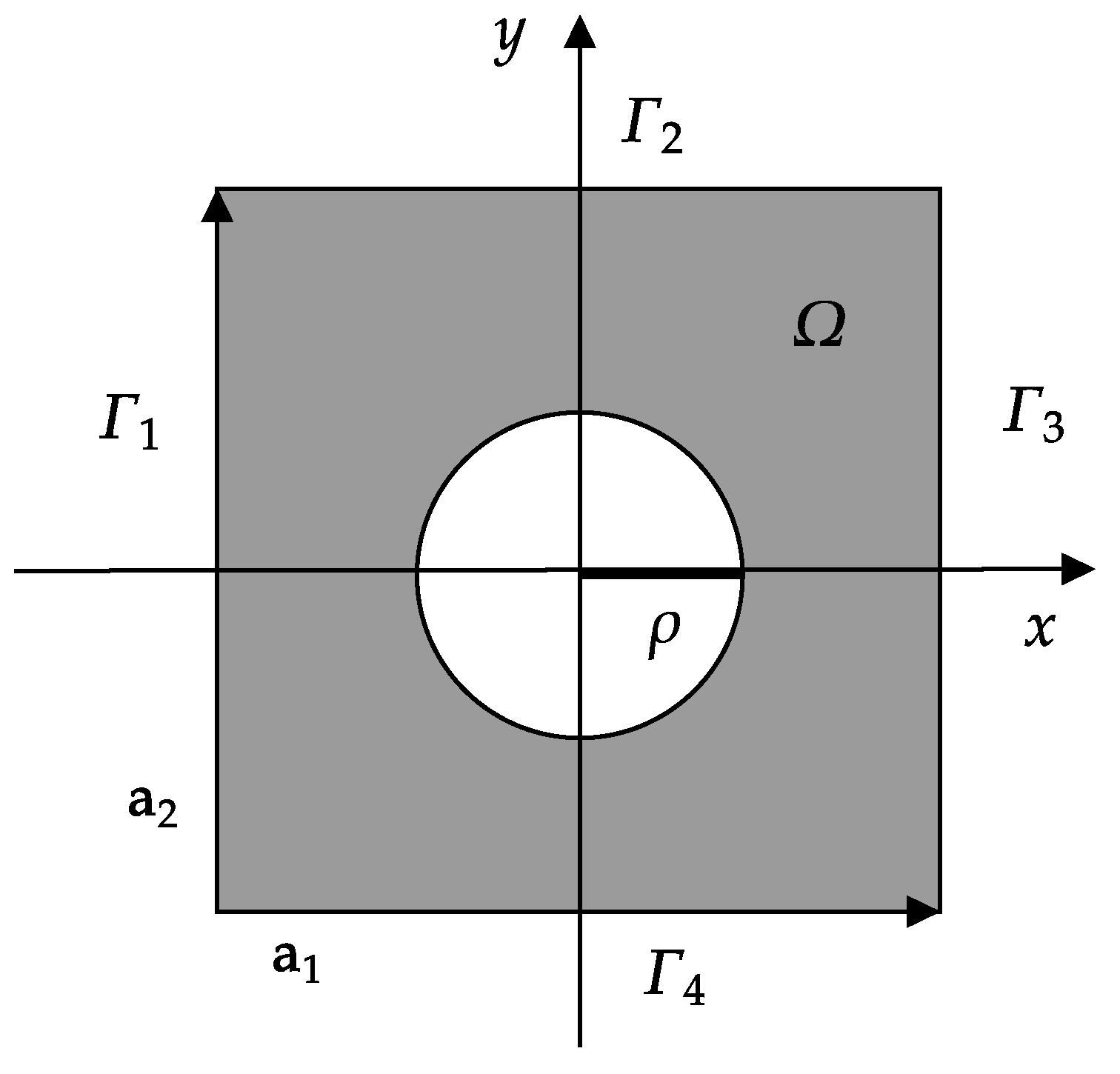
2.1. Model for Band Gap Calculation
2.2. Finite Element Schemes
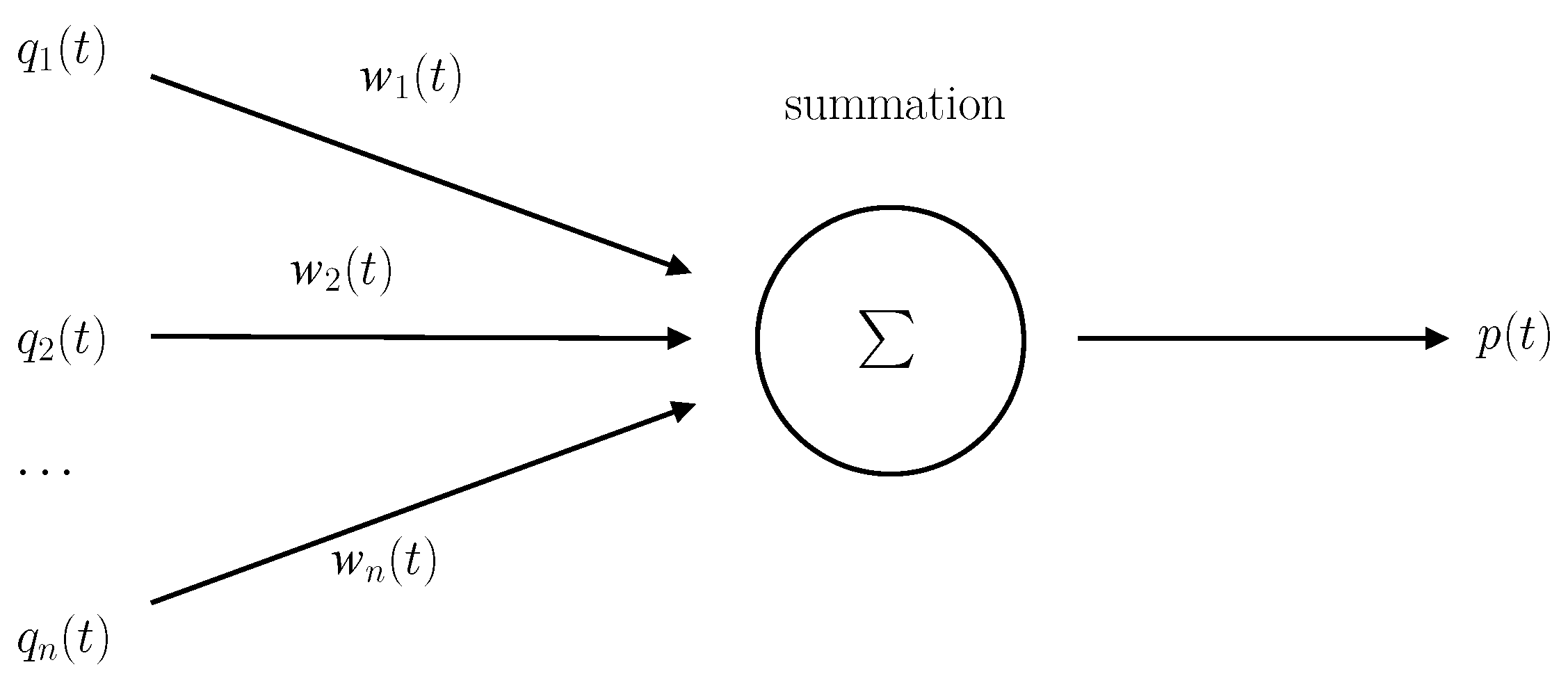
2.3. RNN Model and Algorithm
| Algorithm 1 RNN algorithm for generalized eigenvalue problem |
|
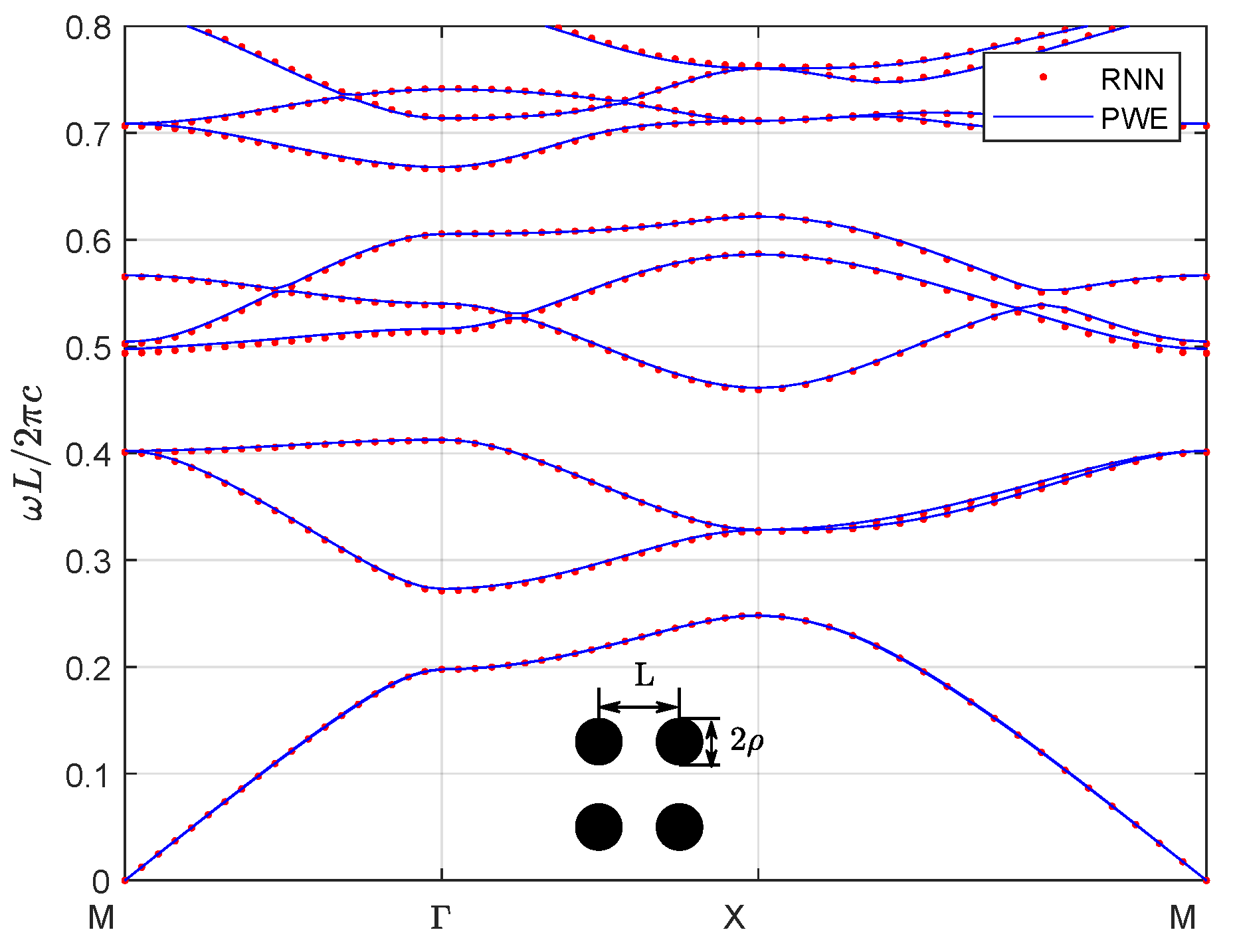
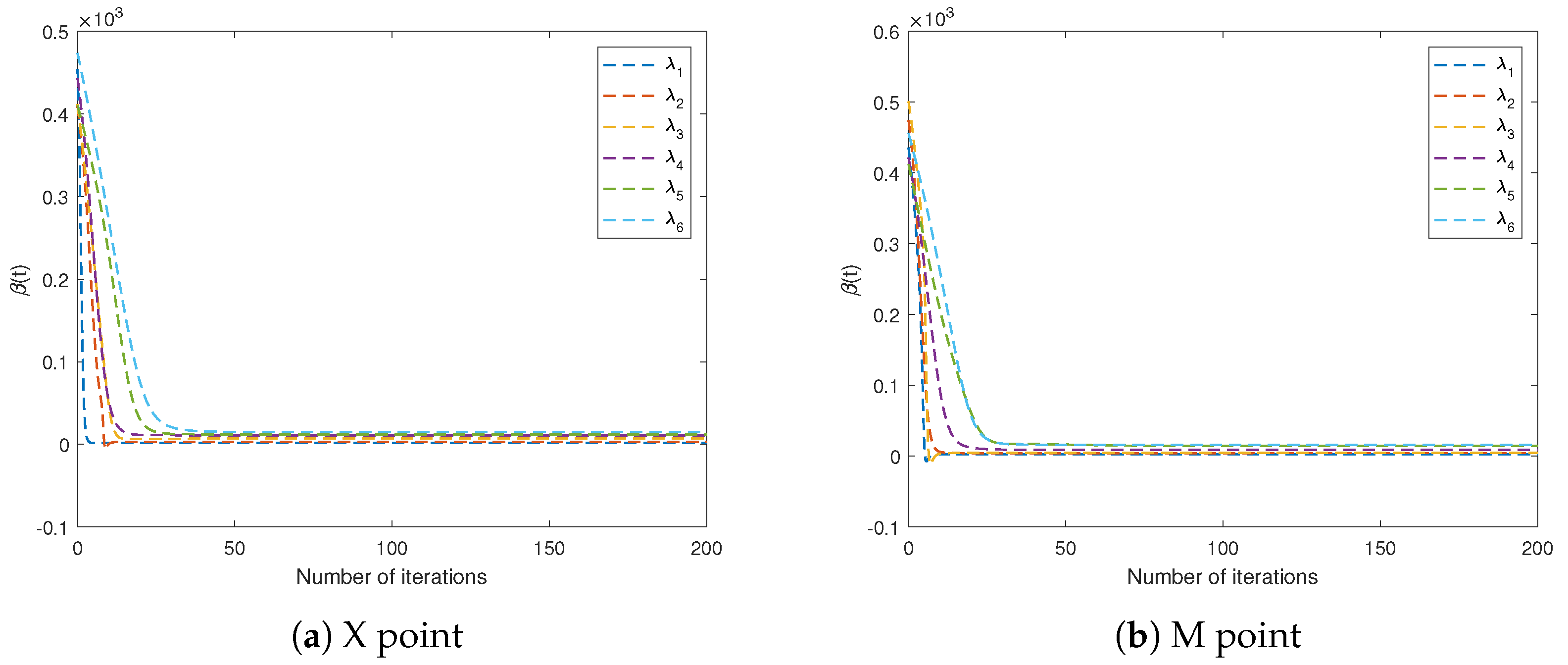
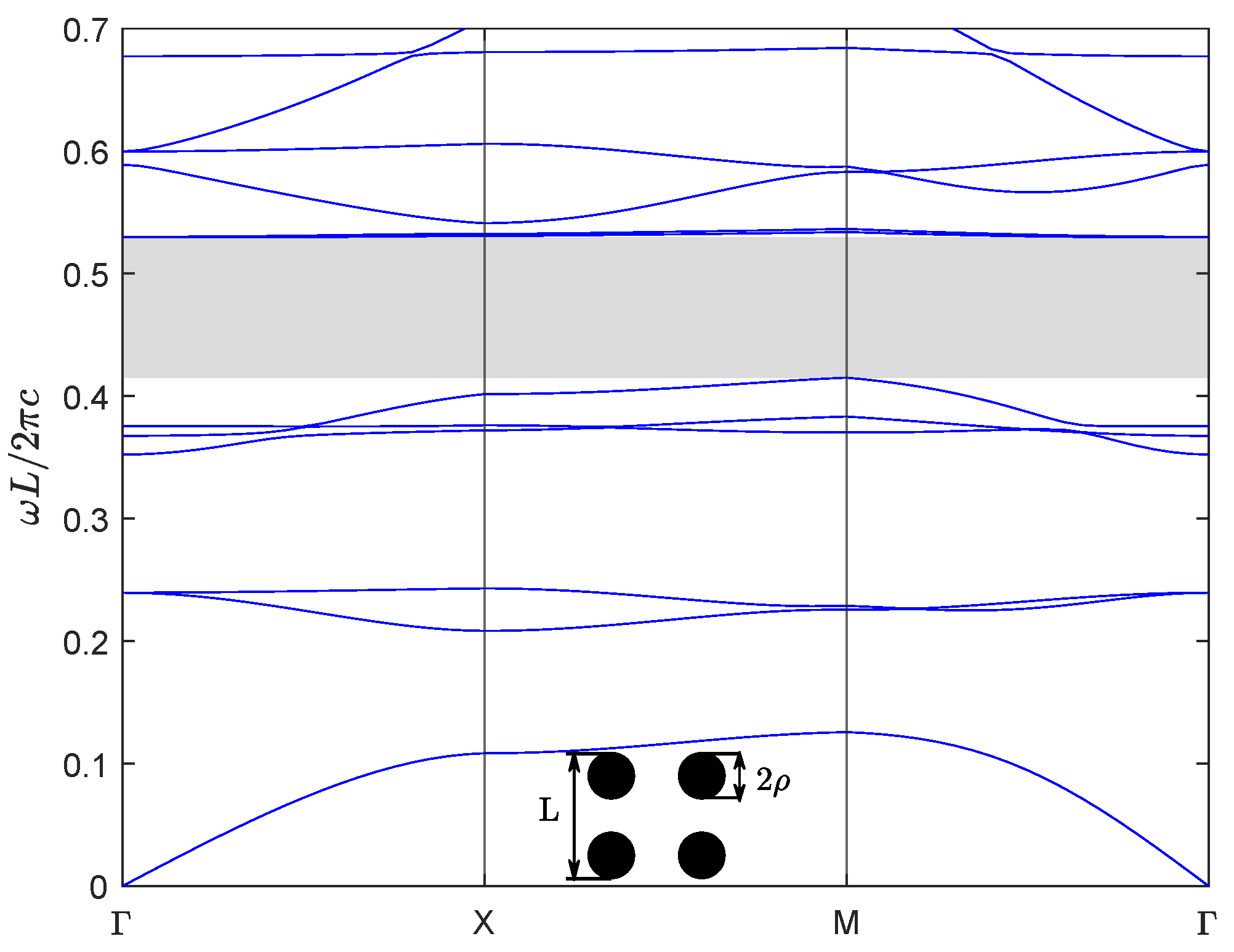
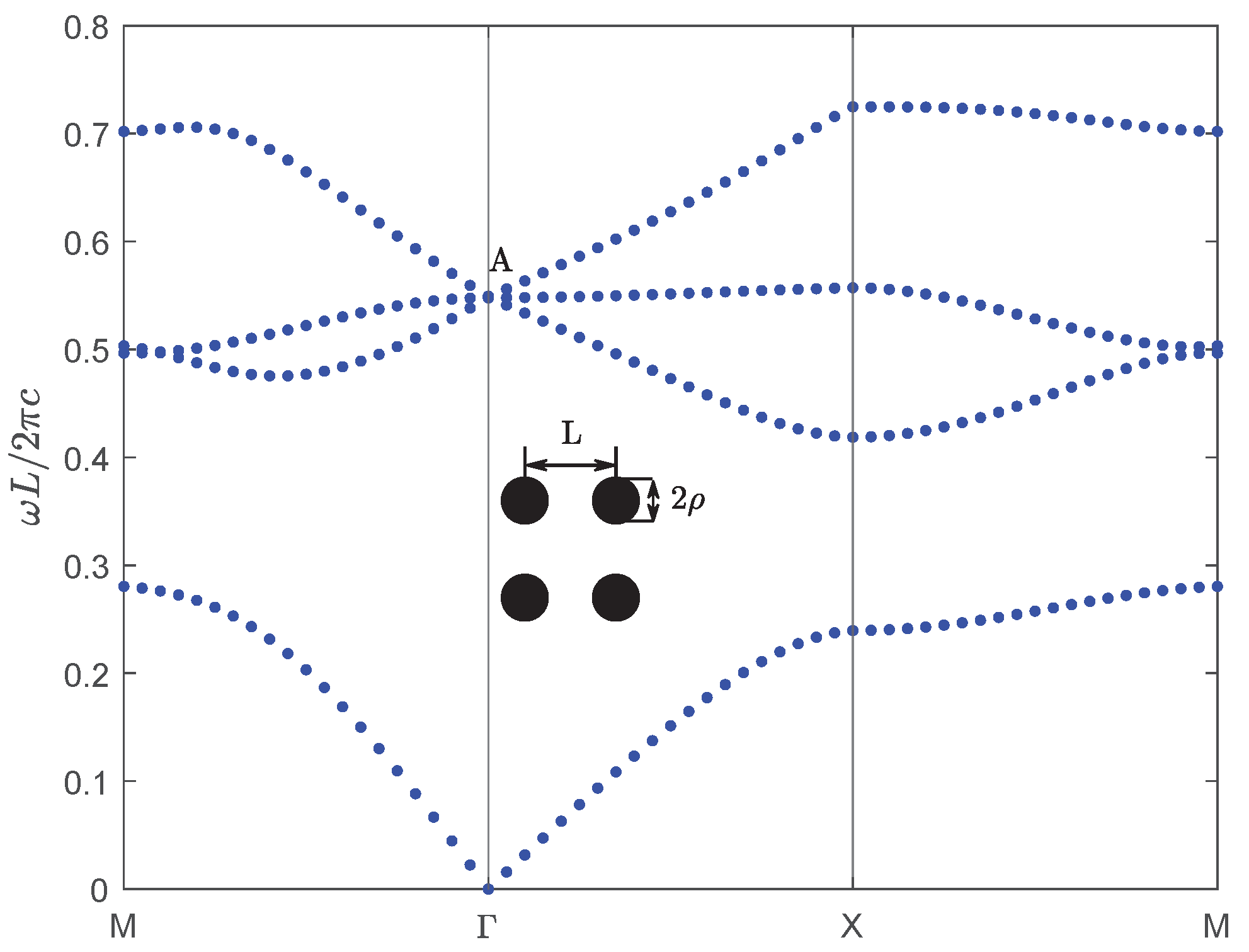
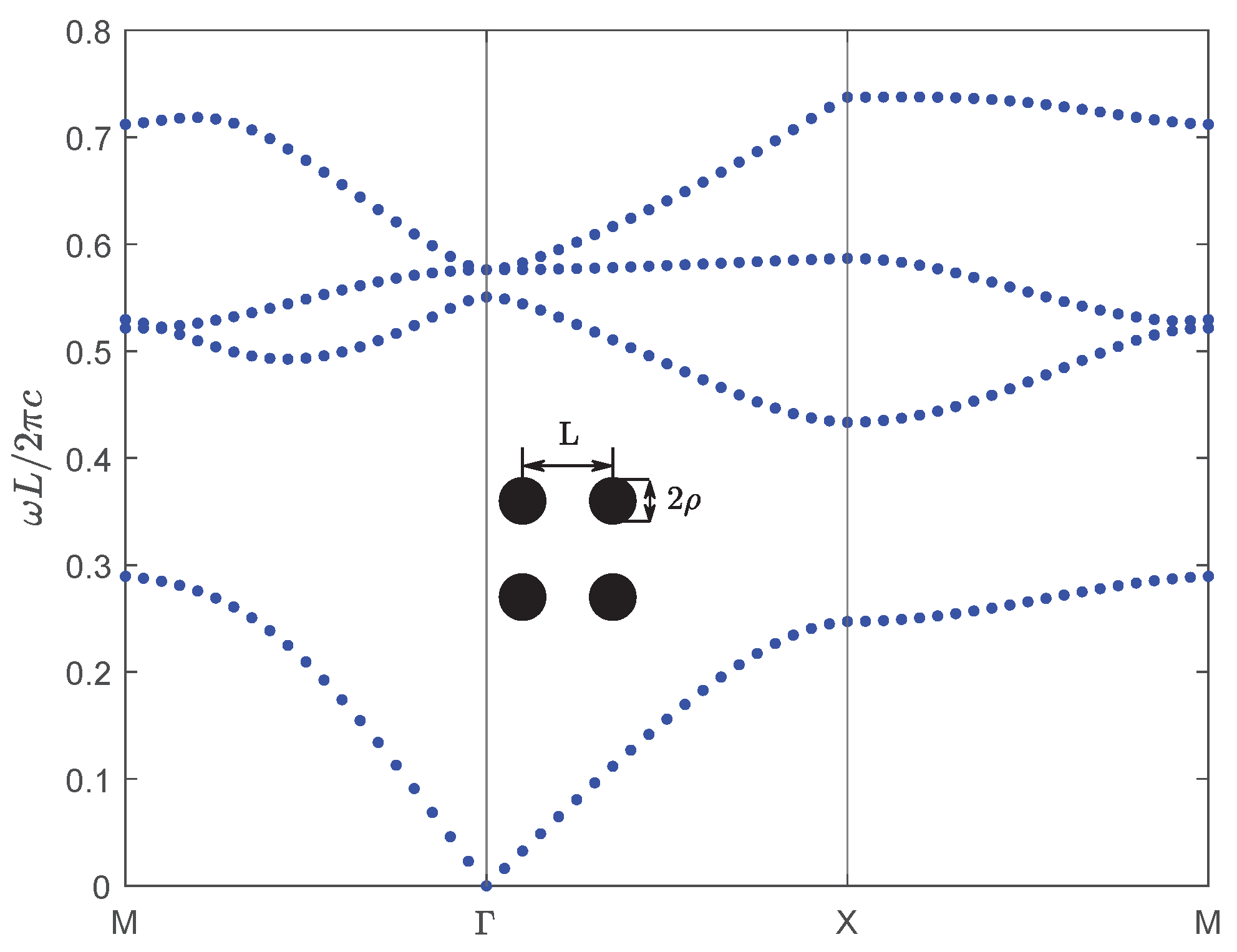
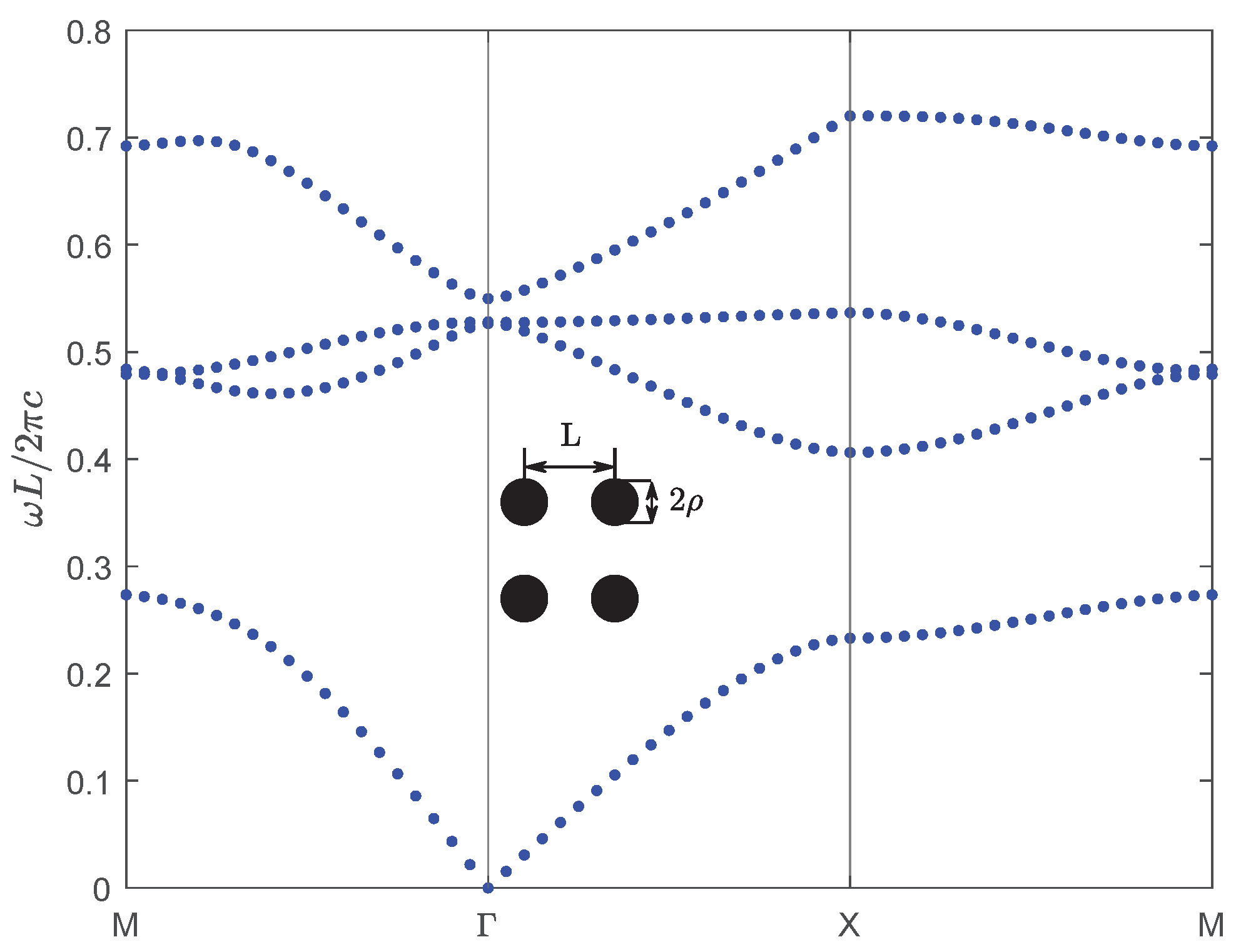
3. Numerical Calculation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zong, Y.X.; Xia, J.B. Photonic band structure of two-dimensional metal/dielectric photonic crystals. J. Phys. D Appl. Phys. 2015, 48, 355103. [Google Scholar] [CrossRef]
- Lu, S.; Li, W.; Guo, H.; Lu, M. Analysis of birefringent and dispersive properties of photonic crystal fibers. Appl. Opt. 2011, 50, 5798–5802. [Google Scholar] [CrossRef]
- Huang, X.; Lai, Y.; Hang, Z.H.; Zheng, H.; Chan, C.T. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nat. Mater. 2011, 10, 582–586. [Google Scholar] [CrossRef]
- Zhong, W.; Zhang, X. Acoustic analog of monolayer graphene and edge states. Phys. Lett. A 2011, 375, 3533–3536. [Google Scholar] [CrossRef]
- Wang, L.G.; Wang, Z.G.; Zhu, S.Y. Zitterbewegung of optical pulses near the Dirac point inside a negative-zero-positive index metamaterial. Europhys. Lett. 2009, 86, 47008. [Google Scholar] [CrossRef]
- Savović, S.; Ivanović, M.; Drljača, B.; Simović, A. Numerical Solution of the Sine–Gordon Equation by Novel Physics-Informed Neural Networks and Two Different Finite Difference Methods. Axioms 2024, 13, 872. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Yu, B. The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems. Commun. Math. Stat. 2018, 6, 1–12. [Google Scholar]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Pei, F.; Cao, F.; Ge, Y. A Novel Neural Network-Based Approach Comparable to High-Precision Finite Difference Methods. Axioms 2025, 14, 75. [Google Scholar] [CrossRef]
- Mazraeh, H.D.; Parand, K. GEPINN: An innovative hybrid method for a symbolic solution to the Lane-Emden type equation based on grammatical evolution and physics-informed neural networks. Astron. Comput. 2024, 48, 100846. [Google Scholar] [CrossRef]
- Mazraeh, H.D.; Parand, K. A three-stage framework combining neural networks and Monte Carlo tree search for approximating analytical solutions to the Thomas–Fermi equation. J. Comput. Sci. 2025, 87, 102582. [Google Scholar] [CrossRef]
- Mazraeh, H.D.; Parand, K. Approximate symbolic solutions to differential equations using a novel combination of Monte Carlo tree search and physics-informed neural networks approach. Eng. Comput. 2025, 1–29. [Google Scholar] [CrossRef]
- Mazraeh, H.D.; Parand, K. An innovative combination of deep Q-networks and context-free grammars for symbolic solutions to differential equations. Eng. Appl. Artif. Intell. 2025, 142, 109733. [Google Scholar] [CrossRef]
- Shi, S.; Chen, C.; Prather, D.W. Plane-wave expansion method for calculating band structure of photonic crystal slabs with perfectly matched layers. J. Opt. Soc. Am. A 2004, 21, 1769–1775. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Chen, C.; Prather, D.W. Second-order accurate FDTD space and time grid refinement method in three space dimensions. IEEE Photon. Technol. Lett. 2006, 18, 1237–1239. [Google Scholar] [CrossRef]
- Xiao, W.; Gong, B.; Sun, J.; Zhang, Z. Finite element calculation of photonic band structures for frequency dependent materials. J. Sci. Comput. 2021, 87, 27. [Google Scholar] [CrossRef]
- Malheiros-Silveira, G.N.; Hernandez-Figueroa, H.E. Prediction of Dispersion Relation and PBGs in 2-D PCs by Using Artificial Neural Networks. IEEE Photon. Technol. Lett. 2012, 24, 1799–1801. [Google Scholar] [CrossRef]
- Liu, L.; Shao, H.; Nan, D. Recurrent neural network model for computing largest and smallest generalized eigenvalue. Neurocomputing 2008, 71, 3589–3594. [Google Scholar] [CrossRef]
- Yi, Z.; Fu, Y.; Tang, H.J. Neural networks based approach for computing eigenvectors and eigenvalues of symmetric matrix. Comput. Math. Appl. 2004, 47, 1155–1164. [Google Scholar] [CrossRef]
- Kong, X.; Du, B.; Feng, X.; Luo, J. Unified and Self-Stabilized Parallel Algorithm for Multiple Generalized Eigenpairs Extraction. IEEE Trans. Signal Process. 2020, 68, 3644–3659. [Google Scholar] [CrossRef]
- Blake, B.; Cotler, J.; Pehlevan, C.; Zavatone-Veth, J.A. Dynamically Learning to Integrate in Recurrent Neural Networks. arXiv 2025, arXiv:2503.18754v1. [Google Scholar] [CrossRef]
- Tavakkoli, V.; Chedjou, J.C.; Kyamakya, K. A Novel Recurrent Neural Network-Based Ultra-Fast, Robust, and Scalable Solver for Inverting a “Time-Varying Matrix”. Sensors 2019, 19, 4002. [Google Scholar] [CrossRef]
- Tang, Y.; Li, J. Another neural network based approach for computing eigenvalues and eigenvectors of real skew-symmetric matrices. Comput. Math. Appl. 2010, 60, 1385–1392. [Google Scholar] [CrossRef]
- Tang, Y.; Li, J. Notes on “Recurrent neural network model for computing largest and smallest generalized eigenvalue”. Neurocomputing 2010, 73, 1006–1012. [Google Scholar] [CrossRef]
- Zhu, L.; Xu, W. The inverse eigenvalue problem of structured matrices from the design of Hopfield neural networks. Appl. Math. Comput. 2016, 273, 1–7. [Google Scholar] [CrossRef]
- Liu, L.; Wu, W. Dynamical system for computing largest generalized eigenvalue. Lect. Notes Comput. Sci. 2006, 3971, 399–404. [Google Scholar] [CrossRef]
- Liu, Y.; You, Z.; Cao, L. A recurrent neural network computing the largest imaginary or real part of eigenvalues of real matrices. Comput. Math. Appl. 2007, 53, 41–53. [Google Scholar] [CrossRef]
- Luo, R.B.; Zeng, W.; Wu, Y.D.; Jiang, W.L.; Tang, B.; Zhong, M.; Liu, Q.J. First-principles calculations on electronic, optical and photocatalytic properties of BiNbO4. Mater. Sci. Semicond. Process. 2022, 140, 106391. [Google Scholar] [CrossRef]
- Zhai, H.; Chen, B.; Luo, H.; Li, H.; Zheng, L.; Yang, J.; Liu, Z. The stability and dielectric performance of BiNbO4 prepared by citrate method assisting sintering process. Phys. Status Solidi A 2016, 213, 2525–2530. [Google Scholar] [CrossRef]


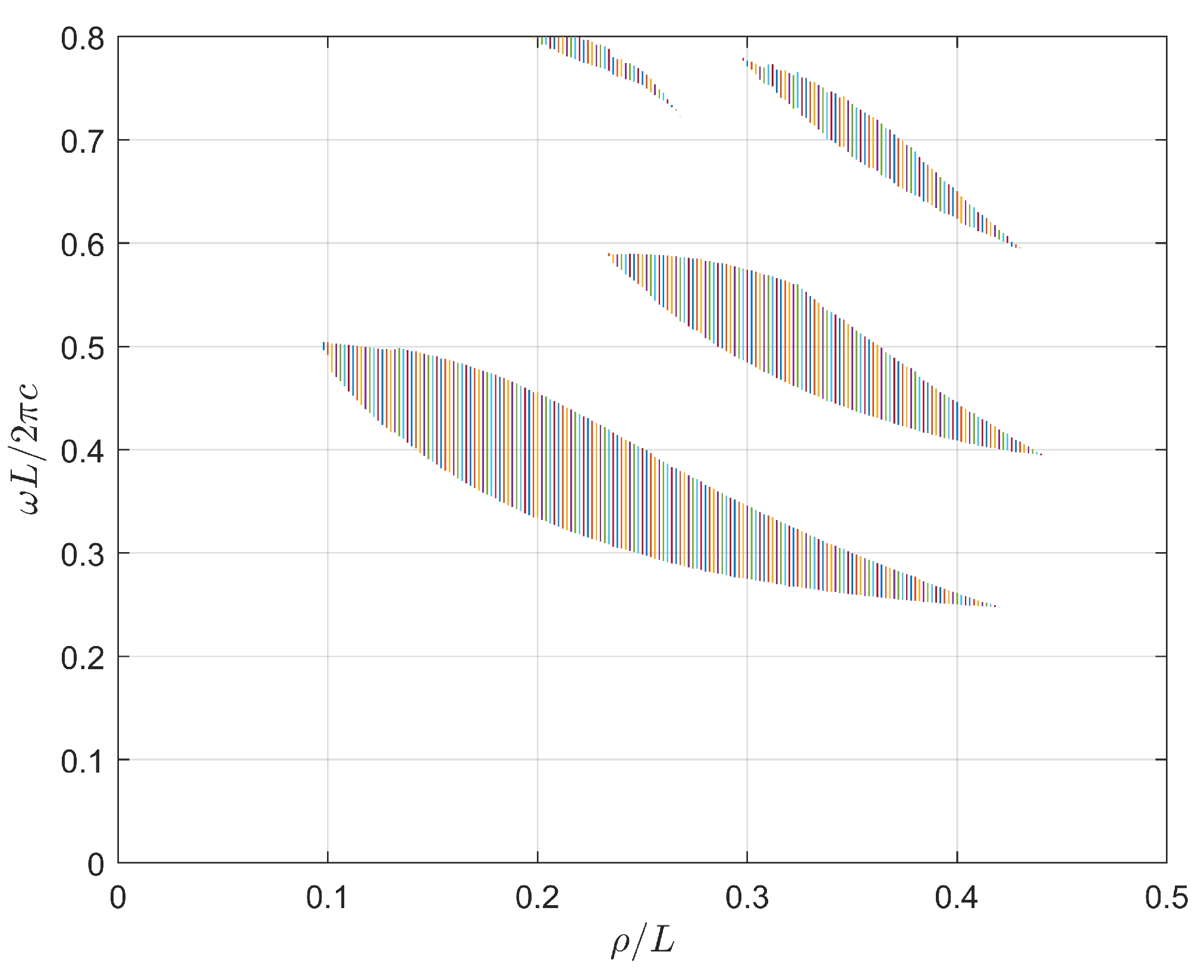
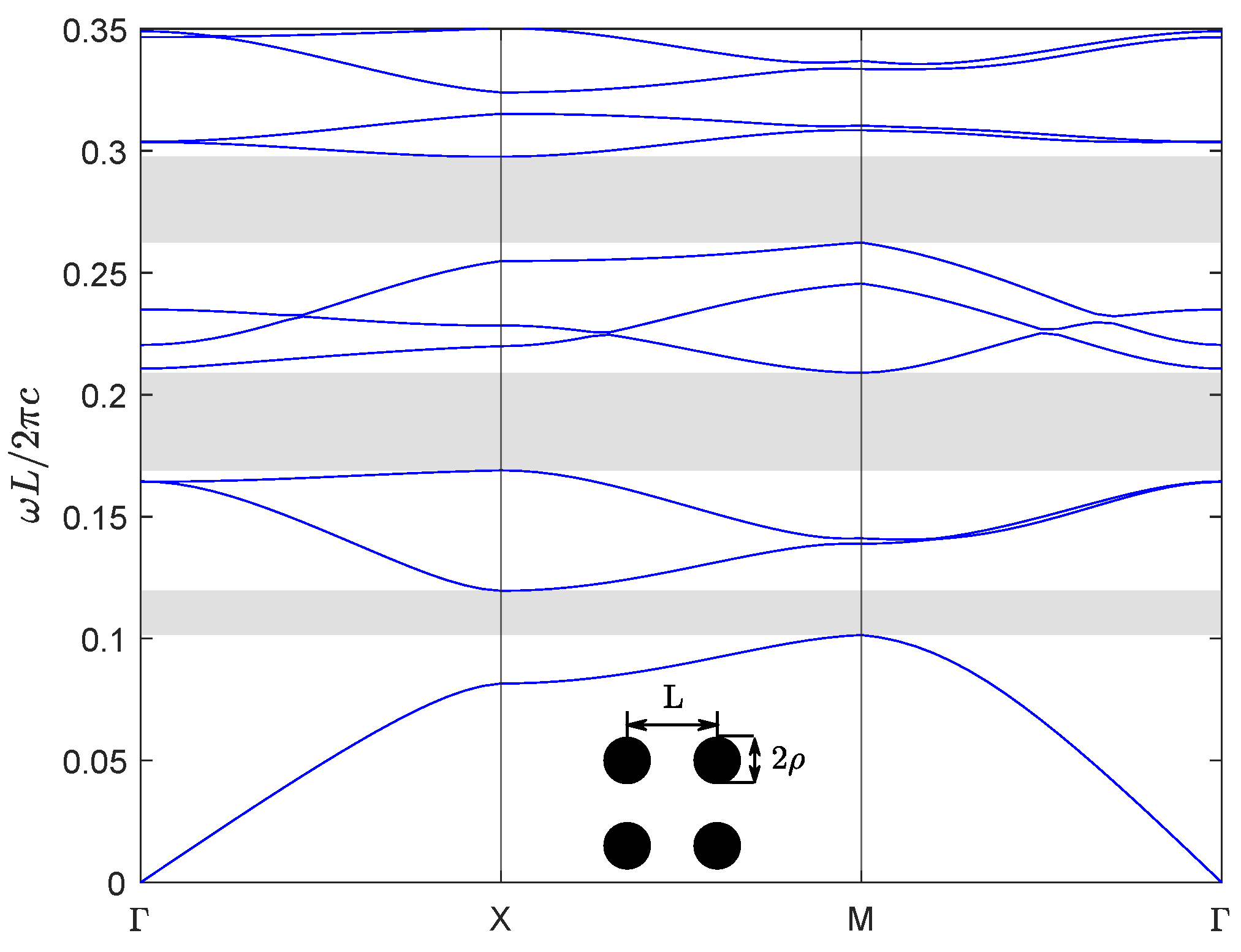
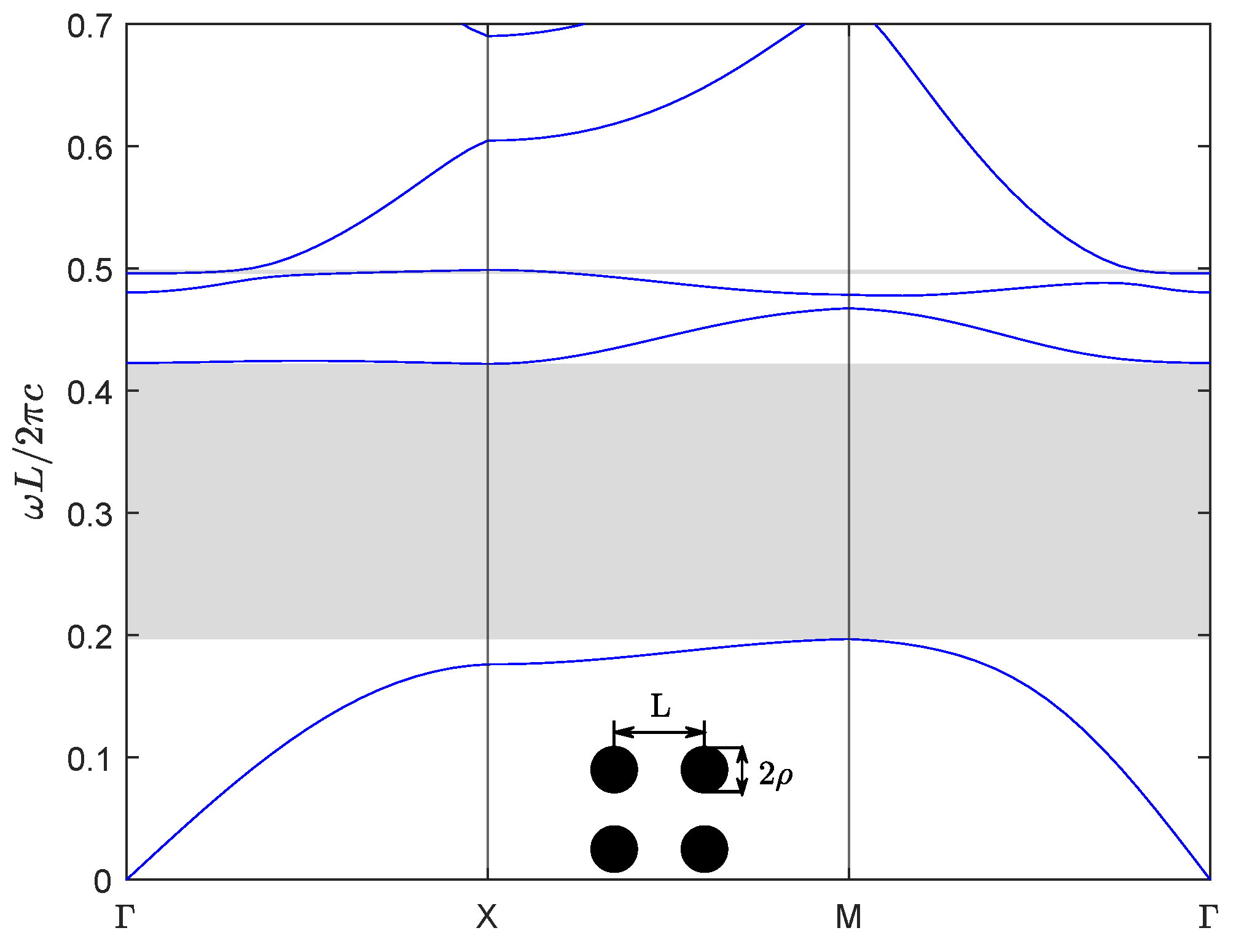
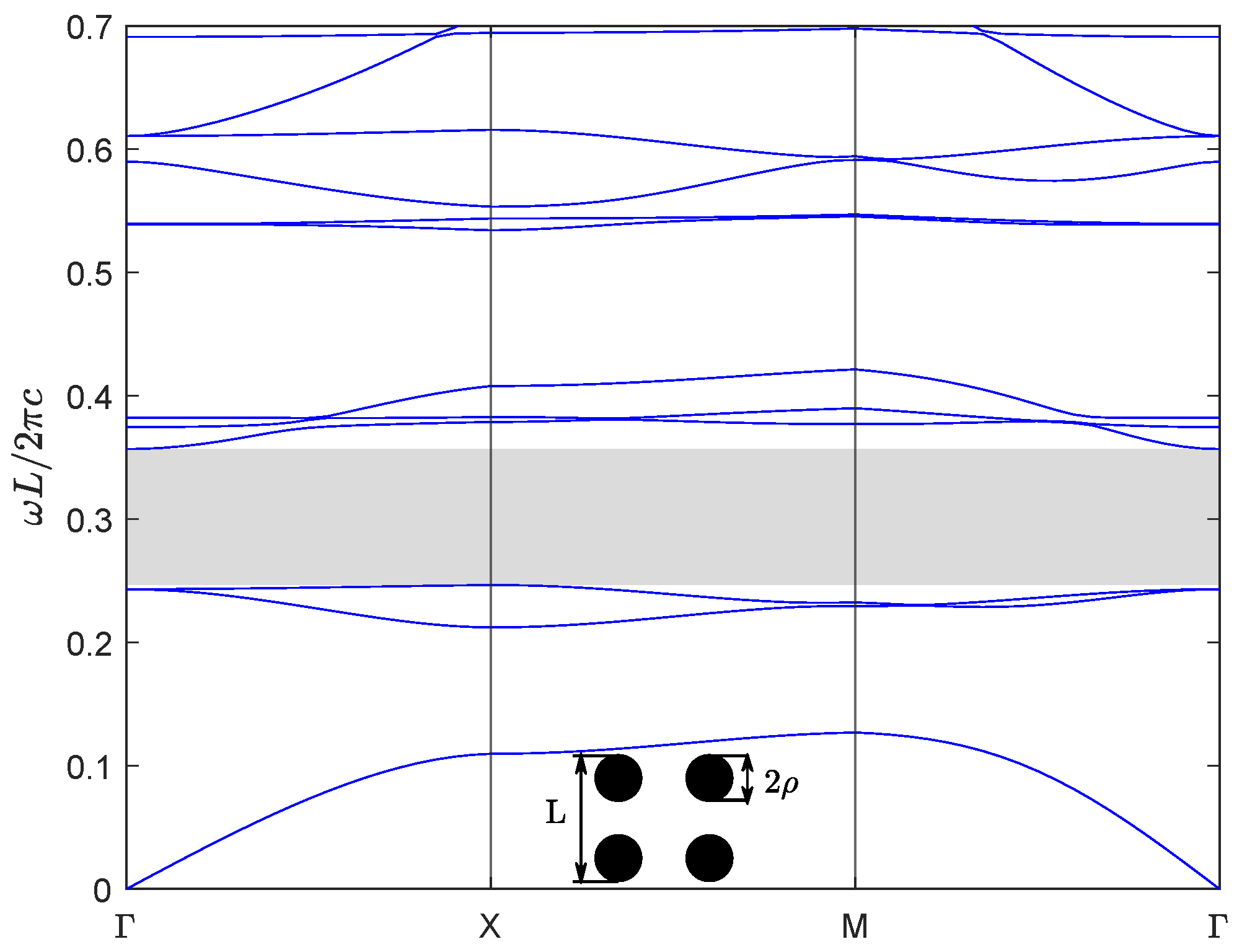

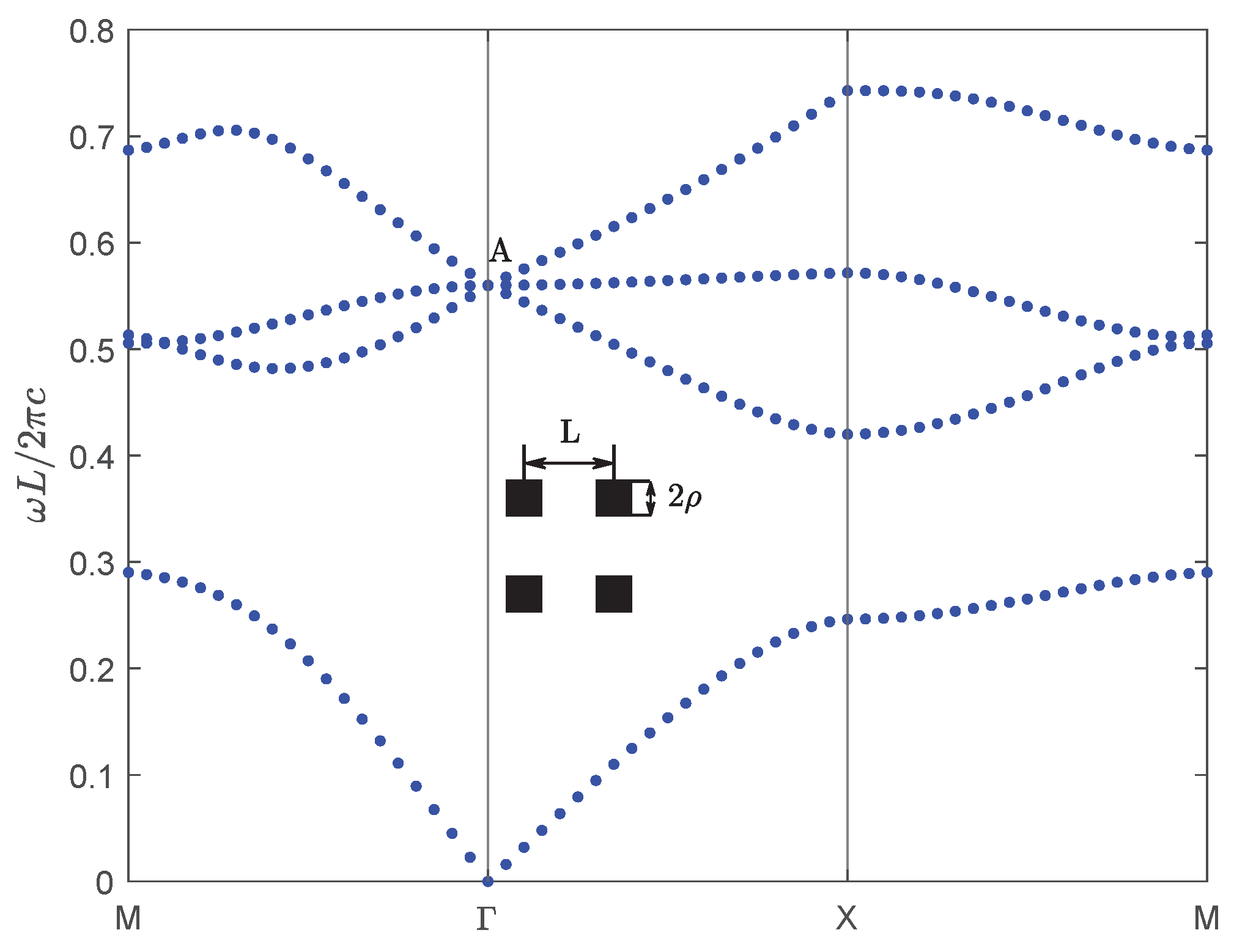
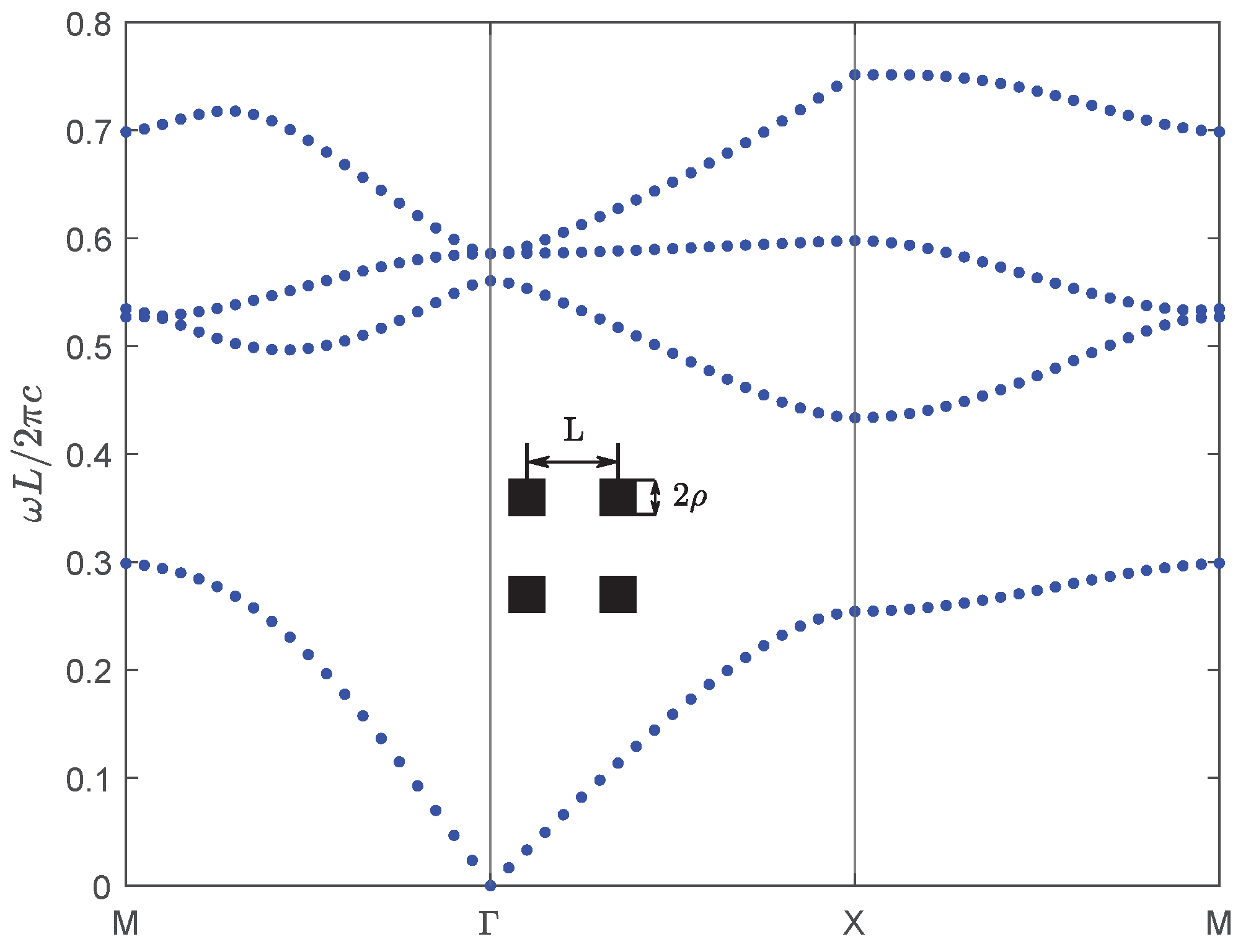
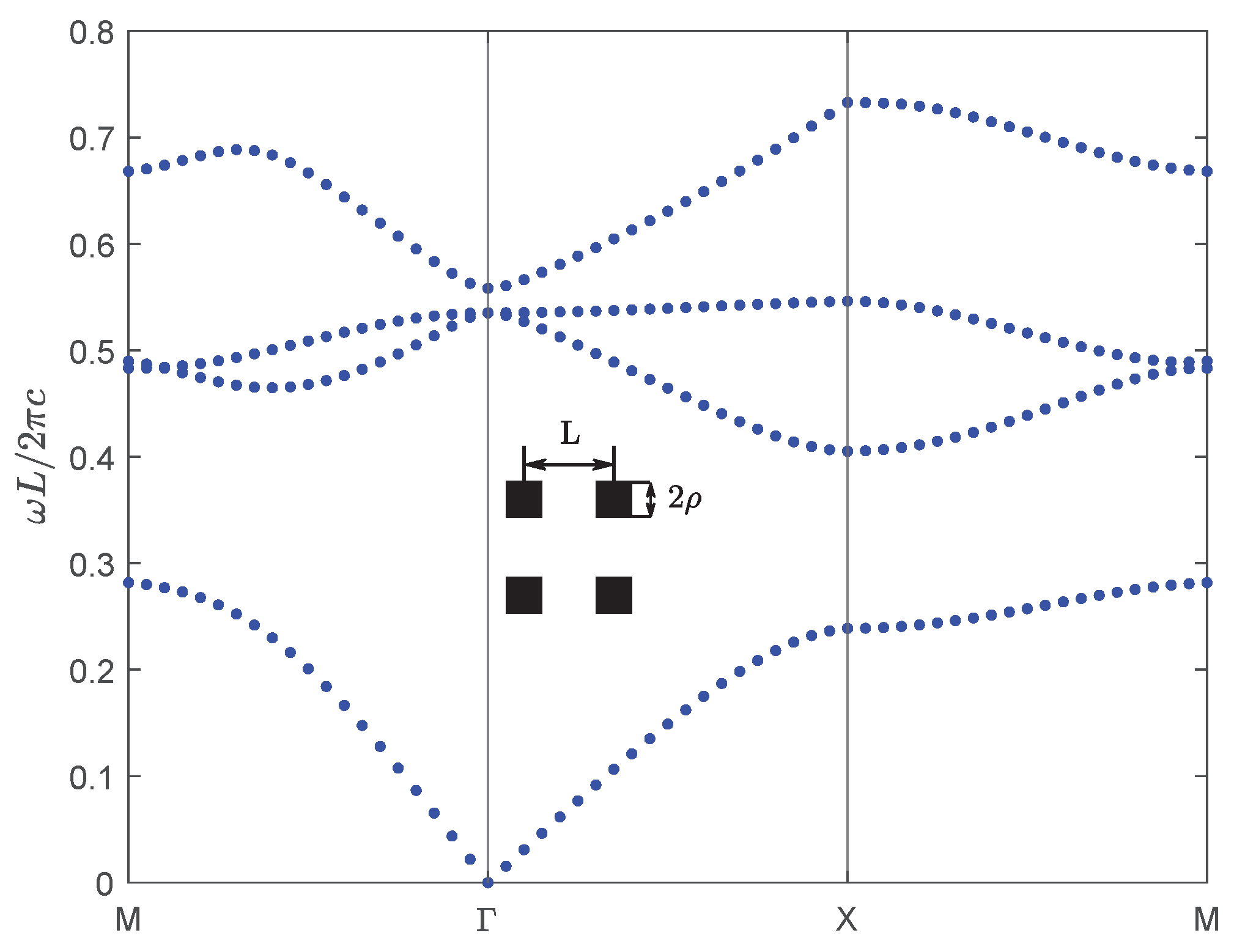

| Band | Band | ||
|---|---|---|---|
| 1 | 1.28 | 6 | 2.10 |
| 2 | 1.83 | 7 | 2.47 |
| 3 | 5.10 | 8 | 4.87 |
| 4 | 1.58 | 9 | 7.26 |
| 5 | 2.93 | 10 | 7.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yuan, J. Numerical Method for Band Gap Structure and Dirac Point of Photonic Crystals Based on Recurrent Neural Network. Axioms 2025, 14, 445. https://doi.org/10.3390/axioms14060445
Wang Y, Yuan J. Numerical Method for Band Gap Structure and Dirac Point of Photonic Crystals Based on Recurrent Neural Network. Axioms. 2025; 14(6):445. https://doi.org/10.3390/axioms14060445
Chicago/Turabian StyleWang, Yakun, and Jianhua Yuan. 2025. "Numerical Method for Band Gap Structure and Dirac Point of Photonic Crystals Based on Recurrent Neural Network" Axioms 14, no. 6: 445. https://doi.org/10.3390/axioms14060445
APA StyleWang, Y., & Yuan, J. (2025). Numerical Method for Band Gap Structure and Dirac Point of Photonic Crystals Based on Recurrent Neural Network. Axioms, 14(6), 445. https://doi.org/10.3390/axioms14060445






