Improving Stability and Reducing Vibrations of the Smooth and Discontinuous Oscillator Using a Proportional–Derivative Controller
Abstract
1. Introduction
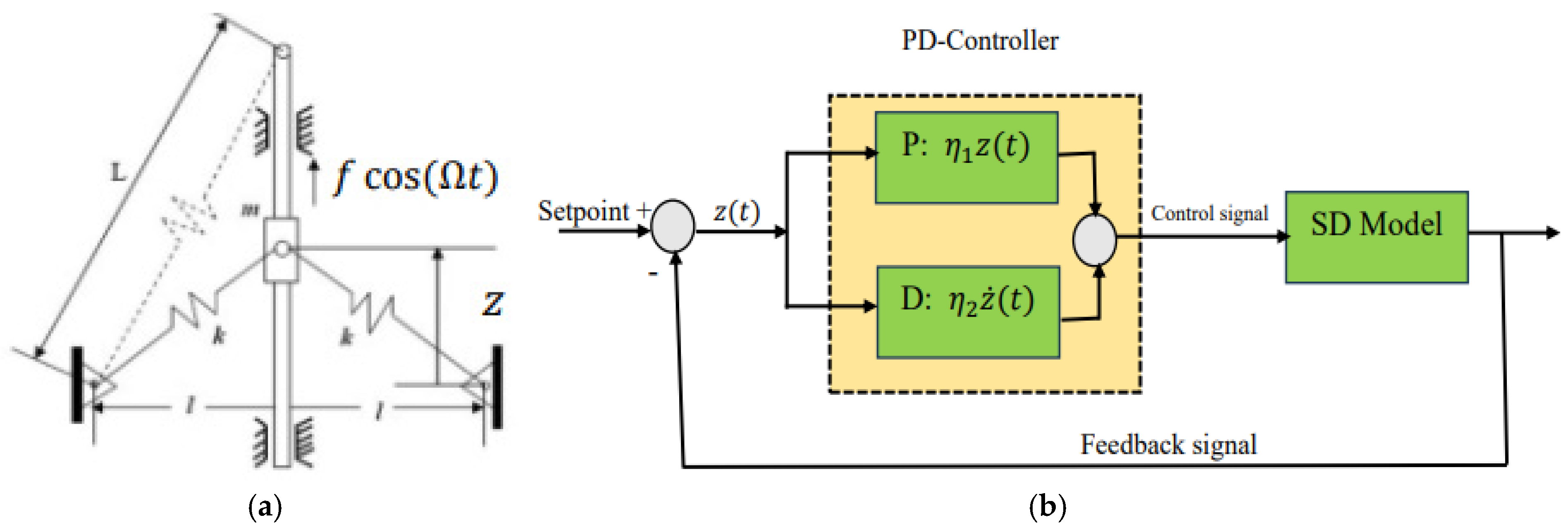
2. Smooth and Discontinuous Oscillator Model
3. Analytical Realization and Autonomous Amplitude-Phase Equations
4. Results and Discussions
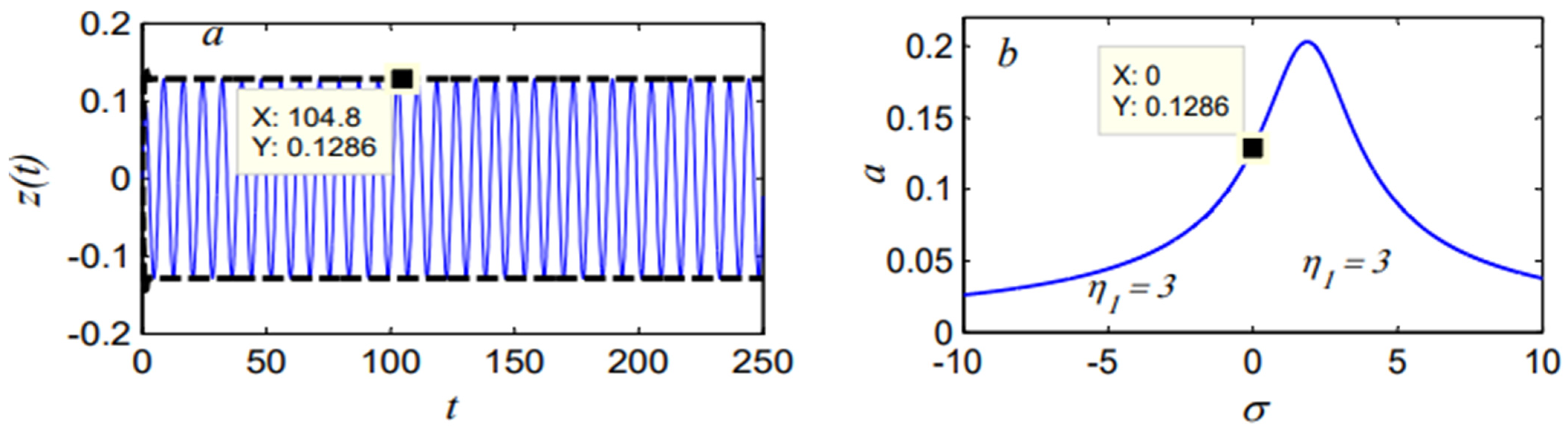
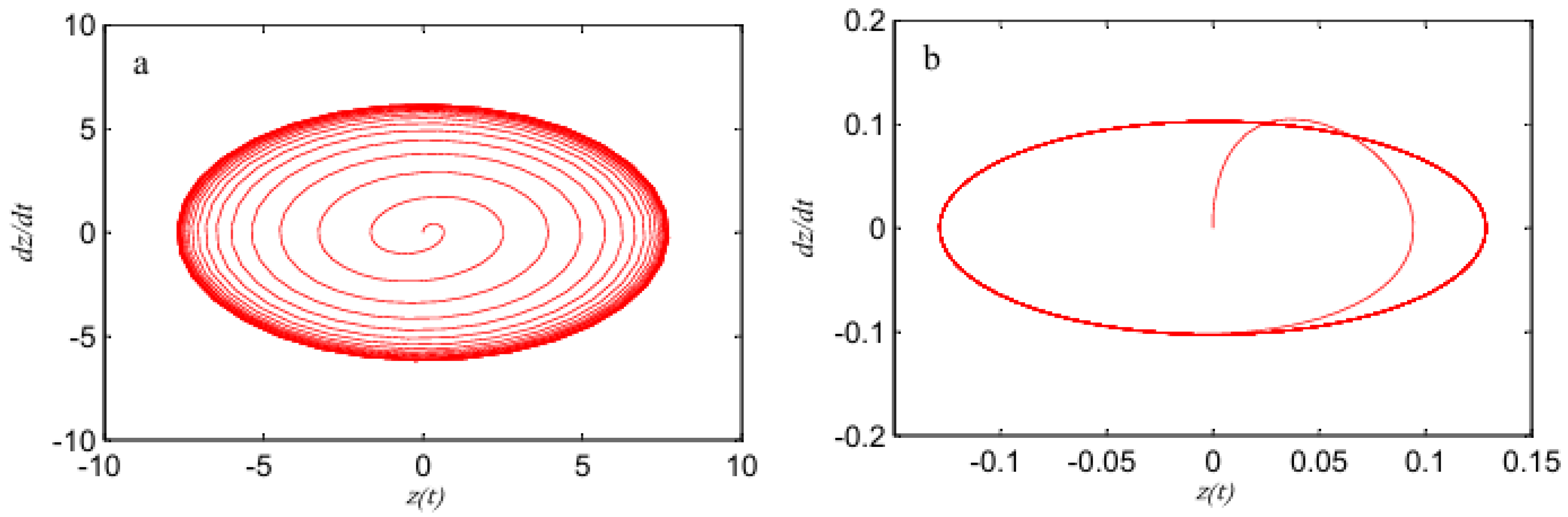
4.1. Uncontrolled Model
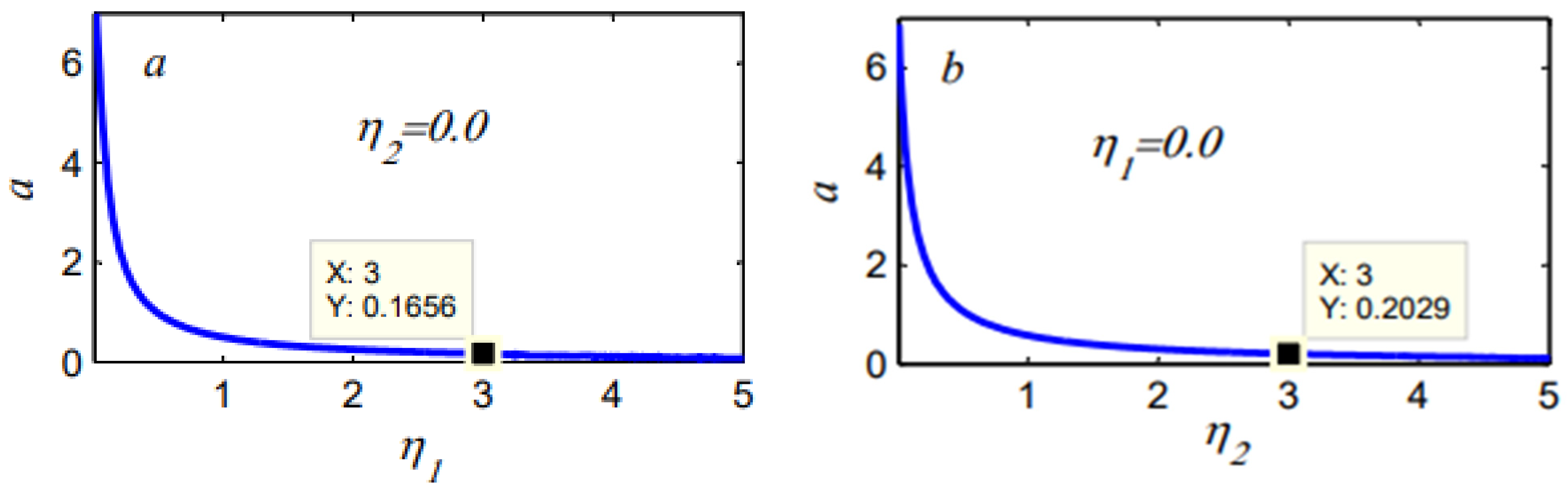
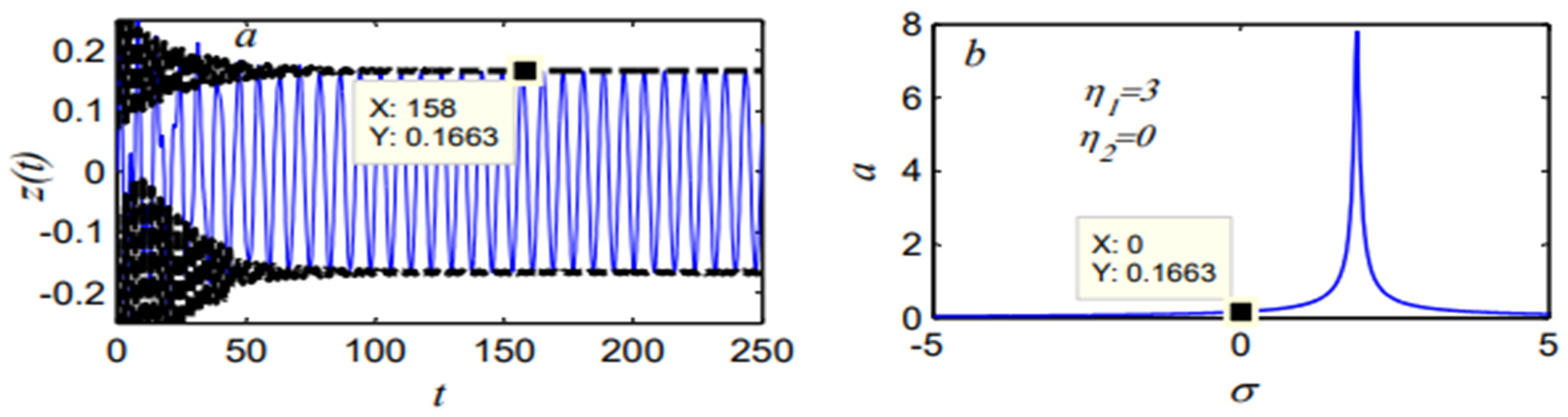
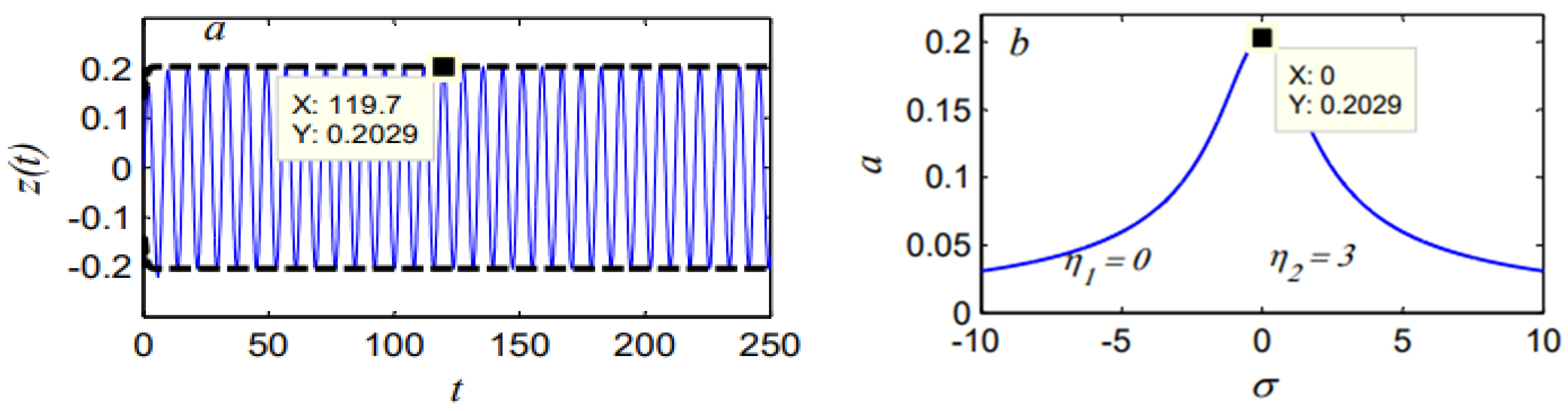
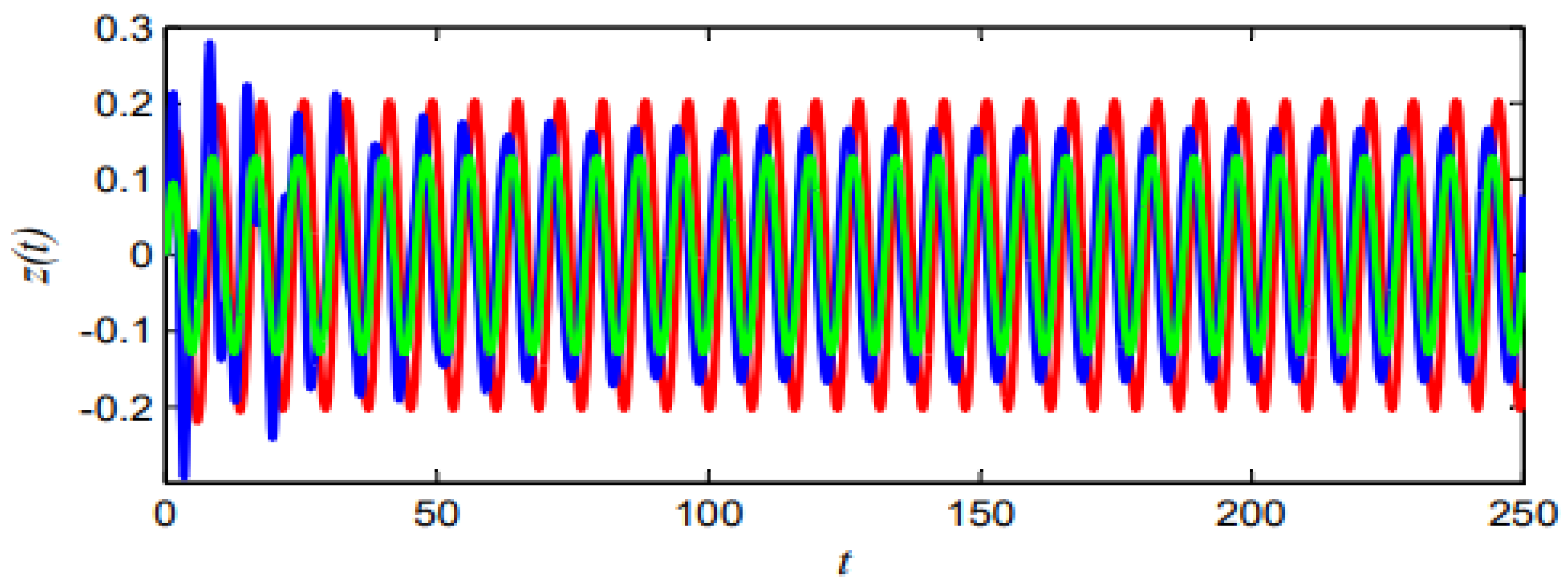
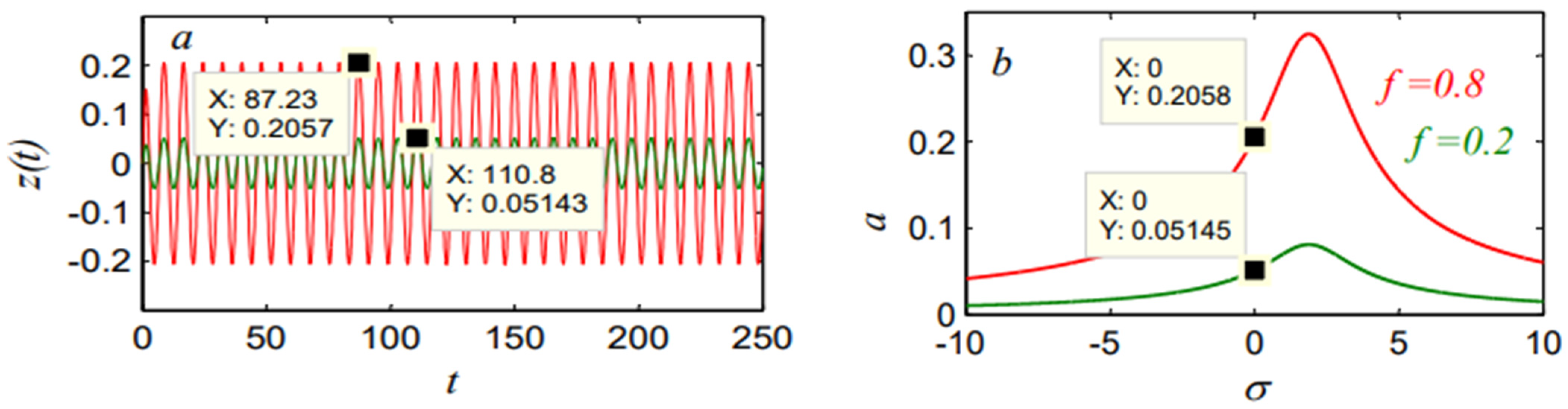
4.2. Controlled Model
4.3. Comparison with Previous Studies
5. Conclusions
- (1)
- Introducing the D-Controller to the SD-Oscillator has modified the damping coefficient;
- (2)
- Introducing the P-Controller to the SD-Oscillator has modulated the natural frequency;
- (3)
- The D-Controller and the P-Controller are not sufficient to suppress the vibrations of the SD Oscillator;
- (4)
- The PD-Controller combines features of the P-Controller and the D-Controller, so we used it to control the vibrating system;
- (5)
- The efficiency of the PD-Controller is about 61;
- (6)
- There is a high closeness between the numerical solutions (from time histories) and the approximate solutions (from perturbation analysis).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Position, velocity, and acceleration of the SD Oscillator. | |
| Linear damping coefficients of the SD Oscillator. | |
| Linear natural frequency of the SD Oscillator. | |
| The external force frequency of the SD Oscillator. | |
| The external force of the SD Oscillator.s | |
| Nonlinearity coefficients. | |
| The proportional gain of the SD Oscillator. | |
| The derivative gain of the SD Oscillator. |
References
- Zhao, Y.-Y.; Xu, J. Effects of delayed feedback control on nonlinear vibration absorber system. J. Sound Vib. 2007, 308, 212–230. [Google Scholar] [CrossRef]
- Xu, J.; Chung, K.W.; Zhao, Y.Y. Delayed saturation controller for vibration suppression in stainless-steel beam. Nonlinear Dyn. 2010, 62, 177–193. [Google Scholar] [CrossRef]
- Saeed, N.A.; El-Ganini, W.A.; Eissa, M. Nonlinear time delay saturation-based controller for suppression of nonlinear beam vibrations. Appl. Math. Model. 2013, 37, 8846–8864. [Google Scholar] [CrossRef]
- Liao, H. Stability analysis of duffing oscillator with time delayed and/or fractional derivatives. Mech. Based Des. Struct. Mach. 2016, 44, 283–305. [Google Scholar] [CrossRef]
- Andreaus, U.; Casini, P. Dynamics of friction oscillators excited by a moving base and/or driving force. J. Sound Vib. 2001, 245, 685–699. [Google Scholar] [CrossRef]
- Pia, P.F.; Nayfeh, A.H. Three-dimensional nonlinear vibrations of composite beams—I. Equations of motion. Nonlinear Dyn. 1990, 1, 477–502. [Google Scholar]
- Pia, P.F.; Nayfeh, A.H. Three-dimensional nonlinear vibrations of composite beams—II. Flapwise excitations. Nonlinear Dyn. 1991, 2, 1–34. [Google Scholar]
- Pia, P.F.; Nayfeh, A.H. Three-dimensional nonlinear vibrations of composite beams—III. Chordwise excitations. Nonlinear Dyn. 1991, 2, 137–156. [Google Scholar]
- Saeed, N.A.; Moatimid, G.M.; Elsabaa, F.M.F.; Ellabban, Y.Y. Time-delayed control to suppress a nonlinear system vibration utilizing the multiple scales homotopy approach. Arch. Appl. Mech. 2021, 91, 1193–1215. [Google Scholar] [CrossRef]
- Sun, X.; Xu, J.; Fu, J. The effect and design of time delay in feedback control for a nonlinear isolation system. Mech. Syst. Signal Process. 2017, 87, 206–217. [Google Scholar] [CrossRef]
- Mao, X.; Ding, W. Nonlinear dynamics and optimization of a vibration reduction system with time delay. Commun. Nonlinear Sci. Numer. Simul. 2023, 122, 107220. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, G.; Xiang, M.; Sun, H.; Wang, X.; Xie, X. Vibration control for the nonlinear resonant response of a piezoelectric elastic beam via time-delayed feedback. Smart Mater. Struct. 2019, 28, 095010. [Google Scholar] [CrossRef]
- El-Shourbagy, S.M.; Saeed, N.A.; Kamel, M.; Raslan, K.R.; Abouel Nasr, E.; Awrejcewicz, J. On the Performance of a Nonlinear Position-Velocity Controller to Stabilize Rotor-Active Magnetic-Bearings System. Symmetry 2021, 13, 2069. [Google Scholar] [CrossRef]
- El-Shourbagy, S.M.; Saeed, N.A.; Kamel, M.; Raslan, K.R.; Aboudaif, M.K.; Awrejcewicz, J. Control Performance, Stability Conditions, and Bifurcation Analysis of the Twelve-Pole Active Magnetic Bearings System. Appl. Sci. 2021, 11, 10839. [Google Scholar] [CrossRef]
- Abd El-Salam, M.N.; Amer, Y.A.; Darwesh, F.O. Effect of negative velocity feedback control on the vibration of a nonlinear dynamical system. Int. J. Dyn. Control 2023, 11, 2842–2855. [Google Scholar] [CrossRef]
- Kay, I. Optimal PI–PD Controller Design for Pure Integrating Processes with Time Delay. J. Control Autom. Electr. Syst. 2021, 32, 563–572. [Google Scholar] [CrossRef]
- Junior, A.D.S.; Birkner, C.; Jazar, R.N.; Marzbani, H. Coupled lateral and longitudinal controller for over-actuated vehicle in evasive maneuvering with sliding mode control strategy. IEEE Access 2023, 11, 33792–33811. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Problems in perturbation. Appl. Opt. 1986, 25, 3145. [Google Scholar]
- Santhosh, B.; Narayanan, S.; Padmanabhan, C. Discontinuity induced bifurcations in nonlinear systems. Procedia IUTAM 2016, 19, 219–227. [Google Scholar] [CrossRef][Green Version]
- Amer, Y.A.; Abdullah, R.E.; Khaled, O.M.; Mahdy, A.M.S.; El-Salam, M.N. Vibration Control of Smooth and Discontinuous Oscillator via Negative Derivative Feedback. J. Vib. Eng. Technol. 2024, 12, 2351–2363. [Google Scholar] [CrossRef]

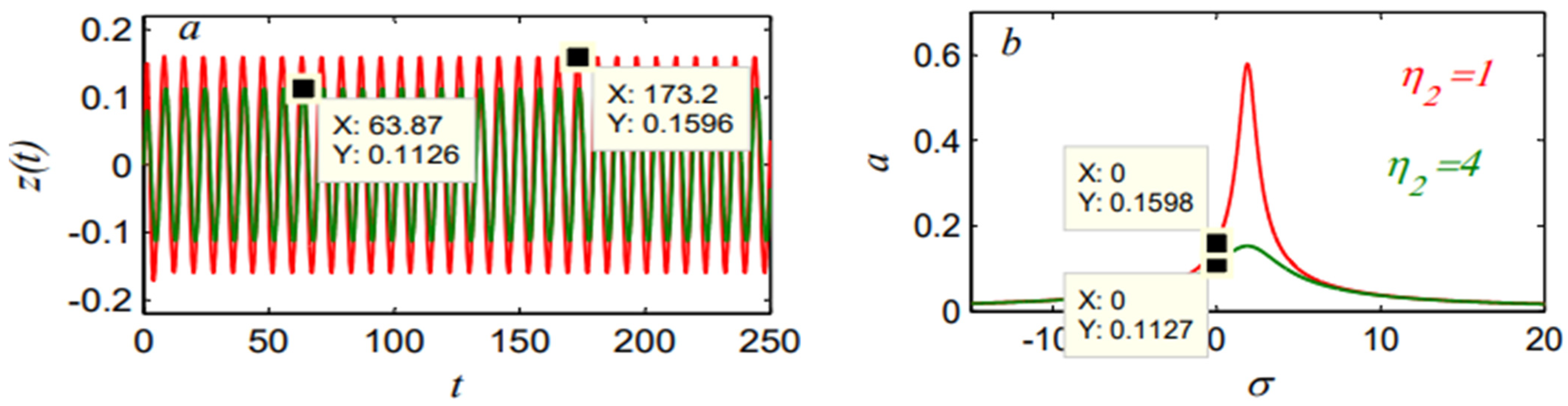
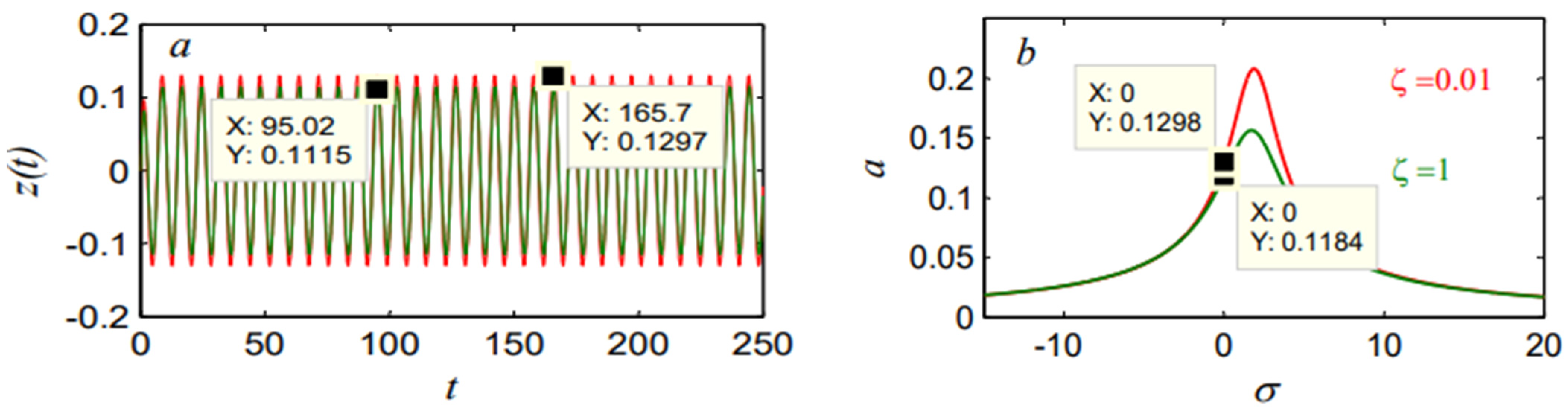
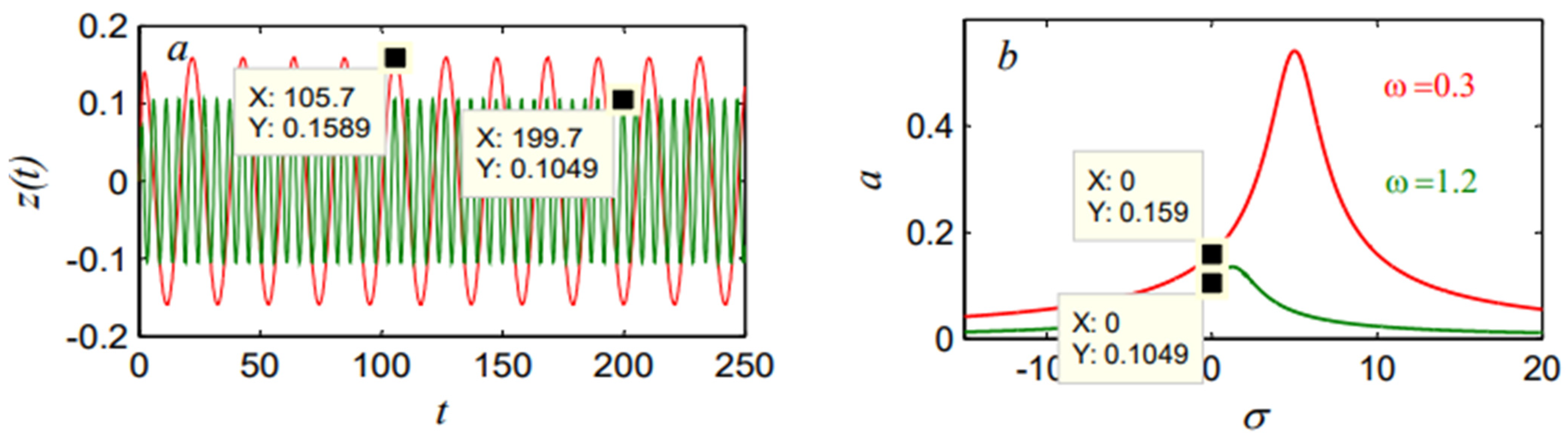


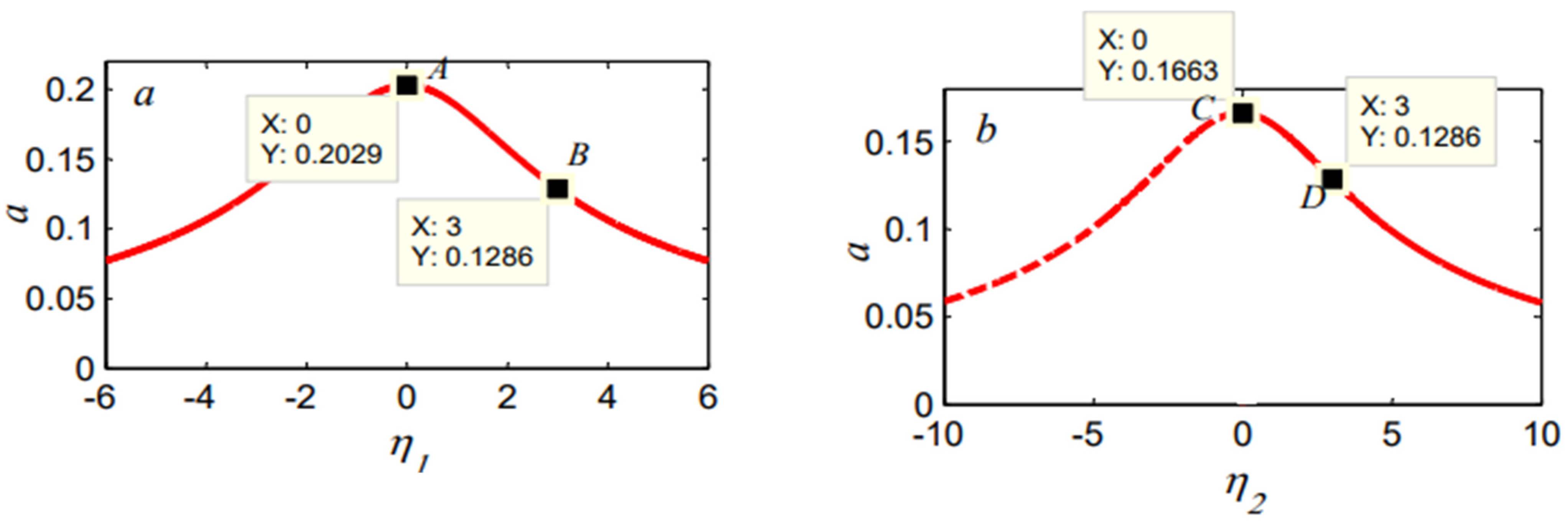
| Control Type | Amplitude Before the Controller | Amplitude After the Controller | Reduction Rate | |
|---|---|---|---|---|
| P-Controller | 7.76 | 0.1663 | 47 | 97.5% |
| D-Controller | 7.76 | 0.2029 | 38 | 97% |
| PD-Controller | 7.76 | 0.1286 | 61 | 98.5% |
| Feature | This Study | Ref. [20] |
|---|---|---|
| Control type | The PD-Controller | The NDF-Controller |
| The resonance case | The primary resonance | The Simultaneous resonance |
| Analytical method | The perturbation technique | The perturbation technique |
| Approximate solution | Up to the second approximation | Up to the first approximation |
| Signal Used | Position and its derivative | Negative derivative signal filtered by a second-order system |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd El-Salam, M.N.; Hussein, R.K.; El-Shourbagy, S.M. Improving Stability and Reducing Vibrations of the Smooth and Discontinuous Oscillator Using a Proportional–Derivative Controller. Axioms 2025, 14, 444. https://doi.org/10.3390/axioms14060444
Abd El-Salam MN, Hussein RK, El-Shourbagy SM. Improving Stability and Reducing Vibrations of the Smooth and Discontinuous Oscillator Using a Proportional–Derivative Controller. Axioms. 2025; 14(6):444. https://doi.org/10.3390/axioms14060444
Chicago/Turabian StyleAbd El-Salam, M. N., Rageh K. Hussein, and Sabry M. El-Shourbagy. 2025. "Improving Stability and Reducing Vibrations of the Smooth and Discontinuous Oscillator Using a Proportional–Derivative Controller" Axioms 14, no. 6: 444. https://doi.org/10.3390/axioms14060444
APA StyleAbd El-Salam, M. N., Hussein, R. K., & El-Shourbagy, S. M. (2025). Improving Stability and Reducing Vibrations of the Smooth and Discontinuous Oscillator Using a Proportional–Derivative Controller. Axioms, 14(6), 444. https://doi.org/10.3390/axioms14060444






