On the Strong Convergence of Combined Generalized Equilibrium and Fixed Point Problems in a Banach Space
Abstract
1. Introduction
- (i)
- Skew-symmetric, i.e.,
- (ii)
- Convex with respect to its second argument.
- (iii)
- Continuous.
2. Preliminaries
- (i)
- represents the set of fixed points of T, i.e.,
- (ii)
- A point is called an asymptotic fixed point of T if there exists a sequence that converges weakly to p and satisfies . The set of all asymptotic fixed points of T is denoted by .
- (iii)
- The mapping T is called relatively nonexpansive if
- (iv)
- T is closed if for any sequence such that and , it follows that .
- (i)
- (ii)
- H is monotone, i.e.,
- (iii)
- For each , we have
- (iv)
- For each , the mapping is convex and lower semicontinuous.
- (a)
- The set is nonempty for every .
- (b)
- The mapping is uniquely defined.
- (c)
- The operator is firmly nonexpansive, satisfying the inequality
- (d)
- The set of fixed points of coincides with the solution set of the CGEP , i.e.,
- (e)
- The solution set is both closed and convex.
3. Main Result
| Algorithm 1: Iterative algorithm for combined equilibrium problem |
Initialization: Let , and . |
Iterative Steps: Step 1. Calculate:
Step 2. For and return to Step 1. |
- Step 1. By applying Lemmas 3, 4, and 11, it follows that is a closed convex set. Consequently, the projection is well defined.
- Step 2. We establish that is a closed and convex set. According to its concept, is clearly both closed and convex. For all , we verify that maintains these properties. Initially, is closed and convex. The closedness of follows naturally, so it remains to demonstrate its convexity. From the concept of ,
- Step 3. We demonstrate that is contained within for all . Suppose that for ,
- Step 4. Next, prove that , , , , and are bounded. Additionally, we prove that exists, and .
- Step 5. We now demonstrate that as , the sequences , , , and , where is a point in .
- Step 6. We now demonstrate that . It remains to be shown that also belongs to .
- Step 7. Finally, we demonstrate that . Let in (24), and we have
| Algorithm 2: Iterative algorithm for equilibrium problem |
Initialization: Choose . Let and . |
Iterative Steps: Step 1. Calculate
Step 2. Let and return Step 1. |
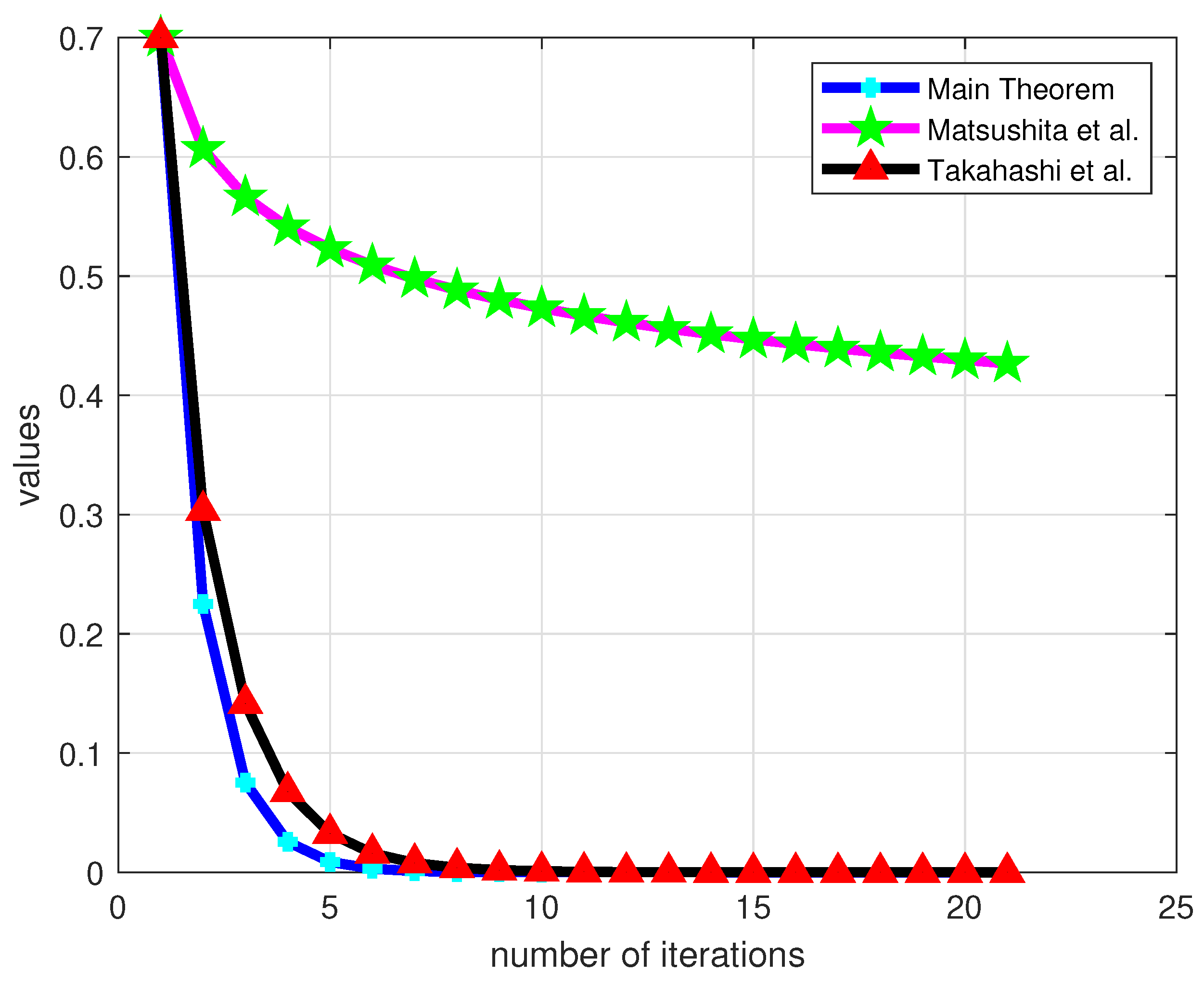
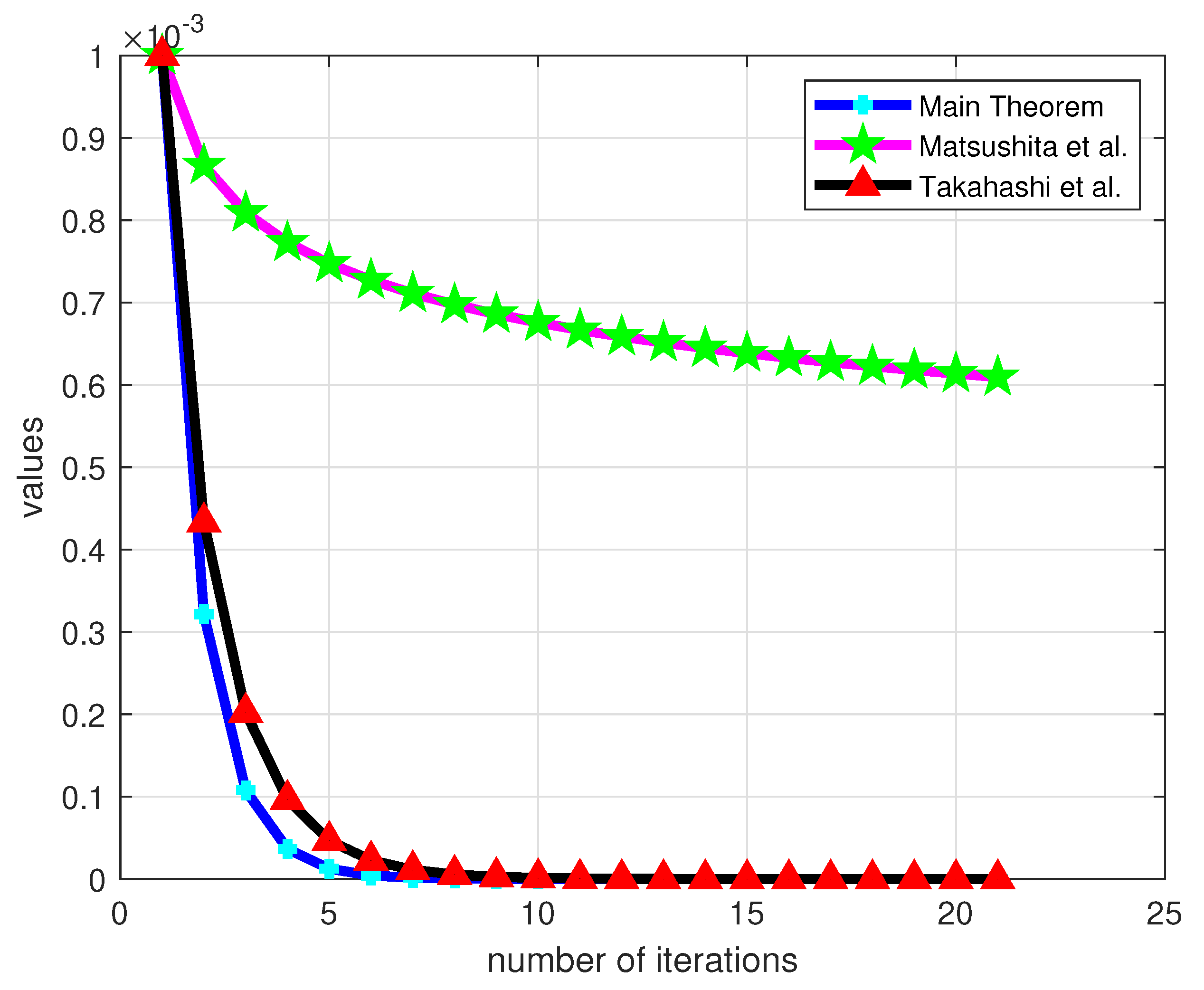
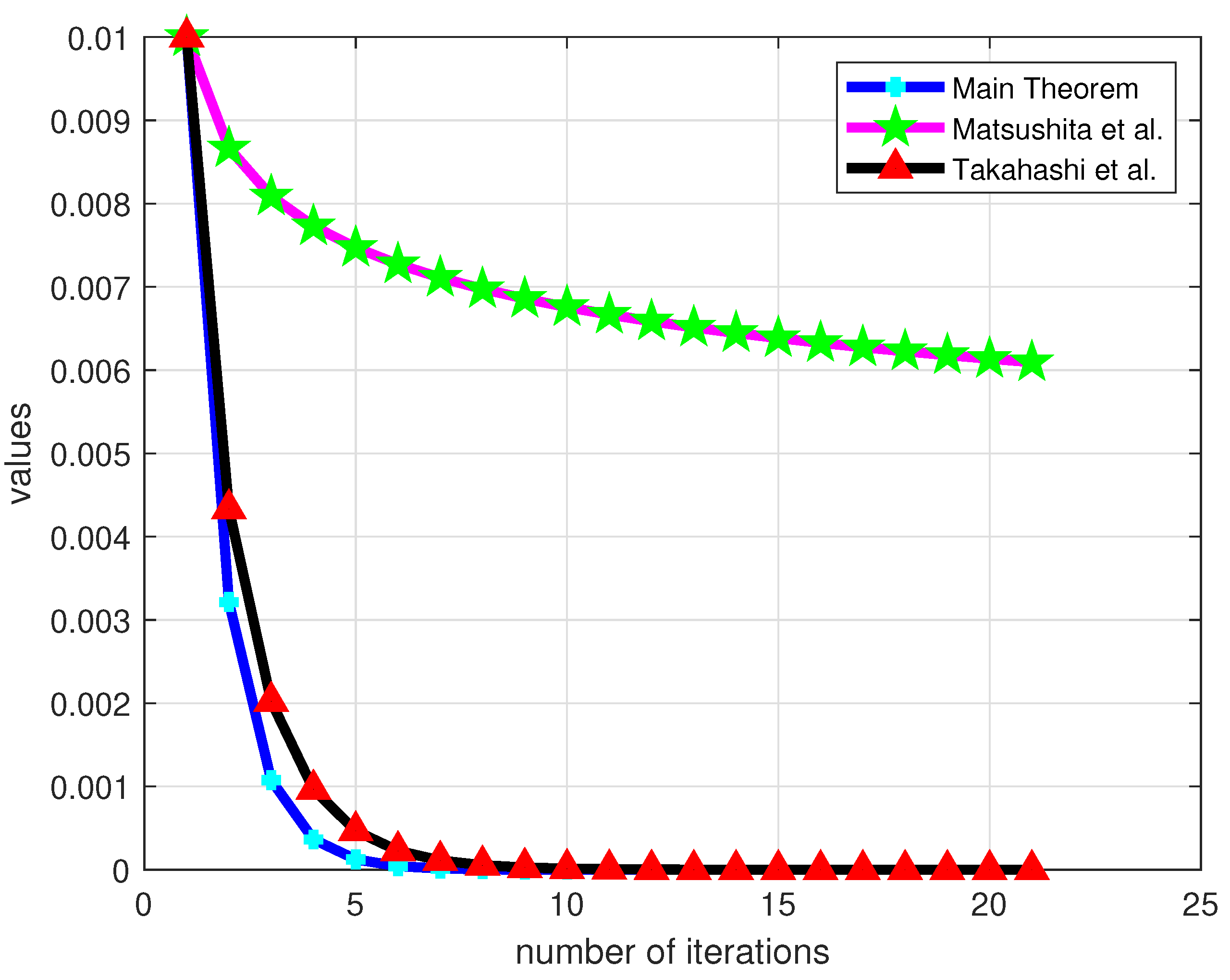
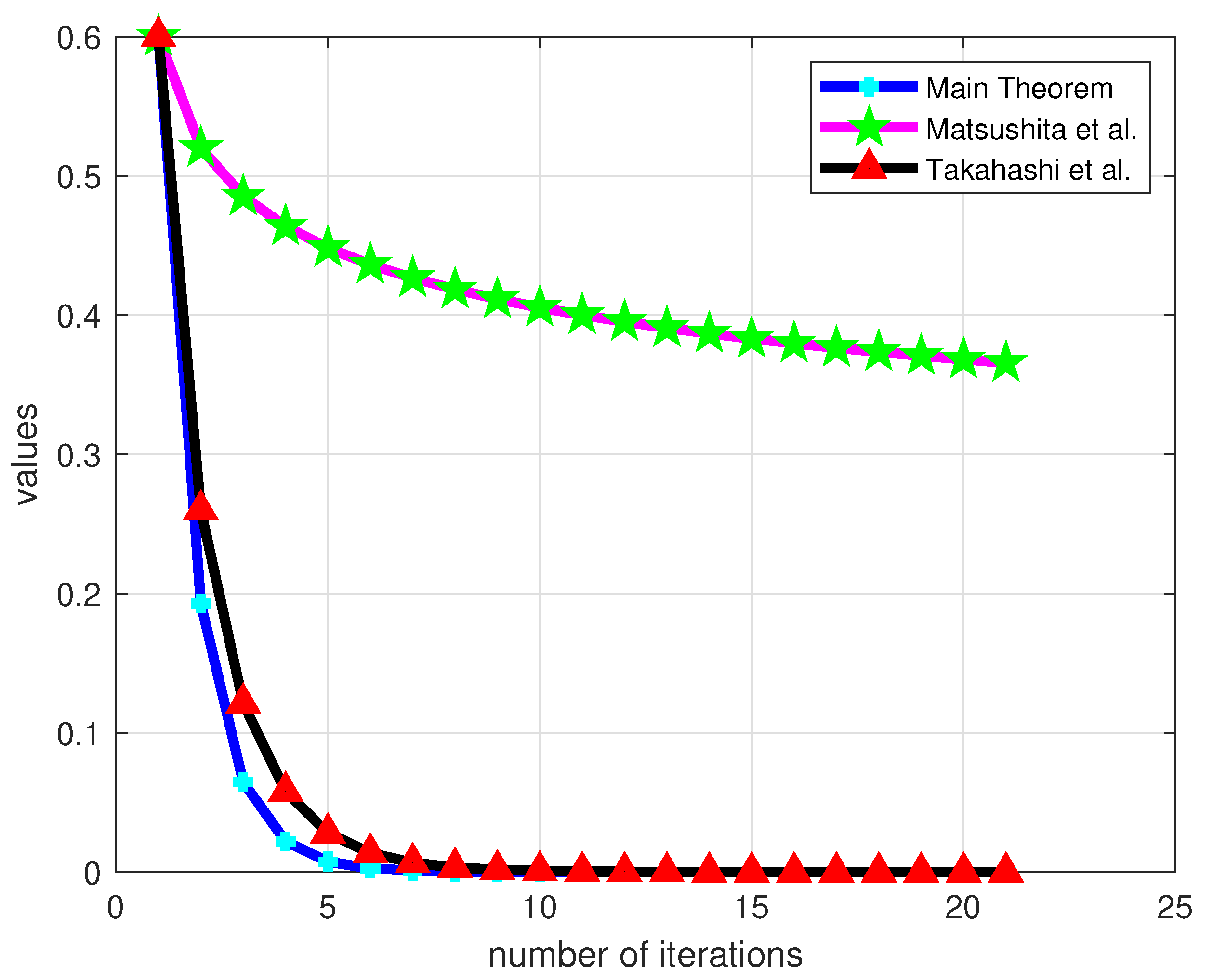
Numerical Example
4. Conclusions
- (i)
- In [25], a strong convergence theorem was established for nonexpansive mapping in a real Hilbert spaces. In contrast, our theorem extends this result to a broader context by proving convergence in two uniformly convex and uniformly smooth real Banach space and for two relatively nonexpansive mappings.
- (ii)
5. Future Direction
- (i)
- Our work is useful from a theoretical and applied perspective, as the result of this paper enables the further development of fixed point theory and its application by using the concept of a specific notion of Galois bundles, as has been introduced to describe fixed points [7].
- (ii)
- A direction for future research is also to extend the method proposed in this paper to an extragradient iterative approach for the considered problems, assuming that is monotone, within the framework of a uniformly smooth and strictly convex Banach space , which generalizes the setting of a uniformly smooth and uniformly convex Banach space.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Browder, F.E. Nonexpansive nonlinear operators in a Banach space. Proc. Natl. Acad. Sci. USA 1965, 54, 1041–1044. [Google Scholar] [CrossRef] [PubMed]
- Goebel, K.; Kirk, W.A. A fixed point theorem for asymptotically nonexpansive mappings. Proc. Am. Math. Soc. 1972, 35, 171–174. [Google Scholar] [CrossRef]
- Kirk, W.A. A fixed point theorem for mappings which do not increase distances. Am. Math. Mon. 1965, 72, 1004–1006. [Google Scholar] [CrossRef]
- Kirk, W.A. Fixed point theorems for non-Lipschitzian mappings of asymptotically non-expansive type. Isr. J. Math. 1974, 17, 339–346. [Google Scholar] [CrossRef]
- Byrne, C. A unified treatment for some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 2004, 20, 103–120. [Google Scholar] [CrossRef]
- Vanderlugt, A. Optical Signal Processing; John Wiley and Sons: New York, NY, USA, 1992. [Google Scholar]
- Sancho, A.A. Fixed points of automorphisms of the vector bundle moduli space over a compact Riemann surface. Mediterr. J. Math. 2024, 21, 20. [Google Scholar] [CrossRef]
- Banach, S. Sur les Operations dans les Ensembles Abstraits et Leur Application aux Equations Integrales. Fundam. Math. 1992, 3, 133–181. [Google Scholar] [CrossRef]
- Hitchin, N. Stable bundles and integrable systems. Duke Math. J. 1987, 54, 91–114. [Google Scholar] [CrossRef]
- Nash, J. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Younis, M.; Chen, L.; Singh, D. Recent Developments in Fixed Point Theory: Theoretical Foundations and Real-World Applications; Springer: Singapore, 2024. [Google Scholar] [CrossRef]
- Suwannaut, S.; Kangtunyakarn, A. The Combination of the set of solutions of equilibrium problem for convergence theorem of the set of fixed points of strictly pseudo-contractive mappings and variational inequalities problem. Fixed Point Theory Appl. 2013, 2013, 291. [Google Scholar] [CrossRef][Green Version]
- Bnouhachem, A. A hybrid iterative method for a combination of equilibria problem, a combination of variational inequality problems and a hierarchical fixed point problem. Fixed Point Theory Appl. 2014, 2014, 163. [Google Scholar] [CrossRef]
- Kazmi, K.R.; Ali, R.; Rizvi, S.H. Common solution of a combination of split general variational-like inequality problems and a family of generalized asymptotically nonexpansive mappings. J. Adv. Math. Stud. 2017, 10, 200–215. [Google Scholar]
- Khan, S.A.; Kazmi, K.R.; Cholamjiak, W.; Dutta, H. Convergence analysis for combination of equilibrium problem k-nonspreading set-valued mappings. Proyecciones J. Math. 2020, 39, 599–619. [Google Scholar] [CrossRef]
- Zuhovickii, S.I.; Poljak, R.A.; Primak, M.E. Two methods of search for equilibrium points of n-person concave games. Sov. Math. Dokl. 1969, 10, 279–282. [Google Scholar]
- Fan, K. Minimax Inequalities and Applications. In Inequality III; Shisha, O., Ed.; Academic Press: New York, NY, USA, 1972; pp. 103–113. [Google Scholar]
- Brézis, H.; Nirenberg, L.; Stampacchia, G. A remark on Ky Fan’s minimax principle. Boll. Dell’Unione Mat. Ital. 1972, 6, 293–300. [Google Scholar]
- Blum, E.; Oettli, W. From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63, 123–145. [Google Scholar]
- Marino, G.; Colao, V.; Muglia, L.; Yao, Y. Krasnoselski-Mann iteration for hierarchical fixed-points and equilibrium problem. Bull. Aust. Math. Soc. 2009, 79, 187–200. [Google Scholar] [CrossRef]
- Daniele, P.; Giannessi, F.; Mougeri, A. (Eds.) Equilibrium Problems and Variational Models; Nonconvex Optimization and its Application; Kluwer Academic Publications: Norwell, MA, USA, 2003; Volume 68. [Google Scholar]
- Moudafi, A. Second order differential proximal methods for equilibrium problems. J. Inequalities Pure Appl. Math. 2003, 4, 18. [Google Scholar]
- Hartman, P.; Stampacchia, G. On some non-linear elliptic differential-functional equation. Acta Math. 1966, 115, 271–310. [Google Scholar] [CrossRef]
- Korpelevich, G.M. The extragradient method for finding saddle points and other problems. Matecon 1976, 12, 747–756. [Google Scholar]
- Nadezhkina, N.; Takahashi, W. Strong convergence theorem by a hybrid method for nonexpansive mappings and Lipschitz continuous monotone mapping. SIAM J. Optim. 2006, 16, 1230–1241. [Google Scholar] [CrossRef]
- Ceng, L.C.; Hadjisavvas, N.; Wong, N.C. Strong convergence theorem by a hybrid extragradient-like approximation method for variational inequalities and fixed point problems. J. Glob. Optim. 2010, 46, 635–646. [Google Scholar] [CrossRef]
- Ceng, L.C.; Guu, S.M.; Yao, J.C. Finding common solution of variational inequality, a general system of variational inequalities and fixed point problem via a hybrid extragradient method. Fixed Point Theory Appl. 2011, 2011, 1–22. [Google Scholar] [CrossRef]
- Ceng, L.C.; Wang, C.Y.; Yao, J.C. Strong convergence theorems by a relaxed extragradient method for a general system of variational inequalities. Math. Methods Oper. Res. 2008, 67, 375–390. [Google Scholar] [CrossRef]
- Farid, M.; Ali, R.; Cholamjiak, W. An inertial iterative algorithm to find common solution of a split generalized equilibrium and a variational inequality problem in Hilbert spaces. J. Math. 2021, 2021, 3653807. [Google Scholar] [CrossRef]
- Rouhani, B.D.; Kazmi, K.R.; Farid, M. Common solutions to some systems of variational inequalities and fixed point problems. Fixed Point Theory 2017, 18, 167–190. [Google Scholar] [CrossRef]
- Matsushita, S.; Takahashi, W. Weak and strong convergence theorems for relatively nonexpansive mappings in Banach spaces. Fixed Point Theory Appl. 2004, 2004, 37–47. [Google Scholar] [CrossRef]
- Takahashi, W.; Zembayashi, K. Strong and weak convergence theorem for equilibrium problems and relatively nonexpansive mmapings in Banach spaces. Nonlinear Anal. 2009, 70, 45–57. [Google Scholar] [CrossRef]
- Kamimura, S.; Takahashi, W. Strong convergence of a proximal-type algorithim in a Banach space. SIAM J. Optim. 2002, 13, 938–945. [Google Scholar] [CrossRef]
- Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Nakajo, K. Strong convergence for gradient projection method and relatively nonexpansive mappings in Banach spaces. Appl. Math. Comput. 2017, 271, 251–258. [Google Scholar] [CrossRef]
- Zhang, S. Generalized mixed equilibrium problem in Banach spaces. Appl. Math. Mech. 2009, 30, 1105–1112. [Google Scholar] [CrossRef]
- Alber, Y.I. Metric and generalized projection operators in Banach spaces: Properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type; Dekker: New York, NY, USA, 1996; pp. 15–50. [Google Scholar]
| No. of Iterations | Main Theorem | Takahashi et al. [32] | Matsushita [31] |
|---|---|---|---|
| cpu Time (in seconds) | cpu Time (in seconds) | cpu Time (in seconds) | |
| 1 | 0.225082 | 0.303333 | 0.606667 |
| 2 | 0.075319 | 0.141556 | 0.566222 |
| 3 | 0.025535 | 0.067632 | 0.541057 |
| 4 | 0.008713 | 0.032689 | 0.523022 |
| 5 | 0.002984 | 0.015909 | 0.509074 |
| 6 | 0.001025 | 0.007778 | 0.497762 |
| 7 | 0.000353 | 0.003815 | 0.488280 |
| 8 | 0.000121 | 0.001876 | 0.480142 |
| 9 | 0.000042 | 0.000924 | 0.473029 |
| 10 | 0.000014 | 0.000456 | 0.466722 |
| 11 | 0.000005 | 0.000225 | 0.461065 |
| 12 | 0.000002 | 0.000111 | 0.455942 |
| 13 | 0.000001 | 0.000055 | 0.451266 |
| 14 | 0.000000 | 0.000027 | 0.446968 |
| 15 | 0.000000 | 0.000014 | 0.442995 |
| No. of Iterations | Main Theorem | Takahashi et al. [32] | Matsushita [31] |
|---|---|---|---|
| cpu Time (in seconds) | cpu Time (in seconds) | cpu Time (in seconds) | |
| 1 | 0.000322 | 0.000433 | 0.000867 |
| 2 | 0.000108 | 0.000202 | 0.000809 |
| 3 | 0.000036 | 0.000097 | 0.000773 |
| 4 | 0.000012 | 0.000047 | 0.000747 |
| 5 | 0.000004 | 0.000023 | 0.000727 |
| 6 | 0.000001 | 0.000011 | 0.000711 |
| 7 | 0.000001 | 0.000005 | 0.000698 |
| 8 | 0.000000 | 0.000003 | 0.000686 |
| 9 | 0.000000 | 0.000001 | 0.000676 |
| 10 | 0.000000 | 0.000001 | 0.000667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlNemer, G.; Ali, R.; Farid, M. On the Strong Convergence of Combined Generalized Equilibrium and Fixed Point Problems in a Banach Space. Axioms 2025, 14, 428. https://doi.org/10.3390/axioms14060428
AlNemer G, Ali R, Farid M. On the Strong Convergence of Combined Generalized Equilibrium and Fixed Point Problems in a Banach Space. Axioms. 2025; 14(6):428. https://doi.org/10.3390/axioms14060428
Chicago/Turabian StyleAlNemer, Ghada, Rehan Ali, and Mohammad Farid. 2025. "On the Strong Convergence of Combined Generalized Equilibrium and Fixed Point Problems in a Banach Space" Axioms 14, no. 6: 428. https://doi.org/10.3390/axioms14060428
APA StyleAlNemer, G., Ali, R., & Farid, M. (2025). On the Strong Convergence of Combined Generalized Equilibrium and Fixed Point Problems in a Banach Space. Axioms, 14(6), 428. https://doi.org/10.3390/axioms14060428