Involutions of the Moduli Space of Principal E₆-Bundles over a Compact Riemann Surface

Abstract

In this paper, the fixed points of involutions on the moduli space of principal $E_6$-bundles over a compact Riemann surface X are investigated. In particular, it is proved that the combined action of a representative $\sigma$ of the outer involution of $E_6$ with the pull-back action of a surface involution $\tau$ admits fixed points if and only if a specific topological obstruction in $H^2\left(X/\tau ,{\pi }_0\left(E_6^{\sigma }\right)\right)$ vanishes. For an involution $\tau$ with $2k$ fixed points, it is proved that the fixed point set is isomorphic to the moduli space of principal H-bundles over the quotient curve $X/\tau$, where H is either $F_4$ or $PSp(8,\mathbb{C})$ and it consists of $2^{g-k+1}$ components. The complex dimensions of these components are computed, and their singular loci are determined as corresponding to H-bundles admitting non-trivial automorphisms. Furthermore, it is checked that the stability of fixed $E_6$-bundles implies the stability of their corresponding H-bundles over $X/\tau$, and the behavior of characteristic classes is discussed under this correspondence. Finally, as an application of the above results, it is proved that the fixed points correspond to octonionic structures on $X/\tau$, and an explicit construction of these octonionic structures is provided.

1. Introduction

Given a compact Riemann surface X of genus $g\ge 2$ and a complex reductive Lie group G, a principal G-bundle over X is a holomorphic complex variety E together with a projection map $E\to X$ that makes E locally isomorphic to $X\times G$ such that E admits a transitive and free right action of G in it. From Ramanathan’s notion of stability for these objects [1,2,3], the moduli space ${\mathcal{M}}_G\left(X\right)$ that parametrizes S-equivalence classes of semi-stable principal G-bundles is a complex algebraic variety admitting the subset of stable bundles as an open dense and smooth subvariety.

The geometry of the space ${\mathcal{M}}_G\left(X\right)$ has been intensively studied, due to its relevance to mathematics and other fields, such as theoretical physics. Indeed, in geometry, principal G-bundles are the base for constructing G-Higgs bundles, which naturally arise as solutions of Hitchin’s equations [4] and whose moduli space construction requires the non-abelian Hodge theory developed by Simpson [5,6,7]. From the perspective of theoretical physics, principal bundles appear in the description of instantons, as solutions to the self-dual Yang–Mills equations [8], and also in the study of the moduli spaces of monopoles, which are equipped with natural hyperkähler metrics and provide insights into the dynamics and scattering of magnetic monopoles [9].

The specific case of the structure group $E_6$ is quite interesting because of its rich geometry. Indeed, $E_6$ is, of all the complex simple Lie groups of exceptional type, the only one that admits non-trivial outer automorphisms. Specifically, it admits a non-trivial outer involution, coming from the symmetries of its Dynkin diagram, which incorporates geometrically interesting symmetries into the group. The different representatives of the outer involution in $Aut\left(E_6\right)$ have as a subgroup of fixed points either the simple exceptional complex Lie group $F_4$ or the projective group $PSp(8,\mathbb{C})$, of type $C_4$. From these data, inclusions of groups $F_4\hookrightarrow E_6$ and $PSp(8,\mathbb{C})\hookrightarrow E_6$ appear that incorporate $F_4$ and symplectic geometries in the group $E_6$. In addition, the group $E_6$ is the only simple exceptional complex Lie group that has a non-trivial center, which is isomorphic to ${\mathbb{Z}}_3$. This also incorporates new symmetries at the level of principal $E_6$-bundles [10]. All of this has led to a great deal of interest in the principal bundles with structure group $E_6$, both in geometry and theoretical physics [11]. Thus, principal $E_6$-bundles are employed to describe how the different fundamental forces might emerge from a single fundamental interaction at extremely high energies, so this Lie group arises in the formulation of Grand Unified Theories (GUTs) [12,13]. Moreover, in certain formulations of string theory, particularly in the context of heterotic string theory, the group $E_6$ emerges as a possible gauge symmetry [14]. Specifically, in the $E_8\times E_8$ heterotic string theory, compactification on a six-dimensional Calabi–Yau manifold can lead to an effective four-dimensional theory with a gauge group $E_6$, which can further break down to the standard model gauge groups [14,15].

The above geometric characteristics have a great impact when studying the fixed points of the automorphisms of the moduli space ${\mathcal{M}}_{E_6}\left(X\right)$ of principal $E_6$-bundles over X. For a general reductive complex Lie structure group G, Fringuelli [16] proved that the automorphism group of the moduli space ${\mathcal{M}}_G\left(X\right)$ is generated by three families of automorphisms: the action of an outer automorphism of G, the pull-back action of an automorphism of the base curve X, and the tensor-product action of an element of $H^1(X,Z\left(G\right))$, where $Z\left(G\right)$ is the center of Z. This extends previous results concerning vector bundles [17] and Higgs bundles [18]. Several works have dealt with automorphisms defined by the action of an inner automorphism of G, by studying the fixed points of the action of an outer involution [19,20] or analyzing the components and the Hitchin integrable system of the fixed point locus in particular interesting cases, such as $Spin(8,\mathbb{C})$ [21]. There are also works that construct fixed points for the action of $H^1(X,Z\left(G\right))$, using Prym varieties as the main technique in the case of vector bundles [22] or specific techniques in the case of the gauge group $E_6$ [10]. However, the preceding literature has not addressed the case of the fixed points of the automorphisms defined as the composition of the action of an outer automorphism of the structure group and the pull-back action of an automorphism of the curve, in the case of orthogonal bundles of even rank over a hyperelliptic curve [23]. This led to the construction of orthogonal $({\sigma }_X,\sigma )$-bundles over X, where $\sigma$ is an outer involution of the Lie group $SO(2n,\mathbb{C})$ and $\sigma$ is an involution of X.

While the general methodology shares conceptual foundations with previous works such as [20,23], this paper extends significantly beyond those studies by applying these techniques to the exceptional Lie group $E_6$, which possesses fundamentally different geometric properties from other Lie groups like $SO(2n,\mathbb{C})$. The application to $E_6$-bundles is not merely a straightforward extension, as $E_6$ has a distinctive structure as an exceptional Lie group with a unique outer automorphism pattern and a non-trivial center isomorphic to ${\mathbb{Z}}_3$. This research also provides novel topological results, including the precise number of connected components, dimensional analysis, characteristic class computations, and a detailed description of the singular locus. These aspects have not been addressed in previous works. Furthermore, this paper establishes an original connection between fixed points and octonionic geometry, demonstrating that fixed points of the automorphism $\Phi$ correspond bijectively to octonionic structures on the quotient curve $X/\tau$. This connection leverages the relationship between $E_6$, $F_4$, and the geometry of octonions, yielding a geometric interpretation with potential applications in geometry and mathematical physics. Specifically, the octonionic structures are key in string theory and M-theory compactifications due to their relationship with exceptional holonomy manifolds, and this correspondence allows us to understand how octonionic structures emerge from the study of principal bundle automorphisms. The explicit construction of octonionic structures from fixed points (Theorem 2) provides techniques for investigating theoretical models in which $E_6$ appears as a gauge symmetry, especially in heterotic string theory contexts where compactification on Calabi–Yau manifolds leads to effective theories with $E_6$ gauge groups.

The main object of study in this research is the moduli space ${\mathcal{M}}_{E_6}\left(X\right)$ of principal $E_6$-bundles over a compact Riemann surface X of genus $g\ge 2$ equipped with an involution $\tau :X\to X$. Given an automorphism $\sigma$ of $E_6$ representing the outer involution that $E_6$ admits, the map $\Phi :{\mathcal{M}}_{E_6}\left(X\right)\to {\mathcal{M}}_{E_6}\left(X\right)$ defined by $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$, where $E^{\tau }={\tau }^{*}E$, is an automorphism of ${\mathcal{M}}_{E_6}\left(X\right)$. The main purpose of this paper is to describe and analyze the fixed points of the automorphism $\Phi$. Notice that it results from combining the action of the outer automorphism of $E_6$ with the pull-back action of an automorphism of the curve, which has not been studied before in the preceding literature. In particular, the main result proves that the fixed point subvariety of $\Phi$ is isomorphic to the moduli space ${\mathcal{M}}_H(X/\tau )$ of H-bundles over the quotient curve $X/\tau$, where H is the fixed point subgroup of $\sigma$, either $F_4$ or $PSp(8,\mathbb{C})$. It is also proved that the fixed point locus consists of $2^{g-k+1}$ components, where $\tau$ fixes $2k$ points of X (Theorem 1). For that, the obstruction for the automorphism $\Phi$ to admit fixed points is characterized for a general reductive complex group G as an element of the cohomology set $H^2(X/\tau ,{\pi }_0\left(G^{\sigma }\right))$, where $G^{\sigma }$ denotes the subgroup of fixed points of $\sigma$ (Proposition 1). Novel results are also provided by computing the dimension of the fixed point subvariety (Proposition 2) and characterizing its singular locus (Proposition 3) and the stability of the fixed points (Proposition 4).

The topology of the fixed point subvariety of $\Phi$ is also deeply analyzed in this paper through the study of its characteristic classes. In particular, every fixed point E of $\Phi$ induces a principal H-bundle over $X/\tau$, where H is the fixed point subgroup of $\sigma$ (either $F_4$ of $PSp(8,\mathbb{C})$), and it is proved that the second Chern class of $E_H$ is equal to that of E, if $H=F_4$, and half of that of E, if $H=PSp(8,\mathbb{C})$ (Proposition 5).

From the above results, a novel geometric application is developed, establishing a concrete correspondence between fixed points of $\Phi$ and octonionic geometric structures on the quotient curve $X/\tau$. Recall that the groups $F_4$ and $E_6$ arise naturally from the geometry of octonions. Specifically, they are subgroups of the automorphism group of the complexified algebra of $3\times 3$ Hermitian matrices over the octonions (the so-called Albert algebra) [24,25]. Octonionic structures on manifolds and bundles have been intensively studied, since they are closely related to manifolds with a holonomy group, like $G_2$ or $Spin\left(7\right)$, so they are crucial in string theory and M-theory compactifications [26]. In this paper, it is proved that the fixed points of $\Phi$ and the octonionic structures on $X/\tau$ are in bijective correspondence (Proposition 6), and an explicit construction of octonionic structures is given from the analysis of fixed points made (Theorem 2).

The structure of this paper is as follows. The main result is established and proved in Section 2, where relevant geometric properties of the fixed point subvariety of $\Phi$, such as the dimension, stability, and singular locus, are also provided. In Section 3, the relationship between the Chern classes of a fixed point of $\Phi$ and the Chern class of the induced reduction of structure group to the fixed point subgroup of $\sigma$ is given. The application of the above results of fixed points to the study of octonionic structures, including the connection of fixed points with octonionic structures on $X/\tau$, is provided in Section 4. In Section 5, the explicit construction of octonionic structures on bundles, designed from the above study, is developed. Finally, the main conclusions are drawn.

2. Involutions of the Moduli Space of Principal $E_6$-Bundles

Let X be a compact Riemann surface of genus $g\ge 2$, G be a complex reductive Lie group, and ${\mathcal{M}}_G\left(X\right)$ be the moduli space of principal G-bundles over X. If $\sigma$ is an automorphism of G, then $\sigma$ acts on ${\mathcal{M}}_G\left(X\right)$ as follows. If E is a principal G-bundle over X, then $\sigma \left(E\right)$ has the same total space as E, but it is equipped with the action of G given by $e·g=e{\sigma }^{-1}\left(g\right)$, for $e\in E$ and $g\in G$ [10,19,20]. This defines an automorphism of ${\mathcal{M}}_G\left(X\right)$. Indeed, if $\sigma$ has a finite order, then the induced automorphism of ${\mathcal{M}}_G\left(X\right)$ has the same order as $\sigma$. Notice also that, if $\sigma$ is an inner automorphism, then $E\cong \sigma \left(E\right)$, so it induces the identity on ${\mathcal{M}}_G\left(X\right)$, but this is not the case if $\sigma$ represents an outer automorphism of G [10,20]. If, in addition, X is equipped with an automorphism $\tau$, then the pull-back action also defines an automorphism of ${\mathcal{M}}_G\left(X\right)$, with the same order as that of $\tau$. The composition of these two actions gives an automorphism $\Phi :{\mathcal{M}}_G\left(X\right)\to {\mathcal{M}}_G\left(X\right)$ defined by $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$, where $E^{\tau }$ denotes the pull-back ${\tau }^{*}E$.

As a first step, in this section, a necessary and sufficient condition for the above automorphism $\Phi$ to admit fixed points is provided in the case where both $\sigma$ and $\tau$ are involutions. Notice that, in this case, $\Phi$ is also an involution. This is performed for a general complex reductive Lie group G. After that, the study is particularized for the case of $G=E_6$, providing a characterization of the fixed points of the automorphism $\Phi$ when $\sigma$ represents the unique outer automorphism that $E_6$ admits (that has order 2) and $\tau$ is an involution of X. In addition, some results are proved concerning the components of the fixed point locus, its dimension, and the stability of the fixed points mentioned above.

Lemma 1. 

Let X be a compact Riemann surface of genus $g\ge 2$ with an involution $\tau :X\to X$, G be a complex semisimple Lie group, $\sigma \in Aut\left(G\right)$ be an automorphism of order 2, and $\Phi :{\mathcal{M}}_G\left(X\right)\to {\mathcal{M}}_G\left(X\right)$ be the involution defined by $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$, where $E^{\tau }={\tau }^{*}E$. If $E\in {\mathcal{M}}_G\left(X\right)$ is a fixed point of Φ, then E admits a reduction of the structure group of E to the fixed point subgroup $G^{\sigma }$ over the quotient curve $X/\tau$.

Proof. 

Let us establish the correspondence between the fixed points of $\Phi$ and the reductions of the structure group. If E is a fixed point of $\Phi$, then $\Phi \left(E\right)\cong E$, meaning that there exists an isomorphism $f:\sigma \left(E^{\tau }\right)\to E$.

Consider the commutative diagram

$$\begin{array}{ccc}\hfill E& \to & X\\ \hfill \downarrow & & \downarrow \pi \\ \hfill E/\tau & \to & X/\tau ,\end{array}$$

where $\pi :X\to X/\tau$ is the quotient map and $\tau$ acts on E by taking the pull-back. Notice that, although the action of $\tau$ on E is not free in general, the quotient space $E/\tau$, which forms a bundle over $X/\tau$, can be considered.

For the fixed point E of $\Phi$, the isomorphism $f:\sigma \left(E^{\tau }\right)\to E$ can be equivalently expressed as an isomorphism $f:\sigma \left(E\right)\to E^{\tau }$. This isomorphism satisfies the condition that $\tau \circ f\circ \tau =\sigma {\left(f\right)}^{-1}$, since $\tau$ is an involution.

Then, this isomorphism f induces a reduction of the structure group of E to $G^{\sigma }$ over the quotient curve $X/\tau$ as follows. Define $E_{\sigma }$ as the subset of E consisting of points that are fixed by the combined action of $\tau$ and $\sigma$ through f,

$$E_{\sigma }=\{p\in E\mid \tau \left(f\left(p\right)\right)=p\}.$$

It is easily checked that $E_{\sigma }$ is a principal $G^{\sigma }$-bundle over $X/\tau$. Indeed, if $p\in E_{\sigma }$ and $g\in G^{\sigma }$, then $\tau \left(f\right(p·g\left)\right)=\tau \left(f\right(p)·\sigma (g\left)\right)=\tau \left(f\right(p\left)\right)·\sigma \left(g\right)=p·g$, which shows that $E_{\sigma }$ is preserved by the action of $G^{\sigma }$.

The projection map $E_{\sigma }\to X/\tau$ is well defined, since, if $p\in E_{\sigma }$, then, the projection of p to X is mapped by $\tau$ to the projection of $\tau \left(f\right(p\left)\right)=p$, which means that the projection of p to X is invariant under $\tau$ and thus descends to $X/\tau$.

To fully justify that $E_{\sigma }$ is indeed a reduction of the structure group to $G^{\sigma }$, notice the following. First, we will show that $E_{\sigma }$ is a principal $G^{\sigma }$-bundle over $X/\tau$. We have already established that $E_{\sigma }$ is preserved by the $G^{\sigma }$-action. For the principal bundle structure, it will be verified that this action is free and transitive on the fibers.

• The action is free because it inherits this property from the free action of G on E. Indeed, if $p·g=p$ for some $p\in E_{\sigma }$ and $g\in G^{\sigma }$, then $g=e$ (the identity element) since the G-action on E is free.
• For transitivity on fibers, let $p,q\in E_{\sigma }$ be points projecting to the same point in $X/\tau$. Their projections to X must be in the same $\tau$-orbit. If they project to the same point in X, then there exists a unique $g\in G$ such that $p·g=q$ (by the principal bundle property of E). We need to show that $g\in G^{\sigma }$. Since $p,q\in E_{\sigma }$, we have $\tau \left(f\right(p\left)\right)=p$ and $\tau \left(f\right(q\left)\right)=q$. This implies that

  $$\begin{array}{cc}\hfill & p·g=q,\hfill \\ \hfill & \tau \left(f\right(p\left)\right)·g=\tau \left(f\right(q\left)\right),\hfill \\ \hfill & \tau \left(f\right(p)·\sigma (g\left)\right)=\tau \left(f\right(q\left)\right).\hfill \end{array}$$

Using the properties of the bundle isomorphism f and that $\tau$ is an involution, we obtain $g=\sigma \left(g\right)$, which means $g\in G^{\sigma }$.

If the projections of p and q to X are different but in the same $\tau$-orbit, we can use that the bundle E is locally trivial and the isomorphism f preserves fibers to establish the existence of an element in $G^{\sigma }$ that transforms p into q.

Now, the structure group of $E_{\sigma }$ is easily extended from $G^{\sigma }$ to G, obtaining a principal G-bundle over $X/\tau$. This extended bundle is $E_{\sigma }{\times }_{G^{\sigma }}G$, the quotient of $E^{\sigma }\times G$ by the equivalence relation $(p,g)\sim (p·h,h^{-1}g)$ for $h\in G^{\sigma }$. When pulled back to X through the quotient map $\pi :X\to X/\tau$, this extended bundle is isomorphic to E. The isomorphism maps a point $(p,g)$ in the pulled-back bundle to $p·g$ in E, and this isomorphism is well defined and respects the G-action.

To complete the proof that $E_{\sigma }$ represents a genuine reduction of structure group, we will verify that the extension of $E_{\sigma }$ from a $G^{\sigma }$-bundle to a G-bundle, when pulled back to X, is isomorphic to the original bundle E. For this, it will be shown that the map $\varphi :{\pi }^{*}\left(E_{\sigma }{\times }_{G^{\sigma }}G\right)\to E$ defined by $\varphi \left(\right[(x,p),g\left]\right)=p·g$ is a well-defined G-bundle isomorphism.

The map is well defined, since, if $(x,p)\sim (x,p·h)$ for $h\in G^{\sigma }$, then $\varphi \left(\right[(x,p),g\left]\right)=p·g$ and $\varphi \left([(x,p·h),h^{-1}g]\right)=(p·h)·\left(h^{-1}g\right)=p·g$. It is also G-equivariant, as $\varphi \left(\right[(x,p),gh\left]\right)=p·gh=(p·g)·h=\varphi \left(\right[(x,p),g\left]\right)·h$ for any $h\in G$. Finally, to show it is bijective, we construct an inverse map $\psi :E\to {\pi }^{*}\left(E_{\sigma }{\times }_{G^{\sigma }}G\right)$. For any $q\in E$ projecting to $x\in X$, there exists a point $p\in E_{\sigma }$ projecting to $\left[x\right]\in X/\tau$ and an element $g\in G$ such that $q=p·g$. The map $\psi \left(q\right)=\left[\right(x,p),g]$ is well defined and provides the required inverse.

Conversely, given a principal $G^{\sigma }$-bundle F over $X/\tau$, extending its structure group to G and pulling back to X yields a principal G-bundle over X that is a fixed point of $\Phi$. The isomorphism f in this case is induced by the action of $G^{\sigma }$ on F.

Therefore, there is a one-to-one correspondence between the fixed points of $\Phi$ and principal $G^{\sigma }$-bundles over the quotient curve $X/\tau$, or equivalently, reductions of the structure group from G to $G^{\sigma }$ over $X/\tau$, as stated. □

Proposition 1. 

Let X be a compact Riemann surface of genus $g\ge 2$ with an involution $\tau :X\to X$, G be a complex semisimple Lie group, and $\sigma \in Aut\left(G\right)$ be an automorphism of order 2. Then, the involution $\Phi :{\mathcal{M}}_G\left(X\right)\to {\mathcal{M}}_G\left(X\right)$ defined by $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$, where $E^{\tau }={\tau }^{*}E$, admits a fixed point if and only if the topological obstruction ${\omega }_2\in H^2(X/\tau ,{\pi }_0\left(G^{\sigma }\right))$ vanishes, where $G^{\sigma }$ denotes the fixed point subgroup of σ.

Proof. 

A fixed point of $\Phi$ is a principal G-bundle E over X such that $\Phi \left(E\right)\cong E$, meaning that there exists an isomorphism $f:\sigma \left(E^{\tau }\right)\to E$. By Lemma 1, this isomorphism can be viewed as a reduction of the structure group of E to the fixed point subgroup $G^{\sigma }$ over the quotient curve $X/\tau$.

Let $\pi :X\to X/\tau$ be the quotient map. Choose a covering $\left\{U_i\right\}$ of $X/\tau$ with local trivializations of the pull-back bundle ${\pi }_{*}\left(E\right)$. On the overlaps $U_i\cap U_j$, the transition functions $g_{ij}:U_i\cap U_j\to G$ satisfy the cocycle condition $g_{ij}{g}_{jk}{g}_{ki}=id$. The involution $\Phi$ acts on these transition functions via $\Phi \left(g_{ij}\right)=\sigma \left(g_{ij}^{\tau }\right)$.

For a fixed point of $\Phi$, there must exist functions $h_i:U_i\to G$ such that $\sigma \left(g_{ij}^{\tau }\right)=h_i{g}_{ij}{h}_j^{-1}$. Define the cohomology class ${\omega }_2$ by the cocycle $\left\{c_{ijk}\right\}$ on triple intersections $U_i\cap U_j\cap U_k$, where

$$c_{ijk}=\sigma \left(g_{ij}^{\tau }\right)\sigma \left(g_{jk}^{\tau }\right)\sigma \left(g_{ki}^{\tau }\right)·{\left(g_{ij}{g}_{jk}{g}_{ki}\right)}^{-1}.$$

Since $\sigma$ has order 2, these cocycles take values in ${\pi }_0\left(G^{\sigma }\right)$, the component group of the fixed point subgroup. The obstruction ${\omega }_2$ vanishes precisely when this cocycle is cohomologically trivial, which completes the proof. □

The simple complex Lie group $E_6$ is one of the groups of exceptional type classified by Cartan. It can be defined as the group of automorphisms of a certain holomorphic symmetric 3-form defined on a 27-dimensional complex vector space. Specifically, $E_6$ is the subgroup of $GL(27,\mathbb{C})$ that preserves a non-degenerate, symmetric trilinear form $\Phi$ defined on a 27-dimensional complex vector space W. Indeed, W gives the fundamental 27-dimensional representation of $E_6$ [11,27,28].

The group $E_6$ is simply connected, and there is only one more simple complex group whose Lie algebra is ${\mathfrak{e}}_6$, which is $\mathbb{P}{E}_6=E_6/Z\left(E_6\right)$. The rank of $E_6$ is 6 and admits 72 roots. Since $E_6$ is simply connected, its group of outer automorphisms, $Out\left(E_6\right)$, coincides with the group of symmetries of its Dynkin diagram. Therefore, $Out\left(E_6\right)\cong {\mathbb{Z}}_2$, and the unique non-trivial outer automorphism of $E_6$, $\left[\sigma \right]$, acts on the center $Z\left(E_6\right)$, which is isomorphic to ${\mathbb{Z}}_3$, by sending each $\mu$ in $Z\left(E_6\right)$ to ${\mu }^2$ [11,27].

Wolf and Gray [29] proved that there are exactly two non-conjugate representatives in $Aut\left(E_6\right)$ of the outer automorphism $\left[\sigma \right]\in Out\left(E_6\right)$, with fixed point subgroups isomorphic to $F_4$ and $PSp(8,\mathbb{C})$, respectively. The group $F_4$ is the rank 4 simple complex Lie group of exceptional type that can be viewed as the group of automorphisms of certain 26-dimensional complex vector spaces that preserves a certain non-degenerate holomorphic symmetric 3-form and a non-degenerate holomorphic symmetric 2-form. On its part, $PSp(8,\mathbb{C})$ is the centerless complex Lie group of type $C_4$.

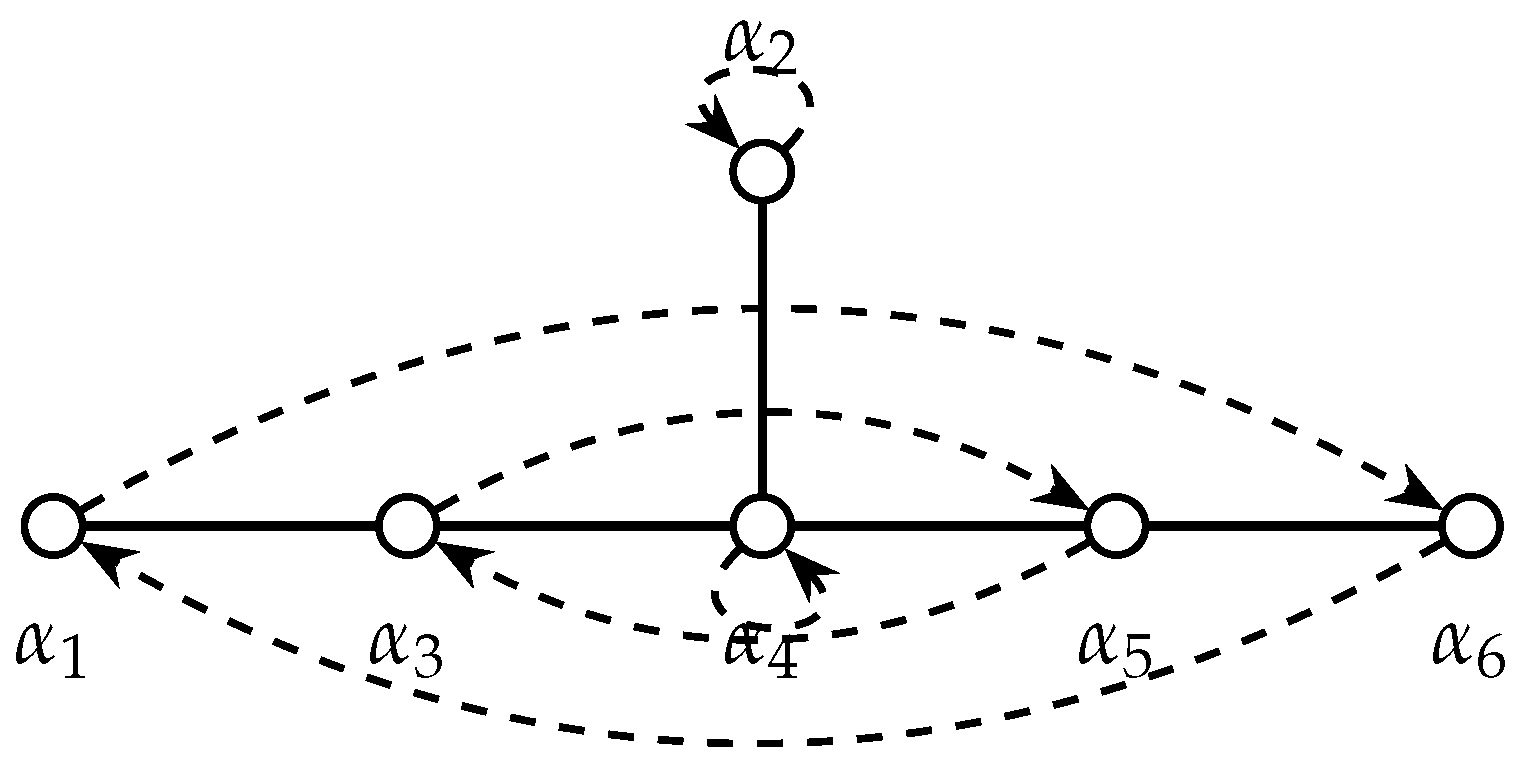
More precisely, the first representative of $\left[\sigma \right]$, denoted by ${\sigma }_1$, corresponds to the diagram automorphism of $E_6$ that fixes the central node of the Dynkin diagram and interchanges the pairs of nodes at the same distance from it. Explicitly, ${\sigma }_1$ interchanges the nodes ${\alpha }_1$ and ${\alpha }_6$, and ${\alpha }_3$ and ${\alpha }_5$, while fixing ${\alpha }_2$ and ${\alpha }_4$, according to Figure 1.

Figure 1. A Dynkin diagram of the simple complex Lie group $E_6$ with the action of its outer involution $\sigma$.

To identify the fixed point subgroup of ${\sigma }_1$, consider the root system of $E_6$ as embedded in ${\mathbb{R}}^8$ with a specific inner product. Precisely, let ${\left\{e_i\right\}}_{i=1}^8$ be the standard basis of ${\mathbb{R}}^8$, and define the subspace $V\subset {\mathbb{R}}^8$ by

$$V=\left\{x=\sum _{i=1}^8{x}_i{e}_i\in {\mathbb{R}}^8\mid \sum _{i=1}^8{x}_i=0\right\}.$$

Then, the root system of $E_6$ consists of the vectors in V defined by

$$\begin{array}{cc}\hfill & \pm (e_i-e_j),1\le i<j\le 6,\hfill \\ \hfill & \pm \left({\displaystyle \frac{1}{2}}\sum _{i=1}^8{\epsilon }_i{e}_i\right),{\epsilon }_i=\pm 1,\sum _{i=1}^8{\epsilon }_i=0,\prod _{i=1}^8{\epsilon }_i=1,\hfill \end{array}$$

A system of simple roots for $E_6$ can be chosen as

$$\begin{array}{cc}\hfill {\alpha }_1& ={\displaystyle \frac{1}{2}}(e_1+e_8-e_2-e_3-e_4-e_5-e_6-e_7),\hfill \\ \hfill {\alpha }_2& =e_1+e_2,\hfill \\ \hfill {\alpha }_3& =e_2-e_1,\hfill \\ \hfill {\alpha }_4& =e_3-e_2,\hfill \\ \hfill {\alpha }_5& =e_4-e_3,\hfill \\ \hfill {\alpha }_6& =e_5-e_4,\hfill \end{array}$$

and the Cartan matrix of $E_6$ with respect to the simple roots above is

$$A_{E_6}=\left(\begin{array}{cccccc}2& 0& -1& 0& 0& 0\\ 0& 2& 0& -1& 0& 0\\ -1& 0& 2& -1& 0& 0\\ 0& -1& -1& 2& -1& 0\\ 0& 0& 0& -1& 2& -1\\ 0& 0& 0& 0& -1& 2\end{array}\right).$$

See [25,30] for further details and explicit computations. The fixed points of ${\sigma }_1$ are precisely those elements in $E_6$ that commute with the action of ${\sigma }_1$ on the root system. Indeed, they form a root system of type $F_4$, since the fixed simple roots are

$$\begin{array}{cc}\hfill {\beta }_1& ={\alpha }_2,\hfill \\ \hfill {\beta }_2& ={\alpha }_4,\hfill \\ \hfill {\beta }_3& ={\alpha }_3+{\alpha }_5,\hfill \\ \hfill {\beta }_4& ={\alpha }_1+{\alpha }_6,\hfill \end{array}$$

which generate a root system of type $F_4$ [25,30,31]; thus, the fixed point subgroup of ${\sigma }_1$ is isomorphic to the complex Lie group $F_4$.

The second representative of the outer involution $\left[\sigma \right]$, denoted ${\sigma }_2$, can be constructed by composing ${\sigma }_1$ with a suitable inner automorphism. Specifically, let $\theta$ be the inner automorphism corresponding to conjugation by the element $exp\left(\pi i{h}_{\alpha }\right)$, where $h_{\alpha }$ is the coroot associated with a specific root $\alpha$. By choosing $\alpha$ appropriately, ${\sigma }_2=\theta \circ {\sigma }_1$ is another automorphism of order 2 representing the non-trivial outer involution of $E_6$ that is not conjugate to ${\sigma }_1$. By analyzing the action of ${\sigma }_2$ on the root system of $E_6$, it is easily checked that the fixed roots generate a root system corresponding to the Lie algebra $\mathfrak{sp}(8,\mathbb{C})$. Since the center of the specific $G^{{\sigma }_2}$ with Lie algebra $\mathfrak{sp}(8,\mathbb{C})$ must be contained in the center of $E_6$, isomorphic to ${\mathbb{Z}}_3$, it must be isomorphic to $PSp(8,\mathbb{C})$.

The combined action of a representative $\sigma$ of the outer involution of $E_6$ with the pull-back action of an involution $\tau :X\to X$ gives an automorphism $\Phi$ of order 2 of the moduli space of principal $E_6$-bundles over X, defined by

$$\Phi \left(E\right)=\sigma \left(E^{\tau }\right),$$

(1)

where $E^{\tau }={\tau }^{*}E$. In this section, the action of this automorphism on principal $E_6$-bundles over the compact Riemann surface is examined. First, it is proved that the obstruction for $\Phi$ to admit fixed points is an element of the cohomology $H^2\left(X/\tau ,{\pi }_0\left(E_6^{\sigma }\right)\right)$, where $E_6^{\sigma }$ denotes the subgroup of fixed points of $\sigma$. Indeed, this obstruction result is proved for a general semisimple group.

In the next result, the fixed points of the combined involution $\Phi$ of the moduli space ${\mathcal{M}}_{E_6}\left(X\right)$ of principal $E_6$-bundles are studied, specifying the analysis made in Proposition 1 and considering the data concerning the possibilities for the fixed point subgroups of the different representatives of the outer involution that $E_6$ admits.

Theorem 1. 

Let X be a compact Riemann surface of genus $g\ge 2$ with an involution τ having $2k$ fixed points, $\left[\sigma \right]$ be the outer involution of $E_6$, and σ be a representative of $\left[\sigma \right]$ with fixed point subgroup H (either $F_4$ or $PSp(8,\mathbb{C})$). Then, the fixed point set of the involution $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$ of the moduli space ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1) is non-empty, it is isomorphic to the moduli space ${\mathcal{M}}_H(X/\tau )$, and it consists of $2^{g-k+1}$ components (in particular, it must be that $k\le g+1$).

Proof. 

Let $Y=X/\tau$ be the quotient curve, which, by the Riemann–Hurwitz formula, has genus $\hat{g}={\displaystyle \frac{g-k+1}{2}}$. The involution $\tau$ has $2k$ fixed points, which project to k branch points on Y.

Recall that a principal $E_6$-bundle E over X is a fixed point of $\Phi$ if and only if there exists an isomorphism $\phi :\sigma \left(E^{\tau }\right)\to E$. Such bundles correspond to reductions of the structure group to the fixed point subgroup H of $\sigma$ over the quotient curve Y, by Lemma 1. The obstruction to the existence of a fixed point lies in $H^2(Y,{\pi }_0\left(H\right))$ by Proposition 1 and, since H is connected (notice that both $F_4$ and $PSp(8,\mathbb{C})$ are connected groups), ${\pi }_0\left(H\right)=\left\{1\right\}$, so this obstruction vanishes automatically. In particular, the fixed point subvariety is non-empty.

The above reduction of the structure group is unique. To check this, notice that, if $E\otimes S$ is another fixed point of $\Phi$, for some $S\in H^1(X,Z\left(E_6\right))=H^1(X,{\mathbb{Z}}_3)$, then,

$$\sigma \left({(E\otimes S)}^{\tau }\right)\cong E\otimes \sigma \left(L^{\tau }\right)\cong E\otimes {\left(S^{\tau }\right)}^{-1},$$

since $\sigma \left(E^{\tau }\right)\cong E$ and $\sigma$ acts on the center of $E_6$ by $\sigma \left(\lambda \right)={\lambda }^2$. If $E\otimes S$ is fixed by $\Phi$, then,

$$E\otimes (S\otimes S^{\tau })\cong E.$$

By taking a suitable trivialization of E with open subset U, it follows that $S\otimes S^{\tau }{|}_U=1$, from which $S^{\tau }{{|}_{{\tau }^{-1}\left(U\right)}\cong S^2|}_U$. But this is not possible, since S is locally a third root of unity (so different from $S^2$), and X is connected, so a locally constant function must be constant. This proves that the reduction of the structure group is unique, so the map ${\mathcal{M}}_H\left(Y\right)\to \mathcal{M}\left(E_6\right)$ is injective and falls into the fixed point subvariety. This gives the isomorphism between the fixed point subvariety and the moduli space ${\mathcal{M}}_H(X/\tau )$ announced.

Finally, the moduli space of fixed points then consists of principal H-bundles over Y, but with additional twisting coming from the possible liftings of the involution to the bundle. These twistings are classified by

$$H^1(Y,{\mathbb{Z}}_2)\cong {\left({\mathbb{Z}}_2\right)}^{2\widehat{g}}\cong {\left({\mathbb{Z}}_2\right)}^{g-k+1},$$

giving a total of $2^{g-k+1}$ components, each isomorphic to ${\mathcal{M}}_H\left(Y\right)$, for H equal to $F_4$ or $PSp(8,\mathbb{C})$, which concludes the result. □

Remark 1. 

Note that, when a compact Riemann surface admits an involution, the number of fixed points of this involution is always even. This is a result that follows from the Riemann–Hurwitz formula for branched covers. Therefore, the assumption of Theorem 1 that the number of fixed points of τ is $2k$ does not entail any loss of generality.

Remark 2. 

In the proof of Theorem 1, it has been used that $\hat{g}={\displaystyle \frac{g-k+1}{2}}$ is a positive integer number, since it is the genus of $Y=X/\tau$. Indeed, since τ is a holomorphic map of degree 2 from X to Y with $2k$ ramification points (the fixed points of τ), each with ramification index $e_p=2$, by the Riemann–Hurwitz formula it is obtained that

$$2g-2=2(2h-2)+\sum _{p\in Ram\left(\tau \right)}(e_p-1)=2(2h-2)+2k·1=4h-4+2k,$$

where h denotes the genus of $X/\tau$. Simplifying the above equation, it is obtained that

$$2g-2=4h-4+2k\Rightarrow g=2h+k-1.$$

Therefore, rearranging to isolate the expression in question, it follows that $g-k+1=2h$, so the genus of Y, which must be a positive integer, coincides with the number $\hat{g}={\displaystyle \frac{g-k+1}{2}}$.

The moduli space ${\mathcal{M}}_{E_6}\left(X\right)$ of principal $E_6$-bundles over a compact Riemann surface X of genus $g\ge 2$ has complex dimension $78(g-1)$, where 78 is the dimension of the Lie algebra ${\mathfrak{e}}_6$. For the components of the fixed point subvariety of the involution $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$ given in Theorem 1, the dimension of each of them is computed in the next result.

Proposition 2. 

Let X be a compact Riemann surface of genus $g\ge 2$ with an involution τ having $2k$ fixed points and $\left[\sigma \right]$ be the outer involution of $E_6$, represented by the order 2 automorphism σ, with fixed point subgroup H. Then, each component of the fixed point set of Φ on ${\mathcal{M}}_{E_6}\left(X\right)$ has complex dimension:

1.

${\displaystyle \frac{dim\left({\mathfrak{f}}_4\right)(g-k+1)}{2}}=26(g-k+1)$ if $H\cong F_4$.

2.

${\displaystyle \frac{dim\left(\mathfrak{sp}\right(8,\mathbb{C}\left)\right)(g-k+1)}{2}}=18(g-k+1)$ if $H\cong PSp(8,\mathbb{C})$.

Proof. 

By Theorem 1, for a fixed point E of the involution $\Phi$, there exists a principal H-bundle $E_H$ over the quotient curve $Y=X/\tau$ such that E is obtained from $E_H$ by the extension of the structure group. The dimension of the moduli space of principal H-bundles over Y is given by $dim\left(H\right)(\hat{g}-1)$, where $\hat{g}$ is the genus of Y. By the Riemann–Hurwitz formula, the genus $\hat{g}$ of $Y=X/\tau$ satisfies

$$2g-2=2(2\widehat{g}-2)+2k,$$

from which $\hat{g}={\displaystyle \frac{g-k+1}{2}}$.

For $H=F_4$, the dimension of the Lie algebra ${\mathfrak{f}}_4$ is 52 [25,30]; thus, the dimension of each component is

$$dim\left(F_4\right)(\hat{g}-1)=52·{\displaystyle \frac{g-k+1}{2}}=26(g-k+1).$$

Similarly, for $H=PSp(8,\mathbb{C})$, the dimension of the Lie algebra $\mathfrak{sp}(8,\mathbb{C})$ is 36; thus, the dimension of each component is

$$dim(PSp(8,\mathbb{C}))(\hat{g}-1)=36·{\displaystyle \frac{g-k+1}{2}}=18(g-k+1),$$

concluding the result. □

The fixed point components of the involution $\Phi$ given in Theorem 1 may contain singular points, which correspond to principal H-bundles over $Y=X/\tau$ with non-trivial automorphisms, as proved in the following result.

Proposition 3. 

Let X be a compact Riemann surface of genus $g\ge 2$ with a fixed non-trivial involution τ, σ be an automorphism of order 2 of $E_6$, representing its outer involution, with a subgroup of fixed points H, Φ be the involution of ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1), and ${\mathcal{M}}_{\Phi }^H\left(X\right)$ be a component of the fixed point set of Φ on the moduli space ${\mathcal{M}}_{E_6}\left(X\right)$, corresponding to principal H-bundles over $Y=X/\tau$. Then, the singular locus of ${\mathcal{M}}_{\Phi }^H\left(X\right)$ consists of those $E_6$-bundles E for which the corresponding principal H-bundle $E_H$ admits non-trivial automorphisms. Moreover, if $E_H$ is a stable principal H-bundle over Y, then it corresponds to a smooth point of ${\mathcal{M}}_{\Phi }^H\left(X\right)$.

Proof. 

The moduli space ${\mathcal{M}}_H\left(Y\right)$ of principal H-bundles over Y is constructed as the quotient of the space of stable principal H-bundles by the action of the gauge group [5]. The points in ${\mathcal{M}}_H\left(Y\right)$ with non-trivial stabilizers under this action correspond to bundles with non-trivial automorphisms, and these points are precisely the singular points of ${\mathcal{M}}_H\left(Y\right)$. Since each component ${\mathcal{M}}_{\Phi }^H\left(X\right)$ is isomorphic to ${\mathcal{M}}_H\left(Y\right)$, the singular locus of ${\mathcal{M}}_{\Phi }^H\left(X\right)$ corresponds to those bundles E for which the associated H-bundle $E_H$ has non-trivial automorphisms, as stated.

For a stable principal H-bundle $E_H$, any automorphism must preserve the stability condition. An automorphism of $E_H$ is a G-equivariant map $f:E_H\to E_H$ covering the identity map on Y. Such a map corresponds to a section of the associated bundle $E_H{\times }_{Ad}H$, where Ad denotes the adjoint action of H on itself.

Since the action of a non-central element of H would induce reductions of the structure group that violate the stability condition, any such section for a stable bundle must take values in the center $Z\left(H\right)$ of H.

Now, the center of H is trivial for the two possible subgroups of fixed points, $H=F_4$ or $H=PSp(8,\mathbb{C})$, so stable H-bundles have no non-trivial automorphisms, and the corresponding fixed point components are also smooth. This concludes the result. □

In the following results, the stability conditions of a fixed point of the involution $\Phi$ defined in (1) as an $E_6$-bundle are related to the stability of its corresponding reduction of structure group to $F_4$ or $PSp(8,\mathbb{C})$, according to Theorem 1.

Proposition 4. 

Let X be a compact Riemann surface of genus $g\ge 2$ with a fixed non-trivial involution τ, σ be an automorphism of order 2 of $E_6$, representing its outer involution, and E be a semi-stable principal $E_6$-bundle over X. If E is a fixed point of the involution $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$ defined in (1), then, the corresponding principal H-bundle $E_H$ over $X/\tau$ given by Theorem 1 is also semi-stable, where H is either $F_4$ or $PSp(8,\mathbb{C})$.

Proof. 

Following Ramanathan’s notion of stability for principal bundles [1,2,3], a principal G-bundle E over a Riemann surface is semi-stable if and only if for every reduction of the structure group to a parabolic subgroup $P\subset G$ with Levi component L and every anti-dominant character $\chi$ of L, the degree of the associated line bundle $L_{\chi }$ is non-positive, where G is any reductive complex Lie group.

Let E be a semi-stable principal $E_6$-bundle over X that is a fixed point of the involution $\Phi$, meaning that there exists an isomorphism $\phi :\sigma \left(E^{\tau }\right)\to E$, and $E_H$ be the corresponding principal H-bundle over $Y=X/\tau$, where H is either $F_4$ or $PSp(8,\mathbb{C})$. Suppose, for contradiction, that $E_H$ is not semi-stable. Then, there exists a reduction of the structure group to a parabolic subgroup $P_H\subset H$ with Levi component $L_H$ and an anti-dominant character $\chi$ of $L_H$ such that $deg\left(L_{\chi }\right)>0$. This reduction induces a reduction of the structure group of E to a parabolic subgroup $P\subset E_6$ that contains $P_H$. More precisely, recall that the maximal parabolic subgroups of $E_6$ are in one-to-one correspondence with subsets of the set of simple roots $\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6\}$. Under the outer automorphism $\sigma$, the simple roots are permuted as follows: $\sigma \left({\alpha }_1\right)={\alpha }_6$, $\sigma \left({\alpha }_3\right)={\alpha }_5$, $\sigma \left({\alpha }_2\right)={\alpha }_2$, and $\sigma \left({\alpha }_4\right)={\alpha }_4$. For a parabolic subgroup $P_H$ of $H=F_4$, the corresponding simple roots in the subsystem of fixed roots are $\{{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\}$, which map to $\{{\alpha }_2,{\alpha }_4,{\alpha }_3+{\alpha }_5,{\alpha }_1+{\alpha }_6\}$ in the root system of $E_6$. Thus, a reduction of the structure group of $E_H$ to $P_H$ corresponds to a reduction of the structure group of E to a parabolic subgroup P of $E_6$ that is stable under the action of $\sigma$, and similar reasoning works for $PSp(8,\mathbb{C})$.

The character $\chi$ of $L_H$ extends to a character of the Levi component L of P. Due to the compatibility with the involution $\Phi$, the degree of the associated line bundle for E satisfies

$$deg\left(L_{\chi }^E\right)=2deg\left(L_{\chi }^{E_H}\right),$$

since the pull-back map ${\pi }^{*}:H^2(Y,\mathbb{Z})\to H^2(X,\mathbb{Z})$ multiplies degrees by the degree of the covering, which is 2. Now, recalling that $deg\left(L_{\chi }^{E_H}\right)>0$, it follows that $deg\left(L_{\chi }^E\right)>0$, contradicting the semi-stability of E. Therefore, $E_H$ must be semi-stable. □

Corollary 1. 

Let X be a compact Riemann surface of genus $g\ge 2$ with a fixed non-trivial involution τ and σ be an automorphism of order 2 of $E_6$, representing its outer involution. Then, the stable fixed point subvariety of the involution Φ defined in (1) consists of components isomorphic to the moduli space of stable principal H-bundles over $X/\tau$, where H is isomorphic to $F_4$ or $PSp(8,\mathbb{C})$.

Proof. 

By Proposition 4, if E is a semi-stable principal $E_6$-bundle that is fixed by $\Phi$, then, the corresponding principal H-bundle $E_H$ over $Y=X/\tau$ is also semi-stable.

Conversely, given a semi-stable principal H-bundle $E_H$ over Y, the induced principal $E_6$-bundle E over X obtained by extending the structure group from H to $E_6$ is also semi-stable, since the forgetful map ${\mathcal{M}}_H\left(X\right)\to {\mathcal{M}}_G\left(X\right)$ respects semi-stability, where H is a subgroup of a reductive Lie group G [20,21]. This establishes a bijection between fixed points of $\Phi$ in the moduli space of semi-stable principal $E_6$-bundles and the moduli space of semi-stable principal H-bundles.

For stable bundles, if E is a stable principal $E_6$-bundle that is a fixed point of $\Phi$, then $E_H$ is also stable. This follows from the fact that stability is a stronger condition than semi-stability, requiring strict inequality in the degree condition for proper parabolic reductions (the same argument of the proof of Proposition 4 works). This concludes the result. □

Remark 3. 

By Proposition 3 and Corollary 1, it follows that every stable H-bundle over $Y=X/\tau$ gives a smooth point in the corresponding component of the fixed point subvariety of the automorphism Φ of ${\mathcal{M}}_{E_6}\left(X\right)$, where H is the subgroup $F_4$ or $PSp(8,\mathbb{C})$ of $E_6$. This smooth point is obtained by extension of the structure group and applying the push-forward ${\pi }_{*}$, where $\pi :X\to Y$ is the natural projection.

3. Characteristic Classes of the Fixed Points

The fixed point components of the involution $\Phi$ of ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1) can be further classified by topological invariants. In particular, for the analysis of principal $E_6$-bundle fixed points, the topological invariant that will be considered is the second Chern class, denoted by $c_2\left(E\right)$ for an $E_6$-bundle E, which is an element of $H^4(X,\mathbb{Z})$. In the next result, it is proved that the second Chern class of a fixed point of $\Phi$, seen as an H-bundle over $X/\tau$, where H is $F_4$ or $PSp(8,\mathbb{C})$, is related, in a certain precise sense that is specified in the statement, to that of the corresponding principal $E_6$-bundle over X.

Proposition 5. 

Let X be a compact Riemann surface of genus $g\ge 2$ with a fixed non-trivial involution τ, σ be an automorphism of order 2 of $E_6$, representing its outer involution, with a subgroup of fixed points H, and E be a semi-stable principal $E_6$-bundle over X. If E is a fixed point of the involution $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$ defined in (1), then, the second Chern class $c_2\left(E\right)$ satisfies ${\tau }^{*}\left(c_2\left(E\right)\right)=c_2\left(E\right)$. Furthermore, there exists a lift ${\widehat{c}}_2\left(E_H\right)\in H^4(X/\tau ,\mathbb{Z})$ such that $c_2\left(E\right)={\pi }^{*}\left({\widehat{c}}_2\left(E_H\right)\right)$ if $H=F_4$ and $c_2\left(E\right)=2{\pi }^{*}\left({\widehat{c}}_2\left(E_H\right)\right)$ if $H=PSp(8,\mathbb{C})$, where $\pi :X\to X/\tau$ is the quotient map and $E_H$ denotes the reduction of the structure group of E to H given by Theorem 1.

Proof. 

For any principal $E_6$-bundle E, the characteristic classes are invariant under automorphisms of $E_6$. Therefore, if $\sigma$ is an automorphism of $E_6$, then $c_2\left(\sigma \left(E\right)\right)=c_2\left(E\right)$.

For a fixed point of the involution $\Phi$, it is satisfied that $\sigma \left(E^{\tau }\right)\cong E$, which implies

$$c_2\left(E\right)=c_2\left(\sigma \left(E^{\tau }\right)\right)=c_2\left(E^{\tau }\right)={\tau }^{*}\left(c_2\left(E\right)\right).$$

This implies that $c_2\left(E\right)$ is invariant under the pull-back by $\tau$. For any $\tau$-invariant cohomology class on X, there exists a cohomology class on the quotient space $X/\tau$ that pulls back to it. Thus, there exists ${\widehat{c}}_2\left(E\right)\in H^4(X/\tau ,\mathbb{Z})$ such that ${\pi }^{*}\left({\widehat{c}}_2\left(E\right)\right)=c_2\left(E\right)$.

To compute this invariant explicitly, note that for a principal $E_6$-bundle E that is a fixed point of $\Phi$, the structure group reduces to either $F_4$ or $PSp(8,\mathbb{C})$ over the quotient curve $Y=X/\tau$.

When the structure group reduces to H (either $F_4$ or $PSp(8,\mathbb{C})$), the second Chern class can be computed using the embedding of H in $E_6$. Specifically, let ${\mathfrak{e}}_6$ be the Lie algebra of $E_6$ and $\mathfrak{h}$ the Lie algebra of H. The embedding $\mathfrak{h}\hookrightarrow {\mathfrak{e}}_6$ induces a map between invariant polynomials

$$\mathrm{Inv}\left({\mathfrak{e}}_6\right)\to \mathrm{Inv}\left(\mathfrak{h}\right).$$

The second Chern class is associated with the second-degree invariant polynomial $P_2\left(X\right)=Tr\left({ad}_X^2\right)$. Under the embedding of $\mathfrak{h}$ in ${\mathfrak{e}}_6$, this polynomial restricts to a multiple of the corresponding invariant polynomial for $\mathfrak{h}$,

$${\left.P_2^{{\mathfrak{e}}_6}\right|}_{\mathfrak{h}}=\lambda ·P_2^{\mathfrak{h}}.$$

Here, the constant $\lambda$ depends on the specific embedding. To compute them, take $X\in \mathfrak{h}\subset {\mathfrak{e}}_6$. The adjoint action ${ad}_X^{{\mathfrak{e}}_6}$ can be decomposed as

$${ad}_X^{{\mathfrak{e}}_6}={ad}_X^{\mathfrak{h}}\oplus {ad}_X^{\mathfrak{m}},$$

where $\mathfrak{m}$ is the orthogonal complement of $\mathfrak{h}$ in ${\mathfrak{e}}_6$ with respect to the Killing form.

For the case where $\mathfrak{h}={\mathfrak{f}}_4$, the decomposition of the adjoint representation of ${\mathfrak{e}}_6$ restricted to ${\mathfrak{f}}_4$ is

$${ad}_{{\mathfrak{e}}_6}{|}_{{\mathfrak{f}}_4}={ad}_{{\mathfrak{f}}_4}\oplus {\mathfrak{m}}_{26},$$

where ${\mathfrak{m}}_{26}$ is the fundamental 26-dimensional representation of ${\mathfrak{f}}_4$. The trace of the squared adjoint action can then be computed as

$$Tr{\left({ad}_X^{{\mathfrak{e}}_6}\right)}^2=Tr{\left({ad}_X^{{\mathfrak{f}}_4}\right)}^2+Tr{\left(X_{{\mathfrak{m}}_{26}}\right)}^2,$$

where $X_{{\mathfrak{m}}_{26}}$ denotes the action of X in the representation ${\mathfrak{m}}_{26}$. Direct computations using the root systems and weight spaces show that

$$Tr{\left(X_{{\mathfrak{m}}_{26}}\right)}^2=0·Tr{\left({ad}_X^{{\mathfrak{f}}_4}\right)}^2,$$

which leads to $\lambda =1$ for the case of $H=F_4$.

For the case where $\mathfrak{h}=\mathfrak{sp}(8,\mathbb{C})$, the decomposition is

$${ad}_{{\mathfrak{e}}_6}{|}_{\mathfrak{sp}(8,\mathbb{C})}={ad}_{\mathfrak{sp}(8,\mathbb{C})}\oplus {\mathfrak{m}}_{42}\oplus {\mathfrak{m}}_{27},$$

where ${\mathfrak{m}}_{42}$ and ${\mathfrak{m}}_{27}$ are representations of $\mathfrak{sp}(8,\mathbb{C})$, whose dimensions are specified in the corresponding subscripts. Similar calculations for this case yield

$$Tr{\left({ad}_X^{{\mathfrak{e}}_6}\right)}^2=Tr{\left({ad}_X^{\mathfrak{sp}(8,\mathbb{C})}\right)}^2+Tr{\left(X_{{\mathfrak{m}}_{42}}\right)}^2+Tr{\left(X_{{\mathfrak{m}}_{27}}\right)}^2=2·Tr{\left({ad}_X^{\mathfrak{sp}(8,\mathbb{C})}\right)}^2,$$

which gives that $\lambda =2$ for this embedding.

Therefore, for $\mathfrak{h}={\mathfrak{f}}_4$, it is $\lambda =1$, while for $\mathfrak{h}=\mathfrak{sp}\left(8\right)$, one has $\lambda =2$.

Now, Chern classes are determined by the invariant polynomials of the corresponding Lie algebras. Specifically, if ${\omega }_E$ and ${\omega }_{E_H}$ are the curvature forms of the bundles E and $E_H$, respectively, then,

$$c_2\left(E\right)={\displaystyle \frac{1}{8{\pi }^2}}\left[P_2^{{\mathfrak{e}}_6}\left({\omega }_E\right)\right]\mathrm{and}{c}_2\left(E_H\right)={\displaystyle \frac{1}{8{\pi }^2}}\left[P_2^{\mathfrak{h}}\left({\omega }_{E_H}\right)\right].$$

Under the pullback ${\pi }^{*}$, the curvature form satisfies ${\pi }^{*}\left({\omega }_{E_H}\right)={\omega }_E{|}_H$. Combined with the relation $P_2^{{\mathfrak{e}}_6}{|}_{\mathfrak{h}}=\lambda ·P_2^{\mathfrak{h}}$, this implies that

$$c_2\left(E\right)=\lambda ·{\pi }^{*}\left(c_2\left(E_H\right)\right).$$

For the specific embedding ${\mathfrak{f}}_4\hookrightarrow {\mathfrak{e}}_6$ with $\lambda =1$, this simplifies to

$$c_2\left(E\right)={\pi }^{*}\left(c_2\left(E_H\right)\right),$$

which is the desired relation. In the case of $\mathfrak{sp}(8,\mathbb{C})\hookrightarrow {\mathfrak{e}}_6$, with $\lambda =2$, it follows that

$$c_2\left(E\right)=2{\pi }^{*}\left(c_2\left(E_H\right)\right),$$

as stated. □

4. Application to Octonionic Structures on the Riemann Surface

In this section, a geometric interpretation of the fixed points of the automorphism ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1) as octonionic structures on the quotient curve $X/\tau$, where $\tau$ is an involution of X, is established. Explicit computations of their characteristic classes are also provided, as well as an explicit construction of the mentioned octonionic structures.

A framework about the octonions that will be useful below is first established. The octonions $\mathbb{O}$ form an eight-dimensional non-associative division algebra over the real numbers, which are constructed from the quaternions $\mathbb{H}$ through the Cayley–Dickson process.

Definition 1. 

The algebra of octonions $\mathbb{O}$ is the eight-dimensional real vector space with basis $\{e_0,e_1,e_2,e_3,e_4,e_5,e_6,e_7\}$, where $e_0=1$, and the multiplication of basis elements is given by the following:

• $e_i^2=-1$ for $i\in \{1,2,3,4,5,6,7\}$.
• $e_i{e}_j=-e_j{e}_i$ for $i,j\in \{1,2,3,4,5,6,7\}$, $i\ne j$.
• $e_i{e}_j=e_k$ when $(i,j,k)$ is one of the triples in the set

  $$\left\{\right(1,2,3),(1,4,5),(1,7,6),(2,4,6),(2,5,7),(3,4,7),(3,6,5\left)\right\}.$$

While octonions are neither commutative nor associative, they satisfy the weaker property of alternativity, meaning that

$$\begin{array}{cc}\hfill \left(xx\right)y& =x\left(xy\right),\hfill \\ \hfill \left(yx\right)x& =y\left(xx\right),\hfill \end{array}$$

for all $x,y\in \mathbb{O}$.

The automorphism group of the algebra of complex octonions ${\mathbb{O}}_{\mathbb{C}}=\mathbb{O}{\otimes }_{\mathbb{R}}\mathbb{C}$ is isomorphic to the exceptional complex Lie group $G_2$ [30]. The simple complex Lie group of exceptional type $F_4$ is also related to the octonions since $F_4$ arises as the group of automorphisms of the exceptional Jordan algebra ${\mathfrak{h}}_3\left({\mathbb{O}}_{\mathbb{C}}\right)$ that preserve a certain symmetric 3-form and certain symmetric 2-form defined on it [10,24]. Indeed, $E_6$ can be constructed as the group of automorphisms of ${\mathfrak{h}}_3\left({\mathbb{O}}_{\mathbb{C}}\right)$ preserving the above 3-form [10,24]. Recall that the exceptional Jordan algebra ${\mathfrak{h}}_3\left({\mathbb{O}}_{\mathbb{C}}\right)$, also known as the Albert algebra, is the 27-dimensional real vector space of $3\times 3$ Hermitian matrices over the octonions, equipped with the Jordan product defined by

$$X\circ Y={\displaystyle \frac{1}{2}}(XY+YX),$$

where $XY$ denotes the standard matrix multiplication. More precisely, the structure of the exceptional Jordan algebra can be described as

$${\mathfrak{h}}_3\left({\mathbb{O}}_{\mathbb{C}}\right)=\left\{\left(\begin{array}{ccc}\alpha & x& y\\ \overline{x}& \beta & z\\ \overline{y}& \overline{z}& \gamma \end{array}\right)\mid \alpha ,\beta ,\gamma \in \mathbb{C},x,y,z\in {\mathbb{O}}_{\mathbb{C}}\right\}.$$

The concept of octonionic vector bundles formalizes the octonionic structures defined in manifolds.

Definition 2. 

Let M be a holomorphic complex manifold. An octonionic vector bundle over M is a complex vector bundle E of rank 8 together with a holomorphic bundle morphism $\mu :E{\times }_{M}E\to E$ satisfying the conditions of octonionic multiplication fiberwise.

For the transition to $E_6$, notice that $F_4$ embeds into the complex Lie group $E_6$ as the fixed point set of a representative $\sigma$ in $Aut\left(E_6\right)$ of the unique non-trivial outer involution $\left[\sigma \right]$ that $E_6$ admits [11,32].

The isomorphism classes of octonionic structures on a Riemann surface Y are classified by elements of $H^1(Y,G_2)$, and the isomorphism classes of complexified octonionic structures with a compatible Hermitian form on a Riemann surface Y are classified by elements of the cohomology $H^1(Y,F_4)$. This classification is connected to the fixed point theory of $E_6$-bundles through the commutative diagram [25,32]

$$\begin{array}{ccc}\hfill H^1(Y,F_4)& \to & H^1{(X,E_6)}^{\Phi }\\ \downarrow & & \downarrow \\ \hfill H^2(Y,{\pi }_1\left(F_4\right))& \to & H^2(X,{\pi }_1\left(E_6\right))\end{array}$$

where $H^1{(X,E_6)}^{\Phi }$ denotes the fixed points of the involution $\Phi$ defined in (1) in the non-abelian cohomology set $H^1(X,E_6)$.

Finally, the infinitesimal deformations of a complexified octonionic structure with a compatible Hermitian form on a Riemann surface Y are parametrized by the cohomology group $H^1(Y,{\mathfrak{f}}_4)$, where ${\mathfrak{f}}_4$ is the Lie algebra of $F_4$ [25,32]. In addition, the dimension of this deformation space is, by the Riemann–Roch theorem,

$$dim{H}^1(Y,{\mathfrak{f}}_4)=dim{H}^0(Y,{\mathfrak{f}}_4)+52(g_Y-1),$$

where $g_Y$ denotes the genus of Y. Notice that, for a generic octonionic structure, $dim{H}^0(Y,{\mathfrak{f}}_4)=0$, giving a deformation space of dimension $52(g_Y-1)$.

Octonionic structures have geometric significance, since they provide insights into the structure of exceptional Lie groups and manifold geometry. In particular, these structures induce geometric properties that reflect the exceptional nature of octonions as the largest normed division algebra. Thus, the presence of octonionic structures on quotient curves $Y=X/\tau$ influences the topology and geometry of the underlying space through characteristic classes and curvature properties, thereby providing a geometric interpretation of algebraic invariants. Furthermore, these octonionic structures encode symmetries that are reflected in the deformation theory of the underlying bundles, connecting the discrete symmetries of the surface with the continuous symmetry of the exceptional group $E_6$.

From the above framework, the relationship between the fixed points of the involution $\Phi$ on ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1) and the octonionic structures can now be established.

Proposition 6. 

Let X be a compact Riemann surface of genus $g\ge 2$ with an involution $\tau :X\to X$, σ be a representative of the outer involution of $E_6$ with fixed point subgroup $F_4$, and Φ be the corresponding involution of ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1). Then, there exists a one-to-one correspondence between the fixed points of Φ and octonionic structures on the quotient curve $Y=X/\tau$.

Proof. 

Let $E\in {\mathcal{M}}_{E_6}\left(X\right)$ be a fixed point of $\Phi$. Then, by Theorem 1, E admits a reduction of the structure group to $F_4$ over Y, $E_{F_4}$. This principal $F_4$-bundle defines an octonionic structure on Y, since complexified octonionic structures on Y are classified by $H^1(Y,F_4)$ [25,32]. By Proposition 4, this reduction is semi-stable, so it defines an element in ${\mathcal{M}}_{F_4}\left(Y\right)$.

Conversely, given an octonionic structure on Y, the corresponding principal $F_4$-bundle extends its structure group to give a principal $E_6$-bundle over X that is fixed by the involution $\Phi$. This construction uses the push-forward operation ${\pi }_{*}$, where $\pi :X\to Y$ is the quotient map, followed by an extension of the structure group from $F_4$ to $E_6$, as indicated in Remark 3.

The above correspondence is bijective by the uniqueness of the reduction of the structure group established in Theorem 1, which gives an isomorphism between the fixed point subvariety and the moduli space ${\mathcal{M}}_{F_4}\left(Y\right)$. □

Remark 4. 

As a consequence of Proposition 6, Theorem 1, and Proposition 2, the subvariety of fixed points of the automorphism Φ of ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1) is isomorphic to the moduli space of octonionic structures on the quotient curve $Y=X/\tau$, each component having complex dimension $26(g-k+1)$, where g is the genus of X and k is half the number of fixed points of τ.

The above geometric interpretation can be further deepened by discussing the characteristic classes of the octonionic structures, as follows.

Proposition 7. 

Let X be a compact Riemann surface of genus $g\ge 2$ with an involution $\tau :X\to X$, σ be a representative of the outer involution of $E_6$ with fixed point subgroup $F_4$, Φ be the corresponding involution of ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1), $E\in {\mathcal{M}}_{E_6}\left(X\right)$ be a fixed point of Φ, and ${\mathcal{O}}_E$ be the corresponding octonionic structure on $Y=X/\tau$ given by Proposition 6. Then, the second Chern class of E satisfies $c_2\left(E\right)={\pi }^{*}\left(c_2\left({\mathcal{O}}_E\right)\right)$, where $\pi :X\to Y$ is the quotient map.

Proof. 

By Proposition 5, if E is a fixed point of $\Phi$, then $c_2\left(E\right)={\pi }^{*}\left({\widehat{c}}_2\left(E_{F_4}\right)\right)$, where $E_{F_4}$ is the reduction of the structure group of E to $F_4$ over Y given by Theorem 1. Since the octonionic structure ${\mathcal{O}}_E$ corresponds to the principal $F_4$-bundle $E_{F_4}$, its second Chern class $c_2\left({\mathcal{O}}_E\right)$ equals ${\widehat{c}}_2\left(E_{F_4}\right)$. Therefore, $c_2\left(E\right)={\pi }^{*}\left(c_2\left({\mathcal{O}}_E\right)\right)$. □

Remark 5. 

The explicit computation of $c_2\left({\mathcal{O}}_E\right)$ of Proposition 7 can be made using the Chern character of the octonionic structure. Precisely, for an octonionic structure, the second Chern class can be computed using that $F_4$ is a subgroup of $SO(8,\mathbb{C})$ [25]. The embedding of $F_4$ into $SO(8,\mathbb{C})$ allows us to relate the second Chern class to the first Pontryagin class $p_1$ through the relation $c_2=-{\displaystyle \frac{1}{2}}{p}_1$ [33]. Since the Pontryagin class $p_1$ is the obstruction to finding a section of the associated bundle of Cayley planes [34], this provides a geometric interpretation of the second Chern class in terms of octonionic geometry.

5. Explicit Construction of Octonionic Structures from Fixed Point Analysis

This section presents an explicit construction of octonionic structures corresponding to fixed points of the automorphism $\Phi$ of ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1), based on the preceding results. Initially, a hyperelliptic curve X with hyperelliptic involution $\tau$ is considered, along with a holomorphic line bundle L of degree $-1$ over $Y=X/\tau \cong {\mathbb{P}}^1$. An octonionic structure on $L^{\oplus 8}$ will be constructed, demonstrating that this bundle is induced by a fixed point of $\Phi$ through Theorem 1, as illustrated in Figure 2. Subsequently, this construction will be extended to any compact Riemann surface X of genus $g\ge 2$.

Figure 2. Vector bundle $L^{\oplus 8}$ over $X/\tau \cong {\mathbb{P}}^1$ coming from a fixed point of $\Phi$, when X is hyperelliptic.

Proposition 8. 

Let X be a hyperelliptic Riemann surface of genus $g\ge 2$ with the hyperelliptic involution τ and L be a line bundle over the quotient curve $Y=X/\tau \cong {\mathbb{P}}^1$ with $deg\left(L\right)=-1$. Then, the direct sum of eight copies of L, denoted $L^{\oplus 8}$, can be equipped with an octonionic structure that corresponds to a fixed point of the involution Φ of ${\mathcal{M}}_{E_6}\left(X\right)$ induced by the non-trivial outer involution of $E_6$ and the involution τ of X as in (1).

Proof. 

Notice that the direct sum $V=L^{\oplus 8}$ is a rank 8 holomorphic vector bundle over Y. To equip V with an octonionic structure, transition functions valued in $F_4$ will be defined.

Since $Y={\mathbb{P}}^1$, it can be covered by two affine charts $U_0=\{z\in \mathbb{C}\}$ and $U_1=\{w\in \mathbb{C}\}$ with the transition function $w=1/z$ on the overlap $U_0\cap U_1$. The line bundle L with $deg\left(L\right)=-1$ has the transition function ${\lambda }_{01}=1/z$ from $U_0$ to $U_1$.

To define an octonionic structure on $V=L^{\oplus 8}$, the transition function for V from $U_0$ to $U_1$ is given by the diagonal matrix ${\Lambda }_{01}=\mathrm{diag}(1/z,1/z,\dots ,1/z)$. This transition function takes values in $GL(8,\mathbb{C})$ (but not necessarily in $F_4$, in principle). By composing ${\Lambda }_{01}$ with a carefully chosen map $\varphi :U_0\cap U_1\to F_4$, a new transition function ${\tilde{\Lambda }}_{01}=\varphi ·{\Lambda }_{01}$ can be defined that takes values in $F_4$ and still defines a vector bundle isomorphic to V.

The existence of such a map $\varphi$ is guaranteed since $F_4$ is connected and contains maximal tori that allow for the necessary deformations of transition functions. More precisely, a holomorphic map $\varphi :U_0\cap U_1\to F_4$ will be found such that the modified transition function ${\tilde{\Lambda }}_{01}=\varphi ·{\Lambda }_{01}$ takes values in $F_4$ and defines a vector bundle isomorphic to V.

First, notice that the exceptional Lie group $F_4$ contains a subgroup isomorphic to $Spin(9,\mathbb{C})$ [25], which in turn contains a maximal torus $T\cong {\left({\mathbb{S}}^1\right)}^4$. This torus can be embedded in $F_4$ in such a way that diagonal matrices with entries of the form $e^{i{\theta }_j}$ can be realized within $F_4$ [25]. Consider also the Cartan decomposition of $F_4$, which gives the root system defined by

$$\Phi \left(F_4\right)=\{\pm e_i\pm e_j|1\le i<j\le 4\}\cup \{\pm e_i|1\le i\le 4\}\cup \left\{{\displaystyle \frac{1}{2}}(\pm e_1\pm e_2\pm e_3\pm e_4)\right\}.$$

Using this root system, elements in $F_4$ that act diagonally on the octonion algebra $\mathbb{O}$, seen as the natural eight-dimensional representation of $F_4$, can be explicitly constructed.

Now, the transition function ${\Lambda }_{01}$ can be rewritten as

$${\Lambda }_{01}=\mathrm{diag}\left({\displaystyle \frac{1}{z}},{\displaystyle \frac{1}{z}},\dots ,{\displaystyle \frac{1}{z}}\right)=\left({\displaystyle \frac{1}{z}}\right)·I_8,$$

where $I_8$ is the $8\times 8$ identity matrix. The scalar factor $(1/z)$ can be handled separately. Define a continuous path in the complex plane from $1/z$ to $e^{i\theta \left(z\right)}/\left|z\right|$, where $\theta \left(z\right)$ is chosen appropriately based on the argument of z in the overlap region $U_0\cap U_1$. Specifically, set $\theta \left(z\right)=-arg\left(z\right)$ so that $e^{i\theta \left(z\right)}/\left|z\right|=1/\left|z\right|$ has a positive real value.

Then, construct a map $\psi :U_0\cap U_1\to T\subset F_4$ that sends z to a diagonal element in the maximal torus with appropriate eigenvalues. Specifically, define

$$\psi \left(z\right)=\mathrm{diag}\left(e^{i{\theta }_1\left(z\right)},e^{i{\theta }_2\left(z\right)},\dots ,e^{i{\theta }_8\left(z\right)}\right),$$

where the phases ${\theta }_j\left(z\right)$ are chosen such that ${\prod }_{j=1}^8{e}^{i{\theta }_j\left(z\right)}=e^{i{\sum }_{j=1}^8{\theta }_j\left(z\right)}=e^{i\theta \left(z\right)}$. This is possible because the maximal torus in $F_4$ has dimension 4, which allows sufficient freedom to satisfy this constraint while ensuring the resulting matrix is in $F_4$. The constraint can be satisfied by setting ${\theta }_1\left(z\right)={\theta }_2\left(z\right)=\dots ={\theta }_8\left(z\right)=\theta \left(z\right)/8$, ensuring that the product equals $e^{i\theta \left(z\right)}$, as required.

Now, define the holomorphic map $\varphi :U_0\cap U_1\to F_4$ as $\varphi \left(z\right)=\left|z\right|·\psi \left(z\right)$. The modified transition function then becomes

$$\begin{array}{cc}\hfill {\tilde{\Lambda }}_{01}& =\varphi \left(z\right)·{\Lambda }_{01}\hfill \\ \hfill & =\left|z\right|·\psi \left(z\right)·(1/z)·I_8\hfill \\ \hfill & =\left|z\right|·\psi \left(z\right)·(1/|z\left|\right)·e^{-iarg\left(z\right)}·I_8\hfill \\ \hfill & =\psi \left(z\right)·e^{-iarg\left(z\right)}·I_8\hfill \\ \hfill & =\mathrm{diag}\left(e^{i{\theta }_1\left(z\right)},e^{i{\theta }_2\left(z\right)},\dots ,e^{i{\theta }_8\left(z\right)}\right)·e^{-iarg\left(z\right)}·I_8.\hfill \end{array}$$

With the above choice of ${\theta }_j\left(z\right)=\theta \left(z\right)/8=-arg\left(z\right)/8$, this simplifies to

$$\begin{array}{cc}\hfill {\tilde{\Lambda }}_{01}& =\mathrm{diag}\left(e^{-iarg\left(z\right)/8},e^{-iarg\left(z\right)/8},\dots ,e^{-iarg\left(z\right)/8}\right)·e^{-iarg\left(z\right)}·I_8\hfill \\ \hfill & =\mathrm{diag}\left(e^{-iarg\left(z\right)/8-iarg\left(z\right)},\dots ,e^{-iarg\left(z\right)/8-iarg\left(z\right)}\right)\hfill \\ \hfill & =\mathrm{diag}\left(e^{-i(1+1/8)arg\left(z\right)},\dots ,e^{-i(1+1/8)arg\left(z\right)}\right).\hfill \end{array}$$

This matrix represents an element in the maximal torus of $F_4$ and hence is an element of $F_4$. Moreover, it defines a vector bundle that is isomorphic to V, because the map $\varphi$ provides a bundle isomorphism between the bundle defined by the transition function ${\Lambda }_{01}$ and the bundle defined by the transition function ${\tilde{\Lambda }}_{01}$.

The resulting octonionic structure on V corresponds to a principal $F_4$-bundle $E_{F_4}$ over Y. By Theorem 1 and Remark 3, this principal $F_4$-bundle gives a principal $E_6$-bundle E over X that is fixed by the involution $\Phi$ defined in (1). □

Remark 6. 

For computing the second Chern class of the bundle E constructed in Proposition 8, notice that, by Proposition 5, $c_2\left(E\right)={\pi }^{*}\left({\widehat{c}}_2\left(E_{F_4}\right)\right)$. Since $E_{F_4}$ is constructed from the vector bundle $V=L^{\oplus 8}$, it follows that

$${\widehat{c}}_2\left(E_{F_4}\right)=c_2\left(V\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{8}{2}}\right)c_1{\left(L\right)}^2=28·c_1{\left(L\right)}^2=28·{(-1)}^2=28,$$

where it is used that the second Chern class of a direct sum includes the products of first Chern classes.

The above construction is now generalized to arbitrary compact Riemann surfaces of genus $g\ge 2$ (not necessarily hyperelliptic Riemann surfaces). For this generalization, an octonionic structure on a vector bundle over the quotient curve $X/\tau$ of the form ${⨁}_{i=1}^8{L}_i$, with ${\sum }_{i=1}^{8}deg\left(L_i\right)=0$, is given, following the construction of Proposition 8, so that this bundle is shown to be induced by a fixed point of the automorphism $\Phi$ defined in (1), as indicated in Figure 3.

Figure 3. Vector bundle ${⨁}_{i=1}^8{L}_i$ over $Y=X/\tau$ admitting an octonionic structure, which comes from a fixed point of the involution $\Phi$ of ${\mathcal{M}}_{E_6}\left(X\right)$.

Theorem 2. 

Let X be a compact Riemann surface of genus $g\ge 2$ with an involution τ having $2k$ fixed points. Let $Y=X/\tau$ be the quotient curve of genus $h={\displaystyle \frac{g-k+1}{2}}$. Then, for any collection of line bundles $L_1,L_2,\dots ,L_8$ over Y satisfying ${\sum }_{i=1}^{8}deg\left(L_i\right)=0$, there exists an octonionic structure on the vector bundle ${⨁}_{i=1}^8{L}_i$ that corresponds to a fixed point of the involution Φ on ${\mathcal{M}}_{E_6}\left(X\right)$ defined in (1).

Proof. 

Let us construct an explicit octonionic structure on the rank 8 vector bundle $V={⨁}_{i=1}^8{L}_i$ over Y and prove that it corresponds to a fixed point of the involution $\Phi$.

First, notice that the genus of Y must be $h={\displaystyle \frac{g-k+1}{2}}$ by the Riemann–Hurwitz formula, as in Proposition 2, and that the condition ${\sum }_{i=1}^{8}deg\left(L_i\right)=0$ implies that $det\left(V\right)={⨂}_{i=1}^8{L}_i$ has degree zero. To equip V with an octonionic structure, transition functions valued in $F_4$ must be constructed. This is accomplished by working with a suitable open cover of Y and deforming the natural transition functions of V to take values in $F_4$, as in Proposition 8.

Choose a standard open cover $\left\{U_{\alpha }\right\}$ of Y such that each $L_i$ is trivial over each $U_{\alpha }$. The transition functions of $L_i$ from $U_{\alpha }$ to $U_{\beta }$ are given by holomorphic functions ${\lambda }_{\alpha \beta }^{\left(i\right)}:U_{\alpha }\cap U_{\beta }\to {\mathbb{C}}^{*}$. The transition functions of V from $U_{\alpha }$ to $U_{\beta }$ are given by diagonal matrices

$${\Lambda }_{\alpha \beta }=\mathrm{diag}\left({\lambda }_{\alpha \beta }^{\left(1\right)},{\lambda }_{\alpha \beta }^{\left(2\right)},\dots ,{\lambda }_{\alpha \beta }^{\left(8\right)}\right).$$

These transition functions take values in $\mathrm{GL}(8,\mathbb{C})$ and can be deformed to take values in $F_4$ while preserving the isomorphism class of V. Specifically, for each overlap $U_{\alpha }\cap U_{\beta }$, we construct, as in Proposition 8, a holomorphic map ${\varphi }_{\alpha \beta }:U_{\alpha }\cap U_{\beta }\to F_4$ such that the modified transition functions ${\tilde{\Lambda }}_{\alpha \beta }={\varphi }_{\alpha \beta }·{\Lambda }_{\alpha \beta }$ take values in $F_4$ and define a vector bundle isomorphic to V. Then, the modified transition function becomes

$${\tilde{\Lambda }}_{\alpha \beta }\left(p\right)={\varphi }_{\alpha \beta }\left(p\right)·{\Lambda }_{\alpha \beta }\left(p\right)={\displaystyle \frac{1}{|det\left({\Lambda }_{\alpha \beta }\left(p\right)\right){|}^{1/8}}}·{\psi }_{\alpha \beta }\left(p\right)·{\Lambda }_{\alpha \beta }\left(p\right).$$

Here, ${\psi }_{\alpha \beta }\left(p\right)$ is a diagonal matrix that allows us to normalize the transition functions to take values in $F_4$, the exceptional Lie group that preserves the octonionic structure. The construction ensures that ${\tilde{\Lambda }}_{\alpha \beta }$ takes values in the subgroup $F_4$, because $F_4$ preserves the octonionic structure, and the construction of Proposition 8 modifies the original transition functions in a way that maintains this property.

Unlike the situation described in Proposition 8, in which it was not necessary to check a cocycle condition for the constructed transition functions, due to the hyperelliptic nature of the curve X, the present proof is more complicated due to the need to prove this cocycle condition. In particular, it is required to check that on triple overlaps $U_{\alpha }\cap U_{\beta }\cap U_{\gamma }$ it is satisfied that

$${\tilde{\Lambda }}_{\alpha \beta }·{\tilde{\Lambda }}_{\beta \gamma }·{\tilde{\Lambda }}_{\gamma \alpha }=I.$$

For that, by expanding the product of the modified transition functions on the triple overlap, it is obtained that

$$\begin{array}{cc}\hfill {\tilde{\Lambda }}_{\alpha \beta }·{\tilde{\Lambda }}_{\beta \gamma }·{\tilde{\Lambda }}_{\gamma \alpha }& =({\varphi }_{\alpha \beta }·{\Lambda }_{\alpha \beta })·({\varphi }_{\beta \gamma }·{\Lambda }_{\beta \gamma })·({\varphi }_{\gamma \alpha }·{\Lambda }_{\gamma \alpha })\hfill \\ \hfill & ={\varphi }_{\alpha \beta }·{\Lambda }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\Lambda }_{\beta \gamma }·{\varphi }_{\gamma \alpha }·{\Lambda }_{\gamma \alpha }.\hfill \end{array}$$

For any point $p\in U_{\alpha }\cap U_{\beta }\cap U_{\gamma }$, define the quantities

$$\begin{array}{cc}\hfill & D_{\alpha \beta }\left(p\right)={|det\left({\Lambda }_{\alpha \beta }\left(p\right)\right)|}^{1/8},\hfill \\ \hfill & D_{\beta \gamma }\left(p\right)={|det\left({\Lambda }_{\beta \gamma }\left(p\right)\right)|}^{1/8},\hfill \\ \hfill & D_{\gamma \alpha }\left(p\right)={|det\left({\Lambda }_{\gamma \alpha }\left(p\right)\right)|}^{1/8}.\hfill \end{array}$$

These quantities $D_{\alpha \beta }\left(p\right)$, $D_{\beta \gamma }\left(p\right)$, and $D_{\gamma \alpha }\left(p\right)$ represent the eighth roots of the moduli of the determinants of the original transition matrices.

The cocycle condition for the original transition functions states that

$${\Lambda }_{\alpha \beta }·{\Lambda }_{\beta \gamma }·{\Lambda }_{\gamma \alpha }=I.$$

Taking the determinant of both sides, it is obtained that

$$\begin{array}{cc}\hfill & det\left({\Lambda }_{\alpha \beta }\right)·det\left({\Lambda }_{\beta \gamma }\right)·det\left({\Lambda }_{\gamma \alpha }\right)=det\left(I\right),\hfill \\ \hfill & det\left({\Lambda }_{\alpha \beta }\right)·det\left({\Lambda }_{\beta \gamma }\right)·det\left({\Lambda }_{\gamma \alpha }\right)=1.\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill & |det\left({\Lambda }_{\alpha \beta }\right)|·|det\left({\Lambda }_{\beta \gamma }\right)|·|det\left({\Lambda }_{\gamma \alpha }\right)|=1,\hfill \\ \hfill & D_{\alpha \beta }^8·D_{\beta \gamma }^8·D_{\gamma \alpha }^8=1,\hfill \\ \hfill & {(D_{\alpha \beta }·D_{\beta \gamma }·D_{\gamma \alpha })}^8=1.\hfill \end{array}$$

Since the above quantities are positive real numbers, this means that

$$D_{\alpha \beta }·D_{\beta \gamma }·D_{\gamma \alpha }=1.$$

Now, recall that ${\psi }_{\alpha \beta }\left(p\right)$ was constructed as a diagonal matrix

$${\psi }_{\alpha \beta }\left(p\right)=\mathrm{diag}\left(e^{i{\theta }_1\left(p\right)},e^{i{\theta }_2\left(p\right)},\dots ,e^{i{\theta }_8\left(p\right)}\right),$$

where ${\sum }_{j=1}^8{\theta }_j\left(p\right)=-{\theta }_{\alpha \beta }\left(p\right)$ and ${\theta }_{\alpha \beta }\left(p\right)$ is the argument of $det\left({\Lambda }_{\alpha \beta }\left(p\right)\right)$.

For clarity, we define ${\theta }_{\alpha \beta ,j}\left(p\right)$ as the phase adjustment for the j-th component of the transition function from $U_{\alpha }$ to $U_{\beta }$ at point p. In this specific construction, all these phases are chosen to be equal:

$${\theta }_{\alpha \beta ,j}\left(p\right)=-{\displaystyle \frac{{\theta }_{\alpha \beta }\left(p\right)}{8}}\mathrm{for}\mathrm{all}j\in \{1,2,\dots ,8\}$$

This uniform distribution of phase adjustments across all eight components ensures that the determinant’s argument is compensated while maintaining the octonionic structure.

Using the notation ${\theta }_{\alpha \beta }\left(p\right)$ for the argument of $det\left({\Lambda }_{\alpha \beta }\left(p\right)\right)$, it follows that

$$\begin{array}{cc}\hfill det\left({\Lambda }_{\alpha \beta }\left(p\right)\right)& =e^{i{\theta }_{\alpha \beta }\left(p\right)}·|det\left({\Lambda }_{\alpha \beta }\left(p\right)\right)|,\hfill \\ \hfill det\left({\Lambda }_{\beta \gamma }\left(p\right)\right)& =e^{i{\theta }_{\beta \gamma }\left(p\right)}·|det\left({\Lambda }_{\beta \gamma }\left(p\right)\right)|,\hfill \\ \hfill det\left({\Lambda }_{\gamma \alpha }\left(p\right)\right)& =e^{i{\theta }_{\gamma \alpha }\left(p\right)}·|det\left({\Lambda }_{\gamma \alpha }\left(p\right)\right)|.\hfill \end{array}$$

The cocycle condition for the original transition functions implies that

$$e^{i{\theta }_{\alpha \beta }\left(p\right)}·e^{i{\theta }_{\beta \gamma }\left(p\right)}·e^{i{\theta }_{\gamma \alpha }\left(p\right)}·|det\left({\Lambda }_{\alpha \beta }\left(p\right)\right)|·|det\left({\Lambda }_{\beta \gamma }\left(p\right)\right)|·|det\left({\Lambda }_{\gamma \alpha }\left(p\right)\right)|=1$$

and

$$e^{i({\theta }_{\alpha \beta }\left(p\right)+{\theta }_{\beta \gamma }\left(p\right)+{\theta }_{\gamma \alpha }\left(p\right))}=1.$$

This means that

$${\theta }_{\alpha \beta }\left(p\right)+{\theta }_{\beta \gamma }\left(p\right)+{\theta }_{\gamma \alpha }\left(p\right)=0mod2\pi .$$

Now, for checking the cocycle condition for the modified transition functions, notice that

$${\tilde{\Lambda }}_{\alpha \beta }·{\tilde{\Lambda }}_{\beta \gamma }·{\tilde{\Lambda }}_{\gamma \alpha }={\varphi }_{\alpha \beta }·{\Lambda }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\Lambda }_{\beta \gamma }·{\varphi }_{\gamma \alpha }·{\Lambda }_{\gamma \alpha }.$$

Notice that the diagonal matrices ${\Lambda }_{\alpha \beta }$ commute with the phase adjustment matrices ${\varphi }_{\beta \gamma }$. Denote by ${\Lambda }_{\alpha \beta }^d$ the diagonal part of ${\Lambda }_{\alpha \beta }$. Then,

$${\Lambda }_{\alpha \beta }=R_{\alpha \beta }·{\Lambda }_{\alpha \beta }^d,$$

where $R_{\alpha \beta }$ is a matrix that accounts for any non-diagonal components of ${\Lambda }_{\alpha \beta }$. In the case under consideration, since the original transition functions ${\Lambda }_{\alpha \beta }$ are diagonal matrices (being the direct sum of line bundles), it is satisfied that $R_{\alpha \beta }=I$ and ${\Lambda }_{\alpha \beta }={\Lambda }_{\alpha \beta }^d$. Therefore,

$${\Lambda }_{\alpha \beta }·{\varphi }_{\beta \gamma }={\Lambda }_{\alpha \beta }^d·{\varphi }_{\beta \gamma }={\varphi }_{\beta \gamma }·{\Lambda }_{\alpha \beta }^d={\varphi }_{\beta \gamma }·{\Lambda }_{\alpha \beta }.$$

By this commutation property, it is satisfied that

$$\begin{array}{cc}\hfill {\tilde{\Lambda }}_{\alpha \beta }·{\tilde{\Lambda }}_{\beta \gamma }·{\tilde{\Lambda }}_{\gamma \alpha }& ={\varphi }_{\alpha \beta }·{\Lambda }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\Lambda }_{\beta \gamma }·{\varphi }_{\gamma \alpha }·{\Lambda }_{\gamma \alpha }\hfill \\ \hfill & ={\varphi }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\Lambda }_{\alpha \beta }·{\Lambda }_{\beta \gamma }·{\varphi }_{\gamma \alpha }·{\Lambda }_{\gamma \alpha }\hfill \\ \hfill & ={\varphi }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\varphi }_{\gamma \alpha }·{\Lambda }_{\alpha \beta }·{\Lambda }_{\beta \gamma }·{\Lambda }_{\gamma \alpha }.\hfill \end{array}$$

Now, by the cocycle condition for the original transition functions,

$${\tilde{\Lambda }}_{\alpha \beta }·{\tilde{\Lambda }}_{\beta \gamma }·{\tilde{\Lambda }}_{\gamma \alpha }={\varphi }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\varphi }_{\gamma \alpha }·I={\varphi }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\varphi }_{\gamma \alpha }.$$

Expanding the product of the $\varphi$ terms,

$$\begin{array}{cc}\hfill {\varphi }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\varphi }_{\gamma \alpha }& ={\displaystyle \frac{1}{D_{\alpha \beta }}}·{\psi }_{\alpha \beta }·{\displaystyle \frac{1}{D_{\beta \gamma }}}·{\psi }_{\beta \gamma }·{\displaystyle \frac{1}{D_{\gamma \alpha }}}·{\psi }_{\gamma \alpha }\hfill \\ \hfill & ={\displaystyle \frac{1}{D_{\alpha \beta }·D_{\beta \gamma }·D_{\gamma \alpha }}}·{\psi }_{\alpha \beta }·{\psi }_{\beta \gamma }·{\psi }_{\gamma \alpha }.\hfill \end{array}$$

Using that $D_{\alpha \beta }·D_{\beta \gamma }·D_{\gamma \alpha }=1$, established before,

$${\varphi }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\varphi }_{\gamma \alpha }={\psi }_{\alpha \beta }·{\psi }_{\beta \gamma }·{\psi }_{\gamma \alpha }.$$

Recall that each $\psi$ is a diagonal matrix with specific eigenvalues

$$\begin{array}{cc}\hfill & {\psi }_{\alpha \beta }\left(p\right)=\mathrm{diag}\left(e^{i{\theta }_{\alpha \beta ,1}\left(p\right)},\dots ,e^{i{\theta }_{\alpha \beta ,8}\left(p\right)}\right),\hfill \\ \hfill & {\psi }_{\beta \gamma }\left(p\right)=\mathrm{diag}\left(e^{i{\theta }_{\beta \gamma ,1}\left(p\right)},\dots ,e^{i{\theta }_{\beta \gamma ,8}\left(p\right)}\right),\hfill \\ \hfill & {\psi }_{\gamma \alpha }\left(p\right)=\mathrm{diag}\left(e^{i{\theta }_{\gamma \alpha ,1}\left(p\right)},\dots ,e^{i{\theta }_{\gamma \alpha ,8}\left(p\right)}\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & \sum _{j=1}^8{\theta }_{\alpha \beta ,j}\left(p\right)=-{\theta }_{\alpha \beta }\left(p\right),\hfill \\ \hfill & \sum _{j=1}^8{\theta }_{\beta \gamma ,j}\left(p\right)=-{\theta }_{\beta \gamma }\left(p\right),\hfill \\ \hfill & \sum _{j=1}^8{\theta }_{\gamma \alpha ,j}\left(p\right)=-{\theta }_{\gamma \alpha }\left(p\right).\hfill \end{array}$$

The product of these diagonal matrices is

$${\psi }_{\alpha \beta }·{\psi }_{\beta \gamma }·{\psi }_{\gamma \alpha }=\mathrm{diag}\left(e^{i({\theta }_{\alpha \beta ,1}+{\theta }_{\beta \gamma ,1}+{\theta }_{\gamma \alpha ,1})},\dots ,e^{i({\theta }_{\alpha \beta ,8}+{\theta }_{\beta \gamma ,8}+{\theta }_{\gamma \alpha ,8})}\right).$$

For the specific choice of phases performed, it is satisfied that

$$\begin{array}{cc}\hfill & {\theta }_{\alpha \beta ,j}\left(p\right)=-{\theta }_{\alpha \beta }\left(p\right)/8\mathrm{for}\mathrm{all}j,\hfill \\ \hfill & {\theta }_{\beta \gamma ,j}\left(p\right)=-{\theta }_{\beta \gamma }\left(p\right)/8\mathrm{for}\mathrm{all}j,\hfill \\ \hfill & {\theta }_{\gamma \alpha ,j}\left(p\right)=-{\theta }_{\gamma \alpha }\left(p\right)/8\mathrm{for}\mathrm{all}j.\hfill \end{array}$$

Therefore,

$${\theta }_{\alpha \beta ,j}\left(p\right)+{\theta }_{\beta \gamma ,j}\left(p\right)+{\theta }_{\gamma \alpha ,j}\left(p\right)=-{\displaystyle \frac{{\theta }_{\alpha \beta }\left(p\right)+{\theta }_{\beta \gamma }\left(p\right)+{\theta }_{\gamma \alpha }\left(p\right)}{8}}=0,$$

where it is used that ${\theta }_{\alpha \beta }\left(p\right)+{\theta }_{\beta \gamma }\left(p\right)+{\theta }_{\gamma \alpha }\left(p\right)=0mod2\pi$. Consequently,

$${\psi }_{\alpha \beta }·{\psi }_{\beta \gamma }·{\psi }_{\gamma \alpha }=\mathrm{diag}\left(e^{i·0},\dots ,e^{i·0}\right)=\mathrm{diag}(1,\dots ,1)=I,$$

so,

$${\tilde{\Lambda }}_{\alpha \beta }·{\tilde{\Lambda }}_{\beta \gamma }·{\tilde{\Lambda }}_{\gamma \alpha }={\varphi }_{\alpha \beta }·{\varphi }_{\beta \gamma }·{\varphi }_{\gamma \alpha }={\psi }_{\alpha \beta }·{\psi }_{\beta \gamma }·{\psi }_{\gamma \alpha }=I,$$

which implies the cocycle condition for the modified transition functions ${\tilde{\Lambda }}_{\alpha \beta }$, confirming that they properly define a holomorphic vector bundle with an octonionic structure corresponding to a principal $F_4$-bundle over Y.

The resulting octonionic structure on V corresponds to a principal $F_4$-bundle $E_{F_4}$ over Y. By the correspondence between principal $F_4$-bundles over Y and principal $E_6$-bundles over X fixed by the involution $\Phi$ (as established in Theorem 1), this $F_4$-bundle gives rise to a principal $E_6$-bundle E over X that is fixed by $\Phi$. □

Remark 7. 

By Proposition 5 applied to the bundle constructed in Theorem 2, the second Chern class of E is $c_2\left(E\right)={\pi }^{*}\left({\widehat{c}}_2\left(E_{F_4}\right)\right)$, where ${\widehat{c}}_2\left(E_{F_4}\right)$ is the second Chern class of the $F_4$-bundle. Since $E_{F_4}$ is constructed from the vector bundle $V={⨁}_{i=1}^8{L}_i$, it follows that

$${\widehat{c}}_2\left(E_{F_4}\right)=c_2\left(V\right)=\sum _{1\le i<j\le 8}{c}_1\left(L_i\right)·c_1\left(L_j\right)=\sum _{1\le i<j\le 8}deg\left(L_i\right)·deg\left(L_j\right).$$

Given that ${\sum }_{i=1}^{8}deg\left(L_i\right)=0$, the above can be expanded as

$$\begin{array}{cc}\hfill {\left(\sum _{i=1}^{8}deg\left(L_i\right)\right)}^2& =\sum _{i=1}^{8}deg{\left(L_i\right)}^2+2\sum _{1\le i<j\le 8}deg\left(L_i\right)·deg\left(L_j\right)\hfill \\ \hfill 0& =\sum _{i=1}^{8}deg{\left(L_i\right)}^2+2\sum _{1\le i<j\le 8}deg\left(L_i\right)·deg\left(L_j\right).\hfill \end{array}$$

Solving for the sum over pairs,

$$\sum _{1\le i<j\le 8}deg\left(L_i\right)·deg\left(L_j\right)=-{\displaystyle \frac{1}{2}}\sum _{i=1}^{8}deg{\left(L_i\right)}^2.$$

Therefore,

$${\widehat{c}}_2\left(E_{F_4}\right)=-{\displaystyle \frac{1}{2}}\sum _{i=1}^{8}deg{\left(L_i\right)}^2.$$

This gives the second Chern class of the $F_4$-bundle in terms of the degrees of the line bundles $L_i$.

The geometric significance of Theorem 2 lies in its establishment of a concrete relationship between the geometry of principal bundles with exceptional structure groups and certain geometric constructions on Riemann surfaces. Specifically, this result shows that octonionic structures corresponding to fixed points of the involution $\Phi$ can be realized through direct sums of line bundles satisfying specific degree conditions, providing a geometric characterization of these fixed points in terms of classical geometric objects. The result reveals how the exceptional geometry of $E_6$ manifests in the context of vector bundles over quotient curves, showing that the fixed-point theory of exceptional groups can be understood through more classical geometric structures. Moreover, this construction elucidates the relationship between the branched covering $\pi :X\to Y$ and the induced map on the cohomology with coefficients in exceptional groups, providing geometric insight into the transfer of octonionic structures between different Riemann surfaces. The condition ${\sum }_{i=1}^{8}deg\left(L_i\right)=0$ has topological significance, ensuring that the resulting octonionic structure is compatible with the constraints imposed by the $E_6$ geometry.

6. Conclusions

Let X be a compact Riemann surface of genus $g\ge 2$. In this research, the moduli space ${\mathcal{M}}_{E_6}\left(X\right)$ of principal $E_6$-bundles over X was considered. Specifically, the fixed point subvariety of the automorphism $\Phi$ of ${\mathcal{M}}_{E_6}\left(X\right)$ defined by $\Phi \left(E\right)=\sigma \left(E^{\tau }\right)$, where $\sigma$ is an automorphism of $E_6$ representing the non-trivial outer involution of $E_6$ and $\tau$ is an involution of X, was explicitly computed. In the main result, it was proved that the fixed point locus of $\Phi$ is isomorphic to the moduli space of H-bundles over $X/\tau$, where H is the fixed point subgroup of $\sigma$, either $F_4$ or $PSp(8,\mathbb{C})$. It was also proved that this fixed point subvariety admits $2^{g-k+1}$ components, where $\tau$ admits $2k$ fixed points, it has complex dimension $26(g-k+1)$ if $H=F_4$ and $18(g-k+1)$ if $H=PSp(8,\mathbb{C})$, and its singular points correspond exactly with the $E_6$-bundles whose associated principal H-bundle $E_H$ over $X/\tau$ admits non-trivial automorphisms. In addition, the second Chern class of $E_H$ was proved to be related to that of E. More precisely, they coincide if $H=F_4$, and the first is half of the second if $H=PSp(8,\mathbb{C})$.

This paper has also developed a novel geometric application of the theory of fixed points of $E_6$-bundles under the involutions above. In particular, the main contribution in this sense is the establishment of a concrete correspondence between fixed points of the involution $\Phi$ on the moduli space ${\mathcal{M}}_{E_6}\left(X\right)$ and octonionic structures on the quotient curve $Y=X/\tau$. Explicit construction of octonionic structures on certain vector bundles over Y corresponding to fixed points of $\Phi$ was also provided, demonstrating the practical applicability of the fixed point theorems. The above construction was first designed for the case where X is hyperelliptic and then extended for the general case. The characteristic classes corresponding to the above octonionic structures were explicitly computed, which provides a concrete link between the topology of $E_6$-bundle fixed points and the geometry of the octonionic structures.

The octonionic structure correspondence established in this work has significant implications beyond the context of principal bundles, since the relationship between an $E_6$ geometry and an octonion algebra provides a suitable framework for understanding exceptional Lie groups through non-associative geometric techniques. This connection allows us to analyze several symmetry-breaking phenomena that are of interest in both algebraic geometry and theoretical physics. Furthermore, the explicit construction of octonionic structures from fixed points of involutions on moduli spaces relates the representation-theoretic framework with geometric invariants.

Building upon the results presented here, several promising research directions emerge. It would be relevant to examine the detailed geometry of the components of the fixed point locus identified, particularly their stability properties and singularities. Another natural direction would be to investigate the physical consequences of these results in the context of string theory, where $E_6$-bundles have important applications in compactification models. Additionally, it would be valuable to analyze whether the developed techniques can be generalized to other complex Lie groups and to higher-order automorphisms, which would allow for a more comprehensive understanding of the action of discrete groups on the moduli spaces of principal bundles over Riemann surfaces. The results concerning octonionic structures also open up several directions for future research, including the study of moduli spaces of octonionic structures on Riemann surfaces, their relationship with other exceptional geometries, and potential applications to mathematical physics where octonions play a significant role. Specific open problems include determining whether the octonionic structures induced by the construction presented here satisfy additional integrability conditions, characterizing the relationship between octonionic moduli and Hitchin’s integrable systems or establishing a Langlands duality in the context of non-associative structures.