A Fractional PDE-Based Model for Nerve Impulse Transport Solved Using a Conforming Virtual Element Method: Application to Prosthetic Implants
Abstract
1. Introduction
- Formulation of a novel mathematical model for nerve impulse transport, based on physical principles, with direct implications for the design and optimization of sensory prosthetics.
- Modeling of the governing equation as a two-dimensional nonlinear partial differential equation with a fractional time derivative (), enhancing the realism of physiological processes.
- Development of a VEM-based numerical framework, effectively addressing challenges posed by fractional-order derivatives.
- A methodological foundation based on regularity theory for nonlinearity, discrete maximal regularity, and the fractional Grünwald–Letnikov approximation, ensuring both stability and consistency.
- Theoretical guarantees of existence and uniqueness of the approximate solution, with proofs establishing stability, a priori error bounds, and optimal convergence rates.
- Numerical validation through -norm and -norm convergence analysis across different mesh configurations, demonstrating the robustness of the proposed approach.
- Applicability of the model to biomedical engineering, particularly in sensory prosthetic design, reinforcing its practical significance.
2. Physical Processes and Governing Equations
2.1. Time-Fractional Diffusion and Reactions
2.2. The Resultant Model
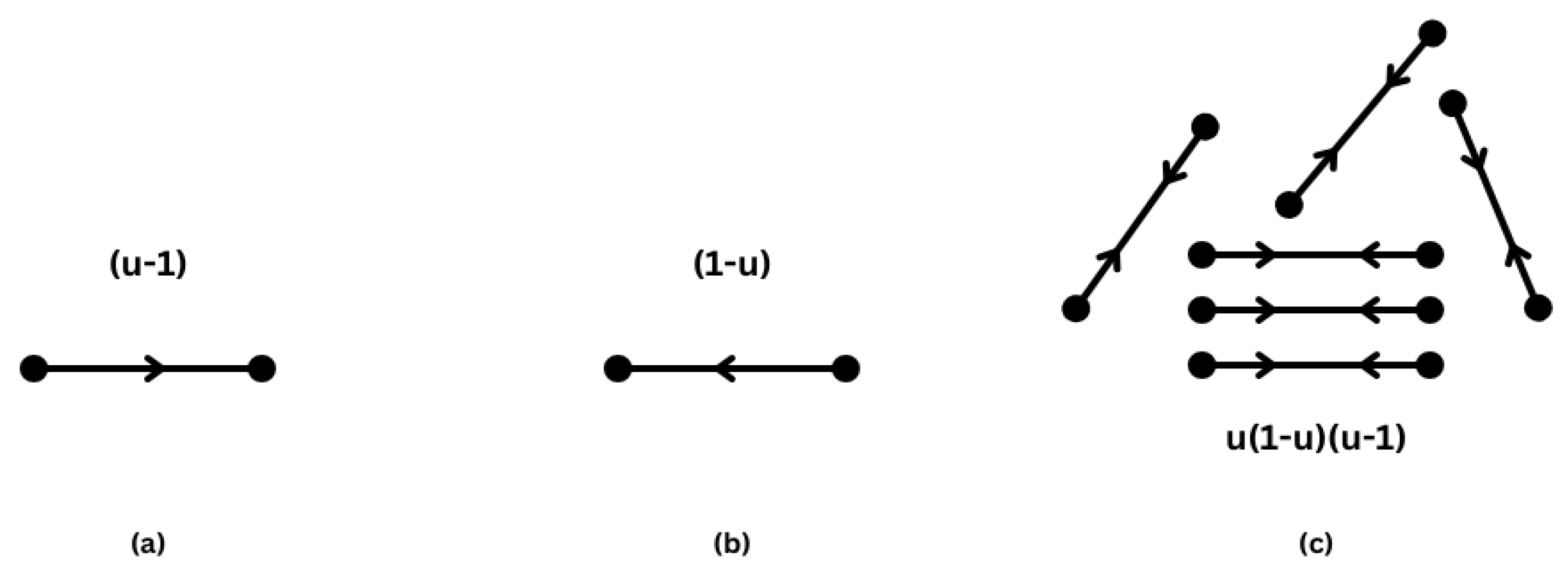
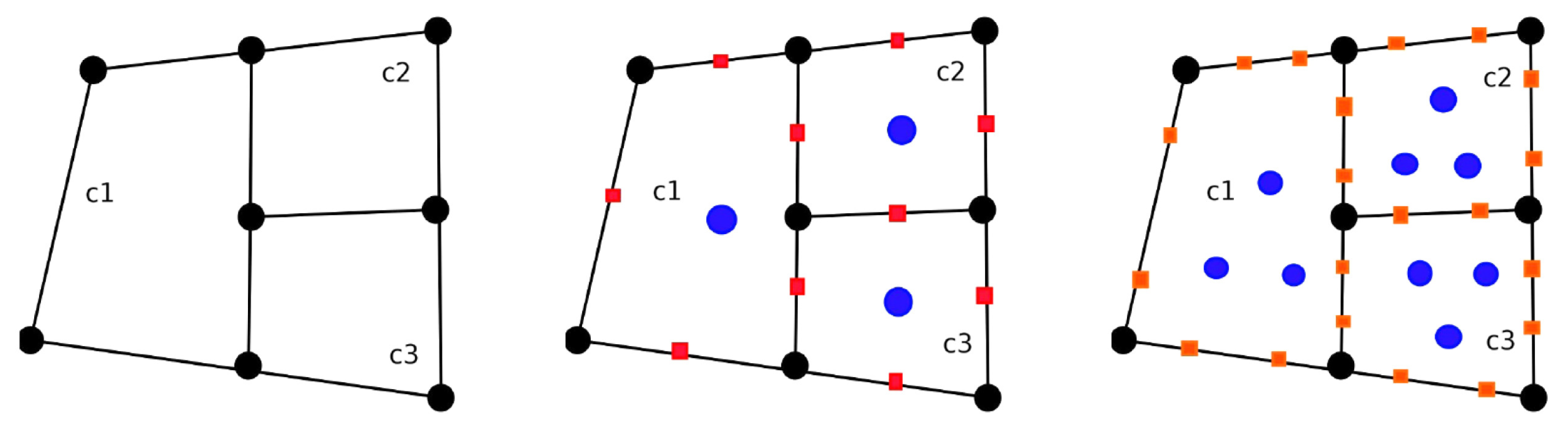
3. The Virtual Element Method
- For a ball with radius , E has a star shape;
- The distance between any two of its vertices is .
- (D1)
- The vertex values for , where the vertices of an element E for are denoted by ;
- (D2)
- On each edge e of for , the values of at the internal Gauss–Lobatto quadrature points;
- (D3)
- The polynomial moments for :
3.1. Virtual Element Discretization
- Stabilization for Stiffness Term:
- Stabilization for Mass Term:
3.2. Fully Discrete VEM
3.3. VEM Implementation
3.3.1. Hardware Specifications
- Device: HP Z2 Tower G9 Workstation Desktop PC.
- Processor: 13th Gen Intel(R) Core(TM) i7-13700K 3.40 GHz for efficient computations.
- Memory: 128 GB RAM.
- Storage: Solid State Drive (SSD) for faster data access and execution (1.86 TB).
3.3.2. Software and Implementation
- Software: MATLAB (Version R2021a).
- Key MATLAB Toolboxes: Symbolic Math Toolbox, Optimization Toolbox, Parallel Computing Toolbox.
- Numerical Method: Newton’s method is used to iteratively solve the nonlinear system, leveraging automatic differentiation via the Jacobian function.
- Convergence Criteria: The iterative solver stops when , where is a predefined tolerance level.
4. Theoretical Analysis and a Priori Error Estimates
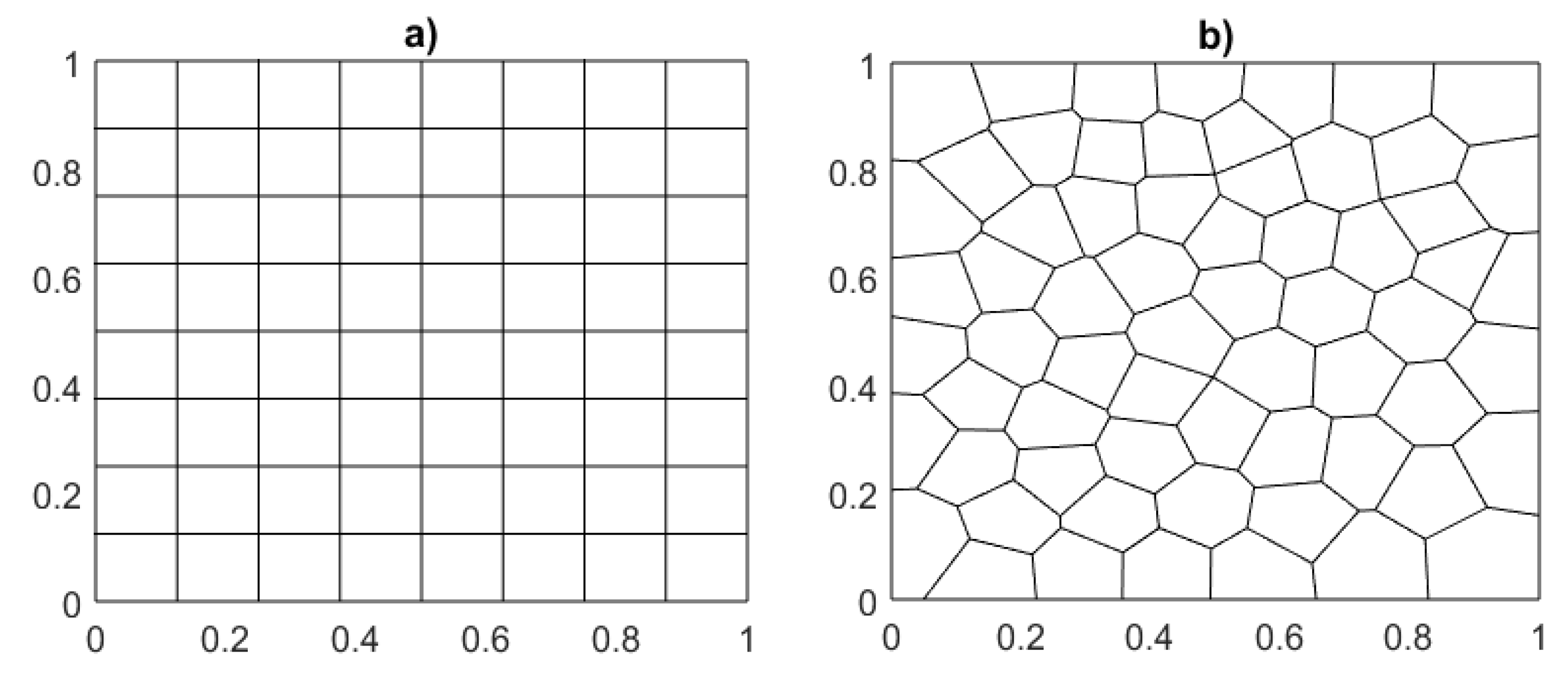
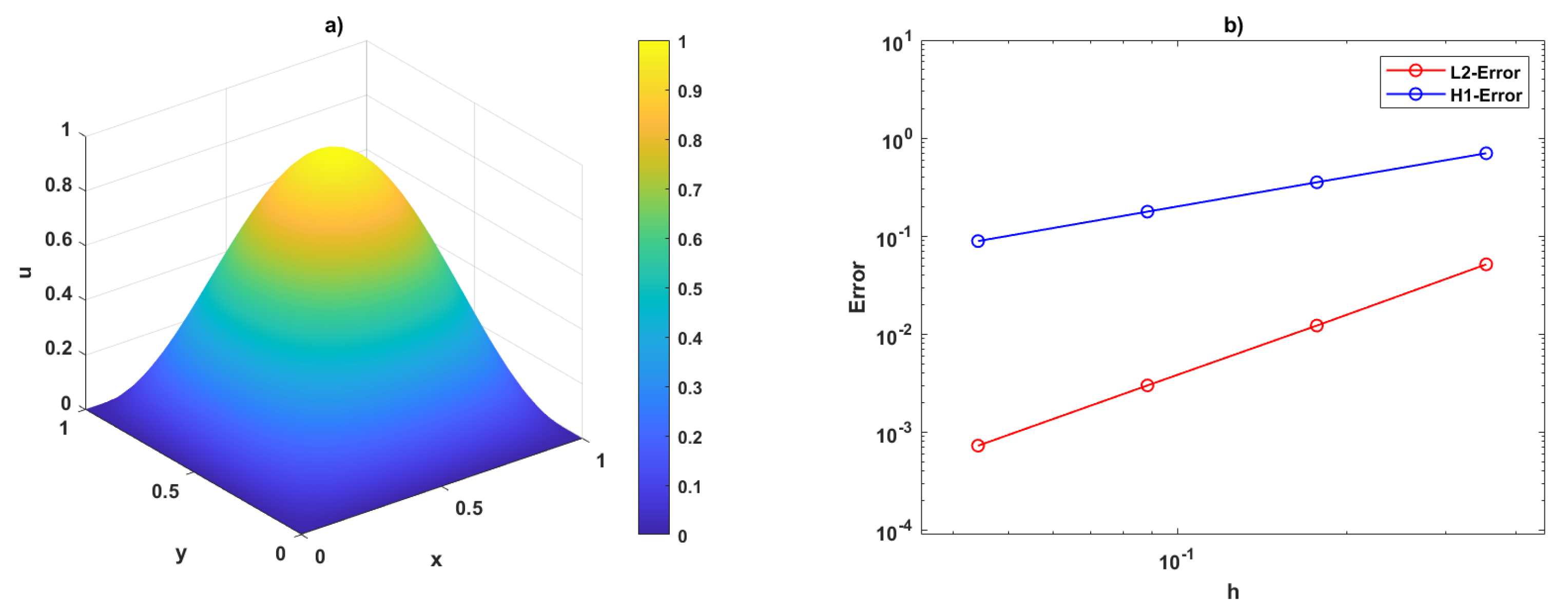
5. Numerical Results
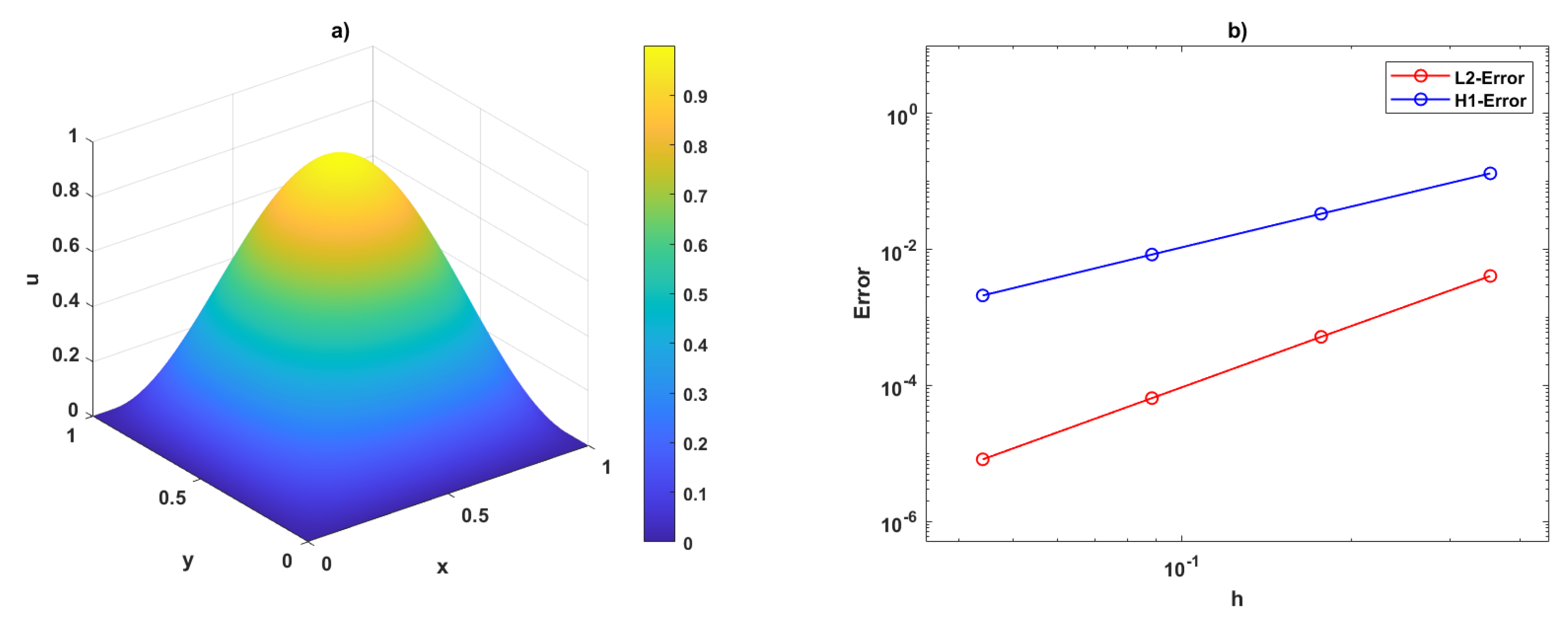
Example 1
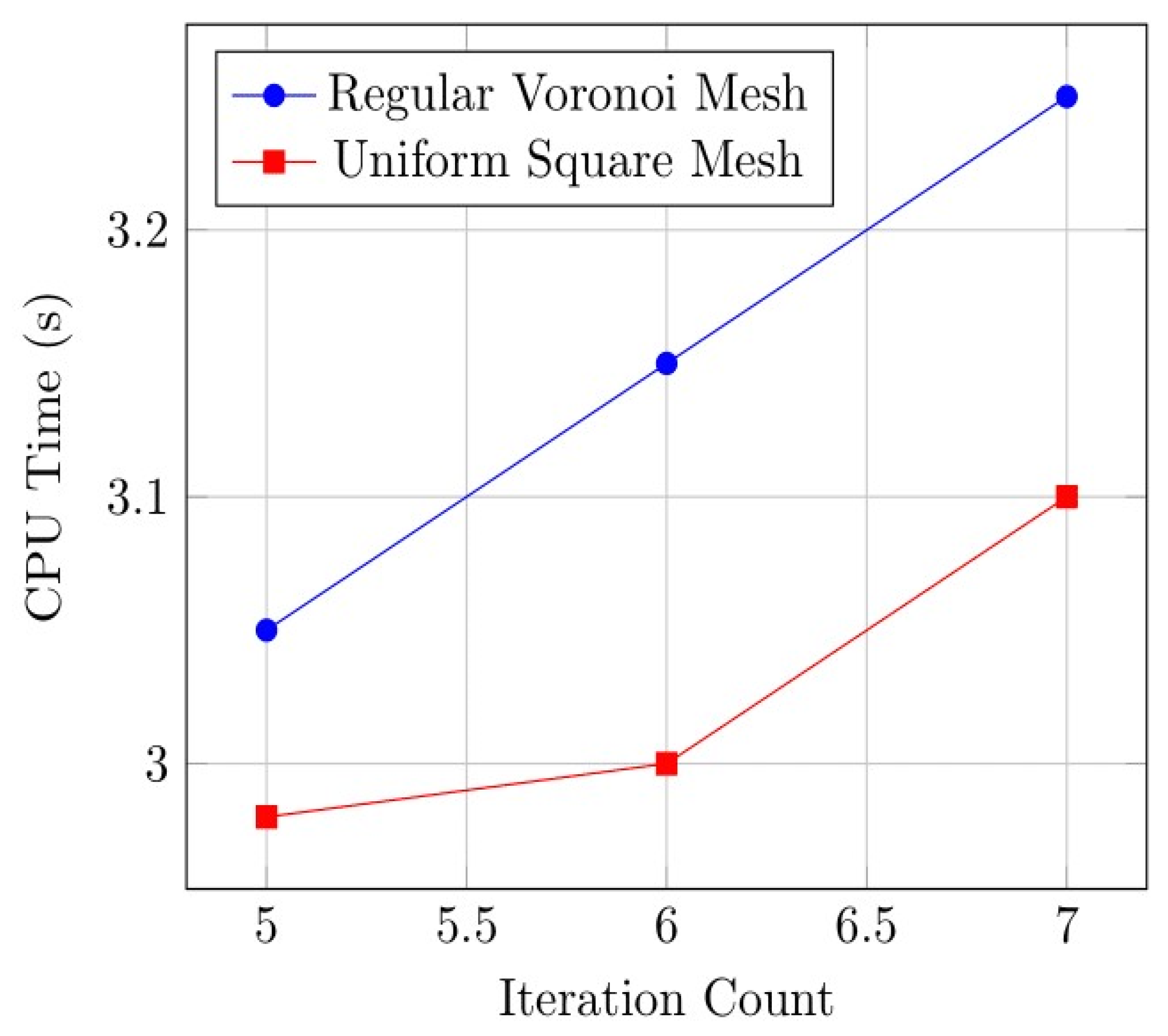
- Figure 9 illustrates the differences in computational efficiency between square and Voronoi meshes. The plot compares iteration count and CPU time, showing that a reduction in iterations leads to decreased computational cost, reflecting the solver’s efficiency across mesh types.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| VEM | Virtual Element Method |
| PDEs | Partial Differential Equations |
| GL | Grünwald–Letnikov |
| RL | Riemann–Liouville |
References
- Podlubny, I. (Ed.) Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1999; Volume 198. [Google Scholar]
- Wazwaz, A.M. Linear and Nonlinear Integral Equations: Methods and Applications, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J.E. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Baeumer, B.; Kov’acs, M.; Sankaranarayanan, H. Higher order Grünwald approximations of fractional derivatives and fractional powers of operators. Trans. Am. Math. Soc. 2014, 367, 813–834. [Google Scholar] [CrossRef]
- Sousa, E. Finite difference approximations for a fractional advection diffusion problem. J. Comput. Phys. 2009, 228, 4038–4054. [Google Scholar] [CrossRef]
- Acosta, G.; Borthagaray, J. A Fractional Laplace Equation: Regularity of Solutions and Finite Element Approximations. SIAM J. Numer. Anal. 2015, 55. [Google Scholar] [CrossRef]
- Acosta, G.; Bersetche, F.; Borthagaray, J. A short FE implementation for a 2d homogeneous Dirichlet problem of a Fractional Laplacian. Comput. Math. Appl. 2017, 74, 784–816. [Google Scholar] [CrossRef]
- Ervin, V.; Roop, J. Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Equ. 2006, 22, 558–576. [Google Scholar] [CrossRef]
- Esen, A.; Ucar, Y.; Yagmurlu, N.; Tasbozan, O. A Galerkin Finite Element Method to Solve Fractional Diffusion and Fractional Diffusion-Wave Equations. Math. Model. Anal. 2013, 18, 260–273. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. A Petrov-Galerkin Finite Element Method for Fractional Convection-Diffusion Equations. SIAM J. Numer. Anal. 2015, 54, 481–503. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, L.; Liu, J. Application of the LDG method using generalized alternating numerical flux to the fourth-order time-fractional sub-diffusion model. Appl. Math. Lett. 2025, 168, 109580. [Google Scholar] [CrossRef]
- Luo, W.H.; Huang, T.Z.; Wu, G.C.; Gu, X.M. Quadratic spline collocation method for the time fractional subdiffusion equation. Appl. Math. Comput. 2016, 276, 252–265. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Gu, X.M.; Ostermann, A. A Preconditioning Technique for an All-at-once System from Volterra Subdiffusion Equations with Graded Time Steps. J. Sci. Comput. 2021, 88, 11. [Google Scholar] [CrossRef]
- Gu, X.M.; Wu, S.L. A parallel-in-time iterative algorithm for Volterra partial integro-differential problems with weakly singular kernel. J. Comput. Phys. 2020, 417, 109576. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Brezzi, F.; Cangiani, A.; Manzini, G.; Marini, L.D.; Russo, A. Basic principles of Virtual Element Methods. Math. Model. Methods Appl. Sci. 2012, 23. [Google Scholar] [CrossRef]
- Ahmad, B.; Alsaedi, A.; Brezzi, F.; Marini, L.D.; Russo, A. Equivalent projectors for virtual element methods. Comput. Math. Appl. 2013, 66, 376–391. [Google Scholar] [CrossRef]
- Adak, D.; Natarajan, S. Virtual element method for semilinear sine–Gordon equation over polygonal mesh using product approximation technique. Math. Comput. Simul. 2020, 172, 224–243. [Google Scholar] [CrossRef]
- Arrutselvi, M.; Natarajan, E. Virtual element method for nonlinear convection–diffusion–reaction equation on polygonal meshes. Int. J. Comput. Math. 2020, 98, 1852–1876. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Lovadina, C.; Vacca, G. Divergence free virtual elements for the stokes problem on polygonal meshes. ESAIM: Math. Model. Numer. Anal. 2017, 51, 509–535. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Brezzi, F.; Marini, L.D.; Russo, A. Mixed Virtual Element Methods for general second order elliptic problems on polygonal meshes. ESAIM Math. Model. Numer. Anal. 2014, 50, 727–747. [Google Scholar] [CrossRef]
- Antonietti, P.F.; Manzini, G.; Verani, M. The conforming virtual element method for polyharmonic problems. Comput. Math. Appl. 2020, 79, 2021–2034. [Google Scholar] [CrossRef]
- Antonietti, P.; Beirão da Veiga, L.; Manzini, G. (Eds.) The Virtual Element Method and Its Applications; SEMA SIMAI Springer Series; Springer: Berlin/Heidelberg, Germany, 2022; Volume 31. [Google Scholar]
- Dar, Z.M.; Arrutselvi, M.; Chandru, M.; Manzini, G.; Natarajan, S. Analytical and Numerical Methods for Solving Fractional-Order Partial Differential Equations and the Virtual Element Method. SSRN 2024. [Google Scholar] [CrossRef]
- Li, D.; Liao, H.l.; Sun, W.; Wang, J.; Zhang, J. Analysis of L1-Galerkin FEMs for Time-Fractional Nonlinear Parabolic Problems. Commun. Comput. Phys. 2018, 24, 86–103. [Google Scholar] [CrossRef]
- Li, D.; Zhang, J. Efficient implementation to numerically solve the nonlinear time fractional parabolic problems on unbounded spatial domain. J. Comput. Phys. 2016, 322, 415–428. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, M. A local projection stabilization virtual element method for the time-fractional Burgers equation with high Reynolds numbers. Appl. Math. Comput. 2023, 436, 127509. [Google Scholar] [CrossRef]
- Dar, Z.M.; Chandru, M. A virtual element scheme for the time-fractional parabolic PDEs over distorted polygonal meshes. Alex. Eng. J. 2024, 106, 611–619. [Google Scholar] [CrossRef]
- Dar, Z.M.; Arrutselvi, M.; Muthusamy, C.; Natarajan, S.; Manzini, G. Virtual element approximations of the time-fractional nonlinear convection-diffusion equation on polygonal meshes. Math. Eng. 2025, 7, 96–129. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Jin, B.; Li, B.; Zhou, Z. Numerical Analysis of Nonlinear Subdiffusion Equations. SIAM J. Numer. Anal. 2018, 56, 1–23. [Google Scholar] [CrossRef]
- Mascotto, L. Ill-conditioning in the virtual element method: Stabilizations and bases. Numer. Methods Partial Differerential Equ. 2018, 34, 1258–1281. [Google Scholar] [CrossRef]
- Kumar, D.; Chaudhary, S.; Srinivas Kumar, V. Fractional Crank–Nicolson–Galerkin finite element scheme for the time-fractional nonlinear diffusion equation. Numer. Methods Partial Differ. Equ. 2019, 35, 2056–2075. [Google Scholar] [CrossRef]
- Jin, B.; Li, B.; Zhou, Z. An analysis of the Crank-Nicolson method for subdiffusion. IMA J. Numer. Anal. 2017, in press. [Google Scholar] [CrossRef]
- Dimitrov, Y. Numerical approximations for fractional differential equations. J. Fract. Calc. Appl. 2015, 5, 1–45. [Google Scholar]
- Thomée, V. Galerkin Finite Element Method for Parabolic Problems; Springer: Berlin/Heidelberg, Germany, 2006; Volume 1054. [Google Scholar] [CrossRef]
- Chen, H.; Holland, F.; Stynes, M. An analysis of the Grünwald–Letnikov scheme for initial-value problems with weakly singular solutions. Appl. Numer. Math. 2019, 139, 52–61. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag–Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Cangiani, A.; Manzini, G.; Sutton, O.J. Conforming and nonconforming virtual element methods for elliptic problems. IMA J. Numer. Anal. 2016, 37, 1317–1354. [Google Scholar] [CrossRef]



| h | DoF | -Norm | Rate | -Norm | Rate |
| 25 | 5.154952 × 10−2 | – | 5.153625 × 10−2 | – | |
| 81 | 1.224224 × 10−2 | 2.0741 | 1.222845 × 10−2 | 2.0753 | |
| 289 | 3.010066 × 10−3 | 2.0240 | 2.996480 × 10−3 | 2.0289 | |
| 1089 | 7.408137 × 10−4 | 2.0226 | 7.274806 × 10−4 | 2.0423 | |
| h | DoF | -Norm | Rate | -Norm | Rate |
| 25 | 7.005321 × 10−1 | – | 7.005239 × 10−1 | – | |
| 81 | 3.543888 × 10−1 | 0.9831 | 3.543856 × 10−1 | 0.9831 | |
| 289 | 1.778421 × 10−1 | 0.9947 | 1.778407 × 10−1 | 0.9947 | |
| 1089 | 8.900554 × 10−2 | 0.9986 | 8.900493 × 10−2 | 0.9986 | |
| h | DoF | -Norm | Rate | -Norm | Rate |
| 81 | 4.083755 × 10−3 | – | 4.083701 × 10−3 | – | |
| 289 | 5.196267 × 10−4 | 2.9743 | 5.195754 × 10−4 | 2.9754 | |
| 1089 | 6.529531 × 10−5 | 2.9924 | 6.522287 × 10−5 | 2.9939 | |
| 4225 | 8.613596 × 10−6 | 2.9223 | 8.199919 × 10−6 | 2.9917 | |
| h | DoF | -Norm | Rate | -Norm | Rate |
| 81 | 1.319297 × 10−1 | – | 1.319295 × 10−1 | – | |
| 289 | 3.357831 × 10−2 | 1.9742 | 3.357831 × 10−2 | 1.9742 | |
| 1089 | 8.432059 × 10−3 | 1.9936 | 8.432053 × 10−3 | 1.9936 | |
| 4225 | 2.110393 × 10−3 | 1.9984 | 2.110361 × 10−3 | 1.9984 | |
| h | DoF | -Norm | Rate | -Norm | Rate |
| 66 | 2.321432 × 10−2 | – | 2.319921 × 10−2 | – | |
| 256 | 5.294615 × 10−3 | 2.1324 | 5.281239 × 10−3 | 2.1351 | |
| 999 | 1.264779 × 10−3 | 2.0656 | 1.251974 × 10−3 | 2.0767 | |
| 3998 | 2.957565 × 10−4 | 2.0964 | 2.836264 × 10−4 | 2.1421 | |
| h | DoF | -Norm | Rate | -Norm | Rate |
| 66 | 5.001585 × 10−1 | – | 5.001548 × 10−1 | – | |
| 256 | 2.511504 × 10−1 | 0.9938 | 2.511499 × 10−1 | 0.9938 | |
| 999 | 1.260075 × 10−1 | 0.9950 | 1.260075 × 10−1 | 0.9950 | |
| 3998 | 6.293241 × 10−2 | 1.0016 | 6.293263 × 10−2 | 1.0016 | |
| h | DoF | -Norm | Rate | -Norm | Rate |
| 195 | 1.434247 × 10−3 | – | 1.434028 × 10−3 | – | |
| 767 | 1.795089 × 10−4 | 2.9982 | 1.793635 × 10−4 | 2.9991 | |
| 2997 | 2.259150 × 10−5 | 2.9902 | 2.237516 × 10−5 | 3.0029 | |
| 11995 | 2.872416 × 10−6 | 2.9754 | 2.868341 × 10−6 | 2.9636 | |
| h | DoF | -Norm | Rate | -Norm | Rate |
| 195 | 6.064623 × 10−2 | – | 6.064618 × 10−2 | – | |
| 767 | 1.479368 × 10−2 | 2.0354 | 1.479367 × 10−2 | 2.0354 | |
| 2997 | 3.690532 × 10−3 | 2.0031 | 3.690514 × 10−3 | 2.0031 | |
| 11995 | 9.079729 × 10−4 | 2.0231 | 9.078992 × 10−4 | 2.0232 | |
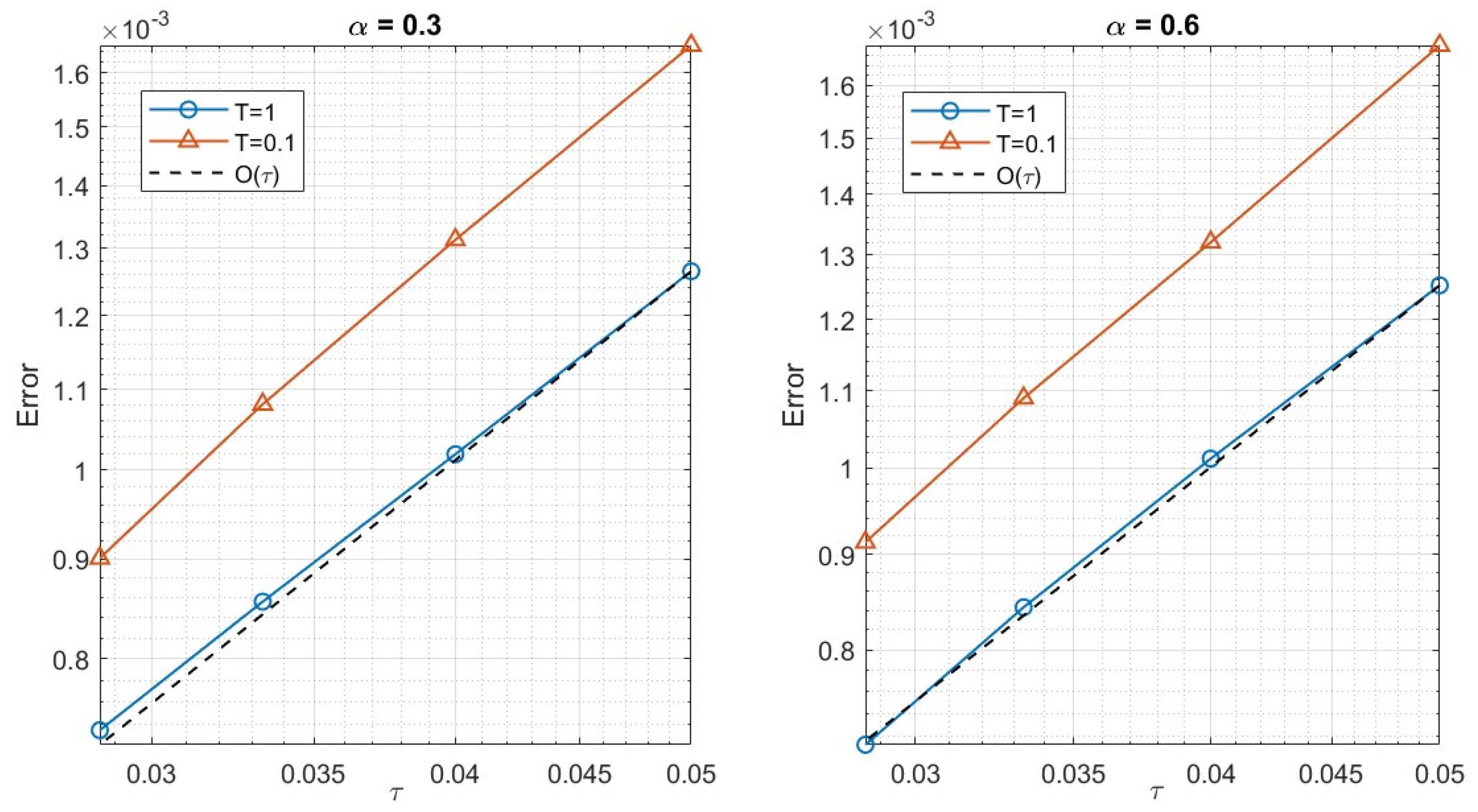
| T | K | -Norm | Rate | -Norm | Rate |
| 1 | 20 | 1.265 × 10−3 | – | 1.252 × 10−3 | – |
| 25 | 1.019 × 10−3 | 0.95 | 1.012 × 10−3 | 0.95 | |
| 30 | 8.561 × 10−4 | 0.96 | 8.431 × 10−4 | 1.00 | |
| 35 | 7.354 × 10−4 | 0.98 | 7.121 × 10−4 | 1.10 | |
| 0.1 | 20 | 1.652 × 10−3 | – | 1.681 × 10−3 | – |
| 25 | 1.313 × 10−3 | 1.03 | 1.320 × 10−3 | 1.08 | |
| 30 | 1.081 × 10−3 | 1.07 | 1.090 × 10−3 | 1.05 | |
| 35 | 9.012 × 10−4 | 1.18 | 9.132 × 10−4 | 1.15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dar, Z.M.; Muthusamy, C.; Ramos, H. A Fractional PDE-Based Model for Nerve Impulse Transport Solved Using a Conforming Virtual Element Method: Application to Prosthetic Implants. Axioms 2025, 14, 398. https://doi.org/10.3390/axioms14060398
Dar ZM, Muthusamy C, Ramos H. A Fractional PDE-Based Model for Nerve Impulse Transport Solved Using a Conforming Virtual Element Method: Application to Prosthetic Implants. Axioms. 2025; 14(6):398. https://doi.org/10.3390/axioms14060398
Chicago/Turabian StyleDar, Zaffar Mehdi, Chandru Muthusamy, and Higinio Ramos. 2025. "A Fractional PDE-Based Model for Nerve Impulse Transport Solved Using a Conforming Virtual Element Method: Application to Prosthetic Implants" Axioms 14, no. 6: 398. https://doi.org/10.3390/axioms14060398
APA StyleDar, Z. M., Muthusamy, C., & Ramos, H. (2025). A Fractional PDE-Based Model for Nerve Impulse Transport Solved Using a Conforming Virtual Element Method: Application to Prosthetic Implants. Axioms, 14(6), 398. https://doi.org/10.3390/axioms14060398








