Domination Parameters of Unit Graphs of Rings

Abstract

Let R be a finite commutative ring with nonzero identity 1. In this paper, domination parameters, the domination number and the total dominating number, of the unit graph $\mathrm{G}(R)$ or the closed unit graph $\overline{\mathrm{G}}(R)$ of R are investigated. To study the domination number of $\mathrm{G}(R)$, we prove that it suffices to consider the case when R is a direct product of fields. Furthermore, we discuss the domination number and total dominating number of the unit graph of the ring of integers modulo n.

1. Introduction

Throughout this paper, all rings are finite and commutative with nonzero identity 1, and $\mathrm{U}(R)$ and $\mathrm{J}(R)$ denote, respectively, the set of units and the Jacobson radical of a ring R. Moreover, ${\mathbb{Z}}_n$ denotes the ring of integers modulo n.

1.1. Unit Graphs of Rings

Assigning a graph to a ring plays an important role in studying the structure of the ring. In 1988, Beck first introduced and studied the zero-divisor graph of a commutative ring in [1]. Since then, zero-divisor graphs, as well as many other graphs associated with rings, have been extensively studied.

With the unit of a ring being an important element of the ring, it is natural to associate a ring with a graph whose edge relationships rely on units of the ring instead of zero divisors. In 1990, Grimaldi first studied the unit graph of ${\mathbb{Z}}_n$. He reported various conclusions about the degree of a vertex, the Hamilton cycles, the covering number, the independence number, and the chromatic polynomial of the unit graph of ${\mathbb{Z}}_n$ in [2]. In 2010, Ashrafi et al. promoted the unit graph $\mathrm{G}({\mathbb{Z}}_n)$ to the unit graph $\mathrm{G}(R)$ for an arbitrary ring R, and reported some characterization conclusions for finite (commutative) rings regarding connectedness, chromatic index, diameter, girth, and planarity of $\mathrm{G}(R)$ in [3]. In recent years, there has been a continuous stream of research on unit graphs associated with a ring. In 2011, Maimani et al. obtained necessary and sufficient conditions for unit graphs to be Hamiltonian in [4]. In 2013, Heydari and Nikmehr studied the unit graph of a left Artinian ring in [5], and Afkhami and Khosh-Ahang investigated the unit graphs of rings of polynomials and power series in [6]. From 2014 to 2021, Su et al. investigated the unit graphs for an arbitrary ring with girth, planarity, higher genus unit graphs, diameter, and radius in [7,8,9,10,11].

Definition 1 

([12], Definitions and Remarks 2.1). Let R be a ring. The unit graph of R, denoted by $\mathrm{G}(R)$, is the simple graph obtained by setting all the elements of R to be vertices and defining distinct vertices x and y to be adjacent if and only if $x+y\in \mathrm{U}(R)$.

When omitting the words “simple" and “distinct" in the definition, we obtain a closed unit graph $\overline{\mathrm{G}}(R)$, and this graph may have loops. Note that $\overline{\mathrm{G}}(R)=\mathrm{G}(R)$ if and only if $2\notin \mathrm{U}(R)$, where $2=1_R+1_R$, $1_R$ is the identity of R.

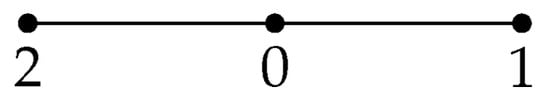
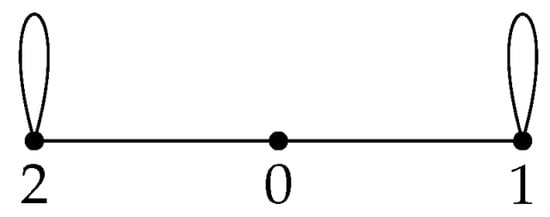
The unit graph $\mathrm{G}({\mathbb{Z}}_3)$ and the closed unit graph $\overline{\mathrm{G}}({\mathbb{Z}}_3)$ are, respectively, described in Figure 1 and Figure 2.

1.2. The Domination Number of Unit Graphs of Rings

Definition 2 

([13]). Let $\mathrm{G}$ be a graph and $V(\mathrm{G})$ be the set of its vertices. A nonempty subset S of $V(\mathrm{G})$ is called a dominating set if every vertex in $V(\mathrm{G})\setminus S$ is adjacent to at least one vertex in S. A subset S of $V(\mathrm{G})$ is called a total dominating set if every vertex in $V(\mathrm{G})$ is adjacent to some vertex in S.

The  domination number  of a graph $\mathrm{G}$, denoted by $\gamma (\mathrm{G})$, is defined as the minimum cardinality of a dominating set in $\mathrm{G}$, and the corresponding dominating set is called a $\gamma$-set  of $\mathrm{G}$. In a similar way, the  total dominating number  of $\mathrm{G}$, denoted by ${\gamma }_t(\mathrm{G})$, is defined as the minimum cardinality of a total dominating set in $\mathrm{G}$, and the corresponding dominating set is called a   ${\gamma }_t$-set  of $\mathrm{G}$.

Remark 1. 

Clearly, a total dominating set of a graph $\mathrm{G}$ must be a dominating set of $\mathrm{G}$, so $\gamma (\mathrm{G})⩽{\gamma }_t(\mathrm{G})$.

Remark 2. 

(i) Let $\mathrm{G}$ be a simple graph. Then, ${\gamma }_t(\mathrm{G})⩾2$, since a is not adjacent to a in $\mathrm{G}$ for any $a\in V(\mathrm{G})$.

(ii) Let R be a ring. Then, ${\gamma }_t(\overline{\mathrm{G}}(R))⩾2$, since a is not adjacent to $-a$ in $\overline{\mathrm{G}}(R)$ for any $a\in R$.

In 2010, Gasper Mekis gave some characterization results for the domination number of unit graphs of rings in [14]. In 2015, Kiani et al. characterized rings with unit graphs having a domination number less than four (see Lemma 7) in [15].This conclusion allows us to determine the structures of certain rings by means of the domination number of their unit graphs.

In 2020, Su et al. investigated the domination number of $\mathrm{G}({\mathbb{Z}}_n)$ when n has exactly three prime divisors in [16]. Throughout [15,16], when n has at most three prime divisors, the domination number of $\mathrm{G}({\mathbb{Z}}_n)$ is calculated, but the total dominating number of $\mathrm{G}({\mathbb{Z}}_n)$ and $\overline{\mathrm{G}}({\mathbb{Z}}_n)$ is not considered completely. In Section 3, we provide additional evidence for some remaining conditions (see Corollary 3).

In addition, let $S={\mathbb{Z}}_{p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}}\cong {\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}$, where $p_1<p_2<p_3$ are primes, ${\alpha }_1,{\alpha }_2,{\alpha }_3$ are positive integers, and ${\alpha }_1{\alpha }_2{\alpha }_3>1$. In [16], Su et al. found a $\gamma$-set of S, and they proved that this specific $\gamma$-set of S is a total dominating set of M, so ${\gamma }_t(\mathrm{G}(S))⩽\gamma (\mathrm{G}(S))$. Using Remark 1, they obtained that $\gamma (\mathrm{G}(S))={\gamma }_t(\mathrm{G}(S)$. So they raised the question in [16] (Remark):

$$\mathrm{Is}\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))\mathrm{true}\mathrm{for}\mathrm{all}n?$$

For this question, we provide four counterexamples and modify the question in Remark 11. However, in the four counterexamples, ${\mathbb{Z}}_n$ is exactly a product of certain fields (i.e., $|\mathrm{J}({\mathbb{Z}}_n)|=1$ using Remark 3). So, we modify the question as

$$\mathrm{Is}\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))\mathrm{true}\mathrm{when} |\mathrm{J}({\mathbb{Z}}_n)|>1?$$

Furthermore, we propose a new conjecture: For a ring R, is $\gamma (\mathrm{G}(R))={\gamma }_t(\mathrm{G}(R))$ true when $|\mathrm{J}(R)|>1$? By coincidence, we observed that $D/\mathrm{J}(M)$ is a total dominating set of $\mathrm{G}(S/\mathrm{J}(S))$, where D is the $\gamma$-set of $\mathrm{G}(S)$ of [16] (see Appendix A), and $\mathrm{J}(R)$ is a special concept of R since it meets the property of Lemma 3. Naturally, this drove us to further explore the relationships between $\gamma (\mathrm{G}(R))$ and ${\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$.

1.3. Layout of the Paper

In this paper, we focus on the unit graph associated with a ring. In Section 2, we introduce some notations of graphs, rings, and unit graphs of rings.

In Section 3, we investigate the relationships between the domination number and total dominating number of unit graphs of rings, and we prove that $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$, where R is a ring with $|\mathrm{J}(R)|⩾2$ (Theorem 1). According to this result, to study the domination number of the unit graph $\mathrm{G}(R)$, it suffices to study the total dominating number of the unit graph associated with the semisimple ring $R/\mathrm{J}(R)$. That is to say, it suffices to consider the cases when R is a direct product of fields using Lemma 5. In particular, to study the domination number of the unit graph of ${\mathbb{Z}}_n$, it suffices to consider the case when ${\mathbb{Z}}_n$ is directly decomposed into fields.

In Section 4, we focus on studying the domination number of $\mathrm{G}({\mathbb{Z}}_n)$ when n has at least four prime divisors. Let $T={\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}$, where $m⩾4$ and $p_1<p_2<\cdots <p_m$ are primes. We find the $\gamma$-set (also a ${\gamma }_t$-set) of $\mathrm{G}(T)$ and $\overline{\mathrm{G}}(T)$ when $p_1⩾3$ and $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$, and then we obtain the domination number and total dominating number of $\mathrm{G}(T)$ and $\overline{\mathrm{G}}(T)$ when $p_1⩾3$ and $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$ (Theorem 2). At the same time, in Theorem 2, we provide the range of the domination number and total dominating number of $\mathrm{G}(T)$ when $p_1=2$.

In Section 5, we provide additional properties of the domination number and total dominating number of $\mathrm{G}({\mathbb{Z}}_n)$ and $\overline{\mathrm{G}}({\mathbb{Z}}_n)$, and then we obtain the domination number and total dominating number when n has exactly four prime divisors (Theorem 3).

2. Preliminaries

In this section, we will review some notions about graphs and rings, and some results about unit graphs of rings, which will be used subsequently.

2.1. Some Notions of Graphs

A graph $\mathrm{G}$ is an ordered triple $(V(\mathrm{G}),E(\mathrm{G}),{\psi }_{\mathrm{G}})$ consisting of a nonempty set $V(\mathrm{G})$ of vertices, a set $E(\mathrm{G})$, disjoint from $V(\mathrm{G})$, of edges, and an incidence function ${\psi }_{\mathrm{G}}$ that associates with each edge of $\mathrm{G}$ an unordered pair of (not necessarily distinct) vertices of $\mathrm{G}$. If e is an edge and u and v are vertices such that ${\psi }_{\mathrm{G}}(e)=\{u,v\}$, then e is said to join u and v, and the vertices u and v are called the ends of e. The ends of an edge are said to be incident with the edge, and vice versa. Two vertices which are incident with a common edge are adjacent. An edge with identical ends is called a loop, and an edge with distinct ends a link. Two or more links with the same pair of ends are said to be parallel edges [17].

A graph is simple [17] if it has no loops or parallel edges. If two vertices u and v are adjacent in a graph $\mathrm{G}$, then we use the usual notation $u\sim v$ in $\mathrm{G}$, and $u\nsim v$ means that u and v are not adjacent. Some other notions used in graph theory are listed in the following (see [17]):

• A bipartite graph is one whose vertex set can be partitioned into two subsets X and Y, so that each edge has one end in X and one end in Y, such a partition $(X,Y)$ is called a bipartition of the graph.
• The degree $d_{\mathrm{G}}(v)$ of a vertex v in $\mathrm{G}$ is the number of edges of $\mathrm{G}$ incident with v, with each loop counting as two edges.
• The open neighborhood of a vertex v in a simple graph $\mathrm{G}$, denoted by $N_{\mathrm{G}}(v)$, is the set of all vertices of $\mathrm{G}$ which are adjacent to v.

2.2. Some Notions of Rings

There exist rings with exactly one maximal ideal; for example, fields. A ring with exactly one maximal ideal is called a local ring [3].

Lemma 1 

([3], Proposition 1.6). Let R be a local ring with exactly one maximal ideal M. Then, the following statements hold:

(i)

$M=R\setminus \mathrm{U}(R)$, where $\mathrm{U}(R)$ is the set of unit elements of R.

(ii)

$1+x\in \mathrm{U}(R)$ for any $x\in M$.

The Jacobson radical $\mathrm{J}(R)$ of a ring R is defined as the intersection of all the maximal ideals of R [3].

Lemma 2 

([3], Proposition 1.9). Let R be a ring. Then, $\mathrm{J}(R)=\{x\in R|1-xR\subseteq \mathrm{U}(R)\}$, where $1-xR=\{1-xr|r\in R\}$.

Lemma 3. 

Let R be a ring and $a\in R$. Then, $a\in \mathrm{U}(R)$ if and only if $a+\mathrm{J}(R)\in \mathrm{U}(R/\mathrm{J}(R)).$

Proof. 

This follows immediately from [18] (Proposition 4.8). □

Remark 3 

([15], Remark 3.15). It is known that every finite commutative ring is isomorphic to a direct product of local rings. Thus, for a given ring R, we may write $R\cong R_1\oplus \cdots \oplus R_n$, where $R_i$ is a local ring with maximal ideal $M_i$ for every $1⩽i⩽n$. It is easy to see that

$$\{R_1\oplus \cdots \oplus R_{i-1}\oplus M_i\oplus R_{i+1}\oplus \cdots \oplus R_n|1⩽i⩽n\}$$

is the set of all maximal ideals of $R_1\oplus \cdots \oplus R_n$ and thus we conclude that the Jacobson radical of R is isomorphic to $\mathrm{J}(R_1\oplus \cdots \oplus R_n)=M_1\oplus \cdots \oplus M_n$. Moreover,

$$R/\mathrm{J}(R)\cong (R_1\oplus \cdots \oplus R_n)/(M_1\oplus \cdots \oplus M_n)\cong (R_1/M_1)\oplus \cdots \oplus (R_n/M_n).$$

In particular, for the ring ${\mathbb{Z}}_n$, let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_s^{{\alpha }_s}$, where $p_1<p_2<\cdots <p_s$ are primes and s is an integer. Then, ${\mathbb{Z}}_n\cong {\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus \cdots \oplus {\mathbb{Z}}_{p_s^{{\alpha }_s}}$, where ${\mathbb{Z}}_{p_1^{{\alpha }_1}},\cdots ,{\mathbb{Z}}_{p_s^{{\alpha }_s}}$ are local rings.

Definition 3 

([19], Page 429, Definition 2.9). A ring R is said to be (Jacobson) semisimple if its Jacobson radical $\mathrm{J}(R)$ is zero.

Lemma 4 

([19], Page 431, Theorem 2.14). If R is a ring, then $R/\mathrm{J}(R)$ is semisimple.

Definition 4 

([19], Page 372, Definition 1.1 and Definition 1.2). Let $(\Sigma ;\supseteq )$ be a poset. The descending chain condition $(\mathbf{DCC})$ is that every decreasing sequence $I_1\supseteq I_2\supseteq \cdots$ in Σ is stationary (i.e., there exists $n\in Z_{+}$ such that $I_n=I_{n+1}=\cdots$ ). A ring R is left [resp. right] Artinian if R satisfies the descending chain condition on left [resp. right] ideals. R is said to be Artinian if R is both left and right Artinian.

Clearly, a finite communicative ring with nonzero identity is Artinian.

Lemma 5 

([19], Page 442, Exercise 3). A commutative semisimple left Artinian ring is a direct product of fields.

2.3. Some Known Results About Unit Graphs of Rings

Lemma 6 

([15], Lemma 4.8). Let R be a ring. Then, $\gamma (\mathrm{G}(R))⩽{\gamma }_t(\mathrm{G}(R))⩽{\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$.

Lemma 7 

([15], Theorem 2.2). Let R be a ring. Then, the following statements hold for the unit graph $\mathrm{G}(R)$:

(i) 

$\gamma (\mathrm{G}(R))=1$ if and only if R is a field.

(ii) 

$\gamma (\mathrm{G}(R))=2$ if and only if either R is a local ring which is not a field, R is isomorphic to the products of two fields such that only one of them has characteristic 2, or $R\cong {\mathbb{Z}}_2\oplus F$, where F is a field.

(iii) 

$\gamma (\mathrm{G}(R))=3$ if and only if R is not isomorphic to the product of two fields such that only one of them has characteristic 2, and $R\cong R_1\oplus R_2$, where $R_i$ is a local ring with maximal ideal $M_i$ in such a way that $R_i/M_i\ncong {\mathbb{Z}}_2$, for $i=1,2$.

Lemma 8 

([15], Lemma 4.2). Let R be a local ring with maximal ideal M such that $|R/M|=2$ and let S be a local ring. If R is not a field, then $\gamma (\mathrm{G}(R\oplus S))={\gamma }_t(\mathrm{G}(R\oplus S))=4$.

Lemma 9 

([15], Lemma 4.3). Let S be a local ring which is not a field. Then, $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus S))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus S))=4$.

Lemma 10 

([15], Lemma 4.5). Let $F_1$ and $F_2$ be two fields in which either both of them have characteristic 2 and none of them is isomorphic to ${\mathbb{Z}}_2$ or none of them has characteristic 2. Then, $\gamma (\mathrm{G}(F_1\oplus F_2))={\gamma }_t(\mathrm{G}(F_1\oplus F_2))=3$.

Lemma 11 

([15], Lemma 3.12). Let $F_1,F_{2}and{F}_3$ be three fields. Then, $\gamma (\mathrm{G}(F_1\oplus F_2\oplus F_3))=4$.

Lemma 12 

([15], Lemma 3.13). Let $F_1,\cdots ,F_k$ be fields. If $k⩾3$, then $\gamma (\mathrm{G}(F_1\oplus \cdots \oplus F_k))⩾k+1$.

Lemma 13 

([12], Proposition 2.4). Let R be a ring. Then, the following statements hold for the unit graph $\mathrm{G}(R)$ of R:

(i) 

If $2\notin \mathrm{U}(R)$, then the unit graph $\mathrm{G}(R)$ is a $|\mathrm{U}(R)|$-regular graph.

(ii) 

If $2\in \mathrm{U}(R)$, then for every $x\in \mathrm{U}(R)$ we have $d_{\mathrm{G}(R)}(x)=\left|\mathrm{U}(R)\right|-1$ and for every $x\in R\setminus \mathrm{U}(R)$ we have $d_{\mathrm{G}(R)}(x)=\left|\mathrm{U}(R)\right|.$

Corollary 1. 

Let R be a ring. Then, the following statements hold for the closed unit graph $\overline{\mathrm{G}}(R)$ of R:

(i) 

If $2\notin \mathrm{U}(R)$, then $\overline{\mathrm{G}}(R)$ is a $|\mathrm{U}(R)|$-regular graph.

(ii) 

If $2\in \mathrm{U}(R)$, then for every $x\in \mathrm{U}(R)$ we have $d_{\overline{\mathrm{G}}(R)}(x)=\left|\mathrm{U}(R)\right|+1$ and for every $x\in R\setminus \mathrm{U}(R)$ we have $d_{\overline{\mathrm{G}}(R)}(x)=\left|\mathrm{U}(R)\right|.$

Proof. 

(i) If $2\notin \mathrm{U}(R)$, then $\mathrm{G}(R)=\overline{\mathrm{G}}(R)$, so $\overline{\mathrm{G}}(R)$ is a $|\mathrm{U}(R)|$-regular graph by Lemma 13.

(ii) If $2\in \mathrm{U}(R)$, then for every $x\in R$, we have $2x\in \mathrm{U}(R)$ if and only if $x\in \mathrm{U}(R)$. Consequently, if $x\in \mathrm{U}(R)$, then $x\sim x$ in $\overline{\mathrm{G}}(R)$, which implies that $d_{\overline{\mathrm{G}}(R)}(x)=d_{\mathrm{G}(R)}(x)+2=\left|\mathrm{U}(R)\right|+1$ by Lemma 13. If $x\in R\setminus \mathrm{U}(R)$, then $x\nsim x$ in $\overline{\mathrm{G}}(R)$, and so $d_{\overline{\mathrm{G}}(R)}(x)=d_{\mathrm{G}(R)}(x)=\left|\mathrm{U}(R)\right|$ by Lemma 13. □

3. The Relationships Between $\mathit{\gamma }(\mathbf{G}(\mathit{R}))$ and ${\mathit{\gamma }}_{\mathit{t}}(\mathbf{G}(\mathit{R}/\mathbf{J}(\mathit{R})))$

In this section, we will investigate the relationships between the domination number and total dominating number of unit graphs of rings.

Lemma 14. 

Let R be a ring. Then, $\gamma (\overline{\mathrm{G}}(R))=\gamma (\mathrm{G}(R))$.

Proof. 

Suppose that D is a dominating set of $\mathrm{G}(R)$. Then, for any $a\in R\setminus D$, there exists $x_a\in D$ such that $a\sim x_a$ in $\mathrm{G}(R)$. Since $E(\mathrm{G}(R))\subseteq E(\overline{\mathrm{G}}(R))$, we have $a\sim x_a$ in $\overline{\mathrm{G}}(R)$. This shows that D is a dominating set of $\overline{\mathrm{G}}(R)$, and, consequently, $\gamma (\overline{\mathrm{G}}(R))⩽\gamma (\mathrm{G}(R))$.

Conversely, suppose that $D^{\prime }$ is a dominating set of $\overline{\mathrm{G}}(R)$. Then, for any $b\in R\setminus D^{\prime }$, there exists $x_b\in D^{\prime }$ such that $b\sim x_b$ in $\overline{\mathrm{G}}(R)$. Since $b\notin D^{\prime }$ and $x_b\in D^{\prime }$, we have $b\sim x_b$ in $G(R)$, and so $D^{\prime }$ is a dominating set of $\mathrm{G}(R)$. Thus, $\gamma (\mathrm{G}(R))⩽\gamma (\overline{\mathrm{G}}(R))$, and hence $\gamma (\overline{\mathrm{G}}(R))=\gamma (\mathrm{G}(R))$. □

In [15] (Theorem 3.20), Lemma 14 has already been pointed out, but we have not found a relevant proof, so we give a detailed proof here.

Lemma 15. 

Let R be a ring. Then, $\gamma (\mathrm{G}(R))⩽{\gamma }_t(\overline{\mathrm{G}}(R))⩽{\gamma }_t(\mathrm{G}(R))$.

Proof. 

Suppose that D is a total dominating set of $\mathrm{G}(R)$. Then, for any $a\in R$, there exist $x_a\in D$ such that $a\sim x_a$ in $\mathrm{G}(R)$. Since $E(\mathrm{G}(R))\subseteq E(\overline{\mathrm{G}}(R))$, we have $a\sim x_a$ in $\overline{\mathrm{G}}(R)$, and so D is a total dominating set of $\overline{\mathrm{G}}(R)$. Thus, ${\gamma }_t(\overline{\mathrm{G}}(R))⩽{\gamma }_t(\mathrm{G}(R))$. Using Lemma 14 and Remark 1, we have $\gamma (\mathrm{G}(R))⩽{\gamma }_t(\overline{\mathrm{G}}(R))⩽{\gamma }_t(\mathrm{G}(R))$. □

Lemma 16. 

Let R be a ring. Then, ${\gamma }_t(\overline{\mathrm{G}}(R)))⩽{\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$.

Proof. 

Suppose that $D=\{x_1+\mathrm{J}(R),\cdots ,x_s+\mathrm{J}(R)\}$ is a total dominating set of $\overline{\mathrm{G}}(R/\mathrm{J}(R))$. Let $D^{\prime }=\{x_1,\cdots ,x_s\}$. To show that $D^{\prime }$ is a total dominating set of $\overline{\mathrm{G}}(R)$, let $y\in R$. Then, there exists $x_i+\mathrm{J}(R)\in D$ such that $(y+\mathrm{J}(R))\sim (x_i+\mathrm{J}(R))$ in $\overline{G}(R/\mathrm{J}(R))$, that is to say, $y+x_i+\mathrm{J}(R)\in \mathrm{U}(R/\mathrm{J}(R))$. It follows from Lemma 3 that $y+x_i\in \mathrm{U}(R)$, and so $y\sim x_i$ in $\overline{\mathrm{G}}(R)$. Thus, $D^{\prime }$ is a total dominating set of $\overline{\mathrm{G}}(R)$, and hence ${\gamma }_t(\overline{\mathrm{G}}(R)))⩽{\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$. □

Corollary 2. 

Let R be a ring. Then,

$$\gamma (\mathrm{G}(R))=\gamma (\overline{\mathrm{G}}(R))⩽{\gamma }_t(\overline{\mathrm{G}}(R))⩽{\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))⩽{\gamma }_t(\mathrm{G}(R/\mathrm{J}(R))).$$

In particular, if $\gamma (\mathrm{G}(R))={\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$, then $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$.

Proof. 

This follows immediately from Lemma 14, Remark 1, Lemma 15, and Lemma 16. □

Lemma 17. 

Let R be a local ring which is not a field. Then, $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))={\gamma }_t(\mathrm{G}(R))=2$.

Proof. 

Let R be a local ring which is not a field. Then, $\gamma (\mathrm{G}(R))=2$ by Lemma 7, and so $2=\gamma (\mathrm{G}(R))⩽{\gamma }_t(\mathrm{G}(R))$ by Remark 1. Since R is a local ring, for any $x\in R$, we have $x\in \mathrm{U}(R)$ or $1+x\in \mathrm{U}(R)$ by Lemma 1, and so $\{0,1\}$ is a total dominating set of $\mathrm{G}(R)$. Hence, ${\gamma }_t(\mathrm{G}(R))⩽2$, which together with $2=\gamma (\mathrm{G}(R))⩽{\gamma }_t(\mathrm{G}(R))$, implies that $\gamma (\mathrm{G}(R))={\gamma }_t(\mathrm{G}(R))=2$. Then, by Lemma 15, we obtain $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))={\gamma }_t(\mathrm{G}(R))=2$. □

Lemma 18. 

Let R be a ring. Then, $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus R))⩽2\gamma (\mathrm{G}(R)).$

Proof. 

Assume that $\gamma (\mathrm{G}(R))=k$ and $D=\{x_1,x_2,\cdots ,x_k\}$ is a $\gamma$-set of $\mathrm{G}(R)$. Let

$$\Phi ={\mathbb{Z}}_2\times D=\{(0,x_1),(0,x_2),\cdots ,(0,x_k),(1,x_1),(1,x_2),\cdots ,(1,x_k)\}.$$

We claim that $\Phi$ is a dominating set of $\mathrm{G}({\mathbb{Z}}_2\oplus R)$. In fact, for any $(a,y)\in ({\mathbb{Z}}_2\oplus R)\setminus \Phi$, we have $y\in R\setminus D$. Since D is a $\gamma$-set of $\mathrm{G}(R)$, there exists $d\in D$ such that $d\sim y$ in $\mathrm{G}(R)$, i.e., $d+y\in \mathrm{U}(R)$ and $d\ne y$.

If $a=0$, then $(0,y)+(1,d)\in \mathrm{U}({\mathbb{Z}}_2\oplus R)$ and $(1,d)\ne (0,y)$, i.e., $(0,y)\sim (1,d)$ in $\mathrm{G}({\mathbb{Z}}_2\oplus R)$.

If $a=1$, then $(1,y)+(0,d)\in \mathrm{U}({\mathbb{Z}}_2\oplus R)$ and $(0,d)\ne (1,y)$, i.e., $(1,y)\sim (0,d)$ in $\mathrm{G}({\mathbb{Z}}_2\oplus R)$.

Hence, $\Phi$ is a dominating set of $\mathrm{G}({\mathbb{Z}}_2\oplus R)$, and consequently, $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus R))⩽2\gamma (\mathrm{G}(R)).$ □

Remark 4. 

It is possibly that $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus R))<2\gamma (\mathrm{G}(R))$. For example, we have by Lemma 11 and Lemma 10 that $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3\oplus {\mathbb{Z}}_5))=4<2·3=2\gamma (\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_5)).$

Lemma 19. 

Let R be a ring. Then, $2{\gamma }_t(\overline{\mathrm{G}}(R))⩽{\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus R))⩽2{\gamma }_t(\mathrm{G}(R))$.

Proof. 

Clearly, $\mathrm{G}({\mathbb{Z}}_2\oplus R)$ is a bipartite graph with the bipartition $V_1=\{0\}\oplus R$ and $V_2=\{1\}\oplus R$.

Suppose that ${\gamma }_t(\mathrm{G}(R))=k$ and $D=\{x_1,\cdots ,x_k\}$ is a ${\gamma }_t$-set of $\mathrm{G}(R)$. Let

$$D^{\prime }={\mathbb{Z}}_2\times D=\{(0,x_1),\cdots ,(0,x_k),(1,x_1),\cdots ,(1,x_k)\}.$$

Then, $D^{\prime }$ is a total dominating set of $\mathrm{G}({\mathbb{Z}}_2\oplus R)$. In fact, for any $(a,b)\in {\mathbb{Z}}_2\oplus R$, we have $b\in R$, and so there exists $x_b\in D$ such that $b\sim x_b$ in $G(R)$. If $a=0$, then $(a,b)\sim (1,x_b)$ in $\mathrm{G}({\mathbb{Z}}_2\oplus R)$. If $a=1$, then $(a,b)\sim (0,x_b)$ in $\mathrm{G}({\mathbb{Z}}_2\oplus R)$. Hence, $D^{\prime }$ is a total dominating set of $\mathrm{G}({\mathbb{Z}}_2\oplus R)$, and, consequently, ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus R))⩽2{\gamma }_t(\mathrm{G}(R))$.

To prove that $2{\gamma }_t(\overline{\mathrm{G}}(R))⩽{\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus R))$, let $D^{\prime \prime }$ be a total dominating set of $\mathrm{G}({\mathbb{Z}}_2\oplus R)$. We claim that ${\mathrm{P}}_R(D^{\prime \prime }\cap V_1)$ is a total dominating set of $\overline{\mathrm{G}}(R)$, where

$${\mathrm{P}}_R(D^{\prime \prime }\cap V_1)=\{r\in R|(\exists a\in {\mathbb{Z}}_2)(a,r)\in D^{\prime \prime }\cap V_1\}=\{r\in R|(0,r)\in D^{\prime \prime }\}.$$

In fact, for any $s\in R$, we have $(1,s)\in {\mathbb{Z}}_2\oplus R$, and so there exists $(0,x_s)\in D^{\prime \prime }\cap V_1$ such that $(1,s)\sim (0,x_s)$ in $\mathrm{G}({\mathbb{Z}}_2\oplus R)$. It follows that $x_s\in {\mathrm{P}}_R(D^{\prime \prime }\cap V_1)$ and $s+x_s\in U(R)$. Thus, ${\mathrm{P}}_R(D^{\prime \prime }\cap V_1)$ is a total dominating set of $\overline{\mathrm{G}}(R)$, and we conclude that ${\gamma }_t(\overline{\mathrm{G}}(R))⩽|{\mathrm{P}}_R(D^{\prime \prime }\cap V_1)|⩽|D^{\prime \prime }\cap V_1|$. Similarly, ${\gamma }_t(\overline{\mathrm{G}}(R))⩽|{\mathrm{P}}_R(D^{\prime \prime }\cap V_2)|⩽|D^{\prime \prime }\cap V_2|$. Thus, $|D^{\prime \prime }|=|D^{\prime \prime }\cap V_1|+|D^{\prime \prime }\cap V_2|⩾2{\gamma }_t(\overline{\mathrm{G}}(R)).$ □

Lemma 20. 

Let F be a field. Then, ${\gamma }_t(\mathrm{G}(F))={\gamma }_t(\overline{\mathrm{G}}(F))=2$ and ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus F))=4$.

Proof. 

Let F be a field. It is clear that $\{0,1\}$ is a total dominating set of $\mathrm{G}(F)$ and $\overline{\mathrm{G}}(F)$, so $\{0,1\}$ is a ${\gamma }_t$-set of $\mathrm{G}(F)$ and $\overline{\mathrm{G}}(F)$ by Remark 2. Thus, ${\gamma }_t(\mathrm{G}(F))={\gamma }_t(\overline{\mathrm{G}}(F))=2$, and so ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus F))=4$ by Lemma 19. □

Lemma 21. 

Let R be a ring, $a\in R$ and $D=\{x_1,x_2,\cdots ,x_k\}$ be a γ-set of $\mathrm{G}(R)$. Let $D/\mathrm{J}(R)=\{x_i+\mathrm{J}(R)|x_i\in D\}$.

(i) 

If $a+\mathrm{J}(R)$ is not adjacent to any vertex of $D/\mathrm{J}(R)$ in $\overline{\mathrm{G}}(R/\mathrm{J}(R))$, then a is not adjacent to any vertex of D in $\mathrm{G}(R)$.

(ii) 

If $a\in D$ and $a+\mathrm{J}(R)$ is not adjacent to any vertex of $D/\mathrm{J}(R)$ in $\mathrm{G}(R/\mathrm{J}(R))$, then a is not adjacent to any vertex of D in $\mathrm{G}(R)$.

Proof. 

Let $R,a,D$ and $D/\mathrm{J}(R)$ be as given in the lemma.

(i) If there exists $x_a\in D$ such that $a\sim x_a$ in $\mathrm{G}(R)$, then $a+x_a\in \mathrm{U}(R)$, which implies that $(a+\mathrm{J}(R))+(x_a+\mathrm{J}(R))=a+x_a+\mathrm{J}(R)\in \mathrm{U}(R/\mathrm{J}(R))$ by Lemma 3. So, $(a+\mathrm{J}(R))\sim (x_a+\mathrm{J}(R))$ in $\overline{\mathrm{G}}(R/\mathrm{J}(R))$. That is to say, $a+\mathrm{J}(R)$ is adjacent to a vertex of $D/\mathrm{J}(R)$ in $\overline{\mathrm{G}}(R/\mathrm{J}(R))$.

(ii) Suppose that $a\in D$ and $a+\mathrm{J}(R)$ is not adjacent to any vertex of $D/\mathrm{J}(R)$ in $\mathrm{G}(R/\mathrm{J}(R))$. If there exists $x_a\in D$ such that $a\sim x_a$ in $\mathrm{G}(R)$, then $a+x_a\in \mathrm{U}(R)$ and $a\ne x_a$, which implies that $(a+\mathrm{J}(R))+(x_a+\mathrm{J}(R))=a+x_a+\mathrm{J}(R)\in \mathrm{U}(R/\mathrm{J}(R))$ by Lemma 3. So $(a+\mathrm{J}(R))\sim (x_a+\mathrm{J}(R))$ in $\overline{\mathrm{G}}(R/\mathrm{J}(R))$. Thus, $a+\mathrm{J}(R)=x_a+\mathrm{J}(R)$, for otherwise, $(a+\mathrm{J}(R))\sim (x_a+\mathrm{J}(R))$ in $\mathrm{G}(R/\mathrm{J}(R))$, a contradiction.

Claim: $D\setminus \{a\}$ is a dominating set of $\mathrm{G}(R)$.

In fact, let $y\in R\setminus (D\setminus \{a\})=(R\setminus D)\cup \{a\}$. If $y\in R\setminus D$, then $y\ne a$ and $y\ne x_a$, since $a\in D$ and $x_a\in D$. Since D is a $\gamma$-set of $\mathrm{G}(R)$, there exists $x_y\in D$ such that $y\sim x_y$ in $\mathrm{G}(R)$.

Noticing that $x_a\in D\setminus \{a\}$ and

$$\begin{array}{ccc}\hfill y\sim ain\mathrm{G}(R)& \iff & y+a\in \mathrm{U}(R)\hfill \\ & \iff & y+a+\mathrm{J}(R)\in \mathrm{U}(R/\mathrm{J}(R))(byLemma3)\hfill \\ & \iff & y+x_a+\mathrm{J}(R)\in \mathrm{U}(R/\mathrm{J}(R))(sincea+\mathrm{J}(R)=x_a+\mathrm{J}(R))\hfill \\ & \iff & y+x_a\in \mathrm{U}(R)(byLemma3)\hfill \\ & \iff & y\sim x_{a}in\mathrm{G}(R),\hfill \end{array}$$

we obtain that there exists $v\in D\setminus \{a\}$ such that $y\sim v$ in $\mathrm{G}(R)$. In addition, since $a\sim x_a$ in $\mathrm{G}(R)$, we have that $D\setminus \{a\}$ is a dominating set of $\mathrm{G}(R)$, which contradicts the fact that D is a $\gamma$-set of $\mathrm{G}(R)$. □

Remark 5. 

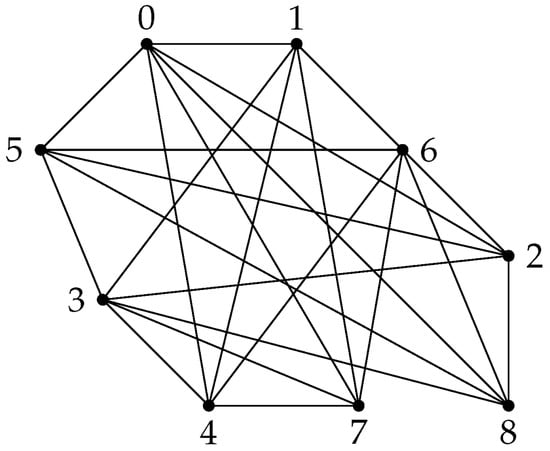
In Lemma 21 (ii), the condition $a\in D$ can not be deleted. For example, in the unit graph $\mathrm{G}({\mathbb{Z}}_9)$ (see Figure 3), $D=\{2,4\}$ is a γ-set of $\mathrm{G}({\mathbb{Z}}_9)$ and $1\notin D$. It is easy to see that $1+\mathrm{J}({\mathbb{Z}}_9)$ is not adjacent to any vertex in $D/\mathrm{J}({\mathbb{Z}}_9)=\{1+\mathrm{J}({\mathbb{Z}}_9),2+\mathrm{J}({\mathbb{Z}}_9)\}$ in $\mathrm{G}({\mathbb{Z}}_9/\mathrm{J}({\mathbb{Z}}_9))\cong G({\mathbb{Z}}_3)$, but $1\sim 4$ in $\mathrm{G}({\mathbb{Z}}_9)$.

Theorem 1. 

Let R be a ring with $|\mathrm{J}(R)|⩾2$. Then, $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R))).$

In particular, if $2\notin \mathrm{U}(R)$, then $\gamma (\mathrm{G}(R))={\gamma }_t(\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))={\gamma }_t(\mathrm{G}(R/\mathrm{J}(R))).$

Proof. 

Assume that R is a ring with $|\mathrm{J}(R)|⩾2$. Using Corollary 2, we only need to verify the inequality

$$\gamma (\mathrm{G}(R))⩾{\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$$

(1)

In fact, suppose that $\gamma (\mathrm{G}(R))=k$ and let $D=\{a_1,a_2,\cdots ,a_k\}$ be a $\gamma$-set of $\mathrm{G}(R)$. Let

$$D/\mathrm{J}(R)=\{a_1+\mathrm{J}(R),a_2+\mathrm{J}(R),\cdots ,a_k+\mathrm{J}(R)\}.$$

Then $|D/\mathrm{J}(R)|⩽\left|D\right|$, and $D/\mathrm{J}(R)$ is a dominating set of $\mathrm{G}(R/\mathrm{J}(R))$ by the proof of [15] (Lemma 3.14). Hence, $D/\mathrm{J}(R)$ is a dominating set of $\overline{\mathrm{G}}(R/\mathrm{J}(R))$ by the proof of Lemma 14.

If $D/\mathrm{J}(R)$ is a total dominating set of $\overline{\mathrm{G}}(R/\mathrm{J}(R))$, then the inequality (1) holds.

If $D/\mathrm{J}(R)$ is not a total dominating set of $\overline{\mathrm{G}}(R/\mathrm{J}(R))$, then there exists $b+\mathrm{J}(R)$ in $D/\mathrm{J}(R)$ such that $b+\mathrm{J}(R)\nsim a+\mathrm{J}(R)$ for any $a+\mathrm{J}(R)\in D/\mathrm{J}(R)$ in $\overline{\mathrm{G}}(R/\mathrm{J}(R))$. We claim that

$$b+\mathrm{J}(R)\subseteq Dand|b+\mathrm{J}(R)|⩾2.$$

(2)

In fact, by Lemma 21 (i), we have $v\nsim w$ in $\mathrm{G}(R)$, for any $v\in b+\mathrm{J}(R)$ and any $w\in D$. So, $b+\mathrm{J}(R)\subseteq D$, since D is a $\gamma$-set of $\mathrm{G}(R)$. Since $|\mathrm{J}(R)|⩾2$, we have $|b+\mathrm{J}(R)|=|\mathrm{J}(R)|⩾2$ using the well-known Lagrange Theorem. Thus, claim (2) holds.

Assume that $b_1+\mathrm{J}(R),b_2+\mathrm{J}(R),\cdots ,b_s+\mathrm{J}(R)$ are all mutually distinct vertexes in $D/\mathrm{J}(R)$ that are not adjacent to any vertex of $D/\mathrm{J}(R)$. Noticing that for any

$$w+\mathrm{J}(R)\in D/\mathrm{J}(R)\setminus \{b_1+\mathrm{J}(R),b_2+\mathrm{J}(R),\cdots ,b_s+\mathrm{J}(R)\},$$

there exists at least one element $u\in w+\mathrm{J}(R)$ such that $u\in D$ by the definition of $D/\mathrm{J}(R)$, we obtain through claim (2) that $2s+(|D/\mathrm{J}(R)|-s)⩽\left|D\right|$; i.e.,

$$|D/\mathrm{J}(R)|+s⩽\left|D\right|.$$

(3)

For each $i\in \{1,2,\cdots ,s\}$, we have by Corollary 1 that $d_{\overline{\mathrm{G}}(R/\mathrm{J}(R))}(b_i+\mathrm{J}(R))⩾1$, so there exists $c_i+J(R)\in (R/\mathrm{J}(R))\setminus (D/\mathrm{J}(R))$ such that $c_i+\mathrm{J}(R)\sim b_i+\mathrm{J}(R)$ in the graph $\overline{\mathrm{G}}(R/\mathrm{J}(R)).$ Let

$$D_t=(D/\mathrm{J}(R))\cup \{c_1+\mathrm{J}(R),c_2+\mathrm{J}(R),\cdots ,c_s+\mathrm{J}(R)\}.$$

It is easy to verify that $D_t$ is a total dominating set of $\overline{\mathrm{G}}(R/\mathrm{J}(R))$, and $|D_t|⩽|D/\mathrm{J}(R)|+s⩽\left|D\right|$ by (3). Consequently, the inequality (1) holds. Thus, $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R))).$

Finally, if $2\notin \mathrm{U}(R)$, then $2+\mathrm{J}(R)\notin \mathrm{U}(R/\mathrm{J}(R))$ by Lemma 3. It follows by Definition 1 that $\overline{\mathrm{G}}(R)=\mathrm{G}(R)$ and $\overline{\mathrm{G}}(R/\mathrm{J}(R))=\mathrm{G}(R/\mathrm{J}(R))$. Thus, $\gamma (\mathrm{G}(R))={\gamma }_t(\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))={\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$ by Lemma 6. □

Remark 6. 

In Theorem 1, the condition $|\mathrm{J}(R)|⩾2$ cannot be deleted. For example, let F be a field. Then, $\gamma (\mathrm{G}(F))=1$ by Lemma 7, but ${\gamma }_t(\overline{\mathrm{G}}(F))=2$ by Lemma 20.

Corollary 3. 

Let $m,n$ be positive integers, and $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$, where $p_1<p_2<\cdots <p_m$ are primes and ${\alpha }_i$’s are positive integers. Then, the following statements hold:

(i) 

If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$.

(ii) 

If $m=1$ and ${\alpha }_1=1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}))=1$, ${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}))=2$.

(iii) 

If $m=1$ and ${\alpha }_1>1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1^{{\alpha }_1}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{{p_1}^{{\alpha }_1}}))=2$.

(iv) 

If $m=2$, ${\alpha }_1{\alpha }_2=1$ and $p_1⩾3$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))=3.$

(v) 

If $m=2$, ${\alpha }_1{\alpha }_2>1$ and $p_1⩾3$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))=3.$

(vi) 

If $m=2$, ${\alpha }_1{\alpha }_2=1$ and $p_1=2$, then $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}))=2$, ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}))=4.$

(vii) 

If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$ and $p_1=2$, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$, and in particular, $\gamma (\mathrm{G}({\mathbb{Z}}_{2^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{2^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))=4.$

(viii) 

If $m=3$ and ${\alpha }_1{\alpha }_2{\alpha }_3>1$, then

$$\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))$$

$$={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))=\left\{\begin{array}{c}6,if{p}_1=2;\hfill \\ 5,if{p}_1=3;\hfill \\ 4,if{p}_1>3.\hfill \end{array}\right.$$

(ix) 

If $m=3$ and ${\alpha }_1{\alpha }_2{\alpha }_3=1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))=4$, and

$${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))=\left\{\begin{array}{c}6,if{p}_1=2;\hfill \\ 5,if{p}_1=3;\hfill \\ 4,if{p}_1>3.\hfill \end{array}\right.$$

Proof. 

Let m and n be as given in the Corollary. Then, ${\mathbb{Z}}_n\cong {\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus \cdots \oplus {\mathbb{Z}}_{p_m^{{\alpha }_m}}$.

(i) If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$, then $|\mathrm{J}({\mathbb{Z}}_n)|⩾2$. By Lemma 3, we have

$$\begin{array}{ccc}\hfill {\mathbb{Z}}_n/\mathrm{J}({\mathbb{Z}}_n)& \cong & {\mathbb{Z}}_{p_1^{{\alpha }_1}}/\langle p_1\rangle \oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}/\langle p_2\rangle \oplus \cdots \oplus {\mathbb{Z}}_{p_m^{{\alpha }_m}}/\langle p_m\rangle \hfill \\ & \cong & {\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}.\hfill \end{array}$$

Thus, $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$ by Theorem 1.

(ii) If $m=1$ and ${\alpha }_1=1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}))=1$ by Lemma 7, ${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}))=2$ by Lemma 20.

(iii) If $m=1$ and ${\alpha }_1>1$, then ${\mathbb{Z}}_{p_1^{{\alpha }_1}}$ is a local ring which is not a field, so $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1^{{\alpha }_1}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{{p_1}^{{\alpha }_1}}))=2$ by Lemma 17.

(iv) If $m=2$, ${\alpha }_1{\alpha }_2=1$ and $p_1⩾3$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))=3$ by Lemma 10, and so $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))=3$ by Lemma 15.

(v) If $m=2$, ${\alpha }_1{\alpha }_2>1$ and $p_1⩾3$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))=3$ by Lemma 7 (iii). It follows by item (iii) that ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}))=3=\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))$, and so ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))=3$ by Lemma 6. Therefore, by Lemma 15 we have $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))=3.$

(vi) If $m=2$, ${\alpha }_1{\alpha }_2=1$ and $p_1=2$, then $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}))=2$ by Lemma 7 (ii), and ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}))=4$ by Lemma 20.

(vii) If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$ and $p_1=2$, then $|\mathrm{J}({\mathbb{Z}}_n)|⩾2$ and $2\notin \mathrm{U}({\mathbb{Z}}_n)$, and so $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$ by Theorem 1. In particular, $\gamma (\mathrm{G}({\mathbb{Z}}_{2^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{2^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}))=4$ by item (iii).

(viii) If $m=3$ and ${\alpha }_1{\alpha }_2{\alpha }_3>1$, then by [16] (Theorem 2.5 and Remark 2.6) we have

$$\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))=\left\{\begin{array}{c}6,if{p}_1=2;\hfill \\ 5,if{p}_1=3;\hfill \\ 4,if{p}_1>3.\hfill \end{array}\right.$$

Thus, by Lemma 15, we obtain

$$\gamma (\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))$$

$$={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}))=\left\{\begin{array}{c}6,if{p}_1=2;\hfill \\ 5,if{p}_1=3;\hfill \\ 4,if{p}_1>3.\hfill \end{array}\right.$$

(ix) If $m=3$ and ${\alpha }_1{\alpha }_2{\alpha }_3=1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))=4$ by Lemma 11.

By Theorem 1 and Corollary 3 item (viii), we obtain

$${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))=\left\{\begin{array}{c}6,if{p}_1=2;\hfill \\ 5,if{p}_1=3;\hfill \\ 4,if{p}_1>3.\hfill \end{array}\right.$$

When $p_1=2$, we have ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))=6$, since $2\notin \mathrm{U}(R)$. By Appendix A, we have ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))⩽5$ when $p_1=3$, and ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))⩽4$ when $p_1>3$. In addition, ${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))⩽{\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))$ by Lemma 15. Hence,

$${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}))=\left\{\begin{array}{c}6,if{p}_1=2;\hfill \\ 5,if{p}_1=3;\hfill \\ 4,if{p}_1>3.\hfill \end{array}\right.$$

□

Remark 7. 

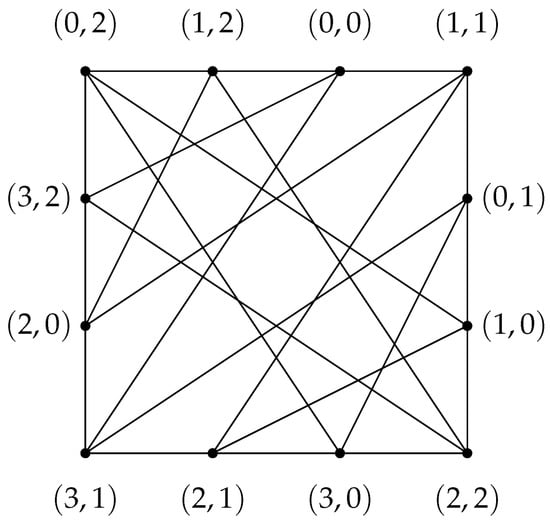
In Theorem 1, for a γ-set D of $G(R)$, $D/\mathrm{J}(R)$ may not be a total dominating set of $(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$.

For example, consider the unit graph $\mathrm{G}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3)$ of the ring ${\mathbb{Z}}_4\oplus {\mathbb{Z}}_3$ (see Figure 4), let $D=\{(0,1),(2,1),(1,2),(3,2)\}$. Then, D is a dominating set of $\mathrm{G}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3)$, and so D is a γ-set of $\mathrm{G}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3)$, since $\gamma (\mathrm{G}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3))=4$ by Corollary 3. But

$$D/\mathrm{J}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3)=\{(0,1),(1,2)\}$$

is not a total dominating set of $\overline{\mathrm{G}}(({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3)/\mathrm{J}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3))=\overline{\mathrm{G}}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3)$, since $(0,1)\nsim (1,2)$ and $(0,1)\nsim (0,1)$ in $\overline{\mathrm{G}}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3)$. According to the proof of Theorem 1, if we add $(1,0)$ and $(0,0)$ to $D/\mathrm{J}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3)$ and obtain $D_t=\{(0,1),(1,2),(1,0),(0,0)\}$, then $D_t$ is a total dominating set of $\overline{\mathrm{G}}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3)$ and $|D_t|=4=\gamma (\mathrm{G}({\mathbb{Z}}_4\oplus {\mathbb{Z}}_3))$.

Remark 8. 

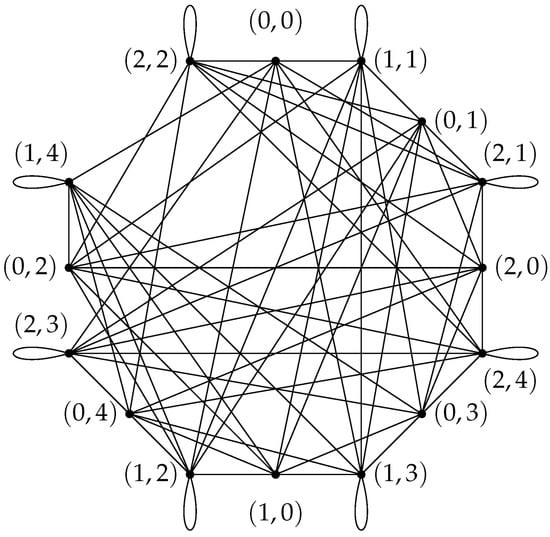
In Theorem 1, the proof is not appropriate when ${\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$ is replaced by ${\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$. For example, consider the unit graph $\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)$. Let $D=\{(0,1),(1,4),(2,2)\}$. Then, D is a dominating set of $\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)$, since

$$\begin{array}{ccc}& & N_{\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)}((0,1))=\{(a,b)\in {\mathbb{Z}}_9\oplus {\mathbb{Z}}_5|a\notin \{0,3,6\}andb\ne 4\}\hfill \\ & & N_{\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)}((1,4))=\{(a,b)\in {\mathbb{Z}}_9\oplus {\mathbb{Z}}_5|a\notin \{2,5,8\}andb\ne 1\}\setminus \{(1,4)\}\hfill \\ & & N_{\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)}((2,2))=\{(a,b)\in {\mathbb{Z}}_9\oplus {\mathbb{Z}}_5|a\notin \{1,4,7\};b\ne 3\}\setminus \{(2,2)\}\hfill \end{array}$$

It follows that D is a γ-set of $\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)$, since $\gamma (\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5))=3$ by Corollary 3. Observe that

$$D/\mathrm{J}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)=\{(0,1),(1,4),(2,2)\}$$

is a total dominating set of $\overline{\mathrm{G}}(({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)/\mathrm{J}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5))=\overline{\mathrm{G}}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_5)$ (see Figure 5), but $D/\mathrm{J}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)$ is not a total dominating set of $\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_5)$, since $(1,4)\nsim (0,1)$ and $(1,4)\nsim (2,2)$. Adding $(1,0)$ to $D/\mathrm{J}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5)$, we obtain that $D_t=\{(0,1),(1,4),(2,2),(1,0)\}$ is a total dominating set of $\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_5)$, but from which we cannot deduce that ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_5))⩽\gamma (\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5))$, since $|D_t|=4>3=\gamma (\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5))$. In fact, we can also obtain that $D_t^{\prime }=\{(0,1),(1,3),(2,2)\}$ is a total dominating set of $\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_5)$, and so ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5))⩽3=\gamma (\mathrm{G}({\mathbb{Z}}_9\oplus {\mathbb{Z}}_5))$.

4. The Unit Graph of the Ring ${\mathbb{Z}}_{\mathit{n}}$

For a ring R, according to Theorem 1, to study the domination number of the unit graph $\mathrm{G}(R)$, it suffices to study the total dominating number of the unit graph associated with the semisimple ring $R/\mathrm{J}(R)$. That is to say, it suffices to consider the cases when R is a direct product of some fields by Lemma 5. In particular, to study the domination number of the unit graph $\mathrm{G}({\mathbb{Z}}_n)$, it suffices to consider the case when ${\mathbb{Z}}_n$ is directly decomposed into certain fields. By Corollary 3, the domination number and the total dominating number of $\mathrm{G}({\mathbb{Z}}_n)$, when n has less than three prime divisors, can be investigated.

In this section, we focus on studying the domination number and the total dominating number of $\mathrm{G}({\mathbb{Z}}_n)$ when n has at least four prime divisors. Without loss of generality, we assume that $T={\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}$, where $p_1<p_2<\cdots <p_m$ are primes and $m⩾4$ is an integer.

4.1. Case $p_1⩾m+1$

Proposition 1. 

Let $p_1⩾m+1$. Then, $\gamma (\mathrm{G}(T)={\gamma }_t(\overline{\mathrm{G}}(T)={\gamma }_t(\mathrm{G}(T))=m+1$.

Proof. 

Let $m,p_i(1⩽i⩽m)$ be as given in the proposition, and let

$$D=\{\underset{mtimes}{\underbrace{(0,0,\cdots ,0)}},\underset{mtimes}{\underbrace{(1,1,\cdots ,1)}},\cdots ,\underset{mtimes}{\underbrace{(m,m,\cdots ,m)}}\}.$$

Then, D is a total dominating set of $\mathrm{G}(T)$. In fact, since $p_1⩾m+1$, we have $D\subseteq T$. Suppose, on the contrary, that there exists $(a_1,a_2,\cdots ,a_m)\in T$ such that $(a_1,a_2,\cdots ,a_m)\nsim (i,i,\cdots ,i)$ (in $\mathrm{G}(T)$) for any $(i,i,\cdots ,i)\in D$. Then, there exists $i_j\in \{1,2,\cdots ,m\}$$(j=0,1,\cdots ,m)$ such that

$$a_{i_0}+0=0,a_{i_1}+1=0,\cdots ,a_{i_m}+m=0.$$

By the well-known pigeonhole principle [20] (Theorem 3.1.1), there exist $s,t\in \{0,1,\cdots ,m\}$ with $s\ne t$ such that $a_{i_s}=a_{i_t}$, but this implies that $a_{i_s}+s=0=a_{i_t}+t=a_{i_s}+t$ in the field ${\mathbb{Z}}_{p_{i_s}}$, and so $s=t$, a contradiction. Thus, D is a total dominating set of $\mathrm{G}(T)$, and hence ${\gamma }_t(\mathrm{G}(T))⩽m+1$. It follows from Remark 1, Lemma 15, and Lemma 12 that

$$m+1⩽\gamma (\mathrm{G}(T))⩽{\gamma }_t(\overline{\mathrm{G}}(T))⩽{\gamma }_t(\mathrm{G}(T))⩽m+1,$$

and consequently, $\gamma (\mathrm{G}(T))={\gamma }_t(\overline{\mathrm{G}}(T))={\gamma }_t(\mathrm{G}(T))=m+1$. □

Remark 9. 

Proposition 1 also holds true when $m=3$ in its proof.

If $p_1⩾m+1$, in the proof of Proposition 1, let

$$D^{\prime }=\{\underset{mtimes}{\underbrace{(b_1,b_1,\cdots ,b_1)}},\underset{mtimes}{\underbrace{(b_2,b_2,\cdots ,b_2)}},\cdots ,\underset{mtimes}{\underbrace{(b_k,b_k,\cdots ,b_k)}}\},$$

where k is a positive integer with $k⩾m+1$, and $b_1,\cdots ,b_k\in \{0,1,\cdots ,p_1-1\}$ are mutually different. One can similarly prove that $D^{\prime }$ is also a total dominating set of $\mathrm{G}(T)$.

4.2. Case $3⩽p_1⩽m⩽p_2$

Let $A_1$ and $A_2$ be nonempty sets. For a subset B of $A_1\times A_2$ (the Cartesian product of $A_1$ and $A_2$), let ${\mathrm{P}}_{A_1}(B)=\{a_1\in A_1|(\exists a_2\in A_2)(a_1,a_2)\in B\}$ and

$${\mathrm{P}}_{A_2}(B)=\{a_2\in A_2|(\exists a_1\in A_1)(a_1,a_2)\in B\}.$$

${\mathrm{P}}_{A_1}(B)$ and ${\mathrm{P}}_{A_2}(B)$ are called, respectively, the projection of B on $A_1$ and the projection of B on $A_2$.

Lemma 22. 

Let $3⩽p_1⩽m⩽p_2$ and let D be a dominating set of $\mathrm{G}(T)$ such that the projection of D on ${\mathbb{Z}}_{p_1}$ is ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)=\{a_1,a_2,\cdots ,a_t\}$, where t is a positive integer. For each $a_i$, let the cardinality of the projection of $(\{a_i\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D$ on ${\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}$ be $k_i$, i.e,

$$|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((\{a_i\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)|=k_i,\forall i=1,2,\cdots ,t$$

Let $z_i=({\sum }_{j=1}^t{k}_j)-k_i,i=1,2,\cdots ,t.$

If $t=1$ or $z_j<m$ for some $j\in \{1,2,\cdots ,t\}$, then $\left|D\right|⩾2m-1$.

Proof. 

Let D, t, $z_i$, $k_i$, $i=1,2,\cdots ,t$ be as given in the lemma. Then, $1⩽t⩽p_1$, since ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)=\{a_1,a_2,\cdots ,a_t\}\subseteq {\mathbb{Z}}_{p_1}$.

If $t=1$, i.e., ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)=\{a_1\}$, then for any $x\in \{(-a_1,x_2,\cdots ,x_m)|x_i\in {\mathbb{Z}}_{p_i},i=2,\cdots ,m\}$ and any $y\in D$, we have $x\nsim y$ in $\mathrm{G}(T)$. It follows that

$$\{(-a_1,x_2,\cdots ,x_m)|x_i\in {\mathbb{Z}}_{p_i},i=2,\cdots ,m\}\subseteq D,$$

since D is a dominating set of $\mathrm{G}(T)$. Hence, $\left|D\right|⩾p_2\cdots p_m⩾p_2{p}_3⩾4m>2m-1$, since $4⩽m⩽p_2<p_3$.

Assume that $t⩾2$ and $z_j<m$ for some $j\in \{1,2,\cdots ,t\}$. Without loss of generality, we assume that $z_1<m$. Since

$$\begin{array}{ccc}& & |{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((\{a_2,a_3,\cdots ,a_t\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)|\hfill \\ & =& |\bigcup _{i=2}^t({\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((\{a_i\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D))|\hfill \\ & ⩽& \sum _{i=2}^t(|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((\{a_i\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D))|)\hfill \\ & =& k_2+k_3+\cdots +k_t=z_1,\hfill \end{array}$$

we may assume that

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((\{a_2,a_3,\cdots ,a_t\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)=\{(b_{j2},b_{j3},\cdots ,b_{jm})|j=1,\cdots ,\ell \},$$

where ℓ is a positive integer and $1⩽\ell ⩽z_1$. Let A be a subset of T such that

$$\begin{array}{ccc}& & (x_1,x_2\cdots ,x_m)\in A\hfill \\ & \iff & x_1=-a_1,x_q=-b_{q-1,q},\forall q\in \{2,3,\cdots ,\ell +1\};and{x}_s\in {\mathbb{Z}}_{p_s},\forall s\in \{\ell +2,\cdots ,m\},\hfill \end{array}$$

that is to say,

$$A=\{(-a_1,-b_{12},-b_{23},\cdots ,-b_{\ell ,\ell +1},x_{\ell +2},\cdots ,x_m)|x_s\in {\mathbb{Z}}_{p_s},s=\ell +2,\cdots ,m\}$$

Then, for any $x\in A$ and any $y\in D$, we have $x\nsim y$ in $\mathrm{G}(T)$, and so $A\subseteq D$, since D is a dominating set of $\mathrm{G}(T)$. Noticing that $1⩽\ell ⩽z_1<m$, we have $1⩽\ell ⩽z_1⩽m-1$.

If $1⩽\ell ⩽m-3$, then $\left|D\right|⩾\left|A\right|=p_m{p}_{m-1}⩾p_2{p}_3⩾4m>2m-1$, since $4⩽m⩽p_2<p_3$.

Assume $m-2⩽\ell ⩽m-1$. Consider the following cases.

Case(i): There exists $i\in \{2,3,\cdots ,m\}$ such that there are at least two elements among $b_{1i},b_{2i},\cdots ,b_{\ell i}$ that are equal. Without loss of generality, assume that $b_{1i}=b_{2i}$.

Let $\Omega$ be a subset of T such that

$$\begin{array}{ccc}& & (x_1,x_2\cdots ,x_i,\cdots ,x_m)\in \Omega \hfill \\ & \iff & x_1=-a_1,x_i=-b_{1i},andthereexists\{j_3,j_4,\cdots ,j_{\ell }\}\subseteq \{2,\cdots ,m\}\setminus \{i\}\hfill \\ & & suchthat{x}_{j_q}=-b_{q{j}_q},q=3,\cdots ,\ell \hfill \end{array}$$

(Note: For example, if $i=3$, we may let $j_q=\left\{\begin{array}{cc}q,\hfill & ifq=4,\cdots ,\ell ;\hfill \\ q-1,\hfill & ifq=3,\hfill \end{array}\right.$ and then

$$\{(-a_1,-b_{32},-b_{13},-b_{44},\cdots ,-b_{\ell \ell },x_{\ell +1},\cdots ,x_m)|x_s\in {\mathbb{Z}}_{p_s},s=\ell +1,\cdots ,m\}\subseteq \Omega .$$

If $i=\ell +1$, we may let $j_q=q-1$ for any $q\in \{3,\cdots ,\ell \}$, and then

$$\{(-a_1,-b_{32},-b_{43},\cdots ,-b_{\ell ,\ell -1},x_{\ell },-b_{1i},x_{l+2},\cdots ,x_m)|x_s\in {\mathbb{Z}}_{p_s},s=l,l+2,\cdots ,m\}\subseteq \Omega .)$$

For any $x\in \Omega$ and any $y\in D$, we have $x\nsim y$ in $\mathrm{G}(T)$, and so $\Omega \subseteq D$, since D is a dominating set of $\mathrm{G}(T)$. It follows that $-a_1\in {\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)=\{a_1,a_2,\cdots ,a_t\}$, and $\left|D\right|⩾|\Omega |⩾p_2$ (since $\ell ⩽m-1$).

When $l=m-2$, we obtain $\left|D\right|⩾|\Omega |⩾p_2{p}_3⩾4m>2m-1$, since $4⩽m⩽p_2<p_3$.

When $l=m-1$, we claim that $-a_1=a_1$. In fact, if $-a_1\ne a_1$, then $-a_1\in \{a_2,\cdots ,a_t\}$, since $-a_1\in {\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)=\{a_1,a_2,\cdots ,a_t\}$. So, $\Omega \subseteq \{a_2,a_3,\cdots ,a_t\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D$, and thus

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}(\Omega )\subseteq {\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((\{a_2,a_3,\cdots ,a_t\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D),$$

which implies that $p_2⩽|\Omega |=|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}(\Omega )|=\ell =m-1<m$, but $p_2⩾m$, a contradiction. Thus, $-a_1=a_1$ in ${\mathbb{Z}}_{p_1}$, and so $a_1=0$, since $p_1⩾3$. Therefore, we have

$$\begin{array}{ccc}& & \left|D\right|⩾|\Omega |+|((\{a_1,a_2,\cdots ,a_t\}\setminus \{-a_1\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D|\hfill \\ & =& |\Omega |+|(\{a_2,\cdots ,a_t\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D|\hfill \\ & ⩾& p_2+\ell ⩾m+(m-1)=2m-1\hfill \end{array}$$

since $m⩽p_2$ and $\ell =m-1$.

Case(ii): $b_{1i},\cdots ,b_{\ell i}$ are mutually different, for any $i\in \{2,\cdots ,m\}.$

Let ${\mathbf{S}}_{\ell }$ denote the symmetric group on the set $\{1,2,\cdots ,\ell \}$, and let $\Psi$ be a subset of T such that

$$\begin{array}{ccc}& & (x_1,x_2\cdots ,x_m)\in \Psi \hfill \\ & \iff & x_1=-a_1,andthereexistsapermutation{j}_1{j}_2\cdots j_{\ell }\in {\mathbf{S}}_{\ell }\hfill \\ & & suchthat{x}_{j_q}=-b_{j_q(q+1)},q=1,2,\cdots ,\ell \hfill \end{array}$$

that is to say,

$$\Psi =\{(-a_1,-b_{j_{1}2},-b_{j_{2}3},\cdots ,-b_{j_{\ell },\ell +1},x_{\ell +2},\cdots ,x_m)|x_i\in {\mathbb{Z}}_{p_i},i=\ell +2,\cdots ,m,j_1\cdots j_{\ell }\in {\mathbf{S}}_{\ell }\}.$$

Then, for any $x\in \Psi$ and any $y\in D$, we have $x\nsim y$ in $\mathrm{G}(T)$, and so $\Psi \subseteq D$, since D is a dominating set of $\mathrm{G}(T)$. Thus, $-a_1\in {\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)=\{a_1,a_2,\cdots ,a_t\}$ and $\left|D\right|⩾|\Psi |$.

In addition, since $((\{a_1,a_2,\cdots ,a_t\}\setminus \{-a_1\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D\subseteq D$, we have

$$\begin{array}{ccc}& & \left|D\right|⩾|\Psi |+|((\{a_1,a_2,\cdots ,a_t\}\setminus \{-a_1\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D|\hfill \\ & ⩾& \left\{\begin{array}{cc}\ell !p_2+1,\hfill & if\ell =m-2;\hfill \\ \ell !+1,\hfill & if\ell =m-1.\hfill \end{array}\right.\hfill \end{array}$$

If $\ell =m-1$, then $\ell !+1⩾2(m-1)+1=2m-1$, since $m-1⩾3$. If $\ell =m-2$, then $\ell !p_2+1⩾2m+1>2m-1$, since $m-2⩾2$ and $p_2⩾m$. Hence, $\left|D\right|⩾2m-1$. □

Proposition 2. 

Let $3⩽p_1⩽m⩽p_2$. Then, $\gamma (\mathrm{G}(T))⩾{\displaystyle \frac{p_1}{p_1-1}}m$. In particular, if $m=(p_1-1)q+r$, where q and r are non-negative integers with $r<p_1-1$, then

$$\gamma (\mathrm{G}(T)⩾\left\{\begin{array}{cc}{p}_{1}q,\hfill & ifr=0;\hfill \\ p_{1}q+r+1,\hfill & ifr\ne 0.\hfill \end{array}\right.$$

Proof. 

Let $3⩽p_1⩽m⩽p_2$ and D be a dominating set of $\mathrm{G}(T)$. Assume that

$${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)=\{a_1,a_2,\cdots ,a_t\}$$

and

$$|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((\{a_i\}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)|=k_i,i=1,2,\cdots ,t$$

Then, $1⩽t⩽p_1$ and $\left|D\right|=k_1+k_2+\cdots +k_t$. Let $z_i=({\sum }_{j=1}^t{k}_j)-k_i,i=1,2,\cdots ,t.$

If $t=1$ or $z_j<m$ for some $j\in \{1,2,\cdots ,t\}$, then $\left|D\right|⩾2m-1$ by Lemma 22. Since $3⩽p_1⩽m$, we have $(2-{\displaystyle \frac{p_1}{p_1-1}})m={\displaystyle \frac{p_1-2}{p_1-1}}m={\displaystyle \frac{m}{p_1-1}}(p_1-2)⩾p_1-2⩾1$, and so $\left|D\right|⩾2m-1⩾{\displaystyle \frac{p_1}{p_1-1}}m$.

If $t>1$ and $z_i⩾m$ for any $i\in \{1,2,\cdots ,t\}$, then we have

$$\left\{\begin{array}{c}{k}_2+k_3+\cdots +k_t=(\sum _{j=1}^t{k}_j)-k_1=z_1⩾m\hfill \\ k_1+k_3+\cdots +k_t=(\sum _{j=1}^t{k}_j)-k_2=z_2⩾m\hfill \\ k_1+k_2+k_4\cdots +k_t=(\sum _{j=1}^t{k}_j)-k_3=z_3⩾m\hfill \\ \cdots \hfill \\ k_1+k_2+\cdots +k_{t-1}=(\sum _{j=1}^t{k}_j)-k_t=z_t⩾m\hfill \end{array}\right.$$

and so $(t-1)\left|D\right|=(t-1)({\sum }_{j=1}^t{k}_j)⩾tm$. Thus, $\left|D\right|⩾{\displaystyle \frac{t}{t-1}}m⩾{\displaystyle \frac{p_1}{p_1-1}}m$, since $t⩽p_1$.

In particular, let $m=(p_1-1)q+r$, where q and r are non-negative integers and $r<p_1-1$.

If $r=0$, then ${\displaystyle \frac{p_1}{p_1-1}}m=p_{1}q$, so $\gamma (\mathrm{G}(T))⩾p_{1}q.$

If $r\ne 0$, then ${\displaystyle \frac{p_1}{p_1-1}}m$ is not an integer but $\left|D\right|$ is an integer and $\left|D\right|⩾{\displaystyle \frac{p_1}{p_1-1}}m$, so

$$\left|D\right|⩾[{\displaystyle \frac{p_1}{p_1-1}}m]+1=[m+{\displaystyle \frac{m}{p_1-1}}]+1=m+[{\displaystyle \frac{m}{p_1-1}}]+1=m+q+1=p_{1}q+r+1,$$

where $\left[x\right]$ is the bracket function. □

Lemma 23. 

Let $3⩽p_1$, $D\subseteq T$ and ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)={\mathbb{Z}}_{p_1}$. If for any $x\in {\mathbb{Z}}_{p_1}$,

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{x\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)$$

is a total dominating set of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$, then D is a total dominating set of $\mathrm{G}(T)$.

Proof. 

Let D be as given in the lemma. For any $(x_1,x_2,\cdots ,x_m)\in T$, let

$$\Lambda ={\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{-x_1\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D).$$

Then, $\Lambda$ is total a dominating set of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$ by assumption, and so there exists $(b_2,b_3,\cdots ,b_m)\in \Lambda$ such that $(x_2,x_3,\cdots ,x_m)\sim (b_2,b_3,\cdots ,b_m)$ in $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$, i.e.,

$$\begin{array}{c}(x_2,x_3\cdots ,x_m)+(b_2,b_3,\cdots ,b_m)\in \mathrm{U}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}) \mathrm{and}\\ (x_2,\cdots ,x_m)\ne (b_2,b_3,\cdots ,b_m)\end{array}$$

Since $(b_2,b_3,\cdots ,b_m)\in \Lambda$, there exists $y\in {\mathbb{Z}}_{p_1}\setminus \{-x_1\}$ such that $(y,b_2,b_3,\cdots ,b_m)\in D$. It follows that $y\ne -x_1$, and thus

$$(x_1,x_2,\cdots ,x_m)+(y,b_2,b_3,\cdots ,b_m)\in \mathrm{U}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$$

In addition, since $(x_2,\cdots ,x_m)\ne (b_2,b_3,\cdots ,b_m)$, we have $(x_1,x_2,\cdots ,x_m)\ne (y,b_2,b_3,\cdots ,b_m)$. Hence, $(x_1,x_2,\cdots ,x_m)\sim (y,b_2,b_3,\cdots ,b_m)$ in $\mathrm{G}(T)$, and consequently, D is a total dominating set of $\mathrm{G}(T)$. □

Proposition 3. 

Let $3⩽p_1⩽m$ and $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$. If $m=(p_1-1)q+r$, where q and r are non-negative integers with $r<p_1-1$, then,

$$\gamma (\mathrm{G}(T)={\gamma }_t(\overline{\mathrm{G}}(T))={\gamma }_t(\mathrm{G}(T)=\left\{\begin{array}{cc}{p}_{1}q,\hfill & ifr=0;\hfill \\ p_{1}q+r+1,\hfill & ifr\ne 0.\hfill \end{array}\right.$$

Proof. 

Let $3⩽p_1⩽m$ and $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$. Using the division algorithm, there is a unique pair of non-negative integers q and r such that $m=(p_1-1)q+r$, where $r<p_1-1$. Consider the following cases:

Case(i): $r=0$. In this case, we have $m=(p_1-1)q$, and so $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m=p_{1}q$. In addition, we have $q⩾2$, for otherwise, $q=1$ implies that $m=p_1-1<p_1$, which contradicts the fact that $3⩽p_1⩽m$. Let $D=A_0\cup A_1\cup A_2\cup \cdots \cup A_{p_1-1}$, where

$$A_0=\{\underset{mtimes}{\underbrace{(0,0,\cdots ,0)}}\}\cup \{\underset{mtimes}{\underbrace{(0,j,\cdots ,j)}}|(p_1-1)q+1⩽j⩽p_{1}q-1\},$$

$$A_i=\{\underset{mtimes}{\underbrace{(i,j,\cdots ,j)}}|(i-1)q+1⩽j⩽iq\},\forall i\in \{1,2,\cdots ,p_1-1\}.$$

Then, $D\subseteq T$, since $p_{1}q-1<p_{1}q⩽p_2<p_3<\cdots <p_m$.

Noticing that $|A_u|=q$ and $A_u\cap A_v=\varnothing$ for any $u,v\in \{0,1,\cdots ,p_1-1\}$ and $u\ne v$, we have $\left|D\right|={\sum }_{i=0}^{p_1-1}\left|A_i\right|=p_{1}q$. In addition, we have ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D)={\mathbb{Z}}_{p_1}$, and for any $x\in {\mathbb{Z}}_{p_1}$,

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{x\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)$$

is a total dominating set of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$ by Remark 9.

(Note: For example, we have

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{0\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)=\{\underset{m-1times}{\underbrace{(j,\cdots ,j)}}|1⩽j⩽(p_1-1)q\},$$

and $|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{0\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)|=(p_1-1)q=m$. Since $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m>m=(m-1)+1$, we immediately find by Remark 9 that ${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{0\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)$ is a total dominating set of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$.)

It follows from Lemma 23 that D is a total dominating set of $\mathrm{G}(T)$, hence

$$p_{1}q⩽\gamma (\mathrm{G}(T))⩽{\gamma }_t(\mathrm{G}(T))⩽\left|D\right|=p_{1}q$$

by Proposition 2 and Remark 1. Consequently, we obtain that $\gamma (\mathrm{G}(T))={\gamma }_t(\mathrm{G}(T))=p_{1}q$.

Case(ii): $r\ne 0$. Since $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$, we have

$$p_2⩾[{\displaystyle \frac{p_1}{p_1-1}}m]+1=[m+{\displaystyle \frac{m}{p_1-1}}]+1=m+[{\displaystyle \frac{m}{p_1-1}}]+1=m+q+1=p_{1}q+r+1.$$

Let $B=B_1\cup B_2\cup \cdots \cup B_{p_1-1}\cup B_0$, where

$$\begin{array}{ccc}& & B_i=\{\underset{mtimes}{\underbrace{(i,j,\cdots ,j)}}|(i-1)q+i⩽j⩽iq+i\},\forall i\in \{1,\cdots ,r\},\hfill \\ & & B_{\ell }=\{\underset{mtimes}{\underbrace{(\ell ,j,\cdots ,j)}}|(\ell -1)q+r+1⩽j⩽\ell q+r\},\forall \ell \in \{r+1,\cdots ,p_1-1\},\hfill \\ & & B_0=\{\underset{mtimes}{\underbrace{(0,0,\cdots ,0)}}\}\cup \{\underset{mtimes}{\underbrace{(0,j,\cdots ,j)}}|(p_1-1)q+r+1⩽j⩽p_{1}q+r\}.\hfill \end{array}$$

Then $B\subseteq T$ ($\because p_{1}q+r<p_2$ ). Noticing that $|B_i|=q+1$ for any $i\in \{0,1,2,\cdots ,r\}$, $|B_{\ell }|=q$ for any $\ell \in \{r+1,r+2,\cdots ,p_1-1\}$ and $B_u\cap B_v=\varnothing$ for any $u,v\in \{0,1,\cdots ,p_1-1\}$ with $u\ne v$, we have $\left|B\right|={\sum }_{i=0}^r|B_i|+{\sum }_{\ell =r+1}^{p_1-1}\left|B_{\ell }\right|=(r+1)(q+1)+(p_1-1-r)q=p_{1}q+r+1$ since $|B_0|=p_{1}q+r-((p_1-1)q+r+1)+1+1=q+1$, $|B_i|=iq+i-((i-1)q+i)+1=q+1$ for any $i\in \{1,\cdots ,r\}$ and $|B_{\ell }|=q$ for any $\ell \in \{r+1,r+2,\cdots ,p_1-1\}$ similarly.

In addition, we have ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(B)={\mathbb{Z}}_{p_1}$, and for any $x\in {\mathbb{Z}}_{p_1}$,

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{x\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap B)$$

is a total dominating set of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$ by Remark 9.

(Note: For example, we have

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{0\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)=\{\underset{m-1times}{\underbrace{(j,\cdots ,j)}}|1⩽j⩽(p_1-1)q+r\},$$

and $|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{0\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)|=(p_1-1)q+r=m$. In addition,

$$\begin{array}{ccc}& & {\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{p_1-1\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)\hfill \\ & =& \{\underset{m-1times}{\underbrace{(j,\cdots ,j)}}|j\in \{0,1,\cdots ,(p_1-2)q+r\}\cup \{(p_1-1)q+r+1,\cdots ,p_{1}q+r\}\},\hfill \end{array}$$

and $|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{p_1-1\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)|=(p_1-1)q+r+1=m+1$.

Since $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m>m=(m-1)+1$, we immediately find through Remark 9 that both

$$\begin{array}{c}{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{0\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D) \mathrm{and}\\ {\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}}((({\mathbb{Z}}_{p_1}\setminus \{p_1-1\})\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\cap D)\end{array}$$

are total dominating sets of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$.)

It follows immediately from Lemma 23 that B is a total dominating set of $\mathrm{G}(T)$, and so

$$p_{1}q+r+1⩽\gamma (\mathrm{G}(T))⩽{\gamma }_t(\mathrm{G}(T))⩽\left|B\right|=p_{1}q+r+1$$

by Proposition 2 and Lemma 1. Hence, $\gamma (\mathrm{G}(T))={\gamma }_t(\mathrm{G}(T))=p_{1}q+r+1$.

Summarizing the above arguments, we obtain by Lemma 15 that

$$\gamma (\mathrm{G}(T)={\gamma }_t(\overline{\mathrm{G}}(T))={\gamma }_t(\mathrm{G}(T))=\left\{\begin{array}{cc}{p}_{1}q,\hfill & ifr=0;\hfill \\ p_{1}q+r+1,\hfill & ifr\ne 0.\hfill \end{array}\right.$$

□

4.3. Case $p_1=2$

Lemma 24. 

If $\ell ⩾4$ is an integer, and $q_1<q_2<\cdots <q_{\ell }$ are primes, then $\ell <q_{\ell -1}<q_{\ell }.$

Proof. 

Assume that $\ell ⩾4$ is an integer, and $q_1<q_2<\cdots <q_{\ell }$ are primes. Then, $q_3⩾5$ and $q_4⩾7$. If $\ell =4$, then $\ell =4<5⩽q_3<q_4.$

If $\ell >4$, then $q_{\ell }>q_{\ell -1}⩾q_4+\ell -5⩾7+\ell -5=\ell +2>\ell$, since $7⩽q_4$. □

Lemma 25. 

Let $p_1=2$. Then, $\gamma (\mathrm{G}(T))⩾2m$.

Proof. 

By Lemma 24, we have $m<p_{m-1}<p_m.$ Let $p_1=2$. Suppose, on the contrary, that D is a dominating set of $\mathrm{G}(T)$ with $\left|D\right|=2m-1$.

Let $V_1=\{0\}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}$, and $V_2=\{1\}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}.$ Then, $T=V_1\cup V_2$ and $V_1\cap V_2=\varnothing$, which implies that $D=(D\cap V_1)\cup (D\cap V_2)$ and $(D\cap V_1)\cap (D\cap V_2)=\varnothing$. Since $\left|D\right|=2m-1$, we have $|D\cap V_1|<m$ or $|D\cap V_2|<m$. Without loss of generality, we assume that $|D\cap V_1|<m$ and let

$$D\cap V_1=\{(0,a_{i2},a_{i3},\cdots ,a_{im})|i=1,2,\cdots ,k\},$$

where $k=|D\cap V_1|<m$. Consider the following cases:

Case(1): $k<m-2$.

Let C be a subset of T such that

$$\begin{array}{ccc}& & (x_1,x_2\cdots ,x_m)\in C\hfill \\ & \iff & x_1=1,x_q=-a_{q-1,q},\forall q\in \{2,3,\cdots ,k+1\};and{x}_s\in {\mathbb{Z}}_{p_s},\forall s\in \{k+2,\cdots ,m\}\hfill \end{array}$$

That is to say,

$$C=\{(1,-a_{12},-a_{23},\cdots ,-a_{k,k+1},x_{k+2},\cdots ,x_m)|x_s\in {\mathbb{Z}}_{p_s},s=k+2,\cdots ,m\}.$$

Then, $x\nsim y$ for any $x\in C$ and any $y\in D$ in $\mathrm{G}(T)$, which implies that $C\subseteq D$, since D is a dominating set of $\mathrm{G}(T)$. Thus, $\left|D\right|⩾\left|C\right|⩾p_{m-1}{p}_m>2m$, since $k<m-2$, $2<p_{m-1}$ and $p_m>m$. But $\left|D\right|=2m-1$, a contradiction.

Case(2): $k=m-2$.

If $a_{12}=a_{22}=\cdots =a_{k2}$, then for any $x\in \{(1,-a_{12},x_3,\cdots ,x_m)|x_i\in {\mathbb{Z}}_{p_i},i=3,\cdots ,m\}$, we have $x\nsim y$ for any $y\in D$. So,

$$\{(1,-a_{12},x_3,\cdots ,x_m)|x_i\in {\mathbb{Z}}_{p_i},i=3,\cdots ,m\}\subseteq D$$

Hence, $\left|D\right|⩾|\{(1,-a_{12},x_3,\cdots ,x_m)|x_i\in {\mathbb{Z}}_{p_i},i=3,\cdots ,m\}|⩾p_{m-1}{p}_m>2m$, since $m⩾4$, $2<p_{m-1}$ and $p_m>m$, which is a contradiction with $\left|D\right|=2m-1$.

If there exist $i,j\in \{2,\cdots ,k\}$ such that $a_{i2}\ne a_{j2}$, without loss of generality, say $a_{12}\ne a_{22}$. Let ${\mathrm{Y}}_1$ and ${\mathrm{Y}}_2$ be, respectively, subsets of T such that

$$\begin{array}{ccc}& & (x_1,x_2\cdots ,x_m)\in {\mathrm{Y}}_1\hfill \\ & \iff & x_1=1,x_q=-a_{q-1,q},\forall q\in \{2,3,\cdots ,k+1\}and{x}_m\in {\mathbb{Z}}_{p_m}\hfill \end{array}$$

(i.e., ${\mathrm{Y}}_1=\{(1,-a_{12},-a_{23},\cdots ,-a_{k,k+1},x_m)|x_m\in {\mathbb{Z}}_{p_m}\}$ ) and

$$\begin{array}{ccc}& & (x_1,x_2,\cdots ,x_m)\in {\mathrm{Y}}_2\hfill \\ & \iff & x_1=1,x_2=-a_{22},x_3=-a_{13},x_q=-a_{q-1,q},\forall q\in \{4,\cdots ,k+1\}and{x}_m\in {\mathbb{Z}}_{p_m}\hfill \end{array}$$

(i.e., ${\mathrm{Y}}_2=\{(1,-a_{22},-a_{13},-a_{34},\cdots ,-a_{k,k+1},x_m)|x_m\in {\mathbb{Z}}_{p_m}\}$.) Then, ${\mathrm{Y}}_1\cap {\mathrm{Y}}_2=\varnothing$, since $a_{12}\ne a_{22}$. Let $\mathrm{Y}={\mathrm{Y}}_1\cup {\mathrm{Y}}_2$. Then, $x\nsim y$ for any $x\in \mathrm{Y}$ and any $y\in D$, which implies that $\mathrm{Y}\subseteq D$ in $\mathrm{G}(T)$, since D is a dominating set of $\mathrm{G}(T)$. Thus, $\left|D\right|⩾\left|\mathrm{Y}\right|=|{\mathrm{Y}}_1|+|{\mathrm{Y}}_2|=2p_m>2m$, since $p_m>m$, which is a contradiction with $\left|D\right|=2m-1$.

Case(3): $k=m-1$.

In this case, we have $|D\cap V_1|=k=m-1$, and so $|D\cap V_2|=m$, since $\left|D\right|=2m-1$, $D=(D\cap V_1)\cup (D\cap V_2)$ and $(D\cap V_1)\cap (D\cap V_2)=\varnothing$.

Subcase(3.1): There exists $i\in \{2,3,\cdots ,m\}$ such that there are at least two elements among $a_{1i},a_{2i},\cdots ,a_{ki}$ that are equal, and without loss of generality, assume that $a_{1i}=a_{2i}$.

Let $C_1$ be a subset of T such that

$$\begin{array}{ccc}& & (x_1,x_2\cdots ,x_i,\cdots ,x_m)\in C_1\hfill \\ & \iff & x_1=1,x_i=-a_{1i},andthereexists\{j_3,j_4,\cdots ,j_k\}\subseteq \{2,\cdots ,m\}\setminus \{i\}\hfill \\ & & suchthat{x}_{j_q}=-a_{q{j}_q},q=3,\cdots ,k\hfill \end{array}$$

(For example, if $i=3$ and $a_{13}=a_{23}$, we may let $j_q=\left\{\begin{array}{cc}q,\hfill & ifq=4,\cdots ,k;\hfill \\ q-1,\hfill & ifq=3,\hfill \end{array}\right.$, then

$$\{(1,-a_{32},-a_{13},-a_{44},\cdots ,-a_{kk},x_m)|x_m\in {\mathbb{Z}}_{p_m}\}\subseteq C_1.$$

If $i=m$ and $a_{1m}=a_{2m}$, we may let $j_q=q-1$ for any $q\in \{3,\cdots ,k\}$, then

$$\{(1,-a_{32},-a_{43},\cdots ,-a_{k,k-1},x_k,-a_{1m})|x_k\in {\mathbb{Z}}_{p_{m-1}}\}\subseteq C_1).$$

For any $x\in C_1$ and any $y\in D$, we have $x\nsim y$ in $\mathrm{G}(T)$, and so $C_1\subseteq D\cap V_2$, since D is a dominating set of $\mathrm{G}(T)$ and $C_1\subseteq V_2$. Hence, $|D\cap V_2|⩾|C_1|⩾p_{m-1}>m$, which is a contradiction with $|D\cap V_2|=m$.

Subcase(3.2): $a_{1i},a_{2i},\cdots ,a_{ki}$ are mutually different, for any $i\in \{2,3,\cdots ,m\}.$

Let ${\mathbf{S}}_k$ denote the symmetric group on the set $\{1,2,\cdots ,k\}$, and let $C_2$ be a subset of T such that

$$\begin{array}{ccc}& & (x_1,x_2\cdots ,x_m)\in C_2\hfill \\ & \iff & x_1=1,andthereexistsapermutation{j}_1{j}_2\cdots j_k\in {\mathbf{S}}_k\hfill \\ & & suchthat{x}_{j_q}=-a_{j_q(q+1)},q=1,2,\cdots ,k\hfill \end{array}$$

that is to say, $C_2=\{(1,-a_{j_{1}2},-a_{j_{2}3},\cdots ,-a_{j_k,k+1})|j_1\cdots j_k\in {\mathbf{S}}_k\}$. Then, for any $x\in C_2$ and any $y\in D$, we have $x\nsim y$ in $\mathrm{G}(T)$, and so $C_2\subseteq D\cap V_2$, since D is a dominating set of $\mathrm{G}(T)$ and $C_2\subseteq V_2$. Hence, $|D\cap V_2|⩾|C_2|⩾k!=(m-1)!⩾2m-2>m$, since $k=m-1$ and $m⩾4$, which is a contradiction with $|D\cap V_2|=m$.

Therefore, we conclude that $\gamma (\mathrm{G}(T))⩾2m$. □

Theorem 2. 

Let m be a positive integer with $m⩾4$, $p_1<p_2<\cdots <p_m$ are primes and $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$, where ${\alpha }_i$ is a positive integer for each $i\in \{1,2,\cdots ,m\}$. Using the division algorithm, there is a unique pair of non-negative integers q and r such that

$$m=(p_1-1)q+r$$

where $0⩽r<p_1-1$.

(i) 

If $p_1=2$ and ${\alpha }_1{\alpha }_2\cdots {\alpha }_m=1$, then $2m⩽\gamma (\mathrm{G}({\mathbb{Z}}_n))⩽2\gamma (\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}).$

(ii) 

If $p_1=2$ and ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$, then $2{\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})⩽\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})\le 2{\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}).$

(iii) 

If $3⩽p_1⩽m$ and $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$, then

$$\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=\left\{\begin{array}{cc}{p}_{1}q,\hfill & ifr=0;\hfill \\ p_{1}q+r+1,\hfill & ifr\ne 0.\hfill \end{array}\right.$$

(iv) 

If $p_1⩾m+1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=m+1.$

(v) 

If $p_1=2$ and $p_2⩾m⩾4$, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=2m.$

Proof. 

Let m and n be as given in the Theorem. Then, ${\mathbb{Z}}_n\cong {\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus \cdots \oplus {\mathbb{Z}}_{p_m^{{\alpha }_m}}$ and ${\mathbb{Z}}_n/\mathrm{J}({\mathbb{Z}}_n)\cong {\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}$.

(i) follows immediately from Lemma 18 and Lemma 25.

(ii) Let $p_1=2$ and ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$. Then, $2\notin \mathrm{U}({\mathbb{Z}}_n)$, which implies by Theorem 1 that $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$. In addition, by Lemma 19, we have

$$2{\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})⩽{\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})⩽2{\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}).$$

Thus, (ii) holds.

(iii) Let $3⩽p_1⩽m$ and $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$. If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m=1$, then by Proposition 3, (iii) holds.

Assume that ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$. By Theorem 1, we have $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$, and so by Proposition 3 we obtain

$$\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$$

$$={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))=\left\{\begin{array}{cc}{p}_{1}q,\hfill & ifr=0;\hfill \\ p_{1}q+r+1,\hfill & ifr\ne 0.\hfill \end{array}\right.$$

It follows from Lemma 6 that $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))$. Finally, by Lemma 15, we have

$$\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=\left\{\begin{array}{cc}{p}_{1}q,\hfill & ifr=0;\hfill \\ p_{1}q+r+1,\hfill & ifr\ne 0.\hfill \end{array}\right.$$

(iv) Let $p_1⩾m+1$. If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m=1$, then by Proposition 1, (iv) holds.

Assume that ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$. By Theorem 1, we have $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$, and so by Proposition 1 we obtain

$$\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))=m+1$$

It follows from Lemma 6 that $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=m+1$. Finally, by Lemma 15, we have $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=m+1$.

(v) Let $p_1=2$ and $p_2⩾m⩾4$. By Proposition 1 and Remark 9, we have

$$\gamma (\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))=m,$$

(4)

since $p_2⩾m=(m-1)+1$.

If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m=1$, then $2m⩽\gamma (\mathrm{G}({\mathbb{Z}}_n))⩽2\gamma (\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$ by Theorem 2 item (i), and so $\gamma (\mathrm{G}({\mathbb{Z}}_n))=2m$ by Equation (4). In addition, by Lemma 19 we have

$$2{\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})⩽{\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})⩽2{\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}).$$

It follows from Equation (4) that ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})=2m$.

If ${\alpha }_1{\alpha }_2\cdots {\alpha }_m>1$, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})=2m$ by Theorem 1. □

Remark 10. 

In Theorem 2, (ii) holds true for all positive integers $m⩾2$ by the proof of (ii).

Theorem 2 (iv) also holds true when $m=3$, since Proposition 1 also holds true when $m=3$ by Remark 9. But Theorem 2 (i) is not true when $m=3$, since $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3\oplus {\mathbb{Z}}_5)=4$ by Lemma 11, but $2m=6$.

As for Theorem 2 (iii), when $m=3$, then $p_1=3$ and $q=r=1$, since $3⩽p_1⩽m$ and $m=(p_1-1)+1$. By Corollary 3 (viii) and (ix), we have

$${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=5=p_{1}q+r+1$$

But $\gamma (\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_5\oplus {\mathbb{Z}}_7)=4\ne 5=p_{1}q+r+1$ by Lemma 11.

As for Theorem 2 (v), when $m=3$ and $p_1=2$, then ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=6=2m$ by Corollary 3 (viii) and (ix), but $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3\oplus {\mathbb{Z}}_5)=4\ne 6=2m$ by Lemma 11.

In Theorem 2, we study several cases of the domination number and total dominating number of ${\mathbb{Z}}_n$. But there are still some situations that we have not fully considered; for example, $3⩽p_1⩽m⩽p_2<{\displaystyle \frac{p_1}{p_1-1}}m$ and $3⩽p_1<p_2<m$. As for the case of $p_1=2$, we only provided a range, without providing an accurate value of the domination number and total dominating number, so this requires more in-depth research.

5. The Unit Graph of the Ring ${\mathbb{Z}}_n$ Associated with Products of Four Residue Class Fields

In this section, we focus on studying the domination number and the total domination number of $\mathrm{G}({\mathbb{Z}}_n)$ when n has exactly four prime divisors. In what follows, we always assume that $S={\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}$, where $p_1<p_2<p_3<p_4$ are primes.

Proposition 4. 

If $p_1=2$, then $\gamma (\mathrm{G}(S))=8$, and ${\gamma }_t(\mathrm{G}(S))=\left\{\begin{array}{cc}10,\hfill & if{p}_2=3;\hfill \\ 8,\hfill & if{p}_2>3.\hfill \end{array}\right.$

Proof. 

Let $p_1=2$. If $p_2>3$, then $p_2⩾5>4$, since $p_2$ is a prime. It follows from Theorem 2 (v) that $\gamma (\mathrm{G}(S))={\gamma }_t(\mathrm{G}(S))=8$.

If $p_2=3$, then $8⩽\gamma (\mathrm{G}(S)⩽2\gamma (\mathrm{G}({\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))=8$ by Theorem 2 (i) and Lemma 11. Thus, $\gamma (\mathrm{G}(S))=8$. As for ${\gamma }_t(\mathrm{G}(S))$, by Lemma 19 we have

$$2{\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))⩽{\gamma }_t(\mathrm{G}(S))⩽2{\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))$$

In addition, by Corollary 3 (ix), we obtain

$${\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))=5$$

Hence, ${\gamma }_t(\mathrm{G}(S))=10$. □

Proposition 5. 

If $p_1=3$ and $p_2=5$, then $\gamma (\mathrm{G}(S))={\gamma }_t(\overline{\mathrm{G}}(S))={\gamma }_t(\mathrm{G}(S))=7$.

Proof. 

Let $p_1=3$ and $p_2=5$. Then, $p_4>p_3⩾7$. Put

$$D=\{(0,1,1,1),(0,2,2,2),(0,3,3,3),(1,0,0,0),(1,2,2,2),(2,3,3,3),(2,4,4,4)\}.$$

Then, $D\subseteq S$. In addition, we have

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}}((({\mathbb{Z}}_{p_1}\setminus \{0\})\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4})\cap D)=\{(0,0,0),(2,2,2),(3,3,3),(4,4,4)\},$$

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}}((({\mathbb{Z}}_{p_1}\setminus \{1\})\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4})\cap D)=\{(1,1,1),(2,2,2),(3,3,3),(4,4,4)\},$$

and

$${\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}}((({\mathbb{Z}}_{p_1}\setminus \{2\})\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4})\cap D)=\{(0,0,0),(1,1,1),(2,2,2),(3,3,3)\}$$

are total dominating sets of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4})$ by Remark 9. It follows from Lemma 23 that D is a total dominating set of $\mathrm{G}(S)$, and so $\gamma (\mathrm{G}(S))⩽{\gamma }_t(\mathrm{G}(S))⩽\left|D\right|=7$ by Remark 1.

Suppose that $D^{\prime }=\{(a_i,b_i,c_i,d_i)\in S|i=1,2,3,4,5,6\}$ is a dominating set of $\mathrm{G}(S)$, and without loss of generality, assume that ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D^{\prime })=\{a_1,a_2,\cdots ,a_t\}$, where $1⩽t⩽3$. Let

$$|{\mathrm{P}}_{{\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}}((\{a_i\}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4})\cap D^{\prime })|=k_i,i=1,2,\cdots ,t$$

and $z_i=({\sum }_{j=1}^t{k}_j)-k_i,i=1,2,\cdots ,t$. Then, $k_1+\cdots +k_t=\left|D^{\prime }\right|=6$. Consider the following cases:

Case (1) $t=1$. Then, $|D^{\prime }|⩾2·4-1=7$ by Lemma 22, a contradiction.

Case (2) $t=2$, i.e., ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D^{\prime })=\{a_1,a_2\}$. Then, $z_2=(k_1+k_2)-k_2=k_1<4$ or $z_1=(k_1+k_2)-k_1=k_2<4$, since $k_1+k_2=\left|D^{\prime }\right|=6$. It follows from Lemma 22 that $|D^{\prime }|⩾7$, a contradiction.

Case (3) $t=3$. Then, ${\mathrm{P}}_{{\mathbb{Z}}_{p_1}}(D^{\prime })=\{a_1,a_2,a_3\}={\mathbb{Z}}_{p_1}$ and $k_1+k_2+k_3=6$.

We claim that $k_i=2$ for any $i\in \{1,2,3\}$. In fact, if $k_j⩾3$ for some $j\in \{1,2,3\}$, then $z_j=(k_1+k_2+k_3)-k_j=6-k_j⩽3<4$, and so $|D^{\prime }|⩾7$ by Lemma 22, a contradiction.

If $k_j=1$ for some $j\in \{1,2,3\}$, say $k_1=1$, then $k_2+k_3=5$, since $k_1+k_2+k_3=6$. It follows from the well-known pigeonhole principle [20] (Theorem 3.1.1) that $k_2⩾3$ or $k_3⩾3$, which also gives a contradiction. Hence, $k_i=2$ for any $i\in \{1,2,3\}$. Without loss of generality, we can assume that

$$a_1=a_4=-1,a_2=a_5=1\mathrm{and}{a}_3=a_6=0\mathrm{in}{\mathbb{Z}}_{p_1}={\mathbb{Z}}_3$$

We will prove that $b_1,b_2,b_3,b_4,b_5$ and $b_6$ are mutually different.

Claim(i): $b_1\ne b_4$ and $b_2\ne b_5$.

Suppose, on the contrary, that $b_1=b_4$. If $c_2=c_5$, then for any $x\in \{(0,-b_1,-c_2,d)|d\in {\mathbb{Z}}_{p_4}\}$ and any $y\in D^{\prime }$, we have $x\nsim y$ in $\mathrm{G}(S)$, and so $\{(0,-b_1,-c_2,d)|d\in {\mathbb{Z}}_{p_4}\}\subseteq D^{\prime }$, since $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. Thus, $|D^{\prime }|⩾p_4>p_3⩾7$, a contradiction. Hence, $c_2\ne c_5$.

For any $y\in D^{\prime }$, we have $(0,-b_1,-c_2,-d_5)\nsim y$ and $(0,-b_1,-c_5,-d_2)\nsim y$ in $\mathrm{G}(S)$, and so

$$\{(0,-b_1,-c_2,-d_5),(0,-b_1,-c_5,-d_2)\}\subseteq D^{\prime },$$

(5)

since $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. It follows that

$$\{(a_3,b_3,c_3,d_3),(a_6,b_6,c_6,d_6)\}=\{(0,-b_1,-c_2,-d_5),(0,-b_1,-c_5,-d_2)\},$$

since $a_3=a_6=0$.

Since $a_1=a_4$, $b_1=b_4$ and $(a_1,b_1,c_1,d_1)\ne (a_4,b_4,c_4,d_4)$, we have $c_1\ne c_4$ or $d_1\ne d_4$. Let

$$\Psi =\{(1,b_1,-c_2,-d_5),(1,b_1,-c_5,-d_2),(-1,b_1,-c_1,-d_4),(-1,b_1,-c_4,-d_1)\}.$$

Then, for any $x\in \Psi$ and any $y\in D^{\prime }$, we have $x\nsim y$ in $\mathrm{G}(S)$, and so

$$\Psi \subseteq D^{\prime }$$

(6)

since $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. Notice that $|D^{\prime }| =6$, by (5) and (6), we immediately have

$$D^{\prime }=\{v_1,v_2,v_3,v_4,v_5,v_6\},$$

where $v_1=(0,-b_1,-c_2,-d_5),v_2=(0,-b_1,-c_5,-d_2),v_3=(1,b_1,-c_2,-d_5),$ $v_4=(1,b_1,-c_5,-d_2),v_5=(-1,b_1,-c_1,-d_4)$ and $v_6=(-1,b_1,-c_4,-d_1)$.

Let

$$\Phi =\{(0,-b_1,c,d)|c\in {\mathbb{Z}}_{p_3}\setminus \{-c_2,-c_5\},d\in {\mathbb{Z}}_{p_4}\}.$$

Then, $\Phi \cap D^{\prime }=\varnothing$, and for any $x\in \Phi$ and any $y\in D^{\prime }$, we have $x\nsim y$ in $\mathrm{G}(S)$. This contradicts with the fact that $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. Thus, $b_1\ne b_4$, and similarly we have $b_2\ne b_5$.

Claim(ii): $b_3\ne b_6$.

Suppose, on the contrary, $b_3=b_6$. If $c_2=c_5$, then for any $x\in \{(1,-b_3,-c_2,d)|d\in {\mathbb{Z}}_{p_4}\}$ and any $y\in D^{\prime }$, we have $x\nsim y$ in $\mathrm{G}(S)$, and so $\{(1,-b_3,-c_2,d)|d\in {\mathbb{Z}}_{p_4}\}\subseteq D^{\prime }$, since $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. Thus, $|D^{\prime }|⩾p_4>p_3⩾7$, a contradiction. Hence, $c_2\ne c_5$.

For any $y\in D^{\prime }$, we have $(1,-b_3,-c_2,-d_5)\nsim y$ and $(1,-b_3,-c_5,-d_2)\nsim y$ in $\mathrm{G}(S)$, and so

$$\{(1,-b_3,-c_2,-d_5),(1,-b_3,-c_5,-d_2)\}\subseteq D^{\prime }.$$

since $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. Noticing that $c_2\ne c_5$, we have $(1,-b_3,-c_2,-d_5)\ne (1,-b_3,-c_5,-d_2)$, which implies that

$$\{(a_2,b_2,c_2,d_2),(a_5,b_5,c_5,d_5)\}=\{(1,-b_3,-c_2,-d_5),(1,-b_3,-c_5,-d_2)\},$$

since $a_2=a_5=1$. It follows that $b_2=b_5=-b_3$, which contradicts with claim(i). Thus, $b_3\ne b_6$.

Claim(iii): $b_1\notin \{b_2,b_5\}$ and $b_4\notin \{b_2,b_5\}$.

Suppose, on the contrary, that $b_1=b_2$. If $c_4=c_5$, then for any $x\in \{(0,-b_1,-c_4,d)|d\in {\mathbb{Z}}_{p_4}\}$ and any $y\in D^{\prime }$, we have $x\nsim y$ in $\mathrm{G}(S)$, and so $\{(0,-b_1,-c_4,d)|d\in {\mathbb{Z}}_{p_4}\}\subseteq D^{\prime }$, since $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. Thus, $|D^{\prime }|⩾p_4>p_3⩾7$, a contradiction. Hence, $c_4\ne c_5$.

For any $y\in D^{\prime }$, we have $(0,-b_1,-c_4,-d_5)\nsim y$ and $(0,-b_1,-c_5,-d_4)\nsim y$ in $\mathrm{G}(S)$, and so

$$\{(0,-b_1,-c_4,-d_5),(0,-b_1,-c_5,-d_4)\}\subseteq D^{\prime },$$

since $D^{\prime }$ is a dominating set of $\mathrm{G}(S)$. It follows that

$$\{(a_3,b_3,c_3,d_3),(a_6,b_6,c_6,d_6)\}=\{(0,-b_1,-c_4,-d_5),(0,-b_1,-c_5,-d_4)\},$$

since $c_4\ne c_5$ and $a_3=a_6=0$. But then $b_3=b_6=-b_1$, which contradicts with claim(ii). Thus, $b_1\ne b_2$. Similarly, we have $b_1\ne b_5$, $b_4\ne b_2$ and $b_4\ne b_5$.

Claim(iv): $b_3\notin \{b_1,b_2,b_4,b_5\}$ and $b_6\notin \{b_1,b_2,b_4,b_5\}$.

Suppose, on the contrary, that $b_3=b_1$. If $c_4=c_6$, then for any $x\in \{(-1,-b_3,-c_4,d)|d\in {\mathbb{Z}}_{p_4}\}$ and any $y\in D^{\prime }$, we have $x\nsim y$$\mathrm{G}(S)$, which implies that $\{(-1,-b_3,-c_4,d)|d\in {\mathbb{Z}}_{p_4}\}\subseteq D^{\prime }$ and so $|D^{\prime }|⩾p_4>p_3⩾7$, a contradiction. Thus, $c_4\ne c_6$.

For any $y\in D^{\prime }$, we have $(-1,-b_3,-c_4,-d_6)\nsim y$ and $(-1,-b_3,-c_6,-d_4)\nsim y$. So

$$\{(-1,-b_3,-c_4,-d_6),(-1,-b_3,-c_6,-d_4)\}\subseteq D^{\prime }.$$

It follows that

$$\{(a_1,b_1,c_1,d_1),(a_4,b_4,c_4,d_4)\}=\{(-1,-b_3,-c_4,-d_6),(-1,-b_3,-c_6,-d_4)\},$$

since $c_4\ne c_6$ and $a_1=a_4=-1$. But then $b_1=b_4=-b_3$, which contradicts with Claim (i). Similarly, we have $b_3\notin \{b_2,b_4,b_5\}$ and $b_6\notin \{b_1,b_2,b_4,b_5\}$.

By claims (i), (ii), (iii), and (iv), we obtain that $b_1,b_2,b_3,b_4,b_5$ and $b_6$ are mutually different elements in ${\mathbb{Z}}_5$, a contradiction. Thus, $7⩽\gamma (\mathrm{G}(S))⩽{\gamma }_t(\mathrm{G}(S))⩽7$. It follows by Lemma 15 that $\gamma (\mathrm{G}(S))={\gamma }_t(\overline{\mathrm{G}}(S))={\gamma }_t(\mathrm{G}(S))=7$. □

Combining the above results, we obtain the main theorem.

Theorem 3. 

Let $R={\mathbb{Z}}_{p_1^{{\alpha }_1}}\oplus {\mathbb{Z}}_{p_2^{{\alpha }_2}}\oplus {\mathbb{Z}}_{p_3^{{\alpha }_3}}\oplus {\mathbb{Z}}_{p_4^{{\alpha }_4}}$, where $p_1<p_2<p_3<p_4$ are primes, ${\alpha }_i$ is a positive integer for each $i\in \{1,2,3,4\}$. Then, we have the following:

(i) 

If $p_1=2$ and ${\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4=1$, then $\gamma (\mathrm{G}(R))=8$, and ${\gamma }_t(\mathrm{G}(R))=\left\{\begin{array}{cc}10,\hfill & if{p}_2=3;\hfill \\ 8,\hfill & if{p}_2>3.\hfill \end{array}\right.$

(ii) 

If $p_1=2$ and ${\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4>1$, then $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))={\gamma }_t(\mathrm{G}(R))=\left\{\begin{array}{cc}10,\hfill & if{p}_2=3;\hfill \\ 8,\hfill & if{p}_2>3.\hfill \end{array}\right.$

(iii) 

If $p_1⩾3$, then $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))={\gamma }_t(\mathrm{G}(R))=\left\{\begin{array}{cc}7,\hfill & if{p}_1=3and{p}_2=5;\hfill \\ 6,\hfill & if{p}_1=3and{p}_2>5;\hfill \\ 5,\hfill & if{p}_1>3.\hfill \end{array}\right.$

Proof. 

(i) follows immediately from Proposition 4.

(ii) follows immediately from Corollary 3 (vii), Lemma 15 and Theorem 3 item (i).

(iii) Assume that $p_1⩾3$. Firstly, let ${\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4=1$.

If $p_1>3$, then $p_1⩾5=4+1$, and so $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))={\gamma }_t(\mathrm{G}(R))=5$ by Proposition 1.

If $p_1=3$ and $p_2>5$, then $p_2⩾7>6={\displaystyle \frac{p_1}{p_1-1}}·4$, and so $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))={\gamma }_t(\mathrm{G}(R))=2p_1=6$ by Proposition 3, since $4=(p_1-1)·2$.

If $p_1=3$ and $p_2=5$, then $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))={\gamma }_t(\mathrm{G}(R))=7$ by Proposition 5.

Finally, assume that ${\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4>1$. Then, $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))$ by Theorem 1. By Lemma 6 and the case of ${\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4=1$, we have

$$\gamma (\mathrm{G}(R))={\gamma }_t(\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R))=\left\{\begin{array}{cc}7,\hfill & if{p}_1=3and{p}_2=5;\hfill \\ 6,\hfill & if{p}_1=3and{p}_2>5;\hfill \\ 5,\hfill & if{p}_1>3.\hfill \end{array}\right.$$

□

Remark 11. 

For Theorem 1, we have not yet investigated whether it applies to an arbitrary ring, especially noncommutative rings, which is also a research topic worth exploring. In addition, we recall the question of [16] (remark): Is $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))$ for all n?

If ${\mathbb{Z}}_n$ is directly decomposed into certain fields, then the answer is negative. For example,

(i) 

n is a prime, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))=1$ and ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=2$ by Corollary 3 (ii).

(ii) 

$n=2p$, where p is a prime, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))=2$ and ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=4$ by Corollary 3 (vi).

(iii) 

$n=3p_2{p}_3$, where $3<p_2<p_3$ are primes, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))=4$ and ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=5$ by Corollary 3 (ix).

(iv) 

$n=2·3p_3{p}_4$, where $3<p_3<p_4$ are primes, then $\gamma (\mathrm{G}({\mathbb{Z}}_n))=8$ and ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))=10$ by Proposition 4.

Here is a special situation, using Theorem 2 (i) and (ii), we find that the domination number and total dominating number of $\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$ are linked to the domination number and total dominating number of $\mathrm{G}({\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$, where $2<p_2<p_3<\cdots <p_m$ are primes.

In addition, from the proof of Lemma 19 and Proposition 4, we know it is the fact that $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_p))\ne {\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_p))$ is caused by $\gamma (\mathrm{G}({\mathbb{Z}}_p))\ne {\gamma }_t(\mathrm{G}({\mathbb{Z}}_p))$, $\gamma (\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))\ne {\gamma }_t(\mathrm{G}({\mathbb{Z}}_2\oplus {\mathbb{Z}}_3\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))$ is caused by $\gamma (\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))\ne {\gamma }_t(\mathrm{G}({\mathbb{Z}}_3\oplus {\mathbb{Z}}_{p_3}\oplus {\mathbb{Z}}_{p_4}))$. However, by Theorem 2 (iii) and (iv), we know that $\gamma (\mathrm{G}({\mathbb{Z}}_{p_1}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_{p_1}\oplus \cdots \oplus {\mathbb{Z}}_{p_m}))$ when $m⩾4$, $p_1⩾3$ and $p_2⩾{\displaystyle \frac{p_1}{p_1-1}}m$.

So we modify the question of [16] (remark) using the following problems:

Open problem 1: Is $\gamma (\mathrm{G}({\mathbb{Z}}_n)={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))$ when $n=p_1{p}_2\cdots p_m$, where $m⩾5$ and $p_1<p_2<\cdots <p_m$ are primes?

In fact, as for the open problem 1, we only need to study the following cases for Theorem 2:

(i) 

$p_1=2$ and $p_2<m$;

(ii) 

$3⩽p_1⩽m⩽p_2<{\displaystyle \frac{p_1}{p_1-1}}m$;

(iii) 

$3⩽p_1<p_2<m$.

Open problem 2: is $\gamma (\mathrm{G}(R))={\gamma }_t(\mathrm{G}(R))$ when $|\mathrm{J}(R)|>1$? In particular, is $\gamma (\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))$ when $|\mathrm{J}({\mathbb{Z}}_n)|>1$?

As for open problem 2, we have $\gamma (\mathrm{G}(R))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$ by Theorem 1 and $\gamma (\mathrm{G}(R))⩽{\gamma }_t(\mathrm{G}(R))⩽{\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$ by Lemma 6. So, if one prove that ${\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))={\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))$, then the answer to problem 2 is positive. By Lemma 15, we have ${\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))⩽{\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$. But we do not know whether ${\gamma }_t(\overline{\mathrm{G}}(R/\mathrm{J}(R)))⩾{\gamma }_t(\mathrm{G}(R/\mathrm{J}(R)))$.

In particular, is ${\gamma }_t(\mathrm{G}({\mathbb{Z}}_n))={\gamma }_t(\overline{\mathrm{G}}({\mathbb{Z}}_n))$ when ${\mathbb{Z}}_n$ is directly decomposed into some fields? Regarding this question, with Theorem 3 we can assume that $n=p_1{p}_2\cdots p_m$, $m⩾5$ and $p_1<p_2<\cdots <p_m$ are primes, and consider the following cases by Theorem 2:

(i) 

$3⩽p_1⩽m⩽p_2<{\displaystyle \frac{p_1}{p_1-1}}m$;

(ii) 

$3⩽p_1<p_2<m$.

Notice that a ${\gamma }_t$-set of $\overline{\mathrm{G}}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$ may be not a total dominating set of $\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$. For example, $\{1,2\}$ is a ${\gamma }_t$-set of $\overline{\mathrm{G}}({\mathbb{Z}}_3)$, but $\{1,2\}$ is not a total dominating set of $\mathrm{G}({\mathbb{Z}}_3)$. However, one can observe that $\{0,1\}$ is a total dominating set of $\mathrm{G}({\mathbb{Z}}_3)$. So, how to construct a total dominating set of $\mathrm{G}({\mathbb{Z}}_{p_1}\oplus {\mathbb{Z}}_{p_2}\oplus \cdots \oplus {\mathbb{Z}}_{p_m})$ is another problem.