Influence of Heat Transfer on Stress Components in Metallic Plates Weakened by Multi-Curved Holes
Abstract
1. Introduction
2. Formulation of the Problem
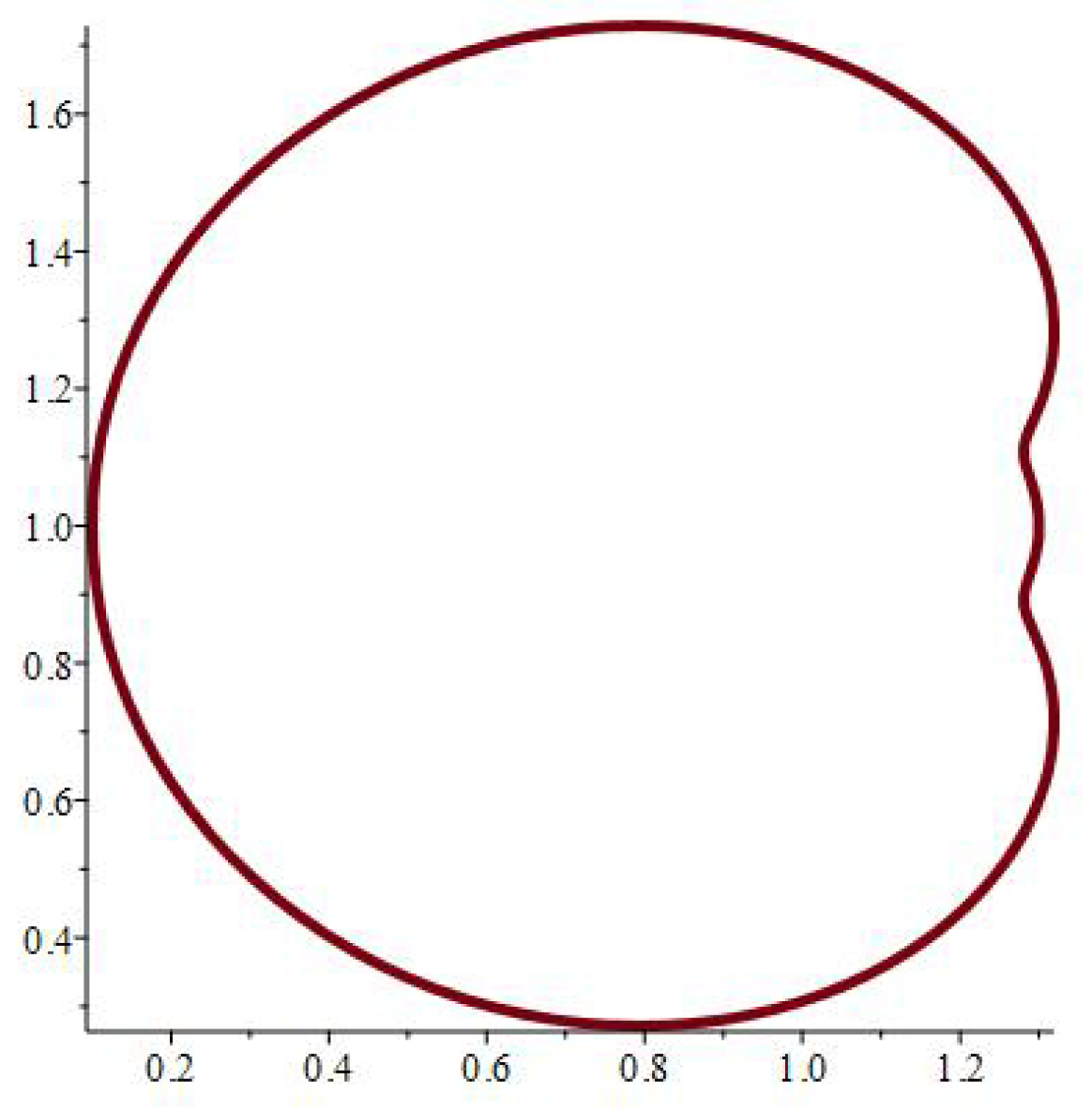
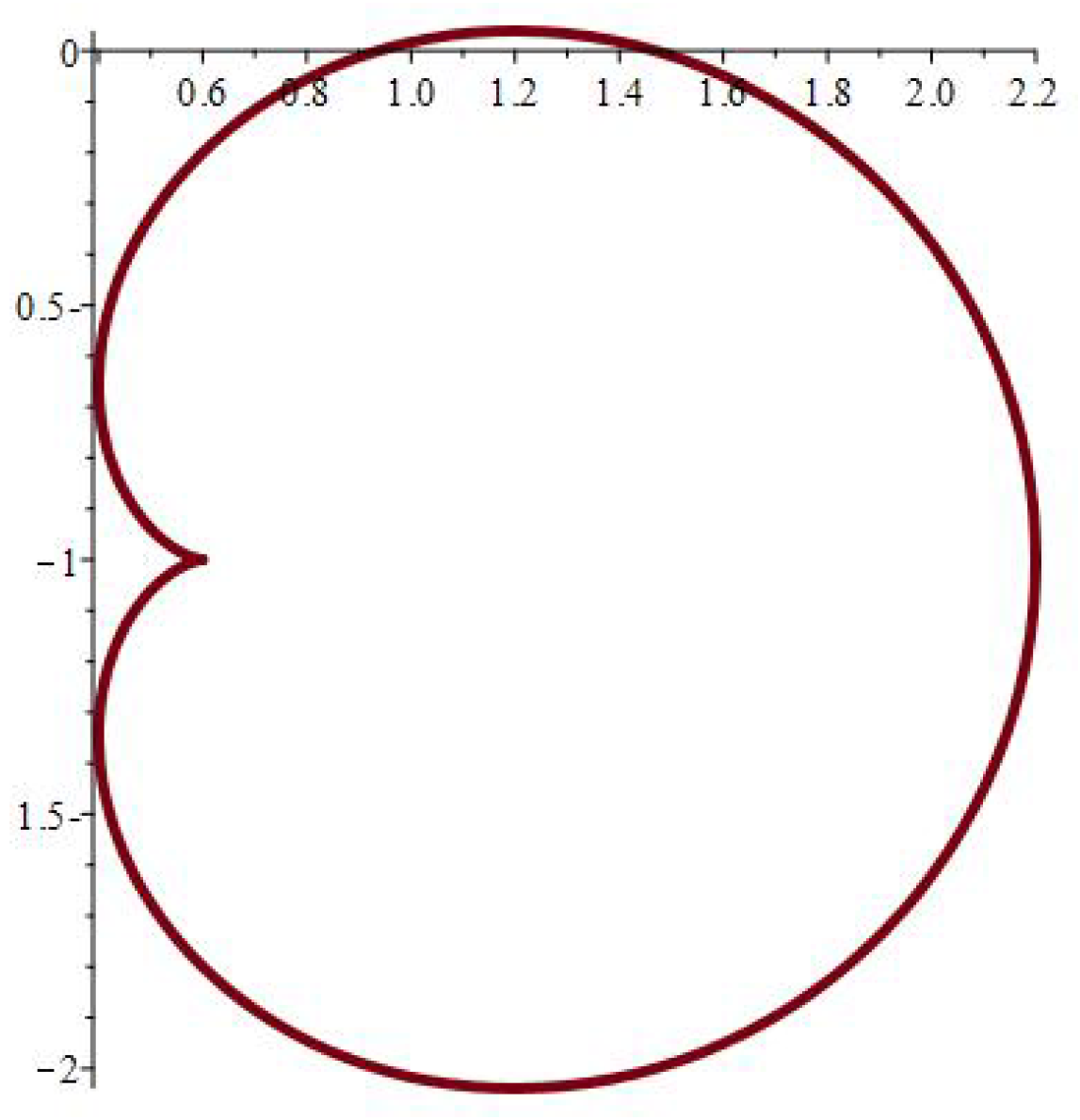
3. Conformal Mapping and Special Cases
4. Method of Solution
5. Applications
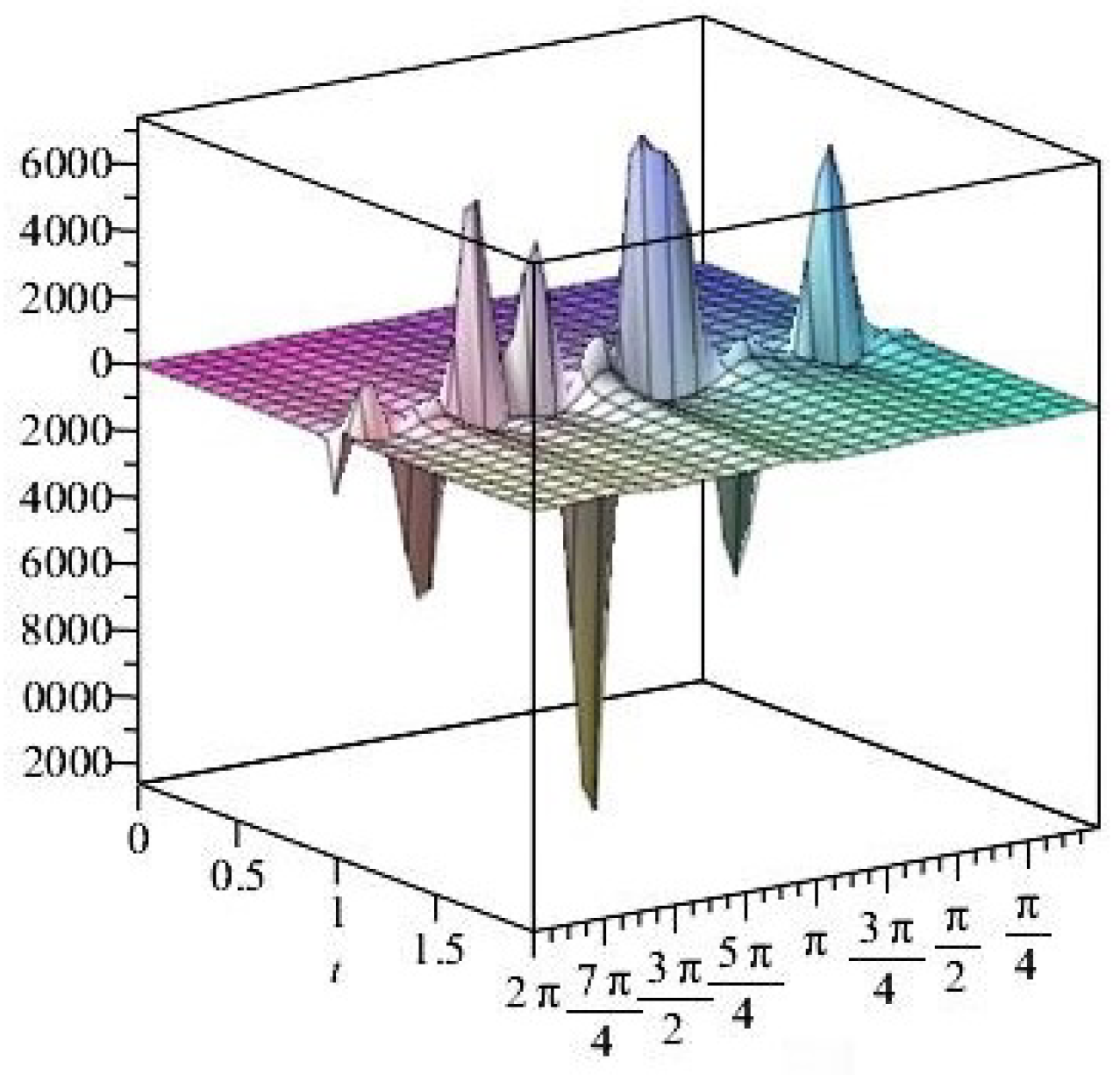

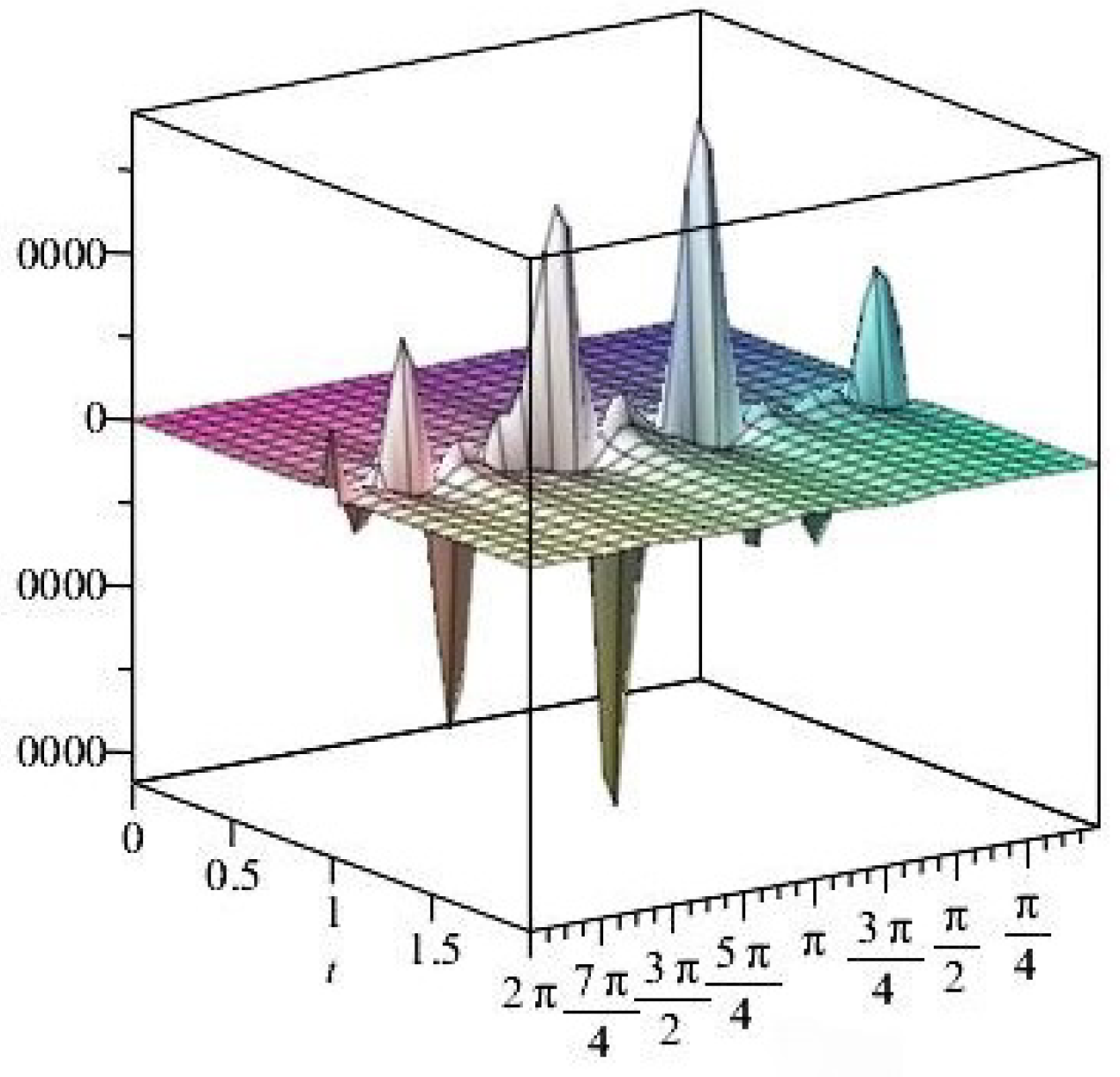
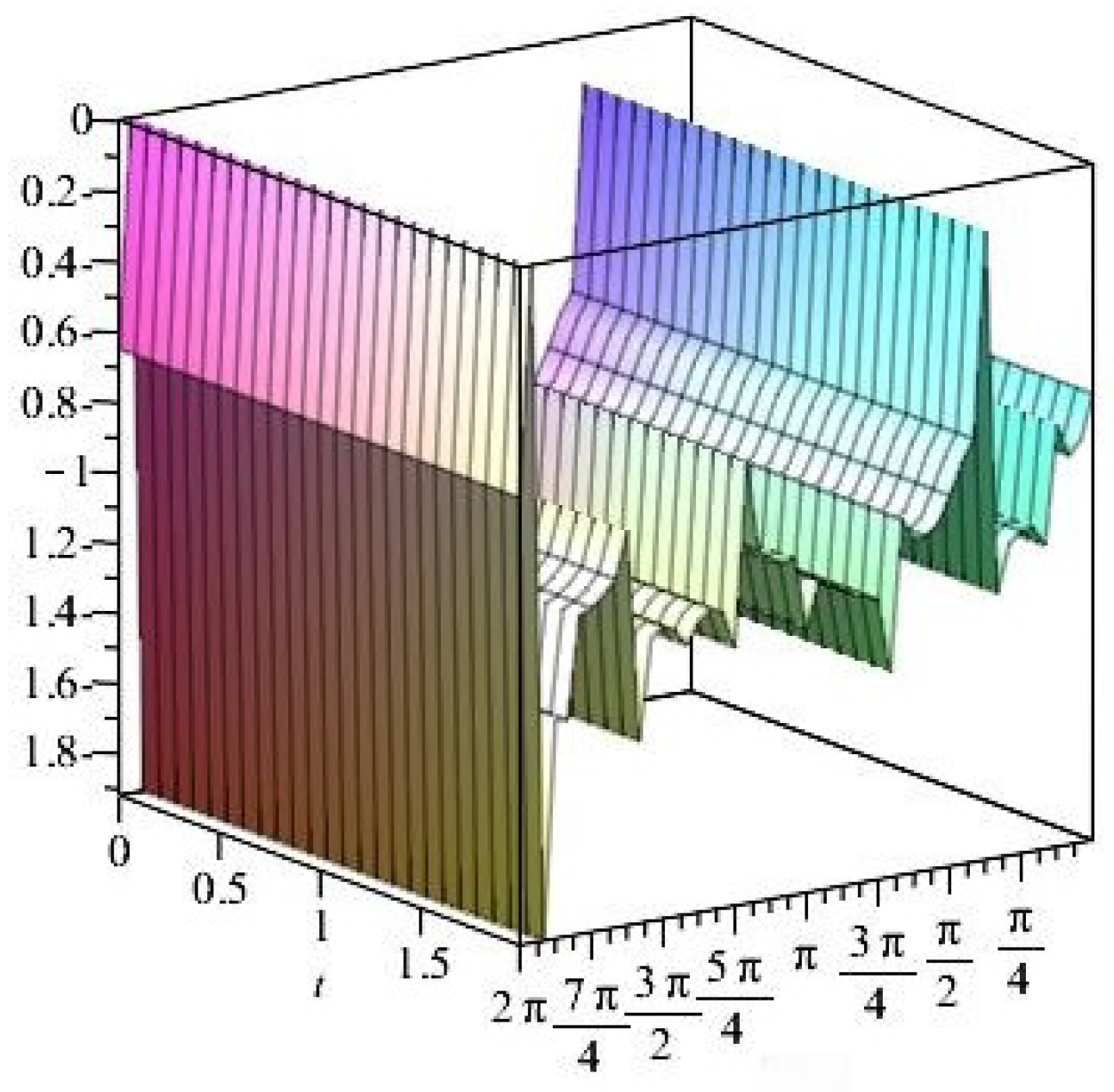
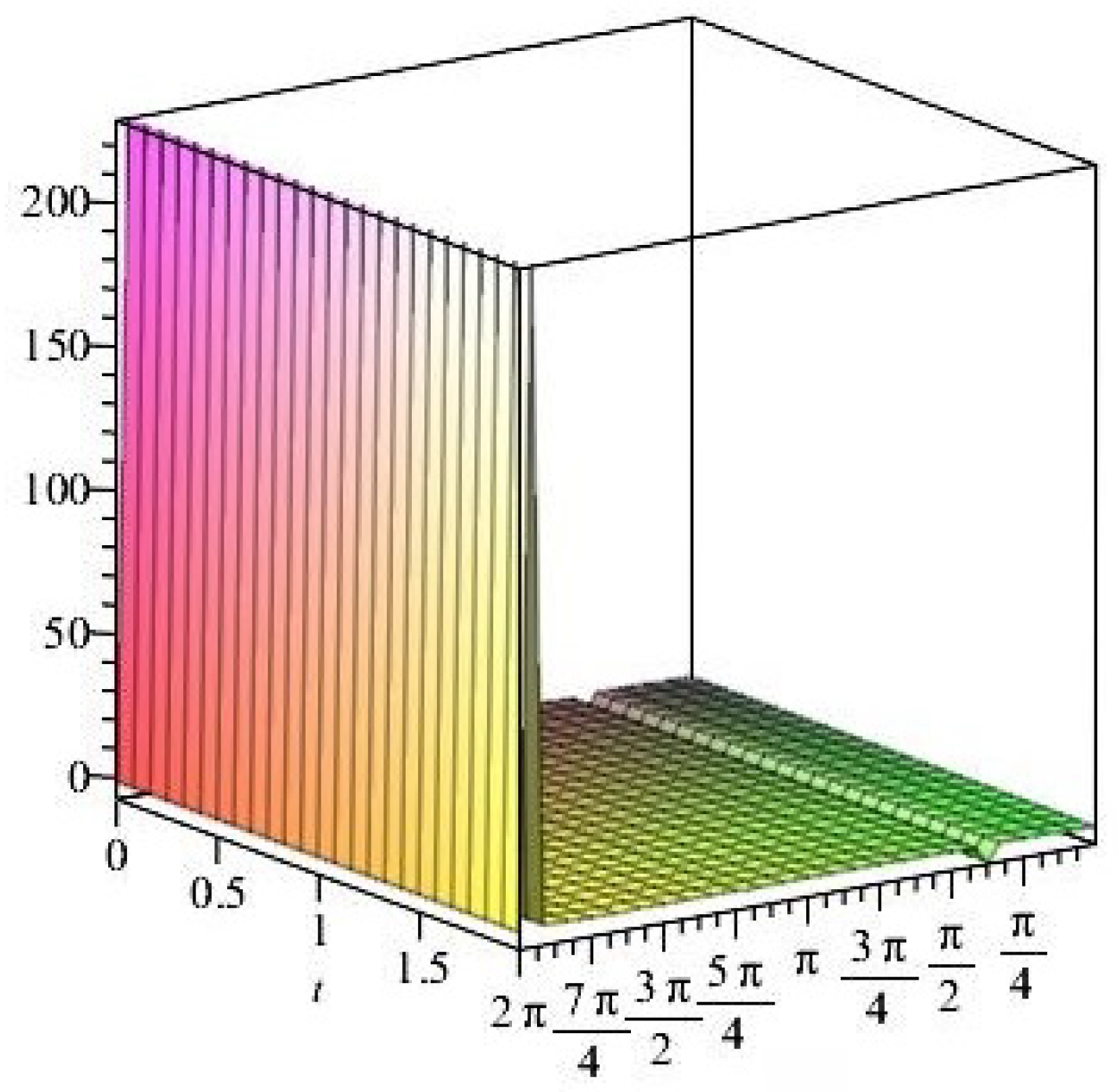
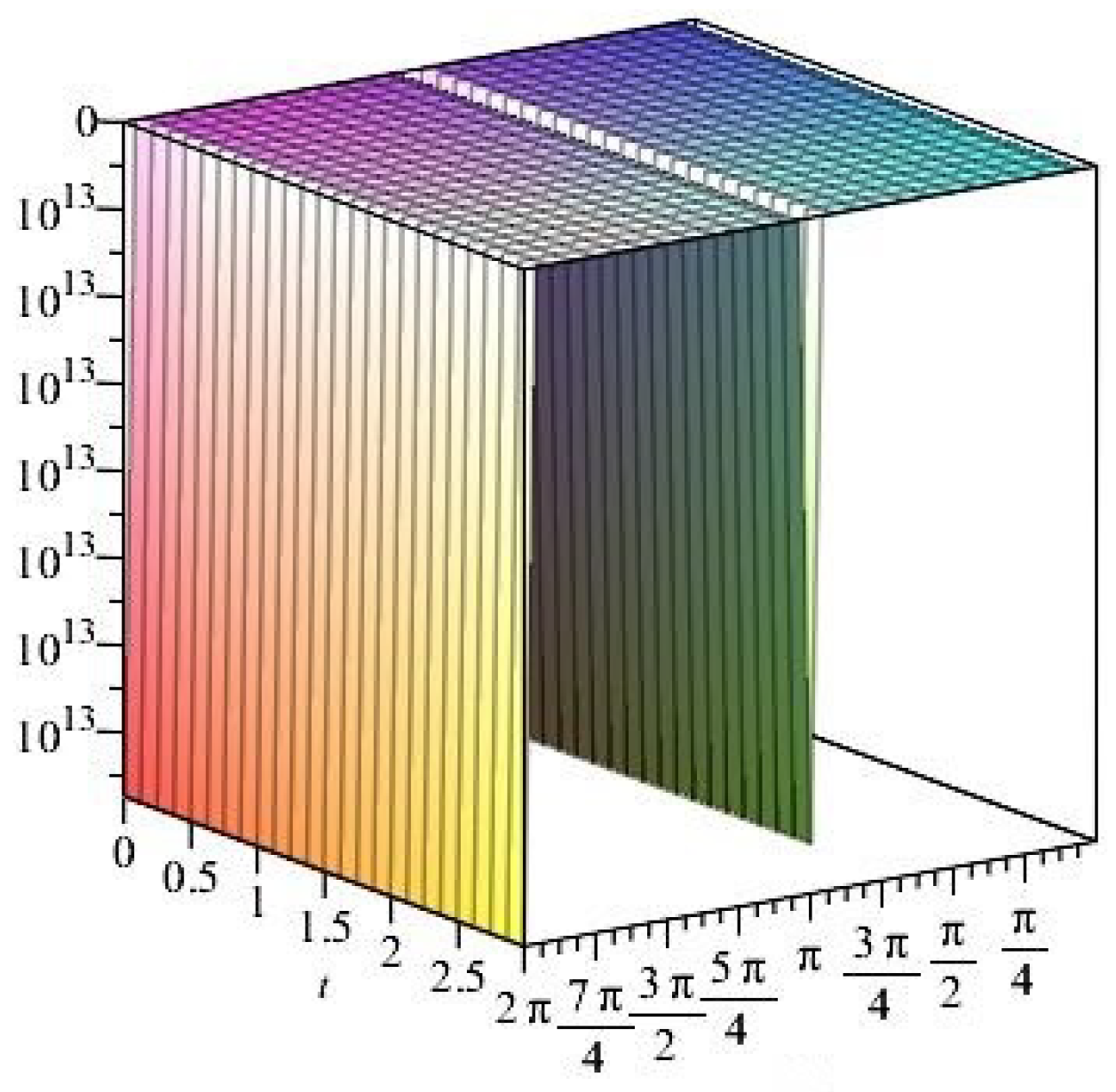
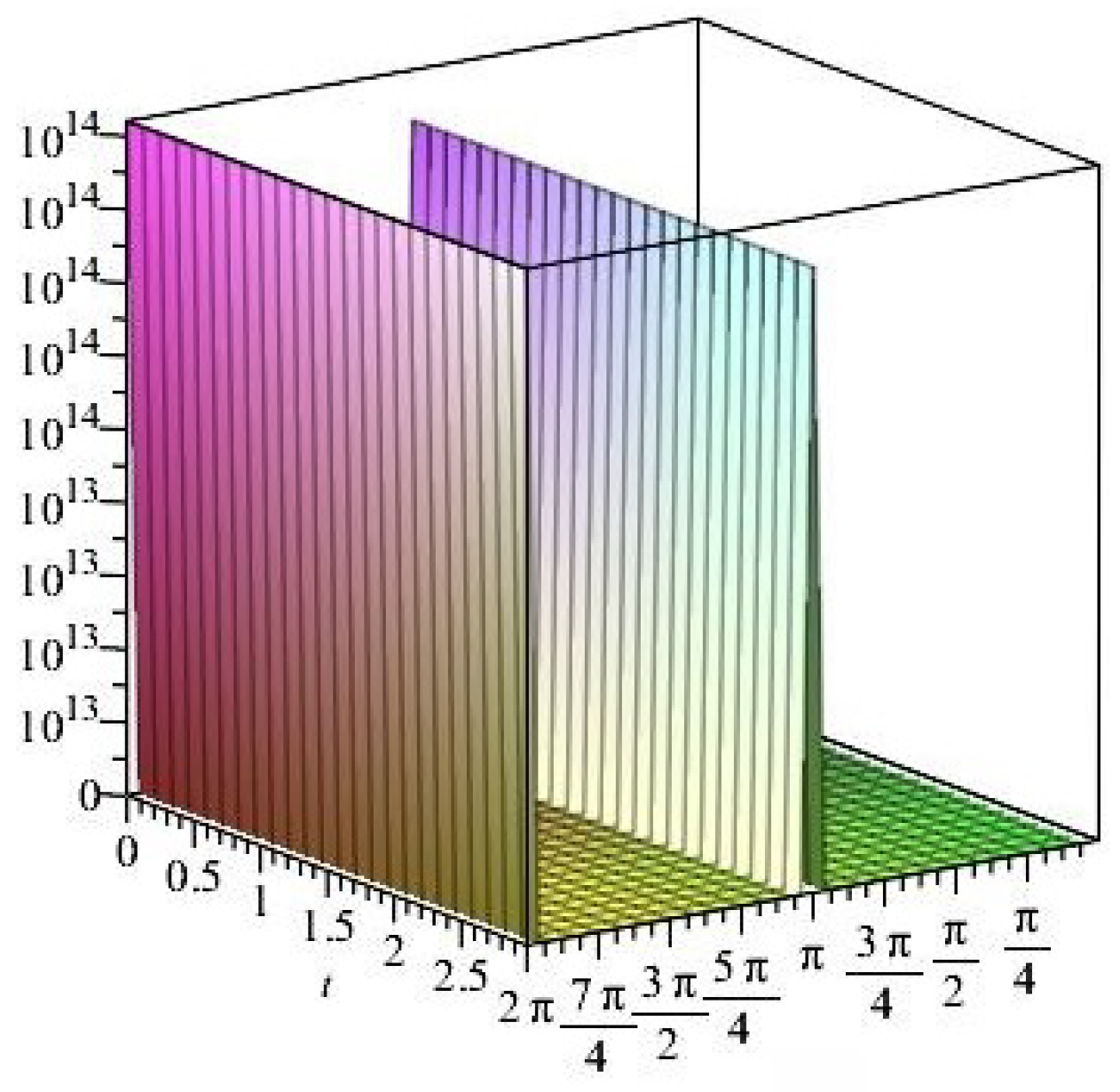
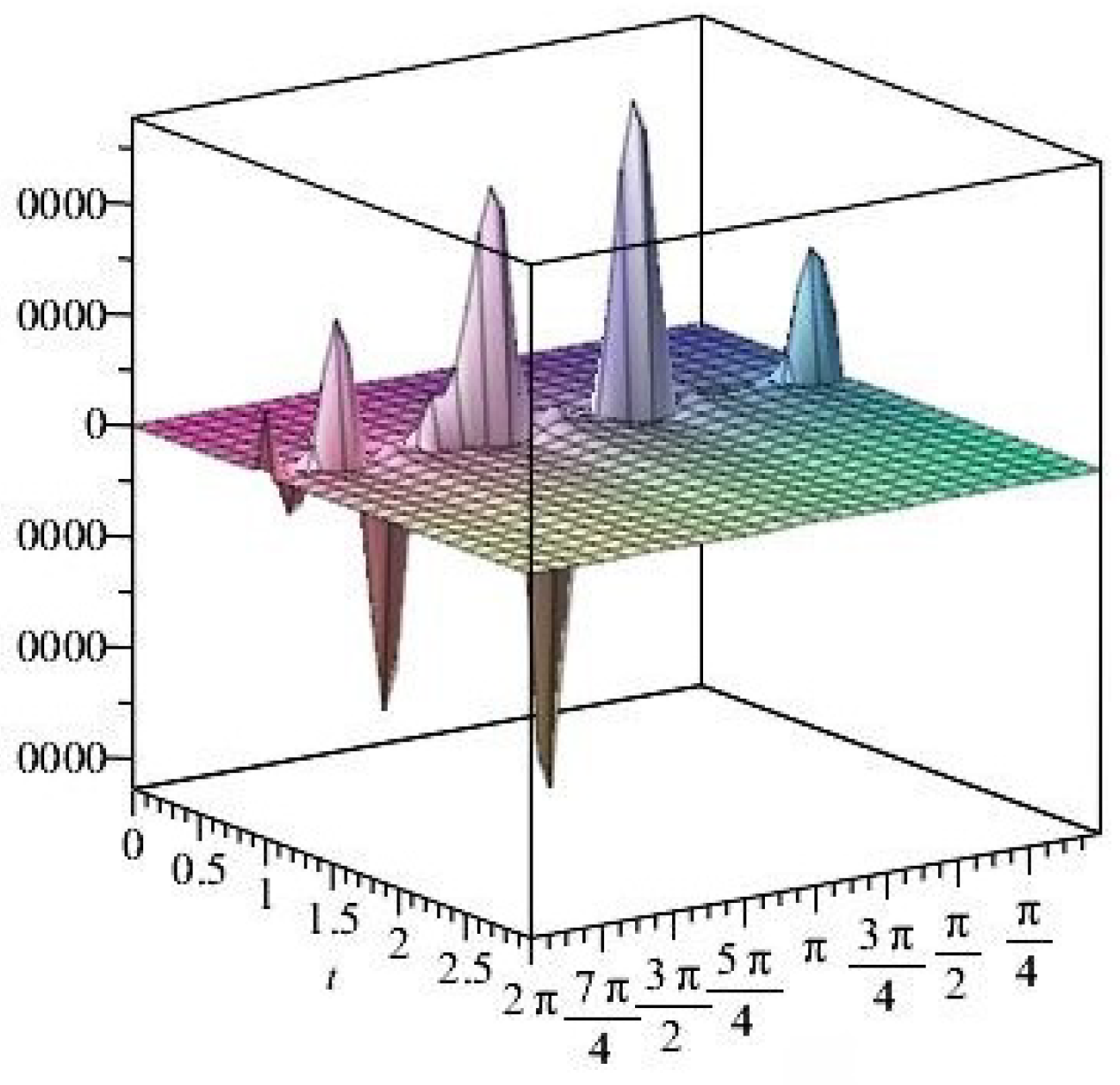
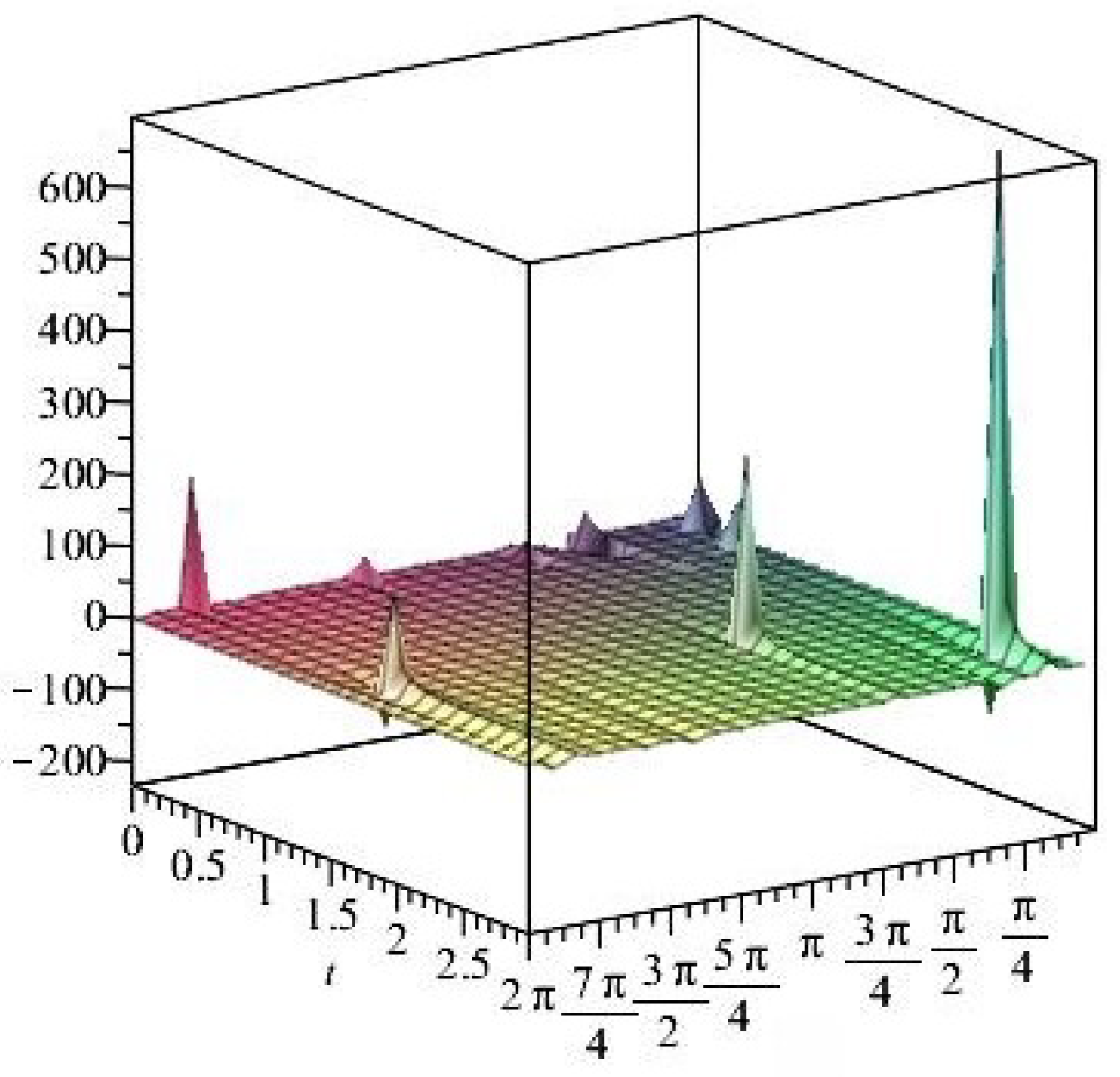
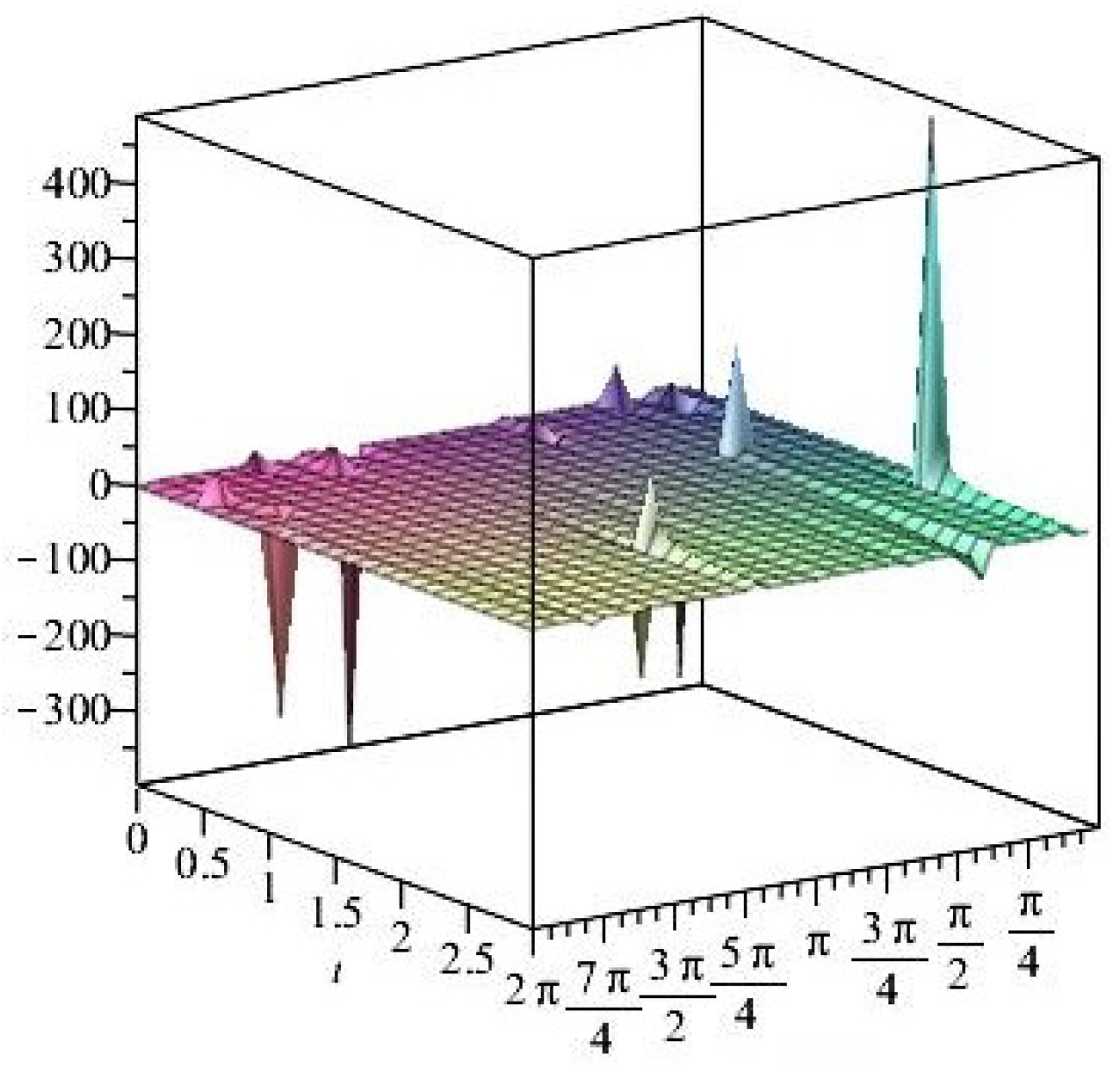
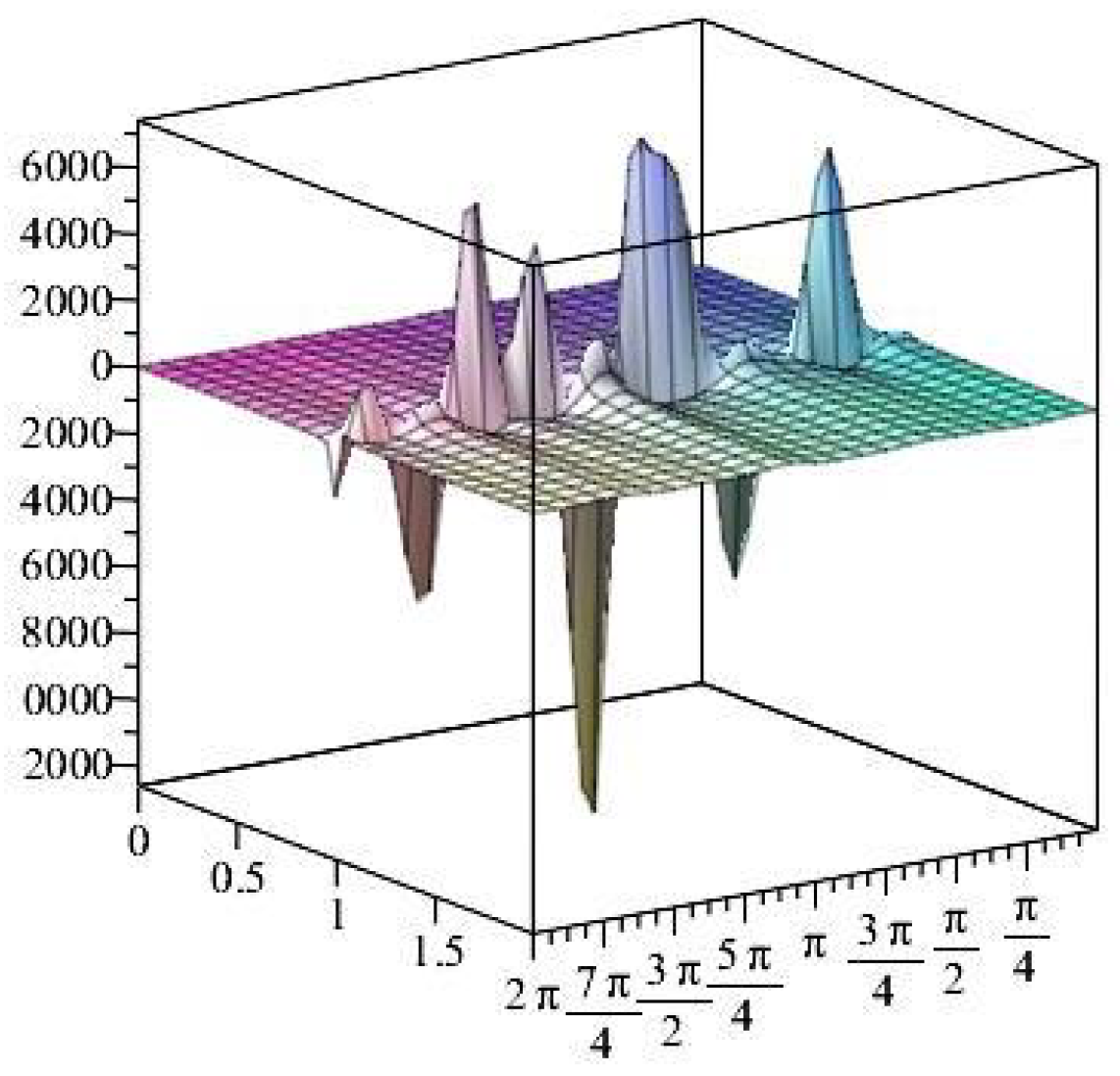
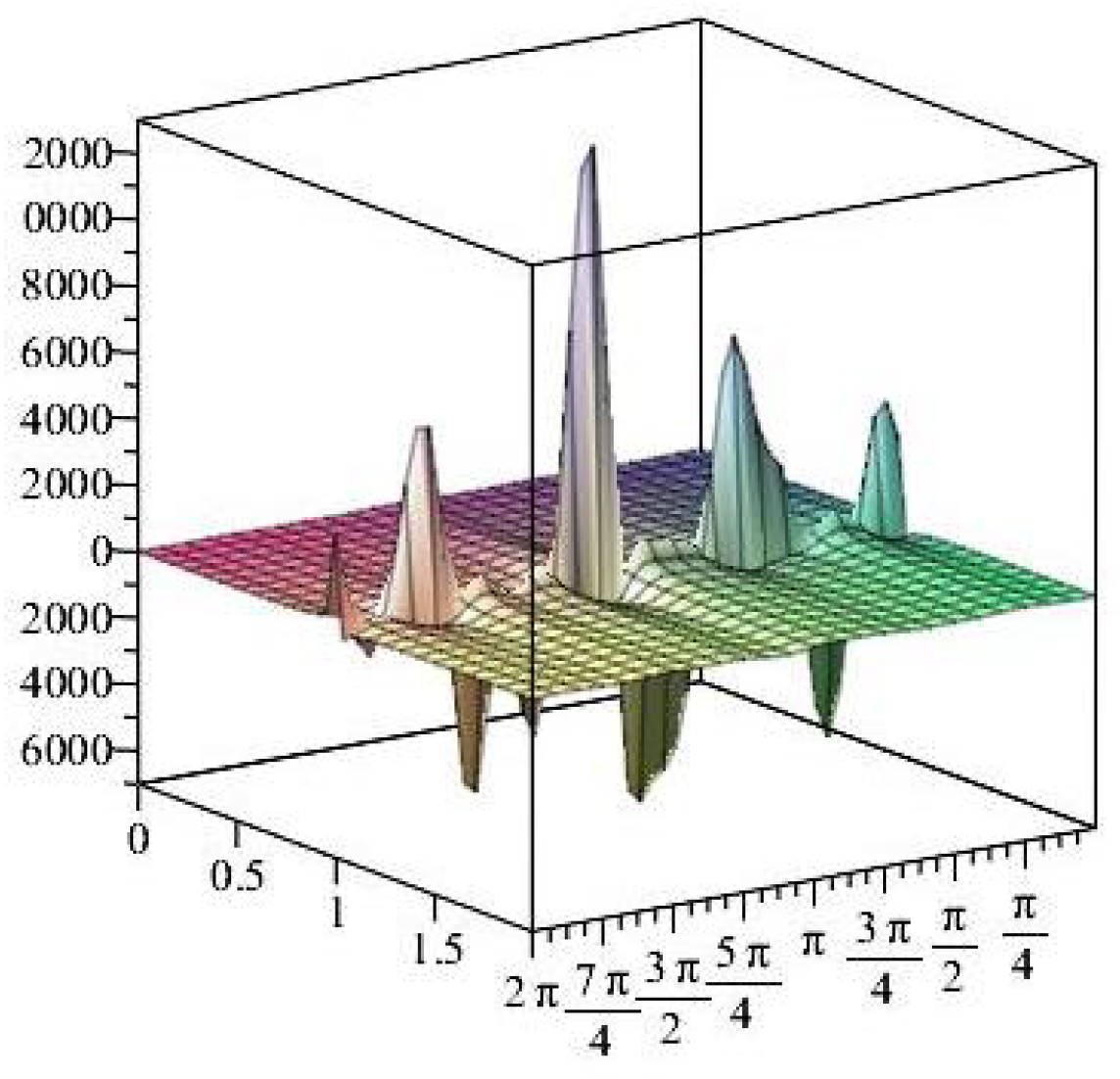

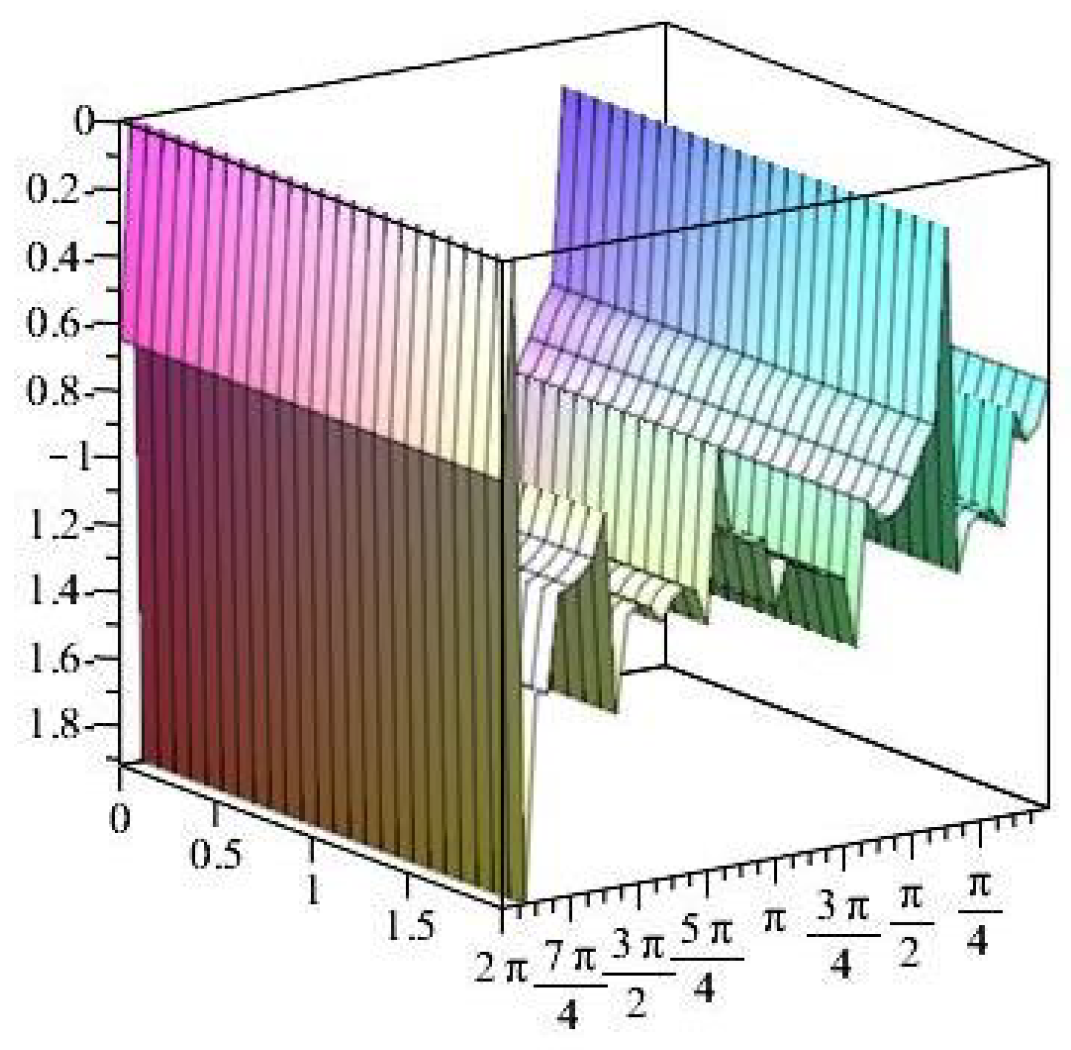
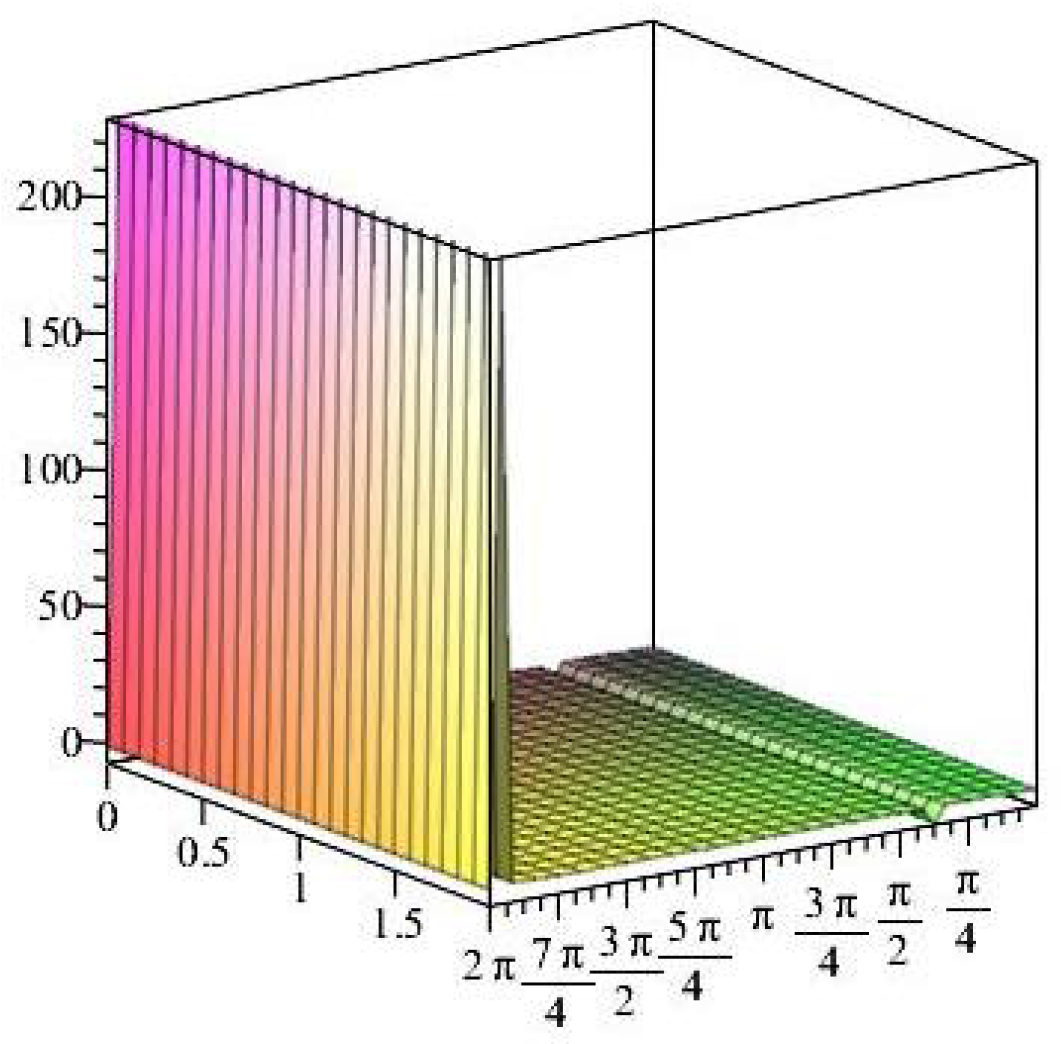
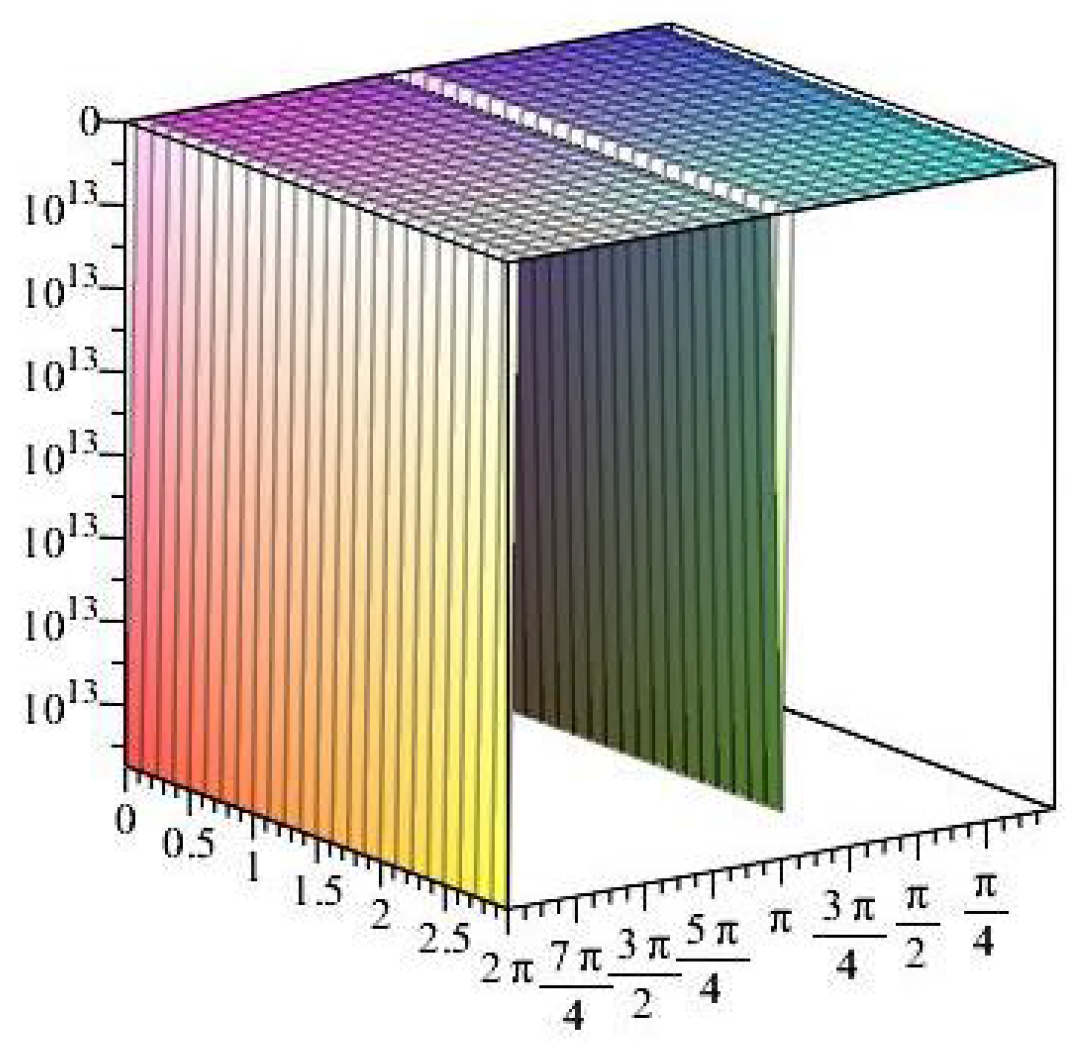
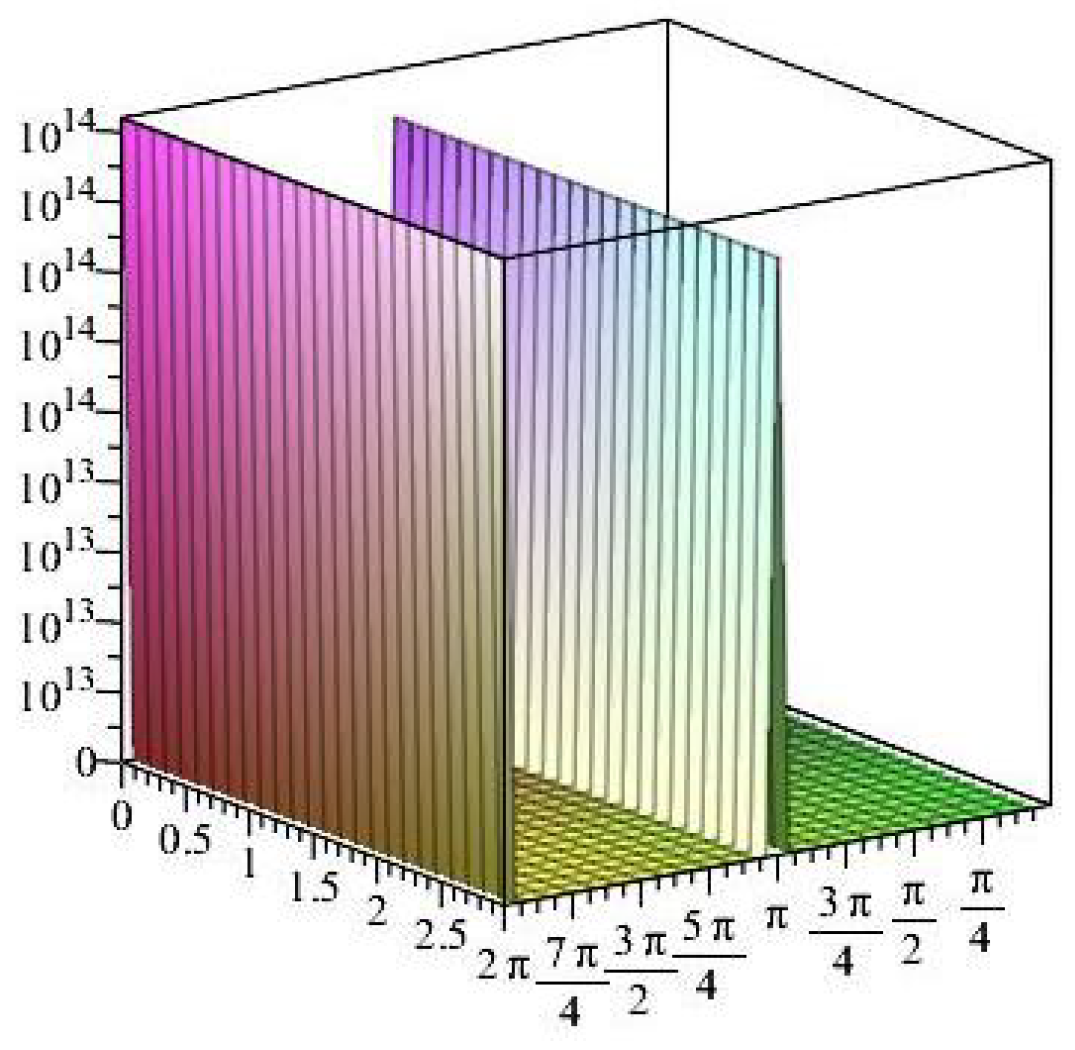
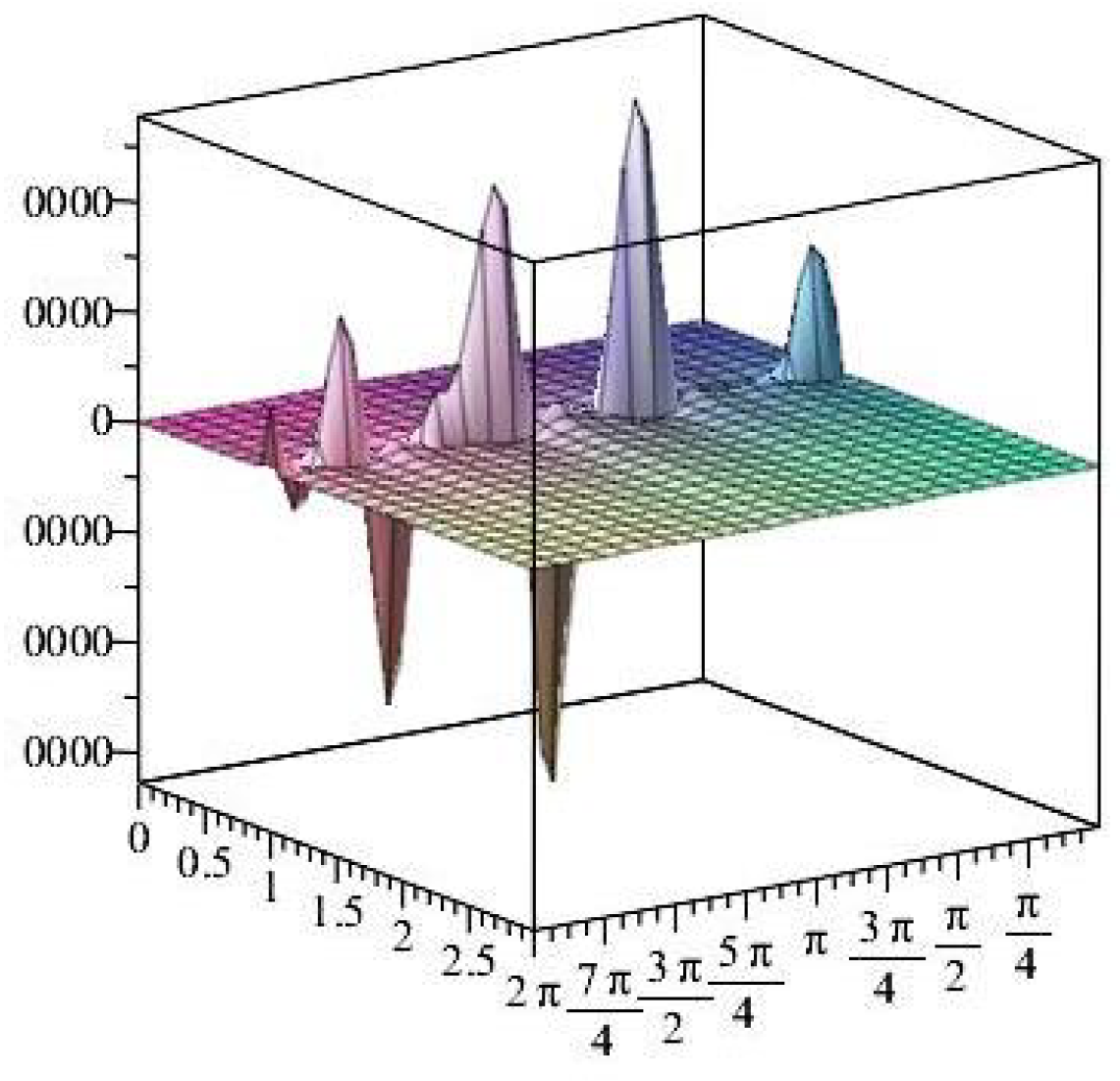
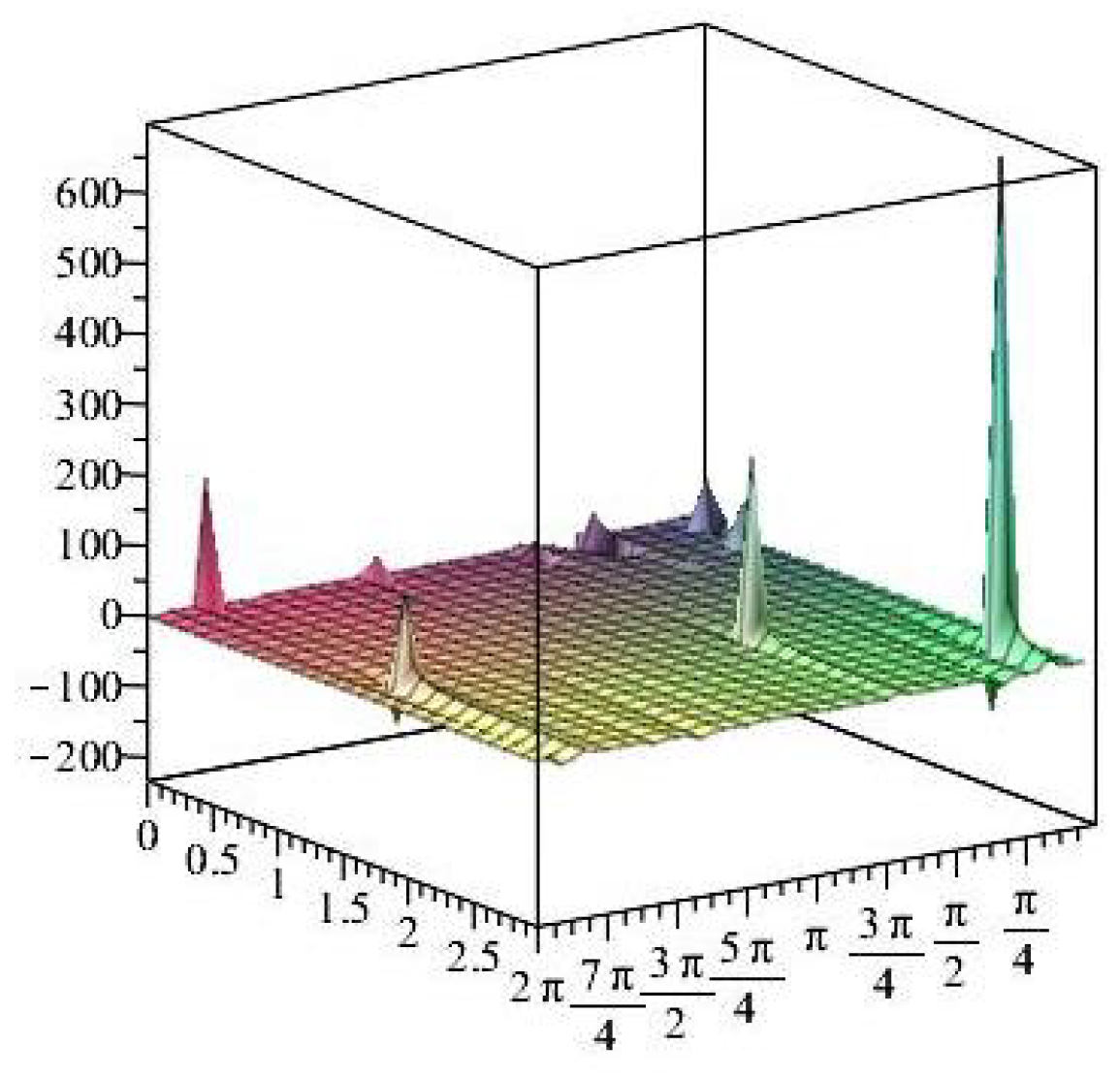
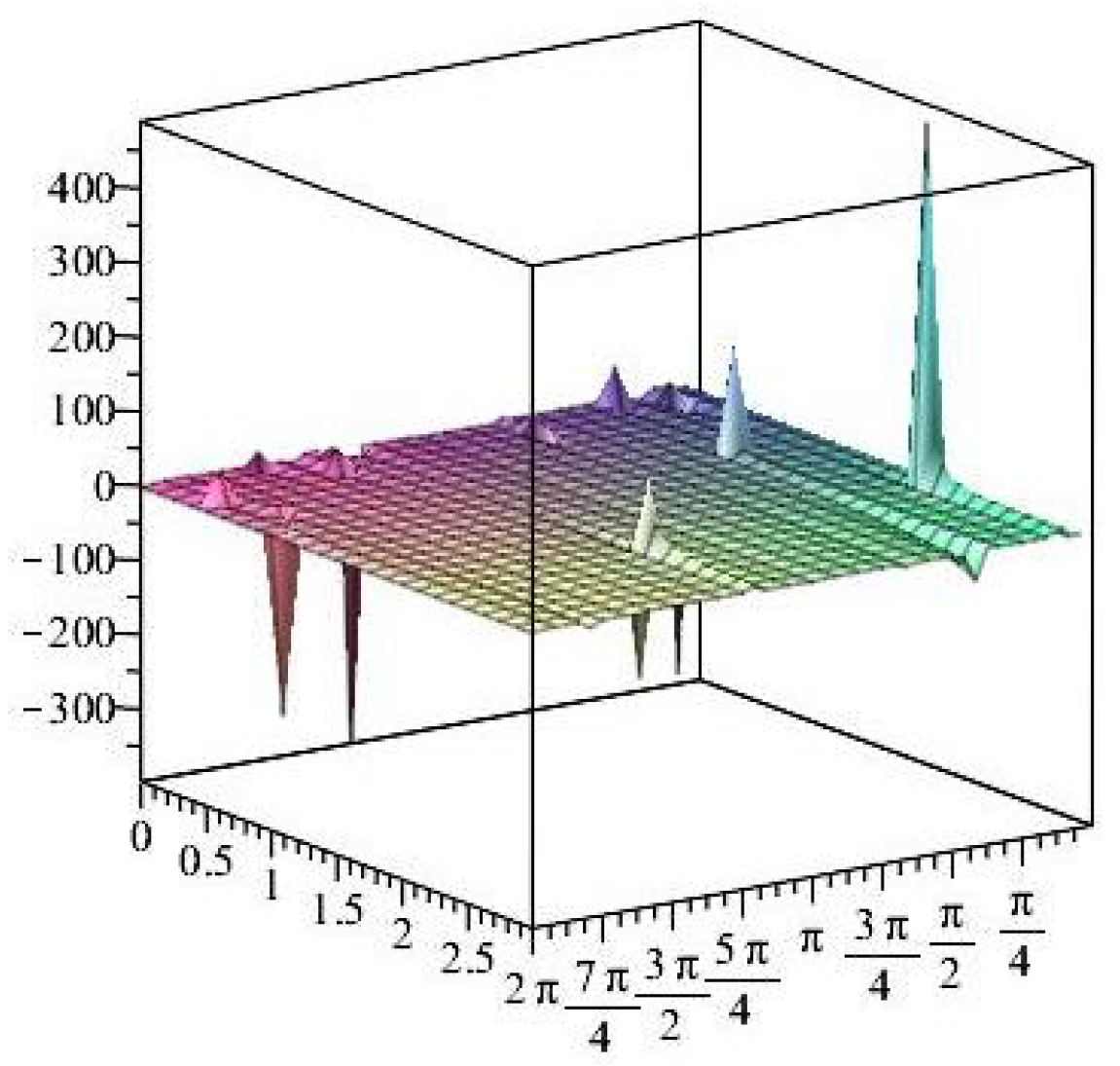
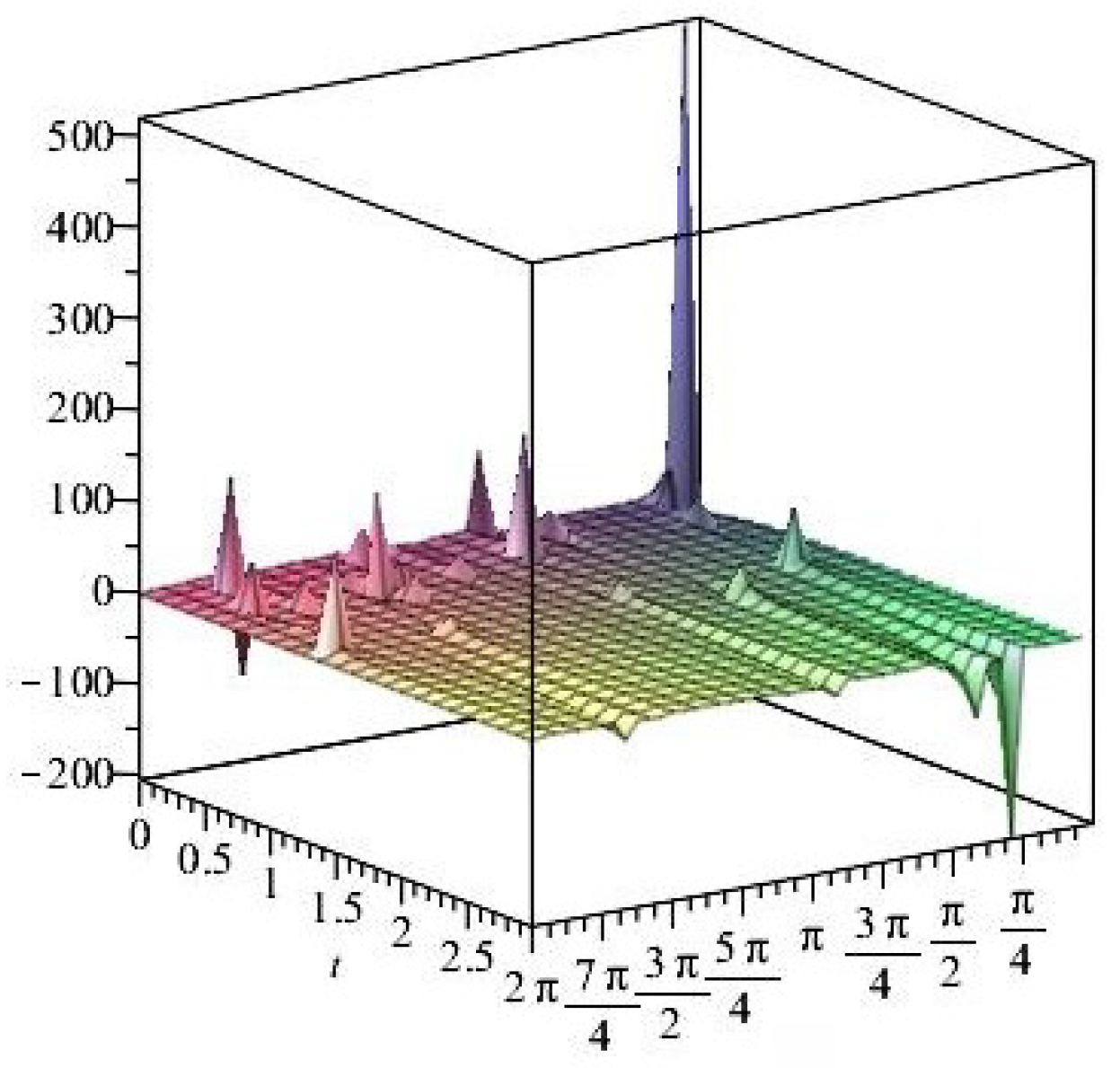
- For
6. Discussion and Conclusions
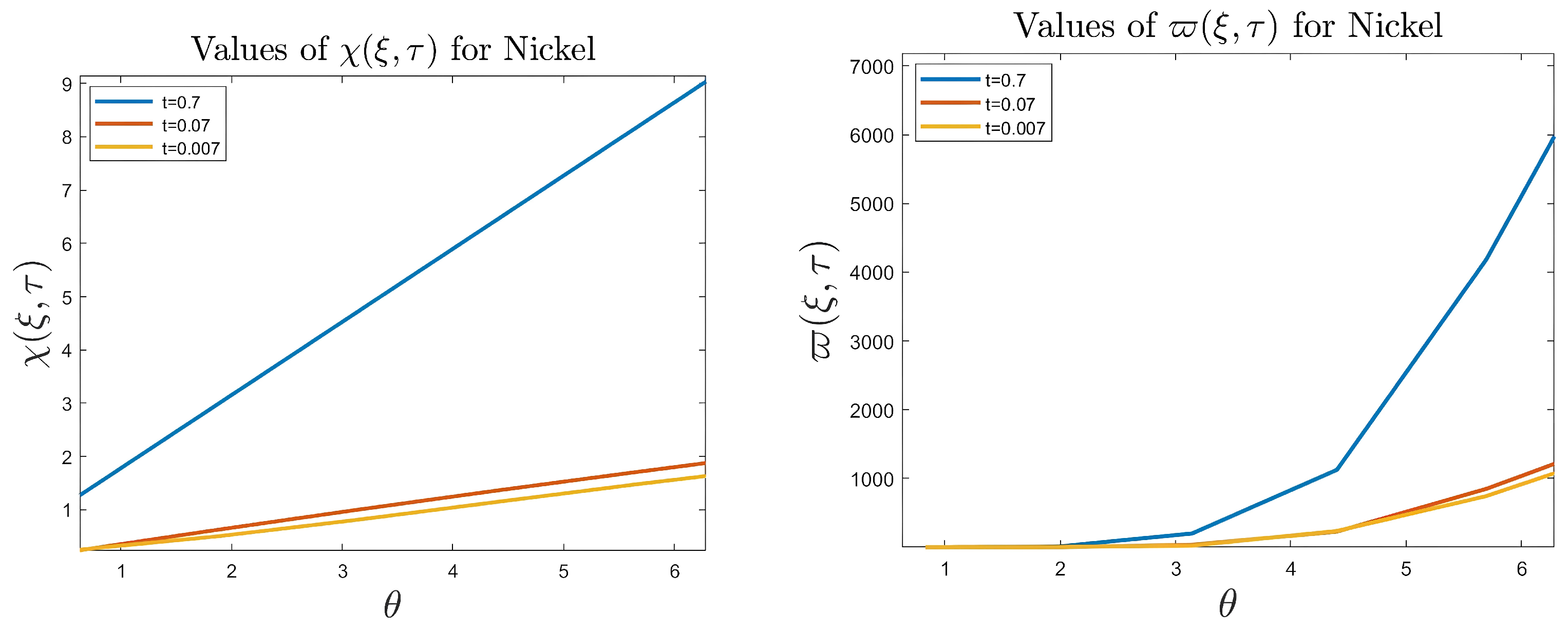
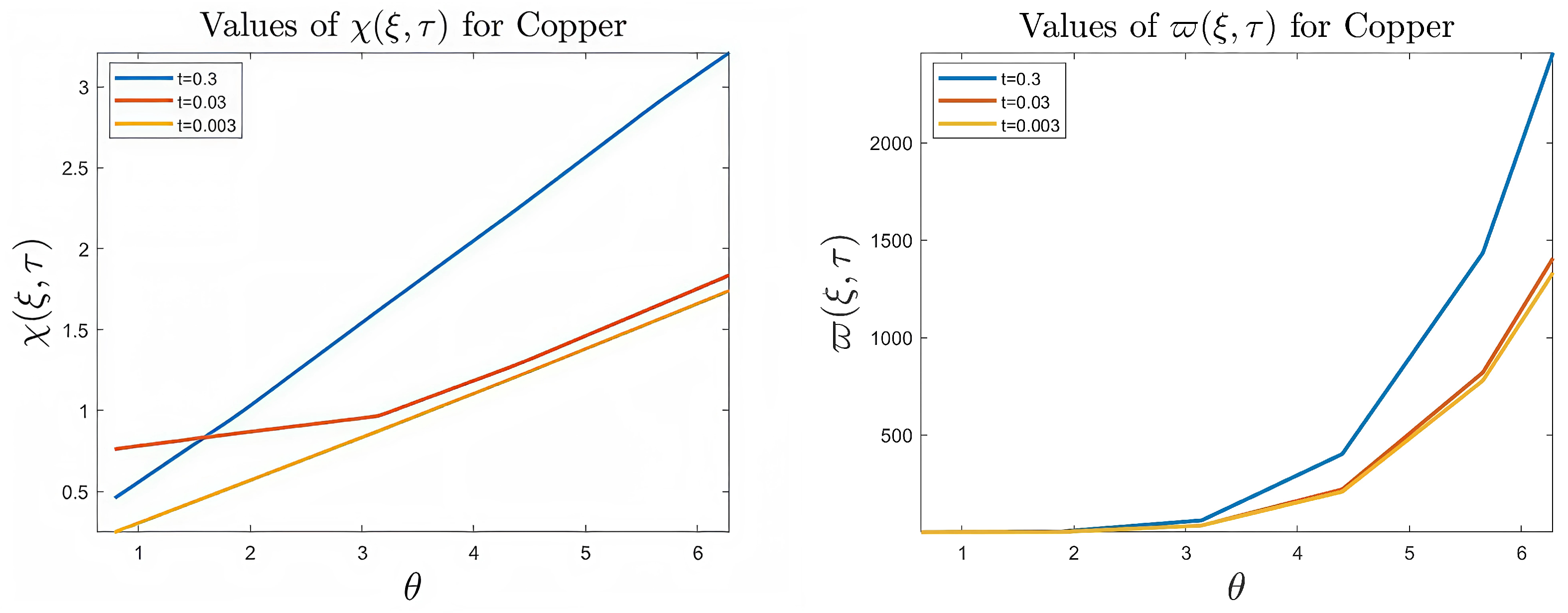
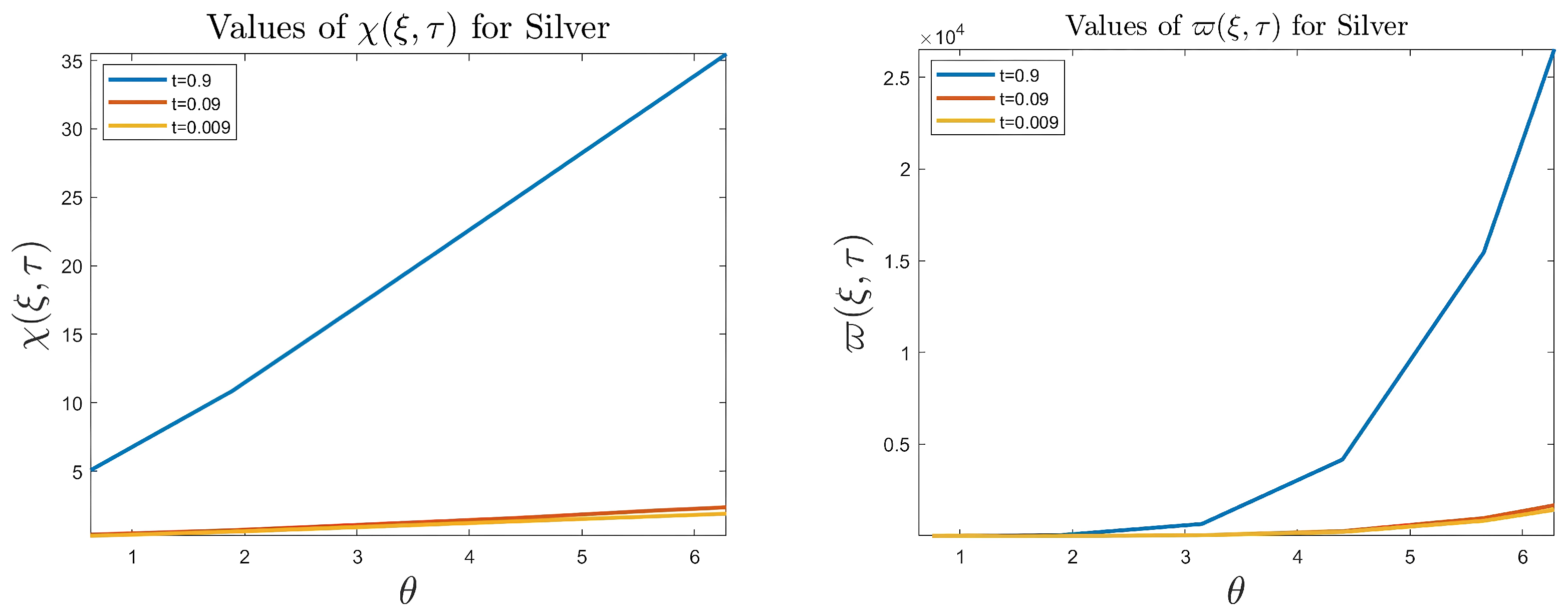
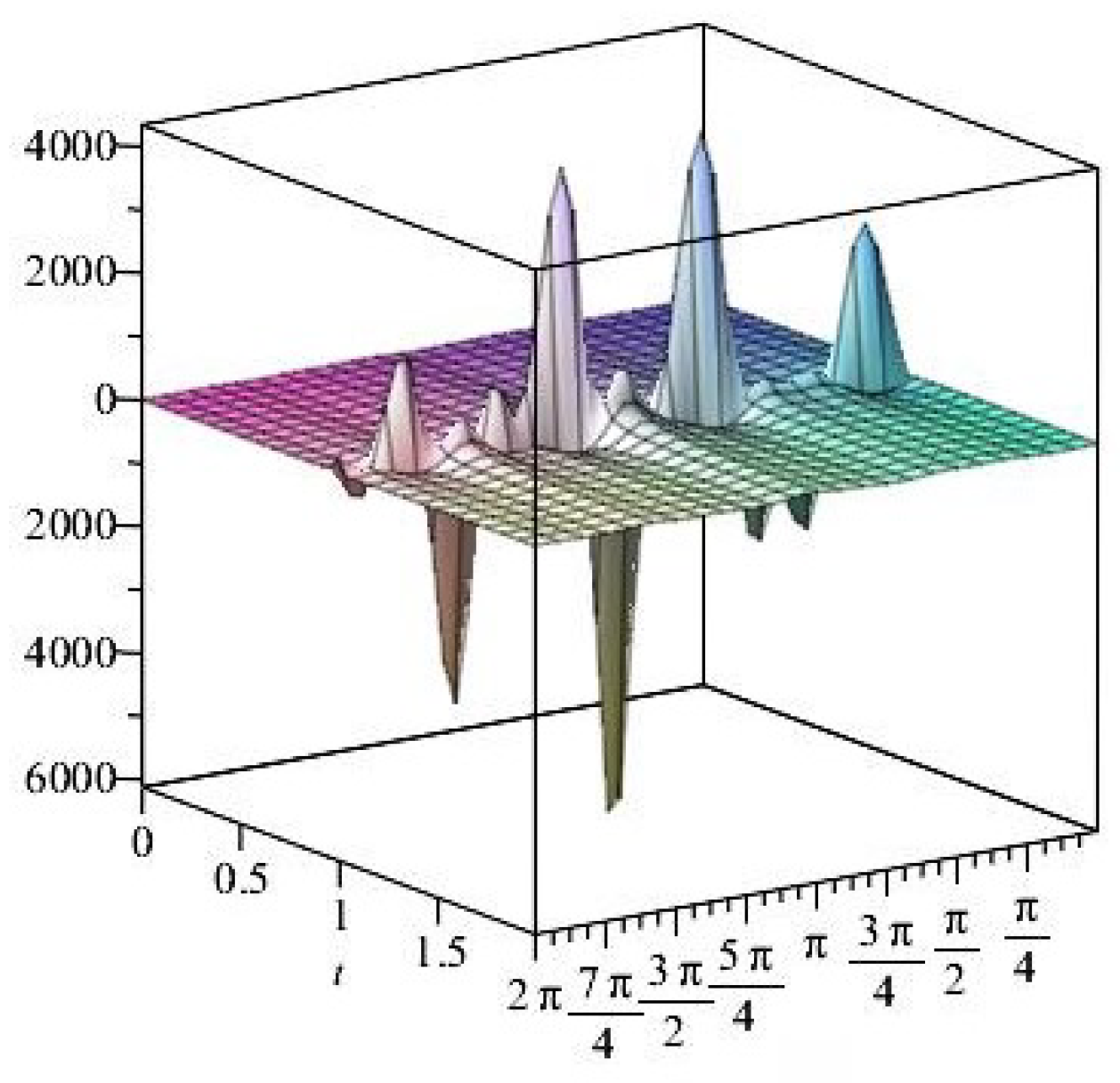
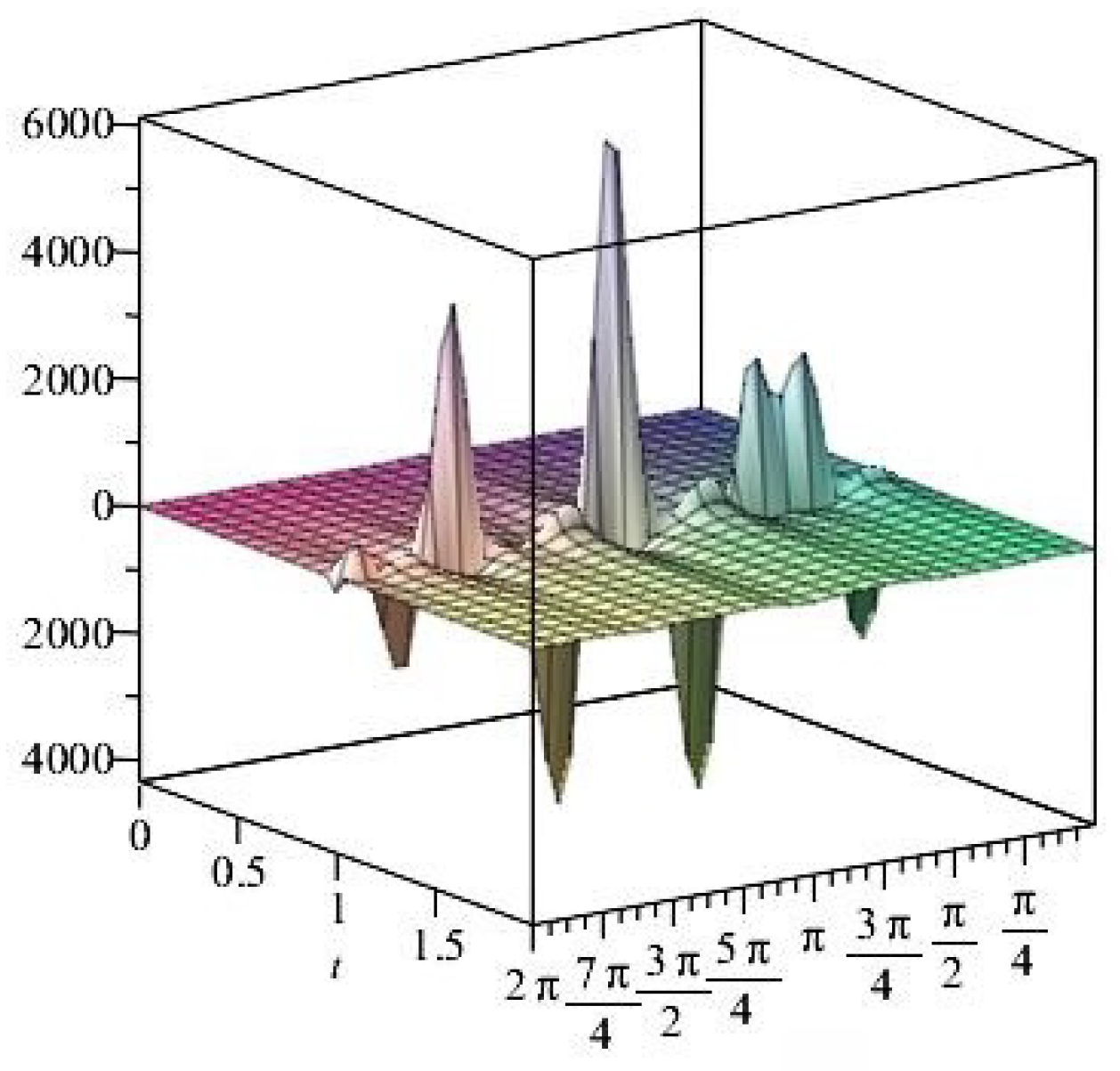
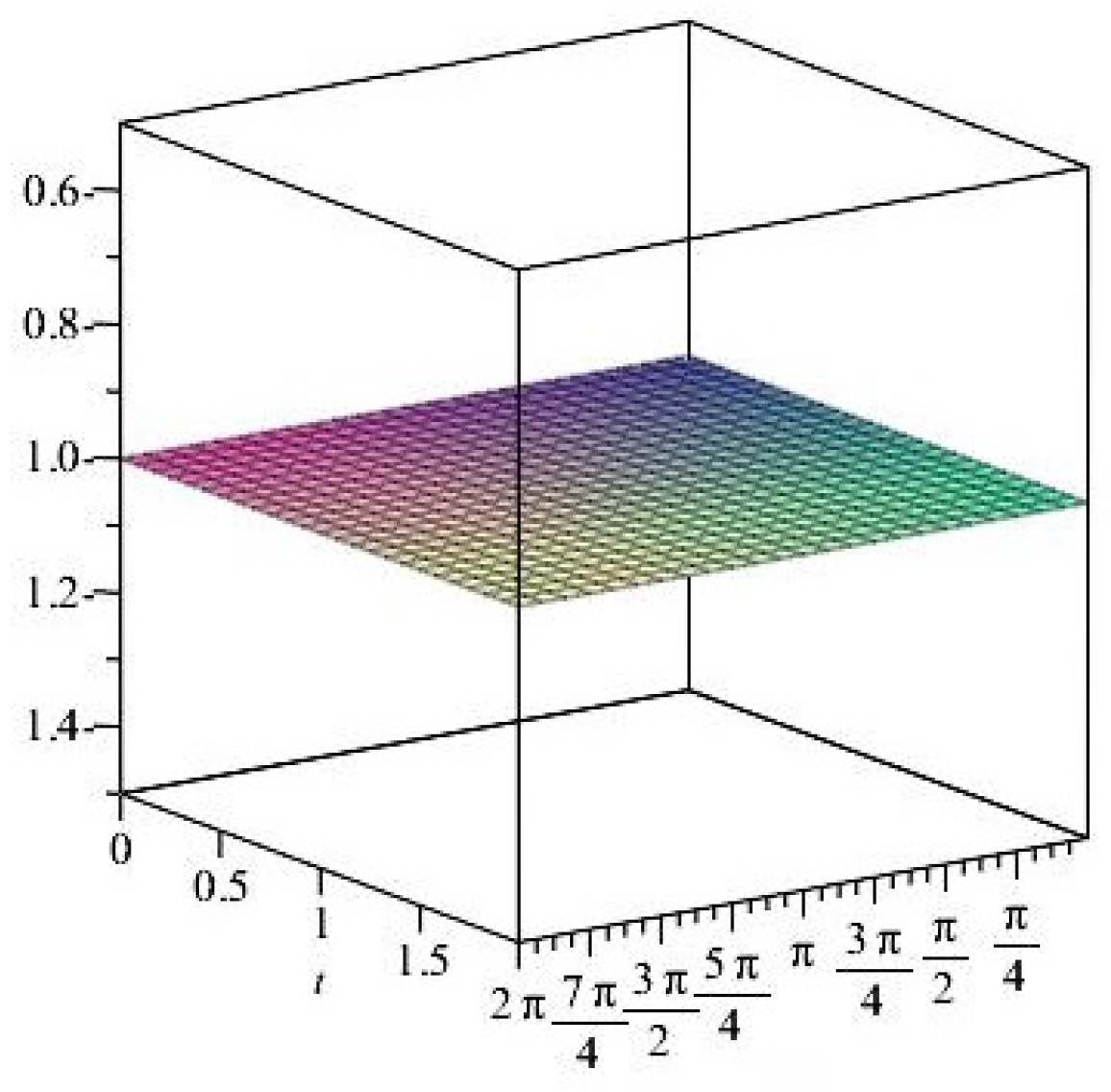
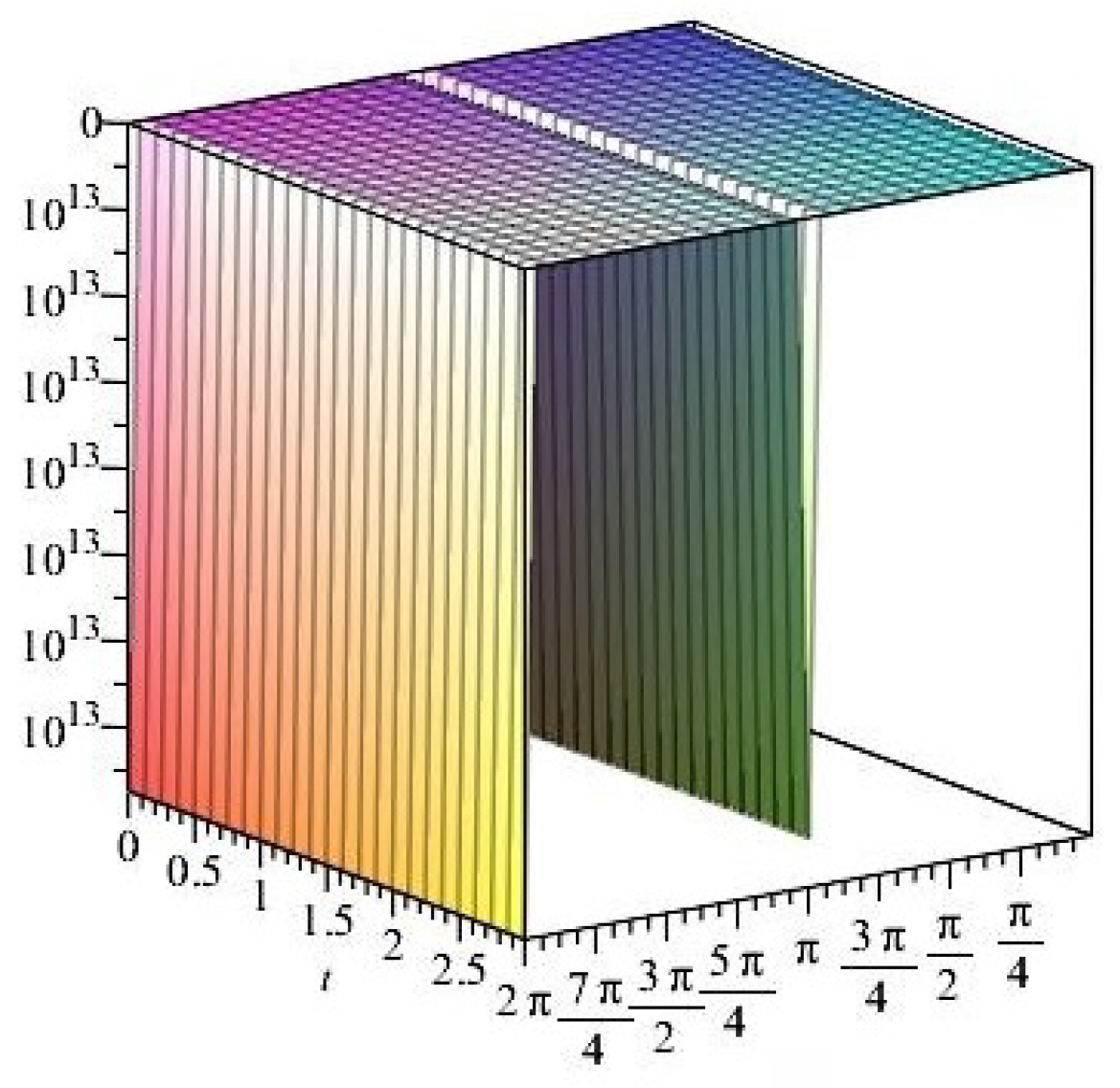
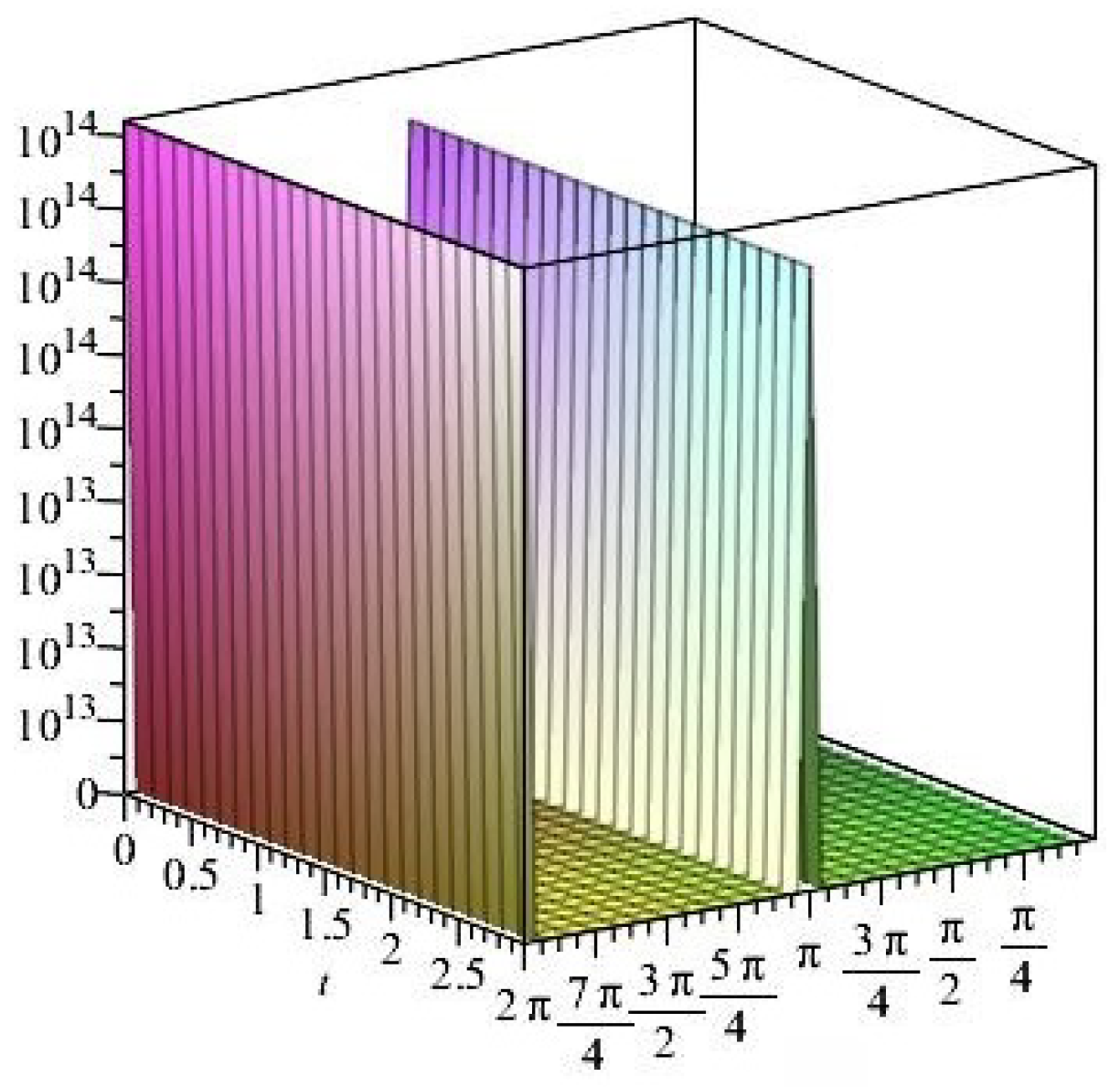
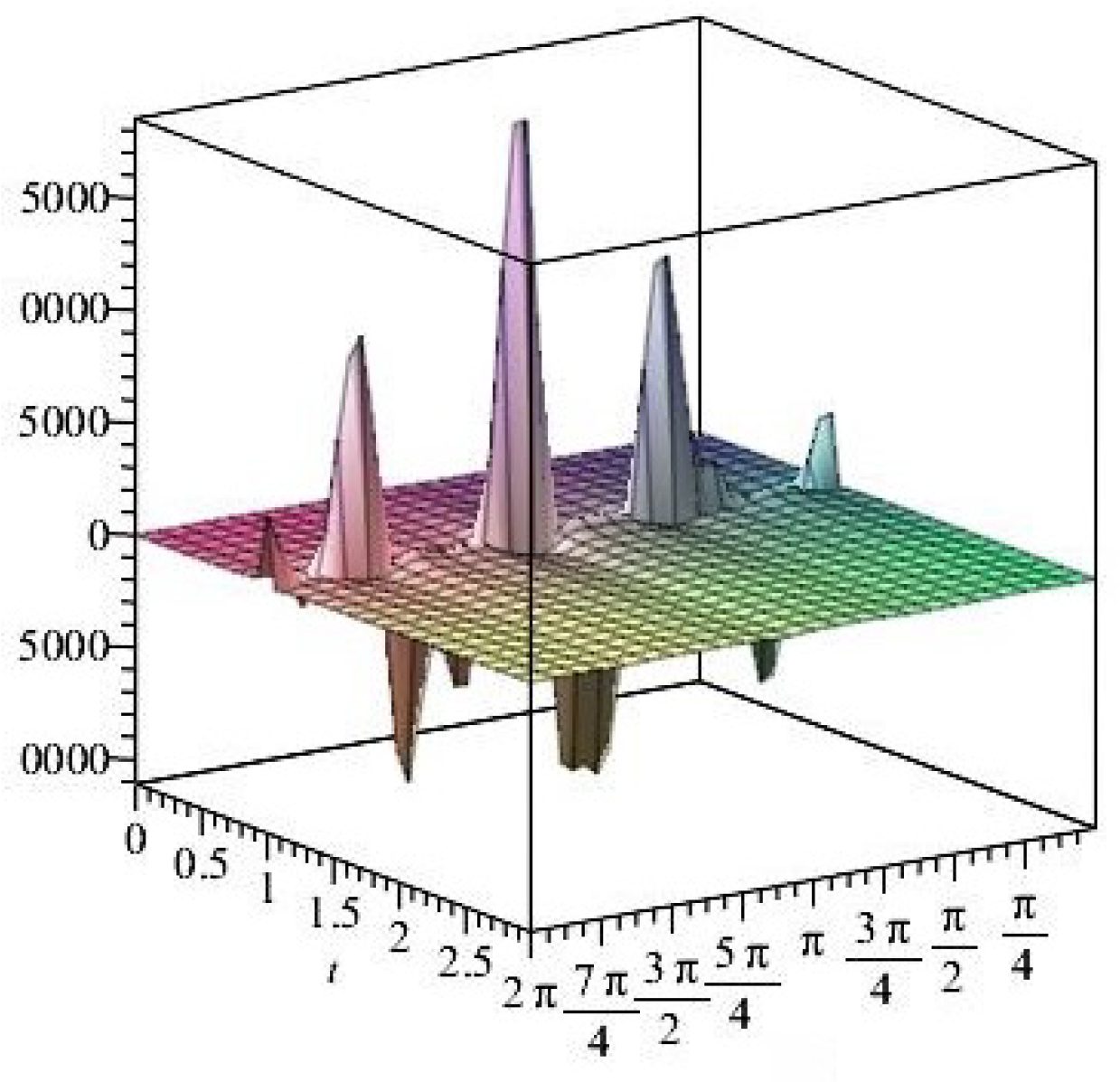
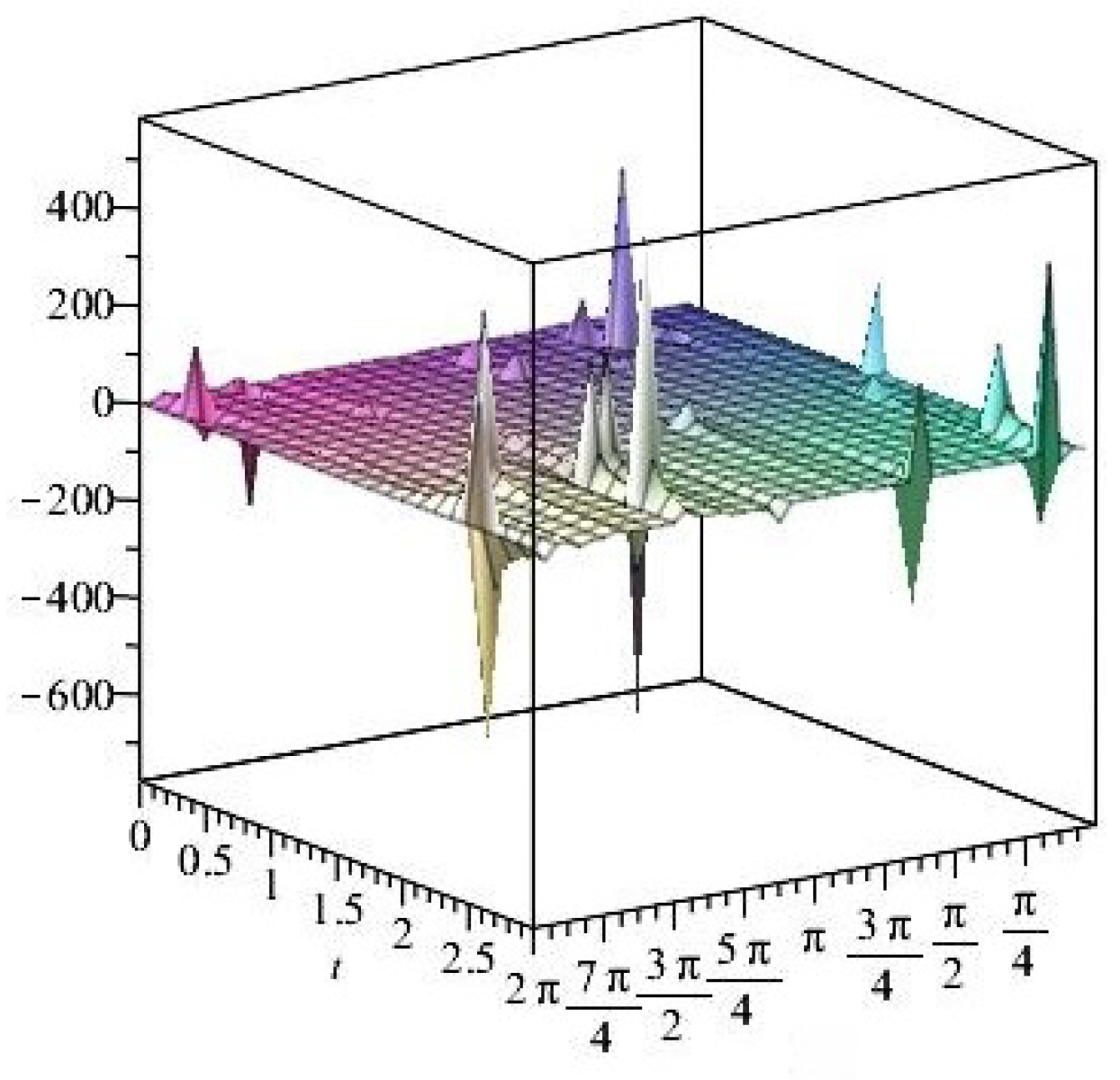
- It is noticed from the resulting values of the stress ratios that the stress remains positive between the minimum and maximum tensile values; see Figure 17 and Figure 22, and, as a special case, when there is no stress change, then see Figure 40. Meanwhile, for a rigid curvilinear center, the stress ratios across a large surface domain are illustrated in Figure 27.
- The numerical results indicate that, besides the boundary conditions that restricted the domain of the problem, acting stress forces, and heat conduction at various times, the two Goursat functions provide increasing values with respect to increasing time (0,1). Therefore, a general visualization of the amplitude of waves or energy levels is determined. See Table 1, Table 2 and Table 3.
- The current model appears in more general physical phenomena. For example, in ceramic thermoelastic plates, the coupling of many curvilinear holes in a metallic ceramic plate under the effect of uniform stress forces in the presence of heat conduction necessitates a thorough examination of both thermal and mechanical stress factors. Numerical approaches, stress intensity factors, and fracture mechanics are crucial in forecasting material performance and failure. To optimize the design and reduce the danger of failure, special attention should be paid to the hole arrangement, thermal gradient, and material qualities.
- Study the physical model in the presence of a normal magnetic field.
- Expand the study to include the effect of the external forces near the edges of the plate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nowacki, W. Thermoelasticity; Pergamon Press: Warsaw, Poland, 2013; Available online: https://shop.elsevier.com/books/thermoelasticity/nowacki/978-0-08-024767-0 (accessed on 22 October 2013).
- Khaldjigitov, A.; Tilovov, O.; Xasanova, Z. A new approach to problems of thermoelasticity in stresses. J. Therm. Stress. 2024, 47, 1228–1241. [Google Scholar] [CrossRef]
- Manickam, G.; Haboussi, M.; D’Ottavio, M.; Kulkarni, V.; Chettiar, A.; Gunasekaran, V. Nonlinear thermo-elastic stability of variable stiffness curvilinear fibres based layered composite beams by shear deformable trigonometric beam model coupled with modified constitutive equations. Int. J. Non-Linear Mech. 2023, 148, 104303. [Google Scholar] [CrossRef]
- Yuan, X.; Jiang, Q.; Zhou, Z.; Yang, F. Stress analysis of anti-plane finite elastic solids with hole by the method of fundamental solutions using conformal mapping technique. Arch. Appl. Mech. 2022, 92, 1823–1839. [Google Scholar] [CrossRef]
- Lu, A.Z.; Xu, Z.; Zhang, N. Stress analytical solution for an infinite plane containing two holes. Int. J. Mech. Sci. 2017, 128, 224–234. [Google Scholar] [CrossRef]
- Hsieh, M.L.; Hwu, C. Green’s functions for anisotropic elastic plates containing polygonal holes. Int. J. Mech. Sci. 2024, 276, 109396. [Google Scholar] [CrossRef]
- Savruk, M.P. Stress Concentration Near Curvilinear Holes and Notches with Nonsmooth Contours. Mater. Sci. 2021, 57, 331–343. [Google Scholar] [CrossRef]
- Hsieh, M.L.; Hwu, C. A full field solution for an anisotropic elastic plate with a hole perturbed from an ellipse. Eur. J. Mech. A/Solids 2023, 97, 104823. [Google Scholar] [CrossRef]
- Guo, J.; Lu, Z. Line field analysis and complex variable method for solving elastic-plastic fields around an anti-plane elliptic hole. Sci. China Phys. Mech. Astron. 2011, 54, 1495–1501. [Google Scholar] [CrossRef]
- Abdou, M.A. Fundamental problems for infinite plate with a curvilinear hole having finite poles. Appl. Math. Comput. 2002, 125, 79–91. [Google Scholar] [CrossRef]
- Abdou, M.A.; Ibrahim, E.; Basseem, M. The stress and strain components for a weakened elastic plate by two curvilinear holes in presence of heat. Curr. Sci. Int. 2022, 11, 199–216. Available online: https://www.curresweb.com/index.php/CSI1/article/view/81 (accessed on 30 May 2022).
- Abdou, M.A.; Monaquel, S.J. Integro Differential Equation and Fundamental Problems of an Infinite Plate with a Curvilinear Hole Having Strong Pole. Int. J. Contemp. Math. Sci. 2011, 6, 199–208. Available online: https://www.researchgate.net/profile/M-Abdou-3/publication/267677313_Integro_differential_equation_and_fundamental_problems_of_an_infinite_plate_with_a_curvilinear_hole_having_strong_pole/links/5523e5c80cf2c815e073650b/Integro-differential-equation-and-fundamental-problems-of-an-infinite-plate-with-a-curvilinear-hole-having-strong-pole.pdf (accessed on 1 January 2011).
- Mattei, O.; Lim, M. Explicit analytic solution for the plane elastostatic problem with a rigid inclusion of arbitrary shape subject to arbitrary far-field loadings. J. Elast. 2021, 144, 81–105. [Google Scholar] [CrossRef]
- Alhazmi, S.; Abdou, M.A.; Basseem, M. The stresses components in position and time of weakened plate with two holes conformally mapped into a unit circle by a conformal mapping with complex constant coefficients. AIMS Math. 2023, 8, 11095–11112. Available online: https://www.aimspress.com/aimspress-data/math/2023/5/PDF/math-08-05-562.pdf (accessed on 9 March 2023). [CrossRef]
- Trefethen, L.N. Numerical conformal mapping with rational functions. Comput. Methods Funct. Theory 2020, 20, 369–387. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Alhendi, N.G. New Approach of Normal and Shear Stress Components for Multiple Curvilinear Holes Which Weakened a Flexible Plate. Symmetry 2024, 16, 360. [Google Scholar] [CrossRef]
- Jan, A.R. The solution of a complex integro differential equation in the right half-plane via an infinite plate weakened by a curvilinear hole. Appl. Math. 2024, 18, 493–503. [Google Scholar] [CrossRef]
- Parkus, H. Thermoelasticity; Springer: Berlin, Germany, 1976. [Google Scholar] [CrossRef]
- Abdou, M.A.; Basseem, M. Thermopotential function in position and time for a plate weakened by curvilinear hole. Arch. Appl. Mech. 2022, 92, 867–883. [Google Scholar] [CrossRef]
- Abdou, M.A.; Aseeri, S.A. Closed forms of Goursat functions in presence of heat for curvilinear holes. J. Therm. Stress. 2009, 32, 1126–1148. [Google Scholar] [CrossRef]
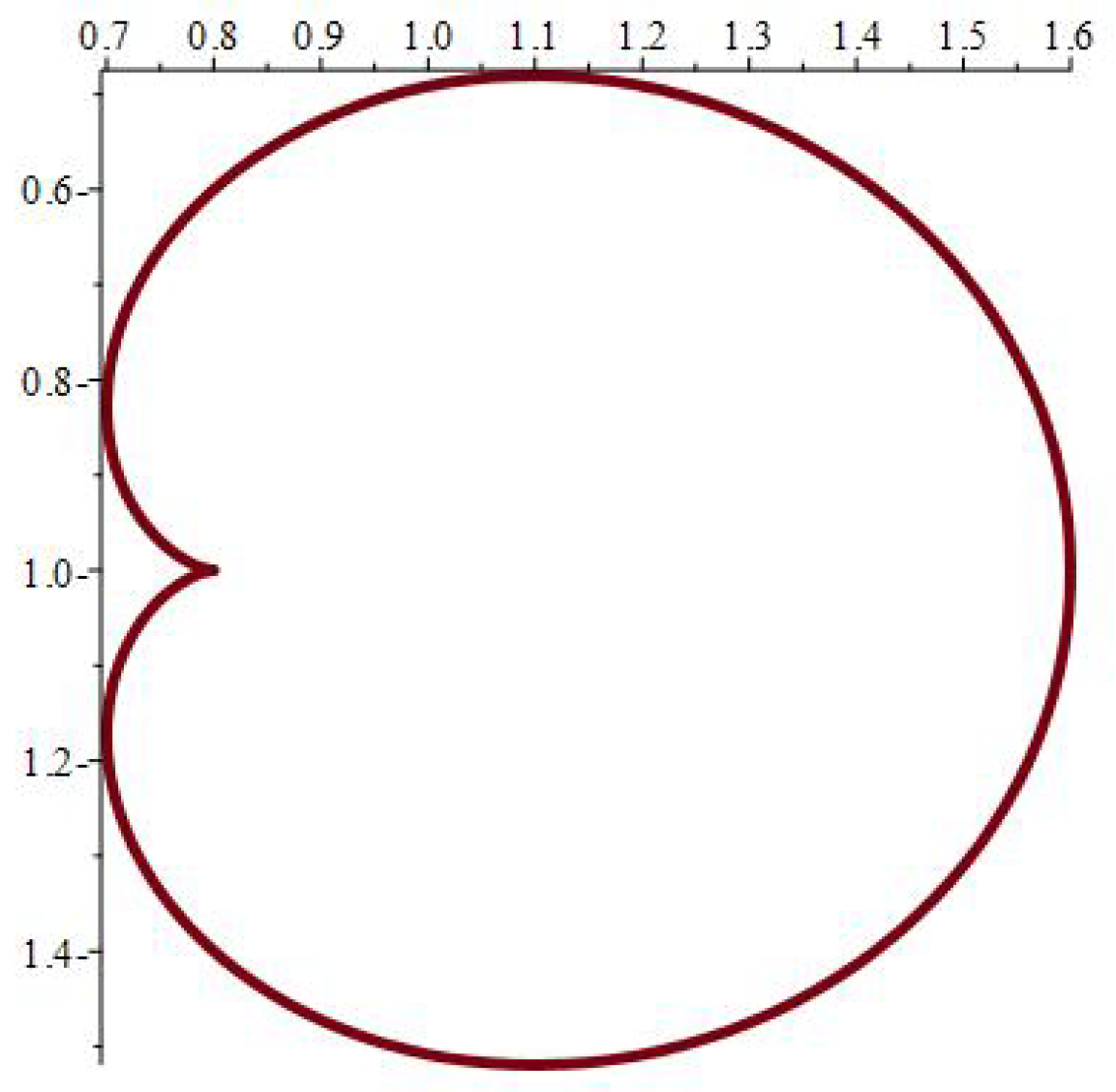

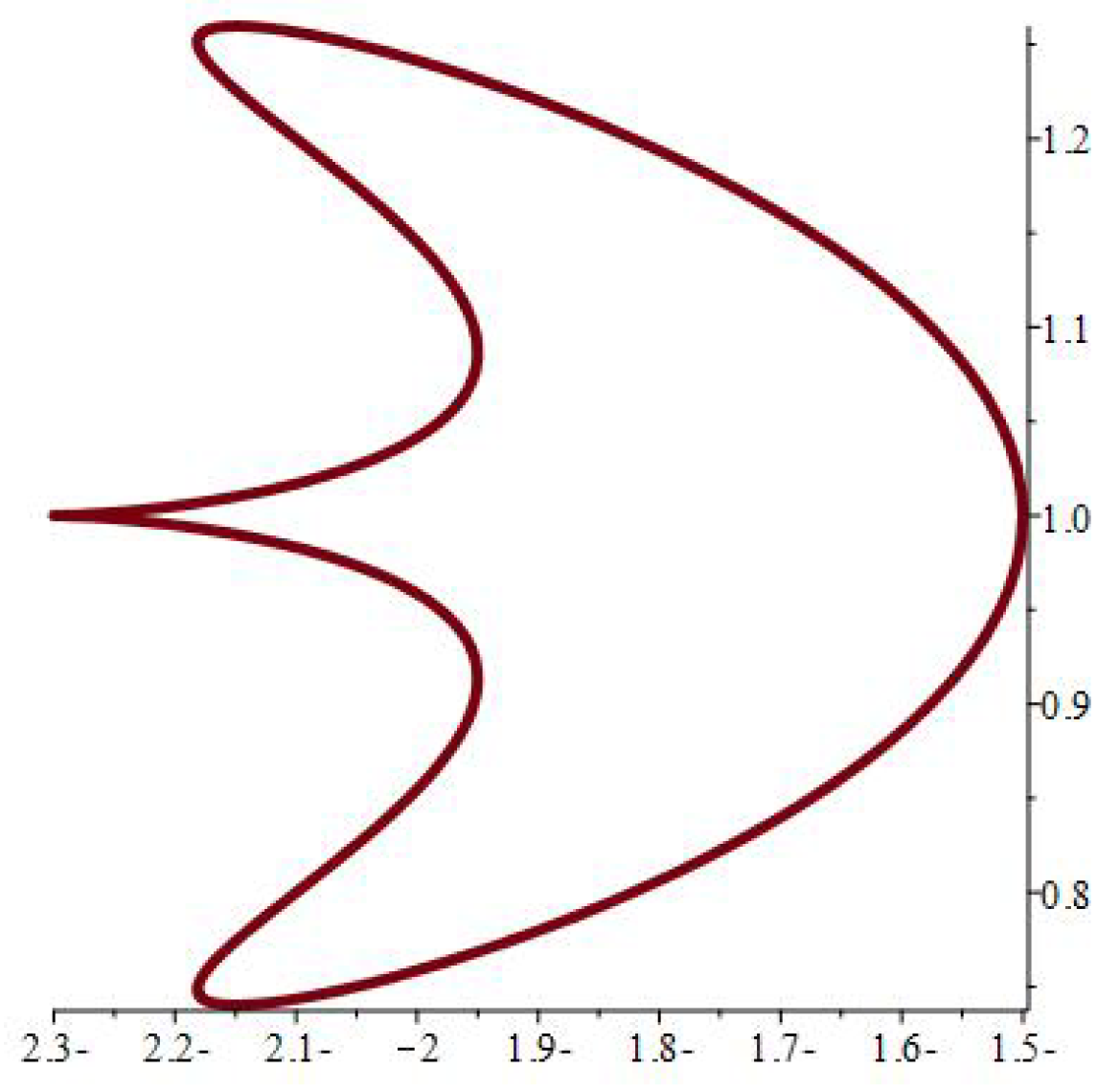
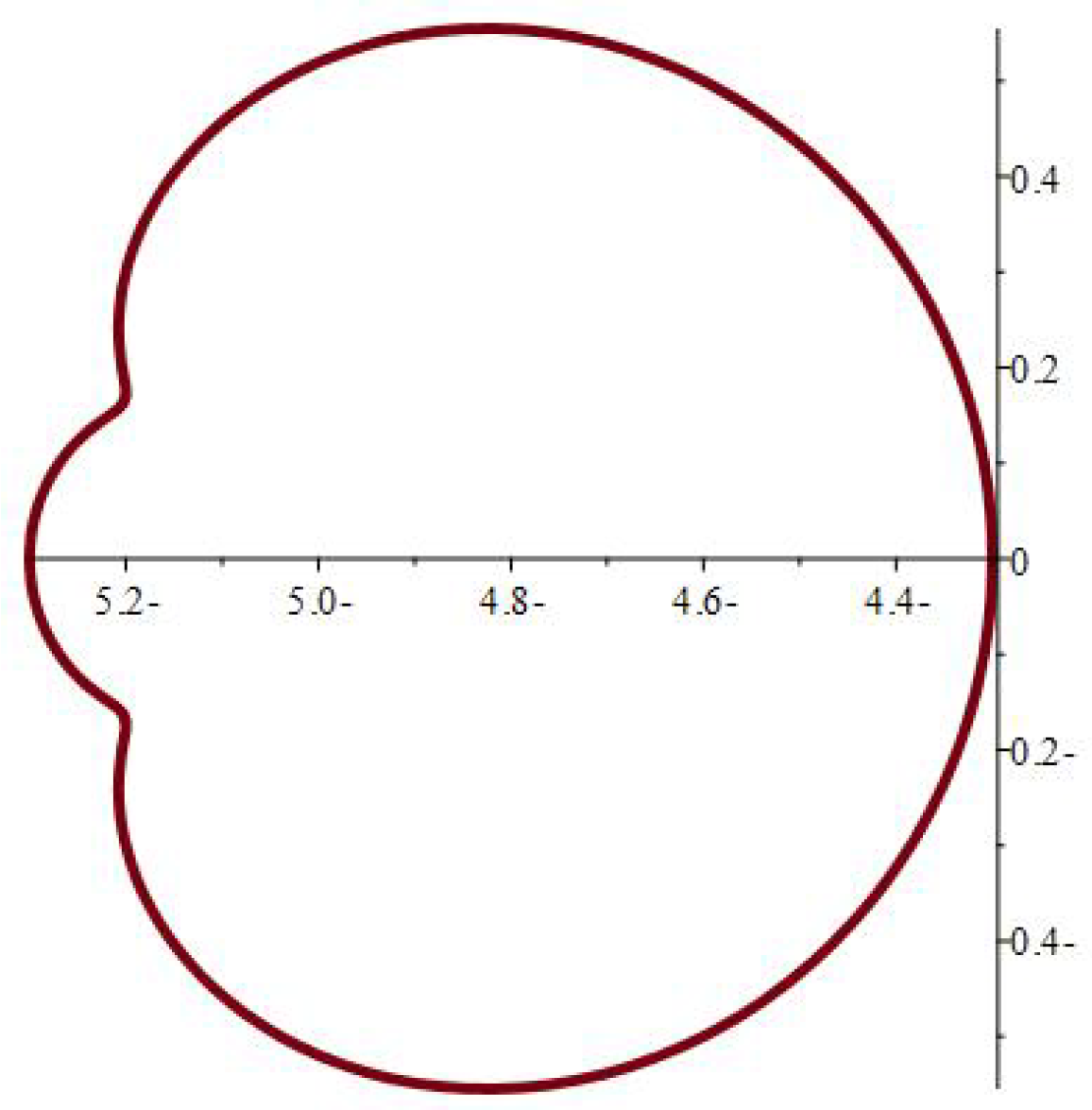
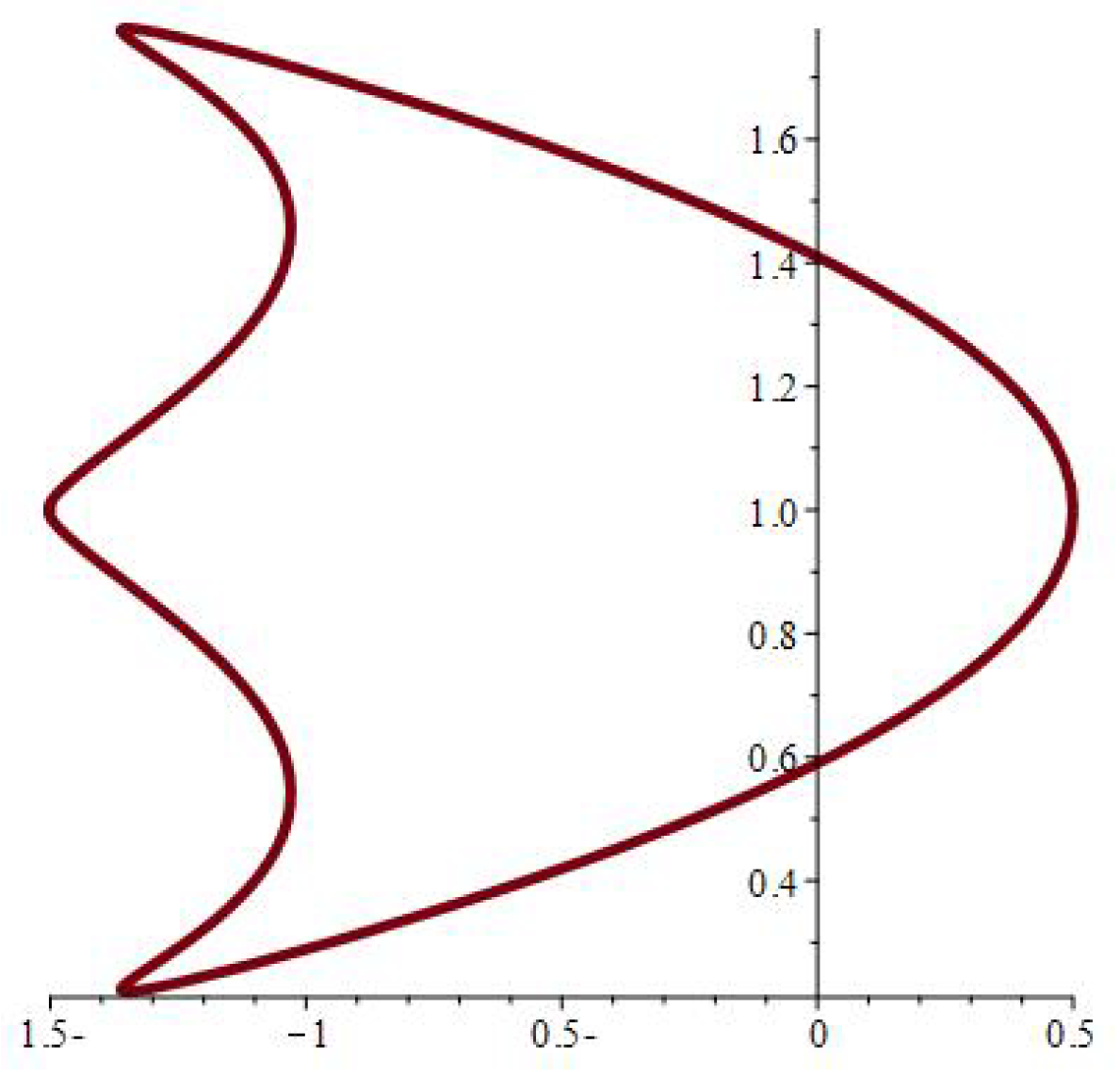
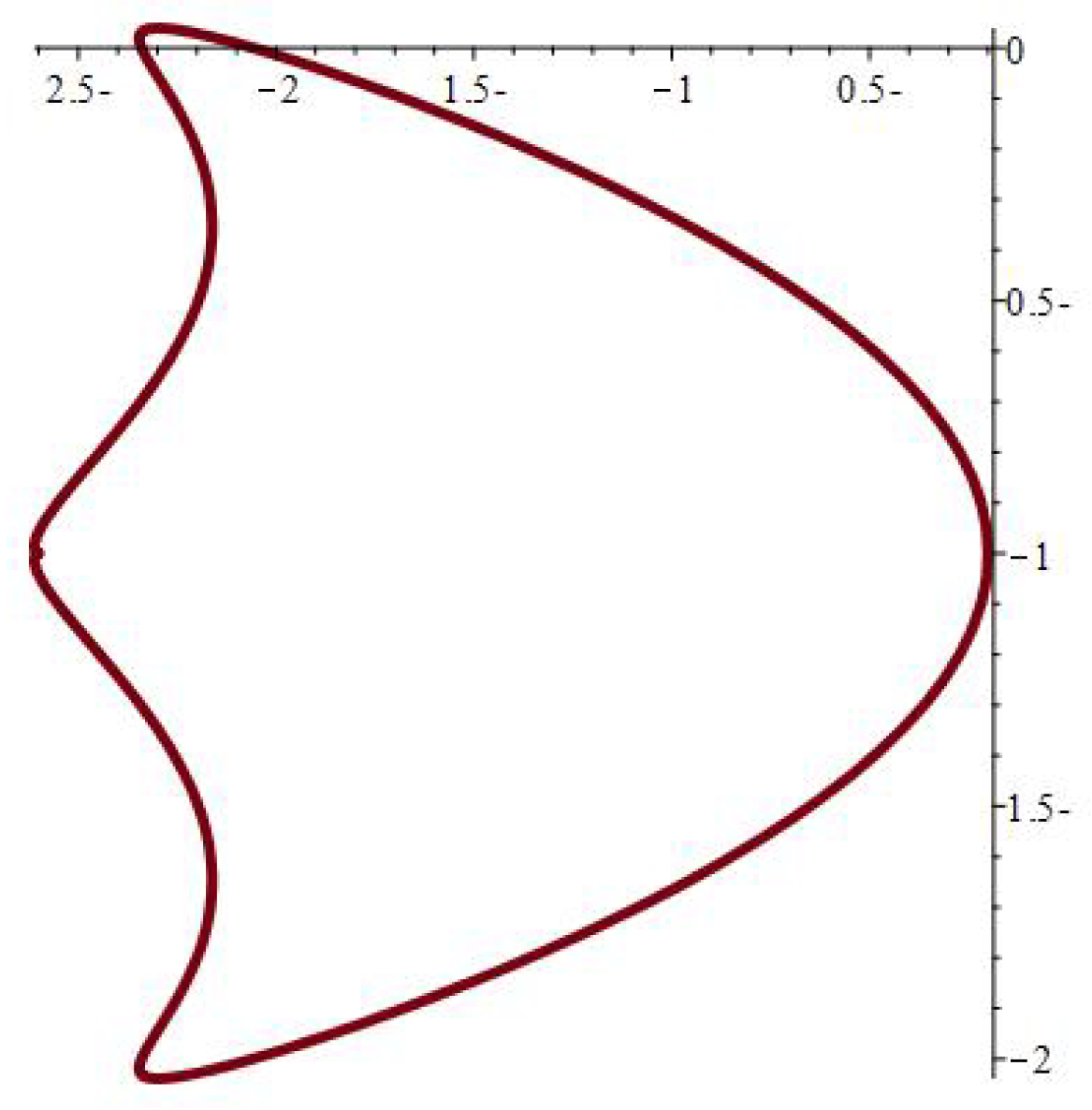
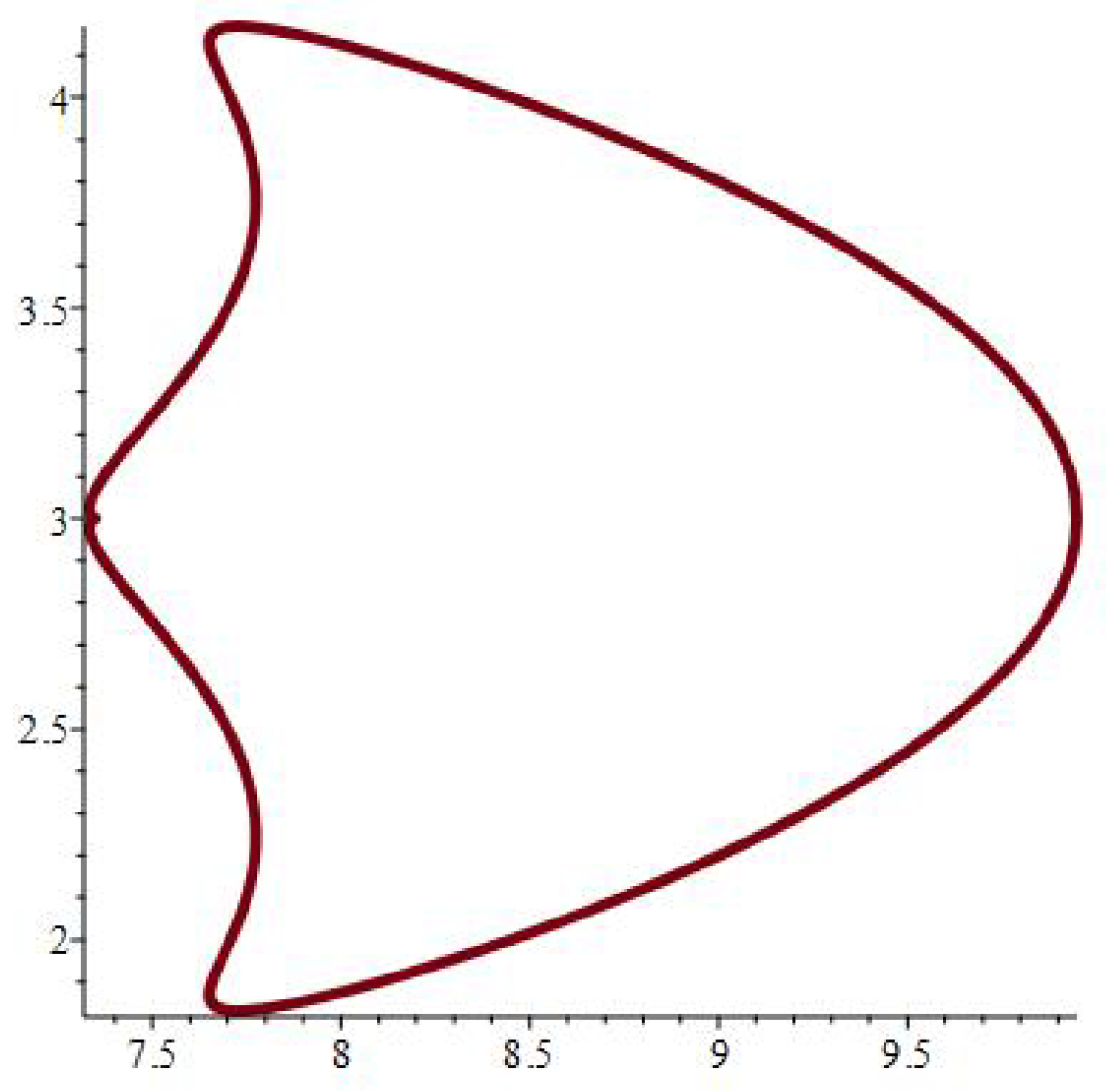
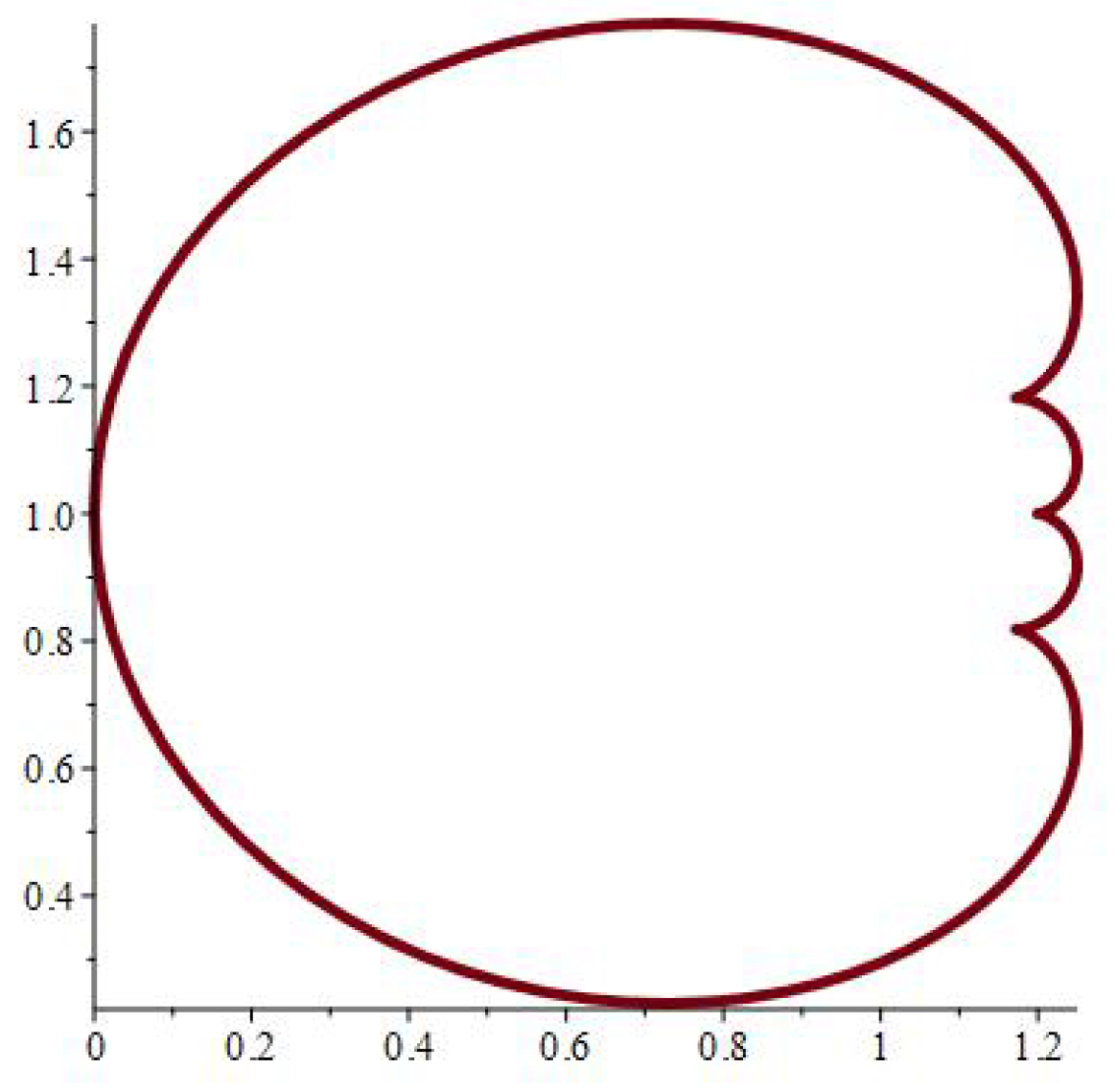
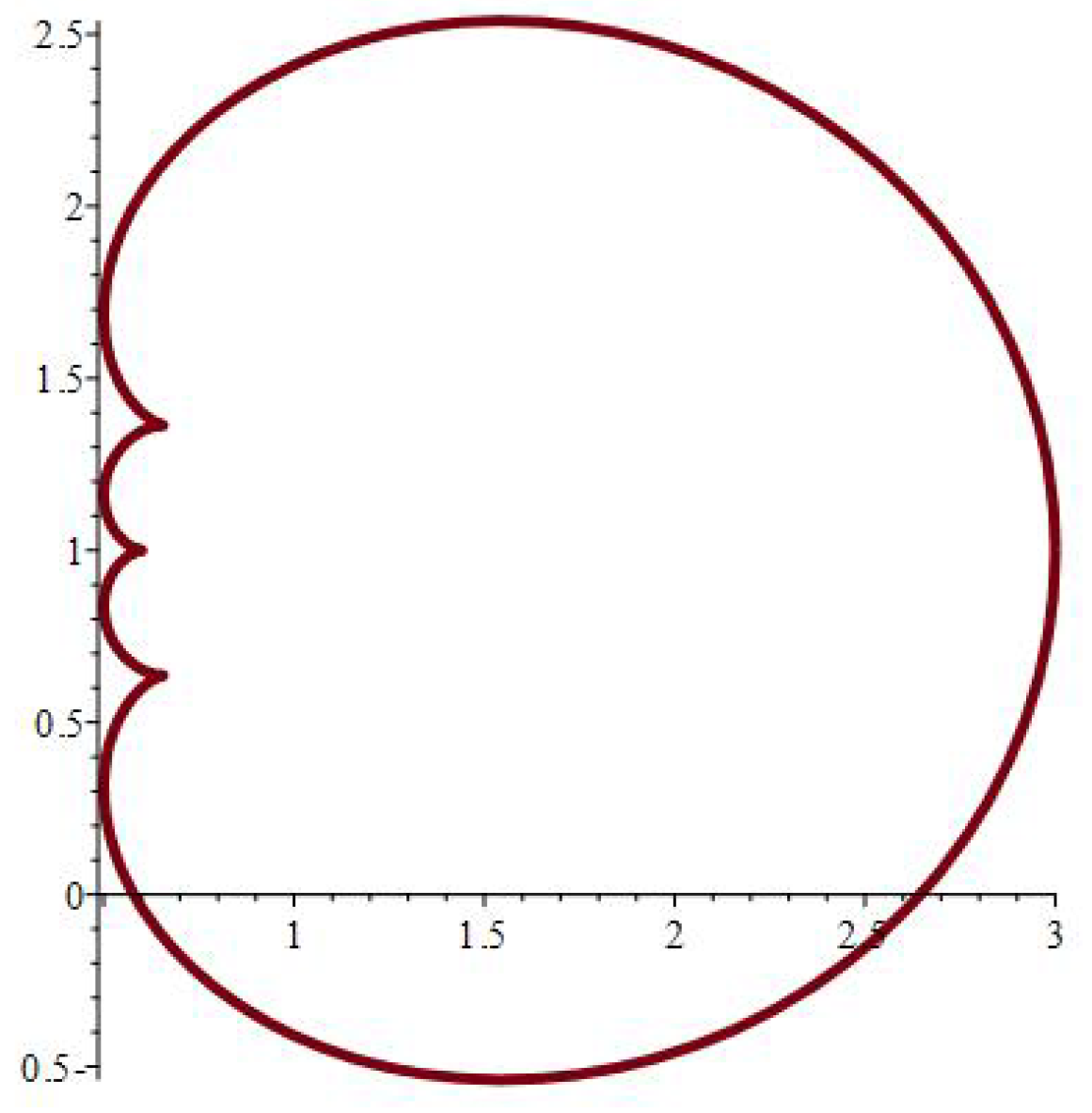


| at 0.7 | at 0.07 | at 0.007 | ||||
|---|---|---|---|---|---|---|
| 0.025220037 | 184.0879069 | 5.12 × 10−3 | 37.37648203 | 4.51 × 10−3 | 32.94411269 | |
| 0.053984223 | 51.54308234 | 0.010960744 | 10.46510401 | 9.66 × 10−3 | 9.224077468 | |
| 0.088736947 | 153.420847 | 0.01801671 | 31.1499632 | 0.0158802392 | 27.45597877 | |
| 0.159031781 | 3477.81632 | 0.32289185 | 706.122099 | 0.028460104 | 622.385114 | |
| 0.176643094 | 5972.582 | 0.035864916 | 1212.64945 | 0.0316117995 | 1068.8449 | |
| at 0.3 | at 0.03 | at 0.003 | ||||
|---|---|---|---|---|---|---|
| 1.87 × 10−3 | 267.395128 | 1.06 × 10−3 | 152.888095 | 1.01 × 10−3 | 144.848484 | |
| 4.004 × 10−3 | 85.87675 | 2.28 × 10−3 | 49.1016152 | 2.17 × 10−3 | 46.519609 | |
| 6.58 × 10−3 | 75.616998 | 3.76 × 10−3 | 43.23541322 | 3.56 × 10−3 | 40.9618816 | |
| 0.0117982313 | 1155.158774 | 6.745 × 10−3 | 660.48332 | 6.39 × 10−3 | 625.751852 | |
| 0.013104777 | 1977.265528 | 7.49 × 10−3 | 1130.53802 | 7.098 × 10−3 | 1071.08874 | |
| at 0.9 | at 0.09 | at 0.009 | ||||
|---|---|---|---|---|---|---|
| 5.062551691 | 2967.25322 | 1.113 × 10−3 | 187.0622331 | 9.45 × 10−4 | 159.0078336 | |
| 0.03777875 | 955.77569 | 2.38 × 10−3 | 60.2542223 | 2.024 × 10−3 | 51.217678 | |
| 0.062099102 | 810.253444 | 3.914 × 10−3 | 51.0801766 | 3.327 × 10−3 | 43.41949785 | |
| 0.111292208 | 11,829.25233 | 7.016 × 10−3 | 745.74233 | 5.963 × 10−3 | 633.90066 | |
| 0.1236168 | 20240.346 | 7.7931 × 10−3 | 1275.9964 | 6.624 × 10−3 | 1084.6305 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, F.M.; Alhendi, N.G. Influence of Heat Transfer on Stress Components in Metallic Plates Weakened by Multi-Curved Holes. Axioms 2025, 14, 369. https://doi.org/10.3390/axioms14050369
Alharbi FM, Alhendi NG. Influence of Heat Transfer on Stress Components in Metallic Plates Weakened by Multi-Curved Holes. Axioms. 2025; 14(5):369. https://doi.org/10.3390/axioms14050369
Chicago/Turabian StyleAlharbi, Faizah M., and Nafeesa G. Alhendi. 2025. "Influence of Heat Transfer on Stress Components in Metallic Plates Weakened by Multi-Curved Holes" Axioms 14, no. 5: 369. https://doi.org/10.3390/axioms14050369
APA StyleAlharbi, F. M., & Alhendi, N. G. (2025). Influence of Heat Transfer on Stress Components in Metallic Plates Weakened by Multi-Curved Holes. Axioms, 14(5), 369. https://doi.org/10.3390/axioms14050369






