A Layer-Adapted Numerical Method for Singularly Perturbed Partial Functional-Differential Equations

Abstract

This article describes an effective computing method for singularly perturbed parabolic problems with small negative shifts in convection and reaction terms. To handle the small negative shifts, the Taylor series expansion is used. The asymptotically equivalent singularly perturbed parabolic convection–diffusion–reaction problem is then discretized with the Crank–Nicolson method on a uniform mesh for the time derivative and a hybrid method on Shishkin-type meshes for the space derivative. The method’s stability and parameter-uniform convergence are established. To substantiate the theoretical findings, the numerical results are presented in tables and graphs are plotted. The present results improve the existing methods in the literature. Due to the effect of the small negative shifts in Examples 1 and 2, the numerical results using Shishkin and Bakhvalov–Shishkin meshes are almost the same. Since there are no small shifts in Examples 3 and 4, the numerical results using the Bakhvalov–Shishkin mesh are more efficient than using the Shishkin mesh. We conclude that the present method using the Bakhvalov–Shishkin mesh performs well for singularly perturbed problems without small negative shifts.

1. Introduction

Differential-difference equations are used to mathematically model a variety of situations in real life, like micro-scale heat transfer [1], the hydrodynamics of liquid helium [2], second-sound theory [2], optically bistable devices [3], diffusion in polymers [4], control of chaotic systems [5], and a variety of models for physiological processes or diseases [6,7]. A differential-difference equation is said to be retarded if the delay argument does not occur in the highest order derivative term; otherwise, it is said to be a neutral differential-difference equation. A differential-difference equation is a differential equation for which the evolution not only depends on the current state of the system but also on the past history [5]. A differential-difference equation involves subtracting or adding a small positive parameter, such as $\mu$, to one or more arguments of the unknown function z or its derivatives. This parameter $\mu$ is considered to be a negative shift if it is subtracted, and a positive shift if it is added. A differential equation is referred to as a singularly perturbed differential-difference equation if it exhibits properties with both singular perturbation problems and differential-difference equations. A functional-differential equation is another name for a differential-difference equation. We introduce the following singularly perturbed parabolic functional differential with negative shifts in the convection and reaction terms:

$$\begin{array}{c}\hfill \left({\displaystyle \frac{\partial z}{\partial t}}+{\mathcal{L}}_{\epsilon ,\mu }\right)(x,t)=f(x,t),(x,t)\in D={\wedge }_x\times {\wedge }_t=(0,1)\times (0,T],\end{array}$$

(1)

subject to the initial condition

$$z(x,0)=\varphi \left(x\right),x\in {\overline{\wedge }}_x,$$

(2)

and the interval boundary conditions

$$\left\{\begin{array}{cc}z(x,t)=\psi (x,t),\hfill & (x,t)\in [-\mu ,0]\times {\overline{\wedge }}_t,\hfill \\ z(1,t)=\phi (1,t),\hfill & t\in {\overline{\wedge }}_t,\hfill \end{array}\right.$$

(3)

where ${\mathcal{L}}_{\epsilon ,\mu }=-\epsilon {\displaystyle \frac{{\partial }^{2}z}{\partial x^2}}+a\left(x\right){\displaystyle \frac{\partial z}{\partial x}}(x-\mu ,t)+b\left(x\right)z(x-\mu ,t)$, $\overline{D}={\overline{\wedge }}_x\times {\overline{\wedge }}_t=[0,1]\times [0,T]$ for some fixed number $T>0$ and $\partial D={\overline{\wedge }}_x\cup {\overline{\wedge }}_t$. The parameter $\epsilon (0<\epsilon \ll 1)$ is a perturbation parameter and $\mu$ ($0<\mu$) is a small delay parameter (or negative shift) satisfying $\mu <\epsilon$. The functions $a\left(x\right),b\left(x\right),\varphi \left(x\right),\psi (x,t),\phi (1,t)$, and $f(x,t)$ are assumed to be sufficiently smooth and bounded to guarantee the existence of a unique solution, $a\left(x\right)$ is assumed to satisfy $a\left(x\right)\ge \alpha >0,x\in \overline{\Omega },$ for some constant $\alpha$ , and (1) contains negative shifts in the convection and reaction terms. With the above conditions, the problem has a boundary layer near $x=1$. When $\mu =0$, (1) would reduce to the singularly perturbed parabolic differential equation.

Various numerical solutions have been developed in the literature for a singularly perturbed parabolic problem with a delay term and advance term in both reaction terms in [8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Some numerical methods have been developed for a singularly perturbed parabolic problem with delay in the reaction terms only in [22] using a new class of non-standard finite difference methods based on interpolation, the $\theta$–method, and Micken’s techniques; the implicit Euler method in temporal discretization; the hybrid scheme consisting of the midpoint upwind method in the outer region and the cubic spline method in the inner region on a Shishkin mesh for spatial discretization in [23]; and the implicit Euler method for the time direction and fitted exponential cubic spline method for space direction are developed in [24]. Some numerical methods are developed for solving different types of singularly perturbed problems in [25,26,27].

Different numerical methods for solving singularly perturbed parabolic functional-differential equations with negative shifts in convection and reaction terms of the form in (1)–(3) are constructed and analyzed in [28] using a three-step Taylor Galerkin finite element scheme-based monotone Schwarz iterative method, a complete flux scheme in [29], a domain decomposition Taylor Galerkin finite element approximation in [30], a finite element domain decomposition approximation in [31], the Crank–Nicolson method for time direction and upwind method on Shishkin mesh for space direction are used in [32], the $\theta$–method in time and non-standard method in space directions are used in [33], the Crank–Nicolson method for time direction and exponentially fitted finite difference method for space direction are developed in [34], and the Crank–Nicolson method for time and midpoint upwind method on a Shishkin mesh with Richardson extrapolation in space direction are used in [35]. According to a number of studies, although these shifts are very small, they have significant effects on the solution and should not be ignored [36]. Therefore, it is crucial to look into robust numerical techniques for solving (1)–(3). To this end, we propose and analyze a Crank–Nicolson method in time direction and a hybrid numerical method on Shishkin-type meshes in space direction to solve the problem under consideration.

This paper is arranged as follows. Section 2 examines the solution’s bounds and derivatives. Section 3 describes the Shishkin-type meshes (Shishkin and Bakhvalov–Shishkin meshes) as well as the hybrid finite difference method. Section 4 examines the uniform convergence of the present method. Section 5 discusses numerical results using tables and figures.

Throughout the paper, C denotes a generic positive constant independent of $\epsilon$, the space mesh parameters, and the time step.

2. The Continuous Problem

2.1. A Priori Estimates for the Negative Shifts

For the case $\mu <\epsilon$, using Taylor series approximation for terms containing a delay is appropriate [37]. Now, approximating $z(x-\mu ,t)$ and $z_x(x-\mu ,t)$ yields the following:

$$\begin{array}{cc}\hfill z(x-\mu ,t)& \approx z(x,t)-\mu z_x(x,t)+{\displaystyle \frac{{\mu }^2}{2}}{z}_{xx}(x,t)+O\left({\mu }^3\right),\hfill \\ \hfill z_x(x-\mu ,t)& \approx z_x(x,t)-\mu z_{xx}(x,t)+O\left({\mu }^2\right).\hfill \end{array}$$

(4)

Plugging (4) into (1)–(3), we obtain an asymptotically equivalent time-dependent singularly perturbed convection–diffusion–reaction continuous problem of the following form:

$$\begin{array}{c}\hfill \left({\displaystyle \frac{\partial z}{\partial t}}+\mathcal{L}\right)(x,t)=f(x,t),(x,t)\in D,\end{array}$$

(5)

with the initial condition

$$z(x,0)=\varphi \left(x\right)\ge 0,x\in {\overline{\wedge }}_x,$$

(6)

and the boundary conditions

$$z(0,t)=\psi \left(t\right),z(1,t)=\phi \left(t\right)\ge 0,t\in {\overline{\wedge }}_t,$$

(7)

where $\mathcal{L}=-c_{\epsilon }{z}_{xx}+p\left(x\right)z_x+b\left(x\right)z,c_{\epsilon }\left(x\right)=\epsilon +\mu a\left(x\right)-{\displaystyle \frac{{\mu }^2}{2}}b\left(x\right)$ and $p\left(x\right)=a\left(x\right)-\mu b\left(x\right)$. Assume $0<c_{\epsilon }\left(x\right)\le \epsilon +\mu \alpha -{\displaystyle \frac{{\mu }^2}{2}}\beta =c_{\epsilon }$, where $\alpha$ and $\beta$ are the lower bounds for $a\left(x\right)$ and $b\left(x\right)$, respectively. Furthermore, we assume $p\left(x\right)=a\left(x\right)-\mu b\left(x\right)\ge \gamma >0$, which implies the occurrence of a boundary layer of width $O\left(\epsilon \right)$ near $x=1$.

2.2. Solution Bounds

The existence and uniqueness of the solution for (1)–(3) can be guaranteed by the sufficient smoothness of $\psi \left(t\right),\varphi \left(x\right),$ and $\phi \left(t\right)$ as well as the compatibility condition at the corner points as stated below.

$$\left\{\begin{array}{c}\varphi \left(0\right)=\psi \left(0\right),\varphi \left(1\right)=\phi \left(0\right),\hfill \\ {\displaystyle \frac{\partial \psi \left(0\right)}{\partial t}}-c_{\epsilon }\left(0\right){\displaystyle \frac{{\partial }^2\varphi \left(0\right)}{\partial x^2}}+p\left(0\right){\displaystyle \frac{\partial \varphi \left(0\right)}{\partial x}}+b\left(0\right)\varphi \left(0\right)=f(0,0),\hfill \\ {\displaystyle \frac{\partial \phi \left(0\right)}{\partial t}}-c_{\epsilon }\left(1\right){\displaystyle \frac{{\partial }^2\varphi \left(1\right)}{\partial x^2}}+p\left(1\right){\displaystyle \frac{\partial \varphi \left(1\right)}{\partial x}}+b\left(1\right)\varphi \left(1\right)=f(1,0).\hfill \end{array}\right.$$

Now, we provide the bounds on the derivatives of the solution of (1)–(3). In order to obtain the bounds, one requires some information about the solution.

Lemma 1. 

The solution $z(x,t)$ of (5)–(7) satisfies

$$\begin{array}{cc}\hfill \left|z\right(x,t)-\varphi (x\left)\right|& \le Ct,\hfill \\ \hfill \left|z\right(x,t)-\psi (t\left)\right|& \le C(1-x),(x,t)\in \overline{D},\hfill \end{array}$$

where a constant C is independent of $c_{\epsilon }$.

To show the bounds of the solution $z(x,t)$ of (5)–(7), we assume, without loss of generality, $\varphi \left(x\right)=0$. Since $\varphi \left(x\right)$ is sufficiently smooth, using the property of norm, we prove the following lemma:

Lemma 2. 

The solution $z(x,t)$ of (5)–(7) is bounded as

$$\left|z(x,t)\right|\le C,(x,t)\in \overline{D}.$$

Proof of Lemma 2. 

From the inequality

$$\left|z\right(x,t)-\varphi (x\left)\right|\le Ct,$$

we have

$$\left|z\right(x,t\left)\right|-\left|\varphi \right(x\left)\right|\le \left|z\right(x,t)-\varphi (x\left)\right|\le Ct.$$

This implies that

$$\left|z(x,t)\right|\le Ct+\left|\varphi \left(x\right)\right|,(x,t)\in \overline{D}.$$

Since $t\in [0,T]$ and $\varphi \left(x\right)$ is bounded, it implies that

$$\left|z\right(x,t\left)\right|\le C,$$

which is the required result. □

The problem (5)–(7) satisfies the following maximum principle.

Lemma 3. 

Let Θ be a sufficiently smooth function defined on D which satisfies $\Theta (x,t)\ge 0$, $\forall (x,t)\in \partial D$. Then, $\left({\displaystyle \frac{\partial }{\partial t}}+\mathcal{L}\right)\Theta (x,t)\ge 0$; $(x,t)\in D$ implies that $\Theta (x,t)\ge 0$, $\forall (x,t)\in \overline{D}$.

Proof of Lemma 3. 

Assume $\Theta (x^{*},t^{*})\in \overline{D}$ such that $\Theta (x^{*},t^{*})=\underset{(x,t)\in \overline{D}}{min}\Theta (x,t)<0.$ It is clear that $(x^{*},t^{*})\notin \partial D$, i.e.,  $(x^{*},t^{*})\in D$. Since $\Theta (x^{*},t^{*})=\underset{(x,t)\in \tilde{D}}{min}\Theta (x,t),$ which implies that ${\Theta }_x(x^{*},t^{*})=0$, ${\Theta }_t(x^{*},t^{*})=0$ and ${\Theta }_{xx}(x^{*},t^{*})\ge 0$. Now,

$$\left({\displaystyle \frac{\partial }{\partial t}}+\mathcal{L}\right)\Theta (x^{*},t^{*})<0,$$

which is a contradiction to the assumption $\left({\displaystyle \frac{\partial }{\partial t}}+\mathcal{L}\right)\Theta (x,t)\ge 0$. Hence, $\Theta (x,t)\ge 0,\forall (x,t)\in \overline{D}$. □

The following stability bound is an immediate consequence of the above maximum principle for the solution of Equation (1).

Lemma 4. 

The solution $z(x,t)$ of (5)–(7) is bounded as

$$\left|z(x,t)\right|\le max\left\{\left|\varphi \left(x\right)\right|,\left|\psi \left(t\right)\right|,\left|\phi \left(t\right)\right|\right\}+{\beta }^{-1}∥f∥.$$

Proof of Lemma 4. 

We define two barrier functions ${\varpi }^{\pm }$ as

$${\varpi }^{\pm }(x,t)=max\left\{\left|\varphi \left(x\right)\right|,\left|\psi \left(t\right)\right|,\left|\phi \left(t\right)\right|\right\}+{\beta }^{-1}∥f∥\pm z(x,t).$$

After evaluating the barrier functions under the initial and boundary conditions, the required bound follows. □

3. The Discrete Problem

The time derivative is discretized using the Crank–Nicolson method with a uniform step size. Following this, the discretization of the space derivative is done via the hybrid method on Shishkin-type meshes.

3.1. Time Semi-Discrete Problem

The problem is discretized using the Crank–Nicolson method on an equidistant mesh for the time derivative. Now, using the mesh size $\kappa$, the interval $[0,T]$ is divided into N sub-intervals with spacing $\kappa ={\displaystyle \frac{T}{N_t}}$. Therefore, the time interval $[0,T]$ is given by

$${\wedge }_t^{N_t}=\{0=t_0<t_1<\dots t_{N_t-1}<t_{N_t}=T\}.$$

Thus, the mesh points for the time interval $[0,T]$ are given by $\{t_n=n\kappa ,0\le n\le N_t\}$. Now, the time semi-discrete problem on ${\wedge }_t^{N_t}$ is given by

$$\left(I+{\displaystyle \frac{\kappa }{2}}\mathcal{L}\right){\widehat{z}}^{n+1}\left(x\right)={\displaystyle \frac{\kappa }{2}}\left(f^{n+1}\left(x\right)+f^n\left(x\right)\right)+\left(I-{\displaystyle \frac{\kappa }{2}}\mathcal{L}\right){\widehat{z}}^n\left(x\right),$$

(8)

with semi-discrete conditions

$$\left\{\begin{array}{cc}\widehat{z}(x,0)=\varphi \left(x\right),\hfill & x\in {\overline{\wedge }}_x,\hfill \\ {\widehat{z}}^{n+1}\left(0\right)={\psi }^{n+1},{\widehat{z}}^{n+1}\left(1\right)={\phi }^{n+1},\hfill & t_{n+1}\in {\overline{\wedge }}_t,\hfill \end{array}\right.$$

(9)

where ${\widehat{z}}^{n+1}\left(x\right)$ represents the semi-discrete numerical solution to (5) and (6) at the ${(n+1)}^{th}$ time level. We can rewrite (8) and (9) in the form

$$\begin{array}{c}\hfill -c_{\epsilon }{\widehat{z}}_{xx}^{n+1}\left(x\right)+p\left(x\right){\widehat{z}}_x^{n+1}\left(x\right)+q\left(x\right){\widehat{z}}^{n+1}\left(x\right)=K\left(x\right),\end{array}$$

(10)

where $K\left(x\right)=c_{\epsilon }{\widehat{z}}_{xx}^n\left(x\right)-p\left(x\right){\widehat{z}}_x^n\left(x\right)-r\left(x\right){\widehat{z}}^n\left(x\right)+f^n\left(x\right)+f^{n+1}\left(x\right)$, $q\left(x\right)=b\left(x\right)+{\displaystyle \frac{2}{\kappa }}$, $r\left(x\right)=b\left(x\right)-{\displaystyle \frac{2}{\kappa }}$ and with semi-discrete conditions in (9). The time semi-discretization satisfies the following semi-discrete maximum principle.

Lemma 5. 

Let $\tilde{\Theta }\left(x\right)$ be a smooth function of the semi-discrete problem such that $\tilde{\Theta }\left(0\right)\ge 0$, $\tilde{\Theta }\left(1\right)\ge 0$. If  ${\mathcal{L}}^{N_t}\tilde{\Theta }\left(x\right)\ge 0$$\forall x\in (0,1)$, then $\tilde{\Theta }\left(x\right)\ge 0$$\forall x\in [0,1]$.

Proof of Lemma 5. 

Assume $\xi \in [0,1]$ such that $\tilde{\Theta }\left(\xi \right)=\underset{x\in [0,1]}{min}\tilde{\Theta }\left(x\right)$ and $\tilde{\Theta }\left(\xi \right)<0$; clearly, $x\notin \{0,1\}.$ Therefore, ${\displaystyle \frac{\partial \tilde{\Theta }}{\partial x}}\left(\xi \right)=0$ and ${\displaystyle \frac{{\partial }^2\tilde{\Theta }}{\partial x^2}}\left(\xi \right)\ge 0$. Now, we have

$${\mathcal{L}}^{N_t}\tilde{\Theta }\left(\xi \right)=-c_{\epsilon }{\displaystyle \frac{{\partial }^2\tilde{\Theta }}{\partial x^2}}\left(\xi \right)+p\left(\xi \right){\displaystyle \frac{\partial \tilde{\Theta }}{\partial x}}\left(\xi \right)+q\left(\xi \right)\tilde{\Theta }\left(\xi \right)\le 0,$$

which contradicts the assumption ${\mathcal{L}}^{N_t}\tilde{\Theta }\left(\xi \right)\ge 0$, $\forall x\in (0,1)$. It immediately follows that $\tilde{\Theta }\left(\xi \right)\ge 0$. Thus, $\tilde{\Theta }\left(x\right)\ge 0$ for $x\in [0,1]$. □

The local truncation error (LTE) of the Crank–Nicolson method for the time semi-discretization is given by $e_{n+1}=z(x,t_{n+1})-{\widehat{z}}^{n+1}\left(x\right)$, where ${\widehat{z}}^{n+1}\left(x\right)$ is the numerical solution of the boundary value problem

$$\begin{array}{c}\hfill -c_{\epsilon }{\widehat{z}}_{xx}^{n+1}\left(x\right)+p\left(x\right){\widehat{z}}_x^{n+1}\left(x\right)+q\left(x\right){\widehat{z}}^{n+1}\left(x\right)=K\left(x\right),\end{array}$$

with semi-discrete conditions

$${\widehat{z}}^{n+1}\left(0\right)={\psi }^{n+1},{\widehat{z}}^{n+1}\left(1\right)={\phi }^{n+1},t_{n+1}\in {\overline{\wedge }}_t,$$

where ${\widehat{z}}^{n+1}\left(x\right)$ represents the semi-discrete numerical solution to (5)–(6) at the ${(n+1)}^{th}$ time level. This error quantifies the contribution of each time step to the global error of the time semi-discretization.

Lemma 6. 

The LTE bound in the time direction is given by

$$\parallel e_{n+1}\parallel \le C{\kappa }^3.$$

Proof of Lemma 6. 

Approximating $\widehat{z}(x,t_n)$ and $\widehat{z}(x,t_{n+1})$ using Taylor series centering at $t_{n+{\displaystyle \frac{1}{2}}}$

$$\begin{array}{cc}\hfill \widehat{z}(x,t_{n+1})& =\widehat{z}(x,t_{n+{\displaystyle \frac{1}{2}}})+{\displaystyle \frac{\kappa }{2}}{\widehat{z}}_t(x,t_{n+{\displaystyle \frac{1}{2}}})+{\displaystyle \frac{{\kappa }^2}{8}}{\widehat{z}}_{tt}(x,t_{n+{\displaystyle \frac{1}{2}}})+O({\kappa }^3),\hfill \\ \hfill \widehat{z}(x,t_n)& =\widehat{z}(x,t_{n+{\displaystyle \frac{1}{2}}})-{\displaystyle \frac{\kappa }{2}}{\widehat{z}}_t(x,t_{n+{\displaystyle \frac{1}{2}}})+{\displaystyle \frac{{\kappa }^2}{8}}{\widehat{z}}_{tt}(x,t_{n+{\displaystyle \frac{1}{2}}})+O\left({\kappa }^3\right).\hfill \end{array}$$

(11)

From (11), we have

$${\displaystyle \frac{\widehat{z}(x,t_{n+1})-\widehat{z}(x,t_n)}{\kappa }}={\widehat{z}}_t(x,t_{n+{\displaystyle \frac{1}{2}}})+O\left({\kappa }^2\right).$$

(12)

Using (12) in (5), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\widehat{z}(x,t_{n+1})-\widehat{z}(x,t_n)}{\kappa }}& =c_{\epsilon }{\widehat{z}}_{xx}(x,t_{n+{\displaystyle \frac{1}{2}}})-p(x){\widehat{z}}_x(x,t_{n+{\displaystyle \frac{1}{2}}})-q(x)\widehat{z}(x,t_{n+{\displaystyle \frac{1}{2}}})\hfill \\ & +f(x,t_{n+{\displaystyle \frac{1}{2}}})+O({\kappa }^2),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill f(x,t_{n+{\displaystyle \frac{1}{2}}})& ={\displaystyle \frac{f(x,t_{n+1})+f(x,t_n)}{2}}+O\left({\kappa }^2\right),\hfill \\ \hfill \widehat{z}(x,t_{n+{\displaystyle \frac{1}{2}}})& ={\displaystyle \frac{\widehat{z}(x,t_{n+1})+\widehat{z}(x,t_n)}{2}}+O\left({\kappa }^2\right).\hfill \end{array}$$

Since the error $e_{n+1}=z(x,t_{n+1})-\widehat{z}(x,t_{n+1})$ satisfies the semi-discrete problem

$$\begin{array}{c}\hfill \mathcal{L}{e}_{n+1}=O\left({\kappa }^3\right),e_{n+1}\left(0\right)=0=e_{n+1}\left(1\right).\end{array}$$

Applying the semi-discrete maximum principle, we obtain

$$\parallel e_{n+1}\parallel \le C{\kappa }^3,$$

(13)

which is the required bound for the local truncation error. □

The LTE $e_{n+1}$ quantifies each time step to the global error given by $E_n={\displaystyle \sum _{\lambda =1}^n}{e}_{\lambda }$. The global error is the measure of the contribution of the LTE at each time step, which is given by $e_n=z(x,t_n)-{\widehat{z}}^n\left(x\right).$

Lemma 7. 

The global error estimate at $t_n$ is bounded by

$$\parallel E_n\parallel \le C{\kappa }^2.$$

Proof of Lemma 7. 

Using the local error estimate up to the $n^{th}$ time step given in Lemma 6, the global error estimate at the $n^{th}$ time step is given by

$$\begin{array}{cc}\hfill \parallel E_n\parallel & =\parallel \sum _{p=1}^n{e}_p\parallel ,n\le {\displaystyle \frac{T}{\kappa }},\hfill \\ \hfill & \le \parallel e_1\parallel +\parallel e_2\parallel +\dots +\parallel e_n\parallel ,\hfill \\ \hfill & \le C_1\left(n\kappa \right){\kappa }^2\mathrm{using}\left(13\right)\hfill \\ \hfill & \le C_{1}T{\kappa }^2,\mathrm{since}n\kappa \le T,\hfill \\ \hfill & =C{\kappa }^2,\mathrm{where}C=C_{1}T,\hfill \end{array}$$

where C is a positive constant independent of $\kappa$ and $c_{\epsilon }$. □

Lemma 7 concludes second-order uniform convergence for the time semi-discretization process. The next theorem helps us to study the parameter-uniform convergence for space discretization. The following theorem is helpful to find the error bound in the semi-discrete problem.

Theorem 1. 

The derivatives of the solution ${\widehat{z}}^{n+1}\left(x\right)$ of (9) and (10) are bounded by

$$\left|{\displaystyle \frac{d^l{\widehat{z}}^{n+1}\left(x\right)}{d{x}^l}}\right|\le C\left(1+c_{\epsilon }^{-l}exp\left({\displaystyle \frac{-\gamma (1-x)}{c_{\epsilon }}}\right)\right),0\le l\le 4.$$

Proof of Theorem 1. 

See [38]. □

3.2. Shishkin-Type Solution Decomposition

Since the bounds on the derivatives of the solution are not sharp enough for the proof of parameter-uniform convergence, Shishkin-type decomposition is needed to derive stronger bounds. This is done by splitting the solution ${\widehat{z}}^{n+1}\left(x\right)$ into a regular component $r^{n+1}\left(x\right)$ and a singular component $s^{n+1}\left(x\right)$ and doing error bounds separately for each. Let

$${\widehat{z}}^{n+1}\left(x\right)=r^{n+1}\left(x\right)+s^{n+1}\left(x\right),$$

(14)

where the regular component $r^{n+1}\left(x\right)$ is the solution to the non-homogeneous equation

$$\left\{\begin{array}{cc}{\mathcal{L}}^{N_t}{r}^{n+1}\left(x\right)=K\left(x\right),\hfill & x\in {\wedge }_x,\hfill \\ r^{n+1}\left(0\right)={\widehat{z}}^{n+1}\left(0\right),\hfill \end{array}\right.$$

(15)

and the singular component $s^{n+1}\left(x\right)$ is the solution to the homogeneous equation

$$\left\{\begin{array}{cc}{\mathcal{L}}^{N_t}{s}^{n+1}\left(x\right)=0,\hfill & x\in {\wedge }_x,\hfill \\ s^{n+1}\left(0\right)=0,\hfill & \\ s^{n+1}\left(1\right)={\widehat{z}}^{n+1}\left(1\right)-r^{n+1}\left(1\right).\hfill \end{array}\right.$$

(16)

Now, we state the bounds for regular and singular components.

Theorem 2. 

Let $r^{n+1}\left(x\right)$ be the regular solution. Then, $r^{n+1}\left(x\right)$ and its derivative satisfy the bound

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{d^l{r}^{n+1}\left(x\right)}{d{x}^l}}\right|\le C(1+c_{\epsilon }^{2-l}),l=0,1,2,x\in {\wedge }_x.\end{array}$$

In general, the derivatives are bounded by

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{d^l{r}^{n+1}\left(x\right)}{d{x}^l}}\right|\le C,l=0,1,2,3x\in {\wedge }_x.\end{array}$$

Proof of Theorem 2. 

For the proof, one can refer to [34,38]. □

Theorem 3. 

Let $s^{n+1}\left(x\right)$ be the solution of (5)–(7). The bounds of $s^{n+1}\left(x\right)$ and its derivatives satisfy

$$\left|{\displaystyle \frac{d^l{s}^{n+1}\left(x\right)}{d{x}^l}}\right|\le C{c}_{ϵ}^{-l}exp\left({\displaystyle \frac{-\gamma (1-x)}{c_{\epsilon }}}\right),l=0,1,2,3x\in {\wedge }_x.$$

Proof of Theorem 3. 

Consider the barrier function

$${\Psi }^{\pm }(x,t_{n+1})=Cexp\left({\displaystyle \frac{-\gamma (1-x)}{c_{\epsilon }}}\right)\pm s^{n+1}\left(x\right),x\in {\overline{\wedge }}_x.$$

Evaluating the barrier functions ${\Psi }^{\pm }(x,t_{n+1})$ at the boundaries and on the whole domain together with the discrete maximum principle yields the required result for $l=0$. For $l=1,2,3$, one can see the proof in [38,39]. □

3.3. Fully Discrete Problem

In this subsection, the space domain is discretized via layer-adapted Shishkin-type meshes of Shishkin and Bakhvalov–Shishkin meshes. The space domain $[0,1]$ is split into two sub-domains with $[0,1-\sigma ]$ an outer region and with $(1-\sigma ,1]$ a boundary layer region, where $1-\sigma$ is the transition parameter, which separates the coarse and fine portions of the mesh. Now, the space domain is given by

$${\wedge }_x^{N_x}=\left\{0=x_0,\dots ,x_{N_x/2}=1-\sigma ,\dots ,x_{N_x}=1\right\}.$$

Shishkin-type meshes are characterized by the Shishkin mesh transition parameter. Therefore, the transition parameter for all Shishkin-type meshes is given by

$$\sigma =min\left\{{\displaystyle \frac{1}{2}},{\displaystyle \frac{{\sigma }_0{c}_{\epsilon }}{\gamma }}ln{N}_x\right\},$$

where ${\sigma }_0$ denotes a constant that represents the order of the method and $\sigma$ depends on $c_{\epsilon }$ and $N_x$. Here, $N_x$ is the number of mesh intervals in the space direction. The mesh points for the Shishkin mesh are defined as

$$x_i=\left\{\begin{array}{cc}{\displaystyle \frac{2(1-\sigma )}{N_x}}i,\hfill & i=0,\dots ,{\displaystyle \frac{N_x}{2}},\hfill \\ (1-\sigma )+{\displaystyle \frac{2\sigma }{N_x}}\left(i-{\displaystyle \frac{N_x}{2}}\right),\hfill & i={\displaystyle \frac{N_x}{2}}+1,\dots ,N_x,\hfill \end{array}\right.$$

for $N_x\ge 4$ being a positive even integer. From the definition of $x_i$, we denote the space mesh size $h_i$ as follows:

$$h_i=\left\{\begin{array}{cc}H={\displaystyle \frac{2(1-\sigma )}{N_x}},\hfill & i=1,\dots ,{\displaystyle \frac{N_x}{2}},\hfill \\ h={\displaystyle \frac{2\sigma }{N_x}},\hfill & i={\displaystyle \frac{N_x}{2}}+1,\dots ,N_x.\hfill \end{array}\right.$$

With the same transition parameter, the mesh points for the Bakhvalov–Shishkin mesh are defined as

$$x_i=\left\{\begin{array}{cc}{\displaystyle \frac{2(1-\sigma )}{N_x}}i,\hfill & i=0,\dots ,{\displaystyle \frac{N_x}{2}},\hfill \\ 1+{\displaystyle \frac{2c_{\epsilon }}{\gamma }}ln\left({\displaystyle \frac{N_x^2-2(N_x-1)(N_x-i)}{N_x^2}}\right),\hfill & i={\displaystyle \frac{N_x}{2}}+1,\dots ,N_x,\hfill \end{array}\right.$$

From the definition of $x_i$, we denote the space mesh size $h_i$ as follows:

$$h_i=\left\{\begin{array}{cc}H={\displaystyle \frac{2(1-\sigma )}{N_x}},\hfill & i=1,\dots ,{\displaystyle \frac{N_x}{2}},\hfill \\ h=x_i-x_{i-1},\hfill & i={\displaystyle \frac{N_x}{2}}+1,\dots ,N_x.\hfill \end{array}\right.$$

The analysis has been carried out by assuming that $\sigma ={\displaystyle \frac{{\sigma }_0{c}_{\epsilon }}{\gamma }}ln{N}_x$; otherwise, $N_x$ is exponentially large compared to $c_{\epsilon }$. It is clear from the above equation that $N_x^{-1}\le H\le 2N_x^{-1},h={\displaystyle \frac{2{\sigma }_0}{\gamma }}{c}_{\epsilon }{N}_x^{-1}ln{N}_x$, and the uniform mesh can be obtained by choosing $\sigma =1/2$. We define the discretized domain $D^{N_x,N_t}={\wedge }_x^{N_x}\times {\wedge }_t^{N_t}$. Before formulating the numerical method, we introduce the difference operators for a given mesh function $v(x_i,t_n)=v_i^n$ as follows:

$$\begin{array}{c}\hfill {\delta }_x^{+}{v}_i^n={\displaystyle \frac{v_{i+1}^n-v_i^n}{h_i}},{\delta }_x^{-}{v}_i^n={\displaystyle \frac{v_i^n-v_{i-1}^n}{h_{i-1}}},{\delta }_x^0{v}_i^n={\displaystyle \frac{v_{i+1}^n-v_{i-1}^n}{h_i+h_{i-1}}},\\ \hfill {\delta }_x^2{v}_i^n={\displaystyle \frac{({\delta }_x^{+}{v}_i^n-{\delta }_x^{-}{v}_i^n)}{{\tilde{h}}_i}}{\delta }_t^{-}{v}_i^n={\displaystyle \frac{v_i^n-v_i^{n-1}}{\kappa }},\end{array}$$

where ${\tilde{h}}_i:=(h_i+h_{i-1})/2,i=1,\dots ,N$. Now, we discretize (8) and (9) in the space direction by means of a hybrid numerical scheme on a Shishkin-type mesh, where we use the central difference scheme in the boundary layer region and the midpoint upwind scheme [40] in the outer region. Let the fully discrete approximation be denoted as $Z_i^{n+1}$ for the semi-discrete form ${\widehat{z}}^{n+1}\left(x\right)$. The totally discrete numerical scheme now takes the following form:

$${\delta }_t^{-}{Z}_i^{n+1}+{\displaystyle \frac{1}{2}}\left({\mathcal{L}}_{hyb}^{N_x,N_t}{Z}_i^n+{\mathcal{L}}_{hyb}^{N_x,N_t}{Z}_i^{n+1}\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}\left(f_{i-{\displaystyle \frac{1}{2}}}^n+f_{i-{\displaystyle \frac{1}{2}}}^{n+1}\right),\hfill & 0<i\le {\displaystyle \frac{N_x}{2}},\hfill \\ {\displaystyle \frac{1}{2}}\left(f_i^n+f_i^{n+1}\right),\hfill & {\displaystyle \frac{N_x}{2}}<i<N_x,\hfill \end{array}\right.$$

Multiplying both sides of the above equation by 2, we obtain

$$\left(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t}\right)Z_i^{n+1}=\left\{\begin{array}{cc}{f}_{i-{\displaystyle \frac{1}{2}}}^n+f_{i-{\displaystyle \frac{1}{2}}}^{n+1}-{\mathcal{L}}_{hyb}^{N_x,N_t}{Z}_i^n,\hfill & 0<i\le {\displaystyle \frac{N_x}{2}},\hfill \\ f_i^n+f_i^{n+1}-{\mathcal{L}}_{hyb}^{N_x,N_t}{Z}_i^n,\hfill & {\displaystyle \frac{N_x}{2}}<i<N_x,\hfill \end{array}\right.$$

(17)

where

$${\mathcal{L}}_{hyb}^{N_x,N_t}{Z}_i^{n+1}=\left\{\begin{array}{c}\begin{array}{cc}\hfill {\mathcal{L}}_{mup}^{N_x,N_t}{Z}_i^{n+1}& =-c_{i-{\displaystyle \frac{1}{2}}}{\delta }_x^2{Z}_i^{n+1}+p_{i-{\displaystyle \frac{1}{2}}}{\delta }_x^{-}{Z}_i^{n+1}+q_{i-{\displaystyle \frac{1}{2}}}{Z}_{i-{\displaystyle \frac{1}{2}}}^{n+1},0<i\le {\displaystyle \frac{N_x}{2}},\hfill \\ \hfill {\mathcal{L}}_{cen}^{N_x,N_t}{Z}_i^{n+1}& =-c_i{\delta }_x^2{Z}_i^{n+1}+p_i{\delta }_x^0{Z}_i^{n+1}+q_i{Z}_i^{n+1},{\displaystyle \frac{N_x}{2}}<i<N_x,\hfill \end{array}\hfill \end{array}\right.$$

with the following discrete conditions:

$$\left\{\begin{array}{cc}{Z}_i^0={\varphi }_i,\hfill & 1\le i\le N_x-1,\hfill \\ Z_0^{n+1}={\psi }^{n+1},Z_N^{n+1}={\phi }^{n+1},\hfill & 1\le n\le N_t-1.\hfill \end{array}\right.$$

(18)

Equation (17) can be written as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\mathcal{L}}_{mup}^{N_x,N_t}& \equiv -c_{i-{\displaystyle \frac{1}{2}}}{\delta }_x^2{Z}_i^{n+1}+p_{i-{\displaystyle \frac{1}{2}}}{\delta }_x^{-}{Z}_i^{n+1}+q_{i-{\displaystyle \frac{1}{2}}}{Z}_{i-{\displaystyle \frac{1}{2}}}^{n+1}=c_{i-{\displaystyle \frac{1}{2}}}{\delta }_x^2{Z}_i^n\hfill \\ & -p_{i-{\displaystyle \frac{1}{2}}}{\delta }_x^{-}{Z}_i^n-r_{i-{\displaystyle \frac{1}{2}}}{Z}_{i-{\displaystyle \frac{1}{2}}}^n+f_{i-{\displaystyle \frac{1}{2}}}^{n+1}+f_{i-{\displaystyle \frac{1}{2}}}^n,0<i\le {\displaystyle \frac{N_x}{2}},\hfill \\ \hfill {\mathcal{L}}_{cen}^{N_x,N_t}& \equiv -c_i{\delta }_x^2{Z}_i^{n+1}+p_i{\delta }_x^0{Z}_i^{n+1}+q_i{Z}_i^{n+1}=c_i{\delta }_x^2{Z}_i^n-p_i{\delta }_x^0{Z}_i^n-r_i{Z}_i^n\hfill \\ & +f_i^{n+1}+f_i^n,{\displaystyle \frac{N_x}{2}}<i<N_x.\hfill \end{array}\hfill \end{array}\right.$$

(19)

Equation (19) yields the following tridiagonal system of equations:

$$A^{-}{Z}_{i-1}^{n+1}+A^0{Z}_i^{n+1}+A^{+}{Z}_{i+1}^{n+1}=g_i^n,i=1,2,\dots ,N_x-1,$$

(20)

with the discrete conditions in (18) and where the coefficients for $0<i<{\displaystyle \frac{N_x}{2}}$ are given by

$$\begin{array}{cc}\hfill A_{mup}^{-}& ={\displaystyle \frac{-2c_{i-\frac{1}{2}}}{h_{i-1}(h_i+h_{i-1})}}-{\displaystyle \frac{p_{i-\frac{1}{2}}}{h_{i-1}}}+{\displaystyle \frac{q_{i-\frac{1}{2}}}{2}},A_{mup}^0={\displaystyle \frac{2c_{i-\frac{1}{2}}}{h_i{h}_{i-1}}}+{\displaystyle \frac{p_{i-\frac{1}{2}}}{h_{i-1}}}+{\displaystyle \frac{q_{i-\frac{1}{2}}}{2}}\hfill \\ \hfill B_{mup}^{-}& ={\displaystyle \frac{2c_{i-\frac{1}{2}}}{h_{i-1}(h_i+h_{i-1})}}+{\displaystyle \frac{p_{i-\frac{1}{2}}}{h_{i-1}}}-{\displaystyle \frac{r_{i-\frac{1}{2}}}{2}},B_{mup}^0={\displaystyle \frac{-2c_{i-\frac{1}{2}}}{h_i{h}_{i-1}}}-{\displaystyle \frac{p_{i-\frac{1}{2}}}{h_{i-1}}}-{\displaystyle \frac{r_{i-\frac{1}{2}}}{2}},\hfill \\ \hfill A_{mup}^{+}& ={\displaystyle \frac{-2c_{i-\frac{1}{2}}}{h_i(h_i+h_{i-1})}},B_{mup}^{+}={\displaystyle \frac{2c_{i-\frac{1}{2}}}{h_i(h_i+h_{i-1})}},\hfill \end{array}$$

(21)

and the coefficients for ${\displaystyle \frac{N_x}{2}}\le i<N_x$ are given by

$$\begin{array}{cc}\hfill A_{cen}^{-}& ={\displaystyle \frac{-2c_i}{h_{i-1}(h_i+h_{i-1})}}-{\displaystyle \frac{p_i}{h_i+h_{i-1}}},B_{cen}^{-}={\displaystyle \frac{2c_i}{h_{i-1}(h_i+h_{i-1})}}+{\displaystyle \frac{p_i}{h_i+h_{i-1}}},\hfill \\ \hfill A_{cen}^0& ={\displaystyle \frac{2c_i}{h_i{h}_{i+1}}}+q_i,B_{cen}^0={\displaystyle \frac{-2c_i}{h_i{h}_{i+1}}}-r_i,\hfill \\ \hfill A_{cen}^{+}& ={\displaystyle \frac{-2c_i}{h_i(h_i+h_{i-1})}}+{\displaystyle \frac{p_i}{h_{i-1}+h_i}},B_{cen}^{+}={\displaystyle \frac{2c_i}{h_i(h_i+h_{i-1})}}-{\displaystyle \frac{p_i}{h_{i-1}+h_i}},\hfill \end{array}$$

(22)

The right-hand side is given by

$$g_i^n=\left\{\begin{array}{c}{B}_{mup}^{-}{Z}_{i-1}^n+B_{mup}^0{Z}_i^n+B_{mup}^{+}{Z}_{i+1}^n+f_{i-{\displaystyle \frac{1}{2}}}^{n+1}+f_{i-{\displaystyle \frac{1}{2}}}^n,\hfill \\ B_{cen}^{-}{Z}_{i-1}^n+B_{cen}^0{Z}_i^n+B_{cen}^{+}{Z}_{i+1}^n+f_i^{n+1}+f_i^n.\hfill \end{array}\right.$$

We used the following notations: $p_i=p\left(x_i\right),p_{i-{\displaystyle \frac{1}{2}}}={\displaystyle \frac{p_i+p_{i-1}}{2}},q_i=q\left(x_i\right),q_{i-{\displaystyle \frac{1}{2}}}={\displaystyle \frac{q_i+q_{i-1}}{2}},r_i=r\left(x_i\right),r_{i-{\displaystyle \frac{1}{2}}}={\displaystyle \frac{r_i+r_{i-1}}{2}}.$ The coefficient matrix of the discrete scheme in (20) with the discrete boundary conditions in (18) gives $(N_x-1)\times (N_x-1)$ linear equations. The coefficient matrix at each time level is diagonally dominant and satisfies the M-matrix criterion. We use the Thomas algorithm to solve the linear equations since the matrix inversion method of solving the linear equations is sensitive to round-off errors.

4. Convergence Analysis

In this section, the stability of the present method is discussed, and, by using the truncation error, we obtain the parameter-uniform error estimate. The tridiagonal systems in (18) and (20) have the following properties. Suppose ${\sigma }_0{\parallel p\parallel }_{\infty }<{\displaystyle \frac{N_x}{ln{N}_x}}$ and $\gamma N_x\ge {(\parallel b\parallel }_{\infty }+{\kappa }^{-1})$; then, we have

$$\left\{\begin{array}{cc}{A}_{cen,i}^{-}<0,A_{cen,i}^{+}<0,A_{mup,i}^{-}<0,A_{mup,i}^{+}<0,\hfill & 1\le i\le N_x-1,\hfill \\ \left|r_{cen,1}^{+}\right|<\left|r_{cen,1}^c\right|,\left|A_{cen,i}^{-}\right|+\left|A_{cen,i}^{+}\right|<|A_{cen,i}^c|,\hfill & 1\le i\le N_x/2,\hfill \\ \left|r_{mup,N-1}^{-}\right|<\left|r_{mup,N-1}^c\right|,\left|A_{mup,i}^{-}\right|+\left|A_{mup,i}^{+}\right|<\left|A_{mup,i}^c\right|,\hfill & N_x/2<i<N_x.\hfill \end{array}\right.$$

The M-matrix properties are thus satisfied by the tridiagonal matrix in (20). The solution Z of (17) can be decomposed into the regular and singular components R and S, respectively, where $Z=R+S$ and R is the solution of the following non-homogeneous problem on $(x_i,t_n)\in D$:

$$\begin{array}{cc}\hfill \left(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t}\right)R_i^n& =\left\{\begin{array}{cc}{f}_{i-{\displaystyle \frac{1}{2}}}^n+f_{i-{\displaystyle \frac{1}{2}}}^{n+1}-{\mathcal{L}}_{hyb}^{N_x,N_t}{R}_i^n,\hfill & 0<i\le {\displaystyle \frac{N_x}{2}},\hfill \\ f_i^n+f_i^{n+1}-{\mathcal{L}}_{hyb}^{N_x,N_t}{R}_i^n,\hfill & {\displaystyle \frac{N_x}{2}}<i<N_x,\hfill \end{array}\right.\hfill \\ \hfill R_0^n& =r(0,t_n),R_N^n=r(1,t_n),t_n\in {\wedge }_t^{N_t},\hfill \\ \hfill R_i^n& =Z(x_i,t_n),(x_i,t_n)\in D,\hfill \end{array}$$

(23)

and S satisfies

$$\begin{array}{cc}\hfill \left(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t}\right)S_i^n& =\left\{\begin{array}{cc}-{\mathcal{L}}_{hyb}^{N_x,N_t}{S}_i^n,\hfill & 0<i\le {\displaystyle \frac{N_x}{2}},\hfill \\ -{\mathcal{L}}_{hyb}^{N_x,N_t}{S}_i^n,\hfill & {\displaystyle \frac{N_x}{2}}<i<N_x,\hfill \end{array}\right.\hfill \\ \hfill S_0^n& =\psi \left(t_n\right)-r(0,t_n),S_N^n=\phi \left(t_n\right)-r(1,t_n),t_n\in {\wedge }_t^{N_t},\hfill \\ \hfill S_i^n& =0,(x_i,t_n)\in D,\hfill \end{array}$$

(24)

where ${\mathcal{L}}_{hyb}^{N_x,N_t}{R}_i^n$ is defined in the form

$${\mathcal{L}}_{hyb}^{N_x,N_t}{R}_i^n=\left\{\begin{array}{cc}{\mathcal{L}}_{mup}^{N_x,N_t}{R}_i^n,\hfill & \mathrm{for}1\le i\le N/2,\hfill \\ {\mathcal{L}}_{cen}^{N_x,N_t}{R}_i^n,\hfill & \mathrm{for}N/2<i<N_x.\hfill \end{array}\right.$$

Similarly, ${\mathcal{L}}_{hyb}^{N_x,N_t}{S}_i^n$ is defined in the form above. The error can be written in the form

$$|Z_i^n-z(x_i,t_n)|\le |R_i^n-r(x_i,t_n)|+|S_i^n-s(x_i,t_n)|.$$

(25)

The error for the singular and regular components may now be estimated independently.

Theorem 4. 

The error bound in the regular component for the Shishkin mesh is given by

$$|R_i^n-r(x_i,t_n)|\le \left\{\begin{array}{cc}C(N_x^{-1}(\epsilon +N_x^{-1})+{\kappa }^2),\hfill & \mathrm{for}1\le i\le N_x/2,\hfill \\ C(N_x^{-2}+{\kappa }^2),\hfill & \mathrm{for}{N}_x/2<i\le N_x-1,\hfill \end{array}\right.$$

and, for the Bakhvalov–Shishkin mesh, is given by

$$|R_i^n-r(x_i,t_n)|\le C(N_x^{-2}+{\kappa }^2),\mathrm{for}1\le i\le N_x-1.$$

Proof of Theorem 4. 

The truncation error for the regular component can be expressed as follows:

$$(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)=\left\{\begin{array}{cc}{f}_{i-{\displaystyle \frac{1}{2}}}^n+f_{i-{\displaystyle \frac{1}{2}}}^{n+1}-\left(2{\delta }_t^{-}+{\mathcal{L}}_{mup}^{N_x,N_t}\right)r_{i-{\displaystyle \frac{1}{2}}}^n-{\mathcal{L}}_{mup}^{N_x,N_t}{R}_{i-{\displaystyle \frac{1}{2}}}^{n+1},\hfill & \\ \mathrm{for}i\le {\displaystyle \frac{N_x}{2}},\hfill \\ f_i^n+f_i^{n+1}-\left(2{\delta }_t^{-}+{\mathcal{L}}_{cen}^{N_x,N_t}\right)r_i^n-{\mathcal{L}}_{cen}^{N_x,N_t}{R}_i^{n+1},\hfill & \\ \mathrm{for}i>{\displaystyle \frac{N_x}{2}},\hfill \end{array}\right.$$

(26)

for $(x_i,t_n)\in D$. Firstly, considering the case (i.e., $i>{\displaystyle \frac{N_x}{2}}$), from (26), we have

$$\begin{array}{cc}\hfill (2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)& =\left({\displaystyle \frac{\partial }{\partial t}}+{\mathcal{L}}^{N_x,N_t}\right)r(x_i,t_n)-(2{\delta }_t^{-}+{\mathcal{L}}_{cen}^{N_x,N_t})r(x_i,t_n)\hfill \\ & +\left({\displaystyle \frac{\partial }{\partial t}}+{\mathcal{L}}^{N_x,N_t}\right)r(x_i,t_{n+1})-{\mathcal{L}}_{cen}^{N_x,N_t}r(x_i,t_{n+1}),\hfill \end{array}$$

Rearranging the terms in the above equation, we have

$$\begin{array}{cc}\hfill (2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)& =({\mathcal{L}}^{N_x,N_t}-{\mathcal{L}}_{cen}^{N_x,N_t})r_i^n+({\mathcal{L}}^{N_x,N_t}-{\mathcal{L}}_{cen}^{N_x,N_t})r_i^{n+1}\hfill \\ & +\left({\displaystyle \frac{\partial }{\partial t}}-2{\delta }_t^{-}\right)r(x_i,t_n)+{\displaystyle \frac{\partial r(x_i,t_{n+1})}{\partial t}}.\hfill \end{array}$$

(27)

Using the Taylor series expansion for the last two terms in (27) and applying the modulus, we obtain

$$|\left({\displaystyle \frac{\partial }{\partial t}}-2{\delta }_t^{-}\right)r(x_i,t_n)+{\displaystyle \frac{\partial r(x_i,t_{n+1})}{\partial t}}|\le {\displaystyle \frac{{\kappa }^2}{12}}\parallel {\displaystyle \frac{{\partial }^{3}r}{\partial t^3}}\parallel .$$

(28)

The Taylor series expansion for the first two terms in (27), together with the triangular inequality and the estimate in (28), yields

$$\begin{array}{cc}\hfill |(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)|& \le C[N_x^{-2}+{\kappa }^2+h_i(h_{i-1}+h_i)\left(c_{\epsilon }\parallel {\displaystyle \frac{{\partial }^{4}r}{\partial x^4}}\parallel +\parallel {\displaystyle \frac{{\partial }^{3}r}{\partial x^3}}\parallel \right)\hfill \\ & +{\displaystyle \frac{{\kappa }^2}{12}}\parallel {\displaystyle \frac{{\partial }^{3}r}{\partial t^3}}\parallel ],\hfill \end{array}$$

(29)

for $(x_i,t_n)\in D$. Using Lemma 7 and the fact that $h_i\le 2N^{-1},h_i+h_{i-1}\le 4N^{-1}$, we obtain

$$|(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)|\le C(N_x^{-2}+{\kappa }^2),(x_i,t_n)\in D.$$

(30)

Since the discrete maximum principle is satisfied by the operator $(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)$, the inequality in (30) simplifies to

$$\left|(R-r)\right|\le C(N_x^{-2}+{\kappa }^2),(x_i,t_n)\in D,$$

(31)

on the Shishkin mesh. Using the same manner and the fact that $N_x^{-2}{ln}^2{N}_x\le N_x^{-2}$, we can obtain the following bound:

$$\left|(R-r)\right|\le C(N_x^{-2}+{\kappa }^2),(x_i,t_n)\in D,$$

(32)

on the Bakhvalov–Shishkin mesh. Secondly, considering the case (i.e., $i\le {\displaystyle \frac{N_x}{2}}$), from (26), we have

$$\begin{array}{cc}\hfill (2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)& =\left({\displaystyle \frac{\partial }{\partial t}}+{\mathcal{L}}^{N_x,N_t}\right)r(x_i,t_n)-(2{\delta }_t^{-}+{\mathcal{L}}_{mup}^{N_x,N_t})r(x_i,t_n)\hfill \\ & +\left({\displaystyle \frac{\partial }{\partial t}}+{\mathcal{L}}^{N_x,N_t}\right)r(x_i,t_{n+1})-{\mathcal{L}}_{mup}^{N_x,N_t}r(x_i,t_{n+1}),\hfill \end{array}$$

Using the same method of analysis as used for $i>{\displaystyle \frac{N_x}{2}}$ and using Lemma 7 for the derivatives

$$\begin{array}{cc}\hfill |(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)|& \le C[N_x^{-1}(c_{\epsilon }+N_x^{-1})+{\kappa }^2+(c_{\epsilon }+h_i)(h_{i-1}+h_i)\parallel {\displaystyle \frac{{\partial }^{3}r}{\partial x^3}}\parallel \hfill \\ & +h_i^2\left(\parallel {\displaystyle \frac{{\partial }^{2}r}{\partial x^2}}\parallel +\parallel {\displaystyle \frac{\partial r}{\partial x}}\parallel \right)+{\displaystyle \frac{{\kappa }^2}{12}}\parallel {\displaystyle \frac{{\partial }^{3}r}{\partial t^3}}\parallel ],\hfill \end{array}$$

(33)

for $(x_i,t_n)\in D$. Using Lemma 7 and the fact that $h_i\le 2N^{-1},h_i+h_{i-1}\le 4N^{-1}$, we obtain

$$|(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)|\le C(N_x^{-1}(c_{\epsilon }+N_x^{-1})+{\kappa }^2),(x_i,t_n)\in D.$$

(34)

Since the operator $(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(R-r)$ satisfies the discrete maximum principle, the inequality in (34) reduces to

$$\left|(R-r)\right|\le C(N_x^{-1}(c_{\epsilon }+N_x^{-1})+{\kappa }^2),(x_i,t_n)\in D,$$

(35)

on the Shishkin mesh. Continuing in the same manner and using the fact that $c_{\epsilon }\le N_x^{-1}$ , we can obtain the following bound

$$\left|(R-r)\right|\le C(N_x^{-2}+{\kappa }^2),(x_i,t_n)\in D,$$

(36)

on the Bakhvalov–Shishkin mesh. □

Theorem 5. 

The error bound in the singular component for the Shishkin mesh is given by

$$|R_i^n-r(x_i,t_n)|\le \left\{\begin{array}{cc}C(N_x^{-1}(\epsilon +N_x^{-1})+{\kappa }^2),\hfill & for1\le i\le N_x/2,\hfill \\ C(N_x^{-2}{ln}^2{N}_x+{\kappa }^2),\hfill & for{N}_x/2<i\le N_x-1,\hfill \end{array}\right.$$

and, for the Bakhvalov–Shishkin mesh, is given by

$$|R_i^n-r(x_i,t_n)|\le C(N_x^{-2}+{\kappa }^2),for1\le i\le N_x-1,$$

Proof of Theorem 5. 

Using the continuous solution decomposition in (16) and the difference equation in (24), we derive the error bound for the singular component as

$$(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(S-s)=\left\{\begin{array}{c}\left({\displaystyle \frac{\partial }{\partial t}}-{\delta }_t^{-}\right)s_{i-{\displaystyle \frac{1}{2}}}^n+({\mathcal{L}}^{N_x,N_t}-{\mathcal{L}}_{mup}^{N_x,N_t})s_{i-{\displaystyle \frac{1}{2}}}^n\hfill \\ +{\displaystyle \frac{\partial s}{\partial t}}(x_{i-{\displaystyle \frac{1}{2}}},t_{n+1})+{\mathcal{L}}_{mup}^{N_x,N_t}{S}_{i-{\displaystyle \frac{1}{2}}}^{n+1},i\le {\displaystyle \frac{N_x}{2}},\hfill \\ \left({\displaystyle \frac{\partial }{\partial t}}+{\mathcal{L}}^{N_x,N_t}\right)s(x_i,t_n)-(2{\delta }_t^{-}+{\mathcal{L}}_{cen}^{N_x,N_t})s(x_i,t_n)\hfill \\ +\left({\displaystyle \frac{\partial }{\partial t}}+{\mathcal{L}}^{N_x,N_t}\right)s(x_i,t_{n+1}),i>{\displaystyle \frac{N_x}{2}},\hfill \end{array}\right.$$

(37)

As done in [40], the right-hand side of (37) could possibly represent the truncation error of the two boundary value problems by fixing t. As a result, we obtain

$$\left|(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(S-s)\right|\le \left\{\begin{array}{cc}C(N_x^{-1}(\epsilon +N_x^{-1})+{\kappa }^2),\hfill & \mathrm{for}i\le {\displaystyle \frac{N_x}{2}},\hfill \\ C(N_x^{-2}{ln}^2{N}_x+{\kappa }^2),\hfill & \mathrm{for}i>{\displaystyle \frac{N_x}{2}},\hfill \end{array}\right.$$

(38)

for $(x_i,t_n)\in D$. Using the fact that the discrete operator $|(2{\delta }_t^{-}+{\mathcal{L}}_{hyb}^{N_x,N_t})(S-s)|$ satisfies the discrete maximum principle and the inverse operator is uniformly bounded, it immediately follows that (38) becomes

$$\left|(S-s)(x_i,t_n)\right|\le \left\{\begin{array}{cc}C(N_x^{-1}(\epsilon +N_x^{-1})+{\kappa }^2),\hfill & \mathrm{for}i\le {\displaystyle \frac{N_x}{2}},\hfill \\ C(N_x^{-2}{ln}^2{N}_x+{\kappa }^2),\hfill & \mathrm{for}i>{\displaystyle \frac{N_x}{2}},\hfill \end{array}\right.$$

(39)

for the Shishkin mesh. Following a similar pattern and using the fact that $c_{\epsilon }\le N_x^{-1}$ and $N_x^{-2}{ln}^2{N}_x\le N_x^{-2}$, we can obtain the following bound

$$\left|(S-s)\right|\le C(N_x^{-2}+{\kappa }^2),(x_i,t_n)\in D,$$

(40)

for the Bakhvalov–Shishkin mesh. Putting (31), (35), and (39) in (25) completes the proof of the error bound for the Shishkin mesh. The proof of the error bound for the Bakhvalov–Shishkin mesh is completed using (32), (36), and (40) in (25). □

The main result of our studies is the parameter-uniform convergence of the numerical solution, which is addressed by the following theorem.

Theorem 6. 

Let z the continuous solution in (5)–(7) and Z be the corresponding numerical solution of the fully discrete problem in (18). Then, the parameter-uniform error bound associated with the Shishkin mesh satisfies

$$\underset{i,n}{max}|z(x_i,t_n)-Z_i^n|\le \left\{\begin{array}{c}C(N_x^{-1}(\epsilon +N_x^{-1})+{\kappa }^2),for1\le i\le N_x/2,\hfill \\ C(N_x^{-2}{ln}^2{N}_x+{\kappa }^2),for{N}_x/2<i\le N_x-1,\hfill \end{array}\right.$$

and the parameter-uniform error bound satisfied by the Bakhvalov–Shishkin mesh is

$$\underset{i,n}{max}|z(x_i,t_n)-Z_i^n|\le C(N_x^{-2}+{\kappa }^2),for1\le i\le N_x-1,$$

Proof of Theorem 6. 

The proof immediately follows from Theorems 4 and 5. □

5. Numerical Computations and Discussion

In this section, we carry out numerical computations to corroborate the performance of the present method with the theoretical results discussed in the previous sections.

Example 1. 

Consider a singularly perturbed parabolic problem [35]

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial z}{\partial t}}-\epsilon {\displaystyle \frac{{\partial }^{2}z}{\partial x^2}}+(2-x^2){\displaystyle \frac{\partial z(x-\mu ,t)}{\partial x}}+(x^2+1+cos\left(\pi x\right))z(x-\mu ,t)=10t^2(1-x)e^{-t},\hfill \\ (x,t)\in [0,1]\times [0,1],\hfill \\ \left\{\begin{array}{cc}z(x,0)=0,\hfill & 0\le x\le 1\hfill \\ z(x,t)=0,\mu \le x\le 0,z(1,t)=0,\hfill & 0\le t\le 1.\hfill \end{array}\right.\hfill \end{array}\right.$$

Example 2. 

Consider a singularly perturbed parabolic problem [35]

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial z}{\partial t}}-\epsilon {\displaystyle \frac{{\partial }^{2}z}{\partial x^2}}+(2-x^2){\displaystyle \frac{\partial z(x-\mu ,t)}{\partial x}}+(3-x)z(x-\mu ,t)=sin\left(\pi x(1-x)\right)e^t,\hfill \\ (x,t)\in [0,1]\times [0,1],\hfill \\ \left\{\begin{array}{cc}z(x,0)=0,\hfill & 0\le x\le 1\hfill \\ z(x,t)=0,\mu \le x\le 0,z(1,t)=0,\hfill & 0\le t\le 1.\hfill \end{array}\right.\hfill \end{array}\right.$$

Since the exact solutions for the Examples 1 and 2 are not available, we use the following double mesh principle to calculate the maximum absolute errors for each $(\epsilon ,\mu )$ as

$$e_{\epsilon ,\mu }^{N_x,N_t}=\underset{0\le i\le N_x;0\le n\le N_t}{max}|Z^{N_x,N_t}(x_i,t_n)-Z^{2N_x,2N_t}(x_i,t_n)|,$$

(41)

where $Z^{N_x,N_t}$ is the numerical solution with $(N_x,N_t)$ mesh points and $Z^{2N_x,2N_t}$ is the numerical solution at the finer mesh with $(2N_x,2N_t)$ mesh points. The following formula is used to calculate $(\epsilon ,\mu )$-maximum errors:

$$e^{N_x,N_t}=\underset{\epsilon ,\mu }{max}{e}_{\epsilon ,\mu }^{N_x,N_t}.$$

(42)

Furthermore, the numerical rate of convergence is computed by

$${\rho }_{\epsilon ,\mu }^{N_x,N_t}={log}_2\left({\displaystyle \frac{e_{\epsilon ,\mu }^{N_x,N_t}}{e_{\epsilon ,\mu }^{2N_x,2N_t}}}\right).$$

(43)

The $(\epsilon ,\mu )$–maximum rates of convergence are calculated using

$${\rho }^{N_x,N_t}=\underset{\epsilon ,\mu }{max}{\rho }_{\epsilon ,\mu }^{N_x,N_t}.$$

(44)

To investigate the effect of small negative shifts on numerical solutions and the practicality of the present method, we considered the singularly perturbed parabolic problem without small negative shifts. In this scenario, replacing $c_{\epsilon }$ by $\epsilon$ with $\mu =0$ is the same for the continuous problem, formulation of numerical method, and convergence analysis.

Example 3. 

Consider a singularly perturbed parabolic problem [39]

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial z}{\partial t}}-\epsilon {\displaystyle \frac{{\partial }^{2}z}{\partial x^2}}+\left(1+x^2+{\displaystyle \frac{1}{2}}sin\left(\pi x\right)\right){\displaystyle \frac{\partial z}{\partial x}}+\left(1+x^2+sin\left({\displaystyle \frac{\pi t}{2}}\right)\right)z\hfill \\ =x^3{(1-x)}^3+t(1-t)sin\left(\pi t\right),(x,t)\in [0,1]\times [0,1],\hfill \\ \left\{\begin{array}{cc}z(x,0)=0,\hfill & 0\le x\le 1\hfill \\ z(0,t)=0,z(1,t)=0,\hfill & 0\le t\le 1.\hfill \end{array}\right.\hfill \end{array}\right.$$

Since the exact solution for Example 3 is not given, we use the formulas (41)–(44) to calculate the maximum errors and rate of convergence.

Example 4. 

Consider a singularly perturbed parabolic problem [38]

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial z}{\partial t}}-\epsilon {\displaystyle \frac{{\partial }^{2}z}{\partial x^2}}+{\displaystyle \frac{\partial z}{\partial x}}=f(x,t),(x,t)\in [0,1]\times [0,1],\hfill \\ \left\{\begin{array}{cc}u(x,0)=u_0\left(x\right),\hfill & 0\le x\le 1\hfill \\ u(0,t)=0,u(1,t)=0,\hfill & 0\le t\le 1,\hfill \end{array}\right.\hfill \end{array}\right.$$

where the source function $f(x,t)=e^{-t}\left[-e^{-1/\epsilon }+(1-e^{-1/\epsilon })(1-x)+e^{-(1-x)/\epsilon }\right]$ and the initial function $u_0\left(x\right)=e^{-1/\epsilon }+(1-e^{-1/\epsilon })x-e^{-(1-x)/\epsilon }$ are chosen from the analytical solution given by

$$z(x,t)=e^{-t}\left[e^{-1/\epsilon }+(1-e^{-1/\epsilon })x-e^{-(1-x)/\epsilon }\right].$$

Since the exact solution for the Example 4 is available, the maximum absolute errors for each $(\epsilon ,\mu )$ are calculated as

$$e_{\epsilon ,\mu }^{N_x,N_t}=\underset{0\le i\le N_x;0\le n\le N_t}{max}|Z^{N_x,N_t}(x_i,t_n)-z^{N_x,N_t}(x_i,t_n)|,$$

(45)

where $Z^{N_x,N_t}$ is the numerical solution with $(N_x,N_t)$ mesh points and $z^{N_x,N_t}$ is the exact solution. Similarly, formulas in (42)–(44) are used.

Table 1. Computations of $e_{\epsilon ,\mu }^{N_x,N_t},e^{N_x,N_t}$, and ${\rho }^{N_x,N_t}$ using $N_x=N_t$, $\mu =0.5\epsilon$ for Example 1.

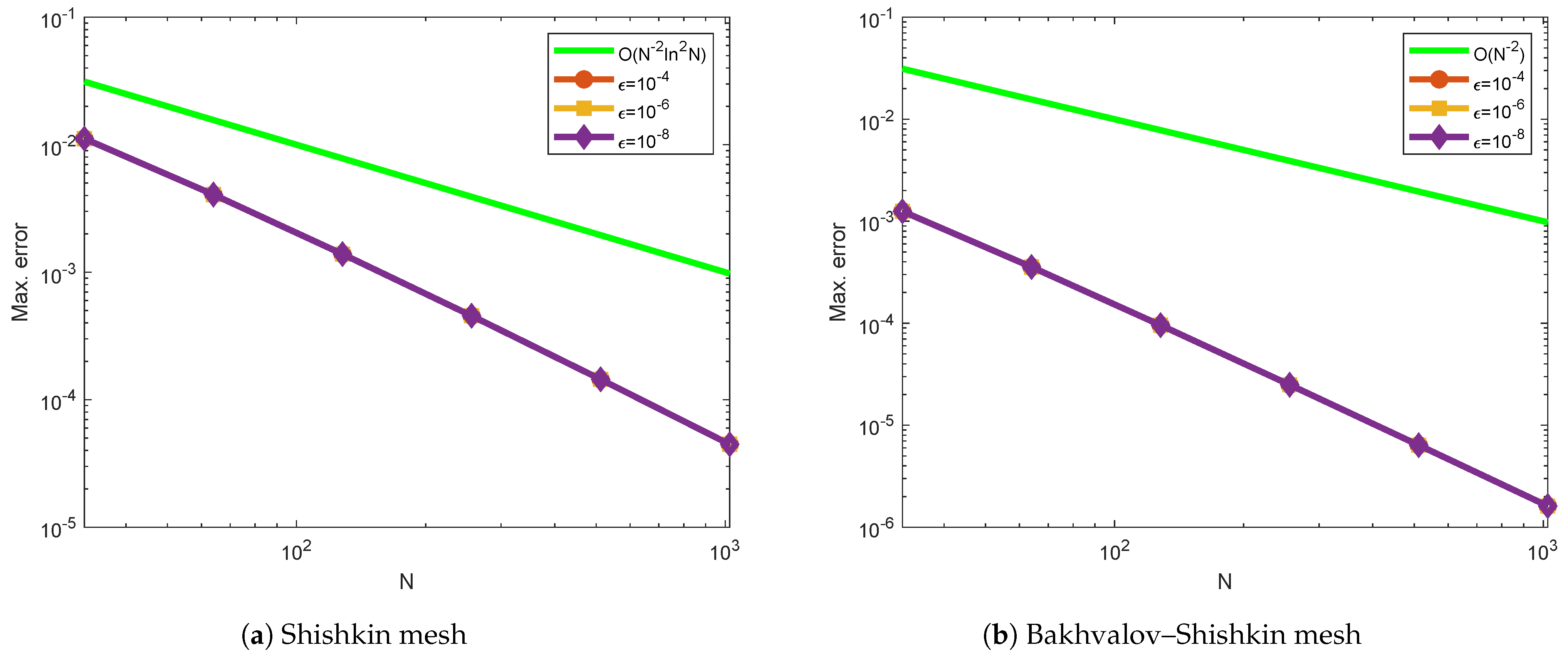
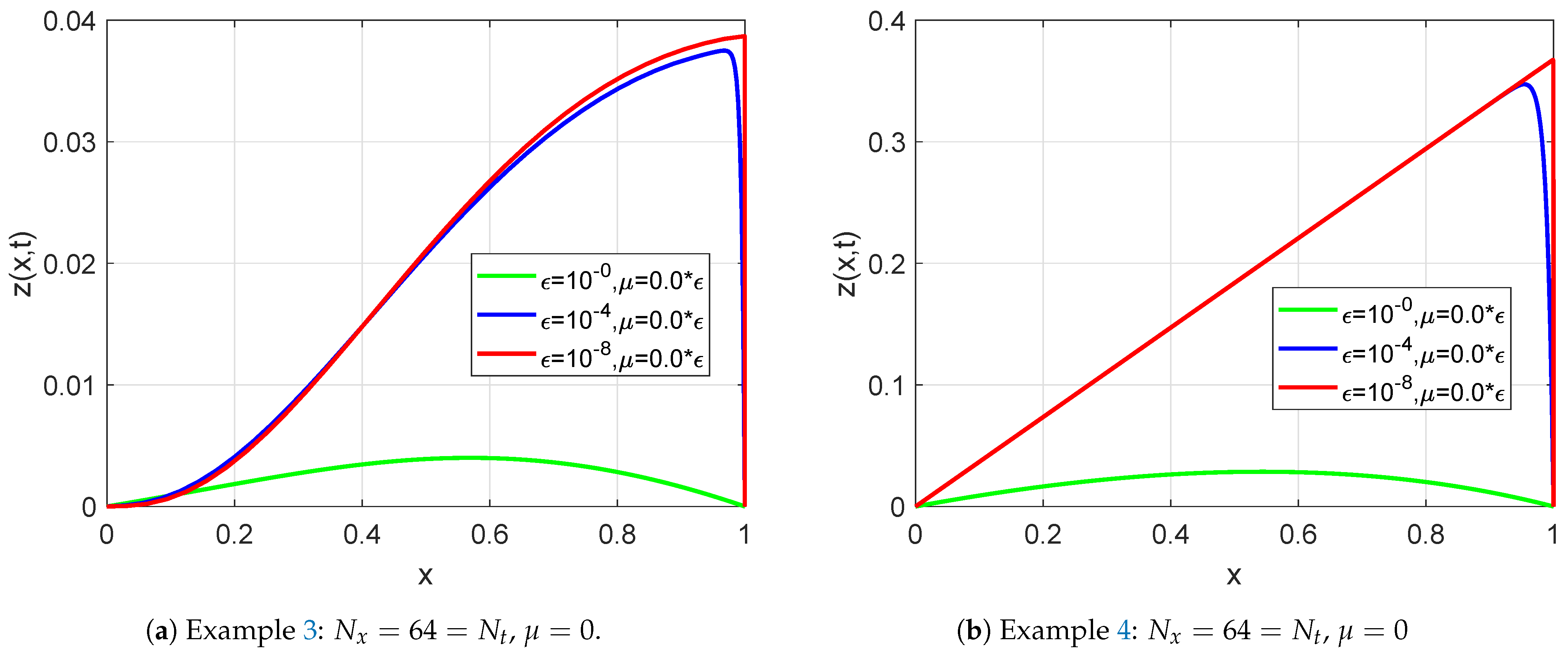
$\mathit{\epsilon }\downarrow$	${\mathit{N}}_{\mathit{x}}=32$	64	128	256	512	1024
Shishkin mesh
${10}^{-3}$	4.1184 $\times {10}^{-3}$	1.1994 $\times {10}^{-3}$	3.1433 $\times {10}^{-4}$	7.7236 $\times {10}^{-5}$	1.8156 $\times {10}^{-5}$	4.2266 $\times {10}^{-6}$
${10}^{-4}$	4.2975 $\times {10}^{-3}$	1.2828 $\times {10}^{-3}$	3.4791 $\times {10}^{-4}$	9.0082 $\times {10}^{-5}$	2.2718 $\times {10}^{-5}$	5.6105 $\times {10}^{-6}$
${10}^{-5}$	4.3151 $\times {10}^{-3}$	1.2911 $\times {10}^{-3}$	3.5133 $\times {10}^{-4}$	9.1473 $\times {10}^{-5}$	2.3310 $\times {10}^{-5}$	5.8734 $\times {10}^{-6}$
${10}^{-6}$	4.3169 $\times {10}^{-3}$	1.2919 $\times {10}^{-3}$	3.5167 $\times {10}^{-4}$	9.1611 $\times {10}^{-5}$	2.3368 $\times {10}^{-5}$	5.8994 $\times {10}^{-6}$
${10}^{-7}$	4.3171 $\times {10}^{-3}$	1.2920 $\times {10}^{-3}$	3.5170 $\times {10}^{-4}$	9.1625 $\times {10}^{-5}$	2.3374 $\times {10}^{-5}$	5.9020 $\times {10}^{-6}$
${10}^{-8}$	4.3171 $\times {10}^{-3}$	1.2920 $\times {10}^{-3}$	3.5171 $\times {10}^{-4}$	9.1626 $\times {10}^{-5}$	2.3374 $\times {10}^{-5}$	5.9023 $\times {10}^{-6}$
$e^{N_x,N_t}$	4.3171 $\times {10}^{-3}$	1.2920 $\times {10}^{-3}$	3.5171 $\times {10}^{-4}$	9.1627 $\times {10}^{-5}$	2.3375 $\times {10}^{-5}$	5.9023 $\times {10}^{-6}$
${\rho }^{N_x,N_t}$	1.7405	1.8771	1.9405	1.9708	1.9856
Bakhvalov–Shishkin mesh
${10}^{-3}$	3.6722 $\times {10}^{-3}$	1.0496 $\times {10}^{-3}$	2.6770 $\times {10}^{-4}$	6.0196 $\times {10}^{-5}$	1.0005 $\times {10}^{-5}$	1.0352 $\times {10}^{-6}$
${10}^{-4}$	3.8406 $\times {10}^{-3}$	1.1385 $\times {10}^{-3}$	3.0783 $\times {10}^{-4}$	7.9533 $\times {10}^{-5}$	1.9985 $\times {10}^{-5}$	4.8703 $\times {10}^{-6}$
${10}^{-5}$	3.8559 $\times {10}^{-3}$	1.1469 $\times {10}^{-3}$	3.1110 $\times {10}^{-4}$	8.0895 $\times {10}^{-5}$	2.0604 $\times {10}^{-5}$	5.1904 $\times {10}^{-6}$
${10}^{-6}$	3.8575 $\times {10}^{-3}$	1.1477 $\times {10}^{-3}$	3.1142 $\times {10}^{-4}$	8.1021 $\times {10}^{-5}$	2.0656 $\times {10}^{-5}$	5.2138 $\times {10}^{-6}$
${10}^{-7}$	3.8576 $\times {10}^{-3}$	1.1478 $\times {10}^{-3}$	3.1145 $\times {10}^{-4}$	8.1034 $\times {10}^{-5}$	2.0661 $\times {10}^{-5}$	5.2160 $\times {10}^{-6}$
${10}^{-8}$	3.8576 $\times {10}^{-3}$	1.1478 $\times {10}^{-3}$	3.1145 $\times {10}^{-4}$	8.1035 $\times {10}^{-5}$	2.0662 $\times {10}^{-5}$	5.2162 $\times {10}^{-6}$
$e^{N_x,N_t}$	3.8576 $\times {10}^{-3}$	1.1478 $\times {10}^{-3}$	3.1145 $\times {10}^{-4}$	8.1035 $\times {10}^{-5}$	2.0662 $\times {10}^{-5}$	5.2163 $\times {10}^{-6}$
${\rho }^{N_x,N_t}$	1.7488	1.8818	1.9424	1.9716	1.9859

and

Table 2. Computations of $e_{\epsilon ,\mu }^{N_x,N_t},e^{N_x,N_t}$, and ${\rho }^{N_x,N_t}$ using $N_x=N_t$, $\mu =0.5\epsilon$ for Example 2.

$\mathit{\epsilon }\downarrow$	${\mathit{N}}_{\mathit{x}}=32$	64	128	256	512	1024
Shishkin mesh
${10}^{-3}$	7.5337 $\times {10}^{-3}$	2.1534 $\times {10}^{-3}$	5.6966 $\times {10}^{-4}$	1.4486 $\times {10}^{-4}$	3.6710 $\times {10}^{-5}$	9.8759 $\times {10}^{-6}$
${10}^{-4}$	7.9721 $\times {10}^{-3}$	2.3169 $\times {10}^{-3}$	6.2460 $\times {10}^{-4}$	1.6187 $\times {10}^{-4}$	4.1060 $\times {10}^{-5}$	1.0279 $\times {10}^{-5}$
${10}^{-5}$	8.0169 $\times {10}^{-3}$	2.3337 $\times {10}^{-3}$	6.3042 $\times {10}^{-4}$	1.6384 $\times {10}^{-4}$	4.4378 $\times {10}^{-5}$	1.2296 $\times {10}^{-5}$
${10}^{-6}$	8.0214 $\times {10}^{-3}$	2.3354 $\times {10}^{-3}$	6.3100 $\times {10}^{-4}$	1.6404 $\times {10}^{-4}$	4.5584 $\times {10}^{-5}$	1.3293 $\times {10}^{-5}$
${10}^{-7}$	8.0219 $\times {10}^{-3}$	2.3356 $\times {10}^{-3}$	6.3106 $\times {10}^{-4}$	1.6406 $\times {10}^{-4}$	4.5721 $\times {10}^{-5}$	1.3430 $\times {10}^{-5}$
${10}^{-8}$	8.0219 $\times {10}^{-3}$	2.3356 $\times {10}^{-3}$	6.3107 $\times {10}^{-4}$	1.6406 $\times {10}^{-4}$	4.5735 $\times {10}^{-5}$	1.3444 $\times {10}^{-5}$
$e^{N_x,N_t}$	8.0219 $\times {10}^{-3}$	2.3356 $\times {10}^{-3}$	6.3107 $\times {10}^{-4}$	1.6406 $\times {10}^{-4}$	4.5736 $\times {10}^{-5}$	1.3446 $\times {10}^{-5}$
${\rho }^{N_x,N_t}$	1.7802	1.8879	1.9436	1.8428	1.7662
Bakhvalov–Shishkin mesh
${10}^{-3}$	7.1064 $\times {10}^{-3}$	2.0070 $\times {10}^{-3}$	5.1962 $\times {10}^{-4}$	1.2398 $\times {10}^{-4}$	2.5523 $\times {10}^{-5}$	1.1837 $\times {10}^{-6}$
${10}^{-4}$	7.5472 $\times {10}^{-3}$	2.1847 $\times {10}^{-3}$	5.8855 $\times {10}^{-4}$	1.5242 $\times {10}^{-4}$	3.8564 $\times {10}^{-5}$	9.7055 $\times {10}^{-6}$
${10}^{-5}$	7.5903 $\times {10}^{-3}$	2.2015 $\times {10}^{-3}$	5.9459 $\times {10}^{-4}$	1.5450 $\times {10}^{-4}$	4.2760 $\times {10}^{-5}$	1.1882 $\times {10}^{-5}$
${10}^{-6}$	7.5945 $\times {10}^{-3}$	2.2033 $\times {10}^{-3}$	5.9518 $\times {10}^{-4}$	1.5478 $\times {10}^{-4}$	4.3958 $\times {10}^{-5}$	1.2883 $\times {10}^{-5}$
${10}^{-7}$	7.5950 $\times {10}^{-3}$	2.2035 $\times {10}^{-3}$	5.9524 $\times {10}^{-4}$	1.5494 $\times {10}^{-4}$	4.4094 $\times {10}^{-5}$	1.3019 $\times {10}^{-5}$
${10}^{-8}$	7.5950 $\times {10}^{-3}$	2.2035 $\times {10}^{-3}$	5.9524 $\times {10}^{-4}$	1.5495 $\times {10}^{-4}$	4.4107 $\times {10}^{-5}$	1.3033 $\times {10}^{-5}$
$e^{N_x,N_t}$	7.5950 $\times {10}^{-3}$	2.2035 $\times {10}^{-3}$	5.9524 $\times {10}^{-4}$	1.5495 $\times {10}^{-4}$	4.4109 $\times {10}^{-5}$	1.3035 $\times {10}^{-5}$
${\rho }^{N_x,N_t}$	1.7853	1.8883	1.9417	1.8127	1.7587

indicate the generated maximum point-wise errors $e_{\epsilon ,\mu }^{N_x,N_t}$ and uniform errors $e^{N_x,N_t}$ for Examples 1 and 2, respectively.

Table 3. Comparison of $e^{N_x,N_t}$ and ${\rho }^{N_x,N_t}$ using $N_x=N_t$, $\mu =0.3\epsilon$ for Example 1.

	${\mathit{N}}_{\mathit{x}}=16$	32	64	128	256
Present result using Shishkin mesh
$e^{N_x,N_t}$	1.1780 $\times {10}^{-2}$	4.3171 $\times {10}^{-3}$	1.2920 $\times {10}^{-3}$	3.5171 $\times {10}^{-4}$	9.1626 $\times {10}^{-5}$
${\rho }^{N_x,N_t}$	1.4482	1.7405	1.8771	1.9406
Present result using Bakhvalov–Shishkin mesh
$e^{N_x,N_t}$	1.0698 $\times {10}^{-2}$	3.8576 $\times {10}^{-3}$	1.1478 $\times {10}^{-3}$	3.1145 $\times {10}^{-4}$	8.1035 $\times {10}^{-5}$
${\rho }^{N_x,N_t}$	1.4716	1.7488	1.8818	1.9424
Result in [35] Before Extrapolation
$e^{N_x,N_t}$	1.3567 $\times {10}^{-2}$	7.7535 $\times {10}^{-3}$	4.1434 $\times {10}^{-3}$	2.5115 $\times {10}^{-3}$	-
${\rho }^{N_x,N_t}$	0.8072	0.9040	0.7223
Result in [35] After Extrapolation
$e^{N_x,N_t}$	7.5907 $\times {10}^{-3}$	2.3678 $\times {10}^{-3}$	8.2018 $\times {10}^{-4}$	2.5398 $\times {10}^{-4}$	-
${\rho }^{N_x,N_t}$	1.6807	1.5295	1.6912

and

Table 4. Comparison of $e^{N_x,N_t}$ and ${\rho }^{N_x,N_t}$ using $N_x=N_t$, $\mu =0.9\epsilon$ for Example 2.

	${\mathit{N}}_{\mathit{x}}=16$	32	64	128	256
Present method using Shishkin mesh
$e^{N_x,N_t}$	2.4022 $\times {10}^{-2}$	8.0219 $\times {10}^{-3}$	2.3356 $\times {10}^{-3}$	6.3107 $\times {10}^{-4}$	1.6406 $\times {10}^{-4}$
${\rho }^{N_x,N_t}$	1.5823	1.7802	1.8879	1.9436
Present method using Bakhvalov–Shishkin mesh
$e^{N_x,N_t}$	2.2966 $\times {10}^{-2}$	7.5950 $\times {10}^{-3}$	2.2035 $\times {10}^{-3}$	5.9524 $\times {10}^{-4}$	1.5495 $\times {10}^{-4}$
${\rho }^{N_x,N_t}$	1.5964	1.7853	1.8883	1.9417
Result in [35] Before Extrapolation
$e^{N_x,N_t}$	1.2759 $\times {10}^{-2}$	6.2559 $\times {10}^{-3}$	3.5761 $\times {10}^{-3}$	2.1620 $\times {10}^{-3}$	-
${\rho }^{N_x,N_t}$	1.0282	0.8068	0.7260
Result in [35] After Extrapolation
$e^{N_x,N_t}$	6.0561 $\times {10}^{-3}$	1.5012 $\times {10}^{-3}$	4.6110 $\times {10}^{-4}$	1.4750 $\times {10}^{-4}$	-
${\rho }^{N_x,N_t}$	2.0123	1.7030	1.6444

demonstrate the comparison of maximum point-wise errors and rates of convergence using the present method and other methods in the literature. Figure 1 and Figure 2 display the numerical simulations for Examples 1 and 2. The maximum point-wise errors for Examples 3 and 4 are provided in

Table 5. Computations of $e_{\epsilon ,\mu }^{N_x,N_t},e^{N_x,N_t}$, and ${\rho }^{N_x,N_t}$ using $N_x=N_t$, $\mu =0$ for Example 3.

$\mathit{\epsilon }\downarrow$	${\mathit{N}}_{\mathit{x}}=32$	64	128	256	512	1024
Shishkin mesh
${10}^{-4}$	1.2027 $\times {10}^{-3}$	4.0510 $\times {10}^{-4}$	1.3450 $\times {10}^{-4}$	4.3745 $\times {10}^{-5}$	1.3839 $\times {10}^{-5}$	4.2766 $\times {10}^{-6}$
${10}^{-5}$	1.2028 $\times {10}^{-3}$	4.0503 $\times {10}^{-4}$	1.3444 $\times {10}^{-4}$	4.3705 $\times {10}^{-5}$	1.3817 $\times {10}^{-5}$	4.2652 $\times {10}^{-6}$
${10}^{-6}$	1.2028 $\times {10}^{-3}$	4.0503 $\times {10}^{-4}$	1.3444 $\times {10}^{-4}$	4.3701 $\times {10}^{-5}$	1.3815 $\times {10}^{-5}$	4.2640 $\times {10}^{-6}$
${10}^{-7}$	1.2028 $\times {10}^{-3}$	4.0503 $\times {10}^{-4}$	1.3444 $\times {10}^{-4}$	4.3701 $\times {10}^{-5}$	1.3815 $\times {10}^{-5}$	4.2639 $\times {10}^{-6}$
${10}^{-8}$	1.2028 $\times {10}^{-3}$	4.0503 $\times {10}^{-4}$	1.3444 $\times {10}^{-4}$	4.3701 $\times {10}^{-5}$	1.3815 $\times {10}^{-5}$	4.2639 $\times {10}^{-6}$
$e^{N_x,N_t}$	1.2028 $\times {10}^{-3}$	4.0510 $\times {10}^{-4}$	1.3450 $\times {10}^{-4}$	4.3745 $\times {10}^{-5}$	1.3839 $\times {10}^{-5}$	4.2766 $\times {10}^{-6}$
${\rho }^{N_x,N_t}$	1.5700	1.5907	1.6204	1.6604	1.6942
Bakhvalov–Shishkin mesh
${10}^{-4}$	1.2637 $\times {10}^{-4}$	3.3122 $\times {10}^{-5}$	8.5789 $\times {10}^{-6}$	2.2252 $\times {10}^{-6}$	5.8937 $\times {10}^{-7}$	1.6389 $\times {10}^{-7}$
${10}^{-5}$	1.2610 $\times {10}^{-4}$	3.2858 $\times {10}^{-5}$	8.4058 $\times {10}^{-6}$	2.1261 $\times {10}^{-6}$	5.3620 $\times {10}^{-7}$	1.3564 $\times {10}^{-7}$
${10}^{-6}$	1.2607 $\times {10}^{-4}$	3.2831 $\times {10}^{-5}$	8.3883 $\times {10}^{-6}$	2.1164 $\times {10}^{-6}$	5.3105 $\times {10}^{-7}$	1.3300 $\times {10}^{-7}$
${10}^{-7}$	1.2607 $\times {10}^{-4}$	3.2829 $\times {10}^{-5}$	8.3865 $\times {10}^{-6}$	2.1154 $\times {10}^{-6}$	5.3054 $\times {10}^{-7}$	1.3273 $\times {10}^{-7}$
${10}^{-8}$	1.2607 $\times {10}^{-4}$	3.2828 $\times {10}^{-5}$	8.3864 $\times {10}^{-6}$	2.1153 $\times {10}^{-6}$	5.3049 $\times {10}^{-7}$	1.3271 $\times {10}^{-7}$
$e^{N_x,N_t}$	1.2637 $\times {10}^{-4}$	3.3122 $\times {10}^{-5}$	8.5789 $\times {10}^{-6}$	2.2252 $\times {10}^{-6}$	5.8937 $\times {10}^{-7}$	1.6389 $\times {10}^{-7}$
${\rho }^{N_x,N_t}$	1.9318	1.9489	1.9469	2.0685	1.8464

and

Table 6. Computations of $e_{\epsilon ,\mu }^{N_x,N_t},e^{N_x,N_t}$, and ${\rho }^{N_x,N_t}$ using $N_x=N_t$, $\mu =0$ for Example 4.

$\mathit{\epsilon }\downarrow$	${\mathit{N}}_{\mathit{x}}=32$	64	128	256	512	1024
Shishkin mesh
${10}^{-2}$	6.5303 $\times {10}^{-3}$	1.9044 $\times {10}^{-3}$	6.4562 $\times {10}^{-4}$	2.1118 $\times {10}^{-4}$	6.6890 $\times {10}^{-5}$	2.0650 $\times {10}^{-5}$
${10}^{-3}$	1.0327 $\times {10}^{-2}$	3.4661 $\times {10}^{-3}$	1.0499 $\times {10}^{-3}$	2.8323 $\times {10}^{-4}$	7.1519 $\times {10}^{-5}$	2.2079 $\times {10}^{-5}$
${10}^{-4}$	1.1076 $\times {10}^{-2}$	3.9934 $\times {10}^{-3}$	1.3397 $\times {10}^{-3}$	4.2548 $\times {10}^{-4}$	1.2681 $\times {10}^{-4}$	3.5204 $\times {10}^{-5}$
${10}^{-5}$	1.1159 $\times {10}^{-2}$	4.0580 $\times {10}^{-3}$	1.3831 $\times {10}^{-3}$	4.5217 $\times {10}^{-4}$	1.4246 $\times {10}^{-4}$	4.3420 $\times {10}^{-5}$
${10}^{-6}$	1.1167 $\times {10}^{-2}$	4.0647 $\times {10}^{-3}$	1.3877 $\times {10}^{-3}$	4.5509 $\times {10}^{-4}$	1.4432 $\times {10}^{-4}$	4.4558 $\times {10}^{-5}$
${10}^{-7}$	1.1168 $\times {10}^{-2}$	4.0653 $\times {10}^{-3}$	1.3881 $\times {10}^{-3}$	4.5539 $\times {10}^{-4}$	1.4451 $\times {10}^{-4}$	4.4676 $\times {10}^{-5}$
${10}^{-8}$	1.1168 $\times {10}^{-2}$	4.0654 $\times {10}^{-3}$	1.3882 $\times {10}^{-3}$	4.5542 $\times {10}^{-4}$	1.4453 $\times {10}^{-4}$	4.4688 $\times {10}^{-5}$
$e^{N_x,N_t}$	1.1168 $\times {10}^{-2}$	4.0654 $\times {10}^{-3}$	1.3882 $\times {10}^{-3}$	4.5542 $\times {10}^{-4}$	1.4453 $\times {10}^{-4}$	4.4689 $\times {10}^{-5}$
${\rho }^{N_x,N_t}$	1.4579	1.5502	1.6079	1.6558	1.6934
Bakhvalov–Shishkin mesh
${10}^{-2}$	1.1649 $\times {10}^{-3}$	3.1490 $\times {10}^{-4}$	7.9954 $\times {10}^{-5}$	1.9744 $\times {10}^{-5}$	4.8508 $\times {10}^{-6}$	1.1969 $\times {10}^{-6}$
${10}^{-3}$	1.2416 $\times {10}^{-3}$	3.5010 $\times {10}^{-4}$	9.2907 $\times {10}^{-5}$	2.3694 $\times {10}^{-5}$	5.8718 $\times {10}^{-6}$	1.4282 $\times {10}^{-6}$
${10}^{-4}$	1.2506 $\times {10}^{-3}$	3.5520 $\times {10}^{-4}$	9.5345 $\times {10}^{-5}$	2.4773 $\times {10}^{-5}$	6.3063 $\times {10}^{-6}$	1.5819 $\times {10}^{-6}$
${10}^{-5}$	1.2515 $\times {10}^{-3}$	3.5574 $\times {10}^{-4}$	9.5665 $\times {10}^{-5}$	2.4902 $\times {10}^{-5}$	6.3693 $\times {10}^{-6}$	1.6113 $\times {10}^{-6}$
${10}^{-6}$	1.2516 $\times {10}^{-3}$	3.5579 $\times {10}^{-4}$	9.5682 $\times {10}^{-5}$	2.4924 $\times {10}^{-5}$	6.3758 $\times {10}^{-6}$	1.6145 $\times {10}^{-6}$
${10}^{-7}$	1.2516 $\times {10}^{-3}$	3.5579 $\times {10}^{-4}$	9.5683 $\times {10}^{-5}$	2.4926 $\times {10}^{-5}$	6.3765 $\times {10}^{-6}$	1.6150 $\times {10}^{-6}$
${10}^{-8}$	1.2516 $\times {10}^{-3}$	3.5579 $\times {10}^{-4}$	9.5683 $\times {10}^{-5}$	2.4926 $\times {10}^{-5}$	6.3766 $\times {10}^{-6}$	1.6151 $\times {10}^{-6}$
$e^{N_x,N_t}$	1.2516 $\times {10}^{-3}$	3.5579 $\times {10}^{-4}$	9.5683 $\times {10}^{-5}$	2.4926 $\times {10}^{-5}$	6.3766 $\times {10}^{-6}$	1.6151 $\times {10}^{-6}$
${\rho }^{N_x,N_t}$	1.8147	1.8947	1.9406	1.9668	1.9812

to investigate the effect of small negative shifts on numerical solutions and the feasibility of the present method.

Table 7. Comparison of maximum errors for Example 3 with [39].

	${\mathit{N}}_{\mathit{x}}=32$	64	128	256	512	1024
	${\mathit{N}}_{\mathit{t}}=\mathbf{16}$	32	64	128	256	512
Present result using Shishkin mesh
$e^{N_x,N_t}$	1.0680 $\times {10}^{-3}$	3.7299 $\times {10}^{-4}$	1.2732 $\times {10}^{-4}$	4.1711 $\times {10}^{-5}$	1.3327 $\times {10}^{-5}$	4.1416 $\times {10}^{-6}$
${\rho }^{N_x,N_t}$	1.5177	1.5507	1.6100	1.6461	1.6861	-
Present result using Bakhvalov–Shishkin mesh
$e^{N_x,N_t}$	2.3367 $\times {10}^{-4}$	6.6981 $\times {10}^{-5}$	1.7999 $\times {10}^{-5}$	4.6858 $\times {10}^{-6}$	1.1936 $\times {10}^{-6}$	3.0273 $\times {10}^{-7}$
${\rho }^{N_x,N_t}$	1.8026	1.8958	1.9415	1.9730	1.9792
Result in [39]
$e^{N_x,N_t}$	0.274 $\times {10}^{-2}$	0.157 $\times {10}^{-2}$	0.847 $\times {10}^{-3}$	0.442 $\times {10}^{-3}$	0.226 $\times {10}^{-3}$	0.114 $\times {10}^{-3}$
${\rho }^{N_x,N_t}$	0.804	0.888	0.939	0.970	0.985

and

Table 8. Comparison of maximum errors for Example 4.

	${\mathit{N}}_{\mathit{x}}=16$	32	64	128	256	512
	${\mathit{N}}_{\mathit{t}}=\mathbf{16}$	32	64	128	256	512
Present result using Shishkin mesh
$e^{N_x,N_t}$	2.7313 $\times {10}^{-2}$	1.1168 $\times {10}^{-2}$	4.0654 $\times {10}^{-3}$	1.3882 $\times {10}^{-3}$	4.5542 $\times {10}^{-4}$	1.4453 $\times {10}^{-4}$
${\rho }^{N_x,N_t}$	1.2902	1.4579	1.5502	1.6079	1.6558
Present result using Bakhvalov–Shishkin mesh
$e^{N_x,N_t}$	3.9792 $\times {10}^{-3}$	1.2516 $\times {10}^{-3}$	3.5579 $\times {10}^{-4}$	9.5683 $\times {10}^{-5}$	2.4926 $\times {10}^{-5}$	6.3766 $\times {10}^{-6}$
${\rho }^{N_x,N_t}$	1.6687	1.8147	1.8947	1.9406	1.9668
Result in [41]
$e^{N_x,N_t}$	7.2411 $\times {10}^{-2}$	4.9395 $\times {10}^{-2}$	3.0647 $\times {10}^{-2}$	1.7952 $\times {10}^{-2}$	1.0184 $\times {10}^{-2}$	5.6568 $\times {10}^{-3}$
${\rho }^{N_x,N_t}$	0.553	0.689	0.772	0.818	0.848
Result in [42]
$e^{N_x,N_t}$	7.3819 $\times {10}^{-2}$	3.4129 $\times {10}^{-2}$	1.5763 $\times {10}^{-2}$	9.1086 $\times {10}^{-3}$	8.4498 $\times {10}^{-3}$	8.3345 $\times {10}^{-3}$
${\rho }^{N_x,N_t}$	1.1130	1.1145	0.7812	0.1081	0.0198

show the comparison of maximum point-wise errors and convergence rates for Examples 3 and 4. Figure 3 and Figure 4 depict the numerical simulations for Examples 3 and 4, respectively. Figure 1, Figure 2, Figure 3 and Figure 4 show the formation of a strong boundary layer near $x=1$ as $\epsilon \to 0$. Figure 5, Figure 6, Figure 7 and Figure 8 exhibit the log–log scale plots of the maximum errors for each Example. The log–log plots suggest the theoretical (green-colored) and numerical (the other colors) errors. These log–log plots suggest the uniform convergence of the method. For $\epsilon$ values equal to ${10}^{-4},{10}^{-6}$, and ${10}^{-8}$, the maximum point-wise errors are almost the same. This causes overlapping in the log–log plot. Due to this reason, we observe a single curve for numerical results (purple-colored overlapped numerical results for ${10}^{-4},{10}^{-6}$, and ${10}^{-8}$) and a single curve for theoretical results as stated in Theorem 6 (red-colored). Due to this overlapping, we have only two curves (line graphs) in all log–log plots. Figure 9 depicts the effect of the perturbation parameter $\epsilon$ and small negative shifts via line graphs for Examples 1 and 2, while Figure 10 shows the effect of the perturbation parameter $\epsilon$ through line graphs for Examples 3 and 4, respectively. As the perturbation parameter size decreases, the layer thickness increases. Since we have not calculated the maximum errors for $N_x=N_t=2048$ in all Tables, we have not included the rate of convergence (${\rho }^{N_x,N_t}$) in the last rows. This is because of the low precision in our computer memory. When the number of mesh points increases, our computer becomes busy.

6. Conclusions

This study presents a computational method for a singularly perturbed parabolic functional differential equation with small negative shifts. The terms involving small negative shifts are approximated using the Taylor series approximation. The resulting singularly perturbed parabolic convection–diffusion–reaction equation is discretized by a Crank–Nicolson method in the time direction on a uniform mesh and a hybrid difference method on Shishkin-type meshes in the space direction. The stability and uniform convergence of the present method are established very well. Theoretically, we have proved that the present method provides an almost-second-order $\epsilon$–uniform convergence using a Shishkin mesh and second-order $\epsilon$–uniform convergence using a Bakhvalov–Shishkin mesh. To validate the applicability of the present method, Examples 1 and 2 were computed for different values of the perturbation parameter and small negative shifts. As can be observed from Table 1, Table 2, Table 3 and Table 4, maximum point-errors and rate of convergence using Shishkin and Bakhvalov–Shishkin meshes are almost the same for Examples 1 and 2. This is the effect of the small negative shifts in the governing differential equation. Since there are no small shifts in the governing differential equation for Examples 3 and 4, the maximum point-errors and rate of convergence using the Bakhvalov–Shishkin mesh are more efficient than using the Shishkin mesh. The Bakhvalov–Shishkin mesh produces the best solutions for the Examples 3 and 4 because there are no small negative shifts.