Hybrid Integral Inequalities on Fractal Set
Abstract
1. Introduction
2. Preliminaries
- •
- and belong to .
- •
- .
- •
- .
- •
- .
- •
- .
- •
- .
- •
- and .
- 1.
- (Local fractional integration is anti-differentiation) Suppose that . Then, we have
- 2.
- (Local fractional integration by parts) Suppose that and .Then, we have
3. Main Results
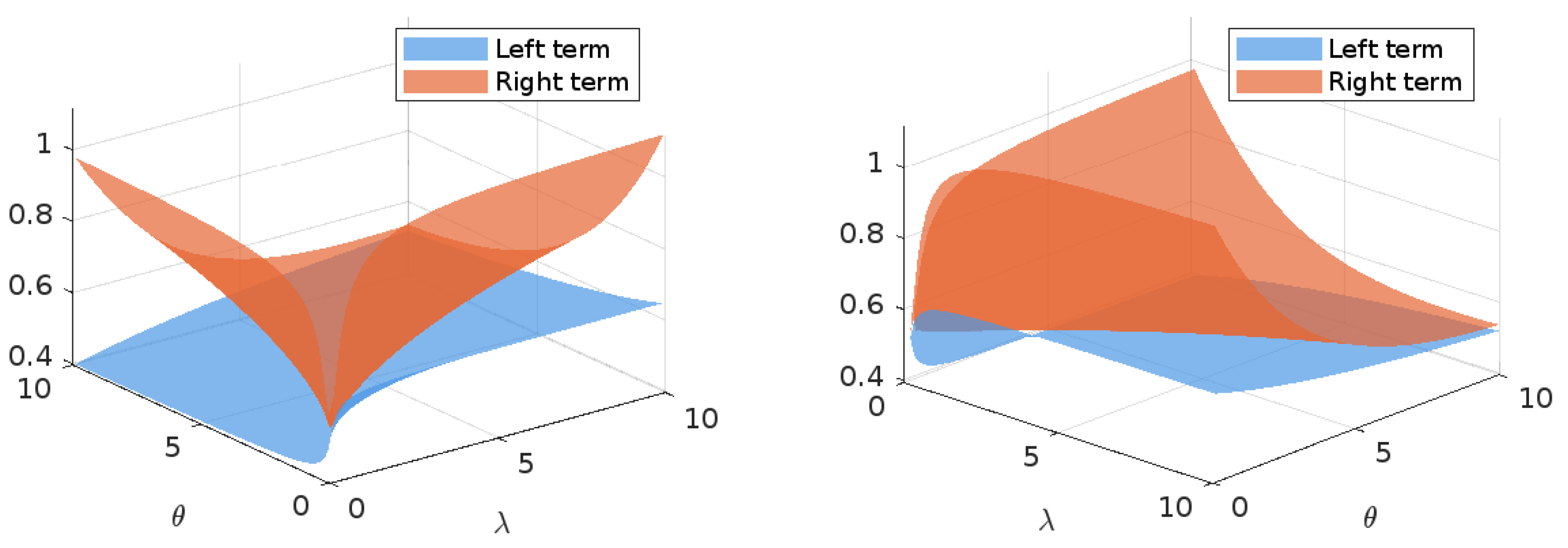
4. Numerical Example and Graphical Illustration
5. Applications
5.1. Quadrature Formula
5.2. Special Means
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pečarić, J.E.; Proschan, F.; Tong, Y.L. Convex functions, partial orderings, and statistical applications. In Mathematics in Science and Engineering; Academic Press, Inc.: Boston, MA, USA, 1992; Volume 187. [Google Scholar]
- Noor, M.A.; Noor, K.I.; Iftikhar, S. Newton inequalities for p-harmonic convex functions. Honam Math. J. 2018, 40, 239–250. [Google Scholar]
- Ögülmü, H.; Sarikaya, M.Z. Some Hermite-Hadamard type inequalities for h-convex functions and their applications. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 813–819. [Google Scholar] [CrossRef]
- Sitthiwirattham, T.; Nonlaopon, K.; Ali, M.A.; Budak, H. Riemann-Liouville fractional Newton’s type inequalities for differentiable convex functions. Fractal Fract. 2022, 6, 175. [Google Scholar] [CrossRef]
- Laribi, N.; Meftah, B. 3/8-Simpson type inequalities for differentiable s-convex functions. Jordan J. Math. Stat. 2023, 16, 79–98. [Google Scholar]
- Meftah, B.; Lakhdari, A.; Saleh, W. 2-point left Radau-type inequalities via s-convexity. J. Appl. Anal. 2023, 29, 341–346. [Google Scholar] [CrossRef]
- Rebiai, G.; Meftah, B. 2-point right Radau inequalities for differentiable s-convex functions. J. Interdiscip. Math. 2024, 27, 1243–1255. [Google Scholar] [CrossRef]
- Berkane, A.; Meftah, B.; Lakhdari, A. Right-Radau-type inequalities for multiplicative differentiable s-convex functions. J. Appl. Math. Inform. 2024, 42, 785–800. [Google Scholar]
- Liu, X.L.; Xu, H.Y.; Shokri, A.; Lakhdari, A.; Meftah, B. Some Error Bounds for 2-Point Right Radau Formula in the Setting of Fractional Calculus via s-Convexity. J. Math. 2024, 2024, 6709056. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Shang, J.; Wang, Y.; Chen, M.; Dai, J.; Zhou, X.; Kuttner, J.; Hilt, G.; Shao, X.; Gottfried, J.; Wu, K. Assembling molecular Sierpiński triangle fractals. Nat. Chem. 2015, 7, 389–393. [Google Scholar] [CrossRef]
- Yang, Y.J.; Baleanu, D.; Yang, X.J. Analysis of fractal wave equations by local fractional Fourier series method. Adv. Math. Phys. 2013, 2013, 632309. [Google Scholar] [CrossRef]
- Gao, F.; Zhong, W.P.; Shen, X.M. Applications of Yang-Fourier transform to local fractional equations with local fractional derivative and local fractional integral. Adv. Mater. Res. 2012, 461, 306–310. [Google Scholar]
- Mo, H.; Sui, X.; Yu, D. Generalized convex functions on fractal sets and two related inequalities. Abst. Appl. Anal. 2014, 2014, 636751. [Google Scholar] [CrossRef]
- Khan, Z.A.; Rashid, S.; Ashraf, R.; Baleanu, D.; Chu, Y.M. Generalized trapezium-type inequalities in the settings of fractal sets for functions having generalized convexity property. Adv. Differ. Equ. 2020, 2020, 657. [Google Scholar] [CrossRef]
- Saleh, W.; Meftah, B.; Lakhdari, A.; Kiliçman, A. Exploring the Companion of Ostrowski’s Inequalities via Local Fractional Integrals. Eur. J. Pure Appl. Math. 2023, 16, 1359–1380. [Google Scholar] [CrossRef]
- Sarıkaya, M.Z.; Budak, H.; Erden, S. On new inequalities of Simpson’s type for generalized convex functions. Korean J. Math. 2019, 27, 279–295. [Google Scholar]
- Luo, C.; Wang, H.; Du, T. Fejér-Hermite-Hadamard type inequalities involving generalized h-convexity on fractal sets and their applications. Chaos Solitons Fractals 2020, 131, 109547. [Google Scholar] [CrossRef]
- Sun, W. Local fractional Ostrowski-type inequalities involving generalized h-convex functions and some applications for generalized moments. Fractals 2021, 29, 2150006. [Google Scholar] [CrossRef]
- Du, T.; Wang, H.; Khan, M.A.; Zhang, Y. Certain integral inequalities considering generalized m-convexity on fractal sets and their applications. Fractals 2019, 27, 1950117. [Google Scholar] [CrossRef]
- Du, T.; Xu, L. Hermite-Hadamard-and Pachpatte-type integral inequalities for generalized subadditive functions in the fractal sense. Miskolc Math. Notes 2024, 25, 645–658. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Du, T. Properties and 2α-fractal weighted parametric inequalities for the fractal (m,h)-preinvex mappings. Fractals 2023, 31, 2350134. [Google Scholar] [CrossRef]
- Yu, Y.; Du, T. Certain error bounds on the Bullen type integral inequalities in the framework of fractal spaces. J. Nonlinear Funct. Anal. 2022, 2022, 24. [Google Scholar]
- Yu, Y.; Liu, J.; Du, T. Certain error bounds on the parameterized integral inequalities in the sense of fractal sets. Chaos Solitons Fractals 2022, 161, 112328. [Google Scholar] [CrossRef]
- Sun, W. Hermite-Hadamard type local fractional integral inequalities with Mittag-Leffler kernel for generalized preinvex functions. Fractals 2021, 29, 2150253. [Google Scholar] [CrossRef]
- Razzaq, A.; Javed, I.; González, F.M. Hermite-Hadamard inequalities for generalized (m-F)-convex function in the framework of local fractional integrals. Ann. Univ. Craiova–Math. Comput. Sci. Ser. 2024, 51, 198–222. [Google Scholar] [CrossRef]
- Napoles Valdes, J.E.; Guzmán, P.M.; Bayraktar, B. Milne-type integral inequalities for modified (h,m)-convex functions on fractal sets. Probl. Anal. Issues Anal. 2024, 13, 106–127. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, W. On general local fractional integral inequalities for generalized h-preinvex functions on Yang’s fractal sets. Fractals 2024, 32, 2440025. [Google Scholar] [CrossRef]
- Ge-JiLe, H.; Rashid, S.; Farooq, F.B.; Sultana, S. Some inequalities for a new class of convex functions with applications via local fractional integral. J. Funct. Spaces 2021, 2021, 6663971. [Google Scholar] [CrossRef]
- Sun, W. Some new inequalities for generalized h-convex functions involving local fractional integral operators with Mittag-Leffler kernel. Math. Methods Appl. Sci. 2021, 44, 4985–4998. [Google Scholar] [CrossRef]
- Sun, W. Some Hermite–Hadamard type inequalities for generalized h-preinvex function via local fractional integrals and their applications. Adv. Differ. Equ. 2020, 2020, 426. [Google Scholar] [CrossRef]
- Du, T.; Yuan, X. On the parameterized fractal integral inequalities and related applications. Chaos Solitons Fractals 2023, 170, 113375. [Google Scholar] [CrossRef]
- Xu, H.; Lakhdari, A.; Saleh, W.; Meftah, B. Some new parametrized inequalities on fractal set. Fractals 2024, 32, 2450063. [Google Scholar] [CrossRef]
- Li, H.; Lakhdari, A.; Jarad, F.; Xu, H.; Meftah, B. An expanded analysis of local fractional integral inequalities via generalized (s,P)-convexity. J. Inequal. Appl. 2024, 2024, 78. [Google Scholar] [CrossRef]
- Xu, H.; Lakhdari, A.; Jarad, F.; Abdeljawad, T.; Meftah, B. On multiparametrized integral inequalities via generalized α-convexity on fractal set. Math. Methods Appl. Sci. 2025, 48, 980–1002. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Rashid, S.; Hammouch, Z.; Chu, Y.M. Some new local fractional inequalities associated with generalized (s,m)-convex functions and applications. Adv. Differ. Equ. 2020, 2020, 406. [Google Scholar] [CrossRef]
- Butt, S.I.; Khan, D.; Seol, Y. Fractal perspective of superquadratic functions with generalized probability estimations. PLoS One 2025, 20, e0313361. [Google Scholar] [CrossRef]
- Butt, S.; Inam, H.; Dokuyucu, M. New fractal Simpson estimates for twice local differentiable generalized convex mappings. Appl. Comput. Math. 2024, 23, 474–503. [Google Scholar]
- Butt, S.I.; Agarwal, P.; Yousaf, S.; Guirao, J.L. Generalized fractal Jensen and Jensen-Mercer inequalities for harmonic convex function with applications. J. Inequal. Appl. 2022, 2022, 1. [Google Scholar] [CrossRef]
- Iftikhar, S.; Kumam, P.; Erden, S. Newton’s-type integral inequalities via local fractional integrals. Fractals 2020, 28, 2050037. [Google Scholar] [CrossRef]
- Bin-Mohsin, B.; Lakhdari, A.; Karabadji, N.; Awan, M.U.; Ben Makhlouf, A.; Meftah, B.; Dragomir, S.S. An Extension of Left Radau Type Inequalities to Fractal Spaces and Applications. Axioms 2024, 13, 653. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science Publisher: New York, NY, USA, 2012. [Google Scholar]
- Chen, G.-S. Generalizations of Hölder’s and some related integral inequalities on fractal space. J. Funct. Spaces Appl. 2013, 2013, 198405. [Google Scholar] [CrossRef]
- Yu, S.; Mohammed, P.O.; Xu, L.; Du, T. An improvement of the power-mean integral inequality in the frame of fractal space and certain related midpoint-type integral inequalities. Fractals 2022, 30, 2250085. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meftah, B.; Saleh, W.; Awan, M.U.; Ciurdariu, L.; Lakhdari, A. Hybrid Integral Inequalities on Fractal Set. Axioms 2025, 14, 358. https://doi.org/10.3390/axioms14050358
Meftah B, Saleh W, Awan MU, Ciurdariu L, Lakhdari A. Hybrid Integral Inequalities on Fractal Set. Axioms. 2025; 14(5):358. https://doi.org/10.3390/axioms14050358
Chicago/Turabian StyleMeftah, Badreddine, Wedad Saleh, Muhammad Uzair Awan, Loredana Ciurdariu, and Abdelghani Lakhdari. 2025. "Hybrid Integral Inequalities on Fractal Set" Axioms 14, no. 5: 358. https://doi.org/10.3390/axioms14050358
APA StyleMeftah, B., Saleh, W., Awan, M. U., Ciurdariu, L., & Lakhdari, A. (2025). Hybrid Integral Inequalities on Fractal Set. Axioms, 14(5), 358. https://doi.org/10.3390/axioms14050358





