Hopf Bifurcation and Optimal Control in an Ebola Epidemic Model with Immunity Loss and Multiple Delays

Abstract

This paper studies the effects of resource limitations, immunity decay, and delays on an Ebola epidemic model and an optimal control strategy. The model includes two types of delays: a delay in the incubation period of infected individuals and a delay in treatment. Conditions for a Hopf bifurcation at the endemic equilibrium are verified, with its direction and stability analyzed via normal form theory and the center manifold theorem. We also studied the optimal control problem for the SIRD delay model using educational campaigns and Ebola survivors’ immunity as control variables. Furthermore, we formulate an optimization problem based on Pontryagin’s maximum principle. This problem uses a modified Runge-Kutta approach with delays to discover the best control strategy to reduce infections and intervention costs. Finally, simulation results confirm analytical conclusions and show the practical implications of the optimum Ebola control plan using the dde23 MATLAB R2024a built-in solver and DDE-Biftool.

1. Introduction

Ebola virus disease was first discovered in 1976, and among infectious diseases, it is one of the most perilous known to humanity. The death rates for people infected with this disease are very high and may reach 90 percent in some cases [1]. The Ebola virus spreads widely among humans in several ways, and infection occurs during the processes of consumption, cooking, or preparation. Individuals may encounter infected animals and come into contact with clothing or items that contain the bodily fluids of an infected person; contact with their urine, feces, semen, or saliva can cause transmission to occur. Ebola enters the body through the liver or when the nose, mouth, or eyes are bitten. In addition, the Ebola virus is also spread to humans by fruit bats, chimpanzees, and monkeys [2,3]. From 2 to 21 days is the range for Ebola’s incubation period, with symptoms such as skin rash, vomiting, diarrhea, and tremors, and severe cases can lead to internal and external bleeding [1,4]. The epidemic had a severe impact on many countries. To curb the rapid spread of the disease, quarantining—a time-tested method—is implemented to isolate those suspected of being infected. Even though it has proved effective in controlling the disease, it also poses significant challenges for public health. Furthermore, direct contact with the deceased during burial ceremonies can facilitate the transmission of the disease [5,6].

The dynamics of Ebola transmission have been extensively studied, revealing insights into the disease’s spread and control. Zoonotic transmission between dogs and humans [7], the progression of the disease through different stages [8], and the impact of density-dependent treatment approaches on Ebola transmission [9] have been explored. A modified mathematical model incorporating quarantining as a control strategy has also been developed [10]. In addition, research has focused on direct and indirect transmission routes; as stated in [11], the models incorporated a composite nonlinear incidence function along with density-independent treatment. The significance of vaccination in reducing mortality among confirmed Ebola patients is highlighted in an observational study [12]. A comprehensive eight-dimensional nonlinear differential equations model is presented to better understand Ebola transmission dynamics [13]. The role of optimal control strategies in human–bat transmission dynamics is also investigated [14]. This study aims to model the dynamics of Ebola by incorporating time delay, immunity, quarantining, and nonlinear perturbations as control mechanisms. The influence of quarantine, medical resource availability, the latent period, and treatment delays were key factors in this study, especially during the early phases of model development. As the research progressed, additional characteristics of Ebola were integrated to enhance the model. The critical roles of quarantine and medical resources, along with the latent period’s significance in Ebola dynamics, are central to this research. This study, inspired by previous research [15], aims to develop computational models focusing on time delays and quarantine for effective Ebola control, particularly in outbreaks like those in Western Guinea. The research also draws inspiration from studies that used modeling methods to understand and mitigate Ebola [16,17].

Delay differential equations (DDEs) offer a more complex dynamic than ordinary differential equations, as the introduction of time delays can destabilize previously stable equilibria, leading to population fluctuations [18,19,20]. This makes the study of delays essential for understanding population dynamics, especially in the context of epidemics, where various infectious diseases exhibit different types of delays during their spread. A comprehensive overview of the relevance of DDEs in population dynamics and epidemics is given in [21]. Various scenarios with the inclusion of delays have been analyzed by researchers, including vaccination periods [22], asymptomatic carriage and infection periods [23], immunity periods, and incubation or latent periods [23,24,25,26]. In [27], the research focuses on an SEIRS model, specifically examining the impact of constant delays on both immune periods and the latent period, and [23] analyzes a model with delays in both asymptomatic carriage period and incubation. In addition, the authors of [28] examined the stability of periodic solutions within a delayed feedback control system and the existence of bifurcation.

Hopf bifurcation in virus infection models with three delays and CTL responses is the focus of study in [29]. A delayed SIQR epidemic model is explored, and different pairs of delays are used as bifurcation parameters in [30]. A delayed SEIS epidemic model, including an analysis of Hopf bifurcation, is explored in [31].

In a more detailed study, the authors of [32] developed a model of the Ebola epidemic that takes into account the loss of immunity, limited medical resources, and the identification and isolation of susceptible individuals. However, their analysis was limited to the disease-free equilibrium, and they did not include time delays or control measures. Our study extends this work by introducing two critical time delays: the incubation period delay and the treatment initiation delay. These delays provide a more realistic representation of disease progression and medical response. In addition, we present two optimal control strategies—quarantine and immune enhancement—allowing us to study their impact on disease control. Furthermore, unlike the original study, we analyze the stability of the endemic equilibrium and explore the conditions under which Hopf bifurcation occurs, leading to periodic outbreaks. This expanded analysis provides deeper insights into disease dynamics and the effectiveness of public health measures.

The inclusion of two time delays, ${\tau }_1$ (incubation period delay) and ${\tau }_2$ (treatment delay), is of biological and mathematical importance. The incubation delay ${\tau }_1$ captures the period between infection and contagion, which affects the early dynamics of the outbreak. The treatment delay ${\tau }_2$ represents the delay in medical intervention, which affects recovery rates and disease persistence. Mathematically, these delays act as bifurcation parameters, meaning that if they exceed certain critical thresholds, the system undergoes Hopf bifurcation, leading to persistent oscillations in the spread of the disease. This suggests that reducing treatment delays could be an effective strategy to prevent periodic outbreaks and control an epidemic more efficiently.

The rest of this article is organized as follows: In Section 2, we develop a mathematical model that incorporates multiple time delays, and for the solution, we establish boundedness and positivity. Section 3 presents an analysis of the disease-free equilibrium local stability and derives the conditions necessary for the local stability of the interior equilibrium point. Section 4 provides a comprehensive analysis of Hopf bifurcation, focusing on both the stability characteristics of the resulting periodic solutions and the direction in which the bifurcation occurs. Further, in Section 5, the associated optimal control system’s formulation and solution are detailed. Numerical simulations confirm the theoretical results in Section 6.

2. Formulation of the Model and Analysis of Solution Positivity

Our study is built upon the epidemiological model proposed in [32], which considers the dynamics of infection, recovery, and deceased individuals who are not yet buried. We extend this model by incorporating time delays and control strategies to analyze disease dynamics more comprehensively.

This model employs a $SIRD$ framework to classify the population into four categories: susceptible (S), infectious (I), recovered (R), and deceased individuals awaiting burial (D). It also explores the latent period for those exposed to the infection, specifically measuring the time from the initial Ebola virus infection to the appearance of symptoms. This period can be affected by the overall viral transmission rate within the community and the individual’s immune response. It is understood that recovered individuals, labeled as R, gradually lose their immunity over time and reintegrate into the susceptible population. Moreover, in light of the widespread nature of the virus, effective tracing and quarantining of susceptible individuals can play a critical role in controlling the outbreak. This is mainly demonstrated through a decrease in the transmission probability, denoted as u.

In our study, we define (for susceptible individuals) the latent period ${\tau }_1$; these parameters represent the time intervals that elapse from the moment an individual is infected until they become capable of transmitting the infection, and for the delay in treatment, we denote this as ${\tau }_2$; this represents when infected individuals do not recover immediately after infection but only after a period of delay due to treatment such as diagnosis and medical intervention.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dS}{dt}}=\Lambda -(I(t-{\tau }_1)+\epsilon D)(1-u)\beta S-dS+\theta R,\hfill \\ \hfill & {\displaystyle \frac{dI}{dt}}=(I(t-{\tau }_1)+\epsilon D)(1-u)\beta S-\gamma I-\mu (b,I)I(t-{\tau }_2)-dI-fI,\hfill \\ \hfill & {\displaystyle \frac{dR}{dt}}=\gamma I+\mu (b,I)I(t-{\tau }_2)-dR-\theta R,\hfill \\ \hfill & {\displaystyle \frac{dD}{dt}}=fI-\rho D,\hfill \end{array}$$

(1)

with the initial conditions

$$\begin{array}{c}S\left(\nu \right)={\Psi }_1\left(\nu \right);I\left(\nu \right)={\Psi }_2\left(\nu \right);R\left(\nu \right)={\Psi }_3\left(\nu \right);D\left(\nu \right)={\Psi }_4\left(\nu \right).\end{array}$$

(2)

Here, $\tau =max\left\{{\tau }_1,{\tau }_2\right\}$, ${\Psi }_i\in \mathbb{C}\left([-\tau ,0],{\mathbb{R}}_{+}\right);(i=1,\cdots ,4)$, with $\nu \in [-\tau ,0],$ and ${\Psi }_i\left(\nu \right)>0.$ Further, ${\displaystyle \mu (b,I)={\mu }_0+({\mu }_1-{\mu }_0)\frac{b}{I+b}}$ is described in detail in [33]. In the model equations, the deceased compartment D only accumulates individuals who die due to infection at a rate of $fI$. Naturally deceased individuals with a rate of d from the compartments $S,I$, and R do not enter into D and are directly removed from the system. Furthermore, our model includes time delays, with a particular focus on the disease latent period represented by the parameter ${\tau }_1$ and the delay in treatment denoted by ${\tau }_2$, where ${\tau }_1,{\tau }_2\ge 0$. The model parameters are defined in

Table 1. Table of parameters used in model (1).

Parameters	Description	Value	Source
$\Lambda$	Susceptible individual recruitment rate	555	[34]
$\beta$	Chance of transmission from infectious to susceptible	0.05	[35]
$\epsilon$	Modification parameter for deceased individuals	0.45	[35]
u	Rate of individuals being tracked and quarantined	0.5	Assumed
$\gamma$	Natural rate of recovery	0.4389	[36]
$\rho$	Rate of incineration or burial of deceased bodies	0.015	Assumed
f	Rate of disease-induced deaths	0.9764	[36]
$\theta$	Rate of immunity	0.75	Assumed
d	Rate of natural mortality in humans	0.9704	[36]
${\mu }_1$	Highest recovery rate achievable with treatment	0.31	Assumed
${\mu }_0$	Minimum rate of recovery through treatment	5.32	Assumed
b	Limit resources of the health care system	0.41	Assumed

.

To model the interactions between the four compartments, we propose the following assumptions:

• The variable u ranges from 0 to 1; when $u=0$, the quarantine measures are ineffective, while $u=1$ indicates that the quarantine is fully enforced;
• Delayed effects: Individuals infected at time $t-{\tau }_1$ become infectious later at time t, so we express their contribution to infectivity as $\beta I(t-{\tau }_1)S$. Likewise, $\mu (b,I)I(t-{\tau }_2)$ captures the treatment delay from $t-{\tau }_2$ to recovery at time t for infectious individuals.

The disease-free equilibrium (DFE) point of the model (1) is given by $E_0=(S_0,0,0,0)$, where $S_0=\Lambda /d$. A critical parameter, the basic reproduction number (BRN), represented as ${\mathcal{R}}_0$, often influences the stability of the equilibrium points within the system. This important factor shows how many new infections one sick person can cause while they are contagious in a population where everyone else is at risk of becoming infected.

We determine the basic reproduction number of model (1) $R_0$ for the system using the next-generation matrix [37,38]. It is similar to that used in [32]. However, for the reader’s interest, we provide a sketch of the idea. The disease-free equilibrium (DFE) of the system (1) is given by $E_0=\left(S_0,0,0,0\right),\mathrm{where}{S}_0=\Lambda /d.$ At the DFE, the matrices $\mathcal{F}$ and $\mathcal{V}$, representing the rate of appearance of new infections and the rate of transfer between compartments, respectively, are defined as follows:

$$\mathcal{F}=\left(\begin{array}{c}(1-u)\beta (I+\epsilon D)S\\ 0\end{array}\right),\mathcal{V}=\left(\begin{array}{c}(\gamma +\mu (b,I\left)\right)I+fI+dI\\ \rho D-fI\end{array}\right).$$

The Jacobian matrices of $\mathcal{F}$ and $\mathcal{V}$ at $E_0$ are computed as

$$F\left(E_0\right)=\left(\begin{array}{cc}(1-u)\beta S_0& (1-u)\epsilon \beta S_0\\ 0& 0\end{array}\right),V\left(E_0\right)=\left(\begin{array}{cc}\gamma +{\mu }_1+f+d& 0\\ -f& \rho \end{array}\right).$$

The next-generation matrix is given by

$$F{V}^{-1}\left(E_0\right)=F\left(E_0\right)V^{-1}\left(E_0\right).$$

By computing the spectral radius of $F{V}^{-1}\left(E_0\right)$, we obtain

$$R_0={\displaystyle \frac{\beta S_0(1-u)}{\gamma +{\mu }_1+f+d}}+{\displaystyle \frac{f\epsilon \beta S_0(1-u)}{(d+\gamma +{\mu }_1+f)\rho }}.$$

Here, the first term represents the expected number of secondary cases produced by an infected individual in a fully susceptible population, while the second term accounts for the contribution of deceased but not yet buried individuals.

Solution Positivity and Boundedness

We provide the following lemma, which is pertinent to this field, to prove the positivity and eventual boundedness of the solutions $S\left(t\right)$, $I\left(t\right)$, $R\left(t\right)$, and $D\left(t\right)$ of model (1).

Lemma 1.

Let $\left(S\right(t),I(t),R(t),D(t\left)\right)$ with the initial conditions given by (2) be the solution to system (1). Then,

$$S\left(t\right),I\left(t\right),R\left(t\right),D\left(t\right)>0,\mathit{for}\mathit{all}t\ge 0.$$

(3)

Moreover, if $\rho >d$ holds for $N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right)$, then

$$\underset{t\to +\infty }{lim\; sup}N\left(t\right)\le \Lambda /d.$$

Proof. 

From (2), it is clear that $S\left(0\right),I\left(0\right),R\left(0\right),D\left(0\right)>0$. Suppose we assume that there exists $t_1>0$ such that $S\left(t\right),I\left(t\right),R\left(t\right),D\left(t\right)>0$ for any $0\le t<t_1$. Further, assume that $S\left(t_1\right)=0$ and $S\left(t\right),I\left(t\right),R\left(t\right),D\left(t\right)>0$ for any $0\le t<t_1$.

From the first equation of (1), we obtain $(\mathrm{d}S/\mathrm{d}t)\left(t_1\right)\ge \Lambda +\theta R>0.$ This contradicts the fact that $S\left(t_1\right)=0$ and $S\left(t\right)>0$ for $0\le t<t_1$. Now, from the remaining equations of (1), we obtain

$$\begin{array}{cc}\hfill & I\left(t\right)={\mathrm{e}}^{-(f+d)t}\left[I\left(0\right)+{\int }_0^t{\mathrm{e}}^{(f+d)s}((1-u)\beta (I(s-{\tau }_1)+\epsilon D\left(s\right))S\left(s\right)\right.\hfill \\ \hfill & -\gamma I\left(s\right)-\mu (b,I\left(s\right))I(s-{\tau }_2))\mathrm{d}s,\hfill \\ \hfill & R\left(t\right)={\mathrm{e}}^{-(\theta +d)t}\left[R\left(0\right)+{\int }_0^t{\mathrm{e}}^{(\theta +d)s}(\gamma I\left(s\right)+\mu (b,I\left(s\right))I(s-{\tau }_2))\mathrm{d}s\right],\hfill \\ \hfill & D\left(t\right)={\mathrm{e}}^{-\left(\rho \right)t}\left[D\left(0\right)+{\int }_0^t{\mathrm{e}}^{\left(\rho \right)s}\left(fI\left(s\right)\right)\mathrm{d}s\right],\mathrm{for}t>0.\hfill \end{array}$$

From the above equations and the fact that $S\left(t_1\right)>0$, we have $I\left(t_1\right)>0,R\left(t_1\right)>0$ and $D\left(t_1\right)>0$ for some $t_1\in [0,t].$ This proves (3).

Consider the delayed system in (1) as

$$N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right),\mathrm{where}\tau =max\{{\tau }_1,{\tau }_2\}.$$

By using (1) and (2), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}N\left(t\right)=& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}(S\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right))\hfill \\ \hfill =& \Lambda -(I(t-{\tau }_1)+\epsilon D)(1-u)\beta S-dS+\theta R+(I(t-{\tau }_1)+\epsilon D)(1-u)\beta S-\gamma I\hfill \\ \hfill & -\mu (b,I)I(t-{\tau }_2)-dI-fI+\gamma I+\mu (b,I)I(t-{\tau }_2)-dR-\theta R-\rho D+fI,\hfill \\ \hfill =& \Lambda -d\left(S\right(t)+I(t)+R(t)+D(t\left)\right)-(\rho -d)D\left(t\right)\hfill \\ \hfill \le & \Lambda -dN\left(t\right).\hfill \\ \hfill N\left(\theta \right)=& {\varphi }_1\left(\theta \right)+{\varphi }_2\left(\theta \right)+{\varphi }_3\left(\theta \right)+{\varphi }_4\left(\theta \right)\ge 0,\theta \in [-\overline{\tau },0),\hfill \\ \hfill \mathrm{with}N\left(0\right)=& {\varphi }_1\left(0\right)+{\varphi }_2\left(0\right)+{\varphi }_3\left(0\right)+{\varphi }_4\left(0\right)>0.\hfill \end{array}$$

Based on the discussion above and the use of the comparison principle, as a result, $lim\underset{\begin{array}{c}t\to +\infty \end{array}}{sup}N\left(t\right)\le \Lambda /d$. □

3. Stability Analysis

This section focuses on the examination of the stability characteristics of the equilibrium points in system (1). First, we present the results concerning the local asymptotic stability of $E_0$.

3.1. Local Stability of Disease-Free Equilibrium

The (DFE) of model (1) is given by $E_0=(\Lambda /d,0,0,0)$. The Jacobian matrix at $E_0$ is represented by

$$J\left(E_0\right)=\left(\begin{array}{cccc}-d& -e^{-\lambda {\tau }_1}\varrho & \theta & -ϵ\varrho \\ 0& \varrho e^{-\lambda {\tau }_1}-\gamma -d-f-{\mu }_1{e}^{-\lambda {\tau }_2}& 0& \varrho ϵ\\ 0& \gamma +{\mu }_1{e}^{-\lambda {\tau }_2}& -d-\theta & 0\\ 0& f& 0& -\rho \end{array}\right),$$

where $\varrho =\beta S_0(1-u)$. The system’s characteristic equation is expressed as follows:

$$\begin{array}{cc}\hfill \Rightarrow & {\lambda }^4+U_3{\lambda }^3+U_2{\lambda }^2+U_1\lambda +U_0+e^{-\lambda {\tau }_1}(V_3{\lambda }^3+V_2{\lambda }^2+V_1\lambda +V_0)\hfill \\ \hfill & +e^{-\lambda {\tau }_2}(W_3{\lambda }^3+W_2{\lambda }^2+W_1\lambda +W_0)=0.\hfill \end{array}$$

(4)

Appendix A outlines the specific forms of $U_i$, $V_i$, and $W_i$ for $i=0,1,2,3$. Given the two different delays of ${\tau }_1$ and ${\tau }_2$, we state the following theorems:

Theorem 1.

The $DFE$ $E_0$ is locally asymptotically stable for ${\tau }_1={\tau }_2=0$ if ${\mathcal{R}}_0<1$.

Proof. 

If ${\tau }_1={\tau }_2=0$, this means the system is without time delay. For the proof, refer to Theorem 2 in [32]. □

Theorem 2.

Suppose (A5) has a positive root; then, the $DFE$$E_0$ is locally asymptotically stable for ${\tau }_1\in \left[0,{\tau }_1^{*}\right)$ with ${\tau }_2=0$.

Theorem 3.

Suppose (A9) has a positive root; then, the $DFE$$E_0$ is locally asymptotically stable for ${\tau }_2\in \left[0,{\tau }_2^{*}\right)$, with ${\tau }_1=0$.

Theorem 4.

Suppose (A13) has a positive root; then, the $DFE$$E_0$ is locally asymptotically stable for $\tau \in [0$, $\left.{\tau }^{*}\right)$, where ${\tau }_1={\tau }_2=\tau$.

Remark 1.

For details on the proofs of Theorems 2–4, please refer to Appendix C.

3.2. Stability Analysis of Interior Equilibria and Hopf Bifurcation

If $R_0>1$, the system described by (1) demonstrates the presence of a unique endemic equilibrium, denoted by $E^{*}=(S^{*},I^{*},R^{*},D^{*})$. By using the same method as in [32], we find

$$\begin{array}{cc}\hfill n_0& =\gamma +{\mu }_0+f+d,n_1=d+\gamma +f+{\mu }_1,m\left(1+{\displaystyle \frac{\epsilon f}{\rho }}\right)=(1-u)\beta ,p_0=n_0-{\displaystyle \frac{\theta \left(\gamma +{\mu }_0\right)}{d+\theta }},\hfill \\ \hfill p_1=& n_1-{\displaystyle \frac{\theta \left(\gamma +{\mu }_1\right)}{d+\theta }},A=bm{p}_1+d{n}_0,B=d{n}_1,\Delta =B^2(R_0-{\displaystyle \frac{A}{B}}{)}^2+4bBm{p}_0\left(R_0-1\right),\hfill \end{array}$$

$$I^{*}={\displaystyle \frac{B\left(R_0-\frac{A}{B}\right)+\sqrt{\Delta }}{2m{p}_0}},S^{*}={\displaystyle \frac{n_0{I}^{*}+n_{1}b}{(I^{*}+b)m}},R^{*}={\displaystyle \frac{(\gamma +{\mu }_0)I^{*}+(\gamma +{\mu }_1)b}{(\theta +d)(b+I^{*})}}{I}^{*},D^{*}={\displaystyle \frac{f}{\rho }}{I}^{*}.$$

(5)

The Jacobian matrix at the equilibrium point $E^{*}$ can be written in the following form:

$$J\left(E^{*}\right)=\left(\begin{array}{cccc}-a_2-d& -a_1{e}^{-\lambda {\tau }_1}& \theta & -a_1ϵ\\ a_2& a_1{e}^{-\lambda {\tau }_1}-a_3{e}^{-\lambda {\tau }_2}-\gamma -d-f& 0& a_1ϵ\\ 0& a_3{e}^{-\lambda {\tau }_2}+\gamma & -d-\theta & 0\\ 0& f& 0& -\rho \end{array}\right),$$

where

$$a_1=\beta S^{*}(1-u),a_2=\beta (1-u)(I^{*}+D^{*}ϵ),a_3={\displaystyle \frac{I^{*}{\mu }_0(I^{*}+2b)+b^2{\mu }_1}{(I^{*}+b{)}^2}}.$$

(6)

At the endemic equilibrium $E^{*}$, the characteristic equation of the linearized model system (1) is

$$\begin{array}{cc}\hfill & {\lambda }^4+{\Xi }_3{\lambda }^3+{\Xi }_2{\lambda }^2+{\Xi }_1\lambda +{\Xi }_0+e^{-\lambda {\tau }_1}({\aleph }_3{\lambda }^3+{\aleph }_2{\lambda }^2+{\aleph }_1\lambda +{\aleph }_0)\hfill \\ \hfill & +e^{-\lambda {\tau }_2}({{\rm Y}}_3{\lambda }^3+{{\rm Y}}_2{\lambda }^2+{{\rm Y}}_1\lambda +{{\rm Y}}_0)=0\hfill \end{array}$$

(7)

where the expressions for ${\Xi }_i$, ${\aleph }_i$, and ${{\rm Y}}_i$, $i=0,1,2,3$, are given in Appendix B.

Theorem 5.

If ${\mathcal{R}}_0>1$ and ${\mu }_0>{\mu }_1$, then the endemic point $E^{*}$ for ${\tau }_1={\tau }_2=0$ is locally asymptotically stable.

For different delays of ${\tau }_1$ and ${\tau }_2$, we have the following theorems:

Theorem 6.

Suppose ${\tau }_2=0$; it can be concluded that for all ${\tau }_1\ge 0$, the endemic equilibrium $E^{*}$ of system (1) remains locally asymptotically stable.

Theorem 7.

Suppose ${\tau }_2={\tau }_2^{*}$, and the conditions ${\mathbf{L}}_{11}$ and ${\mathbf{L}}_{12}$ (see Appendix C) hold. Then, system (1) undergoes a Hopf bifurcation near $E^{*}$, leading to the emergence of a family of periodic solutions from $E^{*}$. Furthermore, for ${\tau }_2\in [0,{\tau }_2^{*})$ with ${\tau }_1=0$, the endemic equilibrium $E^{*}$ remains locally asymptotically stable.

Theorem 8.

Suppose ${\tau }_1={\tau }_2=\tau ={\tau }^{*}$, and the conditions ${\mathbf{L}}_{21}$ and ${\mathbf{L}}_{22}$ (see Appendix C) hold. Then, system (1) experiences a Hopf bifurcation near the endemic equilibrium $E^{*}$, leading to the emergence of a family of periodic solutions from $E^{*}$. If $\tau \in [0,{\tau }^{*})$, the equilibrium $E^{*}$ remains locally asymptotically stable.

Remark 2.

Appendix C provides the proofs of Theorems 5–8.

4. Hopf Bifurcation: Direction and Stability

In this section, we investigate the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions of system (1) with ${\tau }_1={\tau }_2=\tau .$ We analyze the properties of Hopf bifurcation at the critical value $\tau ={\tau }_K^j$ using the center manifold theorem and the normal form theory [39]. We show that for any one of the critical values, $\tau ={\tau }_K^j(j=0,1,2,\dots ,$$K=1,2,3)$ by $\widehat{\tau }.$ Suppose ${\vartheta }_1=S-S^{*},{\vartheta }_2=I-I^{*},{\vartheta }_3=R-R^{*}$ and ${\vartheta }_4=D-D^{*}.$

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}=& \Lambda -(1-u)\beta (({\vartheta }_2(t-\tau )+I^{*})+\epsilon ({\vartheta }_4+D^{*}))({\vartheta }_1+S^{*})-d({\vartheta }_1+S^{*})+\theta ({\vartheta }_3+R^{*}),\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}=& (1-u)\beta (({\vartheta }_2(t-\tau )+I^{*})+\epsilon ({\vartheta }_4+D^{*}))({\vartheta }_1+S^{*})-\gamma ({\vartheta }_2+I^{*})\hfill \\ \hfill & -\mu (b,({\vartheta }_2+I^{*}))({\vartheta }_2(t-{\tau }_2)+I^{*})-f({\vartheta }_2+I^{*})-d({\vartheta }_2+I^{*}),\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}=& \gamma ({\vartheta }_2+I^{*})+\mu (b,({\vartheta }_2+I^{*}))({\vartheta }_2(t-{\tau }_2)+I^{*})-\theta ({\vartheta }_3+R^{*})-d({\vartheta }_3+R^{*}),\hfill \\ \hfill {\displaystyle \frac{dD}{dt}}=& f({\vartheta }_2+I^{*})-\rho ({\vartheta }_4+D^{*}).\hfill \end{array}$$

(8)

The linearization of system (8) at $\vartheta =({\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4)=(0,0,0,0)$ is given by

$$\begin{array}{cc}\hfill & \dot{{\vartheta }_1}=l_1{\vartheta }_1+l_2{\vartheta }_3+l_3{\vartheta }_4+l_4{\vartheta }_2(t-\tau ),\hfill \\ \hfill & \dot{{\vartheta }_2}=m_1{\vartheta }_1+m_2{\vartheta }_2+m_3{\vartheta }_4+m_4{\vartheta }_2(t-\tau ),\hfill \\ \hfill & \dot{{\vartheta }_3}=n_1{\vartheta }_2+n_2{\vartheta }_3+n_3{\vartheta }_2(t-\tau ),\hfill \\ \hfill & \dot{{\vartheta }_4}=p_1{\vartheta }_2+p_2{\vartheta }_4,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & l_1=-d-(I^{*}+\epsilon D^{*})(1-u)\beta ,l_2=\theta ,l_3=-(1-u)\beta \epsilon S^{*},l_4=-(1-u)\beta S^{*},\hfill \\ \hfill & {\displaystyle m_1=(I^{*}+\epsilon D^{*})(1-u)\beta ,m_2=-\gamma +\frac{I^{*}b({\mu }_1-{\mu }_0)}{{(I^{*}+b)}^2}-d-f,m_3=\epsilon S^{*}(1-u)\beta ,}\hfill \\ \hfill & m_4=(1-u)\beta S^{*}-\left({\displaystyle {\mu }_0+({\mu }_1-{\mu }_0)\frac{b}{I^{*}+b}}\right),n_1=\gamma -\left({\displaystyle \frac{I^{*}b({\mu }_1-{\mu }_0)}{{(I^{*}+b)}^2}}\right),n_2=-\theta -d,\hfill \\ \hfill & {\displaystyle n_3={\mu }_0+({\mu }_1-{\mu }_0)\frac{b}{I^{*}+b},p_1=f,p_2=-\rho .}\hfill \end{array}$$

Given $\widehat{\tau }=\tau +\mu$, with $\mu \in \mathbb{R}$, define $S\left(t\right)={\vartheta }_1\left(\tau t\right),I\left(t\right)={\vartheta }_2\left(\tau t\right),R\left(t\right)={\vartheta }_3\left(\tau t\right)$ and $D\left(t\right)={\vartheta }_4\left(\tau t\right)$.

Thus, $\mu =0$ serves as the Hopf bifurcation parameter. As a result, we work within the fixed phase space $C=C([-1,0],{\mathbb{R}}^4)$, which does not depend on the delay $\tau$. Within space C, system (8) is reformulated into a functional differential equation as

$$\dot{\vartheta }\left(t\right)=Y\left(\mu ,{\vartheta }_t\right)+L_{\mu }\left({\vartheta }_t\right)$$

(9)

where $\vartheta \left(t\right)=({\vartheta }_1\left(t\right),{\vartheta }_2\left(t\right),{\vartheta }_3\left(t\right),{\vartheta }_4\left(t\right))\in R^4$ and $L_r:\to R$ with

$$L_{\mu }\left(\nu \right)=(\widehat{\tau }+\mu )\left(B_1\left[\begin{array}{c}{\nu }_1\left(0\right)\hfill \\ {\nu }_2\left(0\right)\hfill \\ {\nu }_3\left(0\right)\hfill \\ {\nu }_3\left(0\right)\hfill \end{array}\right]+B_2\left[\begin{array}{c}{\nu }_1(-1)\hfill \\ {\nu }_2(-1)\hfill \\ {\nu }_3(-1)\hfill \\ {\nu }_3(-1)\hfill \end{array}\right]\right),$$

$$\begin{array}{cc}\hfill B_1=\left(\begin{array}{cccc}{l}_1& 0& l_2& l_3\\ m_1& m_2& 0& m_3\\ 0& n_1& n_2& 0\\ 0& p_1& 0& p_2\end{array}\right),& B_2=\left(\begin{array}{cccc}0& l_4& 0& 0\\ 0& m_4& 0& 0\\ 0& n_3& 0& 0\\ 0& 0& 0& 0\end{array}\right)\hfill \end{array}$$

(10)

and

$$Y(\mu ,\nu )=(\widehat{\tau }+\mu )\left[\begin{array}{c}-(1-u)\beta ({\nu }_2(-1)+\epsilon {\nu }_4\left(0\right)){\nu }_1\left(0\right)\\ (1-u)\beta ({\nu }_2(-1)+\epsilon {\nu }_4\left(0\right)){\nu }_1\left(0\right)-\mu (b,{\nu }_2\left(0\right)){\nu }_2(-1)\\ \mu (b,{\nu }_2\left(0\right)){\nu }_2(-1)\\ 0\end{array}\right],$$

where $\nu \left(\varrho \right)={({\nu }_1\left(\varrho \right),{\nu }_2\left(\varrho \right),{\nu }_3\left(\varrho \right),{\nu }_4\left(\varrho \right))}^T\in C$. There is a function $\eta (\varrho ,\mu )$ with bounded variation for $\varrho \in [-1,0]$, according to the Riesz representation theorem, such that

$$L_{\mu }\nu ={\int }_{-1}^{0}d\eta (\varrho ,0)\nu \left(\varrho \right),\nu \in C.$$

Actually, we may have

$$\eta (\varrho ,\mu )=(\widehat{\tau }+\mu )\left(\begin{array}{cccc}{l}_1& 0& l_2& l_3\\ m_1& m_2& 0& m_3\\ 0& n_1& n_2& 0\\ 0& p_1& 0& p_2\end{array}\right)\delta \varrho -(\widehat{\tau }+\mu )\left(\begin{array}{cccc}0& l_4& 0& 0\\ 0& m_4& 0& 0\\ 0& n_3& 0& 0\\ 0& 0& 0& 0\end{array}\right)\delta (\varrho +1),$$

with $\delta$ being the Dirac delta function. For $\nu \in C^1\left([-1,0],R^4\right)$, we define

$$A\left(\mu \right)\nu =\left\{\begin{array}{cc}{\displaystyle {\int }_{-1}^{0}d\eta (s,\mu )\nu \left(s\right)}\hfill & \varrho =0\hfill \\ {\displaystyle \frac{d\nu \left(\varrho \right)}{d\varrho }}\hfill & \varrho \in [-1,0),\hfill \end{array}\right.$$

and

$$R\left(\mu \right)\nu =\left\{\begin{array}{cc}Y(\mu ,\nu )\hfill & \varrho =0\hfill \\ 0\hfill & \varrho \in [-1,0).\hfill \end{array}\right.$$

Then, model (9) is equivalent to

$$\dot{{\vartheta }_t}=R\left(\mu \right){\vartheta }_t+A\left(\mu \right){\vartheta }_t,$$

(11)

where ${\vartheta }_t={\vartheta }_{t+\varrho }$ for $\varrho \in [-1,0]$. For $\varsigma \in C^1\left([0,1],{\left(R^4\right)}^{*}\right)$, define

$$A^{*}\left(\varsigma \right)s=\left\{\begin{array}{cc}{\displaystyle {\int }_{-1}^0\varsigma (-t)d{\eta }^T(t,0)}\hfill & s=0\hfill \\ {\displaystyle \frac{d\varsigma \left(s\right)}{ds}}\hfill & s\in (-1,0].\hfill \end{array}\right.$$

Consider the bilinear

$$<\varsigma ,\nu >=\overline{\varsigma }\left(0\right)\nu \left(0\right)-{\int }_{-1}^0{\int }_{\xi =0}^{\varrho }{\varsigma }^T(\xi -\varrho )d\eta \left(\varrho \right)\nu \left(\xi \right)d\xi .$$

(12)

Given that $A\left(0\right)$ and $A^{*}$ are adjoint operators, the eigenvectors of A and $A^{*}$ corresponding to $i\omega t$ and $-i\omega t$, respectively, are $\varkappa \left(\varrho \right)={(1,{\varkappa }_1,{\varkappa }_2,{\varkappa }_3)}^T{e}^{i\varrho {\omega }_0\widehat{\tau }}$ and ${\varkappa }^{*}\left(\varrho \right)=D\left(1,{\varkappa }_1^{*},{\varkappa }_2^{*},{\varkappa }_3^{*}\right)e^{i{\omega }_0\widehat{\tau }}$. In this context, $\eta \left(\varrho \right)=\eta (\varrho ,0)$. In light of the established definitions of the function $\eta (\varrho ,\mu )$ and the operator $A\left(0\right)$, it becomes evident that we can express the following relationship in a more generalized form:

$$\widehat{\tau }\left[\begin{array}{cccc}{l}_1& 0& l_2& l_3\\ m_1& m_2& 0& m_3\\ 0& n_1& n_2& 0\\ 0& p_1& 0& p_2\end{array}\right]\varkappa \left(0\right)+\widehat{\tau }\left[\begin{array}{cccc}0& l_4& 0& 0\\ 0& m_4& 0& 0\\ 0& n_3& 0& 0\\ 0& 0& 0& 0\end{array}\right]\varkappa (-1)=\mathrm{i}{\omega }_0\widehat{\tau }\varkappa \left(0\right).$$

For $\varkappa (-1)=\varkappa \left(0\right){\mathrm{e}}^{-\mathrm{i}{\omega }_0\widehat{\tau }}$, we obtain

$\left\{\begin{array}{c}{\displaystyle {\varkappa }_1=\frac{m_1\left(p_2-i{\omega }_0\right)}{m_3{p}_1-\left(p_2-i{\omega }_0\right)\left(m_4{e}^{-i{\omega }_0\widehat{\tau }}+m_2-i{\omega }_0\right)},}\hfill \\ {\displaystyle {\varkappa }_2=-\frac{{\varkappa }_1\left(n_1+n_3{e}^{-i{\omega }_0\widehat{\tau }}\right)}{n_2-i{\omega }_0},{\varkappa }_3=-\frac{p_1{\varkappa }_1}{p_2-i{\omega }_0}.}\hfill \end{array}\right.$

The eigenvector ${\varkappa }^{*}\left(s\right)=D\left(1,{\varkappa }_1^{*},{\varkappa }_2^{*},{\varkappa }_3^{*}\right){\mathrm{e}}^{\mathrm{i}{\omega }_0\widehat{\tau }s}$ of $A^{*}$ corresponding to $-\mathrm{i}{\omega }_0\widehat{\tau }$ can be similarly obtained, where $\left\{\begin{array}{c}{\displaystyle {\varkappa }_1^{*}=-\frac{l_1+i{\omega }_0}{m_1},{\varkappa }_2^{*}=-\frac{l_2}{n_2+i{\omega }_0},{\varkappa }_3^{*}=-\frac{l_3{m}_1-l_1{m}_3-i{m}_3{\omega }_0}{m_1\left(p_2+i{\omega }_0\right)}.}\hfill \end{array}\right.$

By using (12), we can determine the value of D needed to ensure that $〈{\varkappa }^{*}\left(s\right),\varkappa \left(\varrho \right)〉=1$.

$$\begin{array}{cc}\hfill 〈{\varkappa }^{*}\left(s\right),\varkappa \left(\varrho \right)〉=& \overline{D}{\left(1,{\varkappa }_1,{\varkappa }_2,{\varkappa }_3\right)}^{\mathrm{T}}\left(1,{\overline{\varkappa }}_1^{*},{\overline{\varkappa }}_2^{*},{\overline{\varkappa }}_3^{*}\right)\hfill \\ & -{\int }_{-1}^0{\int }_{\xi =0}^{\varrho }\overline{D}\left(1,{\overline{\varkappa }}_1^{*},{\overline{\varkappa }}_2^{*},{\overline{\varkappa }}_3^{*}\right){\mathrm{e}}^{-\mathrm{i}{\omega }_0\widehat{\tau }(\xi -\varrho )}\mathrm{d}\eta \left(\varrho \right){\left(1,{\varkappa }_1,{\varkappa }_2,{\varkappa }_4\right)}^{\mathrm{T}}{\mathrm{e}}^{\mathrm{i}{\omega }_0\widehat{\tau }\xi }\mathrm{d}\xi \hfill \end{array}$$

$$=\overline{D}\left\{1+{\varkappa }_1{\overline{\varkappa }}_1^{*}+{\varkappa }_3{\overline{\varkappa }}_3^{*}+{\varkappa }_2{\overline{\varkappa }}_2^{*}-{\int }_{-1}^0\left(1,{\overline{\varkappa }}_1^{*},{\overline{\varkappa }}_2^{*},{\overline{\varkappa }}_3^{*}\right)\varrho {\mathrm{e}}^{\mathrm{i}{\omega }_0\widehat{\tau }\varrho }\mathrm{d}\eta \left(\varrho \right){\left(1,{\varkappa }_1,{\varkappa }_2,{\varkappa }_3\right)}^{\mathrm{T}}\right\}$$

$$=\overline{D}\left\{1+{\varkappa }_1{\overline{\varkappa }}_1^{*}+{\varkappa }_3{\overline{\varkappa }}_3^{*}+{\varkappa }_2{\overline{\varkappa }}_2^{*}+\widehat{\tau }{\varkappa }_1{\mathrm{e}}^{-\mathrm{i}{\omega }_0\widehat{\tau }}(l_4+m_4{\overline{\varkappa }}_1^{*}+n_3{\overline{\varkappa }}_2^{*})\right\}.$$

Therefore, we can choose D as

$$D={\displaystyle \frac{1}{1+{\overline{\varkappa }}_1{\varkappa }_1^{*}+{\overline{\varkappa }}_2{\varkappa }_2^{*}+{\overline{\varkappa }}_3{\varkappa }_3^{*}+\widehat{\tau }{\overline{\varkappa }}_1{\mathrm{e}}^{\mathrm{i}{\omega }_0\widehat{\tau }}(l_4+m_4{\varkappa }_1^{*}+n_3{\varkappa }_2^{*})}},$$

such that $〈{\varkappa }^{*},\overline{\varkappa }\left(\varrho \right)〉=0,〈{\varkappa }^{*},\varkappa \left(\varrho \right)〉=1$. Assume ${\vartheta }_t$ is the solution to (11) under the specific condition where the parameter $\mu$ is set to zero. Now, we define

$$z\left(t\right)=〈{\varkappa }^{*},{\vartheta }_t〉,M(t,\varrho )={\vartheta }_t\left(\varrho \right)-2Re\left\{z\left(t\right)\varkappa \left(\varrho \right)\right\}.$$

(13)

On the center manifold $C_0$, we have $M(t,\varrho )=M(z\left(t\right)\overline{z}\left(t\right),\varrho )$, and

$$M(z,\overline{z},\varrho )=M_{20}\left(\varrho \right){\displaystyle \frac{z^2}{2}}+M_{11}z\overline{z}+M_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+M_{30}{\displaystyle \frac{z^3}{6}}+\dots$$

(14)

We concentrate on the real solution ${\vartheta }_t\in C_0$ of (11), assuming that M remains real if ${\vartheta }_t$ is real. The local coordinates for the center manifold $C_0$ in the directions of ${\varkappa }^{*}$ and ${\overline{\varkappa }}^{*}$ are denoted by z and $\overline{z}$. With $\mu =0$, we obtain

$$\dot{z}\left(t\right)=i\omega \widehat{\tau }z+{\varkappa }^{*}\left(0\right)Y(0,2Re\{z\left(t\right)\varkappa \left(\varrho \right)+M(z,\overline{z},0))\}\stackrel{\mathrm{def}}{=}i\omega \widehat{\tau }z+Y_0(z.\overline{z}){\varkappa }^{*}\left(0\right).$$

We write the equation as $\dot{z}\left(t\right)=i\omega \widehat{\tau }z+g(z·\overline{z})$, where

$$g(z,\overline{z})=g_{20}{\displaystyle \frac{z^2}{2}}+g_{11}z\overline{z}+g_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+g_{21}{\displaystyle \frac{z^2\overline{z}}{2}}+\dots$$

(15)

Equations (14) and (15) imply that

$$\begin{array}{cc}\hfill {\vartheta }_t\left(\varrho \right)=& 2Re\left\{z\left(t\right)\varkappa \left(\varrho \right)\right\}+M(t,\varrho )=M_{20}\left(\varrho \right){\displaystyle \frac{z^2}{2}}+M_{11}z\overline{z}+M_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+({(1,{\varkappa }_1,{\varkappa }_2,{\varkappa }_3)}^T{e}^{i{\omega }_0\widehat{\tau }\varrho }z\hfill \\ \hfill & +{(1,\overline{{\varkappa }_1},\overline{{\varkappa }_2},\overline{{\varkappa }_3})}^T{e}^{-i{\omega }_0\widehat{\tau }\varrho }\overline{z}+\dots \hfill \end{array}$$

From Equation (13), we have $\varkappa \left(\varrho \right)={(1,{\varkappa }_1,{\varkappa }_2,{\varkappa }_3)}^T{e}^{i{\omega }_0\widehat{\tau }}$ and $\vartheta =({\vartheta }_{1t}\left(\varrho \right),$${\vartheta }_{2t}\left(\varrho \right)$, ${\vartheta }_{3t}\left(\varrho \right)$, and ${\vartheta }_{4t}\left(\varrho \right))=M(t,\varrho )+z\varkappa \left(\varrho \right)+z\varkappa \left(\varrho \right)$; then,

$$\begin{array}{cc}\hfill & {\vartheta }_{1t}\left(0\right)=z+\overline{z}+M_{20}^{\left(1\right)}\left(0\right){\displaystyle \frac{z^2}{2}}+M_{11}^{\left(1\right)}\left(0\right)z\overline{z}+M_{02}^{\left(1\right)}\left(0\right){\displaystyle \frac{{\overline{z}}^2}{2}}+O\left(|z,\overline{z}{|}^3\right),\hfill \\ \hfill & {\vartheta }_{2t}\left(0\right)=z{\varkappa }_1+\overline{z{\varkappa }_1}+M_{20}^{\left(2\right)}\left(0\right){\displaystyle \frac{z^2}{2}}+M_{11}^{\left(2\right)}\left(0\right)z\overline{z}+M_{02}^{\left(2\right)}\left(0\right){\displaystyle \frac{{\overline{z}}^2}{2}}+O\left(|z,\overline{z}{|}^3\right),\hfill \\ \hfill & {\vartheta }_{3t}\left(0\right)=z{\varkappa }_2+\overline{z{\varkappa }_2}+M_{20}^{\left(3\right)}\left(0\right){\displaystyle \frac{z^2}{2}}+M_{11}^{\left(3\right)}\left(0\right)z\overline{z}+M_{02}^{\left(3\right)}\left(0\right){\displaystyle \frac{{\overline{z}}^2}{2}}+O\left(|z,\overline{z}{|}^3\right),\hfill \\ \hfill & {\vartheta }_{4t}\left(0\right)=z{\varkappa }_3+\overline{z{\varkappa }_3}+M_{20}^{\left(4\right)}\left(0\right){\displaystyle \frac{z^2}{2}}+M_{11}^{\left(4\right)}\left(0\right)z\overline{z}+M_{02}^{\left(4\right)}\left(0\right){\displaystyle \frac{{\overline{z}}^2}{2}}+O\left(|z,\overline{z}{|}^3\right),\hfill \\ \hfill & {\vartheta }_{1t}(-1)=z{e}^{-i{\omega }_0\widehat{\tau }}+\overline{z}{e}^{i{\omega }_0\widehat{\tau }}+M_{20}^{\left(1\right)}(-1){\displaystyle \frac{z^2}{2}}+M_{11}^{\left(1\right)}(-1)z\overline{z}+M_{02}^{\left(1\right)}(-1){\displaystyle \frac{{\overline{z}}^2}{2}}+O\left(|z,\overline{z}{|}^3\right),\hfill \\ \hfill & {\vartheta }_{2t}(-1)=z{\varkappa }_1{e}^{-i{\omega }_0\widehat{\tau }}+\overline{z{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}+M_{20}^{\left(2\right)}(-1){\displaystyle \frac{z^2}{2}}+M_{11}^{\left(2\right)}(-1)z\overline{z}+M_{02}^{\left(2\right)}(-1){\displaystyle \frac{{\overline{z}}^2}{2}}+O\left(|z,\overline{z}{|}^3\right).\hfill \end{array}$$

Along with (10), we can have

$$\begin{array}{cc}g(z,\overline{z})\hfill & =f_0(z,\overline{z})\overline{{\varkappa }^{*}}\left(0\right)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & =f(0,{\vartheta }_t)\overline{{\varkappa }^{*}}\left(0\right)\hfill & \end{array}$$

(17)

$$\begin{array}{cc}\hfill & =\widehat{\tau }\overline{D}\left(1,{\overline{{\varkappa }_1}}^{*},{\overline{{\varkappa }_2}}^{*},{\overline{{\varkappa }_3}}^{*}\right)\left[\begin{array}{c}-(1-u)\beta ({\vartheta }_{2t}(-1)+\epsilon {\vartheta }_{4t}\left(0\right)){\vartheta }_{1t}\left(0\right)\\ (1-u)\beta ({\vartheta }_{2t}(-1)+\epsilon {\vartheta }_{4t}\left(0\right)){\vartheta }_{1t}\left(0\right)-\mu (b,{\vartheta }_{2t}\left(0\right)){\vartheta }_{2t}(-1)\\ \mu (b,{\vartheta }_{2t}\left(0\right)){\vartheta }_{2t}(-1)\\ 0\end{array}\right]\hfill & \end{array}$$

(18)

$$\begin{array}{cc}\hfill & =\widehat{\tau }\overline{D}\left(p_1{z}^2+2p_{2}z\overline{z}+p_3{\overline{z}}^2+p_4{z}^2\overline{z}\right)+\mathrm{higher}\mathrm{order}\mathrm{terms}\hfill & \end{array}$$

(19)

with

$$\begin{array}{cc}\hfill p_1=& \beta (u-1)(\overline{{\varkappa }_1^{*}}-1)(-{\varkappa }_3ϵ+{\varkappa }_1(-e^{-i{\omega }_0\widehat{\tau }})),\hfill \\ \hfill p_2=& -{\displaystyle \frac{1}{2}}\beta (u-1)(\overline{{\varkappa }_1^{*}}-1)e^{-i{\omega }_0\widehat{\tau }}(\overline{{\varkappa }_1}{e}^{2i{\omega }_0\widehat{\tau }}+ϵ(\overline{{\varkappa }_3}+{\varkappa }_3)e^{i{\omega }_0\widehat{\tau }}+{\varkappa }_1),\hfill \\ \hfill p_3=& \beta (u-1)(1-\overline{{\varkappa }_1^{*}})(ϵ\overline{{\varkappa }_3}+\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}),\hfill \\ \hfill p_4=& {\displaystyle \frac{1}{2}}\beta (u-1)(\overline{{\varkappa }_1^{*}}-1)e^{-i{\omega }_0\widehat{\tau }}(\stackrel{(1)}{M_{20}(0)}\overline{{\varkappa }_1}(-e^{2i{\omega }_0\widehat{\tau }})-e^{i{\omega }_0\widehat{\tau }}(ϵ(\stackrel{\left(1\right)}{M_{20}(0)}\overline{{\varkappa }_3}+2{\varkappa }_3\stackrel{\left(1\right)}{M_{11}\left(0\right)}\hfill \\ & +2\stackrel{\left(4\right)}{M_{11}\left(0\right)}+\stackrel{\left(4\right)}{M_{20}\left(0\right)})+2\stackrel{\left(2\right)}{M_{11}(-1)}+\stackrel{\left(2\right)}{M_{20}(-1)}-2{\varkappa }_1\stackrel{\left(1\right)}{M_{11}\left(0\right)}).\hfill \end{array}$$

From (15) and (16), we obtain

$$g_{20}=2\widehat{\tau }\overline{D}{p}_1,g_{11}=2\widehat{\tau }\overline{D}{p}_2,g_{02}=2\widehat{\tau }\overline{D}{p}_3,g_{21}=2\widehat{\tau }\overline{D}{p}_4.$$

We are also required to determine $M_{20}\left(\varrho \right)$ and $M_{11}\left(\varrho \right)$. By using (11) and (13), we obtain

$$\begin{array}{cc}\hfill \dot{M}& =\dot{{\vartheta }_t}-\dot{z}\varkappa -\dot{\overline{z}}\dot{\varkappa }\hfill & \end{array}$$

(20)

$$\begin{array}{cc}\hfill & =\left\{\begin{array}{cc}AM-2Re\left\{{\varkappa }^{*}\left(0\right)Y_0\overline{\varkappa }\left(\varrho \right)\right\},\hfill & -1\le \varrho <0\hfill \\ AM-2Re\left\{q^{*}\left(0\right)Y_0\overline{q}\left(\varrho \right)+Y_0\right\}\hfill & \varrho =0\hfill \end{array}\right.\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & \stackrel{\mathrm{def}}{=}AM+G(z,\overline{z},\varrho ),\hfill & \end{array}$$

(22)

where

$$G(z,\overline{z},\varrho )=G_{20}\left(\varrho \right){\displaystyle \frac{z^2}{2}}+G_{11}\left(\varrho \right)z\overline{z}+G_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+\dots$$

(23)

Notice that on the center manifold $C_0$ close to the origin,

$$\dot{M}=M_z\dot{z}+M_{\overline{z}}\dot{\overline{z}}.$$

(24)

Therefore, we obtain

$$\left(A-2i{\omega }_0\widehat{\tau }\right)M_{20}\left(\varrho \right)=-G_{20}\left(\varrho \right),A{M}_{11}\left(\varrho \right)=-G_{11}\left(\varrho \right).$$

(25)

From system (20), for $\varrho \in [-1,0)$,

$$G(z,\overline{z},\varrho )=-{\varkappa }^{*}\left(0\right){\overline{Y}}_0\overline{\varkappa }\left(\varrho \right)-{\overline{\varkappa }}^{*}\left(0\right)Y_0\overline{\varkappa }\left(\varrho \right)=-\overline{g}(z,\overline{z})\overline{\varkappa }\left(\varrho \right)-g(z,\overline{z})\varkappa \left(\varrho \right).$$

(26)

By comparing the coefficient with (23), we obtain

$$G_{20}\left(\varrho \right)=-{\overline{g}}_{02}\overline{\varkappa }\left(\varrho \right)-g_{20}\varkappa \left(\varrho \right),$$

(27)

and

$$G_{11}=-{\overline{g}}_{11}\overline{\varkappa }\left(\varrho \right)-g_{11}\varkappa \left(\varrho \right).$$

(28)

From (25), (28), and the def. of A, we obtain

$${\dot{M}}_{20}\left(\varrho \right)=2i{\omega }_0\widehat{\tau }{M}_{20}\left(\varrho \right)+{\overline{g}}_{02}\overline{\varkappa }\left(\varrho \right)+g_{20}\varkappa \left(\varrho \right),$$

Noticing $\varkappa \left(\varrho \right)=\varkappa \left(0\right)e^{i{\omega }_0\widehat{\tau }}$, we have

$$M_{20}\left(\varrho \right)={\displaystyle \frac{i{g}_{20}}{\widehat{\tau }{\omega }_0}}\varkappa \left(0\right)e^{i\varrho {\omega }_0\widehat{\tau }}+{\displaystyle \frac{{\overline{ig}}_{02}}{3\widehat{\tau }{\omega }_0}}\overline{\varkappa }\left(0\right)e^{-i\varrho {\omega }_0\widehat{\tau }}+X_1{e}^{2i\varrho {\omega }_0\widehat{\tau }},$$

(29)

where a constant vector in ${\mathbb{R}}^4$ is defined as $X_2=({X_2}^{\left(1\right)},{X_2}^{\left(2\right)},{X_2}^{\left(3\right)},{X_2}^{\left(4\right)})$. A similar result can be obtained:

$$M_{11}\left(\varrho \right)={\displaystyle \frac{i{g}_{11}}{\widehat{\tau }{\omega }_0}}\varkappa \left(0\right)e^{i\varrho {\omega }_0\widehat{\tau }}+{\displaystyle \frac{{\overline{ig}}_{11}}{\widehat{\tau }{\omega }_0}}\overline{\varkappa }\left(0\right)e^{-i\varrho {\omega }_0\widehat{\tau }}+X_2.$$

(30)

In the following, we determine $X_1$ and $X_2$. By using the definition of A and (25), we obtain

$${\int }_{-1}^0{M}_{20}\left(\varrho \right)d\eta \left(\varrho \right)=-G_{20}\left(0\right)+2i{\omega }_0\widehat{\tau }{M}_{20}\left(0\right),$$

(31)

$${\int }_{-1}^0{M}_{11}\left(\varrho \right)d\eta \left(\varrho \right)=-G_{11}\left(0\right),$$

(32)

where $\eta \left(\varrho \right)=\eta (0,\varrho )$. From (20) and (23), we have

$$G_{11}\left(0\right)=-g_{11}\varkappa \left(0\right)-{\overline{g}}_{11}\overline{\varkappa }\left(0\right)+2\widehat{\tau }{\left(d_1,d_2,d_3,d_4\right)}^T,$$

(33)

$$G_{20}\left(0\right)=-g_{20}\varkappa \left(0\right)-{\overline{g}}_{02}\overline{\varkappa }\left(0\right)+2\widehat{\tau }{\left(c_1,c_2,c_3,c_4\right)}^T.$$

(34)

The coefficients of $z^2$ and $z\overline{z}$ in $f_0(z,\overline{z})$ are given, respectively, as follows, where ${\left(c_1,c_2,c_3,c_4\right)}^T=C_1$ and $\left(d_1,d_2,d_3,d_4\right)=D_1$:

$$C_1=\left[\begin{array}{c}{c}_1\hfill \\ c_2\hfill \\ c_3\hfill \\ c_4\hfill \end{array}\right]=\left[\begin{array}{c}-(1-u)\beta ({\varkappa }_1{e}^{-i{\omega }_0\widehat{\tau }}+\epsilon {\varkappa }_3)\\ (1-u)\beta ({\varkappa }_1{e}^{-i{\omega }_0\widehat{\tau }}+\epsilon {\varkappa }_3)-\mu (b,{\varkappa }_1){\varkappa }_1{e}^{-i{\omega }_0\widehat{\tau }}\\ \mu (b,{\varkappa }_1){\varkappa }_1{e}^{-i{\omega }_0\widehat{\tau }}\\ 0\end{array}\right],$$

$$\mathrm{and}{D}_1=\left[\begin{array}{c}{d}_1\hfill \\ d_2\hfill \\ d_3\hfill \\ d_4\hfill \end{array}\right]=\left[\begin{array}{c}-(1-u)\beta (Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\}+\epsilon Re\left\{{\varkappa }_3\right\})\\ (1-u)\beta (Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\}+\epsilon Re\left\{{\varkappa }_3\right\})-\mu (b,Re\left\{{\varkappa }_1\right\})Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\})\\ \mu (b,Re\left\{{\varkappa }_1\right\})Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\})\\ 0\end{array}\right],$$

By inserting (29) and (33) into (31) and observing that

$$\varkappa \left(0\right)\left(i\omega \widehat{\tau }I-{\int }_{-1}^0{e}^{i\omega \widehat{\tau }}d\eta \left(\varrho \right)\right)=0.$$

and

$$\overline{\varkappa }\left(0\right)\left(-i\omega \widehat{\tau }I-{\int }_{-1}^0{e}^{-i\omega \widehat{\tau }}d\eta \left(\varrho \right)\right)=0.$$

we finally have

$$\left(2i{\omega }_0\widehat{\tau }I-{\int }_{-1}^0{e}^{2i\omega \widehat{\tau }}d\eta \left(\varrho \right)\right)X_1=2\widehat{\tau }{C}_1,$$

(35)

which leads to $C^{*}{X}_1=2C_1$, where

$$C^{*}=\left[\begin{array}{cccc}{\gimel }_{11}& {\gimel }_{12}& {\gimel }_{13}& {\gimel }_{14}\\ {\gimel }_{21}& {\gimel }_{22}& {\gimel }_{23}& {\gimel }_{24}\\ {\gimel }_{31}& {\gimel }_{32}& {\gimel }_{33}& {\gimel }_{34}\\ {\gimel }_{41}& {\gimel }_{42}& {\gimel }_{43}& {\gimel }_{44}\end{array}\right],D^{*}=\left[\begin{array}{cccc}-l_1& -l_4& -l_2& -l_3\\ -m_1& -m_2-m_4& 0& -m_3\\ 0& -n_1-n_3& -n_2& 0\\ 0& -p_1& 0& -p_2\end{array}\right].$$

where

$$\begin{array}{cc}\hfill & {\gimel }_{11}=2i{\omega }_0-l_1,{\gimel }_{12}=-l_4{e}^{-2i\omega \widehat{\tau }},{\gimel }_{13}=-l_2,{\gimel }_{14}=-l_3,{\gimel }_{21}=-m_1,\hfill \\ \hfill & {\gimel }_{22}=2i{\omega }_0-m_2-m_4{e}^{-2i\omega \widehat{\tau }},{\gimel }_{23}=0,{\gimel }_{24}=-m_3,{\gimel }_{31}=0,{\gimel }_{32}=-n_1-n_3{e}^{-2i\omega \widehat{\tau }},\hfill \\ \hfill & {\gimel }_{33}=-n_2+2i{\omega }_0,{\gimel }_{34}=0,{\gimel }_{41}=0,{\gimel }_{42}=-p_1,{\gimel }_{43}=0,{\gimel }_{44}=2i{\omega }_0-p_2.\hfill \end{array}$$

We can compute $g_{21}$ using $M_{11}\left(\varrho \right)$ and $M_{20}\left(\varrho \right)$, which can be calculated from (29) and (30); that is,

$$\left[\begin{array}{cccc}{\gimel }_{11}& {\gimel }_{12}& {\gimel }_{13}& {\gimel }_{14}\\ {\gimel }_{21}& {\gimel }_{22}& {\gimel }_{23}& {\gimel }_{24}\\ {\gimel }_{31}& {\gimel }_{32}& {\gimel }_{33}& {\gimel }_{34}\\ {\gimel }_{41}& {\gimel }_{42}& {\gimel }_{43}& {\gimel }_{44}\end{array}\right]X_1=2\left[\begin{array}{c}{c}_1\\ c_2\\ c_3\\ 0\end{array}\right],$$

where

$$\begin{array}{cc}& c_1=\beta (u-1)\left({\varkappa }_3ϵ+{\varkappa }_1{e}^{-i{\omega }_0\widehat{\tau }}\right),\hfill \\ & c_2=\beta (1-u)\left({\varkappa }_3ϵ+{\varkappa }_1{e}^{-i{\omega }_0\widehat{\tau }}\right)-{\varkappa }_1\left({\displaystyle \frac{b\left({\mu }_1-{\mu }_0\right)}{b+{\varkappa }_1}}+{\mu }_0\right)e^{-i{\omega }_0\widehat{\tau }},\hfill \\ & c_3={\varkappa }_1\left({\displaystyle \frac{b\left({\mu }_1-{\mu }_0\right)}{b+{\varkappa }_1}}+{\mu }_0\right)e^{-i{\omega }_0\widehat{\tau }}.\hfill \end{array}$$

It follows that

$$\begin{array}{cccc}\hfill X_1^{\left(1\right)}& ={\displaystyle \frac{2}{M_1}}\left|\begin{array}{cccc}{c}_1& {\gimel }_{12}& {\gimel }_{13}& {\gimel }_{14}\\ c_2& {\gimel }_{22}& {\gimel }_{23}& {\gimel }_{24}\\ c_3& {\gimel }_{32}& {\gimel }_{33}& {\gimel }_{34}\\ 0& {\gimel }_{42}& {\gimel }_{43}& {\gimel }_{44}\end{array}\right|,X_1^{\left(2\right)}\hfill & \hfill ={\displaystyle \frac{2}{M_1}}\left|\begin{array}{cccc}{\gimel }_{11}& c_1& {\gimel }_{13}& {\gimel }_{14}\\ {\gimel }_{21}& c_2& {\gimel }_{23}& {\gimel }_{24}\\ {\gimel }_{31}& c_3& {\gimel }_{33}& {\gimel }_{34}\\ {\gimel }_{41}& 0& {\gimel }_{43}& {\gimel }_{44}\end{array}\right|,X_1^{\left(3\right)}& ={\displaystyle \frac{2}{M_1}}\left|\begin{array}{cccc}{\gimel }_{11}& {\gimel }_{12}& c_1& {\gimel }_{14}\\ {\gimel }_{21}& {\gimel }_{22}& c_2& {\gimel }_{24}\\ {\gimel }_{31}& {\gimel }_{32}& c_3& {\gimel }_{34}\\ {\gimel }_{41}& {\gimel }_{42}& 0& {\gimel }_{44}\end{array}\right|,\hfill \end{array}$$

$$X_1^{\left(4\right)}={\displaystyle \frac{2}{M_1}}\left|\begin{array}{cccc}{\gimel }_{11}& {\gimel }_{12}& {\gimel }_{13}& c_1\\ {\gimel }_{21}& {\gimel }_{22}& {\gimel }_{23}& c_2\\ {\gimel }_{31}& {\gimel }_{32}& {\gimel }_{33}& c_3\\ {\gimel }_{41}& {\gimel }_{42}& {\gimel }_{43}& 0\end{array}\right|,\mathrm{where}{M}_1=\left|\begin{array}{cccc}{\gimel }_{11}& {\gimel }_{12}& {\gimel }_{13}& {\gimel }_{14}\\ {\gimel }_{21}& {\gimel }_{22}& {\gimel }_{23}& {\gimel }_{24}\\ {\gimel }_{31}& {\gimel }_{32}& {\gimel }_{33}& {\gimel }_{34}\\ {\gimel }_{41}& {\gimel }_{42}& {\gimel }_{43}& {\gimel }_{44}\end{array}\right|.$$

Similarly, substituting (30) and (35) into (32), we obtain

$$\left[\begin{array}{cccc}-l_1& -l_4& -l_2& -l_3\\ -m_1& -m_2-m_4& 0& -m_3\\ 0& -n_1-n_3& -n_2& 0\\ 0& -p_1& 0& -p_2\end{array}\right]X_2=2\left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ 0\end{array}\right],$$

where

$$\begin{array}{cc}\hfill d_1=& -(1-u)\beta (Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\}+\epsilon Re\left\{{\varkappa }_3\right\}),\hfill \\ \hfill d_2=& (1-u)\beta (Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\}+\epsilon Re\left\{{\varkappa }_3\right\})-\mu (b,Re\left\{{\varkappa }_1\right\})Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\},\hfill \\ \hfill d_3=& \mu (b,Re\left\{{\varkappa }_1\right\})Re\left\{\overline{{\varkappa }_1}{e}^{i{\omega }_0\widehat{\tau }}\right\}.\hfill \end{array}$$

Therefore, we obtain

$$\begin{array}{ccc}& X_2^{\left(1\right)}={\displaystyle \frac{2}{M_2}}\left|\begin{array}{cccc}{d}_1& -l_4& -l_2& -l_3\\ d_2& -m_2-m_4& 0& -m_3\\ d_3& -n_1-n_3& -n_2& 0\\ 0& -p_1& 0& -p_2\end{array}\right|,\hfill & \hfill X_2^{\left(2\right)}={\displaystyle \frac{2}{M_2}}\left|\begin{array}{cccc}-l_1& d_1& -l_2& -l_3\\ -m_1& d_2& 0& -m_3\\ 0& d_3& -n_2& 0\\ 0& 0& 0& -p_2\end{array}\right|,\\ & X_2^{\left(3\right)}={\displaystyle \frac{2}{M_2}}\left|\begin{array}{cccc}-l_1& -l_4& d_1& -l_3\\ -m_1& -m_2-m_4& d_2& -m_3\\ 0& -n_1-n_3& d_3& 0\\ 0& -p_1& 0& -p_2\end{array}\right|,\hfill & \hfill X_2^{\left(4\right)}={\displaystyle \frac{2}{M_2}}\left|\begin{array}{cccc}-l_1& -l_4& -l_2& d_1\\ -m_1& -m_2-m_4& 0& d_2\\ 0& -n_1-n_3& -n_2& d_3\\ 0& -p_1& 0& 0\end{array}\right|,\end{array}$$

where

$$M_2=\left|\begin{array}{cccc}-l_1& -l_4& -l_2& -l_3\\ -m_1& -m_2-m_4& 0& -m_3\\ 0& -n_1-n_3& -n_2& 0\\ 0& -p_1& 0& -p_2\end{array}\right|.$$

$$\begin{array}{cc}\hfill {\mu }_2& =-{\displaystyle \frac{Re\left\{c_1\left(0\right)\right\}}{Re\left\{{\lambda }^{\prime }\left(\widehat{\tau }\right)\right\}}},c_1\left(0\right)={\displaystyle \frac{g_{21}}{2}}+{\displaystyle \frac{i}{2{\omega }_0\widehat{\tau }}}\left(g_{20}{g}_{11}-2{\left|g_{11}\right|}^2-{\displaystyle \frac{{\left|g_{02}\right|}^2}{3}}\right),\hfill \\ \hfill T_2& =-{\displaystyle \frac{{\mu }_{2}Im\left\{{\lambda }^{\prime }\left(\widehat{\tau }\right)\right\}+Im\left\{c_1\left(0\right)\right\}}{{\omega }_0\widehat{\tau }}},{\beta }_2=2Re\left(c_1\left(0\right)\right).\hfill \end{array}$$

(36)

The main result is deduced based on the conclusion of Hassard et al. [39]. The stability of the bifurcating periodic solution is influenced by ${\beta }_2$: the solution will be stable (unstable) if ${\beta }_2<0$ (${\beta }_2>0$). ${\mu }_2$ determines the direction of the Hopf bifurcation; if ${\mu }_2>0$ (${\mu }_2<0$), the Hopf bifurcation is supercritical (subcritical). Finally, $T_2$ determines the period of the bifurcating periodic solution, which increases (decreases) if $T_2>0$ ($T_2<0$).

5. Delay Model: Optimal Control

The subsequent section explores the optimal control problem associated with model (1). We delve into the existence and characterization of the problem.

5.1. Formulation

Based on the delay model outlined in Equation (1), we have formulated an optimal control problem that focuses on two main strategies. Let us first introduce the control set of Lebesgue square integrable functions over time $[0,T]$.

$$U=\left\{v_i\left(t\right)\in L^2[0,T]:a_0\le v_i\left(t\right)\le a_1,0\le t\le T\right\},i=1,2$$

where $v_i,(i=1,2)$ is the control variable with $a_0$ and $a_1$ as the minimum and the maximum values of the control variables. The first strategy aims to increase the quarantine rate of susceptible individuals through targeted education campaigns. The second strategy seeks to enhance the immunity of Ebola survivors through a comprehensive approach, which includes nutritional support, regular medical follow-ups, physical and mental rehabilitation, and the prevention of secondary infections. Additionally, the plan emphasizes the importance of adequate rest, stress management, and participation in support groups or clinical trials as vital components for recovery and long-term health.

To implement these strategies, the model is modified by introducing the control variable $v_1\left(t\right)$ in place of the parameter u, which governs the quarantine rate. In a similar manner, the parameter $\theta$, related to immunity enhancement, is replaced by the control variable $v_2\left(t\right)$. Then, the delay model can be expressed in the following manner for the control problem:

$$\left.\begin{array}{cc}\hfill & {\displaystyle \frac{dS}{dt}=\Lambda -(1-v_1\left(t\right))\beta (I(t-{\tau }_1)+\epsilon D)S-dS+(1-v_2\left(t\right))R,}\hfill \\ \hfill & {\displaystyle \frac{dI}{dt}=(1-v_1\left(t\right))\beta (I(t-{\tau }_1)+\epsilon D)S-\gamma I-I(t-{\tau }_2)\mu (b,I)-dI-fI,}\hfill \\ \hfill & {\displaystyle \frac{dR}{dt}=\gamma I+I(t-{\tau }_2)\mu (b,I)-(1-v_2\left(t\right))R-dR,}\hfill \\ \hfill & {\displaystyle \frac{dD}{dt}=fI-\rho D.}\hfill \end{array}\right\}$$

(37)

$$\left\{\begin{array}{c}S\left(\nu \right)={\Psi }_1\left(\nu \right);I\left(\nu \right)={\Psi }_2\left(\nu \right);R\left(\nu \right)={\Psi }_3\left(\nu \right);D\left(\nu \right)={\Psi }_4\left(\nu \right),\\ {\Psi }_i\in \mathbb{C}\left([-\tau ,0],{\mathbb{R}}_{+}\right);(i=1,\cdots ,4),\mathrm{with}\nu \in [-\tau ,0],\mathrm{and}{\Psi }_i\left(\nu \right)>0.\end{array}\right.$$

(38)

This section focuses on managing the movement of individuals into quarantine and achieving permanent immunity, either through natural recovery or full vaccination. Our primary objective is to determine the optimal rate at which individuals should enter quarantine areas and the necessary density for an effective response during health crises. To achieve this, we propose educational programs that raise public awareness about disease transmission, emphasizing the importance of following health precautions. This approach not only promotes responsible behavior but also helps minimize implementation costs.

We assume the population dynamics to be proportional to the infectious, recovered, and deceased (but not yet buried) populations, scaled by factors $A_1$, $A_2$, and $A_3$, respectively. The losses due to control measures are modeled as being proportional to the square of the control intensity, with scaling factors $B_1/2$ and $B_2/2$. The objective function is given as follows. We introduce control variables $v_i\left(t\right)$, which are designed to balance awareness and control measures, allowing for an effective response to public health emergencies while minimizing disruptions to daily life.

$$\begin{array}{cc}\hfill J(v_1\left(t\right),v_2\left(t\right))=& {\int }_0^T\left[A_{1}I+A_{2}R+A_{3}D+{\displaystyle \frac{1}{2}}\left(B_1{v}_1^2+B_2{v}_2^2\right)\right]dt.\hfill \end{array}$$

(39)

Here, the non-negative weight coefficient is $A_i$ (where $i=1,2,3$). Our goal is to identify an optimal set of variables represented as $\left(v_1(·),v_2(·)\right)$ such that

$$J\left(\widehat{v_1}(·),\widehat{v_2}(·)\right)=min\left\{J\left(v_1(·),v_2(·)\right)\mid \left(v_1(·),v_2(·)\right)\in U\right\},$$

where the optimal set U is defined as follows:

$$U=\{\left(v_1(·),v_2(·)\right)\mid ,v_i(·)\in [0,1]\}$$

(40)

where $v_i(·)$ is Lebesgue measurable.

5.2. Existence and Characterization

In this part of our study, we focus on finding out if there is a best way to control a given system within a limited time frame. Specifically, we look at the system described by the Equations (37)–(40). Our goal is to determine if an optimal set of control strategies exists that can effectively manage the system’s behavior over this period.

Theorem 9.

There exists an optimal control $v^{\prime }\left(t\right)=\left(\widehat{v_1},\widehat{v_2}\right)\in U$ for the optimal solution $\widehat{S},\widehat{I},\widehat{R},\widehat{D}$ such that

$$J\left(\widehat{v_1},\widehat{v_2}\right)=\underset{\left(v_1,v_2\right)\in U}{min}J\left(v_1,v_2\right),$$

subject to the conditions in (37) and (38), with the state variables $\widehat{S},\widehat{I},\widehat{R},\widehat{D}$ remaining bounded on the interval $[0,T]$.

Proof. 

To show the existence of the control variables, the objective function satisfies the following properties:

(i)

The set of control variables and state variables is non-empty. This is derived from the property that the nonlinear functions in Equation (37) exhibit uniform Lipschitz continuity.

(ii)

The space of the control variables is closed and convex. Since the function space $L^p$ is known to be closed and convex, this property is satisfied.

(iii)

The right-hand side (RHS) of the control model in Equation (37) is bounded. The boundedness of both the state and control variables ensures this condition.

(iv)

The objective function is convex with respect to the control variables $w_i$ for $i=1,2$. Let $u,v\in U$ with $0<\sigma <1$. From Equation (39), we have

$$\begin{array}{cc}\hfill J(\sigma u+(1-\sigma \left)v\right)& \le {\displaystyle \underset{0}{\overset{T}{\int }}}\left[A_{1}I+A_{2}R+A_{3}D\right]dt+{\displaystyle \underset{0}{\overset{T}{\int }}}\left[{\displaystyle \frac{1}{2}}\sigma B_1{v}_1^2+{\displaystyle \frac{1}{2}}(1-\sigma )B_2{v}_2^2\right]dt\hfill \\ \hfill & \le \sigma J\left(u\right)+(1-\sigma )J\left(v\right).\hfill \end{array}$$

This proves the convexity of the objective function.

(v)

There exist positive constants $w_1$ and $w_2$ such that

$$J(v_1,v_2)\ge w_1{\left({\displaystyle \sum _{i=1}^2}{\left|v_i\left(t\right)\right|}^2\right)}^{1/2}-w_2.$$

(41)

From Equation (39), we can observe that

$$w_1={\displaystyle \frac{1}{2}}min\{B_1,B_2\},w_2>0.$$

Thus, the existence and uniqueness of the optimal control variables are established using the Filippov-type lemma [40]. □

As described in [41], the optimal control $v^{\prime }\left(t\right)=\left(\widehat{v_1},\widehat{v_2}\right)$ is characterized by the application of Pontryagin’s maximum principle and the formulation of the Hamiltonian function H, considering a delay in the state.

Theorem 10.

Let the optimal control variables be $\widehat{v_1}$ and $\widehat{v_2}$, and let the optimal state variables $\widehat{S},\widehat{I},\widehat{R}$, and $\widehat{D}$ be related to the control system (37); then, there exists an adjoint variable

$$\lambda \left(t\right):=({\lambda }_1\left(t\right),{\lambda }_2\left(t\right),{\lambda }_3\left(t\right),{\lambda }_4\left(t\right))\in {\mathbb{R}}^4,$$

that satisfies the criteria established by the adjoint equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\lambda }_1}{dt}=}& -\left[{\lambda }_1\left(-\beta (1-v_1\left(t\right))\left(\widehat{I}(t-{\tau }_1)+\widehat{D}ϵ\right)-d\right)+\beta {\lambda }_2(1-v_1\left(t\right))\left(\widehat{I}(t-{\tau }_1)+\widehat{D}ϵ\right)\right],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_2}{dt}=}& -{\lambda }_3\left(\gamma -{\displaystyle \frac{\widehat{I}(t-{\tau }_2)b\left({\mu }_1-{\mu }_0\right)}{(\widehat{I}+b{)}^2}}\right)+{\lambda }_2\left({\displaystyle \frac{\widehat{I}(t-{\tau }_2)b\left({\mu }_1-{\mu }_0\right)}{(\widehat{I}+b{)}^2}}-\gamma -d-f\right)+f{\lambda }_4+A_1\hfill \\ \hfill & +{\chi }_{[0,T-{\tau }_2]}\left(t\right)({\lambda }_2(t+{\tau }_2)\left(-{\displaystyle \frac{b\left({\mu }_1-{\mu }_0\right)}{\widehat{I}+b}}-{\mu }_0\right)+{\lambda }_3(t+{\tau }_2)\left({\displaystyle \frac{b\left({\mu }_1-{\mu }_0\right)}{\widehat{I}+b}}+{\mu }_0\right))\hfill \\ \hfill & +{\chi }_{[0,T-{\tau }_1]}\left(t\right)(-\beta \widehat{S}(1-u){\lambda }_1(t-{\tau }_1)+\left(\beta \widehat{S}(1-u)\right){\lambda }_2(t-{\tau }_1),\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_3}{dt}=}& -[{\lambda }_3(-d+v_2\left(t\right)-1)+A_2+{\lambda }_1(1-v_2\left(t\right))],\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_4}{dt}=}& -[A_3-{\lambda }_4\rho -\beta {\lambda }_1\widehat{S}(1-v_1\left(t\right))ϵ+\beta {\lambda }_2\widehat{S}(1-v_1\left(t\right))ϵ].\hfill \end{array}$$

(42)

For $i\in \{1,2,3,4\},$ the transversality condition

$${\lambda }_i\left(T\right)=0$$

(43)

holds. Furthermore, we present the corresponding optimal controls below:

$$\begin{array}{cc}\hfill & \widehat{v_1}=min\left\{max\left\{{\displaystyle \frac{\widehat{S}\beta (\widehat{I}(t-{\tau }_1)+\widehat{D}ϵ)({\lambda }_2\left(t\right)-{\lambda }_1\left(t\right))}{B_1}},a_1\right\},a_0\right\},\hfill \\ & \widehat{v_1}=min\left\{max\left\{{\displaystyle \frac{\widehat{R}({\lambda }_1\left(t\right)-{\lambda }_3\left(t\right))}{B_2}},a_1\right\},a_0\right\}.\hfill \end{array}$$

(44)

Proof. 

The Hamiltonian is defined as

$$\begin{array}{cc}\hfill H=& A_{1}I+A_{2}R+A_{3}D+{\displaystyle \frac{1}{2}}[B_1{v}_1^2+B_2{v}_2^2]+{\lambda }_1[\Lambda -(I(t-{\tau }_1)+\epsilon D)(1-v_1\left(t\right))\beta S-dS\hfill \\ \hfill & +(1-v_2\left(t\right))R]+{\lambda }_2[(I(t-{\tau }_1)(1-v_1\left(t\right))\beta +\epsilon D)S-\gamma I-I(t-{\tau }_2)\mu (b,I)\hfill \\ \hfill & -dI-fI]+{\lambda }_3[\gamma I+I(t-{\tau }_2)\mu (b,I)-(1-v_2\left(t\right))R-dR]+{\lambda }_4[-\rho D+fI].\hfill \end{array}$$

(45)

We define the characteristic function as follows:

$${\chi }_{[t_i,t_f]}\left(t\right)=\left\{\begin{array}{c}1t\in [t_i,t_f]\hfill \\ 0\mathrm{otherwise}.\hfill \end{array}\right.$$

As a result of Pontryagin’s maximum principle, adjoint variables ${\lambda }_i$ (for $i=1,\cdots ,4$) exist and satisfy the following canonical equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\lambda }_1}{dt}}& =-\left[{\displaystyle \frac{\partial H}{\partial S}}\left(t\right)\right];{\displaystyle \frac{d{\lambda }_3}{dt}}=-\left[{\displaystyle \frac{\partial H}{\partial R}}\left(t\right)\right];{\displaystyle \frac{d{\lambda }_4}{dt}}=-\left[{\displaystyle \frac{\partial H}{\partial D}}\left(t\right)\right];\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_2}{dt}}& =-\left[{\displaystyle \frac{\partial H}{\partial I}}\left(t\right)+{\chi }_{\left[0,T-{\tau }_1\right]}\left(t\right){\displaystyle \frac{\partial H}{\partial I\left(t-{\tau }_1\right)}}\left(t\right)+{\chi }_{\left[0,T-{\tau }_2\right]}\left(t\right){\displaystyle \frac{\partial H}{\partial I(t-{\tau }_2)}}\left(t\right)\right].\hfill \end{array}$$

(46)

We impose (43) and manipulate the above inequalities by including the derivatives of the respective variables; additional understanding can be gained through adjoint Equation (42). We obtain the following from deriving the optimality condition:

$${\displaystyle \frac{\partial H}{\partial v_1}=0,\mathrm{at}{v}_1=\widehat{v_1},\frac{\partial H}{\partial v_2}=0,\mathrm{at}{v}_2=\widehat{v_2}.}$$

Thus, we have

$$\widehat{v_1}={\displaystyle \frac{\widehat{S}\beta (\widehat{I}(t-{\tau }_1)+\widehat{D}ϵ)({\lambda }_2\left(t\right)-{\lambda }_1\left(t\right))}{B_1}},\widehat{v_2}={\displaystyle \frac{\widehat{R}({\lambda }_1\left(t\right)-{\lambda }_3\left(t\right))}{B_2}}.$$

(47)

From the corresponding optimal controls in (44), if the values of $v_i$$(i=1,2)$ are greater than 1, we consider them as 1; if they are negative, we treat them as 0. This completes the proof. □

We have the state equations from the corresponding optimality system by substituting $\widehat{v_1}$ and $\widehat{v_2}$ into (37) and (42), as shown below:

$$\left\{\begin{array}{cc}\hfill & {\displaystyle \frac{d\widehat{S}}{dt}=\Lambda -(1-\widehat{v_1}\left(t\right))\beta (\widehat{I}(t-{\tau }_1)+\epsilon \widehat{D})\widehat{S}-d\widehat{S}+(1-\widehat{v_2}\left(t\right))\widehat{R},}\hfill \\ \hfill & {\displaystyle \frac{d\widehat{I}}{dt}=(1-\widehat{v_1}\left(t\right))\beta (\widehat{I}(t-{\tau }_1)+\epsilon \widehat{D})\widehat{S}-\gamma \widehat{I}-\widehat{I}(t-{\tau }_2)\mu (b,\widehat{I})-f\widehat{I}-d\widehat{I},}\hfill \\ \hfill & {\displaystyle \frac{d\widehat{R}}{dt}=\gamma \widehat{I}+\mu (b,\widehat{I})\widehat{I}(t-{\tau }_2)-(1-\widehat{v_2}\left(t\right))\widehat{R}-d\widehat{R},}\hfill \\ \hfill & {\displaystyle \frac{d\widehat{D}}{dt}=f\widehat{I}-\rho \widehat{D},}\hfill \end{array}\right.$$

(48)

For the optimal system variables, the initial conditions are as defined in (2). The adjoint system is described by (42), with the transversality conditions described by (43), and $\widehat{v_1}$ and $\widehat{v_2}$ are the optimal controls that conform to (44).

6. Numerical Simulations

In this section, we employ numerical simulations to illustrate our theoretical findings using the dde23 MATLAB built-in solver and DDE-Biftool [42], a MATLAB package for numerical continuation and bifurcation analysis of delay differential equations (DDEs). The manual for the latest version of DDE-Biftool is available in [43].

System (1) is represented by the following form for the parametric values provided in Table 1.

$$\left\{\begin{array}{c}{\displaystyle \frac{dS\left(t\right)}{dt}=555+0.75R\left(t\right)-0.9704S\left(t\right)-0.025(I\left(t\right)+0.45D\left(t\right))S\left(t\right),}\hfill \\ {\displaystyle \frac{dI\left(t\right)}{dt}=-2.3857I\left(t\right)-(5.32-2.0541/(0.41+I\left(t\right)))I\left(t\right)+0.025(I\left(t\right)+0.45D\left(t\right))S\left(t\right),}\hfill \\ {\displaystyle \frac{dR\left(t\right)}{dt}=0.4389I\left(t\right)+(5.32-2.0541/(0.41+I\left(t\right)))I\left(t\right)-1.7204R\left(t\right),}\hfill \\ {\displaystyle \frac{dD\left(t\right)}{dt}=0.9764I\left(t\right)-0.015D\left(t\right).}\hfill \end{array}\right.$$

(49)

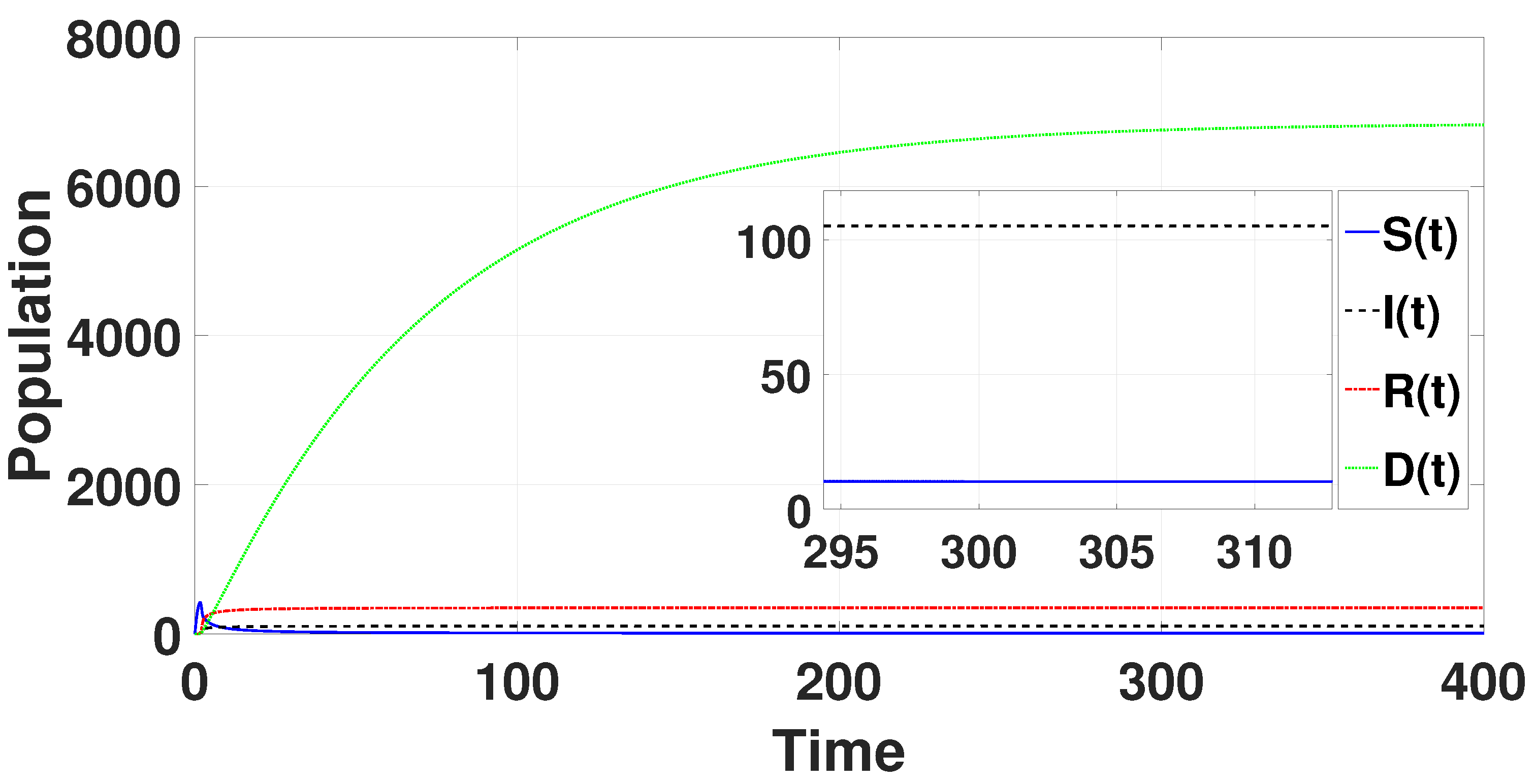
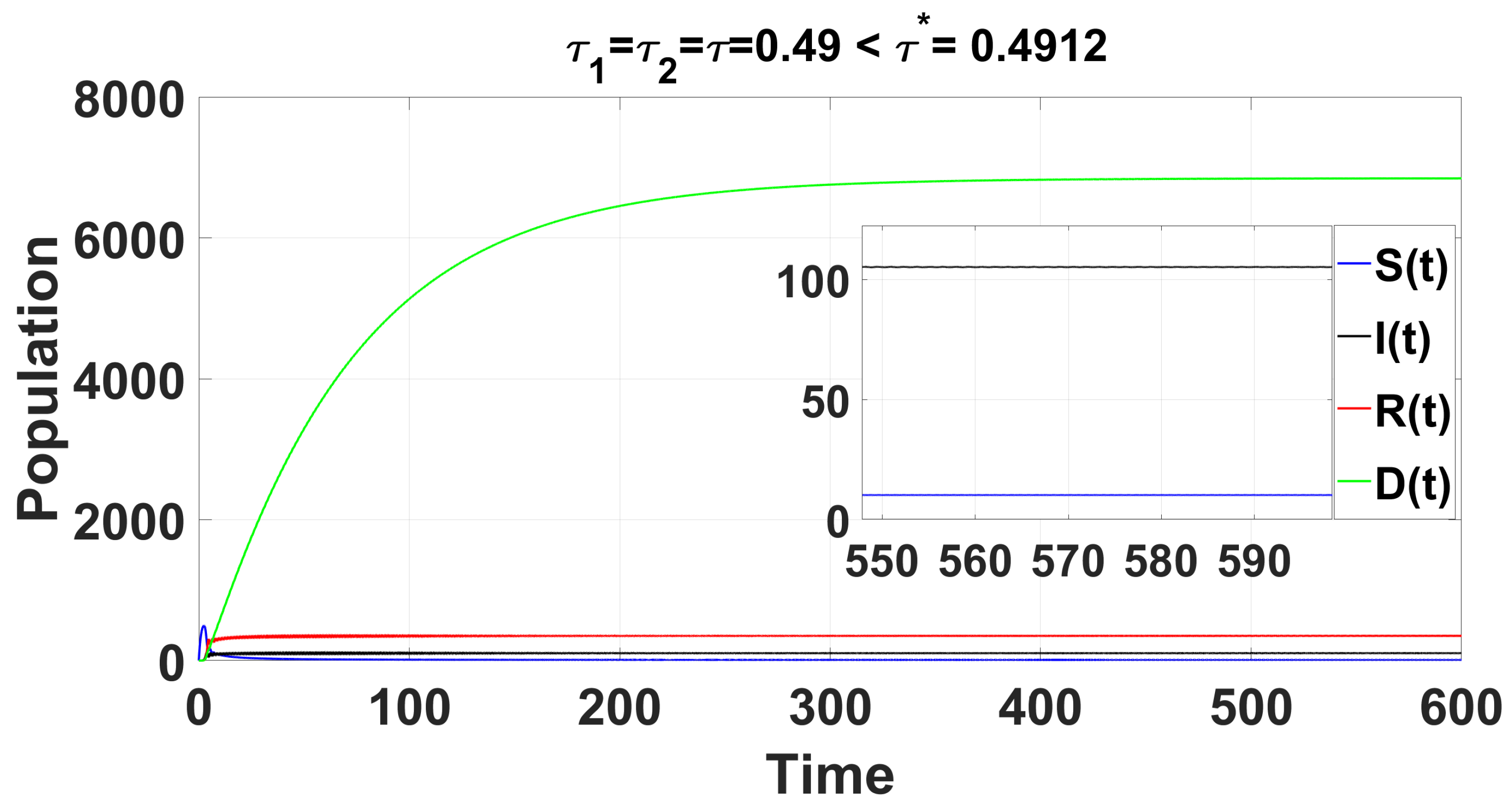
System (49) has a unique endemic equilibrium $E^{*}(S^{*},I^{*},R^{*},D^{*})$ as $R_0=160.671>1$ for the parametric values provided in Table 1. By using the above-mentioned Matlab tool, the unique endemic equilibrium is determined to be $E^{*}$ = (10.1495, 105.157, 350.815, 6845.02), which for ${\tau }_1={\tau }_2=0$ is locally asymptotically stable (refer to Figure 1).

In Figure 2, the solution curves are presented. Theorem 6 confirms that no Hopf bifurcation occurs in system (49). For ${\tau }_1>0$, and ${\tau }_2=0$; furthermore, according to (A21), we find $v_1^4+6559.79v_1^3+467010.03v_1^2+525023.58v_1+114.12=0,$ where $f_{10}=114.12>0$; then, point $E^{*}$ remains locally asymptotically stable for all ${\tau }_1>0$ with ${\tau }_2=0.$

Now, for ${\tau }_2>0$ and ${\tau }_1=0$, we find ${\omega }_{20}=4.5056$ and ${\tau }_2^{*}=0.4885$. Additionally, we have $g_2^{\prime }\left(v_{20}\right)=2.75303\times {10}^6>0$. Thus, we can conclude that the equilibrium point $E^{*}$ is locally asymptotically stable when conditions $\left({\mathbf{L}}_{11}\right)$ and $\left({\mathbf{L}}_{12}\right)$ (see Appendix C) are satisfied for ${\tau }_2\in [0,{\tau }_2^{*})$. However, as ${\tau }_2$ approaches ${\tau }_2^{*}$, $E^{*}$ will switch stability, becoming unstable and undergoing a Hopf bifurcation at ${\tau }_2={\tau }_2^{*}$. This transition leads to the emergence of a family of periodic solutions bifurcating from $E^{*}$ near ${\tau }_2^{*}$.

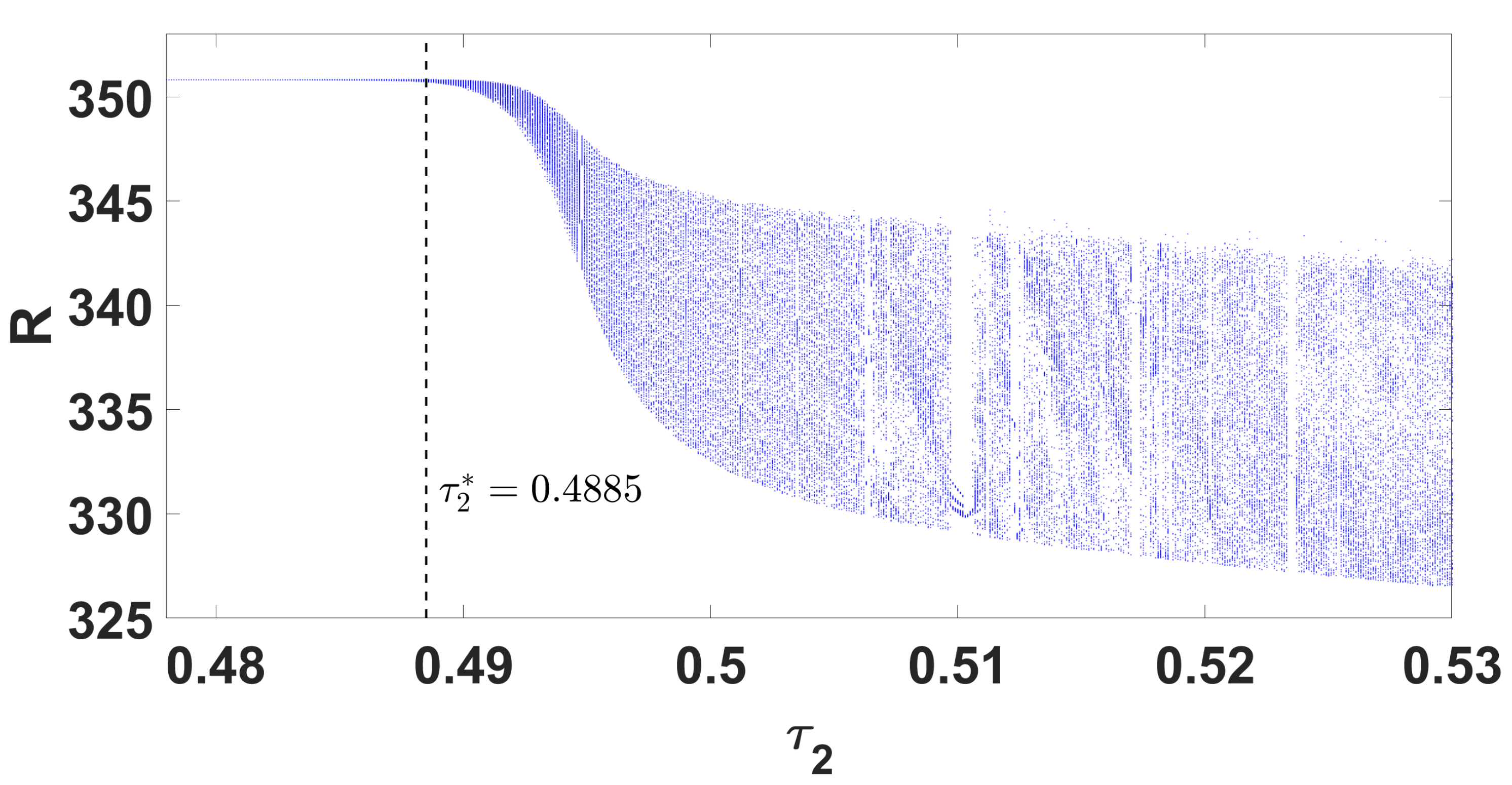
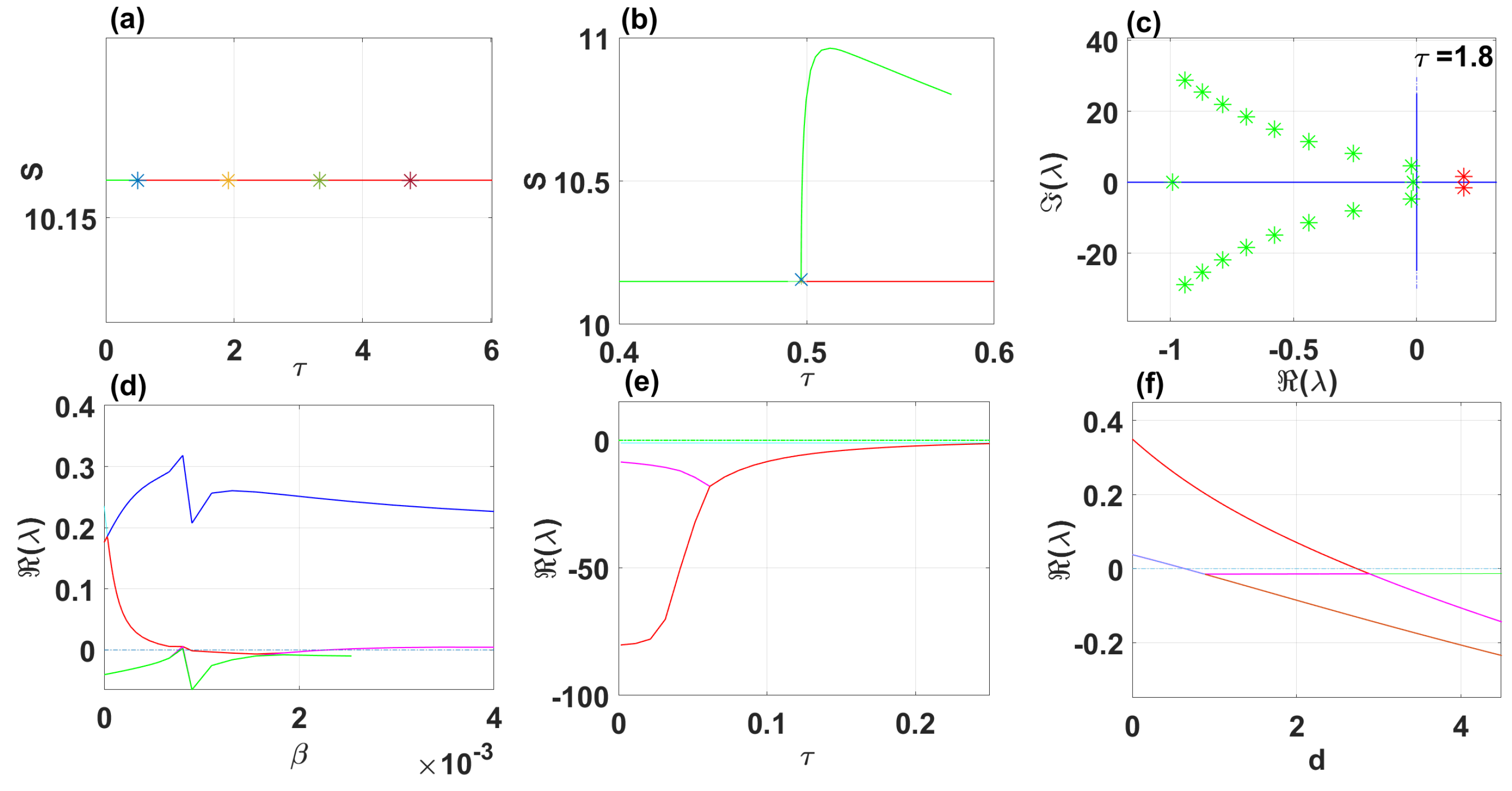
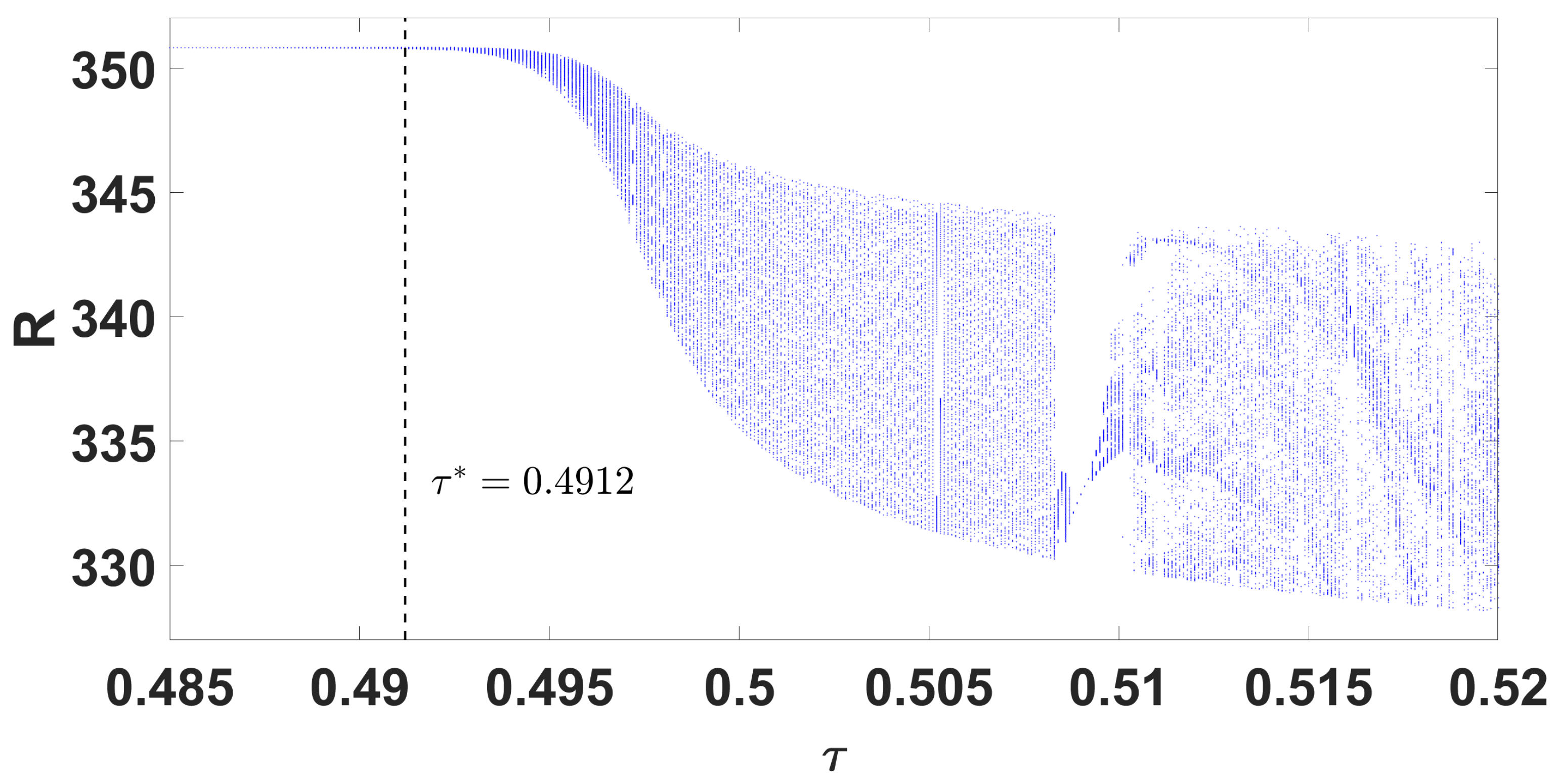
By using DDE-Biftool, we find that when ${\tau }_2\in [0,6]$, there are four critical delays: ${\tau }_2^{*}=\{0.49,1.9,3.3,4.71\}$ (see Figure 3). Notice that the stability switches occur at the Hopf bifurcation points, leading to a total of seven stability switches. The stable and unstable regions of the branch are represented in green and red, respectively. The branch of periodic solutions emerges from the first critical delay at the Hopf bifurcation point ${\tau }_2^{*}=0.49$ (see Figure 3b). This behavior is further illustrated by the bifurcation diagram in Figure 4, with additional solution curves shown in Figure 5 and Figure 6.

Through theoretical analysis, we have determined ${\tau }_2^{*}=0.4885$. Meanwhile, when using DDE-Biftool, the first critical delay is ${\tau }_2^{*}=0.49$. This indicates that our theoretical result is very close to the outcome obtained from DDE-Biftool. The Figure 7 illustrates the projection of the solutions in the $(S,I,R)$ phase space influenced by the delay.

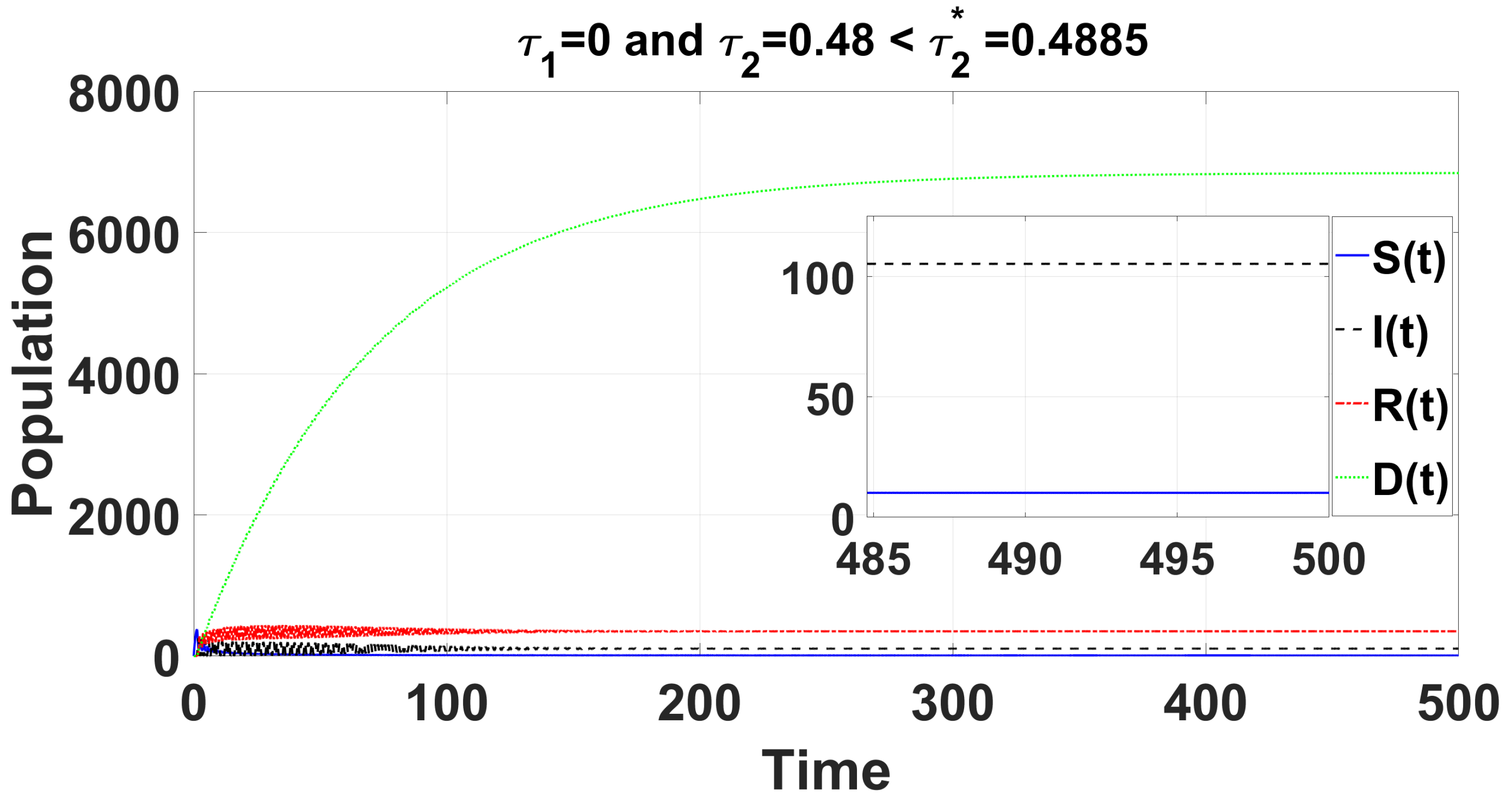
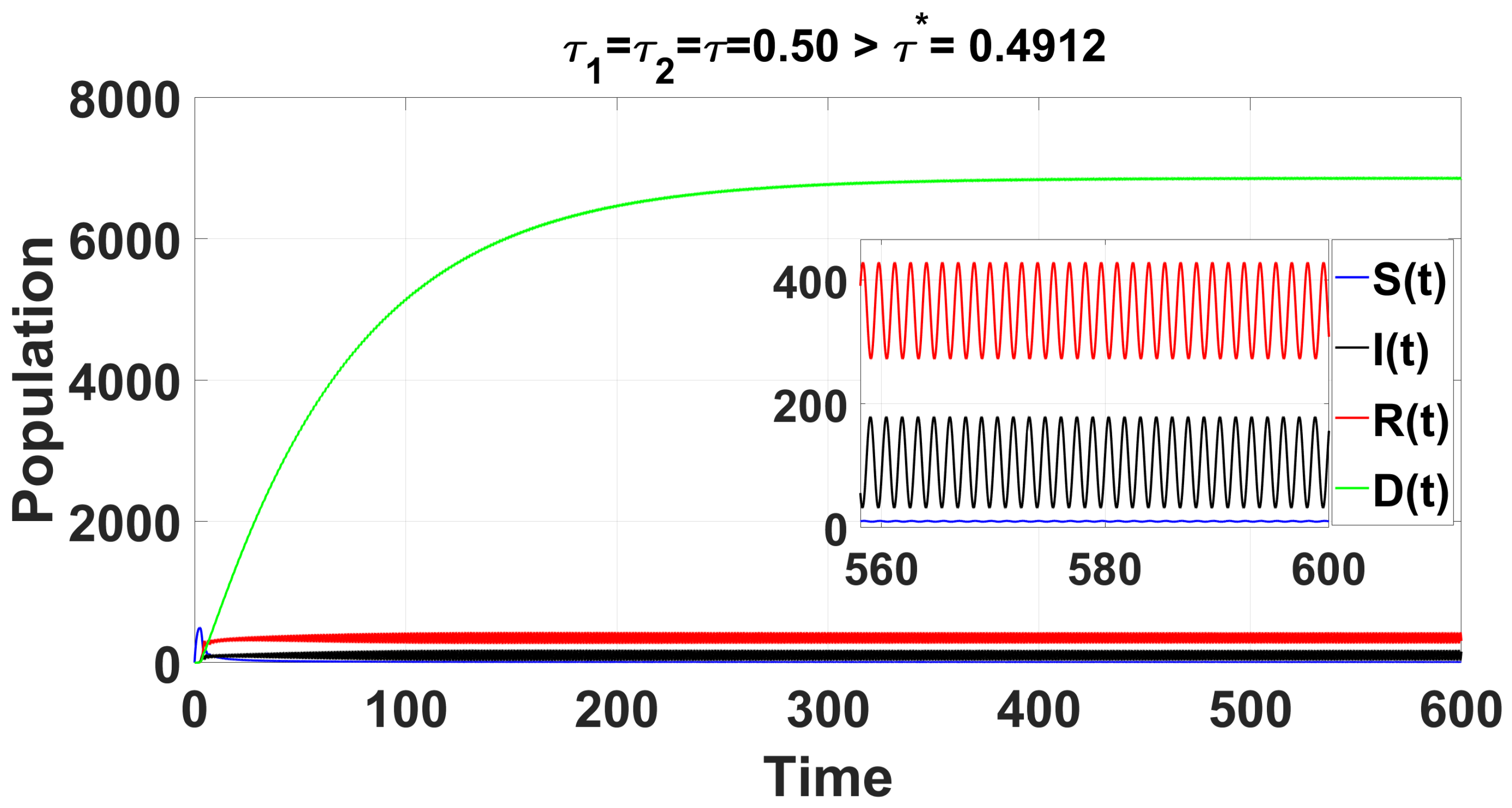
Through complex computations, we find that $\left(L_{21}\right)$ and $\left(L_{22}\right)$ (see Appendix C) are satisfied when ${\tau }_1={\tau }_2=\tau \in [0,{\tau }^{*}]$. This leads to the following results: ${\omega }_0=4.4801$, ${\tau }^{*}=0.4912$, $g_3^{\prime }\left(v_{30}\right)=2.71022\times {10}^6>0$, and ${\displaystyle \frac{\mathrm{d}\lambda \left({\tau }_0\right)}{\mathrm{d}\tau }}=3.205-2.3754\mathrm{i}$. From Equation (36) in Section 4, we determine that $c_1\left(0\right)=-0.0034-0.0175\mathrm{i}$, ${\mu }_2=0.0011>0$, ${\beta }_2=-0.0068<0$, and $T_2=0.0091>0$. As illustrated by the computer simulations (see Figure 8), the positive equilibrium $E^{*}$ is asymptotically stable when $0\le \tau <{\tau }^{*}$. 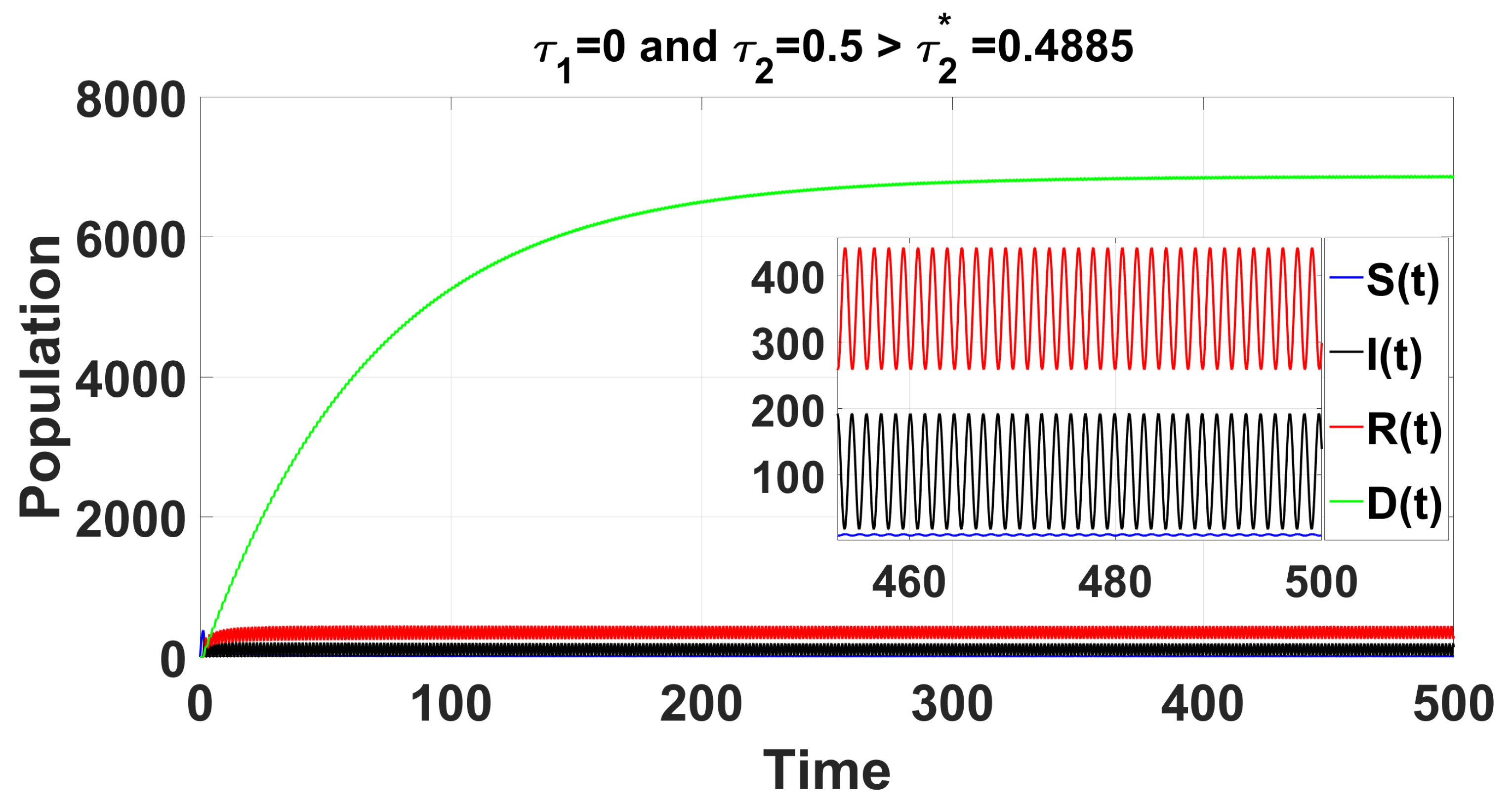Once $\tau$ exceeds the critical value ${\tau }^{*}$, a Hopf bifurcation occurs, causing $E^{*}$ to lose stability, giving rise to a family of periodic solutions that bifurcate from $E^{*}$.

When using DDE-Biftool with $\tau \in [0,6]$, four critical delays are identified: ${\tau }^{*}=\{0.49,1.91,3.32,4.74\}$ (see Figure 9). Notably, stability switches occur at the Hopf bifurcation points, resulting in a total of seven stability switches. The stable and unstable portions of the branch are represented in green and red, respectively. The branch of periodic solutions emanates from the first critical time delay at the Hopf bifurcation point ${\tau }^{*}=0.49$ (see Figure 9). It is important to note that through our theoretical analysis, we find ${\tau }^{*}=0.4912$, whereas when using DDE-Biftool, the first critical delay is ${\tau }^{*}=0.49$. This indicates that our theoretical result is very close to the outcome from DDE-Biftool.

The conditions ${\beta }_2<0$ and ${\mu }_2>0$ indicate a supercritical Hopf bifurcation, with bifurcation occurring for $\tau >{\tau }^{*}$. The periodic solutions bifurcating from $E^{*}$ at ${\tau }^{*}$ are stable, as depicted in Figure 10; system (49) also undergoes a Hopf bifurcation near $\tau ={\tau }^{*}$, which is demonstrated in the bifurcation diagram (Figure 9b and Figure 11). The right side of Figure 12 denotes the projection of the solutions in $(S,I,R)$.

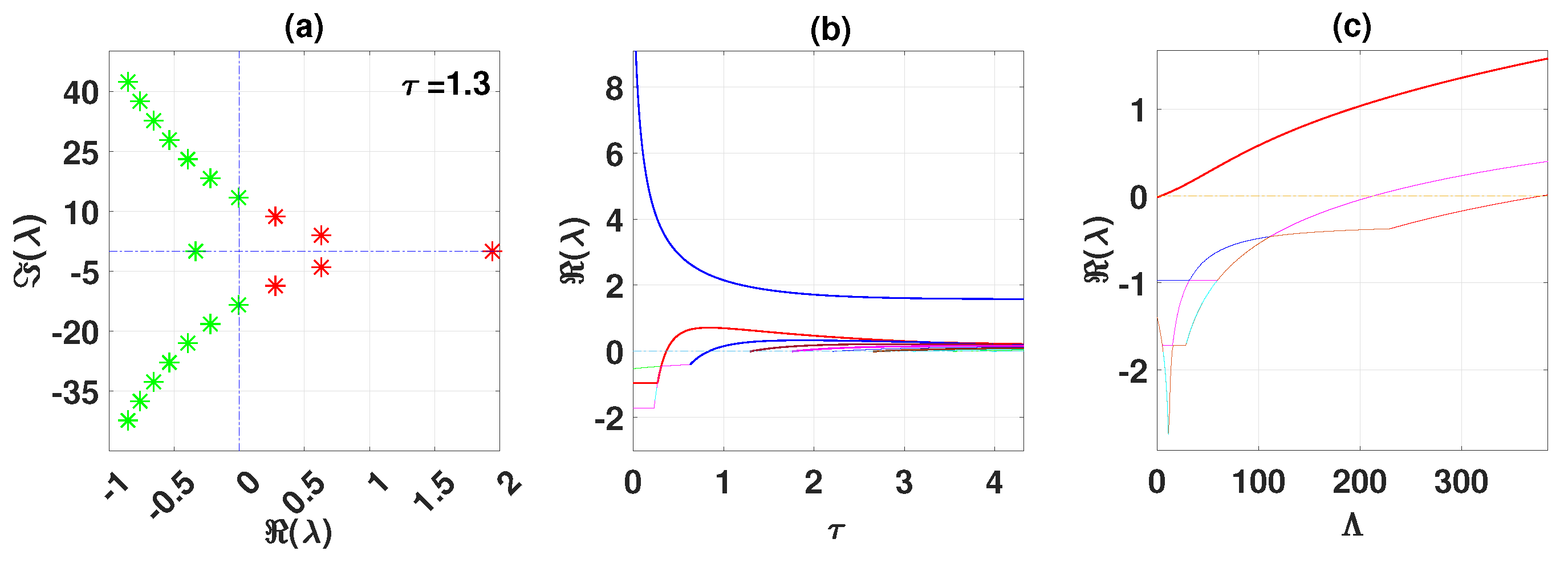
Figure 13 shows eigenvalues of the disease-free branch with $\tau =1.3$ (a). (b) and (c) show the real parts of eigenvalues vs. $\tau$ and $\Lambda$, respectively.

Optimal Control Strategies: Numerical Analysis

This section examines the best control strategy using a numerical example for the $SIRD$ model. We analyzed the results to better understand how different strategies can impact the spread of the disease. The initial population distribution is given by $\left(S\right(\nu ),I(\nu ),R(\nu ),D(\nu \left)\right)=(2,3,2,1)$. From the adjoint and state equations, we first derive the optimality system and, subsequently, solve pandemic model (1) with time delay, control system (37), adjoint Equation (42), the initial conditions (2), and the transversality conditions (43); simulations were carried out using a numerical method derived from the standard Runge-Kutta.

The dynamics of an infected human population can be analyzed by comparing scenarios with and without control interventions. In the given analysis, we refer to the specific parameter values outlined in

Table 2. Assigned numerical values for the parameters of model (1).

Parameter	Value	Source	Parameter	Value	Source
$\Lambda$	5.87	Assumed	$\beta$	0.0165	Assumed
u	0.02	Assumed	$ϵ$	0.45	[35]
$\gamma$	0.4389	[36]	f	0.48	[44]
$\rho$	0.4	Assumed	d	0.104	Assumed
$\theta$	0.75	Assumed	${\mu }_1$	0.31	Assumed
${\mu }_0$	0.21	Assumed	b	0.41	Assumed

, which provide a basis for understanding the effectiveness of these interventions.

As illustrated in Figure 14, Figure 15 and Figure 16, the model depicts two distinct scenarios: the solid lines represent the population without any form of control, and the dashed lines signify the population under implemented control measures. The weights assigned in the objective function are $A_1=10$, $A_2=3$, $A_3=3$, $B_1=300$, and $B_2=0.02$, and these are essential for determining the priorities of different control strategies, influencing the model’s outcomes.

The numerical simulations of the SIRD model investigated the impact of two control strategies, efficiency of quarantine protocols ($v_1$) and immunity enhancement ($v_2$), on achieving a (DFE) $(S_0,0,0,0)$. Each control strategy was tested individually and in combination, revealing both their strengths and limitations.

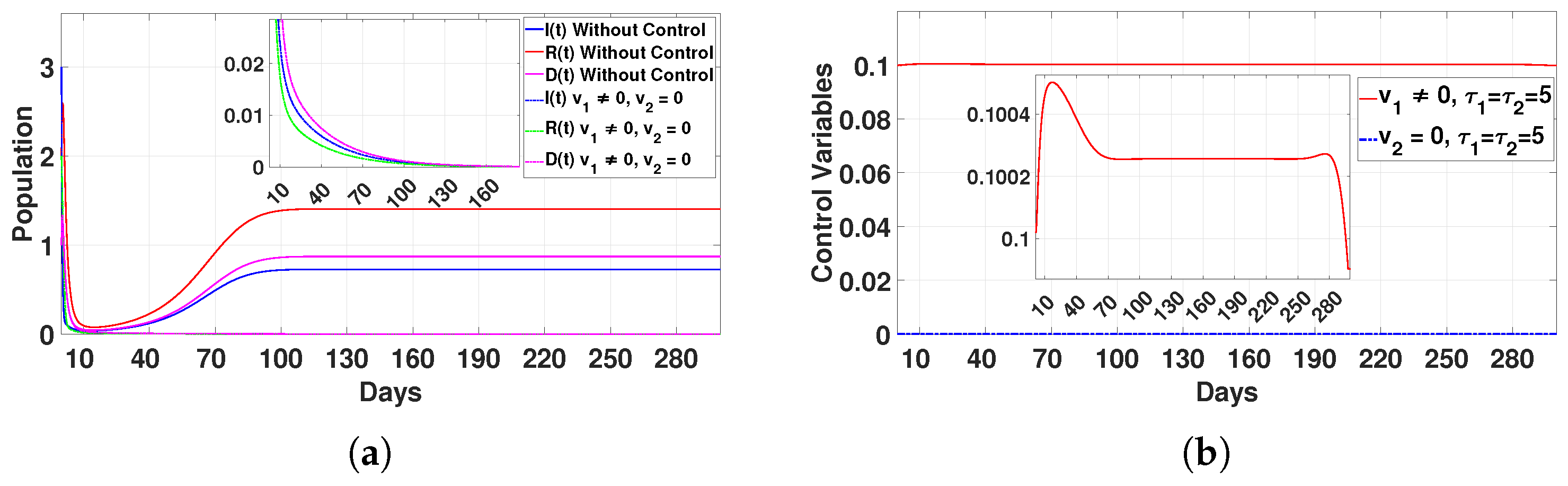
• Case 1: Quarantine protocols only ($v_1\ne 0,v_2=0$)
  In this case, the populations of infected individuals (I), recovered individuals (R), and deceased individuals (D) dropped to zero after 160 days, as shown in Figure 14a. The control $v_1$ was applied at the maximum level for 15 days. After that, we gradually reduced the control application until it was maintained for 70 days at a decreased level. We continued to apply the control at this consistent level for a total of 280 days, after which we significantly decreased the application by 295 days. This approach was effective in reducing disease transmission, but it required long-term implementation, which may be resource-intensive.
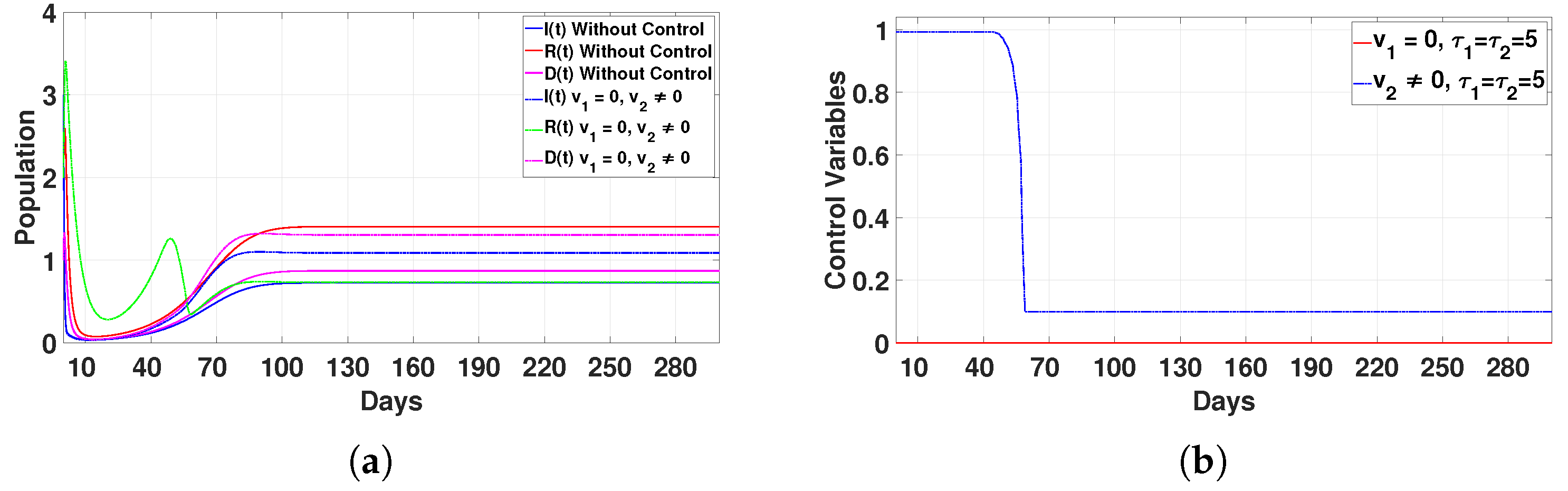
• Case 2: Immunity enhancement only ($v_1=0,v_2\ne 0$)
  In this scenario, the infected (I) and deceased (D) populations increase slightly, and the recovered individuals (R) decrease, as shown in Figure 15a. The control $v_2$ is applied at its maximum level for 50 days, and then it drops sharply until day 60, after which it remains stable, as shown in Figure 15b. This strategy alone is not sufficient to eliminate the disease, so we conclude that applying this control by itself is ineffective.
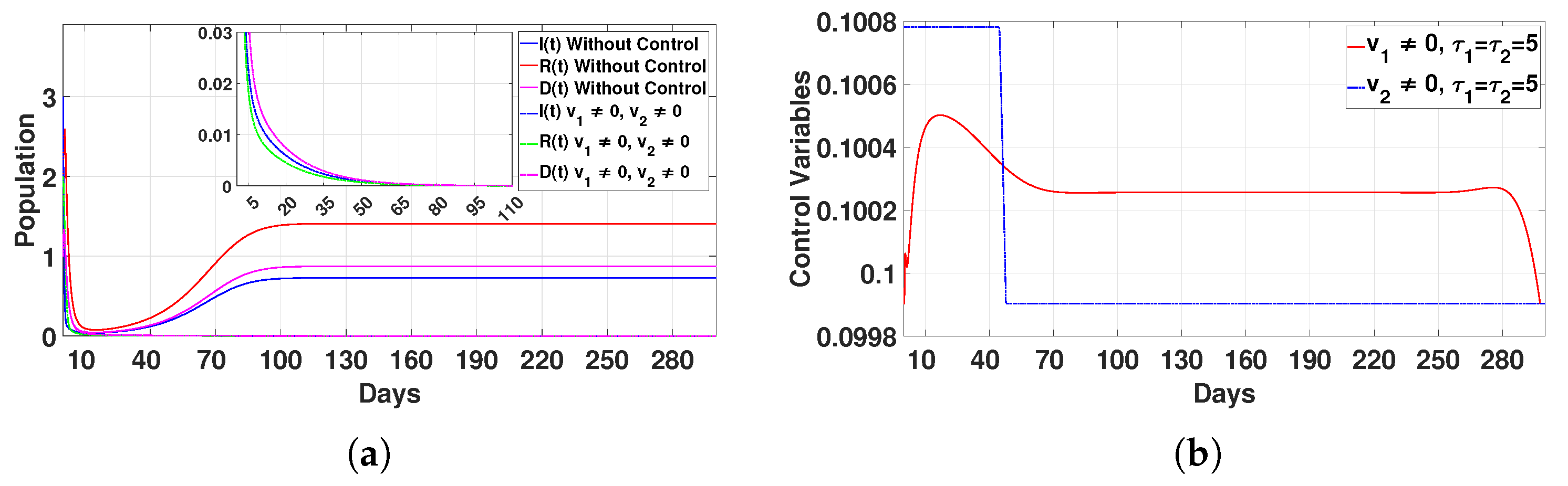
• Case 3: Combined control strategy ($v_1\ne 0,v_2\ne 0$)
  The combined application of two controls yielded the most efficient results. Populations (I), (R), and (D) dropped to zero after 95 days, as presented in Figure 16a. The controls were applied for 20 days ($v_1$) and 50 days ($v_2$), as displayed in Figure 16b. This integrated approach addressed multiple aspects of disease dynamics simultaneously, achieving faster and more sustainable results than any single intervention.

Each strategy has its advantages and disadvantages. Quarantine protocols ($v_1$) are effective at reducing transmission but require sustained effort, resources, and time. Immunity enhancement ($v_2$) does not prevent new infections and is insufficient to achieve a disease-free state. The combined strategy, while highly effective, may require significant coordination and investment. These findings are crucial for public health planning. They demonstrate that while individual controls can lead to disease-free outcomes, a combined approach is the most robust and efficient. By implementing these strategies, communities can enhance their resilience to outbreaks, save lives, and promote long-term public health stability.

7. Discussion

In this work, we propose a delayed $SIRD$ model system that highlights three key concepts: (i) the inclusion of a separate compartment for dead but not yet buried individuals, (ii) the loss of immunity, and (iii) the introduction of a treatment recovery function, $\mu (b,I)$, which measures the impact of limited medical resources. The influence of hospital beds and vaccines on disease dynamics was recently detailed by Wang et al. [32], and numerous mathematical models in epidemiology have thoroughly explored the issue of whether recovered individuals have temporary or permanent immunity [45,46]. The results obtained in this paper complement the research work in the literature [32]; our study extends the work of Wang et al. [32] by examining how delay parameters influence system dynamics. Consequently, our proposed model system (1) is made more realistic, particularly when considering diseases like Ebola; after a period of immunity, a recovered person can become susceptible again, as their immunity may only be temporary. We incorporated two time delays into the proposed $SIRD$ epidemic model: the latent period for susceptible individuals and treatment delay (due to limited medical resources, also known as the treatment period).

The analysis covers optimal control strategies and explores the model’s solution positivity, boundedness, stability, and Hopf bifurcation to understand better how to manage the system. Additionally, this study investigates the effect of time delay parameters on the dynamics of the model system. The significance of quarantine and boosting immunity in controlling the spread of infection is proven. This paper highlights the importance of quarantine and enhanced immunity in managing an infected population. The primary focus is to examine how the delay parameter influences the system dynamics. Additionally, we explore strategies to enhance quarantine measures, improve disease tracking, and boost immunity levels. Quarantine programs, in particular, are essential for safeguarding individuals and curbing the spread of infectious diseases. This is especially evident in the case of Ebola, where quarantine plays a critical role, underscoring the importance of public awareness regarding seasonal quarantine practices.

Additionally, we found that the combined application of both controls yielded the most efficient results, achieving a disease-free state within 95 days, whereas applying only quarantine protocols took 160 days to reach the same outcome. For various ranges of delay parameters (${\tau }_1$ and ${\tau }_2$), the sufficient conditions for local stability of the DFE are explored in Theorems 2–4. The existence of the endemic equilibrium, which is valid when $R_0>1$, is directly derived from [32]. We have used the comparison theorem to establish solution boundedness and applied the elementary theory of functional differential equations to ensure the existence and uniqueness of solutions for the proposed model system. Moreover, local stability conditions for the endemic equilibrium $E^{*}$ are discussed regarding different delay parameter values. In Theorems 7–8, the critical values of both time delays are determined, and the occurrence of Hopf bifurcations is analyzed by treating the delays as bifurcation parameters. Our analysis shows that if the values of time delay ${\tau }_2$ and the ${\tau }_1={\tau }_2=\tau$ parameters for system (1) are below their corresponding critical values, the endemic equilibrium remains stable. However, if any delay parameters exceed their critical values, the stability of the endemic equilibrium is lost. One-parameter bifurcation diagrams for different bifurcation parameters are presented in Figure 4 and Figure 11, and the threshold values of the delay parameters are calculated. We used DDE-Biftool to analyze the endemic equilibrium branch and plot the branch of periodic solutions originating from the first bifurcation point, ${\tau }_2^{*}$, with ${\tau }_1={\tau }_2={\tau }^{*}$. Additionally, we examined the eigenvalues along the endemic equilibrium branch for ${\tau }_2=3$ and ${\tau }_1=0$, as well as for ${\tau }_1={\tau }_2=\tau =1.8$. We also plotted the real parts of the eigenvalues with respect to $\beta$, ${\tau }_2$ (with ${\tau }_1={\tau }_2=\tau$), and d, respectively. See Figure 3 and Figure 9. We used the same tool to plot the eigenvalues along the disease-free equilibrium branch for ${\tau }_1={\tau }_2=\tau =1.3$. Additionally, we plotted the real parts of the eigenvalues as functions of $\tau$ and $\Lambda$, respectively.

The study of Hopf bifurcation properties, such as direction and stability, uses a center manifold and normal form theory. The parametric values in (49) corresponding to the endemic equilibrium, where $R_0>1)$, are discussed. For stability results related to various delay parameters, see Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, Figure 8, and Figure 10. Our study builds on the work of [32] by incorporating public immunity to evaluate its impact on disease control. It also extends this model by introducing incubation and treatment period delays to analyze their effects on hospital resources and recovery rates. Additionally, we explore strategies to enhance quarantine measures, improve disease tracking, and boost immunity levels. Quarantine programs, in particular, are essential for safeguarding individuals and curbing the spread of infectious diseases. This is especially evident in the case of Ebola, where quarantine plays a critical role, underscoring the importance of public awareness regarding seasonal quarantine practices.