Bäcklund Transformation for Solving a (3+1)-Dimensional Integrable Equation
Abstract
1. Introduction
2. A Bäcklund Transformation of Three Dimensions
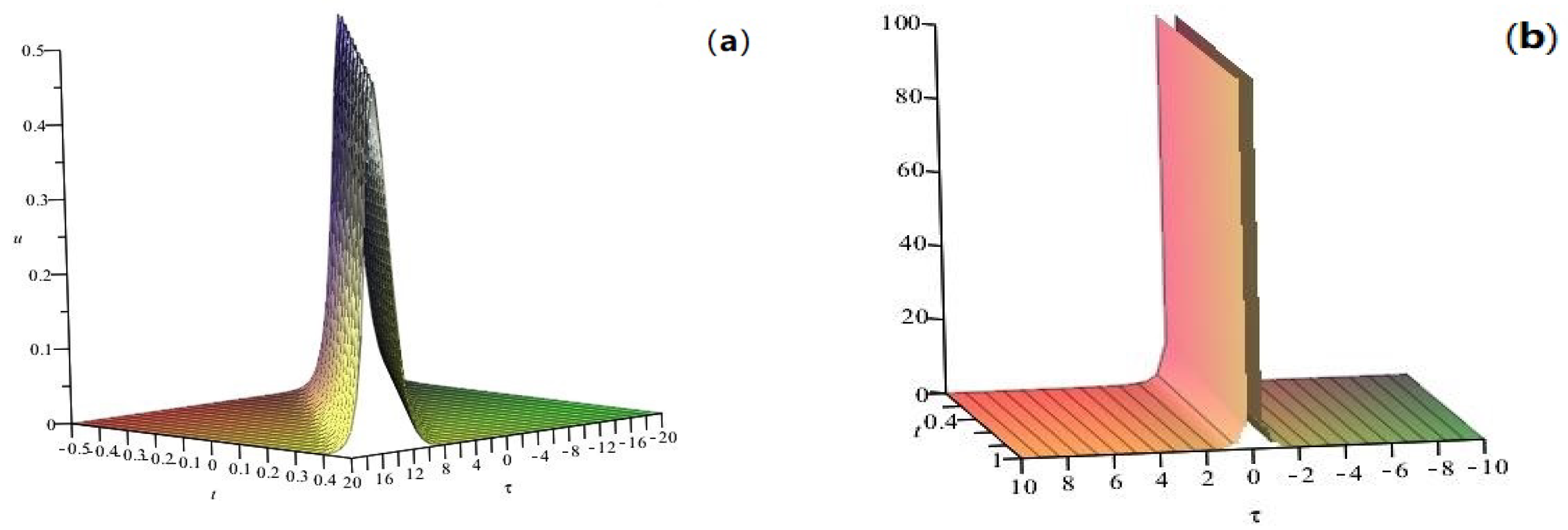
3. A Type of New Soliton Solutions
4. Superposition Formula
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.H. General Derivation of Bäcklund transformations from Inverse Scattering Problems. Phys. Rev. Lett. 1974, 57, 925–928. [Google Scholar] [CrossRef]
- Tu, G.Z. Bäcklund transformation and conservation laws of the Boussinesq equation. Acta Math. Appl. Sin. Engl. Ser. 1981, 4, 63–68. [Google Scholar]
- Wahlquist, H.; Estabrook, F. Bäcklund Transformation for Solutions of the Korteweg-de Vries Equation. Phys. Rev. Lett. 1985, 31, 1386. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Zhang, Y.F. Bäcklund transformation, nonlinear superposition principle and infinite conservation laws of Benjamin equation. Appl. Math. Mech. 2001, 22, 1017–1021. [Google Scholar]
- Konopelchenko, B.G.; Dubrovsky, V.G. Bäcklund-calogero group and general form of integrable equations for the two-dimensional Gelfand-Dikij-Zakharov-Shabat problem bilocal approach. Physica D 1985, 16, 79–98. [Google Scholar] [CrossRef]
- Chen, H.H. A Bäcklund Transformation in two dimensions. J. Math. Phys. 1975, 16, 2382. [Google Scholar] [CrossRef]
- Konopelchenko, B.G. On the general structure of nonlinear evolution equations integrable the two-dimensional matrix spectural problem. Commun. Math. Phys. 1982, 87, 105–125. [Google Scholar] [CrossRef]
- Lü, X.; Ma, W.X.; Khalique, C.M. A direct bilinear Backlund transformation of a (2+1)-dimensional Korteweg-de Vries-like model. Appl. Math. Lett. 2015, 50, 37–42. [Google Scholar] [CrossRef]
- Rogers, B.G. Konopelchenkow. A (2+1)-dimensional sine-Gordon system: Its auto-Bäcklund transformation. Phy. Lett. A 1992, 172, 39–48. [Google Scholar]
- Lü, X. New bilinear Bäcklund transformation with multisoliton solutions for the (2+1)-dimensional Sawada-Kotera model. Nonlinear Dyn. 2014, 76, 161–168. [Google Scholar] [CrossRef]
- Yin, Y.H.; Lü, X.; Ma, W.X. Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 2022, 108, 4181–4194. [Google Scholar] [CrossRef]
- Ma, W.X.; Abdeljabbar, A. A bilinear Bäcklund transformation of a (3+1)-dimensional generalized KP equation. Appl. Math. Lett. 2012, 25, 1500–1504. [Google Scholar] [CrossRef]
- Zhang, L. Tian, M. Construction of Lax Pairs for Two Kinds of (3+1)-Dimensional Equation. J. Gansu Lianhe Univ. (Nat. Sci.) 2013, 27, 31–32. [Google Scholar]
- Ablowitz, M.J.; Yaacov, D.B.; Fokas, A.S. On the inverse Scattering Transform for the Kadomtsev-Petviashvili Equation. Stud. Appl. Math. 1983, 69, 135–143. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.Q.; Yu, X.C. Some New Exact Traveling Wave Solutions of the (3+1)-Dimensional Kadomtsev-Petviashvili Equation. J. Qufu Norm. Univ. (Nat. Sci.) 2006, 32, 27–29. [Google Scholar]
- Li, D.S.; Lv, Z.S.; Zhang, H.Q. Exact Solutions of the (3+1)-Dimensional KP and KdV-Type Equations. Commun. Theor. Phys. 2003, 39, 267–270. [Google Scholar]
- Zhang, H.Y.; Zhang, Y.F. Analysis on the M-rogue wave solutions of a generalized (3+1)-dimensional KP equation. Appl. Math. Lett. 2020, 102, 106145. [Google Scholar] [CrossRef]
- Ma, Y.L.; Wazwaz, A.M.; Li, B.Q. A new (3+1)-dimensional Kadomtsev–CPetviashvili equation and its integrability, multiple-solitons, breathers and lump waves, Mathe. Comput. Simulat. 2021, 187, 505–519. [Google Scholar] [CrossRef]
- Ozisik, M.; Secer, A.; Bayram, M. Soliton Waves with the (3+1)-Dimensional Kadomtsev-Petviashvili-Boussinesq Equation in Water Wave Dynamics. Symmetry 2023, 15, 165. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Gui, L.L.; Feng, B.L. Solutions of Cauchy Problems for the Gardner Equation in Three Spatial Dimensions. Symmetry 2025, 17, 102. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Gui, L.L. Solutions of Cauchy Problems for the Caudrey-Dodd-Gibbon-Kotera-Sawada equation in three spatial and two temporal dimensions. Axioms 2024, 14, 11. [Google Scholar] [CrossRef]
- Chadan, K.; Colton, D.; Pivrinta, L.; Rundell, W. An Introduction to Inverse Scattering and Inverse Spectral Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1987. [Google Scholar]
- Zhang, Y.F.; Tam, H.W. Discussion on integrable properties for higher-dimensional variable-coefficient nonlinear partial differential equations. J. Math. Phys. 2013, 54, 013516. [Google Scholar] [CrossRef]
- Wazwaz, A.M. New solutions of distinct physical structures to high-dimensional nonlinear evolution equations. Appl. Math. Comp. 2008, 196, 363–370. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, B.; Gui, L.; Zhang, Y.; Han, S. Bäcklund Transformation for Solving a (3+1)-Dimensional Integrable Equation. Axioms 2025, 14, 225. https://doi.org/10.3390/axioms14030225
Feng B, Gui L, Zhang Y, Han S. Bäcklund Transformation for Solving a (3+1)-Dimensional Integrable Equation. Axioms. 2025; 14(3):225. https://doi.org/10.3390/axioms14030225
Chicago/Turabian StyleFeng, Binlu, Linlin Gui, Yufeng Zhang, and Siqi Han. 2025. "Bäcklund Transformation for Solving a (3+1)-Dimensional Integrable Equation" Axioms 14, no. 3: 225. https://doi.org/10.3390/axioms14030225
APA StyleFeng, B., Gui, L., Zhang, Y., & Han, S. (2025). Bäcklund Transformation for Solving a (3+1)-Dimensional Integrable Equation. Axioms, 14(3), 225. https://doi.org/10.3390/axioms14030225