Study on Discrete Mosquito Population-Control Models with Allee Effect
Abstract
1. Introduction
2. Wild Mosquito Population Development Model
- When breeding sites are abundant relative to the population size and environmental constraints are minimal (), the mating rate approaches its maximum value a, indicating that resource availability no longer significantly limits reproduction.
- When breeding sites are limited relative to the population size and environmental constraints are substantial (), the mating rate can be approximated as , reflecting the reduced reproductive efficiency due to intense competition for scarce resources.
2.1. The Existence and Stability of Fixed Points
- The fixed point is locally asymptotically stable if there exists a neighborhood U of such that, for any initial value , the trajectory remains within U and converges to as .
- The fixed point is semi-stable if, for initial values on one side of (e.g., or ), the trajectory converges to , while for initial values on the other side, the trajectory diverges away from .
- The system exhibits bistability if there exist two distinct asymptotically stable fixed points and , and the final state of the system (converging to or ) depends on the initial value .
- (1)
- When , the only fixed point is globally asymptotically stable;
- (2)
- When , the unique positive fixed point is semi-stable;
- (3)
- When , the positive fixed point is unstable, and is locally asymptotically stable on . The trivial fixed point is locally asymptotically stable on .
- (1)
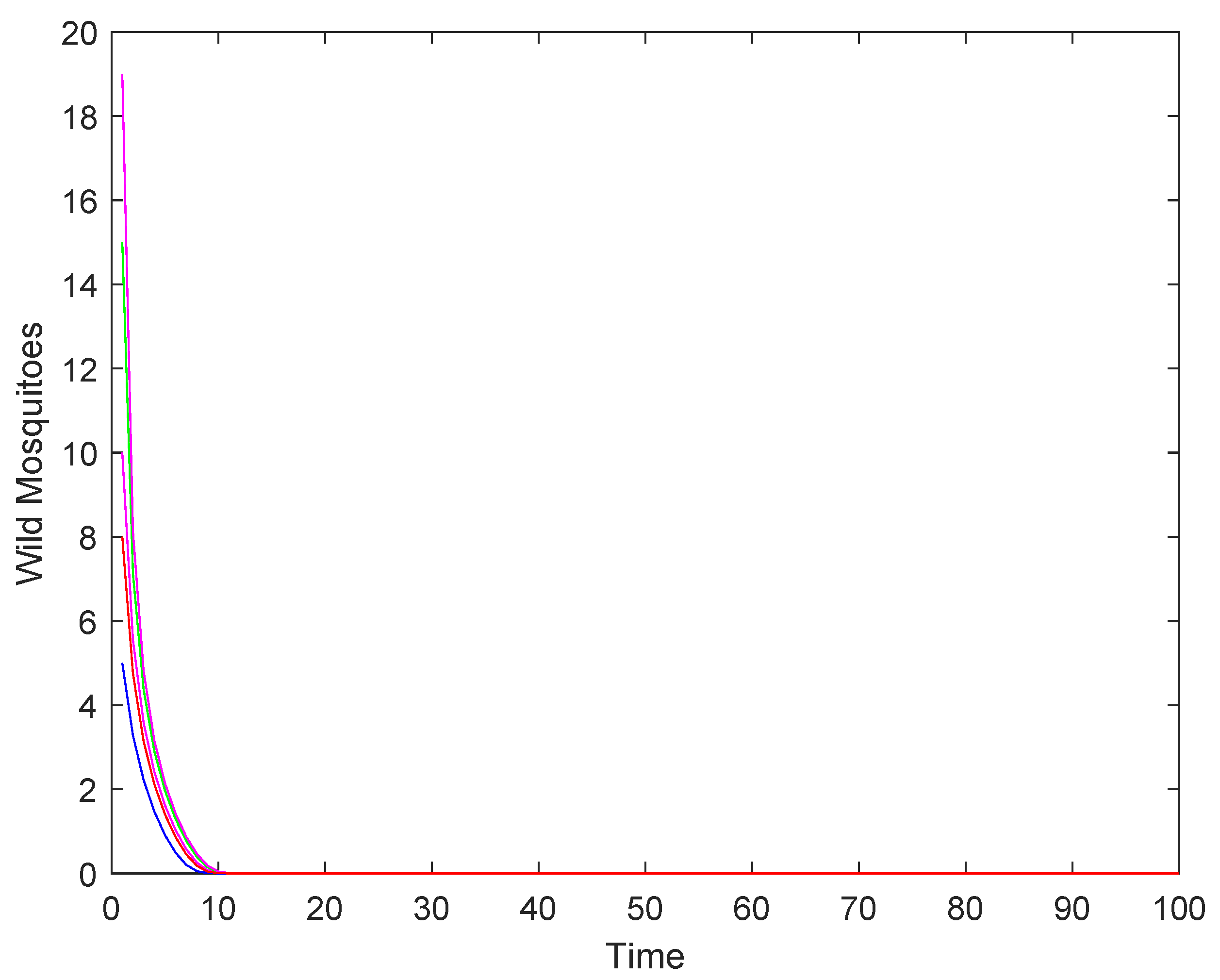
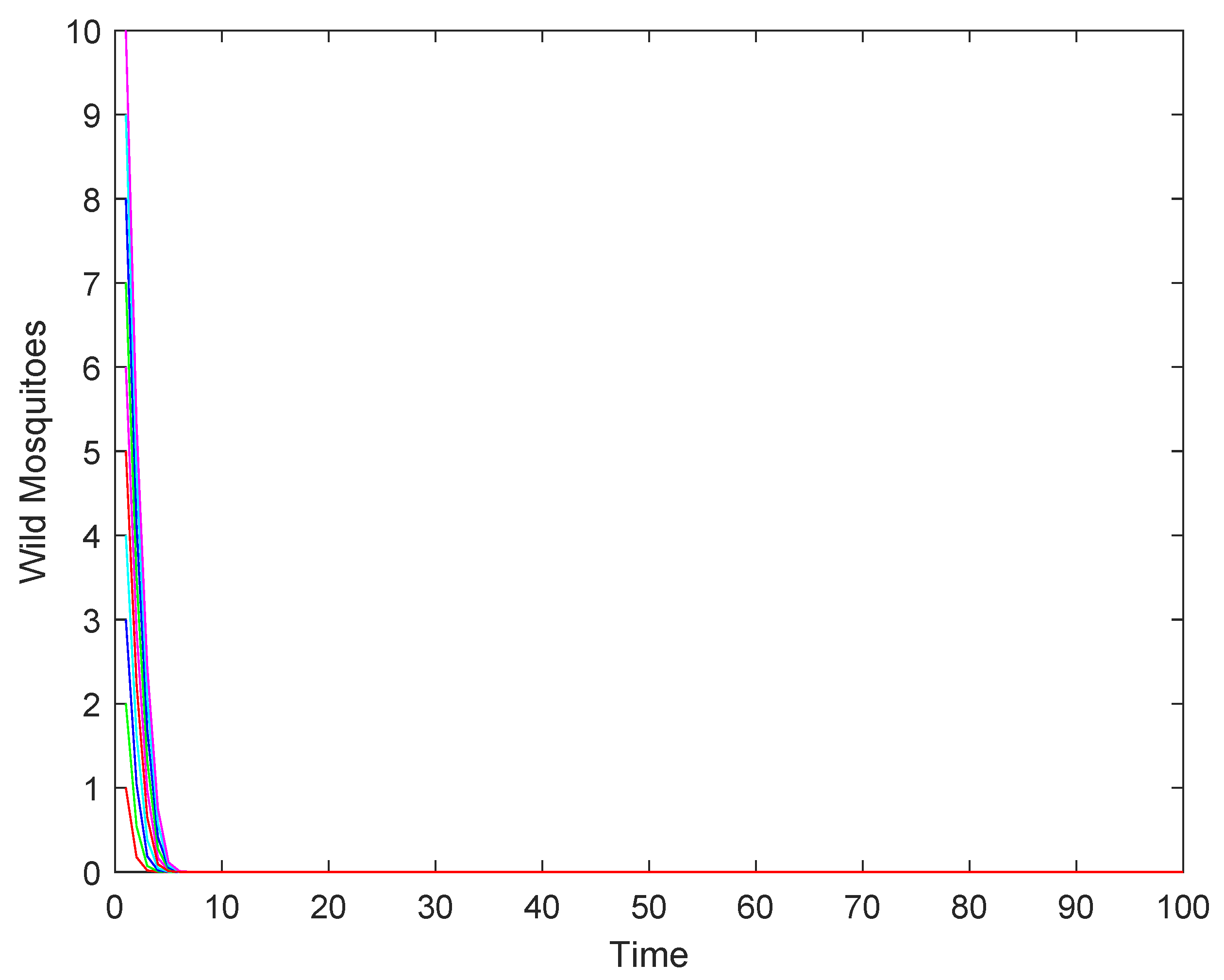
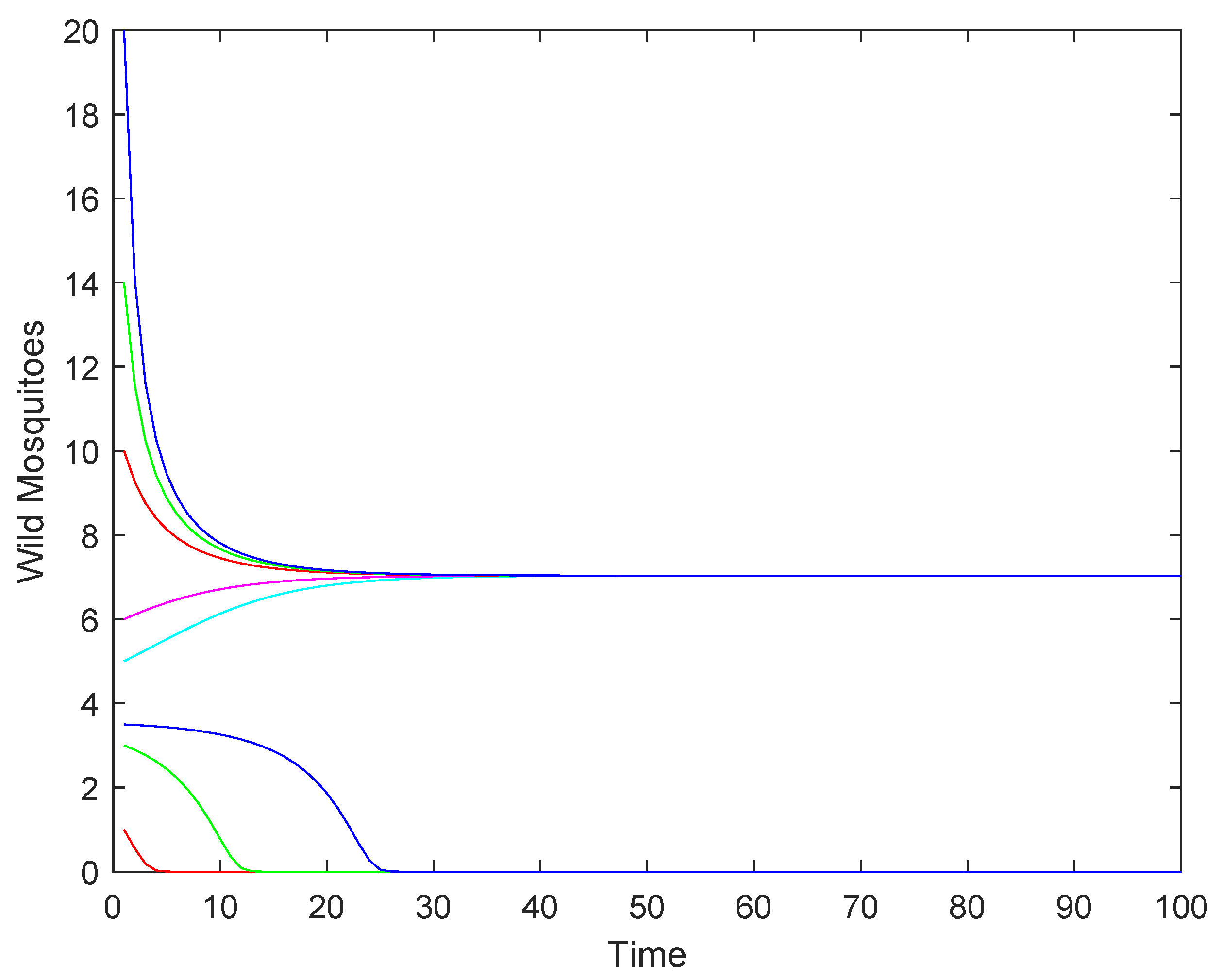
- When the intrinsic growth rate , the wild mosquito population will eventually decline to extinction, regardless of the initial population size. This indicates that the population cannot sustain itself under these conditions.
- (2)
- When the intrinsic growth rate , the population may either stabilize at the equilibrium or decline to extinction, depending on whether the initial population size is above or below . This represents a critical threshold where the population’s fate is determined by its starting size.
- (3)
- When the intrinsic growth rate : if the initial population size is above , the population will stabilize at the equilibrium ; if the initial population size is below , the population will decline to extinction.
2.2. Numerical Simulations
3. Constant Release of Sterile Mosquitoes
3.1. The Existence and Stability of Fixed Points
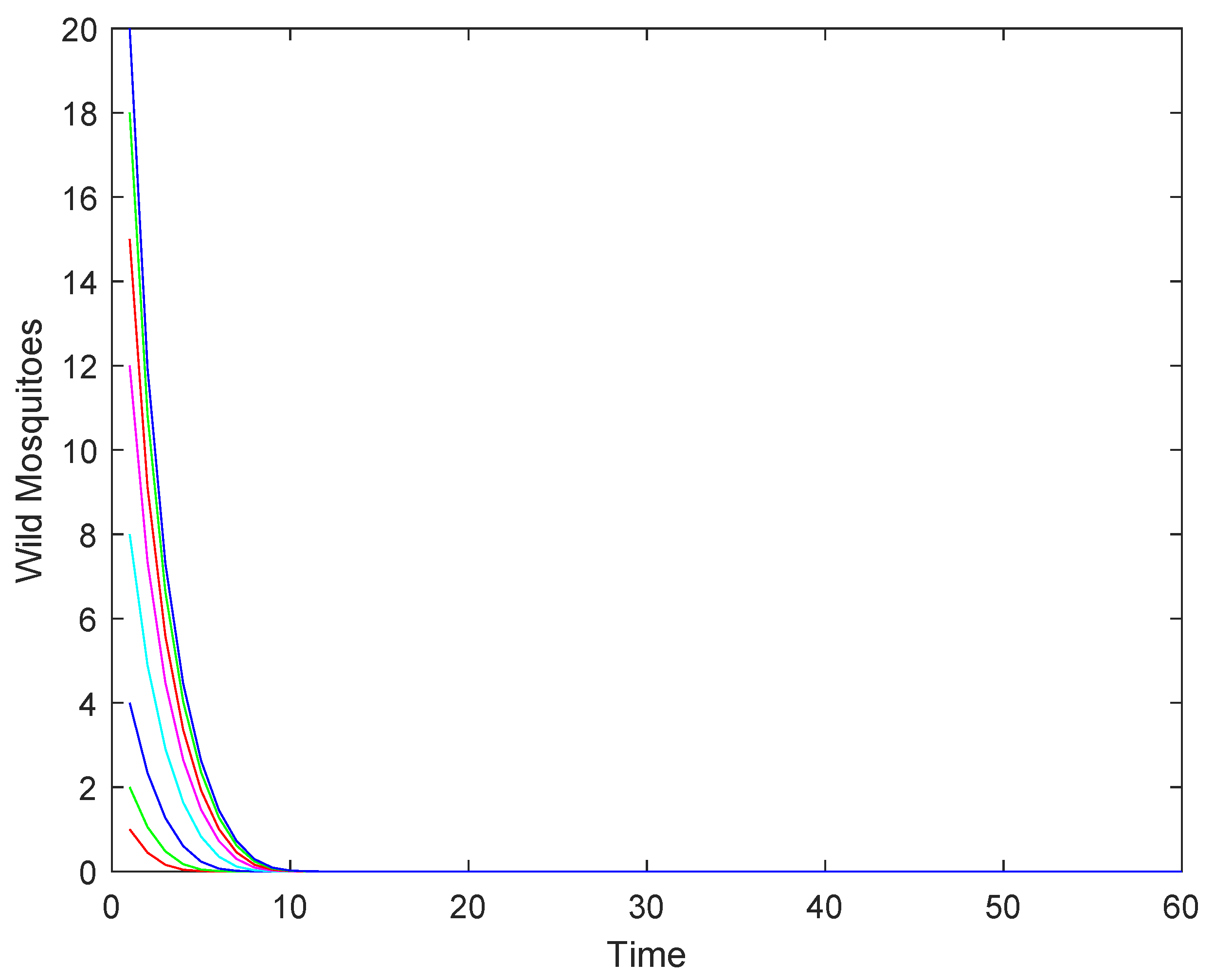
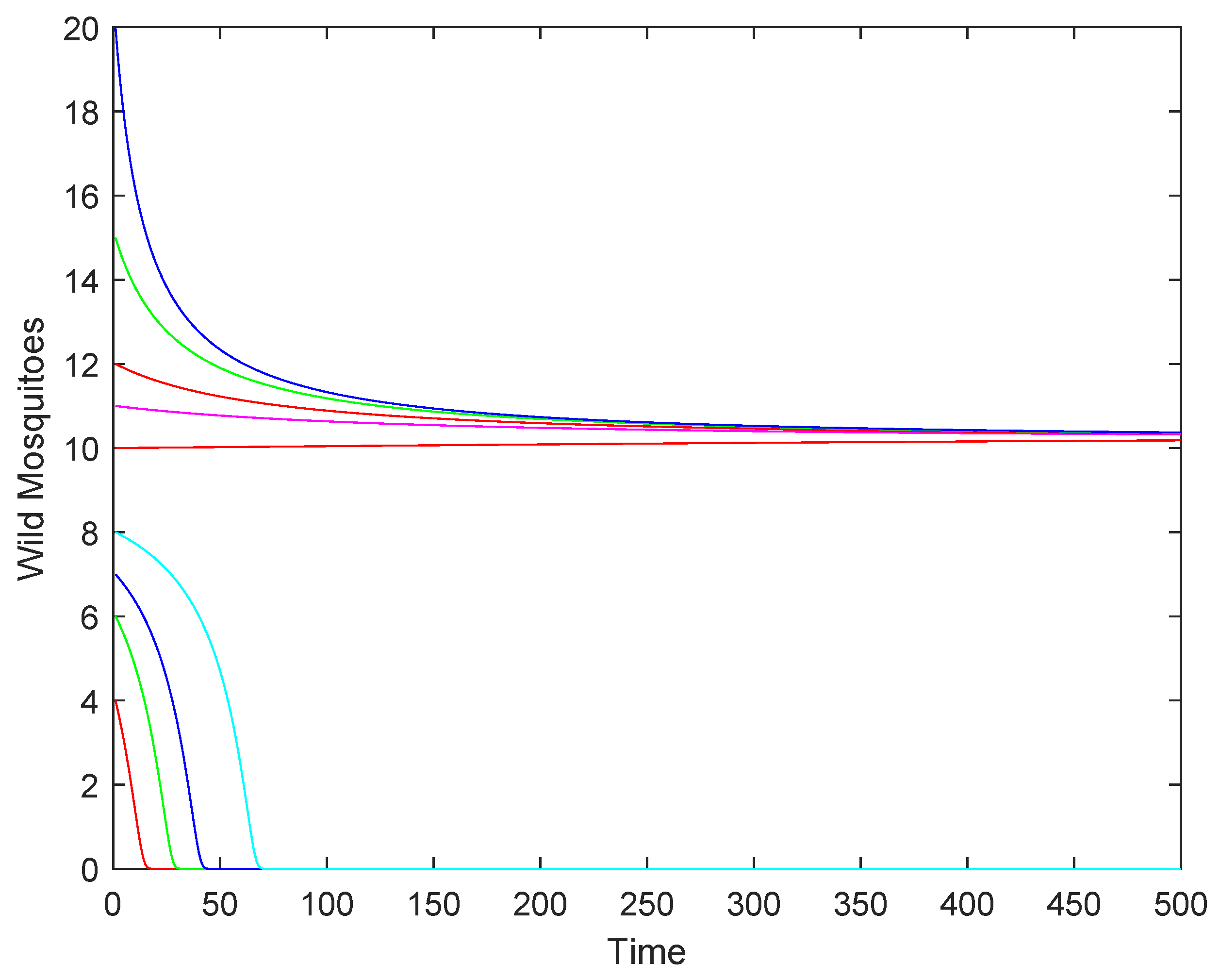
- (1)
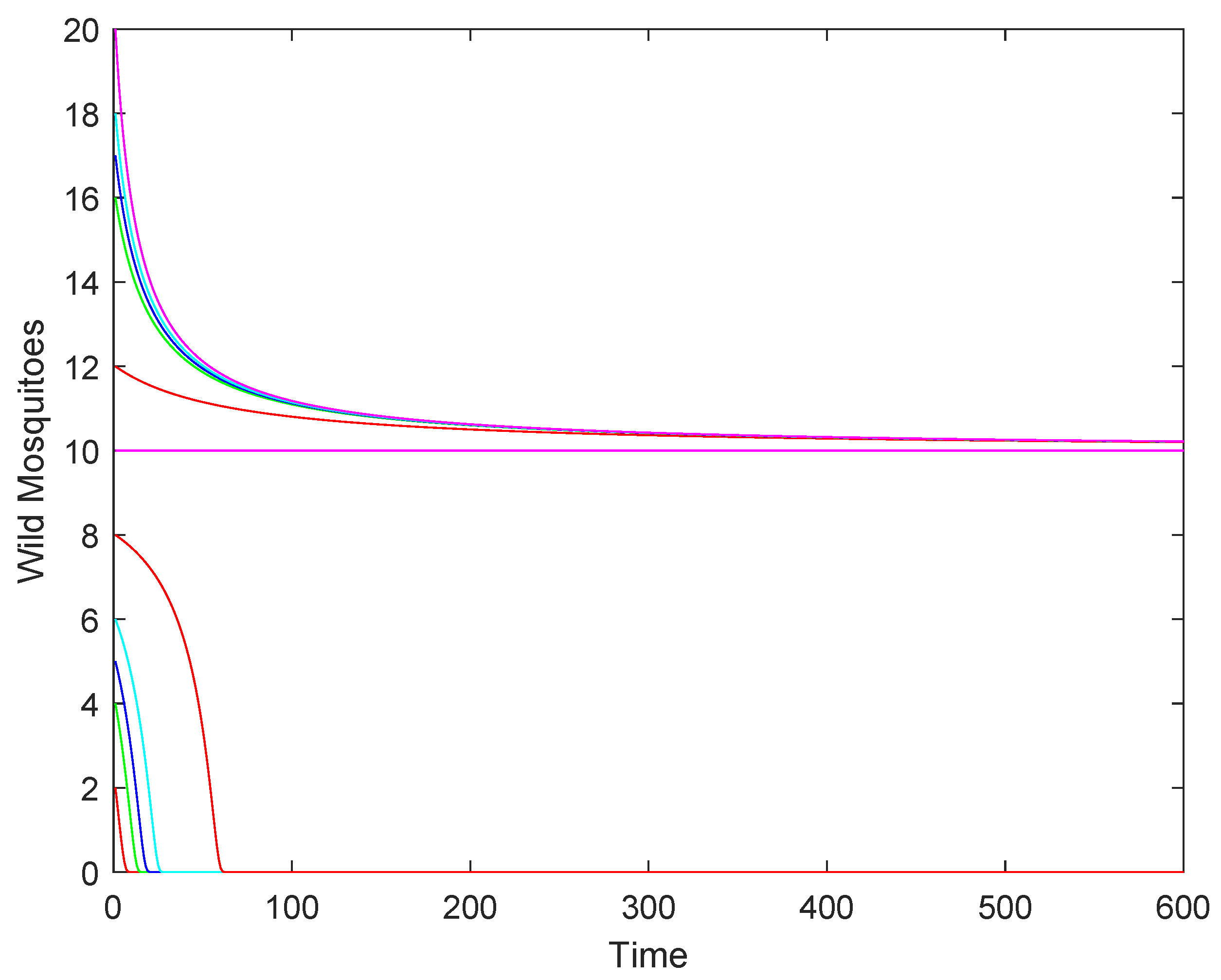
- If , the wild mosquito population will eventually be eradicated. This indicates that the sterile mosquito release strategy is effective in driving the population to extinction.
- (2)
- If , the population may either stabilize at the equilibrium or decline to extinction, depending on the initial population size. This represents a critical scenario where the success of eradication depends on the starting conditions.
- (3)
- If : when the initial population size is above , the population will stabilize at the higher equilibrium , while when the initial population size is below , the population will decline to extinction.
3.2. Numerical Simulations
4. Proportional Release of Sterile Mosquitoes
4.1. The Existence and Stability of Fixed Points
- (1)
- If , then model (13) has no positive fixed points, and the trivial fixed point is globally asymptotically stable.
- (2)
- If , then model (13) has a unique positive fixed point , which is semi-stable.
- (3)
- If , then model (13) has two positive fixed points, and , where the fixed point is unstable, while is locally asymptotically stable on . The trivial fixed point is locally asymptotically stable on .
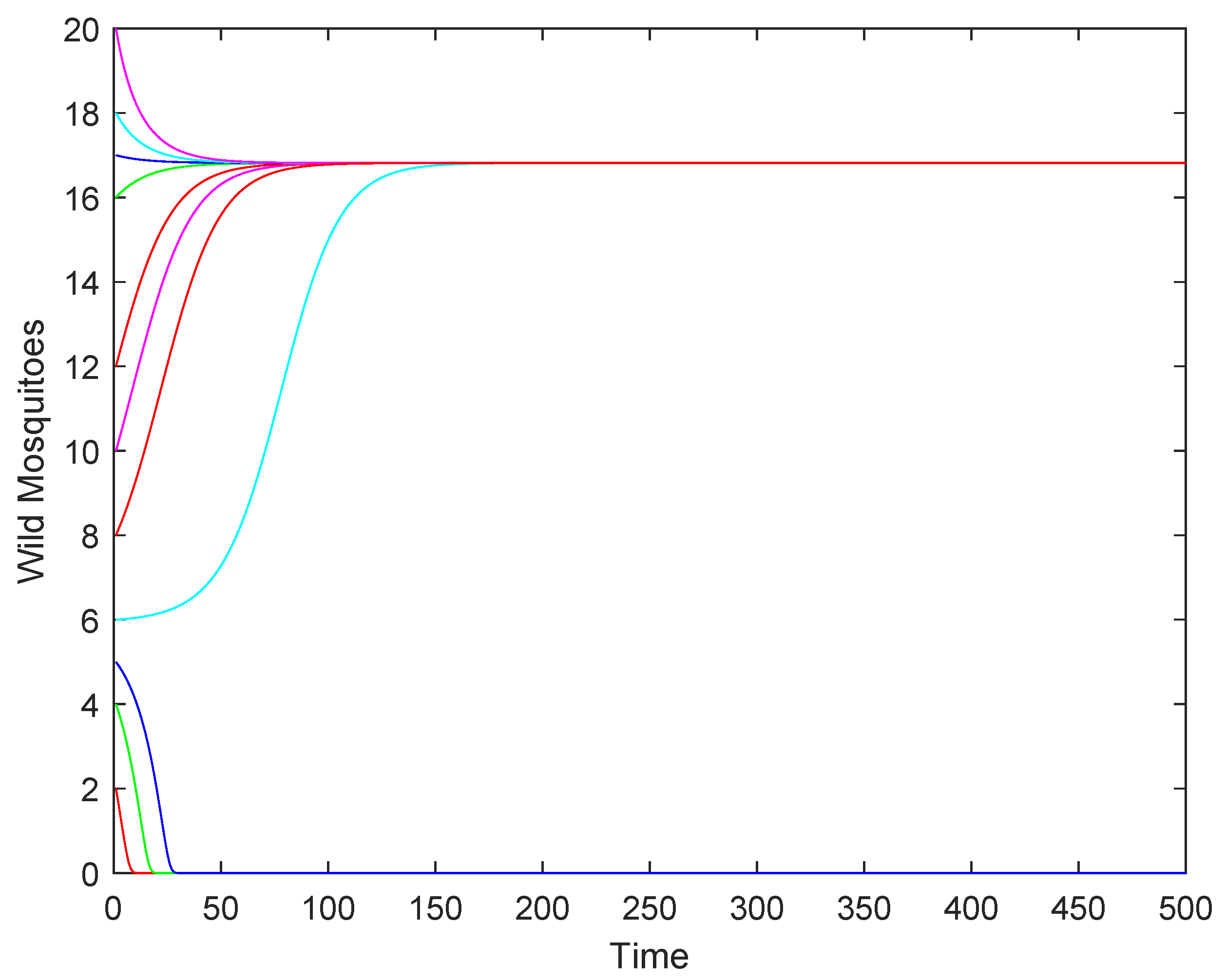
- (1)
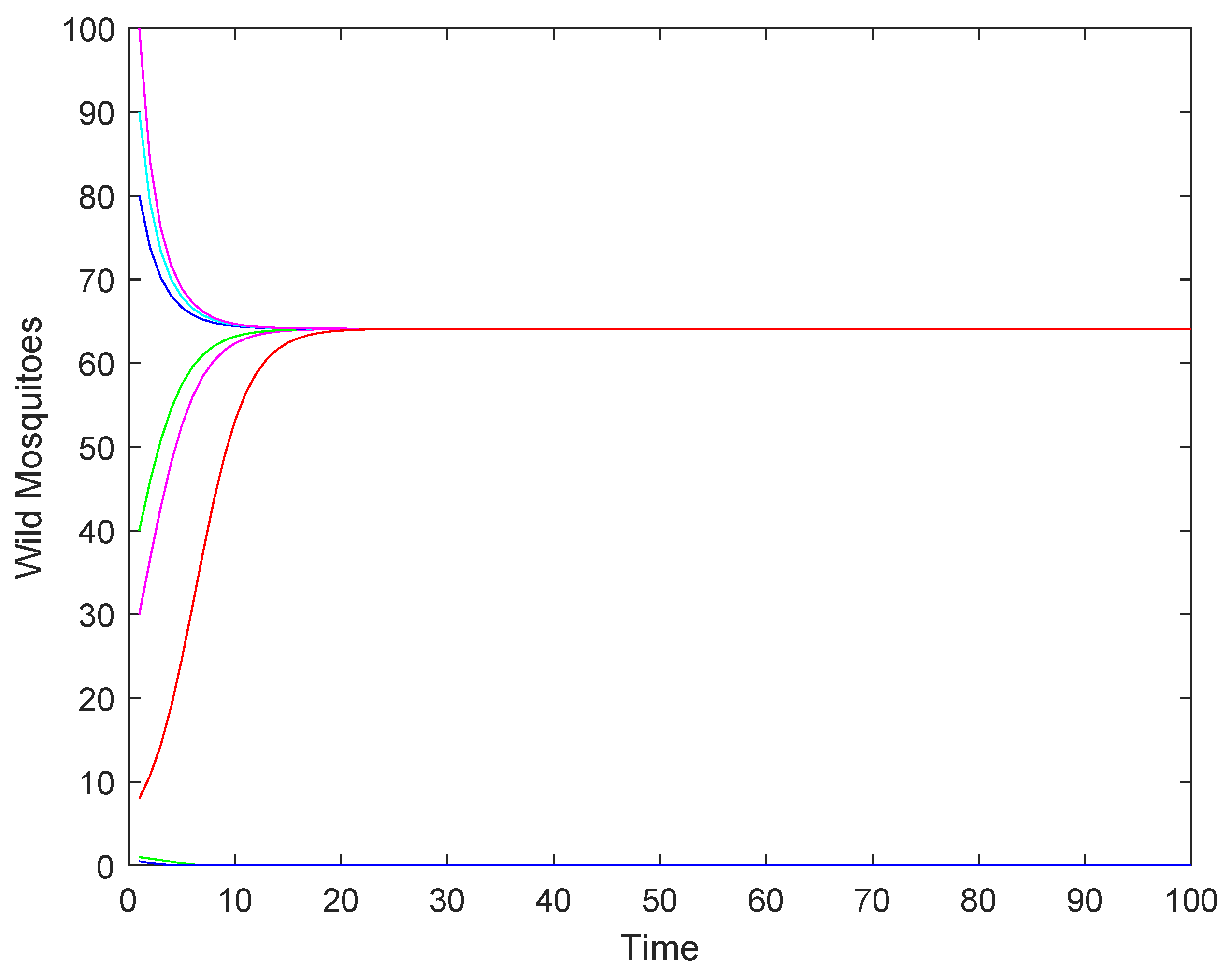
- If the release rate b is sufficiently large (), the wild mosquito population will eventually be eradicated, regardless of the initial population size. This indicates that a high release rate of sterile mosquitoes can effectively suppress and eliminate the wild population.
- (2)
- If the release rate b equals the threshold (), the population may either stabilize at the equilibrium or decline to extinction, depending on the initial population size. This represents a critical scenario where the success of eradication depends on the starting conditions.
- (3)
- If the release rate b is below the threshold (), the population may either stabilize at the higher equilibrium or decline to extinction, depending on whether the initial population size is above or below a certain threshold.
4.2. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Almeida, L.; Duprez, M.; Privat, Y.; Vauchelet, N. Optimal control strategies for the sterile mosquitoes technique. J. Differ. Equ. 2022, 311, 229–266. [Google Scholar] [CrossRef]
- Benedict, M.Q.; Robinson, A.S. The first releases of transgenic mosquitoes: An argument for the sterile insect technique. Trends Parasitol. 2003, 19, 349–355. [Google Scholar] [CrossRef] [PubMed]
- Stone, C.M. Transient population dynamics of mosquitoes during sterile male releases: Modelling mating behaviour and perturbations of life history parameters. PLoS ONE 2013, 8, e76228. [Google Scholar] [CrossRef] [PubMed]
- Bond, J.G.; Osorio, A.R.; Avila, N.; Gomez-Simuta, Y.; Marina, C.F.; Fernandez-Salas, I.; Liedo, P.; Dor, A.; Carvalho, D.O.; Bourtzis, K.; et al. Optimization of irradiation dose to Aedes aegypti and Ae. albopictus in a sterile insect technique program. PLoS ONE 2019, 14, e0212520. [Google Scholar] [CrossRef] [PubMed]
- Yu, J. Modeling mosquito population suppression based on delay differential equations. SIAM J. Appl. Math. 2018, 78, 3168–3187. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, D.; Li, Y.; Yang, C.; Wu, Y.; Liang, X.; Liang, Y.; Pan, X.; Hu, L.; Sun, Q.; et al. Incompatible and sterile insect techniques combined eliminate mosquitoes. Nature 2019, 572, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Li, J.; Yu, J. One discrete dynamical model on the Wolbachia infection frequency in mosquito populations. Sci. China Math. 2022, 65, 1749–1764. [Google Scholar] [CrossRef]
- Yu, J.; Li, J. Dynamics of interactive wild and sterile mosquitoes with time delay. J. Biol. Dyn. 2019, 13, 606–620. [Google Scholar] [CrossRef] [PubMed]
- Yu, J. Existence and stability of a unique and exact two periodic orbits for an interactive wild and sterile mosquito model. J. Differ. Equ. 2020, 269, 10395–10415. [Google Scholar] [CrossRef]
- Yu, J.; Li, J. Global asymptotic stability in an interactive wild and sterile mosquito model. J. Differ. Equ. 2020, 269, 6193–6215. [Google Scholar] [CrossRef]
- Li, J. Modelling of transgenic mosquitoes and impact on malaria transmission. J. Biol. Dyn. 2011, 5, 474–494. [Google Scholar] [CrossRef]
- Li, J.; Yuan, Z. Modelling releases of sterile mosquitoes with different strategies. J. Biol. Dyn. 2015, 9, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Li, J. Discrete-time models for interactive wild and sterile mosquitoes with general time steps. Math. Biosci. 2022, 346, 108797. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.S. Mathematical Ecology Modelling and Research Methods; Science Press: Beijing, China, 1988. (In Chinese) [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, L.; Yang, Y.; Zhang, W.; Huang, M.; Zhou, X. Study on Discrete Mosquito Population-Control Models with Allee Effect. Axioms 2025, 14, 193. https://doi.org/10.3390/axioms14030193
Hong L, Yang Y, Zhang W, Huang M, Zhou X. Study on Discrete Mosquito Population-Control Models with Allee Effect. Axioms. 2025; 14(3):193. https://doi.org/10.3390/axioms14030193
Chicago/Turabian StyleHong, Liang, Yanhua Yang, Wen Zhang, Mingzhan Huang, and Xueyong Zhou. 2025. "Study on Discrete Mosquito Population-Control Models with Allee Effect" Axioms 14, no. 3: 193. https://doi.org/10.3390/axioms14030193
APA StyleHong, L., Yang, Y., Zhang, W., Huang, M., & Zhou, X. (2025). Study on Discrete Mosquito Population-Control Models with Allee Effect. Axioms, 14(3), 193. https://doi.org/10.3390/axioms14030193





