Error Estimators for a Krylov Subspace Iterative Method for Solving Linear Systems of Equations with a Symmetric Indefinite Matrix

Abstract

This paper describes a Krylov subspace iterative method designed for solving linear systems of equations with a large, symmetric, nonsingular, and indefinite matrix. This method is tailored to enable the evaluation of error estimates for the computed iterates. The availability of error estimates makes it possible to terminate the iterative process when the estimated error is smaller than a user-specified tolerance. The error estimates are calculated by leveraging the relationship between the iterates and Gauss-type quadrature rules. Computed examples illustrate the performance of the iterative method and the error estimates.

1. Introduction

Consider the linear system of equations

$$A\mathbf{x}=\mathbf{b},$$

(1)

where $A\in {\mathbb{R}}^{m\times m}$ is a large, symmetric, nonsingular, and indefinite matrix and $\mathbf{x}$ and $\mathbf{b}$ are real vectors. Such systems arise in various areas of applied mathematics and engineering. When A is too large to make its factorization feasible or attractive, an iterative solution method has to be employed. Among the most well-known iterative methods for solving linear systems of the kind (1) are MINRES or SYMMLQ by Paige and Saunders (see [1,2]). However, none of these methods allow for easy estimation of the error in the computed iterates. This can make it difficult to decide when to terminate the iterations.

For a symmetric, positive definite matrix A, the conjugate gradient method is typically used to solve (1). Various techniques are available to estimate the A-norm of the error in the iterates determined by the conjugate gradient method. These techniques leverage the relationship between the conjugate gradient method and Gauss-type quadrature rules applied to integrate the function $f\left(t\right)=t^{-1}$. The quadrature rules are determined with respect to an implicitly defined non-negative measure defined by the matrix A, the right-hand side $\mathbf{b}$, and the initial iterate ${\mathbf{x}}_0$ (see, for example, Almutairi et al. [3], Golub and Meurant [4,5], Meurant and Tichý [6] and references therein).

Error estimation of iterates in cases where the matrix A is nonsingular, symmetric, and indefinite has not received much attention in the literature. We observe that the application of A-norm estimates of the error in the iterates is meaningful when A is symmetric and positive definite [7]. However, this is not the case when A is symmetric and indefinite. In this paper, we estimate the Euclidean norm of the error for each iterate produced by an iterative method, which is described below.

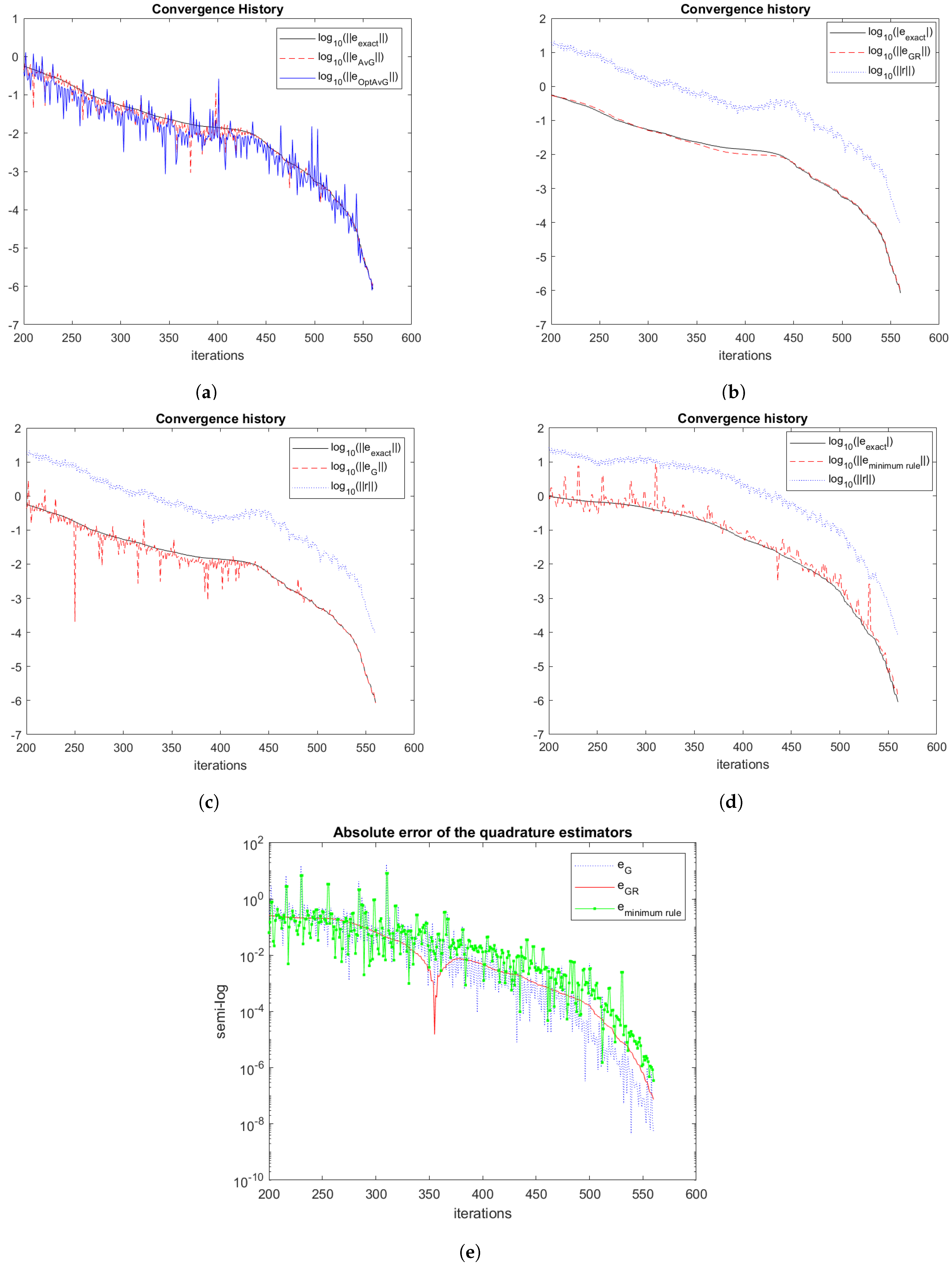
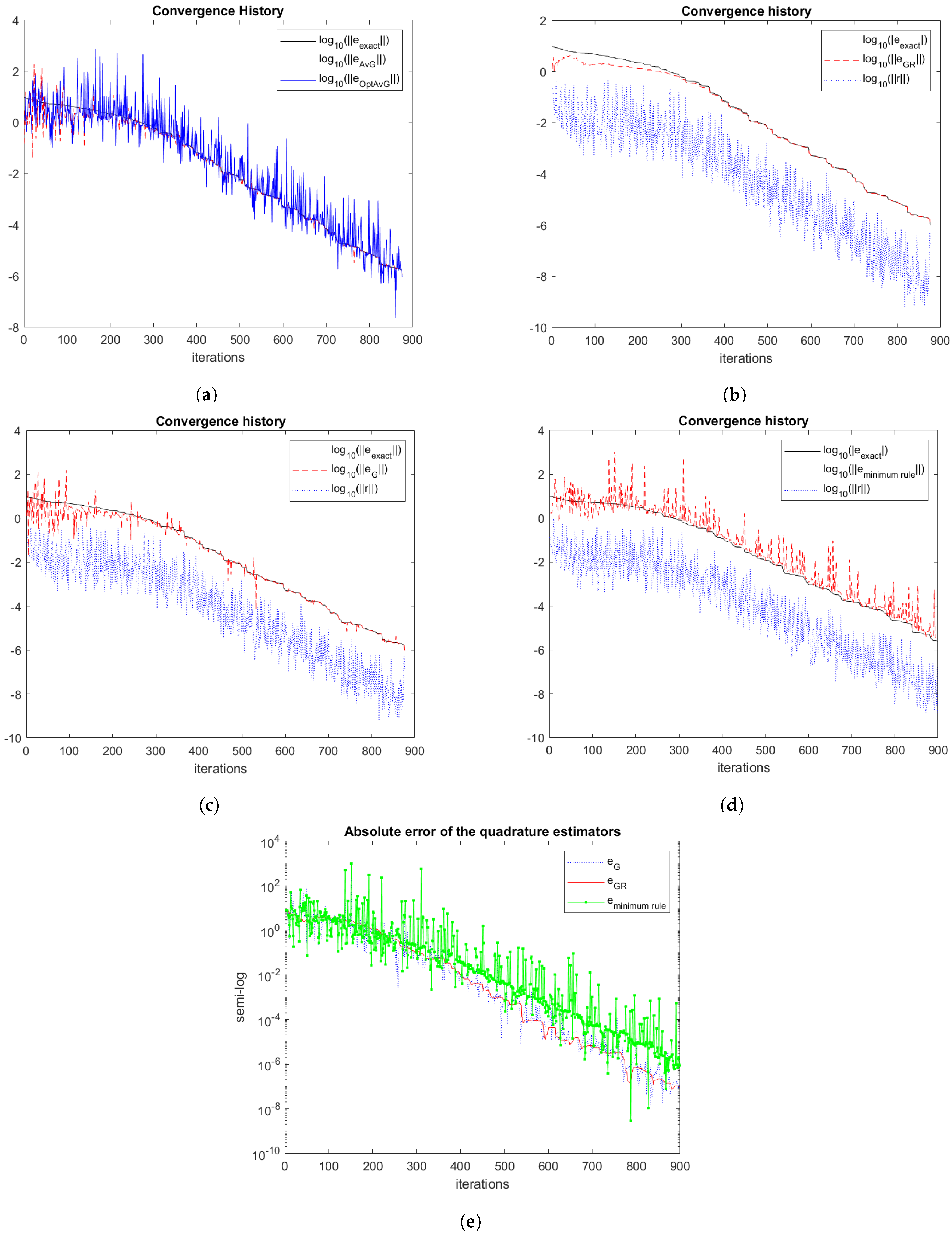
In their work, Calvetti et al. [8] introduced a Krylov subspace method for the iterative solution of (1). They proposed estimating the Euclidean norm of the error in the iterates generated by their method using pairs of associated Gauss and anti-Gauss quadrature rules. However, the quality of the error norm estimates determined in this manner is mixed. Examples of computed results demonstrate that some error norm estimates are significantly exaggerated compared to the actual error norm in the iterates.

This paper presents novel methods for calculating the Euclidean norm of the error in the iterates computed using the iterative method described in Section 2 and [8]. In particular, the anti-Gauss rule used in [8] is replaced by other quadrature rules.

For notational simplicity, we start with the initial approximate solution ${\mathbf{x}}_0=\mathbf{0}$. Consequently, the kth approximate solution ${\mathbf{x}}_k$ determined by the iterative method discussed in this paper lives in the Krylov subspace:

$${\mathcal{K}}_k(A,\mathbf{b})=\mathrm{span}\{\mathbf{b},A\mathbf{b},\dots ,A^{k-1}\mathbf{b}\},k=1,2,\dots ,$$

(2)

i.e.,

$${\mathbf{x}}_k=p_{k-1}\left(A\right)\mathbf{b},k=1,2,\dots ,$$

(3)

for a suitable iteration polynomial $p_{k-1}$ in ${\Pi }_{k-1}$, where ${\Pi }_{k-1}$ is the set of all polynomials of degree less than or equal to $k-1$. We require that the iteration polynomials satisfy

$$p_{k-1}\left(0\right)=0,k=1,2,\dots .$$

(4)

Then

$$p_{k-1}\left(t\right)=t{q}_{k-2}\left(t\right)$$

(5)

fulfills condition (4) for a polynomial $q_{k-2}\in {\Pi }_{k-2}$.

We introduce the residual error related to ${\mathbf{x}}_k$ as

$${\mathbf{r}}_k=\mathbf{b}-A{\mathbf{x}}_k$$

(6)

and let ${\mathbf{x}}_{*}$ denote the solution of (1). Then the error ${\tilde{\mathbf{e}}}_k={\mathbf{x}}_{*}-{\mathbf{x}}_k$ in ${\mathbf{x}}_k$ can be expressed as

$${\tilde{\mathbf{e}}}_k=A^{-1}{\mathbf{r}}_k.$$

(7)

Equations (6) and (7) yield

$${\tilde{\mathbf{e}}}_k^t{\tilde{\mathbf{e}}}_k={\mathbf{r}}_k^t{A}^{-2}{\mathbf{r}}_k={(\mathbf{b}-A{\mathbf{x}}_k)}^t{A}^{-2}(\mathbf{b}-A{\mathbf{x}}_k)={\mathbf{b}}^t{A}^{-2}\mathbf{b}-2{\mathbf{b}}^t{A}^{-1}{\mathbf{x}}_k+{\mathbf{x}}_k^t{\mathbf{x}}_k,$$

(8)

where the superscript ^t denotes transposition. We may calculate the Euclidean norm of the vector ${\tilde{\mathbf{e}}}_k$ by using the terms found on the right-hand side of Equation (8). It is straightforward to compute the term ${\mathbf{x}}_k^t{\mathbf{x}}_k$, and using (5), the expression $2{\mathbf{b}}^t{A}^{-1}{\mathbf{x}}_k$ can be calculated as

$$2{\mathbf{b}}^t{A}^{-1}{\mathbf{x}}_k=2{\mathbf{b}}^t{q}_{k-2}\left(A\right)\mathbf{b}.$$

Hence, the expression $2{\mathbf{b}}^t{A}^{-1}{\mathbf{x}}_k$ can be evaluated without using $A^{-1}$. The iterative method has to be chosen so that recursion formulas for the polynomials $q_{k-2}$, $k=2,3,\dots$ easily can be computed. Finally, we have to estimate ${\mathbf{b}}^t{A}^{-2}\mathbf{b}$, which by setting $f\left(t\right)=1/t^2$, can be written as the following matrix functional

$$\mathcal{F}\left(A\right)={\mathbf{b}}^{t}f\left(A\right)\mathbf{b}.$$

(9)

We use Gauss-type quadrature rules determined by the recurrence coefficients of the iterative method to approximate (9).

The structure of this paper is as follows. Section 2 outlines the iterative Krylov subspace method employed for the solution of (1). This method was discussed in [8]. We review the method for the convenience of the reader. Our presentation differs from that in [8]. The iterative method is designed to facilitate the evaluation of the last two terms on the right-hand side of (8). Section 3 explores various Gauss-type quadrature rules that are employed to estimate the first term on the right-hand side of (8). The quadrature rules used in this study include three kinds of Gauss-type rules, namely averaged and optimally averaged rules by Laurie [9] and Spalević [10], respectively, as well as Gauss-Radau rules with a fixed quadrature node at the origin. Additionally, we describe how to update the quadrature rules cost-effectively as the number of iterations grows. This section improves on the quadrature rules considered in [8]. Section 4 describes the use of these quadrature rules to estimate the Euclidean norm of the errors ${\tilde{\mathbf{e}}}_k$, $k=1,2,\dots$. Section 5 provides three computed examples and Section 6 contains concluding remarks.

The iterates determined by an iterative method often converge significantly faster when a suitable preconditioner is applied (see, e.g., Saad [11] for discussions and examples of preconditioners). We assume that the system (1) is preconditioned when this is appropriate.

2. The Iterative Scheme

This section revisits the iterative method considered in [8] for solving linear systems of Equation (1) with a nonsingular, symmetric, and indefinite matrix A. We begin by discussing some fundamental properties of the method. Subsequently, we describe updating formulas for the approximate solutions ${\mathbf{x}}_k$. This method can be seen as a variation of the SYMMLQ scheme discussed in [1,12].

It is convenient to introduce the spectral factorization of the coefficient matrix (1),

$$A=U\Lambda U^t,$$

where $\Lambda \in {\mathbb{R}}^{m\times m}$ is a diagonal matrix with diagonal elements ${\left\{{\lambda }_k\right\}}_{k=1}^m$ and the matrix $U\in {\mathbb{R}}^{m\times m}$ is orthogonal. The spectral factorization is used for the description of the iterative method but does not have to be computed for the solution of (1). Defining ${\mathbf{b}}^{\prime }={[b_1^{\prime },b_2^{\prime },\dots ,b_m^{\prime }]}^t=U^t\mathbf{b}$, the functional (9) can be written as

$$\mathcal{F}\left(A\right)={\mathbf{b}}^{\prime t}f(\Lambda ){\mathbf{b}}^{\prime }=\sum _{k=1}^{m}f\left({\lambda }_k\right)b_k^{\prime 2}={\int }_{-\infty }^{\infty }f\left(x\right)dw\left(x\right),$$

(10)

where the measure $dw$ has jump discontinuities at the eigenvalues ${\lambda }_k$ of A.

Our iterative method is based on the Lanczos algorithm. Let $I_k\in {\mathbb{R}}^{k\times k}$ denote the identity matrix. By applying $1\le k\ll m$ steps of the Lanczos process to A with initial vector $\mathbf{b}$, the following Lanczos decomposition is obtained:

$$A{\mathcal{V}}_k={\mathcal{V}}_k{T}_k+{\mathbf{f}}_k{\mathbf{e}}_k^t,$$

(11)

where ${\mathbf{f}}_k\in {\mathbb{R}}^m$ and ${\mathcal{V}}_k=[{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_k]\in {\mathbb{R}}^{m\times k}$ are such that ${\mathcal{V}}_k^t{\mathcal{V}}_k=I_k$, ${\mathcal{V}}_k^t{\mathbf{f}}_k=\mathbf{0}$, and

$${\mathbf{v}}_1=\mathbf{b}/\parallel \mathbf{b}\parallel .$$

(12)

Additionally, $T_k$ is a symmetric, tridiagonal $k\times k$ matrix, ${\mathbf{e}}_k$ denotes the kth column of the identity matrix, and $\parallel ·\parallel$ represents the Euclidean vector norm. The columns of the matrix ${\mathcal{V}}_k$ span the Krylov subspace (2), i.e.,

$$\mathrm{range}\left({\mathcal{V}}_k\right)={\mathcal{K}}_k(A,\mathbf{b}).$$

(13)

It is assumed that all subdiagonal entries of $T_k$ are nonvanishing; otherwise, the recursion formulas of the Lanczos process break down, and the solution of (1) can be formulated as a linear combination of the vectors ${\mathbf{v}}_j$ that are available at the time of breakdown. The recursion relation for the columns of ${\mathcal{V}}_k$ is established by Equation (11) and, in conjunction with (12), shows that

$${\mathbf{v}}_j=S_{j-1}\left(A\right)\mathrm{b},j=1,2,\dots ,k,$$

(14)

for certain polynomials $S_j$ of degree j.

Theorem 1.

The polynomials $S_j$ determined by (14) are orthonormal with respect to the inner product

$$(g,h)=\mathcal{I}\left(gh\right)$$

(15)

induced by the operator $\mathcal{I}\left(f\right)={\int }_{-\infty }^{\infty }f\left(x\right)dw\left(x\right)$.

Proof. 

We have

$$\begin{array}{ccc}\hfill (S_{j-1},S_{\ell -1})& =& {\displaystyle {\int }_{-\infty }^{\infty }{S}_{j-1}\left(x\right)S_{\ell -1}\left(x\right)dw\left(x\right)}\hfill \\ & =& {\mathbf{b}}^t\left(U{S}_{j-1}(\Lambda )S_{\ell -1}(\Lambda )U^t\right)\mathbf{b}\hfill \\ & =& {\mathbf{b}}^t\left(U{S}_{j-1}(\Lambda )U^t\right)\left(U{S}_{\ell -1}(\Lambda )U^t\right)\mathbf{b}\hfill \\ & =& {\mathbf{b}}^t{S}_{j-1}\left(A\right)S_{\ell -1}\left(A\right)\mathbf{b}\hfill \\ & =& {\left(S_{j-1}\left(A\right)\mathbf{b}\right)}^t\left(S_{\ell -1}\left(A\right)\mathbf{b}\right)\hfill \\ & =& {\mathbf{v}}_j^t{\mathbf{v}}_{\ell }=\left\{\begin{array}{cc}0,& j\ne \ell ,\hfill \\ 1,& j=\ell ,\hfill \end{array}\right.\hfill \end{array}$$

because the columns ${\mathbf{v}}_j$, $1\le j\le k$, of the matrix ${\mathcal{V}}_k$ are orthogonal and of unit norm (see (11)).    □

We also use the related decomposition to (11):

$$A{\mathcal{V}}_{k-1}={\mathcal{V}}_k{T}_{k,k-1},$$

(16)

where $T_{k,k-1}$ is the leading submatrix of $T_k$ of order $k\times (k-1)$.

We use the QR factorization for $T_k$, that is,

$$T_k=Q_k{R}_k,\mathrm{for}{Q}_k,R_k\in {\mathbb{R}}^{k\times k},$$

(17)

where $Q_k^t{Q}_k=I_k$ and the matrix $R_k={\left[r_{j\ell }^{\left(k\right)}\right]}_{j,\ell =1}^k$ is upper triangular. Similarly, we introduce the factorization

$$T_{k,k-1}=Q_k\left[\begin{array}{c}{\overline{R}}_{k-1}\\ 0\end{array}\right]=Q_{k,k-1}{\overline{R}}_{k-1},$$

(18)

where the $(k-1)\times (k-1)$ matrix ${\overline{R}}_{k-1}$ is the leading submatrix of $R_k$ and $Q_{k,k-1}\in {\mathbb{R}}^{k\times (k-1)}$ is the leading submatrix of $Q_k$.

Theorem 2.

Combine the QR factorization (17) with the Lanczos decomposition (11). This defines a new iterative process with iteration polynomials that comply with (4).

Proof. 

Let $k>1$. By applying the QR factorization (17) within the Lanczos decomposition (11), we obtain

$$A{\mathcal{V}}_k={\mathcal{V}}_k{Q}_k{R}_k+{\mathbf{f}}_k{\mathbf{e}}_k^t.$$

(19)

Multiplying (19) by $Q_k$ from the right-hand side, letting ${\tilde{V}}_k:={\mathcal{V}}_k{Q}_k$, and defining ${\tilde{T}}_k=R_k{Q}_k$, we obtain

$$A{\tilde{V}}_k={\tilde{V}}_k{\tilde{T}}_k+{\mathbf{f}}_k{\mathbf{e}}_k^t{Q}_k.$$

(20)

The column vectors of the matrix expressed as ${\tilde{V}}_k=[{\tilde{\mathbf{v}}}_1^{\left(k\right)},{\tilde{\mathbf{v}}}_2^{\left(k\right)},\dots ,{\tilde{\mathbf{v}}}_k^{\left(k\right)}]$ are orthonormal, and the matrix ${\tilde{T}}_k$ is symmetric and tridiagonal. To expose the relation between the first column ${\mathbf{v}}_1$ of ${\mathcal{V}}_k$ and the first column ${\tilde{\mathbf{v}}}_1^{\left(k\right)}$ of ${\tilde{V}}_k$, we multiply (19) by ${\mathbf{e}}_1$ from the right. This yields

$$A{\mathcal{V}}_k{\mathbf{e}}_1={\tilde{V}}_k{R}_k{\mathbf{e}}_1+{\mathbf{f}}_k{\mathbf{e}}_k^t{\mathbf{e}}_1,k>1,$$

which simplifies to

$$A{\mathbf{v}}_1=r_{11}^{\left(k\right)}{\tilde{\mathbf{v}}}_1^{\left(k\right)},$$

where $r_{11}^{\left(k\right)}{\mathbf{e}}_1=R_k{\mathbf{e}}_1$. For a suitable choice of the sign of $r_{11}^{\left(k\right)}$, we have

$${\tilde{\mathbf{v}}}_1^{\left(k\right)}=A\mathbf{b}/\parallel A\mathbf{b}\parallel .$$

(21)

Since $T_k$ is tridiagonal, the orthogonal matrix $Q_k$ in the QR factorization (17) has upper Hessenberg form. As a result, only the last two entries of the vector expressed as ${\mathbf{e}}_k^t{Q}_k$ are non-zero. Hence, the decomposition (20) differs from a Lanczos decomposition by potentially having non-zero entries in the last two columns of the matrix ${\mathbf{f}}_k{\mathbf{e}}_k^t{Q}_k$.

Suppose that the matrix ${\overline{V}}_{k-1}$ consists of the first $k-1$ columns of ${\tilde{V}}_k$. Then,

$${\overline{V}}_{k-1}={\mathcal{V}}_k{Q}_{k,k-1},$$

(22)

where $Q_{k,k-1}$ is defined by Equation (18). Typically, ${\overline{V}}_{k-1}\ne {\tilde{V}}_{k-1}$; additional details can be found in Section 4. When the last column is removed from each term in (20), the following decomposition results:

$$A{\overline{V}}_{k-1}={\overline{V}}_{k-1}{\tilde{T}}_{k-1}+{\overline{\mathbf{f}}}_{k-1}{\mathbf{e}}_{k-1}^t.$$

(23)

In (23), the matrix ${\tilde{T}}_{k-1}$ is the $(k-1)\times (k-1)$ leading submatrix of ${\tilde{T}}_{k-1}$. Furthermore, ${\overline{V}}_{k-1}^t{\overline{\mathbf{f}}}_{k-1}=\mathbf{0}$, and ${\overline{V}}_{k-1}^t{\overline{V}}_{k-1}=I_{k-1}$. As a result, according to (21), we have that (23) is a Lanczos decomposition with the starting vector ${\tilde{\mathbf{v}}}_1^{\left(k\right)}$ of ${\overline{V}}_{k-1}$ proportional to the vector $A\mathbf{b}$. Similarly to (13), we have

$$\mathrm{range}\left({\overline{V}}_{k-1}\right)={\mathcal{K}}_{k-1}(A,A\mathrm{b}).$$

(24)

To determine the iteration polynomials (3) and the corresponding approximate solutions ${\mathbf{x}}_k$ of (3), we impose the following requirement for certain vectors ${\mathbf{w}}_{k-1}\in {\mathbb{R}}^{k-1}$:

$${\mathbf{x}}_k=p_{k-1}\left(A\right)\mathbf{b}={\overline{V}}_{k-1}{\mathbf{w}}_{k-1}.$$

(25)

It follows from (24) that any polynomial $p_{k-1}$ determined by (25) fulfills (4). This completes the proof.    □

Remark 1.

We chose ${\mathbf{w}}_{k-1}$ in (25) and, thereby, $p_{k-1}$ in ${\Pi }_{k-1}$ in a manner that guarantees the residual error (6) for the approximate solution ${\mathrm{x}}_k$ of (1) satisfies the Petrov-Galerkin condition, i.e.,

$$\mathbf{0}={\mathcal{V}}_{k-1}^t{\mathbf{r}}_k={\mathcal{V}}_{k-1}^t\mathbf{b}-{\mathcal{V}}_{k-1}^{t}A{\overline{V}}_{k-1}{\mathbf{w}}_{k-1},$$

(26)

which, according to (12) and the factorization (22), simplifies to

$$\parallel \mathbf{b}\parallel {\mathbf{e}}_1={\left(A{\mathcal{V}}_{k-1}\right)}^t{\mathcal{V}}_k{Q}_{k,k-1}{\mathbf{w}}_{k-1}.$$

(27)

Remark 2.

Replacing the matrix ${\overline{V}}_{k-1}$ in (26) with ${\mathcal{V}}_{k-1}$ recovers the SYMMLQ method [1]. However, the iteration polynomial $p_{k-1}$ associated with the SYMMLQ method typically does not satisfy condition (4). Our method implements a QR factorization of matrix $T_k$, akin to the SYMMLQ method implementation by Fischer ([12], Section 6.5). In contrast, Paige and Saunders’ [1] implementation of the SYMMLQ method relies on an LQ factorization of $T_k$.

Remark 3.

Equation (26) shows that the iterative method is a Petrov-Galerkin method. In each step of the method, the dimension of the solution subspace (24) is increased by one, and the residual error is required to be orthogonal to the subspace $\left({\mathcal{K}}_{k-1}(A,\mathbf{b})\right)$, cf. (13). This secures convergence of the iterates (25) to the solution ${\mathbf{x}}_{*}$ of (1) as k increases.

Using Theorems 1 and 2, along with Remark 1, we can simplify the right-hand side of (7). First, using (16) and (18), we obtain

$${\left(A{\mathcal{V}}_{k-1}\right)}^t{\mathcal{V}}_k{Q}_{k,k-1}=T_{k,k-1}^t{Q}_{k,k-1}={\overline{R}}_{k-1}^t.$$

(28)

Subsequently, by substituting (28) into (27), we obtain

$${\overline{R}}_{k-1}^t{\mathbf{w}}_{k-1}=\parallel \mathbf{b}\parallel {\mathbf{e}}_1.$$

(29)

We can evaluate ${\mathbf{w}}_{k-1}$ by forward substitution using (29). The rest of this section focuses on evaluating the right-hand side of (8).

Section 4 presents iterative formulas to efficiently update the approximate solutions ${\mathbf{x}}_k$. The remainder of this section discusses the evaluation of the right-hand side of (8). From (24) and (25), it can be deduced that ${\mathrm{x}}_k$ lives in ${\mathcal{K}}_{k-1}(A,A\mathrm{b})$. Consequently, there is a vector ${\mathbf{y}}_{k-1}\in {\mathbb{R}}^{k-1}$ such that

$$A^{-1}{\mathrm{x}}_k={\mathcal{V}}_{k-1}{\mathbf{y}}_{k-1}.$$

(30)

Using the decomposition (16), the kth iterate generated by our iterative method can be written as

$${\mathbf{x}}_k=A{\mathcal{V}}_{k-1}{\mathbf{y}}_{k-1}={\mathcal{V}}_k{T}_{k,k-1}{\mathbf{y}}_{k-1}.$$

Furthermore, according to (22) and (25), we have

$${\mathbf{x}}_k={\mathcal{V}}_k{Q}_{k,k-1}{\mathbf{w}}_{k-1}.$$

This implies that

$$Q_{k,k-1}{\mathbf{w}}_{k-1}=T_{k,k-1}{\mathbf{y}}_{k-1}.$$

(31)

Multiplying (31) by $Q_{k,k-1}^t$ from the left and using (18) yields

$${\mathbf{w}}_{k-1}=Q_{k,k-1}^t{T}_{k,k-1}{\mathbf{y}}_{k-1}={\overline{R}}_{k-1}{\mathbf{y}}_{k-1}.$$

(32)

By successively applying (12), (29), (30), and (32), we obtain

$${\mathbf{b}}^t{A}^{-1}{\mathbf{x}}_k={\mathbf{b}}^t{\mathcal{V}}_{k-1}{\mathbf{y}}_{k-1}=\parallel \mathbf{b}\parallel {\mathbf{e}}_1^t{\mathbf{y}}_{k-1}=\parallel \mathbf{b}\parallel {\mathbf{e}}_1^t{\overline{R}}_{k-1}^{-1}{\mathbf{w}}_{k-1}={\mathbf{w}}_{k-1}^t{\mathbf{w}}_{k-1}.$$

(33)

According to (25), it follows that ${\mathbf{x}}_k^t{\mathbf{x}}_k={\mathbf{w}}_{k-1}^t{\mathbf{w}}_{k-1}$. Combining this with (33) shows that Equation (8) can be represented as

$${\tilde{\mathbf{e}}}_k^t{\tilde{\mathbf{e}}}_k={\mathbf{r}}_k^t{A}^{-2}{\mathbf{r}}_k={\mathbf{b}}^t{A}^{-2}\mathbf{b}-{\mathbf{w}}_{k-1}^t{\mathbf{w}}_{k-1}.$$

The term ${\mathbf{w}}_{k-1}^t{\mathbf{w}}_{k-1}$ can easily be computed using (29). Section 3 describes several Gauss-type quadrature rules that are applied to compute estimates of ${\mathbf{b}}^t{A}^{-2}\mathbf{b}$ in Section 4.

3. Quadrature Rules

This section considers the approximation of integrals like

$$\mathcal{I}\left(f\right)={\int }_a^{b}f\left(x\right)dw\left(x\right)$$

(34)

by Gauss-type quadrature rules, where $[a,b]\subseteq [-\infty ,\infty ]$ and $dw$ denotes a non-negative measure with an infinite number of support points such that all moments ${\mu }_j={\int }_a^b{x}^{j}dw\left(x\right)$ exist, for $j=0,1,2,\dots$. In this section, we assume that ${\mu }_0=1$. Let

$${\mathcal{Q}}_n\left(f\right)=\sum _{i=1}^n{w}_i^{\left(n\right)}f\left({\xi }_i^{\left(n\right)}\right)$$

denote an n-node quadrature rule to approximate (34). Then

$${\int }_a^{b}f\left(x\right)dw\left(x\right)={\mathcal{Q}}_n\left(f\right)+{\mathcal{E}}_n\left(f\right),$$

where ${\mathcal{E}}_n\left(f\right)$ is the remainder term. This term vanishes for all polynomials in ${\Pi }_d$ for some non-negative integer d. The value of d is referred to as the degree of precision of the quadrature rule. It is well known that the maximum value of d for an n-node quadrature rule is $2n-1$. This value is achieved by the n-node Gauss rule (see, e.g., [13] for a proof). The latter rule can be written as

$${\mathcal{G}}_n\left(f\right)=\sum _{i=1}^n{w}_i^{\left(n\right)}f\left({\xi }_i^{\left(n\right)}\right).$$

(35)

The nodes ${\xi }_i^{\left(n\right)}$, $i=1,2,\dots ,n$, are the eigenvalues of the matrix

$$T_n=\left[\begin{array}{ccccc}{\alpha }_1& {\beta }_1& & & \mathbf{0}\\ {\beta }_1& {\alpha }_2& {\beta }_2& & \\ & \ddots & \ddots & \ddots & \\ & & {\beta }_{n-2}& {\alpha }_{n-1}& {\beta }_{n-1}\\ \mathbf{0}& & & {\beta }_{n-1}& {\alpha }_n\end{array}\right]\in {\mathbb{R}}^{n\times n},$$

(36)

and the weights $w_i^{\left(n\right)}$ are the square of the first elements of normalized eigenvectors.

The entries ${\alpha }_i$ and ${\beta }_i$ of $T_n$ are obtained from the recursion formula for the sequence of monic orthogonal polynomials ${\left\{P_i\right\}}_{i=0}^{\infty }$ associated with the inner product (15):

$$P_{i+1}\left(x\right)=(x-{\alpha }_i)P_i\left(x\right)-{\beta }_i^2{P}_{i-1}\left(x\right),i=0,1,2,\dots ,$$

(37)

where $P_{-1}\left(x\right)\equiv 0$ and $P_0\left(x\right)\equiv 1$. The values of ${\alpha }_i$ and ${\beta }_i$ in (37) can be determined from the following formulas (see, e.g., Gautschi [13] for details):

$${\alpha }_i={\displaystyle \frac{(x{P}_i,P_i)}{(P_i,P_i)}},{\beta }_i^2={\displaystyle \frac{(P_i,P_i)}{(P_{i-1},P_{i-1})}};$$

They also can be computed by the Lanczos process, which is presented in Algorithm 1.

Algorithm 1: The Lanczos algorithm.

It is straightforward to demonstrate that

$${\mathcal{G}}_n\left(f\right)={\mathbf{e}}_1^{t}f\left(T_n\right){\mathbf{e}}_1,$$

(38)

where ${\mathbf{e}}_1={[1,0,\dots ,0]}^t$.

We are interested in measures $dw$ with support in two real intervals $[a,b]$ and $[c,d]$, where $a<b<0<c<d$. The following result sheds light on how the nodes of the Gauss rule (35) are allocated for such measures.

Theorem 3.

Let $d\omega$ be a non-negative measure with support on the union of bounded real intervals $[a,b]$ and $[c,d]$, where $a<b<c<d$. Then, the Gauss rule (35) has at most one node in the open interval $(b,c)$.

Proof. 

The result follows from [14] (Theorem 3.41.1). □

The following subsection reviews some Gauss-type quadrature rules that are used to estimate the error in approximate solutions ${\mathbf{x}}_k$ of (1) that are generated by the iterative method proposed in Section 2.

Selected Gauss-Type Quadrature Rules

In [9], Laurie presented anti-Gauss quadrature rules. A recent analysis of anti-Gauss rules was also carried out by Díaz de Alba et al. [15]. Related investigations can be found in [16,17]. The $(n+1)$-point anti-Gauss rule ${\breve{\mathcal{G}}}_{n+1}$, which is associated with the Gauss rule (35), is defined by the property

$$\left(\mathcal{I}-{\breve{\mathcal{G}}}_{n+1}\right)\left(f\right)=-\left(\mathcal{I}-{\mathcal{G}}_n\right)\left(f\right),\mathrm{for}\mathrm{all}f\in {\Pi }_{2n+1}.$$

(39)

The following tridiagonal matrix is used to determine the rule ${\breve{\mathcal{G}}}_{n+1}$:

$${\breve{T}}_{n+1}=\left[\begin{array}{cccccc}{\alpha }_1& {\beta }_1& & & & \mathbf{0}\\ {\beta }_1& {\alpha }_2& {\beta }_2& & & \\ & \ddots & \ddots & \ddots & & \\ & & {\beta }_{n-2}& {\alpha }_{n-1}& {\beta }_{n-1}& \\ & & & {\beta }_{n-1}& {\alpha }_n& \sqrt{2}{\beta }_n\\ \mathbf{0}& & & & \sqrt{2}{\beta }_n& {\alpha }_{n+1}\end{array}\right]{\mathbb{R}}^{(n+1)\times (n+1)}.$$

Similarly to (38), we have

$${\breve{\mathcal{G}}}_{n+1}\left(f\right)={\mathbf{e}}_1^{t}f\left({\breve{T}}_{n+1}\right){\mathbf{e}}_1.$$

Moreover,

$${\breve{\mathcal{G}}}_n\left(f\right)=\mathcal{I}\left(f\right),\mathrm{for}\mathrm{all}f\in {\Pi }_{2n-1}.$$

Further, Laurie [9] introduced the averaged Gauss quadrature rule associated with ${\mathcal{G}}_n$. It has $2n+1$ nodes and is given by

$${\mathcal{A}}_{2n+1}={\displaystyle \frac{1}{2}}\left({\mathcal{G}}_n+{\breve{\mathcal{G}}}_{n+1}\right).$$

(40)

The property (39) suggests that the quadrature error for ${\mathcal{A}}_{2n+1}$ is smaller than the error for ${\mathcal{G}}_n$. Indeed, it follows from (39) that the degree of precision of ${\mathcal{A}}_{2n+1}$ is no less than $2n+1$. This implies that the difference

$${\mathcal{A}}_{2n+1}\left(f\right)-{\mathcal{G}}_n\left(f\right)$$

(41)

can be used to estimate the quadrature error

$$\mathcal{I}\left(f\right)-{\mathcal{G}}_n\left(f\right).$$

(42)

Computed results in [18] illustrate that for numerous integrands and various values of n, the difference (41) provides fairly accurate approximation of the quadrature error (42). The accuracy of these estimates depends both on the integrand and the value of n.

In [10], Spalević presented optimal averaged Gauss quadrature rules, which usually have a higher degree of precision than averaged Gauss rules with the same number of nodes. The symmetric tridiagonal matrix for the optimal averaged Gauss quadrature rule ${\widehat{\mathcal{A}}}_{2n+1}$ with $2n+1$ nodes is defined as follows. Introduce the reverse matrix of $T_n$, which is given by

$$T_n^{\prime }=\left[\begin{array}{ccccc}{\alpha }_n& {\beta }_{n-1}& & & \mathbf{0}\\ {\beta }_{n-1}& {\alpha }_{n-1}& {\beta }_{n-2}& & \\ & \ddots & \ddots & \ddots & \\ & & {\beta }_2& {\alpha }_2& {\beta }_1\\ \mathbf{0}& & & {\beta }_1& {\alpha }_1\end{array}\right]\in {\mathbb{R}}^{n\times n},$$

as well as the concatenated matrix

$${\widehat{T}}_{2n+1}=\left[\begin{array}{ccc}{T}_n& {\beta }_n{\mathbf{e}}_n& \mathbf{0}\\ {\beta }_n{\mathbf{e}}_n^t& {\alpha }_{n+1}& {\beta }_{n+1}{\mathbf{e}}_1^t\\ \mathbf{0}& {\beta }_{n+1}{\mathbf{e}}_1& T_n^{\prime }\end{array}\right]\in {\mathbb{R}}^{(2n+1)\times (2n+1)}.$$

The nodes of the rule ${\widehat{\mathcal{A}}}_{2n+1}$ are the eigenvalues, and the weights are the squared first components of normalized eigenvectors of the matrix ${\widehat{T}}_{2n+1}$. It is worth noting that n of the nodes of ${\widehat{\mathcal{A}}}_{2n+1}$ agree with the nodes of ${\mathcal{G}}_n$. Similarly to Equation (38), we have

$${\widehat{\mathcal{A}}}_{2n+1}\left(f\right)={\mathbf{e}}_1^{t}f\left({\widehat{T}}_{2n+1}\right){\mathbf{e}}_1.$$

The degree of precision for this quadrature rule is at least $2n+2$. Analyses of the degree of precision of the rules ${\widehat{\mathcal{A}}}_{2n+1}$ and the location of their largest and smallest nodes for several measures for which explicit expressions for coefficients ${\alpha }_i$ and ${\beta }_i$ are known can be found in [19] and references therein. An estimate of the quadrature error in the Gauss rule (35) is given by

$${\widehat{\mathcal{A}}}_{2n+1}\left(f\right)-{\mathcal{G}}_n\left(f\right).$$

(43)

Numerical examples provided in [18] show this estimate to be quite accurate for a wide range of integrands. As the rule ${\widehat{\mathcal{A}}}_{2n+1}$ typically has strictly higher degree of precision than Laurie’s averaged Gauss rule (40), we expect the quadrature error estimate (43) to generally be more accurate than the estimate (41), particularly for integrands with high-order differentiability.

In the computations, we use the representation

$${\widehat{\mathcal{A}}}_{2n+1}\left(f\right)={\displaystyle \frac{{\beta }_{n+1}^2}{{\beta }_n^2+{\beta }_{n+1}^2}}{\mathcal{G}}_n\left(f\right)+{\displaystyle \frac{{\beta }_n^2}{{\beta }_n^2+{\beta }_{n+1}^2}}{\mathcal{G}}_{n+1}^{*}\left(f\right),$$

where

$${\mathcal{G}}_{n+1}^{*}\left(f\right)={\mathbf{e}}_1^{t}f\left(T_{n+1}^{*}\right){\mathbf{e}}_1$$

with

$$T_{n+1}^{*}=\left[\begin{array}{cccccc}{\alpha }_1& {\beta }_1& & & & \mathbf{0}\\ {\beta }_1& {\alpha }_2& {\beta }_2& & & \\ & \ddots & \ddots & \ddots & & \\ & & {\beta }_{n-2}& {\alpha }_{n-1}& {\beta }_{n-1}& \\ & & & {\beta }_{n-1}& {\alpha }_n& {\beta }_n^{*}\\ \mathbf{0}& & & & {\beta }_n^{*}& {\alpha }_{n+1}\end{array}\right]\in {\mathbb{R}}^{(n+1)\times (n+1)}$$

and ${\beta }_n^{*}=\sqrt{{\beta }_n^2+{\beta }_{n+1}^2}$.

We finally consider the Gauss-Radau quadrature rule ${\mathcal{R}}_{n+1,0}\left(f\right)$, which has $n+1$ nodes, with one node anchored at 0. This rule can be written as

$${\mathcal{R}}_{n+1,0}\left(f\right)=w_0^{(n+1)}f\left(0\right)+\sum _{i=1}^n{w}_i^{(n+1)}f\left({\xi }_{i,0}^{(n+1)}\right).$$

(44)

To maximize the degree of precision, which is $2n$, the n nodes ${\xi }_{i,0}^{(n+1)}$, $i=1,2,\dots ,n$, are suitably chosen. The rule ${\mathcal{R}}_{n+1,0}\left(f\right)$ can be expressed as

$${\mathcal{R}}_{n+1,0}\left(f\right)={\mathbf{e}}_1^{t}f\left(T_{n+1,0}\right){\mathbf{e}}_1,$$

where

$$T_{n+1,0}=\left[\begin{array}{cccccc}{\alpha }_1& {\beta }_1& & & & \mathbf{0}\\ {\beta }_1& {\alpha }_2& {\beta }_2& & & \\ & \ddots & \ddots & \ddots & & \\ & & {\beta }_{n-2}& {\alpha }_{n-1}& {\beta }_{n-1}& \\ & & & {\beta }_{n-1}& {\alpha }_n& {\beta }_n\\ \mathbf{0}& & & & {\beta }_n& {\tilde{\alpha }}_{n+1}\end{array}\right]\in {\mathbb{R}}^{(n+1)\times (n+1)},$$

(45)

and the entry ${\tilde{\alpha }}_{n+1}$ is chosen so that $T_{n+1,0}$ has an eigenvalue at the origin. Details on how to determine ${\tilde{\alpha }}_{n+1}$ are provided by Gautschi [13,20] and Golub [21].

Theorem 4.

Let the nodes ${\left\{{\xi }_{i,0}^{(n+1)}\right\}}_{i=1}^{n+1}$ of the rule (44) and the nodes ${\left\{{\xi }_i^{\left(n\right)}\right\}}_{i=1}^n$ of the rule (35) be ordered according to increasing magnitude. Then ${\xi }_{0,0}^{(n+1)}=0$ and

$$|{\xi }_{i,0}^{(n+1)}| > |{\xi }_i^{\left(n\right)}|,i=1,\dots ,n.$$

Proof. 

The last subdiagonal entry of the matrix (45) is non-vanishing since the measure $dw$ in (34) has infinitely many support points. By the Cauchy interlacing theorem, the eigenvalues of the leading principal $n\times n$ submatrix (36) of the symmetric tridiagonal $(n+1)\times (n+1)$ matrix (45) strictly interlace the eigenvalues of the latter. Since one of the eigenvalues of (45) vanishes, the theorem follows. □

The measure $dw$ has no support at the origin. We therefore apply the Gauss-Radau rules with $f\left(0\right)=0$ in (44).

Finally, we compute error-norm estimates by using the “minimum rule”:

$${\mathcal{A}}_{4n+2}^{min}\left(f\right)=min\{{\mathcal{A}}_{2n+1}\left(f\right),{\widehat{\mathcal{A}}}_{2n+1}\left(f\right)\}.$$

(46)

It typically has $3n+2$ distinct nodes. This rule is justified by the observation that the rules ${\mathcal{A}}_{2n+1}\left(f\right)$ and ${\widehat{\mathcal{A}}}_{2n+1}\left(f\right)$ sometimes overestimate the error norm.

4. Error-Norm Estimation

This section outlines how the quadrature rules discussed in the previous section can be used to estimate the Euclidean norm of the error in the iterates ${\mathbf{x}}_k$, $k=0,1,\dots$, determined by the iterative method described in Section 2. The initial iterate is assumed to be ${\mathbf{x}}_0=\mathbf{0}$. Then the iterate ${\mathbf{x}}_n$ lives in the Krylov subspace (cf. (24) and (25)),

$${\mathcal{K}}_{n-1}(A,A\mathbf{b})=\mathrm{span}\left\{A\mathbf{b},A^2\mathbf{b},\dots ,A^{n-1}\mathbf{b}\right\},$$

The residual corresponding to the iterate ${\mathbf{x}}_n$ is defined in (6). We use the relation (7) to obtain the Euclidean norm of the error, cf. (8). Our task is to estimate the first term in the right-hand side of (8). In this section, the measure is defined by (10). In particular, the measure has support in intervals on the negative and positive real axis. These intervals exclude an interval around the origin.

We turn to the computation of the iterates ${\mathbf{x}}_k$ described by (25). The computations can be structured in such a way that only a few m-vectors need to be stored. Let the $k\times k$ real matrix $T_k$ be given by (36) with $n=k$, i.e.,

$$T_k=\left[\begin{array}{ccccccc}{\alpha }_1& {\beta }_1& & & & & \mathbf{0}\\ {\beta }_1& {\alpha }_2& {\beta }_2& & & & \\ & {\beta }_2& {\alpha }_3& & & & \\ & & & \ddots & \ddots & & \\ & & & \ddots & {\alpha }_{k-2}& {\beta }_{k-2}& \\ & & & & {\beta }_{k-2}& {\alpha }_{k-1}& {\beta }_{k-1}\\ \mathbf{0}& & & & & {\beta }_{k-1}& {\alpha }_k\end{array}\right].$$

(47)

Based on the discussion following Equation (12), we may assume that the ${\beta }_j$ are nonzero. This ensures that the eigenvalues of $T_k$ are distinct. We can compute the QR factorization (17) of $T_k$ by applying a sequence of $k-1$ Givens rotations to $T_k$,

$$G_k^{\left(j\right)}:=\left[\begin{array}{cccc}{I}_{j-1}& & & \\ & \phantom{-}{c}_j& s_j& \\ & -s_j& c_j& \\ & & & I_{k-j-1}\end{array}\right]\in {\mathbb{R}}^{k\times k},c_j^2+s_j^2=1,s_j\ge 0,$$

(48)

This yields an orthogonal matrix $Q_k$ and an upper triangular matrix $R_k$ given by

$$\begin{array}{c}{Q}_k:=G_k^{\left(1\right)T}{G}_k^{\left(2\right)T}\cdots G_k^{(k-1)T},\hfill \\ R_k:=G_k^{(k-1)}{G}_k^{(k-2)}\cdots G_k^{\left(1\right)}{T}_k.\hfill \end{array}$$

(49)

For a discussion on Givens rotations, see, e.g., ([2], Chapter 5). In our iterative method, the matrix $Q_k$ is not explicitly formed; instead, we use the representation in (49). Since $T_k$ is tridiagonal, the upper triangular matrix $R_k$ has nonzero entries solely on the diagonal and the two adjacent superdiagonals.

Application of k steps of the Lanczos process to the matrix A with initial vector $\mathbf{b}$ results in the matrix $T_k$, as shown in (47). By performing one more step, analogous to (11), we obtain the following Lanczos decomposition:

$$A{\mathcal{V}}_{k+1}={\mathcal{V}}_{k+1}{T}_{k+1}+{\mathbf{f}}_{k+1}{\mathbf{e}}_{k+1}^t.$$

(50)

We observe that the last subdiagonal element of the symmetric tridiagonal matrix $T_{k+1}$ can be calculated as ${\beta }_k=\parallel {\mathbf{f}}_k\parallel$ right after the kth Lanczos step is completed. This is convenient when evaluating the tridiagonal matrices (45) associated with Gauss-Radau quadrature rules.

We can express the matrix $T_{k+1}$ in terms of its QR factorization as follows:

$$T_{k+1}=Q_{k+1}{R}_{k+1},$$

(51)

whose factors can be computed from $Q_k$ and $R_k$ in a straightforward manner. Indeed, we have

$$\begin{array}{ccc}\hfill Q_{k+1}& =& \left[\begin{array}{cc}{Q}_k& \mathbf{0}\\ {\mathbf{0}}^t& 1\end{array}\right]G_{k+1}^{\left(k\right)T},\hfill \\ \hfill Q_{k+1,k}& =& \left[\begin{array}{cc}{Q}_k& \mathbf{0}\\ {\mathbf{0}}^t& 1\end{array}\right]G_{k+1,k}^{\left(k\right)T},\hfill \end{array}$$

(52)

wherein $Q_{k+1}$ is a $(k+1)\times (k+1)$ real orthogonal matrix; $Q_{k+1,k}$ is a $(k+1)\times k$ real matrix; $G_{k+1}^{\left(k\right)}$ is defined by (48); and $G_{k+1,k}^{\left(k\right)}$ is a real $(k+1)\times k$ matrix, which is made up of the first k columns of $G_{k+1}^{\left(k\right)}$.

We express the matrices in terms of their columns to derive updating formulas for the computation of the triangular matrix $R_{k+1}$ in (51) from $R_k$ in (49):

$$R_k=[{\mathbf{r}}_1^{\left(k\right)},{\mathbf{r}}_2^{\left(k\right)},\dots ,{\mathbf{r}}_k^{\left(k\right)}],R_{k+1}=[{\mathbf{r}}_1^{(k+1)},{\mathbf{r}}_2^{(k+1)},\dots ,{\mathbf{r}}_k^{(k+1)},{\mathbf{r}}_{k+1}^{(k+1)}].$$

A comparison between (17) and (51) yields the following results:

$${\mathbf{r}}_j^{(k+1)}=\left[\begin{array}{c}{\mathbf{r}}_j^{\left(k\right)}\\ 0\end{array}\right],1\le j<k,$$

and

$$\begin{array}{ccc}\hfill {\mathbf{r}}_k^{(k+1)}& =& G_{k+1}^{\left(k\right)}\left[\begin{array}{c}{\mathbf{r}}_k^{\left(k\right)}\\ {\beta }_k\end{array}\right],\hfill \\ \hfill {\mathbf{r}}_{k+1}^{(k+1)}& =& G_{k+1}^{\left(k\right)}{G}_{k+1}^{(k-1)}{T}_{k+1}{\mathbf{e}}_{k+1}.\hfill \end{array}$$

(53)

Thus, the elements of all the matrices $R_1,R_2,\dots ,R_{k+1}$ can be calculated in just $O\left(k^2\right)$ arithmetic floating-point operations (flops).

As defined by (18), the matrix expressed as ${\overline{R}}_k={\left[{\overline{r}}_{j\ell }^{\left(k\right)}\right]}_{j,\ell =1}^k$ is the leading principal submatrix of $R_{k+1}$ of order k, and differs from $R_k={\left[r_{j\ell }^{\left(k\right)}\right]}_{j,\ell =1}^k$ only in its last diagonal entry. From Equation (53) and the fact that ${\beta }_k$ is nonzero, it follows that ${\overline{r}}_{kk}^{\left(k\right)}>r_{kk}^{\left(k\right)}\ge 0$. When $T_k$ is nonsingular, we obtain that $r_{kk}^{\left(k\right)}>0$. Here we assume that the diagonal entries of the upper triangular matrix in all QR factorizations are non-negative.

We turn to the computation of the columns of the matrix ${\tilde{V}}_{k+1}$, that is,

$${\tilde{V}}_{k+1}=[{\tilde{\mathbf{v}}}_1^{(k+1)},{\tilde{\mathbf{v}}}_2^{(k+1)},\dots ,{\tilde{\mathbf{v}}}_{k+1}^{(k+1)}]:={\mathcal{V}}_{k+1}{Q}_{k+1},$$

(54)

from columns of ${\tilde{V}}_k$, where ${\mathcal{V}}_{k+1}$ is obtained by the modified Lanczos scheme (50), see Algorithm 1, and $Q_{k+1}$ is determined by (52). Substituting (52) into the right-hand side of (54) yields

$$\begin{array}{ccc}\hfill {\tilde{V}}_{k+1}& =& [{\mathcal{V}}_k,{\mathbf{v}}_{k+1}]Q_{k+1}=[{\tilde{V}}_k,{\mathbf{v}}_{k+1}]G_{k+1}^{\left(k\right)T}\hfill \\ \hfill & =& [{\overline{V}}_{k-1},c_k{\tilde{\mathbf{v}}}_k^{\left(k\right)}+S_k{\mathbf{v}}_{k+1},-S_k{\tilde{\mathbf{v}}}_k^{\left(k\right)}+c_k{\mathbf{v}}_{k+1}].\hfill \end{array}$$

(55)

As a result, the initial $k-1$ columns of the matrix ${\tilde{V}}_{k+1}$ correspond to those of ${\overline{V}}_{k-1}$. The columns ${\tilde{\mathbf{v}}}_k^{(k+1)}$ and ${\tilde{\mathbf{v}}}_{k+1}^{(k+1)}$ in ${\tilde{V}}_{k+1}$ are linear combinations obtained from the last columns of both ${\tilde{V}}_k$ and ${\mathcal{V}}_{k+1}$.

Given the solution ${\mathbf{w}}_{k-1}$ of the linear system (29) and considering that ${\overline{R}}_k$ is upper triangular, with ${\overline{R}}_{k-1}$ as the leading principal submatrix of order $k-1$, the computation of the solution ${\mathbf{w}}_k={[{\eta }_1,{\eta }_2,\dots ,{\eta }_k]}^t$ of ${\overline{R}}_k^t{\mathbf{w}}_k=\parallel \mathbf{b}\parallel {\mathbf{e}}_1$ is inexpensive. We find that

$${\mathbf{w}}_k=\left[\begin{array}{c}{\mathbf{w}}_{k-1}\\ {\eta }_k\end{array}\right],{\eta }_k=-({\overline{r}}_{k-2,k}^{\left(k\right)}{\eta }_{k-2}+{\overline{r}}_{k-1,k}^{\left(k\right)}{\eta }_{k-1})/{\overline{r}}_{kk}^{\left(k\right)}.$$

Note that the computation of ${\mathbf{w}}_k$ from ${\mathbf{w}}_{k-1}$ only requires the last column of the matrix ${\overline{R}}_k$.

We are now in a position to compute ${\mathbf{x}}_{k+1}$ from ${\mathbf{x}}_k$. Using Equations (25) and (55), we obtain

$${\mathbf{x}}_{k+1}={\overline{V}}_k{\mathbf{w}}_k={\overline{V}}_{k-1}{\mathbf{w}}_{k-1}+{\eta }_k{\tilde{\mathbf{v}}}_k^{(k+1)}={\mathbf{x}}_k+{\eta }_k{\tilde{\mathbf{v}}}_k^{(k+1)},$$

Note that only the last few columns of ${\mathcal{V}}_k$ and ${\tilde{V}}_k$ are required to update the iterate ${\mathbf{x}}_{k+1}$.

Algorithm 1 shows pseudo-code for computing the nontrivial elements of the matrix $T_n$ in (36) and the matrix $\mathcal{V}$ in (50). Each iteration requires the evaluation of one matrix-vector product with the matrix A and a few operations with m-vectors. The latter only require $O\left(m\right)$ flops.

5. Computed Examples

This section illustrates the performance of the iterative method of Section 2 and the error estimates of Section 4 when applied to three linear systems of Equation (1). In all examples, the matrix A is symmetric, nonsingular, and indefinite. All computations were carried out on a laptop computer using MATLAB R2024b. The initial approximate solution was set to ${\mathrm{x}}_0=\mathbf{0}$, and iterations were terminated once the Euclidean norm of the error fell below ${10}^{-6}$.

The matrix $A\in {\mathbb{R}}^{m\times m}$ in the computed examples were determined from their spectral factorization (2), where the eigenvector matrix U is a random orthogonal matrix and the eigenvalues are distributed on the positive and negative real axis. The exact solution for all examples is ${\mathbf{x}}_{*}={[1,1,\dots ,1]}^t\in {\mathbb{R}}^m$. The approximation of the Euclidean norm of the errors in the iterates was done using the quadrature rules of Section 3.

Problem 1.

In this example, we set $m=491$. The spectrum of the symmetric matrix A is in the union of the intervals: $[-150,-10]\cup [1,350]$. The eigenvalues of A are given by

$${\lambda }_i=\left\{\begin{array}{cc}i-151\hfill & \mathrm{for}1\le \mathrm{i}\le 141,\hfill \\ i-141\hfill & \mathrm{for}142\le \mathrm{i}\le 491.\hfill \end{array}\right.$$

We have $\mathrm{cond}\left(A\right)=350$. Figure 1 displays numerical results for this example. The plots show the convergence history of the Gauss, Gauss-Radau, optimal averaged Gauss, and minimum ${\mathcal{A}}_{4n+2}^{min}\left(f\right)$ quadrature rules. The plots show all rules considered to be convergent. Furthermore, the Gauss-Radau and ${\mathcal{A}}_{4n+2}^{min}\left(f\right)$ rules display the fastest convergence.

Problem 2.

Let $m=200$ and let the spectrum of the symmetric matrix A be in the union of two intervals: $[-7.3891,-2.7456]\cup [1.0513,148.4132]$. The eigenvalues of A are given by

$${\lambda }_i=\left\{\begin{array}{cc}exp(i/20)\hfill & \mathrm{for}1\le \mathrm{i}\le 100,\hfill \\ -exp(i/100)\hfill & \mathrm{for}101\le \mathrm{i}\le 200.\hfill \end{array}\right.$$

Thus, the matrix A has 100 negative eigenvalues, and its condition number is $\mathrm{cond}\left(A\right)\approx 147$. Figure 2 shows the convergence history for the Gauss, Gauss-Radau, optimal averaged Gauss, and ${\mathcal{A}}_{4n+2}^{min}\left(f\right)$ rules.

Problem 3.

In this example, we use the symmetric matrix $A\in {\mathbb{R}}^{100\times 100}$ with eigenvalues

$${\lambda }_i=\left\{\begin{array}{cc}-i^{-2}\hfill & \mathrm{for}1\le \mathrm{i}\le 50,\hfill \\ i^{-3}\hfill & \mathrm{for}51\le \mathrm{i}\le 100.\hfill \end{array}\right.$$

Thus, the matrix A has 50 negative eigenvalues, with its spectrum in the intervals of $[-1,-4·{10}^{-4}]\cup [{10}^{-6},7.5386·{10}^{-6}]$ and $\mathrm{cond}\left(A\right)=1.25·{10}^8$. Figure 3 displays the convergence history for the Gauss, Gauss-Radau, optimal averaged Gauss, and minimum ${\mathcal{A}}_{4n+2}^{min}\left(f\right)$ rules.

6. Concluding Remarks

This paper describes novel techniques for estimating the Euclidean norm of the error in iterates obtained with a Krylov subspace iterative method. The method is designed to solve linear systems of equations with a symmetric, nonsingular, indefinite matrix. The error norm estimates are obtained by using the relation between the Krylov subspace iterative method and Gauss-type quadrature rules. The computed results demonstrate the performance of the iterative method and the error norm estimates. Among the considered quadrature rules, the rules (44) and (46) provide the most accurate error-norm estimates.