On Zero-Divisor Graphs of Z_n When n Is Square-Free

Abstract

In this article, some properties of the zero-divisor graph $\Gamma \left(Z_n\right)$ are investigated when n is a square-free positive integer. It is shown that the zero-divisor graph $\Gamma \left(Z_n\right)$ of ring $Z_n$ is a $(2^k-2)$-partite graph when the prime decomposition of n contains k distinct square-free primes using the method of congruence relation. We present some examples, accompanied by graphic representations, to achieve the desired results. It is also obtained that the zero-divisor graph $\Gamma \left(Z_n\right)$ is Eulerian if n is a square-free odd integer. Since $Z_n$ is a semisimple ring when n is square-free, the results can be generalized to characterize semisimple rings and modules, as well as rings satisfying Artinian and Noetherian conditions through the properties of their zero-divisor graphs. We endeavored to show that $\Gamma \left(R\right)$ is a partite graph with a certain condition on n and also that $\Gamma \left(R\right)$ is a complete graph when $n=p^2$ for a prime p as part of a corollary. To prove these results, we employed the assistance of several theoretic congruence relations that grabbed our attention, making the investigation more interesting.

1. Introduction

Graph theory is regarded as one of the most intriguing topics, offering a powerful means to visualize the interconnections between objects. Its applications span various fields in both the social and natural sciences, employing its inherent visual representation to simplify complex properties. For a more comprehensive exploration of graph theory, we refer the readers to [1,2,3,4]. Moreover, graph theory serves as a valuable tool in numerous branches of mathematics, including algebra [5,6,7,8,9,10,11].

The zero-divisor graph of a commutative ring was first introduced by Beck in 1988 [12] to explore the structure of the underlying ring. Since then, this concept has been extensively studied by various researchers [13,14,15,16]. The study of zero-divisor graphs has also been extended to noncommutative rings [17]. Redmond [18] further generalized this concept to arbitrary rings, demonstrating that, for any ring R, any two vertices in $\Gamma \left(R\right)$ are connected by a path of length at most 3.

It has also been shown that, for any ring R, if $\Gamma \left(R\right)$ contains a cycle, the length of the shortest cycle is at most 4. Anderson introduced various structural properties of zero-divisor graphs, proving that $\Gamma \left(R\right)$ is always connected to diam($\Gamma \left(R\right))\le 3$. Additionally, they discussed conditions under which $\Gamma \left(R\right)$ becomes a complete graph or a star graph [19].

Beck [12] defined a zero-divisor graph $\Gamma \left(R\right)$ of a ring R as a graph whose vertex set $V\left(R\right)$ consists of the set of all the elements of R and whose edge set $E\left(R\right)$ is defined by the relation on the elements of R as $x,y\in V\left(R\right)$, which are adjacent if and only if $xy=0$ for distinct $x,y\in R$, and it is noted that the relation in a zero-divisor graph $\Gamma \left(R\right)$ is always symmetric while R is a commutative ring. If the ring is commutative, then $\Gamma \left(R\right)$ is a simple graph and $\Gamma \left(R\right)$ is an empty graph, while R is an integral domain with a slight modification in the definition. The zero-divisor graph is slightly different from the definition provided by Beck [12] and is defined by considering the nonzero zero-divisors as vertex sets instead of taking all the elements of the ring as vertex sets [19]. The intention of Anderson and Livingston [19] was to simplify $\Gamma \left(R\right)$ so that it could be visualized in a simple way without losing the relevant pieces of information contained in it.

Later, many properties of $\Gamma \left(R\right)$ were studied, including diameter, girth, and chromatic number (see [19,20]).

Other scholars, such as Weiner [21], explored certain important features of simple rings. David [22] enhanced the previous work by determining the Weiner complexity of a finite field’s zero-divisor graph and establishing an upper bound for the semisimple case. We also wish to discover characteristics associated with semisimple rings.

A ring R is called simple if it has no proper nonzero two-sided ideals, and an R module M is called simple if it is non-trivial and lacks any proper nonzero submodules. In number theory, a simple ring or module can be treated as a prime number since $Z_n$ is simple and n is prime. Simple submodules serve as the module’s building blocks, just as primes do for numbers. A module is labeled as semisimple (or completely reducible) if it is a sum of simple (irreducible) submodules. A ring R with unity is semisimple if its module $R_R$ is semisimple. When a positive integer n is square-free, its prime decomposition is as simple as the semisimple finite ring $Z_n$. For any prime p, the semisimple ring $R=Z_p\times Z_p\times \dots \times Z_p$ exists. This prompted us to investigate the features of zero-divisor graphs of $Z_n$ where n is square-free. Because $Z_n$ is a semisimple ring and n is square-free, our inquiry became fascinating. We aimed to learn about the ring-theoretic features of the semisimple ring in terms of its zero-divisor graphs. We sought to examine the connection between the ring-theoretic features of semisimple ring R and the graph-theoretic properties of $\Gamma \left(R\right)$ in relation to the number-theoretic aspects. We discovered a good correlation between R and $\Gamma \left(R\right)$ for $R=Z_n$.

This article attempts to demonstrate that $\Gamma \left(R\right)$ is a partite graph with a certain constraint on n, as well as a complete graph when $n=p^2$ for a prime number p. We also evaluated the Eulerian nature of $\Gamma \left(Z_n\right)$. To prove the results, we employed a number-theoretic congruence relation, which piqued our curiosity and made the inquiry more exciting. The remaining work is outside the scope of this article and is being studied; it may result in a sequel to this work.

We present some examples to achieve the results. It should be noted that $\Gamma \left(Z_n\right)$ is always connected and that the diameter and girth of this graph are small. Some examples of zero-divisor graphs $Z_n$ are provided below (Figure 1).

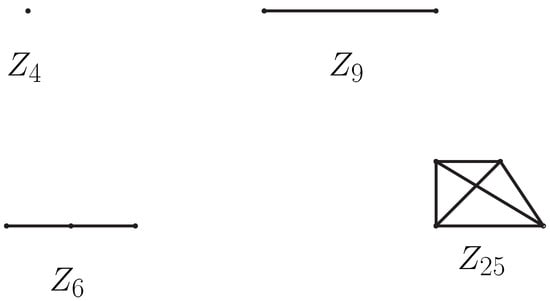
Figure 1. Zero-divisor graphs.

2. Key Definitions and Notations

Definition 1

([4]). A graph G is a collection of objects in which the objects are pairwise related in some sense. The objects are called vertices and the related or linked vertices are called edges. Formally, it consists of two sets V and E, where E is a set of unordered pairs $\{u,v\}$ for some $u,v\in V$ called the edge set of G and is denoted by $G=(V,E)$. If V is a finite set, then G is called a finite graph.

Definition 2.

Two integers a and b are congruent modulo m iff they have the same remainder when divided by m [3], denoted by $a\equiv b\left(modm\right)$.

Property 1

([3]). The linear congruence equation

$$ax\equiv b\left(\mathrm{mod}m\right)$$

has a solution if and only if $d|b$, where $d=\mathit{gcd}(a,m)$.

A path in a graph is an alternating sequence of distinct vertices and edges such that consecutive vertices in the sequence are adjacent to the graph. For an unweighted graph, the length of a path is the number of edges on the path. The eccentricity of a vertex is defined as the maximum distance of a vertex to all other vertices and is denoted by $e\left(V\right)$. If a path is closed, that is, the starting and end vertices are the same, then the path is called a cycle. A graph is called connected if it always finds a path between any two vertices. A cycle-free connected graph is called a tree. A star graph $S_n$ of order n, sometimes simply known as n-star, is a tree on n nodes with one node having vertex degree $n-1$ and the other $n-1$ having vertex degree 1.

Definition 3

([4]). The center of a graph is the set of all vertices of minimum eccentricity, and the radius of a graph is the minimum eccentricity of any graph vertex in a graph.

Definition 4

([19]). Let R be a commutative ring with 1 and let $Z\left(R\right)$ be its set of nonzero zero-divisors. We associated a simple graph $\Gamma \left(R\right)$ to R with the vertex set $V=Z\left(R\right)$, the set of nonzero zero-divisors of R, and, for distinct $x,y\in Z\left(R\right)$, the vertices x and y are adjacent if and only if $xy=0$.

A graph is called a bipartite graph if the vertex set can be partitioned into two sets $V_1$ and $V_2$ for which no two vertices from the same set can be adjacent. A graph is called a k-partite graph if the vertices can be partitioned into k disjoint sets so that no two vertices within the same set are adjacent. It should be noted that, if $k=2$, then the graph is called a bipartite graph.

A complete k- partite graph is a k-partite graph such that every pair of graph vertices in the k sets are adjacent. If there are $p,q,\dots ,r$ graph vertices in the k sets, the complete k-partite graph is denoted by $K_{p,q,\dots ,r}$. If $n=2$, then the graph is said to be a complete bipartite graph.

A graph that is complete k-partite for some k is called a complete multipartite graph. A Turán graph is a complete multipartite graph whose partite sets are as nearly equal in cardinality as possible.

3. Zero-Divisor Graph of Z_n for Square-Free n

In this section, the two main results are proved, and some properties are discussed.

Theorem 1.

If $n=p_1{p}_2$, the product of two distinct primes, then

1. 

$\Gamma \left(Z_{p_1{p}_2}\right)$ is a complete bipartite graph $K_{p_1-1,p_2-1}$. In particular, if $p_1=2$, then $\Gamma \left(Z_{p_1{p}_2}\right)$ is a star graph and the center of $\Gamma \left(Z_{p_1{p}_2}\right)$=$p_2$.

2. 

diameter, i.e., diam($\Gamma \left(Z_{p_1{p}_2}\right))=2$.

3. 

radius, rad($\Gamma \left(Z_{p_1{p}_2}\right))=1$, if $p_1=2$ and otherwise 2.

Proof. 

• Let us consider

  $$V=\{n_1,n_2,n_3,\dots ,n_t\}$$

  to be the set of all nonzero zero-divisors of $Z_{p_1{p}_2}$. Then, by the properties of zero-divisor, we know that, for each i,

  $$(n_i,p_1{p}_2)\ne 1.$$

  Since 0 is always a zero-divisor element,

  $$t=p_1{p}_2-1-\varphi \left(p_1{p}_2\right),$$

  where $\varphi$ is a Euler’s totient function, it follows that

  $$t=p_1{p}_2-1-(p_1-1)(p_2-1)$$

  $$t=p_1+p_2-2.$$

  Therefore,

  $$t=|V(\Gamma Z_{p_1{p}_2})|=p_1+p_2-2,$$

  where V is the set of vertices of $\Gamma \left(Z_{p_1{p}_2}\right)$. Now, one of the ways to determine the zero-divisor elements of $Z_{p_1,p_2}$ is to solve for the incongruent solution of the congruent equation.

  $$kx\equiv 0\left(\mathrm{mod}{p}_1{p}_2\right)$$

  (1)

  where k is a nonzero zero-divisor element of $Z_{p_1{p}_2}$. Now, Equation (1) has a solution as

  $$gcd(p_1{p}_2,k)\mid 0.$$

  We may assume that

  $$k=p_1\mathrm{or}k=p_2.$$

  Then,

  $$kx\equiv 0\left(\mathrm{mod}{p}_1{p}_2\right)$$

  can be written as

  $$p_{1}x\equiv 0\left(\mathrm{mod}{p}_1{p}_2\right)$$

  (2)

  $$or$$

  $$p_{2}x\equiv 0\left(\mathrm{mod}{p}_1{p}_2\right).$$

  (3)

  Now, from Equation (2),

  $$p_1{p}_2\mid p_{1}x.$$

  Therefore,

  $$p_{1}x=p_1{p}_{2}l,$$

  for some l. We note that, for incongruent solution, l must be less than $p_1{p}_2$. It follows that

  $$x=p_{2}l.$$

  Thus, the incongruent solutions of Equation (2) are provided by those integers that are multiples of $p_2$ and less than $p_1{p}_2$. Similarly, the incongruent solutions of Equation (3) are provided by those integers that are less than $p_1{p}_2$ and multiples of $p_1$. For instance, if $p_1$ = 3 and $p_2$ = 7, then the solutions of these two congruence Equations (2) and (3) will be multiples of 7 and 3, i.e., $\{7,14\}$ and $\{3,6,9,12,15,18\}$, respectively. Now, let us consider $V_1$ = all the incongruent solutions of Equation (2) and $V_2$ = all the incongruent solutions of Equation (3). Then,

  $$|V(\Gamma \left(Z_{p_1{p}_2}\right))| = |V_1\cup V_2| = t.$$

  Since $p_1$ and $p_2$ are distinct primes,

  $$V_1\cap V_2=\varphi .$$

  Moreover, no two vertices in $V_i$ are connected for each i = $1,2,$ and every vertex of $V_1$ is connected to every vertex of $V_2$. If possible, assume

  $$v_1,v_2\in V_1$$

  are connected; then, we have

  $$v_1{v}_2\equiv 0\left(\mathrm{mod}{p}_1{p}_2\right).$$

  Since $v_1,v_2\in V_1$

  $$v_1=p_2{l}_1\mathrm{and}{v}_2=p_2{l}_2,$$

  where $l_1,l_2<p_1$. It follows that

  $$p_1{p}_2\mid p_1{l}_1{p}_2{l}_2\Rightarrow p_2{l}_1{l}_2=p_{1}m.$$

  Since $p_1$ is prime and $l_1,l_2<p_1$, we have $p_1\mid p_2$, which is a contradiction that $p_1$ and $p_2$ are distinct primes. Since

  $$|V_1|=p_1-1\mathrm{and}\left|V_2\right|=p_2-1,$$

  we have $\Gamma \left(Z_{p_1{p}_2}\right)$, which is a complete bipartite graph, i.e., $\Gamma \left(Z_{p_1{p}_2}\right)=K_{p_1-1}{,}_{p_2-1}$ (Figure 2).
  

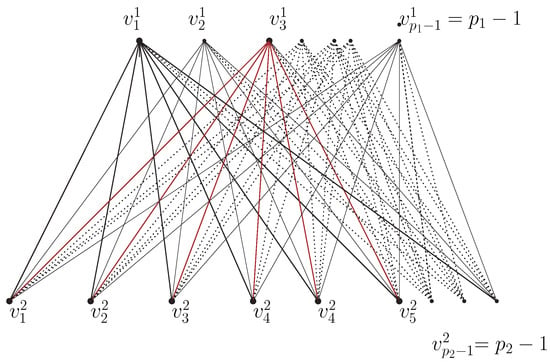  Figure 2. Bipartite representations of the graph $\Gamma \left(Z_{p_1{p}_2}\right)$, where $p_1$ and $p_2$ are distinct prime numbers.
  If any of the primes $p_1$ or $p_2$ are 2, say, $p_1=2$, then $|V_1|=1$, and the only vertex in $V_1$ must have an edge with every vertex in $V_2$, so $\Gamma \left(Z_{p_1{p}_2}\right)$ is a star graph (Figure 3).
  

  Figure 3. Schematic representations of $\Gamma \left(Z_{p_1{p}_2}\right)$ as star graph for $p_1=2$.
• To prove this, we consider an example as shown in Figure 2. Since $\Gamma \left(Z_{p_1{p}_2}\right)$ is a bipartite graph, diameter $\Gamma \left(Z_{p_1{p}_2}\right)=2$ and chromatic number $\chi \left(Z_{p_1{p}_2}\right)=2.$
• Radius, rad($\Gamma \left(Z_{p_1{p}_2}\right))$, is the minimum eccentricity of all the vertices of $\Gamma \left(Z_{p_1{p}_2}\right)$, which is 2 (Figure 2).

   □

For instance, if $p_1=3$ and $p_2=5$, then the zero-divisor graph $\Gamma \left(Z_{p_1{p}_2}\right)$ can be drawn as Figure 4.

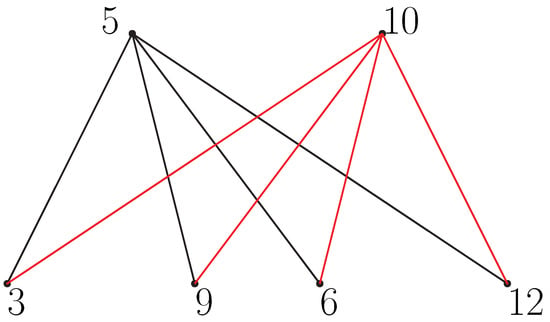
Figure 4. The complete bipartite graph $\Gamma \left(Z_{15}\right)=K_{2,4}$, where $p_1=3$ and $p_2=5$.

Theorem 2.

If $n=p_1{p}_2{p}_3\dots p_k$ is a square-free prime factorization, then the nonzero zero-divisor graph $\Gamma \left(Z_n\right)$ is a ($2^k-2$)-partite graph.

Proof. 

If n is a prime, i.e., $n=p_1$, then the nonzero zero-divisor graph $\Gamma \left(Z_n\right)$ is a null graph. Hence, in this case, the result is true.

If n = $p_1{p}_2$, then, by Theorem 1, the nonzero zero-divisor graph $\Gamma \left(Z_n\right)$ is a bipartite graph, i.e., ($2^2-2$)-partite graph. Thus, the result is true in this case also.

In the proof of Theorem 1, it can be observed that the partition of the vertex set is obtained by taking the incongruent solution of the two congruent equations

$$p_{1}x\equiv 0\left(\mathrm{mod}n\right)\mathrm{and}{p}_{2}x\equiv 0\left(\mathrm{mod}n\right),$$

respectively.

Now, we assume that n = $p_1{p}_2{p}_3$. Let $V=\{n_1,n_2,n_3,\dots ,n_t\}$ be the set of nonzero zero-divisor elements of $Z_{p_1{p}_2{p}_3}$. We know that, for each i,

$$(n_i,n)\ne 1.$$

It follows that the number of nonzero zero-divisors, which is also the number of vertices in $\Gamma \left(Z_{p_1{p}_2{p}_3}\right)$, can be obtained by

$$\begin{array}{cc}\left|V\right|\hfill & =n-\varphi \left(n\right)-1,\mathrm{where}\varphi \mathrm{denotes}\mathrm{the}\mathrm{Euler}\mathrm{totient}\mathrm{function}.\hfill \\ & =p_1{p}_2{p}_3-\varphi \left(p_1{p}_2{p}_3\right)-1\hfill \\ & =p_1(p_2-1)+p_2(p_3-1)+p_3(p_1-1).\hfill \end{array}$$

For any $m\in V$, we have m as a zero-divisor of $Z_n$. It follows that there exists $x,1\le x<n$ such that $n\mid mx$. Therefore, to list all such zero-divisors of $Z_n$, we must solve for the incongruent solution of the congruent equation

$$mx\equiv 0\left(\mathrm{mod}n\right).$$

(4)

Equation (4) is solvable as $gcd(m,n)\mid 0.$ Since $n=p_1{p}_2{p}_3$ is a product of three distinct primes and $0<m<n$, some possible values of m include any one of the primes or products of primes by taking two primes at a time, namely

$$p_1,p_2,p_3,p_1{p}_2,p_1{p}_3,p_2{p}_3.$$

For our convenience, depending upon the choices of m, we may consider the following cases to solve the congruence Equation (4).

Case I: For each i, let $m=p_i$. In this case, we shall have three linear congruence equations, namely

$$p_{i}x\equiv 0\left(\mathrm{mod}n\right),$$

where $i=1,2,3$. These three congruence equations can be thought as ${}^{3}C_1$ number of choices. Now, for each i, $n\mid p_{i}x$, whence $x{p}_i=\left(p_1{p}_2{p}_3\right)\times r,r=1,2,3,\dots$. In this way, we shall obtain 3 sets of solutions for each i, i = $1,2,3$. As we are looking for nonzero zero-divisors of $Z_n$ only, x must be greater than 0 and less than n, i.e., $0<x<n$. Now, for a fixed i, $(i=1,2,3)$, the equation $x{p}_i=p_1{p}_2{p}_2\times r$ can be reduced to

$$x=p_2{p}_{3}r\mathrm{or}x=p_1{p}_{3}r\mathrm{or}x=p_1{p}_{2}r.$$

Since $0<x<p_1{p}_2{p}_3$, we have $r=1,2,3,\dots ,p_i-1$ for each corresponding to choice of $i=1,2,3$. Let us denote these solution sets by $S_{m_i}$, corresponding to each i. We note that then three sets of solutions can be thought of as 3 = ${}^{3}C_1$ sets of solutions (number of combinations of picking 1 member at a time from the set of 3 members).

Case II: $m=p_i{p}_j$, $i\ne j$.

In this case, we shall have ${}^{3}C_2$ sets of solutions as we can choose two members from a set of 3 members by $3C_2$ ways. Thus, the congruence equation reduces to

$$p_i{p}_{j}x\equiv 0\left(\mathrm{mod}n\right),i\ne j$$

whence

$$p_i{p}_{j}x=p_1{p}_2{p}_{3}r,r=0,1,2,3,\dots$$

For fixed $i\mathrm{and}j$,

$$x=p_{l}r,\mathrm{where}l=1,2,3.$$

We note that $i\ne j\ne l.$ Since $0<x<p_1{p}_2{p}_3$, we obtain $r=1,2,3,\dots ,p_i{p}_j,$ respectively. That is, any set of solutions of these ${}^{3}C_2$ congruence equations must be multiples of $p_l$. Let us denote these sets of solutions by $S_{m_{ij}}$, corresponding to $p_i$ and $p_j$. It is to be noted that there are

$${}^{3}C_1+{}^{3}C_2=(2^k-2)$$

sets of solutions, which may not be mutually disjoint. This process may be continued for n as product of 4, 5, …distinct primes. Suppose

$$n=p_1{p}_2{p}_3\dots p_k.$$

Let

$$V=\{n_1,n_2,n_3,n_5,\dots ,n_q\}$$

be set of nonzero zero-divisor elements of $\Gamma \left(Z_n\right)$. Then,

$$(n_i,n)\ne 1.$$

Thus, the number of nonzero zero-divisors can be obtained by

$$|V(\Gamma Z_n)|=p_1{p}_2{p}_3\dots p_k-1-\varphi (p_1{p}_2{p}_3\dots p_k).$$

Let $m\in V$. Since m is a zero-divisor, there exists $x,1\le x<n$ such that

$$n\mid mx.$$

Therefore, to list all such zero-divisors of $Z_n$, we must solve the congruence equation

$$mx\equiv 0\left(\mathrm{mod}n\right)$$

(5)

Since m and x are both variables, we have to fix one. For our convenience, we are fixing m by choosing some particular value of m. We would like to note that we are choosing m in such a way so that the totality of such solutions for x provides us the complete set of nonzero zero-divisors of ring $Z_n$ and further leads to a partition to the vertex set of the nonzero zero-divisor graph $\Gamma \left(Z_n\right)$ in the formation of a partite graph.

Now, Equation (5) is solvable as $gcd(m,n)\mid 0$ since $n=p_1{p}_2{p}_3\dots p_k$ is a product of k distinct primes and ($0<m<n$). To fix m, we choose the zero divisor, which is a product of prime by taking at most $K-1$ primes from $p_1,p_2,p_3,\dots ,p_k$ at a time. In this way, we shall have the following cases.

• $m=p_i,i=1,2,\dots ,k\left(\mathrm{picking}\mathrm{one}\mathrm{prime}\mathrm{at}\mathrm{a}\mathrm{time}\right).$
• $m=p_i{p}_j,1<i\ne j<k\left(\mathrm{picking}\mathrm{two}\mathrm{distinct}\mathrm{primes}\mathrm{at}\mathrm{a}\mathrm{time}\right)$
  and so on. After $k-2$ steps, we have
• $m=p_1{p}_2\dots p_{i-1}{p}_{i+1}\dots p_k\left(\mathrm{picking}\mathrm{k}-1\mathrm{distinct}\mathrm{primes}\mathrm{at}\mathrm{a}\mathrm{time}\right)$.

In this way, we shall have

$${}^{k}C_1+{}^{k}C_2+\dots +{}^{k}C_{k-1}=2^k-2$$

numbers of equations corresponding to which we shall have $2^k-2$ sets of solutions. Now, we solve the $(2^k-2)$ equations to obtain the complete list of nonzero zero-divisors of $Z_n$.

Case (1): If $m=p_i$ for some $p_i$ (picking one prime at a time), then Equation (5) reduces to

$$p_{i}x\equiv 0\left(\mathrm{mod}n\right),\mathrm{for}\mathrm{fixed}i.$$

It follows that

$$p_1{p}_2{p}_3\dots p_k{p}_{i}x.$$

Whence,

$$x=\left(p_1{p}_2{p}_3{p}_{i-1}{p}_{i+1}\dots p_k\right)\times r,r=0,1,2,3,\dots$$

Since $0<x<n$, we have $0<r<p_i;\mathrm{that}\mathrm{is},r=1,2,3,\dots ,p_i-1.$ In this way, we shall obtain k sets of solutions for each i, $i=1,2,3,\dots ,k.$ Let us denote these solution sets by $S_{m_i}$, corresponding to $p_i$. We note that k = ${}^{k}C_1$ (number of combinations of picking 1 member at a time from the sets of k members).

Case (2): $m=p_i{p}_j,i\ne j \left(\mathrm{picking}\mathrm{two}\mathrm{primes}\mathrm{at}\mathrm{a}\mathrm{time}\right).$ In this case, we shall have ${}^{k}C_2$ sets of solutions as we can choose two members from a set of k members by ${}^{k}C_2$ ways. Thus, the congruence equation reduces to

$$p_i{p}_{j}x\equiv 0\left(\mathrm{mod}\mathrm{n}\right),i\ne j.$$

Whence, $p_i{p}_{j}x=p_1{p}_2{p}_3\dots p_{k}r,r=0,1,2,3\dots$

For fixed $i\mathrm{and}j$, $i\ne j$ (without loss of generality, we assume $i<j$), we have

$$x=p_1{p}_2\dots p_{i-1}{p}_{i+1}\dots p_{j-1}{p}_{j+1}\dots p_{k}r.$$

Since $0<x<p_1{p}_2\dots p_i{p}_{i+1}..p_j{p}_{j+1}\dots p_k$, we obtain $r=1,2,3,\dots ,p_i{p}_j-1.$ Let us denote these sets of solutions by $S_{m_{i,j}}$, corresponding to $p_i$ and $p_j$. Continuing in this manner, we have the following case.

In this ${(k-1)}^{th}$ case, $(k-1)$ primes are picked at a time and we shall have ${}^{k}C_{k-1}$ sets of solutions corresponding to the congruence equations

$$m_{i}x\equiv 0\left(\mathrm{mod}\mathrm{n}\right),$$

where $m_i=p_1{p}_2{p}_3\dots p_{i-1}{p}_{i+1}\dots p_k.$ Whence,

$$x\equiv 0\left(\mathrm{mod}{p}_i\right),$$

where

$$0<x<p_1{p}_2\dots p_{i-1}{p}_i{p}_{i+1}\dots p_k.$$

Let us denote the ${}^{k}C_{k-1}=k$ sets of solutions by

$$S_{m_{1,2,\dots ,i-1,i+1,\dots ,k}},i=1,2,3,4,\dots ,k.$$

For each i, the solution set $S_{m_{1,2,\dots ,i-1,i+1,\dots ,k}}$ is provided by

$$x=p_{i}r,r=1,2,\dots ,p_1{p}_2{p}_3\dots p_{i-1}.p_{i+1}\dots p_k-1.$$

Therefore, in total, we shall have

$${}^{k}C_1{+}^k{C}_2{+}^k{C}_3+\dots {+}^k{C}_{k-1}=(2^k-2)$$

sets of solutions of the congruence equation,

$$mx\equiv 0\left(\mathrm{mod}\mathrm{n}\right).$$

The construction of the $(2k-2)$-partite graph is the most important part of the theorem. The remaining portion of the proof discusses the construction process. We note that these $2^k-2$ sets of solutions may not be pairwise disjoint but collectively exhaust the set of all nonzero zero-divisors. In other words, the union of all such sets of solutions forms the set of all nonzero zero-divisors. In our next step, we would like to re-structure the $2^k-2$ sets of solutions in such a way that they are pairwise disjoint and their union is the set of all nonzero zero-divisors of ring $Z_n$, which in fact forms a partition of the vertex set of the zero-divisor graph $\Gamma \left(Z_n\right)$. Now, we shall show that the $2^k-2$ sets of solutions will act as a partition of the vertex set and form a $(2^k-2)$-partite graph. These $2^k-2$ sets are split into $k-1$ levels. We shall start with the innermost level. The innermost level corresponds to sets of solutions

$$S_{m_i},i=1,2,3,4,5,\dots ,k.$$

Let us denote them by

$$V_i^1=S_{m_i},$$

where

$$S_{m_i}=\{p_1{p}_2\dots p_{i-1}{p}_{i+1}\dots p_k,2p_1{p}_2\dots p_{i-1}{p}_{i+1}\dots p_k,\dots ,(p_i-1)p_1{p}_2\dots p_{i-1}{p}_{i+1}\dots p_k\}.$$

That is, it is the collection of integers that are multiples of $p_1{p}_2\dots p_{i-1}{p}_{i+1}\dots p_k$ (mod n). In this way, we shall have

$$V_i^1,i=1,2,3,4,\dots ,k$$

sets of vertices, and since $p_i^{\prime }s$ are distinct primes, these sets of vertices are pairwise disjoint. In the next outer level, i.e., $k-2\left(\mathrm{level}\right)$, we consider those sets of solutions for which each solution m is a multiple of the primes $p_1,p_2,p_3,\dots ,p_k$ by removing a pair of primes at a time and denoted by $S_{m_{i,j}}$, constructing the next level of vertices as follows:

$$\begin{array}{cc}{V}_t^2\hfill & =S_{m_{i,j}}-S_{m_i}-S_j\hfill \\ & =S_{m_{i,j}}-S_{m_i}\cup S_{m_j},t=1,2,3,4,\dots {,}^k{C}_{k-2},\hfill \end{array}$$

where ‘−’ stands for the difference in sets and repeated use of ‘−’ is for cumulative difference in the sense that, if $X-A-B$, then we mean that it is $X-(A\cup B)$. Then it can be verified that $V_t^{k-2}$ is pairwise disjoint and

$$\left(\bigcup _t{V}_t^2\right)\cup \left(\bigcup _t{V}_t^1\right)=\left(\bigcup _i{S}_{m_i}\right)\cup \left(\bigcup _{i,j}{S}_{m_{i,j}}\right).$$

Now, the next outer level should be

$$V_t^3,t=1,2,\dots {,}^k{C}_{k-3}$$

by considering those sets of solutions for which each solution m is a multiple of the primes $p_1,p_2,p_3,\dots ,p_k$ by removing three primes at a time. Then,

$$\begin{array}{cc}{V}_t^3\hfill & =S_{m_{i,j,k}}-S_{m_{i,j}}-S_{m_{i,k}}-S_{m_{j,k}}-S_{m_i}-S_{m_j}-S_{m_k}\hfill \\ & =S_{m_{i,j,k}}-S_{m_{i,j}}\cup S_{m_{i,k}}\cup S_{m_{j,k}}-S_{m_i}\cup S_{m_j}\cup S_{m_k}\hfill \end{array}$$

where

$$t=1,2,3,4,\dots {,}^k{C}_{k-3}.$$

It can be observed that $V_t^{k-3}$ is pairwise disjoint and

$$\left(\bigcup _t{V}_t^1\right)\cup \left(\bigcup _t{V}_t^2\right)\cup \left(\bigcup _t{V}_t^3\right)=\left(\bigcup _{i,j,k}{S}_{m_{i,j,k}}\right)\cup \left(\bigcup _{i,j}{S}_{m_{i,j}}\right)\cup \left(\bigcup _i{S}_{m_i}\right).$$

Continuing this process, the outermost level would be $(k-1)\mathrm{level}$, for which corresponding sets are $V_t^1,$ where $t=1,2,3,4,\dots {,}^k{C}_{k-(k-1)}$. Now, we consider sets of solutions for which each solution m is a multiple of the primes $p_1,p_2,\dots ,p_k$ by removing $k-1$ of primes at a time and construct the next level of vertices as follows:

$$\begin{array}{cc}{V}_t^{k-1}\hfill & =S_{m_{1,2,\dots ,i-1,i+1,\dots ,k}}-\Sigma S_{m_{1,2,\dots ,i_{r-1},i_{r+1},\dots ,i_{s-1},i_{s+1},\dots ,k}}-\dots -S_{m_{i_1}}-S_{m_{i_2}}-\dots -S_{m_{i_{k-1}}}\hfill \\ & =S_{m_{1,2,\dots ,i-1,i+1,\dots ,k}}-\left(\bigcup S_{m_{1,2,\dots ,i_r-1,i_r+1,\dots ,i_s-1,i_s+1,\dots ,k}}\right)\cup \dots \cup \left(\bigcup _l{S}_{m_{i_l}}\right),\hfill \end{array}$$

where t = 1,2,3,…,k and

$$\begin{array}{cc}\left({\bigcup }_t{V}_t^1\right)\cup \left({\bigcup }_t{V}_t^2\right)\cup \dots \cup \left({\bigcup }_t{V}_t^{k-1}\right)=\hfill & \left({\bigcup }_{i_1,i_2,\dots ,i_{k-1}}{S}_{m_{i_1,i_2,\dots ,i_{k-1}}}\right)\hfill \\ & \cup \left({\bigcup }_{i_1^{\prime },i_2^{\prime },\dots ,i_{k-2}^{\prime }}{S}_{m_{i_1^{\prime },i_2^{\prime },\dots ,i_{k-2}^{\prime }}}\right)\hfill \\ & \cup \dots \cup \left({\bigcup }_i{S}_{m_i}\right),\hfill \end{array}$$

where the sum $\Sigma S_{m_{1,2,\dots ,i_{r-1},i_{r+1},\dots ,i_{s-1},i_{s+1},\dots ,k}}$ runs over all combinations by picking k − 2 distinct elements from k − 1 elements from i₁,i₂,i₃…i_k−1>.

Next, we claim that no two vertices in the same set of the above partition of the vertex set are connected by an edge.

From the construction of level sets, it can be observed that, for an arbitrary $V_t^m$, we can always find a prime $p_i$ such that $p_i\nmid v$ for all $v\in V_t^m$. For instance, if

$$v\in V_t^1=S_{m_i},$$

then $p_i\nmid v$. Moreover, if

$$v\in V_t^2=S_{m_{i,j}}-S_{m_i}-S_{m_j},$$

then $p_i\nmid v$ and $p_j\nmid v$ and so on.

Now, if $v_1,v_2\in V_i^j$ are connected, then

$$v_1{v}_2=0\left(\mathrm{mod}n\right).$$

It follows that $n|v_1{v}_2$. Since $p_i|n$, we have $p_i|v_1{v}_2$, which is a contradiction to $p_i\nmid v_1$ and $p_i\nmid v_2.$ Therefore, any two vertices are non-adjacent whenever they are from the same level set.

The rest of the proof demonstrates the edge construction of the zero-divisor graph $\Gamma \left(Z_n\right)$. If $u\in V_i^1$, $v\in V_j^1$, $i\ne j$, then $p_l$ is divisor of u except $p_i$ and divisor of v except $p_j$. Since $i\ne j$, it follows that all $p_l$ divide $uv$; that is, $uv\equiv 0\left(\mathrm{mod}n\right)$. Thus, {$u,v$} is an edge of the zero-divisor graph. Hence, every vertex of an innermost level $V_i^1$ is adjacent to all vertices of another same level set $V_j^1$.

Again, every vertex $v\in V_j^1=S_{m_i}$ must have edge with every vertex of the next outer level set

$$V_t^2=S_{m_{p,q}}-S_{m_p}-S_{m_q}$$

for which i is different from p and q, and no vertex of $V_i^1$ can have an edge with any vertex of

$$V_t^2=S_{m_{p,q}}-S_{m_p}-S_{m_q}$$

for which i either coincides with p or q.

Similarly, it can be observed that every vertex of innermost level $v\in V_i^1=S_{m_i}$ must have edge with every vertex of the next outer level set

$$V_t^3=S_{m_{p,q,r}}-S_{m_{p,q}}-S_{m_{p,r}}-S_{m_{q,r}}-S_{m_p}-S_{m_q}-S_{m_r}.$$

for which i is different from $p,q$ and r, and no vertex of $V_i^{k-1}$ can have an edge with any vertex of $V_t^{k-3}$ for which any one i either coincides with p or q or r.

Continuing in this process, we obtain every vertex $v\in V_i^1=S_{m_p}$ must have an edge with every vertex of the outermost level set

$$v\in V_t^{k-1}=S_{m_{1,2,\dots ,i-1,i+1,\dots ,k}}-\Sigma S_{m_{1,2,\dots ,i_{r-1},i_{r+1},\dots ,i_{s-1},i_{s+1},\dots ,k}}-\dots -S_{m_{i_1}}-S_{m_{i_2}}-\dots -S_{m_{i_{k-1}}}.$$

only.

Moreover, every vertex $v\in V_s^2=S_{m_{i,j}}-S_{m_i}-S_{m_j}$ must have edge with every vertex of an another set of the same level

$$V_t^2=S_{m_{p,q}}-S_{m_p}-S_{m_q}$$

for which i and j are different from p and q, and no vertex of $V_s^2$ can have an edge with any vertex of $V_t^2$ for which any one i or j either coincides with p or q.

Similarly, every vertex of $v\in V_s^2=S_{m_{i,j}}-S_{m_i}-S_{m_j}$ must have edge with every vertex of the next outer level set

$$V_t^3=S_{m_{p,q,r}}-S_{m_{p,q}}-S_{m_{p,r}}-S_{m_{q,r}}-S_{m_p}-S_{m_q}-S_{m_r}.$$

for which i and j are different from $p,q$ and r, and no vertex of $V_s^{k-2}$ can have an edge with any vertex of $V_t^{k-3}=V_t^{k-3}$ for which i or j either coincides with p or q or r. Continuing in this way, it can be obtained that every vertex of each set of second most inner level has an edge with every vertex of only one set of second outermost level, and no vertex of a set of second innermost level can have an edge with any vertex of any set from the outermost level.

This process will continue until the outermost level is reached. In the most outer level, the vertices of $V_i^{k-1}$ are nonadjacent to the vertices of $V_j^{k-1}$ for $i\ne j$.

In this way, we obtain a ($2^k-2$)-partite structure of the nonzero zero-divisor graph $\Gamma \left(Z_n\right)$.    □

4. Algorithm to Determine $\mathbf{\Gamma }\left({\mathit{Z}}_{\mathit{n}}\right)$ When n Is Square-Free

The entire process, from determining the zero divisor elements of $Z_n$ to building the partite structures of $\Gamma \left(Z_n\right)$ that are addressed in the previously discussed theorems, is demonstrated via an algorithm (see Algorithm 1). The algorithm is designed to simplify the complex process of proving the theorems.

Algorithm 1 An algorithm to identifies the zero divisor elements of $Z_n$ and to creates the partite structures of $\Gamma \left(Z_n\right)$.

Step 1: Find the number of nonzero zero-divisors of $Z_n$, which is provided by $$|V\left(Z_n\right)|=p_1{p}_2{p}_3..p_n\left(\mathrm{say}\right)-1-\varphi (p_1{p}_2{p}_3\dots p_n).$$ Step 2: Find out the number of partitions, which is provided by $${}^{n}C_1{+}^n{C}_2{+}^n{C}_3+\dots {+}^n{C}_{n-1}=2^k-2$$ Step 3: List all the congruence equations in order to obtain the nonzero zero-divisors by using the equations $$p_{1}x\equiv 0\left(\mathrm{mod}\mathrm{n}\right).$$ $$p_1{p}_{2}x\equiv 0\left(\mathrm{mod}\mathrm{n}\right).$$ $$p_1{p}_2{p}_{3}x\equiv 0\left(\mathrm{mod}\mathrm{n}\right).$$ $$p_1{p}_2{p}_3{p}_{4}x\equiv 0\left(\mathrm{mod}\mathrm{n}\right).$$ $$\dots \dots \dots \dots$$ $$\dots \dots \dots \dots$$ $$\dots \dots \dots \dots$$ $$p_1{p}_2{p}_3{p}_4\dots p_{n-1}x\equiv 0\left(\mathrm{mod}\mathrm{n}\right).$$ Step 4: Find the incongruent solutions for all the congruence equations listed in Step 3. Step 5: Partition the set of solutions into level sets $V_j^i$. Step 6: Formation of edges, that is, connecting of vertices to obtain edges.

5. Examples

Example 1.

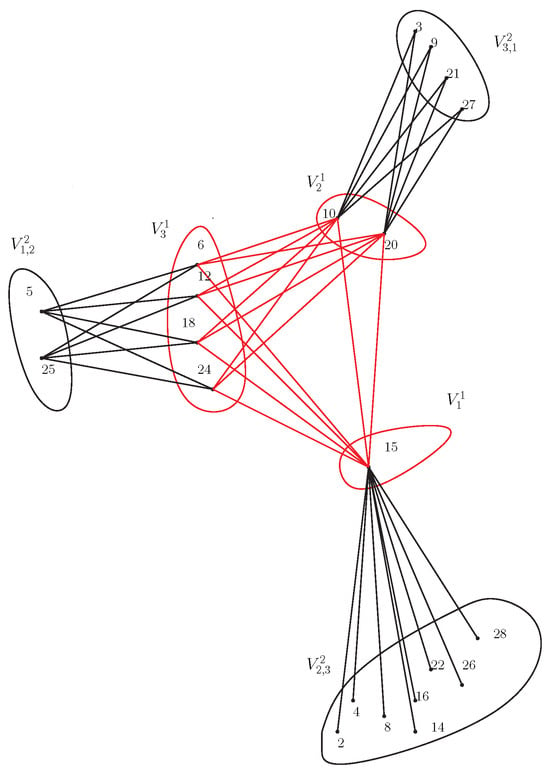
(3-distinct primes) For 3-distinct primes, $p_1,p_2$, and $p_3$, if

$$n=p_1{p}_2{p}_3,$$

then $Z_n$ is a ring in which n is square-free. For instance, if $p_1=2,p_2=3,p_3=5$, then, using the above algorithm, we can construct a nonzero zero-divisor graph of $Z_{30}$ (see Figure 5).

Figure 5. Zero-divisor graph of $Z_{30}$.

The number of nonzero zero-divisor elements will be provided by

$$\begin{array}{cc}\left|V\right|\hfill & =2·3·5-1-\varphi (2·3·5)\hfill \\ & =30-1-\varphi \left(2\right)\varphi \left(3\right)\varphi \left(5\right)\hfill \\ & =29-1·2·4\hfill \\ & =29-8\hfill \\ & =21.\hfill \end{array}$$

According to step 1 of the algorithm, the number of partitions should be

$${}^{3}C_1+{}^{3}C_2=6.$$

Thus, the graph must be a 6-partite graph.

Let us denote V as the set of nonzero zero divisor elements of $Z_{30}$, Then,

$$V=\{2,3,4,5,6,8,9,10,12,14,15,16,18,20,21,22,24,25,26,27,28\}.$$

The vertex set V can be obtained using the algorithm in terms of solution sets using the method described above. The number of incongruent equations will be $2x\equiv 0\left(\mathrm{mod}30\right),3x\equiv 0\left(\mathrm{mod}30\right)$ and $5x\equiv 0\left(\mathrm{mod}30\right)$ by picking 1 member at a time. Similarly, $(2·3)x\equiv 0\left(\mathrm{mod}30\right),(2·5)x\equiv 0\left(\mathrm{mod}30\right)\mathit{and}(3·5)x\equiv 0\left(\mathrm{mod}30\right)$ by picking 2 member at a time. Solving the incongruent solution of the given congruence equations, we obtain 6 disjoint subsets of the vertices, which can be denoted by $V_1^1,V_2^1,V_3^1,V_{1,2}^2,V_{2,3}^2,V_{3,1}^2$.

$$\begin{array}{cc}{V}_1^1\hfill & =15x\hfill \\ \\ V_2^1\hfill & =10x\hfill \\ \\ V_3^1\hfill & =6x\hfill \\ \\ V_{1,2}^2\hfill & =5x-10x-15x\hfill \\ \\ V_{2,3}^2\hfill & =2x-6x-10x\hfill \\ \\ V_{3,1}^2\hfill & =3x-6x-15x,\hfill \end{array}$$

i.e., solutions of the above equations are provided by

$$\begin{array}{cc}{V}_1^1\hfill & =\left\{15\right\}.\hfill \\ \\ V_2^1\hfill & =\{10,20\}.\hfill \\ \\ V_3^1\hfill & =\{6,12,18,24\}.\hfill \\ \\ V_{1,2}^2\hfill & =\{5,25\}.\hfill \\ \\ V_{2,3}^2\hfill & =\{2,4,8,14,16,22,26,28\}.\hfill \\ \\ V_{3,1}^2\hfill & =\{3,9,21,27\}.\hfill \end{array}$$

Now, edges can be formed using step 6. Once the edges are formed, we obtain a 6-partite graph as in Figure 5. It can be verified that

$$V_1^1\cup V_2^1\cup V_3^1\cup V_{1,2}^2\cup V_{2,3}^2\cup V_{1,3}^2=V.$$

Remark 1.

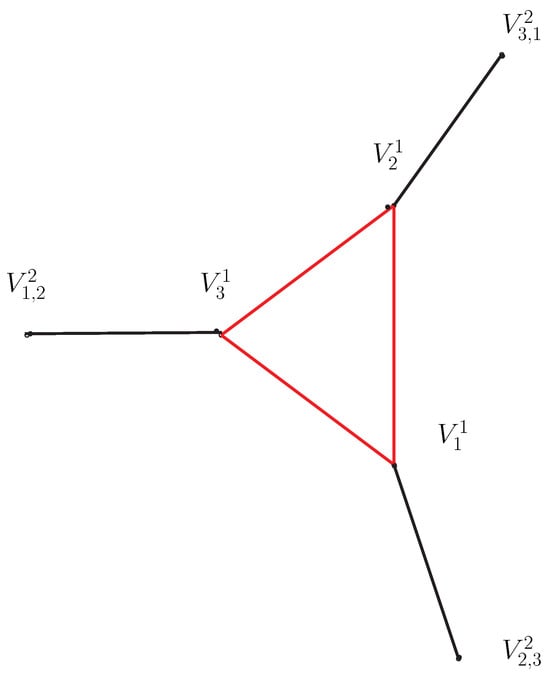
For convenience, the zero-divisor graph $\Gamma \left(Z_{30}\right)$ has been represented by a single linked edge between two level sets. This means that, if elements of one level set $V_i^k$ are connected to elements of another level set $V_j^l$, the corresponding two level sets are connected by an edge. This minimizes the difficulty of constructing the zero-divisor graph, which can take the shape depicted in Figure 6. This phenomenon can be described as the merging of vertices and edges.

Figure 6. Simplified form of $\Gamma \left(Z_{30}\right)$ by merging vertices and edges.

Example 2.

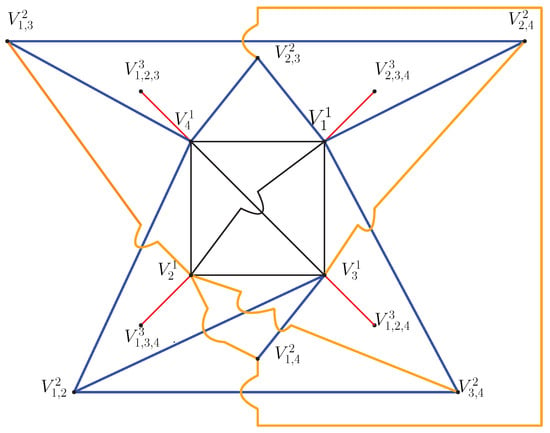
(4-distinct primes) Let

$$n=p_1{p}_2{p}_3{p}_4,$$

$$p_1=2,p_2=5,p_3=7,p_4=11.$$

Then, $Z_n$ = $Z_{770}$. The total number of nonzero zero-divisor elements of $Z_{770}$ is provided by

$$\begin{array}{cc}\left|V\right|\hfill & =2·5·7·11-1-\varphi (2·5·7·11)\hfill \\ & =770-1-\varphi \left(2\right)\varphi \left(5\right)\varphi \left(7\right)\varphi \left(11\right)\hfill \\ & =769-1·4·6·10\hfill \\ & =769-240\hfill \\ & =529\mathit{elements}.\hfill \end{array}$$

Here, $K=4,$ so the number of partitions must be

$${}^{4}C_1{+}^4{C}_2{+}^4{C}_3=4+6+4=14.$$

The graph must be a 14-partite graph. Now, to list out all the vertices of $\Gamma \left(Z_{770}\right)$, we must find all the incongruent solutions of the congruence equations according to steps 3 and 4. Using step 5, we can construct 14 disjoint subsets of the vertices that partitioned the vertices. Finally, using step 6, a 14-partite graph can be constructed that is depicted in the simplified form (see Figure 7).

Figure 7. Simplified form of the zero-divisor graph of $Z_{770}$.

Partitioning the vertices as level subsets of $\Gamma \left(Z_{770}\right)$ is as follows:

$$\begin{array}{cc}{V}_1^1\hfill & =\{385,770\}.\hfill \\ V_2^1\hfill & =\{154,308,462,610,770\}.\hfill \\ V_3^1\hfill & =\{110,220,330,440,550,660,770\}.\hfill \\ V_4^1\hfill & =\{70,140,210,280,350,420,490,560,630,700,770\}.\hfill \\ V_{1,2}^2\hfill & =\{77,231,539,693\}.\hfill \\ V_{1,3}^2\hfill & =\{55,165,275,495,605,715\}.\hfill \\ V_{1,4}^2\hfill & =\{35,105,175,245,315,455,525,595,665,735\}.\hfill \\ V_{2,3}^2\hfill & =\{22,44,66,88,132,176,198,242,264,\hfill \\ & 286,352,374,396,418,484,506,528,572,594,\hfill \\ & 638,682,704,726,748\}.\hfill \\ V_{2,4}^2\hfill & =\{14,28,42,56,84,98,112,126,168,182,196,224,238,\hfill \\ & 252,266,294,322,336,364,378,392,406,434,448,476,\hfill \\ & 504,518,532,546,574,588,602,644,658,672,686,714,\hfill \\ & 728,742,756\}.\hfill \end{array}$$

$$\begin{array}{cc}{V}_{3,4}^2\hfill & =\{10,20,30,40,50,60,80,90,100,120,130,150,160,\hfill \\ & 170,180,190,200,230,240,250,260,270,290,300,310,\hfill \\ & 320,340,360,370,380,390,400,410,430,450,460,470,\hfill \\ & 480,500,510,520,530,540,570,580,590,600,610,620,\hfill \\ & 640,650,670,680,690,710,720,730,740,750,760\}.\hfill \\ V_{1,2,3}^3\hfill & =\{11,33,99,121,143,187,209,253,297,319,341,363,\hfill \\ & 407,429,451,473,517,561,583,627,649,671,737,759\}.\hfill \\ V_{1,4,3}^3\hfill & =\{5,15,25,45,65,75,85,95,115,125,135,\hfill \\ & 145,155,185,195,205,215,225,235,255,265,\hfill \\ & 285,295,305,325,335,345,355,365,375,395\hfill \\ & 405,415,425,435,445,465,475,485,505,515,\hfill \\ & 535,454,555,565,575,585,615,625,635,645,\hfill \\ & 655,675,685,695,705,725,745,755,765\}.\hfill \\ V_{1,2,4}^3\hfill & =\{7,21,49,63,91,119,133,147,161,189,203,\hfill \\ & 217,259,273,287,301,329,343,357,371,385,\hfill \\ & 413,427,441,469,483,497,511,553,567,581,\hfill \\ & 609,623,637,651,679,707,721,749,763\}.\hfill \\ V_{2,3,4}^3\hfill & =\{2,4,6,8,12,16,18,24,26,32,34,36,\hfill \\ & 38,46,48,52,54,58,62,64,68,72,74,76,78,\hfill \\ & 82,86,92,94,96,102,104,106,108,114,116,\hfill \\ & 118,122,124,128,134,136,138,142,144,146,\hfill \\ & 148,152,156,158,162,164,166,172,174,178,\hfill \\ & 184,186,188,194,202,204,206,208,212,214,\hfill \\ & 216,218,222,226,228,232,234,236,244,246,\hfill \\ & 248,254,256,258,262,268,272,274,276,278,\hfill \\ & 282,284,288,292,296,298,302,304,306,312,\hfill \\ & 314,316,318,324,326,328,332,334,338,342,\hfill \\ & 344,346,348,354,356,358,362,366,368,372,376,\hfill \\ & 382,384,386,388,394,398,402,404,408,412,\hfill \\ & 414,416,422,424,426,428,432,436,438,442,\hfill \\ & 444,446,452,454,456,458,464,466,468,472,\hfill \\ & 474,478,482,486,488,492,494,496,498,502,\hfill \\ & 508,512,514,516,522,524,526,534,536,538,\hfill \\ & 542,544,548,552,554,556,558,562,568,576,\hfill \\ & 578,582,584,586,592,596,598,604,606,608,\hfill \\ & 612,614,618,622,624,626,628,632,634,636,\hfill \\ & 642,646,648,652,654,656,662,664,666,668,\hfill \\ & 674,676,678,684,688,692,694,696,698,702,\hfill \\ & 706,708,712,716,718,722,724,732,734,736,\hfill \\ & 738,744,746,752,754,758,762,764,766,768\}.\hfill \end{array}$$

Remark 2.

For convenience, we denote the level sets as

$$V_{\mathit{suffixes}\mathit{of}\mathit{primes}{p}_i’\mathrm{s}\mathit{separated}\mathit{by}\mathit{comma}}^r,$$

where r represents the levels and $p_i$ denotes the family of distinct primes whose product appears in the congruence relation, which particularly means that $V_i^1=S_{m_i}$ and $V_{1,2}^2=S_{m_{p,q}}$. It is to be noted that $S_i=S_{m_i}-\left\{0\right\}$. For illustration, $V_i^1$ is a partition of the vertex set corresponding to solution set $S_i$ (a simple component of $Z_n$) obtained corresponding to the congruence relation $p_{i}x\equiv 0\left(\mathit{mod}n\right)$, and $V_{i,j}^2$ is a partition of the vertex set corresponding to solution set $S_i⨁S_j$ (direct sum of two simple components $Z_i$ and $Z_j$ of $Z_n$) obtained corresponding to the congruence relation $p_i{p}_{j}x\equiv 0\left(\mathit{mod}n\right)$ in level 2. This syntax makes it easy to discover edges in such a way that, if any suffixes are missing in a certain level set, vertices in that set must be connected to all vertices in another level set containing only the missing suffixes. The graph edges can then be drawn using Table 1 and Table 2. A similar table can be used to determine the edges and vertices of a nonzero zero-divisor graph of a semisimple ring R, which is the direct sum of its simple components.

Table 1. Formation of partite graphs of $Z_{30}$.

Equations	Solution Sets	Partition Sets	Edge Formations
$2x\equiv 0\left(\mathrm{mod}30\right)$	$S_1=S_{m_1}\cup \left\{0\right\}=\{0,15\}$	$V_1^1=S_1-\left\{0\right\}$	$V_{2,3}^2,V_2^1,V_3^1$
$3x\equiv 0\left(\mathrm{mod}30\right)$	$S_2=S_{m_2}\cup \left\{0\right\}=\{0,10,20\}$	$V_2^1=S_2-\left\{0\right\}$	$V_3^1,V_1^1,V_{3,1}^2$
$5x\equiv 0\left(\mathrm{mod}30\right)$	$S_3=S_{m_2}\cup \{0,6,12,18,24\}$	$V_3^1=S_3-\left\{0\right\}$	$V_2^1,V_1^1,V_{1,2}^2$
$6x\equiv 0\left(\mathrm{mod}30\right)$	$S_1⨁S_2$	$V_{1,2}^2=S_1⨁S_2-S_1\cup S_2$	$V_3^1$
$10x\equiv 0\left(\mathrm{mod}30\right)$	$S_1⨁S_3$	$V_{2,3}^2=S_1⨁S_3-S_1\cup S_3$	$V_1^1$
$15x\equiv 0\left(\mathrm{mod}30\right)$	$S_2⨁S_3$	$V_{3,1}^2=S_2⨁S_3-S_2\cup S_3$	$V_2^1$

Table 2. Formation of partite graphs of $Z_{770}$.

Equations	Solution Sets	Partition Sets	Edge Formations
$2x\equiv 0\left(\mathrm{mod}770\right)$	$S_1=S_{m_1}\cup \left\{0\right\}$	$V_1^1=S_{m_1}=S_1-\left\{0\right\}$	$V_2^1,V_3^1,V_4^1,V_{2,3}^2,V_{3,4}^2,V_{2,4}^2,V_{2,3,4}^3$
$5x\equiv 0\left(\mathrm{mod}770\right)$	$S_2=S_{m_2}\cup \left\{0\right\}$	$V_2^1=S_{m_2}=S_2-\left\{0\right\}$	$V_1^1,V_3^1,V_4^1,V_{1,3}^2,V_{3,4}^2,V_{1,4}^2,V_{1,3,4}^3$
$7x\equiv 0\left(\mathrm{mod}770\right)$	$S_3=S_{m_3}\cup \left\{0\right\}$	$V_3^1=S_{m_3}=S_3-\left\{0\right\}$	$V_1^1,V_2^1,V_4^1,V_{1,2}^2,V_{2,4}^2,V_{2,3}^2,V_{1,2,4}^3$
$11x\equiv 0\left(\mathrm{mod}770\right)$	$S_4=S_{m_4}\cup \left\{0\right\}$	$V_4^1=S_{m_4}=S_4-\left\{0\right\}$	$V_1^1,V_2^1,V_3^1,V_{2,3}^2,V_{1,2}^2,V_{1,3}^2,V_{1,2,3}^3$
$2.5x\equiv 0\left(\mathrm{mod}770\right)$	$S_1⨁S_2=S_{m_{1,2}}\cup \left\{0\right\}$	$V_{1,2}^2=S_1⨁S_2-S_1\cup S_2$	$V_3^1,V_4^1,V_{3,4}^2$
$2.7x\equiv 0\left(\mathrm{mod}770\right)$	$S_1⨁S_3$	$V_{1,3}^2=S_1⨁S_3-S_1\cup S_3$	$V_4^1,V_2^1,V_{2,4}^2$
$2.11x\equiv 0\left(\mathrm{mod}770\right)$	$S_1⨁S_4$	$V_{1,4}^2=S_1⨁S_4-S_1\cup S_4$	$V_2^1,V_3^1,V_{2,3}^2$
$5.7x\equiv 0\left(\mathrm{mod}770\right)$	$S_2⨁S_3$	$V_{2,3}^2=S_2⨁S_3-S_2\cup S_3$	$V_1^1,V_4^1,V_{1,4}^2$
$5.11x\equiv 0\left(\mathrm{mod}770\right)$	$S_2⨁S_4$	$V_{2,4}^2=S_2⨁S_4-S_2\cup S_4$	$V_1^1,V_3^1,V_{1,3}^2$
$7.11x\equiv 0\left(\mathrm{mod}770\right)$	$S_3⨁S_4$	$V_{3,4}^2=S_3⨁S_4-S_3\cup S_4$	$V_1^1,V_2^1,V_{1,2}^2$
$2.5.7x\equiv 0\left(\mathrm{mod}770\right)$	$S_1⨁S_2⨁S_3$	$V_{1,2,3}^3=S_1⨁S_2⨁S_3-\left[\{S_1⨁S_2\}\cup \{S_1⨁S_3\}\cup \{S_2⨁S_3\}\right]$	$V_4^1$
$2.7.11x\equiv 0\left(\mathrm{mod}770\right)$	$S_1⨁S_3⨁S_4$	$V_{1,3,4}^3=S_1⨁S_3⨁S_4-\left[\{S_1⨁S_3\}\cup \{S_1⨁S_4\}\cup \{S_3⨁S_4\}\right]$	$V_2^1$
$5.7.11x\equiv 0\left(\mathrm{mod}770\right)$	$S_2⨁S_3⨁S_4$	$V_{2,3,4}^3=S_2⨁S_3⨁S_4-\left[\{S_2⨁S_3\}\cup \{S_2⨁S_4\}\cup \{S_3⨁S_4\}\right]$	$V_1^1$
$5.11.2x\equiv 0\left(\mathrm{mod}770\right)$	$S_1⨁S_2⨁S_4$	$V_{2,4,1}^3=S_1⨁S_2⨁S_4-\left[\{S_1⨁S_2\}\cup \{S_1⨁S_4\}\cup \{S_2⨁S_4\}\right]$	$V_3^1$

Theorem 3

([23]). For a prime p, $\Gamma \left(Z_{p^2}\right)$ is a complete graph.

Proof. 

Let

$$V=\{n_1,n_2,n_3\dots n_k\}$$

be the set of vertices of nonzero zero divisors of $\left(Z_{p^2}\right)$. Then, for each i, $(n_i,p^2)\ne 1.$ Since 0 is always a zero divisor element of $Z_{p^2}$, if k represents arbitrary elements V, then $(k,p^2)\ne 1$. Therefore,

$$\begin{array}{cc}\left|V\right|\hfill & =p^2-1-\varphi \left(p^2\right)\hfill \\ & =p^2-1-p^{2-1}(p-1)\hfill \\ & =p^2-1-p(p-1)\hfill \\ & =p^2-1-p^2+p\hfill \\ & =(p-1)\mathrm{elements}.\hfill \end{array}$$

(6)

That is, total number of vertices in Γ($Z_{p^2}$) is p − 1 Now, in order to list all the vertices of Γ($Z_{p^2}$) we shall find all the incongruent solutions of the congruent equation

$$\begin{array}{c}\hfill kx\equiv 0\left(\mathrm{mod}{p}^2\right),\end{array}$$

where k is a nonzero zero-divisor of $Z_{p^2}$.

Now, the congruence linear equation has solution as

$$gcd(kx,p^2)\mid 0.$$

Since k is element of $Z_{p^2}$, we have

$$0<k<p^2.$$

From Equation (6), we obtain

$$p^2\mid (kx-0),\mathrm{It}\mathrm{follows}\mathrm{that}$$

$$p\mid x\mathrm{or}p\mid k.$$

If $p\mid x$, we must obtain $k<p.$ Since $\left|V\right|=p-1$, the zero-divisors are $p,2p,3p,\dots ,(p-1)p.$ Since every vertex is a multiple of p, the product of any two vertices is divisible by $p^2$. Hence, each vertex is connected to every vertex of $\Gamma \left(Z_{p^2}\right).$ Therefore, $\Gamma \left(Z_{p^2}\right)$ is a complete graph $K_{p-1}$, where p is a prime number.   □

Example 3.

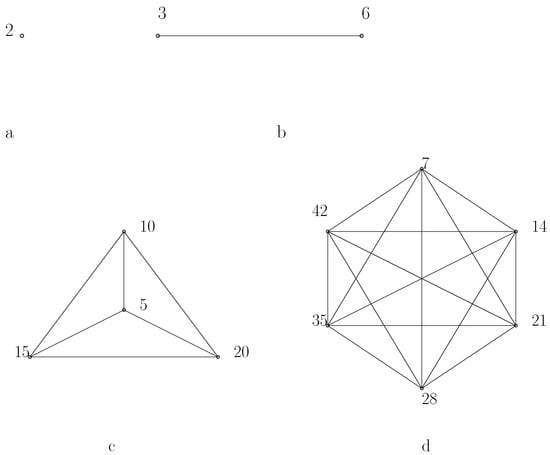
The zero-divisor graphs of $z_{2.2}$, $z_{3.3}$, $z_{5.5}$, and $z_{7.7}$ are shown in Figure 8.

Figure 8. Zero-divisor graphs (a) $\Gamma \left(Z_4\right)$, (b) $\Gamma \left(Z_9\right)$, (c) $\Gamma \left(Z_{25}\right)$, and (d) $\Gamma \left(Z_{49}\right)$.

Remark 3.

It is obtained that $\Gamma \left(Z_n\right)$ when n is square-free is a partite graph. It can be seen that $Zpq$ is a complete bipartite graph, while $Z_{p^2}$ is a complete graph. On the other hand, the semisimple ring $\Gamma (Z_p\times Z_p)$ is not a complete graph. In particular, it is a complete bipartite graph. In fact, $\Gamma (Z_p\times Z_p)$ is a Turán graph. This observation leads to a conjecture that, for any finite semisimple ring, the zero-divisor graph of them is a partite graph and some of its subgraphs are Turán graphs. We will take this as a sequel to our current study.

Remark 4.

It should be emphasized that semisimple rings are just as simple as square-free integers in that they may be written as the direct sum of their simple components, and they can be grouped together with square-free integers that are products of their different prime factors. The multiplicative structure of ring $Z_n$ can be represented as combinatorial by examining the zero-divisor graph $\Gamma \left(Z_n\right)$ when n is square-free will. The structure of $\Gamma \left(Z_n\right)$ is more complicated if n is not square-free. Rings can be categorized according to their divisors by studying zero-divisor graphs. Of all the crucial characteristics of graphs, the Eulerian nature is the most ancient and original use of graphs, which is where graph theory originated. Here, we discuss the Eulerian nature of $\Gamma \left(Z_n\right)$. For instance, the zero-divisor graph $\Gamma \left(Z_n\right)$ is Eulerian if n is a square-free odd integer.

Theorem 4.

The zero-divisor graph $\Gamma \left(Z_n\right)$ is Eulerian if n is a square-free odd integer.

Proof. 

Let $n=p_1{p}_2\dots p_k$ represent the prime decomposition of n. Given that n is an odd integer, each of the prime factors $p_1,p_2,\dots ,p_k$ must be odd. To prove that $\Gamma \left(Z_n\right)$ is Eulerian, simply show that it is connected and that the degree of each vertex is even. Since $\Gamma \left(Z_n\right)$ is connected, we assert that each vertex is of even degree. Let $v_j\in V_j^1$. Then, the degree of $v_j$ is provided by

$$deg\left(v_j\right)=\sum _{i=1,i\ne j}^{{}^{k-1}C_1}(p_i-1)+\sum _{r<s,r\ne j,s\ne j}^{{}^{k-1}C_2}(p_r-1)(p_s-1)+\dots +(p_{i_1}-1)(p_{i_2}-1)\dots (p_{i_{k-1}}-1),$$

(7)

where $i_1<i_2<\dots <i_{k-1}$ and $i_1,i_2,\dots ,i_{k-1}\ne j$. Again, if $v_{i,j}\in V_{i,j}^2$, then the degree $deg\left(v_{i,j}\right)$ of $v_{i,j}$ is provided by

$$\sum _{r,r\ne i,j}^{{}^{k-2}C_1}(p_r-1)+\sum _{r<s,r\ne i,j;s\ne i,j}^{{}^{k-2}C_2}(p_r-1)(p_s-1)+\dots +(p_{i_1}-1)(p_{i_2}-1)\dots (p_{i_{k-2}}-1),$$

(8)

where $i_1<i_2<\dots <i_{k-2}$ and $i_1,i_2,\dots ,i_{k-2}\ne i,j$. For $v_{i_1,i_2,\dots ,i_{k-1}}\in V_{i_1,i_2,\dots ,i_{k-1}}^{k-1}$, we obtain

$$deg\left(v_{i_1,i_2,\dots ,i_{k-1}}\right)=p_{i_k}-1,$$

(9)

where $i_k\ne i_1,i_2,\dots ,i_{k-1}$.

$p_i-1$ must be even since each $p_i,i=1,2,\dots ,k$ is an odd number. From Equations (7)–(9), the expression of degree of each vertex must be even since sums of products of even integers are even numbers.   □

6. Conclusions

The zero-divisor graph $\Gamma \left(Z_n\right)$ of $Z_n$ for which n is linearly factored is investigated, and it is shown that $\Gamma \left(Z_n\right)$ of ring $Z_n$ is a $r=(2^k-2)$-partite graph, where $n=p_1{p}_2\dots p_k$ ($p_1,p_2,\dots ,p_k$ are k distinct primes). We note that $Z_n$ for $n=p_1{p}_2\dots p_k$ (where $p_1,p_2,\dots ,p_k$ are distinct primes) is a semisimple ring. We believe that the results obtained can be used as tools to investigate the nature and properties of the zero-divisor graphs of semisimple rings and modules. It should be noted that the results obtained are only applicable to ring $Z_n$ but may not be applicable to an arbitrary ring of order n. For example, the rings $Z_4$ and $Z_2\times Z_2$ are of order $4=2^2$, but $\Gamma \left(Z_4\right)$ and $\Gamma (Z_2\times Z_2)$ are two different graphs.

The study of zero-divisor graphs provides a bridge between algebra and graph theory. Graph theory and number theory have been widely used in computer science, cryptography, and network analysis and are promising tools in theoretical computer science. The study of ring theory, along with graph theory and number theory, could provide interesting avenues for further research in network analysis and security. In algebraic aspects, the results obtained can be generalized to characterize semisimple rings and modules, as well as rings satisfying Artinian and Noetherian conditions.