New μ-Synchronization Criteria for Nonlinear Drive–Response Complex Networks with Uncertain Inner Couplings and Variable Delays of Unknown Bounds

Abstract

Since the research of $\mu$-synchronization helps to explore how complex networks (CNs) work together to produce complex behaviors, the $\mu$-synchronization task for uncertain time-delayed CNs is studied in our work. Especially, bounded external perturbations and variable delays of unknown bounds containing coupling delays, internal delays, and pulse delays are all taken into consideration, making the model more general. Through the $\mu$-stable theory together with the hybrid impulsive control technique, the problems caused by uncertain inner couplings, time-varying delays, and perturbations can be solved, and novel synchronization criteria are gained for the $\mu$-synchronization of the considered CNs. Different from traditional models, it is not necessary for the coupling matrices to meet the zero-row-sum condition, and the control protocol relaxes the constraint of time delays on impulse intervals. Moreover, numerical experiments and image encryption algorithms are carried out to verify our theoretical results’ effectiveness.

1. Introduction

Complex networks (CNs) are very common in daily life [1,2], such as social networks, retrieval systems of the scientific literature, power networks, commercial networks, biological neural networks (NNs), and cellular NNs. CNs, as carriers of information dissemination, exhibit diverse synchronization phenomena. In fact, the ability of the network to achieve synchronization lies on the network’s topology and the dynamic properties of the nodes, as well as the strength of the external control. By studying the phenomenon of synchronization, we can better understand the evolution process of complex networks over time and their potential in engineering applications.

1.1. The Background and Related Works

Various categories of synchronization have been presented, such as phase synchronization [3,4], complete synchronization [5], generalized synchronization [6], finite-time synchronization [7,8,9], projective synchronization [10], and $\mu$-synchronization [11,12,13,14]. $\mu$-Synchronization is a generalized synchronization associated with the $\mu$-function that can be converted to an exponential or logarithmic synchronization and has thus received focused attention from researchers. The $\mu$-synchronization of CNs is particularly valuable in scenarios that are affected by noise, uncertainties, or other disturbances. Its applications span a wide range of fields, including secure communication, distributed computing, control systems, coupled oscillators, etc. There are several control methods for the synchronization of CNs, such as pinning control [15,16], optimal control [17], adaptive control [18], decentralized control [19], event-triggered control [20,21], and impulsive control [11,12,13,14,22]. Impulsive control only applies brief control inputs at specific time instants, rather than continuous control, which can significantly reduce the overall energy consumption. For achieving the $\mu$-synchronization of multi-link CNs, a distributed delayed impulsive controller is presented by establishing a Halanay-like inequality [11]. By combining the benefits of two control theories, namely, pulse control theory and event-driven control theory, Zhang et al. [12] presented an impulsive control approach aiming for the $\mu$-synchronization tasks of CNs. The $\mu$-synchronization task of coupled NNs was investigated via the integration method based on pulse effects [13]. By means of an impulsive delay inequality approach, Guan et al. studied the $\mu$-stabilization and $\mu$-synchronization tasks of CNs with variable time delays [14]. In [22], utilizing the average impulsive interval approach, a secure impulsive controller was introduced to ensure the bounded synchronization of dynamic networks.

In many actual CNs, there exist inherent time delays in the information interactions among nodes, which significantly impact their synchronization task. Based on the decomposing technique, Liu et al. [23] investigated the anti-synchronization issue for coupled complex CNs with asynchronous variable time delays. Luo et al. [24] solved the finite-time synchronization problems of the uncertain variable time-delayed CNs by a feedback controller. Tan et al. [25] dealt with the synchronization task of CNs affected by time delays with a discrete distribution. Han et al. [26] explored complex function projective synchronization issues for CNs, in which coupling delays were considered. Intermittent control strategies were applied in [27] to achieve finite-time synchronization for delayed fuzzy CNs. The preassigned-time synchronization tasks were investigated for fuzzy memristive NNs with variable delays by putting forward a general controller in [28]. Through the Lyapunov–Krasovskii theory, the synchronization of Markovian jumping chaotic NNs with distributed time-varying delays was analyzed in [29]. Xing et al. presented the double-ring NN model with multiple bounded time delays and discussed its stability using the Coates flow graph method in [30]. In the above synchronization results, the time delay is assumed to be bounded, and the change rate of the time delay is restricted to a limited range of intervals.

In addition, there exist parameter uncertainties caused by factors such as system modeling errors, time delays, and external disturbances in practical complex networks. Parameter uncertainties including inner coupling states, node dynamics, and outer coupling topologies can affect the system’s synchronization behavior. He et al. [31] investigated the n-dimensional multi-time delayed fractional order NNs with parameter uncertainty by adopting an active control strategy, in which the parameter uncertainty involved belonged to uncertain outer couplings. Gu et al. [32] considered the synchronization tasks for memristor-based dynamical CNs with parameter uncertainty through a comparison principle and the Lyapunov method, in which parameter uncertainty describes the synaptic connection weight among different nodes. Fan et al. [33] investigated synchronization in multi-weighted CNs with parameter uncertainties that were added to the weight constant matrices of the node’s state vector. Selvaraj et al. [34] investigated the synchronization of non-linear uncertainty CNs in view of a feedback control strategy. Mirshamsi et al. [35] proposed a bounded control approach for linear time-invariant systems that considered time-varying uncertainty in state and input matrices. However, the $\mu$-synchronization of CNs with internal coupling parameter uncertainty has been rarely studied.

Further, unknown external disturbances [36,37,38] can generally affect the synchronization behaviors between the drive–response CNs. Through a simple error feedback control strategy, Du et al. studied the function projective synchronization (FPS) task for CNs subjected to external perturbations [39]. In [40], by introducing the stability theory, Du et al. presented a new control method for addressing the issue of modified FPS for fractional order CNs with external perturbations. With the help of the Lyapunov stability theory and comparison criteria, the mean square exponential synchronization of CNs with stochastic perturbations was explored in [41]. By introducing a disturbance observer, the asymptotical synchronization task was focused on nonidentical CNs affected by unknown external perturbations in [42]. Liang et al. explored the synchronization task of switched duplex NNs under external stochastic disturbances by introducing channel matrices [43]. Research on the fixed-time synchronization task for delayed CNs in the presence of stochastic perturbations using the impulsive pinning control was studied in [44]. Shukla et al. [45] presented the condition for the El Niño chaotic system to achieve function matrix projective synchronization under the controller, which uses the functional projective matrix information. However, to date, few works consider how to design specific controllers for the $\mu$-synchronization of uncertain CNs with unknown external perturbations and unbounded time delays, especially in the case where the coupling topology is not limited by dissipative coupling. This is also the main research motivation for this article.

1.2. The Research Aim and Highlights

Since studying $\mu$-synchronization helps to shed light on how CNs work together to produce complex behaviors and cognitive functions, our goal is to achieve $\mu$-synchronization for the considered CNs. The research question is how to design a controller to achieve $\mu$-synchronization for the uncertain time-delayed CNs. Given by the aforementioned discussions, to achieve $\mu$-synchronization for a type of unbounded time-delayed CNs with external disturbances and uncertainties of inner couplings, new synchronization criteria are derived. The highlights of this article contain the following aspects: (1) The time-delayed CNs that include uncertain couplings and external perturbations are modeled. In particular, all time delays, namely, coupling delays, internal delays, and pulse sampling delays, have non-metrizable bounds. (2) Unlike the pulse control protocols in [46,47,48], the hybrid pulse controllers in this paper allow the sampling delay to be unbounded, and new synchronization conditions are obtained for the uncertain time-delayed networks studied. (3) There is no need for the model’s external coupling matrices to meet the condition of dissipative coupling, and the control protocol relaxes the constraint of time delays on pulse intervals.

Notations: I denotes the unit matrix with a certain dimension. $\overline{B}>0$ denotes a positive definite matrix. ∀${\Lambda }_1\subseteq R$, ${\Lambda }_2\subseteq R^m$, $1\le m\le n$, $C^1({\Lambda }_1,{\Lambda }_2)=$$\{o$: ${\Lambda }_1\to {\Lambda }_2\}$, in which o is continuously differentiable. $PC({\Lambda }_1,{\Lambda }_2)=\{o^{*}$: ${\Lambda }_1\to {\Lambda }_2\}$ stands for the space of all piecewise continuous functions from ${\Lambda }_1$ to ${\Lambda }_2$, with the segmentation points satisfying $o^{*}\left(t^{+}\right)=o^{*}\left(t\right)$, and $o^{*}\left(t^{-}\right)$ exists. Let $PC{B}_r=\{\overline{o}\in PC([-r,0],R^n)$, $r>0$, with the norm $|\overline{o}|={\sup }_{-r\le s\le 0}\parallel \overline{o}\left(s\right)\parallel$. ${\lambda }_{max}\left(\mathrm{{\rm Y}}\right)$ and ${\lambda }_{min}\left(\mathrm{{\rm Y}}\right)$ are the maximum and minimum eigenvalues of the matrix $\mathrm{{\rm Y}}$ individually. $X=\{\mu \left(t\right)\in C^1(R_{+},[1,+\infty ))\}$ denotes the family of all non-decreasing functions on $[0,+\infty )$, which satisfies $\mu \left(t\right)\to \infty$ as $t\to \infty$.

2. Model and Background Description

In view of the delay and uncertainty phenomena in neural networks, the CNs considered in this article are formulated as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=-\overline{\mathcal{D}}{x}_i\left(t\right)+\overline{\mathcal{A}}\varphi \left(x_i\left(t\right)\right)+\overline{\mathcal{B}}h\left(x_i(t-v_1\left(t\right))\right)+c_1{\displaystyle \sum _{j=1}^N}{\tilde{\mathcal{H}}}_{ij}({\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right))\psi \left(x_j\left(t\right)\right)\hfill \\ +c_2{\displaystyle \sum _{j=1}^N}{\tilde{\mathcal{G}}}_{ij}({\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right))\psi \left(x_j(t-v_2\left(t\right))\right),t>0,\hfill \\ x_i\left(s\right)={\epsilon }_i\left(s\right),s\in (-\infty ,0],\hfill \end{array}\right.\end{array}$$

(1)

where $x_i\left(t\right)=(x_{1i}\left(t\right),x_{2i}\left(t\right),\cdots$, $x_{ni}{\left(t\right))}^T$ refers to the node’s state values, $i=1,2,\cdots$, N. $\overline{\mathcal{A}}$, $\overline{\mathcal{B}}$, and $\overline{\mathcal{D}}\in R^{n\times n}$ are known weight matrices, and $\psi (·)\in R^n$ is the function that stands for the coupling behavior among nodes. $\varphi (·)$, $h(·)\in R^n$ are the functions that describe the nodes’ nonlinear behavior. $c_1$ and $c_2$ denote the coupling strengths, in which $c_1>0$, $c_2>0$. $\tilde{\mathcal{H}}$, $\tilde{\mathcal{G}}\in R^{N\times N}$ denote the outer coupling matrices between different coupled nodes. It is mentioned that ${\tilde{\mathcal{H}}}_{ij}>0$ and ${\tilde{\mathcal{G}}}_{ij}>0$ if there is a coupling between nodes i and j; otherwise, ${\tilde{\mathcal{H}}}_{ij}={\tilde{\mathcal{G}}}_{ij}=0$. ${\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right)$, ${\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right)\in R^{n\times n}$ are the matrices reflecting the inner-coupling situations, where ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ denote certainty coupling matrices, and $\Delta {\mathrm{\Gamma }}_1\left(t\right)$ and $\Delta {\mathrm{\Gamma }}_2\left(t\right)$ denote the uncertainty parts. $v_1\left(t\right)$ and $v_2\left(t\right)$ are the unbounded delays with $0\le v_i\left(t\right)\le \infty (i=1,2)$, and ${\epsilon }_i\left(s\right)\in PC{B}_r$ is the original condition of node i.

We treat the CNs (1) as the drive system, and then take the response system with external disturbances and controllers as the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{y}}_i\left(t\right)=-\overline{\mathcal{D}}{y}_i\left(t\right)+\overline{\mathcal{A}}\varphi \left(y_i\left(t\right)\right)+\overline{\mathcal{B}}h\left(y_i(t-v_1\left(t\right))\right)+c_1{\displaystyle \sum _{j=1}^N}{\tilde{\mathcal{H}}}_{ij}({\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right))\psi \left(y_j\left(t\right)\right)\hfill \\ +c_2\sum _{j=1}^N{\tilde{\mathcal{G}}}_{ij}({\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right))\psi \left(y_j(t-v_2\left(t\right))\right)+{\eta }_i\left(t\right)+u_i\left(t\right),t\ne t_k,\hfill \\ e_i\left(t\right)=\mathrm{\Theta }{e}_i(t^{-}-{\vartheta }_k),t=t_k,k\in {\mathbb{Z}}_{+},\hfill \\ y_i\left(s\right)={\phi }_i\left(s\right),s\in (-\infty ,0),\hfill \end{array}\right.\end{array}$$

(2)

where $y_i\left(t\right)=(y_{1i}\left(t\right),y_{2i}\left(t\right),\cdots$, $y_{ni}{\left(t\right))}^T$ is the node’s response state values, $i=1,2,\cdots$, N. ${\phi }_i(·)\in PC{B}_r$ is the original condition of node i in response networks. ${\eta }_i\left(t\right)\in R^n$ is the bounded external disturbance vector in the response system, which satisfies $\parallel {\eta }_i\left(t\right)\parallel \le w_i$. Here, $\parallel {\eta }_i\left(t\right)\parallel$ stands for the modulus of vector ${\eta }_i\left(t\right)$.

To accomplish the synchronization task, the controller in this paper contains information feedback techniques and impulse sampling schemes. $e_i\left(t\right)=y_i\left(t\right)-x_i\left(t\right)$ denotes the system synchronization error, and the controller employing the feedback information is further designed as below:

$$\begin{array}{c}\hfill u_i\left(t\right)=-{\tilde{d}}_{1}sgn\left(e_i\left(t\right)\right)/{\parallel e_i\left(t\right)\parallel }_1,\end{array}$$

(3)

in which $sgn(·)$ refers to the sign vector function, and ${\tilde{d}}_1={\displaystyle \frac{1}{2N}}{\sum }_{i=1}^N{w}_i^2$ is the control gains. The delayed impulsive controller of the response CNs is designed as

$$\begin{array}{c}\hfill e_i\left(t\right)=\mathrm{\Theta }{e}_i(t^{-}-{\vartheta }_k),t=t_k,k\in {\mathbb{Z}}_{+},\end{array}$$

(4)

in which $\mathrm{\Theta }$ with size $n\times n$ denotes the gain matrix of the controller, and ${\vartheta }_k$ denotes the impulsive delay satisfying $0\le {\vartheta }_k\le \infty$. Let $F\left(T\right)$ be the set consisting of pulse instants, namely, $F\left(T\right)=\left\{t_k\right|t_k-t_{k-1}\le T,k\in {\mathbb{Z}}_{+},T>0\}$, in which $t_k\to \infty$ as $k\to \infty$.

Remark 1.

The uncertain time-delayed CNs studied in this article take into account multiple factors, such as the uncertain inner couplings, the nonlinear external couplings, the unbounded internal delays, the unbounded coupling delays, and the unbounded impulsive delays, which are more general in the real world. Moreover, the bounded external disturbance vector and the hybrid controller of the error signal are considered in the response system, further enhancing the practicality and generality of the model.

On the basis of CNs (1) and (2), the error system is derived as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{e}}_i\left(t\right)=-\overline{\mathcal{D}}{e}_i\left(t\right)+\overline{\mathcal{A}}\varphi \left(e_i\left(t\right)\right)+\overline{\mathcal{B}}h\left(e_i(t-v_1\left(t\right))\right)+c_1{\displaystyle \sum _{j=1}^N}{\tilde{\mathcal{H}}}_{ij}({\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right))\psi \left(e_j\left(t\right)\right)\hfill \\ +c_2{\displaystyle \sum _{j=1}^N}{\tilde{\mathcal{G}}}_{ij}({\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right))\psi \left(e_j(t-v_2\left(t\right))\right)+{\eta }_i\left(t\right)-{\tilde{d}}_{1}sgn\left(e_i\left(t\right)\right)/{\parallel e_i\left(t\right)\parallel }_1,t\ne t_k,\hfill \\ e_i\left(t\right)=\mathrm{\Theta }{e}_i(t^{-}-{\vartheta }_k),t=t_k,k\in {\mathbb{Z}}_{+},\hfill \\ e_i\left(s\right)={\phi }_i\left(s\right)-{\epsilon }_i\left(s\right),s\in (-\infty ,0].\hfill \end{array}\right.\end{array}$$

(5)

Note $\varphi \left(e_i\left(t\right)\right)=\varphi \left(y_i\left(t\right)\right)-\varphi \left(x_i\left(t\right)\right)$, $h\left(e_i(t-v_1\left(t\right))\right)=h\left(y_i(t-v_1\left(t\right))\right)-h\left(x_i(t-v_1\left(t\right))\right)$ and $\psi \left(e_j(t-v_2\left(t\right))\right)=\psi \left(y_j(t-v_2\left(t\right))\right)-\psi \left(x_j(t-v_2\left(t\right))\right)$, $i=1,2,\cdots$, N. Then, the synchronization task of the drive–response CNs can be regarded as the $\mu$-stable objective for the error network.

Assumption 1.

For the functions $\varphi (·),h(·)$, and $\psi (·)$, the three conditions

$$\begin{array}{c}\hfill \parallel \varphi \left(\varrho \right)-\varphi \left(\theta \right)\parallel \le l_{\varphi }\parallel \varrho -\theta \parallel ,\parallel h\left(\varrho \right)-h\left(\theta \right)\parallel \le l_h\parallel \varrho -\theta \parallel ,\parallel \psi \left(\varrho \right)-\psi \left(\theta \right)\parallel \le l_{\psi }\parallel \varrho -\theta \parallel \end{array}$$

hold, ∀ϱ, $\theta \in R^n$, $l_{\varphi }>0$, $l_h>0$, and $l_{\psi }>0$.

Assumption 2.

For the matrices $\tilde{\mathcal{H}}$ and $\tilde{\mathcal{G}}$, which describe the network’s topological structure, the two conditions

$$\begin{array}{c}\hfill \sum _{j=1}^N{\left({\tilde{\mathcal{H}}}_{ij}\right)}^2\le L_{\tilde{\mathcal{H}}},\sum _{j=1}^N{\left({\tilde{\mathcal{G}}}_{ij}\right)}^2\le L_{\tilde{\mathcal{G}}}\end{array}$$

hold, in which $L_{\tilde{\mathcal{H}}}>0$, $L_{\tilde{\mathcal{G}}}>0$.

Assumption 3.

$\Delta {\mathrm{\Gamma }}_1\left(t\right)$ and $\Delta {\mathrm{\Gamma }}_2\left(t\right)$ denote the uncertainty parts of internal coupling, which are norm-bounded and could be described as

$$\begin{array}{c}\hfill \Delta {\mathrm{\Gamma }}_1\left(t\right)=E_{{\mathrm{\Gamma }}_1}\mathrm{\Omega }\left(t\right)F_{{\mathrm{\Gamma }}_1},\Delta {\mathrm{\Gamma }}_2\left(t\right)=E_{{\mathrm{\Gamma }}_2}\mathrm{\Omega }\left(t\right)F_{{\mathrm{\Gamma }}_2},\end{array}$$

in which $E_{{\mathrm{\Gamma }}_1},E_{{\mathrm{\Gamma }}_2},F_{{\mathrm{\Gamma }}_1},and F_{{\mathrm{\Gamma }}_2}$ are constant matrices, and the uncertainty matrix $\mathrm{\Omega }\left(t\right)$ is bounded by ${\mathrm{\Omega }}^T\left(t\right)\mathrm{\Omega }\left(t\right)\le I$.

Assumption 4.

The inequality conditions with regard to $\mu \left(t\right)$

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\mu \left(t_{k-1}\right)}}\le {\mu }_{\tilde{p}},{\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_1\left(t\right))}}\le {\mu }_1,{\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_2\left(t\right))}}\le {\mu }_2,\cdots ,{\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_n\left(t\right))}}\le {\mu }_n,\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\tilde{\mu }(t_k-{\vartheta }_k)}}\le {\mu }_{\tilde{q}},\hfill \end{array}$$

can be satisfied if ${\mu }_i\ge 1(i=1,2,\cdots ,n)$, ${\mu }_{\tilde{p}}\ge 1$, ${\mu }_{\tilde{q}}\ge 1$, and $\tilde{\mu }\left(t\right)=\left\{\begin{array}{cc}1,\hfill & ift<0,\hfill \\ \mu \left(t\right),\hfill & else.\hfill \end{array}\right.$

3. Synchronization Analysis Results

Then, according to the assumptions in Section 2 and the Lemmas in Appendix A, the $\mu$-synchronization for uncertain time-delayed CNs with external disturbances is explored. Sufficient conditions are calculated to reach the $\mu$-synchronization for CNs (1) and (2). By Definition A1 in Appendix A, the error dynamical system (5) reaching $\mu$-stable is equivalent to our ultimate synchronization task.

Theorem 1.

The μ-synchronization of CNs (1) and (2) under Assumptions 1–4 and the hybrid impulsive controller can be reached if

(i)

$\ln {\mu }_{\tilde{p}}+[a+\gamma (b_1{\mu }_1+b_2{\mu }_2)]T<\ln \gamma ,$

(ii)

$$\begin{gathered} -\mathcal{R}\overline{\mathcal{D}}-{\overline{\mathcal{D}}}^T\mathcal{R}+{\xi }_1\mathcal{R}\overline{\mathcal{A}}{\overline{\mathcal{A}}}^T\mathcal{R}+{\xi }_1^{-1}{l}_{\varphi }^{2}I+{\varsigma }_1\mathcal{R}\overline{\mathcal{B}}{\overline{\mathcal{B}}}^T\mathcal{R}+c_1{\sigma }_1{L}_{\tilde{\mathcal{H}}}\mathcal{R}{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_1^T\mathcal{R}+c_1{\sigma }_2{L}_{\tilde{\mathcal{H}}}\mathcal{R}{E}_{{\mathrm{\Gamma }}_1} \\ {E}_{{\mathrm{\Gamma }}_1}^T\mathcal{R}+c_2{\sigma }_3{L}_{\tilde{\mathcal{G}}}\mathcal{R}{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_2^T\mathcal{R}+c_2{\sigma }_4{L}_{\tilde{\mathcal{G}}}\mathcal{R}{E}_{{\mathrm{\Gamma }}_2}{E}_{{\mathrm{\Gamma }}_2}^T\mathcal{R}+c_1({\sigma }_1^{-1}+{\sigma }_2^{-1}{\lambda }_{max}\left(F_{{\mathrm{\Gamma }}_1}^T{F}_{{\mathrm{\Gamma }}_1}\right))l_{\psi }^{2}NI+ \\ {\nu }_1\mathcal{R}\mathcal{R}\le a\mathcal{R}, \end{gathered}$$

(iii)

${\varsigma }_1^{-1}{l}_h^{2}I\le b_1\mathcal{R},$

(iv)

$c_2({\sigma }_3^{-1}+{\sigma }_4^{-1}{\lambda }_{max}\left(F_{{\mathrm{\Gamma }}_2}^T{F}_{{\mathrm{\Gamma }}_2}\right))l_{\psi }^{2}NI\le b_2\mathcal{R},$

(v)

${\nu }_1^{-1}\le {\lambda }_{min}\left(\mathcal{R}\right),$

(vi)

$\left[\begin{array}{cc}-{\displaystyle \frac{1}{\gamma {\mu }_{\tilde{q}}}}\mathcal{R}& Q\\ Q^T& -\mathcal{R}\end{array}\right]\le 0,$

in which $\mu \left(t\right)\in X$, matrix Q is with size $n\times n$, $\gamma >1$, and ${\xi }_1$, ${\varsigma }_1$, ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_3$, ${\sigma }_4$, ${\nu }_1$, a, $b_1$, $b_2>0$. Moreover, the control gain matrix is set as $\mathrm{\Theta }={\mathcal{R}}^{-1}{Q}^T$.

Proof. 

We establish a proper form of Lyapunov function as

$$\begin{array}{c}\hfill W\left(t\right)=\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{e}_i\left(t\right).\end{array}$$

(6)

When $t\ne t_k$, calculating the derivative of $W\left(t\right)$ along the solution of error system (5), it can be obtained that

$$\begin{array}{cc}\hfill & D^{+}W\left(t\right)\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\dot{e}}_i\left(t\right)\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}[-\overline{\mathcal{D}}{e}_i\left(t\right)+\overline{\mathcal{A}}\varphi \left(e_i\left(t\right)\right)+\overline{\mathcal{B}}h\left(e_i(t-v_1\left(t\right))\right)+c_1\sum _{j=1}^N{\tilde{\mathcal{H}}}_{ij}({\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right))\psi \left(e_j\left(t\right)\right)\hfill \\ \hfill & +c_2\sum _{j=1}^N{\tilde{\mathcal{G}}}_{ij}({\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right))\psi \left(e_j(t-v_2\left(t\right))\right)+{\eta }_i\left(t\right)-{\tilde{d}}_{1}sgn\left(e_i\left(t\right)\right)/{\parallel e_i\left(t\right)\parallel }_1].\hfill \end{array}$$

(7)

According to the operation rule of matrix quadratic form, one has

$$\begin{array}{c}\hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}(-\overline{\mathcal{D}})e_i\left(t\right)=\sum _{i=1}^N{e}_i^T\left(t\right)(-\mathcal{R}\overline{\mathcal{D}}-{\overline{\mathcal{D}}}^T\mathcal{R})e_i\left(t\right).\end{array}$$

(8)

By Lemma A1 and Assumption 1, it can be obtained that

$$\begin{array}{cc}\hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}\overline{\mathcal{A}}\varphi \left(e_i\left(t\right)\right)\le & \sum _{i=1}^N{\xi }_1{e}_i^T\left(t\right)\mathcal{R}\overline{\mathcal{A}}{\overline{\mathcal{A}}}^T\mathcal{R}{e}_i\left(t\right)+\sum _{i=1}^N{\xi }_1^{-1}{\parallel \varphi \left(e_i\left(t\right)\right)\parallel }^2\hfill \\ \hfill \le & \sum _{i=1}^N{\xi }_1{e}_i^T\left(t\right)\mathcal{R}\overline{\mathcal{A}}{\overline{\mathcal{A}}}^T\mathcal{R}{e}_i\left(t\right)+\sum _{i=1}^N{\xi }_1^{-1}{l}_{\varphi }^2{e}_i^T\left(t\right)e_i\left(t\right).\hfill \end{array}$$

(9)

Similarly, by Lemma A1 and Assumption 1, it is easy to obtain that

$$\begin{array}{cc}\hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}\overline{\mathcal{B}}h\left(e_i(t-v_1\left(t\right))\right)& \le \sum _{i=1}^N{\varsigma }_1{e}_i^T\left(t\right)\mathcal{R}\overline{\mathcal{B}}{\overline{\mathcal{B}}}^T\mathcal{R}{e}_i\left(t\right)+\sum _{i=1}^N{\varsigma }_1^{-1}{\parallel h\left(e_i(t-v_1\left(t\right))\right)\parallel }^2\hfill \\ \hfill & \le \sum _{i=1}^N{\varsigma }_1{e}_i^T\left(t\right)\mathcal{R}\overline{\mathcal{B}}{\overline{\mathcal{B}}}^T\mathcal{R}{e}_i\left(t\right)+\sum _{i=1}^N{\varsigma }_1^{-1}{l}_h^2{e}_i^T(t-v_1\left(t\right))e_i(t-v_1\left(t\right)).\hfill \end{array}$$

(10)

By Lemma A1 and Assumptions 1–3, one can obtain that

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}\left[c_1\sum _{j=1}^N{\tilde{\mathcal{H}}}_{ij}({\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right))\psi \left(e_j\left(t\right)\right)\right]\hfill \\ \hfill \le & c_1{\sigma }_1\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_1^T{\left({\tilde{\mathcal{H}}}_{ij}\right)}^2\mathcal{R}{e}_i\left(t\right)+c_1{\sigma }_1^{-1}\sum _{i=1}^N\sum _{j=1}^N{\parallel \psi \left(e_j\left(t\right)\right)\parallel }^2\hfill \\ \hfill & +c_1{\sigma }_2\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right)\mathcal{R}{E}_{{\mathrm{\Gamma }}_1}{E}_{{\mathrm{\Gamma }}_1}^T{\left({\tilde{\mathcal{H}}}_{ij}\right)}^2\mathcal{R}{e}_i\left(t\right)+c_1{\sigma }_2^{-1}\sum _{i=1}^N\sum _{j=1}^N{\psi }^T\left(e_j\left(t\right)\right)F_{{\mathrm{\Gamma }}_1}^T{F}_{{\mathrm{\Gamma }}_1}\psi \left(e_j\left(t\right)\right)\hfill \\ \hfill \le & c_1{\sigma }_1{L}_{\tilde{\mathcal{H}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_1^T\mathcal{R}{e}_i\left(t\right)+c_1{\sigma }_1^{-1}{l}_{\psi }^{2}N\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +c_1{\sigma }_2{L}_{\tilde{\mathcal{H}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{E}_{{\mathrm{\Gamma }}_1}{E}_{{\mathrm{\Gamma }}_1}^T\mathcal{R}{e}_i\left(t\right)+c_1{\sigma }_2^{-1}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_{max}(F_{{\mathrm{\Gamma }}_1}^T{F}_{{\mathrm{\Gamma }}_1}){\psi }^T\left(e_j\left(t\right)\right)\psi \left(e_j\left(t\right)\right)\hfill \\ \hfill \le & c_1{\sigma }_1{L}_{\tilde{\mathcal{H}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_1^T\mathcal{R}{e}_i\left(t\right)+c_1({\sigma }_1^{-1}+{\sigma }_2^{-1}{\lambda }_{max}\left(F_{{\mathrm{\Gamma }}_1}^T{F}_{{\mathrm{\Gamma }}_1}\right))l_{\psi }^{2}N\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\hfill \\ \hfill & +c_1{\sigma }_2{L}_{\tilde{\mathcal{H}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{E}_{{\mathrm{\Gamma }}_1}{E}_{{\mathrm{\Gamma }}_1}^T\mathcal{R}{e}_i\left(t\right).\hfill \end{array}$$

(11)

Similarly, by Lemma A1 and Assumptions 1–3, one can obtain

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}\left[c_2\sum _{j=1}^N{\tilde{\mathcal{G}}}_{ij}({\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right))\psi \left(e_j(t-v_2\left(t\right))\right)\right]\hfill \\ \hfill \le & c_2{\sigma }_3\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_2^T{\left({\tilde{\mathcal{G}}}_{ij}\right)}^2\mathcal{R}{e}_i\left(t\right)+c_2{\sigma }_3^{-1}\sum _{i=1}^N\sum _{j=1}^N{\parallel \psi \left(e_j(t-v_2\left(t\right))\right)\parallel }^2\hfill \\ \hfill & +c_2{\sigma }_4\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right)\mathcal{R}{E}_{{\mathrm{\Gamma }}_2}{E}_{{\mathrm{\Gamma }}_2}^T{\left({\tilde{\mathcal{G}}}_{ij}\right)}^2\mathcal{R}{e}_i\left(t\right)+c_2{\sigma }_4^{-1}\sum _{i=1}^N\sum _{j=1}^N{\psi }^T\left(e_j(t-v_2\left(t\right))\right)F_{{\mathrm{\Gamma }}_2}^T{F}_{{\mathrm{\Gamma }}_2}\psi \left(e_j(t-v_2\left(t\right))\right)\hfill \\ \hfill \le & c_2{\sigma }_3{L}_{\tilde{\mathcal{G}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_2^T\mathcal{R}{e}_i\left(t\right)+c_2{\sigma }_3^{-1}{l}_{\psi }^{2}N\sum _{i=1}^N{e}_i^T(t-v_2\left(t\right))e_i(t-v_2\left(t\right))\hfill \\ \hfill & +c_2{\sigma }_4{L}_{\tilde{\mathcal{G}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{E}_{{\mathrm{\Gamma }}_2}{E}_{{\mathrm{\Gamma }}_2}^T\mathcal{R}{e}_i\left(t\right)+c_2{\sigma }_4^{-1}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_{max}\left(F_{{\mathrm{\Gamma }}_2}^T{F}_{{\mathrm{\Gamma }}_2}\right){\psi }^T\left(e_j(t-v_2\left(t\right))\right)\psi \left(e_j(t-v_2\left(t\right))\right)\hfill \\ \hfill \le & c_2{\sigma }_3{L}_{\tilde{\mathcal{G}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_2^T\mathcal{R}{e}_i\left(t\right)+c_2{\sigma }_4{L}_{\tilde{\mathcal{G}}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{E}_{{\mathrm{\Gamma }}_2}{E}_{{\mathrm{\Gamma }}_2}^T\mathcal{R}{e}_i\left(t\right)\hfill \\ \hfill & +c_2({\sigma }_3^{-1}+{\sigma }_4^{-1}{\lambda }_{max}\left(F_{{\mathrm{\Gamma }}_2}^T{F}_{{\mathrm{\Gamma }}_2}\right))l_{\psi }^{2}N\sum _{i=1}^N{e}_i^T(t-v_2\left(t\right))e_i(t-v_2\left(t\right)).\hfill \end{array}$$

(12)

By Lemma A1, it is calculated that

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}[{\eta }_i\left(t\right)-{\tilde{d}}_{1}sgn\left(e_i\left(t\right)\right)/\parallel e_i\left(t\right){\parallel }_1]\hfill \\ \hfill \le & {\nu }_1\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathcal{R}}^T{e}_i\left(t\right)+{\nu }_1^{-1}\sum _{i=1}^N\parallel {\eta }_i{\left(t\right)\parallel }^2-2{\lambda }_{min}\left(\mathcal{R}\right)\sum _{i=1}^N{e}_i^T\left(t\right)\widetilde{d_1}sgn\left(e_i\left(t\right)\right)/{\parallel e_i\left(t\right)\parallel }_1\hfill \\ \hfill \le & {\nu }_1\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathcal{R}}^T{e}_i\left(t\right)+{\nu }_1^{-1}\sum _{i=1}^N{w}_i^2-2{\lambda }_{min}\left(\mathcal{R}\right){\tilde{d}}_1·N\hfill \\ \hfill =& {\nu }_1\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}{\mathcal{R}}^T{e}_i\left(t\right)+({\nu }_1^{-1}-{\lambda }_{min}\left(\mathcal{R}\right))\sum _{i=1}^N{w}_i^2\hfill \\ \hfill \le & {\nu }_1\sum _{i=1}^N{e}_i^T\left(t\right)\mathcal{R}\mathcal{R}{e}_i\left(t\right).\hfill \end{array}$$

(13)

Based on conditions (i)–(vi), bringing together (7)–(13), one has

$$\begin{array}{cc}\hfill & D^{+}W\left(t\right)\hfill \\ \hfill \le & \sum _{i=1}^N{e}_i^T\left(t\right)[-\mathcal{R}\overline{\mathcal{D}}-{\overline{\mathcal{D}}}^T\mathcal{R}+{\xi }_1\mathcal{R}\overline{\mathcal{A}}{\overline{\mathcal{A}}}^T\mathcal{R}+{\xi }_1^{-1}{l}_{\varphi }^{2}I+{\varsigma }_1\mathcal{R}\overline{\mathcal{B}}{\overline{\mathcal{B}}}^T\mathcal{R}+c_1{\sigma }_1{L}_{\tilde{\mathcal{H}}}\mathcal{R}{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_1^T\mathcal{R}\hfill \\ \hfill & +c_1{\sigma }_2{L}_{\tilde{\mathcal{H}}}\mathcal{R}{E}_{{\mathrm{\Gamma }}_1}{E}_{{\mathrm{\Gamma }}_1}^T\mathcal{R}+c_1({\sigma }_1^{-1}+{\sigma }_2^{-1}{\lambda }_{max}\left(F_{{\mathrm{\Gamma }}_1}^T{F}_{{\mathrm{\Gamma }}_1}\right))l_{\psi }^{2}NI+c_2{\sigma }_3{L}_{\tilde{\mathcal{G}}}\mathcal{R}{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_2^T\mathcal{R}\hfill \\ \hfill & +c_2{\sigma }_4{L}_{\tilde{\mathcal{G}}}\mathcal{R}{E}_{{\mathrm{\Gamma }}_2}{E}_{{\mathrm{\Gamma }}_2}^T\mathcal{R}+{\nu }_1\mathcal{R}\mathcal{R}]e_i\left(t\right)+\sum _{i=1}^N{e}_i^T(t-v_1\left(t\right))\left({\varsigma }_1^{-1}{l}_h^{2}I\right)e_i(t-v_1\left(t\right))\hfill \\ \hfill & +\sum _{i=1}^N{e}_i^T(t-v_2\left(t\right))c_2({\sigma }_3^{-1}+{\sigma }_4^{-1}{\lambda }_{max}\left(F_{{\mathrm{\Gamma }}_2}^T{F}_{{\mathrm{\Gamma }}_2}\right))l_{\psi }^{2}NI{e}_i(t-v_2\left(t\right))\hfill \\ \hfill \le & aW\left(t\right)+b_{1}W(t-v_1\left(t\right))+b_{2}W(t-v_2\left(t\right)).\hfill \end{array}$$

(14)

Let $e\left(t\right)=[e_1^T\left(t\right),e_2^T\left(t\right),\cdots$, $e_N^T{\left(t\right)]}^T$; when $t=t_k,k\in {\mathbb{Z}}_{+}$, we have

$$\begin{array}{cc}\hfill W\left(t_k\right)=& \sum _{i=1}^N{e}_i^T\left(t_k\right)\mathcal{R}{e}_i\left(t_k\right)=\sum _{i=1}^N{\left[\mathrm{\Theta }{e}_i(t_k^{-}-{\vartheta }_k)\right]}^T\mathcal{R}\left[\mathrm{\Theta }{e}_i(t_k^{-}-{\vartheta }_k)\right]\hfill \\ \hfill =& \sum _{i=1}^N{e}_i^T(t_k^{-}-{\vartheta }_k){\mathrm{\Theta }}^T\mathcal{R}\mathrm{\Theta }{e}_i(t_k^{-}-{\vartheta }_k).\hfill \end{array}$$

(15)

In the light of Lemma A2, it can be concluded that

$$\begin{array}{c}\hfill {\mathrm{\Theta }}^T\mathcal{R}\mathrm{\Theta }-{\displaystyle \frac{1}{\gamma {\mu }_{\tilde{q}}}}\mathcal{R}\le 0.\end{array}$$

(16)

Thus, the following inequality holds:

$$\begin{array}{cc}\hfill W\left(t_k\right)\le & {\displaystyle \frac{1}{\gamma {\mu }_{\tilde{q}}}}\sum _{i=1}^N{e}_i^T(t_k^{-}-{\vartheta }_k)\mathcal{R}{e}_i(t_k^{-}-{\vartheta }_k)\hfill \\ \hfill =& {\displaystyle \frac{1}{\gamma {\mu }_{\tilde{q}}}}W(t_k^{-}-{\vartheta }_k).\hfill \end{array}$$

(17)

By Lemma A3, combining (14)–(16) with (17), we have

$$\begin{array}{c}\hfill W\left(t\right)\le {\displaystyle \frac{\gamma \mu \left(0\right){\sup }_{-\infty <s\le 0}W\left(s\right)}{\mu \left(t\right)}},t\ge 0,\end{array}$$

(18)

and the relationship below can be derived:

$$\begin{array}{c}\hfill \parallel e\left(t\right)\parallel \le \sqrt{{\displaystyle \frac{\gamma \mu \left(0\right){\lambda }_{max}\left(\mathcal{R}\right){\left|e\left(0\right)\right|}^2}{{\lambda }_{min}\left(\mathcal{R}\right)\mu \left(t\right)}}}.\end{array}$$

(19)

According to the comparison principle, the objective of the $\mu$-synchronization of CNs (1) and (2) can be obtained. Due to $\mu \left(t\right)\to \infty$ as $t\to \infty$, then $\parallel e\left(t\right)\parallel \to 0$ as $t\to \infty$, the error NNs become $\mu$-stable. The above process completes the proof. □

Remark 2.

The network model in [11] has uncertainty in system dynamics, while the parameter uncertainty of the network model in this paper is reflected in the inner coupling matrix. For these two different types of parameter uncertainty, different inequality analysis methods, assumptions, and lemmas are used in the proof process of the Theorem. Additionally, the controllers used in the two articles are different. In [11], it only adopts a distributed pulse controller, while this paper designs a hybrid controller that includes a feedback controller and a time-delay pulse controller.

Remark 3.

The global μ-synchronization task for nonlinear CNs was studied in [49] by adopting a delayed impulsive control approach. In our article, to achieve the synchronization of the drive–response CNs, a hybrid impulsive controller containing both information feedback of error signals and impulse sampling factors is proposed. In contrast, the control scheme in this paper makes the results more applicable under external disturbances.

Remark 4.

In [50,51], the impulsive interval T was set considering the factor of the bound of time delays. From condition (i) of Theorem 1, it can be seen that the pulse interval T is not affected by the values of time delays in this article. Therefore, the constraint on the impulsive interval T is relaxed in the proposed model. Moreover, in [52], the synchronization for semi-Markov impulsive coupled NNs was reached under the state feedback controller, yet the time-varying delays were bounded parameters. In [53], the synchronization algorithm for nonlinear NNs with variable topology was proposed, yet the change rate of the time delay was within a bounded interval. In this article, CNs (1) and (2) can reach synchronization even if the proposed model has unbounded time delays.

Remark 5.

The synchronization task of CNs with parameter uncertainty was investigated in [31,33,34,54]. The parameter uncertainty involved belonged to the outer coupling matrices [31,54], the connection weight matrices [33], and the nonlinear dynamics state of nodes [34]. In our article, the model considers the uncertainty of inner-coupling matrices, and novel μ-synchronization criteria of complex systems are derived. In addition, in [55], the impulsive synchronization of randomly coupled CNs was explored, in which the outer coupling matrices should satisfy the zero-row-sum condition. However, there is no need for the external coupling matrices in the proposed model to satisfy the dissipative coupling condition.

Based on Theorem 1, three specific cases are shown below, which indicates that the synchronization under the sense of power, log, and exponential can be achieved by our impulsive control scheme.

Corollary 1.

Supposing that Assumptions 1–3 and situations (ii)–(v) hold, let $\mu \left(t\right)={(1+\kappa t)}^{\rho }$, $v_1\left(t\right)={\iota }_{1}t$, $v_2\left(t\right)={\iota }_{2}t$, and ${\vartheta }_k={\iota }_3{t}_k$, in which $\kappa >0,\rho >0$, and $0\le {\iota }_1,{\iota }_2,{\iota }_3<1$. If ∃$\gamma >1,T>0$, such that the two inequalities

$$\rho \ln (1+\kappa T)+aT+\gamma [{\displaystyle \frac{b_1}{{(1-{\iota }_1)}^{\rho }}}+{\displaystyle \frac{b_2}{{(1-{\iota }_2)}^{\rho }}}]T<\ln \gamma ,$$

and

$$\left[\begin{array}{cc}-{\displaystyle \frac{{(1-{\iota }_3)}^{\rho }}{\gamma }}\mathcal{R}& Q\\ Q^T& -\mathcal{R}\end{array}\right]\le 0.$$

hold. Then, it can be well recognized that CNs (1) and (2) further reach synchronization in the power sense using the control matrix $\mathrm{\Theta }={\mathcal{R}}^{-1}{Q}^T$.

Proof. 

Comparing the conditions of Theorem 1 and Corollary 1, if Assumption 4 holds, the conclusion of Corollary 1 is correct. Clearly, when $t\ge 0$, it is calculated that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\mu \left(t_{k-1}\right)}}={\left[{\displaystyle \frac{1+\kappa t_k}{1+\kappa t_{k-1}}}\right]}^{\rho }={\left[{\displaystyle \frac{1+\kappa t_{k-1}+\kappa (t_k-t_{k-1})}{1+\kappa t_{k-1}}}\right]}^{\rho }\le {(1+\kappa T)}^{\rho },\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_1\left(t\right))}}={\left[{\displaystyle \frac{1+\kappa t}{1+\kappa (1-{\iota }_1)t}}\right]}^{\rho }={\displaystyle \frac{1}{{\left[\frac{1+\kappa (1-{\iota }_1)t}{1+\kappa t}\right]}^{\rho }}}\le {\displaystyle \frac{1}{{(1-{\iota }_1)}^{\rho }}},\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_2\left(t\right))}}={\left[{\displaystyle \frac{1+\kappa t}{1+\kappa (1-{\iota }_2)t}}\right]}^{\rho }={\displaystyle \frac{1}{{\left[\frac{1+\kappa (1-{\iota }_2)t}{1+\kappa t}\right]}^{\rho }}}\le {\displaystyle \frac{1}{{(1-{\iota }_2)}^{\rho }}},\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\tilde{\mu }(t_k-{\vartheta }_k)}}={\left[{\displaystyle \frac{1+\kappa t_k}{1+\kappa (1-{\iota }_3)t_k}}\right]}^{\rho }={\displaystyle \frac{1}{{\left[\frac{1+\kappa (1-{\iota }_3)t_k}{1+\kappa t_k}\right]}^{\rho }}}\le {\displaystyle \frac{1}{{(1-{\iota }_3)}^{\rho }}}.\hfill \end{array}$$

Let ${\mu }_{\tilde{p}}={(1+\kappa T)}^{\rho }$, ${\mu }_1={\displaystyle \frac{1}{{(1-{\iota }_1)}^{\rho }}}$, ${\mu }_2={\displaystyle \frac{1}{{(1-{\iota }_2)}^{\rho }}}$, and ${\mu }_{\tilde{q}}={\displaystyle \frac{1}{{(1-{\iota }_3)}^{\rho }}}$; according to the proof strategy of Theorem 1, it shows that CNs (1) and (2) reach power synchronization. □

Corollary 2.

Provided that Assumptions 1–3 and situations (ii)–(v) hold true, let $\mu \left(t\right)=\ln (e+\alpha t)$, $v_1\left(t\right)=t+[e-{(t+e)}^{{\rho }_1}]/\alpha$, $v_2\left(t\right)=t+[e-{(t+e)}^{{\rho }_2}]/\alpha$, and ${\vartheta }_k=\iota t_k$, in which $0<\alpha ,{\rho }_1,{\rho }_2<1$, and $0\le \iota <1$. If ∃$\gamma >1,T>0$, such that the two inequalities

$$\ln [1+\ln (1+{\displaystyle \frac{\alpha T}{e}})]+[a+\gamma ({\displaystyle \frac{b_1}{{\rho }_1}}+{\displaystyle \frac{b_2}{{\rho }_2}})]T<\ln \gamma ,$$

and

$$\left[\begin{array}{cc}-{\displaystyle \frac{1}{\gamma [1-\ln (1-\iota \left)\right]}}\mathcal{R}& Q\\ Q^T& -\mathcal{R}\end{array}\right]\le 0.$$

hold, then CNs (1) and (2) are log-synchronized under the existence of the control matrix $\mathrm{\Theta }={\mathcal{R}}^{-1}{Q}^T$.

Proof. 

When $t\ge 0$, one can obtain that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\mu \left(t_{k-1}\right)}}={\displaystyle \frac{\ln (e+\alpha t_k)}{\ln (e+\alpha t_{k-1})}}=1+{\displaystyle \frac{\ln [1+\frac{\alpha (t_k-t_{k-1})}{e+\alpha t_{k-1}}]}{\ln (e+\alpha t_{k-1})}}\le 1+\ln (1+\alpha T/e),\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_1\left(t\right))}}={\displaystyle \frac{\ln (e+\alpha t)}{\tilde{\mu }[({(t+e)}^{{\rho }_1}-e)/\alpha ]}}={\displaystyle \frac{\ln (e+\alpha t)}{{\rho }_1\ln (e+t)}}\le {\displaystyle \frac{1}{{\rho }_1}},\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_2\left(t\right))}}={\displaystyle \frac{\ln (e+\alpha t)}{\tilde{\mu }[({(t+e)}^{{\rho }_2}-e)/\alpha ]}}={\displaystyle \frac{\ln (e+\alpha t)}{{\rho }_2\ln (e+t)}}\le {\displaystyle \frac{1}{{\rho }_2}},\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\tilde{\mu }(t_k-{\vartheta }_k)}}={\displaystyle \frac{\ln (e+\alpha t_k)}{\ln (e+\alpha (1-\iota )t_k)}}=1+{\displaystyle \frac{\ln \left[\frac{e+\alpha t_k}{e+\alpha (1-\iota )t_k}\right]}{\ln [e+\alpha (1-\iota )t_k]}}\le 1-\ln (1-\iota ).\hfill \end{array}$$

Select ${\mu }_{\tilde{p}}=1+\ln (1+\alpha T/e)$, ${\mu }_1={\displaystyle \frac{1}{{\rho }_1}}$, ${\mu }_2={\displaystyle \frac{1}{{\rho }_2}}$, and ${\mu }_{\tilde{q}}=1-\ln (1-\iota )$; according to the analysis strategy of Theorem 1, it indicates that CNs (1) and (2) reach log synchronization. □

Corollary 3.

Given that Assumptions 1–3 and situations (ii)–(v) hold, let $\mu \left(t\right)=\exp \left(\beta t\right)$, $0\le v_1\left(t\right),v_2\left(t\right)\le v$, $0\le {\vartheta }_k\le \eta$, in which $\beta >0,v<\infty$, and $\eta <\infty$. If ∃$\gamma >1,T>0$, such that the two inequalities

$$\beta T+[a+\gamma (b_1+b_2)\exp \left(\beta v\right)]T<\ln \gamma ,$$

and

$$\left[\begin{array}{cc}-{\displaystyle \frac{1}{\gamma \exp \left(\beta \eta \right)}}\mathcal{R}& Q\\ Q^T& -\mathcal{R}\end{array}\right]\le 0.$$

hold. In this case, CNs (1) and (2) achieve synchronization in the exponential sense by employing the hybrid pulse controller, where the matrix $\mathrm{\Theta }={\mathcal{R}}^{-1}{Q}^T$.

Proof. 

When $t\ge 0$, one has

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\mu \left(t_{k-1}\right)}}={\displaystyle \frac{\exp \left(\beta t_k\right)}{\exp \left(\beta t_{k-1}\right)}}=\exp \left[\beta (t_k-t_{k-1})\right]\le \exp \left(\beta T\right),\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_1\left(t\right))}}={\displaystyle \frac{\exp \left(\beta t\right)}{\exp \left[\beta (t-v_1\left(t\right))\right]}}=\exp \left[\beta v_1\left(t\right)\right]\le \exp \left(\beta v\right),\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t\right)}{\tilde{\mu }(t-v_2\left(t\right))}}={\displaystyle \frac{\exp \left(\beta t\right)}{\exp \left[\beta (t-v_2\left(t\right))\right]}}=\exp \left[\beta v_2\left(t\right)\right]\le \exp \left(\beta v\right),\hfill \\ \hfill & {\displaystyle \frac{\mu \left(t_k\right)}{\tilde{\mu }(t_k-{\vartheta }_k)}}={\displaystyle \frac{\exp \left(\beta t_k\right)}{\exp \left[\beta (t_k-{\vartheta }_k)\right]}}=\exp \left(\beta {\vartheta }_k\right)\le \exp \left(\beta \eta \right).\hfill \end{array}$$

Choosing ${\mu }_{\tilde{p}}=\exp \left(\beta T\right)$, ${\mu }_1=\exp \left(\beta v\right)$, ${\mu }_2=\exp \left(\beta v\right)$, and ${\mu }_{\tilde{q}}=\exp \left(\beta \eta \right)$, according to the strategy of Theorem 1, it shows that CNs (1) and (2) reach exponential synchronization. □

4. Numerical Simulations

The experiments in this section are conducted to verify the correctness of the theoretical results in Section 3. The correctness of the conditions in Theorem 1 is verified through two numerical experiments.

Example 1.

First, the drive NNs containing 6 nodes with unbounded changeable delays and inner couplings of uncertainty are considered as

$$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)=& -\overline{\mathcal{D}}{x}_i\left(t\right)+\overline{\mathcal{A}}\varphi \left(x_i\left(t\right)\right)+\overline{\mathcal{B}}h\left(x_i(t-v_1\left(t\right))\right)\hfill \\ \hfill & +c_1\sum _{j=1}^6{\tilde{\mathcal{H}}}_{ij}({\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right))\psi \left(x_j\left(t\right)\right)+c_2\sum _{j=1}^6{\tilde{\mathcal{G}}}_{ij}({\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right))\psi \left(x_j(t-v_2\left(t\right))\right)\hfill \end{array}$$

(20)

in which $x_i\left(t\right)={(x_{i1}\left(t\right),x_{i2}\left(t\right))}^T$, $c_1=0.1$, $c_2=0.15$, $v_1\left(t\right)=0.03t$, $v_2\left(t\right)=0.04t$. The nonlinear functions are set as $\varphi \left(x_i\left(t\right)\right)=h\left(x_i\left(t\right)\right)=\psi \left(x_i\left(t\right)\right)=1/8{(tanh\left(x_{i1}\left(t\right)\right),tanh\left(x_{i2}\left(t\right)\right))}^T$. It can be obtained that $l_{\varphi }=l_h=l_{\psi }=1/8$ through a simple calculation, such that Assumption 1 holds. The response system is depicted as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{y}}_i\left(t\right)=-\overline{\mathcal{D}}{y}_i\left(t\right)+\overline{\mathcal{A}}\varphi \left(y_i\left(t\right)\right)+\overline{\mathcal{B}}h\left(y_i(t-v_1\left(t\right))\right)+c_1\sum _{j=1}^6{\tilde{\mathcal{H}}}_{ij}({\mathrm{\Gamma }}_1+\Delta {\mathrm{\Gamma }}_1\left(t\right))\psi \left(y_j\left(t\right)\right)\hfill \\ +c_2\sum _{j=1}^6{\tilde{\mathcal{G}}}_{ij}({\mathrm{\Gamma }}_2+\Delta {\mathrm{\Gamma }}_2\left(t\right))\psi \left(y_j(t-v_2\left(t\right))\right)+{\eta }_i\left(t\right)-{\tilde{d}}_{1}sgn\left(e_i\left(t\right)\right)/{\parallel e_i\left(t\right)\parallel }_1,t\ne t_k,\hfill \\ e_i\left(t\right)=\mathrm{\Theta }{e}_i(t^{-}-{\vartheta }_k),t=t_k,k\in Z_{+},\hfill \end{array}\right.\end{array}$$

(21)

The constant matrices $\overline{\mathcal{D}}$, $\overline{\mathcal{A}}$, $\overline{\mathcal{B}}$ are set, respectively, as

$$\begin{array}{c}\hfill \overline{\mathcal{D}}=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right],\overline{\mathcal{A}}=\left[\begin{array}{cc}2.2& -0.2\\ -3.2& 1.6\end{array}\right],\overline{\mathcal{B}}=\left[\begin{array}{cc}-1.0& -0.2\\ -0.3& -1.5\end{array}\right].\end{array}$$

The certainty inner coupling matrices are set, respectively, as

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_1=\left[\begin{array}{cc}0.9& 0\\ 0& 0.2\end{array}\right],{\mathrm{\Gamma }}_2=\left[\begin{array}{cc}0.3& 0\\ 0& 0.8\end{array}\right].\end{array}$$

The parametric uncertainties of internal coupling are selected, respectively, as

$$\begin{array}{c}\hfill \Delta {\mathrm{\Gamma }}_1\left(t\right)=E_{{\mathrm{\Gamma }}_1}\mathrm{\Omega }\left(t\right)F_{{\mathrm{\Gamma }}_1}=\left[\begin{array}{cc}-0.1& 0\\ 0& -0.1\end{array}\right]\left[\begin{array}{cc}\sin \left(t\right)& 0\\ 0& \cos \left(t\right)\end{array}\right]\left[\begin{array}{cc}-0.1& 0\\ 0& -0.1\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill \Delta {\mathrm{\Gamma }}_2\left(t\right)=E_{{\mathrm{\Gamma }}_2}\mathrm{\Omega }\left(t\right)F_{{\mathrm{\Gamma }}_2}=\left[\begin{array}{cc}0.3& 0\\ 0& 0.3\end{array}\right]\left[\begin{array}{cc}\sin \left(t\right)& 0\\ 0& \cos \left(t\right)\end{array}\right]\left[\begin{array}{cc}0.3& 0\\ 0& 0.3\end{array}\right].\end{array}$$

The topological matrices $\tilde{\mathcal{H}}$ and $\tilde{\mathcal{G}}$ are selected, respectively, as

$$\begin{array}{c}\hfill \tilde{\mathcal{H}}=\left[\begin{array}{cccccc}1& 0& 1& 0& 1& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 1& 0& 0\\ 0& 0& 2& 1& 0& 0\\ 0& 0& 1& 0& 1& 0\\ 0& 0& 0& 1& 0& 2\end{array}\right],\tilde{\mathcal{G}}=\left[\begin{array}{cccccc}1& 0& 1& 0& 0& 0\\ 0& 2& 1& 0& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 0& 0& 0& 1& 0& 1\\ 0& 0& 0& 1& 1& 0\\ 0& 0& 0& 1& 0& 1\end{array}\right].\end{array}$$

Assumption 2 is satisfied with $L_{\tilde{\mathcal{H}}}=L_{\tilde{\mathcal{G}}}=5$. Due to ${\mathrm{\Omega }}^T\left(t\right)\mathrm{\Omega }\left(t\right)\le I$, Assumption 3 holds. The function $\mu \left(t\right)$ and the delay parameter ${\vartheta }_k$ in Assumption 4 are set, respectively, as $\mu \left(t\right)=\sqrt{1+5t},$${\vartheta }_k=t_k/50,$$k\in {\mathbb{Z}}_{+}.$ Let ${\xi }_1=2$, ${\varsigma }_1=4$, ${\sigma }_1=1$, ${\sigma }_2=0.5$, ${\sigma }_3=5$, ${\sigma }_4=0.1$, ${\nu }_1=3$, $a=1000$, $b_1=0.01$, $b_2=1.005$, $\gamma =10$, and $T=0.001$. Then, it can be obtained that ${\mu }_{\tilde{p}}=1.0025$, ${\mu }_{\tilde{q}}=1.0102$, ${\mu }_1=1.0153$, ${\mu }_2=1.0206$ by calculation. According to the proof process of Corollary 1, Assumption 4 holds.

To satisfy the remaining conditions in Corollary 1, the following feasible solutions are obtained by using the Matlab LMI toolbox:

$$\begin{array}{c}\hfill \mathcal{R}=\left[\begin{array}{cc}8.1506& 0\\ 0& 12.0142\end{array}\right],Q=\left[\begin{array}{cc}1.28& 0\\ 0.24& 0.95\end{array}\right].\end{array}$$

Hence, the control matrix Θ is set as

$$\begin{array}{c}\hfill \mathrm{\Theta }=\left[\begin{array}{cc}0.1570& 0.0294\\ 0& 0.0791\end{array}\right].\end{array}$$

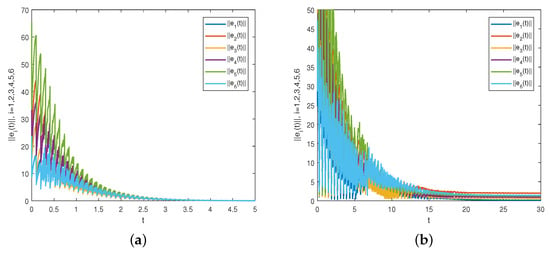
We randomly choose the initial values for six nodes from $[-50,50]$. The state trajectories of $\parallel e_i\left(t\right)\parallel$ converging to 0 with respect to a proper value of Θ are presented in Figure 1a, which implies that CNs (20) and (21) have achieved synchronization. Figure 1b is a description of the non-synchronization result under an improper value of ${\mathrm{\Theta }}^{*}=\mathrm{\Theta }+0.2I$ due to the state trajectories of $\parallel e_i\left(t\right)\parallel$ not converging to 0. That is, CNs (20) and (21) cannot reach synchronization with respect to the changed value of matrix ${\mathrm{\Theta }}^{*}$ since the inequality condition in Corollary 1 no longer holds.

Remark 6.

By selecting a series of parameters whose values conform to the conditions in Theorem 1 through calculation, for example, the values of the parameters ${\mu }_{\tilde{p}}$, a, γ, $b_1$, $b_2$, ${\mu }_1$, ${\mu }_2$, and T in the experiment conform to condition (i); the values of the parameters $\overline{\mathcal{D}}$, $\overline{\mathcal{A}}$, $\overline{\mathcal{B}}$, ${\mathrm{\Gamma }}_1$, ${\mathrm{\Gamma }}_2$, $E_{{\mathrm{\Gamma }}_1}$, $F_{{\mathrm{\Gamma }}_1}$, $E_{{\mathrm{\Gamma }}_2}$, $L_{\tilde{\mathcal{H}}}$, $L_{\tilde{\mathcal{G}}}$, $\mathcal{R}$, ${\xi }_1$, ${\varsigma }_1$, $c_1$, $c_2$, ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_3$, ${\sigma }_4$, $l_{\varphi }$, $l_{\psi }$, ${\nu }_1$, a, and N in the experiment conform to condition (ii); the values of the parameters ${\varsigma }_1$, $l_h$, $b_1$, and $\mathcal{R}$ in the experiment conform to condition (iii); and the values of the parameters γ, ${\mu }_{\tilde{q}}$, Q, and $\mathcal{R}$ in the experiment conform to condition (vi). Additionally, the correctness of the conditions in Theorem 1 is verified from the experimental results in Figure 1. Theoretical results and numerical experiments jointly demonstrate that uncertain time-delayed CNs can achieve μ-synchronization under the designed hybrid controller.

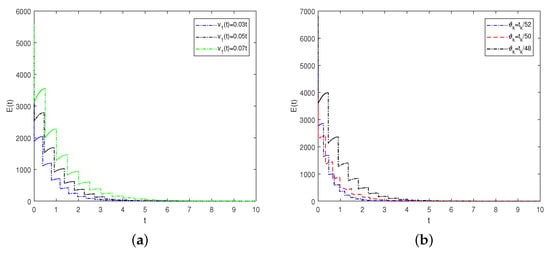
The changes in system parameters will significantly affect the synchronization stability of CNs. Our focus is on discussing two different types of time delays, namely, internal delays and impulsive delays. The total synchronization error of CNs (20) and (21) is defined as $E\left(t\right)={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{∥y_i\left(t\right)-x_i\left(t\right)∥}^2$. First, we study the effect of fine-tuning the internal delay $v_1\left(t\right)$ while keeping other network parameters unchanged. The internal delay gradually changes with $0.03t$ as the initial value and $0.02t$ as the step size, and the variation of the synchronization speeds can be seen in Figure 2a. Second, the impulsive delays ${\vartheta }_k$ are set to $t_k/52$, $t_k/50$, and $t_k/48$, while the remaining parameters are kept unchanged. As can be seen in Figure 2b, the black, red, and blue curves denote the time evolution of the total synchronization error under the influence of different impulsive delays. Overall, the total synchronization error curves indicate that the efficiency of network synchronization slows down as the internal or impulsive delay increases.

Example 2.

Consider a complex nonlinear network composed of six neuron nodes, where each decoupled node satisfies the following chaotic system:

$${\dot{x}}_i\left(t\right)=-\overline{\mathcal{D}}{x}_i\left(t\right)+\overline{\mathcal{A}}\varphi \left(x_i\left(t\right)\right)+\overline{\mathcal{B}}h\left(x_i(t-v_1\left(t\right))\right)$$

(22)

where $x_i\left(\begin{array}{c}t\end{array}\right)=\left(\begin{array}{c}{x}_{i1}\left(\begin{array}{c}t\end{array}\right),x_{i2}\left(\begin{array}{c}t\end{array}\right)\end{array}\right)$ is the state vector of the i-th node, and the bounded delay is set as $v_1\left(t\right)=e^t/(1+e^t)$.

The weight matrices are set as $\overline{\mathcal{D}}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$, $\overline{\mathcal{A}}=\left[\begin{array}{cc}1+{\displaystyle \frac{\pi }{4}}& 20\\ \\ 0.1& 1+{\displaystyle \frac{\pi }{4}}\end{array}\right]$, $\overline{\mathcal{B}}=\left[\begin{array}{cc}{\displaystyle \frac{-13\sqrt{2}\pi }{40}}& 0.1\\ \\ 0.1& {\displaystyle \frac{-13\sqrt{2}\pi }{40}}\end{array}\right]$.

The nonlinear activation functions are set as

$$\varphi \left(x_i\left(t\right)\right)=h\left(x_i\left(t\right)\right)=({\displaystyle \frac{1}{2}}\left(\right|x_{i1}\left(t\right)+1|-|x_{i1}\left(t\right)-1\left|\right),{\displaystyle \frac{1}{2}}\left(\right|x_{i2}\left(t\right)+1|-|x_{i2}\left(t\right)-1\left|\right)).$$

When the initial value of each node in this system is $\left[\begin{array}{c}0,0.5\end{array}\right]$, the behavior of the system exhibits chaos [13]. For neural networks (22) that include both external and internal couplings, the external coupling function is set as

$$\psi \left(x_i\left(t\right)\right)=({\displaystyle \frac{1}{8}}\left(\right|x_{i1}\left(t\right)+1|-|x_{i1}\left(t\right)-1\left|\right),{\displaystyle \frac{1}{8}}\left(\right|x_{i2}\left(t\right)+1|-|x_{i2}\left(t\right)-1\left|\right)).$$

It can be obtained that $l_{\varphi }=l_h=1,l_{\psi }=1/4$ using the inequality scaling principle, such that Assumption 1 holds.

Let the certainty inner coupling matrices be

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_1=\left[\begin{array}{cc}0.3& 0\\ 0& 0.4\end{array}\right],{\mathrm{\Gamma }}_2=\left[\begin{array}{cc}0.3& 0\\ 0& 0.5\end{array}\right].\end{array}$$

The uncertainties of internal coupling are set, respectively, as

$$\begin{array}{c}\hfill \Delta {\mathrm{\Gamma }}_1\left(t\right)=E_{{\mathrm{\Gamma }}_1}\mathrm{\Omega }\left(t\right)F_{{\mathrm{\Gamma }}_1}=\left[\begin{array}{cc}-0.2& 0\\ 0& -0.3\end{array}\right]\left[\begin{array}{cc}\sin \left(t\right)& 0\\ 0& \cos \left(t\right)\end{array}\right]\left[\begin{array}{cc}-0.2& 0\\ 0& -0.3\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill \Delta {\mathrm{\Gamma }}_2\left(t\right)=E_{{\mathrm{\Gamma }}_2}\mathrm{\Omega }\left(t\right)F_{{\mathrm{\Gamma }}_2}=\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right]\left[\begin{array}{cc}\sin \left(t\right)& 0\\ 0& \cos \left(t\right)\end{array}\right]\left[\begin{array}{cc}0.4& 0\\ 0& 0.2\end{array}\right].\end{array}$$

The values for the outer topological matrices $\tilde{\mathcal{H}}$ and $\tilde{\mathcal{G}}$ are set, respectively, as

$$\begin{array}{c}\hfill \tilde{\mathcal{H}}=\left[\begin{array}{cccccc}1& 0& 1& 0& 1& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 1& 0& 0\\ 0& 1& 2& 1& 0& 0\\ 1& 1& 1& 0& 1& 0\\ 0& 0& 0& 1& 0& 2\end{array}\right],\tilde{\mathcal{G}}=\left[\begin{array}{cccccc}1& 0& 1& 0& 0& 0\\ 0& 2& 1& 0& 1& 0\\ 0& 0& 2& 0& 0& 0\\ 0& 1& 0& 1& 0& 1\\ 1& 0& 0& 1& 1& 0\\ 0& 2& 0& 1& 0& 1\end{array}\right].\end{array}$$

Let $L_{\tilde{\mathcal{H}}}=L_{\tilde{\mathcal{G}}}=6$; then Assumption 2 is satisfied. Similarly as before, ${\mathrm{\Omega }}^T\left(t\right)\mathrm{\Omega }\left(t\right)\le I$; then Assumption 3 is satisfied. The function $\mu \left(t\right)$ and the delay parameter ${\vartheta }_k$ in Assumption 4 are set, respectively, as $\mu \left(t\right)=exp\left(0.2t\right),$${\vartheta }_k=t_k/40,$$k\in {\mathbb{Z}}_{+}.$ Let ${\xi }_1=0.2$, ${\varsigma }_1=12$, ${\sigma }_1=1$, ${\sigma }_2=0.5$, ${\sigma }_3=5$, ${\sigma }_4=0.1$, ${\nu }_1=3$, $a=1200$, $b_1=0.02$, $b_2=1.015$, $\gamma =10$, $\eta =3$, $T=0.001$, and $v=1$. Then, we can obtain ${\mu }_{\tilde{p}}=1.0002$, ${\mu }_{\tilde{q}}=1.8221$, ${\mu }_1=1.2214$, and ${\mu }_2=1.2214$. Through the proof process of Corollary 3, Assumption 4 is satisfied.

To make the remaining conditions in Corollary 3 hold true, the following feasible solutions are obtained by using the Matlab LMI toolbox:

$$\begin{array}{c}\hfill \mathcal{R}=\left[\begin{array}{cc}4.8563& 0\\ 0& 8.2438\end{array}\right],Q=\left[\begin{array}{cc}0.72& 0\\ 0.81& 0.68\end{array}\right].\end{array}$$

Then, the control gain matrix Θ is set as

$$\begin{array}{c}\hfill \mathrm{\Theta }=\left[\begin{array}{cc}0.1483& 0.1668\\ 0& 0.0825\end{array}\right].\end{array}$$

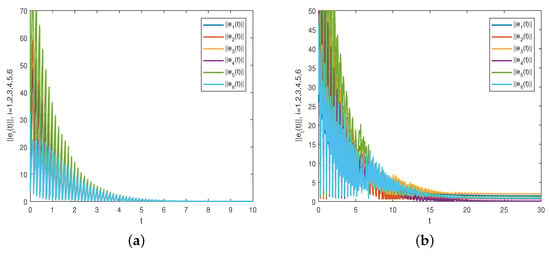
First, the conditions of Corollary 3 are satisfied by validation. Then, in Figure 3a, it can be observed that the state trajectories of $\parallel e_i\left(t\right)\parallel$ under the useful matrix Θ converge to 0, which means that CNs (20) and (21) have achieved synchronization. On the other hand, Figure 3b is a display of the non-synchronization situation between CNs (20) and (21) through plotting the state trajectories of $\parallel e_i\left(t\right)\parallel$. The reason is that the value of the control matrix is changed to ${\mathrm{\Theta }}^{*}=\mathrm{\Theta }-0.2I$ so that the conditions of Corollary 3 are no longer met. Furthermore, synchronization is not achieved with the time evolution of $\parallel e_i\left(t\right)\parallel$ not converged to 0.

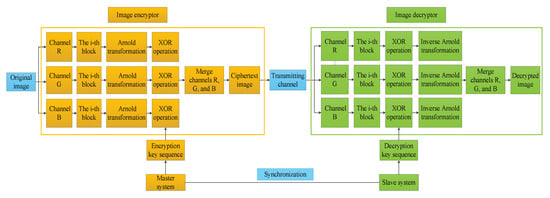
Next, network synchronization will be used for image encryption and decryption. A flowchart of the image encryption and decryption algorithm is shown in Figure 4. This scheme divides digital color images into three two-dimensional matrices by image channel. Divide each two-dimensional matrix into several sub-blocks and perform the Arnold transformation on pixel positions within each sub-block. Then, create a key using the sequence generated by the chaotic system, and encrypt each sub-block by the key. Finally, merge each of the three channels to obtain a color encrypted image.

Let the colored digital image $\mathcal{I}$ with size $\mathcal{M}\times \mathcal{N}$ be the image to be encrypted. The encryption steps are as follows:

Step 1: Divide $\mathcal{I}$ into three two-dimensional matrices, ${\mathcal{I}}_1$, ${\mathcal{I}}_2$, and ${\mathcal{I}}_3$, corresponding to channels R, G, and B, respectively.

Step 2: To enhance the universality of the algorithm, pad the three matrices ${\mathcal{I}}_1$, ${\mathcal{I}}_2$, and ${\mathcal{I}}_3$ with values 0 so that their dimensions meet Equation (23).

$$\left\{\begin{array}{c}\mathrm{mod}\left({\mathcal{M}}^{\prime },\sqcap \right)=0;\hfill \\ \mathrm{mod}({\mathcal{N}}^{\prime },\sqcap )=0.\hfill \end{array}\right.$$

(23)

Here, $\sqcap$ is the block size. The dimensions of the zero-padded image are ${\mathcal{M}}^{\prime }$ and ${\mathcal{N}}^{\prime }$. According to Equation (23), the matrices ${\mathcal{I}}_1$, ${\mathcal{I}}_2$, and ${\mathcal{I}}_3$ can be evenly divided into blocks of size $\sqcap \times \sqcap$. Therefore, each two-dimensional matrix can be divided into $\overline{n}={\mathcal{M}}^{\prime }\times {\mathcal{N}}^{\prime }/{\sqcap }^2$ blocks after padding.

Step 3: The spatial position of image pixels can be changed by the discrete Arnold transformation, which is a two-dimensional reversible mapping and is often used as a permutation method in the image encryption field. Taking ${\mathcal{I}}_1$ as an example, perform the discrete Arnold transformation on the position coordinates of the pixels in the image, that is,

$$\begin{array}{c}\hfill \left[\begin{array}{c}{i}_x^{\prime }\\ i_y^{\prime }\end{array}\right]={\mathcal{A}}^{n^{\prime }}\left[\begin{array}{c}{i}_x\\ i_y\end{array}\right](\mathrm{mod}\sqcap ),\mathcal{A}=\left[\begin{array}{cc}1& \tilde{a}\\ \tilde{b}& \tilde{a}\tilde{b}+1\end{array}\right]\\ \hfill \end{array}$$

(24)

where $\mathcal{A}$ is the transformation matrix, and $\tilde{a},\tilde{b}\in R$, $n^{\prime }$ represents the number of iterations. ${\left(\begin{array}{c}{i}_x,i_y\end{array}\right)}^T$ is the pixel coordinate in the i-th block of ${\mathcal{I}}_1$. Let ${\mathcal{I}}_R$ be the image after the Arnold transformation, and ${\left(\begin{array}{c}{i}_x^{\prime },i_y^{\prime }\end{array}\right)}^T$ is the coordinate of the corresponding pixel in the i-th block of ${\mathcal{I}}_R$. Similarly, by performing the Arnold transformation on the pixel coordinates in ${\mathcal{I}}_2$ and ${\mathcal{I}}_3$, the images ${\mathcal{I}}_G$ and ${\mathcal{I}}_B$ can be obtained with changed pixel coordinates, respectively.

Step 4: Assume that two chaotic sequences generated by the chaotic system in the encryptor are as follows:

$$X_1=({\tilde{x}}_1\left(1\right),{\tilde{x}}_1\left(2\right),\cdots ,{\tilde{x}}_1\left(\widehat{n}\right))$$

(25)

where $\widehat{n}={\sqcap }^2$, and the encrypted key sequence is calculated as

$$Key\left(\tilde{n}\right)=\mathrm{mod}(floor(X_1\left(\tilde{n}\right)\times {10}^{\overline{r}}),256)$$

(26)

where $\overline{r}$ is an adjustable integer, and $\tilde{n}=1,2,\cdots$, $\widehat{n}$.

Step 5: After Arnold transformation, each of the pixel values in ${\mathcal{I}}_R$, ${\mathcal{I}}_G$, and ${\mathcal{I}}_B$ ranges from 0 to 255, which can be represented by an 8-bit binary number. By performing a bitwise XOR operation between the pixel values of each sub-block of ${\mathcal{I}}_R$, ${\mathcal{I}}_G$ and ${\mathcal{I}}_B$ with $Key\left(\tilde{n}\right)$, we can obtain the encrypted image in channels R, G, and B, respectively, as follows:

$$\left\{\begin{array}{c}{\mathcal{I}}_{R1}^i(i_x^{\prime },i_y^{\prime })={\mathcal{I}}_R^i(i_x^{\prime },i_y^{\prime })\oplus Key\left(\tilde{n}\right)\hfill \\ {\mathcal{I}}_{G1}^i(i_x^{\prime },i_y^{\prime })={\mathcal{I}}_G^i(i_x^{\prime },i_y^{\prime })\oplus Key\left(\tilde{n}\right)\hfill \\ {\mathcal{I}}_{B1}^i(i_x^{\prime },i_y^{\prime })={\mathcal{I}}_B^i(i_x^{\prime },i_y^{\prime })\oplus Key\left(\tilde{n}\right)\hfill \end{array}\right.$$

(27)

where ⊕ denotes the XOR operation, and ${\mathcal{I}}_{R1}^i$, ${\mathcal{I}}_{G1}^i$, and ${\mathcal{I}}_{B1}^i$ denote the i-th block of images ${\mathcal{I}}_{R1}$, ${\mathcal{I}}_{G1}$, and ${\mathcal{I}}_{B1}$, respectively.

Step 6: The encrypted images from the three channels are merged to obtain the final encrypted image called ${\mathcal{I}}_E$.

The decryption process involves performing the reverse operation on the encrypted image, which is completely opposite to the encryption process. The image decryption process is as follows:

Step 1: Divide ${\mathcal{I}}_E$ into three two-dimensional matrices, referred to as ${\tilde{\mathcal{I}}}_1$, ${\tilde{\mathcal{I}}}_2$, and ${\tilde{\mathcal{I}}}_3$, which correspond to channels R, G, and B, respectively.

Step 2: The decrypted chaotic sequence generated by the chaotic system in the decryptor is as follows:

$$Y_1=({\tilde{y}}_1\left(1\right),{\tilde{y}}_1\left(2\right),\cdots ,{\tilde{y}}_1\left(\widehat{n}\right)).$$

(28)

Additionally, the decrypted key sequence is calculated as

$$Key1\left(\tilde{n}\right)=\mathrm{mod}(floor(Y_1\left(\tilde{n}\right)\times {10}^{\overline{r}}),256)$$

(29)

where $\overline{r}$ is an adjustable integer, and $\tilde{n}=1,2,\cdots$, $\widehat{n}$.

Step 3: Decrypt the encrypted images of three channels using the key sequence $Key1\left(\tilde{n}\right)$ as follows:

$$\left\{\begin{array}{c}{\mathcal{I}}_{R2}^i(i_x^{\prime },i_y^{\prime })={\tilde{\mathcal{I}}}_1^i(i_x^{\prime },i_y^{\prime })\oplus Key1\left(\tilde{n}\right)\hfill \\ {\mathcal{I}}_{G2}^i(i_x^{\prime },i_y^{\prime })={\tilde{\mathcal{I}}}_2^i(i_x^{\prime },i_y^{\prime })\oplus Key1\left(\tilde{n}\right)\hfill \\ {\mathcal{I}}_{B2}^i(i_x^{\prime },i_y^{\prime })={\tilde{\mathcal{I}}}_3^i(i_x^{\prime },i_y^{\prime })\oplus Key1\left(\tilde{n}\right)\hfill \end{array}\right.$$

(30)

where ${\tilde{\mathcal{I}}}_1^i$, ${\tilde{\mathcal{I}}}_2^i$, and ${\tilde{\mathcal{I}}}_3^i$ are the i-th block of images ${\tilde{\mathcal{I}}}_1$, ${\tilde{\mathcal{I}}}_2$, and ${\tilde{\mathcal{I}}}_3$, respectively. ${\mathcal{I}}_{R2}$, ${\mathcal{I}}_{G2}$, and ${\mathcal{I}}_{B2}$ denote the decrypted images of the channels R, G, and B in the first stage, respectively. ${\mathcal{I}}_{R2}^i$, ${\mathcal{I}}_{G2}^i$, and ${\mathcal{I}}_{B2}^i$ are the i-th block of images ${\mathcal{I}}_{R2}$, ${\mathcal{I}}_{G2}$, and ${\mathcal{I}}_{B2}$, respectively.

Step 4: The position coordinates of the pixels in the images ${\mathcal{I}}_{R2}$, ${\mathcal{I}}_{G2}$, and ${\mathcal{I}}_{B2}$ are carried out by the inverse Arnold transformation as follows:

$$\begin{array}{c}\hfill \left[\begin{array}{c}{i}_x\\ i_y\end{array}\right]={\mathcal{A}}^{-n^{\prime }}\left[\begin{array}{c}{i}_x^{\prime }\\ i_y^{\prime }\end{array}\right]\left(\begin{array}{cc}\mathrm{mod}& \sqcap \end{array}\right),{\mathcal{A}}^{-1}=\left[\begin{array}{cc}\tilde{a}\tilde{b}+1& -\tilde{a}\\ -\tilde{b}& 1\end{array}\right]\\ \hfill \end{array}$$

(31)

where ${\mathcal{A}}^{-1}$ denotes the inverse transformation matrix, $\tilde{a},\tilde{b}\in R$, $n^{\prime }$ represents the number of iterations, and ${\left(\begin{array}{c}{i}_x^{\prime },i_y^{\prime }\end{array}\right)}^T$ denotes the pixel’s position coordinate of the i-th block in the images ${\mathcal{I}}_{R2}$, ${\mathcal{I}}_{G2}$, and ${\mathcal{I}}_{B2}$. Let ${\tilde{\mathcal{I}}}_R$, ${\tilde{\mathcal{I}}}_G$, and ${\tilde{\mathcal{I}}}_B$ be the decrypted images after the inverse Arnold transformation in channels R, G, and B, respectively. ${\left(\begin{array}{c}{i}_x,i_y\end{array}\right)}^T$ denotes the position coordinate of the pixel in the i-th block of the images ${\tilde{\mathcal{I}}}_R$, ${\tilde{\mathcal{I}}}_G$, and ${\tilde{\mathcal{I}}}_B$.

Step 5: Remove the zero pixels of the images ${\tilde{\mathcal{I}}}_R$, ${\tilde{\mathcal{I}}}_G$, and ${\tilde{\mathcal{I}}}_B$ padded during the encryption process; then the results are referred to as ${\tilde{\mathcal{I}}}_{R1}$, ${\tilde{\mathcal{I}}}_{G1}$, and ${\tilde{\mathcal{I}}}_{B1}$, respectively.

Step 6: By merging three channels of the decrypted images ${\tilde{\mathcal{I}}}_{R1}$, ${\tilde{\mathcal{I}}}_{G1}$, and ${\tilde{\mathcal{I}}}_{B1}$, we obtain the final decrypted image called ${\mathcal{I}}_D$.

Remark 7.

The decryption process must use exactly the same key as the encryption process to obtain the correct decrypted image. In other words, the response system and the driving system must be synchronized so that the chaotic sequences generated by the encryption and decryption ends are the same. Since the encryption key and the decryption key are identical, the decrypted image is indistinguishable from the original image.

Use a $512\times 512\times 3$ color digital image “Parrot” as the image to be encrypted, as shown in Figure 5a. The encryption and decryption algorithm is simulated and verified on the Matlab R2024a platform in the Windows 10 operating system environment. Figure 5a–c show the original image, ciphertext image, and correctly decrypted image, respectively. From a visual perspective, the ciphertext image does not have a correlation with the original image.

(1)

Histogram analysis.

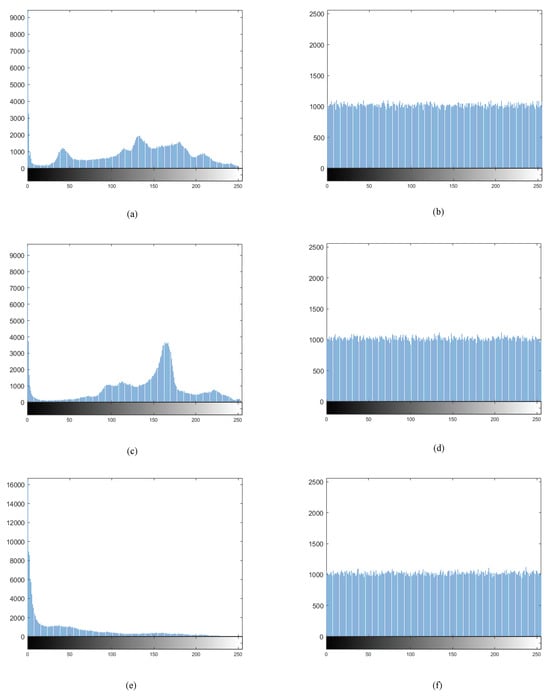
In the image histogram, the horizontal axis ranges from 0 to 255, and the vertical axis represents the frequency of the value of each pixel appearing in the entire image. Therefore, the distribution of pixel values in the image can be reflected through the histogram. Figure 6a–f show the histograms of the R, G, and B channels of the image before and after encryption, respectively. From Figure 6, it can be seen that the histograms of channels R, G, and B in the original image fluctuate, while the histograms of the three channels in the ciphertext image are evenly distributed and have pseudo-random properties, which can hide the statistical characteristics of the original image and effectively resist histogram-based statistical attacks on images.

(2)

Correlation of pixel values between adjacent positions.

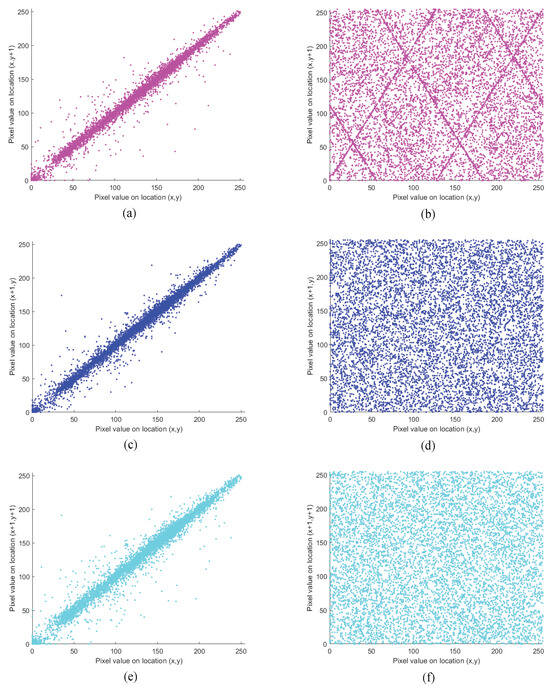
The ability of an image to resist attacks is inversely proportional to the correlation between its adjacent pixel values. To test the resistance of the image to attacks, 5000 pairs of adjacent pixels are randomly selected in the horizontal, vertical, and diagonal directions for correlation analysis. To compare the correlation of pixel values between adjacent positions of images before and after encryption more intuitively, a point graph is drawn in Figure 7, with the horizontal axis representing the pixel values of random point positions and the vertical axis representing the pixel values of adjacent positions.

Figure 7a–b show the correlation coefficient plots of pixel values between adjacent positions of images before and after encryption in the horizontal direction, respectively. Figure 7c–d show the correlation coefficient plots of pixel values between adjacent positions of images before and after encryption in the vertical direction, respectively. Figure 7e–f show the correlation coefficient plots of pixel values between adjacent positions of images before and after encryption in the diagonal direction, respectively. It can be seen that the pixel values of adjacent positions in all three directions of the original image have strong correlation, and the distribution of pixel points shows a linear relationship. The correlation between adjacent pixel values in all three directions in the ciphertext image is almost zero, and the distribution of pixel points is completely random. Therefore, there is no correlation between the distribution of adjacent pixel values in the ciphertext image, whether in horizontal, vertical, or diagonal directions. This encryption algorithm completely changes the pixel values and shuffles pixel positions of the original image, and thus has strong resistance to attacks.

(3)

Information entropy analysis.

Information entropy represents the degree of confusion of information in a system; therefore, in an image, information entropy represents the confusion degree of the pixel values in the image. It is defined as follows:

$$H\left(x\right)=-\sum _{i=0}^{255}\tilde{p}\left(x_i\right){\log }_2\tilde{p}\left(x_i\right)$$

(32)

where $\tilde{p}\left(x_i\right)$ represents the proportion of pixel value $x_i$ in the image. According to Equation (32), the maximum theoretical information entropy of an image is 8. After calculation, the information entropy of the original image is $6.3918$, and the information entropy of the ciphertext image is $7.9998$. It can be seen that the information entropy of the ciphertext image is very close to the maximum theoretical information entropy value, indicating that the degree of chaos in the ciphertext image is approaching the theoretical limit. Therefore, this encryption algorithm can effectively resist attacks based on image information entropy.

(4)

Analysis of key capacity.

A good encryption algorithm requires a sufficiently large key space, generally not less than $2^{128}$. In this scheme, the size of the key space is simply estimated as

$$\tilde{\mathrm{\Omega }}={\left(100\times {10}^{\tilde{\mathrm{x}}}\right)}^{3\tilde{N}}$$

(33)

where $\tilde{N}$ denotes the number of nodes in the network and $\tilde{N}=6$ in the experiment. $\tilde{\mathrm{x}}$ is a positive integer related to the precision of computer floating-point numbers, with a value of 14. It can be obtained that the key space of the proposed scheme is much larger than $2^{128}$, which can effectively resist brute-force attacks.

5. Conclusions

With the purpose of achieving $\mu$-synchronization for the proposed CNs, our work studies the $\mu$-synchronization task for CNs subjected to uncertain inner couplings, unbounded time delays, and external disturbances. For the CNs studied, there is no need for the coupling topology to satisfy the zero-row-sum condition, allowing for the application of the network more widespread. The three types of time delays are unbounded, which makes the model and results better applied to real engineering scenarios, such as image encryption. Several milder sufficient conditions are gained utilizing the new hybrid pulse control technique, under which the considered CNs can reach $\mu$-synchronization. To sum up, we adopt the hybrid pulse controller containing both the error feedback information and the pulse control factor to make the proposed CNs achieve $\mu$-synchronization by the Lyapunov method. In the future, one field of focus will be the finite-time synchronization of fuzzy CNs with high-order topologies via adaptive event-triggering impulsive control.