1. Introduction
The subject of unitary subsemigroups has been recognized as being connected to the issue of whether semigroup amalgams can be embedded, following Howie’s foundational research in [
1]. This has been extended to almost unitary subsemigroups, again by Howie [
2], regarding the embeddability of semigroup amalgams. Renshaw [
3] further applied Howie’s work to quasi unitary subsemigroups. Al Subaiei and Renshaw [
4] generalized it to posemigroups and established various connections with flatness properties and amalgamation in pomonoids. N. Alam and N. M. Khan (see [
5,
6]) used the technique of semigroup dominions and obtained results concerning the embeddability of special semigroup amalgams for almost unitary and quasi unitary semigroups, respectively. In this work, we will generalize their findings in [
5,
6] to the category of pomonoids, exploring new properties and implications within this wider category.
A monoid
S is called a partially ordered monoid, or a pomonoid, if it is equipped with a partial-order relation ≤ that is compatible with the binary operation on
S.
Among the most natural examples of pomonoids are
and
, where both pomonoids are equipped with the natural order. A mapping
, where
S and
T are pomonoids, is referred to as a pomonoid morphism if
f is a monoid morphism that is also monotone, i.e.,
implies
. A pomonoid morphism
is said to be an epimorphism (epi for short) if, whenever
are pomonoid morphisms, such that
, it implies that
. It is a well-known fact that every surjective morphism is an epimorphism in any category, but in the category of pomonoids, the converse does not hold. In the category of pomonoids, the natural embedding
i of
into
, where both pomonoids are equipped with the natural order, is an epimorphism.
J. R. Isbell in [
7] introduced the notion of dominion and related it to epimorphism. In the category of semigroups, due to the famous Isbell’s zigzag theorem, this notion has been helpful for the investigation of epimorphism-related problems (see [
8,
9]). The systematic study of epimorphism and dominions has been initiated by N. Sohail [
10] and B. Al Subaie [
11]. N. Sohail [
12] obtained the analog of Isbell’s zigzag theorem for pomonoids. Ahanger, Shah and Khan [
13] successfully extended many of the classical results of N. M. Khan [
14] and P. M. Higgins [
15] in the category of posemigroups using the zigzag theorem.
Let
U be a subpomonoid of a pomonoid
S and
. When for all pomonoids
T and all pomonoid morphisms
we have that
and then, we say that
d is dominated by
U. The
dominion of
U in
S is the set of all elements of
S dominated by
U and it is denoted by
. One can easily prove that
. If
, we conclude that
U is closed in
S, and
U is said to be absolutely closed if
for every pomonoid
S that contains
U as a subpomonoid. For a subpomonoid
U of a pomonoid
S, let
denote the monoid dominion of
U in
S. One can easily observe that
. Therefore, if
U is closed in
S as a pomonoid, then it is also closed in
S as a monoid.
We call the triple
a pomonoid amalgam if it consists of a pomonoid
U (referred to as the core of the amalgam), a family of pomonoids
, as well as a set of order embeddings
for each
. An amalgam is said to be weakly embeddable (resp. poembeddable) in a pomonoid
Z whenever there are pomonoid monomorphisms (resp. order embeddings)
such that
for every
. Furthermore, the amalgam is strongly embeddable (resp. poembeddable) in
Z when
. Whenever there exists an order isomorphism
such that
, then we refer to the pomonoid amalgam
as a special amalgam. It is evident from [
16] that a pomonoid amalgam is (weakly, strongly) embeddable (resp. poembeddable) in a pomonoid if and only if it is naturally (weakly, strongly) embeddable (resp. poembeddable) in its free product.
The following result establishes the relation between pomonoid amalgams and dominions of Pomonoids.
Theorem 1 ([
11], Theorem 4.1.1)
. Let and be the natural maps from and , respectively, into the free product of the ordered amalgam . Also, let U be a subpomonoid of pomonoids and , and let be an order isomorphism. Then, Thus, we can conclude that the special pomonoid amalgam is strongly poembeddable if and only if U is closed in S.
The characterization of posemigroup dominion established by Sohail and Tart [
17] is known as the zigzag theorem for posemigroups and is described as follows.
Theorem 2 ([
17], Theorem 5)
. Let U be a subpomonoid of a pomonoid S. Then, if and only if orwhere, The inequalities outlined above are referred to as zigzag in
S over
U with value
d. The first scheme of the zigzag inequalities (
1) produces
This means that
Similarly, the second scheme (
2) of the zigzag inequalities produces
whence
2. Epimorphisms–Amalgams and Quasi Po-Unitary Pomonoids
This section will examine the relationship between quasi po-unitary pomonoids and the embeddability of special pomonoid amalgams. We have established that when U is quasi po-unitary in S, the special pomonoid amalgam is strongly poembeddable. In fact, this relation has been demonstrated for the unordered case.
Theorem 3 ([
6])
. Let U be a quasi unitary submonoid of a monoid S, and then U is closed in S. In the category of pomonoids (see [
4,
11]), unitary properties have been extended to various types of unitary structures, leading to a refined order relation. Let
U be a subpomonoid of a pomonoid
S. Then, the following can be stated:
- 1
U is upper strongly left po-unitary (USLPU) in S if ;
- 2
U is lower strongly left po-unitary (LSLPU) in S if ;
- 3
U is strongly left po-unitary (SLPU) in S if or ;
- 4
U is left po-unitary (LPU) in S if ;
- 5
U is left unitary (LU) in S if .
where and . Next, we further extend these properties to quasi po-unitary-type properties.
Let U be the subpomonoid of a pomonoid S. Let us assume that there is a -morphism such that and . We say as follows:
- 6
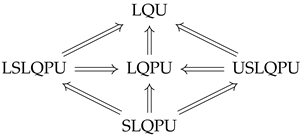
U is upper strongly left quasi po-unitary (USLQPU) in S if ;
- 7
U is lower strongly left quasi po-unitary (LSLQPU) in S if ;
- 8
U is strongly left quasi po-unitary (SLQPU) in S if or ;
- 9
U is left quasi po-unitary (LQPU) in S if ;
- 10
U is left quasi unitary (LQU) in S if .
Versions for these conditions for the right-hand and both sides are defined in a comparable way. The two-sided version is equivalent to both the left-handed and right-handed versions.
The following diagram indicates the implications among these classes of semigroups.
Further; if
U is any of the above subpomonoids of a pomonoid
S with
as a
-morphism; then for any
,
Therefore, for every
and
, we have
Theorem 4. Let U be a subpomonoid of a pomonoid S. The subpomonoid U is closed in S whenever U is an LQPU in S.
Proof. Let
U be a subpomonoid of a pomonoid
S such that
U is LQPU in
S. Take any
. By Theorem 2,
d has zigzag inequalities of the type (
1) and (
2). From the left columns in schemes (
1) and (
2), respectively, we have
Therefore,
Therefore,
Continuing in this fashion, we have
And so, by using Equation (
6) and the zigzag inequalities (
1), we obtain
Therefore,
Once again,
So,
Continuing in this fashion, we have
Finally, by using Equation (
6), zigzag inequalities (
2), and Equation (
5), we obtain
As
and
U is LQPU in
S, we obtain that all of
Now,
Hence,
, as required. □
In a dual manner, we can establish the following.
Theorem 5. Let U be a subpomonoid of a pomonoid S. If U is RQPU in S, then U is closed in S.
A subpomonoid U of a pomonoid S is quasi po-unitary (QPU) in S if it is both LQPU and RQPU in S.
The following results are now immediate.
Corollary 1. A quasi po-unitary subpomonoid U of a pomonoid S is closed in S.
Corollary 2. Let U be a subpomonoid of a pomonoid S. If U is either SLQPU, LSLQPU, or USLQPU in S, then it is closed in S.
Dually, we may prove the following.
Corollary 3. Let U be a subpomonoid of a pomonoid S. If U is either SRQPU, LSRQPU, or USRQPU in S, then it is closed in S.
From Theorem 1 and Corollary 1, we can conclude the following.
Corollary 4. The special pomonoid amalgam with a QPU core U is strongly poembeddable.
3. Epimorphisms–Amalgams and Almost Po-Unitary Pomonoids
This section explores the connection between almost po-unitary pomonoids and the poembeddability of special pomonoid amalgams. We have demonstrated that when U is almost po-unitary in S, the special pomonoid amalgam is strongly poembeddable. Moreover, this relationship has been established for the unordered case.
Theorem 6 ([
5])
. Let U be a submonoid of a monoid S. The submonoid U is closed in S whenever U is almost-unitary in S. Let S be a pomonoid and be the maps. The map is called a left translation of S if the following conditions are satisfied:
- (ALPU1)
for all ;
- (ALPU2)
is monotone.
In contrast, the map is referred to as a right translation if the following conditions are satisfied:
- (ALPU3)
for all ;
- (ALPU4)
is monotone.
A left translation and a right translation are called linked if for every , the following applies:
- (ALPU5)
,
and the pair is called a bitranslation of S.
Let U be a nonempty subset of the pomonoid S. The subset U is called an almost left po-unitary (ALPU) in S whenever there exist mappings (called associated mappings) that satisfy the following:
- (ALPU6)
is called a bitranslation of S;
- (ALPU7)
(i.e., commutes with );
- (ALPU8)
and ;
- (ALPU9)
;
- (ALPU10)
U is left po-unitary in .
Dually, we can define an almost right po-unitary subset of S. A subset U of S is said to be almost po-unitary in S if it is both ALPU and ARPU in S.
As in the unordered case, we have the following (see Lemma 4.7 in [
3]).
Lemma 1. Let U be the ALPU subset of a pomonoid S. Then, U is LQPU.
Lemma 2. Let U be the ALPU subset of a pomonoid S. Then, is a subpomonoid of S containing U.
Proof. Clearly,
and so
. Let
, then
that is,
, as required. □
In view of Lemma 2 condition (ALPU10), the definition of ALPU makes sense.
Theorem 7. Let U be a subpomonoid of a pomonoid S. If U is ALPU in S, then U is closed in S.
Proof. Let
U be a subpomonoid of a pomonoid
S such that
U is ALPU in
S. Take any
. By Theorem 2,
d has zigzag inequalities of the type (
2). Therefore, we have
Therefore,
Next, we have
Thus, we have
Continuing in this fashion, we have
Also,
We obtain the inequality
And
This gives the inequality
Continuing like this, we have
Finally, we have
Therefore, we obtain the inequality
Since
U is LPU in
, it follows that all of
and
are in
U.
Now,
Thus,
and, so
. Since
, it follows that
as required. □
Conversely, we can demonstrate the following.
Theorem 8. Let U be a subpomonoid of a pomonoid S. If U is ARPU in S, then it is closed in S.
Thus, the next result is immediate.
Corollary 5. Let U be a subpomonoid of a pomonoid S. If U is APU in S, then it is closed in S.
From Theorem 1 and Corollary 5, we can conclude the following.
Corollary 6. The special pomonoid amalgam with an APU core U is strongly poembeddable.