Estimation for Longitudinal Varying Coefficient Partially Nonlinear Models Based on QR Decomposition

Abstract

To address the estimation efficiency issues arising from multicollinearity and longitudinal data correlation in the varying coefficient partially nonlinear models (VCPNLM), a method based on QR decomposition and quadratic inference function (QIF) is proposed to obtain the orthogonality estimation of parameter components and varying coefficient functions. QR decomposition eliminates the pathology of the design matrix, and combines the adaptive weighting of the relevant structures within the group by QIF to effectively capture the complex correlation structure of longitudinal data. The theoretical analysis proves the asymptotic nature of the estimator, and the efficiency of the estimation method proposed in this paper is verified by simulation experiments.

1. Introduction

In recent years, longitudinal data have attracted much attention due to their wide applications in domains like biomedicine, economics and social sciences. This kind of data results from repeatedly observing the same subject at various time intervals. As a result, multiple measurement results of the same subject exhibit temporal or spatial dependence, which makes the traditional independent and identically distributed assumption no longer applicable. To address this issue, the VCPNLM has become one of the research hotspots, as it combines the interpretability of parametric models with the flexibility of nonparametric models. Li and Mei [1] put forward a profile nonlinear least squares estimation approach to estimate the parameter vector and coefficient function vector of the VCPNLM, and further derived the asymptotic characteristics of the obtained estimators.

Important progress has been made in model estimation in existing studies. Yu et al. [2] constructed robust estimators for the partially linear additive model under functional data. Yan et al. [3] explored the empirical likelihood inference targeting the partially linear errors-in-variables model under longitudinal data. VCPNLM, based on mode regression, a robust two-stage method for estimation and variable selection, was proposed by Xiao and Liang [4]. Zhao et al. [5] put forward a new orthogonality-based empirical likelihood inference method through orthogonal estimation techniques and empirical likelihood inference methods, which is used to estimate the parametric and nonparametric components in a class of varying coefficient partially linear instrumental variable models for longitudinal data. Liang and Zeger [6] applied the generalized estimating equation to longitudinal data analysis for effective handling of its correlation issue. For the varying coefficient partially nonlinear quantile regression model under randomly left-censored data, Xu et al. [7] introduced a three-stage estimation weighting method. A comprehensive overview of longitudinal data analysis methods can be found in Diggle et al. [8].

The VCPNLM has received widespread attention in statistical research due to its flexibility in capturing dynamic relationships between variables and adaptability to complex data structures [4,6,7]. It integrates the advantages of varying coefficient models and partially nonlinear models, making it a powerful tool for practical applications such as biomedical research, economic forecasting, and environmental monitoring. However, the complexity of the model structure and the characteristics of real-world data pose great challenges to accurate parameter estimation, which motivates the need for further improvements in existing methods.

Despite the notable advancements mentioned above, significant challenges still exist in the existing methods for estimating the VCPNLM. For instance, the estimation of nonlinear parameters is easily disturbed by nonparametric components and longitudinal correlation structures, leading to reduced estimation efficiency; when there is multicollinearity among explanatory variables, the ill-posed nature of the design matrix will further decrease the stability of estimation. Such issues severely limit the performance and practicality of the model in practical applications.

To address the above issues, existing studies have proposed a variety of improved methods. For example, Qu et al. [9] used the QIF to advance the estimating equation, and this method maintains optimal performance even as the working correlation structure is misspecified. Bai et al. [10] applied the quadratic inference function to handle longitudinal data, and the results demonstrate that the proposed estimation method exhibits excellent asymptotic properties. For semiparametric varying coefficient partially linear models, Tian et al. [11] proposed penalized QIF. Schumaker [12] utilized B-spline basis functions to approximate the varying coefficient part, which improves the computational efficiency. For linear models with randomly missing responses, Wei et al. [13] introduced a model averaging approach. Jiang et al. [14] proposed an estimation method for the VCPNLM based on the exponential squared loss function. Xiao and Chen [15] advanced a procedure for local bias-corrected cross-sectional nonlinear least squares estimation. By adopting an orthogonality-projection method, Yang and Yang [16] developed smooth-threshold estimating equations for VCPNLM. Additional studies focusing on this model include Refs. [7,17,18,19]. These investigations address various data scenarios and model settings, offering targeted estimation methods and inference strategies to further supplement and optimize the research framework within this field.

This paper proposes an orthogonal estimation framework that integrates QR decomposition and the QIF. QR decomposition can effectively eliminate the ill-posed nature of the design matrix and improve numerical stability. The QIF method avoids the limitations of traditional generalized estimating equations by adaptively weighting the intra-group correlation structure, significantly enhancing estimation efficiency. This study not only provides a new theoretical tool for longitudinal data analysis but also offers a feasible solution to complex modeling problems in practical applications.

The structure of this paper is arranged as follows: Section 2 introduces the model specification and estimation method, including the specific implementation of QR decomposition and QIF; Section 3 addresses the asymptotic properties of the estimators; Section 4 verifies the superiority of the proposed method using simulation experiments; Appendix A contains the proof process of the key conclusions.

2. Models and Methods

Consider the VCPNLM introduced by Li and Mei [1]:

$$Y=X^T\alpha \left(U\right)+g\left(Z,\beta \right)+\epsilon ,$$

(1)

where $Y\in R$ is the response variable, $X\in R^p$, $U\in R$, and $Z\in R^r$ are covariates, $\alpha \left(U\right)={\left({\alpha }_1\left(U\right),{\alpha }_2\left(U\right),\dots ,{\alpha }_p\left(U\right)\right)}^T$ and ${\alpha }_k\left(U\right),k=1,2,\dots ,p$ are unknown smooth functions, $g(·,·)$ is a nonlinear function with a known form, $\beta ={\left({\beta }_1,{\beta }_2,\dots ,{\beta }_q\right)}^T$ denotes a q-dimensional unknown parameter vector, and $\epsilon$ is the model error with mean zero and variance ${\sigma }^2$.

2.1. Estimation of Parameter Vector

Considering the model (1) under longitudinal data, suppose the j-th observation of the i-th individual satisfies

$$\begin{array}{c}{Y}_{ij}=X_{ij}^T\alpha \left(U_{ij}\right)+g\left(Z_{ij},\beta \right)+{\epsilon }_{ij},i=1,2,\dots ,n,j=1,2,\dots ,n_i,\end{array}$$

(2)

among them, ${\epsilon }_{ij}$ has a mean of zero, and $X_{ij}\in R^p,Z_{ij}\in R^r,U_{ij}$ are covariates.

Based on the idea of Schumaker [12], the unknown function ${\alpha }_k\left(·\right),k=1,2,\dots ,p$ is approximated through basis functions. The B-spline basis functions are denoted by the vector $B\left(u\right)={\left(B_1\left(u\right),B_2\left(u\right),\dots ,B_L\left(u\right)\right)}^T$. The dimension L is defined as $L=K+M$, where K and M represent the number of interior knots and the order of the spline, respectively. Then ${\alpha }_k\left(u\right)$ is approximately expressed as

$$\begin{array}{c}{\alpha }_k\left(u\right)\approx B{\left(u\right)}^T{\gamma }_k,k=1,2,\dots ,p;\end{array}$$

(3)

here, ${\gamma }_k={\left({\gamma }_{k1},{\gamma }_{k2},\dots ,{\gamma }_{kL}\right)}^T$ are the coefficient vector for the B-spline basis functions. model (2) is expressed as

$$Y_{ij}\approx W_{ij}^T\gamma +g\left(Z_{ij},\beta \right)+{\epsilon }_{ij},i=1,2,\dots ,n,j=1,2,\dots ,n_i,$$

(4)

define $W_{ij}=I_p\otimes B\left(U_{ij}\right)·X_{ij}$, where ⊗ is the Kronecker product, and let $\gamma ={\left({\gamma }_1^T,{\gamma }_2^T,\dots ,{\gamma }_p^T\right)}^T$, $Y_i={\left(Y_{i1},Y_{i2},\dots ,Y_{i{n}_i}\right)}^T$, $W_i={\left(W_{i1},W_{i2},\dots ,W_{i{n}_i}\right)}^T$, $g(Z_i,\beta )=\left(g(Z_{i1},\beta ),g(Z_{i2},\beta ),\dots ,\right.$ ${\left.g(Z_{i{n}_i},\beta )\right)}^T$, ${\epsilon }_i={\left({\epsilon }_{i1},{\epsilon }_{i2},\dots ,{\epsilon }_{i{n}_i}\right)}^T$. Then model (4) is expressed as

$$Y_i\approx W_i\gamma +g\left(Z_i,\beta \right)+{\epsilon }_i,i=1,2,\dots ,n.$$

(5)

We first state a fundamental result on the QR decomposition of full-column-rank matrices, which is essential for the subsequent steps.

Lemma 1

(QR Decomposition for Full-Column-Rank Matrices). Let $W\in {\mathbb{R}}^{m\times k}$ be a matrix with full column rank k. Then, an orthogonal matrix $Q\in {\mathbb{R}}^{m\times m}$ and an upper triangular matrix $R\in {\mathbb{R}}^{k\times k}$ exist, satisfying

$$W=Q\left(\begin{array}{c}R\\ \mathbf{0}\end{array}\right),$$

where $\mathbf{0}$ is a $(m-k)\times k$ zero matrix. Moreover, Q can be partitioned as $Q=(Q_1,Q_2)$, with $Q_1\in {\mathbb{R}}^{m\times k}$ and $Q_2\in {\mathbb{R}}^{m\times (m-k)}$, satisfying $Q_2^{\top }{Q}_1=\mathbf{0}$.

We now proceed with the derivation from Equation (5). Suppose that for all $i=1,2,\dots ,n$, the matrices $W_i$ have full column rank, their QR decomposition can be expressed as

$$\begin{array}{c}{W}_i=Q_i\left(\begin{array}{c}{R}_i\\ \mathbf{0}\end{array}\right),\end{array}i=1,2,\dots ,n,$$

(6)

where the definitions of $Q_i$, R, and $\mathbf{0}$ are the same as those in Lemma 1 above. The matrix $Q_i$ can be divided into two parts as $Q_i=\left(Q_{i1},Q_{i2}\right)$, where $Q_{i1}$ is a $n_i\times pL$ matrix and $Q_{i2}$ is a $n_i\times \left(n_i-pL\right)$ matrix. Substitute the decomposition of $Q_i$ into (6) to obtain $W_i=Q_{i1}{R}_i$, from the properties of orthogonal matrices, $Q_{i2}^T{Q}_{i1}=0$ can be derived, and then $Q_{i2}^T{W}_i=Q_{i2}^T{Q}_{i1}{R}_i=0$ is obtained. Multiplying both sides of Equation (5) by $Q_{i2}^T$, we get

$$Q_{i2}^T{Y}_i\approx Q_{i2}^{T}g\left(Z_i,\beta \right)+Q_{i2}^T{\epsilon }_i,i=1,2,\dots ,n.$$

(7)

Obviously, model (7) is a regression model containing only unknown parameters. Following Liang [6], the generalized estimating equation for $\beta$ can be formulated as

$$\sum _{i=1}^n{g}^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{V}_i^{-1}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))=0,$$

(8)

among them, $g^{\left(1\right)}(Z_i,\beta )={(g^{\left(1\right)}(Z_{i1},\beta ),\dots ,g^{\left(1\right)}(Z_{i{n}_i},\beta ))}^T$, $V_i=Q_{i2}^T{\mathsf{\Sigma }}_i{Q}_{i2}$, ${\mathsf{\Sigma }}_i$ is the covariance matrices of $Y_i$, and the structure of $V_i$ can also be expressed as $V_i=A_i^{{\displaystyle \frac{1}{2}}}R\left(\rho \right)A_i^{{\displaystyle \frac{1}{2}}}$ according to the method of Liang [6], where $A_i$ is a diagonal matrix, $R\left(\rho \right)$ is a working correlation matrix, and $\rho$ is a correlation parameter. Since a consistent estimator of $\rho$ is not always available in practice, we adopt the QIF method to approximate the working correlation matrix $R^{-1}\left(\rho \right)$ through several basis matrices, thereby avoiding directly specifying the correlation structure. Drawing on the classic specifications proposed by Qu et al. [9] and combined with the correlation structure characteristics of the data in this study, we select a set of basis matrices $M_1,M_2,\dots ,M_s$ with corresponding coefficients $a_1,a_2,\dots ,a_s$ that satisfy

$$R^{-1}\left(\rho \right)\approx a_1{M}_1+a_2{M}_2+\cdots +a_s{M}_s.$$

(9)

Substituting (9) into (8), we obtain

$$\sum _{i=1}^n{g}^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}(a_1{M}_1+\cdots +a_s{M}_s)A_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))=0.$$

(10)

Define the extended score function as follows:

$$G_n\left(\beta \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\eta }_i\left(\beta \right)\triangleq {\displaystyle \frac{1}{n}}\sum _{i=1}^n\left(\begin{array}{c}{g}^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}{M}_1{A}_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))\\ g^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}{M}_2{A}_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))\\ ⋮\\ g^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}{M}_s{A}_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))\end{array}\right).$$

(11)

Thus, the QIF for $\beta$ can be defined as

$$M_n\left(\beta \right)=G_n^T\left(\beta \right){\mathsf{\Phi }}_n^{-1}\left(\beta \right)G_n\left(\beta \right),$$

(12)

where ${\mathsf{\Phi }}_n\left(\beta \right)={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\eta }_i\left(\beta \right){\eta }_i^T\left(\beta \right)$, in this case, we obtain the estimator $\widehat{\beta }$ of $\beta$ by minimizing the objective function $M_n\left(\beta \right)$:

$$\widehat{\beta }=arg\underset{\beta }{min}{M}_n\left(\beta \right).$$

(13)

2.2. Estimation of the Coefficient Functions

The QIF effectively handles the correlation in longitudinal data and improves estimation efficiency by constructing a set of estimating equations. Therefore, after obtaining the initial estimates of the parameters $\beta$, we also use the QIF method to estimate the coefficient functions ${\alpha }_k\left(u\right),k=1,2,\dots ,p.$

Substitute the estimator of into Equation (5), resulting in

$${\tilde{Y}}_i\approx W_i\gamma +{\epsilon }_i,i=1,2,\dots ,n,$$

(14)

where ${\tilde{Y}}_i=Y_i-g_i\left(Z_i,\widehat{\beta }\right)$, assuming that the covariance matrix of ${\tilde{Y}}_i$ is ${\mathsf{\Psi }}_i$, and its structure is expressed following Liang [6] as ${\mathsf{\Psi }}_i=A_i^{{\displaystyle \frac{1}{2}}}R\left(\rho \right)A_i^{{\displaystyle \frac{1}{2}}}$, where $A_i$ and $R\left(\rho \right)$ are defined as in the previous subsection. Assuming $V_i$ is known, construct the estimating equation

$$\underset{i=1}{\sum ^n}{W}_i^T{\mathsf{\Psi }}_i^{-1}\left({\tilde{Y}}_i-W_i\gamma \right)=0.$$

(15)

In practical applications, $V_i$ is usually unknown. Based on this, we still adopt the QIF method and use $M_1,M_2,\dots ,M_s$ to approximate $R_i^{-1}$, then we have

$$\underset{i=1}{\sum ^n}{W}_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}\left(a_1{M}_1+a_2{M}_2+\cdots +a_s{M}_s\right)A_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)=0.$$

(16)

Define the extended score function as follows:

$$G_n\left(\gamma \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\phi }_i\left(\gamma \right)\triangleq {\displaystyle \frac{1}{n}}\sum _{i=1}^n\left(\begin{array}{c}{W}_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}{M}_1{A}_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)\\ W_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}{M}_2{A}_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)\\ ⋮\\ W_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}{M}_s{A}_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)\end{array}\right).$$

(17)

Thus, the QIF for $\gamma$ is defined as follows:

$$Q_n\left(\gamma \right)=G_n^T\left(\gamma \right)C_n^{-1}\left(\gamma \right)G_n\left(\gamma \right),$$

(18)

where $C_n\left(\gamma \right)={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\phi }_i\left(\gamma \right){\phi }_i^T\left(\gamma \right)$. In this case, we obtain the estimator $\widehat{\gamma }$ of $\gamma$ by minimizing the objective function $Q_n\left(\gamma \right)$,

$$\widehat{\gamma }=argmin{Q}_n\left(\gamma \right).$$

(19)

Thus, the estimate of the coefficient function ${\alpha }_k\left(u\right)$ can be expressed as

$${\widehat{\alpha }}_k\left(u\right)\approx B{\left(u\right)}^T{\widehat{\gamma }}_k,k=1,2,\dots ,p,$$

(20)

where ${\widehat{\gamma }}_k$ is the component corresponding to the k-th coefficient function in $\widehat{\gamma }$.

3. Main Conclusions

This section studies the asymptotic properties of the estimators $\widehat{\beta }$ and ${\widehat{\alpha }}_k\left(u\right),$$k=1,2,\dots ,p$, assuming that ${\beta }_0$ and ${\alpha }_0(·)$ are the true values of $\beta$ and $\alpha (·)$, respectively, ${\gamma }_0$ is the true value of $\gamma$, and ${\alpha }_{k0}(·)$ and ${\gamma }_{k0}$ correspond to the k-th elements of ${\alpha }_0(·)$ and $\gamma$, respectively. First, we present some common regularity conditions in longitudinal data analysis as follows:

(C1)

The support $\mathsf{\Omega }$ of the random variable U is bounded, and its probability density function $f_u\left(·\right)$ has continuous second-order derivatives.

(C2)

The varying coefficient functions ${\alpha }_1\left(u\right),\dots ,{\alpha }_p\left(u\right)$ are continuously differentiable of order r on $\left[0,1\right]$, where $r>2$.

(C3)

For arbitrary Z, $g\left(Z,\beta \right)$ exhibits continuity with respect to $\beta$, and $g\left(Z,\beta \right)$ has continuous partial derivatives of order r.

(C4)

${sup}_i∥E\left({\epsilon }_i{\epsilon }_i^T\right)∥<\infty$ holds, and there exists some $\delta >0$ satisfying $E\left({∥{\epsilon }_i∥}^{2+\delta }\right)<\infty$.

(C5)

The covariates $X_{ij}$ and $Z_{ij}$ are assumed to satisfy the following conditions: $\underset{ij}{sup}E\left\{{∥X_{ij}∥}^4\right\}<\infty$, $\underset{ij}{sup}E\left\{{∥Z_{ij}∥}^4\right\}<\infty$, $i=1,2,\dots ,n,j=1,2,\dots ,n_i.$

(C6)

Let $t_1,\dots ,t_k$ be interior nodes on $\left[0,1\right]$. Furthermore, let $t_0=0,t_{k+1}=1,{\xi }_i=t_i-t_{i-1},$ then a constant $C_0$ exists such that:${\displaystyle \frac{max\left\{{\xi }_i\right\}}{min\left\{{\xi }_i\right\}}}\le C_0,max\left\{\left|{\xi }_{i+1}-{\xi }_i\right|\right\}=o\left(K^{-1}\right)$

(C7)

Define $P_{ik}=Q_{i2}{A}_i^{-\frac{1}{2}}{M}_k{A}_i^{-\frac{1}{2}}{Q}_{i2}^T$, then we have:

$${\displaystyle \frac{1}{n}}\sum _{i=1}^{n}E\left\{g^{\left(1\right)}{(Z_i,\beta )}^T{P}_{ik}{g}^{\left(1\right)}(Z_i,\beta )\right\}\stackrel{P}{\to }{D}_k,k=1,2,\dots ,s.$$

$${\displaystyle \frac{1}{n}}\sum _{i=1}^{n}E\left\{g^{\left(1\right)}{(Z_i,\beta )}^T{P}_{il}^T{V}_i{P}_{il}{g}^{\left(1\right)}(Z_i,\beta )\right\}\stackrel{P}{\to }{\mathsf{\Omega }}_{lk},l,k=1,2,\dots ,s.$$

Among them, $D_k$ and ${\mathsf{\Omega }}_{lk}$ are constant matrices, and $\stackrel{P}{\to }$ denotes convergence in probability. Define ${\mathsf{\Omega }}_0={\left({\mathsf{\Omega }}_{lk}\right)}_{ps\times ps}$ and ${\mathsf{\Gamma }}_0={(D_1^T,\dots ,D_s^T)}^T$, additionally, assume that ${\mathsf{\Omega }}_0$ and ${\mathsf{\Gamma }}_0^T{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0$ are both invertible.

It is noted that conditions (C1) to (C5) are common conditions in VCPNLM components, condition (C6) indicates that $t_0,\dots ,t_{k+1}$ is a uniform partition sequence over the interval $\left[0,1\right]$, and condition (C7) is used for subsequent proofs.

Theorem 1.

Under conditions (C1) to (C7), and when $n\to \infty$, thus

$$\sqrt{n}(\widehat{\beta }-{\beta }_0)\stackrel{L}{\to }N(0,\mathsf{\Sigma }),$$

where the matrix $\mathsf{\Sigma }={\left({\mathsf{\Gamma }}_0^T{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0\right)}^{-1}$, $\stackrel{L}{\to }$ denotes convergence in distribution.

Theorem 2.

Under conditions (C1) to (C7), the number of nodes $K=O\left(n^{\frac{1}{2r+1}}\right)$, and when $n\to \infty$, it follows that

$$∥{\widehat{\alpha }}_k\left(·\right)-{\alpha }_{k0}\left(·\right)∥=O_p\left(n^{-\frac{r}{2r+1}}\right),k=1,2,\dots ,p,$$

in which $∥·∥$ denotes the function’s $L_2$ norm.

4. Simulation Study

This section assesses the finite-sample performance of the proposed orthogonality estimation method based on QR decomposition and QIF in VCPNLM through a Monte Carlo simulation study. We define the following model:

$$Y=X^T\alpha \left(U\right)+g\left(Z,\beta \right)+\epsilon ,$$

among them, the covariates $X,Z={(Z_1,Z_2)}^T$ both follow normal distributions, $g(Z,\beta )$ is defined as $g(Z,\beta )={\beta }_1{Z}_1+{\beta }_{2}exp\left(Z_2\right)$, with the parameter vector $\beta ={({\beta }_1,{\beta }_2)}^T={(0.8,-0.5)}^T$. Additionally, $U\sim U(0,1)$, the coefficient function $\alpha \left(U\right)=sin\left(2\pi U\right)$, the error term $\epsilon$ follows an AR(1) process, and its structure is: ${\epsilon }_{i,j}=0.5{\epsilon }_{i,j-1}+v_{i,j}$, where $v_{i,j}\sim N(0,0.5\sqrt{1-{0.5}^2})$.

The sample size is set to $n=100,150,200$; for the i-th subject, the number of repeated measurements is $m_i\equiv 8$, and 1000 simulation runs are conducted for each case. The method combining QR decomposition and QIF proposed in this paper (OQIF) is compared with the profile nonlinear least squares method (PNLS) introduced by Li and Mei [1]. After sorting out,

Table 1. The bias and standard deviation of ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$ measured using distinct methods.

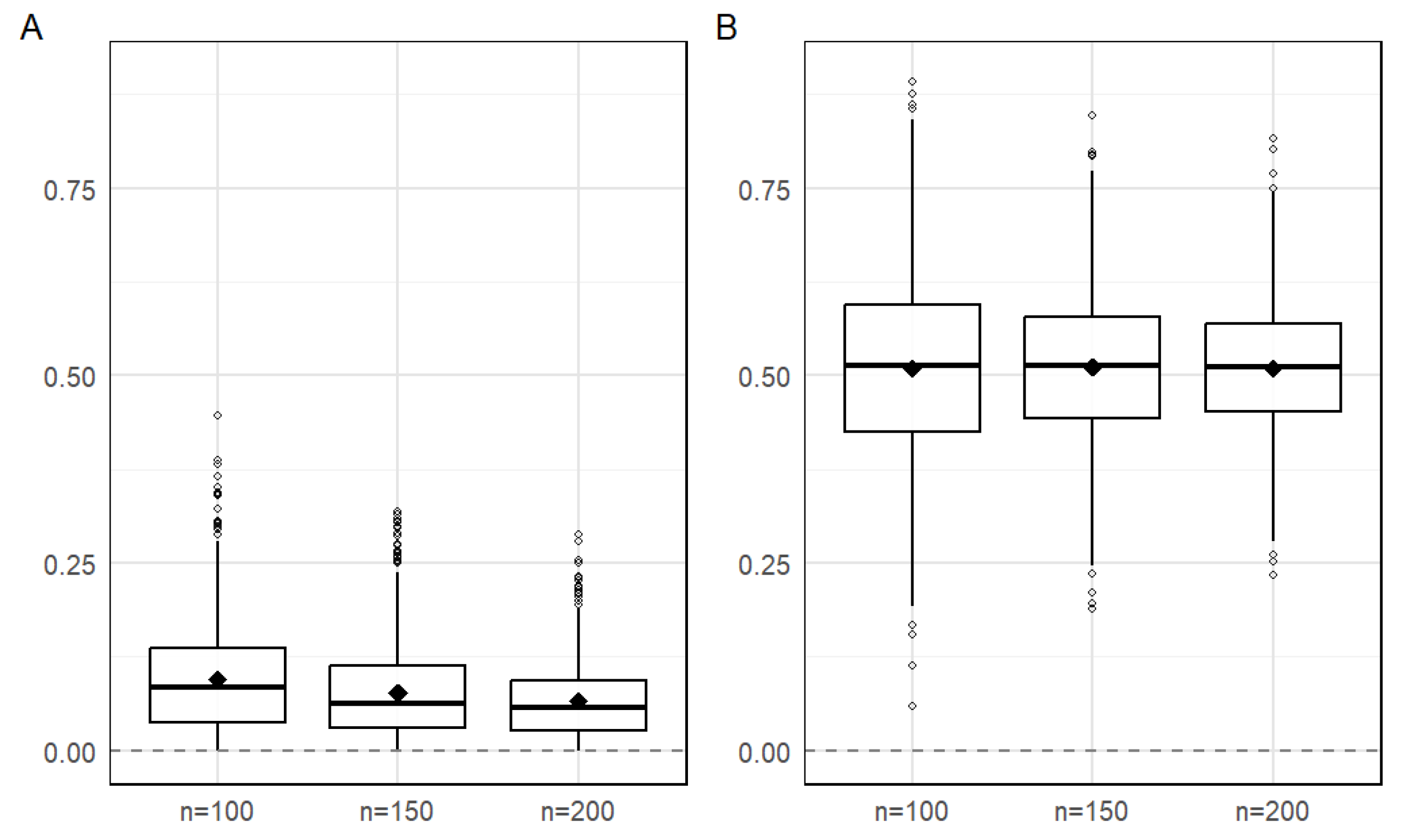
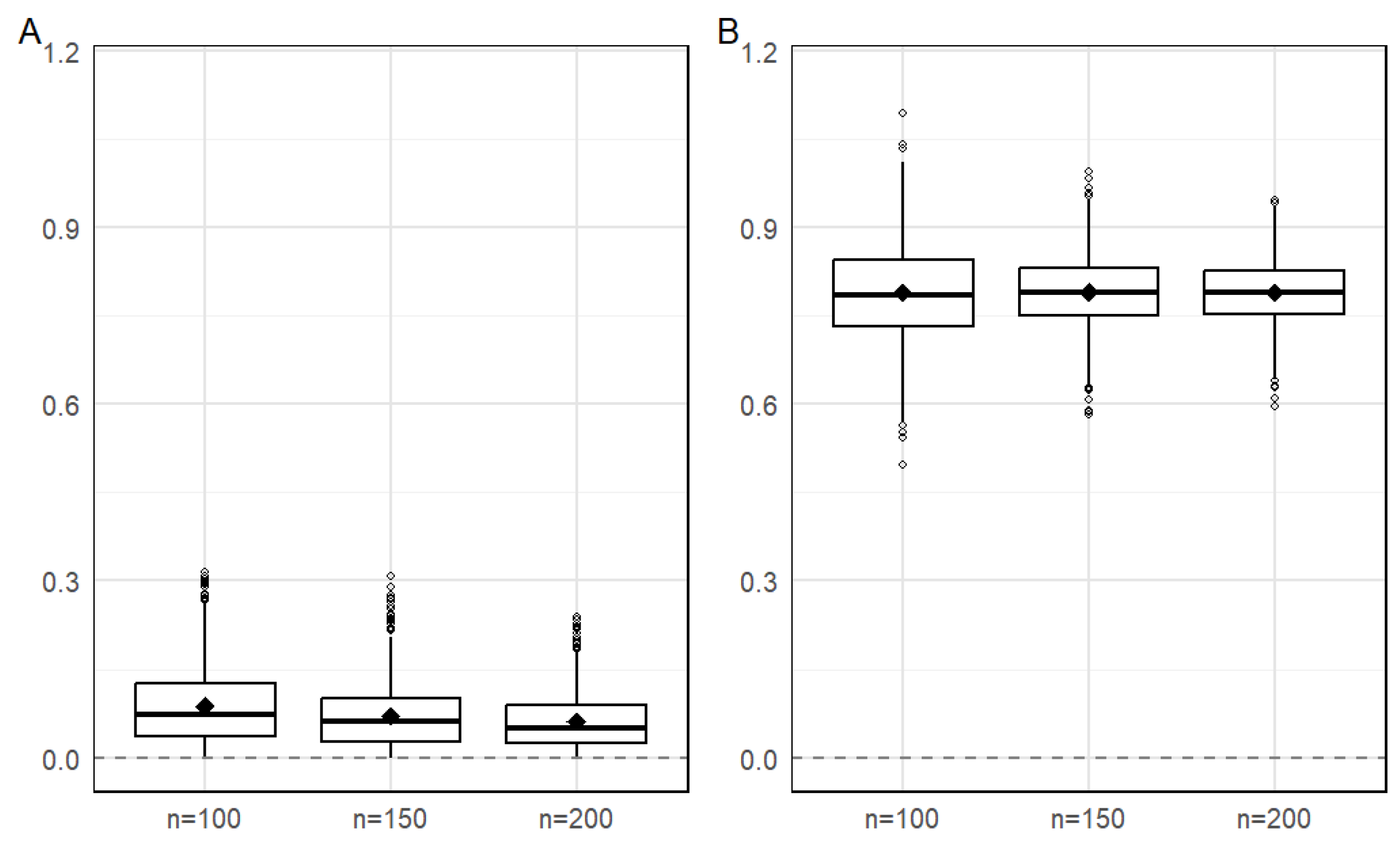
Method	Parameter	$\mathit{n}=100$		$\mathit{n}=150$		$\mathit{n}=200$
		Bias	SD	Bias	SD	Bias	SD
OQIF	${\widehat{\beta }}_1$	0.00257	0.02012	0.00123	0.01890	0.00079	0.01568
	${\widehat{\beta }}_2$	−0.00390	0.03890	−0.00235	0.03568	−0.00157	0.02946
PNLS	${\widehat{\beta }}_1$	0.01457	0.03012	0.01235	0.02789	0.00988	0.02346
	${\widehat{\beta }}_2$	−0.02789	0.05890	−0.02457	0.05235	−0.02012	0.04457

and

Table 2. Confidence interval length and coverage probability comparison.

Method	Parameter	$\mathit{n}=100$		$\mathit{n}=150$		$\mathit{n}=200$
		Length	Coverage	Length	Coverage	Length	Coverage
OQIF	${\widehat{\beta }}_1$	0.07671	0.943	0.07190	0.947	0.05971	0.951
	${\widehat{\beta }}_2$	0.14853	0.937	0.13551	0.941	0.11329	0.948
PNLS	${\widehat{\beta }}_1$	0.11329	0.911	0.10065	0.918	0.08541	0.925
	${\widehat{\beta }}_2$	0.20995	0.899	0.18773	0.905	0.15946	0.912

are obtained.

As illustrated in Table 1, increasing the sample size leads to a reduction in both bias and standard deviation for both methods. Notably, the OQIF method demonstrates smaller bias and standard deviation, indicating superior estimation accuracy. Although larger sample sizes generally enhance the precision of both methods, the OQIF method outperforms in terms of bias control.

The results in Table 2 show that the mean length for the confidence interval of the OQIF method is significantly shorter than that of the PNLS method, demonstrating higher estimation efficiency; the coverage rate of the OQIF method is closer to the ideal 95%, while although the coverage rate of the PNLS method has improved, it is still below 95%.

In conclusion, as the sample size grows from 100 to 200, the OQIF method demonstrates higher estimation accuracy and stronger robustness across all evaluation indicators. These trend analyses further confirm the theoretical advantages and practical application value of the OQIF method in handling nonlinear longitudinal data.

We further conducted 1000 simulations and plotted boxplots of the 1000 RMSE values for parameters ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$, as shown in Figure 1 and Figure 2. From the figures, we can observe the following: The RMSE values of ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$ for both methods decrease as the sample size increases; however, the OQIF method already exhibits good performance with a small sample size (n = 100), while the PNLS method requires a larger sample size to achieve similar accuracy. The boxplots of the OQIF method are more symmetric and compact, indicating that the distribution of its estimators is closer to the normal distribution and has better statistical properties. Additionally, the OQIF method has significantly fewer outliers than the PNLS method, demonstrating stronger robustness against abnormal data. This suggests that the overall performance of the OQIF method in parameter estimation is superior to that of the PNLS method, with more pronounced advantages especially in cases of finite samples.

Next, we estimate the coefficient function $\widehat{\alpha }\left(U\right)$, simulate 1000 times, and draw the box plot of the RMSE of $\widehat{\alpha }\left(U\right)$ under different samples, resulting in Figure 3 below.

As can be seen from the above boxplots, with the increase in sample size, the error distributions of both the OQIF method and the PNLS method become more concentrated, but the OQIF method has much smaller errors than the PNLS method. This further verifies the superiority of the OQIF method in the VCPNLM.