Simple Two-Sided Convergence Method for a Special Boundary Value Problem with Retarded Argument

Abstract

This study utilizes approximation techniques to address a boundary value problem involving a differential equation with a delayed argument. The problem is approached through analytical techniques by transforming it firstly into an equivalent integral equation. Specifically, we derive a Fredholm–Volterra integral equation that encapsulates the delayed behavior inherent in the original differential equation. The Fredholm operator in this equation features a degenerate kernel, which enables simplification and facilitates the construction of successive approximations. To solve this integral equation, we employ the two-sided convergence method, a powerful iterative technique that generates two sequences of approximate solutions—lower and upper bounds—that converge monotonically toward the exact solution. This method is particularly well-suited for problems with delayed arguments, as it ensures both stability and convergence under appropriate conditions on the kernel functions. The main objective of the study is to demonstrate the applicability and accuracy of the Simple Two-Sided Convergence Method for this class of boundary value problems. A numerical example is presented to illustrate the theoretical results, and the obtained approximations are compared with the exact analytical solution. All computations were carried out using Maple, ensuring precise numerical evaluation.

1. Introduction

Differential equations with retarded (or delayed) arguments constitute a significant subclass of functional differential equations, arising naturally in various fields such as population dynamics, control theory, electrical circuits, and engineering systems, where after-effect phenomena are observed. Historically, the study of such equations can be traced back to the 18th century, particularly to Euler’s investigation of curves that resemble their own evolutes a problem that inherently involves delayed relationships between variables. Despite their long-standing presence in mathematical modeling, a comprehensive and systematic theoretical framework for retarded differential equations only began to emerge in the 20th century.

The first comprehensive approach to this was presented in the dissertation referenced in [1]. Subsequently, the problem was addressed using the method of successive approximations, and the solutions were analyzed within the framework of positive linear systems through the use of positive operators [2]. One of the widely used analytical approaches for solving boundary value problems is the integral equation method [3,4]. For the boundary condition $x\left(T\right)=x_T$ in the problem (1) has been studied for $\tau \left(t\right)\equiv 0$ and $\tau \left(t\right)\equiv$ const in [5]. Additionally, in [6], some problems were approximated using the CAS Wavelet method. Although two-sided monotone iteration techniques have been employed in earlier studies, our approach introduces a new analytical framework by transforming the original boundary value problem into an equivalent Fredholm–Volterra integral equation with a degenerate kernel. This hybrid structure enables the construction of monotone lower and upper approximations under less restrictive smoothness conditions on the kernel functions, compared with classical methods applied to purely Fredholm or Volterra forms. Moreover, the proposed Simple Two-Sided Convergence Method provides a direct convergence proof that relies on the monotonicity and continuity properties of both operators simultaneously. In contrast to previously developed iterative methods, such as the modified two-sided and monotone iterative approaches, our study introduces a simplified analytical structure described below. The main novelty of the proposed Simple Two-Sided Convergence Method lies in its analytical formulation based on transforming the delayed boundary value problem into an equivalent Fredholm–Volterra integral equation with a degenerate kernel. Unlike classical monotone iteration or upper and lower solution methods, the present approach simultaneously exploits the monotonicity properties of both Fredholm and Volterra operators within a unified convergence framework. This hybrid structure enables the method to achieve convergence under weaker smoothness and regularity assumptions while still guaranteeing the existence and uniqueness of the solution. In the present study. We employ the Simple Two-Sided Convergence Method to solve problem (1). This technique transforms the original boundary value problem into an equivalent integral equation. Unlike the classical theory, which typically yields Fredholm-type integral equations, our approach leads to a Fredholm–Volterra integral equation with a degenerate kernel—offering a novel analytical structure for delayed argument problems.

Differential equations with delayed arguments appear in various applied fields such as control theory and population dynamics. The novelty of this study lies in constructing a Simple Two-Sided Convergence Method that integrates Fredholm and Volterra operators within a degenerate kernel framework. This design enables convergence under weaker smoothness conditions than previous two-sided monotone iteration approaches. Parallel to developments in delay differential equations, recent studies have focused on advanced approximation and operator-based techniques applicable to a broader class of functional problems. For instance, the use of Hardy averaging operators in variable exponent Sobolev spaces has been explored in [7], while [8] presents multi-soliton and breather wave solutions based on the linear superposition principle. Additionally, optimal boundary control strategies for complex systems, such as the Schrödinger equation, have been proposed in [9,10]. These contributions, though not exclusively centered on delay equations, reflect a growing interdisciplinary interest in applying functional analysis, operator theory, and control methods to boundary value problems with nonlocal or delayed structures. They also reinforce the analytical foundation upon which the Simple Two-Sided Convergence Method can be further developed.

Foundational works by Hale [11] and Elsgolts [12] provided the essential groundwork for the theory of functional differential equations with deviating arguments. Krasnoselskii’s research on positive linear systems [13] significantly influenced the numerical treatment of such equations. A broad spectrum of studies has addressed delay differential boundary value problems from both theoretical and computational perspectives. Linear cases were examined in [14], while [15,16] introduced analytical and numerical approaches for more general retarded systems. Recent developments include advanced numerical methods presented in [17,18,19,20,21,22]. Maly and Jafari [23] offered problem-specific approximations for delayed equations, and Smith [24] contributed the concept of monotonicity in dynamical systems, relevant to the stability analysis of solutions.

In this context, the current study focuses on a special class of boundary value problems defined by a second-order differential equation with a retarded argument. By transforming the original problem into an equivalent Fredholm–Volterra İntegral Equation and applying the Simple Two-Sided Convergence Method, we aim to obtain accurate approximations of the solution. This approach enables not only a rigorous analytical formulation but also an efficient numerical implementation. The results are compared with exact solutions to assess the reliability and performance of the method.

2. An Equivalent Integral Equation

A boundary value problem involving a delayed argument differential equation is of the form

$$\begin{gathered} x^{″}\left(t\right)+a\left(t\right)x\left(t-\tau \left(t\right)\right)=f\left(t\right), \left(0\le t\le T\right), \\ x\left(t\right)=\phi \left(t\right) \left({\lambda }_0\le t\le 0\right)\hspace{1em}x\left(T\right)=x\left(c\right)\left(0\le c\le T\right). \end{gathered}$$

(1)

where $a(t$)$\ge 0$, $f(t)\ge 0$ and $\tau \left(t\right)\ge 0$ $(0\le t\le T)$ and $\phi \left(t\right)$ $\left({\lambda }_0\le t\le 0\right)$.

To facilitate the application of analytical approximation methods, we first reformulate the boundary value problem (1) into an equivalent integral equation. This transformation provides a more tractable framework for the analysis and numerical solution of the original differential equation involving a retarded argument. In the problem (1) if we take $\lambda \left(t\right)=t-\tau \left(t\right)$ then $t_0\in \left[0,T\right]$ is a point located at the left side of $T$ such that conditions $\lambda \left(t_0\right)=0$ and $\lambda \left(t\right)\le 0 (0\le t\le t_0)$ are satisfied, where ${\lambda }_0={min}_{0\le t\le t_0}\lambda (t)$. We assume that $\lambda \left(t\right)$ is a nondecreasing function in the interval $\left[t_0,T\right]$ and the equation $\lambda \left(t\right)=\sigma$ has a differentiable continuous solution $t=\gamma (\sigma )$ for arbitrary $\sigma \in \left[0,\lambda \left(t\right)\right].$ It can be seen that if $x^{\ast }(t)$ is a solution of the boundary value problem (1) than $x^{\ast }(t)$ is also the solution of the equation:

$$\begin{array}{c}{x}^{\ast }\left(t\right)=\widehat{h}\left(t\right)+t{\int }_0^T{\displaystyle \frac{T-s}{T-c}}a\left(s\right)x(s-\tau (s))ds-t{\int }_0^c{\displaystyle \frac{c-s}{T-c}}a\left(s\right)x(s-\tau (s))ds\hfill \\ -{\int }_0^t\left(t-s\right)a\left(s\right)x\left(s-\tau \left(s\right)\right)ds.\hfill \end{array}$$

(2)

Here,

$$\widehat{h}\left(t\right)=\phi \left(0\right)-t{\int }_0^T{\displaystyle \frac{T-s}{T-c}}f\left(s\right)ds+t{\int }_0^c{\displaystyle \frac{c-s}{T-c}}f(s)ds+{\int }_0^t\left(t-s\right)f\left(s\right)ds.$$

Let $\sigma =s- \tau \left(s\right)$. Therefore Equation (2) can be written as follows:

$$\begin{gathered} x^{\ast }\left(t\right)=h\left(t\right)+t{\int }_0^{\lambda (T)}{\displaystyle \frac{T-\gamma \left(\sigma \right)}{T-c}}a\left(\gamma \left(\sigma \right)\right){\gamma }^{\prime }\left(\sigma \right)x\left(\sigma \right)d\sigma \\ -t{\int }_0^{\lambda (c)}{\displaystyle \frac{c-\gamma \left(\sigma \right)}{T-c}}a\left(\gamma \left(\sigma \right)\right){\gamma }^{\prime }\left(\sigma \right)x\left(\sigma \right)d\sigma \\ -{\int }_0^{\lambda (t)}\left(t-\gamma (\sigma )\right)a\left(\gamma (\sigma )\right){\gamma }^{\prime }\left(\sigma \right)x(\sigma )d\sigma , \end{gathered}$$

(3)

where

$$\begin{gathered} h\left(t\right)=\widehat{h}\left(t\right)+{\int }_{{\lambda }_0}^0{\displaystyle \frac{T-\gamma \left(\sigma \right)}{T-c}}a\left(\gamma \left(\sigma \right)\right){\gamma }^{\prime }\left(\sigma \right)\phi (\sigma )d\sigma -{\int }_{{\lambda }_0}^0{\displaystyle \frac{c-\gamma \left(\sigma \right)}{T-c}}a\left(\gamma \left(\sigma \right)\right){\gamma }^{\prime }\left(\sigma \right)\phi (\sigma )d\sigma \\ -{\int }_{{\lambda }_0}^0\left(t-\gamma (\sigma )\right)a\left(\gamma (\sigma )\right){\gamma }^{\prime }\left(\sigma \right)\phi (\sigma )d\sigma . \end{gathered}$$

(4)

Let us calculate

$$\begin{gathered} K_1\left(\sigma \right)={\displaystyle \frac{T-\gamma \left(\sigma \right)}{T-c}} a\left(\gamma \left(\sigma \right)\right) a\left(\gamma \left(\sigma \right)\right){\gamma }^{\prime }\left(\sigma \right), \\ {K}_2\left(\sigma \right)=-{\displaystyle \frac{c-\gamma \left(\sigma \right)}{T-c}} a\left(\gamma \left(\sigma \right)\right) a\left(\gamma \left(\sigma \right)\right){\gamma }^{\prime }\left(\sigma \right), \\ K\left(t,\sigma \right)=-(t-\gamma \left(\sigma \right))a\left(\gamma \left(\sigma \right)\right){\gamma }^{\prime }\left(\sigma \right), \\ {x}^{\ast }\left(t\right)=h\left(t\right)+t{\int }_0^{\lambda \left(T\right)}{K}_1\left(\sigma \right)x^{\ast }\left(\sigma \right)d\sigma +t{\int }_0^{\lambda \left(c\right)}{K}_2\left(\sigma \right)x^{\ast }\left(\sigma \right)d\sigma +{\int }_0^{\lambda \left(t\right)}K\left(t,\sigma \right)x^{\ast }\left(\sigma \right)d\sigma , \end{gathered}$$

(5)

or

$$x\left(t\right)=h\left(t\right)+t(F_{\lambda }^{T}x+F_{\lambda }^{c}x)+V_{\lambda }x,$$

(6)

where

$$\begin{gathered} F_{\lambda }^{T}x\equiv {\int }_0^{\lambda \left(T\right)}{K}_1\left(\sigma \right)x\left(\sigma \right)d\sigma \\ {F}_{\lambda }^{c}x\equiv {\int }_0^{\lambda \left(T\right)}{K}_2\left(\sigma \right)x\left(\sigma \right)d\sigma , \end{gathered}$$

is the Fredholm operator, and

$$V_{\lambda }x\equiv {\int }_0^{\lambda \left(t\right)}K\left(t,\sigma \right)x(\sigma )d\left(\sigma \right)$$

is the Volterra operator. Equation (6) is a Fredholm–Volterra integral equation, and it is equivalent to the problem (1). Importantly, this integral equation is equivalent to the original boundary value problem (1), and the solution of one directly yields the solution of the other.

3. Simple Two-Sided Convergence Method

In this section, we will consider the solution of the Fredholm–Volterra type integral Equation (6) with the improved Simple Two-Sided Convergence Method. Equation (6) is equivalent to Problem (1), defined in a more general form. Thanks to this equivalence, the approximate solution method that is known for integral equations can be directly applied to the original problem. The Simple Two-Sided Convergence Method provides a powerful tool by recognizing the possibility of lower and upper bounds of the solution separately, especially the existence and uniqueness of the solution. In addition, the monotonic convergence of the solution sequences and the fact that the solution remains within an arithmetically narrowing interval increase the numerical stability and robustness of the method. In order for the method to be applied successfully, it is important that the integral operators used have some monotonicity and continuous dependency properties.

Therefore, the properties of Fredholm and Volterra operators, which form the theoretical basis of the method, are as given. Suppose that the signs of the $\gamma \prime \left(t\right)$ function is fixed in the intervals $[0,\lambda (T)]$. Let $x\left(t\right)\ge 0 (0\le t\le T)$. Therefore the Fredholm operator $F_{\lambda }x$ is non-decreasing and the Volterra operator $V_{\lambda }x$ is non-increasing.

We construct the approximations for the Fredholm–Volterra integral equation related to Problem (1) using the following rule. Using the following approach, we aim to develop approximations for the Fredholm–Volterra integral Equation (6), which is equivalent to Problem (1). Let us choose the first approximations ${\underset{\_}{x}}_0\left(t\right)$ and ${\overline{x}}_0\left(t\right)$.

such that

$$\begin{gathered} {\underset{\_}{x}}_0\left(t\right)\le h\left(t\right)+t\left(F_{\lambda }^T{\underset{\_}{x}}_0+F_{\lambda }^c{\underset{\_}{x}}_0\right)+V_{\lambda }{\overline{x}}_0, \\ {\overline{x}}_0\left(t\right)\ge h\left(t\right)+t\left(F_{\lambda }^T{\overline{x}}_0+F_{\lambda }^c{\overline{x}}_0\right)+V_{\lambda }{\underset{\_}{x}}_0, \end{gathered}$$

(7)

and

$${\underset{\_}{x}}_0\left(t\right)\le {\overline{x}}_0\left(t\right).$$

(8)

The inequalities are satisfied. Next, let us get the approximations:

$$\begin{array}{c}{\underset{\_}{x}}_n\left(t\right)=h\left(t\right)+t(F_{\lambda }^T{\underset{\_}{x}}_{n-1}+F_{\lambda }^c{\underset{\_}{x}}_{n-1})+V_{\lambda }{\overline{x}}_{n-1},\hfill \\ {\overline{x}}_n\left(t\right)=h\left(t\right)+t(F_{\lambda }^T{\overline{x}}_{n-1}+F_{\lambda }^c{\overline{x}}_{n-1})+V_{\lambda }{\underset{\_}{x}}_{n-1}\hspace{1em}\left(n=\mathrm{1,2},\dots \right).\hfill \end{array}$$

(9)

Next, let us define the equations.

First, let us prove that the inequalities if

$${\underset{\_}{x}}_n\left(t\right)\le {\underset{\_}{x}}_{n+1}\left(t\right)\hspace{1em}\mathrm{ve}\hspace{1em}{\overline{x}}_n\left(t\right)\ge {\overline{x}}_{n+1}\left(t\right)\left(n=\mathrm{0,1},2,\dots \right)$$

(10)

and

$${\underset{\_}{x}}_n\left(t\right)\le {\overline{x}}_n\left(t\right)$$

(11)

are true. For this, let us apply the Inductive Proof Method. From (7) and (9), it is seen that, for $n=1$,

$${\underset{\_}{x}}_0\left(t\right)\le {\underset{\_}{x}}_1\left(t\right)\hspace{1em}\mathrm{ve}\hspace{1em}{\overline{x}}_0\left(t\right)\ge {\overline{x}}_1\left(t\right).$$

Let us assume that for $n-1$ için

$${\underset{\_}{x}}_{n-1}\left(t\right)\le {\underset{\_}{x}}_n\left(t\right)\hspace{1em}\mathrm{ve}\hspace{1em}{\overline{x}}_{n-1}\left(t\right)\ge {\overline{x}}_n\left(t\right).$$

If $F_{\lambda }^{T}x$, $F_{\lambda }^{c}x$ are increasing, ve $V_{\lambda }x$ is decreasing the operators

$$\begin{gathered} {\underset{\_}{x}}_n\left(t\right)\le h\left(t\right)+t\left(F_{\lambda }^T{\underset{\_}{x}}_n+F_{\lambda }^c{\underset{\_}{x}}_n\right)+V_{\lambda }{\overline{x}}_n={\underset{\_}{x}}_{n+1}\left(t\right), \\ {\overline{x}}_n\left(t\right)\ge h\left(t\right)+t\left(F_{\lambda }^T{\overline{x}}_n+F_{\lambda }^c{\overline{x}}_n\right)+V_{\lambda }{\underset{\_}{x}}_n={\overline{x}}_{n+1}\left(t\right). \end{gathered}$$

From the inequality,

$${\underset{\_}{x}}_n\left(t\right)\le {\underset{\_}{x}}_{n+1}\left(t\right)\hspace{1em}\mathrm{ve}\hspace{1em}{\overline{x}}_n\left(t\right)\ge {\overline{x}}_{n+1}\left(t\right)$$

(12)

is obtained. According to the inductive proof method, the inequality (12) is true for every $nϵ\mathbb{N}$ Now let us see the truth of (8).

For $n=0$, the truth of (11) is seen from (8). Let us assume that

$${\underset{\_}{x}}_n\left(t\right)\le {\overline{x}}_n\left(t\right),$$

where $F_{\lambda }x$ and $F_{\lambda }x$ are monotone operators and

$$\begin{gathered} {\underset{\_}{x}}_{n+1}\left(t\right)=h\left(t\right)+t\left(F_{\lambda }^T{\underset{\_}{x}}_n+F_{\lambda }^c{\underset{\_}{x}}_n\right)+V_{\lambda }{\overline{x}}_n, \\ \le h\left(t\right)+t\left(F_{\lambda }^T{\overline{x}}_n+F_{\lambda }^c{\overline{x}}_n\right)+V_{\lambda }{\underset{\_}{x}}_n={\overline{x}}_{n+1}\left(t\right) \end{gathered}$$

According to the inductive method, (11) is true for every $nϵ\mathbb{N}$.

As a result, it was found that the lower approximations increase monotonically, the upper approximations decrease monotonically, and the higher approximations remain bounded above by the upper approximations.

Before presenting the main theorem, we explicitly state the assumptions required for the convergence of the proposed method.

• The kernel functions $K\left(x,t\right)$ and $H\left(x,t\right)$ in the Fredholm and Volterra operators are continuous and bounded on $\left[\mathrm{0,1}\right]x\left[\mathrm{0,1}\right]$
• The delay function $\tau \left(t\right)$ is continuously differentiable and nondecreasing on $\left[\mathrm{0,1}\right]$, satisfying $(0\le \tau \left(t\right)t\le T)$.
• The right-hand side $f\left(x\right)$ is continuous on $\left[\mathrm{0,1}\right]$
• The kernel functions $K_1\left(x,t\right)$ and $K_2\left(x,t\right)$ are continuous and bounded over], and the $\left[a,b\right]$ delay function $\tau \left(t\right)$ is continuously differentiable, nondecreasing, and satisfies $\tau \left(t\right)\le t$. Under these mild assumptions, the Fredholm and Volterra operators are monotone and compact. Hence, the constructed approximation sequences converge both monotonically and uniformly in the supremum norm $C \left[\mathrm{0,1}\right]$. Convergence may fail only if the kernel loses boundedness or the delay function becomes non-monotone.

Under these conditions, the operators $F$ and $V$ defined in Equations (4) and (5) are monotone and compact. Hence, the successive approximations constructed in (9)–(11) are well-defined and remain within the closed convex cone determined by the initial bounds. These explicit assumptions ensure that all theoretical steps in the convergence analysis are transparent and reproducible.

The theorem below demonstrates that the approximations given in (9) converge to the solution of Problem (1) using the Simple Two-Sided Convergence Method.

Theorem 1. 

Let us assume that

$$q={\int }_0^{\lambda \left(T\right)}\left(\left|K_1\left(\sigma \right)\right|+\left|K\left(T,\sigma \right)\right|\right)d\left(\sigma \right)+{\int }_0^{\lambda \left(C\right)}\left|K_2\left(\sigma \right)\right|d\left(\sigma \right)<1.$$

Under these conditions, Problem (1) possesses a unique solution, which coincides with the limit of the lower and upper approximations defined by expressions (9). The convergence rate is specified by the formula below:

$$\Vert {\overline{x}}_n-{\underset{\_}{x}}_n\Vert \le q^n\Vert {\overline{x}}_0-{\underset{\_}{x}}_0\Vert .$$

Proof. 

From the explanations given above, it is seen that

$$\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }{\underset{\_}{x}}_n=x\left(t\right) \underset{\mathrm{n}\to \mathrm{\infty }}{\lim }{\overline{x}}_0=x\left(t\right).$$

When the successive approximations (9) are taken as limits for $n\to \infty$, it is concluded that the functions $\underset{\_}{x}\left(t\right)$ and $\overline{x}\left(t\right)$ are the solutions of problem (1).

Now, let us find the speed of convergence.

Difference ${\overline{x}}_n(t)-{\underset{\_}{x}}_n(t)$ from (9),

$${\overline{x}}_n\left(t\right)-{\underset{\_}{x}}_n\left(t\right)=t\left[F_{\lambda }^T\left({\overline{x}}_{n-1}-{\underset{\_}{x}}_{n-1}\right)+F_{\lambda }^c\left({\overline{x}}_{n-1}-{\underset{\_}{x}}_{n-1}\right)\right]-V_{\lambda }\left({\overline{x}}_{n-1}-{\underset{\_}{x}}_{n-1}\right),$$

is possible. From here, we get

$$\begin{gathered} \left|{\overline{x}}_n\left(t\right)-{\underset{\_}{x}}_n\left(t\right)\right|\le \left[{\int }_0^{\lambda \left(T\right)}\left|K_1\left(\sigma \right)\right|d\left(\sigma \right)+{\int }_0^{\lambda \left(C\right)}\left|K_2\left(\sigma \right)\right|d\left(\sigma \right)+{\int }_0^{\lambda \left(T\right)}\left|K\left(T,\sigma \right)\right|d\left(\sigma \right)\right]\left|\left|{\overline{x}}_{n-1}\left(t\right)-{\underset{\_}{x}}_{n-1}\left(t\right)\right|\right|, \\ \le \left[{\int }_0^{\lambda \left(T\right)}\left(\left|K_1\left(\sigma \right)\right|+\left|K\left(T,\sigma \right)\right|\right)d\left(\sigma \right)+{\int }_0^{\lambda \left(C\right)}\left|K_2\left(\sigma \right)\right|d\left(\sigma \right)\right]||{\overline{x}}_{n-1}\left(t\right)-{\underset{\_}{x}}_{n-1}\left(t\right)||. \end{gathered}$$

Due to the acceptance of $q<1$, we obtain

$$\left|{\overline{x}}_n\left(t\right)-{\underset{\_}{x}}_n\left(t\right)\right|\le q^n\Vert {\overline{x}}_0\left(t\right)-{\underset{\_}{x}}_0\left(t\right)\Vert .$$

In this framework, the two-sided approximation method, which is constructed by using the monotonicity and continuous dependence properties of the operators, shows that the solution not only exists but also converges uniquely and rapidly. This approach is both theoretically sound and reliable in practice, and is an effective tool especially in the numerical solution of mixed integral equations of the Fredholm–Volterra type. □

Example 1. 

Let us consider the boundary value problem:

$$\begin{gathered} {\mathit{x}}^{″}\left(\mathit{t}\right)+tx\left(t-\frac{1}{2}\sqrt{t}\right)=-2t^3+2t^{\frac{5}{2}}+\frac{5}{2}{t}^2-\frac{3}{2} t^{\frac{3}{2}}-4 \left(0\le t\le 1\right), \\ x\left(t\right)=0\hspace{1em}\left(-1/16\le t\le 0\right) , x\left(\frac{1}{2}\right)=x\left(1\right)\left(0\le \frac{1}{2}\le 1\right). \end{gathered}$$

(13)

This equation can be written as the Fredholm–Volterra integral equation:

$$\begin{gathered} x\left(t\right)=2.872933230t-2t^2-0.1714285714t^{{\displaystyle \frac{7}{2}}}+0.2083333333t^4+0.1269841270t^{{\displaystyle \frac{9}{2}}}-0.1t^5 \\ +{\displaystyle \frac{t}{8}}\underset{0}{\overset{1/2}{\int }}\left[3+4\sigma -16{\sigma }^2+{\displaystyle \frac{3+28\sigma -80{\sigma }^2}{\sqrt{1+16\sigma }}}\right]x\left(\sigma \right)d\sigma \\ -{\displaystyle \frac{t}{8}}\underset{0}{\overset{1/2-\sqrt{2}/4}{\int }}\left[1-4\sigma -16{\sigma }^2+{\displaystyle \frac{1+4\sigma -80{\sigma }^2}{\sqrt{1+16\sigma }}}\right]x\left(\sigma \right)d\sigma \\ -{\displaystyle \frac{1}{16}}\underset{0}{\overset{t-\sqrt{t}/2}{\int }}\left[\left(4t-1\right)+\left(16t-12\right)\sigma -16{\sigma }^2+{\displaystyle \frac{\left(4t-1\right)+(48t-20)\sigma -80{\sigma }^2}{\sqrt{1+16\sigma }}}\right]x\left(\sigma \right)d\sigma \end{gathered}$$

(14)

Let

$$\begin{gathered} h\left(t\right)=2.872933230t-2t^2-0.1714285714t^{{\displaystyle \frac{7}{2}}}+0.2083333333t^4+0.1269841270t^{{\displaystyle \frac{9}{2}}}-0.1t^5 \\ {K}_1\left(\sigma \right)=\frac{1}{8}\left[3+4\sigma -16{\sigma }^2+{\displaystyle \frac{3+28\sigma -80{\sigma }^2}{\sqrt{1+16\sigma }}}\right] \\ {K}_2\left(\sigma \right)=\frac{1}{8}\left[1-4\sigma -16{\sigma }^2+{\displaystyle \frac{1+4\sigma -80{\sigma }^2}{\sqrt{1+16\sigma }}}\right] \\ K\left(t,\sigma \right)=-{\displaystyle \frac{1}{16}}[\left(4t-1\right)+\left(16t-12\right)\sigma -16{\sigma }^2+{\displaystyle \frac{\left(4t-1\right)+(48t-20)\sigma -80{\sigma }^2}{\sqrt{1+16\sigma }}}] \end{gathered}$$

and

$$F_{\lambda }^{T}x\equiv {\int }_0^{1/2}{K}_1\left(\sigma \right)x\left(\sigma \right)d\sigma ,$$

$$F_{\lambda }^{c}x\equiv {\int }_0^{1/2-\sqrt{2}/4}{K}_2\left(\sigma \right)x\left(\sigma \right)d\sigma$$

$$V_{\lambda }x\equiv -{\int }_0^{t-{\displaystyle \frac{\sqrt{t}}{2}}}K\left(t,\sigma \right)x\left(\sigma \right)d\left(\sigma \right).$$

As a result, the integral Equation (14) can be expressed as

$$x\left(t\right)=h\left(t\right)+t{F}_{\lambda }^{T}x+t{F}_{\lambda }^{c}x+V_{\lambda }x,$$

and this equation is equivalent to problem (13). The analytical solution of Equation (13) is $x\left(t\right)=-2t^2+3t$.

$$q=0.11979<1$$

was found for this problem. This satisfies the condition $q<1$ from Theorem 1, ensuring convergence.

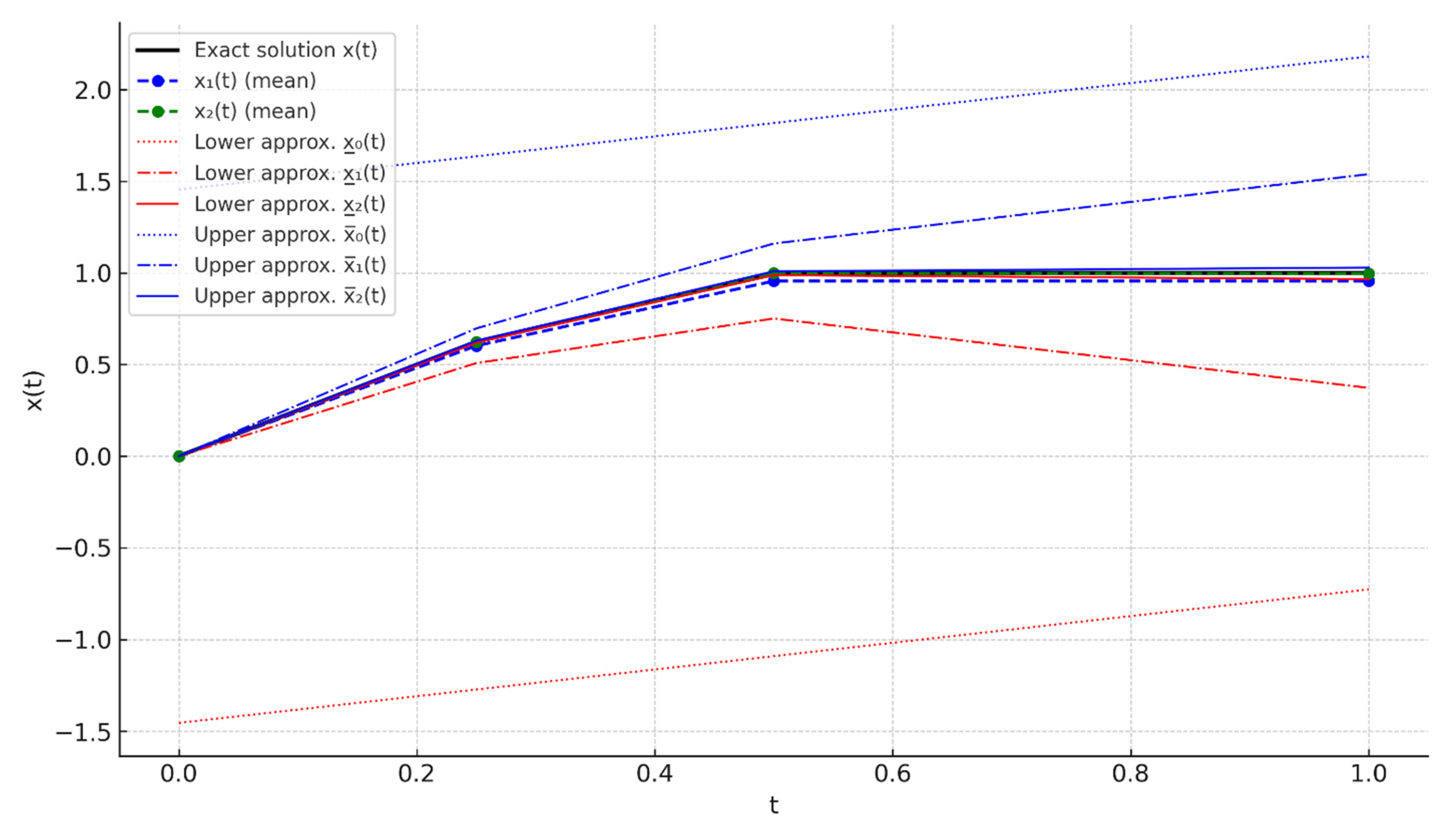
The second approximations were obtained by using the Two-Sided Convergence Method for some special values of the solution of this equation and for the inequalities ${\underset{\_}{x}}_i\left(t\right)\le {\underset{\_}{x}}_{i+1}\left(t\right)$, ${\overline{x}}_{i+1}\left(t\right)\le {\overline{x}}_i\left(t\right)$ and ${\underset{\_}{x}}_i\left(t\right)\le {\overline{x}}_i\left(t\right), (i=\mathrm{0,1})$.

Table 1. The monotonic behavior of the lower and upper approximations across iterations $n=0,1,2$.

${\mathit{t}}_{\mathit{i}}$	${\underset{\_}{\mathit{x}}}_0\left(\mathit{t}\right)$	${\underset{\_}{\mathit{x}}}_1\left(\mathit{t}\right)$	${\underset{\_}{\mathit{x}}}_2\left(\mathit{t}\right)$
0.000000	$-1.45455$	0	0
0.250000	$-1.27273$	0.50782	0.61905
0.500000	$-1.09091$	0.75120	0.98745
1.000000	$-0.72727$	0.37241	0.96635
${\mathit{t}}_{\mathit{i}}$	${\overline{\mathit{x}}}_0\left(\mathit{t}\right)$	${\overline{\mathit{x}}}_1\left(\mathit{t}\right)$	${\overline{\mathit{x}}}_2\left(\mathit{t}\right)$
0.000000	1.45455	0	0
0.250000	1.63636	0.69721	0.62943
0.500000	1.81818	1.16029	1.00872
1.000000	2.18182	1.53908	1.02925

shows the first approximations

$${\underset{\_}{x}}_0\left(t\right)={\displaystyle \frac{8}{11}}t-{\displaystyle \frac{16}{11}}, {\overline{x}}_0\left(t\right)={\displaystyle \frac{8}{11}}t-{\displaystyle \frac{16}{11}},$$

and the inequalities

$${\mathit{x}}_{\mathit{i}}\left(\mathbf{t}\right)={\displaystyle \frac{{\underset{\_}{x}}_i\left(t\right)+{\overline{\mathit{x}}}_{\mathit{i}}\left(\mathit{t}\right)}{2}}, (i=\mathrm{1,2})$$

are in

Table 2. The convergence rate and absolute errors for each iteration of the Simple Two-Sided Convergence Method.

${\mathit{t}}_{\mathit{i}}$	$\mathit{x}(\mathit{t})$	${\mathit{x}}_1({\mathit{t}}_{\mathit{i}})$	${\mathit{x}}_2({\mathit{t}}_{\mathit{i}})$	$\mathit{ϵ}\left({\mathit{t}}_{\mathit{i}}\right)$
0.000000	0.00	$0.00$	0.00000	0.00000
0.250000	$0.6250$	$0.60251$	0.62425	0.00075
0.500000	1.00	$0.95574$	0.99809	0.00191
1.000000	1.00	$0.95574$	0.99708	0.00292

.

The inequalities

$${\underset{\_}{x}}_i\left(t\right)\le {\underset{\_}{x}}_{i+1}\left(t\right), {\overline{x}}_{i+1}\left(t\right)\le {\overline{x}}_i\left(t\right) \mathrm{and} {\underset{\_}{x}}_i\left(t\right)\le {\overline{x}}_i\left(t\right), (i=\mathrm{0,1})$$

are shown in Table 1 for some special values, the first approximations being

$${\underset{\_}{x}}_0\left(t\right)={\displaystyle \frac{8}{11}}t-{\displaystyle \frac{16}{11}}, {\overline{x}}_0\left(t\right)={\displaystyle \frac{8}{11}}t-{\displaystyle \frac{16}{11}}.$$

In Table 2, the second approximations are obtained by using the Two-Side Convergence Method for the same values of the solution of the following equation:

$${\mathit{x}}_{\mathit{i}}\left(\mathbf{t}\right)={\displaystyle \frac{{\underset{\_}{x}}_i\left(t\right)+{\overline{\mathit{x}}}_{\mathit{i}}\left(\mathit{t}\right)}{2}}, \left(i=\mathrm{1,2}\right).$$

To strengthen the numerical validation, we extended the analysis by computing the convergence rate and absolute errors for each iteration of the Simple Two-Sided Convergence Method. For the numerical example given by Equation (13), the error norm was defined as

$$E_n={}_{t\in \left[\mathrm{0,1}\right]}{}^{max}\left|x\left(t\right)-{\displaystyle \frac{1}{2}}\left({\overline{x}}_n\left(t\right)-{\underset{\_}{x}}_n\left(t\right)\right)\right|,$$

which was evaluated for $(n=\mathrm{0,1},\mathrm{2,3})$. Numerical experiments, performed using Maple, validate the theoretical findings. The method exhibits robustness against small perturbations in τ(t)\tau(t)τ(t) and a(t)a(t)a(t), confirming stability and continuous dependence on input data. The results demonstrate that $E_n$ decreases geometrically with where $x\left(t\right)$ denotes the exact analytical solution, and ${\overline{x}}_n\left(t\right)$, ${\underset{\_}{x}}_n\left(t\right)$ represent the lower and upper approximations obtained at the nnn-th iteration. The computed results demonstrate that $E_n$ decreases monotonically and geometrically with respect to $n$, confirming the theoretical convergence stated in Theorem 1. In addition, since the Fredholm kernel in Equation (6) is degenerate, the corresponding numerical computations reduce to finite sums, resulting in minimal computational cost. Consequently, the proposed method ensures both high numerical efficiency and strong agreement with the analytical solution, as reflected in Table 1 and Table 2 and Figure 1.

Table 1 and Table 2 confirm the theoretical results:

• Table 1 illustrates the monotonic behavior of the lower and upper approximations across iterations $n=0,1,2$.
• Table 2 compares the midpoints $x_n\left(t\right)=1/2(x_n\left(t\right)+x_n\left(t\right))$ with the exact solution, highlighting the rapid convergence and small error $ϵ\left(t_i\right)$.

4. Conclusions

The main objective of this study was to apply the Simple Two-Sided Convergence Method to solve a boundary value problem involving a differential equation with a retarded (delayed) argument. To this end, the original differential equation was first transformed into an equivalent Fredholm–Volterra integral equation, which provided a more tractable framework for analysis and numerical computation. Following the formulation of the integral equation, the Simple Two-Sided Convergence Method was employed to generate sequences of lower and upper approximate solutions. These approximations converged monotonically towards the exact solution, demonstrating the method’s effectiveness and reliability. The computed approximations showed a strong agreement with the known analytical solution of Problem (1), confirming the accuracy and rapid convergence of the method. All symbolic and numerical computations were performed using Maple 2023 software, which significantly facilitated the implementation of the method and ensured the precision of the results. In conclusion, the findings of this study demonstrate that the Simple Two-Sided Convergence Method is a highly effective, reliable, and accurate approach for solving boundary value problems with delayed arguments. The method’s flexibility and strong convergence properties suggest that it can be successfully applied to a broader class of more complex problems with similar structures.

In this study, we proposed and analyzed a Simple Two-Sided Convergence Method for a boundary value problem with a retarded argument by reformulating it as a Fredholm–Volterra integral equation with a degenerate kernel. This formulation provides a unified framework that captures both delayed and integral effects simultaneously. The main theoretical contribution lies in proving monotone and rapid convergence of the constructed lower and upper approximations under explicitly stated operator conditions. In contrast, the present approach integrates both operator types, leading to stronger convergence guarantees and a simpler computational implementation. Compared with the previous two-sided monotone iteration approaches, the present technique achieves convergence under weaker regularity assumptions and offers greater computational efficiency due to the degenerate kernel structure. Consequently, the proposed approach can be considered a robust and general tool for solving delayed boundary value problems and may be extended to nonlinear, multi-dimensional, or optimal control formulations in future studies. The word “simple” in Simple Two-Sided Convergence Method reflects its computational efficiency—the degenerate kernel reduces integral operations to finite algebraic computations. The method guarantees monotone and uniform convergence under weaker assumptions. Future work will extend the approach to nonlinear delayed systems, multidimensional problems, and optimal control formulations.