A Trust-Enhancing Variant of the Binary Randomized Response Technique
Abstract
1. Introduction
2. Trust Enhancement in RRT Models
2.1. Previous Models
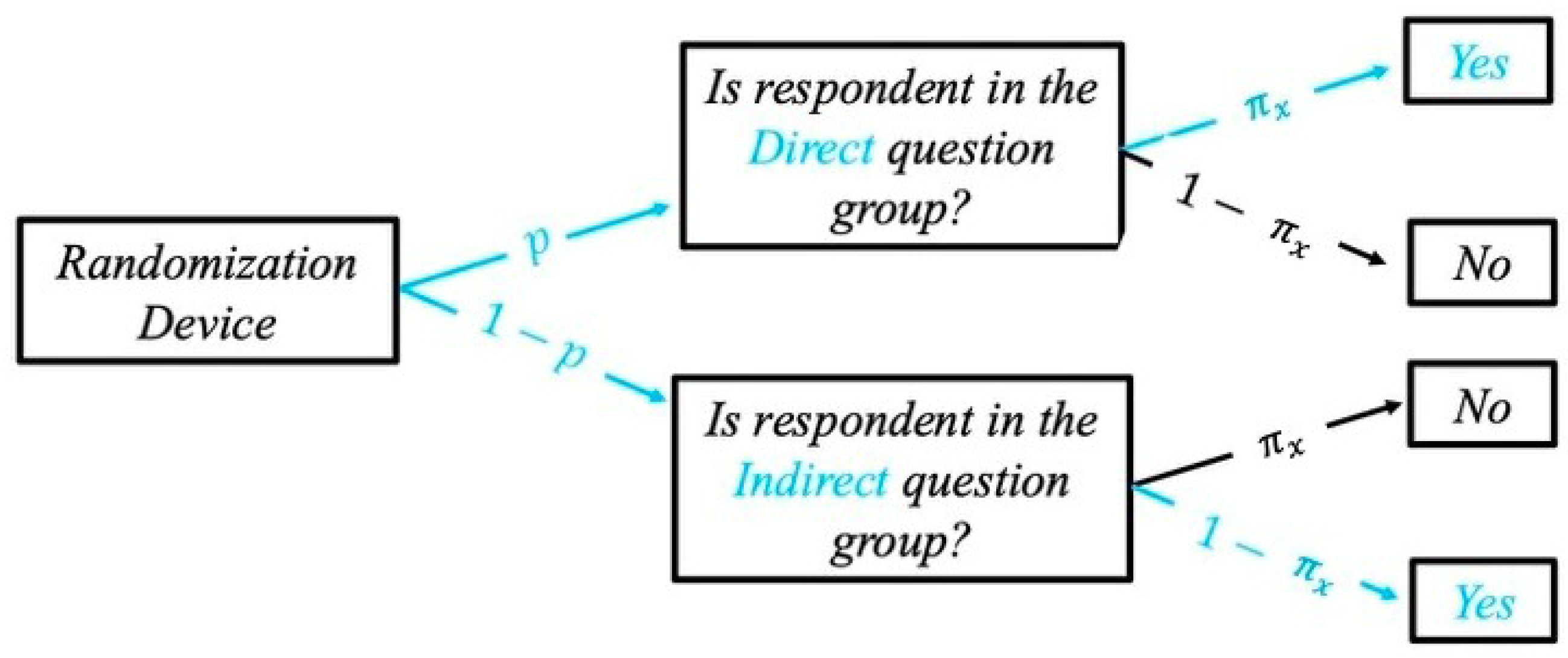
2.1.1. Warner’s Model
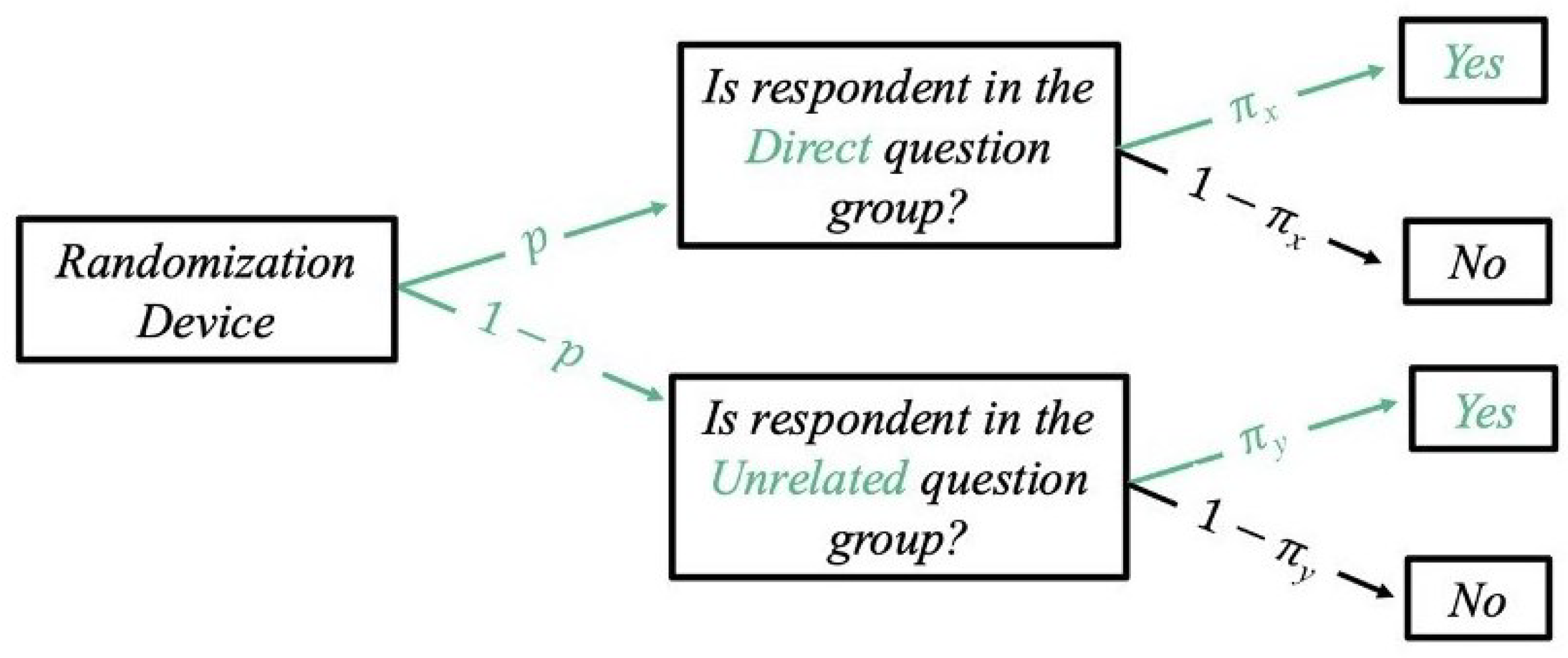
2.1.2. Greenberg’s Model
2.1.3. Lovig’s Mixture Model That Accounts for Untruthfulness
3. Proposed Trust-Enhanced Binary RRT Framework
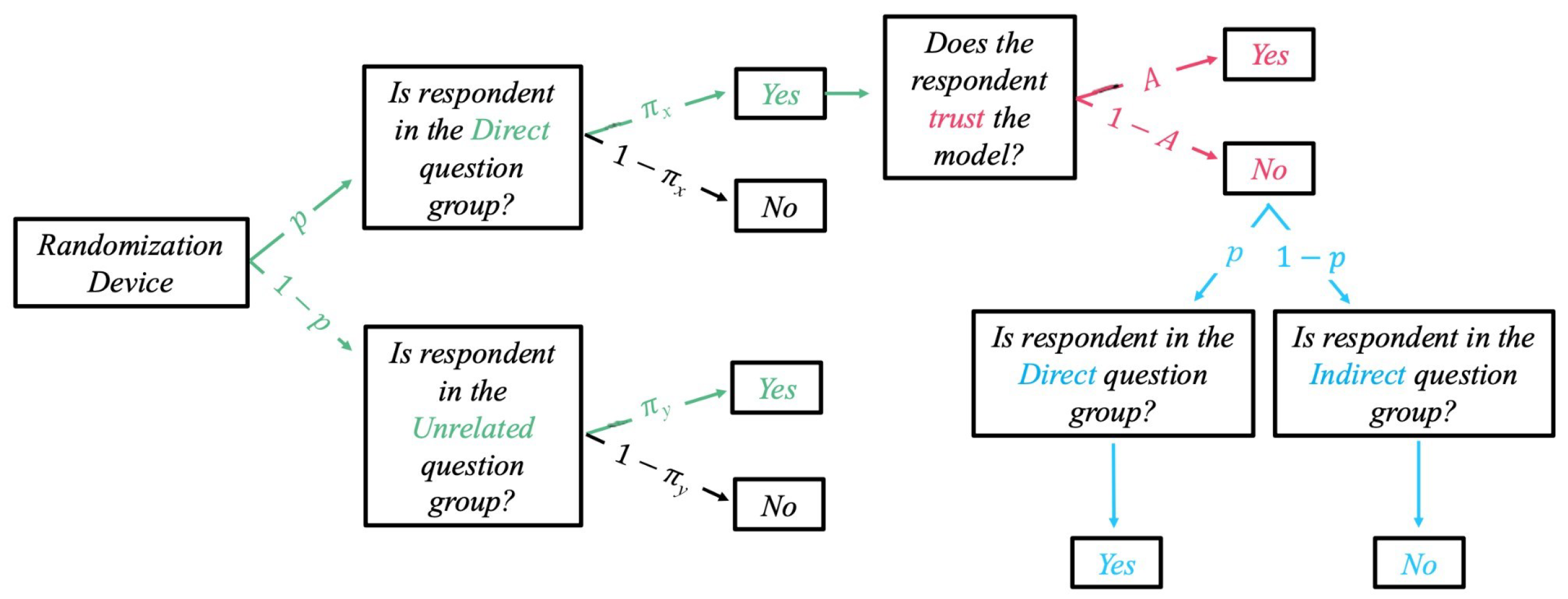
3.1. Our Proposed Enhanced-Trust Greenberg Model (Model-I)
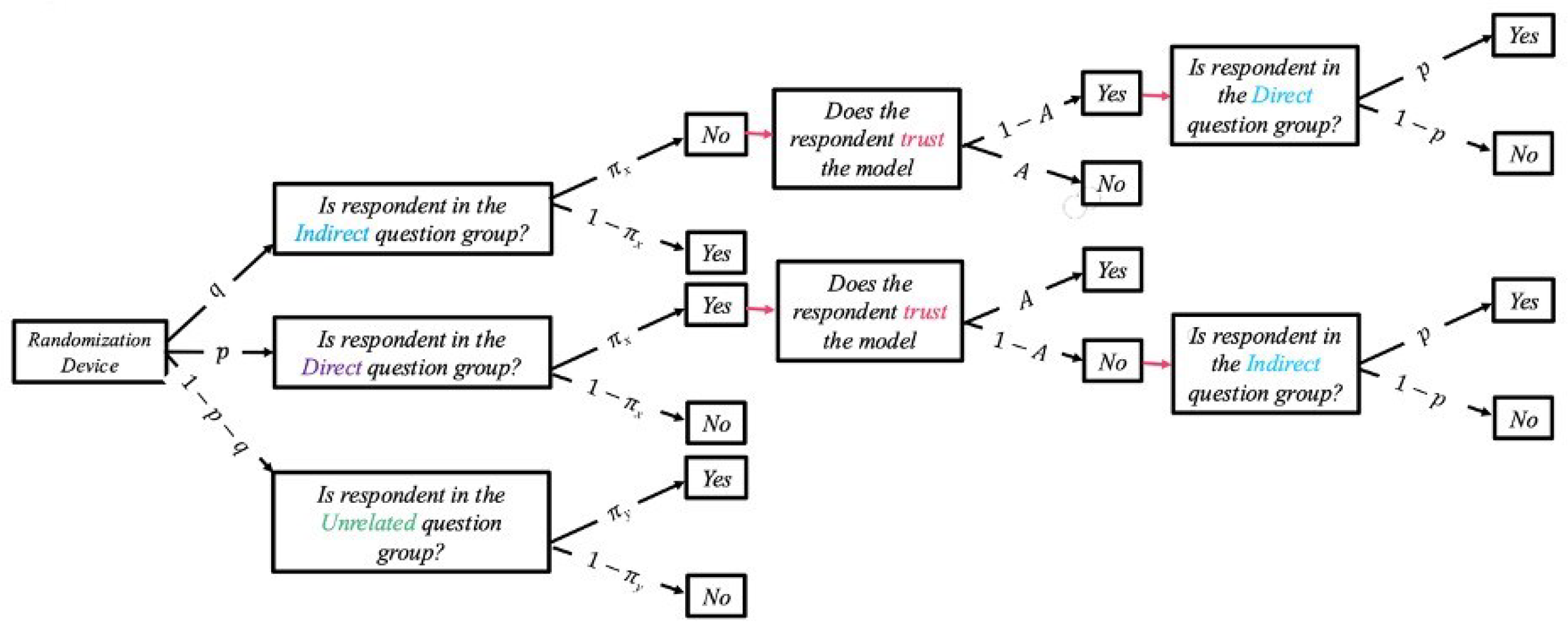
3.2. Our Proposed Enhanced-Trust Lovig Model (Model-II)
3.3. Effectiveness of the Mixture Model When Accounting for Untruthfulness
- Question 1 (With Greenberg Model): Do you trust the model?
- Question 2 (Proposed Model-I): Do you have the sensitive trait?
- Question 2 (Proposed Model-II): Do you have the sensitive trait?
3.4. Preservation of Privacy in the Proposed Models
3.5. Proposed Unified Metric
3.6. Privacy of the Proposed Models
4. Simulation Study
4.1. Numerical Results
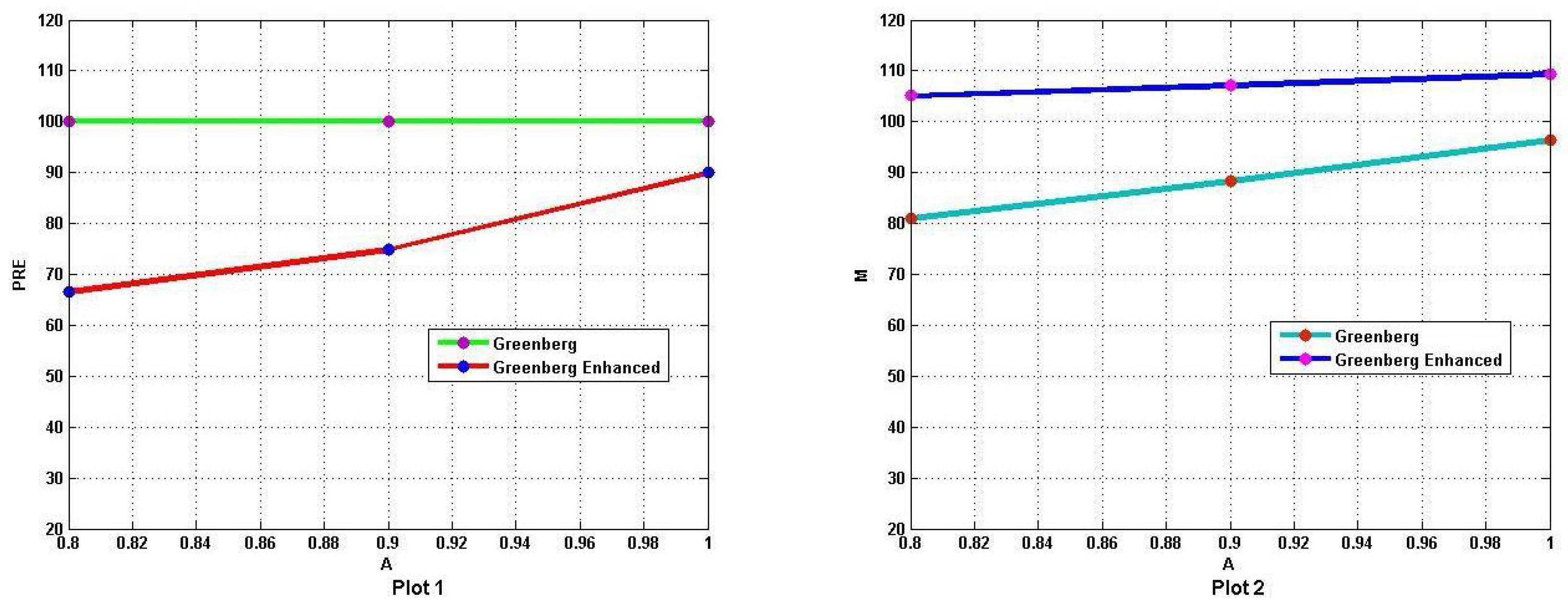
4.2. Graphical Comparison of the Models
4.3. Estimator Stability Under Different Models
- Greenberg Model:
- Enhanced-Trust Greenberg Model:
- Lovig Model:
- Enhanced-Trust Lovig Model:
5. Study Limitations and Future Directions
5.1. Limitations
5.2. Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Warner, S.L. Randomized response: A survey technique for eliminating evasive answer bias. J. Am. Stat. Assoc. 1965, 60, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Greenberg, B.G.; Abul-Ela, A.-L.A.; Simmons, W.R.; Horvitz, D.G. The unrelated question randomized response model: Theoretical framework. J. Am. Stat. Assoc. 1969, 64, 520–539. [Google Scholar] [CrossRef]
- Mangat, N.S.; Singh, R. An alternative randomized response procedure. Biometrika 1990, 77, 439–442. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, B.; Singh, S. Estimation of the sensitivity level of personal interview survey questions. J. Stat. Plan. Inference 2002, 100, 239–247. [Google Scholar] [CrossRef]
- Kim, J.-M.; Warde, W.D. A mixed randomized response model. J. Stat. Plan. Inference 2005, 113, 211–221. [Google Scholar] [CrossRef]
- Lovig, M.; Khalil, S.; Rahman, S.; Sapra, P.; Gupta, S. A mixture binary RRT model with a unified measure of privacy and efficiency. Commun. Stat. - Simul. Comput. 2023, 52, 2727–2737. [Google Scholar] [CrossRef]
- Parker, M.; Gupta, S.; Khalil, S. A Mixture Quantitative Randomized Response Model That Improves Trust in RRT Methodology. Axioms 2024, 13, 11. [Google Scholar] [CrossRef]
- Jones, E.E.; Sigall, H. The bogus pipeline: A new paradigm for measuring affect and attitude. Psychol. Bull. 1971, 76, 349–364. [Google Scholar] [CrossRef]
- Reynolds, W.M. Development of a reliable and valid short form of the Marlowe-Crowne SDB scale. J. Clin. Psychol. 1982, 38, 119–125. [Google Scholar] [CrossRef]
- Ostapczuk, M.; Musch, J.; Moshagen, M. A randomized-response investigation of the education effect in attitudes towards foreigners. Eur. J. Soc. Psychol. 2009, 39, 920–931. [Google Scholar] [CrossRef]
- Striegel, H.; Simon, P.; Hansel, J.; Niess, A.M.; Ulrich, R. Doping and drug use in elite sports: An analysis using the randomized response technique. Med. Sci. Sport. Exerc. 2006, 38, S247. [Google Scholar] [CrossRef]
- Kalucha, G.; Khalil, S.; Gupta, M.; Gupta, S. Estimating the Prevalence of Depression Among College Students — Field Validation of a Complex Randomized Response Technique. J. Stat. Theory Pract. 2025, 19, 96. [Google Scholar] [CrossRef]
- Lanke, J. On the degree of protection in randomized interviews. Int. Stat. Rev. Rev. Int. Stat. 1976, 44, 197–203. [Google Scholar] [CrossRef]
- Fligner, M.A.; Policello, G.E.; Singh, J. A comparison of two randomized response survey methods with consideration for the level of respondent protection. Commun. Stat. Theory Methods 1977, 6, 1511–1524. [Google Scholar] [CrossRef]
- Gupta, S.; Mehta, S.; Shabbir, J.; Khalil, S. A unified measure of respondent privacy and model efficiency in quantitative RRT models. J. Stat. Theory Pract. 2018, 12, 506–511. [Google Scholar] [CrossRef]


| Symbol | Description |
|---|---|
| n | sample size (number of respondents). |
| p | probability that the respondent is in the direct question group. |
| q | probability that the respondent is in the indirect question group. |
| probability that the respondent is in the unrelated question group. | |
| prevalence of the sensitive trait in the target population. | |
| proportion of the unrelated trait in the target population (such as prevalence of April births). | |
| A | proportion of respondents who trust the underlying RRT model and provide a response as per the model instructions. |
| proportion of the respondents who do not trust the RRT methodology to protect their privacy if the model-based response is incriminating, and switch their response from “yes” to “no”, or from “no” to “yes” to avoid incrimination and maintain social desirability. | |
| probability of the respondent entering a “yes” response for Warner’s Model. | |
| probability of the respondent entering a “yes” response for Greenberg’s model. | |
| probability of the respondent entering a “yes” response for Lovig’s model. | |
| probability of the respondent entering a “yes” response for the Enhanced-Trust Greenberg model. | |
| probability of the respondent entering a “yes” response for the Enhanced-Trust Lovig model. | |
| the probability of direct questioning utilized in the Greenberg model for the assessment of Trust. | |
| the probability of the unrelated trait in the Greenberg model for the assessment of Trust. | |
| the estimated value of the parameter . |
| Model | p | q | 1-p-q | A | Var | M | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Greenberg | 0.7 | 0.3 | 0 | 1 | 1.0002 | 0.4001 | 0.0010 | 0.0010 | 0.0968 | 0.0968 | 96.4091 | 99.1116 |
| 0.9 | 0.9006 | 0.3999 | 0.0012 | 0.0011 | 0.1064 | 0.1062 | 88.3861 | 94.2058 | ||||
| 0.8 | 0.8005 | 0.4003 | 0.0015 | 0.0013 | 0.1181 | 0.1178 | 80.9979 | 88.5820 | ||||
| Greenberg | 0.7 | 0.3 | 0 | 1 | 0.9998 | 0.3994 | 0.0009 | 0.0009 | 0.0968 | 0.1132 | 109.3931 | 103.9980 |
| Enhanced | 0.9 | 0.8998 | 0.4000 | 0.0009 | 0.0009 | 0.0995 | 0.1128 | 107.2141 | 109.1430 | |||
| 0.8 | 0.8002 | 0.3988 | 0.0010 | 0.0010 | 0.1023 | 0.1121 | 105.1185 | 106.8716 | ||||
| Lovig | 0.7 | 0.15 | 0.15 | 1 | 1.0001 | 0.4002 | 0.0016 | 0.0017 | 0.4286 | 0.4291 | 252.2162 | 251.2180 |
| 0.9 | 0.8998 | 0.4006 | 0.0021 | 0.0020 | 0.4545 | 0.4551 | 219.3250 | 225.2544 | ||||
| 0.8 | 0.7999 | 0.4006 | 0.0026 | 0.0025 | 0.4839 | 0.4842 | 188.0234 | 194.8597 | ||||
| Lovig | 0.7 | 0.15 | 0.15 | 1 | 1.0002 | 0.4005 | 0.0016 | 0.0015 | 0.4286 | 0.4283 | 272.9501 | 279.7032 |
| Enhanced | 0.9 | 0.9006 | 0.3998 | 0.0016 | 0.0017 | 0.4333 | 0.4334 | 266.5181 | 254.9553 | |||
| 0.8 | 0.7998 | 0.3991 | 0.0017 | 0.0017 | 0.4381 | 0.4387 | 260.1536 | 251.2456 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, S.; Jayaraj, N.; Gupta, M.; Trisandhya, P. A Trust-Enhancing Variant of the Binary Randomized Response Technique. Axioms 2025, 14, 864. https://doi.org/10.3390/axioms14120864
Gupta S, Jayaraj N, Gupta M, Trisandhya P. A Trust-Enhancing Variant of the Binary Randomized Response Technique. Axioms. 2025; 14(12):864. https://doi.org/10.3390/axioms14120864
Chicago/Turabian StyleGupta, Sat, Nikita Jayaraj, Mala Gupta, and Pidugu Trisandhya. 2025. "A Trust-Enhancing Variant of the Binary Randomized Response Technique" Axioms 14, no. 12: 864. https://doi.org/10.3390/axioms14120864
APA StyleGupta, S., Jayaraj, N., Gupta, M., & Trisandhya, P. (2025). A Trust-Enhancing Variant of the Binary Randomized Response Technique. Axioms, 14(12), 864. https://doi.org/10.3390/axioms14120864





