Optimizing Textile Manufacturing with an M^X/G/1 Queueing Model: Two Heterogeneous Services, Bernoulli Vacations, and Disaster–Repair Interventions

Abstract

This study investigates an $M^X/G/1$ queueing system tailored to the textile manufacturing industry, incorporating two heterogeneous service types, Bernoulli vacation schedules, and the effects of disasters and repairs. The system handles bulk fabric arrivals following a Poisson process, where customers can opt for either standard finishing or advanced finishing services. Disasters such as equipment malfunctions cause system interruptions, necessitating stochastic repair periods, while Bernoulli vacation schedules allow the machines to take probabilistic vacations based on operational conditions. By employing the supplementary variable technique, the probability generating function (PGF) for the number of customers in the system is obtained. Key performance metrics are derived alongside rate arguments to analyze system behavior comprehensively. Numerical techniques are utilized to explore and illustrate the influence of model parameters, providing practical insights for optimizing resource allocation, enhancing production efficiency, and maintaining system reliability in textile manufacturing operations.

1. Introduction

Queueing systems play a vital role in the analysis and optimization of service and manufacturing processes, especially during interruptions, service variability, and in crucial workload management. This study focuses on modeling an $M^X/G/1$ queueing system characterized by two heterogeneous services, Bernoulli vacation schedules, and the influence of disasters and repairs. The concept of heterogeneous services reflects real-world settings where a server offers two distinct types of service differing in complexity, resource requirements, or in time. Disasters represent system-wide failures that interrupt operations, necessitating repair periods to restore functionality. The inclusion of a Bernoulli vacation schedule adds flexibility by allowing the server to probabilistically decide on taking a vacation. In this study, these features are integrated into a unified framework to derive key system performance metrics, including the probability generating function (PGF) for the number of customers in the system, using the supplementary variable technique.

The present study contributes to the literature on bulk-arrival single-server systems by formulating an $M^X/G/1$ model that simultaneously incorporates heterogeneous service choice, Bernoulli-type vacations, and disaster–repair interruptions within a unified analytical framework. Earlier works of certain model addresses these mechanisms only in isolation or partial combinations, whereas the current model captures their joint influence through a coupled supplementary-variable structure and modified steady-state balance equations. This integrated formulation enables system descriptors that explicitly reflect the interaction among service heterogeneity, probabilistic vacations, and breakdown–repair cycles, yielding structural and parametric behaviors not observed in models with only one or two of these features. This establishes the technical novelty and broadens the applicability of $M^X/G/1$ queueing models to more realistic operational environments.

The development of this model is grounded upon significant prior work. The integration of disasters and repairs builds on the foundational work of Afanasyev [1], who examined the busy period in queueing systems with vacations, providing insights into the probabilistic structure of service interruptions. Afthab Begum et al. [2] extended disaster models by including working breakdowns. Arumuganathan and Jeyakumar [3] studied bulk queueing systems with service feedback and control policies. In a related context, Barron [4] developed a replenishment inventory model under random environments with stock- and age-dependent cost functions, bridging queueing theory and inventory control under stochastic conditions. Similarly, Choi and Lim [5] proposed a Markovian queueing model with an alternating server and queue-length-based threshold control, contributing to adaptive service mechanisms. Choudhury and Paul [6] examined two-phase queueing systems with feedback, while Choudhury and Deka [7] explored single-server systems operating under Bernoulli vacation schedules in disaster-prone environments. Fu et al. [8] analyzed optimization decisions in customer-intensive services under bounded rationality, incorporating behavioral uncertainty through Gumbel distributions. Guendouzi and Bouzebda [9] optimized a GI/M/2/N queue with heterogeneous servers, working vacations, and impatience using the Bat algorithm, demonstrating the potential of metaheuristic techniques in queue optimization. Jeyakumar and Logapriya [10,11,12] further explored non-terminating vacation policies, single vacation policies, and compulsory vacation policies in queueing systems under disaster and repair conditions. Jeyakumar and Senthilnathan [13] provided insights into the behavior of bulk queueing systems with multiple vacations and breakdowns, emphasizing their relevance to real-world operations. The role of Bernoulli vacation schedules is highlighted by Jingjing et al. [14]. Kadi et al. [15] analyzed an M/M/1/K queue with single working vacation, feedback, and impatience under an N-policy. Collectively, these studies form the foundation on which the present comprehensive queueing model is developed to address real-world challenges in manufacturing and service industries.

In addition to these foundational contributions, several recent studies have advanced the analysis and optimization of queueing systems under modern operational complexities. Ke and Pearn [16] discussed optimal management policies in vacation models, while Kim and Lee [17] analyzed working breakdowns in M/G/1 queues. Kumar and Arivudainambi [18] examined queueing systems with catastrophes. The inclusion of heterogeneous services is inspired by Madan [19] and Madan et al. [20], who studied two-stage and multi-type service models. Mahanta et al. [21] and Mytalas and Zazanis [22] extended disaster models by considering working breakdowns and MAV policies, respectively. Niranjan et al. [23] studied bulk queueing models with load balancing and vacation, relevant to distributed and industrial service systems. Palaniammal and Kumar [24] further investigated the implications of heterogeneity on queueing performance across various industries. Applications of similar models in manufacturing environments have been demonstrated by Park et al. [25] in stochastic disaster systems. Sasikala et al. [26] focused on Bernoulli vacation schedules in retrial queueing systems, while Singh C.J., Jain M., and Kumar B. [27] analyzed an $M^X/G/1$ unreliable retrial queue with the option of additional service and Bernoulli vacation. Xie et al. [28] investigated equilibrium and optimization in multi-server queues with heterogeneous information and reneging. Yechiali [29] examined queues with system disasters and impatient customers, contributing substantially to research on vacation policies. Zhu and Wang [30] explored strategic joining in single-server Markovian queues with Bernoulli working vacations, revealing the behavioral dynamics of customers in such systems. Collectively, these recent developments emphasize a growing research interest in queueing models with vacations, customer heterogeneity, and stochastic disruptions—providing strong motivation for the present study.

Accordingly, the current work proposes a queueing model featuring two heterogeneous services, Bernoulli vacation schedules, and disaster–repair interventions, which is formulated to optimize textile manufacturing operations. The model captures realistic production characteristics such as probabilistic breakdowns, rest periods, and service variability, offering a unified analytical framework for improving efficiency and reliability in manufacturing environments.

The comparison in

Table 1. Comparison of the Present Study with Existing Related Works.

Year	Model	Heterogeneous Services	Bulk Arrivals	Bernoulli Vacation	Disaster/ Breakdown	Repair Mechanism	Application
2000	M/M/1 with Catastrophes	✗	✗	✗	✓	✓	Theoretical
2007	Queue with Disasters and Impatience	✗	✗	✗	✓	✓	Theoretical
2014	Single-Server with Bernoulli Vacation	✗	✗	✓	✓	✗	✗
2011	Two-Stage/Multi-Type Service Models	✓	✗	✗	✗	✗	✗
2018	Bulk Queue with Feedback	✗	✓	✗	✗	✗	✗
2020	Retrial Queue with Bernoulli Vacation	✗	✗	✓	✗	✗	✗
2024	Bulk Queue with Load Balancing and Vacation	✗	✓	✓	✗	✗	✗
2025	GI/M/2/N with Working Vacation, Feedback, and Impatience	✓	✗	✓	✗	✗	✗
Present Study	Two Heterogeneous Services, Bernoulli Vacation, and Disaster–Repair	✓	✓	✓	✓	✓	✓

clearly highlights that most existing studies address only one or two aspects, such as vacations, breakdowns, or service heterogeneity, in isolation. The present work uniquely combines bulk arrivals, two heterogeneous services, Bernoulli vacation schedules, and disaster–repair mechanisms within a unified $M^X/G/1$ queueing framework. Furthermore, the model is applied to a real-world textile manufacturing scenario, providing both analytical insight and practical relevance. This integrated approach distinguishes the present study from earlier theoretical models and offers a novel contribution toward performance optimization and operational reliability in industrial systems.

The aim of this model is to analyze complex queueing scenarios that arise in industries where bulk arrivals, diverse service options, and system disruptions are common. In a textile manufacturing unit, fabric rolls (customers) arrive in bulk for processing. The server (machine) provides two types of finishing services that are Standard Finishing and Advanced Finishing. Finishing services play a crucial role in enhancing the properties and appearance of fabrics to meet specific customer demands. Finishing is often the final stage of production that adds value to the product, ensuring it meets both functional and aesthetic requirements. Customers may opt for standard fabric finishing (basic chemical treatments for durability) or advanced finishing (waterproofing, anti-bacterial coatings, or wrinkle resistance) based on their needs and budget. Occasionally, the machine (server) undergoes disasters like machine malfunctions due to wear and tear in standard finishing service (service 1) and high-tech failures due to issues in UV curing machines in advanced finishing services (service 2), requiring repair before resuming operations. During periods of low workload, the machine may enter a Bernoulli vacation state for maintenance or energy conservation. This model helps in evaluating the system performance, optimizing machine utilization, improve production efficiency, and in maintaining high customer satisfaction while managing the inherent uncertainties in manufacturing operations.

Beyond textile manufacturing, similar queueing dynamics are observed in other industrial and service sectors. For instance, in automobile assembly lines, robotic units often alternate between routine operations and calibration (vacation periods), while different service stations handle heterogeneous assembly or finishing tasks. In semiconductor fabrication plants, equipment frequently undergoes maintenance and repair cycles, and production batches (bulk arrivals) must queue for standard or specialized processing steps. Likewise, in healthcare service systems, diagnostic centers face bulk patient arrivals, where medical devices or testing units provide heterogeneous services (basic vs. advanced tests) and occasionally undergo service interruptions or recalibrations.

Thus, the proposed queueing model with heterogeneous services, Bernoulli vacations, and disaster–repair mechanisms capture a wide range of real-world operations, providing valuable insights for optimizing resource utilization, improving service efficiency, and maintaining customer satisfaction under uncertainty.

The present study can be extended in several meaningful directions to enhance its analytical scope and practical relevance. Future research may incorporate customer impatience, reneging, or feedback mechanisms to model situations where fabric batches or customers withdraw or rejoin the system depending on service delays. The framework can also be generalized to multi-server or parallel-machine environments, reflecting large-scale textile or manufacturing systems with coordinated operations and load balancing. Introducing finite buffer capacity and priority-based service rules would allow analysis of preferential treatment for high-value or urgent orders. Moreover, the development of data-driven or machine learning-based control policies could optimize vacation scheduling, repair decisions, and service switching in real time. Further, integrating the queueing framework with inventory or supply-chain models would provide a holistic view of production and material flow. Allowing general or state-dependent distributions for repair and vacation times could also capture practical uncertainties in maintenance processes. Finally, future studies may conduct simulation-based validation or empirical analysis using industrial data to evaluate economic and energy efficiency, thereby strengthening the real-world applicability of the proposed model.

The paper is organized as follows. Section 2 presents the mathematical model of the queueing system with two heterogeneous services, Bernoulli vacations, and disaster–repair mechanisms. Section 3 details the derivation of the steady-state equations using the supplementary variable approach and the probability generating function (PGF) methodology. Section 4 analyzes the queue size distribution and key performance measures, while Section 5 illustrates the numerical results and discusses the impact of various system parameters. Finally, Section 6 concludes the study and highlights potential directions for future research.

2. Model Formulation

The system considers a bulk-arrival process in which customer batches arrive according to a Poisson process with rate $\lambda .$The size of each arriving batch is modeled by the random variable C. A batch of customers $i$ with the parameters $\lambda ,\lambda >0$joins the system with a provided with two kinds of heterogeneous service under first come, first serve discipline. The mean batch size is denoted by $E\left(C\right)$. An arriving customer has the option to select either the first service with a probability ‘p’ or second service with a probability ‘$1-p$’. Let ${\mu }_1\left(x\right)$ and ${\mu }_2\left(x\right)$ be the hazard rate function of the of both the services, with the corresponding density functions ${S_1}^{\prime }$ and ${S_2}^{\prime }$and with the mean service times $E\left(S_1\right)$ and $E\left(S_2\right).$ After completing service, the server may either take vacation with probability $b$ or with probability $1-b$, where the server may wait in the system to serve the arriving customer. Let $v\left(x\right)$ be the hazard rate function of the vacation, with the mean vacation time being $E\left(L\right).$ All vacation periods are independent of each other. Finally, disaster is assumed to happen in the system during either the first or second kind of service. With the disaster rate $\delta$, it removes all the customers, including the one being served by the system, and the system is immediately moved to a repair period. Let $r\left(x\right)$ be the hazard rate function of the repair period with density function $R^{\prime }$ and mean repair time $E\left(R\right).$ The customers who arrive during repair time may wait in the queue.

In this model, we aim to derive the KolmogorovChapman equations for a bulk arrival single-server queueing system with two different kinds of heterogeneous service, server vacations, and disasters requiring repairs. Let $S_{i,t},\mathrm{i}=1,2$ and $L_t$ be introduced as supplementary variables to obtain a Markov Process as $\left\{N_t,\mathsf{\Omega }\left(t\right),S_{i,t},R_t,L_t,t\ge 0\right\}$.

Let $N_t$ and $\mathsf{\Omega }\left(t\right)$ be the system size and random variable corresponding to server’s status at a time t. For the various server’s states, the limiting probabilities are defined as follows:

Server’s idle state: $P_0$ at $\Omega \left(t\right)=0$ represents the probability that the system is empty and the server is idle. Server’s busy state (first kind of service): $P_n^{\left(s1\right)}\left(x\right)$ at $\Omega \left(t\right)=1$ represents the joint probability of having $n$ customers in the system and the server busy with the first kind of service. Server’s busy state (second kind of service): $P_n^{\left(s2\right)}\left(x\right)$ at $\Omega \left(t\right)=2$ represents the joint probability of having $n$ customers in the system and the server busy with the second kind of service. Server’s repair state: $R_n\left(x\right)$ at $\Omega \left(t\right)=3$ represents the probability of having $n$ customers in the system and the server undergoing repairs. Server’s vacation state: $L_n\left(x\right)$ at $\Omega \left(t\right)=4$ represents the probability of having $n$ customers in the system and the server is on vacation. Symbols and notations are listed in Appendix A.

3. Supplementary Variable Approach to Steady-State Differential Equations

The supplementary variable technique is a powerful tool in queueing theory for deriving steady-state differential equations and analyzing system performance. This method is particularly effective for systems with bulk arrivals, general service distributions, and stochastic disruptions like disasters and repairs. Building on our earlier studies on single vacation policies [5] and non-terminating vacation models in $M^X/G/1$ queues [6], this work extends the application of the supplementary variable technique to explore steady-state behaviors in two different heterogeneous services.

The governing equations for various states of the system are framed for $n>0as$

$$0=-\lambda P_0+{\int }_0^{\infty }{L}_0\left(x\right)v\left(x\right)dx+(1-b)\left({\int }_0^{\infty }{P}_1^{\left(s2\right)}\left(x\right){\mu }_2\left(x\right)dx+{\int }_0^{\infty }\begin{array}{c}{P}_1^{\left(s1\right)}\left(x\right){\mu }_1\left(x\right)dx+\\ {\int }_0^{\infty }{R}_0\left(x\right)r\left(x\right)dx\end{array}\right)$$

(1)

$$\left({\displaystyle \frac{d}{dx}}+\lambda +{\mu }_1\left(x\right)+\delta \right)P_n^{\left(s1\right)}\left(x\right)=\lambda {{\sum }_{i=1}^{n-1}{C}_{i}P}_{n-i}^{\left(s1\right)}\left(x\right),n\ge 1$$

(2)

$$\left({\displaystyle \frac{d}{dx}}+\lambda +{\mu }_2\left(x\right)\right)P_n^{\left(s2\right)}\left(x\right)=\lambda {{\sum }_{i=1}^{n-1}{C}_{i}P}_{n-i}^{\left(s2\right)}\left(x\right),n\ge 1$$

(3)

$$\left({\displaystyle \frac{d}{dx}}+\lambda +r\left(x\right)\right)R_n\left(x\right)=\lambda {{\sum }_{i=1}^{n-1}{C}_{i}R}_{n-i}\left(x\right),n\ge 1$$

(4)

$$\left({\displaystyle \frac{d}{dx}}+\lambda +v\left(x\right)\right)L_n\left(x\right)=\lambda {{\sum }_{i=1}^{n-1}{C}_{i}L}_{n-i}\left(x\right),n\ge 1$$

(5)

With the boundary conditions

$$P_n^{\left(s1\right)}\left(0\right)=p\left({\int }_0^{\infty }{L}_n\left(x\right)v\left(x\right)dx+{\int }_0^{\infty }{P}_{n+1}^{\left(s2\right)}\left(x\right){\mu }_2\left(x\right)dx+{\int }_0^{\infty }\begin{array}{c}{P}_{n+1}^{\left(s1\right)}\left(x\right){\mu }_1\left(x\right)dx+{\int }_0^{\infty }{R}_n\left(x\right)r\left(x\right)dx+\\ \lambda C_n{P}_0\end{array}\right)$$

(6)

$$P_n^{\left(s2\right)}\left(0\right)=(1-p)\left({\int }_0^{\infty }{L}_n\left(x\right)v\left(x\right)dx+{\int }_0^{\infty }{P}_{n+1}^{\left(s2\right)}\left(x\right){\mu }_2\left(x\right)dx+{\int }_0^{\infty }\begin{array}{c}{P}_{n+1}^{\left(s1\right)}\left(x\right){\mu }_1\left(x\right)dx+{\int }_0^{\infty }{R}_n\left(x\right)r\left(x\right)dx\\ +\lambda C_n{P}_0\end{array}\right)$$

(7)

$$R_0\left(0\right)=\delta \left({\sum }_{n=1}^{\infty }{\int }_0^{\infty }{P}_n^{\left(s1\right)}\left(x\right)dx+{\sum }_{n=1}^{\infty }{\int }_0^{\infty }{P}_n^{\left(s2\right)}\left(x\right)dx\right)$$

(8)

$$L_n\left(0\right)=b\left({\int }_0^{\infty }{P}_n^{\left(s2\right)}\left(x\right){\mu }_2\left(x\right)dx+{\int }_0^{\infty }{P}_{n+1}^{\left(s1\right)}\left(x\right){\mu }_1\left(x\right)dx\right)$$

(9)

4. PGF-Based Steady-State Analysis

We derive the steady-state probability generating function (PGF) by systematically linking each balance equation to the corresponding operational condition of the system. Intermediate steps are outlined to clarify how the supplementary variables capture service heterogeneity, vacation decisions, and disaster–repair dynamics. By presenting the derivation in a stepwise manner, the structure of the PGF becomes transparent, showing how each component of the model contributes to the steady-state representation.

To obtain the PGF, we define the functions as

$$\begin{array}{c}{P}^{\left(s1\right)}\left(x,z\right)={\sum }_{n=1}^{\infty }{P}_n^{\left(s1\right)}\left(x\right)z^n,P_n^{\left(s1\right)}\left(z\right)={\sum }_{n=1}^{\infty }{P}_n^{\left(s1\right)}{z}^n\\ P^{\left(s2\right)}\left(x,z\right)={\sum }_{n=1}^{\infty }{P}_n^{\left(s2\right)}\left(x\right)z^n,P_n^{\left(s2\right)}\left(z\right)={\sum }_{n=1}^{\infty }{P}_n^{\left(s2\right)}{z}^n\\ L\left(x,z\right)={\sum }_{n=0}^{\infty }{L}_n\left(x\right)z^n,R\left(x,z\right)={\sum }_{n=0}^{\infty }{R}_n\left(x\right)z^n\end{array}$$

(10)

By multiplying Equations (2)–(9) with certain powers of $z$ and summing it over $n$, we obtain the PDEs as

$$\begin{array}{c}{\displaystyle \frac{d}{dx}}{P}^{\left(s1\right)}\left(x,z\right)+\left(\lambda +{\mu }_1\left(x\right)+\delta -\lambda C\left(z\right)\right)P^{\left(s1\right)}\left(x,z\right)=0\\ {\displaystyle \frac{d}{dx}}{P}^{\left(s2\right)}\left(x,z\right)+\left(\lambda +{\mu }_2\left(x\right)+\delta -\lambda C\left(z\right)\right)P^{\left(s2\right)}\left(x,z\right)=0\\ {\displaystyle \frac{d}{dx}}R\left(x,z\right)+\left(\lambda +r\left(x\right)-\lambda C\left(z\right)\right)R\left(x,z\right)=0\\ {\displaystyle \frac{d}{dx}}L\left(x,z\right)+\left(\lambda +v\left(x\right)-\lambda C\left(z\right)\right)L\left(x,z\right)=0\end{array}$$

(11)

$$\begin{array}{c}{P}^{\left(s1\right)}\left(0,z\right)=\left(p\right)({\int }_0^{\infty }\left(L\left(x,z\right)-L_0\left(x\right)\right)v\left(x\right)dx+{\int }_0^{\infty }\left({{\displaystyle \frac{1}{z}}{P}^{\left(s2\right)}\left(x,z\right)-P}_1^{\left(s2\right)}\left(x\right)\right){\mu }_2\left(x\right)dx+\\ {\int }_0^{\infty }\left({{\displaystyle \frac{1}{z}}{P}^{\left(s1\right)}\left(x,z\right)-P}_1^{\left(s1\right)}\left(x\right)\right){\mu }_1\left(x\right)dx+{\int }_0^{\infty }\left({R\left(x,z\right)-R}_0\left(x\right)\right)r\left(x\right)dx+\lambda C(z)P_0)\end{array}$$

(12)

$$\begin{array}{c}{P}^{\left(s2\right)}\left(0,z\right)=\left(1-p\right)({\int }_0^{\infty }\left(L\left(x,z\right)-L_0\left(x\right)\right)v\left(x\right)dx+{\int }_0^{\infty }\left({{\displaystyle \frac{1}{z}}{P}^{\left(s2\right)}\left(x,z\right)-P}_1^{\left(s2\right)}\left(x\right)\right){\mu }_2\left(x\right)dx+\\ {\int }_0^{\infty }\left({{\displaystyle \frac{1}{z}}{P}^{\left(s1\right)}\left(x,z\right)-P}_1^{\left(s1\right)}\left(x\right)\right){\mu }_1\left(x\right)dx+{\int }_0^{\infty }\left({R\left(x,z\right)-R}_0\left(x\right)\right)r\left(x\right)dx+\lambda C(z)P_0)\end{array}$$

(13)

$$R\left(0,z\right)=\delta \left({\int }_0^{\infty }{P}^{\left(s1\right)}\left(x,1\right)dx+{\int }_0^{\infty }{P}^{\left(s1\right)}\left(x,1\right)dx\right)$$

(14)

$$L\left(0,z\right)=b\left({\int }_0^{\infty }{P}_n^{\left(s1\right)}\left(x,z\right){\mu }_2\left(x\right)dx+{\int }_0^{\infty }{P}_n^{\left(s2\right)}\left(x,z\right){\mu }_1\left(x\right)dx\right)$$

(15)

Upon solving Equation (11), we have

$$\begin{array}{c}{P}^{\left(s1\right)}\left(x,z\right)=P^{\left(s1\right)}\left(0,z\right)(1-S_1\left(x\right))e^{-\left(\lambda +\delta -\lambda C\left(z\right)\right)x}\\ P^{\left(s2\right)}\left(x,z\right)=P^{\left(s2\right)}\left(0,z\right)(1-S_2\left(x\right))e^{-\left(\lambda +\delta -\lambda C\left(z\right)\right)x}\\ R\left(x,z\right)=R\left(0,z\right)(1-R\left(x\right))e^{-\left(\lambda -\lambda C\left(z\right)\right)x}\\ L\left(x,z\right)=L\left(0,z\right)(1-L\left(x\right))e^{-\left(\lambda -\lambda C\left(z\right)\right)x}\end{array}$$

(16)

By integrating the Equation (16) again, we have

$$\begin{array}{c}{P}^{\left(s1\right)}\left(z\right)=P^{\left(s1\right)}\left(0,z\right)\left({\displaystyle \frac{1-S_1^{*}(\lambda +\delta -\lambda C(z\left)\right)}{\lambda +\delta -\lambda C\left(z\right)}}\right)\\ P^{\left(s2\right)}\left(z\right)=P^{\left(s2\right)}\left(0,z\right)\left({\displaystyle \frac{1-S_2^{*}(\lambda +\delta -\lambda C(z\left)\right)}{\lambda -\lambda C\left(z\right)}}\right)\\ R\left(z\right)=R\left(0,z\right)\left({\displaystyle \frac{1-R^{*}(\lambda -\lambda C(z\left)\right)}{\lambda -\lambda C\left(z\right)}}\right)\\ L\left(z\right)=L\left(0,z\right)\left({\displaystyle \frac{1-L^{*}(\lambda -\lambda C(z\left)\right)}{\lambda -\lambda C\left(z\right)}}\right)\end{array}$$

(17)

$S_1^{*}\left(\lambda +\delta -\lambda C\left(z\right)\right)and{S}_2^{*}\left(\lambda +\delta -\lambda C\left(z\right)\right)$ represent the Laplace-Stieltjes transforms of the first and second types of service time distributions, respectively. Similarly, $R^{*}\left(\lambda -\lambda C\left(z\right)\right)$ denotes the Laplace-Stieltjes transform of the repair time distributions, and $L^{*}\left(\lambda -\lambda C\left(z\right)\right)$ corresponds to the Laplace-Stieltjes transform of the vacation time distribution. These transforms are essential in expressing the steady-state characteristics of the queueing system.

Equations (13)–(16) are evaluated to determine and obtain the integral equations as,

$${\int }_0^{\mathrm{\infty }}{P}^{\left(s1\right)}\left(x,z\right){\mu }_1\left(x\right)dx=P^{\left(s1\right)}\left(0,z\right)S_1^{\mathrm{*}}(\lambda +\delta -\lambda C(z\left)\right)$$

(18)

$${\int }_0^{\infty }{P}^{\left(s2\right)}\left(x,z\right){\mu }_2\left(x\right)dx=P^{\left(s2\right)}\left(0,z\right)S_2^{*}(\lambda +\delta -\lambda C(z\left)\right)$$

(19)

$${\int }_0^{\infty }R\left(x,z\right)r\left(x\right)dx=R\left(0,z\right)R^{*}(\lambda -\lambda C(z\left)\right)$$

(20)

$${\int }_0^{\infty }L\left(x,z\right)v\left(x\right)dx=L\left(0,z\right)L^{*}(\lambda -\lambda C(z\left)\right)$$

(21)

In the given queueing system, it is assumed that no customers are present immediately after the completion of a vacation period or a repair period that follows a disaster. This condition arises because the system state resets at the end of these events. Consequently, the joint probabilities associated with the number of customers in the system and the system’s phase simplify PGFs $L\left(0,z\right)as{L}_0\left(0\right)$ and $R\left(0,z\right)as{R}_0\left(0\right)$.

5. Queue Size Distribution Under Different Operational States

The analysis of the queue size distribution proceeds by decomposing the overall PGF into parts associated with the key operational states of the system—busy operation, vacation periods, disaster epochs, and repair phases. Each resulting expression is accompanied by brief interpretative remarks illustrating how the model parameters influence the distribution under these conditions. This separation of structural components provides clearer insight into how the combined effects of bulk arrivals, service heterogeneity, vacations, and breakdown–repair cycles shape the system’s queue length behavior.

Queueing systems are subjected to disruptions like vacations, repairs, and varying server availability, and the queue size distribution depends significantly on the operational state of the server. By deriving the PGFs for different states, such as when the server is busy, under repair, or on vacation, this enables us to compute key performance metrics like mean queue length and waiting time.

$$P^{\left(s1\right)}\left(0,z\right)={\displaystyle \frac{zp\left(\delta \left(P^{\left(s1\right)}\left(1\right)+P^{\left(s2\right)}\left(1\right)\right)R^{*}\left(A_z\right)-\lambda P_0{H}_z\right)}{z-\left(p{S}_1^{*}\left(A_z+\delta \right)+(1-p).S_2^{*}(A_z+\delta )\right)\left(zb{L}^{*}\left(A_z\right)+1\right)}}$$

(22)

where $A_z=\lambda -\lambda C\left(z\right)$, and $H_z={\displaystyle \frac{1}{1-b}}-C\left(z\right)$.

Therefore Equation (17) becomes

$$P^{\left(s1\right)}\left(z\right)={\displaystyle \frac{zp\left(\delta \left(P^{\left(s1\right)}\left(1\right)+P^{\left(s2\right)}\left(1\right)\right)R^{*}\left(A_z\right)-\lambda P_0{H}_z\right)}{z-\left(p{S}_1^{*}\left(A_z+\delta \right)+(1-p).S_2^{*}(A_z+\delta )\right)\left(zb{L}^{*}\left(A_z\right)+1\right)}}\left({\displaystyle \frac{1-S_1^{*}(A_z+\delta )}{A_z+\delta }}\right)$$

(23)

To establish the existence of a unique root inside the unit disk, we apply Rouche’s theorem. If possible, let ${z=z}_{\theta }$ be the unique solution of $z=\left(p{S}_1^{*}\left(A_z+\delta \right)+(1-p).S_2^{*}(A_z+\delta )\right)\left(zb{L}^{*}\left(A_z\right)+1\right)$. In that case, equality becomes $\lambda P_0{H}_{z_{\theta }}=\delta \left(P^{\left(s1\right)}\left(1\right)+P^{\left(s2\right)}\left(1\right)\right)R^{*}\left(A_{z_{\theta }}\right)$. Let us set $\pi ={\displaystyle \frac{H_{z_{\theta }}}{R^{\mathrm{*}}\left(A_{z_{\theta }}\right)}}$.

Results:

The probability generating functions (PGFs) for the size of the system at different epochs—corresponding to the first kind of service, second kind of service, repair phase, and vacation phase—are derived as follows:

The PGF at the epoch of the first kind of service is given as

$$P^{\left(s1\right)}\left(z\right)={\displaystyle \frac{zp\left(\pi \lambda P_0{R}^{*}\left(A_z\right)-\lambda P_0{H}_z\right)}{z-\left(p{S}_1^{*}\left(A_z+\delta \right)+(1-p).S_2^{*}(A_z+\delta )\right)\left(zb{L}^{*}\left(A_z\right)+1\right)}}\left({\displaystyle \frac{1-S_1^{*}(A_z+\delta )}{A_z+\delta }}\right)$$

(24)

The PGF at the epoch of the second kind of service is given as

$$P^{\left(s2\right)}\left(z\right)={\displaystyle \frac{z(1-p)\left(\pi \lambda P_0{R}^{*}\left(A_z\right)-\lambda P_0{H}_z\right)}{z-\left(p{S}_1^{*}\left(A_z+\delta \right)+(1-p).S_2^{*}(A_z+\delta )\right)\left(zb{L}^{*}\left(A_z\right)+1\right)}}\left({\displaystyle \frac{1-S_2^{*}(A_z+\delta )}{A_z+\delta }}\right)$$

(25)

The PGF at the epoch under repair is given as

$$R\left(z\right)={\displaystyle \frac{\lambda P_0\left(\pi -\frac{b}{1-b}\right)\left(P\left(1-S_1^{*}\left(\delta \right)\right)+(1-P)(1-S_2^{*}\left(\delta \right))\right)\left(1-R^{*}\left(A_z\right)\right)}{(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)A_z}}$$

(26)

The PGF at the epoch of under vacation is given as

$$L\left(z\right)={\displaystyle \frac{zb\left(\pi \lambda P_0{R}^{*}\left(A_z\right)-\lambda P_0{H}_z\right)\left(p{S}_1^{*}\left(A_z+\delta \right)+\left(\left(1-p\right).S_2^{*}\left(A_z+\delta \right)\right)\right)\left(1-L^{*}\left(A_z\right)\right)}{{(z-\left(p{S}_1^{*}\left(A_z+\delta \right)+(1-p).S_2^{*}(A_z+\delta )\right)\left(zb{L}^{*}\left(A_z\right)+1\right)A}_z}}$$

(27)

Using the normalizing condition$atz=1$, the probability $P_0$ is obtained when the server being idle as

$$P_0={\left(1+{\displaystyle \frac{\lambda \left(\pi -\frac{b}{1-b}\right)\left\{\left(p\left(1-S_1^{*}\left(\delta \right)\right)+(1-p)\left(1-S_2^{*}\left(\delta \right)\right)\right)\left(1+\delta E\left(R\right)\right)+\delta \left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)\right\}}{\delta \left(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)\right)}}\right)}^{-1}$$

(28)

Finally, the total PGF of queue size $X\left(z\right)$ is obtained as

$$\begin{array}{c}X\left(z\right)={\left(1+{\displaystyle \frac{\lambda \left(\pi -\frac{b}{1-b}\right)\left\{\left(p\left(1-S_1^{*}\left(\delta \right)\right)+(1-p)\left(1-S_2^{*}\left(\delta \right)\right)\right)\left(1+\delta E\left(R\right)\right)+\delta \left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)\right\}}{\delta \left(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)\right)}}\right)}^{-1}[1+\\ {\displaystyle \frac{z\left(\pi \lambda P_0{R}^{*}\left(A_z\right)-\lambda P_0{H}_z\right)}{z-\left(p{S}_1^{*}\left(A_z+\delta \right)+\left(1-p\right).S_2^{*}\left(A_z+\delta \right)\right)\left(zb{L}^{*}\left(A_z\right)+1\right)}}({\displaystyle \frac{p\left(1-S_1^{*}\left(A_z+\delta \right)\right)+\left(1-p\right)\left(1-S_2^{*}\left(A_z+\delta \right)\right)}{A_z+\delta }}+\\ {\displaystyle \frac{b\left(p{S}_1^{*}\left(A_z+\delta \right)+\left(\left(1-p\right).S_2^{*}\left(A_z+\delta \right)\right)\right)\left(1-L^{*}\left(A_z\right)\right)}{A_z}})+{\displaystyle \frac{\lambda P_0\left(\pi -\frac{b}{1-b}\right)\left(P\left(1-S_1^{*}\left(\delta \right)\right)+(1-P)(1-S_2^{*}\left(\delta \right))\right)\left(1-R^{*}\left(A_z\right)\right)}{(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)A_z}}]\end{array}$$

(29)

Also, due to disaster, the PGF of the total number of customers removed from the queueing system is given as

$$X_d\left(z\right)={\displaystyle \frac{z\delta \left(\pi R^{*}\left(A_z\right)-H_z\right)\left(1-(b+1)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)\right)}{\left(z-\left(p{S}_1^{*}\left(A_z+\delta \right)+\left(1-p\right).S_2^{*}\left(A_z+\delta \right)\right)\left(zb{L}^{*}\left(A_z\right)+1\right)\right)\left(\pi -\frac{b}{1-b}\right)}}\left({\displaystyle \frac{1-S_1^{*}(A_z+\delta )}{(1-S_1^{*}\left(\delta \right)){(A}_z+\delta )}}+{\displaystyle \frac{1-S_2^{*}(A_z+\delta )}{(1-S_2^{*}\left(\delta \right)){(A}_z+\delta )}}\right)$$

(30)

6. Performance Measures

The expected queue length ($E\left(Q_L\right))$ and waiting time $(E\left(W_T)\right)$ of the customer in the system are derived using L’ Hospital’s rule. By applying this rule to the PGF obtained from the Equation (29), the mean queue length of the customer in the queue and mean waiting time of the customer are calculated. It produces valuable insights into the performance of the queueing system.

$$E\left(Q_L\right)={\displaystyle \frac{\begin{array}{c}\lambda E\left(c\right)\left(\frac{\left(\delta \left({1-\left(b+1\right)S}_a\right)\right)}{\delta \left({1-\left(b+1\right)S}_a\right)+\lambda {\lambda }_c\left(S_c\left(1+\delta E\left(R\right)\right)+\delta S_{a}E\left(L\right)\right)}\right)\\ \left(\begin{array}{c}{S}_d{\lambda }_c\left(\frac{\lambda }{\delta }-\frac{b\lambda }{2}E\left(L\right)\right)+S_c\left(S_e+{\lambda }_c\left(S_f-\frac{\lambda }{\delta }\left(b+1\right)S_d\right)-S_a\left(\left(b+1\right)S_e-{\lambda }_c\left(\left(b+1\right)S_f+\frac{1}{\delta E\left(c\right)}-\frac{\lambda }{\delta }E\left(L\right)\right)\right)\right)\\ +S_a\left(S_g+{\lambda }_c\left(S_h-S_d\left(\frac{b(b+1)}{2}\lambda E\left(L\right)-\frac{\lambda }{\delta }\left(1+b\right)\right)\right)-S_a\left(S_g-{\lambda }_c\left(1+b\right)\right)\right)\end{array}\right)\end{array}}{{\left({1-(b+1)S}_a\right)}^2}}$$

(31)

$$E\left(W_T\right)={\displaystyle \frac{\begin{array}{c}\left(\frac{\left(\delta \left({1-\left(b+1\right)S}_a\right)\right)}{\delta \left({1-\left(b+1\right)S}_a\right)+\lambda {\lambda }_c\left(S_c\left(1+\delta E\left(R\right)\right)+\delta S_{a}E\left(L\right)\right)}\right)\\ \left(\begin{array}{c}{S}_d{\lambda }_c\left(\frac{\lambda }{\delta }-\frac{b\lambda }{2}E\left(L\right)\right)+S_c\left(S_e+{\lambda }_c\left(S_f-\frac{\lambda }{\delta }\left(b+1\right)S_d\right)-S_a\left(\left(b+1\right)S_e-{\lambda }_c\left(\left(b+1\right)S_f+\frac{1}{\delta E\left(c\right)}-\frac{\lambda }{\delta }E\left(L\right)\right)\right)\right)\\ +S_a\left(S_g+{\lambda }_c\left(S_h-S_d\left(\frac{b(b+1)}{2}\lambda E\left(L\right)-\frac{\lambda }{\delta }\left(1+b\right)\right)\right)-S_a\left(S_g-{\lambda }_c\left(1+b\right)\right)\right)\end{array}\right)\end{array}}{{\left({1-(b+1)S}_a\right)}^2}}$$

(32)

where${\lambda }_c=\left(\pi -{\displaystyle \frac{b}{1-b}}\right)$

$$S_d=p{S}_1^{{*}^{\prime }}\left(\delta \right)+(1-p)p{S}_2^{{*}^{\prime }}\left(\delta \right);S_a=(p{S}_1^{*}\left(\delta \right)+\left(1-p\right)S_2^{*}\left(\delta \right)),$$

$$S_c=p{(1-S}_1^{*}\left(\delta \right))+\left(1-p\right){(1-S}_2^{*}\left(\delta \right));S_h={\displaystyle \frac{b\lambda }{2}}E\left(L^2\right)-{\displaystyle \frac{b}{2E\left(c\right)}}E\left(L\right)$$

$$S_e={\displaystyle \frac{\pi \lambda }{\delta }}E\left(R\right)-\delta ;S_f={\displaystyle \frac{\lambda }{{\delta }^2}}+{\displaystyle \frac{\lambda }{2}}E\left(R^2\right);S_g={\displaystyle \frac{b}{2}}E\left(L\right)\left(\lambda E\left(R\right)-1\right)$$

Also, ${R^{*}}^{\prime }\left(0\right)$ and ${L^{*}}^{\prime }\left(0\right)$ are the mean repair time and mean vacation time; ${R^{*}}^{″}\left(0\right)$ and ${L^{*}}^{″}\left(0\right)$ are the second moment repair time and vacation time.

7. Rate Arguments

Disasters in the system can occur either before the commencement of a repair period or at the conclusion of a busy period. Consequently, the rate at which disasters occur is expressed as

$$r_d={\displaystyle \frac{\lambda P_0\left(\pi -\frac{b}{1-b}\right)\left(P\left(1-S_1^{*}\left(\delta \right)\right)+(1-P)(1-S_2^{*}\left(\delta \right))\right)}{(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)}}$$

(33)

At the end of a busy period, the server may proceed to take a vacation. Hence, the rate of normal busy period completion is expressed as

$$r_{nbpc}={\displaystyle \frac{z\lambda P_0\left(\pi R^{*}\left(A_z\right)-H_z\right)\left(P\left(1-S_1^{*}\left(\delta \right)\right)+(1-P)(1-S_2^{*}\left(\delta \right))\right)}{z-\left(p{S}_1^{*}\left(A_z+\delta \right)+(1-p).S_2^{*}(A_z+\delta )\right)\left(zb{L}^{*}\left(A_z\right)+1\right)}}$$

(34)

Every busy period is initiated either following the conclusion of the previous busy period or after the occurrence of a disaster. Accordingly, the rate of initiation of a busy period is given as

$$r_{sbp}=\lambda P_0\left(P\left(1-S_1^{*}\left(\delta \right)\right)+\left(1-P\right)\left(1-S_2^{*}\left(\delta \right)\right)\right)\left(\begin{array}{c}{\displaystyle \frac{z\left(\pi R^{*}\left(A_z\right)-H_z\right)}{z-\left(p{S}_1^{*}\left(A_z+\delta \right)+\left(1-p\right).S_2^{*}\left(A_z+\delta \right)\right)\left(zb{L}^{*}\left(A_z\right)+1\right)}}\\ +{\displaystyle \frac{\left(\pi -\frac{b}{1-b}\right)}{(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)}}\end{array}\right)$$

(35)

A customer leaves the system either after his first essential service or second optional service. Therefore, the rate of customers leaving the system (due to service completion) is given as

$$r_{clsc}={\displaystyle \frac{\lambda P_0\left(\pi -\frac{b}{1-b}\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)}{(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)}}$$

(36)

If a customer suffers disaster only during the first essential service, therefore, the rate of customers leaving (due to disaster) is given as

$$r_{cld}=\lambda \left({E\left(c\right)-P}_0{\displaystyle \frac{\left(\pi -\frac{b}{1-b}\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)}{(1-\left(b+1\right)\left(p\left(S_1^{*}\left(\delta \right)\right)+(1-p)\left(S_2^{*}\left(\delta \right)\right)\right)}}\right)$$

(37)

8. Numerical Illustration

Numerical technique was applied to compute the queue size distribution for various states in the illustrated real-life situation that exist in textile production. Parameters $\mu ,r,v$ are assumed to be distributed in exponential. The numerical parameters were chosen as illustrative values to highlight the behavioral impact of service choice, vacations, and disaster–repair dynamics. Real industrial datasets that jointly capture all these features are not readily available, but the selected ranges are consistent with those used in related queueing studies.

In a textile manufacturing unit, the arrival rate of fabric rolls to the manufacturing unit is $\lambda$, where they choose between standard finishing or advanced finishing services based on their specific needs. Standard finishing involves basic chemical treatments aimed at enhancing fabric durability, with a processing rate ${\mu }_1=5$, while advanced finishing includes high-tech processes like waterproofing, anti-bacterial coatings, or UV curing for wrinkle resistance, processed at a rate ${\mu }_2=6$. Both services are susceptible to disasters; standard finishing faces machine malfunctions due to wear and tear, and advanced finishing encounters high-tech failures such as UV curing machine breakdowns at a disaster rate $\delta$. After a disaster, the machine undergoes a repair phase at a rate $r$before resuming operations. Additionally, during periods of low workload, the machine may enter a Bernoulli vacation state for maintenance with a rate $v.$

To analyze the described textile production system, the tables below summarize the key parameters, and the graphs represent the impact of these parameters on the performance metrics. These visualizations provide a clear understanding of the system’s behavior under different scenarios, highlighting the effects of disasters in different service.

From

Table 2. Performance measures with $\mathsf{\lambda }=2 \mathrm{a}\mathrm{n}\mathrm{d} \mathsf{\delta }=3$.

$\mathit{p}$	${\mathit{P}}_0$	$\mathit{E}\left({\mathit{Q}}_{\mathit{L}}\right)$	$\mathit{E}\left({\mathit{W}}_{\mathit{T}}\right)$
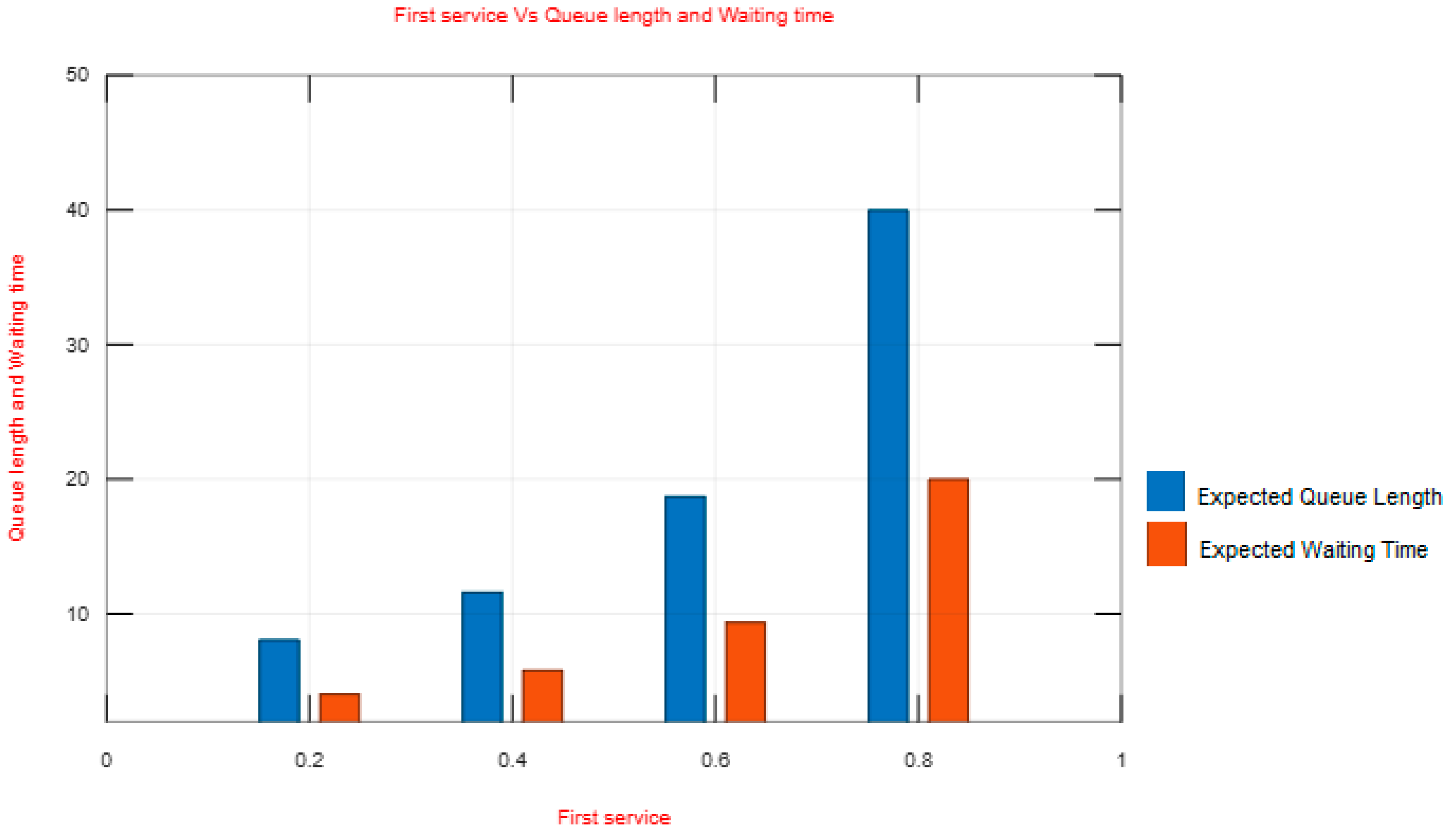
0.2	0.0675	8.033	4.017
0.4	0.0520	11.585	5.792
0.6	0.0356	18.683	9.341
0.8	0.0183	39.965	19.983

and Figure 1, it is evident that as the probability $p$ of opting for the standard finishing service of the first kind increases, the idle time of the fabric rolls decreases, while the queue length and expected waiting time increase. This occurs because the service rate for standard finishing ${\mu }_1$ is lower than that of advanced finishing ${\mu }_2$.

From

Table 3. Performance measures with $\delta =4,p=0.25,\mathrm{a}\mathrm{n}\mathrm{d}b=0.5$.

$\mathit{\lambda }$	${\mathit{P}}_0$	$\mathit{E}\left({\mathit{Q}}_{\mathit{L}}\right)$	$\mathit{E}\left({\mathit{W}}_{\mathit{T}}\right)$
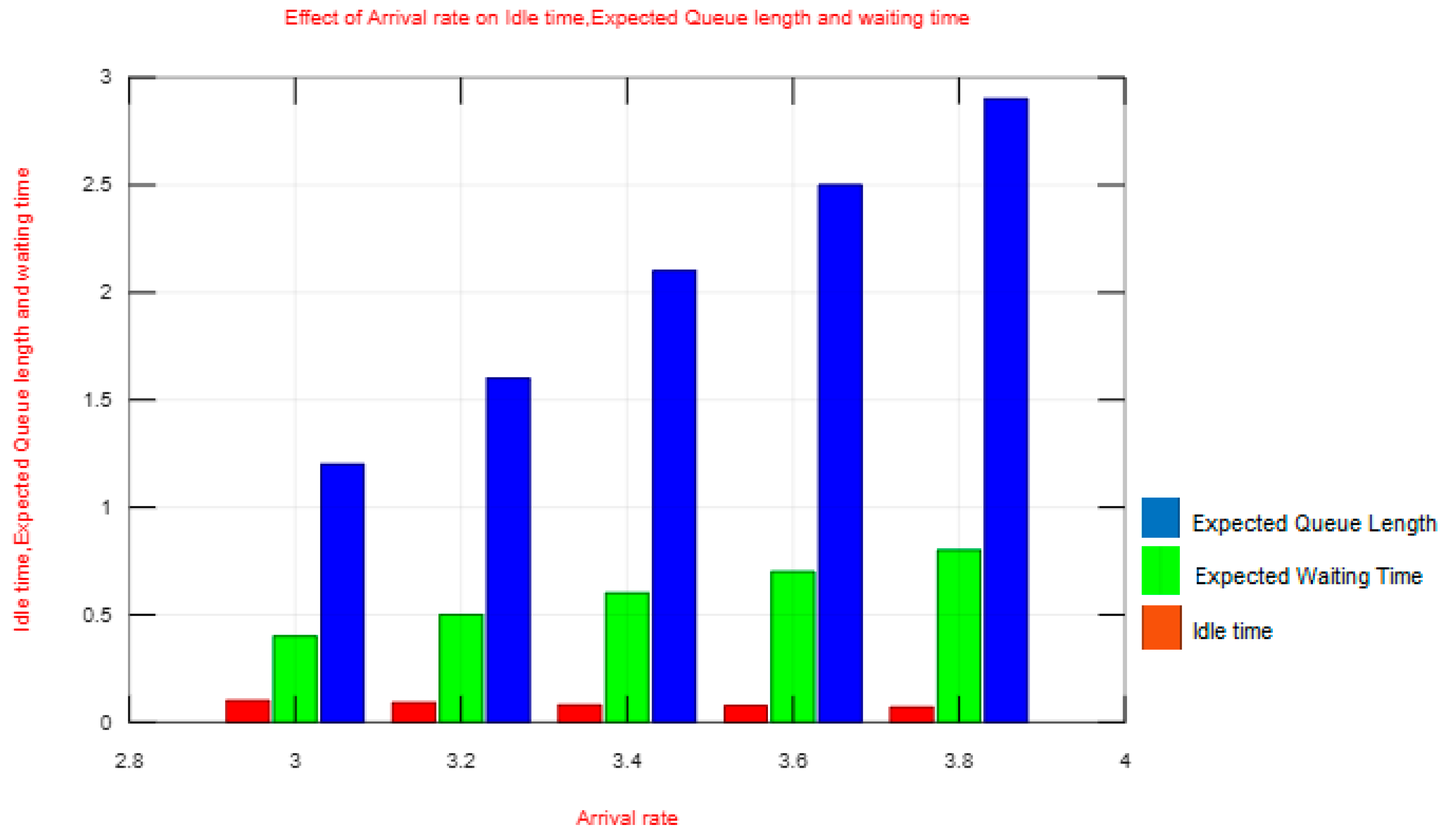
3.0	0.0974	1.2013	0.4004
3.2	0.0898	1.6357	0.5111
3.4	0.0831	2.0700	0.6088
3.6	0.0772	2.5032	0.6953
3.8	0.0719	2.9353	0.7725

and Figure 2, it is clear that an increase in the arrival rate of fabric rolls leads to a rise in both the queue length and expected waiting time, reflecting the added workload on the system. Conversely, when the disaster rate increases, as also shown in

Table 4. Performance measures with $\lambda =2,p=0.25,\mathrm{a}\mathrm{n}\mathrm{d}b=0.5$.

$\mathit{\delta }$	${\mathit{P}}_0$	$\mathit{E}\left({\mathit{Q}}_{\mathit{L}}\right)$	$\mathit{E}\left({\mathit{W}}_{\mathit{T}}\right)$
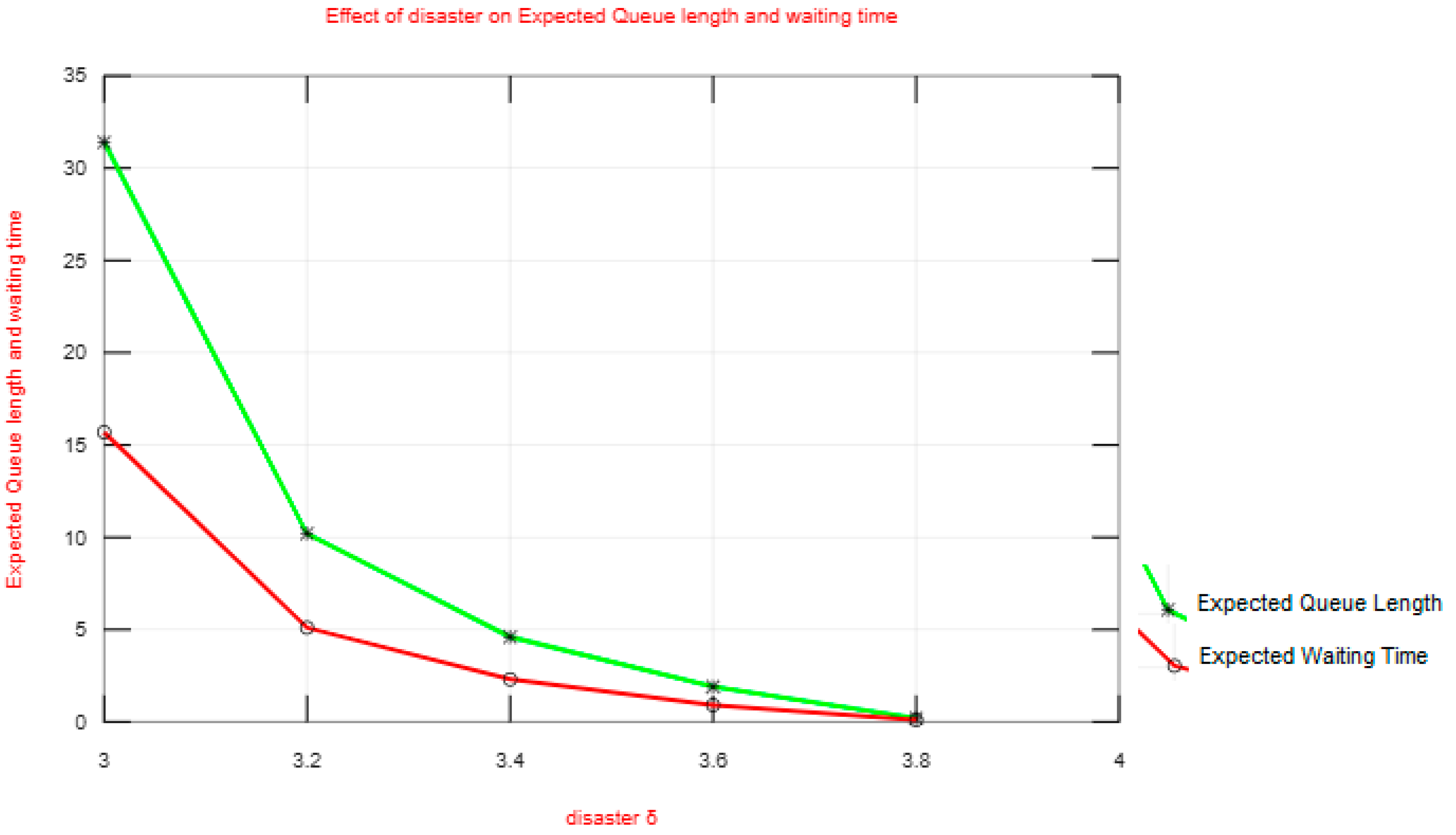
3.0	0.0227	31.453	15.727
3.2	0.0537	10.161	5.080
3.4	0.0823	4.566	2.283
3.6	0.1087	1.877	0.938
3.8	0.1332	0.228	0.114

and Figure 3, the queue length and expected waiting time decrease, indicating reduced service continuity due to frequent interruptions requiring repairs.

Although the model is motivated by textile manufacturing operations, empirical datasets that jointly capture bulk arrivals, heterogeneous services, Bernoulli vacations, and disaster–repair behavior are not currently available; therefore, the numerical results presented here serve as theoretical illustrations, with analytical correctness verified through consistency with known $M^X/G/1$ special cases.

9. Conclusions

In this article, an $M^X/G/1$ queueing model with two heterogeneous services and a Bernoulli vacation schedule is examined in the context of disasters and repairs within the textile manufacturing industry. We derive the queue size distributions for various steady states, along with quality metrics, using the supplementary variable technique. Numerical examples are provided to illustrate the approach, demonstrating the disaster, impact waiting times, and queue lengths for the two service types in textile production. The numerical analysis reveals key insights: as the arrival rate and the probability of opting for the service increase, both the server’s busy period and customer waiting times also rise. Conversely, when the disaster rate increases, leading to more frequent system interruptions, the server’s busy period and customer waiting time decrease. These findings highlight the critical role of managing service options, machine downtime, and operational disruptions in optimizing production efficiency and minimizing delays in textile manufacturing.