1. Introduction
Crohn’s disease [
1] is a chronic inflammatory intestinal disorder that may involve any region of the digestive tract, with the terminal ileum and colon being the most commonly affected areas. Dysregulation of the immune system is the central pathological feature of Crohn’s disease [
2,
3]. Normally, the immune response helps the body defend against foreign pathogens. But in Crohn’s disease, it mounts an aberrant response to commensal gut microbiota and dietary antigens, resulting in chronic intestinal inflammation. This inflammation not only damages the normal structure and function of the affected parts of the intestine but can also lead to a series of complications that, in severe cases, may even threaten the patient’s life. In a healthy state, gut bacteria are kept in check by phagocytes, maintaining a homeostatic balance. In Crohn’s disease, however, this delicate balance is disrupted, leading to a pathological cycle where phagocyte activity against bacteria perpetuates inflammation and tissue damage. Crucially, Crohn’s disease manifests clinically as a chronic and relapsing condition. The fluctuating and unpredictable nature of core symptoms, such as abdominal pain, diarrhea, and fatigue, poses persistent and substantial challenges for disease management, the selection of treatment strategies, and patient quality of life.
The pathogenesis of Crohn’s disease involves complex interactions among genetic, environmental, and immunological factors [
4,
5,
6]. Despite significant advances in clinical research, the precise mechanisms driving the pathologic interactions between gut bacteria and phagocytes remain poorly understood. As an effective approach, reaction-diffusion dynamical systems have attracted widespread attention in recent research [
7,
8,
9,
10,
11]. Therefore, mathematicians employ mathematical modeling to examine gut dysbiosis, propose simplified models to simulate the immune responses that triggers inflammation, and thus investigate the pathogenesis of Crohn’s disease [
12,
13,
14].
In [
12], Nadin et al. characterized the patchy inflammatory patterns in the intestinal tract that are characteristic of Crohn’s disease. To explain this phenomenon, they proposed a diffusion system modeling bacteria-phagocyte interactions (
1) and demonstrated the occurrence of Turing instability. Turing instability refers to a phenomenon in which, under certain conditions, the homogeneous equilibrium state of a reaction-diffusion system may become unstable upon the introduction of diffusion terms, leading to the spontaneous emergence of spatial patterns.
where
denotes the bacterial biomass,
denotes the phagocyte biomass, and
denotes the Laplace operator. The Neumann boundary conditions
at
and
represent no-flux conditions, modeling a closed environment.
,
are continuous functions with non-negative values, defined on the interval
. All other parameters are positive, with their biological meanings summarized in
Table 1.
Shi et al. [
13] conducted further investigations on the system (
1). Through multiscale analysis, they derived amplitude equations governing Turing pattern structures under varying bacterial biomass conditions, and proposed a numerical metric for assessing the severity of Crohn’s disease.
To better align the bacteria-phagocyte interaction model with biological reality, Shi et al. introduced the interference between phagocytes during phagocytosis of bacteria into the system in [
14]. They investigated the complex spatiotemporal dynamics generated by the system (
2) near the Turing-Hopf bifurcation point through bifurcation analysis. In addition, they also focused on the effects of intestinal permeability and phagocyte diffusion rate on the pattern structure of Crohn’s disease.
In biological systems, immune responses are never instantaneous [
16]. Numerous studies have investigated the associated time delays [
17,
18,
19]. Cherraf et al. [
17] incorporated both time delays and diffusion processes when modeling tumor-immune system interactions. In [
18], Yang et al. found that intracellular time delay in HIV infection models can induce Hopf bifurcations, destabilizing immune-presence equilibria. Riha et al. [
19] developed a model with fractional order and time delay to describe the interactions between the tumor immune system and external treatments.
In Crohn’s disease, intestinal phagocytes, such as macrophages, require a certain amount of time to detect bacteria, migrate to the site of infection, and initiate effector functions. Although this is physiologically significant, most previous studies in Crohn’s disease [
12,
13,
14] have simplified immune activation as an instantaneous process (i.e.,
), which may overlook some critical dynamic changes. Within the framework of our model, this delay is specifically attributed to the intracellular execution time of phagocytosis, the core effector function. This process involves multiple biochemical steps, including recognition, internalization, and degradation, and is considered the most significant rate-limiting stage [
20,
21]. Therefore, we specifically correlate the phagocytic rate at time
t with the bacterial biomass at an earlier time
, modifying the phagocytic term in the model (
2) to
. This formulation captures the biological principle that the clearance efficacy observed at the present moment is determined by bacterium-phagocyte encounters that occurred at a prior time. We model
as a constant delay, based on the core biological assumption that the mean time required for a phagocyte to complete a successful phagocytic event is relatively stable for a given host at a specific stage of disease progression. This duration is primarily set by intrinsic physiological constraints dictated by the host’s genetic background and immune status. Given that time delays are well-known to induce Hopf bifurcations and subsequent oscillatory dynamics in such systems, we propose the following model (
3) to investigate its Hopf bifurcation.
In the term , the parameter s quantifies the negative effect of phagocyte concentration on epithelial resistance, thereby exerting a positive net effect on bacterial density. Activated phagocytes n damage the intestinal epithelium by releasing inflammatory mediators. The resulting epithelial gaps, represented by the term , create new colonization niches for bacteria m, which in turn recruit additional phagocytes to the site, further exacerbating epithelial porosity and perpetuating a self-sustaining cycle of inflammation.
The functional response term for phagocytosis,
is adopted from prior works [
12,
13,
14] to facilitate comparison. Within this structure, the parameters are endowed with distinct physical meanings through the defined relationship
Here,
a represents the maximum engulfment rate, with its reciprocal
defining the average handling time per bacterium. The parameter
r functions as the baseline half-saturation constant, specifying the bacterial density required for the engulfment rate to reach half of its maximum under idealized conditions. Consequently, the ratio
defines the encounter rate, characterizing phagocyte search efficiency. This interlocked set of definitions ensures that all parameters possess clear and independent biological interpretations.
Our analysis focuses on the stability of the positive equilibrium and the direction of the Hopf bifurcation. Specifically, the derivation of the bifurcation direction utilizes normal form and center manifold theory, an approach that is universally applied in the bifurcation analysis of systems [
22,
23].
The paper is structured in the following manner.
Section 2 establishes the positivity, boundedness, and global stability of the solutions to the ordinary differential system (
4) without time delay.
Section 3 investigates the local stability of the positive equilibrium point and the occurrence of Hopf bifurcation in the delayed system (
3) and
Section 4 analyzes the direction and stability of the spatial Hopf bifurcation.
Section 5 validates the theoretical results through numerical simulations and explores the influence of time delay and other parameters on the system’s dynamic behavior. The final section concludes the paper.
3. Stability Analysis of the Partial Differential Model with Delay
It is important to note that both the time delay
and diffusion terms do not affect the existence or the values of the equilibrium points. This is because, at an equilibrium, the system states are constant in time, nullifying the effect of the delay, and spatially homogeneous, nullifying the Laplacian diffusion terms. Consequently, the conditions for finding equilibrium points are identical to those of the homogeneous system. Therefore, the equilibrium point formulas (
8) remain valid for system (
3).
In this section, we analyze the stability of the equilibrium point
and the emergence of Hopf bifurcation for the system (
3).
The linearized system at
is
where
and
Therefore, the equation of the characteristic takes the form
where
,
and
.
Lemma 1. Assuming that and are satisfied, the system (
3)
behaves stably when . Proof. The detailed proof for the case when
can be found in [
14]. Briefly speaking, (
15) can be written in
with
and
for
. Hence all roots of (
15) possess negative real parts for
. □
can be easily obtained under and , then Lemma 2 holds.
Lemma 2. Assuming that and are satisfied, the value does not satisfy Equation (
15)
for any . When
, let
be the solutions of (
15). Euler’s formula provides a representation of eigenvalues through their real and imaginary components.
Square both sides of the two equations in (
16) and then add them together, we can obtain
Define
, then (
17) is equivalent to
and the roots of (
18) take the form
Through the computation, it is found that
Under the hypothesis
and
, there will be two possible situations.
Lemma 3. Assuming that and are satisfied, the following statements hold.
- (i)
In , Equation (
15)
has no purely imaginary root. - (ii)
In , Equation (
15)
has two roots at , where
Let
be the root of Equation (
15), where its real part is 0 and its imaginary part is
as
approaches
. Therefore, we derive the transversality condition.
Lemma 4. Assuming that , and are satisfied, we can obtain Proof. Using
and (
15), the following expression can be obtained.
Therefore
. □
Define
. The situation where
for some
may occur. This paper addresses
In summary, the Theorem 4 is obtained.
Theorem 4. For system (
3),
assuming that and are satisfied, the statements below hold. - (i)
In , is locally stable. The system (
3)
will asymptotically converge to it. - (ii)
In , for , is locally stable. The system (
3)
will asymptotically converge to it. - (iii)
In , for , exhibits instability.
- (iv)
In , the system (
3)
also undergoes a Hopf bifurcation. When with , the bifurcating periodic solutions arising from the bifurcation are spatially homogeneous. Otherwise, the bifurcating periodic solutions are not spatially homogeneous.
5. Numerical Simulations
To confirm the accuracy of the results above, we use MATLAB R2020a for numerical simulation.
For the system (3), the values of the parameters are shown in
Table 1. By calculation, we can obtain the positive equilibrium point
and
Therefore both
and
are satisfied, and
is met. Through further calculation, it is obtained that
,
,
.
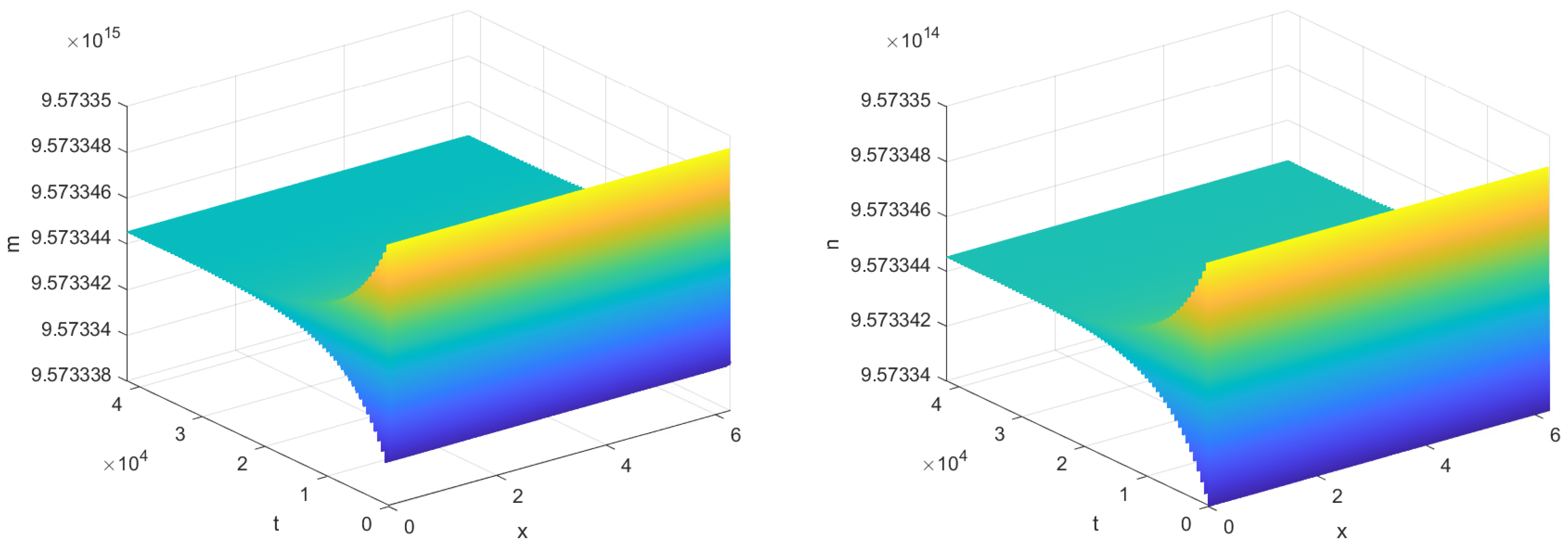
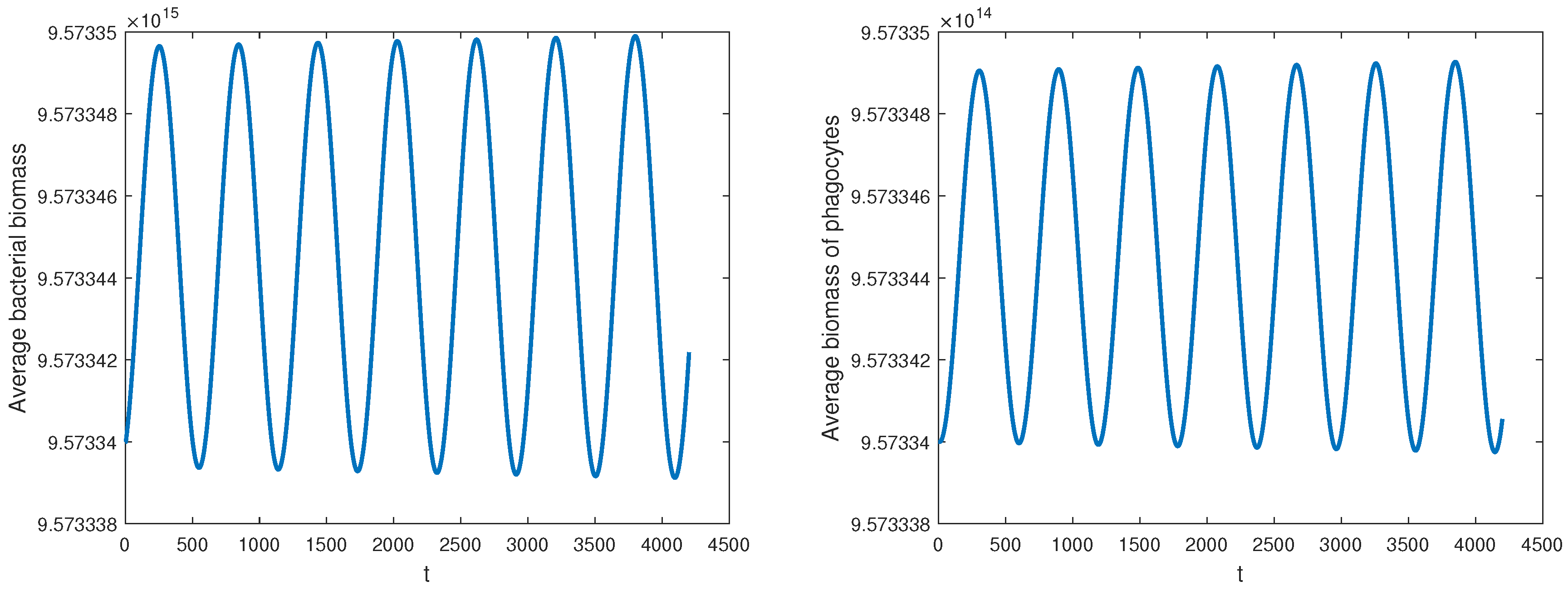
Theorem 4(ii) implies that when
,
is locally asymptotically stable. This can be shown in
Figure 1, where
is chosen. Theorem 4(iii) implies that the equilibrium
loses its stability as
increases through
, giving rise to a Hopf bifurcation. According to Theorem 5,
It can be concluded from the above results that the bifurcation proceeds in the forward direction. The bifurcating periodic solutions are locally asymptotically stable. Moreover, the period of the solutions emerging from the bifurcation decreases with increasing
.
Figure 2 illustrates this behavior at the value
.
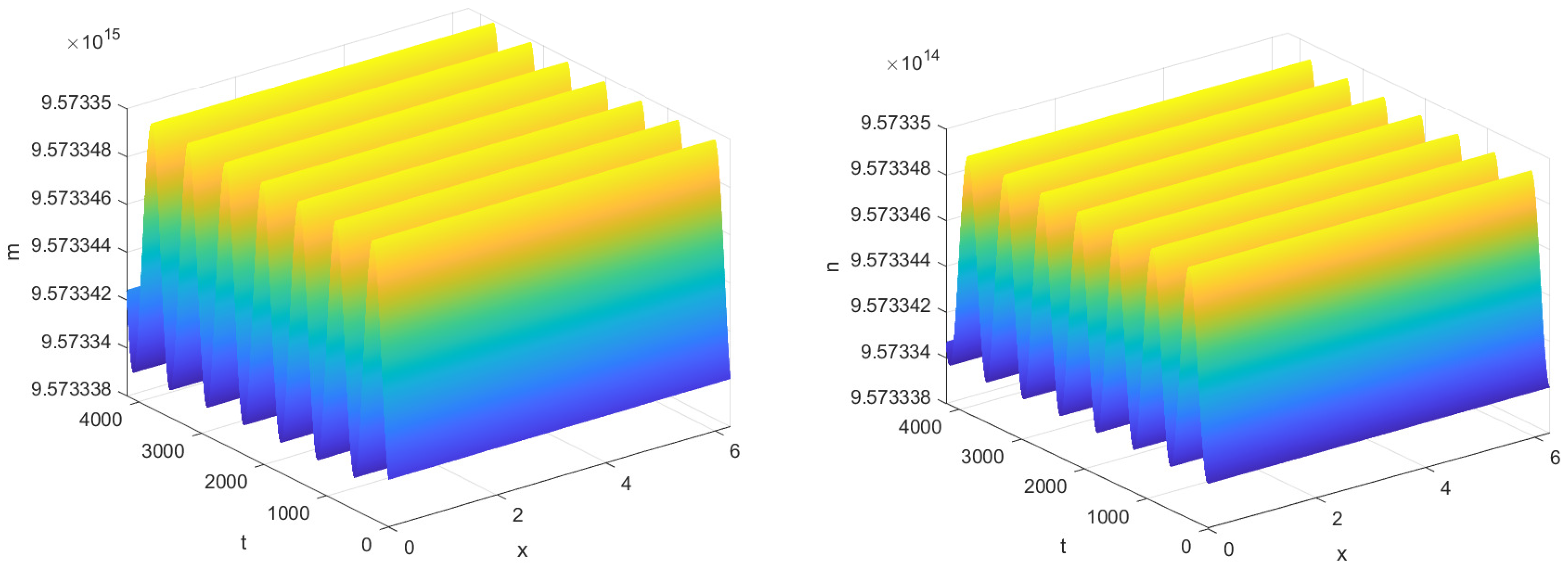
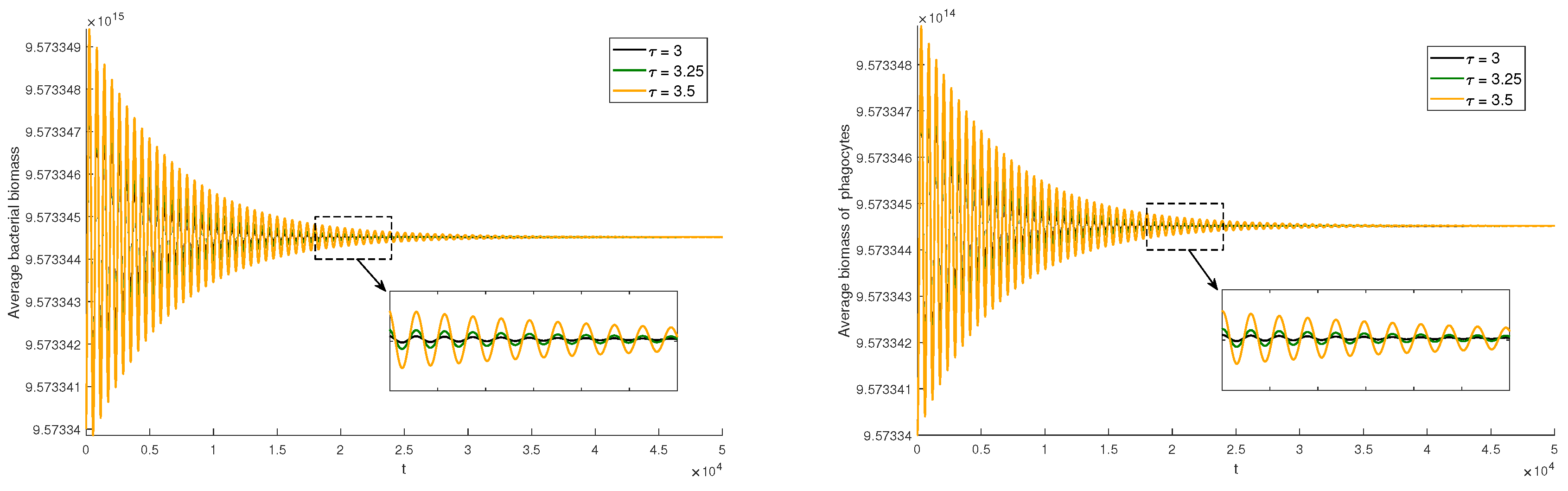
As shown in
Figure 3,
Figure 4 and
Figure 5, time delay plays a critical role in inflammatory responses, where even minor variations can lead to significant changes in system dynamics. Specifically, when
, the time it takes for the system to reach steady state is significantly longer than when there is no time delay, i.e.,
. This is because the introduction of time delay causes a lag in the response of phagocytes to bacterial signals, resulting in the system’s current state being dependent on its past state, slowing down the convergence to steady state. Notably, as shown in
Figure 4, when
, the stabilization time of the system increases with increasing
, indicating that delays in immune regulation may prolong infection recovery time. And as shown in
Figure 5, when
, the system transitions into a stable periodic oscillatory state. This shift suggests that excessive delays in immune responses may lead to recurrent inflammation.
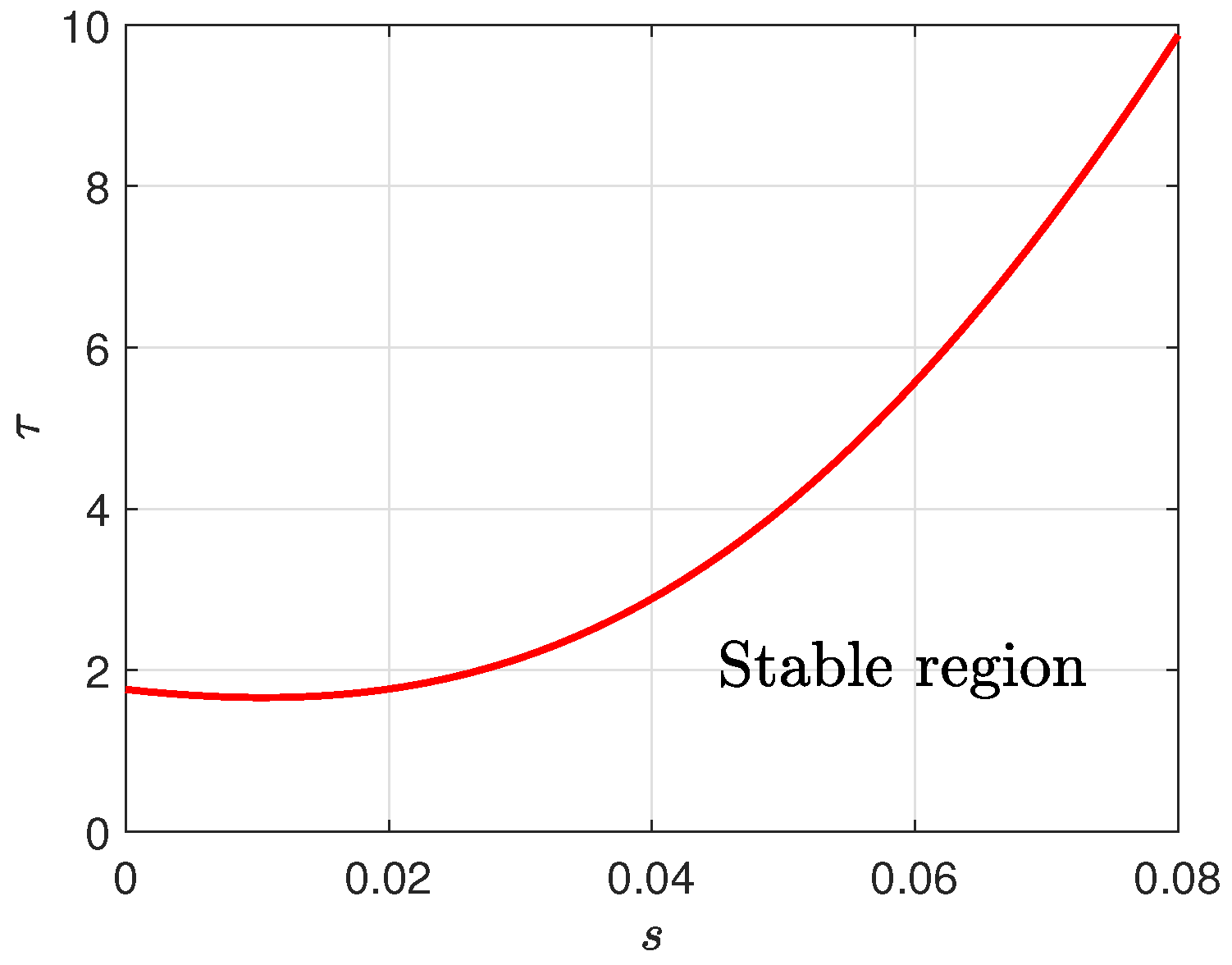
Since intestinal permeability serves as a critical pathological marker in Crohn’s disease, we analyze the interactions between the parameter
s and the time delay
to elucidate their effects on system dynamics. As illustrated in
Figure 6, at fixed
, increased intestinal permeability can prolong the time required to reach steady state, manifesting as a postponement in the onset of oscillations. This phenomenon may correspond to the early stage of Crohn’s disease, where despite impaired barrier function, dynamic balance is temporarily maintained through immune regulation. Conversely, when intestinal permeability is constant, an increase in time delay can lead to a decrease in system stability, making oscillations more likely. This reflects the immune regulatory dysfunction observed clinically: delayed immune responses fail to suppress inflammation in time, leading to disease progression.
To identify which parameters have a greater impact on the system’s behavior, a local sensitivity and elasticity analysis is performed [
29]. The analysis focuses on the equilibrium point
of the system (3). The sensitivity coefficient
measures the absolute change in a component of
E resulting from an infinitesimal change in a parameter, i.e.,
where
is a component of the equilibrium. In contrast, the elasticity coefficient
is a dimensionless measure, representing the percentage change in an equilibrium component in response to a 1% change in a parameter, i.e.,
This normalization allows for a direct comparison of the relative importance of parameters with different units.
The results in
Table 2 reveal key drivers of the system’s dynamics. The high elasticity (
) of the intestinal permeability coefficient
a and phagocyte mortality rate
v signifies that proportional changes in these parameters will cause the most pronounced proportional shifts in the system’s steady state. This highlights their roles as potential control points in the pathological process. Conversely, while the bacterial growth rate
p has a lower relative impact (low
), its substantial absolute effect (high
) suggests it acts as a powerful direct driver of bacterial load.
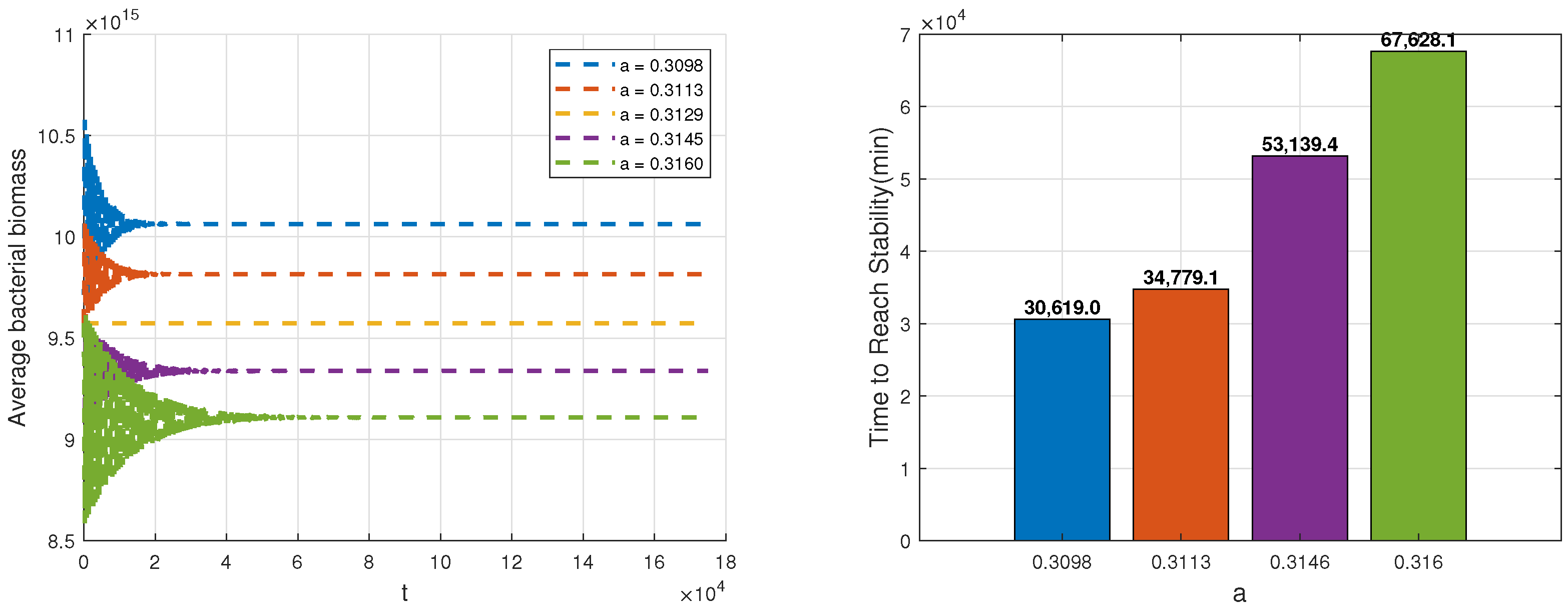
Based on the above analysis, we examine the influence of parameters
a,
v and
p on both the spatial average biomass of bacteria and the time required to reach equilibrium. A step size of
is used to determine the time to reach stability. We consider the system to reach equilibrium when the variation in average bacterial biomass remains below
for 50 consecutive steps. As shown in
Figure 7, an increase in maximum engulfment rate by phagocytes can reduce bacterial biomass but also prolongs the stabilization time, indicating that phagocytes require more time to regulate the inflammatory response. For example, when
, the average bacterial biomass is relatively low, but the system takes 67,628.1 min, approximately 4.7 days, to reach stability.
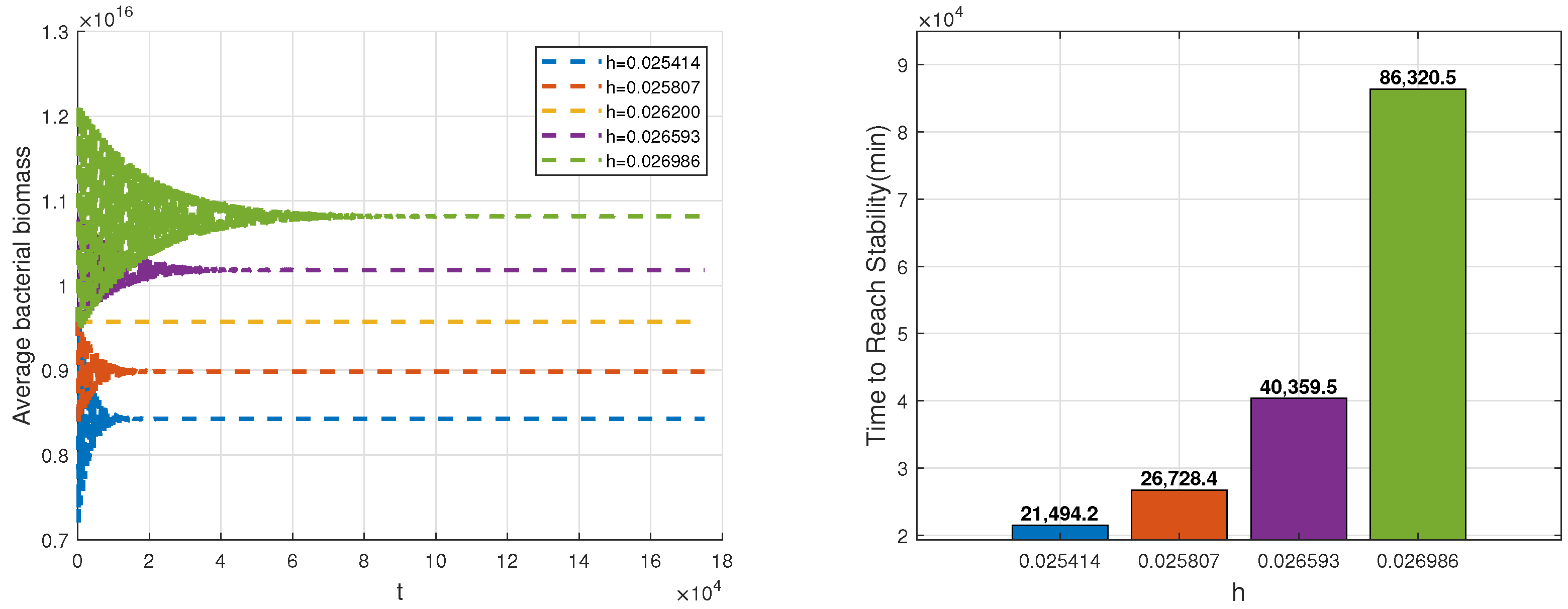
Figure 8 demonstrates that when the phagocytosis death rate increases, the average bacterial biomass rises, and the time for bacteria to stabilize shortens. However, despite the rapid stabilization of bacteria, the infection is not effectively cleared. At last,
Figure 9 reveals that an increase in the rate of bacterial increase leads to higher average bacterial biomass and a longer stabilization time. The persistent stimulation of the immune system by bacteria prolongs the duration of infection.
6. Conclusions
Crohn’s disease, a chronic inflammatory bowel disorder, arises from dysregulated interactions between intestinal phagocytes and gut microbiota. In this paper, we establish a delay differential model of the phagocyte–bacteria interactions to study the dynamic behavior of these interactions. First, we prove the positivity, boundedness, existence, uniqueness, and global stability of the solutions for the ordinary differential system without a time delay. We investigate the stability of the positive equilibrium point and analyze the existence of Hopf bifurcation for the partial differential system with a time delay. Our study reveals that when the delay exceeds a critical value a forward Hopf bifurcation occurs, provided that , destabilizing the positive equilibrium and giving rise to periodic oscillations. By applying normal form theory and center manifold theory, we systematically derive the bifurcation direction and stability criteria for the bifurcating periodic solutions.
Numerical simulations verify the theoretical results. Comparing the temporal changes in average biomass of bacteria and phagocytes with and without time delay, we find that the delay significantly slows down the system’s approach to a steady state. This indicates that the time delay in immune regulation may prolong inflammation recovery time. We analyze the interactions between intestinal permeability s (a key pathological marker of Crohn’s disease) and time delay from different perspectives. When is fixed, increased intestinal permeability prolongs the time required for the system to reach steady state, corresponding to the early stage of Crohn’s disease. When s remains constant, increased time delay makes the system more susceptible to oscillations, matching clinically observed immune regulation dysfunctions. Finally, we conduct sensitivity analysis on other parameters to study their effects on average bacterial biomass and the time required to reach stability. The results show that an increased maximum engulfment rate by phagocytes a reduces bacterial biomass but prolongs stabilization time, while an increased phagocyte death rate v shortens stabilization time but increases average bacterial biomass. Additionally, an increased rate of bacterial increase p leads to higher average bacterial biomass and longer stabilization time. These findings provide insights into the dynamic equilibrium in immune systems.