Total Decoupling of 2D Lattice Vibration

Abstract

Lattice structures find broad application in aerospace, automotive, biomedical, and energy systems owing to their exceptional structural stability. These systems typically exhibit complex internal couplings that facilitate vibration propagation across the entire network. The primary objective of this study is to achieve total decoupling of 2D lattice vibration system, which involves eliminating all inter-subsystem interactions while preserving spectrum. Building upon prior research, we develop structure-preserving isospectral transformation flow (SPITF) framework to address this challenge. Two principle results are established: first, the equations of motion are systematically derived for lattice vibration systems; second, total decoupling is successfully realized for such systems. Numerical experiments validate the decoupling capability of lattice vibration systems.

1. Introduction

Coupled systems consist of two or more subsystems interconnected through dynamic linkages and exhibit significant mutual interactions. Such systems are prevalent across numerous multidisciplinary fields, including engineering and scientific research. Representative examples include mechanical coupling between structural components in building seismic analysis, multi-body interactions among the deck, cables, and towers in bridge dynamics, and vibroacoustic coupling between structural vibration and acoustic propagation. These coupling effects induce intricate emergent behaviors, such as multivariate correlations, which considerably complicate system modeling, performance analysis, and controller design. The decomposition of a multi-degree-of-freedom system into mutually independent single-degree-of-freedom subsystems constitutes a significant research objective, as it facilitates targeted analysis and optimization of specific components while improving the efficiency of complex system design and modification. This represents the fundamental objective of decoupling.

Second-order linear dynamical systems constitute a cornerstone model in scientific and engineering disciplines [1]. Such systems are typically governed by the following equation:

$$\mathbf{M}\ddot{\mathbf{x}}\left(t\right)+\mathbf{C}\dot{\mathbf{x}}\left(t\right)+\mathbf{K}\mathbf{x}\left(t\right)=\mathbf{f}\left(t\right),$$

(1)

where $\mathbf{M}$,$\mathbf{C}$, and $\mathbf{K}$ represent the given coefficient matrices. Mathematically, this family of systems admits mature and rigorous analytical and computational methods. Considerable theoretical and numerical advances have been made in decoupling second-order linear dynamical systems [1,2].

Undamped systems, where $\mathbf{C}=0$, can be interpreted as a generalized eigenvalue problem (GEP). The eigenvectors obtained from its solution form a congruence transformation matrix, which effectively decouples the system. Based on this theoretical foundation, classical modal analysis has been developed to decouple classically damped systems [3], which are characterized by symmetric coefficient matrices with positive-definite $\mathbf{M}$, non-negative-definite $\mathbf{C}$ and $\mathbf{K}$, and satisfaction of the Caughey-O’Kelly commutativity condition [4] [Theorem 2].

$$\mathbf{C}{\mathbf{M}}^{-1}\mathbf{K}=\mathbf{K}{\mathbf{M}}^{-1}\mathbf{C}.$$

For general non-proportionally damped systems, several decoupling methods have been developed, as reported in [5,6,7,8,9,10]. However, most existing approaches depend on complete spectral information of the system, a requirement that is often infeasible in practical engineering applications.

Spectral decomposition constitutes another analytical technique for decoupling second-order linear dynamical systems. Any solution $(\lambda ,\mathbf{u})\in \mathbb{C}\times {\mathbb{C}}^n$ to the quadratic eigenvalue problem (QEP) [1,11,12]

$$Q\left(\lambda \right)\mathbf{u}=0$$

yields a fundamental solution

$$\mathbf{x}\left(t\right)=\mathbf{u}{e}^{\lambda t}$$

to the differential system (1). The spectral properties of the quadratic pencil

$$Q\left(\lambda \right):=Q(\lambda ;\mathbf{M},\mathbf{C},\mathbf{K})={\lambda }^2\mathbf{M}+\lambda \mathbf{C}+\mathbf{K}$$

(2)

dictates the dynamic behavior of the system. For example, the quadeig in [13] and the polyeig in Matlab R2011b. Nevertheless, this method depends on obtaining the complete set of eigeninformation, a demanding requirement that is often infeasible in practical applications.

The phase synchronization technique [14,15] converts non-classically damped modes into classically damped forms, thereby enabling system decoupling through classical modal analysis. In contrast to classically damped modes characterized by real eigenvectors, non-classically damped modes exhibit complex conjugate eigenvector pairs [16]. This approach alters modal properties by synchronizing phase differences among modal components via phase shifts, reflecting the fundamental principle of phase synchronization. Nevertheless, the method still requires complete eigeninformation of the system.

In our previous work on decoupling second-order linear dynamical systems, we developed the structure-preserving isospectral transformation flow (SPITF) algorithm [17]. This framework enables decoupling without requiring complete spectral information. Specifically, SPITF constructs a transformation matrix that preserves the Lancaster structure. Through simultaneous congruence transformations applied to the coefficient matrices $\mathbf{M}$, $\mathbf{C}$, and $\mathbf{K}$, total decoupling is achieved. Preservation of the Lancaster structure ensures invariance of the system’s spectral properties, thereby maintaining consistent dynamic characteristics during decoupling. The theoretical foundation of the SPITF algorithm will be comprehensively presented in Section 4.

Second-order nonlinear dynamical systems occur more frequently in practical applications. Although decoupling techniques for linear systems have been extensively studied, their extension to nonlinear systems remains limited. Nonlinear systems exhibit inherently complex coupling mechanisms that pose substantially greater challenges for analysis and decoupling compared to their linear counterparts. Consequently, research on decoupling for second-order nonlinear dynamical systems carries significant theoretical and practical importance.

This paper addresses the decoupling of 2D lattice vibration systems, a representative category of second-order nonlinear dynamical systems. Consider a 2D network comprising n masses interconnected by normal springs and dampers in a specified configuration. An example of a 3-mass system is illustrated in Figure 1, where each mass connects to a fixed end with different sprint elements while the internal sprints consist of one spring and one damper. The configuration in Figure 1 depicts a fundamental 2D lattice system, with Figure 2 demonstrating more complex architectures featuring multi-layered spring networks. Such lattice systems find broad applicability across scientific and engineering disciplines [18,19,20,21,22,23,24,25]. In medical domain, they enable analysis of soft tissue elasticity in skin lesions [26,27]. In quantum materials research, they enable investigation of the interplay between quantum and topological phase formation [28]. These systems typically exhibit complex dynamics characterized by multi-degree-of-freedom coupling, presenting substantial challenges in theoretical modeling, numerical implementation, and computational simulation. Consequently, developing decoupling methodologies for these systems carries significant theoretical importance while offering substantial potential for practical engineering applications.

This paper extends the SPITF framework to second-order nonlinear dynamical systems, achieving total decoupling of 2D lattice vibration systems. The work is organized into five sections. Section 2 develops a mathematical model for 2D lattice vibration systems, with rigorous validation of dynamic properties to ensure analytical soundness. Section 3 addresses system nonlinearity through linearization, transforming the model into a standard second-order linear ODE system. This transformation represents an essential prerequisite for achieving total decoupling. Building on this foundation, Section 4 reviews the SPITF framework for decoupling second-order linear dynamical systems, establishing the core methodology for total decoupling of 2D lattice systems. Finally, Section 5 presents experimental results and corresponding analyses.

2. Model Development

This section addresses vibration analysis in lattice systems within ${\mathbb{R}}^2$ space. Key notations and definitions are first introduced, followed by the development of a mathematical model. Lastly, the model’s validity is verified through dynamic behavior analysis.

Let $\mathfrak{K}=\left[k_{ij}\right]$ denote the matrix whenever masses $m_i$ and $m_j$ are connected by a spring with stiffness $k_{ij}$. We shall use the diagonal element $k_{ii}$ to denote the stiffness of a spring attached solely by the mass $m_i$ to a fixed end but not others. Likewise, let $\mathfrak{C}=\left[c_{ij}\right]$ be matrix recording damper linkages. In a sense, both matrices can be considered as adjacency matrices. For each mass $m_i$, let ${\mathbb{K}}_i$ denote the set of masses linked to $m_i$ by a spring and ${\mathbb{C}}_i$ the set of masses linked to $m_i$ by a damper. We may also assume that the mass $m_i$ is attached to a set of fixed rotational joints at ${\mathbf{b}}_i^{\left(j\right)}$ with spring stiffness $k_{ii}^{\left(j\right)}$ and damping $c_{ii}^{\left(j\right)}$, $j\in {\mathbb{F}}_i$. If ${\mathbb{F}}_i=\varnothing$, then $m_i$ is a free end.

Using vector notation, the following discussion remains valid in higher dimension. It is more convenient to use the position ${\mathbf{x}}_i$ of the mass $m_i$ to describe the equation of motion. Assume that the rest position of $m_i$ is at ${\mathbf{a}}_i$. For small deformation, we may assume also that the Hooke’s law is applicable [29]. Assume additionally that the springs are allowed to move translationally in the direction joining the masses and, thus, involve no angular nor torsional movement. Then the equation of motion is given by the nonlinear differential system

$$\begin{array}{ccc}\hfill m_i{\ddot{\mathbf{x}}}_i& =& -{\displaystyle \sum _{j\in {\mathbb{F}}_i}}{c}_{ii}^{\left(j\right)}{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^2}}{\dot{\mathbf{x}}}_i\hfill \\ \hfill & & -{\displaystyle \sum _{j\in {\mathbb{F}}_i}}{k}_{ii}^{\left(j\right)}{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel -\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel )\hfill \\ \hfill & & -{\displaystyle \sum _{j\in {\mathbb{C}}_i}}{c}_{ij}{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{x}}_j){({\mathbf{x}}_i-{\mathbf{x}}_j)}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2}}({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j)\hfill \\ \hfill & & -{\displaystyle \sum _{j\in {\mathbb{K}}_i}}{k}_{ij}{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{x}}_j}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel ).\hfill \end{array}$$

(3)

The first two terms are the linear damping and elastic restoring forces between mass $m_i$ and fixed point ${\mathbf{b}}_i^{\left(j\right)}$, whereas the latter two are the corresponding forces between masses $m_i$ and $m_j$, with both pairs generated by dampers and springs, respectively. It is important to note that the system might have additional equilibrium points. An equilibrium point of the system (3) necessarily satisfies the system of equations

$$\begin{array}{ccc}\hfill g_i({\mathbf{x}}_1,\dots ,{\mathbf{x}}_n)& :=& {\displaystyle \sum _{j\in {\mathbb{F}}_i}}{k}_{ii}^{\left(j\right)}{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel -\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel )\hfill \\ \hfill & & +{\displaystyle \sum _{j\in {\mathbb{K}}_i}}{k}_{ij}{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{x}}_j}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel )=0,i=1,\dots n\hfill \end{array}$$

(4)

which certainly is satisfied by the initial rest position. It is possible that at new equilibrium, the lattice has been distorted and the springs are exerting forces. However, forces from all directions add to zero and, hence, the lattice stays stable.

Suppose that there are n masses which are linked internally according to the configuration specified by the index subsets ${\mathbb{K}}_i$ and ${\mathbb{C}}_i$, and peripherally by ${\mathbb{F}}_i$, $i=1,\dots ,n$. The total kinetic energy T is given by

$$T={\displaystyle \frac{1}{2}}\sum _{i=1}^n{m}_i{\dot{\mathbf{x}}}_i^{\top }{\dot{\mathbf{x}}}_i.$$

(5)

Each spring has a quadratic potential due to the change of its linear length. The total potential energy P is given by

$$\begin{array}{c}\hfill P={\displaystyle \frac{1}{2}}\{\sum _{i=1}^n\sum _{j\in {\mathbb{F}}_i}{k}_{ii}^{\left(j\right)}(\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel -\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel )}^2+\sum _{i<j}{k}_{ij}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j{\parallel )}^2\},\end{array}$$

(6)

where we assume that $k_{ij}=0$ if $m_i$ and $m_j$ are not linked. The total energy within the system is

$$E\left(t\right)=T\left(t\right)+P\left(t\right),$$

(7)

which is time dependent. we now argue that (3) is always dissipative in the following sense.

Lemma 1.

If damping is present, the total energy of the system (3) decreases.

Proof. 

Out goal is to show that ${\displaystyle \frac{dE}{dt}}\le 0$ and is zero only under special circumstances. We first calculate

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dT}{dt}}=\sum _{i=1}^n{m}_i{\dot{\mathbf{x}}}_i^{\top }{\ddot{\mathbf{x}}}_i=& -& \sum _{i=1}^n\sum _{j\in {\mathbb{F}}_i}{c}_{ii}^{\left(j\right)}{\dot{\mathbf{x}}}_i^{\top }{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^2}}{\dot{\mathbf{x}}}_i\hfill \\ & -& \sum _{i=1}^n\sum _{j\in {\mathbb{F}}_i}{k}_{ii}^{\left(j\right)}{\dot{\mathbf{x}}}_i^{\top }{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel -\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel )\hfill \\ & -& \sum _{i=1}^n\sum _{j\in {\mathbb{C}}_i}{c}_{ij}{\dot{\mathbf{x}}}_i^{\top }{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{x}}_j){({\mathbf{x}}_i-{\mathbf{x}}_j)}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2}}({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j)\hfill \\ & -& \sum _{i=1}^n\sum _{j\in {\mathbb{K}}_i}{k}_{ij}{\dot{\mathbf{x}}}_i^{\top }{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{x}}_j}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel ).\hfill \end{array}$$

Terms in the third double sum appear in pairs such as ${\dot{\mathbf{x}}}_i^{\top }({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j)$ and ${\dot{\mathbf{x}}}_j({\dot{\mathbf{x}}}_j-{\dot{\mathbf{x}}}_i)$ which we can combine into

$$\sum _{i=1}^n\sum _{j\in {\mathbb{C}}_i}{c}_{ij}{\dot{\mathbf{x}}}_i^{\top }{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{x}}_j){({\mathbf{x}}_i-{\mathbf{x}}_j)}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2}}({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j)=\sum _{i<j}{c}_{ij}{({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j)}^{\top }{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{x}}_j){({\mathbf{x}}_i-{\mathbf{x}}_j)}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2}}({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j).$$

Likewise, terms in the last double sum appear in pairs such as ${\dot{\mathbf{x}}}_i^{\top }({\mathbf{x}}_i-{\mathbf{x}}_j)$ and ${\dot{\mathbf{x}}}_j^{\top }({\mathbf{x}}_j-{\mathbf{x}}_i)$ which we can combine to

$$\sum _{i=1}^n\sum _{j\in {\mathbb{K}}_i}{k}_{ij}{\dot{\mathbf{x}}}_i^{\top }{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{x}}_j}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel )=\sum _{i<j}{k}_{ij}{\displaystyle \frac{({\dot{\mathbf{x}}}_i^{\top }-{\dot{\mathbf{x}}}_j^{\top })({\mathbf{x}}_i-{\mathbf{x}}_j)}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel ).$$

we can also calculate

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dP}{dt}}& =& \sum _{i=1}^n\sum _{j\in {\mathbb{F}}_i}{k}_{ii}^{\left(j\right)}{\displaystyle \frac{{\dot{\mathbf{x}}}_i^{\top }({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)})}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel -\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel )\hfill \\ & & +\sum _{i<j}{k}_{ij}{\displaystyle \frac{({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j^{\top })({\mathbf{x}}_i-{\mathbf{x}}_j)}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel ).\hfill \end{array}$$

Together, we find that

$${\displaystyle \frac{dE}{dt}}=-\sum _{i=1}^n\sum _{j\in {\mathbb{F}}_i}{c}_{ii}^{\left(j\right)}{\dot{\mathbf{x}}}_i^{\top }{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^2}}{\dot{\mathbf{x}}}_i-\sum _{i<j}{c}_{ij}{({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j)}^{\top }{\displaystyle \frac{({\mathbf{x}}_i-{\mathbf{x}}_j){({\mathbf{x}}_i-{\mathbf{x}}_j)}^{\top }}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2}}({\dot{\mathbf{x}}}_i-{\dot{\mathbf{x}}}_j).$$

Clearly, every term on the right-hand side is non-negative. So ${\displaystyle \frac{dE}{dt}}\le 0$. Further more, ${\displaystyle \frac{dE}{dt}}=0$ unless every term is exactly zero.  ☐

Lemma 1 indicates that the nonlinear system (3) continuously dissipates energy during vibration. The motion ceases when the total energy is depleted, while remaining independent of variations in the original rest positions ${\mathbf{a}}_i$, fixed-end points ${\mathbf{b}}_i$, positions ${\mathbf{x}}_i$, or initial velocity ${\dot{\mathbf{x}}}_i$. Nevertheless, the system is not guaranteed to return to its original rest position. Under certain configurations, alternative equilibrium positions may exist for fixed ${\mathbf{a}}_i$ and ${\mathbf{b}}_i$ when the initial velocity is altered. This results from the inherent nonlinear coupling characteristics of lattice vibration systems. This aspect requires further investigation beyond the present scope.

3. Linearized System

To achieve total decoupling of 2D lattice vibration systems using the SPITF framework, the second-order nonlinear system (3) developed in Section 2 requires linearization. This process determines the coefficient matrices $\mathbf{M}$, $\mathbf{C}$, and $\mathbf{K}$, thereby enabling the application of SPITF to accomplish decoupling.

The linear system can model the nonlinear system only in the vicinity of an equilibrium point. Assuming that the vibration is tiny, we should be able to consider the linearized system near the rest position [30]. The linearization is actually an approximation for the displacement vectors ${\mathbf{z}}_i:={\mathbf{x}}_i-{\mathbf{a}}_i$.

Lemma 2.

For (3), the first-order approximation of the displacement vector ${\mathbf{z}}_i$ is given by the

$$\begin{array}{ccc}\hfill m_i{\ddot{\mathbf{z}}}_i& =& -{\displaystyle \sum _{j\in {\mathbb{F}}_i}}{c}_{ii}^{\left(j\right)}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^2}}{\dot{\mathbf{z}}}_i-{\displaystyle \sum _{j\in {\mathbb{C}}_i}}{c}_{ij}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{a}}_j){({\mathbf{a}}_i-{\mathbf{a}}_j)}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{a}}_j{\parallel }^2}}({\dot{\mathbf{z}}}_i-{\dot{\mathbf{z}}}_j)\hfill \\ \hfill & & -{\displaystyle \sum _{j\in {\mathbb{F}}_i}}{k}_{ii}^{\left(j\right)}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^2}}{\mathbf{z}}_i-{\displaystyle \sum _{j\in {\mathbb{K}}_i}}{k}_{ij}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{a}}_j){({\mathbf{a}}_i-{\mathbf{a}}_j)}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{a}}_j{\parallel }^2}}({\mathbf{z}}_i-{\mathbf{z}}_j).\hfill \end{array}$$

(8)

Proof. 

It suffices to demonstrate the linearization of the second and fourth summations on the right-hand side of (3). Rewrite

$$\begin{array}{ccc}\hfill f_i({\mathbf{x}}_1,\dots ,{\mathbf{x}}_n)& :=& {\displaystyle \sum _{j\in {\mathbb{F}}_i}}{k}_{ii}^{\left(j\right)}{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel -\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel )\hfill \\ \hfill & =& {\displaystyle \sum _{j\in {\mathbb{F}}_i}}{k}_{ii}^{\left(j\right)}({\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)})-{\displaystyle \sum _{j\in {\mathbb{F}}_i}}{k}_{ii}^{\left(j\right)}\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel {\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}}{\parallel {\mathbf{x}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel }},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \widetilde{f_i}({\mathbf{x}}_1,\dots ,{\mathbf{x}}_n)& :=& {\displaystyle \sum _{j\in {\mathbb{K}}_i}}{k}_{ij}{\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{x}}_j}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel -\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel )\hfill \\ \hfill & =& {\displaystyle \sum _{j\in {\mathbb{K}}_i}}{k}_{ij}({\mathbf{x}}_i-{\mathbf{x}}_j)-{\displaystyle \sum _{j\in {\mathbb{K}}_i}}{k}_{ij}\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel {\displaystyle \frac{{\mathbf{x}}_i-{\mathbf{x}}_j}{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }}.\hfill \end{array}$$

(10)

The actions of the Fréchet derivatives of Equations (9) and (10) on $({\mathbf{z}}_1,\dots ,{\mathbf{z}}_n)$ at $({\mathbf{a}}_1,\dots ,{\mathbf{a}}_n)$ are given by

$$\begin{array}{ccc}\hfill f_i^{\prime }({\mathbf{a}}_1,\dots ,{\mathbf{a}}_n).({\mathbf{z}}_1,\dots ,{\mathbf{z}}_n)& =& \sum _{j\in {\mathbb{F}}_i}{k}_{ii}^{\left(j\right)}{\mathbf{z}}_i\hfill \\ & & -\sum _{j\in {\mathbb{F}}_i}{k}_{ii}^{\left(j\right)}\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel ({\displaystyle \frac{{\mathbf{z}}_i}{\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}\parallel }}-{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^3}}{\mathbf{z}}_i),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {{\tilde{f}}_i}^{\prime }({\mathbf{a}}_1,\dots ,{\mathbf{a}}_n).({\mathbf{z}}_1,\dots ,{\mathbf{z}}_n)& =& \sum _{j\in {\mathbb{K}}_i}{k}_{ij}({\mathbf{z}}_i-{\mathbf{z}}_j)\hfill \\ & & -\sum _{j\in {\mathbb{K}}_i}{k}_{ij}\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel ({\displaystyle \frac{{\mathbf{z}}_i-{\mathbf{z}}_j}{\parallel {\mathbf{a}}_i-{\mathbf{a}}_j\parallel }}-{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{a}}_j){({\mathbf{a}}_i-{\mathbf{a}}_j)}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{a}}_j{\parallel }^3}}({\mathbf{z}}_i-{\mathbf{z}}_j)).\hfill \end{array}$$

Upon substitution and simplification, we obtain the expression for the summations of the last two terms in (8).  ☐

We can rewrite the Equation (8) as the standard second-order linear ODE system

$$\mathbf{M}\ddot{\mathbf{z}}+\mathbf{C}\dot{\mathbf{z}}+\mathbf{K}\mathbf{z}=0,$$

(11)

except that the coefficient matrices are block structured in a special way. The matrices $\mathbf{M}$, $\mathbf{C}$, and $\mathbf{K}$ are respectively the mass, damping, and stiffness matrices. For convenience, denote the matrices

$$\begin{array}{ccc}& & \left\{\begin{array}{ccc}\hfill {\mathbf{C}}_{ii}& :=& \sum _{j\in {\mathbb{F}}_i}{c}_{ii}^{\left(j\right)}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^2}},\hfill \\ \hfill {\mathbf{K}}_{ii}& :=& \sum _{j\in {\mathbb{F}}_i}{k}_{ii}^{\left(j\right)}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}){({\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)})}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{b}}_i^{\left(j\right)}{\parallel }^2}},\hfill \end{array}\right.i=1,\dots ,n,\hfill \\ & & {\mathbf{C}}_{ij}:=c_{ij}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{a}}_j){({\mathbf{a}}_i-{\mathbf{a}}_j)}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{a}}_j{\parallel }^2}},j\in {\mathbb{C}}_i,\hfill \\ & & {\mathbf{K}}_{ij}:=k_{ij}{\displaystyle \frac{({\mathbf{a}}_i-{\mathbf{a}}_j){({\mathbf{a}}_i-{\mathbf{a}}_j)}^{\top }}{\parallel {\mathbf{a}}_i-{\mathbf{a}}_j{\parallel }^2}},j\in {\mathbb{K}}_i,\hfill \end{array}$$

where for each i, the existence of $(i,j)$ depends on the index subsets ${\mathbb{C}}_i$ and ${\mathbb{K}}_i$, respectively; otherwise, they are set to zero matrices. Note all these $2\times 2$ matrices are symmetric and positive semi-definite. Note also that ${\mathbf{C}}_{ij}={\mathbf{C}}_{ji}$ and ${\mathbf{K}}_{ij}={\mathbf{K}}_{ji}$. Then

$$\begin{array}{ccc}\mathbf{M}\hfill & :=& \left[\begin{array}{cccc}{m}_1& 0& & 0\\ 0& m_2& & 0\\ & & \ddots & \\ 0& 0& & m_n\end{array}\right]\otimes \mathbf{I},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill \mathbf{C}& :=& \left[\begin{array}{ccccc}\sum _{j=1}^n{\mathbf{C}}_{1j}& -{\mathbf{C}}_{12}& -{\mathbf{C}}_{13}& \dots & -{\mathbf{C}}_{1n}\\ -{\mathbf{C}}_{12}& \sum _{j=1}^n{\mathbf{C}}_{2j}& -{\mathbf{C}}_{23}& & -{\mathbf{C}}_{2n}\\ -{\mathbf{C}}_{13}& -{\mathbf{C}}_{23}& \sum _{j=1}^n{\mathbf{C}}_{3j}& & -{\mathbf{C}}_{3n}\\ ⋮& & & \ddots & \\ -{\mathbf{C}}_{1n}& & & & \sum _{j=1}^n{\mathbf{C}}_{nj}\end{array}\right],\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \mathbf{K}& :=& \left[\begin{array}{ccccc}\sum _{j=1}^n{\mathbf{K}}_{1j}& -{\mathbf{K}}_{12}& -{\mathbf{K}}_{13}& \dots & -{\mathbf{K}}_{1n}\\ -{\mathbf{K}}_{12}& \sum _{j=1}^n{\mathbf{K}}_{2j}& -{\mathbf{K}}_{23}& & -{\mathbf{K}}_{2n}\\ -{\mathbf{K}}_{13}& -{\mathbf{K}}_{23}& \sum _{j=1}^n{\mathbf{K}}_{3j}& & -{\mathbf{K}}_{3n}\\ ⋮& & & \ddots & \\ -{\mathbf{K}}_{1n}& & & & \sum _{j=1}^n{\mathbf{K}}_{nj}\end{array}\right],\hfill \end{array}$$

(14)

with ⊗ standing for the Kronecker product. For a free-end system, ${\mathbf{C}}_{ii}={\mathbf{K}}_{ii}=0$. With the coefficient matrices $\mathbf{M}$, $\mathbf{C}$, and $\mathbf{K}$ now determined, total decoupling of the 2D lattice vibration system can be realized.

4. Total Decoupling

Total decoupling requires a stringent condition than simultaneous diagonalization, specifically the preservation of eigeninformation throughout the decoupling process. The SPITF framework is founded on the Lancaster form [31]

$$L\left(\lambda \right):=L(\lambda ;\mathbf{M},\mathbf{C},\mathbf{K})=\left[\begin{array}{cc}\mathbf{C}& \mathbf{M}\\ \mathbf{M}& 0\end{array}\right]\lambda +\left[\begin{array}{cc}\mathbf{K}& 0\\ 0& -\mathbf{M}\end{array}\right],$$

(15)

which enables linearization of the QEP (2). There must exist a matrix $\mathbf{T}$ that performs a congruence transformation on $L\left(\lambda \right)$, such that the structure remains invariant under this transformation [32], namely

$${\mathbf{T}}^{\top }L\left(\lambda \right)\mathbf{T}=L(\lambda ;{\mathbf{M}}_D,{\mathbf{C}}_D,{\mathbf{K}}_D)=\left[\begin{array}{cc}{\mathbf{C}}_D& {\mathbf{M}}_D\\ {\mathbf{M}}_D& 0\end{array}\right]\lambda +\left[\begin{array}{cc}{\mathbf{K}}_D& 0\\ 0& -{\mathbf{M}}_D\end{array}\right],$$

(16)

where ${\mathbf{M}}_D$, ${\mathbf{C}}_D$ and ${\mathbf{K}}_D$ are the coefficient matrices of the total decoupled system and $\lambda$ denotes the invariant spectrum. The implementation procedure is detailed in this section.

The initial coefficient matrices ${\mathbf{M}}_0$, ${\mathbf{C}}_0$ and ${\mathbf{K}}_0$ of the second-order linear system (11) are employed to construct the Lancaster structure

$${\mathcal{A}}_0=\left[\begin{array}{cc}{\mathbf{K}}_0& 0\\ 0& -{\mathbf{M}}_0\end{array}\right],{\mathcal{B}}_0=\left[\begin{array}{cc}{\mathbf{C}}_0& {\mathbf{M}}_0\\ {\mathbf{M}}_0& 0\end{array}\right].$$

(17)

Given the symmetry of the matrices defined in Equations (12)–(14), there exists a one-parameter $2n\times 2n$ transformation $\mathbf{T}\left(t\right)$ satisfying

$$\left\{\begin{array}{ccccc}\hfill \mathcal{A}\left(t\right)& =& {\mathbf{T}}^{\top }\left(t\right){\mathcal{A}}_0\mathbf{T}\left(t\right)\hfill & =& \left[\begin{array}{cc}\mathbf{K}\left(t\right)& 0\\ 0& -\mathbf{M}\left(t\right)\end{array}\right],\hfill \\ \hfill \mathcal{B}\left(t\right)& =& {\mathbf{T}}^{\top }\left(t\right){\mathcal{B}}_0\mathbf{T}\left(t\right)\hfill & =& \left[\begin{array}{cc}\mathbf{C}\left(t\right)& \mathbf{M}\left(t\right)\\ \mathbf{M}\left(t\right)& 0\end{array}\right],\hfill \end{array}\right.$$

(18)

where $\mathbf{T}\left(t\right)$ start from ${\mathbf{I}}_{2n}$ with $t=0$. It means this transformation maintain Lancaster structure for all t during decoupling, thereby ensuring that $\left(\mathcal{A}\right(t),\mathcal{B}(t\left)\right)$ are isospectral to $({\mathcal{A}}_0,{\mathcal{B}}_0)$ for any t.

Differentiate Equation (18) with respect to the parameter t, we can find

$$\left\{\begin{array}{ccc}\hfill \dot{\mathcal{A}}\left(t\right)& =& {\dot{\mathbf{T}}}^{\top }\left(t\right){\mathcal{A}}_0\mathbf{T}\left(t\right)+{\mathbf{T}}^{\top }\left(t\right){\mathcal{A}}_0\dot{\mathbf{T}}\left(t\right)={\mathcal{R}}^{\top }\left(t\right)\mathcal{A}\left(t\right)+\mathcal{A}\left(t\right)\mathcal{R}\left(t\right),\hfill \\ \hfill \dot{\mathcal{B}}\left(t\right)& =& {\dot{\mathbf{T}}}^{\top }\left(t\right){\mathcal{B}}_0\mathbf{T}\left(t\right)+{\mathbf{T}}^{\top }\left(t\right){\mathcal{B}}_0\dot{\mathbf{T}}\left(t\right)={\mathcal{R}}^{\top }\left(t\right)\mathcal{B}\left(t\right)+\mathcal{B}\left(t\right)\mathcal{R}\left(t\right),\hfill \end{array}\right.$$

(19)

the block matrix $\mathcal{R}\left(t\right)\in {\mathbb{R}}^{2n}$ is determined by the following equation

$$\dot{\mathbf{T}}\left(t\right)=\mathbf{T}\left(t\right)\mathcal{R}\left(t\right)=\mathbf{T}\left(t\right)\left[\begin{array}{c}{\mathbf{R}}_{11}\left(t\right){\mathbf{R}}_{12}\left(t\right)\\ {\mathbf{R}}_{21}\left(t\right){\mathbf{R}}_{22}\left(t\right)\end{array}\right],$$

(20)

where ${\mathbf{R}}_{ij}\left(t\right),i,j=1,2$ are all $n\times n$ matrices. By synthesizing all the information, there are $n(n+1)/2+2n^2$ equations must be satisfied:

$$\left\{\begin{array}{ccc}\hfill \mathbf{K}\left(t\right){\mathbf{R}}_{12}\left(t\right)-{\mathbf{R}}_{21}^{\top }\left(t\right)\mathbf{M}\left(t\right)& =& 0,\hfill \\ \hfill {\mathbf{R}}_{12}^{\top }\left(t\right)\mathbf{M}\left(t\right)+\mathbf{M}\left(t\right){\mathbf{R}}_{12}\left(t\right)& =& 0,\hfill \\ \hfill \mathbf{M}\left(t\right){\mathbf{R}}_{11}\left(t\right)-\mathbf{M}\left(t\right){\mathbf{R}}_{22}\left(t\right)+{\mathbf{R}}_{12}^{\top }\left(t\right)\mathbf{C}\left(t\right)& =& 0.\hfill \end{array}\right.$$

(21)

We define the matrix $\mathcal{R}\left(t\right)$ through two free parameter matrices $\mathbf{D}\left(t\right)$ and $\mathbf{N}\left(t\right)$, establishing the parameterization

$$\mathcal{R}\left(t\right)=\left[\begin{array}{cc}\mathbf{D}\left(t\right)& 0\\ 0& \mathbf{D}\left(t\right)\end{array}\right]\left[\begin{array}{cc}-{\displaystyle \frac{\mathbf{C}\left(t\right)}{2}}& -\mathbf{M}\left(t\right)\\ \mathbf{K}\left(t\right)& {\displaystyle \frac{\mathbf{C}\left(t\right)}{2}}\end{array}\right]+\left[\begin{array}{cc}\mathbf{N}\left(t\right)& 0\\ 0& \mathbf{N}\left(t\right)\end{array}\right].$$

(22)

Clearly, $\mathbf{D}\left(t\right)\in {\mathbb{R}}^{n\times n}$ is an skew-symmetric matrix. The substitution of (22) into (19) gives rise to an autonomous differential system

$$\left\{\begin{array}{ccc}\hfill \dot{\mathbf{K}}\left(t\right)& =& {\displaystyle \frac{1}{2}}(\mathbf{C}\left(t\right)\mathbf{D}\left(t\right)\mathbf{K}\left(t\right)-\mathbf{K}\left(t\right)\mathbf{D}\left(t\right)\mathbf{C}\left(t\right))+{\mathbf{N}}^{\top }\left(t\right)\mathbf{K}\left(t\right)+\mathbf{K}\left(t\right)\mathbf{N}\left(t\right),\hfill \\ \hfill \dot{\mathbf{C}}\left(t\right)& =& (\mathbf{M}\left(t\right)\mathbf{D}\left(t\right)\mathbf{K}\left(t\right)-\mathbf{K}\left(t\right)\mathbf{D}\left(t\right)\mathbf{M}\left(t\right))+{\mathbf{N}}^{\top }\left(t\right)\mathbf{C}\left(t\right)+\mathbf{C}\left(t\right)\mathbf{N}\left(t\right),\hfill \\ \hfill \dot{\mathbf{M}}\left(t\right)& =& {\displaystyle \frac{1}{2}}(\mathbf{M}\left(t\right)\mathbf{D}\left(t\right)\mathbf{C}\left(t\right)-\mathbf{C}\left(t\right)\mathbf{D}\left(t\right)\mathbf{M}\left(t\right))+{\mathbf{N}}^{\top }\left(t\right)\mathbf{M}\left(t\right)+\mathbf{M}\left(t\right)\mathbf{N}\left(t\right),\hfill \end{array}\right.$$

(23)

for the matrices $\mathbf{M}\left(t\right)$, $\mathbf{C}\left(t\right)$, and $\mathbf{K}\left(t\right)$, which is independent of the choice of $\mathbf{D}\left(t\right)$ and $\mathbf{N}\left(t\right)$.

For a spring-mass-damper system, since mass properties are generally dominated by diagonal terms in the mass matrix [27], it is reasonable to approximate ${\mathbf{M}}_0=\mathbf{I}$. Throughout the transition, we seek to further ensure that $\mathbf{M}\left(t\right)\equiv \mathbf{I}$. By ensuring $\dot{\mathbf{M}}\left(t\right)=0$, we find that

$$\mathbf{N}\left(t\right)={\displaystyle \frac{1}{4}}(\mathbf{C}\left(t\right)\mathbf{D}\left(t\right)-\mathbf{D}\left(t\right)\mathbf{C}\left(t\right))+\mathbf{S}\left(t\right)$$

(24)

with $\mathbf{S}\left(t\right)=-{\mathbf{S}}^{\top }\left(t\right)$. The structure of flow $\mathbf{T}\left(t\right)$ is given in the following form

$$\dot{\mathbf{T}}\left(t\right)=\left[\begin{array}{cc}{\mathbf{T}}_{11}\left(t\right)& {\mathbf{T}}_{12}\left(t\right)\\ {\mathbf{T}}_{21}\left(t\right)& {\mathbf{T}}_{22}\left(t\right)\end{array}\right]\left[\begin{array}{cc}{\displaystyle \frac{1}{4}}\mathbf{C}\left(t\right)\mathbf{D}\left(t\right)-{\displaystyle \frac{3}{4}}\mathbf{D}\left(t\right)\mathbf{C}\left(t\right)+\mathbf{S}\left(t\right)& -\mathbf{D}\left(t\right)\\ \mathbf{D}\left(t\right)\mathbf{K}\left(t\right)& {\displaystyle \frac{1}{4}}(\mathbf{C}\left(t\right)\mathbf{D}\left(t\right)+\mathbf{D}\left(t\right)\mathbf{C}\left(t\right))+\mathbf{S}\left(t\right)\end{array}\right].$$

(25)

Total decoupling of system (11) requires appropriate selection of the $n(n-1)$-dimensional parameter matrices $\mathbf{D}\left(t\right)$ and $\mathbf{S}\left(t\right)$ to govern the transformation flow (25), thereby generating the spectrum-preserving transformation $\mathbf{T}\left(t\right)$. This objective is achieved through the formulation of an open-loop optimal control problem

$$\begin{array}{ccc}& \underset{\mathbf{x}\in {\mathbb{R}}^n}{min}& h\left(\mathbf{x}\right),\hfill \\ & \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{o}& \dot{\mathbf{x}}=g\left(\mathbf{x}\right)\mathbf{u},\mathbf{x}\left(0\right)={\mathbf{x}}_0.\hfill \end{array}$$

(26)

The control $\mathbf{u}$ may be chosen to minimize the deviation between $\dot{\mathbf{x}}$ and $-\nabla h\left(\mathbf{x}\right)$. This reduces to finding the least-squares solution $\mathbf{u}$ to problem

$$\underset{\mathbf{x}\in {\mathbb{R}}^n}{min}{\parallel g\left(\mathbf{x}\right)\mathbf{u}+\nabla h\left(\mathbf{x}\right)\parallel }_2.$$

Hence, the problem (26) translates into solving the closed-loop dynamical system

$$\dot{\mathbf{x}}=-g\left(\mathbf{x}\right)g{\left(\mathbf{x}\right)}^{†}\nabla h\left(\mathbf{x}\right),$$

(27)

where $g{\left(\mathbf{x}\right)}^{†}$ stands for the Moore-Penrose generalized inverse of $g\left(\mathbf{x}\right)$.

Let ${\mathcal{P}}_C$ and ${\mathcal{P}}_K$ denote projection operators such that ${\mathcal{P}}_C\left(\mathbf{C}\left(t\right)\right)$ and ${\mathcal{P}}_K\left(\mathbf{K}\left(t\right)\right)$ extract the components of $\mathbf{C}\left(t\right)$ and $\mathbf{K}\left(t\right)$, respectively, that deviate from the specified patterns. To precisely characterize this deviation, we define the operators $\mathcal{D}\left(\mathbf{C}\right(t\left)\right)$ and $\mathcal{D}\left(\mathbf{K}\right(t\left)\right)$ which set all off-diagonal elements of $\mathbf{C}\left(t\right)$ and $\mathbf{K}\left(t\right)$ to zero, respectively. This establishes the formal definition:

$$\left\{\begin{array}{ccc}\hfill {\mathcal{P}}_C\left(\mathbf{C}\left(t\right)\right)& =& \mathbf{C}\left(t\right)-\mathcal{D}\left(\mathbf{C}\right(t\left)\right),\hfill \\ \hfill {\mathcal{P}}_K\left(\mathbf{K}\left(t\right)\right)& =& \mathbf{K}\left(t\right)-\mathcal{D}\left(\mathbf{K}\right(t\left)\right).\hfill \end{array}\right.$$

The matrices $\mathbf{C}\left(t\right)$ and $\mathbf{K}\left(t\right)$ are derived from (18) as follows:

$$\left\{\begin{array}{ccc}\hfill \mathbf{C}\left(t\right)& =& \mathbf{C}\left(\mathbf{T}\left(t\right)\right)={\mathbf{T}}_{11}^{\top }\left(t\right){\mathbf{C}}_0{\mathbf{T}}_{11}\left(t\right)+{\mathbf{T}}_{21}^{\top }\left(t\right){\mathbf{T}}_{11}\left(t\right)+{\mathbf{T}}_{11}^{\top }\left(t\right){\mathbf{T}}_{21}\left(t\right),\hfill \\ \hfill \mathbf{K}\left(t\right)& =& \mathbf{K}\left(\mathbf{T}\left(t\right)\right)={\mathbf{T}}_{11}^{\top }\left(t\right){\mathbf{K}}_0{\mathbf{T}}_{11}\left(t\right)-{\mathbf{T}}_{21}^{\top }\left(t\right){\mathbf{T}}_{21}\left(t\right).\hfill \end{array}\right.$$

(28)

Define the objective function as:

$$f\left(\mathbf{T}\left(t\right)\right):={\displaystyle \frac{1}{2}}\left\{\alpha \left(t\right)\parallel {\mathcal{P}}_C{\left(\mathbf{C}\left(t\right)\right)\parallel }_F^2+\beta \left(t\right){\parallel {\mathcal{P}}_K\left(\mathbf{K}\left(t\right)\right)\parallel }_F^2\right\},$$

(29)

$\alpha \left(t\right)$ and $\beta \left(t\right)$ are adjustable weights, where ${\parallel ·\parallel }_F$ denotes the Frobenius norm, respectively. This readily yields

$$\begin{array}{c}\hfill -\nabla f\left(\mathbf{T}\left(t\right)\right)=\left[\begin{array}{c}\mathbf{vec}(-2\alpha \left(t\right)({\mathbf{C}}_0{\mathbf{T}}_{11}\left(t\right)+{\mathbf{T}}_{21}\left(t\right))\left({\mathcal{P}}_C\left(\mathbf{C}\left(t\right)\right)\right)-2\beta \left(t\right){\mathbf{K}}_0{\mathbf{T}}_{11}\left(t\right)\left({\mathcal{P}}_K\left(\mathbf{K}\left(t\right)\right)\right))\\ \mathbf{vec}(-2\alpha \left(t\right){\mathbf{T}}_{11}\left(t\right)\left({\mathcal{P}}_C\left(\mathbf{C}\left(t\right)\right)\right)+2\beta \left(t\right){\mathbf{T}}_{21}\left(t\right)\left({\mathcal{P}}_K\left(\mathbf{K}\left(t\right)\right)\right))\\ 0\\ 0\end{array}\right].\end{array}$$

(30)

Given the skew-symmetry of matrices $\mathbf{D}\left(t\right)$ and $\mathbf{S}\left(t\right)$, their strictly upper triangular components are represented by vectors $\mathbf{d}\left(t\right)$ and $\mathbf{s}\left(t\right)$, respectively, leading to the compact representation:

$$\left[\begin{array}{c}\mathbf{vec}\left(\mathbf{S}\right(t\left)\right)\\ \mathbf{vec}\left(\mathbf{D}\right(t\left)\right)\end{array}\right]=\mathbf{Z}\left(t\right)\left[\begin{array}{c}\mathbf{s}\left(t\right)\\ \mathbf{d}\left(t\right)\end{array}\right],$$

(31)

where $\mathbf{Z}\left(t\right)\in {\mathbb{R}}^{2n^2\times n(n-1)}$ denotes the linear transformation matrix. Consequently, we define

$$\begin{array}{c}\hfill g\left(\mathbf{T}\left(t\right)\right):=\left[\begin{array}{cc}\hfill \mathbf{I}\otimes {\mathbf{T}}_{11}\left(t\right)& {\displaystyle \frac{1}{4}}(\mathbf{I}\otimes \left({\mathbf{T}}_{11}\left(t\right)\mathbf{C}\left(t\right)\right))-{\displaystyle \frac{3}{4}}(\mathbf{C}\left(t\right)\otimes {\mathbf{T}}_{11}\left(t\right))+\mathbf{K}\left(t\right)\otimes {\mathbf{T}}_{12}\left(t\right)\\ \hfill \mathbf{I}\otimes {\mathbf{T}}_{21}\left(t\right)& {\displaystyle \frac{1}{4}}(\mathbf{I}\otimes \left({\mathbf{T}}_{21}\left(t\right)\mathbf{C}\left(t\right)\right))-{\displaystyle \frac{3}{4}}(\mathbf{C}\left(t\right)\otimes {\mathbf{T}}_{21}\left(t\right))+\mathbf{K}\left(t\right)\otimes {\mathbf{T}}_{22}\left(t\right)\\ \hfill \mathbf{I}\otimes {\mathbf{T}}_{12}\left(t\right)& {\displaystyle \frac{1}{4}}(\mathbf{I}\otimes \left({\mathbf{T}}_{12}\left(t\right)\mathbf{C}\left(t\right)\right))+{\displaystyle \frac{1}{4}}(\mathbf{C}\left(t\right)\otimes {\mathbf{T}}_{12}\left(t\right))-\mathbf{I}\otimes {\mathbf{T}}_{11}\left(t\right)\\ \hfill \mathbf{I}\otimes {\mathbf{T}}_{22}\left(t\right)& {\displaystyle \frac{1}{4}}(\mathbf{I}\otimes \left({\mathbf{T}}_{22}\left(t\right)\mathbf{C}\left(t\right)\right))+{\displaystyle \frac{1}{4}}(\mathbf{C}\left(t\right)\otimes {\mathbf{T}}_{22}\left(t\right))-\mathbf{I}\otimes {\mathbf{T}}_{21}\left(t\right)\end{array}\right]\mathbf{Z}\left(t\right).\end{array}$$

(32)

Then, the control vectors $\mathbf{d}\left(t\right)$ and $\mathbf{s}\left(t\right)$ are obtained via the least-squares solution of

$$\begin{array}{c}\hfill g\left(\mathbf{T}\left(t\right)\right)\left[\begin{array}{c}\mathbf{s}\left(t\right)\hfill \\ \mathbf{d}\left(t\right)\hfill \end{array}\right]=-\nabla f\left(\mathbf{T}\left(t\right)\right).\end{array}$$

(33)

In summary, the total decoupling of system (11) is equivalent to solving the initial value problem

$$\begin{array}{c}\hfill \dot{\mathbf{T}}\left(t\right)=-g\left(\mathbf{T}\left(t\right)\right)g{\left(\mathbf{T}\left(t\right)\right)}^{†}\nabla f\left(\mathbf{T}\left(t\right)\right),\mathbf{T}\left(0\right)=\left[\begin{array}{cc}\mathbf{I}& 0\\ 0& \mathbf{I}\end{array}\right].\end{array}$$

(34)

5. Numerical Experiments

This section describes three numerical experiments designed to achieve total decoupling of the 2D lattice vibration system. The transformation $\mathbf{T}$ is first obtained by numerically solving the initial value problem (34). Subsequently, this matrix is applied in the congruence transformation (16) to derive the decoupled system’s coefficient matrices ${\mathbf{M}}_D$, ${\mathbf{C}}_D$ and ${\mathbf{K}}_D$. In this context, total decoupling requires that ${\mathbf{M}}_D$, ${\mathbf{C}}_D$ and ${\mathbf{K}}_D$ attain block-diagonal forms. Specifically, each block in these matrices corresponds to a $2\times 2$ submatrix representing an independent single-degree-of-freedom subsystem.

The numerical implementation utilizes Matlab’s ODE15s solvers [33], which control global error by bounding the local error at each integration step. The InitialStep is set to ${10}^{-10}$ with auto_control enabled (control_intensity $=10$). The tolerances AbsTol and RelTol are set to ${10}^{-10}$. Although no rigorous theory currently relates final accuracy to tolerance settings, precision can be enhanced by reducing these tolerances when necessary. This work aims to achieve total decoupling of system (11). Since $\mathbf{T}\left(t\right)$ converges to a point ${\mathbf{T}}^{*}$ that constitutes a local minimizer of the objective function $f\left(\mathbf{T}\right)$, the system is considered decoupled when $f\left({\mathbf{T}}^{*}\right)$ approaches zero within specified tolerance. Numerical results are reported with four significant digits.

Example 1.

For a spring-mass-damper system with the configuration shown in Figure 1, we randomly generate a set of coefficient matrices where ${\mathbf{M}}_0=I$ and

$$\begin{array}{c}\hfill {\mathbf{C}}_0=\left[\begin{array}{cccccc}\hfill 1.0195& \hfill 0.2014& \hfill -0.1163& \hfill -0.2014& \hfill -0.9032& \hfill 0.0000\\ \hfill 0.2014& \hfill 1.1805& \hfill -0.2014& \hfill -0.3489& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.1163& \hfill -0.2014& \hfill 0.7537& \hfill 0.0319& \hfill -0.0979& \hfill 0.1696\\ \hfill -0.2014& \hfill -0.3489& \hfill 0.0319& \hfill 0.6427& \hfill 0.1696& \hfill -0.2937\\ \hfill -0.9032& \hfill 0.0000& \hfill -0.0979& \hfill 0.1696& \hfill 1.6618& \hfill -0.1696\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.1696& \hfill -0.2937& \hfill -0.1696& \hfill 0.2937\end{array}\right],\\ \hfill {\mathbf{K}}_0=\left[\begin{array}{cccccc}\hfill 0.5435& \hfill 0.0935& \hfill -0.0540& \hfill -0.0935& \hfill -0.4945& \hfill 0.0000\\ \hfill 0.0935& \hfill 0.8441& \hfill -0.0935& \hfill -0.1620& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.0540& \hfill -0.0935& \hfill 0.2017& \hfill -0.0113& \hfill -0.0605& \hfill 0.1048\\ \hfill -0.0935& \hfill -0.1620& \hfill -0.0113& \hfill 0.3436& \hfill 0.1048& \hfill -0.1816\\ \hfill -0.4945& \hfill 0.0000& \hfill -0.0605& \hfill 0.1048& \hfill 1.0553& \hfill -0.1048\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.1048& \hfill -0.1816& \hfill -0.1048& \hfill 0.1816\end{array}\right].\end{array}$$

The initial damping matrix ${\mathbf{C}}_0$ and stiffness matrix ${\mathbf{K}}_0$ exactly follow the structure specified in (13) and (14). Numerical integration of (34) yields a transformation

$$\begin{array}{c}\hfill {\mathbf{T}}^{*}=\left[\begin{array}{cccccccccccc}\hfill 0.7686& \hfill 0.3923& \hfill -0.7417& \hfill 0.1014& \hfill -0.0978& \hfill 0.1297& \hfill -0.4328& \hfill 0.7906& \hfill -0.0586& \hfill 0.9567& \hfill -0.0488& \hfill -0.5026\\ \hfill -0.2552& \hfill 0.1331& \hfill -0.2293& \hfill 0.0959& \hfill -0.0161& \hfill 0.0611& \hfill -0.4087& \hfill 0.0794& \hfill -0.0288& \hfill -0.0751& \hfill 0.0766& \hfill -0.1172\\ \hfill -0.2931& \hfill 1.2096& \hfill 0.0999& \hfill 0.2684& \hfill -0.0128& \hfill -0.1584& \hfill -1.1431& \hfill 0.1579& \hfill 0.2170& \hfill 0.2206& \hfill 1.1345& \hfill -0.1301\\ \hfill -0.4532& \hfill -0.2514& \hfill 0.3903& \hfill 0.1494& \hfill 0.1675& \hfill -0.1144& \hfill -0.6372& \hfill -1.0362& \hfill 0.0961& \hfill -0.1734& \hfill 0.4031& \hfill 0.1982\\ \hfill ine0.5764& \hfill 0.2769& \hfill 0.6326& \hfill 0.0094& \hfill -0.0672& \hfill 0.1134& \hfill -0.0408& \hfill 0.5650& \hfill -0.0639& \hfill 0.5885& \hfill -0.0331& \hfill 0.8364\\ \hfill -0.1244& \hfill -0.1988& \hfill 0.1169& \hfill -0.0219& \hfill 0.1273& \hfill -0.0739& \hfill 0.0938& \hfill -0.7789& \hfill 0.0484& \hfill -0.1623& \hfill 0.2961& \hfill -0.0131\\ \hfill -0.1088& \hfill 0.3552& \hfill 0.1995& \hfill 0.0597& \hfill -0.1425& \hfill -0.0219& \hfill -0.0705& \hfill 0.5297& \hfill 0.3580& \hfill 0.0182& \hfill 0.1638& \hfill 0.1379\\ \hfill 0.7936& \hfill 0.3048& \hfill 0.0770& \hfill 0.0843& \hfill 0.0119& \hfill -0.0101& \hfill -0.1001& \hfill -0.0097& \hfill 0.1574& \hfill 0.9582& \hfill 0.3265& \hfill 0.0490\\ \hfill ine-0.5660& \hfill 0.1025& \hfill -0.3200& \hfill 0.3453& \hfill -0.0566& \hfill -0.0062& \hfill -0.4116& \hfill 0.1731& \hfill 0.9619& \hfill 0.0703& \hfill 0.0205& \hfill -0.3782\\ \hfill -0.5241& \hfill 0.8726& \hfill 0.4750& \hfill 0.1210& \hfill 0.0220& \hfill 0.0093& \hfill -0.1436& \hfill -0.2998& \hfill 0.1108& \hfill -0.2842& \hfill 0.8668& \hfill 0.4887\\ \hfill 0.2838& \hfill 0.0493& \hfill 0.0056& \hfill -0.0557& \hfill -0.1130& \hfill -0.0163& \hfill 0.0670& \hfill 0.4054& \hfill 0.1917& \hfill 0.1974& \hfill -0.1050& \hfill -0.0367\\ \hfill 0.0390& \hfill -0.4727& \hfill 0.8466& \hfill 0.0184& \hfill 0.0106& \hfill 0.0091& \hfill -0.0223& \hfill -0.2110& \hfill -0.0597& \hfill 0.0617& \hfill -0.4864& \hfill 0.8680\end{array}\right]\end{array}$$

that drives the objective function (29) to near-zero values when the iterative computation converges at $t\approx 2\times {10}^5$. Using this matrix, the decoupled damping matrix ${\mathbf{C}}_D$ and stiffness matrix ${\mathbf{K}}_D$ are obtained as follows:

$$\begin{array}{c}\hfill {\mathbf{C}}_D=\left[\begin{array}{cccccc}\hfill 0.4222& \hfill 0.0755& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0755& \hfill 1.3362& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.6878& \hfill -0.1938& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0000& \hfill 0.0000& \hfill -0.1938& \hfill 0.6506& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 2.3299& \hfill -0.2865\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill -0.2865& \hfill 0.1251\end{array}\right],\\ \hfill {\mathbf{K}}_D=\left[\begin{array}{cccccc}\hfill 0.2340& \hfill 0.0024& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0024& \hfill 0.8323& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.1904& \hfill -0.0995& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0000& \hfill 0.0000& \hfill -0.0995& \hfill 0.4174& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 1.3533& \hfill -0.1406\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill -0.1406& \hfill 0.0382\end{array}\right].\end{array}$$

Both matrices ${\mathbf{C}}_D$ and ${\mathbf{K}}_D$ possess a block-diagonal structure composed of $2\times 2$ blocks, indicating total decoupling into three independent subsystems. The dynamic properties of each subsystem are encoded within their respective block structures.

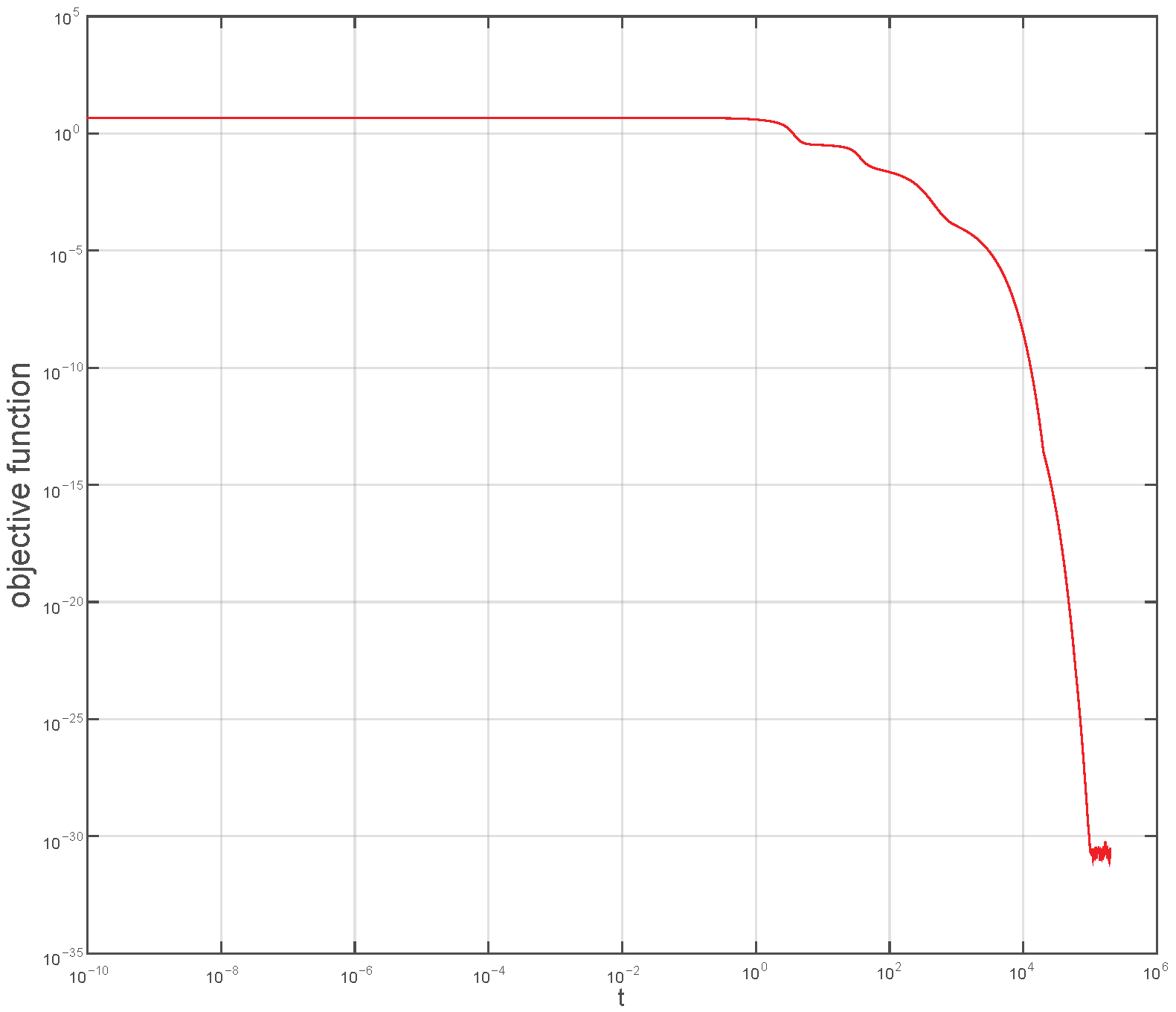
Figure 3 depicts the evolution of the objective function (29) during integration. It is evident that $f\left(\mathbf{T}\right(t\left)\right)$ approaches zero when the system achieves total decoupling.

Example 2.

We consider a system with a specific triangular configuration where one vertex forms a right angle. First, a set of initial damping and stiffness matrices conforming to the structure shown in (13) and (14) are generated by

$$\begin{array}{c}\hfill {\mathbf{C}}_0=\left[\begin{array}{cccccc}\hfill 0.9300& \hfill -0.0768& \hfill -0.2553& \hfill -0.2553& \hfill -0.3320& \hfill 0.3320\\ \hfill -0.0768& \hfill 0.5873& \hfill -0.2553& \hfill -0.2553& \hfill 0.3320& \hfill -0.3320\\ \hfill -0.2553& \hfill -0.2553& \hfill 0.5629& \hfill 0.2553& \hfill -0.3076& \hfill 0.0000\\ \hfill -0.2553& \hfill -0.2553& \hfill 0.2553& \hfill 0.7333& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.3320& \hfill 0.3320& \hfill -0.3076& \hfill 0.0000& \hfill 0.6396& \hfill -0.3320\\ \hfill 0.3320& \hfill -0.3320& \hfill 0.0000& \hfill 0.0000& \hfill -0.3320& \hfill 0.9307\end{array}\right],\\ \hfill {\mathbf{K}}_0=\left[\begin{array}{cccccc}\hfill 1.1939& \hfill 0.1367& \hfill -0.4702& \hfill -0.4702& \hfill -0.3335& \hfill 0.3335\\ \hfill 0.1367& \hfill 0.8037& \hfill -0.4702& \hfill -0.4702& \hfill 0.3335& \hfill -0.3335\\ \hfill -0.4702& \hfill -0.4702& \hfill 0.9449& \hfill 0.4702& \hfill -0.4702& \hfill 0.0000\\ \hfill -0.4702& \hfill -0.4702& \hfill 0.4702& \hfill 0.5206& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.3335& \hfill 0.3335& \hfill -0.4748& \hfill 0.0000& \hfill 0.8083& \hfill -0.3335\\ \hfill 0.3335& \hfill -0.3335& \hfill 0.0000& \hfill 0.0000& \hfill -0.3335& \hfill 0.7702\end{array}\right],\end{array}$$

and ${\mathbf{M}}_0=I$. The congruence transformation

$$\begin{array}{c}\hfill {\mathbf{T}}^{*}=\left[\begin{array}{cccccccccccc}\hfill 0.6353& \hfill -0.5550& \hfill -0.4912& \hfill -0.0027& \hfill -0.0405& \hfill 0.0374& \hfill 0.0484& \hfill 0.4196& \hfill -0.0467& \hfill 0.6296& \hfill -0.5101& \hfill -0.4658\\ \hfill -0.0687& \hfill -0.6779& \hfill -0.0676& \hfill -0.0515& \hfill 0.1132& \hfill -0.0792& \hfill 0.4605& \hfill 0.0465& \hfill 0.1578& \hfill -0.1512& \hfill -0.6057& \hfill -0.1069\\ \hfill 0.3157& \hfill 0.6308& \hfill -0.4077& \hfill 0.0887& \hfill -0.0563& \hfill -0.0203& \hfill -0.5005& \hfill 0.3476& \hfill 0.0250& \hfill 0.4417& \hfill 0.6551& \hfill -0.4216\\ \hfill 0.4784& \hfill -0.2715& \hfill 0.2626& \hfill -0.1522& \hfill 0.1219& \hfill -0.0825& \hfill 1.0107& \hfill 0.1725& \hfill 0.0761& \hfill 0.2538& \hfill -0.1739& \hfill 0.1998\\ \hfill ine0.4926& \hfill -0.0479& \hfill 0.7423& \hfill 0.0436& \hfill -0.0484& \hfill 0.0172& \hfill -0.4061& \hfill 0.5016& \hfill -0.0299& \hfill 0.5633& \hfill 0.0058& \hfill 0.7519\\ \hfill -0.2137& \hfill -0.0128& \hfill 0.0842& \hfill -0.0306& \hfill -0.0499& \hfill -0.0935& \hfill 0.0595& \hfill 0.0934& \hfill 0.1468& \hfill -0.2511& \hfill -0.0262& \hfill 0.0281\\ \hfill -0.1018& \hfill -0.4632& \hfill 0.2898& \hfill -0.0084& \hfill -0.0017& \hfill 0.0119& \hfill 0.0584& \hfill -0.5630& \hfill -0.0317& \hfill -0.1122& \hfill -0.1982& \hfill 0.3055\\ \hfill 0.6276& \hfill 0.0239& \hfill -0.3881& \hfill -0.0262& \hfill 0.0872& \hfill -0.1413& \hfill 0.3281& \hfill -0.1745& \hfill 0.1920& \hfill 0.5931& \hfill 0.1561& \hfill -0.5519\\ \hfill ine0.4928& \hfill -0.1232& \hfill -0.2037& \hfill -0.0407& \hfill -0.0182& \hfill -0.0058& \hfill -0.0648& \hfill -0.4447& \hfill 0.0165& \hfill 0.4487& \hfill 0.0765& \hfill -0.2114\\ \hfill -0.0870& \hfill 0.7728& \hfill 0.1229& \hfill 0.0253& \hfill 0.1022& \hfill 0.0272& \hfill 0.3708& \hfill -0.3634& \hfill 0.0126& \hfill -0.0651& \hfill 1.0029& \hfill 0.1482\\ \hfill 0.2207& \hfill -0.6308& \hfill -0.0845& \hfill 0.0271& \hfill -0.0019& \hfill 0.0220& \hfill -0.3062& \hfill -0.6731& \hfill -0.0324& \hfill 0.2558& \hfill -0.3139& \hfill -0.0587\\ \hfill 0.5946& \hfill -0.0184& \hfill 0.8483& \hfill 0.0473& \hfill -0.0307& \hfill -0.0889& \hfill -0.1717& \hfill -0.0864& \hfill 0.1429& \hfill 0.6501& \hfill 0.0049& \hfill 0.7425\end{array}\right]\end{array}$$

once obtained, yields the decoupled coefficient matrices

$$\begin{array}{c}\hfill {\mathbf{C}}_D=\left[\begin{array}{cccccc}\hfill 0.2679& \hfill -0.1244& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.1244& \hfill 0.2799& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.6982& \hfill 0.6001& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.6001& \hfill 0.9180& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.9160& \hfill -0.5483\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill -0.5483& \hfill 1.3037\end{array}\right],\\ \hfill {\mathbf{K}}_D=\left[\begin{array}{cccccc}\hfill 0.1917& \hfill -0.1119& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.1119& \hfill 0.2369& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 1.5057& \hfill 1.0502& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0000& \hfill 0.0000& \hfill 1.0502& \hfill 0.7798& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 1.1754& \hfill -0.5535\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill -0.5535& \hfill 1.1907\end{array}\right].\end{array}$$

Each $2\times 2$ block matrix corresponds to an independent subsystem, and the composite system formed by these three independent subsystems is dynamically equivalent to the undamped system. Figure 4 presents the variation of the objective function during the integration process. As evidenced by this figure, the system has achieved total decoupling.

Example 3.

In this example, we consider a self-adjoint second-order system with

$$\begin{array}{c}\hfill {\mathbf{C}}_0=\left[\begin{array}{cccccc}\hfill 1.1736& \hfill 0.1896& \hfill -0.1163& \hfill 0.2014& \hfill -0.2258& \hfill -0.3911\\ \hfill 0.1896& \hfill 1.0263& \hfill 0.2014& \hfill -0.3489& \hfill -0.3911& \hfill -0.6774\\ \hfill -0.1163& \hfill 0.2014& \hfill 0.5079& \hfill -0.2014& \hfill -0.3916& \hfill 0.0000\\ \hfill 0.2014& \hfill -0.3489& \hfill -0.2014& \hfill 0.8884& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.2258& \hfill -0.3911& \hfill -0.3916& \hfill 0.0000& \hfill 0.7826& \hfill 0.6772\\ \hfill -0.3911& \hfill -0.6774& \hfill 0.0000& \hfill 0.0000& \hfill 0.6772& \hfill 1.1729\end{array}\right],\\ \hfill {\mathbf{K}}_0=\left[\begin{array}{cccccc}\hfill 0.8598& \hfill 0.1206& \hfill -0.0540& \hfill 0.0935& \hfill -0.1236& \hfill -0.2141\\ \hfill 0.1206& \hfill 0.5329& \hfill 0.0935& \hfill -0.1620& \hfill -0.2141& \hfill -0.3709\\ \hfill -0.0540& \hfill 0.0935& \hfill 0.2961& \hfill -0.0935& \hfill -0.2421& \hfill 0.0000\\ \hfill 0.0935& \hfill -0.1620& \hfill -0.0935& \hfill 0.2492& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.1236& \hfill -0.2141& \hfill -0.2421& \hfill 0.0000& \hfill 0.4908& \hfill 0.4308\\ \hfill -0.2141& \hfill -0.3709& \hfill 0.0000& \hfill 0.0000& \hfill 0.4308& \hfill 0.7461\end{array}\right].\end{array}$$

These initial coefficient matrices conform to the structures of matrices $\mathbf{C}$ and $\mathbf{K}$ as defined in Section 3. While preserving its spectrum

$$\begin{array}{cc}\hfill \{& -0.0099\pm 0.0727i,-0.2282\pm 0.2991i,-0.3197\pm 0.5553i,-0.5557\pm 0.3809i,-0.4705\pm 0.5822i,\hfill \\ & -0.9458,-1.4383\},\hfill \end{array}$$

decoupling the system we find damping and stiffness matrices

$$\begin{array}{ccc}\hfill {\mathbf{C}}_D& =& \left[\begin{array}{cccccc}\hfill 1.1834& \hfill 0.0275& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0275& \hfill 0.3845& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.6314& \hfill -0.0605& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0000& \hfill 0.0000& \hfill -0.0605& \hfill 0.9489& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.9468& \hfill 1.1575\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 1.1575& \hfill 1.4570\end{array}\right],\hfill \\ \hfill {\mathbf{K}}_D& =& \left[\begin{array}{cccccc}\hfill 0.5099& \hfill -0.0801& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill -0.0801& \hfill 0.1386& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.4293& \hfill -0.0712& \hfill 0.0000& \hfill 0.0000\\ \hfill 0.0000& \hfill 0.0000& \hfill -0.0712& \hfill 0.5477& \hfill 0.0000& \hfill 0.0000\\ \hfill ine0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.4928& \hfill 0.6530\\ \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.0000& \hfill 0.6530& \hfill 0.8801\end{array}\right].\hfill \end{array}$$

This decoupling is effected by the transformation

$$\begin{array}{c}\hfill {\mathbf{T}}^{*}=\left[\begin{array}{cccccccccccc}\hfill -0.1630& \hfill 0.5903& \hfill 0.0174& \hfill 0.4490& \hfill -0.0403& \hfill -0.1538& \hfill -0.8408& \hfill 0.0257& \hfill 0.1618& \hfill 0.8251& \hfill 0.5492& \hfill -0.2671\\ \hfill -0.3939& \hfill -0.3549& \hfill -0.6342& \hfill -0.1670& \hfill 0.1356& \hfill 0.1819& \hfill 0.3354& \hfill -0.1838& \hfill -0.3585& \hfill -0.7922& \hfill -0.1907& \hfill -0.2856\\ \hfill 0.0179& \hfill 0.5362& \hfill 0.2550& \hfill -0.2458& \hfill 0.0454& \hfill 0.1180& \hfill 0.5202& \hfill -0.0484& \hfill -0.1546& \hfill -0.6043& \hfill 0.5877& \hfill 0.4756\\ \hfill 1.3160& \hfill 0.0164& \hfill 0.5906& \hfill -0.2416& \hfill -0.1581& \hfill -0.3661& \hfill 0.4431& \hfill 0.2197& \hfill -0.0348& \hfill 0.7970& \hfill -0.1764& \hfill -0.0557\\ \hfill ine-0.4869& \hfill -0.3515& \hfill 0.6822& \hfill 0.3250& \hfill 0.0839& \hfill 0.0797& \hfill -0.5754& \hfill -0.1438& \hfill -0.0584& \hfill 0.1831& \hfill -0.2419& \hfill 0.8278\\ \hfill -0.6394& \hfill 0.4186& \hfill -0.0028& \hfill 0.2682& \hfill 0.0917& \hfill 0.0472& \hfill -0.5392& \hfill -0.1523& \hfill -0.0874& \hfill 0.0009& \hfill 0.5371& \hfill 0.0872\\ \hfill -0.0238& \hfill -0.9783& \hfill -0.0183& \hfill -0.1024& \hfill 0.2267& \hfill -0.2054& \hfill 0.2524& \hfill -0.4105& \hfill 0.1134& \hfill -0.0977& \hfill -0.5872& \hfill -0.3708\\ \hfill 0.7274& \hfill 0.3125& \hfill -0.6809& \hfill 0.0198& \hfill -0.4488& \hfill 0.2411& \hfill 0.0508& \hfill 0.7955& \hfill -0.0079& \hfill 0.6987& \hfill -0.4534& \hfill -0.2544\\ \hfill ine0.2217& \hfill 0.6253& \hfill -0.7049& \hfill 0.0081& \hfill -0.1931& \hfill 0.1573& \hfill 0.2420& \hfill 0.3462& \hfill -0.0640& \hfill 0.1143& \hfill 0.2938& \hfill -0.4327\\ \hfill 0.5360& \hfill 0.0166& \hfill 0.5264& \hfill 0.0625& \hfill 0.5057& \hfill -0.4938& \hfill -0.1949& \hfill -0.8947& \hfill 0.5868& \hfill 0.5987& \hfill 0.8788& \hfill -0.2883\\ \hfill 0.2786& \hfill -0.4102& \hfill -0.1670& \hfill -0.1007& \hfill -0.1807& \hfill 0.1068& \hfill 0.3942& \hfill 0.3113& \hfill -0.0780& \hfill 0.1430& \hfill -0.7142& \hfill 0.0143\\ \hfill 0.3783& \hfill 0.0252& \hfill 0.6960& \hfill -0.0316& \hfill -0.2135& \hfill 0.0626& \hfill -0.0835& \hfill 0.3701& \hfill -0.0063& \hfill 0.4252& \hfill -0.3352& \hfill 0.8064\end{array}\right].\end{array}$$

The block-diagonal configuration of matrices ${\mathbf{C}}_D$ and ${\mathbf{K}}_D$ demonstrates total decoupling. Since these subsystems are mutually independent, their dynamic properties can be analyzed separately, providing complete characterization of the initial system’s behavior.

Figure 5 illustrates the evolution of the objective function, concurrently demonstrating the transformation of the coefficient matrices into block-diagonal form during total decoupling.

6. Conclusions

This paper demonstrates the total decoupling of 2D lattice vibration systems through the SPITF framework. Initially, a nonlinear dynamical model is established for this category of systems and subsequently linearized about its equilibrium configuration, which identifies the coefficient matrices $\mathbf{M}$, $\mathbf{C}$, and $\mathbf{K}$ of the linearized system. Solving an initial value problem then yields a transformation $\mathbf{T}$ that minimizes the objective function $f\left(\mathbf{T}\right)$, thereby achieving system decoupling. Numerical simulations verify the efficacy of this methodology, showing that as the coefficient matrices attain block-diagonal configurations, the objective function converges to zero, thereby validating the decoupling approach.