On Two-Dimensional Closed–Open Topological Field Theories

Abstract

Topological field theories (TFTs) have captured the attention of mathematicians due to their various applications. In categorical terms, an nTFT is defined as a monoidal functor that maps the category of n-dimensional cobordisms to the category of vector spaces. In this paper, we introduce the category of two-dimensional closed–open cobordisms, denoted as $2Co{b}_{CO}$. We demonstrate that the generating morphisms in this category total 35. Furthermore, we establish that the category $2Co{b}_{CO}$ is a monoidal category. We define a triple $(B,\epsilon ,{\epsilon }^{\prime })$ as a doubly Frobenius algebra if both $(B,\epsilon )$ and $(B,{\epsilon }^{\prime })$ are Frobenius algebras. We then introduce the category of doubly Frobenius algebras, wherein the objects are doubly Frobenius algebras and the morphisms are homomorphisms of Frobenius algebras that satisfy specific compatibility conditions. Additionally, we present a new type of 2TFT, which we refer to as the two-dimensional closed–open TFT (denoted as $2TF{T}_{CO}$). We demonstrate that the category of all $2TF{T}_{CO}$, referred to as $2\mathcal{T}\mathcal{F}{\mathcal{T}}_{CO}$, is equivalent to the category of all commutative doubly Frobenius algebras, denoted as $\mathcal{C}\mathcal{F}$.

1. Introduction

The concept of a topological quantum field theory (TFT) emerges from the interplay between physics and mathematics, specifically through the lenses of quantum field theory and topology. This framework enhances our comprehension of quantum phenomena by integrating topological data. TFTs were developed by physicists who were exploring topological invariants of manifolds alongside gauge theory. The mathematical formulation of TFTs allows for a rigorous understanding of these theories, typically framed as a symmetric monoidal functor $T:nCob\to Vect$. Here, $nCob$ denotes the category of cobordisms, while $Vect$ represents the category of vector spaces, facilitating the algebraic interpretation of geometric objects.

The foundational definition of a TFT, introduced by Michael Atiyah [1], built on existing works in mathematical physics, particularly those by Edward Witten, who delved into topological Yang–Mills theory and the invariants of manifolds defined by quantum field theories [2].

Earlier, the functorial approach put forth by Graeme Segal [3] emphasized the categorical structures inherent in field theories defined on Riemann surfaces. Atiyah subsequently utilized Segal’s framework to formulate a purely categorical definition of TFT, known as Atiyah’s axioms. In further developments, Jan Dijkgraaf examined both the categorical and geometric features of two-dimensional topological field theories (2TFTs) [4].

In the context of 2TFTs, the geometric category $2Cob$ comprises objects represented by one-dimensional manifolds and morphisms that correspond to surfaces between these manifolds. Notably, Robbert Abrams demonstrated the equivalence of the objects, when consisting of disjoint unions of circles, to the category of commutative Frobenius algebras [5]. Subsequently, J. Kock provided a comprehensive description of 2TFTs [6]. Recognizing Frobenius algebras as objects within a symmetric monoidal category underscores their pivotal role in characterizing topological field theories in lower dimensions, allowing for the algebraic encoding of duality, non-degenerate bilinear forms, and trace operations. For instance, Lauda and Pfeiffer illustrated that open–closed 2TFTs can be effectively described through knowledge of Frobenius algebras [7]. Recently, Adam Czenk studied extended Frobenius structures relevant to non-oriented genera, aiding in the categorical characterization of TFTs in lower dimensions [8].

Numerous studies have explored TFTs, offering diverse perspectives and methodologies to contextualize them within mathematical physics and algebraic geometry. Getzler and Pandharipande examined the structure of semi-simple two-dimensional topological field theories [9], linking them to quantum cohomology and Gromov–Witten theory. Kimura extended noncommutative generalizations of Frobenius algebras in his investigation of matrix models [10]. Additionally, Juhaz employed surgery techniques to provide a concrete explanation and proof of the equivalence between two-dimensional TFTs and commutative Frobenius algebras [11].

Topological and algebraic tools are utilized in real-life applications to describe decision boundaries in medical data and uncertainty; see [12,13]. These concepts create a link with the idea of closed–open topological field theories. They treat medical data, such as imaging results and clinical labels, as objects within a topological field theory. Additionally, topological field theories can provide algebraic constraints to ensure consistency when merging local rough sets into a global diagnostic conclusion.

2. Preliminaries

In this section, we provide the basic definitions and known results that we will rely on throughout this paper. The section covers both the geometric and algebraic fundamentals.

Definition 1.

A Morse function is defined as a smooth function $f:X\to [0,1]$, where X is a smooth manifold without a boundary. One key characteristic of a Morse function is the presence of only non-degenerate critical points.

Remark 1.

In cases where the manifold X includes a boundary, the function must ensure that the boundary $\partial X$ is mapped entirely to the boundary $\partial [0,1]$ of the interval $[0,1]$. Furthermore, it is essential that the boundary $\partial [0,1]$ contains no critical values of the function.

Theorem 1

([14]). Morse functions on a smooth manifold X always exist and are dense in the space of all smooth maps $f:X\to [0,1]$.

Definition 2.

A one-dimensional open compact manifold refers to a manifold of dimension 1 that has boundaries, and it specifically consists of a disjoint union of closed intervals.

Definition 3

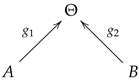
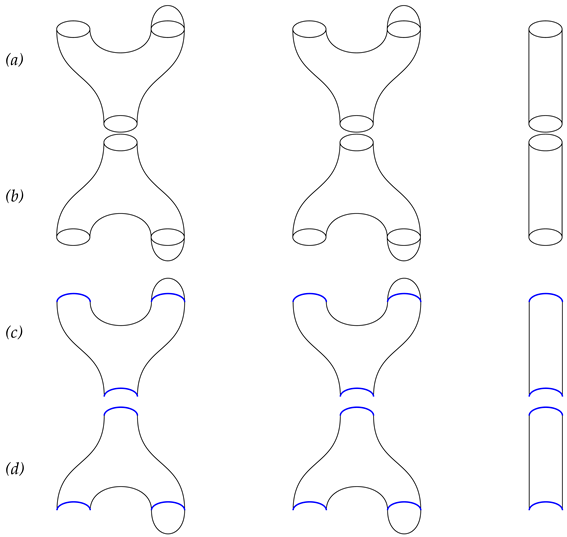
([15]). An open cobordism between two open one-dimensional manifolds A and B can be described using a surface Θ, in which the boundary is decomposed as $\partial \Theta =A\cup B\cup {\partial }_{\mathit{out}}\Theta$. In this context, ${\partial }_{\mathit{out}}\Theta$ acts as a cobordism from $\partial A$ to $\partial B$, with both $\partial A$ and $\partial B$ being compact 0-manifolds.

Furthermore, we have homeomorphisms illustrated by the following diagram:

Within this framework, the mapping $g_1\coprod g_2:A\coprod B\to \partial \Theta \setminus {\partial }_{\mathit{out}}\Theta$ must be a homeomorphism.

Definition 4

([6]). A one-dimensional closed manifold refers to a manifold of dimension 1 without boundaries, and it specifically consists of a disjoint union of circles. A closed cobordism between two closed 1D manifolds A and B is defined as above.

Remark 2.

In the context of closed cobordisms, A and B have no boundaries. Therefore, ${\partial }_{\mathit{out}}\Theta =\varnothing .$

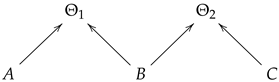
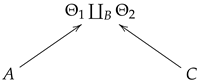
Remark 3.

Cobordisms can be glued together along a common boundary component. Specifically, given two cobordisms ${\Theta }_1$ and ${\Theta }_2$, where Θ is a cobordism between manifolds A and B, and ${\Theta }_2$ is a cobordism between B and C, we can create a new manifold ${\Theta }_1{\coprod }_B{\Theta }_2$ by gluing them along the boundary B. This process is illustrated in the following diagram:

The resulting cobordism can be represented as

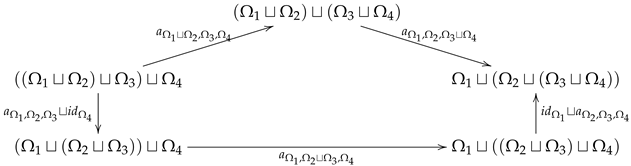
Furthermore, the gluing of cobordisms is associative. If we have three cobordisms ${\Theta }_1$, ${\Theta }_2$, and ${\Theta }_3$, such that ${\Theta }_1$ is a cobordism between A and B, ${\Theta }_2$ is a cobordism between B and C, and ${\Theta }_3$ is a cobordism between C and D, then the following relationship holds:

$$\left({\Theta }_1\coprod _B{\Theta }_2\right)\coprod _C{\Theta }_2={\Theta }_1\coprod _B\left({\Theta }_2\coprod _C{\Theta }_3\right)$$

Definition 5.

The category $2\mathcal{C}{\mathit{ob}}_O$ is composed of the following elements:

1. 

Objects: The objects consist of 1-dimensional compact manifolds, interpreted as a disjoint union of a finite number of closed intervals.

2. 

Morphisms: Morphisms between these objects are defined as equivalence classes of cobordisms. For any object $A\in 2\mathcal{C}{\mathit{ob}}_O$, the identity morphism is characterized by the 2-dimensional cylinder.

Composition of morphisms: Given morphisms $\psi :A\to B$ and ${\psi }^{\prime }:B\to C$, their composition ${\psi }^{\prime }\circ \psi$ forms a cobordism between objects A and C. Specifically, this is expressed as

$${\psi }^{\prime }\circ \psi ={\Theta }_1\coprod _B{\Theta }_2$$

where ${\Theta }_1$ denotes the cobordism corresponding to ψ and ${\Theta }_2$ represents the cobordism that corresponds to ${\psi }^{\prime }$.

Remark 4.

The category $2\mathcal{C}{\mathit{ob}}_C$ is defined analogously to the category $2\mathcal{C}{\mathit{ob}}_O$ with objects being disjoint union of circles.

Definition 6.

([15]). A function $f:\Theta \to [0,1]$, where Θ is an open cobordism connecting two manifolds A and B, is termed Morse if it meets the following criteria: The set of points that map to 0 under f equals A; the set of points that map to 1 equals B; and when restricted to the boundary ${\partial }_{\mathit{out}}\Theta$, f behaves as a Morse function. Furthermore, we also impose that the pre-image of any value in the range of f does not contain any closed components.

Remark 5.

It was stated in [7] that such Morse functions exist on open cobordisms.

Definition 7.

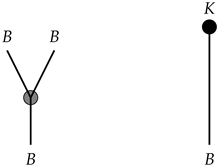
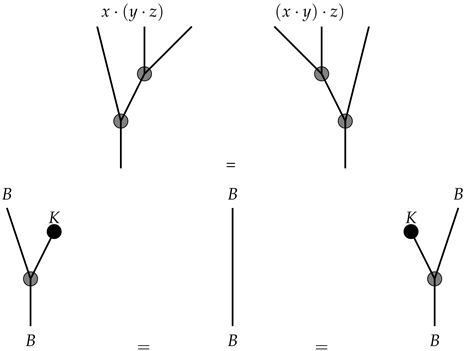
([6]). An associative algebra over a ring K consists of a set B along with two operations: multiplication, represented by the map $m:B\otimes B\to B$, and a unit map, denoted as $i:K\to B$. These operations must satisfy specific commutative diagrams, which are outlined in the following:

In graphical representation, both multiplication and the unit exhibit distinct forms:

The axioms of associativity and identity can be effectively illustrated through graphical representations:

Definition 8.

An algebra B in a symmetric monoidal category $\mathcal{C}$ is termed Frobenius if it is provided with a morphism $\epsilon :B\to K$, known as the Frobenius form. This morphism induces a pairing $\beta =\epsilon \circ m:B\otimes B\to K$, referred to as the Frobenius pairing, which is a symmetric and non-degenerate pairing. This means that there exists a morphism ${\beta }^{\prime }:K\to B\otimes B$, called the Frobenius copairing, such that the compositions of these morphisms,

are the identity. The following is a ribbon graph representation of the above compositions:

Definition 9.

([1]). Let $\mathcal{C}$ denote a monoidal category. An n-dimensional topological field theory (nTFT) is characterized as a symmetric monoidal functor

$$T:n\mathit{Cob}\to \mathcal{C}.$$

This functor must meet certain criteria: specifically, the image of the ($n-1$)-dimensional empty manifold, represented as $T(\varnothing )$, must correspond to the unit object K in the category $\mathcal{C}$. Additionally, the functor should map the disjoint union of $(n-1)$-dimensional manifolds to the tensor product of objects within $\mathcal{C}$.

Remark 6.

We denote $2TF{T}_O$ as a two-dimensional topological field theory $T:2{\mathit{Cob}}_O\to \mathcal{C}$, and $2TF{T}_C$ as another two-dimensional topological field theory $T:2{\mathit{Cob}}_C\to \mathcal{C}$.

Theorem 2

([5]). The category of 2-dimensional open topological field theories, denoted as $2\mathcal{T}\mathcal{F}{\mathcal{T}}_O$, is equivalent to the category of Frobenius algebras, represented by $\mathcal{F}\mathcal{A}$.

Theorem 3

([4]). The category of 2-dimensional closed topological field theories, denoted as $2\mathcal{T}\mathcal{F}{\mathcal{T}}_C$, is equivalent to the category of commutative Frobenius algebras, represented by $\mathcal{C}\mathcal{F}\mathcal{A}$.

3. Two-Dimensional (Closed + Open) Topological Field Theories

In this section, we introduce a new category of cobordisms, which we refer to as the 2D closed + open category, denoted as $2\mathcal{C}{\mathit{ob}}_{CO}$. We also define a new 2D closed–open topological field theory, which we call $TF{T}_{CO}$. Furthermore, we present several results.

Definition 10.

The category $2\mathcal{C}{\mathit{ob}}_{CO}$ consists of the following components:

1. 

Objects: The objects are of the form $C\coprod O$, where C is a disjoint union of a finite number of circles $S^1$ and O is a disjoint union of a finite number of closed intervals.

2. 

Morphisms: For any two objects $X,Y$ in $2\mathcal{C}{\mathit{ob}}_{CO}$, morphisms between X and Y are equivalence classes of cobordisms. We represent X as $C\coprod O$ and Y as $C^{\prime }\coprod O^{\prime }$, where $C,C^{\prime }$ are disjoint unions of circles $S^1$ and $O,O^{\prime }$ are disjoint unions of closed intervals. A morphism f can be expressed as a disjoint union of $f_C$ and $f_O$, where $f_C$ is a cobordism between C and $C^{\prime }$, and $f_O$ is a cobordism between O and $O^{\prime }$.

For any object $X\in 2\mathcal{C}{\mathit{ob}}_{CO}$, the identity morphism is represented by the disjoint union of two 2-dimensional cylinders: one for the closed cobordism and one for the open cobordism.

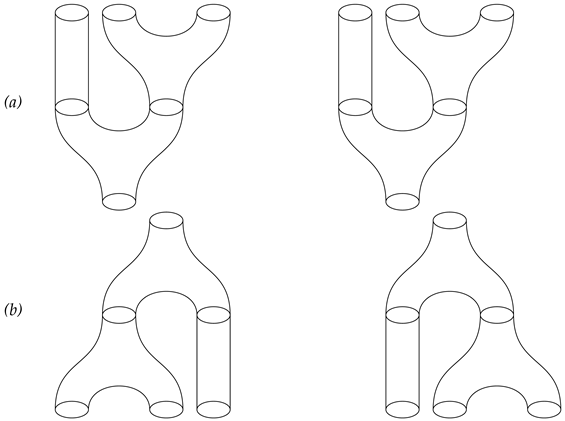
Compositions of morphisms: For morphisms $r:X\to Y$ and $u:Y\to Z$, the composition $u\circ r$ is a cobordism between X and Z. More precisely, we have

$$u\circ r=(N\coprod _{C^{\prime }}{N}^{\prime })\coprod (M\coprod _{O^{\prime }}{M}^{\prime })$$

where $X=C\coprod O,$$Y=C^{\prime }\coprod O^{\prime },$$Z=C^{″}\coprod O^{″}$, N is a cobordism between $C,C^{\prime }$, $N^{\prime }$ is a cobordism between $C^{\prime },C^{″}$, M is a cobordism between $O,O^{\prime }$, and $M^{\prime }$ is a cobordism between $O^{\prime },O^{″}$.

Lemma 1.

The number of generating objects in $2\mathcal{C}{\mathit{ob}}_{CO}$ is three.

Proof. 

The objects in this case are compact manifolds of dimension 1. They can be represented as disjoint unions of circles and closed intervals.

The first generating object consists of a disjoint union of one circle and one closed interval. The second generating object is a disjoint union of a circle and the one-dimensional empty manifold. Finally, the third generating object is the disjoint union of a closed interval and the one-dimensional empty manifold. □

Remark 7.

As previously mentioned, Morse functions always exist on both open and closed cobordisms. Then, we deduce the following modified Morse function.

Definition 11.

Let N be a cobordism of the form $N=C\coprod O$, where C is a closed cobordism with a Morse function f, and O is an open cobordism with a Morse function g. We define $F:N\to [0,1]$ as $F(c,o)=f\left(c\right)\cup g\left(o\right)$. This F is referred to as a modified Morse function on N.

Remark 8.

For a given modified Morse function F on $\Omega =C\coprod O$, critical values coming from C can coincide with critical values coming from O.

Remark 9.

We call a cobordism $C\coprod O$ in $2\mathcal{C}{\mathit{ob}}_{CO}$ if each of C and O has exactly one critical point at most.

Proposition 1.

The number of minimal morphisms in $2\mathcal{C}{\mathit{ob}}_{CO}$ is 35.

Proof. 

Let $\psi :A\to B$ be an arbitrary morphism that is a cobordism of the form $\Omega =\Gamma \coprod \Delta$. Consider a modified Morse function $F=f\coprod g$ on M. Let $F\left(x_1\right),F\left(x_2\right),\dots ,F\left(x_n\right)$ be all the critical values with respect to f, and let $F\left(y_1\right),F\left(y_2\right),\dots ,F\left(y_s\right)$ be all the critical values with respect to g. We arrange the critical values as follows:

$$F\left(x_1\right)<F\left(x_2\right)<\dots <F\left(x_n\right)$$

and

$$F\left(y_1\right)<F\left(y_2\right)<\dots <F\left(y_s\right)$$

such that $F\left(x_i\right)=F\left(y_j\right)$ for $i=j$. This arrangement is possible as Morse functions are dense. For example, we choose a height function F on the given morphism. Then, we smoothly adjust $\Delta$ so that the critical points $x_i$ and $y_j$ from $\Gamma$ and $\Delta$ are aligned at the same level for $i=j$. This results in $F\left(x_i\right)=F\left(y_i\right)$.

Suppose, without loss of generality, that $max\{n,s\}=s$. Then, we have $F\left(x_n\right)<F\left(y_s\right)$.

Next, we cut the cobordism into pieces as follows: We choose non-critical values $d_1,d_2,\dots ,d_n$ such that

$$F\left(x_1\right)<d_1<F\left(x_2\right)<\dots <F\left(x_{n-1}\right)<d_n<F\left(x_n\right).$$

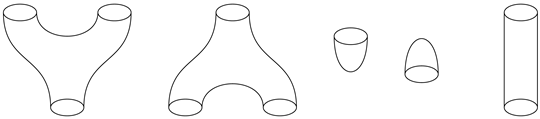
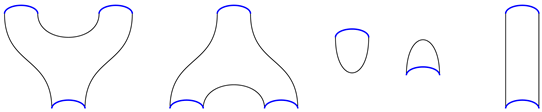
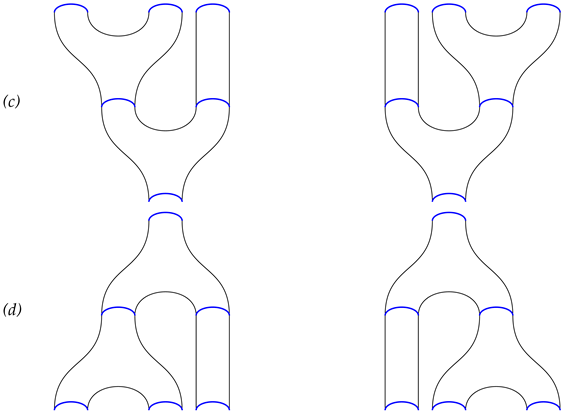
We then cut the cobordism along the pre-images of $d_1,d_2,\dots ,d_n$. Consequently, along the pre-image of each $d_i$, we obtain a cobordism of the form $\Gamma \coprod \Delta$ in which each copy has only one critical point. If the cobordism is of the form $\Gamma \coprod \varnothing$, then all possible minimal morphisms are as follows:

We refer to the cobordisms above as Γ₁, Γ₂, Γ₃, Γ₄ and Γ₅, respectively. If the cobordism is of the form ∅∐Δ, then the following are all possible minimal morphisms:

The above cobordisms are represented by ${\Delta }_1,{\Delta }_2,{\Delta }_3,{\Delta }_4,$ and ${\Delta }_5$, respectively. We have 10 generating morphisms, as represented above. Then, we take each minimal ${\Gamma }_i$ along with the disjoint union of all possible minimal ${\Delta }_j$, which gives us 25 generating morphisms, as delineated below.

	${\Delta }_1$	${\Delta }_2$	${\Delta }_3$	${\Delta }_4$	${\Delta }_5$
${\Gamma }_1$	$({\Gamma }_1,{\Delta }_1)$	$({\Gamma }_1,{\Delta }_2)$	$({\Gamma }_1,{\Delta }_3)$	$({\Gamma }_1,{\Delta }_4)$	$({\Gamma }_1,{\Delta }_5)$
${\Gamma }_2$	$({\Gamma }_2,{\Delta }_1)$	$({\Gamma }_2,{\Delta }_2)$	$({\Gamma }_2,{\Delta }_3)$	$({\Gamma }_2,{\Delta }_4)$	$({\Gamma }_2,{\Delta }_5)$
${\Gamma }_3$	$({\Gamma }_3,{\Delta }_1)$	$({\Gamma }_3,{\Delta }_2)$	$({\Gamma }_3,{\Delta }_3)$	$({\Gamma }_3,{\Delta }_4)$	$({\Gamma }_3,{\Delta }_5)$
${\Gamma }_4$	$({\Gamma }_4,{\Delta }_1)$	$({\Gamma }_4,{\Delta }_2)$	$({\Gamma }_4,{\Delta }_3)$	$({\Gamma }_4,{\Delta }_4)$	$({\Gamma }_4,{\Delta }_5)$
${\Gamma }_5$	$({\Gamma }_5,{\Delta }_1)$	$({\Gamma }_5,{\Delta }_2)$	$({\Gamma }_5,{\Delta }_3)$	$({\Gamma }_5,{\Delta }_4)$	$({\Gamma }_5,{\Delta }_5)$

Each pair $({\Gamma }_i,{\Delta }_j)$ represents the disjoint union ${\Gamma }_i\coprod {\Delta }_j$. This results in a total of 25 generating morphisms, giving us 35 generating morphisms overall. □

Remark 10.

We shall refer to a generating morphism as a minimal morphism; i.e., it is of the form $C\coprod O$ such that each of the cobordisms C and O has at most one critical point.

Example 1.

The following morphism represent a non-minimal morphism in $2\mathcal{C}{\mathit{ob}}_{CO}$ as the closed cobordism has four critical points and the open one has three critical points:

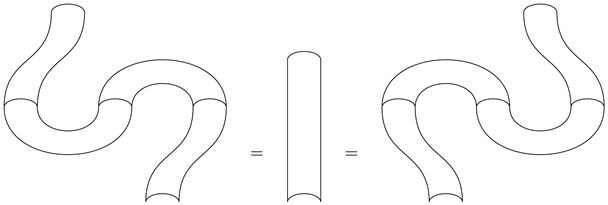
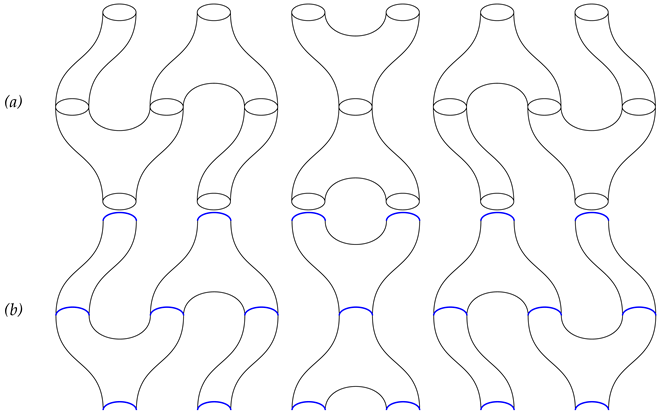
Remark 11.

According to the explanation provided in [6], two cobordisms are considered equivalent if they have the same genus and the same number of incoming and outgoing boundaries. In this paper, we designate the top boundary of a given cobordism as incoming, while the bottom boundary is referred to as outgoing.

Proposition 2.

The following list presents the basic relations between morphisms in $2Co{b}_{CO}$, where each item corresponds to equivalent cobordisms:

1. 

Unit relations:

2. 

Associativity relation and coassociativity relation:

3. 

Frobenius relations:

More relations among morphisms can be represented as a disjoint union. Specifically, let $i_{xj}$ denote the $jth$ cobordism associated with the number i and later x, where $i,j=1,2,3$ and $x=a,b,c$, or d. Then, the expression $i_{xj}\coprod i_{y{j}^{\prime }}^{\prime }$ is equivalent to all possible cases for $j,j^{\prime }=1,2,3$.

Proof. 

This follows directly from Remark 11. □

Remark 12.

For any objects ${\Omega }_1=C\coprod O$, ${\Omega }_2=C^{\prime }\coprod O^{\prime }\in 2\mathcal{C}{\mathit{ob}}_{CO}$, we take "⊔" to be the tensor product in the following sense:

$$(C\coprod O)\bigsqcup (C^{\prime }\coprod O^{\prime })=(C\bigsqcup C^{\prime })\coprod (O\bigsqcup O^{\prime })$$

Remark 13.

We denote the tensor product in $2\mathcal{C}{\mathit{ob}}_{CO}$ using the symbol ⊔, which represents the disjoint union of any objects in the category. Additionally, since the objects in this category consist of disjoint unions of manifolds, we refer to this disjoint union using the notation ∐.

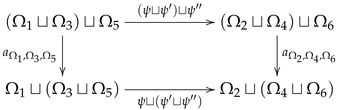
Lemma 2.

For any two objects ${\Omega }_1,{\Omega }_2\in (2\mathcal{C}{\mathit{ob}}_{CO},\bigsqcup )$, we have that ${\Omega }_1\bigsqcup {\Omega }_2$ is isomorphic to ${\Omega }_2\bigsqcup {\Omega }_1,$ i.e., ${\Omega }_1\bigsqcup {\Omega }_2\cong {\Omega }_2\bigsqcup {\Omega }_1.$

Proof. 

First, note that the 2D open cobordism $2Co{b}_O$ and the 2D closed cobordism $2Co{b}_C$ are symmetric, i.e., any two objects in each category commute with each other with respect to the disjoint union $\bigsqcup .$ Write ${\Omega }_1=C\coprod O$ and ${\Omega }_2=C^{\prime }\coprod O^{\prime }.$

$$\begin{array}{cc}\hfill (C\coprod O)\bigsqcup (C^{\prime }\coprod O^{\prime })& =(C\bigsqcup C^{\prime })\coprod (O\bigsqcup O^{\prime })\hfill \\ \hfill & \cong (C^{\prime }\bigsqcup C)\coprod (O^{\prime }\bigsqcup O)\hfill \\ \hfill & =(C^{\prime }\coprod O^{\prime })\bigsqcup (C\coprod O)\hfill \end{array}$$

□

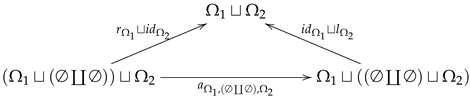
Theorem 4.

The category $(2\mathcal{C}{\mathit{ob}}_{CO},\bigsqcup )$ is a monoidal category.

Proof. 

The unit object in this category is the disjoint union of two copies of the one-dimensional empty manifold, denoted as $\varnothing \coprod \varnothing$. One copy is associated with closed cobordisms, while the other is associated with open cobordisms. Additionally, we consider the family of isomorphisms related to this structure,

$$a={\{a_{{\Omega }_1,{\Omega }_2,{\Omega }_3}:({\Omega }_1\bigsqcup {\Omega }_2)\bigsqcup {\Omega }_3\to {\Omega }_1\bigsqcup ({\Omega }_2\bigsqcup {\Omega }_3)\}}_{{\Omega }_1,{\Omega }_2,{\Omega }_3}\in 2\mathcal{C}{\mathit{ob}}_{CO},$$

a family of isomorphisms $l={\{l_{{\Omega }_i}:(\varnothing \coprod \varnothing )\bigsqcup {\Omega }_i\to {\Omega }_i\}}_{{\Omega }_i\in 2\mathcal{C}{\mathit{ob}}_{CO}}$, and a family of isomorphisms $r={\{r_{{\Omega }_i}:{\Omega }_i\bigsqcup (\varnothing \coprod \varnothing )\to {\Omega }_i\}}_{{\Omega }_i\in 2\mathcal{C}{\mathit{ob}}_{CO}}$. Hence, the following diagrams commute:

1.

For all ${\Omega }_1,{\Omega }_2,{\Omega }_3,{\Omega }_4\in 2Co{b}_{CO}$,

2.

For all ${\Omega }_1,{\Omega }_2\in \mathcal{C}{\mathit{ob}}_{CO}$,

3.

For all $\psi :{\Omega }_1\to {\Omega }_2, {\psi }^{\prime }:{\Omega }_3\to {\Omega }_4, {\psi }^{\prime \prime }:{\Omega }_5\to {\Omega }_6$ in the category $2Co{b}_{CO}$,

4.

For any morphism $\psi :{\Omega }_1\to {\Omega }_2\in 2Co{b}_{CO}$,

□

Definition 12.

Let B be an algebra over a ground field K. We define a triple $(B,\epsilon ,{\epsilon }^{\prime })$ as a doubly Frobenius algebra if both $(B,\epsilon )$ and $(B,{\epsilon }^{\prime })$ are Frobenius algebras, where ε and ${\epsilon }^{\prime }$ are Frobenius forms on B. B is called a symmetric doubly Frobenius algebra if $\epsilon \left(xy\right)=\epsilon \left(yx\right)$ and ${\epsilon }^{\prime }\left(xy\right)={\epsilon }^{\prime }\left(yx\right)$ for all $x,y\in B$.

Example 2.

Let $\mathbb{R}$ denote the set of all real numbers, which forms a field. Consider the space $B=M_{2\times 2}=\left\{\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]:a,b,c,d\in \mathbb{R}\right\}$. This space B is an algebra over $\mathbb{R}$. Our goal is to define a Frobenius structure on B.

We define a linear functional $\epsilon :B\to \mathbb{R}$ such that $\epsilon \left(\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\right)=a+d$. One equivalent definition for an algebra B to qualify as a Frobenius algebra is to show that the kernel of the Frobenius form ε does not contain any non-trivial left ideal.

The set of left ideals in B is given by

$$B_L=\left\{\left[\begin{array}{cc}a& 0\\ b& 0\end{array}\right]:a,b\in \mathbb{R}\right\}.$$

Meanwhile, the kernel of ε is defined as

$$kernel=\left\{\left[\begin{array}{cc}a& b\\ c& -a\end{array}\right]:a,b,c\in \mathbb{R}\right\}.$$

Thus, the only left ideal contained in the kernel is the zero matrix. Consequently, we conclude that $(B,\epsilon )$ is a symmetric Frobenius algebra.

Example 3.

We can define a different Frobenius structure on the algebra from Example 2 by introducing a Frobenius form denoted as ${\epsilon }^{\prime }:B\to \mathbb{R}$, such that ${\epsilon }^{\prime }\left(\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\right)=b+c.$

Following the same reasoning as in Example 2, we find that $(B,{\epsilon }^{\prime })$ is a Frobenius algebra. However, the pair $(B,{\epsilon }^{\prime })$ cannot be symmetric. To demonstrate this, consider the elements $x=\left[\begin{array}{cc}1& 2\\ 0& 0\end{array}\right]$ and $y=\left[\begin{array}{cc}1& 1\\ 2& 2\end{array}\right].$

We have ${\epsilon }^{\prime }\left(xy\right)=5$ and ${\epsilon }^{\prime }\left(yx\right)=4,$ which implies that ${\epsilon }^{\prime }\left(xy\right)\ne {\epsilon }^{\prime }\left(yx\right).$ Therefore, ${\epsilon }^{\prime }$ does not define a symmetric Frobenius structure on $B.$ Consequently, the triple $(B,\epsilon ,{\epsilon }^{\prime })$ is not a symmetric doubly Frobenius algebra.

Definition 13.

Define the category $\mathcal{F}$ of doubly Frobenius algebras over a field K as follows:

1. 

Objects: The objects in this category are symmetric doubly Frobenius algebras.

2. 

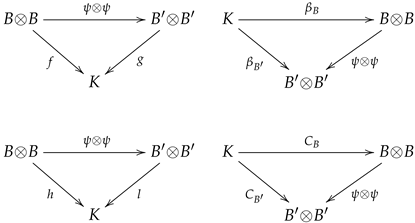
Morphisms: Given two symmetric doubly Frobenius algebras $(B,\epsilon ,{\epsilon }^{\prime })$ and $(B^{\prime },\alpha ,{\alpha }^{\prime })$, a morphism $\psi :(B,\epsilon ,{\epsilon }^{\prime })\to (B^{\prime },\alpha ,{\alpha }^{\prime })$ is a homomorphism of algebras such that the following diagrams commute:

where $f=\epsilon \circ m_B,h={\epsilon }^{\prime }\circ m_B,g=\alpha \circ m_{B^{\prime }},\mathrm{and}l={\alpha }^{\prime }\circ m_{B^{\prime }}.$

Remark 14.

Observe that the category of commutative doubly Frobenius algebras over a field K, denoted by $\mathcal{C}\mathcal{F}$, is included in the category $\mathcal{F}$, specifically $\mathcal{C}\mathcal{F}\subset \mathcal{F}$.

Remark 15.

We mean by $2TF{T}_{CO}$ a two-dimensional closed–open topological field theory:

$$T:2{\mathit{Cob}}_{CO}\to \mathcal{C}$$

Theorem 5.

The category $2\mathcal{T}\mathcal{F}{\mathcal{T}}_{CO}$ of two-dimensional closed–open topological field theories is equivalent to the category $\mathcal{C}\mathcal{F}$ of commutative doubly Frobenius algebras.

Proof. 

Let us first define a functor G from the category of two-dimensional closed–open topological field theories to the category of doubly commutative Frobenius algebras:

$$G:2\mathcal{T}\mathcal{F}{\mathcal{T}}_{CO}\to \mathcal{C}\mathcal{F}.$$

Given an object $T\in 2\mathcal{T}\mathcal{F}{\mathcal{T}}_{CO}$, for minimal morphisms in $2\mathcal{C}{\mathit{ob}}_{CO}$ of the form $C\coprod \varnothing$, T assigns the following linear maps: $\epsilon :B\to K$, $i:K\to B$, $id:B\to B$, $m:B\otimes B\to B$, $\delta :B\to B\otimes B$. For minimal morphisms of the form $\varnothing \coprod O$, let T assign the same linear maps as before. However, the cobordism from a single interval to the empty manifold will be mapped to ${\epsilon }^{\prime }:B\to K$, i.e, $\epsilon =T(S^1\to \varnothing )$, ${\epsilon }^{\prime }=T(D\to \varnothing )$, $i=T(\varnothing \to S^1)=T(\varnothing \to D)$, $id=T(S^1\to S^1)=T(D\to D)$, $m=T(S^1\bigsqcup S^1\to S^1)=T(D\bigsqcup D\to D)$, and $\delta =T(S^1\to S^1\bigsqcup S^1)=T(D\to D\bigsqcup D)$. In this context, $S^1$ denotes a circle, D represents the closed interval, and ∅ represents the empty manifold. Proposition 2 shows that the the identities on B are

where $\beta$ is either $\epsilon \circ m$ or ${\epsilon }^{\prime }\circ m$ and ${\beta }^{\prime }$ is the dual of $\beta .$ Since the value on the circle under any TFT is a commutative Frobenius algebra, this forces the value on the closed interval under T to be a commutative Frobenius algebra. We need to verify that the functor G is full, faithful, and essentially surjective, which would imply that G is an equivalence of categories.

Suppose we have a commutative doubly Frobenius algebra $(B,\epsilon ,{\epsilon }^{\prime })$ over a field K. We must find a $2TF{T}_{CO}$ such that $G\left(2TF{T}_{CO}\right)$ is isomorphic to $(B,\epsilon ,{\epsilon }^{\prime })$. We can define a $2TF{T}_{CO}$, denoted as T, such that for the one-dimensional empty manifold, T assigns K. For the disjoint union of n circles and m intervals, T assigns $B^{\otimes (n+m)}$, where $n+m$ is the sum of the number of circles and closed intervals.

Let $h:B\to B^{\prime }$ be a homomorphism of doubly Frobenius algebras. We want to find a natural transformation $\chi :T\to T^{\prime }$ in $2\mathcal{T}\mathcal{F}{\mathcal{T}}_{CO}$ such that $G\left(\chi \right)=h$. This can be achieved by choosing a closed–open topological field theory T whose values on the circle and closed interval yield B, and similarly for $T^{\prime }$, which yields $B^{\prime }$. Hence, we have $G\left(\chi \right)=h:B\to B^{\prime }$.

Now, let us assume we have two natural transformations $\chi :T\to T^{\prime }$ and ${\chi }^{\prime }:T\to T^{\prime }$, both of which map to the same homomorphism $h:B\to B^{\prime }$ of doubly Frobenius algebras. However, all component functions of $\chi$ are determined by ${\chi }_1:T\left(S^1\right)=T\left(D\right)\to T^{\prime }\left(S^1\right)=T^{\prime }\left(D\right)$ (this follows from Proposition 2), and similarly for ${\chi }^{\prime }$ and hence ${\chi }_1={\chi }_1^{\prime }$, which implies $\chi ={\chi }^{\prime }$. Therefore, G is indeed an equivalence. □

Example 4.

Let $\mathbb{C}$ be the field of all complex numbers, and let B be any commutative algebra over $\mathbb{C}$. Suppose that the dimension of B is n, where $n\in \mathbb{N}$. According to Wedderburn’s theorem ([16], p. 854), we can decompose B as follows:

$$B={\mathbb{C}}_1\oplus {\mathbb{C}}_2\oplus \dots \oplus {\mathbb{C}}_n$$

where each ${\mathbb{C}}_i$ is a copy of the field $\mathbb{C}$.

We can establish a Frobenius form for each component of the direct sum. For example, we can take each ${\epsilon }_i:{\mathbb{C}}_i\to \mathbb{C}$ to be the identity map. Consequently, we can define the Frobenius form ε on B as follows:

$$\epsilon ={\epsilon }_1+{\epsilon }_2+\dots +{\epsilon }_n.$$

Another Frobenius form can be defined by mapping each x in ${\mathbb{C}}_i$ to $3x\in \mathbb{C}$. Thus, the sum of these maps, denoted $\alpha ,$ is a Frobenius form.

As a result, $(B,\epsilon ,\alpha )$ forms a commutative doubly Frobenius algebra. It is important to note that we should assume the category of commutative doubly Frobenius algebras is an additive category to allow for the direct sum.

4. Conclusions

Many studies have investigated topological field theories from the perspectives of both physics and mathematics. To define a topological field theory, we first need to select a category of cobordisms and analyze it geometrically. The dimension plays an important role in this context. When referring to two-dimensional topological field theories, we mean that the objects of the cobordism category are of dimension 1, while the morphisms are of dimension 2. Similarly, in three-dimensional topological field theories (3TFTs), the cobordism category consists of dimension-2 objects and morphisms of dimension 3.

Various explorations have examined the cobordism category. For instance, in dimension 2, researchers have defined a closed cobordism category that is algebraically classified by a commutative Frobenius algebra. In contrast, the open cobordism category is classified by a Frobenius algebra that is not necessarily commutative.

In this paper, we define a new category, which we call the closed–open category of cobordisms, by taking both circles and closed intervals as objects. We also define a closed–open topological field theory (TFT) in dimension 2. We find that the category of all $2TF{T}_{CO}$ is described by commutative doubly Frobenius algebras. The purpose of this investigation is to extend the category of closed cobordisms, denoted as $2{\mathit{Coc}}_C$, and the category of open cobordisms, denoted as $2{\mathit{Cob}}_O$. We combine these two categories into a new category called closed–open cobordisms, represented as $2{\mathit{Cob}}_{CO}$. This generalization differs from the one presented in [7], where morphisms between intervals and circles are permitted. We believe that our new generalization will pave the way for further developments, especially in dimension 3, where we can consider the objects to be the same as those in $2{\mathit{Cob}}_{CO}$ and 1-morphisms to be as in $2{\mathit{Cob}}_{CO}$ as well. However, the interactions between morphisms, known as 2-morphisms, remain unclear.