Third-Order Nonlinear Neutral Delay Differential Equations with Several Deviating Arguments: Improved Oscillation Criteria

Al-Jaser, Asma; Serra-Capizzano, Stefano; Alluqmani, Eman; Qaraad, Belgees

doi:10.3390/axioms14110850

Open AccessArticle

Third-Order Nonlinear Neutral Delay Differential Equations with Several Deviating Arguments: Improved Oscillation Criteria

¹

Department of Mathematical Sciences, College of Science, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh 11671, Saudi Arabia

²

Department of Science and High Technology, University of Insubria, Via Valleggio 11, 22100 Como, Italy

³

Division of Scientific Computing, Department of Information Technology, Uppsala University, Lägerhyddsv 2, hus 2, SE-751 05 Uppsala, Sweden

⁴

Department of Mathematics, Faculty of Sciences, Umm Al-Qura University, P.O. Box 14035, Makkah 21955, Saudi Arabia

⁵

Department of Mathematics, Faculty of Science, Mansoura University, Mansoura 35516, Egypt

^*

Author to whom correspondence should be addressed.

Axioms 2025, 14(11), 850; https://doi.org/10.3390/axioms14110850

Submission received: 18 September 2025 / Revised: 4 November 2025 / Accepted: 11 November 2025 / Published: 18 November 2025

(This article belongs to the Special Issue Applied Mathematics and Numerical Analysis: Theory and Applications, 2nd Edition)

Download

Browse Figures

Versions Notes

Abstract

In this paper, we initiate the study of the asymptotic and oscillatory properties of solutions to third-order functional differential equations. Using the Riccati transformation to eliminate the existence of non-oscillatory solutions, we derive various oscillation criteria that address different models of the studied equation. Our primary focus is on reducing the constraints imposed on oscillation criteria, thereby broadening their applicability. Our results improve, refine, and extend some of the known findings in previous studies. Several examples are presented to illustrate the significance of the main results.

Keywords:

third-order differential equations; delay; oscillation criteria

MSC:

34C10; 22E70; 34K11

1. Introduction

This paper deals with the oscillatory behavior of solutions to a third-order neutral delay differential equation of the form

{(d (⊤) {({(y (⊤) + w (⊤) y (ς (⊤)))}^{″})}^{α})}^{'} + \int_{a}^{b} Π (⊤, s) y^{α} (ϱ (⊤, s)) d s = 0,

(1)

for

⊤ \geq ⊤_{0} > 0,

where

α > 0

is a quotient of two odd positive integers and

0 \leq a < b .

We assume the following assumptions:

(I₁): $Π \in C ([⊤_{0}, \infty) \times (a, b), R),$ $ς \in C ([⊤_{0}, \infty), (0, \infty)),$ $ϱ \in C^{1} ([⊤_{0}, \infty) \times (a, b), R),$ and ${lim}_{⊤ \to \infty} ς (⊤) = {lim}_{⊤ \to \infty} ϱ (⊤, s) = \infty;$
(I₂): $d, w \in C ([⊤_{0}, \infty), R), d > 0$ ,

$\int_{⊤_{0}}^{\infty} d^{- 1 / α} (s) d s = \infty$

and

$0 \leq w (⊤) \leq Φ_{0} < \infty;$
(I₃): $ς (⊤) \leq ⊤$ , $ς^{'} (⊤) \geq ς_{0} > 0,$ $ς \circ ϱ = ϱ \circ ς$ and $ϱ (⊤, s) \leq ⊤ .$ Furthermore, $Π (⊤, s) \geq 0$ does not vanish eventually.

Definition 1.

A solution of (1) is defined as

y \in C ([⊤_{y}, \infty), [0, \infty))

for a certain

⊤_{y} \geq ⊤_{0}

with the corresponding function

ρ (⊤) = y (⊤) + w (⊤) y (ς (⊤)),

(2)

where

d {(ρ^{″})}^{α} \in C ([⊤_{y}, \infty), [0, \infty))

and y satisfies (1) on

[⊤_{y}, \infty),

and

sup {|y (⊤)| : ⊤_{y} \leq ⊤ < \infty} > 0 for all t \geq ⊤_{y} .

Furthermore, if a solution y of (1) has arbitrarily large zeros, it is considered oscillatory; otherwise, it is called a non-oscillatory solution.

Definition 2.

Equation (1) is said to have property N if every solution of (1) is either oscillatory or satisfies

y (⊤) \to 0 as ⊤ \to \infty .

(3)

Oscillation theory and computing are closely linked, especially in solving complex differential equations and dynamic systems. Computational methods inspired by oscillation theory help to analyze the stability and behavior of solutions, particularly in periodic or aperiodic systems. With advances in computing, oscillatory patterns in high-dimensional or nonlinear systems can be efficiently modelled. This connection broadens the practical applications of oscillation theory in areas such as signal processing and control systems [1].

The study of oscillatory behavior in differential equations represents a fundamental area of mathematical research, owing to its wide-ranging applications in physics, engineering, and biology. Oscillation theory focuses on identifying the conditions under which solutions to differential equations exhibit oscillatory behavior, thereby providing valuable insights into their qualitative characteristics. Within this framework, third-order differential equations have received considerable attention, as they serve as effective models for complex dynamical systems, including beam vibrations in mechanics, electrical circuits, and control processes. These equations commonly arise in higher-order systems, where second-order descriptions fall short of capturing the intricate dynamics. A general third-order linear differential equation can be expressed as

y {(⊤)}^{‴} + a_{2} (⊤) y {(⊤)}^{″} + a_{1} (⊤) y {(⊤)}^{'} + a_{0} (⊤) y (⊤) = 0,

where

a_{0} (⊤), a_{1} (⊤),

and

a_{2} (⊤)

are real-valued coefficient functions. Oscillation theory focuses on understanding the zeros of

y (⊤)

, the points at which

y (⊤) = 0

, and determining the nature and frequency of these zeros.

Numerical methods are essential for solving complex differential equations, particularly when analytical solutions are unavailable. These methods approximate solutions by discretising and solving systems of linear and nonlinear equations iteratively, using techniques like finite differences, finite elements, Runge-Kutta methods, and spectral methods plus (preconditioned) Krylov solvers. For oscillatory differential equations, specialized algorithms, such as time-stepping approaches and Fourier transforms, are used to capture periodic behavior and identify frequency components. These methods are crucial in systems where oscillations are central, including mechanical vibrations, electrical circuits, and population dynamics. We refer the reader to [2,3,4,5,6] and references therein for concrete algorithms and the related computational costs also from the perspective of associated numerical linear algebra issues.

Oscillatory solutions are those with infinitely many zeros as

⊤ \to \infty

, while non-oscillatory solutions have at most a finite number of zeros. The study of oscillation for third-order differential equations is particularly challenging due to the interplay between the coefficients and higher derivative terms. Unlike second-order equations, where Sturm’s comparison and separation theorems provide a robust framework, third-order equations often require the development of new methodologies and criteria. Various techniques, including comparison principles, integral averaging, Riccati equations, and Lyapunov functional approaches, have been adapted and extended for the analysis of these equations [7,8,9,10,11,12,13].

In the literature, oscillation criteria have been established for both linear and nonlinear third-order differential equations. Significant progress has been made in studying equations with variable coefficients, delay terms, and forced oscillations. Researchers have developed sufficient conditions for oscillation based on integral inequalities, properties of associated functions, and the asymptotic behavior of coefficients. The motivation for studying the oscillation of third-order differential equations comes from their practical applications and theoretical implications, see [14,15,16,17,18,19,20]. In engineering, they describe stability and resonance phenomena in mechanical and electrical systems. In physics, they model the propagation of waves and the stability of structures. Moreover, in pure mathematics, they contribute to the broader understanding of dynamical systems and spectral theory.

The study of oscillatory behavior in differential equations benefits from the structural insights of Lie algebra. Lie symmetries provide a systematic method for analyzing differential systems. They reveal invariant transformations under which the equations preserve their form. By doing so, these symmetries can simplify complex systems, reduce their dimensionality, or even yield exact solutions. In oscillatory dynamics, the underlying Lie algebraic structures play a key role. They can describe conserved quantities, periodic orbits, and integrability conditions. Identifying the Lie algebra associated with a system also enables classification of its oscillatory regimes. It further provides a deeper geometric understanding of the phase space. This interplay between oscillatory analysis and Lie theory forms a powerful framework. It uncovers hidden patterns and supports the analytical treatment of dynamical systems that would otherwise be intractable [21,22].

In the past decade, significant progress has been achieved in the development of oscillation theory for third-order delay differential equations (see, e.g., [23,24,25,26]). Specifically, the authors in [15,27,28] developed oscillation criteria for nonlinear differential equation of the form

{(d (⊤) {(ρ^{″} (⊤))}^{α})}^{'} + f (y (ϱ (⊤))) = 0

by comparing it to first-order oscillatory differential equations.

Elabbasy et al. in [13] extended the oscillation criteria established by [15,27] to a more general third-order delay differential equation of the form

{(d_{2} (⊤) {({(d_{1} (⊤) {(ρ^{'} (⊤))}^{α_{1}})}^{'})}^{α_{2}})}^{'} + Π (⊤) f (y (ϱ (⊤))) = 0,

which applies to both cases:

\int_{⊤_{0}}^{\infty} d_{k}^{- 1 / α_{k}} (⊤) d t = \infty, and \int_{⊤_{0}}^{\infty} d_{k}^{- 1 / α_{k}} (⊤) d t < \infty, for k = 1, 2 .

Wang, Meng, and Gu [29] investigated the following third-order neutral differential equations with damping and distributed deviating arguments:

{(d_{2} (⊤) {(d_{1} (⊤) {(ρ^{'} (⊤))}^{α})}^{'})}^{'} + d_{3} (⊤) {(d_{1} (⊤) {(ρ^{'} (⊤))}^{α})}^{'} + \int_{a}^{b} f (s, y (ϱ (⊤, s))) d s = 0,

where

0 \leq w (⊤) \equiv \int_{c_{1}}^{c_{2}} w (⊤, s) d s < w *,

they established new oscillation criteria using a refined generalized Riccati transformation and integral averaging techniques. Their results extend previous results.

Tian, Cai, Fu, and Li [30] explored third-order neutral differential equations with distributed deviating arguments:

{(d (⊤) {({(y (⊤) + \int_{c_{1}}^{c_{2}} w (⊤, s) y (ς (⊤, s)) d s)}^{″})}^{α})}^{'} + \int_{a}^{b} Π (⊤, s) y^{α} (ϱ (⊤, s)) d s = 0,

where

α \geq 1,

0 \leq \int_{c_{1}}^{c_{2}} w (⊤, s) d s \leq 1

and

d^{'} (⊤) \geq 0

. Using a generalized Riccati transformation and integral averaging techniques, they obtained Philos-type criteria that ensuring every solution is either oscillatory or converges to zero.

Sun and Zhao [31] examined third-order neutral delay differential equations with distributed deviating arguments:

{(d_{2} (⊤) {(\hat{ρ} (⊤))}^{'})}^{'} + \int_{a}^{b} Π (⊤, s) {|y (ϱ (⊤, s))|}^{α_{3} - 1} y (ϱ (⊤, s)) d s = 0,

where

\hat{ρ} (⊤) = {(|d_{1} (⊤) {|ρ^{'} (⊤)|}^{α_{1} - 1}| ρ^{'} (⊤))}^{α_{2} - 1} (|d_{1} (⊤) {|ρ^{'} (⊤)|}^{α_{1} - 1}| ρ^{'} (⊤)),

\int_{⊤_{0}}^{\infty} d_{i}^{- 1 / α_{i}} (s) d s = \infty,

for

i = 1, 2

and

w (⊤) \neq 1,

and established new oscillatory criteria.

Baculikova and Dzurina [8], Candan in [19,32] established different oscillation criteria for the equation

{(d (⊤) {(ρ (⊤))}^{″})}^{'} + Π (⊤) y (σ (⊤)) = 0, for t \geq ⊤_{0},

(4)

under the condition

0 \leq w (⊤) \leq Φ_{0} < 1 .

(5)

In [33], the authors studied the oscillation of solutions to equation

{(d (⊤) {({(y (⊤) + w (⊤) y (ς (⊤)))}^{″})}^{α})}^{'} + Π (⊤) y^{α} (ϱ (⊤)) = 0

under the condition (5). On the other hand, Han et al. [34] considered the oscillation for third-order neutral differential equation

{(({(y (⊤) + w (⊤) y (ς (⊤)))}^{″}))}^{'} + Π (⊤) y (ϱ (⊤)) = 0,

where

- 1 < w (⊤) \leq 0 .

(6)

Karpuz et al. [35] investigated the oscillation of odd-order delay differential equations of the form

{(d (⊤) y (⊤) + w (⊤) y (ς (⊤)))}^{(n)} + Π (⊤) y (ϱ (⊤)) = 0,

under the condition

- 1 < w (⊤) < 1 .

(7)

This work presents new insights into the oscillatory behavior of third-order differential equation solutions. It extends classical results and employs advanced techniques to establish refined oscillation criteria for a broader class of equations. These results enrich the theoretical framework of oscillation theory and provide valuable tools for applications across diverse scientific fields.

Lemma 1

([35]). Let

z_{1}

,

z_{2}

,

z_{3} \in C ([⊤_{0}, \infty), R)

and

z_{3}

satisfies

z_{3} (⊤) \leq ⊤

and

{lim}_{⊤ \to \infty} z_{3} (⊤) = \infty

for all

⊤ \in [⊤_{0}, \infty);

further, assume that there is a function

j \in C ([⊤_{*}, \infty), R^{+}),

where

⊤_{*} : = {min}_{⊤ \in [⊤_{0}, \infty)} \{z_{3} (⊤)\},

such that

z_{1} (⊤) = j (⊤) + z_{2} (⊤) j (z_{3} (⊤))

for all

⊤ \in [⊤_{0}, \infty) .

Suppose that

{lim}_{t \to \infty} z_{1} (⊤)

exists and

{lim inf}_{⊤ \to \infty} z_{2} (⊤) > - 1 .

Then

{lim sup}_{⊤ \to \infty} j (⊤) > 0

leads to

{lim}_{⊤ \to \infty} z_{1} (⊤) > 0 .

Lemma 2

([36]). Let

g_{1}, g_{2} \in [0, \infty)

. Then

\tilde{g} \leq \{\begin{matrix} 1 if 0 < γ \leq 1, \\ 2^{γ - 1} if 1 \leq γ < \infty, \end{matrix}

where

\tilde{g} = {(g_{1} + g_{2})}^{γ} / (g_{1}^{γ} + g_{2}^{γ}) .

2. Main Results

Here, we suppose the following conditions:

ϱ (⊤, s) \leq ς (⊤) and ϱ^{'} (⊤, s) > 0

(8)

or

ϱ (⊤, s) \geq ς (⊤) .

(9)

The following lemma will play a useful role in the subsequent results:

Lemma 3.

Suppose that

y (⊤)

is a positive solution of (1), and

lim_{⊤ \to \infty} y (⊤) \neq 0 .

(10)

If

\int_{⊤_{0}}^{\infty} \int_{υ}^{\infty} {(d^{- 1} (ς (u)) \int_{u}^{\infty} \int_{a}^{b} Π (t, ζ) d ζ d s)}^{1 / α} d u d υ = \infty,

(11)

where

Π (⊤, s) = min {Π (⊤, s), Π (ς (⊤), s)},

(12)

then

ρ (⊤) > 0, ρ^{'} (⊤) > 0, ρ^{″} (⊤) > 0, {(d (⊤) {(ρ^{″} (⊤))}^{α})}^{'} \leq 0 .

(13)

Proof.

Let

y > 0

be a solution of (1). We can prove the case for

α \geq 1

, as

0 < α \leq 1

follows a similar approach. According to (2), we note that

ρ (⊤) \geq y (⊤) > 0

and

{(d (⊤) {(ρ^{″} (⊤))}^{α})}^{'} = - \int_{a}^{b} Π (⊤, s) y (ϱ (⊤, s)) d s \leq 0 .

(14)

That is,

{(d (⊤) {(ρ^{″} (⊤))}^{α})}^{'} \leq 0

and has one sign. Moreover,

ρ^{″} (⊤)

is a positive and has one sign. Also, either

ρ^{″} (⊤) > 0

or

ρ^{″} (⊤) < 0

for

⊤ \geq ⊤_{1}

. We claim that

ρ^{″} (⊤) > 0

. If not, then there is a constant

M > 0

such that

d (⊤) {(ρ^{″} (⊤))}^{α} \leq - M < 0 .

(15)

Integrating (15) from

⊤_{1}

to ⊤, we have

ρ^{'} (⊤) - ρ^{'} (⊤_{1}) + M^{\frac{1}{α}} \int_{⊤_{1}}^{⊤} d^{\frac{- 1}{α}} (s) d s \leq 0 .

Thus,

lim_{⊤ \to \infty} ρ^{'} (⊤) = - \infty .

Then, using

ρ^{'} (⊤) < 0

and

ρ^{″} (⊤) < 0

, we see that

{lim}_{⊤ \to \infty} ρ (⊤) = - \infty

, that is,

ρ^{″} (⊤) > 0

. Now, suppose that

ρ^{'} (⊤) < 0

. From (1), we have

\begin{matrix} {(d (⊤) {(ρ^{″} (⊤))}^{α})}^{'} + \frac{Φ_{0}^{α}}{ς_{0}} {(d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α})}^{'} \\ \leq & - \int_{a}^{b} Π (⊤, s) y^{α} (ϱ (⊤, s)) d s - Φ_{0}^{α} \int_{a}^{b} Π (ς (⊤), s) y^{α} (ϱ (ς (⊤), s)) d s \\ \leq & - (\int_{a}^{b} Π (⊤, s) y^{α} (ϱ (⊤, s)) + Φ_{0}^{α} Π (ς (⊤), s) y^{α} (ϱ (ς (⊤, s)))) d s \\ \leq & - \int_{a}^{b} Π (⊤, s) (y^{α} (ϱ (⊤, s)) + Φ_{0}^{α} y^{α} (ϱ (ς (⊤, s)))) d s . \end{matrix}

(16)

From (2) and by using Lemma 2, we obtain

\begin{matrix} y^{α} (ϱ (⊤, s)) + Φ_{0}^{α} y^{α} (ϱ (ς (⊤, s))) & \geq & \frac{{(y (ϱ (⊤, s)) + Φ_{0} y (ϱ (ς (⊤, s))))}^{⠀^{α}}}{2^{γ - 1}} \\ \geq & \frac{ρ^{⠀^{α}} (⊤)}{2^{γ - 1}} . \end{matrix}

(17)

Using (12) and (17) in (16), we have

{(d (⊤) {(ρ^{″} (⊤))}^{α})}^{'} + Φ_{0}^{α} \frac{{(d (⊤) {(ρ^{″} (ς (⊤)))}^{α})}^{'}}{ς_{0}} \leq - \frac{1}{2^{α - 1}} ρ^{α} (ϱ (⊤, b)) \int_{a}^{b} Π (⊤, s) d s .

(18)

Integrating (18) from ⊤ to ∞, we get

d (⊤) {(ρ^{″} (⊤))}^{α} + Φ_{0}^{α} \frac{d (⊤) {(ρ^{″} (ς (⊤)))}^{α}}{ς_{0}} \geq \frac{1}{2^{α - 1}} \int_{⊤}^{\infty} ρ^{α} (ϱ (⊤, b)) \int_{a}^{b} Π (⊤, u) d u d s .

Using

ς (⊤) \leq ⊤

and (14), we have

\frac{d (⊤) {(ρ^{″} (⊤))}^{α}}{d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}} \leq 1 .

That is

d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α} - \frac{2^{1 - α} ς_{0}}{(ς_{0} + Φ_{0}^{α})} \int_{⊤}^{\infty} ρ (ϱ (⊤, b)) \int_{a}^{b} Π (⊤, u) d u d s \geq 0 .

(19)

According Lemma 1, we note that

ρ (⊤) = y (⊤) + w (⊤) y (ς (⊤)),

and in view of (10), and since

{lim}_{⊤ \to \infty} ρ (⊤) = L > 0

, we get

ρ^{α} (ϱ (⊤, b)) \geq L^{α} .

In (19), we see that

ρ^{″} (ς (⊤)) - L {(\frac{2^{1 - α} ς_{0}}{(ς_{0} + Φ_{0}^{α})})}^{\frac{1}{α}} {(d^{- 1} (ς (u)))}^{\frac{1}{α}} {(\int_{⊤}^{\infty} \int_{a}^{b} Π (⊤, u) d u d s)}^{\frac{1}{α}} \geq 0 .

Integrating from ⊤ to ∞, we obtain

- ς_{0}^{- 1} ρ^{'} (ς (⊤)) - L {(\frac{2^{1 - α} ς_{0}}{(ς_{0} + Φ_{0}^{α})})}^{\frac{1}{α}} \int_{⊤}^{\infty} {(d^{- 1} (ς (u)))}^{\frac{1}{α}} {(\int_{⊤}^{\infty} \int_{a}^{b} Π (⊤, u) d u d s)}^{\frac{1}{α}} d u \geq 0 .

(20)

Integrating (20) from

⊤_{1}

to ∞, we get

- ς_{0}^{- 2} ρ (ς (⊤_{1})) - L {(\frac{2^{1 - α} ς_{0}}{(ς_{0} + Φ_{0}^{α})})}^{\frac{1}{α}} \int_{⊤_{1}}^{\infty} \int_{v}^{\infty} {(d^{- 1} (ς (u)))}^{\frac{1}{α}} {(\int_{u}^{\infty} \int_{a}^{b} Π (⊤, u) d u d s)}^{\frac{1}{α}} d u d v \geq 0,

this contradicts (11). Thus

ρ^{'} (⊤)

is positive. Hence, the proof is established. □

Lemma 4.

Let ρ be satisfied (13) for

⊤ \geq ⊤_{1}

. Then

\frac{β_{1} (⊤, ⊤_{1})}{ρ^{'} (⊤)} \leq \frac{d^{- 1 / α} (⊤)}{ρ^{″} (⊤)}, where β_{1} (⊤, ⊤_{1}) = \int_{⊤_{1}}^{⊤} d^{- 1 / α} (s) d s,

(21)

and

\frac{β_{2} (⊤, ⊤_{1})}{ρ (⊤)} \leq \frac{d^{- 1 / α} (⊤)}{ρ^{″} (⊤)}, where β_{2} (⊤, ⊤_{1}) = \int_{⊤_{1}}^{⊤} \int_{⊤_{1}}^{s} d^{- 1 / α} (u) d u d s .

(22)

Proof.

According the fact that

d (⊤) {(ρ^{″} (⊤))}^{α}

is nonincreasing. Then we have

\begin{matrix} ρ^{'} (⊤) & \geq & \int_{⊤_{1}}^{⊤} d^{- 1 / α} (⊤) {(d (s) {(ρ^{″} (s))}^{α})}^{\frac{1}{α}} d s \\ \geq & d^{1 / α} (⊤) (ρ^{″} (⊤)) \int_{⊤_{1}}^{⊤} d^{- 1 / α} (⊤) d s . \end{matrix}

Also,

ρ (⊤) - d^{\frac{1}{α}} (⊤) (ρ^{″} (⊤)) \int_{⊤_{1}}^{⊤} \int_{⊤_{1}}^{s} d^{- 1 / α} (u) d u d s \geq 0 .

This completes the proof. □

In the following subsections, we will suppose that there exists a function

ℏ \in C^{1} ([⊤_{0}, \infty), (0, \infty))

for

⊤_{0} < ⊤_{1} \leq ⊤_{1} .

2.1. Oscillation Criteria When (8) Holds

Theorem 1.

Assume that (11) is satisfied,

1 \leq α < \infty .

If

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} [2^{1 - α} ℏ (s) (\int_{a}^{b} Π (⊤, u) d u) - \frac{{(α + 1)}^{(- α + 1)} (ς_{0} + Φ_{0}^{α}) {(ℏ^{'} (s))}^{α + 1}}{ς_{0} {(ℏ (s) β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}}] d s = \infty,

(23)

then (1) has property

N .

Proof.

Let

y > 0

be a solution of (1). As in the proof of Lemma 3, we get (13) and (18). Thus, by using Lemma 4, we obtain (21). Now, define the following function:

ω (⊤) = ℏ (⊤) d (⊤) \frac{{(ρ^{″} (⊤))}^{α}}{ρ^{α} (ϱ (⊤, s))} .

(24)

That is, according to Lemma 3,

ω (⊤) > 0

, and

\begin{matrix} ω^{'} (⊤) & = & ℏ^{'} (⊤) d (⊤) \frac{{(ρ^{″} (⊤))}^{α}}{ρ^{α} (ϱ (⊤, s))} + ℏ (⊤) {(d (⊤) \frac{{(ρ^{″} (⊤))}^{α}}{ρ^{α} (ϱ (⊤, s))})}^{'} \\ = & ℏ^{'} (⊤) d (⊤) \frac{{(ρ^{″} (⊤))}^{α}}{ρ^{α} (ϱ (⊤, s))} + \frac{ℏ (⊤)}{ρ^{α} (ϱ (⊤, s))} {[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'} \\ - α ℏ (⊤) d (⊤) (\frac{{(ρ^{″} (⊤))}^{α} ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{ρ^{2 α} (ϱ (⊤, s))}) ϱ^{'} (⊤, s) . \\ ⠀ \end{matrix}

(25)

In view of (13), (21) and

ϱ (⊤, s) \leq ⊤,

we find

\begin{matrix} ρ^{'} (ϱ (⊤, s)) & \geq & (d^{1 / α} (ϱ (⊤, s)) ρ^{″} (ϱ (⊤, s))) β_{1} (ϱ (⊤), ⊤_{1}) \\ \geq & (d^{1 / α} (⊤) ρ^{″} (⊤)) β_{1} (ϱ (⊤), ⊤_{1}) . \end{matrix}

Using (24) and (25), we get

ω^{'} (⊤) \leq ℏ (⊤) \frac{{[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} + \frac{1}{ℏ (⊤)} ℏ^{'} (⊤) ω (⊤) - α \frac{β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ^{1 / α} (⊤)} ϱ^{'} (⊤, s) ω^{⠀^{(α + 1) / α}} (⊤) .

(26)

Define another function as follows:

ν (⊤) = ℏ (⊤) d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ϱ (⊤, s))} .

(27)

That is, according to Lemma 3,

ν (⊤) > 0

, and

\begin{matrix} ν^{'} (⊤) & = & ℏ^{'} (⊤) d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ϱ (⊤, s))} + ℏ (⊤) {(d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α} \frac{1}{ρ^{α} (ϱ (⊤, s))})}^{'} \\ = & ℏ^{'} (⊤) d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ϱ (⊤, s))} + ℏ (⊤) \frac{{[d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} \\ - α ℏ (⊤) d (ς (⊤)) (\frac{{(ρ^{″} (ς (⊤)))}^{α} ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{ρ^{2 α} (ϱ (⊤, s))}) ϱ^{'} (⊤, s) . \end{matrix}

(28)

Taking (13) and (21) with the fact that

ϱ (⊤, s) \leq ς (⊤)

into account, we have

\begin{matrix} ρ^{'} (ϱ (⊤, s)) & \geq & (α^{1 / α} (ϱ (⊤, s)) ρ^{″} (ϱ (⊤, s))) β_{1} (ϱ (s), ⊤_{1}) \\ \geq & (α^{1 / α} (ς (⊤)) ρ^{″} (ς (⊤))) β_{1} (ϱ (⊤, s), ⊤_{1}) . \end{matrix}

which from (27) and (28) implies that

\begin{matrix} ν^{'} (⊤) & \leq & ℏ (⊤) \frac{{[d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ν (⊤) \\ - α \frac{β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ^{1 / α} (⊤)} ϱ^{'} (⊤, s) ν^{(α + 1) / α} (⊤) . \end{matrix}

(29)

Using (26) and (29), we obtain

\begin{matrix} ω^{'} (⊤) + \frac{1}{ς_{0}} Φ_{0}^{α} (⊤) υ^{'} (⊤) & \leq & \frac{ℏ (⊤)}{ρ^{α} (ϱ (⊤, s))} {(d (⊤) {(ρ^{″} (⊤))}^{α})}^{'} + \frac{1}{ς_{0}} Φ_{0}^{α} {(d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α})}^{'} \\ + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - α \frac{β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ^{1 / α} (⊤)} ϱ^{'} (⊤, s) ω^{(α + 1) / α} (⊤) \\ + \frac{Φ_{0}^{α}}{ς_{0}} [\frac{ℏ^{'} (⊤) υ (⊤)}{ℏ (⊤)} - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s) υ^{(α + 1) / α} (⊤)}{ℏ^{1 / α} (⊤)}] . \end{matrix}

(30)

By (18) and (30), we obtain

\begin{matrix} ω^{'} (⊤) + \frac{Φ_{0}^{α}}{ς_{0}} υ^{'} (⊤) & \leq & - 2^{1 - α} ℏ (⊤) \int_{a}^{b} Π (⊤, s) d s \\ + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{1 / α} (⊤)} ω^{(α + 1) / α} (⊤) \\ + \frac{Φ_{0}^{α}}{ς_{0}} [\frac{ℏ^{'} (⊤)}{ℏ (⊤)} υ (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{1 / α} (⊤)} υ^{(α + 1) / α} (⊤)] . \end{matrix}

(31)

By applying the inequality stated in [37], namely,

B u - A u^{(α + 1) / α} - \frac{α^{α} B^{α + 1}}{{(α + 1)}^{(α + 1)} A^{α}} \leq 0, A > 0,

(32)

we see that

\frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{1 / α} (⊤)} ω^{(α + 1) / α} (⊤) \leq \frac{α^{α}}{{(α + 1)}^{(α + 1)}} \frac{{(\frac{ℏ^{'} (⊤)}{ℏ (⊤)})}^{α + 1}}{{(\frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{1 / α} (⊤)})}^{α}}

(33)

and

\frac{ℏ^{'} (⊤)}{ℏ (⊤)} υ (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{1 / α} (⊤)} υ^{(α + 1) / α} (⊤) \leq \frac{α^{α}}{{(α + 1)}^{(α + 1)}} \frac{{(\frac{ℏ^{'} (⊤)}{ℏ (⊤)})}^{α + 1}}{{(\frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{1 / α} (⊤)})}^{α}} .

(34)

Substituting (33) and (34) into (31), we are led to

\begin{matrix} ω^{'} (⊤) + \frac{1}{ς_{0}} Φ_{0}^{α} υ^{'} (⊤) & \leq & - 2^{1 - α} ℏ (⊤) \int_{a}^{b} Π (⊤, u) d u \\ + {(α + 1)}^{- (α + 1)} \frac{{(ℏ^{'} (⊤))}^{α + 1}}{{(ℏ (⊤) β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}} \\ + \frac{\frac{Φ_{0}^{α}}{ς_{0}}}{{(α + 1)}^{α + 1}} \frac{{((ℏ^{'} (⊤)) +)}^{α + 1}}{{(ℏ (⊤) β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}} . \end{matrix}

(35)

Integrating above inequality from

⊤_{2}

to ⊤, we see that

\begin{matrix} \int_{⊤_{2}}^{⊤} [2^{1 - α} ℏ (s) (\int_{a}^{b} Π (⊤, u) d u) - \frac{ς_{0} + Φ_{0}^{α}}{ς_{0} {(α + 1)}^{α + 1}} \frac{{(ℏ^{'} (s))}^{α + 1}}{{(ℏ (s) β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}}] d s \\ \leq & ω (⊤_{2}) + \frac{Φ_{0}^{α}}{ς_{0}} v (⊤_{2}), \end{matrix}

Hence, the proof is established. □

By Lemma 2, and using a similar approach to the proof of Theorem 1, we derive the subsequent result.

Theorem 2.

Assume that (11) is satisfied and

0 < α \leq 1 .

If

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} [ℏ (s) \int_{a}^{b} Π (⊤, u) d u - \frac{ς_{0} + Φ_{0}^{α}}{ς_{0} {(α + 1)}^{α + 1}} \frac{{(ℏ^{'} (s))}^{α + 1}}{{(ℏ (s) β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}}] d s = \infty,

(36)

then any solution y of (1) is oscillatory or satisfies (3).

Theorem 3.

Assume that (11) is satisfied,

1 \leq α < \infty .

If there exists a function

ℏ \in C^{1} ([⊤_{0}, \infty), (0, \infty))

for

⊤_{0} \leq ⊤_{1} < ⊤_{2}

such that

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} [2^{1 - α} ℏ (s) \int_{a}^{b} Π (⊤, u) d u - \frac{ς_{0} + Φ_{0}^{α}}{4 α ς_{0}} \frac{{(ℏ^{'} (s))}^{2}}{ℏ (s) ϱ^{'} (⊤, s) (β_{2} {(ϱ (s), ⊤_{1})}^{α - 1} β_{1} (ϱ (s), ⊤_{1}))}] d s = \infty,

(37)

then (1) has property

N .

Proof.

Let

y > 0

be a solution of (1), which does not asymptotically approach zero. As in the proof of Lemma 3, we get (13) and (18). By using Lemma 4, we have (21) and (22).

Using the definition of both functions

ω

and v by (24) and (27), respectively. Similarly as in the proof of Theorem 1, we get (25) and (28), which from (25) yields

\begin{matrix} ω^{'} (⊤) & = & ℏ^{'} (⊤) \frac{d (⊤) {(ρ^{″} (⊤))}^{α}}{ρ^{α} (ϱ (⊤, s))} + \frac{ℏ (⊤) {[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} \\ - \frac{α {[ℏ (⊤) d (⊤) {(ρ^{″} (⊤))}^{α}]}^{2} ϱ^{'} (⊤, s)}{ρ^{2 α} (ϱ (⊤, s))} \frac{ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{ℏ (⊤) d (⊤) {(ρ^{″} (⊤))}^{α}} . \end{matrix}

(38)

According to (13), (21), (22) and

ϱ (⊤, s) \leq ⊤

, we have

\begin{matrix} \frac{ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{d (⊤) {(ρ^{″} (⊤))}^{α}} & = & \frac{1}{d (⊤)} \frac{ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{{(ρ^{″} (⊤))}^{α}} \\ \geq & \frac{1}{d (⊤)} \frac{{(d^{\frac{1}{α}} (ϱ (⊤, s)) ρ^{″} (ϱ (⊤, s)))}^{α}}{{(ρ^{″} (⊤))}^{α}} \frac{β_{1} (ϱ (⊤, s), ⊤_{1})}{{(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} \\ \geq & \frac{β_{1} (ϱ (⊤, s), ⊤_{1})}{{(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} . \end{matrix}

(39)

Using (39) in (38), and in view (25), we get

ω^{'} (⊤) \leq \frac{ℏ (⊤) {[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - \frac{α ϱ^{'} (⊤, s) β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ (⊤) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} ω^{2} (⊤) .

(40)

Now, from (28), we see that

\begin{matrix} ν^{'} (⊤) & = & ℏ^{'} (⊤) \frac{d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ϱ (⊤, s))} + ℏ (⊤) \frac{{[d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} \\ - \frac{α {[ℏ (⊤) d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{2} ϱ^{'} (⊤, s)}{ρ^{2 α} (ϱ (⊤, s))} \frac{ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{ℏ (⊤) d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}} . \end{matrix}

(41)

Using (13), (21), (22) and

ϱ (⊤, s) \leq ς (⊤)

, we are led to

\begin{matrix} \frac{ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}} & = & \frac{ρ^{α - 1} (ϱ (⊤, s)) ρ^{'} (ϱ (⊤, s))}{d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}} \\ \geq & \frac{{(d^{\frac{1}{α}} (ϱ (⊤, s)) ρ^{″} (ϱ (⊤, s)))}^{α} β_{1} (ϱ (⊤, s), ⊤_{1})}{d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α} {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} \\ \geq & \frac{β_{1} (ϱ (⊤, s), ⊤_{1})}{{(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} . \end{matrix}

(42)

Combining (42) and (41), and applying (28), we obtain

\begin{matrix} ν^{'} (⊤) & \leq & \frac{ℏ (⊤) {[d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ν (⊤) \\ - \frac{α ϱ^{'} (⊤, s) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{α - 1} β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ (⊤)} ν^{2} (⊤) . \end{matrix}

(43)

By (40) and (43), we get

\begin{matrix} ω^{'} (⊤) + \frac{Φ_{0}^{α} (⊤)}{ς_{0}} υ^{'} (⊤) & \leq & ℏ (⊤) \frac{{[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} + \frac{\frac{Φ_{0}^{α}}{ς_{0}} {[d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{'}}{ρ^{α} (ϱ (⊤, s))} \\ + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ (⊤) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} ω^{2} (⊤) \\ + \frac{Φ_{0}^{α} (⊤)}{ς_{0}} [\frac{ℏ^{'} (⊤)}{ℏ (⊤)} υ (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ (⊤) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} υ^{2} (⊤)] . \end{matrix}

(44)

By applying the inequality stated in [37], namely,

B u - A u^{2} - \frac{1}{4} B^{2} A^{- 1} \leq 0, A > 0,

we see that

\frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ (⊤) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} ω^{2} (⊤) \leq \frac{1}{4} {(\frac{ℏ^{'} (⊤)}{ℏ (⊤)})}^{2} {(\frac{α β_{1} (ϱ (⊤, s), ⊤_{1})}{ℏ (⊤) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}})}^{- 1}

(45)

and

\frac{ℏ^{'} (⊤)}{ℏ (⊤)} υ (⊤) - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ (⊤) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}} υ^{2} (⊤) \leq \frac{1}{4} {(\frac{ℏ^{'} (⊤)}{ℏ (⊤)})}^{2} {(\frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ (⊤) {(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α}})}^{- 1}

(46)

Substituting (45) and (46) into (44), we obtain

ω^{'} (⊤) + \frac{Φ_{0}^{α} υ^{'} (⊤)}{ς_{0}} \leq - ℏ (⊤) \frac{\int_{a}^{b} Π (⊤, u) d u}{2^{α - 1}} + \frac{ς_{0} + Φ_{0}^{α}}{4 α ς_{0}} \frac{{(β_{2} (ϱ (⊤, s), ⊤_{1}))}^{1 - α} {(ℏ^{'} (⊤))}^{2}}{ℏ (⊤) β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)} .

(47)

Integrating (47) from

⊤_{2}

to ⊤, we have

\int_{⊤_{2}}^{⊤} (\frac{ℏ (s) \int_{a}^{b} \tilde{q} (⊤, u) d u}{2^{α - 1}} - \frac{\frac{ς_{0} + Φ_{0}^{α}}{4 α ς_{0}} {(β_{2} (ϱ (s), ⊤_{1}))}^{1 - α} {(ℏ^{'} (s))}^{2}}{ℏ (s) β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)}) d s \leq ω (⊤_{2}) + \frac{Φ_{0}^{α}}{ς_{0}} v (⊤_{2}),

and contradicts (37). The proof is complete. □

From Lemma 2, and following a similar approach to the proof of Theorem 3, we obtain the following result.

Theorem 4.

Assume that (11) is satisfied,

0 < α \leq 1

, and

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} [ℏ (s) \int_{a}^{b} Π (⊤, u) d u - (\frac{ς_{0} + Φ_{0}^{α}}{4 α ς_{0}}) \frac{{(β_{2} (ϱ (s), ⊤_{1}))}^{1 - α} {({(ℏ^{'} (s))}_{⠀^{+}})}^{2}}{ℏ (s) ϱ^{'} (⊤, s) β_{1} (ϱ (s), ⊤_{1})}] d s = \infty .

(48)

Then (1) has property

N .

We now present criteria for the oscillation of (1) under the assumption that (9) holds.

2.2. Oscillation Criteria When (9) Holds

Theorem 5.

Let (11) be satisfied,

1 \leq α < \infty .

If

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} [\frac{ℏ (s) \int_{a}^{b} Π (⊤, u) d u}{2^{α - 1}} - (\frac{(ς_{0} + Φ_{0}^{α})}{ς_{0}}) \frac{{(ℏ^{'} (s))}^{α + 1}}{{(α + 1)}^{α + 1} {(ℏ (s) β_{1} (ς (s), ⊤_{1}) ς^{'} (s))}^{α}}] d s = \infty,

(49)

then (1) has property

N .

Proof.

Let

y > 0

be a solution of (1), which does not asymptotically approach zero. As proof of Lemma 3, we get (13) and (18). That is, by Lemma 4, we obtain (21). Define the positive function

ω (⊤) = ℏ (⊤) d (⊤) \frac{{(ρ^{″} (⊤))}^{α}}{ρ^{α} (ς (⊤))} .

(50)

It follows that

\begin{matrix} ω^{'} (⊤) & = & ℏ^{'} (⊤) d (⊤) \frac{{(ρ^{″} (⊤))}^{α}}{ρ^{α} (ς (⊤))} + ℏ (⊤) {(\frac{d (⊤) {(ρ^{″} (⊤))}^{α}}{ρ^{α} (ς (⊤))})}^{'} \\ = & ℏ^{'} (⊤) d (⊤) \frac{{(ρ^{″} (⊤))}^{α}}{ρ^{α} (ς (⊤))} + ℏ (⊤) \frac{{[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'}}{ρ^{α} (ς (⊤))} \\ - α ℏ (⊤) d (⊤) \frac{{(ρ^{″} (⊤))}^{α} ρ^{α - 1} ς (⊤) ρ^{'} (ς (⊤))}{ρ^{2 α} (ς (⊤))} ς^{'} (⊤) . \end{matrix}

(51)

Using (13), (21) and

ς (⊤) \leq ⊤,

we have

\begin{matrix} ρ^{'} (ς (⊤)) & \geq & β_{1} (ς (⊤), ⊤_{1}) (d^{1 / α} (ς (⊤)) ρ^{″} (ς (⊤))) \\ \geq & β_{1} (ς (⊤), ⊤_{1}) (d^{1 / α} (ς (⊤)) ρ^{″} (⊤)) . \end{matrix}

With the use of (50) and (51), we deduce

ω^{'} (⊤) \leq \frac{ℏ (⊤) {[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'}}{ρ^{α} (ς (⊤))} + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - \frac{α β_{1} (ς (⊤), ⊤_{1}) ς^{'} (⊤)}{ℏ^{\frac{1}{α}} (⊤)} ω^{(α + 1) / α} (⊤) .

(52)

Now, define the following positive function

v (⊤) = ℏ (⊤) d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ς (⊤))} .

(53)

That is,

\begin{matrix} ν^{'} (⊤) & = & ℏ^{'} (⊤) d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ϱ (⊤, s))} + ℏ (⊤) {(d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ς (⊤))})}^{'} \\ = & ℏ^{'} (⊤) d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α}}{ρ^{α} (ς (⊤))} + ℏ (⊤) \frac{{[d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{'}}{ρ^{α} (ς (⊤))} \\ - α ℏ (⊤) d (ς (⊤)) \frac{{(ρ^{″} (ς (⊤)))}^{α} ρ^{α - 1} (ς (⊤)) ρ^{'} (ς (⊤))}{ρ^{2 α} (ς (⊤))} ς^{'} (⊤) . \end{matrix}

(54)

From (13) and (21), we have

ρ^{'} (ς (⊤)) \geq (α^{1 / α} (ς (⊤)) ρ^{″} (ς (⊤))) β_{1} (ς (s), ⊤_{1}),

which from (53) and (54) implies

\begin{matrix} v^{'} (⊤) & \leq & ℏ (⊤) \frac{{[d ς (⊤) {(ρ^{″} ς (⊤))}^{α}]}^{'}}{ρ^{α} (ς (⊤))} + \frac{ℏ^{'} (⊤) v (⊤)}{ℏ (⊤)} \\ - β_{1} (ς (⊤), ⊤_{1}) \frac{α ς^{'} (⊤)}{ℏ^{1 / α} (⊤)} v^{(α + 1) / α} (⊤) . \end{matrix}

(55)

Using (52) and (55), we have

\begin{matrix} ω^{'} (⊤) + Φ_{0}^{α} \frac{υ^{'} (⊤)}{ς_{0}} & \leq & ℏ (⊤) \frac{{[d (⊤) {(ρ^{″} (⊤))}^{α}]}^{'}}{ρ^{α} (ς (⊤))} + \frac{Φ_{0}^{α}}{ς_{0}} \frac{{[d (ς (⊤)) {(ρ^{″} (ς (⊤)))}^{α}]}^{'}}{ρ^{α} (ς (⊤))} \\ + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) - α β_{1} (ς (⊤), ⊤_{1}) \frac{ς^{'} (⊤)}{ℏ^{1 / α} (⊤)} ω^{(α + 1) / α} (⊤) \\ + \frac{Φ_{0}^{α}}{ς_{0}} [\frac{(ℏ^{'} (⊤)) +}{ℏ (⊤)} υ (⊤) - \frac{α β_{1} (ς (⊤), ⊤_{1}) ς^{'} (⊤)}{ℏ^{1 / α} (⊤)} v^{(α + 1) / α} (⊤)] . \end{matrix}

(56)

By (13), (18), (56) and

ϱ (t) \geq ς (t),

we obtain

\begin{matrix} ω^{'} (⊤) + \frac{Φ_{0}^{α}}{ς_{0}} υ^{'} (⊤) & \leq & - ℏ (⊤) \frac{\int_{a}^{b} Π (⊤, u) d u}{2^{α - 1}} + \frac{ℏ^{'} (⊤)}{ℏ (⊤)} ω (⊤) \\ - \frac{α β_{1} (ς (⊤), ⊤_{1}) ς^{'} (⊤)}{ℏ^{1 / α} (⊤)} ω^{(α + 1) / α} (⊤) \\ + \frac{Φ_{0}^{α}}{ς_{0}} [\frac{ℏ^{'} (⊤)}{ℏ (⊤)} υ (⊤) - \frac{α β_{1} (ς (⊤), ⊤_{1}) ς^{'} (⊤)}{ℏ^{1 / α} (⊤)} v^{(α + 1) / α} (⊤)] . \end{matrix}

(57)

Using (57) and (32), we get

\begin{matrix} ω^{'} (⊤) + \frac{Φ_{0}^{α} υ^{'} (⊤)}{ς_{0}} & \leq & - \frac{ℏ (⊤) \int_{a}^{b} Π (⊤, u) d u}{2^{α - 1}} + \frac{{(α + 1)}^{- (α + 1)} {(ℏ^{'} (⊤))}^{α + 1}}{{(ℏ (⊤) β_{1} (ς (⊤), ⊤_{1}) ς^{'} (⊤))}^{α}} \\ + \frac{Φ_{0}^{α}}{ς_{0}} \frac{{(α + 1)}^{- (α + 1)} {(ℏ^{'} (⊤))}^{α + 1}}{{(ℏ (⊤) β_{1} (ς (⊤), ⊤_{1}) ς^{'} (⊤))}^{α}} . \end{matrix}

(58)

Integrating (58) from

⊤_{2}

to ⊤, we have

\begin{matrix} \int_{⊤_{2}}^{⊤} (\frac{ℏ (s) \int_{a}^{b} Π (⊤, u) d u}{2^{α - 1}} - \frac{(ς_{0} + Φ_{0}^{α}) {(ℏ^{'} (s))}^{α + 1}}{ς_{0} {(α + 1)}^{α + 1} {(ℏ (s) β_{1} (ς (s), ⊤_{1}) ς^{'} (s))}^{α}}) d s \\ \leq & ω (⊤_{2}) + \frac{Φ_{0}^{α}}{ς_{0}} v (⊤_{2}), \end{matrix}

which is a contradiction (49). With the latter the proof is complete. □

Using Lemma 2 and proceeding as in the proof of Theorem 5, we obtain the following theorem.

Theorem 6.

Let (11) be satisfied,

0 < α \leq 1

, and for all

⊤_{1} \geq ⊤_{0}

, there is a

⊤_{2} > ⊤_{1}

such that

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} (ℏ (s) (\int_{a}^{b} Π (⊤, u) d u) - \frac{(ς_{0} + Φ_{0}^{α}) {(ℏ^{'} (s))}^{α + 1}}{ς_{0} {(α + 1)}^{α + 1} {(ℏ (s) ς^{'} (s) β_{1} (ς (s), ⊤_{1}))}^{α}}) d s = \infty .

(59)

Then any solution y of (1) is oscillatory or satisfies (3).

Using (51), (54), and applying a similar approach to the proof of Theorem 3, we obtain the following theorem.

Theorem 7.

Let (11) be satisfied and

1 \leq α < \infty .

If

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} [2^{1 - α} ℏ (s) \int_{a}^{b} Π (⊤, u) d u - \frac{{(β_{2} (ς (s), ⊤_{1}))}^{1 - α} (ς_{0} + Φ_{0}^{α}) {(ℏ^{'} (s))}^{2}}{4 α ς_{0} ℏ (s) β_{1} (ς (s), ⊤_{1}) ς^{'} (s)}] d s = \infty,

(60)

then (1) has property

N .

In view of Lemma 2 and Theorem 7, similar to the proof of Theorem 3, we get the following result.

Theorem 8.

Let (11) be satisfied and

0 < α \leq 1 .

If

\underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} (ℏ (s) \int_{a}^{b} Π (⊤, u) d u - \frac{{(β_{2} (ς (s), ⊤_{1}))}^{1 - α} (ς_{0} + Φ_{0}^{α}) {(ℏ^{'} (s))}^{2}}{4 α ς_{0} ℏ (s) β_{1} (ς (s), ⊤_{1}) ς^{'} (s)}) d s = \infty,

(61)

then (1) has property

N .

Remark 1.

Based on Theorems 1–8, we can derive oscillation criteria of (1) for various choices of ℏ.

2.3. Philos-Type Oscillation Criteria

In this section, we will derive Philos-type oscillation results for (1). Suppose that

D_{0} = \{(⊤, s) : t > s \geq ⊤_{0}\}

and

D = \{(⊤, s) : t \geq s \geq ⊤_{0}\} .

Let

Γ

be an element of

C ([D, R),

we say that the function

Γ

has property P if it satisfies the following assumptions:

(I): $Γ (t, ⊤) = 0, t \geq ⊤_{0}; (⊤, s) \in D_{0}, Γ (⊤, s) > 0,$
(II): $Γ$ has a continuous partial derivative with respect to the second variable in $D_{0}$ , which is non-positive.

2.3.1. Philos-Type Criteria When (8) Holds

Theorem 9.

Assume that (11) is satisfied,

1 \leq α < \infty .

If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that

j (⊤, s) \frac{{(Γ (⊤, s))}^{\frac{α}{(α + 1)}}}{ℏ (s)} = - \frac{\partial}{\partial s} Γ (⊤, s) - \frac{ℏ^{'} (s)}{ℏ (s)} Γ (⊤, s), (⊤, s) \in D_{0},

(62)

and

\underset{⊤ \to \infty}{lim sup} Γ^{- 1} (⊤, ⊤_{2}) \int_{⊤_{2}}^{⊤} (\frac{Γ (⊤, s) ℏ (s) \int_{a}^{b} Π (⊤, u) d u}{2^{α - 1}} - G_{1} (⊤, s)) d s = \infty,

(63)

where

G_{1} (⊤, s) = \frac{{(α + 1)}^{- (α + 1)} (ς_{0} + Φ_{0}^{α}) {(j_{-} (⊤, s))}^{α + 1}}{ς_{0} {(ℏ (s) β_{2} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}},

and

j_{-} (⊤, s) : = max {0, - j (⊤, s)}

, then (1) has property

N .

Proof.

Let

y > 0

be a solution of (1). As in Theorem 1, define

ω

and

υ

, we get (31). From (31), we obtain

\begin{matrix} 2^{1 - α} ℏ (⊤) \int_{a}^{b} Π (t, u) d u & \leq & - ω^{'} (⊤) - \frac{Φ_{0}^{α} υ^{'} (⊤)}{ς_{0}} + \frac{ℏ^{'} (⊤) ω (⊤)}{ℏ (⊤)} \\ - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (⊤)} ω^{\frac{α + 1}{α}} (⊤) \\ + \frac{Φ_{0}^{α}}{ς_{0}} (\frac{ℏ^{'} (⊤) υ (⊤)}{ℏ (⊤)} - \frac{α β_{1} (ϱ (⊤, s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (⊤)} υ^{\frac{α + 1}{α}} (⊤)) . \end{matrix}

(64)

Multiplying both sides by

Γ (⊤, s)

, then integrating from

⊤_{2}

to ⊤, we infer that

\begin{matrix} \int_{⊤_{2}}^{⊤} \frac{ℏ (s)}{2^{α - 1}} Γ (⊤, s) (\int_{a}^{b} Π (⊤, u) d u) d s & \leq & - \int_{⊤_{2}}^{⊤} Γ (⊤, s) ω^{'} (s) d s + \int_{⊤_{2}}^{⊤} \frac{Γ (⊤, s) ℏ^{'} (s) ω (s)}{ℏ (s)} d s \\ - \int_{⊤_{2}}^{⊤} \frac{α Γ (⊤, s) β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (s)} ω^{\frac{α + 1}{α}} (⊤) d s \\ - \frac{Φ_{0}^{α}}{ς_{0}} (\int_{⊤_{2}}^{⊤} Γ (⊤, s) υ^{'} (s) d s + \int_{⊤_{2}}^{⊤} \frac{Γ (⊤, s) ℏ^{'} (s) υ (s)}{ℏ (s)} d s) \\ - \frac{Φ_{0}^{α}}{ς_{0}} \int_{⊤_{2}}^{⊤} \frac{Γ (⊤, s) α β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (s)} υ^{\frac{α + 1}{α}} (s) d s . \end{matrix}

Thus, we have

\begin{matrix} \int_{⊤_{2}}^{⊤} \frac{ℏ (s)}{2^{α - 1}} Γ (⊤, s) (\int_{a}^{b} Π (⊤, u) d u) d s & \leq & Γ (⊤, ⊤_{2}) ω (⊤_{2}) \\ - \int_{⊤_{2}}^{⊤} (- \frac{\partial}{\partial (s)} Γ (⊤, s) - \frac{ℏ^{'} (s)}{ℏ (s)} Γ (⊤, s)) ω (s) d s \\ - \int_{⊤_{2}}^{⊤} Γ (⊤, s) \frac{α β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (s)} ω^{\frac{α + 1}{α}} (s) d s \\ + \frac{Φ_{0}^{α}}{ς_{0}} Γ (⊤, ⊤_{2}) υ (⊤_{2}) \\ - \frac{Φ_{0}^{α}}{ς_{0}} \int_{⊤_{2}}^{⊤} [- \frac{\partial}{\partial (s)} Γ (⊤, s) - \frac{1}{ℏ (s)} ℏ^{'} (s) Γ (⊤, s)] υ (s) d s \\ - \int_{⊤_{2}}^{⊤} \frac{α Γ (⊤, s) β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (s)} υ^{\frac{α + 1}{α}} (s) d s, \end{matrix}

that is,

\begin{matrix} \int_{⊤_{2}}^{⊤} \frac{Γ (⊤, s) ℏ (s) \int_{a}^{b} Π (⊤, u) d u}{2^{α - 1}} d s \\ \leq & Γ (⊤, ⊤_{2}) ω (⊤_{2}) + \frac{Φ_{0}^{α}}{ς_{0}} Γ (⊤, ⊤_{2}) υ (⊤_{2}) \\ + \int_{⊤_{2}}^{⊤} [\frac{j_{-} (⊤, s) {(Γ (⊤, s))}^{\frac{α}{α + 1}}}{ℏ (s)} ω (s) - \frac{Γ (⊤, s) α β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (s)} ω^{\frac{α + 1}{α}} (s)] d s \\ + \frac{Φ_{0}^{α}}{ς_{0}} \int_{⊤_{2}}^{⊤} [\frac{j_{-} (⊤, s) {(Γ (⊤, s))}^{\frac{α}{α + 1}}}{ℏ (s)} υ (s) - \frac{Γ (⊤, s) α β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)}{ℏ^{\frac{1}{α}} (s)} υ^{\frac{α + 1}{α}} (s)] d s . \end{matrix}

(65)

Using (65) and (32), we find

\begin{matrix} Γ^{- 1} (⊤, ⊤_{2}) \int_{⊤_{2}}^{⊤} [\frac{Γ (⊤, s) ℏ (s) \int_{a}^{b} Π (t, u) d u}{2^{α - 1}} - \frac{ς_{0} + Φ_{0}^{α}}{ς_{0} {(α + 1)}^{α + 1}} \frac{{(j_{-} (⊤, s))}^{α + 1} {(Γ (⊤, s))}^{α + 1}}{{(ℏ (s) β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}}] d s \\ \leq & ω (⊤_{2}) + \frac{Φ_{0}^{α} υ (⊤_{2})}{ς_{0}}, \end{matrix}

and contradicts (63). As a consequence, the proof is complete. □

According to Theorem 2, similar to the proof of Theorem 9, we obtain the following theorem.

Theorem 10.

Assume that (11) and (62) are satisfied and

0 < α \leq 1

. If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that

\underset{⊤ \to \infty}{lim sup} Γ^{- 1} (⊤, ⊤_{2}) \int_{⊤_{1}}^{⊤} Γ (⊤, s) ℏ (s) F_{1} (⊤, s) d s = \infty,

(66)

where

F_{1} (⊤, s) : = \int_{a}^{b} Π (⊤, u) d u - \frac{⠀_{0} {(α + 1)}^{- (α + 1)} (ς_{0} + Φ_{0}^{α})}{ς {(ℏ (s) β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s))}^{α}} {(j_{-} (⊤, s))}^{α + 1},

j_{-} (⊤, s) : = max {0, j_{-} (⊤, s)},

then (1) has property

N .

Using (18) and (44) in Theorem 3, as in the proof of Theorem 9, we get the following theorem.

Theorem 11.

Assume that (11) is satisfied and

1 \leq α < \infty

. If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that

\frac{j (⊤, s) {(Γ (⊤, s))}^{1 / 2}}{ℏ (s)} = - \frac{\partial}{\partial s} Γ (⊤, s) - \frac{ℏ^{'} (s) Γ (⊤, s)}{ℏ (s)}, (⊤, s) \in D_{0}

(67)

and

\underset{⊤ \to \infty}{lim sup} Γ^{- 1} (⊤, ⊤_{2}) \int_{⊤_{1}}^{⊤} (\frac{1}{2^{α - 1}} Γ (⊤, s) ℏ (s) (\int_{a}^{b} \tilde{Π} (⊤, u) d u) - G_{2} (⊤, s)) d s = \infty,

(68)

where

G_{2} (⊤, s) : = \frac{(ς_{0} + Φ_{0}^{α}) {(j_{-} (⊤, s))}^{2}}{ς_{0} 4 α ℏ (s) {(β_{2} (ϱ (s), ⊤_{1}))}^{α - 1} β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)},

and

j - (⊤, s) : = max {0, - j (⊤, s)},

then (1) has property

N .

From Theorem 4, as in the proof of Theorem 9, we obtain the following result.

Theorem 12.

Assume that (11) and (67) are satisfied, and

0 < α \leq 1

. If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that

\underset{⊤ \to \infty}{lim sup} Γ^{- 1} (⊤, ⊤_{2}) \int_{⊤_{2}}^{⊤} (ℏ (s) (\int_{a}^{b} \tilde{q} (⊤, u) d u) Γ (⊤, s) - F_{2} (⊤, s)) d s = \infty,

(69)

where

F_{2} (⊤, s) = \frac{(ς_{0} + Φ_{0}^{α}) {(j_{-} (⊤, s))}^{2}}{4 α ς_{0} ℏ (s) {(β_{2} (ϱ (s), ⊤_{1}))}^{α - 1} β_{1} (ϱ (s), ⊤_{1}) ϱ^{'} (⊤, s)},

and

j_{-} (⊤, s) : = max {0, - j (⊤, s)},

then (1) has property

N .

By (57) in Theorem 5, as in the proof of Theorem 9, we conclude the following result.

2.3.2. Philos-Type Criteria When (9) Holds

Theorem 13.

Let (11) and (62) be satisfied, and

1 \leq α < \infty

. If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that

\underset{⊤ \to \infty}{lim sup} \frac{1}{Γ (⊤, ⊤_{2})} \int_{⊤_{2}}^{⊤} (\frac{1}{2^{α - 1}} ℏ (s) Γ (⊤, s) (\int_{a}^{b} Π (⊤, u) d u) - G_{3} (⊤, s) d s) = \infty,

(70)

where

G_{3} (⊤, s) = \frac{(ς_{0} + Φ_{0}^{α}) {(j_{-} (⊤, s))}^{α + 1}}{ς_{0} {(α + 1)}^{α + 1} {(ℏ (s) β_{1} (ς (s), ⊤_{1}) ς^{'} (s))}^{α}},

and

j_{-} (⊤, s) : = max {0, - j (⊤, s)},

then (1) has property N.

By Theorem 6, as in the proof of Theorem 9, we conclude the following theorem.

Theorem 14.

Let (11) and (62) be satisfied,

0 < α \leq 1

. If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that

\underset{⊤ \to \infty}{lim sup} \frac{1}{Γ (⊤, ⊤_{2})} \int_{⊤_{2}}^{⊤} (ℏ (s) (\int_{a}^{b} \tilde{q} (⊤, u) d u) Γ (⊤, s) - F_{3} (⊤, s)) d s = \infty,

(71)

where

F_{3} (⊤, s) = \frac{(ς_{0} + Φ_{0}^{α}) {(j_{-} (⊤, s))}^{α + 1}}{ς_{0} {(α + 1)}^{α + 1} {(ℏ (s) β_{1} (ς (s), ⊤_{1}) ς^{'} (s))}^{α}},

and

j_{-} (⊤, s) : = max {0, - j (⊤, s)},

then (1) has property

N .

By Theorem 7, as in the proof of Theorem 9, we get the following result.

Theorem 15.

Let (11) and (67) be satisfied, and

1 \leq α < \infty .

If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that

\underset{⊤ \to \infty}{lim sup} Γ^{- 1} (⊤, ⊤_{2}) \int_{⊤_{2}}^{⊤} (\frac{1}{2^{α - 1}} Γ (⊤, s) ℏ (s) \int_{a}^{b} Π (⊤, u) d u - G_{4} (⊤, s)) d s = \infty,

(72)

where

G_{4} (⊤, s) = \frac{(ς_{0} + Φ_{0}^{α}) {(j_{-} (⊤, s))}^{2}}{4 α ς_{0} {(ℏ (s) β_{2} (ς (s), ⊤_{1}))}^{α - 1} β_{1} (ς (s), ⊤_{1}) ς^{'} (s)},

and

j_{-} (⊤, s) : = max {0, - j (⊤, s)},

then (1) has property

N .

By Theorem 8, as in the proof of that of Theorem 9, we obtain the following theorem.

Theorem 16.

Let (11) be satisfied, and

0 < α \leq 1

. If there exists a function

Γ \in C (D, R)

satisfies property P, for all

⊤_{2} > ⊤_{1} \geq ⊤_{0}

such that (67) holds and

\underset{⊤ \to \infty}{lim sup} Γ^{- 1} (⊤, ⊤_{2}) \int_{⊤_{2}}^{⊤} (\frac{1}{2^{α - 1}} Γ (⊤, s) ℏ (s) \int_{a}^{b} Π (⊤, u) d u - F_{4} (⊤, s)) d s = \infty,

(73)

where

F_{4} (⊤, s) = \frac{(ς_{0} + Φ_{0}^{α}) {(j_{-} (⊤, s))}^{2}}{4 α ς_{0} {(ℏ (s) β_{2} (ς (s), ⊤_{1}))}^{α - 1} β_{1} (ς (s), ⊤_{1}) ς^{'} (s)},

and

j_{-} (⊤, s) : = max {0, - j (⊤, s)},

then (1) has property

N .

Remark 2.

Using Theorems 9–16, we can derive oscillation criteria of (1) for various choices of ℏ and Γ.

3. Examples

Example 1.

Consider the equation

{[⊤ {({[y (⊤) + Φ_{0} y (\frac{⊤}{2})]}^{″})}^{3}]}^{'} + (\frac{λ}{⊤^{6}}) y^{3} (\frac{⊤}{2}) = 0,

(74)

where

λ > 0,

2 > Φ_{0} > 0.3 .

Here,

α = 3, a (⊤) = ⊤, ϱ (⊤, s) = ς (⊤) = \frac{⊤}{2},

ς_{0} = \frac{1}{2}

and

Π (⊤, s) = \frac{λ}{⊤^{6}}

. Set

ℏ (⊤) = ⊤^{5}

That is, we have

\tilde{Π} (⊤, s) = \frac{λ}{⊤^{6}} and β_{1} (⊤, ⊤_{1}) \geq ⊤^{2 / 3} .

Thus, (11) holds. According to Theorem 1, we see that any solution of (74) is oscillatory or satisfies (3) if

λ > 312.5 (1 + 2 Φ_{0}^{3}) .

(75)

On the other hand, by applying the results in [8], we conclude that Corollary 1 leads to

\underset{⊤ \to \infty}{lim inf} \frac{⊤^{3}}{⊤} \int_{⊤}^{\infty} \frac{λ}{2^{6} s^{3}} d s > \frac{6^{3}}{4^{4} {(1 - Φ_{0})}^{3}},

that is

λ > 108 {(1 - Φ_{0})}^{- 3} .

(76)

Hence, (74) has property N if (76) holds.

Remark 3.

In Figure 1, Example 1 demonstrates a clear superiority over the results of the study in [8], and this can be discussed as follows:

1.: For interval $1 > Φ_{0} > 0.3$ , the curve (75) is superior to (76) because it consistently provides the dominant lower bound for $λ,$ while (76) rises sharply and diverges as $Φ_{0}$ approaches 1 from the left.
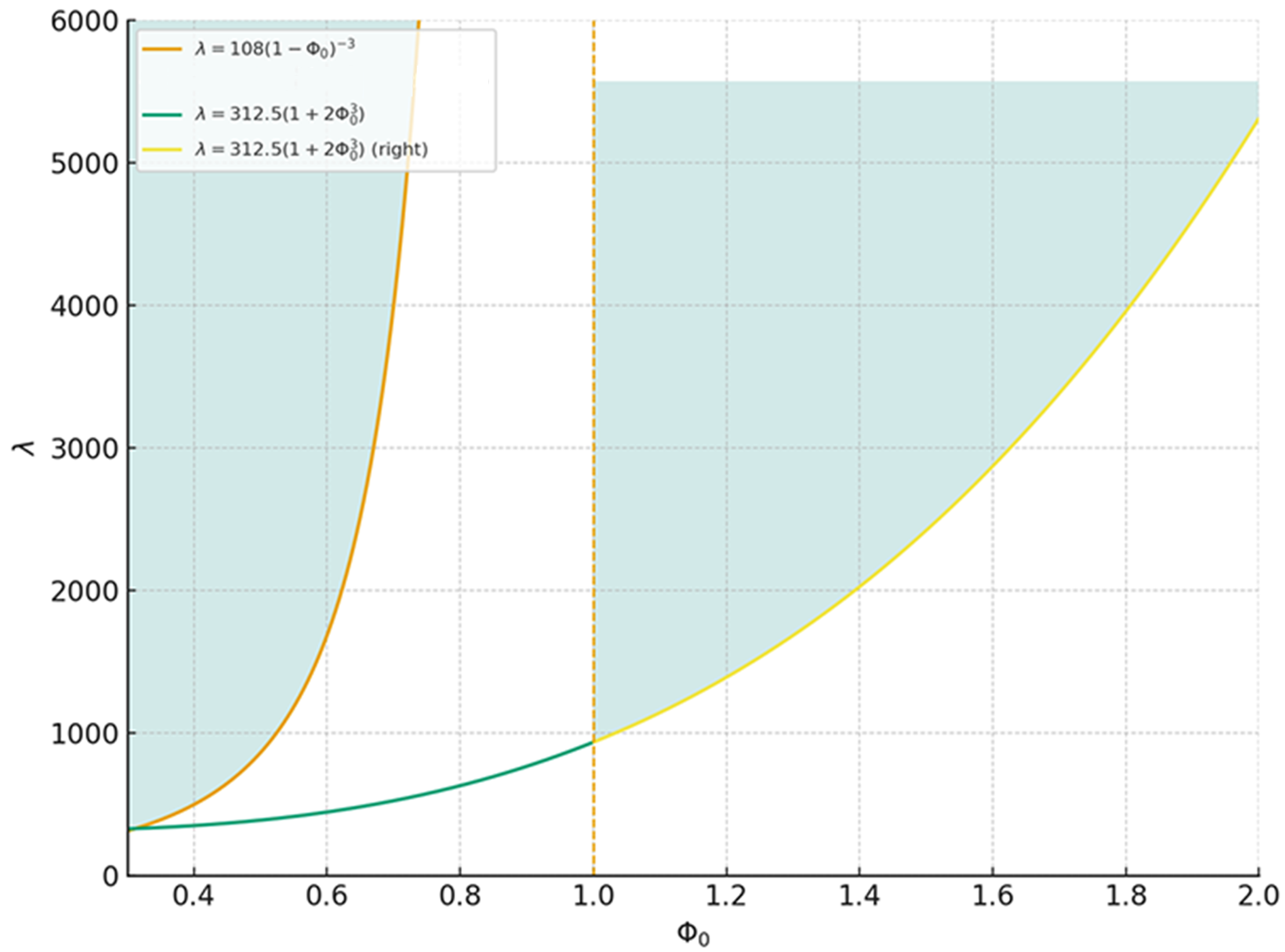
2.: The results in [8] were restricted to the interval $1 > Φ_{0} \geq 0.3$ . Consequently, this results fails to provide any oscillation results once $Φ_{0}$ reaches or exceeds unity. In contrast, our formulation remains valid up to $2 \geq Φ_{0} \geq 1$ (green area enclosed during $2 \geq Φ_{0} \geq 1$ in Figure 1), where the cubic condition dominates and ensures the existence of feasible solutions. This extended validity represents a clear improvement and demonstrates the robustness of our approach.

Example 2.

Consider the equation

{[⊤ {({[y (⊤) + Φ_{0} y (0.5 ⊤)]}^{″})}^{3}]}^{'} + (⊤^{- 6} λ) y^{3} (0.5 ⊤) = 0,

(77)

where

λ > 0,

2 > Φ_{0} > 0.3 .

Here,

α = 3, d (⊤) = ⊤, ϱ (⊤, s) = ς (⊤) = 0.5 ⊤,

ς_{0} = 0.5

and

Π (⊤, s) = λ ⊤^{- 6}

. Set

ℏ (⊤) = ⊤^{5}

. That is, we have

\tilde{Π} (⊤, s) = λ ⊤^{- 6} and β_{1} (⊤, ⊤_{1}) \geq ⊤^{2 / 3} .

Thus, (11) holds. According to Theorem 1, we conclude that any solution of (77) is oscillatory or satisfies (3) if

λ > \frac{2^{5} \cdot 5^{4}}{4^{3}} (1 + 2 Φ_{0}^{3}) .

(78)

According to Theorem 3 and since

β_{2} (⊤, ⊤_{1}) \geq 0.4 ⊤^{\frac{5}{3}},

we see that

[0.25 λ - \frac{5^{4} \cdot 2^{5}}{48} (1 + 2 Φ_{0}^{3})] lim_{⊤ \to \infty} \int_{⊤_{2}}^{⊤} s^{- 1} d s = \infty,

when

λ > \frac{5^{4} \cdot 2^{5} \cdot (1 + 2 Φ_{0}^{3})}{12} .

(79)

Hence, (77) has property N if (79) holds.

Remark 4.

For Example 2, we note that:

1.: At $Φ_{0} = 1 / 3,$ we (78) implies

$λ > \frac{2^{5} \cdot 5^{4} (3^{3} + 2)}{4^{3} 3^{3}} .$

(80)

In view of ([8], Example 1), it is found that the result is obtained as a necessary condition for (77) to has property N was as follows

$λ > \frac{729}{2} .$

(81)

By comparing results (80) and (81), we find that

$\frac{2^{5} \cdot 5^{4} (3^{3} + 2)}{4^{3} 3^{3}} < \frac{729}{2} .$

Thus, our results improve results of [8].
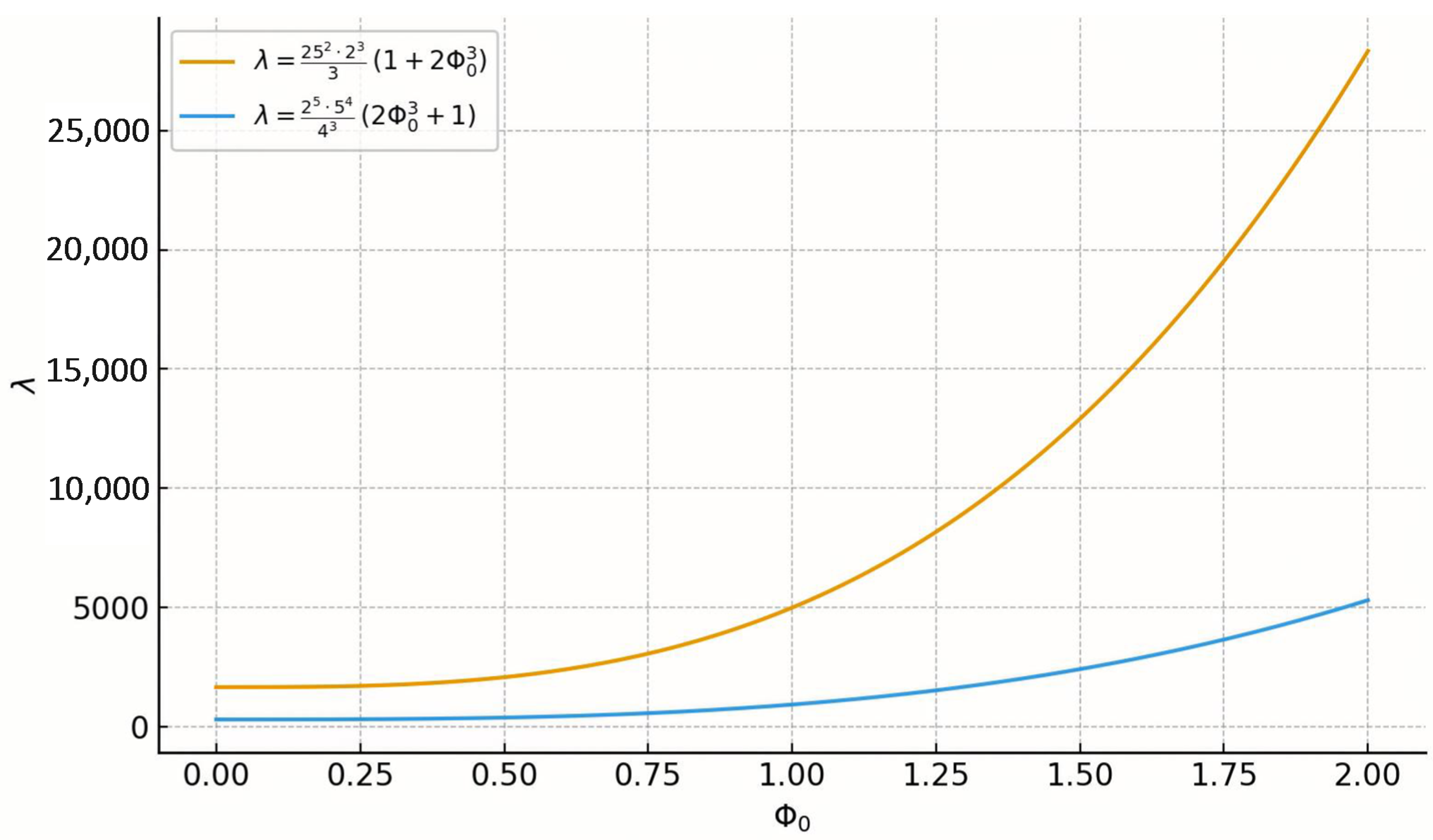
2.: Figure 2 illustrates a direct comparison between Theorem 1 (solid yellow curve) and Theorem 3 (dashed blue curve). It is evident that Theorem 1 consistently provides smaller values of λ across the examined range of $Φ_{0}$ , reflecting a tighter and more efficient bound. In contrast, Theorem 3 grows significantly faster. That is Theorem 1 offers a stronger and more reliable characterization of the oscillatory condition.

Table 1 presents the calculated values of

λ_{1}

and

λ_{2}

corresponding to oscillation conditions (78) and (79) as functions of parameter

Φ_{0}

. The results illustrate the progressive increase of both parameters with

Φ_{0}

.

Example 3.

Consider the equation

{[⊤ {({[y (⊤) + Φ_{0} y (0.5 ⊤)]}^{″})}^{3}]}^{'} + λ ⊤^{- 6} y^{3} (1.5 ⊤) = 0,

(82)

where

λ > 0

and

Φ_{0} > 0 .

Here,

α = 3, d (⊤) = ⊤, ϱ (⊤, s) = 1.5 ⊤, ς (⊤) = 0.5 ⊤,

and

Π (⊤) = λ ⊤^{- 6}

. It is easy to see that

ς^{'} (⊤) = ς_{0} = 0.5,

\tilde{Π} (⊤, s) = min {Π (⊤, s), Π (ς (⊤), s)} = λ ⊤^{- 6},

β_{1} (⊤, ⊤_{1}) = \int_{⊤_{1}}^{⊤} s^{- 1 / 3} d s \geq ⊤^{2 / 3},

and

β_{2} (⊤, ⊤_{1}) : = \int_{⊤_{1}}^{⊤} \int_{⊤_{1}}^{s} u^{- 1 / 3} d u d s \geq 0.4 ⊤^{5 / 3} .

It is clear that (11) hold. By putting

ℏ (⊤) = ⊤^{5}

and according to Theorem 7, we find that

[\frac{λ}{4} - \frac{{(\frac{25}{2})}^{2} \cdot 2^{5} \cdot (1 + 2 Φ_{0}^{3})}{12}] \underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} \frac{1}{s} d s = \infty .

Thus, any solution of (82) is oscillatory or satisfies (3) if

λ > \frac{25^{2} \cdot 2^{3}}{3} \cdot (1 + 2 Φ_{0}^{3}) .

(83)

Also, according to Theorem 5, we note that

(\frac{λ}{4} - \frac{2^{5} \cdot 5^{4}}{4^{4}} (2 Φ_{0}^{3} + 1)) \underset{⊤ \to \infty}{lim sup} \int_{⊤_{2}}^{⊤} s^{- 1} d s = \infty .

Hence, if

4^{3} λ > 2^{5} \cdot 5^{4} (2 Φ_{0}^{3} + 1),

(84)

then (82) has property

N .

Remark 5.

In Figure 3, the results clearly indicate that Theorem 5 (blue curve) yields consistently smaller values of λ across the entire range of

Φ_{0}

. This reflects a tighter and more efficient bound compared to Theorem 7 (yellow curve), whose rapid growth demonstrates weaker control. Thus, for Example 3, we see that Theorem 5 is better than Theorem 7.

Table 2 presents the calculated values of

λ_{1}

and

λ_{2}

corresponding to oscillation conditions (83) and (84) as functions of parameter

Φ_{0}

. The results illustrate the progressive increase of both parameters with

Φ_{0}

.

4. Conclusions

In this work, we examine the oscillatory behavior of solutions to Equation (1). Our results extend and refine previous research by relaxing the conditions placed on the functions involved in the equation. Specifically, we introduce the condition

0 \leq w (⊤) \leq w_{0} < \infty

, in contrast to the more restrictive conditions (5)–(7) that were commonly applied in earlier studies, such as those in [8,19,32,33,34,35]. These previous conditions fail in models where the function

w (⊤)

falls outside the range

- 1 \leq w (⊤) < 1 .

Our proofs rely on various forms of Riccati assumptions, which allow us to derive results applicable to a broad spectrum of models. Furthermore, we investigate the oscillatory behavior of Equation (1) when the condition (9) holds (see Theorems 9–16).

This work presents a novel analysis of the general Equation (1), which, to the best of our knowledge, has not been addressed in previous studies. The approach we take enables the inclusion of a wider range of models, setting our work apart from earlier research and offering new directions for further investigation.

Future studies could extend this work by examining the oscillatory behavior of (1) in the case where the function

w (⊤)

is oscillatory. Additionally, the methodology developed in this paper can be adapted to analyze more generalized equations in the form

{(d_{1} (⊤) (d_{2} (⊤) {({(ρ (⊤))}^{″})}^{α}))}^{'} + \int_{a}^{b} Π (⊤, s) y^{α} (ϱ (⊤, s)) d s = 0,

where

ρ (⊤) = y (⊤) + \int_{c}^{d} w (⊤, s) y (ς (⊤, s)) d s .

In addition to the sufficient conditions established in this work and the detailed analysis we have provided, a natural extension of the present study would be to investigate whether these conditions are close to being necessary. Such an extension would further strengthen the theoretical framework and provide a sharper characterization of the parameter space.

Finally, based on the oscillation criteria examined in this study, it is evident that under Riccati’s assumptions, the solutions maintain a crucial property of boundedness. This ensures that they neither diverge nor exhibit instability over time. By linking oscillatory behavior with stability, we confirm that the solutions remain well-behaved within finite bounds, further supporting the notion of stability in dynamic systems. Thus, the interplay between oscillation and stability offers significant insights into the long-term behavior and boundedness of the system under consideration. In this direction, we emphasize that there is a lot of work to do and we leave it for future investigations.

Author Contributions

Conceptualization, A.A.-J., E.A. and B.Q.; methodology, A.A.-J., B.Q. and E.A.; validation, A.A.-J., B.Q. and E.A.; investigation, A.A.-J. and B.Q.; resources, B.Q. and A.A.-J.; data curation, A.A.-J. and B.Q.; writing—original draft preparation, A.A.-J., E.A. and B.Q.; writing—review and editing, B.Q., A.A.-J., S.S.-C. and E.A.; visualization, A.A.-J., E.A., S.S.-C. and B.Q.; supervision, A.A.-J., S.S.-C., E.A. and B.Q.; project administration, B.Q. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Researchers Supporting Project number (PNURSP2025R406), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.

Data Availability Statement

Data are contained within the article.

Acknowledgments

Authors would like to thank Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R406), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Krasnosel’skii, M.A.; Pokrovskii, A.V. Systems with Hysteresis; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
Al-Jaser, A.; Qaraad, B.; Ramos, H.; Serra-Capizzano, S. New Conditions for Testing the Oscillation of Solutions of Second-Order Nonlinear Differential Equations with Damped Term. Axioms 2024, 13, 105. [Google Scholar] [CrossRef]
Linders, V.; Birken, P. Locally conservative and flux consistent iterative methods. SIAM J. Sci. Comput. 2024, 46, S424–S444. [Google Scholar] [CrossRef]
Dravins, I.; Serra-Capizzano, S.; Neytcheva, M. Spectral Analysis of Preconditioned Matrices Arising from Stage-Parallel Implicit Runge–Kutta Methods of Arbitrarily High Order. SIAM J. Matrix Anal. Appl. 2024, 45, 1007–1034. [Google Scholar] [CrossRef]
McDonald, E.; Pestana, J.; Wathen, A. Preconditioning and iterative solution of all-at-once systems for evolutionary partial differential equations. SIAM J. Sci. Comput. 2018, 40, A1012–A1033. [Google Scholar] [CrossRef]
Ferrari, P.; Furci, I.; Hon, S.; Ayman-Mursaleen, M.; Serra-Capizzano, S. The eigenvalue distribution of special 2-by-2 block matrix-sequences with applications to the case of symmetrized Toeplitz structures. SIAM J. Matrix Anal. Appl. 2019, 40, 1066–1086. [Google Scholar] [CrossRef]
Hale, J.K. Theory of Functional Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar] [CrossRef]
Baculíková, B.; Džurina, J. Oscillation of third-order neutral differential equations. Math. Comput. Model. 2010, 52, 215–226. [Google Scholar] [CrossRef]
Džurina, J.; Grace, S.R.; Jadlovská, I. On nonexistence of Kneser solutions of third-order neutral delay differential equations. Appl. Math. Lett. 2019, 88, 193–200. [Google Scholar] [CrossRef]
Thandapani, E.; Tamilvanan, S.; Jambulingam, E.; Tech, V.T.M. Oscillation of third order half-linear neutral delay differential equations. Int. J. Pure Appl. Math. 2012, 77, 359–368. [Google Scholar]
Jiang, Y.; Li, T. Asymptotic behavior of a third-order nonlinear neutral delay differential equation. J. Inequal. Appl. 2014, 2014, 512. [Google Scholar] [CrossRef]
Tunc, E. Oscillatory and asymptotic behavior of third-order neutral differential equations with distributed deviating arguments. Electron. J. Differ. Equ. 2017, 2017, 1–12. Available online: https://ejde.math.txstate.edu/Volumes/2017/16/tunc.pdf (accessed on 10 November 2025). [CrossRef]
Elabbasy, E.M.; Hassan, T.; Elmatary, B.M. Oscillation criteria for third order delay nonlinear differential equations. Electron. J. Qual. Theory Differ. Equ. 2012, 2012, 1–9. [Google Scholar] [CrossRef]
Graef, J.R.; Tunc, E.; Grace, S.R. Oscillatory and asymptotic behavior of a third-order nonlinear neutral differential equation. Opusc. Math. 2017, 37, 839–852. [Google Scholar] [CrossRef]
Grace, S.R.; Agarwal, R.P.; Pavani, R.; Thandapani, E. On the oscillation of certain third-order nonlinear functional differential equations. Appl. Math. Comput. 2008, 202, 102–112. [Google Scholar] [CrossRef]
Džurina, J.; Thandapani, E.; Tamilvanan, S. Oscillation of solutions to third-order half-linear neutral differential equations. Electron. J. Differ. Equ. 2012, 2012, 1–9. [Google Scholar]
Li, T.; Zhang, C.; Xing, G. Oscillation of third-order neutral delay differential equations. In Abstract and Applied Analysis; Hindawi: London, UK, 2012; Volume 2012, p. 569201. [Google Scholar] [CrossRef]
Li, T.; Rogovchenko, Y.V. On asymptotic behavior of solutions to higher-order sublinear emden–fowler delay differential equations. Appl. Math. Lett. 2017, 67, 53–59. [Google Scholar] [CrossRef]
Candan, T. Asymptotic properties of solutions of third-order nonlinear neutral dynamic equations. Adv. Differ. Equ. 2014, 2014, 35. [Google Scholar] [CrossRef]
Philos, C.G. On the existence of nonoscillatory solutions tending to zero at ∞ for differential equations with positive delays. Arch. Math. 1981, 36, 168–178. [Google Scholar] [CrossRef]
Hall, B.C. Lie Groups, Lie Algebras, and Representations. In Quantum Theory for Mathematicians. Graduate Texts in Mathematics; Springer: New York, NY, USA, 2013; Volume 267, pp. 333–366. [Google Scholar] [CrossRef]
Knapp, A.W. Lie Groups Beyond an Introduction; Birkhäuser: Boston, MA, USA, 1996; Volume 140. [Google Scholar] [CrossRef]
Jadlovská, I.; Chatzarakis, G.E.; Džurina, J.; Grace, S.R. On Sharp Oscillation Criteria for General Third-Order Delay Differential Equations. Mathematics 2021, 9, 1675. [Google Scholar] [CrossRef]
Graef, J.R.; Jadlovská, I.; Tunç, E. Sharp asymptotic results for third-order linear delay differential equations. J. Appl. Anal. Comput. 2021, 11, 2459–2472. [Google Scholar] [CrossRef]
Grace, S.R. Oscillation criteria for third order nonlinear delay differential equations with damping. Opuscula Math. 2015, 35, 485–497. [Google Scholar] [CrossRef]
Baculíková, B.; Džurina, J. Oscillation of the third order Euler differential equation with delay. Math. Bohem. 2014, 139, 649–655. [Google Scholar] [CrossRef]
Baculíková, B.; Džurina, J. Oscillation of third-order nonlinear differential equations. Appl. Math. Lett. 2011, 24, 466–470. [Google Scholar] [CrossRef]
Saker, S.H.; Džurina, J. On the oscillation of certain class of third-order nonlinear delay differential equations. Math. Bohem. 2010, 135, 225–237. [Google Scholar] [CrossRef]
Wang, Y.; Meng, F.; Gu, J. Oscillation criteria of third-order neutral differential equations with damping and distributed deviating arguments. Adv. Differ. Equ. 2021, 2021, 515. [Google Scholar] [CrossRef]
Tian, Y.; Cai, Y.; Fu, Y.; Li, T. Oscillation and asymptotic behavior of third-order neutral differential equations with distributed deviating arguments. Adv. Differ. Equ. 2015, 2015, 267. Available online: https://advancesincontinuousanddiscretemodels.springeropen.com/articles/10.1186/s13662-015-0604-6 (accessed on 10 November 2025). [CrossRef]
Sun, Y.; Zhao, Y. Oscillatory behavior of third-order neutral delay differential equations with distributed deviating arguments. J. Inequal. Appl. 2019, 2019, 207. [Google Scholar] [CrossRef]
Candan, T. Oscillation criteria and asymptotic properties of solutions of third-order nonlinear neutral differential equations. Math. Methods Appl. Sci. 2014, 38, 1379–1392. [Google Scholar] [CrossRef]
Zhong, J.; Ouyang, Z.; Zou, S. Oscillation criteria for a class of third-order nonlinear neutral differential equations. J. Appl. Anal. 2011, 17, 155–163. [Google Scholar] [CrossRef]
Han, Z.; Li, T.; Zhang, C.; Sun, S. An oscillation criterion for third-order neutral delay differential equations. J. Appl. Anal. 2010, 16, 295–303. [Google Scholar] [CrossRef]
Karpuz, B.; Öcalan, Ö.; Öztürk, S. Comparison theorems on the oscillation and asymptotic behavior of higher-order neutral differential equations. Glasgow Math. J. 2010, 52, 107–114. [Google Scholar] [CrossRef]
Thandapani, E.; Li, T. On the oscillation of third-order quasi-linear neutral functional differential equations. Arch. Math. 2011, 47, 181–199. [Google Scholar]
Zhang, S.; Wang, Q. Oscillation of second-order nonlinear neutral dynamic equations on times cales. Appl. Math. Comput. 2010, 216, 2837–2848. [Google Scholar] [CrossRef]

Figure 1. Test of the strength of criteria for Equation (74).

Figure 2. Test of the strength of criteria for Equation (77).

Figure 3. Test of the strength of criteria for Equation (82).

Table 1. Numerical evaluation of

λ_{1}

and

λ_{2}

as functions of

w_{0}

under Conditions (78) and (79).

Table 1. Numerical evaluation of

λ_{1}

and

λ_{2}

as functions of

w_{0}

under Conditions (78) and (79).

		$0.0$	$0.25$	$0.5$	$0.75$	$1.0$	$1.25$	$1.5$	$1.75$	$2.0$
1	$λ_{1} = (2^{5} \cdot 5^{4} / 4^{3}) (1 + 2 Φ_{0}^{3})$	312	322	390	576	937	1533	2421	3662	5312
2	$λ_{2} = (5^{4} \cdot 2^{5} / 12) (1 + 2 Φ_{0}^{3})$	1666	1718	2083	3072	5000	8177	$12, 916$	$19, 531$	$28, 333$

Table 2. Numerical evaluation of

λ_{1}

and

λ_{2}

as functions of

Φ_{0}

under Conditions (83) and (84).

Table 2. Numerical evaluation of

λ_{1}

and

λ_{2}

as functions of

Φ_{0}

under Conditions (83) and (84).

		$Φ_{0} = 0.0$	$Φ_{0} = 0.20$	$Φ_{0} = 0.40$	$Φ_{0} = 0.60$	$Φ_{0} = 0.80$	$Φ_{0} = 1.00$	$Φ_{0} = 1.20$	$Φ_{0} = 1.40$
1	$λ = (25^{2} \cdot 2^{3} / 3) (1 + 2 Φ_{0}^{3})$	16,666.6667	$1693.3333$	$1880.0$	$2386.6667$	$3373.3333$	$5000.0$	$7426.6667$	10,813.3333
2	$λ = (2^{5} \cdot 5^{4} / 4^{3}) (2 Φ_{0}^{3} + 1)$	$312.5$	$317.5$	$352.5$	$447.5$	$632.5$	$937.5$	$1392.5$	$2027.5$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Al-Jaser, A.; Serra-Capizzano, S.; Alluqmani, E.; Qaraad, B. Third-Order Nonlinear Neutral Delay Differential Equations with Several Deviating Arguments: Improved Oscillation Criteria. Axioms 2025, 14, 850. https://doi.org/10.3390/axioms14110850

AMA Style

Al-Jaser A, Serra-Capizzano S, Alluqmani E, Qaraad B. Third-Order Nonlinear Neutral Delay Differential Equations with Several Deviating Arguments: Improved Oscillation Criteria. Axioms. 2025; 14(11):850. https://doi.org/10.3390/axioms14110850

Chicago/Turabian Style

Al-Jaser, Asma, Stefano Serra-Capizzano, Eman Alluqmani, and Belgees Qaraad. 2025. "Third-Order Nonlinear Neutral Delay Differential Equations with Several Deviating Arguments: Improved Oscillation Criteria" Axioms 14, no. 11: 850. https://doi.org/10.3390/axioms14110850

APA Style

Al-Jaser, A., Serra-Capizzano, S., Alluqmani, E., & Qaraad, B. (2025). Third-Order Nonlinear Neutral Delay Differential Equations with Several Deviating Arguments: Improved Oscillation Criteria. Axioms, 14(11), 850. https://doi.org/10.3390/axioms14110850

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Third-Order Nonlinear Neutral Delay Differential Equations with Several Deviating Arguments: Improved Oscillation Criteria

Abstract

1. Introduction

2. Main Results

2.1. Oscillation Criteria When (8) Holds

2.2. Oscillation Criteria When (9) Holds

2.3. Philos-Type Oscillation Criteria

2.3.1. Philos-Type Criteria When (8) Holds

2.3.2. Philos-Type Criteria When (9) Holds

3. Examples

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI