Quasi-Optimal Convergence of a Family of Adaptive Nonconforming Finite Element Methods

Abstract

This study is devoted to the quasi-optimal convergence analysis of a family of adaptive nonconforming elements with high-order terms, which preserve weak continuities. In contrast with the nonconforming $P_1$ element (Crouzeix–Raviart element) the gradient of the discrete solution considered in this paper is not a piecewise constant vector. New quasi-orthogonality and a new discrete upper bound are established for the first time, based on which the convergence of the adaptive algorithm with a standard Dörfler collective marking strategy and quasi-optimality results are eventually established. Some other properties are also investigated, for example, the discrete Helmholtz decomposition for this family of nonconforming elements. Numerical experiments confirm the theoretical results.

1. Introduction

The adaptive finite element method (AFEM) serves as a powerful and dependable approach for numerically solving partial differential equations, with its origins tracing back to the foundational work reported in [1]. For a comprehensive discussion, see the books by Ainsworth [2], Babuška [3], and Verfürth [4], as well as the review articles reported in [5,6], together with their cited references. Recent years have witnessed significant advances in the convergence analysis of AFEMs. The foundational work by Dörfler [7] introduced a key marking strategy, now widely referred to as Dörfler’s marking strategy, and established strict energy reduction of the adaptive conforming $P_1$ element method for the Poisson equation under the condition that the initial mesh (${\mathcal{T}}_0$) satisfies a specific fineness assumption. Morin et al. [8,9] eliminated initial mesh restrictions by introducing the concepts of data oscillation and the interior node property, establishing the convergence rate of the adaptive conforming $P_1$ element method. Carstensen and Hoppe [10] pioneered convergence proofs for the adaptive nonconforming finite element method (ANFEM) and extended results to the mixed finite element method (FEM) [11]. The field of AFEMs has also seen substantial theoretical developments in quasi-optimality analyses. Binev et al. [12] first established the complexity of two-dimensional newest-vertex bisection, demonstrating that the cumulative number of elements added to maintain mesh conformity does not excessively increase the total number of marked elements. Leveraging this property, they proved the optimality of the AFEM by incorporating an additional coarsening step. Later, Stevenson [13] generalized the complexity to three-dimensional newest-vertex bisection and proved coarsening unnecessary for quasi-optimality. The optimal complexity results for adaptive algorithms mentioned above can be understood as follows: if the exact solution can be approximated by a given class of finite element methods at a certain rate (measured as the ratio of accuracy to the number of unknowns), then the sequence of meshes generated by the adaptive algorithm with newest-vertex bisection will achieve this optimal convergence rate, up to a constant multiplicative factor. Cascon et al. advanced the theory by proving the convergence of AFEMs without an interior node property and the quasi-optimality of AFEMs for self-adjoint elliptic problems [14]. More recently, a convergence and optimality result of the adaptive Wilson element method was obtained in [15], where the authors used a special property of the Wilson element whose shape function space is composed of two parts (a conforming $Q_1$ part and a nonconforming bubble-function part) orthogonal to each other, i.e., the Wilson element is very close to conforming with the $Q_1$ element. The first quasi-optimality result of the ANFEM for a second-order elliptic problem was obtained by Becker et al. [16], who considered the nonconforming $P_1$ element (Crouzeix–Raviart element [17]) with an adaptive algorithm based on a balance of contributions of two parts in the estimator in each step. Later, Mao et al. established the quasi-optimality of the adaptive Crouzeix–Raviart element method by using a simple Dörfler collective marking strategy in each step, without comparison of the two contributions in the estimator [18]. The quasi-optimality result of an ANFEM for a fourth-order elliptic problem was obtained by Hu et al. [19], who considered Morley element in their paper. The quasi-optimality results of the adaptive nonconforming $P_1$ element method for optimal control problems were studied in [20,21]. Convergence and optimality analysis of ANFEMs in all these papers crucially relies on the fact that, for the lowest order nonconforming element, the discrete pressure (or the discrete stress) is a piecewise constant vector (tensor).

This paper will establish the quasi-optimal convergence for a family of adaptive nonconforming finite element methods that preserve weak continuities across elements’ edges, where the corresponding discrete pressure is not a piecewise constant vector. The lowest order case in this family is the Lin–Tobiska–Zhou element [22]. To the best of my knowledge, it is the first optimal convergence result using an adaptive algorithm with a nonconforming finite element and high-order terms preserving weak continuities. It will be proven that the adaptive algorithm based on this family of nonconforming finite elements on rectangular meshes is convergent by establishing a new quasi-orthogonality. More importantly, it will be proven that the above-mentioned adaptive algorithm possesses optimal complexity, and a new discrete reliability will be proven by establishing a new discrete Helmholtz decomposition for this family of nonconforming elements for the first time. It is noticed that the nonconforming quadrilateral $P_1$ element [23] also be seen as a member of the family of nonconforming finite elements considered in this paper. Therefore, the convergence and optimality results presented in this paper are valid for the adaptive nonconforming quadrilateral $P_1$ element [23] method applied to general quadrilateral meshes.

This work addresses a gap in prior analyses of adaptive nonconforming methods, which have predominantly relied on the piecewise-constant nature of the discrete stress/pressure field (as in the case of the Crouzeix–Raviart element). New analytical tools are developed, including a novel quasi-orthogonality relation, a discrete reliability bound derived from a novel Helmholtz decomposition tailored to this class of elements, and accompanying technical estimates. These tools are integrated with standard Dörfler marking to establish the convergence and quasi-optimality of the adaptive algorithm for rectangular/quadrilateral meshes.

The rest of this paper is organized as follows. The next section presents the preliminaries, including the notations, the problem under consideration, and the definition of a nonconforming element and some of its key properties. In Section 3, the a posteriori error estimation and the adaptive algorithm will be presented. Section 4 will prove one main result of this paper, i.e., the convergence of the AFEM algorithm will be proven, and a new quasi-orthogonality will be established in the beginning of Section 4. Section 5 will establish a new discrete reliability result and provide an asymptotic estimate for the optimality of the adaptive algorithm, which is the other main result of the paper. Some numerical experiments are presented in Section 6.

2. Preliminaries and Notations

This section introduces some essential notations. Following standard definitions for Sobolev spaces (cf. [24]), the seminorm and norm of a function (v) defined on an open domain (G) are defined as follows:

$${\left|v\right|}_{m,G}={\left({\int }_G\sum _{\left|\alpha \right|=m}{\left|D^{\alpha }v\right|}^2\right)}^{{\displaystyle \frac{1}{2}}},{\parallel v\parallel }_{m,G}={\left({\int }_G\sum _{\left|\alpha \right|\le m}{\left|D^{\alpha }v\right|}^2\right)}^{{\displaystyle \frac{1}{2}}}.$$

Let $\Omega \subset {\mathbb{R}}^2$ be a bounded polygonal domain that is partitioned by a rectangular mesh (${\mathcal{T}}_0$). This paper focuses on the following second-order elliptic problem with discontinuous coefficients: find $u\in V=H_0^1(\Omega )$ such that

$$\left\{\begin{array}{ccccc}\hfill -\mathrm{div}(\mathbf{A}\nabla u)& =\hfill & \hfill f& \mathrm{in}\hfill & \hfill \Omega ,\\ \hfill u& =\hfill & \hfill 0& \mathrm{on}\hfill & \hfill \partial \Omega .\end{array}\right.$$

(1)

where $f\in L^2(\Omega )$ and $\mathbf{A}$ is a positive, piecewise-constant coefficient matrix. Assume that $\mathbf{A}$ remains constant on each element of the initial mesh (${\mathcal{T}}_0$).

Let ${(·,·)}_G$ denote the $L^2\left(G\right)$ inner product, where the subscript $\Omega$ is omitted when $G=\Omega$ for simplicity. For any $f\in L^2(\Omega )$, the variational formulation of the problem (1) can be expressed as follows:

$$\left\{\begin{array}{l}\mathrm{find}u\in H_0^1(\Omega ),\mathrm{such}\mathrm{that}\\ a(u,v)=(f,v),\forall v\in H_0^1(\Omega )\end{array}\right.$$

(2)

where $a(u,v):={\int }_{\Omega }\mathbf{A}\nabla u·\nabla v\mathrm{d}x$.

Let $\#J$ denote the cardinality of a finite set (J). The meshes considered in this paper are described next. Assume that $\mathcal{T}$ is a graded adaptive mesh generated through a refinement process as follows: the domain ($\Omega$) is initially partitioned into elements ($K\in {\mathcal{T}}_0$) of mesh-level 0, where ${\mathcal{T}}_0$ is conforming, meaning that for any distinct elements ($K_1,K_2\in {\mathcal{T}}_0$), their intersection ($\overline{K_1}\cap \overline{K_2}$) is either empty, a common node, or a common edge. Starting from an element ($K\in {\mathcal{T}}_0$), an existing element (K) can be refined by splitting it into four new elements, referred to as its sons and denoted by ${\mathcal{S}}_i\left(K\right)$ for $i=1,2,3,4$. The son elements are formed by connecting the midpoints of opposite edges of the original element (K). For a newly created element ($K^{\prime }={\mathcal{S}}_i\left(K\right)$), the original element (K) is designated as the father element of $K^{\prime }$, denoted by $K=\mathcal{F}\left(K^{\prime }\right)$. When an element (K) undergoes refinement, the domain partition ($\Omega$) is updated by replacing K with its four son elements (${\mathcal{S}}_i\left(K\right)$, $i=1,2,3,4$). The new elements can be refined again and again and so the final partition (${\mathcal{T}}_h$) of $\Omega$ is created.

Definition 1.

For an element ($K\in {\mathcal{T}}_h$) generated from the initial mesh (${\mathcal{T}}_0$) by the refinement process described above, the refinement level ($L\left(K\right)$) is defined as $L\left(K\right):=0$ if $K\in {\mathcal{T}}_0$ and $L\left(K\right):=m\ge 1$ if there exists a chain of m father elements ($K_i$, where $i=1,\dots ,m$, starting from $K_0:=K$ and defined by $K_i:=\mathcal{F}\left(K_{i-1}\right)$ for $i=1,\dots ,m$) such that $K_m\in {\mathcal{T}}_0$.

The above definition of $L\left(K\right)$ is equal to the number of refinement steps required to generate element K from an element in the coarsest mesh (${\mathcal{T}}_0$).

Definition 2.

A mesh (${\mathcal{T}}_h$) generated by the above refinement process from a regular initial mesh (${\mathcal{T}}_0$) is called k-irregular (where $k\ge 0$ and $k\in \mathbb{Z}$) if the following condition holds for any pair of neighboring elements ($K,K^{\prime }\in {\mathcal{T}}_h$) sharing a one-dimensional manifold boundary ($\partial K\cap \partial K^{\prime }$):

$$|L\left(K\right)-L\left(K^{\prime }\right)| \le k.$$

(3)

Here, $L\left(K\right)$ and $L\left(K^{\prime }\right)$ denote the refinement levels of elements K and $K^{\prime }$, respectively.

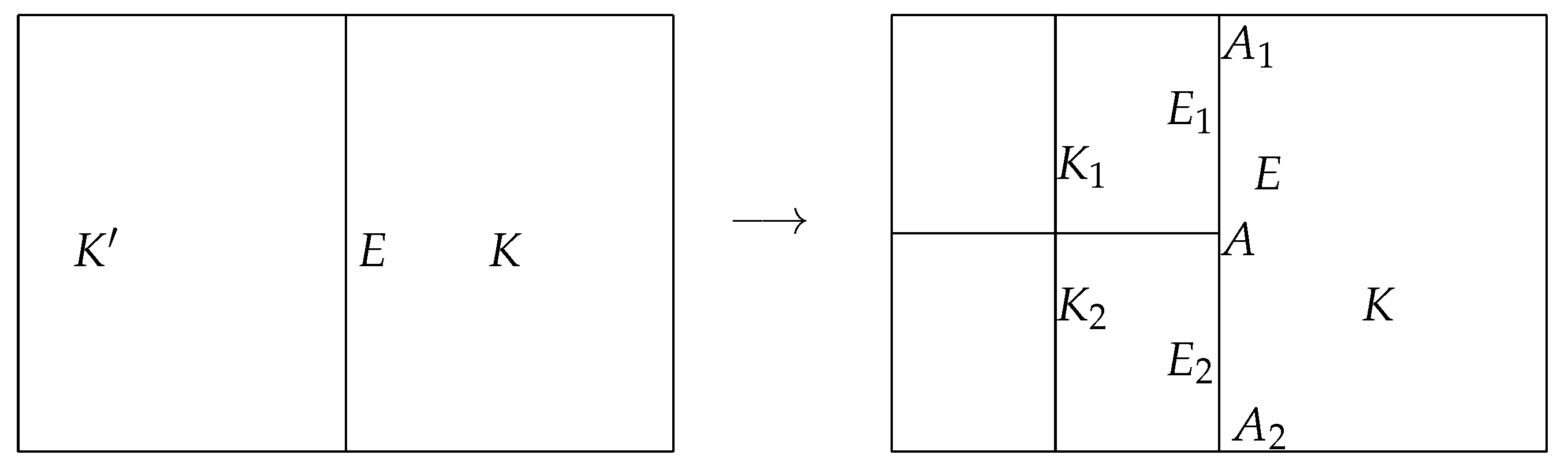
Note that condition (3) does not need to hold for element pairs (K and $K^{\prime }$) sharing a single vertex. A 0-irregular mesh is conforming (without hanging nodes), whereas this work exclusively examines 1-irregular meshes, which permit hanging nodes. AFEMs on quadrilateral meshes without hanging nodes were presented in [25]. The corresponding local refinement procedure for 1-irregular meshes is detailed in Algorithm 1.

Algorithm 1 Local refinement on 1-irregular quadrilateral meshes.

Input: A 1-irregular mesh ${\mathcal{T}}_{\ell }$ with a marked elements set ${\mathcal{M}}_{\ell }$ (If $\ell =0$, ${\mathcal{T}}_0$ is required as a conforming mesh).

(1) For each marked element $K\in {\mathcal{M}}_{\ell }$, subdivide it into 4 smaller elements by connecting the barycenters of its opposite edges (see Figure 1). (2) If any pair of neighboring elements violates the 1-irregularity condition (i.e., (3) with $k=1$), refine the less-refined element by splitting it into 4 sub-elements (as in Step 1). (3) Repeat Step 2 until the 1-irregularity condition holds for all neighboring elements in the mesh.

Output: The refined graded adaptive mesh ${\mathcal{T}}_{\ell +1}=\mathrm{REFINE}({\mathcal{T}}_{\ell },{\mathcal{M}}_{\ell })$.

Figure 1. (Left) Regular interior edge ($E\in {\mathcal{E}}_h^r$) connecting two associated elements (K and $K^{\prime }$); (Right) Hanging node A, along with its neighboring regular nodes ($A_1$ and $A_2$) and its irregular interior edge ($E\in {\mathcal{E}}_h^i$) subdivided into two son edges ($E_1,E_2\in \mathcal{S}\left(E\right)$), where each son edge corresponds to a single element ($K_1$ or $K_2$).

Figure 1. (Left) Regular interior edge ($E\in {\mathcal{E}}_h^r$) connecting two associated elements (K and $K^{\prime }$); (Right) Hanging node A, along with its neighboring regular nodes ($A_1$ and $A_2$) and its irregular interior edge ($E\in {\mathcal{E}}_h^i$) subdivided into two son edges ($E_1,E_2\in \mathcal{S}\left(E\right)$), where each son edge corresponds to a single element ($K_1$ or $K_2$).

The above local bisection refinement result holds for the following complexity result [26].

Lemma 1.

Let ${\mathcal{T}}_k,k=0,\dots n$ be a sequence of quadrilateral meshes generated by Algorithm 1, starting from an initial mesh (${\mathcal{T}}_0$) with ${\mathcal{M}}_k\subset {\mathcal{T}}_k,k=0,\dots n-1$ denoting the marked elements refined at step k. Then, ${\mathcal{T}}_n$ is uniformly shape-regular, with its regularity constant depending only on ${\mathcal{T}}_0$. Furthermore, the total elemental increase satisfies the following:

$$\#{\mathcal{T}}_n-\#{\mathcal{T}}_0\le C_0\sum _{k=0}^{n-1}\#{\mathcal{M}}_k,$$

(4)

where $C_0$ is a constant determined by ${\mathcal{T}}_0$.

Let ${\mathcal{E}}_h\left(K\right)$ denote the set of four edges of an element ($K\in {\mathcal{T}}_h$). Let ${\mathcal{E}}_h:={\bigcup }_{K\in {\mathcal{T}}_h}{\mathcal{E}}_h\left(K\right)$ be the set of all elements’ edges of the mesh. ${\mathcal{E}}_h$ can be decomposed as follows:

$${\mathcal{E}}_h={\mathcal{E}}_h^0\cup {\mathcal{E}}_h^{\Gamma },$$

where ${\mathcal{E}}_h^{\Gamma }$ describes the set of all edges located at the boundary ($\Gamma$) of $\Omega$ and ${\mathcal{E}}_h^0$ denotes the set of edges of ${\mathcal{E}}_h$ located in the interior of $\Omega$. An edge ($\tilde{E}\in {\mathcal{E}}_h$) is called a son edge of an edge ($E\in {\mathcal{E}}_h$) if $\tilde{E}\subset E$ and $|\tilde{E}|<|E|$ (see Figure 1). The set of all son edges of E is denoted by $\mathcal{S}\left(E\right)$. The set of all irregular interior edges (${\mathcal{E}}_h^i$) is defined as follows:

$${\mathcal{E}}_h^i:=\left\{E\in {\mathcal{E}}_h^0\mid \mathcal{S}\left(E\right)\ne \varnothing \right\}.$$

Let $\tilde{E}\in \mathcal{S}\left(E\right)$ be a son edge of $E\in {\mathcal{E}}_h^i$; then, edge E is termed the father edge of $\tilde{E}$ and is written as $E=\mathcal{F}\left(\tilde{E}\right)$. The set of all son edges is defined as

$${\mathcal{E}}_h^s:=\bigcup _{E\in {\mathcal{E}}_h^i}\mathcal{S}\left(E\right).$$

Let ${\mathcal{E}}_h^r$ denote the collection of regular interior edges:

$${\mathcal{E}}_h^r:={\mathcal{E}}_h^0\setminus ({\mathcal{E}}_h^i\cup {\mathcal{E}}_h^s).$$

It is easy to see that set $\mathcal{S}\left(E\right)$ is empty for each regular edge ($E\in {\mathcal{E}}_h^r$). Using these definitions, the set of all interior edges (${\mathcal{E}}_h^0$) can be decomposed as

$${\mathcal{E}}_h^0={\mathcal{E}}_h^r\cup {\mathcal{E}}_h^i\cup {\mathcal{E}}_h^s.$$

Let ${\mathcal{N}}_h\left(K\right)$ to be the set of vertices of any element ($K\in {\mathcal{T}}_h$). The set of all nodes of the mesh (${\mathcal{T}}_h$) reads ${\mathcal{N}}_h:={\cup }_{K\in {\mathcal{T}}_h}{\mathcal{N}}_h\left(K\right)$. Obviously, son edges appear in pairs. The common vertex of a pair of two son edges is called a hanging node.

A node ($P\in {\mathcal{N}}_h$) is defined as a regular node if it does not serve as a hanging node. A representative scenario involving a hanging node (A) and its connected regular nodes ($A_1,A_2$) is illustrated in Figure 1. Specifically, a node ($A\in {\mathcal{N}}_h$) is classified as a hanging node if there exists a mesh element ($K\in {\mathcal{T}}_h$) such that A lies on the boundary ($\partial K$) but is not one of the vertices of K.

For each element ($K\in {\mathcal{T}}_h$) and edge ($E\in {\mathcal{E}}_h$), we define $h_K={\left|K\right|}^{{\displaystyle \frac{1}{2}}}$ and $h_E=\left|E\right|$. For each edge ($E\in {\mathcal{E}}_h$), we define

$${\omega }_E:=\cup \{K\in {\mathcal{T}}_h:\overline{K}\cap E\mathrm{as}\mathrm{a} \mathrm{1-dimensional} \mathrm{manifold}.\}$$

For each element ($K\in {\mathcal{T}}_h$), we define

$${\omega }_K=\cup \{K^{\prime }\in {\mathcal{T}}_h:\overline{K^{\prime }}\cap \overline{K}\ne \varnothing \},$$

and

$${\Omega }_K:=\bigcup _{\tilde{K}\in S\left(K\right)}{\omega }_{\tilde{K}}$$

where

$$S\left(K\right):=\left\{K_0\in {\mathcal{T}}_h:\overline{K}\cap \overline{K_0}\ne \varnothing \right\}$$

is the set of all the neighboring elements of element $K\in {\mathcal{T}}_h$. For any $E\in {\mathcal{E}}_h$, we define

$${\Omega }_E:=\bigcup _{K_i\in {\mathcal{T}}_h,\overline{K_i}\cap E\in {\mathcal{E}}_h}{\Omega }_{K_i}.$$

It is noticed that the shape regularity of rectangular mesh ${\mathcal{T}}_h$ implies the existence of a constant ($C_0$) such that

$$\begin{array}{c}\hfill {\displaystyle \frac{max\{h_x\left(K\right),h_y\left(K\right)\}}{min\{h_x\left(K\right),h_y\left(K\right)\}}}\le C_0,\forall K\in {\mathcal{T}}_h,\end{array}$$

(5)

where $h_x\left(K\right),h_y\left(K\right)$ is the diameter along each coordinate axis of element K. The definition of the shape regularity of general quadrilateral meshes can be found in [24,27].

This study focuses on the following family of nonconforming FEMs with some weak continuity at interelement boundaries, which means the corresponding finite element function preserves the continuity of the integral across internal edges of elements.

The corresponding interpolation operator related to degrees of freedom is presented next. For a reference element ($\widehat{K}={[-1,1]}^2$), we define the polynomial space as follows:

$${\tilde{P}}_n\left(\widehat{K}\right)=\mathrm{span}\{1,\xi ,\eta ,{\xi }^2,{\eta }^2,\dots ,{\xi }^n,{\eta }^n\},n\mathrm{is}\mathrm{a}\mathrm{fixed}\mathrm{non-negative}\mathrm{integer}.$$

(6)

The finite element interpolation operator (${\widehat{\Pi }}_h\widehat{v}$) is defined for any $\widehat{v}\in H^1\left(\widehat{K}\right)$ as follows:

$${\widehat{\Pi }}_h\widehat{v}\in {\tilde{P}}_n\left(\widehat{K}\right),n\ge 2,$$

(7)

and for any boundary ($\widehat{E}$) of $\widehat{K}$,

$${\int }_{\widehat{E}}(\widehat{v}-{\widehat{\Pi }}_h\widehat{v})\mathrm{d}s=0,\forall \widehat{E}\subset \partial \widehat{K};$$

(8)

and

$${\int }_{\widehat{K}}(\widehat{v}-{\widehat{\Pi }}_h\widehat{v})p\mathrm{d}x=0,\forall p\in {\tilde{P}}_{n-2}\left(\widehat{K}\right);$$

(9)

For a reference element ($\widehat{K}$) with four edges (${\widehat{E}}_1,{\widehat{E}}_2,{\widehat{E}}_3$, and ${\widehat{E}}_4$), the degrees of freedom (DOFs) of function $\widehat{v}$ are defined as

$$\left\{{\displaystyle \frac{{\int }_{{\hat{E}}_i}\widehat{v}\mathrm{d}s}{|{\widehat{E}}_i|}},i=1,2,3,4;{\displaystyle \frac{{\int }_{\widehat{K}}\widehat{v}\mathrm{d}x}{|\widehat{K}|}},{\displaystyle \frac{{\int }_{\widehat{K}}\xi \widehat{v}\mathrm{d}x}{|\widehat{K}|}},{\displaystyle \frac{{\int }_{\widehat{K}}\eta \widehat{v}\mathrm{d}x}{|\widehat{K}|}},\dots ,{\displaystyle \frac{{\int }_{\widehat{K}}{\xi }^{n-2}\widehat{v}\mathrm{d}x}{|\widehat{K}|}},{\displaystyle \frac{{\int }_{\widehat{K}}{\eta }^{n-2}\widehat{v}\mathrm{d}x}{|\widehat{K}|}}\right\}.$$

(10)

The nonconforming finite element function space ($V_h$) defined on mesh ${\mathcal{T}}_h$ can be given as

$$V_h^n=\left\{v_h\in L^2(\Omega )|v_h{|}_K\circ F_K\in {\tilde{P}}_n\left(\widehat{K}\right),\forall K\in {\mathcal{T}}_h;{\int }_E〚v_h{〛}_E\mathrm{d}s=0,\forall E\in {\mathcal{E}}_h^r\cup {\mathcal{E}}_h^i\cup {\mathcal{E}}_h^{\Gamma }\right\},$$

(11)

where $F_K$ represents the linear transformation from the standard reference element ($\widehat{K}={[-1,1]}^2$) to the actual rectangular element (K), $〚v_h{〛}_E$ is the jump of $v_h$ across interior edge E, and $〚v_h{〛}_E:=v_h{|}_E$ for any boundary edge ($E\in {\mathcal{E}}_h^{\Gamma }$). Thus, the interpolation operator (${\Pi }_h$) is followed by the above linear mapping.

Remark 1.

The above definition includes a family of nonconforming finite elements. For the low-order case of $n=2$, the above nonconforming finite element is the Lin–Tobiska–Zhou element [22]. In addition, if one defines ${\tilde{P}}_{-1}\left(\widehat{K}\right)=\left\{0\right\}$ in (9), then the quadrilateral/hexahedral nonconforming $P_1$ element [23] is also included in the above nonconforming element family with the case of $n=1$, and the convergence and optimality results presented in this paper are also valid for this element.

Remark 2.

If (8) is replaced by a continuity at the center of E, then the other versions of nonconforming finite elements are obtained, which preserve the continuity at centers of interelement boundaries. In addition, it is easy to see that $\xi \eta$ is not well defined based on the weak continuity condition (continuity at the midpoint or continuity of the integral) on four edges of the reference element ($\widehat{K}={[-1,1]}^2$). Therefore, nonconforming finite elements that preserve some weak continuity across interelement boundaries usually exclude terms of multiplication between ξ and η.

Without any confusion, $V_h^n$ is also denoted as $V_h$ in this paper.

Obviously, for any irregular edge ($E\in {\mathcal{E}}_h^i$), some additional constraints should be imposed on degrees of freedom of E and its two son edges in order to keep the integral continuity across E. One can cite [27] for more details.

Let ${\nabla }_h$ denote the discrete gradient operator and $\nabla \times$ denote the curl operator. The discrete weak form of (2) is defined as

$$\left\{\begin{array}{l}\mathrm{find}{u}_h\in V_h,\mathrm{such}\mathrm{that}\\ a_h(u_h,v_h)=(f,v_h),\forall v_h\in V_h,\end{array}\right.$$

(12)

where $a_h(u_h,v_h):=(\mathbf{A}{\nabla }_h{u}_h,{\nabla }_h{v}_h)={\sum }_{K\in {\mathcal{T}}_h}{\int }_K\mathbf{A}\nabla u_h\nabla v_h\mathrm{d}x$. $⫴·{⫴}_h$ is the following mesh-dependent energy norm:

$$⫴v_h{⫴}_h^2:=a_h(v_h,v_h).$$

Obviously, the above mesh-dependent energy norm is equivalent to the mesh-dependent $H^1$ norm ($\parallel {\nabla }_h{v}_h{\parallel }_{0,\Omega }$), i.e.,

$$c_a⫴v{⫴}_h\le {\parallel {\nabla }_{h}v\parallel }_{0,\Omega }\le C_a⫴v{⫴}_h,\forall v\in V_h\cup H_0^1(\Omega )$$

(13)

where the above constants ($c_a$ and $C_a$) depend on $\mathbf{A}$.

As rectangular meshes are considered in this paper, it is easy to see that for any $v_h\in V_h$, ${\nabla }_h{v}_h·n_E$ is a constant on any line E, where E is parallel to an axis and $n_E$ is a unit normal of E.

Lemma 2.

The following properties hold for the finite element space and the interpolation operator.

(i) 

Operator ${\Pi }_h$ holds for the following stability:

$$\begin{array}{c}\hfill \parallel {\nabla }_h{\Pi }_h{v\parallel }_{0,K}\le {\parallel {\nabla }_{h}v\parallel }_{0,K},\forall v\in H^1\left(K\right)\cup V_h\mathit{and}\forall K\in {\mathcal{T}}_h.\end{array}$$

(14)

(ii) 

Operator ${\Pi }_H$ has the following approximation property with a constant (C) dependent only on the shape regularity of the initial mesh such that

$$\parallel v-{\Pi }_H{v\parallel }_{0,K}\le {C\left|K\right|}^{1/2}{\parallel {\nabla }_{h}v\parallel }_{0,K},\forall v\in H^1\left(K\right)\cup V_H\cup V_h\mathit{and}\forall K\in {\mathcal{T}}_H,$$

(15)

(iii) 

For any three nested meshes (${\mathcal{T}}_h$, ${\mathcal{T}}_H$, and ${\mathcal{T}}_{\mathbb{H}}$, where ${\mathcal{T}}_h$ is finer than ${\mathcal{T}}_H$ and ${\mathcal{T}}_H$ is finer than ${\mathcal{T}}_{\mathbb{H}}$), the following orthogonal properties hold:

$$a_h(v,(I-{\Pi }_H)w)=0,\forall v\in V_H\cup V_{\mathbb{H}},\forall w\in V\cup V_h.$$

(16)

(iv) 

For any two nested meshes (${\mathcal{T}}_h$ and ${\mathcal{T}}_H$, where ${\mathcal{T}}_h$ is finer than ${\mathcal{T}}_H$), and any $v_H\in V_H$, let $P_h{v}_H\in V_h$ be the projection of $v_H$ on space $V_h$ related to the energy norm ($⫴·{⫴}_h$), there exists a conforming bilinear $Q_1$ function ($q_h$) such that

$$\begin{array}{c}\hfill \mathit{A}{\nabla }_h{v}_H-\mathit{A}{\nabla }_h{P}_h{v}_H=\nabla \times q_h.\end{array}$$

(17)

Proof. 

(i) and (ii) are standard results. The proof is limited to (iii) and (iv). The proof begins with (16). By integration by parts, for any $v\in V_H$ and any $w\in V$, one can obtain

$$\begin{array}{cc}\hfill & a_h(v,(I-{\Pi }_H)w)\hfill \\ \hfill & =\sum _{K\in {\mathcal{T}}_h}\left(-{\int }_K(w-{\Pi }_{H}w)\mathrm{div}(\mathbf{A}\nabla v)\mathrm{d}x+{\int }_{\partial K}(w-{\Pi }_{H}w)(\mathbf{A}\nabla v·n)\mathrm{d}s\right)\hfill \\ \hfill & =\sum _{E\in {\mathcal{E}}_H^{\Gamma }}{\mathbf{A}\nabla v|}_E·n_E{\int }_E(w-{\Pi }_{H}w)\mathrm{d}s+\sum _{E\in {\mathcal{E}}_H^0}〚\mathbf{A}\nabla v{〛}_E·n_E{\int }_E(w-{\Pi }_{H}w)\mathrm{d}s\hfill \\ \hfill & =0\hfill \end{array}$$

where (9) and (8) are used in the last two steps. Similarly, one can verify that (16) holds for any $v\in V_{\mathbb{H}}$ and any $w\in V$, any $v\in V_H$ and any $w\in V_h$, or any $v\in V_{\mathbb{H}}$ and any $w\in V_h$.

(iv) is now proven. Since $P_h{v}_H\in V_h$ is the projection of $v_H$ on space $V_h$, one can see that for any $w_h\in V_h$,

$$a_h(P_h{v}_H,w_h)=a_h(v_H,w_h).$$

For any interior element edge ($E\in {\mathcal{E}}_h^0$), ${\varphi }_E$ denotes the related basis function on E. Taking $w_h={\varphi }_E$ and integrating by parts yields

$$0=(\mathbf{A}{\nabla }_h{v}_H-\mathbf{A}{\nabla }_h{P}_h{v}_H,{\nabla }_h{\varphi }_E)=〚\mathbf{A}{\nabla }_h{v}_H-\mathbf{A}{\nabla }_h{P}_h{v}_H{〛}_E·n_E{\int }_E{\varphi }_E\mathrm{d}x,$$

which means $〚\mathbf{A}\nabla v_H-\mathbf{A}\nabla P_h{v}_H{〛}_E·n_E=0$. Therefore, $\mathrm{div}(\mathbf{A}\nabla (v_H-P_h{v}_H))\in L^2(\Omega )$. For any element ($K\in {\mathcal{T}}_h$), ${\varphi }_K$ denotes the related basis function in K. Taking $w_h={\varphi }_E$ and integrating by parts yields

$$0=(\mathbf{A}{\nabla }_h{v}_H-\mathbf{A}{\nabla }_h{P}_h{v}_H,{\nabla }_h{\varphi }_K)={\int }_K\mathrm{div}(\mathbf{A}\nabla (v_H-P_h{v}_H)){\varphi }_K\mathrm{d}x.$$

As the above identity holds for basis functions related to DOFs in the interior of K and noticing that $\mathrm{div}(\mathbf{A}\nabla (v_H-P_h{v}_H)){|}_K\in {\tilde{P}}_{n-2}\left(K\right)$, it must hold that $\mathrm{div}(\mathbf{A}\nabla (v_H-P_h{v}_H)){|}_K=0$, which, together with $\mathrm{div}(\mathbf{A}\nabla (v_H-P_h{v}_H))\in L^2(\Omega )$, leads to $\mathrm{div}(\mathbf{A}\nabla (v_H-P_h{v}_H))=0$. Therefore, there exists a function (q) belonging to $H^1(\Omega )$ with ${\int }_{\Omega }q\mathrm{d}x=0$ such that $\mathbf{A}\nabla (v_H-P_h{v}_H)=\nabla \times q$. For any $K\in {\mathcal{T}}_h$, $\mathbf{A}(v_H-P_h{v}_H){|}_K=a_0+a_{1}x+a_2{x}^2+\dots +a_n{x}^n+b_{1}y+b_2{y}^2+\dots +b_n{y}^n$ with coefficients $a_0,a_1,\dots ,a_n,b_1,b_2,\dots ,b_n$. Then, one can obtain

$${(\nabla \times q)|}_K=(\mathbf{A}\nabla (v_H-P_h{v}_H)){|}_K=\left(\begin{array}{c}{a}_1+2a_{2}x+\dots +n{a}_n{x}^{n-1}\\ b_1+2b_{2}y+\dots +n{b}_n{y}^{n-1}\end{array}\right).$$

Let ${q|}_K={\sum }_{j=0}^n{\sum }_{i=0}^j{c}_{i,j}{x}^i{y}^{j-i}$ and insert it into the above identity. Thus, one can find that $c_{i,j}=0$ when $i>1$ or $j-i>1$, which means ${q|}_K=c_{0,0}+c_{1,0}x+c_{0,1}y+c_{1,1}xy$. Therefore, q is a conforming $Q_1$ function. □

Remark 3.

It is noticed that (17) actually establishes the discrete Helmholtz decomposition for this family of nonconforming finite elements, i.e.,

$$\mathit{A}{\nabla }_h(w_h-v_H)=\mathit{A}{\nabla }_h(w_h-P_h{v}_H)+\nabla \times q_h$$

for any $w_h\in V_h$ and any $v_H\in V_H$, where $q_h$ is a conforming piecewise $Q_1$ function related to mesh ${\mathcal{T}}_h$.

In this paper, when a mesh is denoted as ${\mathcal{T}}_k,k=0,1,2,\dots$, the subscript h is also replaced by k correspondingly, such as ${\mathcal{E}}_k$, ${\mathcal{E}}_k^0,{\mathcal{E}}_k^r,{\mathcal{E}}_k^i,{\mathcal{E}}_k^s,{\mathcal{N}}_k,V_k,u_k,{\nabla }_k$ and so on. In addition, for a subset ($\mathcal{M}\subset {\mathcal{T}}_h$), the notation of ${\parallel ·\parallel }_{\mathcal{M}}^2={\sum }_{K\in \mathcal{M}}{\parallel ·\parallel }_{0,K}^2$ is also adopted.

3. Adaptive Algorithm

This section will present an adaptive nonconforming finite element algorithm. To this end, the reliability and efficiency of the a posteriori error estimation should be established. The following a posteriori error estimator for nonconforming FEMs is presented [28,29].

For any $v\in V_h$, define the normal jump across an interior edge (E) as follows:

$$j_n{\left(v\right)|}_E:=〚\mathbf{A}{\nabla }_{h}v{〛}_E·n_E,\forall E\in {\mathcal{E}}_h,$$

(18)

where $n_E$ is the unit normal of E. For any $v\in V_h$, define the tangential jump across an interior edge (E) as follows:

$$j_t{\left(v\right)|}_E:={\tau }_E(〚{\nabla }_{h}v{〛}_E)=〚{\nabla }_{h}v{〛}_E·t_E,\forall E\in {\mathcal{E}}_h,$$

(19)

where $t_E$ is the unit tangential of E.

For $K\in {\mathcal{T}}_h$, define the residual term for $v\in V_h$ as

$$r_h^2(v,K):=h_K^2{\Vert f+\mathrm{div}\left(\mathbf{A}{\nabla }_{h}v\right)\Vert }_{0,K}^2,$$

(20)

where $h_K:={\left|K\right|}^{{\displaystyle \frac{1}{d}}}$. For $K\in {\mathcal{T}}_h$, define the jump term for $v\in V_h$ as

$$J_h^2(v,K):=\sum _{E\subset \partial K}{h}_K{\Vert j_t\left(v\right)\Vert }_{0,E}^2.$$

(21)

The notation of $r_h^2(v,\mathcal{M}):={\sum }_{K\in \mathcal{M}}{r}_h^2(v,K)$ and $J_h^2(v,\mathcal{M}):={\sum }_{K\in \mathcal{M}}{J}_h^2(v,K)$ is adopted for any subset ($\mathcal{M}\subset {\mathcal{T}}_h$). For brevity, $r_h=r_h(u_h,{\mathcal{T}}_h)$ and $J_h=J_h(u_h,{\mathcal{T}}_h)$ are used as shorthand notations.

Lemma 3.

Let $u_h\in V_h$ be the solution of (12) on mesh ${\mathcal{T}}_h$; then, it holds that

$$h_E\parallel j_n\left(u_h\right){\parallel }_{0,E}^2\le C{h}_E^2{\parallel f+\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_h\right)\parallel }_{0,{\Omega }_E}^2,\forall E\in {\mathcal{E}}_h^0,$$

(22)

where C is a positive constant dependent only on the mesh’s shape regularity and polynomial degree.

Proof. 

If $E\in {\mathcal{E}}_h^r$, let ${\psi }_E$ to be the nonconforming element basis function on E. One can see from the definition of $V_h$ that ${\int }_E〚{\psi }_E{〛}_E\mathrm{d}s=0$. Therefore, direct calculations lead to

$$\begin{array}{ccc}\hfill \parallel j_n\left(u_h\right){\parallel }_{0,E}^2& \le & C{\int }_E{\psi }_E{j}_n^2\left(u_h\right)\mathrm{d}s.\hfill \end{array}$$

Notice that the integral of ${\psi }_E$ on $\partial {\omega }_E$ is zero. By using integration by parts and Cauchy–Schwartz inequality and noticing $(\mathbf{A}{\nabla }_h{u}_h·n_E){|}_E$ is a constant, one can obtain

$$\begin{array}{ccc}\hfill {\int }_E{\psi }_E{j}_n^2\left(u_h\right)\mathrm{d}s& =& {\int }_E(〚\mathbf{A}{\nabla }_h{u}_h{〛}_E·n_E)\left({\psi }_E{j}_n\left(u_h\right)\right)\mathrm{d}s\hfill \\ & & +{\int }_{\partial {\omega }_E}(\mathbf{A}{\nabla }_h{u}_h·n_E)\left({\psi }_E{j}_n\left(u_h\right)\right)\mathrm{d}s\hfill \\ & =& {\int }_{{\omega }_E}\mathbf{A}{\nabla }_h{u}_h{\nabla }_h{\psi }_E{j}_n\left(u_h\right)\mathrm{d}x+{\int }_{{\omega }_E}\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_h\right){\psi }_E{j}_n\left(u_h\right)\mathrm{d}x\hfill \\ & =& {\int }_{{\omega }_E}(f+\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_h\right)){\psi }_E{j}_n\left(u_h\right)\mathrm{d}x\hfill \\ & \le & \parallel f+\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_h\right){\parallel }_{0,{\omega }_E}{\parallel {\psi }_E{j}_n\left(u_h\right)\parallel }_{0,{\omega }_E}\hfill \\ & \le & C{h}_E^{1/2}\parallel f+\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_h\right){\parallel }_{0,{\omega }_E}{\parallel j_n\left(u_h\right)\parallel }_{0,E}.\hfill \end{array}$$

Combining the above two inequalities yields the final result (22). If $E\in {\mathcal{E}}_h^i$, then there must exist an element (K) on one side of E with $\overline{K}\cap E=E$. Meanwhile, there must exist two elements ($K_1$ and $K_2$) on the other side of edge E with $\overline{K_1}\cap E=E_1$ and $\overline{K_2}\cap E=E_2$, where $E_1$ and $E_2$ are two son edges of E (see Figure 1). Let ${\psi }_E$ to be the restriction in K of the nonconforming element basis function related to E. Let ${\psi }_E^i$ to be the restriction in $K_i$ of the nonconforming element basis function related to $E_i$, where $i=1,2$. We define

$$\widetilde{{\psi }_E}=\left\{\begin{array}{l}{\psi }_E,\mathrm{in} K\\ {\psi }_E^i,\mathrm{in} K_i,i=1,2.\end{array}\right.$$

It is easy to see from the definition of $V_h$ that ${\int }_E〚\widetilde{{\psi }_E}〛\mathrm{d}s=0$. Therefore, one can similarly obtain (22). If $E\in {\mathcal{E}}_h^s$, then one can consider the father edge of E, denoted by $\tilde{E}$, which belongs to ${\mathcal{E}}_h^i$, and obtain

$$\begin{array}{c}\hfill h_E\parallel j_n\left(u_h\right){\parallel }_{0,E}^2\le h_E\parallel j_n\left(u_h\right){\parallel }_{0,\tilde{E}}^2\le C{h}_E^2{\parallel f+\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_h\right)\parallel }_{0,{\Omega }_E}.\end{array}$$

□

For any $K\in {\mathcal{T}}_h$, we define the error estimator for $v\in V_h$ as

$${\eta }_h^2(v,K):=r_h^2(v,K)+J_h^2(v,K)=h_K^2{\parallel f+\mathrm{div}(\mathbf{A}\nabla v)\parallel }_{0,K}^2+\sum _{E\subset \partial K}{h}_K{\parallel j_t\left(v\right)\parallel }_{0,E}^2.$$

(23)

For any given subset ($\mathcal{M}\subset {\mathcal{T}}_h$), we define

$${\eta }_h^2(v,\mathcal{M}):=\sum _{K\in \mathcal{M}}{\eta }_h^2(v,K).$$

For brevity, ${\eta }_h={\eta }_h(u_h,{\mathcal{T}}_h)$ is set when $v=u_h$ and $\mathcal{M}={\mathcal{T}}_h$. When the mesh is denoted by ${\mathcal{T}}_k$ with an integer of k, the notation of ${\eta }_k(u_k,\mathcal{M})$ is adopted to represent the error estimator over $\mathcal{M}\subset {\mathcal{T}}_k$, while ${\eta }_k$ is used to denote the error estimator over the entire mesh (${\mathcal{T}}_k$).

Lemma 4 (Global upper bound).

There exists a constant ($C_1>0$) depending on the shape regularity of the mesh (${\mathcal{T}}_h$), the polynomial degree, and $\mathit{A}$ such that for the discrete solution ($u_h\in V_h$) of (12), it holds that

$$⫴u-u_h{⫴}_h^2\le C_1{\eta }_h^2.$$

(24)

Proof. 

Based on the result of [29] (see (4.8) in [29]), one can obtain

$$⫴u-u_h{⫴}_h^2\le C\left(\sum _{K\in {\mathcal{T}}_h}{h}_K^2{\Vert f+\mathrm{div}(\mathbf{A}\nabla u_h)\Vert }_{0,K}^2+\sum _{E\in {\mathcal{E}}_h}{h}_E\left(\Vert j_n\left(u_h\right){\Vert }_{0,E\cap \Omega }^2+{\Vert j_t\left(u_h\right)\Vert }_{0,E}^2\right)\right),$$

which, combined with Lemma 3, leads to (24). □

The efficiency of the a posteriori error estimator is subsequently provided. For a non-negative integer (m), let ${\pi }_m^p$ be the $L^p$-best approximation operator on the set of discontinuous polynomials that belong to ${\tilde{P}}_m\left(K\right)$ over $K\in {\mathcal{T}}_h$. For any $\mathcal{M}\subset {\mathcal{T}}_h$, we define the oscillation term as

$$os{c}_h^2\left(\mathcal{M}\right):=\sum _{K\in \mathcal{M}}{h}_K^2{\parallel f+\mathrm{div}(\mathbf{A}\nabla u_h)-{\pi }_{n-2}^2(f+\mathrm{div}(\mathbf{A}\nabla u_h))\parallel }_{L^2\left(K\right)}^2.$$

For rectangular meshes (${\mathcal{T}}_h$), it is easy to see that $\mathrm{div}(\mathbf{A}\nabla u_h){|}_K\in {\tilde{P}}_{n-2}\left(K\right)$ over $K\in {\mathcal{T}}_h$, which means

$$os{c}_h^2\left(\mathcal{M}\right)=\sum _{K\in \mathcal{M}}{h}_K^2{\parallel f-{\pi }_{n-2}^2\left(f\right)\parallel }_{L^2\left(K\right)}^2,\mathcal{M}\subset {\mathcal{T}}_h.$$

However, the above identity is usually incorrect on general quadrilateral meshes, as the term $\mathrm{div}(\mathbf{A}\nabla u_h)$ will not be a polynomial in general. Refer to [30] for more details. The notation of $os{c}_h=os{c}_h\left({\mathcal{T}}_h\right)$ is adopted for brevity. If the mesh is denoted by ${\mathcal{T}}_k$ with an integer of k, $os{c}_k\left(\mathcal{M}\right)$ is also used to stand for the oscillation term over $\mathcal{M}\subset {\mathcal{T}}_k$ and $os{c}_k$ is used to stand for the oscillation term over the entire mesh (${\mathcal{T}}_k$).

Lemma 5 (Lower bound).

There exists a constant ($C_2>0$) depending on the shape regularity of the mesh ${\mathcal{T}}_h$, the polynomial degree, and $\mathit{A}$ such that the discrete solution ($u_h\in V_h$) of (12) satisfies

$$\begin{array}{cc}\hfill h_E{\parallel j_t\left(u_h\right)\parallel }_{0,E}^2& \le C_2{\parallel {\nabla }_h(u-u_h)\parallel }_{0,{\omega }_E}^2,\forall E\in {\mathcal{E}}_h,\hfill \\ \hfill J_h^2& \le C_2⫴u-u_h{⫴}_h^2,\hfill \end{array}$$

(25)

and

$$\begin{array}{cc}\hfill r_h^2(u_h,K)& \le C_2(\parallel {\mathbf{A}}^{{\displaystyle \frac{1}{2}}}\nabla (u-u_h){\parallel }_{L^2\left(K\right)}^2+os{c}_h^2\left(K\right)),\forall K\in {\mathcal{T}}_h,\hfill \\ \hfill r_h^2& \le C_2(⫴u-u_h{⫴}_h^2+os{c}_h^2),\hfill \end{array}$$

(26)

and

$${\eta }_h^2\le C_2(⫴u-u_h{⫴}_h^2+os{c}_h^2).$$

(27)

The above results can be similarly proven by the arguments in [2,4,30,31,32].

The adaptive finite element algorithm based on the aforementioned error estimator is introduced at the end of this section. Moving forward, ${\mathcal{T}}_k$ is also used to represent a mesh (${\mathcal{T}}_h$) with a non-negative integer (k). The same applies to other associated quantities.

Algorithm 2 $\mathcal{ANFEM}$.

Select a Dörfler marking parameter $\theta \in (0,1]$, choose an initial mesh ${\mathcal{T}}_0$, and initialize $k=0$.

(1) Solve the weak formulation as defined in (12) over the current mesh ${\mathcal{T}}_k$ and obtain the discrete solution $u_k$. (2) Compute the error estimator ${\eta }_k(u_k,K)$ for each element $K\in {\mathcal{T}}_k$. (3) Identify a subset ${\mathcal{M}}_k$ of ${\mathcal{T}}_k$ with the smallest possible number of elements that satisfies the condition: $${\eta }_k^2(u_k,{\mathcal{M}}_k)\ge \theta {\eta }_k^2.$$ (28) (4) Apply the local refinement algorithm specified in Algorithm 1 to the marked elements ${\mathcal{M}}_k$ and generate the refined mesh ${\mathcal{T}}_{k+1}$; (5) Set $k:=k+1$ and return to step (1).

4. Convergence

This section investigates the convergence properties of the previously proposed adaptive nonconforming finite element algorithm. To this end, the following error estimator reduction will be established.

Lemma 6 (Estimator reduction).

Let ${\mathcal{T}}_H,{\mathcal{T}}_h$ be two nested 1-irregular meshes and $M_H={\mathcal{T}}_H\setminus {\mathcal{T}}_h$ be the set of refined elements in the coarse mesh (${\mathcal{T}}_H$). Then, there exist constants ($0<\lambda <1$ and $C_6>0$) that depend on the shape regularity of ${\mathcal{T}}_h$ and $\mathbf{A}$ such that

$${\eta }_h^2\left(u_h\right)\le (1+{\delta }_1){\eta }_H^2\left(u_H\right)-\lambda (1+{\delta }_1){\eta }_H^2(u_H,M_H)+C_6(1+{\displaystyle \frac{1}{{\delta }_1}})\parallel {\mathit{A}}^{{\displaystyle \frac{1}{2}}}{\nabla }_h(u_h-u_H){\parallel }_{0,\Omega }^2,$$

(29)

where the ${\delta }_1$ parameter can be any positive number. Moreover, it holds that

$$os{c}_h^2\le os{c}_H^2-\lambda os{c}_H^2\left(M_H\right).$$

(30)

Proof. 

For any $K\in {\mathcal{T}}_h$, one can use a triangle inequality to obtain

$$\begin{array}{ccc}\hfill {\eta }_h(u_h,K)& =& (h_K^2\parallel f+\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_h\right){\parallel }_{0,K}^2+\sum _{E\subset \partial K}{h}_K\parallel {\tau }_E(〚{\nabla }_h{u}_h{〛}_E){\parallel }_{0,E}^2{)}^{{\displaystyle \frac{1}{2}}}\hfill \\ & \le & (h_K^2\parallel f+\mathrm{div}\left(\mathbf{A}{\nabla }_h{u}_H\right){\parallel }_{0,K}^2+\sum _{E\subset \partial K}{h}_K\parallel {\tau }_E(〚{\nabla }_h{u}_H{〛}_E){\parallel }_{0,E}^2{)}^{{\displaystyle \frac{1}{2}}}\hfill \\ & & +h_K\parallel \mathrm{div}\left(\mathbf{A}{\nabla }_h(u_H-u_h)\right){\parallel }_{0,K}+h_K^{{\displaystyle \frac{1}{2}}}\sum _{E\subset \partial K}\parallel {\tau }_E(〚{\nabla }_h(u_h-u_H){〛}_E){\parallel }_{0,E}\hfill \\ & \le & {\eta }_h(u_H,K)+C\parallel {\mathbf{A}}^{{\displaystyle \frac{1}{2}}}{\nabla }_h(u_h-u_H){\parallel }_{0,{\omega }_K}.\hfill \end{array}$$

where the scaling argument is integrated with trace and inverse inequalities to finalize the above estimation process. Employing Young’s inequality with the ${\delta }_1$ parameter, summing over all elements ($K\in {\mathcal{T}}_h$), and capitalizing on the finite overlap of ${\omega }_T$, the following inequality is established.

$${\eta }_h^2\left(u_h\right)\le (1+{\delta }_1){\eta }_h^2\left(u_H\right)+C(1+{\displaystyle \frac{1}{{\delta }_1}})\parallel {\mathbf{A}}^{{\displaystyle \frac{1}{2}}}{\nabla }_h(u_h-u_H){\parallel }_{0,\Omega }^2.$$

For a refined element ($K\in M_H\subset {\mathcal{T}}_H$), let ${\mathcal{T}}_{h,K}:=\{K^{\prime }\in {\mathcal{T}}_h\mid K^{\prime }\subset K\}$. From Lemma 3.1 in [27], one can see that for any $K^{\prime }\in {\mathcal{T}}_{h,K}$,

$$h_{K^{\prime }}={\left|K^{\prime }\right|}^{{\displaystyle \frac{1}{2}}}\le {\chi }^{{\displaystyle \frac{1}{2}}}{h}_K,$$

(31)

with $0<\chi <1$, which yields

$$\begin{array}{ccc}\hfill {\eta }_h^2\left(u_H\right)& =& {\eta }_h^2(u_H,{\mathcal{T}}_H\setminus M_H)+{\eta }_h^2(u_H,M_H)\hfill \\ & \le & {\eta }_H^2(u_H,{\mathcal{T}}_H\setminus M_H)+{\chi }^{{\displaystyle \frac{1}{2}}}{\eta }_H^2(u_H,M_H)\hfill \\ & =& {\eta }_H^2(u_H,{\mathcal{T}}_H)-(1-{\chi }^{{\displaystyle \frac{1}{2}}}){\eta }_H^2(u_H,M_H).\hfill \end{array}$$

Taking $\lambda =1-{\chi }^{{\displaystyle \frac{1}{2}}}$ and combining the above two inequalities leads to (29). Similarly, from the relation (31), one can obtain (30). □

Remark 4.

Similar to (30), for the following result, it also holds that

$${\mu }_h^2\left({\mathcal{T}}_h\right)\le {\mu }_H^2\left({\mathcal{T}}_H\right)-\lambda {\mu }_H^2\left(M_H\right),$$

(32)

by setting ${\mu }_h^2\left(M_h\right)={\sum }_{K\in M_h}{h}_K^2{\parallel f\parallel }_{0,K}^2$ for any subset ($M_h\subset {\mathcal{T}}_h$).

Lemma 7 (Quasi-orthogonality).

Let ${\mathcal{T}}_H,{\mathcal{T}}_h$ be two nested 1-irregular meshes and $M_H={\mathcal{T}}_H\setminus {\mathcal{T}}_h$ be the set of refined elements in the coarse mesh (${\mathcal{T}}_H$). Let $u_H\in V_H$ and $u_h\in V_h$ be the discrete solutions of (12). Then, there exists a constant ($C_3>0$) depending only on the mesh’s shape regularity and $\mathit{A}$ such that

$$(\mathit{A}{\nabla }_h(u-u_h),{\nabla }_h(u_h-u_H))\le C_{3}os{c}_H\left(M_H\right)⫴u-u_h{⫴}_h.$$

(33)

Proof. 

Using (12), Green’s formula, and Lemma 2, one can obtain

$$\begin{array}{cc}\hfill & a_h(u-u_h,u_h-u_H)\hfill \\ \hfill & =a_h({\Pi }_{h}u-u_h,u_h-u_H)\hfill \\ \hfill & =(f,{\Pi }_{h}u-u_h)-a_h(u_H,{\Pi }_{h}u-u_h)\hfill \\ \hfill & =(f,{\Pi }_{h}u-u_h)-a_h(u_H,{\Pi }_H({\Pi }_{h}u-u_h))-a_h(u_H,(I-{\Pi }_H)({\Pi }_{h}u-u_h))\hfill \\ \hfill & =(f,(I-{\Pi }_H)({\Pi }_{h}u-u_h))-a_h(u_H,(I-{\Pi }_H)({\Pi }_{h}u-u_h))\hfill \\ \hfill & =(f-{\pi }_{n-2}^{2}f,(I-{\Pi }_H)({\Pi }_{h}u-u_h))\hfill \end{array}$$

(34)

where (9) and (16) are used in the last step.

Inserting a Cauchy–Schwartz inequality, the approximate property, (15), and (14) into the above identity leads to

$$\begin{array}{ccc}\hfill a_h(u-u_h,u_h-u_H)& \le & C\sum _{K\in M_H}\parallel f-{\pi }_{n-2}^2{f\parallel }_{0,K}{\parallel (I-{\Pi }_H)({\Pi }_{h}u-u_h)\parallel }_{0,K}\hfill \\ & \le & C\sum _{K\in M_H}{h}_K\parallel f-{\pi }_{n-2}^2{f\parallel }_{0,K}{\parallel {\nabla }_h({\Pi }_{h}u-u_h)\parallel }_{0,K}\hfill \\ & \le & Cos{c}_H\left(M_H\right){\parallel {\nabla }_h\left({\Pi }_h(u-u_h)\right)\parallel }_{0,\Omega }\hfill \\ & \le & Cos{c}_H\left(M_H\right){\parallel {\nabla }_h(u-u_h)\parallel }_{0,\Omega }.\hfill \end{array}$$

□

Remark 5.

Notice that the quasi-orthogonality (33) is a new result compared with quasi-orthogonality results of nonconforming finite elements in the literature [16,19]. Since $os{c}_H^2\left(M_H\right)\le {\mu }_H^2\left(M_H\right)$, it is easy to deduce the following result from (33):

$$(\mathit{A}{\nabla }_h(u-u_h),{\nabla }_h(u_h-u_H))\le C_3{\mu }_H\left(M_H\right)⫴u-u_h{⫴}_h$$

(35)

which was the quasi-orthogonality result obtained in the literature.

The convergence of the adaptive Algorithm 2 will be established next. Before that, a total error is defined as follows:

$$e\left({\mathcal{T}}_k\right):=⫴u-u_k{⫴}_k^2+{\beta }_1{\eta }_k^2+{\beta }_{2}os{c}_k^2,k\in \mathbb{N}.$$

(36)

Theorem 1.

Let ${\left\{{\mathcal{T}}_k\right\}}_{k\ge 0}$ be the sequence of 1-irregular meshes generated by the Algorithm 2, and let ${\left\{u_k\right\}}_{k\ge 0}$ be the corresponding sequence of discrete solutions of (12). Then, there exist constants (${\beta }_1$, ${\beta }_2>0$, and $\rho <1$) depending on the mesh’s shape regularity, polynomial degree, marking parameter ($0<\theta \le 1$), and $\mathit{A}$ such that for all $k=1,2,\dots$,

$$e\left({\mathcal{T}}_{k+1}\right)\le \rho e\left({\mathcal{T}}_k\right),$$

(37)

Proof. 

From Lemma 7 and Young’s inequality, one can obtain

$$\begin{array}{ccc}\hfill ⫴u-u_{k+1}{⫴}_{k+1}^2& =& ⫴u-u_k{⫴}_k^2-⫴u_{k+1}-u_k{⫴}_{k+1}^2-2(\mathbf{A}{\nabla }_{k+1}(u-u_{k+1}),{\nabla }_{k+1}(u_{k+1}-u_k))\hfill \\ & \le & ⫴u-u_k{⫴}_k^2+{\delta }_2⫴u-u_{k+1}{⫴}_{k+1}^2+{\displaystyle \frac{C_3^2}{{\delta }_2}}os{c}_k^2\left(M_k\right)-⫴u_{k+1}-u_k{⫴}_{k+1}^2,\hfill \end{array}$$

where the above constant ($0<{\delta }_2<1$) is to be determined in the subsequent analysis.

It follows from (29) and (30) that

$$\begin{array}{cc} & \left(1-{\delta }_2\right)⫴u-u_{k+1}{⫴}_{k+1}^2+{\beta }_1{\eta }_{k+1}^2+{\beta }_{2}os{c}_{k+1}^2\hfill \\ \le & ⫴u-u_k{⫴}_k^2+{\beta }_1(1+{\delta }_1){\eta }_k^2-{\beta }_1\lambda (1+{\delta }_1){\eta }_k^2(u_k,M_k)\hfill \\ & -\left(1-{\beta }_1{C}_6(1+{\displaystyle \frac{1}{{\delta }_1}})\right)⫴u_{k+1}-u_k{⫴}_{k+1}^2+{\beta }_{2}os{c}_k^2-\left({\beta }_2\lambda -{\displaystyle \frac{C_3^2}{{\delta }_2}}\right)os{c}_k^2\left(M_k\right).\hfill \end{array}$$

Setting

$${\beta }_1={\displaystyle \frac{1}{C_6(1+\frac{1}{{\delta }_1})}}$$

(38)

and

$${\beta }_2={\displaystyle \frac{C_3^2}{{\delta }_2\lambda }},$$

(39)

together with the Döfler marking strategy (28) and the upper bound (24), yields

$$\begin{array}{cc} & \left(1-{\delta }_2\right)⫴u-u_{k+1}{⫴}_{k+1}^2+{\beta }_1{\eta }_{k+1}^2+{\beta }_{2}os{c}_{k+1}^2\hfill \\ \le & ⫴u-u_k{⫴}_k^2+{\beta }_1(1+{\delta }_1){\eta }_k^2+{\beta }_{2}os{c}_k^2-{\beta }_1\lambda (1+{\delta }_1){\eta }_k^2(u_k,M_k)\hfill \\ \le & ⫴u-u_k{⫴}_k^2+{\beta }_1(1+{\delta }_1){\eta }_k^2+{\beta }_{2}os{c}_k^2-{\beta }_1\lambda (1+{\delta }_1)\theta {\eta }_k^2\hfill \\ \le & \left(1-{\displaystyle \frac{{\beta }_1\lambda \theta (1+{\delta }_1)}{3C_1}}\right)⫴u-u_k{⫴}_k^2+{\beta }_1(1+{\delta }_1)\left(1-{\displaystyle \frac{\lambda \theta }{3}}\right){\eta }_k^2+{\beta }_2\left(1-{\displaystyle \frac{{\beta }_1\lambda \theta (1+{\delta }_1)}{3{\beta }_2}}\right)os{c}_k^2.\hfill \end{array}$$

In order to obtain (37), the following conditions need to be further verified:

$$1-{\displaystyle \frac{{\beta }_1\lambda \theta (1+{\delta }_1)}{3C_1}}<1-{\delta }_2,\mathrm{and} 0<{\delta }_2<1;$$

(40)

$$(1+{\delta }_1)\left(1-{\displaystyle \frac{\lambda \theta }{3}}\right)<1,\mathrm{and} {\delta }_1>0.$$

(41)

(40) is equivalent to

$$0<{\delta }_2<min\left(1,{\displaystyle \frac{{\beta }_1\lambda \theta (1+{\delta }_1)}{3C_1}}\right),$$

(42)

and (41) is equivalent to

$$0<{\delta }_1<{\displaystyle \frac{\lambda \theta }{3-\lambda \theta }},$$

(43)

The selection of the ${\delta }_1$, ${\beta }_1$, ${\delta }_2$, and ${\beta }_2$ parameters according to (43), (38), (42), and (39), respectively, finalizes the proof. □

5. Quasi-Optimality

Before establishing the optimality of Algorithm 2, the following discrete upper bound needs to be provided.

Lemma 8 (Discrete upper bound).

Let ${\mathcal{T}}_H,{\mathcal{T}}_h$ be two nested 1-irregular meshes and $M_H={\mathcal{T}}_H\setminus {\mathcal{T}}_h$ be the set of refined elements in the coarse mesh (${\mathcal{T}}_H$). Let $u_H\in V_H$ and $u_h\in V_h$ be two solutions of (12) on ${\mathcal{T}}_H$ and ${\mathcal{T}}_h$, respectively. Then, there exist two positive constants ($C_4$ and $C_5$) dependent only on the mesh’s shape regularity and $\mathit{A}$ such that

$$\#M_H\le C_4(\#{\mathcal{T}}_h-\#{\mathcal{T}}_H).$$

(44)

and

$$⫴u_h-u_H{⫴}_h^2\le C_5(os{c}_H^2\left(M_H\right)+J_H^2(u_H,M_H))$$

(45)

Proof. 

(44) is a direct conclusion, and only (45) is proven here. For any $v_h\in V_h$, the following results can be derived:

$$\begin{array}{cc}\hfill ⫴u_h-u_H{⫴}_h^2& =a_h(u_h-u_H,u_h-v_h)+a_h(u_h-u_H,v_h-u_H)\hfill \\ \hfill & =(f,u_h-v_h)-a_h(u_H,u_h-v_h)+a_h(u_h-u_H,v_h-u_H)\hfill \\ \hfill & =(f,(I-{\Pi }_H)(u_h-v_h))-a_h(u_H,(I-{\Pi }_H)(u_h-v_h))\hfill \\ \hfill & +a_h(u_h-u_H,v_h-u_H)\hfill \\ \hfill & =(f-{\pi }_{n-2}^{2}f,(I-{\Pi }_H)(u_h-v_h))+a_h(u_h-u_H,v_h-u_H).\hfill \end{array}$$

(46)

where (9) and (16) are used in the last step. Let $v_h=P_h{u}_H$ be the projection of $u_H$ on space $V_h$. From (17), one can fin that $\mathbf{A}{\nabla }_h(P_h{u}_H-u_H)=\nabla \times {\psi }_h$, where ${\psi }_h$ is a conforming $Q_1$ function with respect to mesh ${\mathcal{T}}_h$. It is easy to see from the definition of $P_h{u}_H$ that

$$a_h(u_h,P_h{u}_H-u_H)=0.$$

(47)

Let $L_H^c$ represent the standard Lagrange interpolation operator of the conforming $Q_1$ space with respect to mesh ${\mathcal{T}}_H$. By integrating by parts and leveraging the weak continuity of $u_H$, one can find that

$$({\nabla }_H{u}_H,\nabla \times \left(L_H^c{\psi }_h\right))=\sum _{E\in {\mathcal{E}}_H}{\int }_E〚u_H{〛}_E(\nabla L_H^c{\psi }_h·t_E)\mathrm{d}s=0.$$

(48)

Combining (46)–(48) leads to

$$\begin{array}{cc}\hfill ⫴u_h-u_H{⫴}_h^2& =(f-{\pi }_{n-2}^{2}f,(I-{\Pi }_H)(u_h-P_h{u}_H))-({\nabla }_H{u}_H,\nabla \times ({\psi }_h-L_H^c{\psi }_h)).\hfill \end{array}$$

(49)

Using Cauchy–Schwartz inequality, the approximation property of interpolation operator (15) and the triangular inequality, one can obtain

$$\begin{array}{cc}\hfill & (f-{\pi }_{n-2}^{2}f,(I-{\Pi }_H)(u_h-P_h{u}_H))\hfill \\ \hfill & \le C\sum _{K\in {\mathcal{T}}_H\setminus {\mathcal{T}}_h}{h}_K\parallel f-{\pi }_{n-2}^2{f\parallel }_{0,K}{\parallel {\nabla }_h(u_h-P_h{u}_H)\parallel }_{0,K}\hfill \\ \hfill & \le Cos{c}_H\left(M_H\right){\parallel {\nabla }_h(u_h-P_h{u}_H)\parallel }_{0,\Omega }\hfill \end{array}$$

(50)

By integration by parts and using the approximation property of $L_H^c$, one can obtain

$$\begin{array}{cc}\hfill & ({\nabla }_H{u}_H,\nabla \times ({\psi }_h-L_H^c{\psi }_h))\hfill \\ \hfill & =\sum _{E\subset \partial K,K\in {\mathcal{T}}_H\setminus {\mathcal{T}}_h}{\int }_E〚{\nabla }_H{u}_H〛·t_E({\psi }_h-L_H^c{\psi }_h)\mathrm{d}s\hfill \\ \hfill & \le C\sum _{E\subset \partial K,K\in {\mathcal{T}}_H\setminus {\mathcal{T}}_h}{h}_E^{{\displaystyle \frac{1}{2}}}\parallel 〚{\nabla }_H{u}_H〛·t_E{\parallel }_{0,E}{\parallel \nabla {\psi }_h\parallel }_{0,{\Omega }_E}\hfill \\ \hfill & \le C{J}_H(u_H,M_H){\parallel \mathbf{A}{\nabla }_h(P_h{u}_H-u_H)\parallel }_{0,\Omega }\hfill \end{array}$$

(51)

By integration by parts, one can derive

$$({\nabla }_h(u_h-P_h{u}_H),\mathbf{A}{\nabla }_h(P_h{u}_H-u_H))=\sum _{E\in {\mathcal{E}}_h^0}{\int }_E〚(u_h-P_h{u}_H)〛(\nabla \times {\psi }_h)·n_E\mathrm{d}s=0,$$

which means

$$\parallel {\mathbf{A}}^{{\displaystyle \frac{1}{2}}}{\nabla }_h(u_h-P_h{u}_H){\parallel }_{0,\Omega }^2+\parallel {\mathbf{A}}^{{\displaystyle \frac{1}{2}}}{\nabla }_h(P_h{u}_H-u_H){\parallel }_{0,\Omega }^2=\parallel {\mathbf{A}}^{{\displaystyle \frac{1}{2}}}{\nabla }_h(u_h-u_H){\parallel }_{0,\Omega }^2.$$

Combining the above identity with (49)–(51) leads to the final result (45). □

Remark 6.

Notice that the discrete upper bound (45) is a new result compared with discrete upper-bound results of nonconforming finite elements in the literature [16,19]. From (45), it is easy to obtain the following result:

$$⫴u_h-u_H{⫴}_h^2\le C_5{\eta }_H^2(u_H,M_H),$$

(52)

which is the discrete upper bound obtained in the literature [16,19].

To express the optimal complexity, several notations from nonlinear approximation theory are utilized, as developed in the works reported in [12,33]. Let ${\mathcal{H}}_N$ represent the collection of all triangulations $\mathcal{T}$ where the cardinality is $\#\mathcal{T}\le N$.

The approximation class is defined as

$${\mathcal{W}}^s:=\{(u,f)\in (H_0^1(\Omega ),L^2(\Omega )):{\parallel (u,f)\parallel }_{{\mathcal{W}}^s}<+\infty \}$$

(53)

with

$${\parallel (u,f)\parallel }_{{\mathcal{W}}^s}:=\underset{N\ge N_0}{sup}{(N-N_0)}^s\underset{{\mathcal{T}}_h\in {\mathcal{H}}_N}{inf}\left(⫴u-u_h{⫴}_h^2+os{c}_h^2\right).$$

(54)

Remark 7.

It is known that $r_h^2\le {\eta }_h^2\le C_2(⫴u-u_h{⫴}_h^2+os{c}_h^2)$. Hence, $os{c}_h$ in (54) can be equivalently replaced by $r_h$, i.e., one can equivalently redefine the norm (54) as

$${\parallel (u,f)\parallel }_{{\mathcal{W}}^s}:=\underset{N\ge N_0}{sup}{(N-N_0)}^s\underset{{\mathcal{T}}_h\in {\mathcal{H}}_N}{inf}\left(⫴u-u_h{⫴}_h^2+r_h^2\right)$$

(55)

and

$${\parallel (u,f)\parallel }_{{\mathcal{W}}^s}:=\underset{N\ge N_0}{sup}{(N-N_0)}^s\underset{{\mathcal{T}}_h\in {\mathcal{H}}_N}{inf}\left(⫴u-u_h{⫴}_h^2+{\eta }_h^2\right)$$

(56)

and

$${\parallel (u,f)\parallel }_{{\mathcal{W}}^s}:=\underset{N\ge N_0}{sup}{(N-N_0)}^s\underset{{\mathcal{T}}_h\in {\mathcal{H}}_N}{inf}\left(⫴u-u_h{⫴}_h^2+{\eta }_h^2+os{c}_h^2\right)$$

(57)

An AFEM is said to realize optimal convergence rates when, for any $(u,f)\in {\mathcal{W}}^s$, it generates a triangulation (${\mathcal{T}}_k$) with a cardinality of $\#{\mathcal{T}}_k$ alongside a corresponding approximation ($u_k$) such that

$$⫴u-u_k{⫴}_k^2+os{c}_k^2\le C{(\#{\mathcal{T}}_k-\#{\mathcal{T}}_0)}^{-s}.$$

(58)

The following lemma emphasizes the intrinsic relationship between Dörfler marking (28), the set of refined elements, and the total error reduction.

Lemma 9.

Let ${\mathcal{T}}_H$ be the coarse mesh, and let ${\mathcal{T}}_h$ be the refined mesh obtained from ${\mathcal{T}}_H$ based on the set of elements marked for refinement ($M_H={\mathcal{T}}_H\setminus {\mathcal{T}}_h$). Under the hypothesis that

$$⫴u-u_h{⫴}_h^2+os{c}_h^2\le {\chi }^{\prime }(⫴u-u_H{⫴}_H^2+os{c}_H^2),$$

(59)

for some $0<{\chi }^{\prime }<{\displaystyle \frac{1}{2}}$, there exists $0<{\theta }^{\prime }<1$ such that

$${\eta }_H^2(u_H,M_H)\ge {\theta }^{\prime }{\eta }_H^2\left(u_H\right).$$

(60)

Proof. 

Combining the global lower bound (27) and (59) yields

$$\begin{array}{cc} & {\displaystyle \frac{1-2{\chi }^{\prime }}{C_2}}{\eta }_H^2\left(u_H\right)\hfill \\ \le & (1-2{\chi }^{\prime })(⫴u-u_H{⫴}_H^2+os{c}_H^2)\hfill \\ \le & ⫴u-u_H{⫴}_H^2+os{c}_H^2-2⫴u-u_h{⫴}_h^2-2os{c}_h^2\hfill \\ =& ⫴u_H-u_h{⫴}_h^2+2(\mathbf{A}{\nabla }_h(u-u_h),{\nabla }_h(u_H-u_h))-⫴u-u_h{⫴}_h^2+os{c}_H^2-2os{c}_h^2.\hfill \end{array}$$

The second term on the right-hand side of the inequality can be controlled by quasi-orthogonality (33), i.e.,

$$\begin{array}{cc} & 2(\mathbf{A}{\nabla }_h(u-u_h),{\nabla }_h(u_H-u_h))-⫴u-u_h{⫴}_h^2\hfill \\ \le & 2C_3{r}_H\left(M_H\right)⫴u-u_h{⫴}_h-⫴u-u_h{⫴}_h^2\hfill \\ \le & C_3^2{r}_H^2\left(M_H\right)\hfill \\ \le & C_3^2{\eta }_H^2(u_H,M_H),\hfill \end{array}$$

(61)

where the last step applies the Cauchy–Schwartz inequality. Furthermore,

$$\begin{array}{ccc}\hfill os{c}_H^2-2os{c}_h^2& \le & os{c}_H^2-os{c}_h^2\le os{c}_H^2\left(M_H\right)\le {\eta }_H^2(u_H,M_H).\hfill \end{array}$$

(62)

Combining (61), (62), and the discrete upper bound (45) leads to

$$\begin{array}{c}\hfill {\displaystyle \frac{1-2{\chi }^{\prime }}{C_2}}{\eta }_H^2\left(u_H\right)\le (C_5+C_3^2+1){\eta }_H^2(u_H,M_H),\end{array}$$

Taking ${\theta }^{\prime }={\displaystyle \frac{1-2{\chi }^{\prime }}{C_2(C_5+C_3^2+1)}}$ completes the proof. □

Theorem 2.

Assume $(u,f)\in {\mathcal{W}}^s$. A sequence of meshes, denoted by ${\left\{{\mathcal{T}}_k\right\}}_{k\ge 0}$, is generated by the $\mathcal{ANFEM}$ algorithm. Corresponding to these meshes, there are sequences of finite element spaces (${\left\{V_k\right\}}_{k\ge 0}$) and their respective solutions (${\left\{u_k\right\}}_{k\ge 0}$). The error measure (${\epsilon }_k$) is defined as ${\epsilon }_k:=⫴u-u_k{⫴}_k^2+os{c}_k^2$. Under the assumption that the marking parameter (θ) satisfies

$$0<\theta <{\displaystyle \frac{1}{C_2(C_4+C_3^2+1)}},$$

(63)

where $C_2$, $C_3$, and $C_4$ are constants, as already introduced, the following complexity estimate of the $\mathcal{ANFEM}$ algorithm holds: there exists a constant (C) depending on the mesh’s shape regularity, polynomial degree, marking parameter ($0<\theta \le 1$), and $\mathit{A}$ such that

$$\#{\mathcal{T}}_k-\#{\mathcal{T}}_0\le C{\epsilon }_k^{-1/s}.$$

(64)

Proof. 

Based on the assumption of $(u,f)\in {\mathcal{W}}^s$, there exists a mesh (${\mathcal{T}}_{h^{\prime }}\in \mathcal{H}$) such that for $\chi >0$ to be chosen, the following must hold:

$$⫴u-u_{h^{\prime }}{⫴}_{h^{\prime }}^2+os{c}_{h^{\prime }}^2\le \chi (⫴u-u_k{⫴}_k^2+os{c}_k^2)$$

(65)

and

$$\#{\mathcal{T}}_{h^{\prime }}-\#{\mathcal{T}}_0\le {\parallel (u,f)\parallel }_{{\mathcal{W}}^s}^{1/s}{\chi }^{-1/s}{(⫴u-u_k{⫴}_k^2+os{c}_k^2)}^{-1/s}.$$

(66)

Let ${\mathcal{T}}_{h^{*}}\in \mathcal{H}$ be the refinement of ${\mathcal{T}}_k$ with a minimal number of elements such that ${\mathcal{T}}_{h^{*}}$ is a refinement of ${\mathcal{T}}_{h^{\prime }}$. Then, one can obtain

$$\#{\mathcal{T}}_{h^{*}}-\#{\mathcal{T}}_k\le \#{\mathcal{T}}_{h^{\prime }}-\#{\mathcal{T}}_0.$$

From the quasi-orthogonality (33), Young’s inequality, and the global lower bound (27), one can obtain

$$⫴u-u_{h^{*}}{⫴}_{h^{*}}^2+os{c}_{h^{*}}^2\le C^{\prime }(⫴u-u_{h^{\prime }}{⫴}_{h^{\prime }}^2+os{c}_{h^{\prime }}^2)\le C^{\prime }\chi (⫴u-u_k{⫴}_k^2+os{c}_k^2),$$

with constant $C^{\prime }$ dependent on $C_3$ and $C_2$. $C^{\prime }\chi <{\displaystyle \frac{1}{2}}$ is set by choosing $\chi$. Let $M^{*}\subset {\mathcal{T}}_k$ be the set of refined elements in the coarse mesh (${\mathcal{T}}_k$) in order to obtain ${\mathcal{T}}_{h^{*}}$. Based on Lemma 9, there exists $0<\theta <{\displaystyle \frac{1}{C_2(C_4+C_3^2+1)}}$ such that

$${\eta }_k^2(u_k,M^{*})\ge \theta {\eta }_k^2.$$

(67)

Since ${\mathcal{M}}_k$ in the Dörfler marking strategy is chosen to be the set with minimal cardinality satisfying (67), it is easy to find that

$$\#{\mathcal{M}}_k\le \#M^{*}\le C_5(\#{\mathcal{T}}_{h^{*}}-\#{\mathcal{T}}_k)\le C{\epsilon }_k^{-1/s}.$$

(68)

Notice the expression of (36) and let $e_k=e\left({\mathcal{T}}_k\right)$ for simplicity. Since $e_k$ is equivalent to ${\epsilon }_k$, one can see from Theorem 1 that there exists a constant (C) such that, with $0<\rho <1$,

$${\epsilon }_k\le C{\rho }^{k-l}{\epsilon }_l,0\le l\le k.$$

(69)

Together with Lemma 1, this implies that

$$\begin{array}{ccc}\hfill \#{\mathcal{T}}_k-\#{\mathcal{T}}_0& \le & C\sum _{l=0}^{k-1}\#{\mathcal{M}}_l\le C\sum _{l=0}^{k-1}{\epsilon }_l^{-1/s}\hfill \\ & \le & C\left(\sum _{l=0}^{k-1}{\rho }^{(k-l)/s}\right){\epsilon }_k^{-1/s}\le {\displaystyle \frac{C}{1-{\rho }^{1/s}}}{\epsilon }_k^{-1/s}.\hfill \end{array}$$

This completes the proof. □

6. Numerical Examinations

Numerical experiments with the $\mathcal{ANFEM}$ are presented here. In this section, the adaptive Lin–Tobiska–Zhou(LTZ) element method is used in numerical experiments. The number of DOFs in the finest mesh exceeds 10 million in all numerical examples.

Example 1 (Crack problem).

The domain (Ω) is given by $\Omega =\left\{\right|x|+|y|<1\}\setminus \{0\le x\le 1, y=0\}$. In this domain, the solution (u) adheres to the Poisson equation:

$$\begin{array}{c}\hfill -▵u=1,\mathit{in}\Omega \mathit{and}u=g\mathit{on}\partial \Omega .\end{array}$$

By selecting g appropriately, the exact solution u can be expressed in polar coordinates as follows:

$$\begin{array}{c}\hfill u(r,\theta )=r^{{\displaystyle \frac{1}{2}}}sin{\displaystyle \frac{\theta }{2}}-{\displaystyle \frac{1}{4}}{r}^2.\end{array}$$

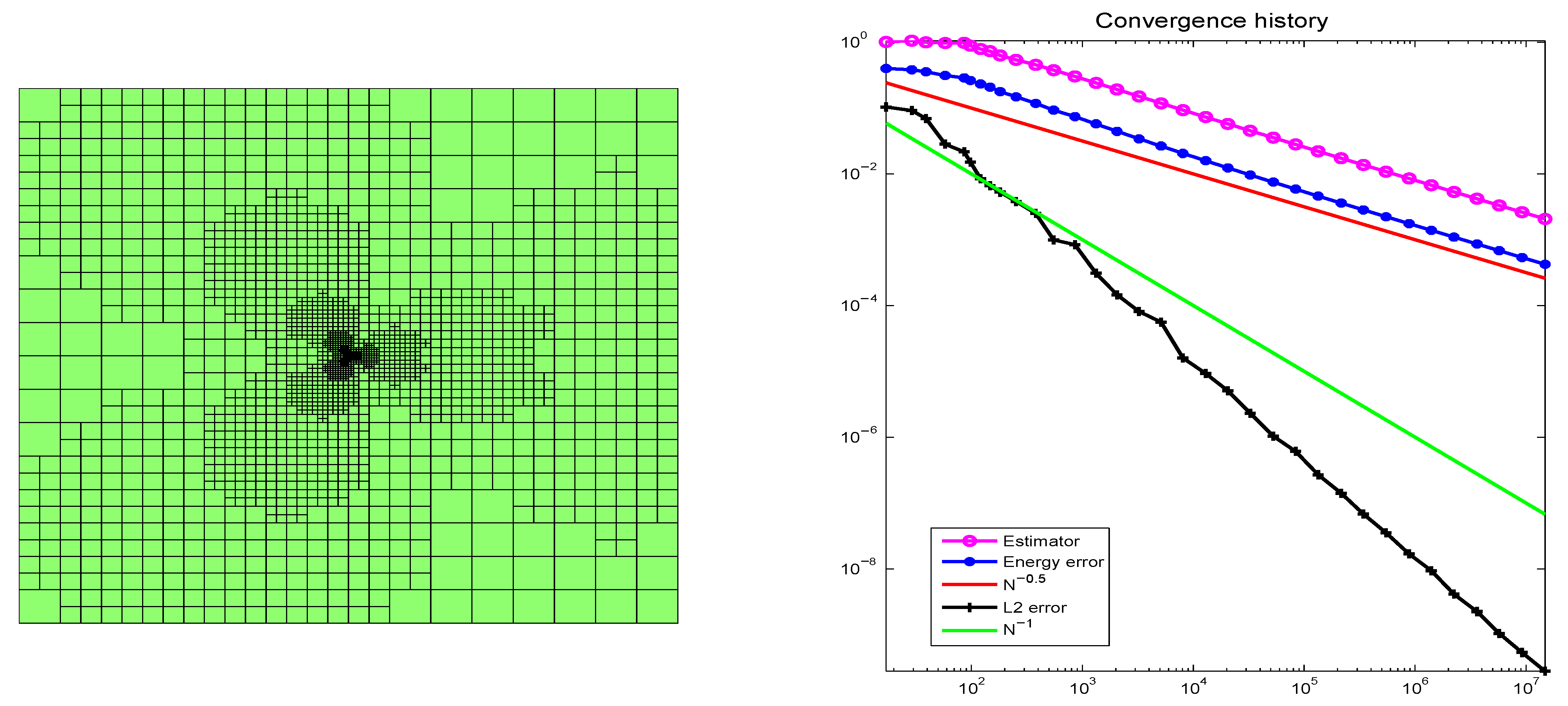
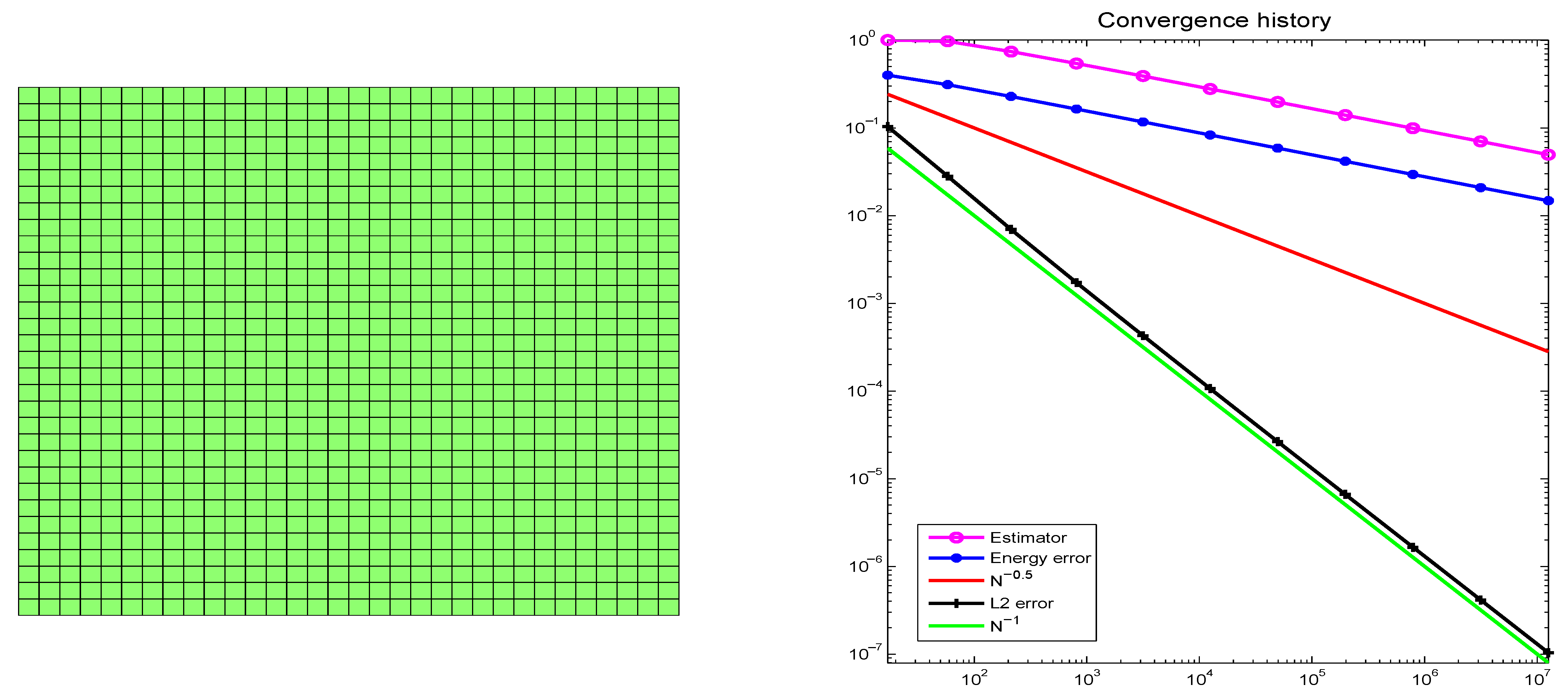
The two pictures in Figure 2 are the 17th-level adaptive mesh generated by the LTZ element method and the corresponding convergence history of the $\mathcal{ANFEM}$ with 14,823,276 DOFs in the final mesh. The two pictures in Figure 3 are the 4th-level uniform mesh generated by the LTZ element method and the corresponding convergence history with 12,588,032 DOFs in the final mesh. Obviously, the adaptive LTZ element method is optimally convergent, while the LTZ element method with uniform refinement is not.

Example 2 (Kellogg problem).

Consider the following elliptic problem with piecewise constant coefficients and a vanishing right-hand side (f). Let $\Omega ={(-1,1)}^2$, $\mathit{A}=RI$ in the first and third quadrants and $\mathit{A}=I$ in the second and fourth quadrants, where R is a constant to be specified later. The problem is defined as follows:

$$\begin{array}{c}\hfill -\mathit{div}(\mathit{A}\nabla u)=0,\mathit{in}\Omega \mathit{and}u=g_D\mathit{on}\partial \Omega .\end{array}$$

The boundary function ($g_D$) is chosen to match an exact solution (u), which is expressed in polar coordinates as follows: $u(r,\varphi )=r^{\tau }\nu \left(\varphi \right)$, where

$$\nu \left(\varphi \right)=\left\{\begin{array}{cc}cos\left(({\displaystyle \frac{\pi }{2}}-\sigma )\tau \right)·cos\left((\varphi -{\displaystyle \frac{\pi }{2}}+\rho )\tau \right),\hfill & \mathit{if}0\le \varphi \le {\displaystyle \frac{\pi }{2}},\hfill \\ cos\left(\rho \tau \right)·cos\left(\right(\varphi -\pi +\sigma \left)\tau \right),\hfill & \mathit{if}{\displaystyle \frac{\pi }{2}}\le \varphi \le \pi ,\hfill \\ cos\left(\sigma \tau \right)·cos\left(\right(\varphi -\pi +\rho \left)\tau \right),\hfill & \mathit{if}\pi \le \varphi \le {\displaystyle \frac{3\pi }{2}},\hfill \\ cos\left(({\displaystyle \frac{\pi }{2}}-\rho )\tau \right)·cos\left((\varphi -{\displaystyle \frac{3\pi }{2}}-\sigma )\tau \right),\hfill & \mathit{if}{\displaystyle \frac{3\pi }{2}}\le \varphi \le 2\pi .\hfill \end{array}\right.$$

The τ, ρ, and σ parameters satisfy the following nonlinear relationships:

$$\left\{\begin{array}{c}R=-tan\left(({\displaystyle \frac{\pi }{2}}-\sigma )\tau \right)·\left(\rho \tau \right),\hfill \\ 1/R=-tan\left(\rho \tau \right)·cot\left(\sigma \tau \right),\hfill \\ R=-tan\left(\sigma \tau \right)·cot({\displaystyle \frac{\pi }{2}}-\rho )\tau ),\hfill \\ 0<\tau <2,\hfill \\ max\{0,\pi \tau -\pi \}<2\tau \rho <min\{\pi \tau ,\pi \},\hfill \\ max\{0,\pi -\pi \tau \}<-2\tau \sigma <min\{\pi \tau ,2\pi -\pi \tau \}.\hfill \end{array}\right.$$

(70)

The solution of u belongs to space $H^{1+s}$ with $s<\tau$. For $\tau =0.1$, solving the above nonlinear equation (Equation (70)) yields

$$R\approx 161.4476387975881,\rho ={\displaystyle \frac{\pi }{4}},\sigma \approx -14.92256510455152.$$

This problem is first solved using the error estimator (23) (called the old estimator hereafter) by the $\mathcal{ANFEM}$ with the LTZ element method. Second, this problem is solved using a modified posteriori error estimator (called the new estimator hereafter) by the $\mathcal{ANFEM}$ with the LTZ element method. For any $v\in V_h$ and any $K\in {\mathcal{T}}_h$, the new estimator is defined as

$$\begin{array}{cc}\hfill {\tilde{\eta }}_{\ell }^2(v,K)& :={\lambda }_K^{-{\displaystyle \frac{1}{2}}}{h}_K^2{\Vert f+\mathrm{div}(\mathbf{A}\nabla v)\Vert }_{L^2\left(K\right)}^2+{\Lambda }_E^{{\displaystyle \frac{1}{2}}}{h}_K\sum _{E\subset \partial K}\Vert 〚\mathbf{A}\nabla v〛·t_E{\Vert }_{0,E}^2,\hfill \end{array}$$

(71)

where

$${\lambda }_K:=\underset{K^{\prime }\subset {\Omega }_K}{min}\mathbf{A}{|}_{K^{\prime }},{\Lambda }_K:=\underset{K^{\prime }\subset {\Omega }_K}{max}\mathbf{A}{|}_{K^{\prime }},{\Lambda }_E:=\underset{K\subset {\omega }_E}{max}{\Lambda }_K.$$

For this new estimator, the following reliability result holds:

$$\begin{array}{c}\hfill \parallel {\mathbf{A}}^{{\displaystyle \frac{1}{2}}}\nabla (u-u_h){\parallel }_{0,\Omega }^2\le C_m{\tilde{\eta }}_h^2(u_h,{\mathcal{T}}_h),\end{array}$$

(72)

where $C_m$ is a constant dependent only on the shape regularity of mesh ${\mathcal{T}}_h$ and independent of $\mathbf{A}$.

The Dörfler parameter is $\theta =0.8$ in all adaptive finite element computations for the Kellogg problem.

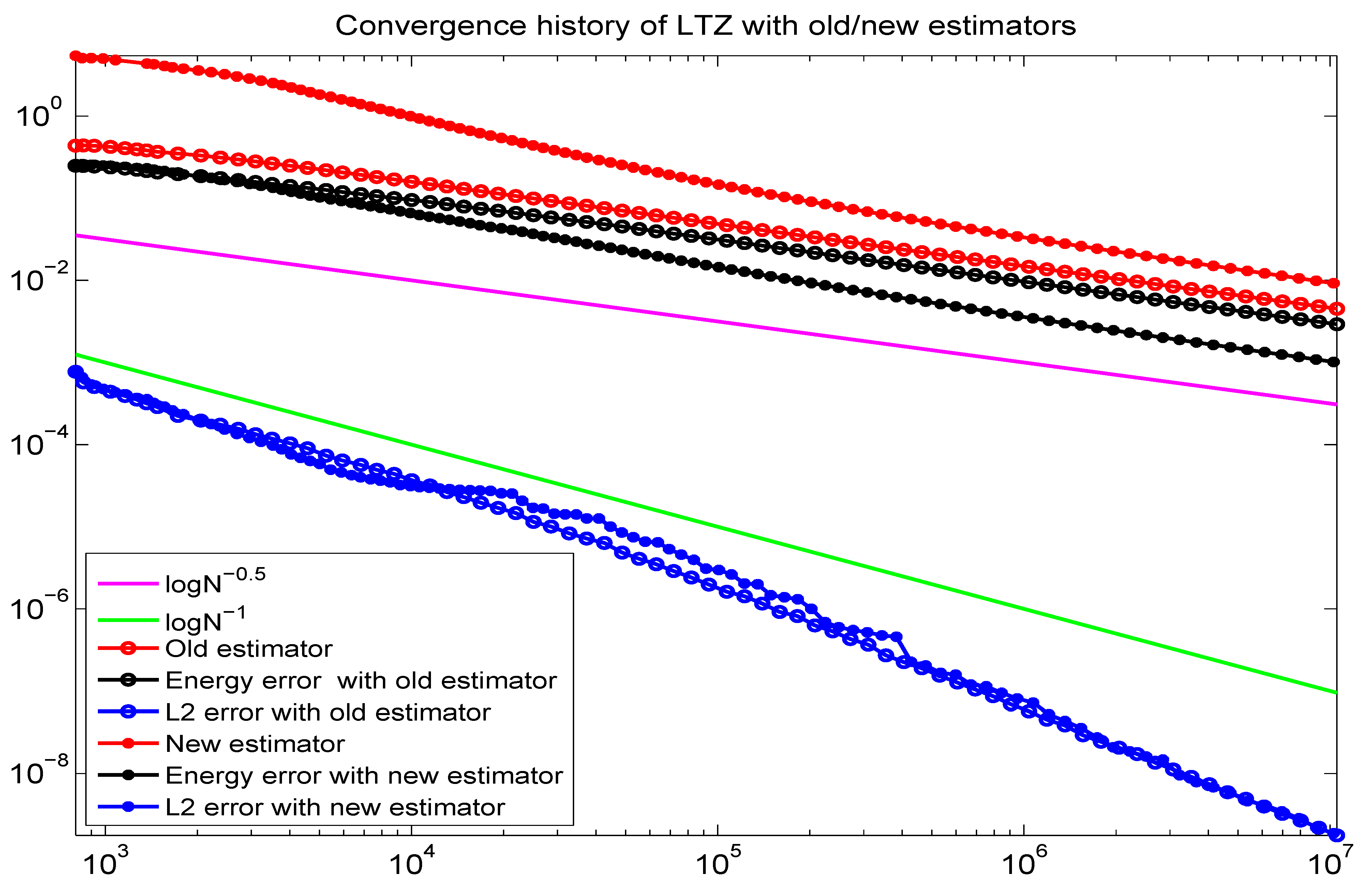
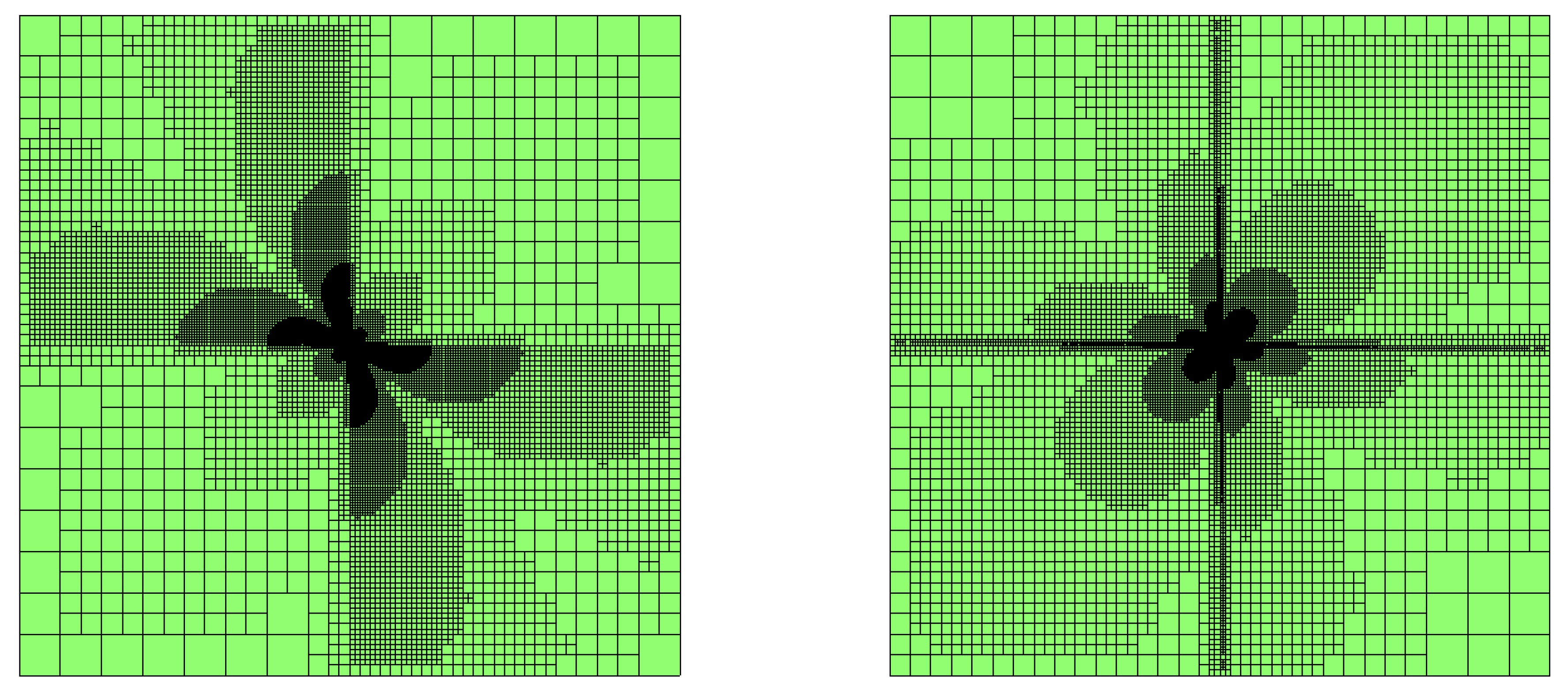
Figure 4 shows the convergence history of the $\mathcal{ANFEM}$ with the LTZ element method using the old estimator and new estimator. Although both adaptive methods converge with the optimal rate, energy norm errors of the adaptive LTZ element method with a new estimator are smaller than those of the old estimator under the same scale.

Figure 5 shows two intermediate meshes generated by the above two ANFEMs. As demonstrated by the two images in Figure 5, the new estimator demonstrates superior efficiency in detecting singularities, consequently achieving more favorable results.