Novel Data-Driven Shrinkage Ridge Parameters for Handling Multicollinearity in Regression Models with Environmental and Chemical Data Applications

Abstract

Multicollinearity among predictor variables is a common challenge in modeling chemical and environmental datasets in physical sciences, often leading to collinearity issues and unreliable parameter estimates when fitting regression models. Ridge regression method emerges as an effective solution to this problem by introducing a penalty term ($k$) that shrinks parameters to mitigate multicollinearity and balances bias and variance. In this study, we propose three novel shrinkage parameters for ridge regression and use them to develop three ridge-type estimators, referred to as SPS1, SPS2, and SPS3, which are designed to enhance parameter estimation based on sample size $\left(n\right)$, number of predictors $\left(p\right)$, and standard error $\left(\sigma \right)$. These shrinkage estimators aim to improve the accuracy of regression models in the presence of multicollinearity. To evaluate the performance of the SPS estimators, we conduct comprehensive Monte Carlo simulations comparing them to ordinary least squares (OLS) and other existing estimators based on the mean squared error (MSE) criteria. The simulation results demonstrate that the SPS estimators outperform OLS and other methods. Additionally, we apply these three shrinkage estimators to two real-world environmental and chemical datasets, showing their ability to address multicollinearity as compared to OLS and other estimators. The proposed SPS estimators offer more stable and accurate regression results, contributing to improved decision-making in environmental modeling, pollution analysis, and other scientific research involving correlated variables.

1. Introduction

Linear regression models are widely employed in physical sciences to analyze relationships between variables in fields such as environmental monitoring, material science, chemistry, and geophysics. A critical assumption in these models is that predictor variables are independent; however, physical systems often exhibit strong interdependencies and correlations among measured factors. This multicollinearity presents significant challenges in regression analysis, as it obscures the individual effect of each variable and leads to unstable coefficient estimates. In some cases, parameter estimates may fluctuate dramatically or change signs unexpectedly, undermining the physical interpretability of the model. Such instability reduces the reliability of conclusions drawn about complex physical phenomena and limits the model’s predictive accuracy, complicating the understanding and management of environmental and physical processes.

While many researchers have proposed different shrinkage or ridge parameters to address multicollinearity, only a few are widely examined in the literature. Initially, Hoerl and Kennard [1] developed a ridge regression method that introduced a penalty parameter $(\mathit{k}$) to reduce the influence of highly correlated variables to remove the effect of multicollinearity. In the shrinkage technique, penalty term is added to stabilize the coefficient estimates, hence improving the statistical model’s predictive accuracy. However, the ridge parameter introduces a slight bias in the estimators. When the penalty parameter is set to zero, ridge regression essentially becomes equivalent to OLS. Over the years, various improvements have been made to ridge regression to enhance its effectiveness in tackling multicollinearity. Rao and Toutenburg [2] proposed generalized ridge regression, offering more flexibility in selecting the penalty terms. Furthermore, the authors in [3,4] improved ridge estimators and the process of shrinking coefficients, enhancing the model’s stability and precision. Most recently, advanced developments by authors [5,6,7,8,9] innovated shrinkage parameters to handle severe multicollinearity, further improving the accuracy, reliability, and predication of regression models. One of the recent studies is Ref. [10], who introduced several two-ridge estimators, which are based on the data structure, for handling collinear datasets.

It is clear from the literature that no single ridge estimator achieves optimal performance across all scenarios, creating a significant research gap in addressing multicollinearity effectively. Existing methods often fail to incorporate critical factors, such as sample size, standard error, and the number of predictors, which are crucial for improving the accuracy and reliability of regression estimates. To bridge this gap, we propose three new estimators, denoted as SPS1, SPS2 and SPS3, that specifically address these issues by incorporating the sample size $\left(\mathit{n}\right)$, standard error $\left(\mathit{\sigma }\right)$, and number of predictors $\left(\mathit{p}\right)$ in their formulations. Our newly proposed estimators are designed to mitigate multicollinearity, shrink regression coefficients, and achieve lower MSE as compared to OLS and other existing estimators. Through extensive simulation analysis and practical applications, the newly proposed SPS estimators consistently outperform both OLS and other existing estimators across various scenarios.

The structure of this paper is organized as follows. Section 2 introduces the statistical models, discusses various ridge estimators, and presents the proposed shrinkage parameters. Section 3 details the simulation study conducted to evaluate the performance of the proposed estimators. In Section 4, two real-life datasets are analyzed to demonstrate the practical advantages of the proposed estimators. Finally, the paper concludes with key findings and remarks in Section 5.

2. Materials and Methods

Consider the following multiple linear regression model:

$$\mathit{y}=\mathit{X}\mathit{\alpha }+\mathit{ϵ},$$

(1)

where $\mathit{y}=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]$ is an $(n\times 1)$ observations response vector, $\mathit{X}=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1p}\\ x_{21}& x_{22}& \dots & x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \dots & x_{np}\end{array}\right]$ is an $(n\times p)$ design matrix, $\mathit{\alpha }=\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_p\end{array}\right]$ is a $(p\times 1)$ unknown parameter vector, and $\mathsf{ϵ}=\left[\begin{array}{c}{ϵ}_1\\ {ϵ}_2\\ ⋮\\ {ϵ}_n\end{array}\right]$ is an $(n\times 1)$ error vector.

The OLS estimator is given as follows:

$${\widehat{\mathit{\alpha }}}_{\mathit{o}\mathit{l}\mathit{s}}={\left({\mathit{X}}^{\mathit{\prime }}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathbf{\prime }}\mathbf{y},$$

(2)

where $Cov\left(\widehat{\mathit{\alpha }}\right)={\mathsf{\sigma }}^2({\mathit{X}}^{\mathbf{\prime }}\mathit{X}{)}^{-1}$. However, when predictors are highly correlated, ${\mathit{X}}^{\mathit{\prime }}\mathit{X}$ becomes nearly singular (|$\mathit{X}$′$\mathit{X}$| ≈ 0), causing unstable estimates and large variances [11]. To address this issue, ridge regression method introduces a shrinkage parameter $k(k> 0)$. Ridge regression estimator is given as follows:

$${\widehat{\mathit{\alpha }}}_{\mathit{R}\mathit{R}}={({\mathit{X}}^{\mathit{\prime }}\mathit{X}+k\mathit{I})}^{-1}{\mathit{X}}^{\mathbf{\prime }}\mathit{y},$$

(3)

where $\mathit{I}$ is the identity matrix. This stabilizes estimates by trading bias for reduced variance. The ridge shrinkage parameter $k$ biases the estimates; however, it reduces their variance compared to OLS estimator [1]. When $k=0,$ the ridge regression estimator approaches the OLS estimator (${\widehat{\mathit{\alpha }}}_{\mathit{o}\mathit{l}\mathit{s}}={\widehat{\mathit{\alpha }}}_{\mathit{R}\mathit{R}}$), and as $k$ → ∞, $\widehat{\alpha }\to 0$.

The regression model (1) can be expressed in its canonical form as follows:

$$\mathit{y}=\mathit{Z}\mathit{\beta }+\mathit{ϵ},$$

(4)

where $\mathit{Z}=\mathit{X}\mathit{Q}$, $\mathit{\beta }=\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_p\end{array}\right]={\mathit{Q}}^{\mathit{\prime }}\mathit{\alpha }$, and $\mathit{Q}$ is an orthogonal matrix such that $\mathit{Q}$′$\mathit{X}$′$\mathit{X}\mathit{Q}$ = Λ, with Λ $= diag ({\lambda }_1, {\lambda }_2, \dots , {\lambda }_{\mathrm{p}})$ representing the eigenvalues of $\mathit{X}$′$\mathit{X}$. In this form, OLS and ridge regression estimator are given in Equation (5) and Equation (6), respectively.

$${\widehat{\mathit{\beta }}}_{\mathit{o}\mathit{l}\mathit{s}}=({\mathbf{Z}}^{\mathbf{\prime }}\mathbf{Z}{)}^{-1}{\mathbf{Z}}^{\mathbf{\prime }}\mathit{y},$$

(5)

$${\widehat{\mathit{\beta }}}_{\mathit{R}\mathit{R}}=({\mathbf{Z}}^{\mathbf{\prime }}\mathbf{Z}+K{)}^{-1}{\mathbf{Z}}^{\mathbf{\prime }}\mathit{y},$$

(6)

where $K = diag(k_1, k_2, \dots , k_{\mathrm{p}}) \mathrm{a}\mathrm{n}\mathrm{d} k_{\mathrm{i}} > 0$ for all $i=1, 2,\dots , p.$

The MSE of the OLS and ridge regression estimator are defined in Equation (7) and Equation (8), respectively.

$$\mathrm{M}\mathrm{S}\mathrm{E}({\widehat{\mathit{\beta }}}_{\mathit{o}\mathit{l}\mathit{s}})={\sigma }^2{\sum }_{i=1}^p{\displaystyle \frac{1}{{\lambda }_{\mathrm{i}}}},$$

(7)

$$\mathrm{S}\mathrm{E}({\widehat{\mathit{\beta }}}_{\mathit{R}\mathit{R}})={\sigma }^2{\sum }_{i=1}^p\left[{\displaystyle \frac{{\lambda }_{\mathrm{i}}}{{\left({\lambda }_{\mathrm{i}}+k_{\mathrm{i}}\right)}^2}}+{\displaystyle \frac{k_{\mathrm{i}} {{\beta }_{\mathrm{i}}}^2}{{\left({\lambda }_{\mathrm{i}}+k_{\mathrm{i}}\right)}^2}}\right].$$

(8)

The first term in Equation (8) represents variance, while the second term captures the bias introduced by ridge regression. As $k$ increases, the variance decreases and the bias increases.

2.1. Ridge Regression Estimators

In ridge regression, $k$ is often referred to as the ridge, shrinkage, or penalty term, and it plays an important role in addressing collinearity in the data. Its value must be estimated from real data, and much of the recent research in ridge regression has focused on developing methods to determine an optimal $k$ value. In this section, we review various statistical approaches for estimating $k$ and their applications in addressing multicollinearity.

2.1.1. Existing Ridge Estimators

Hoerl and Kennard [1] mathematically determined that the optimal ridge parameter $\left(k_{\mathrm{i}}\right)$ equals the estimated error variance divided by the square of the ordinary least squares coefficient estimate, as presented in Equation (9).

$${\widehat{k}}_i={\displaystyle \frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_{\max }^2}},$$

(9)

where ${\widehat{\sigma }}^2$is the estimated error variance and ${\widehat{\beta }}_{\max }=max({\widehat{\beta }}_1, {\widehat{\beta }}_2, \dots ,{\widehat{\beta }}_{\mathrm{p}})$. This estimator is known as HK estimator.

Hoerl et al. [12] further modified the HK estimator, and developed BHK estimator with estimated $k$ defined as follows:

$${\widehat{k}}_{BHK}= {\displaystyle \frac{{\widehat{\sigma }}^2}{\sum _{i=1}^p{\widehat{\beta }}_{\mathrm{i}}^2}}.$$

(10)

Kibria [13] introduced some new ridge estimators based on averages: arithmetic mean, geometric mean, and median for collinearity dataset. These estimators are denoted by KAM, KGM, and Kmed in this work. Their estimated $k$ values are mathematically defined as follows:

$${\widehat{k}}_{AM}={\displaystyle \frac{1}{p}}{\sum }_{i=1}^p{\displaystyle \frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_i^2}},$$

(11)

$${\widehat{k}}_{GM}={\displaystyle \frac{{\widehat{\sigma }}^2}{{\left({\prod }_{i=1}^p{\widehat{\beta }}_i^2\right)}^{1/p}}},$$

(12)

$${\widehat{k}}_{med}=\mathrm{Med}\left({\displaystyle \frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_i^2}}\right)$$

(13)

Khalaf et al. [14] developed a new estimator denoted as KMS by making eigenvalue-based adjustments. The estimated $k$ value for this estimator is expressed as follows:

$${\widehat{k}}_{KMS}={\displaystyle \frac{{\mathsf{\lambda }}_{\max }{\sum }_{i=1}^p\left|{\widehat{\beta }}_{\mathrm{i}}\right|}{\left\{\frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_{\max }^2}\right\}}}.$$

(14)

Most recently, Ref. [15] introduced a few shrinkage parameters to improve and better handle collinear data. Among these, the Balanced Log Ridge Estimator (BLRE) is chosen for comparison with our proposed estimators. The $k$-value for the BLRE is defined as follows:

$${\widehat{k}}_{BLRE}=\left({\displaystyle \frac{1}{p}}{\sum }_{i=1}^p{\gamma }_i\right)\left({\displaystyle \frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_{max}^2}}\right),$$

(15)

where ${\gamma }_i=\ln \left({\lambda }_i\left|\widehat{{\beta }_i}\right|\right)$.

The newly proposed SPS estimators are compared with OLS and above ridge estimators, HK, BHK, KAM, KGM, Kmed, KMS, and BLRE in this research.

2.1.2. Proposed Ridge-Type Estimators

In this study, we proposed three new ridge parameters to establish three new ridge estimators, that referred to as SPS1, SPS2, and SPS3, which are based on data components such as the sample size $\left(n\right)$, the number of predictor variables $\left(p\right)$, and the standard error ($\sigma )$. The ${\widehat{k}}_1, {\widehat{k}}_2 \mathrm{and} {\widehat{k}}_3$ for the three proposed estimators are mathematically defined as follows:

$$\mathrm{SPS}1:\hspace{1em}{\widehat{k}}_1=\widehat{\sigma } p^{(1+{\displaystyle \frac{p}{n}})} \mathrm{l}\mathrm{n}(1+p),$$

(16)

$$\mathrm{SPS}2:\hspace{1em}{\widehat{k}}_2=\widehat{\sigma } p^{(1+{\displaystyle \frac{p}{n}})} \left(1-{\displaystyle \frac{p}{n+p}}\right),$$

(17)

$$\mathrm{SPS}3:\hspace{1em}{\widehat{k}}_3=\widehat{\sigma } p^{(1+{\displaystyle \frac{p}{n}})}+({\displaystyle \frac{{\widehat{\sigma }}^2}{n+p}}).$$

(18)

The proposed ${\widehat{k}}_1, {\widehat{k}}_2 \mathrm{a}\mathrm{n}\mathrm{d} {\widehat{k}}_3$ assist in controlling the influence of correlated independent variables. SPS1 adjusts the penalty with a logarithmic term, which is influenced by both the number of predictors and the sample size. SPS2 introduces a correction factor based on the relationship between $p$ and $n$. SPS3 incorporates both the standard error and the sum of the sample size and number of predictors, providing a more balanced adjustment to the penalty term.

2.2. Mean Squared Error

The estimators’ performance was evaluated using the MSE criterion, a widely used metric in previous similar studies [16,17,18]. The MSE can be defined as follows:

$$MSE\left(\widehat{\mathit{\beta }}\right)={\displaystyle \frac{1}{N}}{\sum }_{j=1}^N{\left({\widehat{\beta }}_{ij}-{\beta }_i\right)}^{\mathbf{\prime }}\left({\widehat{\beta }}_{ij}-{\beta }_i\right) , i=\mathrm{1,2}, \dots ,p.$$

(19)

As the theoretical comparisons can be complex, we examined the performance of these ridge estimators (Equations (9)–(18)) via Monte Carlo simulations, as described in next section.

3. Monte Carlo Simulation Approach

To assess ridge estimators, the predictor variables are generated using Equation (20), where $x_{ij}$ is simulated through a standard approach widely used by researchers [19,20,21].

$$x_{ij}={(1-{\mathsf{\rho }}^{\mathbf{2}})}^{{\displaystyle \frac{1}{2}}} z_{ji}+{\mathsf{\rho }z}_{i, p+1}, j=\mathrm{1,2},\dots ,n; i=\mathrm{1,2},\dots ,p.$$

(20)

To generate the dependent variable, we assumed the following model:

$${\mathit{y}}_{\mathit{j}}={\beta }_0+{\beta }_1{X}_{1j}+{\beta }_2{X}_{2j}+\cdots +{\beta }_p{X}_{pj}+ {ϵ}_j, j=\mathrm{1,2}, \dots , n,$$

(21)

where ${\mathit{y}}_{\mathit{j}}$ represents the dependent variable, $X_{j1}, X_{j2},\dots , X_{jp}$ are the predictor variables and ${\mathit{ϵ}}_{\mathit{j}}$is the error term$\mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r} \mathrm{r}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}$. The number of observations is denoted as$\left(n\right)$, and the β coefficients are selected under the assumption that β′β = 1. For the model in Equation (21), the intercept term is set to zero $\left({\beta }_0=0\right).$

The correlation $\left(\rho \right)$ between the predictor variables are given values $0.80, 0.85, 0.90, 0.95, \mathrm{a}\mathrm{n}\mathrm{d} 0.99$. The error terms ${\mathit{ϵ}}_{\mathit{j}}$ are followed a normal distribution with zero mean and unit variance. The study explored the impact of varying factors, such as the number of independent variables $\left(p\right)$, the error variance $\left({\sigma }^2\right),$ and the sample size ($n)$. The specific values used in the analysis are as follows:

• Sample sizes: $n =10, 20, 50, 100$.
• Number of independent variables: $p = 4, 6, 8, 10$.
• Error variance: ${\sigma }^2=0.5, 1, 4, 5, 7, 10, 11$.

These variations were considered to examine the influence of these factors on the model’s behavior and results. To evaluate the MSE across different values of $\rho , n, \mathrm{a}\mathrm{n}\mathrm{d} p, N = \mathrm{10,000}$simulations were run in R programming. The results are presented in

Table A1. MSE of estimators for $(p=4, n=20)$.

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
1	0.80	0.381722	0.336311	0.239591	0.373687	0.199399	0.206686	0.317793	0.341271	0.096369	0.151097	0.134367
	0.90	0.880447	0.688187	0.469479	0.849001	0.37831	0.394013	0.662817	0.935449	0.092713	0.173259	0.146667
	0.99	10.32911	5.509546	4.453117	9.685212	3.0654	2.808829	8.316298	846.1171	0.03203	0.085875	0.064564
4	0.80	1.066719	0.61152	0.440264	0.972168	0.283993	0.332424	0.628455	0.570306	0.108993	0.189345	0.160515
	0.90	2.430839	1.095047	0.797161	2.148914	0.501131	0.565139	1.38769	18.17153	0.088879	0.173325	0.141207
	0.99	26.21955	8.205079	6.275412	21.78119	2.931802	2.329863	18.18321	2512.741	0.031904	0.050503	0.041198
7	0.80	37.90316	1.024881	0.866454	6.071223	0.758773	0.769288	4.865606	0.797476	0.696769	0.574452	0.652587
	0.90	87.10602	1.501699	1.114106	14.18643	0.693971	0.742622	15.00999	1.048954	0.67604	0.543744	0.630084
	0.99	1027.093	17.28349	6.432572	163.3736	0.568026	1.076394	363.5222	93.58721	0.644037	0.494677	0.592247
11	0.80	102.3447	1.112332	1.018671	6.314481	0.905386	0.918277	8.282985	0.924905	0.870751	0.796783	0.878491
	0.90	241.4098	1.344821	1.086585	14.71329	0.829353	0.864614	25.68358	0.906478	0.848712	0.759732	0.856623
	0.99	3021.616	17.21244	7.991548	189.3703	0.812114	1.380869	808.7333	567.8743	0.851543	0.763881	0.860182

,

Table A2. MSE of estimators for ($p=4, n=50).$

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
1	0.80	0.125058	0.119628	0.098933	0.123936	0.073636	0.081312	0.114858	0.117047	0.066911	0.083504	0.081279
	0.90	0.241146	0.220143	0.162037	0.237221	0.116366	0.116724	0.20462	0.214773	0.082819	0.115915	0.111081
	0.99	2.472887	1.547049	1.04638	2.352433	0.863905	0.929462	1.815929	6.150803	0.071514	0.151194	0.136765
4	0.80	0.364284	0.275261	0.198094	0.346267	0.124553	0.150691	0.245659	0.2267	0.102706	0.149489	0.142146
	0.90	0.722983	0.440899	0.297424	0.666707	0.173679	0.202647	0.401354	0.356539	0.106391	0.173859	0.16255
	0.99	6.957725	2.146644	1.739	5.911761	0.861428	0.834389	4.09908	15.69122	0.041272	0.095354	0.084222
7	0.80	12.72908	0.638914	0.713264	2.047904	0.748878	0.74314	1.16384	0.737304	0.439555	0.358713	0.382736
	0.90	24.57116	0.660869	0.629903	3.469813	0.631487	0.656603	2.223892	0.644284	0.391179	0.297432	0.327522
	0.99	252.8613	2.934918	1.353407	34.47371	0.350447	0.470676	54.08455	2.481519	0.365652	0.257285	0.295085
11	0.80	36.77443	0.806727	0.84138	2.015266	0.889796	0.896574	1.720767	0.89328	0.705462	0.606351	0.681401
	0.90	70.84212	0.787915	0.77263	3.467096	0.829113	0.847421	3.849749	0.81509	0.66381	0.550627	0.636029
	0.99	697.7311	1.716884	0.981795	28.96569	0.565712	0.638804	96.36211	0.769851	0.635996	0.51105	0.60571

,

Table A3. MSE of estimators for ($p=4, n=100).$

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
1	0.80	0.073158	0.071404	0.063338	0.072766	0.045999	0.05657	0.069321	0.06982	0.050248	0.057556	0.057055
	0.90	0.158128	0.149732	0.110135	0.156456	0.083473	0.077761	0.141343	0.144238	0.075882	0.096666	0.095111
	0.99	1.566058	1.090523	0.697096	1.501563	0.578708	0.622701	1.135416	1.177122	0.086637	0.163996	0.15661
4	0.80	0.200462	0.169205	0.117511	0.19395	0.079965	0.100083	0.149279	0.14103	0.087537	0.113945	0.111849
	0.90	0.420866	0.303682	0.197936	0.397744	0.115385	0.125776	0.259076	0.234339	0.104039	0.153283	0.149016
	0.99	4.264437	1.615085	1.089959	3.684344	0.562153	0.596236	2.356495	4.782404	0.051989	0.115022	0.108108
7	0.80	7.214069	0.487329	0.659391	1.144371	0.687347	0.67447	0.624957	0.696449	0.248811	0.228449	0.226216
	0.90	15.43519	0.493008	0.536202	2.250433	0.559319	0.563757	1.215291	0.588141	0.216271	0.182123	0.184494
	0.99	163.2934	1.570553	0.664435	21.7554	0.226123	0.317754	29.20614	0.514066	0.178541	0.121509	0.131159
11	0.80	21.03422	0.756219	0.808184	1.140987	0.878837	0.882705	1.006658	0.88462	0.502603	0.405102	0.446738
	0.90	45.24612	0.65903	0.693989	2.019112	0.7836	0.803695	1.688513	0.787761	0.463454	0.360841	0.404912
	0.99	430.949	1.125724	0.590609	16.33793	0.471055	0.543273	44.92153	0.531209	0.434253	0.321689	0.371107

,

Table A4. MSE of estimators for ($p=10, n=20).$

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
1	0.80	2.284127	1.685051	0.903303	2.250052	0.459175	0.503777	1.615548	2.993322	0.045312	0.101956	0.067479
	0.90	4.859703	3.288467	1.906409	4.77908	0.913367	1.069212	3.519616	384.3484	0.034211	0.08603	0.052673
	0.99	49.86188	30.6844	18.48504	48.93173	8.559488	9.237748	42.45696	76,912.96	0.020737	0.024732	0.015411
4	0.80	6.386834	3.0775	1.49275	6.106473	0.601489	0.759784	3.73593	51.48983	0.123105	0.097429	0.078083
	0.90	13.11762	6.179757	3.015062	12.49789	1.143838	1.487611	8.107051	168.0486	0.101242	0.071659	0.057825
	0.99	137.8711	61.36146	32.09949	130.7863	9.485896	10.09598	107.8657	34,245.33	0.087969	0.023496	0.030116
7	0.80	233.0813	8.785561	2.365695	105.6809	0.68644	0.743248	53.16302	4.074206	0.881932	0.680549	0.765443
	0.90	465.2746	15.70025	4.102241	210.3472	0.676224	0.820967	121.9218	8.796627	0.868034	0.650487	0.741114
	0.99	4894.56	162.8072	38.51122	2172.959	2.614338	6.406677	2193.379	2757.717	0.853483	0.615877	0.714483
11	0.80	617.9034	7.824816	2.268186	164.6607	0.814416	0.857643	99.67967	2.83745	0.950756	0.848628	0.899381
	0.90	1383.508	15.5833	3.963246	365.9745	0.963833	0.988453	270.9978	6.29608	0.947047	0.837536	0.892433
	0.99	13,426.38	128.6827	37.20499	3467.91	1.153153	2.554649	4770.136	110.9893	0.943568	0.825355	0.88445

,

Table A5. MSE of estimators for ($p=10, n=50).$

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
1	0.80	0.417147	0.383421	0.234113	0.414857	0.096117	0.100127	0.341607	0.390564	0.05666	0.124011	0.110414
	0.90	0.908936	0.762117	0.405999	0.900444	0.174632	0.185595	0.654883	0.828499	0.05382	0.14856	0.127847
	0.99	9.54206	5.920085	3.469449	9.375005	1.440231	1.762719	7.175871	2217.959	0.016714	0.095593	0.071293
4	0.80	1.173028	0.756862	0.337056	1.142175	0.113737	0.130868	0.654915	0.714077	0.058551	0.15634	0.132142
	0.90	2.350638	1.266501	0.574634	2.266627	0.184277	0.234889	1.195507	1.314097	0.044798	0.152996	0.123747
	0.99	24.54575	9.054248	4.252182	23.19558	1.294795	1.745523	15.25974	1463.181	0.013079	0.044609	0.032908
7	0.80	42.57609	1.164027	0.662166	19.14574	0.644068	0.59596	4.927942	0.610493	0.636057	0.37501	0.424154
	0.90	85.57156	1.962977	0.679122	36.53429	0.470064	0.44128	10.94429	0.764603	0.585338	0.311992	0.362793
	0.99	881.1069	21.40582	4.526549	363.2619	0.217817	0.345077	236.3235	12.10284	0.540698	0.262777	0.313951
11	0.80	116.0368	1.004509	0.766254	26.70064	0.83824	0.814891	6.989201	0.717093	0.840375	0.648296	0.707707
	0.90	256.6391	2.132952	0.76494	58.58945	0.708274	0.686199	22.20308	0.81693	0.80662	0.585922	0.652807
	0.99	2422.861	14.17891	1.760762	504.0391	0.327292	0.358444	413.1733	5.2177	0.788603	0.555289	0.625595

,

Table A6. MSE of estimators for ($p=10, n=100).$

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
1	0.80	0.137812	0.13459	0.104791	0.137544	0.041796	0.042678	0.127697	0.133745	0.053578	0.082875	0.080015
	0.90	0.266324	0.252747	0.16858	0.265312	0.070546	0.072923	0.225697	0.252204	0.064909	0.115032	0.10977
	0.99	2.650696	1.933346	0.997241	2.616357	0.540492	0.629913	1.835231	2.848495	0.043926	0.173954	0.154299
4	0.80	0.365701	0.31271	0.183118	0.361518	0.064169	0.070038	0.259254	0.284685	0.073789	0.14333	0.135751
	0.90	0.708655	0.522677	0.245601	0.694777	0.077467	0.089712	0.401939	0.472848	0.068705	0.167359	0.155538
	0.99	7.538962	3.348994	1.567945	7.225021	0.516405	0.755272	4.092925	7.998094	0.021802	0.108746	0.093146
7	0.80	13.31037	0.465473	0.602639	6.430089	0.688236	0.608921	0.918523	0.503025	0.397533	0.224757	0.233673
	0.90	27.0539	0.565706	0.497726	12.07412	0.52065	0.451751	1.828595	0.380872	0.344449	0.172584	0.183042
	0.99	257.2537	4.835247	0.917106	107.8683	0.130197	0.145287	40.43949	1.764421	0.285518	0.110668	0.124518
11	0.80	36.2454	0.603839	0.760996	8.880035	0.870757	0.840264	1.276353	0.749229	0.679472	0.445795	0.483727
	0.90	75.55831	0.642997	0.63427	18.13211	0.763342	0.728327	3.215177	0.589775	0.627231	0.378655	0.418069
	0.99	744.5225	2.743864	0.657579	160.6927	0.28449	0.261308	73.79567	0.666285	0.570577	0.308535	0.349748

,

Table A7. MSE of estimators for ($p=6, n=10).$

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
0.5	0.85	3.378658	2.528398	1.762173	3.287537	1.160446	1.072205	2.733217	4.896776	0.066439	0.129521	0.086383
	0.95	11.19735	6.886133	5.346904	10.70042	2.641352	2.717343	9.048494	92.03867	0.067073	0.150705	0.096489
	0.99	52.33269	30.69125	23.98468	50.46642	13.29911	12.07585	46.65281	14,495.49	0.033233	0.074324	0.042417
1	0.85	11.4453	5.273581	4.094192	10.3094	1.896017	1.948777	7.995936	49.78762	0.194721	0.173499	0.151345
	0.95	41.57378	17.65389	14.47399	37.70011	4.968464	4.632178	32.38513	508.4532	0.160245	0.145754	0.119691
	0.99	217.2169	91.83447	71.08078	193.7974	21.65944	15.95904	180.9525	182,157.5	0.145154	0.055667	0.074836
5	0.85	305.9332	15.93175	13.04077	130.7292	2.72492	2.987827	124.3324	11.57589	0.871156	0.731276	0.803255
	0.95	1126.807	76.26366	50.4237	416.4954	7.235105	6.579562	491.7308	76.3393	0.839774	0.694566	0.768471
	0.99	5405.858	480.6797	352.4595	2374.298	30.85213	50.33312	3346.464	399,519.7	0.827058	0.644451	0.740844
10	0.85	1232.287	58.0389	40.75881	305.7432	10.51065	7.637171	429.4527	46.67396	0.955862	0.903286	0.939088
	0.95	3908.595	137.5315	48.76107	943.0356	2.176856	3.358429	1491.989	71.50126	0.962096	0.903055	0.94383
	0.99	21,305.45	591.9954	593.4539	4726.276	62.24463	103.2838	10,093.68	2172.425	0.907581	0.803336	0.865478

and

Table A8. MSE of estimators for ($p=8, n=10).$

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	BHK	KMS	KAM	KGM	Kmed	BLRE	$\mathbf{S}\mathbf{P}\mathbf{S}1$	$\mathbf{S}\mathbf{P}\mathbf{S}2$	$\mathbf{S}\mathbf{P}\mathbf{S}3$
0.5	0.85	0.382213	0.355909	0.247702	0.379287	0.14813	0.133869	0.331037	0.366758	0.070056	0.129137	0.114566
	0.95	1.102372	0.942284	0.584152	1.086712	0.395289	0.428592	0.869086	1.088992	0.068197	0.162643	0.137268
	0.99	7.151624	4.374096	3.41327	6.972188	1.736972	1.979576	5.830794	19372.74	0.033276	0.121457	0.093012
1	0.85	1.371118	0.757422	0.437602	1.276828	0.180411	0.219901	0.682065	0.730715	0.073838	0.160861	0.134973
	0.95	5.208522	2.461426	1.529502	4.82043	0.545255	0.653276	3.060522	9.980913	0.046727	0.13536	0.105492
	0.99	20.81684	6.652062	4.348678	18.70876	1.618902	1.850371	13.30289	2616.95	0.021276	0.049378	0.037687
5	0.85	30.32442	0.773357	0.67011	9.029886	0.597249	0.585316	3.279911	0.536333	0.550313	0.350903	0.404997
	0.95	108.0267	2.864367	0.937737	32.02229	0.41274	0.417908	17.9029	1.265746	0.514929	0.316523	0.370594
	0.99	556.6817	20.42108	5.618645	168.087	0.528299	1.3103	164.3863	14.24792	0.513925	0.314639	0.370418
10	0.85	136.843	1.681656	0.846271	16.41279	0.843225	0.847043	11.8655	0.910318	0.835199	0.694807	0.774308
	0.95	583.8776	2.912145	1.206887	70.05865	0.70819	0.718044	81.40251	1.061343	0.830935	0.684944	0.767827
	0.99	2434.236	8.51515	3.702356	266.2184	0.506051	0.756916	562.6443	2.57801	0.791225	0.615915	0.716577

(Appendix A).

The following steps were used to calculate the MSE for the estimators:

• Data Preparation

Standardize predictors using Equation (20) and compute eigenvalues (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, …, ${\lambda }_p$) and eigenvectors ($e_1$, $e_2$, $e_3$, …, $e_p$) of ${\mathit{X}}^{\mathit{\prime }}\mathit{X}$. Set true coefficients as β = e_maxP, where P = [$e_1$, …, $e_p$] and $e_{\mathrm{m}\mathrm{a}\mathrm{x}}$corresponds to the largest eigenvector (${\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}})$with errors generated from $\mathrm{N}(0,1).$

• Model Estimation

Compute response values using Equations (5) and (6), and derive OLS and other ridge estimates using their formulas.

• MSE Calculation

Repeat the procedure for $N=10000$ Monte Carlo simulations. Calculate the MSE as follows:

$$MSE\left(\widehat{\mathit{\beta }}\right)={\displaystyle \frac{1}{10000}} {\sum }_{J=1}^{10000}{\left({\widehat{\beta }}_{ij}-{\beta }_i\right)}^{\mathbf{\prime }}\left({\widehat{\beta }}_{ij}-{\beta }_i\right) .$$

(22)

Discussion of the Simulation Results

The simulation results presented in Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8 provided a detailed comparison of the performance of OLS, existing ridge estimators (HK, KMS, KAM, KGM, Kmed, and BLRE), and our newly proposed ridge estimators ($\mathrm{S}\mathrm{P}\mathrm{S}1,\mathrm{S}\mathrm{P}\mathrm{S}2,\mathrm{S}\mathrm{P}\mathrm{S}3$). The study evaluated the effects of sample size $\left(n\right)$, number of predictors $\left(p\right)$, correlation coefficient $\left(\rho \right)$, and error variance $\left({\mathsf{\sigma }}^2\right)$ on the mean squared error (MSE) of these estimators. The results highlighted the robustness and efficiency of our newly proposed estimators across a wide range of scenarios. Key observations from the tables are summarized below.

• Performance Across Sample Sizes $\left(n\right)$: The performance of the estimators varies significantly with different sample sizes. As the sample size increased (from $n$ = 10, 20 to $n$ = 100), the MSE tended to decrease across most estimators, which is a common trend in statistical estimation due to the law of large numbers. For instance, in Table A1 ($p$ = 4, $n$ = 20), the MSE for most estimators was higher, whereas in Table A3 ($p$ = 4, $n$ = 100), MSE values were noticeably lower. This improvement is particularly evident in the new SPS estimators, especially the SPS1, which consistently exhibited lower MSE compared to OLS and other existing estimators. This suggests that the SPS estimators, particularly the SPS1, are more stable and efficient as the sample size increases, further supporting their robustness in larger datasets.
• Impact of Number of Predictors $\left(p\right)$: The number of predictors also influenced the MSE of the estimators. As the number of predictors increases from $p$ = 4, 6, 8 and $p$ = 10, the MSE generally increases, especially for estimators like OLS, which struggle more as the model complexity increases. For example, in Table A4 ($p$ = 10, $n$ = 20), the MSE for OLS was considerably higher than in the $p$ = 4 scenarios, reflecting the difficulty of OLS in dealing with more complex models. The proposed SPS estimators continued to show robust performance across different values of $p$, especially the SPS1, which tended to outperform other estimators even as p increased. This highlights that the SPS estimators remain effective even in higher-dimensional settings, where traditional estimators like OLS may fail to perform well.
• Effect of Correlation Coefficient $\left(\rho \right)$: The correlation coefficient had a notable effect on the MSE, with higher correlation leading to increased estimation difficulty. As $\rho$ increased from 0.80 to 0.99, the MSE for most estimators increased, especially for OLS. This is particularly apparent in Table A1, Table A2 and Table A3, where at $\rho$ = 0.99, the MSE for OLS was much higher than at $\rho$ = 0.80. The newly proposed SPS estimators, particularly the SPS1, maintained relatively low MSE even as the correlation increases. This indicates that the SPS estimators are more robust to high correlation, which is often a challenging condition for many existing estimators and OLS. This robustness makes the SPS estimators particularly attractive when high correlations between predictors are present.
• Influence of Error Variance $\left({\mathsf{\sigma }}^2\right)$: The influence of error variance was another critical factor affecting the performance of the estimators. As σ² increased from 0.5 to 11, the MSE generally increased for all estimators, indicating that higher error variance leads to greater estimation uncertainty. However, the newly proposed SPS estimators showed a distinct advantage under high error variance conditions. For instance, in Table A4 ($p$ = 10, $n$ = 20) at σ² = 11, the SPS1 still outperformed OLS and several other existing estimators, suggesting that it can handle larger error variances more effectively. In contrast, traditional estimators like KGM and Kmed showed substantial increases in MSE as error variance rose, especially at $\rho$ = 0.99. This confirms that the SPS estimators, particularly the SPS1, are more robust to high levels of error variance, providing more reliable estimates under such conditions.
• Comparison with existing estimators: When comparing the performance of the newly proposed SPS estimators with existing ones (HK, BHK, KMS, KAM, KGM, Kmed, BLRE), the SPS estimators generally outperform OLS and most of the existing estimators across different conditions, especially under higher correlations and larger error variances. Among the traditional estimators, KAM, KMS, and BHK were the most competitive, showing lower MSE than OLS in many scenarios, particularly at higher sample sizes and moderate to high correlation. However, the SPS estimators, particularly the SPS1, showed consistently superior performance across a wide range of conditions, including high correlation ($\rho$ = 0.99) and large error variances (σ² = 11). The SPS1 consistently provided the lowest MSE across most of the datasets, making it the most reliable estimator in challenging conditions. In contrast, the SPS2 and SPS3 exhibited competitive performance but with slightly higher MSE compared to the SPS1, particularly in cases of very high correlation and large error variances. Nonetheless, they still outperformed OLS and several existing estimators, making them valuable alternatives in many situations.

4. Environmental and Chemical Science Data Applications

Regression analysis involving multicollinear data, especially in environmental, chemical, and physical studies, is of particular interest to many researchers, where predictor interdependence is common.

The performance of our newly developed estimators, OLS, and other existing ridge estimators was evaluated using two real datasets. We considered the environmental Air Pollution Dataset [22] and the chemical Hald Cement Dataset [11], see also: Ref. [23]. These real datasets share features similar to those taken into account in our earlier simulation work.

4.1. Air Pollution Dataset

This environmental dataset contains 20 real-world measurements of urban nitrogen dioxide (NO₂) levels ($y$), along with humidity $\left(X_1\right)$, temperature $\left(X_2\right)$, and air pressure $\left(X_3\right)$. From 15 predictors, we selected only three predictor variables $\left(X_1, X_2 \mathrm{a}\mathrm{n}\mathrm{d} X_3\right)$ as their correlations are obvious. NO₂ ranges from 0.05 ppm (light) to 0.25 ppm (moderate pollution). The natural correlations between weather variables, such as humidity and air pressure, make this dataset useful for testing regression models on atmospheric data. The linear regression model for modeling this dataset can be written as follows:

$$y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+\mathsf{ϵ}.$$

In this equation, ${\beta }_0$ represents the intercept, while ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$ are the coefficients associated with each predictor variable $X_1, X_2 \mathrm{a}\mathrm{n}\mathrm{d} X_3,$ respectively. The term $\mathsf{ϵ}$ reflects the error term, which accounts for the difference between the actual and predicted values.

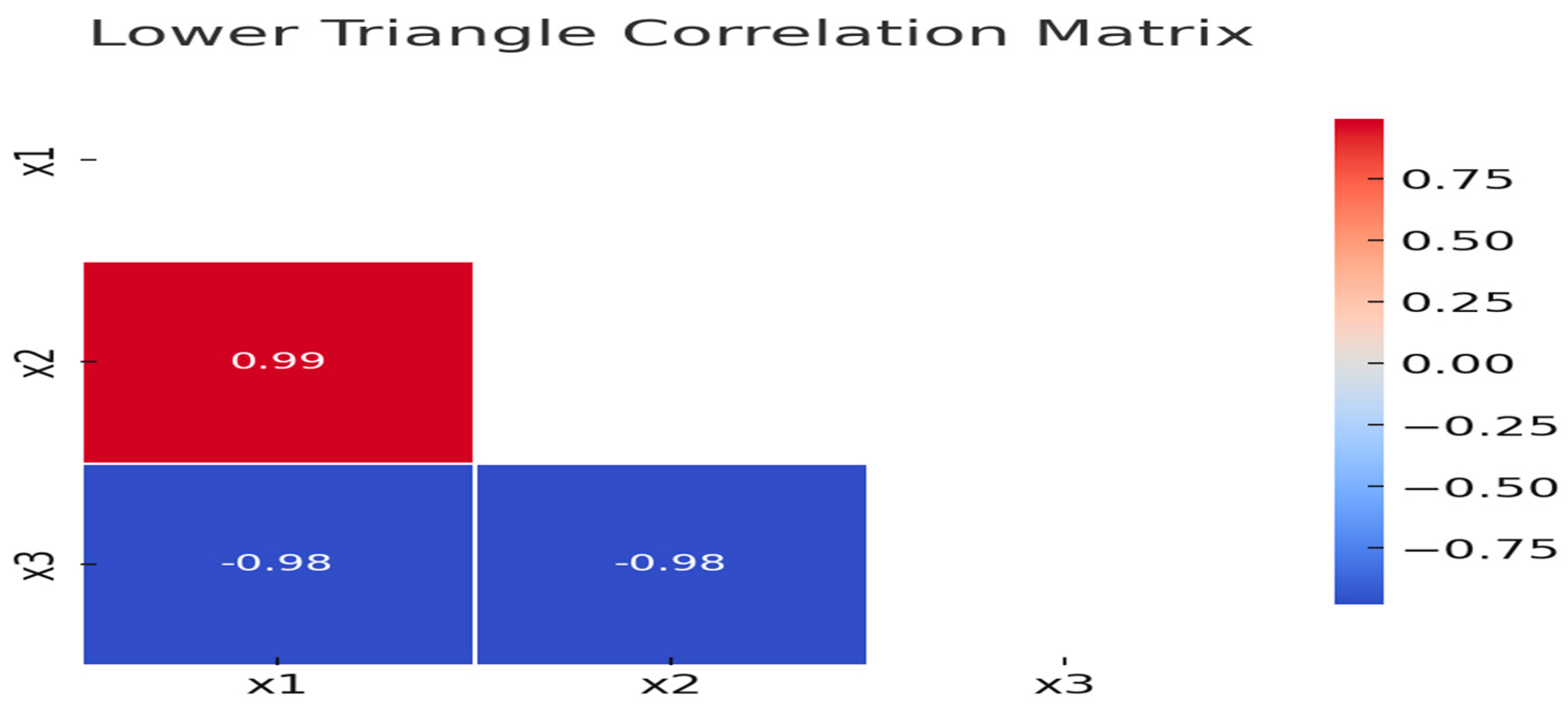
To check if the dataset is affected by multicollinearity, three tools were used: Variance Inflation Factor (VIF), the Condition Number (CN), and a heatmap display. For the CN, the eigenvalues of the data are needed, which are as follows: ${\lambda }_1=1.09, { \lambda }_2=0.05 \mathrm{a}\mathrm{n}\mathrm{d} {\lambda }_3=0.003$.

The presence of near-zero eigenvalues (0.05 and 0.003) shows that the predictors are highly interdependent, with one variable almost perfectly explainable by the others.

When the CN is greater than 30, it indicates the presence of multicollinearity in the dataset.

The CN, calculated as the ratio of the largest to smallest eigenvalue, is as follows:

$$CN={\displaystyle \frac{{\lambda }_{max}}{{\lambda }_{min}}} \cong 363.$$

Additionally, the VIF values for each predictor are as follows:

$$VIF\left(X_1\right)=0.917, VIF\left(X_2\right)= 20 \mathrm{a}\mathrm{n}\mathrm{d} VIF\left(X_3\right)=333.$$

Since all VIF values far exceeded the threshold of 10, this confirms high multicollinearity in the dataset.

From Figure 1, it is also evident that variables exhibit strong correlations with each other; therefore, strong multicollinearity exists in the data. Given that OLS regression would produce unstable coefficient estimates, we employed our newly developed estimators that were designed to handle highly collinear data effectively. These estimators were compared against OLS and other existing methods to demonstrate their superiority in mitigating multicollinearity.

This practical application proved that our proposed estimator’s performance is better compared to the OLS and other existing approaches. These findings, presented in

Table 1. MSE and regression coefficients for air pollution dataset.

Method	MSE	${\widehat{\mathit{\beta }}}_0$	${\widehat{\mathit{\beta }}}_1$	${\widehat{\mathit{\beta }}}_2$	${\widehat{\mathit{\beta }}}_3$
OLS	2.979202	0.038863	0.621592	−0.07121	−0.16889
HK	1.321717	−2.07044	0.038852	0.158958	−0.0168
BHK	0.862875	−0.54526	−2.00902	0.038804	0.035427
KAM	2.447914	2.500708	−0.50237	−1.78161	0.036829
KGM	0.314779	0.038785	2.103305	−0.37532	−0.30316
Kmed	0.370558	−1.70836	0.037444	1.249123	−0.03155
KMS	1.488609	−0.34251	−0.41397	0.038896	0.067531
BLRE	1.256637	1.082581	−0.04478	−2.27084	0.036829
SPS1	0.275383	0.038684	0.097186	−0.72364	−0.30316
SPS2	0.293119	−1.39038	0.038005	5.501533	−0.03155
SPS3	0.293119	−0.23044	−0.61191	0.035118	0.067531

, provided strong confirmation of our earlier simulation results.

4.2. Hald Cement Dataset

This dataset consists of 13 observations with five numerical variables: the dependent variable (y) and four independent variables $X_1 X_2, X_3 \mathrm{a}\mathrm{n}\mathrm{d} X_4$. The regression model is expressed as follows:

$$y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+\mathsf{ϵ}.$$

To check if the dataset is affected by multicollinearity, two indicators were used: the CN and the heatmap. For the CN, the eigenvalues of the data are needed. The eigenvalues are${\lambda }_1=1.57, {\lambda }_2=0.198, {\lambda }_3=0.0126, \mathrm{a}\mathrm{n}\mathrm{d} {\lambda }_4=0.0016$.

Therefore, the CN is approximately 986, which is greater than the threshold of 30. This indicates that the data exhibits multicollinearity. Figure 2 clearly shows that the independent variables are correlated with each other.

The newly proposed and existing estimators were employed to compare their performance based on MSE, in order to identify the best estimator for mitigating multicollinearity.

Table 2. MSE and regression coefficients for Hald Cement Dataset.

Method	MSE	${\widehat{\mathit{\beta }}}_0$	${\widehat{\mathit{\beta }}}_1$	${\widehat{\mathit{\beta }}}_2$	${\widehat{\mathit{\beta }}}_3$	${\widehat{\mathit{\beta }}}_4$
OLS	28.17521	−0.24971	−0.36505	0.715165	0.112926	0.045647
HK	22.90219	−0.36526	0.923205	0.018739	11.45462	−0.23748
HKB	11.97531	0.927308	0.105368	0.310029	−0.24971	−0.33059
KAM	26.99004	0.113338	7.570884	−0.23612	−0.36526	0.506491
KGM	0.456483	11.76045	−0.24971	−0.32693	0.927339	0.007486
Kmed	0.375257	−0.2497	−0.36525	0.480812	0.113403	0.112597
KMS	26.75516	−0.36522	0.927143	0.006745	11.81024	−0.23748
BLRE	21.40995	0.926478	0.112996	0.100843	−0.22143	−0.33059
SPS1	0.333952	0.111636	11.50577	−0.24971	−0.28984	0.506491
SPS2	0.381985	10.58041	−0.2452	−0.36525	0.302918	0.007486
SPS3	0.381985	−0.24964	−0.35208	0.927109	0.003141	0.112597

presents the MSE and regression coefficients for both the newly proposed estimators (SPS1, SPS2, SPS3) and the existing ones based on the real Hald Cement Dataset. It is evident that the results aligned well with the simulation results, validating the performance of the proposed estimators. In the analysis of the Hald Cement Dataset, the newly proposed estimators (SPS1, SPS2, SPS3) were compared with OLS and other existing methods (HK, HKB, KAM, KGM, Kmed, KMS, and BLRE) based on MSE. SPS1 estimator showed the best performance, having the lowest MSE, which was significantly better than OLS and other methods. SPS2 and SPS3 also performed well, with MSE values of 0.381985, outperforming all other methods except Kmed (0.375257).

Overall, the SPS estimators offer a promising alternative for more accurate predictions in modeling this dataset.

5. Conclusions

This study comprehensively evaluated the performance of newly proposed ridge-type shrinkage estimators (SPS1, SPS2, and SPS3) with OLS and other existing estimators, such as HK, KAM, KGM, Kmed, KMS, and BLRE, under various scenarios of multicollinearity including sample size, and error variance. Both simulations and real-world datasets analyses confirmed the superiority of the proposed SPS estimators in mitigating multicollinearity and induced instability while maintaining estimation efficiency.

SPS estimators are recommended for regression analysis involving multicollinear data, particularly in environmental and physical science studies, where predictor interdependence is common.

Future work could explore theoretical extensions in nonlinear or heteroscedastic settings and applications in more complex, big environmental and physical science datasets.