The Fourier Regularization for Solving a Cauchy Problem for the Laplace Equation with Uncertainty

Abstract

The Laplace equation is an important partial differential equation, typically used to describe the properties of steady-state distributions or passive fields in physical phenomena. Its Cauchy problem is one of the classic, serious, ill-posed problems, characterized by the fact that minor disturbances in the data can lead to significant errors in the solution and lack stability. Secondly, the determination of the parameters of the classical Laplace equation is difficult to adapt to the requirements of complex applications. For this purpose, in this paper, the Laplace equation with uncertain parameters is defined, and the uncertainty is represented by fuzzy numbers. In the case of granular differentiability, it is transformed into a granular differential equation, proving its serious ill-posedness. To overcome the ill-posedness, the Fourier regularization method is used to stabilize the numerical solution, and the stability estimation and error analysis between the regularization solution and the exact solution are given. Finally, numerical examples are given to illustrate the effectiveness and practicability of this method.

1. Introduction

This article introduces a numerical method for solving the Laplace equation under imprecise definition, focusing on its Cauchy problem. In simple terms, the Cauchy problem for the Laplace equation [1,2,3,4,5] is to solve the Laplace equation inside a region while prescribing both the function itself and its normal derivative on a portion of the boundary. This problem is a classic example of an ill-posed problem: it fails to satisfy one or more of the three requirements for well-posedness laid down by the French mathematician Hadamard: existence, uniqueness, and stability of the solution. Nevertheless, the Cauchy problem is ubiquitous in science and engineering, wherever one must infer internal or inaccessible boundary information from measurements taken on only part of the surface-typical of non-destructive testing and indirect measurement. Because the problem is inherently ill-posed, standard numerical schemes such as finite-element or finite-difference methods break down; special regularization techniques are indispensable. Their core idea is to introduce suitable constraints or smoothing terms that curb noise amplification and deliver a stable approximate solution. Widely used approaches include the method of fundamental solutions [6,7], regularization methods [8,9], and specialized numerical solvers [10,11].

The Cauchy problem for the Laplace equation is severely ill-posed [12,13,14,15,16,17,18], with its solution ultra-sensitive to Cauchy data, so dedicated stabilization techniques are indispensable; among the earliest and most popular is the quasi-reversibility method of Lattes and Lions [19], in which the original PDE is replaced by a nearby, well-posed equation that can “absorb” noisy data and whose solutions converge to the true solution, while subsequent work has refined and diversified the toolbox: In 2013, Mukanova [20] adopted a Fourier approach to recover missing boundary data on rectangular domains and analyzed mixed initial Cboundary-value problems for Laplace’s equation; In 2014, Cheng et al. [21] introduced a spectral filter for the same geometry, deriving a conventional $H\ddot{o}lder$-type error bound whose stability, however, degrades rapidly; In 2015, He et al. [22] invoked optimal regularization and produced the best-possible $H\ddot{o}lder$ estimate; In 2016, Li [23] derived the optimal error bound between the exact and regularized solutions via best approximation, markedly more stable yet computationally expensive for complex geometries; In 2017, Sun [24] recast the problem as a boundary-integral equation and solved it numerically; In 2018, Liu [25] extended the method of fundamental solutions to arbitrary domains, widening the class of tractable configurations; In 2024, Koleva [26] addressed a Cauchy-type problem with locally dynamic boundary conditions, further broadening the practical scope of the Laplace Cauchy problem, and together these studies chart a steady progression toward greater stability, wider geometrical flexibility, and sharper error control. In 2024, Kaltenbacher and Rundell [27] regularized the classical Cauchy problem of the Laplace equation and two related problems by replacing the integer-order derivatives with fractional-order derivatives. As a result, they transformed the classical severely ill-posed partial differential equation problem into a neighboring well-posed or only slightly ill-posed partial differential equation problem.

It is evident from the reviewed literature that various methods have been proposed to solve the Cauchy problem for the Laplace equation, including the fundamental solution method, integral equation method, numerical solution techniques, and regularization approaches. However, these methods still suffer from certain limitations. Firstly, the computational procedures are often complex and not easily implementable, particularly for highly intricate systems, where the accuracy of the results remains unsatisfactory. Secondly, a common assumption in these studies is that the parameters of the Laplace equation are precisely known. In practical applications, however, the available data may be incomplete or imprecise. To address these shortcomings, we propose to define the Laplace equation with uncertain parameters, using fuzzy numbers to represent the incompleteness and inaccuracy of the data. Furthermore, we will investigate the ill-posedness of the corresponding Cauchy problem and explore suitable regularization methods.

In fact, the Laplace equation with uncertain parameters is also a kind of fuzzy differential equation. Therefore, we have also introduced some research on the inverse problem of fuzzy differential equations.

The concept of fuzzy sets was first proposed by Zadeh [28]. Subsequently, Chang and Zadeh [29] proposed the fuzzy mapping function. With these theoretical foundations, in 1982, Dubois and Prade [30] proposed fuzzy operations based on the expansion principle. Subsequently, Kaleva et al. [31] first solved the Cauchy problem and the fuzzy initial boundary value problem of fuzzy differential equations. Since then, the research on the numerical solutions of fuzzy differential equations has begun [32]. When people solve fuzzy differential equations, they find that since the difference between two fuzzy numbers does not necessarily exist, the definition of the derivative of a fuzzy number is extremely difficult. To solve this thorny problem, many scholars began to study the definition of the derivative of fuzzy numbers [33,34,35,36]. Among them, the methods for solving fuzzy differential equations mainly include those based on differential inclusion theory [37,38], those based on Hukuhara derivatives and generalized Bade derivatives [39,40], etc. However, all these methods have certain drawbacks, such as ignoring the definition of fuzzy derivatives, lacking differentiability, and making the solutions increasingly fuzzy over time. In 2018, Mazandarani [41] proposed a new method for solving fuzzy differential equations, namely granular differentiability. This method overcomes the shortcomings of previous methods, making the solution of fuzzy differential equations simple and fast.

With the deepening research on fuzzy differential equations, it has become evident that, in practical applications, such as solving fuzzy backward heat conduction problems, the governing equations are frequently ill-posed; that is, they fail to satisfy at least one, and often none, of Hadamard’s three requirements for well-posedness. Gong and Yang were the first to investigate such ill-posed problems within fuzzy-number spaces and to develop systematic regularization techniques. In 2015, Gong and Yang et al. [42] studied the inverse problem of fuzzy differential equations by introducing the idea of inverse problems in the space of fuzzy numbers. In 2019, Yang and Gong [43] first proposed the concept of the ill-posedness of fuzzy integral equations. The numerical solution of the stable integral equation is regularized using the classic Tikhonov method. In 2020, Yang and Gong [44] proposed an iterative method for solving the first kind of fuzzy Fredholm integral equation based on the Landweber iterative method. In 2025, Yang and He [45] studied the regularization method of the Backward heat conduction equation with uncertain parameters.

Building on the systematic study of the classical Cauchy problem for the Laplace equation and on the pioneering analysis of ill-posed inverse problems and regularization in fuzzy-number spaces, we now stand on a firmer and broader theoretical platform. These advances allow us to move naturally from “certain” to “uncertain”: instead of treating the coefficients, boundary data, or initial conditions of the Laplace equation as exact real numbers, we endow them with fuzzy numbers that encode measurement errors, cognitive limitations, and environmental fluctuations. The resulting parameter-uncertain Laplace equation overcomes the rigid true-or-false dichotomy of traditional models and supplies a realistic modeling tool for data-scarce, noise-dominated applications in engineering, finance, and geosciences.

Within this framework, we systematically investigate the corresponding Cauchy problem. We establish the existence and uniqueness of solutions in the fuzzy-number space, quantify the violation of Hadamard’s three requirements, and construct a regularization scheme that is compatible with fuzzy data. By introducing the granular derivative, we prove that the regularized solutions converge to the true fuzzy solution in the level-set sense, and we derive explicit stability estimates. Numerical experiments demonstrate that the proposed strategy consistently outperforms classical deterministic algorithms, often by orders of magnitude.

Consequently, the present work breaks the long-standing assumption that parameters must be precise real numbers and delivers a computable, systematic methodology for solving Laplace-equation inversion problems under genuine uncertainty.

The remainder of this paper is organized as follows. Section 2 introduces the basic preliminaries relevant to this study. In Section 3, the Laplace equation with uncertain parameters is defined. Utilizing the concept of granular differentiability, it is transformed into a granular differential equation, and its ill-posed nature is analyzed. Section 4 presents the Fourier regularization method for solving the Cauchy problem of this Laplace equation with uncertain parameters. This section also provides the granular representation of the regularized solution, along with corresponding error estimates and a convergence analysis. A numerical example is provided in Section 5 to demonstrate the practicality and effectiveness of the proposed method. Finally, Section 6 concludes the paper and discusses potential avenues for future research.

2. Preliminaries

In this paper, the fuzzy number space is represented by $E^1$. For $0<\mu \le 1,$ the $\mu$-level set of $\tilde{u}\in E^1$ (or simply the $\mu$-cut) is defined by ${\left[\tilde{u}\right]}_{\mu }=\{x\in {\mathbb{R}}^n|\tilde{u}\left(x\right)\ge \mu \}.$

Definition 1

([41]). Let $\tilde{u}:[a,b]\subseteq {\mathbb{R}}^n\to [0,1]$ be a fuzzy number. The horizontal membership function $u^{gr}:[0,1]\times [0,1]\to [a,b]$ is a representation of $\tilde{u}\left(x\right)$ as $u^{gr}(\mu ,{\alpha }_u)=x$ in which “gr” stands for the granule of information included in $x\in [a,b],\mu \in [0,1]$ is the membership degree of x in $\tilde{u}\left(x\right), {\alpha }_u\in [0,1]$ is called relative-distance-measure (RDM) variable, and $u^{gr}(\mu ,{\alpha }_u)={\underline{u}}^{\mu }+({\overline{u}}^{\mu }-{\underline{u}}^{\mu }){\alpha }_u$.

Note 1

([41]). The horizontal membership function of $\tilde{u}\left(x\right)\in E^1$ is also denoted by $\mathcal{H}\left(\tilde{u}\left(x\right)\right)=u^{gr}(\mu ,{\alpha }_u)$. Moreover, using

$${\mathcal{H}}^{-1}\left(u^{gr}\left(\mu ,{\alpha }_u\right)\right)={\left[\tilde{u}\right]}_{\mu }=\left[\underset{\beta \ge \mu }{\inf }\underset{{\alpha }_u}{\min }{u}^{gr}(\beta ,{\alpha }_u),\underset{\beta \ge \mu }{\sup }\underset{{\alpha }_u}{\max }{u}^{gr}(\beta ,{\alpha }_u)\right],$$

(1)

the μ-level sets of the vertical membership function of $\tilde{u}\left(x\right)$.

The horizontal membership functions of triangular fuzzy number, $\tilde{u}=(a,b,c)$, are as $\mathcal{H}\left(\tilde{u}\right)=[a+(b-a)\mu ]+\left[(1-\mu )(c-a)\right]{\alpha }_u$. The horizontal membership functions of trapezoidal fuzzy number $\tilde{v}=(a,b,c,d)$, then, $\mathcal{H}\left(\tilde{v}\right)=[a+(b-a)\mu ]+[(d-a)-\mu (d-a+b-c)]{\alpha }_v$.

The horizontal membership function $\mathcal{H}\left(\tilde{u}\right)$ is similar to a transition from the vertical membership functions space to the multivariable functions space.

Definition 2

([41]). Two fuzzy numbers $\tilde{u}$ and $\tilde{v}$ are said to be equal if and only if $\mathcal{H}\left(\tilde{u}\right)=\mathcal{H}\left(\tilde{v}\right)$ for all ${\alpha }_u={\alpha }_v\in [0,1],$ and $\mu \in [0,1]$.

Definition 3

([41]). Let $\tilde{u}$ and $\tilde{v}$ be two fuzzy numbers whose horizontal membership function are $u^{gr}(\mu ,{\alpha }_u)$ and $v^{gr}(\mu ,{\alpha }_v)$, respectively, and “${\odot }_{gr}$ ” denotes one of the four basic operations, i.e., addition, subtraction, multiplication, and division. Then, $\tilde{u}{\odot }_{gr}\tilde{v}$ is a fuzzy number $\tilde{m}$ such that $\mathcal{H}\triangleq u^{gr}(\mu ,{\alpha }_u){\odot }_{gr}{v}^{gr}(\mu ,{\alpha }_v)$. It should be that $0\notin v^{gr}(u,{\alpha }_u)$ when “${\odot }_{gr}$” denotes the division operator.

Definition 4

([41]). Let $\tilde{f}:[a,b]\subseteq {\mathbb{R}}^n\to E^1$ include $n\in N$ distinct fuzzy numbers ${\tilde{u}}_1,{\tilde{u}}_2,\dots ,{\tilde{u}}_n$. The horizontal membership function of $\tilde{f}\left(t\right)$ at the point $t\in [a,b]$ is denoted by $\mathcal{H}\left(\tilde{f}\left(t\right)\right)\triangleq f^{gr}(t,\mu ,{\alpha }_f)$, and defined as $f^{gr}:[a,b]\times [0,1]\times \underset{n}{\underbrace{[0,1]\times \dots \times [0,1]}}\to [c,d]\subseteq \mathbb{R}$ in which ${\alpha }_f\triangleq ({\alpha }_{u_1},{\alpha }_{u_2},\dots ,{\alpha }_{u_n})$ are the RDM variables corresponding to the fuzzy numbers.

Definition 5

([41]). The fuzzy-number-valued function $\tilde{f}:[a,b]\subseteq {\mathbb{R}}^n\to E^1$ is said to be granular differentiable (gr-differentiable) at the point $t\in [a,b]$ if there exists a fuzzy number ${\displaystyle \frac{d\tilde{f}\left(t\right)}{dt}}\in E^1$, such that the following limit exists

$$\underset{h\to 0}{\lim }{\displaystyle \frac{\tilde{f}(t+h){\ominus }_{gr}\tilde{f}\left(t\right)}{h}}={\displaystyle \frac{d\tilde{f}\left(t\right)}{dt}}.$$

(2)

Theorem 1

([41]). The fuzzy-number-valued function $\tilde{f}:[a,b]\subseteq {\mathbb{R}}^n\to E^1$ is said to be gr-differentiable at the point $t\in [a,b]$ if and only if its horizontal membership function is differentiable with respect to t at that point. Moreover, $\mathcal{H}\left(\frac{d\tilde{f}\left(t\right)}{dt}\right)={\displaystyle \frac{\partial f^{gr}(t,\mu ,{\alpha }_f)}{\partial t}}.$

Definition 6

([41]). Let $\tilde{f}:[a,b]\subseteq \mathbb{R}\to E^1$ mapping $t\mapsto \tilde{f}\left(t\right)$ be a continuous fuzzy function whose horizontal membership function, i.e., $f^{gr}(t,\mu ,{\alpha }_f)$, is integrable on $t\in [a,b]$. Let ${\int }_a^b\tilde{f}\left(t\right)dt$ denote the integral of $\tilde{f}$ on $[a,b]$. Then, the fuzzy function $\tilde{f}$ is said to be granular integrable on $[a,b]$ if there exists a fuzzy number $\tilde{m}={\int }_a^b\tilde{f}\left(t\right)dt$ such that $\mathcal{H}\left(\tilde{m}\right)={\int }_a^b\mathcal{H}\left(\tilde{f}\left(t\right)\right)dt$.

Remark 1

([41]). Let $\tilde{m}=\tilde{u}{\odot }_{gr}\tilde{v}$. Then, ${\left[\tilde{m}\right]}_{\mu }={\mathcal{H}}^{-1}\left(u^{gr}(\mu ,{\alpha }_u){\odot }_{gr}{v}^{gr}(\mu ,{\alpha }_v)\right)$ always presents μ-level sets of the fuzzy number $\tilde{m}$.

Definition 7

([41]). Based on RDM fuzzy interval arithmetic, the following relations hold for $\tilde{u},\tilde{v},\tilde{w}\in E^1$:

(1)

$\tilde{u}{\ominus }_{gr}\tilde{v}=-\left(\tilde{v}{\ominus }_{gr}\tilde{u}\right)$;

(2)

$\tilde{u}{\ominus }_{gr}\tilde{u}=0$;

(3)

$\tilde{u}{\oslash }_{gr}\tilde{u}=1$; and

(4)

$\left(\tilde{u}{\oplus }_{gr}\tilde{v}\right){\otimes }_{gr}\tilde{w}=\tilde{u}{\otimes }_{gr}\tilde{w}{\oplus }_{gr}\tilde{v}{\otimes }_{gr}\tilde{w}$.

Note 2

([41]). Consider the following fuzzy differential equation

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\dot{\tilde{x}}\left(t\right)=\tilde{f}(t,\tilde{x}\left(t\right)),\hfill & \hfill t\in [t_0,t_f],\\ \tilde{x}\left(t_0\right)={\tilde{x}}_0.\hfill \end{array}\right.\end{array}$$

(3)

where $\tilde{x}:[t_0,t_f]\subseteq \mathbb{R}\to E^1$ includes $n\in \mathbb{N}$ distinct fuzzy numbers ${\tilde{u}}_1,{\tilde{u}}_2,...,{\tilde{u}}_n$, $\dot{\tilde{x}}\left(t\right)$ means gr-derivative of $\tilde{x}$ with respect to t, and ${\tilde{x}}_0\in E^1$ is a fuzzy initial condition. Based on Definition 2, fuzzy differential Equation (4) can be rewritten as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathcal{H}\left(\dot{\tilde{x}}\left(t\right)\right)=\mathcal{H}\left(\tilde{f}(t,\tilde{x}\left(t\right))\right),\hfill & \hfill t\in [t_0,t_f],\\ \mathcal{H}\left(\tilde{x}\left(t_0\right)\right)=\mathcal{H}\left({\tilde{x}}_0\right),\hfill \end{array}\right.\end{array}$$

(4)

then, using Theorem 1, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle \frac{\partial x^{gr}(t,\mu ,\alpha )}{\partial t}}=f^{gr}(t,x^{gr}(t,\mu ,\alpha ),\mu ,\alpha ),\hfill & \hfill t\in [t_0,t_f],\\ x^{gr}(t_0,\mu ,\alpha )=x_0^{gr}(\mu ,\alpha ),\hfill & \hfill \alpha \triangleq ({\alpha }_{u_1},{\alpha }_{u_2},...,{\alpha }_{u_n}).\end{array}\right.\end{array}$$

(5)

Definition 8

Let $\tilde{f}\left(t\right)$ be a bounded and continuous fuzzy-number-valued function, then the fuzzy Fourier transform of $\tilde{f}\left(t\right)$ is given by the following formula

$$\widehat{\tilde{f}}\left(t\right):=\mathcal{F}\left\{\tilde{f}\left(t\right)\right\}={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }\tilde{f}\left(t\right)e^{-iwt}dt=\tilde{F}\left(w\right).$$

(6)

Definition 9

If $\tilde{F}\left(w\right)$ is the fuzzy Fourier transform of $\tilde{f}\left(t\right)$, then the inverse fuzzy Fourier transform of $\tilde{F}\left(w\right)$ is

$${\mathcal{F}}^{-1}\left\{\tilde{F}\left(w\right)\right\}={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }\tilde{F}\left(w\right)e^{iwt}dw=\tilde{f}\left(t\right).$$

(7)

Remark 2.

Let $\tilde{f}\left(x\right)$ be a fuzzy-number-valued function. According to Definition 3, for any $\mu ,{\alpha }_f,{\alpha }_F\in [0,1]$, the following formula holds

$$\mathcal{F}\left\{f^{gr}(t,\mu ,{\alpha }_f)\right\}={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }{f}^{gr}(t,\mu ,{\alpha }_f)e^{-iwt}dt=F^{gr}(w,\mu ,{\alpha }_F).$$

(8)

and Equation (8) can also be rewritten as

$${\mathcal{F}}^{-1}\left\{F^{gr}(w,\mu ,{\alpha }_F)\right\}={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }{F}^{gr}(w,\mu ,{\alpha }_F)e^{iwt}dw=f^{gr}(t,\mu ,{\alpha }_f).$$

(9)

Example 1.

We consider the following a Cauchy problem for the Laplace equation with uncertainty

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}\tilde{u}(x,y)+{\partial }_{y{y}_{gr}}\tilde{u}(x,y)=\tilde{0},\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ \tilde{u}(0,y)=\tilde{\phi }\left(y\right)=\tilde{v}{y}^2,\hfill & \hfill y\in \mathbb{R},\\ {\partial }_{x_{gr}}\tilde{u}(0,y)=\tilde{0},\hfill & \hfill y\in \mathbb{R},\end{array}\right.\end{array}$$

(10)

where $\tilde{v}$ is a fuzzy-number-valued function, i.e., $\tilde{v}=(-1,0,1)$. According to the Definition 1, we have $\mathcal{H}\left(\tilde{v}\right)=(-1+\mu )+2(1-\mu ){\alpha }_v$. According to Note 1, the Cauchy problem of the Laplace equation can be transformed into the following granular differential equation

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)+{\partial }_{y{y}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,\alpha ),\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ u^{gr}(0,y,\mu ,{\alpha }_u)={\phi }^{gr}(y,\mu ,{\alpha }_{\phi })=[-1+\mu )+2(1-\mu )]y^2,\hfill & \hfill y\in \mathbb{R},\\ {\partial }_{x_{gr}}{u}^{gr}(0,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,\alpha ),\hfill & \hfill y\in \mathbb{R}.\end{array}\right.\end{array}$$

(11)

The fuzzy Fourier transform is applied to the variable y, and the equation is obtained

$${\partial }_{x{x}_{gr}}{\widehat{u}}^{gr}(x,\omega ,\mu ,{\alpha }_u)-{\omega }^2{\widehat{u}}^{gr}(x,\omega ,\mu ,{\alpha }_u)=0^{gr}(\mu ,\alpha ),$$

then the general solution is

$${\widehat{u}}^{gr}(x,\omega ,\mu ,{\alpha }_u)=A\left(\omega \right)e^{\omega x}+B\left(\omega \right)e^{-\omega x}.$$

(12)

Apply boundary conditions, the fuzzy Fourier transform of $u^{gr}(0,y,\mu ,{\alpha }_u)=[(-1+\mu )+2(1-\mu ){\alpha }_v]y^2$ is ${\widehat{u}}^{gr}(0,\omega ,\mu ,{\alpha }_u)=-2[(-1+\mu )+2(1-\mu ){\alpha }_v]\pi {\delta }^{″}\left(\omega \right)$, and ${\partial }_{x_{gr}}{u}^{gr}(0,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,\alpha )$ lead to $A\left(\omega \right)=B\left(\omega \right)$. Bring it into $\left(12\right)$ to obtain the following formula

$$\begin{array}{cc}\hfill {\widehat{u}}^{gr}(x,\omega ,\mu ,{\alpha }_u)& =-[(-1+\mu )+2(1-\mu ){\alpha }_v]\pi {\delta }^{″}\left(\omega \right)(e^{\omega x}+e^{-\omega x})\hfill \\ \hfill & =-2[(-1+\mu )+2(1-\mu ){\alpha }_v]\pi {\delta }^{″}\left(\omega \right)\cosh \left(\omega x\right).\hfill \end{array}$$

According to the inverse fuzzy Fourier transform, the final solution is

$$u^{gr}(x,y,\mu ,{\alpha }_u)=[(-1+\mu )+2(1-\mu ){\alpha }_v](y^2-x^2).$$

Definition 10

([46]). Let fuzzy-number-valued function $\tilde{f}\left(x\right)$ be granular improper integrable on infinite interval $[a,\infty )$, where $a\ge 0$. For any fixed $\mu ,\alpha \in [0,1]$, then 2-norm of $f^{gr}(x,\mu ,\alpha )$ on $\mathbb{R}$ is defined as

$$\mathcal{H}\left(\Vert \tilde{f}{\left(x\right)\Vert }_2\right)={\Vert \mathcal{H}\left(\tilde{f}\left(x\right)\right)\Vert }_2={\left({\int }_a^{\infty }{\left(f^{gr}(x,\mu ,\alpha )\right)}^{2}dx\right)}^{\frac{1}{2}}.$$

(13)

3. Ill-Posedness of the Laplace Equation with Uncertainty

In this section, we consider the following a Cauchy problem for the Laplace equation with uncertainty

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}\tilde{u}(x,y)+{\partial }_{y{y}_{gr}}\tilde{u}(x,y)=\tilde{0},\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ \tilde{u}(0,y)=\tilde{\phi }\left(y\right),\hfill & \hfill y\in \mathbb{R},\\ {\partial }_{x_{gr}}\tilde{u}(0,y)=\tilde{0},\hfill & \hfill y\in \mathbb{R},\end{array}\right.\end{array}$$

(14)

where $\tilde{\phi }\left(y\right)$ is the known data. $\tilde{u}(x,y)$, ${\partial }_{x{x}_{gr}}\tilde{u}(x,y)$, ${\partial }_{y{y}_{gr}}\tilde{u}(x,y)$, $\tilde{0}$, $\tilde{u}(0,y)$, $\tilde{\phi }\left(y\right)$, ${\partial }_{x_{gr}}\tilde{u}(0,y)$ are fuzzy-number-valued functions and according to the Definition 1, we have

$$\mathcal{H}\left(\tilde{u}(x,y)\right)=u^{gr}(x,y,\mu ,{\alpha }_u),$$

$$\mathcal{H}\left({\partial }_{x{x}_{gr}}\tilde{u}(x,y)\right)={\partial }_{x{x}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u),$$

$$\mathcal{H}\left({\partial }_{y{y}_{gr}}\tilde{u}(x,y)\right)={\partial }_{y{y}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u),$$

$$\mathcal{H}\left(\tilde{0}\right)=0^{gr}(\mu ,{\alpha }_0),$$

$$\mathcal{H}\left(\tilde{u}(0,y)\right)=u^{gr}(0,y,\mu ,{\alpha }_u),$$

$$\mathcal{H}\left(\tilde{\phi }\left(y\right)\right)={\phi }^{gr}(y,\mu ,{\alpha }_{\phi }),$$

$$\mathcal{H}\left({\partial }_{x_{gr}}\tilde{u}(0,y)\right)={\partial }_{x_{gr}}{u}^{gr}(0,y,\mu ,{\alpha }_u).$$

Our aim is to obtain the data $\tilde{u}(x,·)$ that we are interested in from the known data $\tilde{\phi }\left(x\right)$. According to Definition 1 and Note 2, in order to investigate Equation (14), we consider the following granular partial differential equations

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)+{\partial }_{y{y}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ u^{gr}(0,y,\mu ,{\alpha }_u)={\phi }^{gr}(y,\mu ,{\alpha }_{\phi }),\hfill & \hfill y\in \mathbb{R}.\\ {\partial }_{x_{gr}}{u}^{gr}(0,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill {\alpha }_u,{\alpha }_{\phi }\in [0,1].\end{array}\right.\end{array}$$

(15)

Let $u^{gr}(x,y,\mu ,{\alpha }_u)$ is solution of Equation (15). If $\mathcal{H}\left(\tilde{u}(x,y)\right)$ defines the horizontal membership functions of a fuzzy number, for all $x\in (0,1)$, $(y\in \mathbb{R})$, $\mu ,{\alpha }_u\in [0,1]$, the $\tilde{u}(x,y)$ is a solution of Equation $\left(14\right)$ [45].

We take the fuzzy Fourier transform of the variable y in Equation (14) and obtain the following equation:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}{\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)-{\zeta }^2{\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill x\in (0,1),\zeta \in \mathbb{R},\\ {\widehat{u}}^{gr}(0,\zeta ,\mu ,{\alpha }_u)={\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi }),\hfill & \hfill \zeta \in \mathbb{R}.\\ {\partial }_{x_{gr}}{\widehat{u}}^{gr}(0,\zeta ,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill {\alpha }_u,{\alpha }_{\phi }\in [0,1].\end{array}\right.\end{array}$$

(16)

Then, by separating variables, the solution of Equation (16) can be easily obtained as

$${\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)={\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (x,\zeta ,\mu ,\alpha )={\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (x,|\zeta |,\mu ,\alpha ),$$

(17)

and according to the inverse fuzzy Fourier transform, the solution can be expressed as

$$u^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }{\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (x,|\zeta |,\mu ,\alpha )e^{iy\zeta }d\zeta .$$

(18)

For the solution $u^{gr}(x,y,\mu ,{\alpha }_u)$ of the Equation (15), according to the Note 1, a solution of the Equation $\left(14\right)$ as follows:

$${\mathcal{H}}^{-1}\left(u^{gr}\left(\mu ,{\alpha }_u\right)\right)={\left[\tilde{u}\right]}_{\mu }=\left[\underset{\beta \ge \mu }{\inf }\underset{{\alpha }_u}{\min }{u}^{gr}(\beta ,{\alpha }_u),\underset{\beta \ge \mu }{\sup }\underset{{\alpha }_u}{\max }{u}^{gr}(\beta ,{\alpha }_u)\right].$$

(19)

In the following, we discuss the ill-posedness of the Equation (14).

Definition 11

([47]). If an equation satisfies the following three properties, then it is well-posed.

(1)

There are solutions.

(2)

The solution is unique.

(3)

The solution continuity depends on the definite solution condition.

On the contrary, if only one of these three conditions is not satisfied, then it is ill-posed.

Theorem 2

([45]). If Equation (15) has no solution, then Equation (14) has no solution.

Theorem 3

([45]). If the solution of Equation (15) exists and it is not unique, then a solution of Equation (14) exists and it is not unique.

Theorem 4

([45]). If the problem of granular partial differential Equation (15) is ill-posed, then the problem of the Laplace Equation (14) with uncertainty is said to be ill-posed.

The proof of the above theorem is similar to that in Reference [45], and will not be elaborated here. We already know that the problem of the granular partial differential Equation (15) is highly ill-posed. Thus, the problem of the Laplace Equation (14) with uncertainty is ill-posed.

Example 2.

Consider the following Cauchy problem of the Laplace equation with uncertainty

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}\tilde{u}(x,y)+{\partial }_{y{y}_{gr}}\tilde{u}(x,y)=\tilde{0},\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ \tilde{u}(0,y)=\tilde{\phi }\left(y\right)=\tilde{v}\sin \left(\beta y\right),\hfill & \hfill y\in \mathbb{R},\\ {\partial }_{x_{gr}}\tilde{u}(0,y)=\tilde{0},\hfill & \hfill y\in \mathbb{R},\end{array}\right.\end{array}$$

(20)

where $\tilde{v}$ is a fuzzy-number-valued function and β is a positive constant. According to Note (2), we have the following granular differential equation

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)+{\partial }_{y{y}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ u^{gr}(0,y,\mu ,{\alpha }_u)={\phi }^{gr}(y,\mu ,{\alpha }_{\phi })=v^{gr}(\mu ,{\alpha }_v)\sin \left(\beta y\right),\hfill & \hfill y\in \mathbb{R}.\\ {\partial }_{x_{gr}}{u}^{gr}(0,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill {\alpha }_u,{\alpha }_{\phi }\in [0,1].\end{array}\right.\end{array}$$

(21)

First, we apply a fuzzy Fourier transform to the variable y. Let ${\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)$ be the fuzzy Fourier transform of $u^{gr}(x,y,\mu ,{\alpha }_u)$ with respect to the variable y, i.e.,

$${\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)={\int }_{-\infty }^{+\infty }{u}^{gr}(x,y,\mu ,{\alpha }_u)e^{i\zeta y}d\zeta .$$

(22)

Applying the fuzzy Fourier transform to Equation (21), we get

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}{\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)-{\zeta }^2{\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill x\in (0,1),\zeta \in \mathbb{R},\\ {\widehat{u}}^{gr}(0,\zeta ,\mu ,{\alpha }_u)={\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })=v^{gr}(\mu ,{\alpha }_v){\int }_{-\infty }^{+\infty }\sin \left(\beta y\right)e^{i\zeta y}dy,\hfill & \hfill \zeta \in \mathbb{R}.\\ {\partial }_{x_{gr}}{\widehat{u}}^{gr}(0,\zeta ,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill {\alpha }_u,{\alpha }_{\phi }\in [0,1],\end{array}\right.\end{array}$$

(23)

then

$${\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })=v^{gr}(\mu ,{\alpha }_v)\left[{\displaystyle \frac{i}{2}}(\delta (\zeta -\beta )-\delta (\zeta +\beta ))\right],$$

where $\delta$ is a Dirac delta function. So, the solution is of the form

$${\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)=v^{gr}(\mu ,{\alpha }_v)[A\left(\zeta \right)e^{\zeta x}+B\left(\zeta \right)e^{\zeta x}].$$

Sine ${\partial }_{x_{gr}}{u}^{gr}(0,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0)$, we have

$${\partial }_{x_{gr}}{\widehat{u}}^{gr}(0,\zeta ,\mu ,{\alpha }_u)=\zeta (A\left(\zeta \right)-B\left(\zeta \right))=0,$$

so,

$$A\left(\zeta \right)=B\left(\zeta \right).$$

Therefore, the solution to the equation is

$${\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)=C\left(\zeta \right)\cosh \left(\zeta x\right).$$

The following will determine $C\left(\zeta \right).$ From the boundary condition ${\widehat{u}}^{gr}(0,\zeta ,\mu ,{\alpha }_u)={\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })$, we can obtained as

$$C\left(\zeta \right)={\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })=v^{gr}(\mu ,{\alpha }_v)\left[{\displaystyle \frac{i}{2}}(\delta (\zeta -\beta )-\delta (\zeta +\beta ))\right].$$

Therefore, the solution of the Equation (21) is

$${\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)=v^{gr}(\mu ,{\alpha }_v)\left[{\displaystyle \frac{i}{2}}(\delta (\zeta -\beta )-\delta (\zeta +\beta ))\right]\cosh \left(\zeta x\right).$$

The following formula is obtained from the inverse fuzzy Fourier transform

$$u^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }{\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)e^{i\zeta y}d\zeta ,$$

let us put ${\widehat{u}}^{gr}(x,\zeta ,\mu ,{\alpha }_u)$ in here, we have

$$u^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{i}{4\pi }}{v}^{gr}(\mu ,{\alpha }_v)\left({\int }_{-\infty }^{+\infty }\delta (\zeta -\beta )\cosh \left(\zeta x\right)e^{i\zeta y}d\zeta -{\int }_{-\infty }^{+\infty }\delta (\zeta +\beta )\cosh \left(\zeta x\right)e^{i\zeta y}d\zeta \right).$$

Using the properties of the Dirac delta function, we can get

$$u^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{i}{4\pi }}(\cosh \left(\beta x\right)e^{i\beta y}-\cosh \left(\beta x\right)e^{-i\beta y}),$$

by simplifying, we get

$$u^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{\sinh \left(\beta \right)x}{2\pi }}\sin \left(\beta y\right).$$

First, when $\beta$ is large, $\sinh \left(\beta x\right)$ grows very fast, which means that the solution is very sensitive to small changes in x. This rapid growth indicates the instability of the solution. Second, since the form of the solution depends on the value of $\beta$, different $\beta$ values may lead to different solutions. This indicates that the uniqueness of the solution is questioned. Finally, due to the high frequency oscillation of $\tilde{\phi }\left(y\right)=\tilde{v}\sin \left(\beta y\right)$, any small perturbation can cause the solution to change significantly near $x=0$. This variation amplifies as x increases, causing the solution to become unstable over the entire region.

In summary, by means of the Fourier transform and inverse Fourier transform, we show that the Cauchy problem is ill-posed when $\tilde{\phi }\left(y\right)=\tilde{v}\sin \left(\beta y\right)$ and $\beta$ is large. The instability of the solution, the sensitivity to the data, and the uniqueness of the solution all show this.

We have now shown that the Cauchy problem of the Laplace equation with uncertainty is severely ill-posed, which means that small perturbations in a given Cauchy data can cause explosive growth of the solution. Therefore, a regularization method is needed to stabilize the numerical solution, that is, to find a well-posed problem to approximate the ill-posed problem, so that the solution tends to be stable. In this paper, the Fourier regularization method is used to stabilize the solution of the Cauchy problem with uncertain Laplace equations.

Next, the specific process of the Fourier regularization method, convergence analysis, and error estimation will be introduced in detail.

4. Fourier Regularization and Error Estimates for the Laplace Equation with Uncertainty

In this section, we consider the following Cauchy problem for the Laplace equation with uncertainty

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}\tilde{u}(x,y)+{\partial }_{y{y}_{gr}}\tilde{u}(x,y)=\tilde{0},\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ \tilde{u}(0,y)=\tilde{\phi }\left(y\right),\hfill & \hfill y\in \mathbb{R},\\ {\partial }_{x_{gr}}\tilde{u}(0,y)=\tilde{0},\hfill & \hfill y\in \mathbb{R}.\end{array}\right.\end{array}$$

(24)

Based on Note 2, we mainly consider the Fourier regularization of the granular differential equation of the Laplace equation with uncertainty

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)+{\partial }_{y{y}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ u^{gr}(0,y,\mu ,{\alpha }_u)={\phi }^{gr}(y,\mu ,{\alpha }_{\phi }),\hfill & \hfill y\in \mathbb{R}.\\ {\partial }_{x_{gr}}{u}^{gr}(0,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,{\alpha }_0),\hfill & \hfill {\alpha }_u,{\alpha }_{\phi }\in [0,1].\end{array}\right.\end{array}$$

(25)

We want to find the $\tilde{u}(x,·)$ for a $0<x\le 1$ from the data we know $\tilde{\phi }\left(x\right)$. As shown in the previous section, we have obtained the solution of Equation (25) as follows:

$$u^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }{\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (x,|\zeta |,\mu ,\alpha )e^{iy\zeta }d\zeta .$$

(26)

Now, let us assume that ${\phi }^{gr}(y,\mu ,{\alpha }_{\phi })$ and ${\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })$ are the exact and measured data of the solution of Equation (25) at time $x=0$, respectively, which satisfy

$$\Vert {\phi }^{gr}(y,\mu ,{\alpha }_{\phi })-{\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })\Vert \le \delta ,$$

(27)

where $\delta$ represents the noise level of the measured data.

In order to obtain the convergence of the regular solution and speed up the convergence rate of the regular solution, we need to make a prior bound assumption on $L^2\left(\mathbb{R}\right)$ for the exact solution, so as to find the $H\ddot{o}lder$-type stability estimation of the regular solution. For that, let us assume

$$\Vert u^{gr}(1,y,\mu ,{\alpha }_u)\Vert \le A,$$

(28)

where A is a positive constant, and $\Vert ·\Vert$ represents the $L^2$-norm.

Next, we defined a regularization solution of Equation (25) for the measured data, which we call the Fourier regular solution of Equation (25) as follows:

$$u_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }{\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (|\xi |x){\chi }_{\max }{e}^{i\zeta y}d\zeta ,$$

(29)

where ${\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })$ is the fuzzy Fourier transform of measured data ${\tilde{\phi }}_{\delta }\left(y\right)$, table $\delta$ represents the noisy data with errors, such as the data obtained through manual measurement. The subscript ${\xi }_{\max }$ indicates the Fourier regular solution obtained through Fourier regularization, and ${\chi }_{\max }$ is the characteristic function of the interval $[-{\xi }_{\max },{\xi }_{\max }]$, i.e.

$${\chi }_{\max }=\begin{array}{c}\hfill \left\{\begin{array}{cc}1,\hfill & \hfill x\in [-{\xi }_{\max },{\xi }_{\max }];\\ 0,\hfill & \hfill x\notin [-{\xi }_{\max },{\xi }_{\max }],\end{array}\right.\end{array}$$

(30)

and ${\xi }_{\max }$ will be selected appropriately as regularization parameter.

The following theorem shows that the Fourier regularization defined by us, that is, the Equation (29), is continuously dependent on the given noisy data $u_{\delta }^{gr}(x,y,\mu ,{\alpha }_u)$.

Theorem 5.

Let $u_{{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)$ and $u_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)$ be solution to Equation (29) corresponding to data ${\phi }^{gr}(y,\mu ,{\alpha }_{\phi })$ and ${\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })$, respectively. Additionally, assume that conditions (27) and (28) always hold true. Then, there is

$$\Vert u_{{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)-u_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)\Vert \le {\cosh }^2\left({\xi }_{\max }x\right)\Vert {\phi }^{gr}(y,\mu ,{\alpha }_{\phi })-{\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })\Vert .$$

(31)

Proof. 

Due to the Parseval formula

$$\begin{array}{cc}\hfill & \Vert u_{{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)-u_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u){\Vert }^2\hfill \\ \hfill & =\Vert {\widehat{u}}_{{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)-{\widehat{u}}_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u){\Vert }^2\hfill \\ \hfill & ={\int }_{-\infty }^{+\infty }{\left|\cosh (|\zeta |x)\left({\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })-{\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\right)\right|}^{2}d\zeta \hfill \\ \hfill & ={\int }_{-{\xi }_{\max }}^{+{\xi }_{\max }}{\left|\cosh (|\zeta |x)\left({\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })-{\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\right)\right|}^{2}d\zeta \hfill \\ \hfill & \le {\cosh }^2(|{\xi }_{\max }|x){\int }_{-{\xi }_{\max }}^{+{\xi }_{\max }}{\left|\left({\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })-{\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\right)\right|}^{2}d\zeta \hfill \\ \hfill & \le {\cosh }^2(|{\xi }_{\max }|x)\Vert {\widehat{\phi }}^{gr}(\xi ,\mu ,{\alpha }_{\phi })-{\widehat{\phi }}_{\delta }^{gr}(\xi ,\mu ,{\alpha }_{\phi }){\Vert }^2\hfill \\ \hfill & ={\cosh }^2(|{\xi }_{\max }|x)·{\delta }^2,\hfill \end{array}$$

then, we have

$$\Vert u_{{\xi }_{\max }}^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}(·)\Vert \le {\cosh }^2\left({\xi }_{\max }x\right)\Vert {\phi }^{gr}(·)-{\phi }_{\delta }^{gr}(·)\Vert .$$

(32)

□

The above theorem explains the stability of the Fourier regular solution we have given. The results show that the regularization solution can be kept in a relatively stable range when the input data is measurement data with noise. Thus, the reliability and effectiveness of the scheme in practical application are guaranteed.

Remark 3.

We already know that given noise level δ, there is $\Vert {\phi }^{gr}(·)-{\phi }_{\delta }^{gr}(·)\Vert \le \delta$, Thus, for Equation (32), when $\delta \to 0$, there is

$$\Vert u_{{\xi }_{\max }}^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}(·)\Vert \to 0.$$

According to Equations $\left(26\right)$ and $\left(29\right)$, the total error can be decomposed into two parts

$$\Vert u^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}\Vert \le A_1+A_2,$$

where $A_1$ represents the truncation error, which is

$$A_1={\left({\int }_{|\zeta |\ge {\xi }_{\max }}|{\widehat{\phi }}^{gr}{\left(\zeta \right)cosh(|\zeta |x)|}^{2}d\zeta \right)}^{\frac{1}{2}},$$

by using the relation ${\widehat{\phi }}^{gr}\left(\zeta \right)={\displaystyle \frac{{\widehat{u}}^{gr}(1,\zeta )}{cosh(|\zeta )}}$, we can obtain

$$A_1={\left({\int }_{|\zeta |\ge {\xi }_{\max }}|{\widehat{u}}^{gr}{(1,\zeta )|}^2|{\displaystyle \frac{cosh(|\zeta |x)}{cosh(|\zeta |)}}{|}^{2}d\zeta |\right)}^{\frac{1}{2}},$$

utilizing the properties of hyperbolic functions

$${\displaystyle \frac{cosh(|\zeta |x)}{cosh(|\zeta |)}}\le 2e^{(-|\zeta |(1-x))},$$

so,

$$A_1\le {\left({\int }_{|\zeta |\ge {\xi }_{\max }}|{\widehat{u}}^{gr}{(1,\zeta )|}^2|·4e^{-2|\zeta |(1-x)}d\zeta |\right)}^{\frac{1}{2}}.$$

Since $e^{-2|\zeta |(1-x)}$ is monotonically decreasing when $|\zeta |\ge |{\xi }_{\max }|$ is present, and by using the prior bound condition $\Vert u^{gr}(1,y)\Vert \le A$, we can obtain

$$A_1\le 2e^{-{\xi }_{\max }(1-x)}·\Vert u^{gr}(1,y)\Vert \le 2A{e}^{-{\xi }_{\max }(1-x)}.$$

$A_2$ represents the noise amplification error, that is

$$E_2={\left({\int }_{{\xi }_{\max }}^{-{\xi }_{max}}|({\widehat{\phi }}^{gr}\left(\zeta \right)-{\widehat{\phi }}_{\delta }^{gr}\left(\zeta \right)){cosh(|\zeta |x)|}^2\right)}^{\frac{1}{2}},$$

because $cosh(|\zeta |x)\le cosh\left({\xi }_{\max }x\right)\le e^{{\xi }_{\max }x}$, and $\Vert {\phi }^{gr}-{\phi }_{\delta }^{gr}\Vert \le \delta ,$

$$E_2\le e^{{\xi }_{\max }x}·\delta .$$

Therefore, there is an upper bound for the total error

$$\Vert u^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}\Vert \le 2A{e}^{-{\xi }_{\max }(1-x)}+e^{{\xi }_{\max }x}·\delta .$$

In order to find the optimal ${\xi }_{\max }$, we balance the two errors. Select the equilibrium point as $x=1$, and let

$$2A{e}^{-{\xi }_{\max }(1-1)}=\delta e^{{\xi }_{\max }·1},$$

so,

$$2A=\delta e^{{\xi }_{\max }},$$

Finally, we obtain

$${\xi }_{\max }=\ln \left({\displaystyle \frac{2A}{\delta }}\right).$$

Next, we verify the error estimation.

For any $x\in [0,1]$, substitute ${\xi }_{\max }=\ln {\displaystyle \frac{2A}{\delta }}$ into the upper bound of the total error, and the truncation error term and the noise amplification error term are obtained as follows:

$$2A{e}^{-{\xi }_{\max }(1-x)}=2A{\left({\displaystyle \frac{2A}{\delta }}\right)}^{-(1-x)}=2A{\left({\displaystyle \frac{\delta }{2A}}\right)}^{1-x}={\left(2A\right)}^x{\delta }^{1-x},$$

$$\delta e^{{\xi }_{\max }x}=\delta {\left({\displaystyle \frac{2A}{\delta }}\right)}^x={\left(2A\right)}^x{\delta }^{1-x}.$$

Therefore, the upper bound of the total error is obtained

$$\Vert u^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}{\Vert \le \left(2A\right)}^x{\delta }^{1-x}+{\left(2A\right)}^x{\delta }^{1-x}=2{\left(2A\right)}^x{\delta }^{1-x},$$

when A = 1, we obtain

$$\Vert u^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}\Vert \le 2^{x+1}{\delta }^{1-x}.$$

Next, we will conduct a sensitivity analysis. First, we will discuss the sensitivity to the noise level $\delta$, which is divided into parameter sensitivity:

$${\delta }_{\max }=\ln \left({\displaystyle \frac{2A}{\delta }}\right)\propto \ln \left({\displaystyle \frac{1}{\delta }}\right),$$

when $\delta$ decreases, ${\xi }_{\max }$ increases. However, due to the logarithmic growth, the rate of increase is extremely slow.

And error sensitivity:

$$\tau =\propto {\delta }^{1-x}.$$

here, $\tau$ represents the sensitivity of error. When x is fixed, the error decreases as $\delta$ decreases. However, when x approaches 1, the sensitivity of the error to $\delta$ decreases.

Next, we discuss the sensitivity of the prior bound A, which also includes parameter sensitivity:

$${\delta }_{\max }=\ln \left(2A\right)-\ln \delta ,$$

we can observe that the dependence of parameter A is also logarithmic in nature and relatively insensitive.

And error sensitivity:

$$\tau \propto {\left(2A\right)}^x,$$

based on the above analysis, when x approaches 1, the sensitivity of the error to A blockage increases. When $x=0$, the error is independent of A.

Finally, we discuss the sensitivity of position x, which is divided into error behavior:

$$\tau \propto {\delta }^{1-x},$$

it can be observed that as x increases (i.e., moving away from the boundary), the error also increases, which is consistent with the characteristics of an ill-posed problem.

The regularization effect: At $x=0$, the error is the smallest. The error is the greatest at $x=1$.

After the above analysis, we found that in actual calculations, when the prior bound A is unknown, it is reasonable to take $A=1$. This is because the parameter selection is not very sensitive to A (logarithmically dependent) and the error estimation still maintains the Hölder-type convergence rate. Since the parameter selection is based on the worst-case analysis, it usually maintains stability in actual calculations.

The following theorem states the error estimation of Fourier regular solutions.

Theorem 6.

Let $u^{gr}(x,y,\mu ,{\alpha }_u)$ and $u_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)$ be the exact solution and the Fourier regular solution we defined for the Equation (25), respectively, assuming that Equations (27) and (28) are hold, if we select the following regularization parameter

$${\xi }_{\max }=\ln \left({\displaystyle \frac{2A}{\delta }}\right)$$

(33)

there are the following conclusions

$$\Vert u_{{\xi }_{\max }}^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}{(·)\Vert \le 2\left(2A\right)}^x{\delta }^{1-x}.$$

(34)

Proof. 

Due to the Parseval formula and Equations (26)–(29), we find

$$\begin{array}{cc}\hfill & \Vert u^{gr}(x,y,\mu ,{\alpha }_u)-u_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)\Vert \hfill \\ \hfill & =\Vert {\widehat{u}}^{gr}(x,y,\mu ,{\alpha }_u)-{\widehat{u}}_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)\Vert \hfill \\ \hfill & =\Vert {\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (|\zeta |x)-{\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (|\zeta |x){\chi }_{\max }\Vert \hfill \\ \hfill & \le \Vert {\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (|\zeta |x)-{\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (|\zeta |x){\chi }_{\max }\Vert +\Vert ({\widehat{\phi }}^{gr}(·)-{\widehat{\phi }}_{\delta }^{gr}(·)\cosh (|\zeta |x){\chi }_{\max }\Vert \hfill \\ \hfill & ={\left({\int }_{|\zeta |\ge {\xi }_{\max }}|{\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi }){\cosh (|\zeta |x)|}^{2}d\zeta \right)}^{\frac{1}{2}}+{\left({\int }_{-{\xi }_{\max }}^{+{\xi }_{\max }}|({\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi })-{\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })){\cosh (|\zeta |x)|}^{2}d\zeta \right)}^{\frac{1}{2}}\hfill \\ \hfill & ={\left({\int }_{|\zeta |\ge {\xi }_{\max }}|{\widehat{\phi }}^{gr}(\zeta ,\mu ,{\alpha }_{\phi }){\cosh (|\zeta |)|}^2{\left|{\displaystyle \frac{\cosh (|\zeta |x)}{\cosh (|\zeta |)}}\right|}^{2}d\zeta \right)}^{\frac{1}{2}}+{\left({\int }_{-{\xi }_{\max }}^{+{\xi }_{\max }}|({\widehat{\phi }}^{gr}(·)-{\widehat{\phi }}_{\delta }^{gr}(·)){\cosh (|\zeta |x)|}^{2}d\zeta \right)}^{\frac{1}{2}}\hfill \\ \hfill & ={\left({\int }_{|\zeta |\ge {\xi }_{\max }}{|{\widehat{u}}^{gr}(1,\zeta ,\mu ,{\alpha }_u)|}^2{\left|{\displaystyle \frac{\cosh (|\zeta |x)}{\cosh (|\zeta |)}}\right|}^{2}d\zeta \right)}^{\frac{1}{2}}+{\left({\int }_{-{\xi }_{\max }}^{+{\xi }_{\max }}|({\widehat{\phi }}^{gr}(·)-{\widehat{\phi }}_{\delta }^{gr}(·)){\cosh (|\zeta |x)|}^{2}d\zeta \right)}^{\frac{1}{2}}\hfill \\ \hfill & ={\left({\int }_{|\zeta |\ge {\xi }_{\max }}{|{\widehat{u}}^{gr}(1,\zeta ,\mu ,{\alpha }_u)|}^{2}4e^{2(x-1)|\zeta |}d\zeta \right)}^{\frac{1}{2}}+\cosh \left({\xi }_{\max }x\right){\left({\int }_{-{\xi }_{\max }}^{+{\xi }_{\max }}{\left|{\widehat{\phi }}^{gr}(·){\widehat{\phi }}_{\delta }^{gr}(·)d\zeta \right|}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le 2e^{x-1}{\xi }_{\max }\Vert u^{gr}(1,y,\mu ,{\alpha }_u)\Vert +e^{x{\xi }_{\max }}\Vert {\phi }^{gr}(y,\mu ,{\alpha }_{\phi })-{\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })\Vert \hfill \\ \hfill & \le 2e^{x-1}{\xi }_{\max }A+e^{x{\xi }_{\max }}\delta \hfill \\ \hfill & =2A{\left({\displaystyle \frac{2A}{\delta }}\right)}^{x-1}+{\left({\displaystyle \frac{2A}{\delta }}\right)}^x\delta \hfill \\ \hfill & ={\left(2A\right)}^x{\delta }^{1-x}+{\left(2A\right)}^x{\delta }^{1-x}\hfill \\ \hfill & =2{\left(2A\right)}^x{\delta }^{1-x}.\hfill \end{array}$$

□

We know that in specific applications, the value of A is unknown. So in this article, for ease of calculation, we give $A=1$. The relationship is as follows

$${\xi }_{\max }=\ln \left({\displaystyle \frac{2}{\delta }}\right),$$

(35)

then, we have

$$\Vert u_{{\xi }_{\max }}^{gr}(·)-u_{\delta ,{\xi }_{\max }}^{gr}{(·)\Vert \le \left(2\right)}^{x+1}{\delta }^{1-x}.$$

(36)

5. Numerical Example

We consider the following a Cauchy problem for the Laplace equation with uncertainty

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}\tilde{u}(x,y)+{\partial }_{y{y}_{gr}}\tilde{u}(x,y)=\tilde{0},\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ \tilde{u}(0,y)=\tilde{\phi }\left(y\right)=\tilde{v}{e}^{-y^2},\hfill & \hfill y\in \mathbb{R},\\ {\partial }_{x_{gr}}\tilde{u}(0,y)=\tilde{0},\hfill & \hfill y\in \mathbb{R},\end{array}\right.\end{array}$$

(37)

where $\tilde{v}\left(x\right)$ is a fuzzy-number-valued function, i.e., $\tilde{v}\left(x\right)=(-2,0,2)$, have the following expression

$$\tilde{v}\left(x\right)=\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}x+1,\hfill & \hfill x\in [-2,0),\\ 1,\hfill & \hfill x=0,\\ -{\displaystyle \frac{1}{2}}x+1,\hfill & \hfill x\in (0,2],\\ 0,\hfill & \hfill otherwise.\end{array}\right.\end{array}$$

(38)

and according to Definition 1, $v^{gr}(x,\mu ,{\alpha }_v)=(-2+2\mu )+4(1-\mu ){\alpha }_v$. Based on Note 2, we obtain the granular differential equation as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{x{x}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)+{\partial }_{y{y}_{gr}}{u}^{gr}(x,y,\mu ,{\alpha }_u)=0^{gr}(\mu ,\alpha ),\hfill & \hfill x\in (0,1),y\in \mathbb{R},\\ u^{gr}(0,y,\mu ,{\alpha }_u)={\phi }^{gr}(y,\mu ,{\alpha }_{\phi })=[(-2+2\mu )+4(1-\mu ){\alpha }_v]·e^{-y^2},\hfill & \hfill {\alpha }_u={\alpha }_v\in [0,1],y\in \mathbb{R},\\ {\partial }_x^{gr}{u}^{gr}(0,y,\mu ,{\alpha }_{\phi })=0^{gr}(\mu ,\phi ),\hfill & \hfill y\in \mathbb{R}.\end{array}\right.\end{array}$$

(39)

The variable y in the above equation is transformed by fuzzy Fourier transform, and then the exact solution of the equation is obtained by means of the variable separation method as follows

$$u^{gr}(x,y,\mu ,{\alpha }_u)=[(-2+2\mu )+4(1-\mu ){\alpha }_u]·e^{x^2-y^2}\cos \left(2xy\right),$$

(40)

and according to Note 1, the $\mu$-level sets of the exact solution can be obtained

$${\left[\tilde{u}(x,y)\right]}_{\mu }=[-2+2\mu ,2-2\mu ]·e^{x^2-y^2}\cos \left(2xy\right).$$

(41)

Now, according to the Fourier regularization method, we give the Fourier regular solution as follows

$$u_{\delta ,{\xi }_{\max }}^{gr}(x,y,\mu ,{\alpha }_u)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{+\infty }{\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })\cosh (|\xi |x){\chi }_{\max }{e}^{i\zeta y}d\zeta ,$$

(42)

where ${\chi }_{\max }$ is the characteristic function of the interval $[-{\xi }_{\max },{\xi }_{\max }]$, and ${\widehat{\phi }}_{\delta }^{gr}(\zeta ,\mu ,{\alpha }_{\phi })$ is the fuzzy Fourier transform of the measurement data ${\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })$ obtained by physical instruments, which is usually with errors. Noisy data is generated by the following methods

$${\left({\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })\right)}_i={\left({\phi }^{gr}(y,\mu ,{\alpha }_{\phi })\right)}_i+ϵ·rand{\left(size\left({\phi }^{gr}(y,\mu ,{\alpha }_{\phi })\right)\right)}_i.$$

(43)

The magnitude $\delta$ indicates the noise level of measurement data by physical instruments, and this noise level has an expression as follows:

$$\delta :\triangleq \Vert {\phi }_{\delta }^{gr}(y,\mu ,{\alpha }_{\phi })\Vert ={\left({\displaystyle \frac{1}{N_x}}\sum _{i=1}^{N_x}{|{\phi }_{\delta }^{gr}(y_i,\mu ,{\alpha }_{\phi })-{\phi }^{gr}(y_i,\mu ,{\alpha }_{\phi })|}^2\right)}^{\frac{1}{2}}.$$

(44)

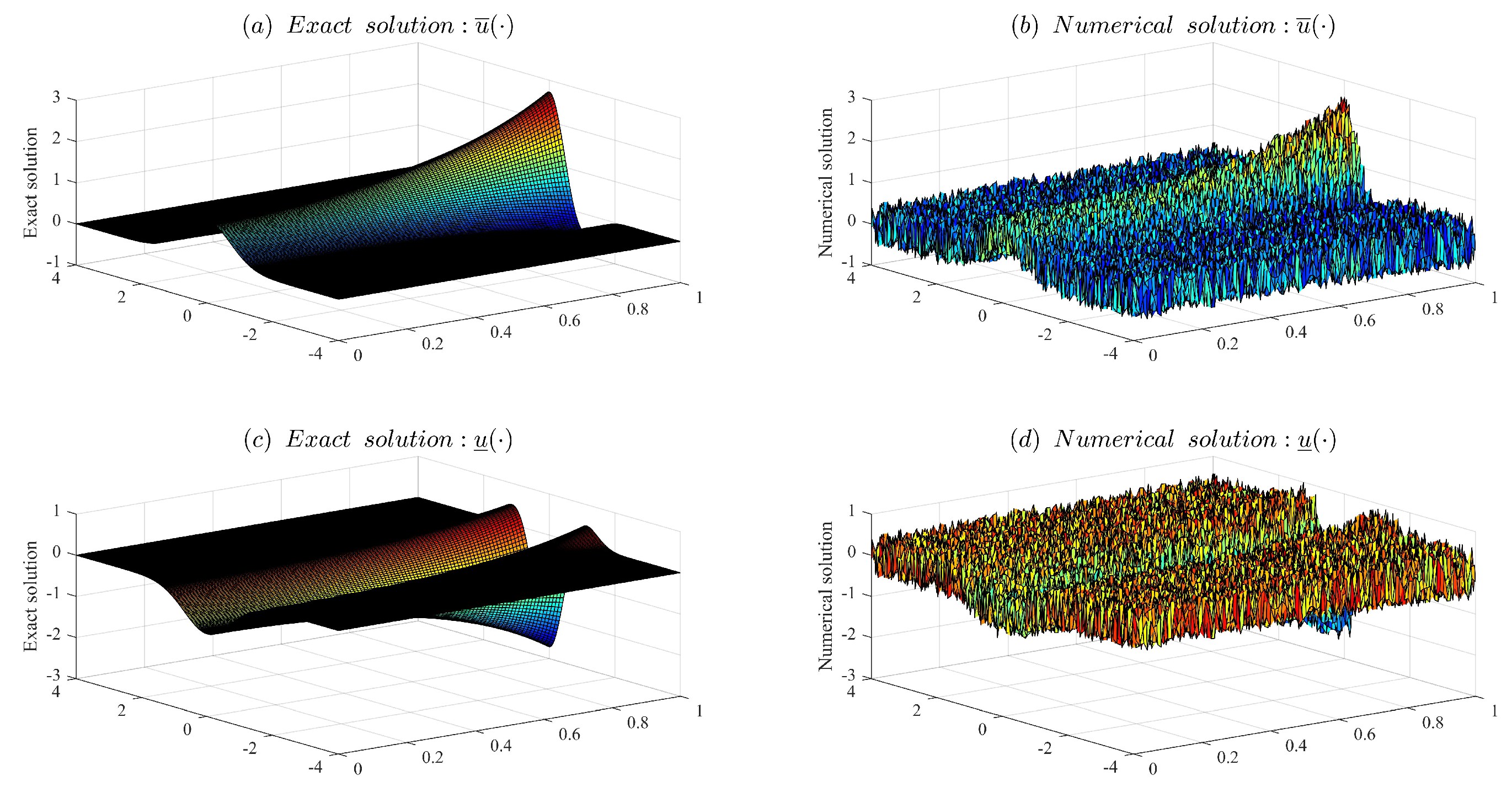
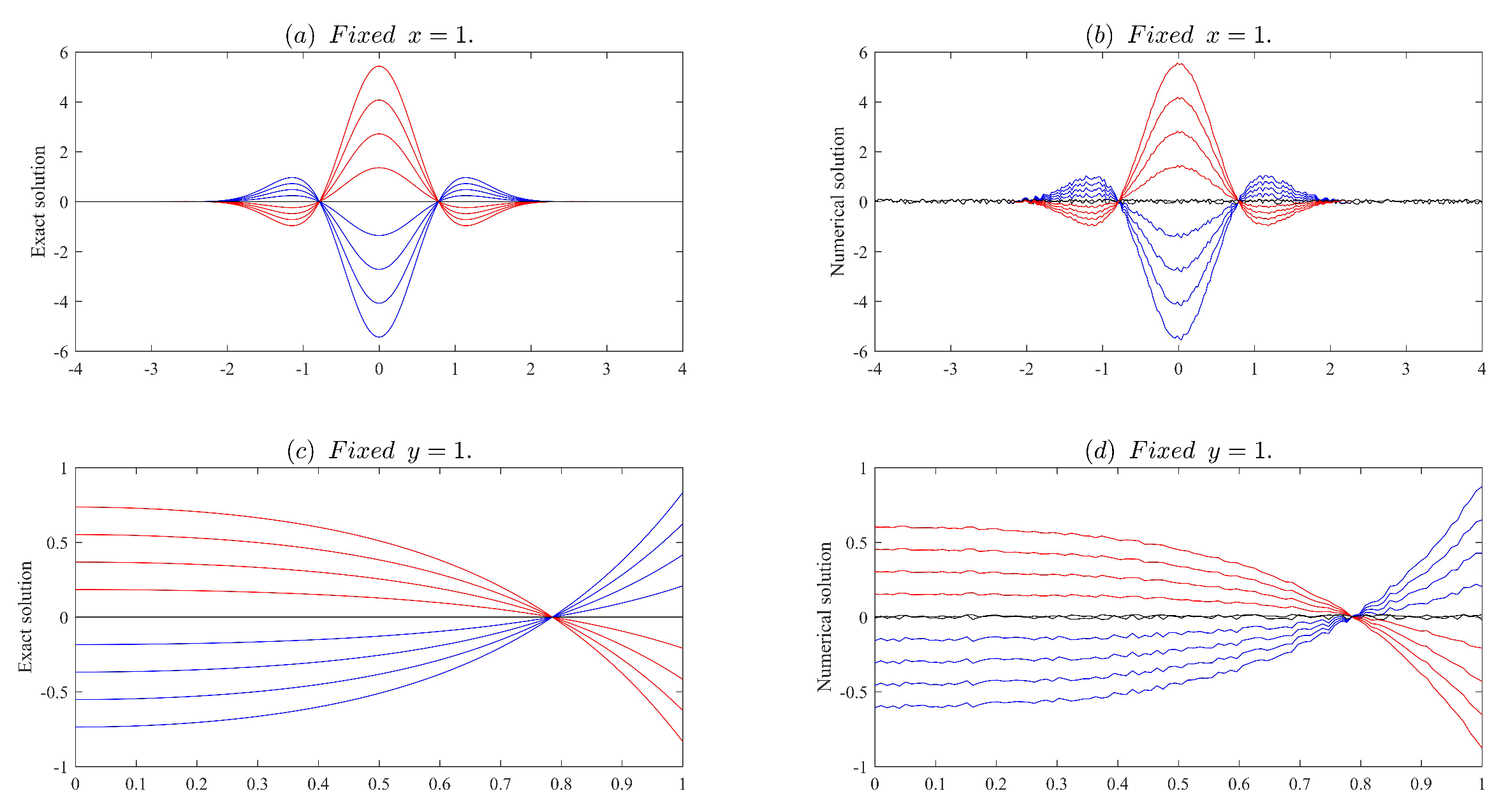
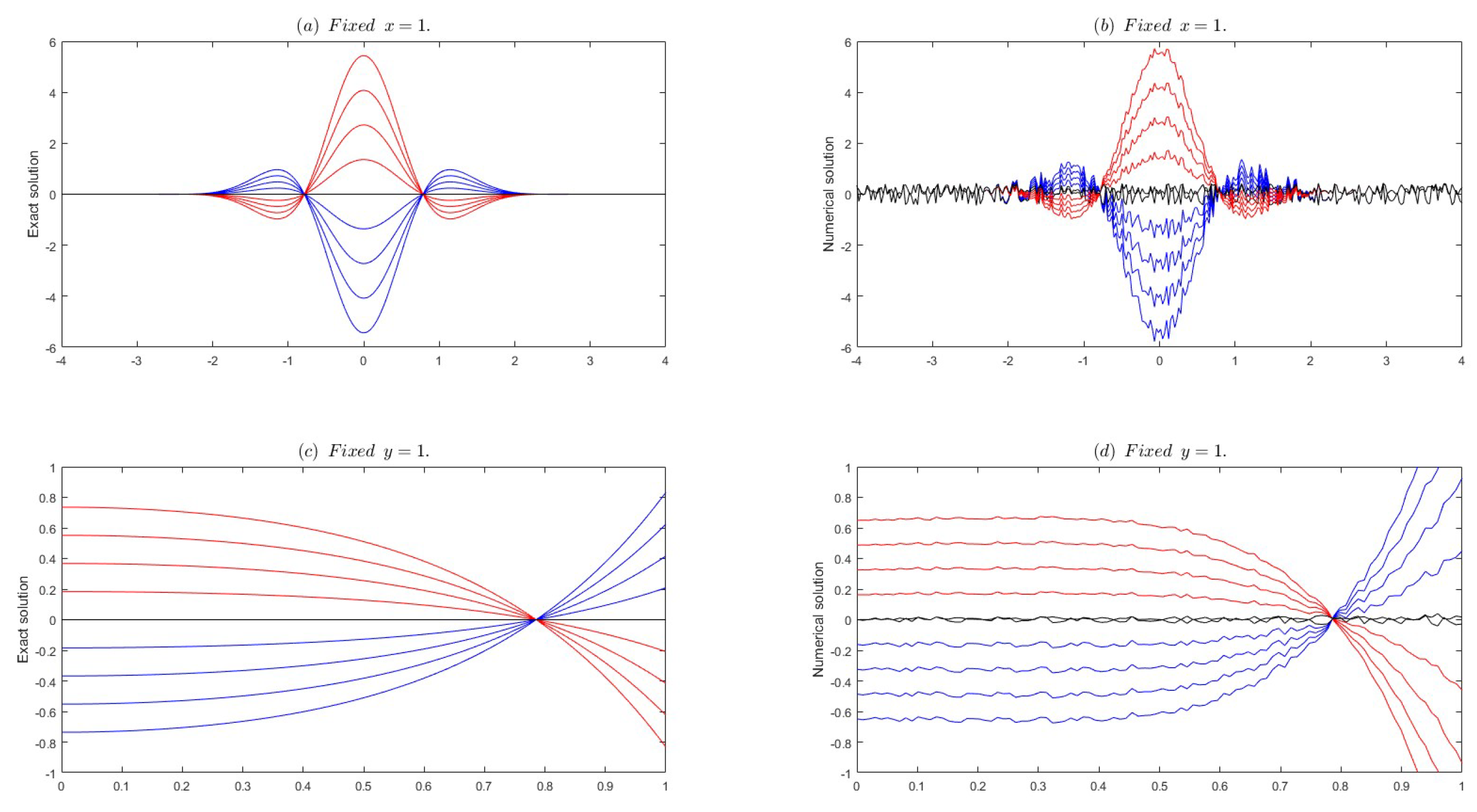
First, we present the unregularized results. Figure 1 shows the comparison between the left and right endpoints of the exact solution and the left and right endpoints of the numerical solution when the noise level $\delta =6\times {10}^{-2}$.

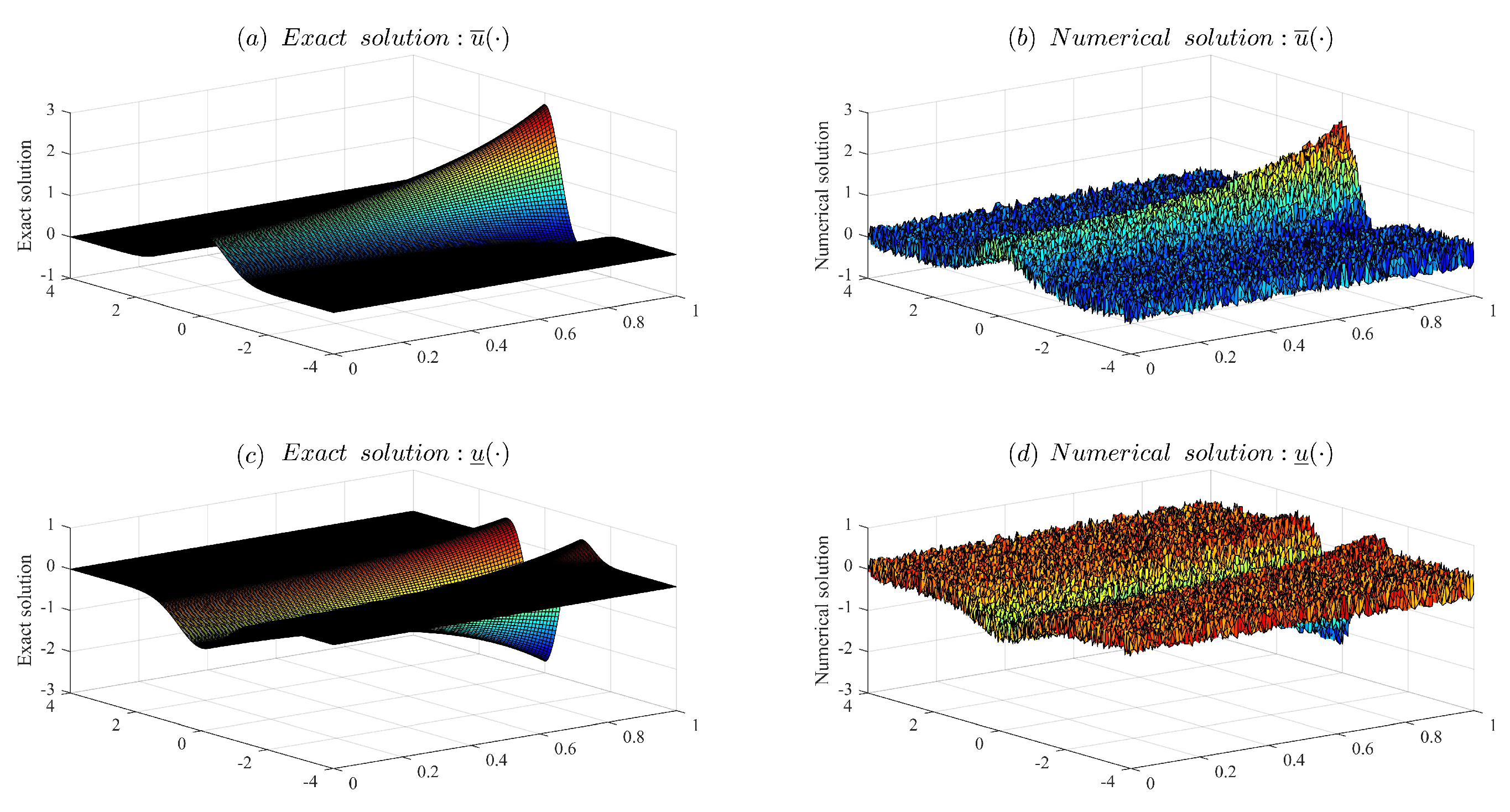
Figure 2 shows the comparison between the left and right endpoints of the exact solution and the left and right endpoints of the numerical solution when the noise level $\delta =6\times {10}^{-4}$.

It can be clearly seen from the figure that as the noise level of the input data decreases, the accuracy of unregularization resolution becomes higher and higher. Therefore, when the input data is not regularized, even very small perturbations in the input data can lead to significant changes in the solution, making the numerical solution extremely unstable. Therefore, in order to overcome this instability, the regularization method needs to be used.

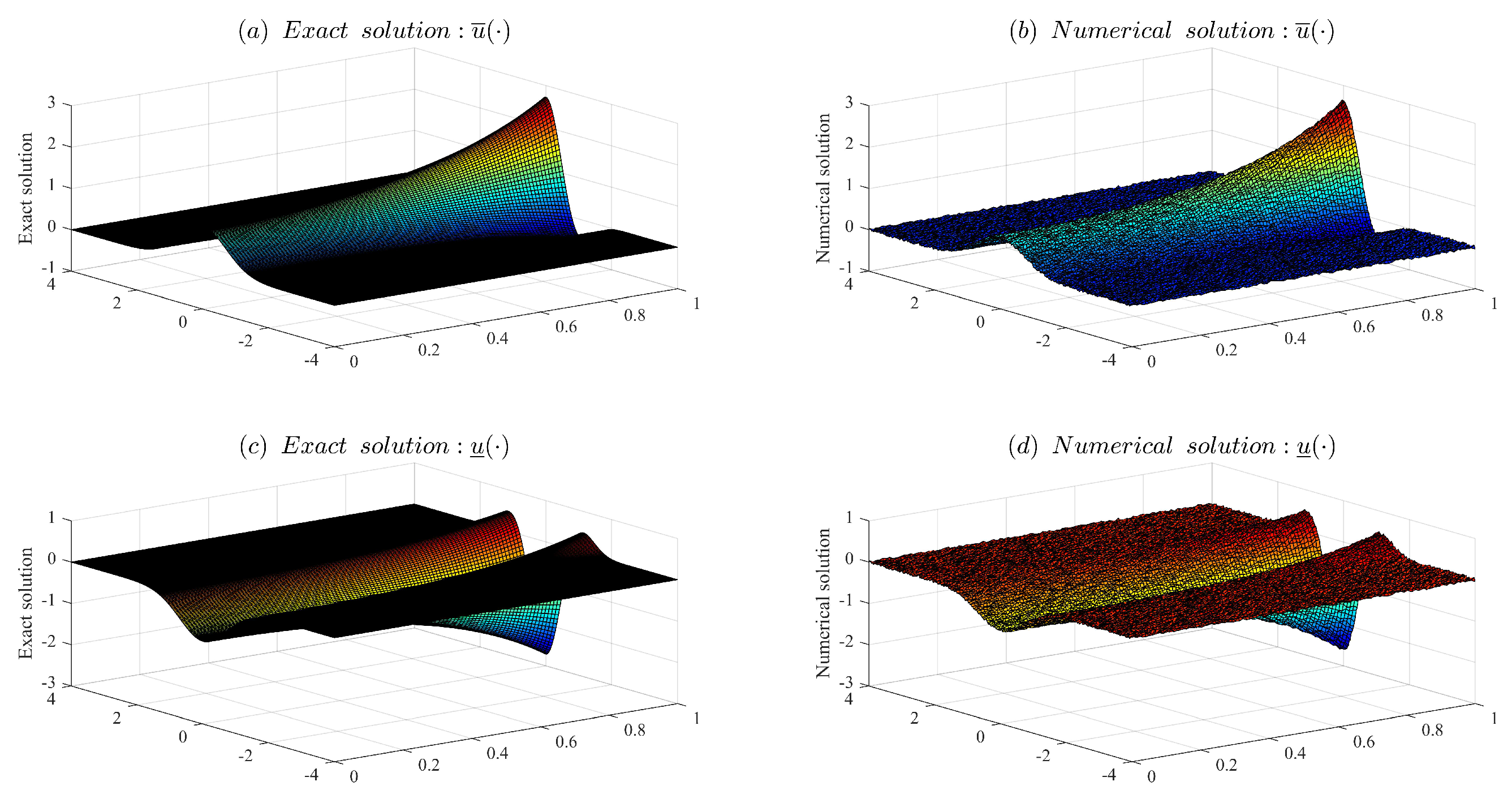
Figure 3 shows the comparison of the relationship between the numerical solution obtained by Fourier regularization and the exact solution when the regularization parameter ${\xi }_{\max }=0.7765$ and the noise level $\delta =6\times {10}^{-2}$.

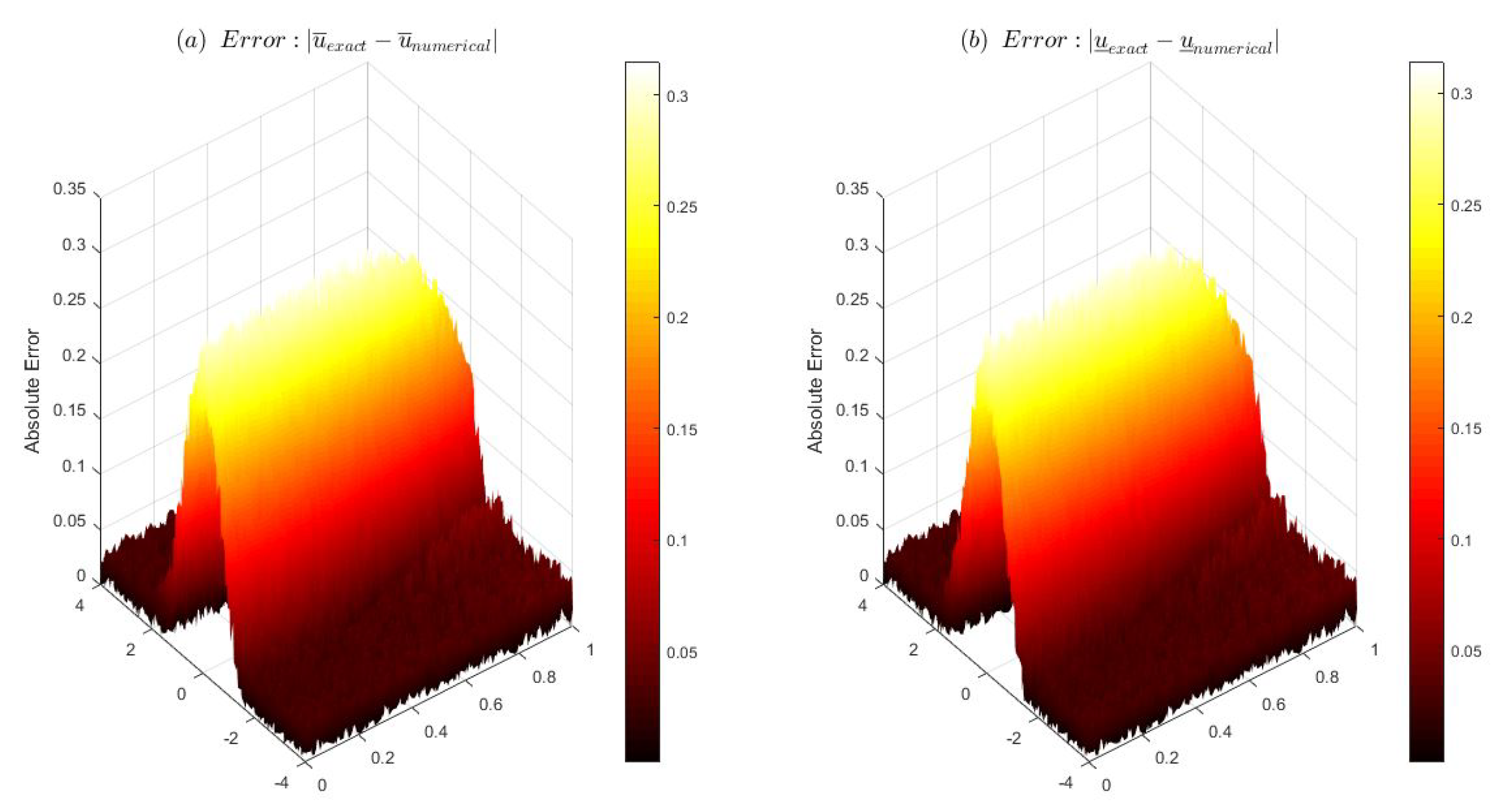
Figure 4 shows the spatial distribution of the absolute error between the numerical solution and the exact solution of the Fourier regularization method. Through the visualization of the three-dimensional error surface, we can intuitively analyze the propagation characteristics of the error within the computational domain.

Figure 4a corresponds to the error distribution at the left endpoint of the solution, and its surface shape reveals the convergence performance of the numerical method in different spatial regions. This is consistent with the theoretical predicted error, verifying the good stability of the algorithm in this region.

Figure 4b corresponds to the error distribution at the right endpoint of the solution, presenting similar distribution characteristics to those of the left endpoint of the solution. The overall topological structure of the error surface indicates that the Fourier regularization method can effectively control the global propagation of the error.

From the above analysis, it is clearly evident that when the regularization parameter is selected according to Equation (33), the result of Fourier regularization approaches the exact solution very stably. This further verifies the correctness and practicality of our theory.

In order to demonstrate the stability of the Fourier regularization method under the concept of granular differentiability, we fix $x=1$ and $y=1$, respectively, and take $\mu =0, 0.25, 0.5, 0.75, 1$ to observe the relationship between the numerical solution and the exact solution obtained by the Fourier regularization method under the concept of granular differentiability. Among them, the red curve represents the left endpoint of the solution, the blue curve represents the right endpoint of the solution, and the black curve represents the solution when $\mu =1$. From this Figure 5, we can also find that when $\mu =1$, under the concept of granular differentiability, the solution obtained through the Fourier regularization method is completely consistent with the solution obtained in the classical sense.

The following figure shows the results of taking $\mu =0, 0.25, 0.5, 0.75$ respectively.

From this example, it can be seen that for ill-posedness problems, perturbations of the input data can cause significant changes in the solution, and regularization methods need to be used to stabilize the numerical solution. For the Fourier regularization method we gave, when the regularization parameter takes values according to Equation (33), the stability between the obtained numerical solution and the exact solution is the best. Furthermore, we also found that when $\mu =1$, the results obtained under the concept of particle differentiability are completely consistent with those in the classical sense. This further proves the convenience and accuracy of the method we gave in solving the Cauchy problem of the Laplace equation.

In order to further verify the effectiveness and practicability of the Fourier regularization method, we also compared the Fourier regularized solutions corresponding to different regularization parameters with the exact solutions. As shown in the figure below:

Figure 6 and Figure 7 show the comparison between the Fourier regular solution and the exact solution when the regularization parameter is ${\xi }_{\max }=1.2014$ and ${\xi }_{\max }=0.3402$, respectively. The results show that for data with noise, if the regularization parameter is set too large or too small, it will affect the outcome of Fourier regularization.

From the above theoretical analysis and numerical examples, it is not difficult to observe that the approach we have described for solving the Cauchy problem of the Laplace equation with uncertain parameters using the Fourier regularization method possesses obvious theoretical simplicity in terms of implementing fuzzy operations and preserving the structure of the solution. We have conducted a detailed analysis of the challenges faced by different methods when applied to unbounded regions and fuzzy environments. Eventually, we discovered the convenience of using the Fourier regularization method in solving such problems. We have demonstrated that, in the context of fuzzy uncertainty, the convergence estimates we derived are consistent in form with the optimal convergence rates in the classical deterministic theory. This provides a theoretical verification of the effectiveness of our method.

6. Conclusions and Prospect

This paper studies the Cauchy problem of the Laplace equation with uncertain parameters and proposes a method based on Fourier regularization to solve this problem. Specifically, the main contributions and achievements of this paper are as follows: Firstly, this paper defines the Laplace equation with uncertain parameters, where the uncertain parameters are represented by fuzzy numbers. This representation method can effectively handle the uncertainties in practical problems and make the model closer to the real situation. Under the concept of granular differentiability, the Laplace equation with uncertain parameters is transformed into a granular differential equation. This transformation not only provides a theoretical basis for the subsequent solution but also offers a new perspective for dealing with fuzzy parameters. Secondly, this paper proposes the Fourier regularization method to solve the Cauchy problem of the Laplace equation with uncertain parameters. By introducing the regularization term, the ill-posedness of the Cauchy problem is effectively overcome, and the numerical solution is stabilized. The granular representation of the regularization solution is given, which not only enriches the theoretical system of the regularization method but also provides a specific computational framework for practical applications. Through two theorems, this paper proves in detail the error estimation and convergence of the proposed regularization method. These theoretical results provide a solid mathematical foundation for the effectiveness and reliability of the method, ensuring its stability in practical applications. Finally, through numerical experiments, this paper verifies the stability and practicability of the proposed method. The experimental results show that this method can effectively handle the Cauchy problem of the Laplace equation with uncertain parameters. Moreover, under specific conditions (such as when $\mu =1$), the obtained results are completely consistent with those in the classical sense, further demonstrating the effectiveness of the proposed method.

Although this paper has made significant progress in dealing with the Cauchy problem of Laplace equations with uncertain parameters, there are still some potential research directions worthy of further exploration. This paper mainly studies the Fourier regularization method. In the future, other regularization methods, such as Tikhonov regularization and iterative regularization, can be explored to further improve the stability and accuracy of the solution. In this paper, uncertain parameters are represented by fuzzy numbers. In the future, more complex uncertainty models, such as random fuzzy numbers and interval fuzzy numbers, can be considered to better describe the uncertainties in practical problems. The method proposed in this paper shows good stability and practicability in numerical experiments. In the future, it can be applied to more practical fields, such as engineering, physics, finance, etc., to solve the uncertainties and inappropriateness in practical problems.

In conclusion, this paper has made significant progress in dealing with the Cauchy problem of the Laplace equation with uncertain parameters, providing new ideas and methods for subsequent research. Future research can be further deepened in both theoretical and application aspects to promote the development of related fields.