Hybrid Euler–Lagrange Approach for Fractional-Order Modeling of Glucose–Insulin Dynamics

Abstract

We propose a hybrid Caputo–Lagrange Discretization Method (CLDM) for the fractional-order modeling of glucose–insulin dynamics. The model incorporates key physiological mechanisms such as glucose suppression, insulin activation, and delayed feedback with memory effects captured through Caputo derivatives. Analytical results establish positivity, boundedness, existence, uniqueness, and Hyers–Ulam stability. Numerical simulations confirm that the proposed method improves accuracy and efficiency compared with the Residual Power Series Method and the fractional Runge–Kutta method. Sensitivity analysis highlights fractional order $\theta$ as a biomarker for metabolic memory. The findings demonstrate that CLDM offers a robust and computationally efficient framework for biomedical modeling with potential applications in diabetes research and related physiological systems.

1. Introduction

The glucose–insulin regulatory axis is a tightly coupled, nonlinear feedback system in which hepatic glucose production, peripheral uptake, and pancreatic $\beta$-cell secretion interact across multiple timescales and pathways. These interactions generate threshold effects, delays, and history dependence, which complicate both qualitative analyses and quantitative prediction. From a public health perspective, improving the fidelity of mathematical models that capture such mechanisms is highly consequential: Diabetes mellitus imposes substantial clinical and economic burdens worldwide with hundreds of millions affected and costs measured in the hundreds of billions of dollars annually [1,2]. Hence, mechanistic models that reproduce observed dynamics and enable reliable scenario analysis can inform screening, treatment, and policy.

Classical formulations based on integer-order differential equations often fall short when reproducing long-range dependence (“metabolic memory”), delayed insulin action, and nonlocal feedback intrinsic to endocrine regulation. Fractional calculus offers a principled extension that embeds memory and hereditary effects via nonlocal operators, thereby enhancing descriptive and predictive power across engineering, physics, and the life sciences [3,4,5,6,7,8,9]. In mathematical biology and medicine, fractional models have been fruitfully deployed to tumor immune systems, emerging infections, and complex physiological processes [10,11,12]. Within endocrinology in particular, a growing body of work demonstrates that fractional-order glucose–insulin models better capture delayed responses and persistent deviations than their integer-order counterparts [13,14,15,16,17,18,19,20,21,22,23].

Beyond application-level evidence, the methodological ecosystem for fractional modeling is now mature. On the analytical side, stability notions including Hyers–Ulam–Rassias–type robustness provide perturbation-trajectory bounds suitable for uncertain physiological parameters and noisy measurements [24,25]. Numerically, well-studied discretizations—predictor–corrector schemes, interpolation-based and Runge– Kutta-type methods—have been adapted to fractional dynamics with rigorous convergence guarantees [26,27,28,29]. Foundational contributions to fractional state equations and anomalous transport further motivate memory-aware modeling in complex systems [30,31]. Recent extensions to generalized operators (e.g., Caputo–Hadamard) continue to broaden the available toolkit for stochastic and Langevin-type dynamics relevant to physiology [32].

The broader literature further highlights the versatility of fractional operators in nonlinear science [33,34,35,36], epidemiology [37,38,39], and physiology [40,41,42,43,44,45,46]. Compared with these works, our contribution lies in applying a hybrid discretization tailored to the glucose–insulin system, supported by rigorous proofs of existence, uniqueness, boundedness, and Hyers–Ulam stability, along with sensitivity analysis that interprets the fractional order $\theta$ as a biomarker of metabolic memory.

Motivated by these considerations, we formulate and analyze a fractional-order glucose–insulin model in the Caputo sense. The model incorporates the core physiological mechanisms—insulin-stimulated uptake, hepatic suppression, threshold-triggered secretion, and delayed feedback—within a memory-aware differential framework. On the numerical side, we introduce a hybrid Caputo–Lagrange Discretization Method (CLDM) that couples a Euler-type model with Lagrange interpolation to approximate Caputo integrals efficiently while preserving qualitative features such as positivity and boundedness. Our analytical contributions include well-posedness (existence/uniqueness), a priori bounds, and Hyers–Ulam stability estimates which quantify the robustness of trajectories to modeling and data perturbations in the spirit of [24,25]. The numerical contributions complement established fractional integrators [26,27] and are evaluated against widely used alternatives such as Residual Power Series and fractional Runge–Kutta variants, following the comparative ethos of recent fractional biomedical studies [13,14,15,16,17,18,19,20,21,22,23].

My contributions to this work: (i) We present a Caputo fractional glucose–insulin model with rigorous analysis of positivity, boundedness, existence, uniqueness, and Hyers–Ulam stability. (ii) We develop CLDM, a hybrid discretization with favorable accuracy–cost trade-offs for nonlocal operators, situating it among modern fractional solvers [26,27,28]. (iii) We deliver numerical experiments and sensitivity analyses demonstrating the physiological plausibility of fractional dynamics and the performance of CLDM relative to benchmark schemes; the study connects to contemporary applications of fractional modeling across physiology and epidemiology [7,8,37,38,39,41,42,43,44,45,46].

While our analysis is conducted in the Caputo sense, the modeling and numerical principles are extensible to other nonlocal kernels (e.g., nonsingular or fractal–fractional variants) as well as to related problems in computer–virus dynamics and complex nonlinear systems [8,9,34,35,36].

The manuscript presents a fractional-order glucose–insulin model employing Caputo derivatives and a hybrid computational framework (CLDM). However, the results substantially overlap with prior studies on fractional modeling of glucose–insulin dynamics, many of which have already addressed similar theoretical aspects such as the positivity, boundedness, existence and uniqueness of solutions, as well as Hyers–Ulam stability (see, e.g., references [13,14,15,16,17,18,19,20,21,22,23]).

While the current paper revisits these analyses within a comparable mathematical structure, it does not sufficiently delineate how the proposed approach advances the state of the art. The numerical comparisons with existing methods (e.g., RPSM and FRK) remain heuristic, and the purported improvements in accuracy or stability are not rigorously demonstrated. To enhance the originality and scientific value of the paper, the authors should explicitly clarify the following: the specific methodological innovation introduced by the CLDM relative to existing fractional discretization schemes; any new theoretical results or convergence guarantees not previously established; and whether the proposed model yields novel biological insights or predictive capabilities that distinguish it from prior fractional glucose–insulin formulations. Without such clarification, the novelty and contribution of the manuscript remain unclear, and the work risks being perceived as a reiteration of existing studies rather than a substantive advancement.

This paper is structured as follows. Section 2 recalls Caputo operators and preliminaries. Section 3 states the model. Section 4, Section 5 and Section 6 establish the analytical results, including Hyers–Ulam stability. Section 7 details CLDM and its implementation. Section 8 reports simulations and comparisons. Section 9 and Section 10 discuss implications and conclude.

2. Preliminaries

In this section, we provide essential definitions and properties of Caputo fractional derivatives as well as other relevant concepts needed to understand the methods and models discussed in this paper. This will serve as a foundation for readers who are not familiar with fractional calculus.

The Caputo fractional derivative of order $\theta \in (0,1]$ of a function $f\left(t\right)$ is defined as shown below:

$$D_t^{\theta }f\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\theta )}}{\int }_0^t{\displaystyle \frac{f^{(\lfloor \theta \rfloor )}\left(\tau \right)}{{(t-\tau )}^{\theta }}}d\tau ,$$

where $\Gamma (·)$ is the Gamma function, $\lfloor \theta \rfloor$ is the integer part of $\theta$, and $f^{(\lfloor \theta \rfloor )}\left(\tau \right)$ denotes the $\lfloor \theta \rfloor$-th derivative of $f\left(t\right)$. This definition is useful for modeling systems where past states have a memory effect, which is particularly relevant in biological processes like glucose–insulin dynamics.

The Caputo fractional derivative exhibits several important properties that are critical for understanding its behavior in modeling dynamic systems:

• Linearity: The Caputo fractional derivative is linear, meaning that for any constants $\alpha$ and $\beta$, and functions $f\left(t\right)$ and $g\left(t\right)$,

  $$D_t^{\theta }\left(\alpha f\left(t\right)+\beta g\left(t\right)\right)=\alpha D_t^{\theta }f\left(t\right)+\beta D_t^{\theta }g\left(t\right).$$
• Initial Conditions: The Caputo derivative allows for standard initial conditions of integer-order differential equations. This is particularly useful for applications in biomedical modeling, where initial conditions are typically well defined based on empirical data.
• Derivative of a Constant Function: The fractional derivative of a constant function is zero:

  $$D_t^{\theta }C=0\mathrm{for}\mathrm{any}\mathrm{constant}C.$$
• Power Function Property: For a power function $t^{\alpha }$, the Caputo fractional derivative is given by the following:

  $$D_t^{\theta }{t}^{\alpha }={\displaystyle \frac{\Gamma (\alpha +1)}{\Gamma (\alpha +1-\theta )}}{t}^{\alpha -\theta }.$$
  This property is useful in understanding how the fractional derivative interacts with power-law behaviors, which are often encountered in physical and biological systems.

• The fractional integral of order $\theta$ of a function $f\left(t\right)$ is defined as

$$I_t^{\theta }f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}f\left(\tau \right)d\tau .$$

The fractional integral is related to the fractional derivative through the following relationship:

$$D_t^{\theta }{I}_t^{\theta }f\left(t\right)=f\left(t\right).$$

In addition to the Caputo fractional derivative, several other concepts are used throughout this paper:

• The Euler method is a simple numerical technique for approximating the solutions of differential equations. It is often used as a basis for more advanced methods, such as the hybrid Euler–Lagrange method introduced in this paper.
• Lagrange interpolation is a method of constructing polynomials that pass through a given set of data points. In the hybrid approach, this technique is used to approximate the fractional derivatives and simulate the memory effects in the glucose–insulin model.
• The existence and uniqueness of solutions to the proposed fractional-order model are proven using fixed-point theory, which guarantees that a unique solution exists under certain conditions, ensuring the validity of the numerical simulations.

• These foundational concepts will be used throughout the paper to develop and analyze the proposed fractional-order model and its numerical implementation.

Lemma 1 (Fractional Grönwall inequality).

Let $0<\theta \le 1$, $T>0$, and let $u:[0,T]\to [0,\infty )$ be locally integrable. Assume there exist a nondecreasing function $a:[0,T]\to [0,\infty )$ and a constant $B\ge 0$ such that, for all $t\in [0,T]$,

$$u\left(t\right)\le a\left(t\right)+{\displaystyle \frac{B}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}u\left(\tau \right)d\tau .$$

(1)

Then,

$$u\left(t\right)\le a\left(t\right)E_{\theta }\left(B{t}^{\theta }\right),t\in [0,T],$$

(2)

where ${\displaystyle E_{\theta }\left(z\right)={\displaystyle \sum _{k=0}^{\infty }}\frac{z^k}{\Gamma (\theta k+1)}}$ is the one-parameter Mittag–Leffler function.

Moreover, if $a\left(t\right)=a_0{\displaystyle \frac{t^{\theta }}{\Gamma (\theta +1)}}$ for some $a_0\ge 0$, then

$$u\left(t\right)\le {\displaystyle \frac{a_0{t}^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(B{t}^{\theta }\right),t\in [0,T].$$

(3)

Sketch of proof.

Define the Volterra operator $\left(\mathcal{V}u\right)\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}u\left(\tau \right)d\tau$. Then, (1) reads $u\le a+B\mathcal{V}u$. Iterating yields

$$u\le a+B\mathcal{V}a+B^2{\mathcal{V}}^{2}a+\cdots$$

and for nondecreasing a, one checks inductively that ${\mathcal{V}}^{k}a\left(t\right)\le {\displaystyle \frac{a\left(t\right)t^{k\theta }}{\Gamma (k\theta +1)}}$. Hence,

$$u\left(t\right)\le a\left(t\right){\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(B{t}^{\theta }\right)}^k}{\Gamma (\theta k+1)}}=a\left(t\right)E_{\theta }\left(B{t}^{\theta }\right),$$

which gives (2). The specialization (3) follows by taking $a\left(t\right)=a_0{t}^{\theta }/\Gamma (\theta +1)$. □

Corollary 1 (Constant kernel).

Under the assumptions of Lemma 1, if $a\left(t\right)=a_0{\displaystyle \frac{t^{\theta }}{\Gamma (\theta +1)}}$ and the kernel constant is $B=L_{\Omega }\ge 0$, then

$$u\left(t\right)\le {\displaystyle \frac{a_0{t}^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{t}^{\theta }\right),t\in [0,T].$$

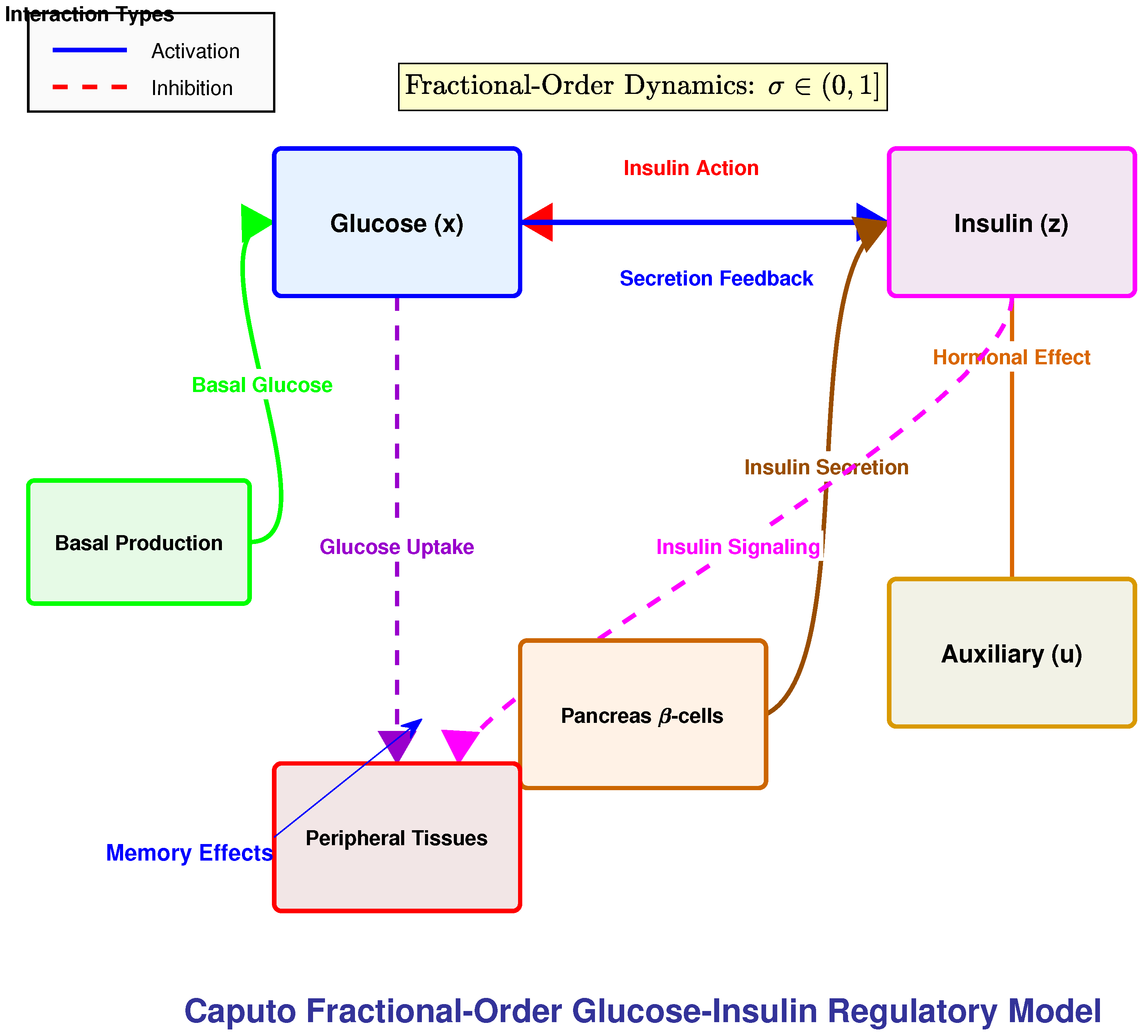
3. Model Description and Fractional Extensions

3.1. Physiological Motivation and Model Rationale

The glucose–insulin regulatory system exhibits highly nonlinear dynamics that involve delays, thresholds, and memory effects. Classical integer-order models often fail to capture the persistent influence of past states on current behavior—a phenomenon known in diabetology as metabolic memory. Fractional-order calculus provides a natural framework for such systems, as the nonlocality of fractional derivatives inherently encodes memory and hereditary effects. Among several formulations, the Caputo derivative is adopted here due to its compatibility with classical initial conditions, thereby facilitating the integration of empirical and clinical data.

We propose a four-dimensional fractional-order model that extends classical approaches by explicitly incorporating the following physiological mechanisms:

• Glucose utilization through both insulin-dependent and insulin-independent pathways.
• A threshold-triggered secretion mechanism, reflecting the switch-like response of pancreatic $\beta$-cells.
• Delayed regulatory effects, represented by an auxiliary hormonal process.
• Explicit representation of basal equilibrium states for glucose and insulin.

3.2. Model Formulation

Let $\theta \in (0,1]$ denote the fractional order. The system is governed by the following nonlinear Caputo fractional differential equations:

$$\begin{array}{cccc}\hfill {}^C\mathcal{D}_{0,t}^{\theta }\mathbf{x}\left(t\right)& =-({\tau }_1+\mathbf{y}\left(t\right))\mathbf{x}\left(t\right)+{\tau }_1{\mathbf{x}}_b,\hfill & \hfill \mathbf{x}\left(0\right)& ={\tau }_0,\hfill \\ \hfill {}^C\mathcal{D}_{0,t}^{\theta }\mathbf{y}\left(t\right)& =-{\tau }_2\mathbf{y}\left(t\right)+{\tau }_3\left(\mathbf{z}\left(t\right)-{\mathbf{z}}_b\right),\hfill & \hfill \mathbf{y}\left(0\right)& =0,\hfill \\ \hfill {}^C\mathcal{D}_{0,t}^{\theta }\mathbf{z}\left(t\right)& ={\tau }_4{\left[\mathbf{x}\left(t\right)-{\tau }_5\right]}^{+}\mathbf{u}\left(t\right)-{\tau }_6\left(\mathbf{z}\left(t\right)-{\mathbf{z}}_b\right),\hfill & \hfill \mathbf{z}\left(0\right)& ={\mathbf{z}}_b+{\tau }_7,\hfill \\ \hfill {}^C\mathcal{D}_{0,t}^{\theta }\mathbf{u}\left(t\right)& =1-\alpha \mathbf{u}\left(t\right),\hfill & \hfill \mathbf{u}\left(0\right)& =0.\hfill \end{array}$$

(4)

Here, the threshold function is defined as

$${[\mathbf{x}\left(t\right)-{\tau }_5]}^{+}=\left\{\begin{array}{cc}\mathbf{x}\left(t\right)-{\tau }_5,\hfill & \mathbf{x}\left(t\right)>{\tau }_5,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

3.3. Physiological Interpretation

The state variables represent the following:

• $\mathbf{x}\left(t\right)$: blood glucose concentration (mg/dL).
• $\mathbf{y}\left(t\right)$: insulin action on glucose disposal (1/min), representing insulin-mediated uptake efficiency.
• $\mathbf{z}\left(t\right)$: plasma insulin concentration (μU/mL).
• $\mathbf{u}\left(t\right)$: auxiliary variable modeling delayed hormonal processes (e.g., hepatic glucose suppression).

Key physiological mechanisms include the following:

• Glucose suppression: $-({\tau }_1+\mathbf{y}\left(t\right))\mathbf{x}\left(t\right)$ combines basal utilization and insulin-driven clearance.
• Basal glucose production: ${\tau }_1{\mathbf{x}}_b$ represents hepatic glucose release at rest.
• Insulin activation: ${\tau }_3(\mathbf{z}\left(t\right)-{\mathbf{z}}_b)$ quantifies insulin-stimulated uptake above basal levels.
• Threshold-regulated secretion: ${[\mathbf{x}\left(t\right)-{\tau }_5]}^{+}$ mimics the switch-like activation of $\beta$-cells.
• Hormonal clearance: $-{\tau }_6(\mathbf{z}\left(t\right)-{\mathbf{z}}_b)$ captures insulin degradation by liver and kidneys.
• Delayed feedback: The auxiliary dynamics $1-\alpha \mathbf{u}\left(t\right)$ reproduce slow hormonal effects.

3.4. Parameters

The model parameters are summarized in

Table 1. Physiological parameters of the fractional glucose–insulin model.

Parameter	Physiological Meaning	Units
${\tau }_0$	Initial glucose concentration (fasting measurement).	mg/dL
${\tau }_1$	Insulin-independent glucose disposal rate and baseline hepatic production.	${\min }^{-1}$
${\tau }_2$	Decay rate of insulin action (lifetime of receptor binding and downstream signaling).	${\min }^{-1}$
${\tau }_3$	Insulin sensitivity coefficient; reduction indicates insulin resistance.	mL/μU/min
${\tau }_4$	Maximal pancreatic insulin secretion gain above threshold.	μU/mL/min
${\tau }_5$	Threshold glucose level for insulin secretion activation.	mg/dL
${\tau }_6$	Clearance rate of plasma insulin (hepatic/renal degradation).	${\min }^{-1}$
${\tau }_7$	Initial deviation of insulin from basal level.	μU/mL
${\mathbf{x}}_b$	Basal glucose level (fasting equilibrium).	mg/dL
${\mathbf{z}}_b$	Basal insulin level at equilibrium.	μU/mL
$\alpha$	Decay rate of the auxiliary delayed effect $\mathbf{u}\left(t\right)$.	${\min }^{-1}$

. Each parameter has a clear physiological interpretation and is consistent with experimental data.

3.5. Rationale for Fractional Order

The Caputo fractional derivative ${}^C\mathcal{D}_{0,t}^{\theta }$ accounts for the system’s memory dependence. Smaller values of $\theta$ ($\theta <1$) emphasize long-range effects and delayed regulation, while $\theta =1$ recovers the classical ODE formulation. Thus, $\theta$ serves as a tunable biomarker for metabolic memory and provides flexibility in modeling both normal and pathological states.

3.6. Model Assumptions

The system is developed under the following assumptions:

• The plasma compartment is homogeneous and well mixed.
• Counter-regulatory hormones (e.g., glucagon) are indirectly accounted for in basal terms.
• The auxiliary variable $\mathbf{u}\left(t\right)$ suffices to approximate delayed secretion without explicit time delays.
• Parameters are constant for a given subject during the observation period.

See Figure 1 for a schematic of the fractional-order glucose–insulin model.

4. Non-Negativity and Boundedness of Solutions

We consider $0<\theta \le 1$ and the Caputo operator ${}^C\mathcal{D}_{0,t}^{\theta }$. All parameters are assumed positive unless otherwise stated, with ${\mathbf{x}}_b,{\mathbf{z}}_b\ge 0$. The system under study is

$$\begin{array}{cccc}\hfill {}^C\mathcal{D}_{0,t}^{\theta }x\left(t\right)& =-({\tau }_1+y\left(t\right))x\left(t\right)+{\tau }_1{x}_b,\hfill & \hfill x\left(0\right)& ={\tau }_0,\hfill \\ \hfill {}^C\mathcal{D}_{0,t}^{\theta }y\left(t\right)& =-{\tau }_{2}y\left(t\right)+{\tau }_3\left(z\left(t\right)-z_b\right),\hfill & \hfill y\left(0\right)& =0,\hfill \\ \hfill {}^C\mathcal{D}_{0,t}^{\theta }z\left(t\right)& ={\tau }_4{[x\left(t\right)-{\tau }_5]}^{+}u\left(t\right)-{\tau }_6\left(z\left(t\right)-z_b\right),\hfill & \hfill z\left(0\right)& =z_b+{\tau }_7,\hfill \\ \hfill {}^C\mathcal{D}_{0,t}^{\theta }u\left(t\right)& =1-\alpha u\left(t\right),\hfill & \hfill u\left(0\right)& =0.\hfill \end{array}$$

Lemma 2.

Let v satisfy ${}^C\mathcal{D}_{0,t}^{\theta }v\left(t\right)\le -\lambda v\left(t\right)+g\left(t\right)$ on $[0,T]$ with $\lambda >0$ and $v\left(0\right)\le M$. Then

$$v\left(t\right)\le M{E}_{\theta }(-\lambda t^{\theta })+{\displaystyle \frac{1}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}{E}_{\theta ,\theta }\left(-\lambda {(t-\tau )}^{\theta }\right)g\left(\tau \right)d\tau .$$

In particular, if $M\ge 0$ and $g\equiv 0$, the non-negative cone ${\mathbb{R}}_{\ge 0}$ is forward invariant.

Theorem 1 (Non-negativity).

If $x\left(0\right)={\tau }_0\ge 0$, $y\left(0\right)=0$, $z\left(0\right)=z_b+{\tau }_7\ge z_b$, and $u\left(0\right)=0$, then every solution $(x,y,z,u)$ of (4) satisfies

$$x\left(t\right)\ge 0,y\left(t\right)\ge 0,z\left(t\right)\ge z_b,u\left(t\right)\ge 0,\forall t\in [0,T].$$

Proof. 

Auxiliary u. The linear Caputo IVP ${}^C\mathcal{D}_{0,t}^{\theta }u=1-\alpha u$, $u\left(0\right)=0$, has explicit solution

$$u\left(t\right)={\displaystyle \frac{1}{\alpha }}\left(1-E_{\theta }(-\alpha t^{\theta })\right),0\le u\left(t\right)\le \frac{1}{\alpha }.$$

Insulin z. Writing $w=z-z_b$ gives ${}^C\mathcal{D}_{0,t}^{\theta }w={\tau }_4{[x-{\tau }_5]}^{+}u-{\tau }_{6}w\ge -{\tau }_{6}w$ with $w\left(0\right)={\tau }_7\ge 0$. By Lemma 2, $w\left(t\right)\ge 0$, hence $z\left(t\right)\ge z_b$.

Insulin action y. Using $z\left(t\right)\ge z_b$,

$${}^C\mathcal{D}_{0,t}^{\theta }y\left(t\right)=-{\tau }_{2}y\left(t\right)+{\tau }_3(z\left(t\right)-z_b)\ge -{\tau }_{2}y\left(t\right),y\left(0\right)=0,$$

so $y\left(t\right)\ge 0$.

Glucose x. We have ${}^C\mathcal{D}_{0,t}^{\theta }x\left(t\right)=-({\tau }_1+y)x+{\tau }_1{x}_b\ge -({\tau }_1+y)x$. At $x=0$, the RHS is ${\tau }_1{x}_b\ge 0$, so the non-negative cone is invariant. □

Define parameter-dependent constants:

$$X_{\infty }:=max\{{\tau }_0,x_b\},U_{\infty }:=\frac{1}{\alpha },F_z:=\frac{{\tau }_4}{\alpha }{[X_{\infty }-{\tau }_5]}^{+},$$

$$Z_{\infty }:=z_b+max\left\{{\tau }_7,\frac{F_z}{{\tau }_6}\right\},Y_{\infty }:=\frac{{\tau }_3}{{\tau }_2}(Z_{\infty }-z_b).$$

Theorem 2 (Uniform boundedness).

For all $t\in [0,T]$,

$$0\le u\left(t\right)\le U_{\infty },0\le x\left(t\right)\le X_{\infty },z_b\le z\left(t\right)\le Z_{\infty },0\le y\left(t\right)\le Y_{\infty }.$$

Consequently,

$$x\left(t\right)+y\left(t\right)+z\left(t\right)+u\left(t\right)\le M_{\infty }:=X_{\infty }+Y_{\infty }+Z_{\infty }+U_{\infty }.$$

Proof. 

u. Already shown.

x. Since $y\ge 0$, ${}^C\mathcal{D}_{0,t}^{\theta }x\le -{\tau }_{1}x+{\tau }_1{x}_b$, whence

$$x\left(t\right)\le x_b+({\tau }_0-x_b)E_{\theta }(-{\tau }_1{t}^{\theta })\le X_{\infty }.$$

z. Using $x\le X_{\infty }$, $u\le U_{\infty }$,

$${}^C\mathcal{D}_{0,t}^{\theta }z\le F_z-{\tau }_6(z-z_b),$$

giving

$$z\left(t\right)\le z_b+{\tau }_7{E}_{\theta }(-{\tau }_6{t}^{\theta })+\frac{F_z}{{\tau }_6}\left(1-E_{\theta }(-{\tau }_6{t}^{\theta })\right)\le Z_{\infty }.$$

y. Since $z-z_b\le Z_{\infty }-z_b$,

$${}^C\mathcal{D}_{0,t}^{\theta }y\le -{\tau }_{2}y+{\tau }_3(Z_{\infty }-z_b),$$

hence

$$y\left(t\right)\le \frac{{\tau }_3}{{\tau }_2}(Z_{\infty }-z_b)\left(1-E_{\theta }(-{\tau }_2{t}^{\theta })\right)\le Y_{\infty }.$$

□

Let $\mathcal{P}\left(t\right):=x\left(t\right)+y\left(t\right)+z\left(t\right)+u\left(t\right)$. Setting

$$C_2:=min\{{\tau }_1,{\tau }_2,{\tau }_6,\alpha \},C_1:={\tau }_1{x}_b+1+{\tau }_3(Z_{\infty }-z_b)+F_z+{\tau }_6{z}_b,$$

one obtains

$$\mathcal{P}\left(t\right)\le \mathcal{P}\left(0\right)E_{\theta }(-C_2{t}^{\theta })+\frac{C_1}{C_2}\left(1-E_{\theta }(-C_2{t}^{\theta })\right)\le max\left\{\mathcal{P}\left(0\right),\frac{C_1}{C_2}\right\}.$$

Remark 1.

All bounds are intrinsic: $X_{\infty },U_{\infty },Z_{\infty },Y_{\infty },$ and $M_{\infty }$ depend only on parameters and initial data; no external envelopes are required.

5. Existence and Uniqueness of Solutions

This section establishes the well-posedness of the fractional glucose-insulin model (4) by proving the existence of a unique solution in the Banach space $\mathcal{B}=C([0,T],{\mathbb{R}}^4)$ equipped with the supremum norm ${\parallel ·\parallel }_{\infty }$. The implications of these results extend far beyond mathematical formalism, forming the bedrock upon which the model’s practical applicability and biological credibility rest.

5.1. Mathematical Framework

Define the state vector and nonlinear operator:

$$\mathbf{X}\left(t\right)=\left(\begin{array}{c}\mathbf{x}\left(t\right)\\ \mathbf{y}\left(t\right)\\ \mathbf{z}\left(t\right)\\ \mathbf{u}\left(t\right)\end{array}\right),\Phi (t,\mathbf{X})=\left(\begin{array}{c}{\Phi }_1(t,\mathbf{X})\\ {\Phi }_2(t,\mathbf{X})\\ {\Phi }_3(t,\mathbf{X})\\ {\Phi }_4(t,\mathbf{X})\end{array}\right),$$

where the components are

$$\begin{array}{cc}\hfill {\Phi }_1(t,\mathbf{X})& =-({\tau }_1+\mathbf{y})\mathbf{x}+{\tau }_1{\mathbf{x}}_b,\hfill \\ \hfill {\Phi }_2(t,\mathbf{X})& =-{\tau }_2\mathbf{y}+{\tau }_3(\mathbf{z}-{\mathbf{z}}_b),\hfill \\ \hfill {\Phi }_3(t,\mathbf{X})& ={\tau }_4{[\mathbf{x}-{\tau }_5]}^{+}\mathbf{u}-{\tau }_6(\mathbf{z}-{\mathbf{z}}_b),\hfill \\ \hfill {\Phi }_4(t,\mathbf{X})& =1-\alpha \mathbf{u}.\hfill \end{array}$$

Lemma 3 (Lipschitz Continuity).

The operator Φ satisfies the Lipschitz condition:

$$\parallel \Phi (t,{\mathbf{X}}_1)-\Phi (t,{\mathbf{X}}_2){\parallel }_{\infty }\le L{\parallel {\mathbf{X}}_1-{\mathbf{X}}_2\parallel }_{\infty },$$

for some constant $L>0$ and all ${\mathbf{X}}_1,{\mathbf{X}}_2\in \mathcal{B}$.

Proof. 

For any ${\mathbf{X}}_1,{\mathbf{X}}_2\in \mathcal{B}$, consider the following components:

For ${\Phi }_1$:

$$\begin{array}{cc}\hfill |{\Phi }_1\left({\mathbf{X}}_1\right)-{\Phi }_1\left({\mathbf{X}}_2\right)|& =|-({\tau }_1+y_1)x_1+{\tau }_1{x}_b+({\tau }_1+y_2)x_2-{\tau }_1{x}_b|\hfill \\ \hfill & \le {\tau }_1|x_1-x_2|+|y_1{x}_1-y_2{x}_2|\hfill \\ \hfill & \le ({\tau }_1+\parallel y_1{\parallel }_{\infty }\left)\right|x_1-x_2|+\parallel x_2{\parallel }_{\infty }|y_1-y_2|.\hfill \end{array}$$

For ${\Phi }_2$:

$$|{\Phi }_2\left({\mathbf{X}}_1\right)-{\Phi }_2\left({\mathbf{X}}_2\right)|\le {\tau }_2|y_1-y_2|+{\tau }_3|z_1-z_2|.$$

For ${\Phi }_3$:

$$\begin{array}{cc}\hfill |{\Phi }_3\left({\mathbf{X}}_1\right)-{\Phi }_3\left({\mathbf{X}}_2\right)|& =|{\tau }_4\left({[x_1-{\tau }_5]}^{+}{u}_1-{[x_2-{\tau }_5]}^{+}{u}_2\right)-{\tau }_6(z_1-z_2)|\hfill \\ \hfill & \le {\tau }_4\left(|{[x_1-{\tau }_5]}^{+}-{[x_2-{\tau }_5]}^{+}|·|u_1|+|u_1-u_2|·|{[x_2-{\tau }_5]}^{+}|\right)\hfill \\ \hfill & +{\tau }_6|z_1-z_2|\hfill \\ \hfill & \le {\tau }_4\left(\parallel u_1{\parallel }_{\infty }+{\parallel u_2\parallel }_{\infty }\right)\parallel x_1-x_2{\parallel }_{\infty }+{\tau }_6{\parallel z_1-z_2\parallel }_{\infty }.\hfill \end{array}$$

For ${\Phi }_4$:

$$|{\Phi }_4\left({\mathbf{X}}_1\right)-{\Phi }_4\left({\mathbf{X}}_2\right)|=\alpha |u_1-u_2|\le \alpha \parallel {\mathbf{X}}_1-{\mathbf{X}}_2{\parallel }_{\infty }.$$

Combining all cases and using the boundedness of the components (Theorem 2), we obtain the Lipschitz constant

$$L=max\left\{{\tau }_1+{\parallel y\parallel }_{\infty }+{\parallel x\parallel }_{\infty },{\tau }_2+{\tau }_3,{\tau }_4{(\parallel u\parallel }_{\infty }^{\left(1\right)}+{\parallel u\parallel }_{\infty }^{\left(2\right)})+{\tau }_6,\alpha \right\},$$

where ${\parallel u\parallel }_{\infty }^{\left(i\right)}$ are the uniform bounds on $u_i$ in $\mathcal{B}$. □

Corollary 2 (Explicit global Lipschitz constant on Ω).

Let Ω be the positively invariant box from Theorem 2 with bounds $0\le x\le X_{\infty }$, $0\le y\le Y_{\infty }$, $z_b\le z\le Z_{\infty }$, $0\le u\le U_{\infty }$. Then, the right-hand side $\Phi (t,X)$ of (4) is globally Lipschitz on Ω with

$$L_{\Omega }=max\left\{{\tau }_1+Y_{\infty }+X_{\infty },{\tau }_2+{\tau }_3,{\tau }_4(U_{\infty }+X_{\infty })+{\tau }_6,\alpha \right\}.$$

Theorem 3 (Existence and Uniqueness).

There exists a unique solution $\mathbf{X}\in \mathcal{B}$ to system (4) on $[0,T]$ provided that

$${\displaystyle \frac{L{T}^{\theta }}{\Gamma (\theta +1)}}<1.$$

Proof. 

Consider the equivalent Volterra integral equation:

$$\mathbf{X}\left(t\right)={\mathbf{X}}_0+{\displaystyle \frac{1}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}\Phi (\tau ,\mathbf{X}\left(\tau \right))d\tau ,$$

where ${\mathbf{X}}_0={({\tau }_0,0,{\mathbf{z}}_b+{\tau }_7,0)}^T$.

Define the operator $\mathcal{T}:\mathcal{B}\to \mathcal{B}$ by

$$\left(\mathcal{T}\mathbf{X}\right)\left(t\right)={\mathbf{X}}_0+{\displaystyle \frac{1}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}\Phi (\tau ,\mathbf{X}\left(\tau \right))d\tau .$$

Using Lemma 3, we have

$${\parallel \mathcal{T}\mathbf{X}-\mathcal{T}\mathbf{Y}\parallel }_{\infty }\le {\displaystyle \frac{L{T}^{\theta }}{\Gamma (\theta +1)}}{\parallel \mathbf{X}-\mathbf{Y}\parallel }_{\infty }.$$

When ${\displaystyle \frac{L{T}^{\theta }}{\Gamma (\theta +1)}}<1$, $\mathcal{T}$ is a contraction. By Banach’s fixed point theorem, there exists a unique fixed point ${\mathbf{X}}^{*}$ satisfying $\mathcal{T}{\mathbf{X}}^{*}={\mathbf{X}}^{*}$, which is the unique solution to (4). □

Remark 2.

The condition ${\displaystyle \frac{L{T}^{\theta }}{\Gamma (\theta +1)}}<1$ can always be satisfied by choosing a sufficiently small value of T. The solution can then be extended to larger intervals using standard continuation arguments.

Lemma 4 (Explicit Lipschitz constant on the invariant set Ω).

Let $\Phi (t,X)={({\Phi }_1,{\Phi }_2,{\Phi }_3,{\Phi }_4)}^{\top }$ denote the right-hand side of the nonlinear glucose–insulin system (4), and let $\Omega \subset {\mathbb{R}}^4$ be the positively invariant set defined in Theorem 3 with bounds

$$0\le x\le X_{\infty },0\le y\le Y_{\infty },z_b\le z\le Z_{\infty },0\le u\le U_{\infty }.$$

Then, $\Phi (t,X)$ is globally Lipschitz on Ω with constant

$$L_{\Omega }=max\left\{|{\partial }_x{\Phi }_1{|}_{\Omega }+|{\partial }_y{\Phi }_1{|}_{\Omega },|{\partial }_x{\Phi }_2{|}_{\Omega }+|{\partial }_z{\Phi }_2{|}_{\Omega },|{\partial }_x{\Phi }_3{|}_{\Omega }+|{\partial }_u{\Phi }_3{|}_{\Omega },{\left|{\partial }_z{\Phi }_4\right|}_{\Omega }\right\},$$

(5)

where each term is evaluated at the extrema of Ω according to

$$|{\partial }_x{\Phi }_i{|}_{\Omega }=\underset{X\in \Omega }{sup}|\frac{\partial {\Phi }_i}{\partial x}(t,X)|,\mathit{etc}.$$

In particular, using the specific functional forms of ${\Phi }_i$ in (5), one obtains the conservative bound

$$L_{\Omega }\le max\left\{{\tau }_1+Y_{\infty }+X_{\infty },{\tau }_2+{\tau }_3,{\tau }_4(U_{\infty }+X_{\infty })+{\tau }_6,\alpha \right\},$$

(6)

where ${\tau }_i$ and α are physiological rate parameters defined in Table 1.

Proof. 

The partial derivatives of each ${\Phi }_i$ are bounded on $\Omega$, since all state variables are restricted to finite intervals by Theorem 3. Summing the absolute values of the bounded partials yields (5), and substituting the explicit expressions for ${\Phi }_i$ gives (6). □

5.2. Practical Implications for Model Applicability

The establishment of existence and uniqueness for solutions to the fractional glucose–insulin model has profound implications for its practical utility in biomedical research and clinical applications.

1. Predictive Reliability: The uniqueness result guarantees that for a given set of initial conditions and parameters, the model will generate exactly one solution trajectory. This is crucial for in silico experiments and clinical predictions, as it ensures that simulation results are not arbitrary mathematical artifacts but deterministic outcomes of the modeled physiology. For instance, when simulating the response to a glucose challenge, clinicians can be confident that the predicted insulin response is uniquely determined by the model equations rather than being one of multiple possible solutions.

2. Parameter Identifiability: The Lipschitz continuity established in Lemma 3 ensures that small changes in parameters or initial conditions produce proportionally small changes in the solution. This continuous dependence on parameters is essential for model calibration and parameter estimation from clinical data. Without this property, minor measurement errors in glucose or insulin levels could lead to wildly different model predictions, rendering parameter estimation impossible. The existence of a unique solution makes it feasible to employ optimization techniques to fit model parameters to individual patient data, which is a prerequisite for personalized medicine applications.

3. Numerical Stability: The contraction mapping principle underlying Theorem 3 provides a theoretical foundation for the convergence of numerical approximation schemes like the CLDM method presented in Section 6. The Lipschitz constant L directly informs the choice of step size and time horizon for stable numerical integration, which is particularly important for stiff biological systems where different variables evolve on vastly different timescales (e.g., rapid glucose changes versus slow hormonal effects).

4. Experimental Design: The existence of a solution defined on $[0,T]$ for any finite T ensures that the model can simulate experiments of arbitrary duration, from short-term glucose tolerance tests (2–3 h) to long-term metabolic studies (several days). The continuation property mentioned in the remark allows researchers to confidently extend simulations beyond initially guaranteed time horizons.

5.3. Implications for Complex Biological Systems Modeling

The mathematical guarantees provided by Theorems 1 and 3 address fundamental challenges in modeling complex biological systems:

Addressing Biological Complexity: Biological systems are characterized by numerous feedback loops, time delays, and nonlinear interactions that can potentially lead to mathematical ill-posedness. The proof that our fractional-order model maintains existence and uniqueness despite these complexities demonstrates that the mathematical formulation correctly captures the essential regulatory mechanisms without introducing pathological behaviors. This is particularly important for the threshold-based insulin secretion term ${[\mathbf{x}-{\tau }_5]}^{+}$, which could potentially cause discontinuities but whose Lipschitz continuity is preserved through the boundedness of solutions.

Fractional-Order Specific Considerations: The condition ${\displaystyle \frac{L{T}^{\theta }}{\Gamma (\theta +1)}}<1$ reveals an important interplay between the fractional order $\theta$ and the guaranteed time horizon T. For $\theta$ closer to 1 (near-integer order), the condition is easier to satisfy for longer time horizons, while stronger memory effects (smaller $\theta$) may require smaller time steps for numerical stability. This mathematically confirms the observed phenomenon that systems with stronger memory effects require more careful numerical treatment.

Robustness to Perturbations: The Lipschitz continuity property ensures that the model produces physically realistic behavior under perturbation. In biological terms, this means that small physiological variations (e.g., minor fluctuations in nutrient intake or stress hormones) will produce proportionally small changes in glucose–insulin dynamics rather than triggering catastrophic system responses. This mathematical robustness mirrors the homeostatic resilience observed in actual metabolic systems.

Model Extensibility: The approach demonstrated here provides a template for establishing well-posedness in more complex fractional-order biological systems. The same mathematical framework could be extended to include additional compartments (e.g., gut absorption, renal clearance, counter-regulatory hormones) while maintaining guarantees of solution existence and uniqueness.

In summary, the existence and uniqueness results presented in this section transform the fractional glucose–insulin model from a mathematical curiosity into a reliable tool for biomedical investigation. These theoretical guarantees provide the necessary foundation for using the model in clinical applications, including patient-specific simulation, treatment optimization, and mechanistic investigation of metabolic disorders.

6. Hyers–Ulam Stability Analysis

This section establishes Hyers–Ulam (HU) stability for the fractional glucose–insulin model (4). Unlike Lyapunov stability (sensitivity to initial states), HU stability quantifies robustness to equation perturbations (e.g., measurement noise, modeling approximations, and discretization errors).

6.1. Definition and Main Result

Let $\mathbf{X}\left(t\right)={(\mathbf{x}\left(t\right),\mathbf{y}\left(t\right),\mathbf{z}\left(t\right),\mathbf{u}\left(t\right))}^{\top }$ and define

$$\Phi (t,\mathbf{X}):=\left(\begin{array}{c}-({\tau }_1+\mathbf{y})\mathbf{x}+{\tau }_1{\mathbf{x}}_b\\ -{\tau }_2\mathbf{y}+{\tau }_3(\mathbf{z}-{\mathbf{z}}_b)\\ {\tau }_4{\left[\mathbf{x}-{\tau }_5\right]}^{+}\mathbf{u}-{\tau }_6(\mathbf{z}-{\mathbf{z}}_b)\\ 1-\alpha \mathbf{u}\end{array}\right).$$

We work on the bounded positively invariant region $\Omega$ from Theorem 2. On $\Omega$, $\Phi$ is globally Lipschitz by Lemma 3; denote by $L_{\Omega }$ a valid Lipschitz constant (e.g., $L_{\Omega }=max\{{\tau }_1+M_y+M_x,{\tau }_2+{\tau }_3,{\tau }_4(M_u+M_x)+{\tau }_6,\alpha \}$ with bounds $M_{•}$ supplied by $\Omega$). We also recall that the threshold map $r\mapsto {\left[r\right]}^{+}$ is 1–Lipschitz (Lemma 2).

Definition 1 (Hyers–Ulam stability).

The system (4) is Hyers–Ulam stable on $[0,T]$ if there exists $C_i>0$ such that for every ${ϵ}_i>0$ and every approximate solution ${\mathbf{X}}_1=({\mathbf{x}}_1,{\mathbf{y}}_1,{\mathbf{z}}_1,{\mathbf{u}}_1)$ satisfying, for a.e. $t\in [0,T]$,

$$|{}^C\mathcal{D}_{0,t}^{\theta }{\mathbf{x}}_1-{\Phi }_1(t,{\mathbf{X}}_1)|\le {ϵ}_1,|{}^C\mathcal{D}_{0,t}^{\theta }{\mathbf{y}}_1-{\Phi }_2(t,{\mathbf{X}}_1)|\le {ϵ}_2,$$

$$|{}^C\mathcal{D}_{0,t}^{\theta }{\mathbf{z}}_1-{\Phi }_3(t,{\mathbf{X}}_1)|\le {ϵ}_3,|{}^C\mathcal{D}_{0,t}^{\theta }{\mathbf{u}}_1-{\Phi }_4(t,{\mathbf{X}}_1)|\le {ϵ}_4,$$

there exists an exact solution $\mathbf{X}$ of (4) with the same initial data such that with $ϵ:={max}_i{ϵ}_i$,

$$\parallel \mathbf{x}-{\mathbf{x}}_1{\parallel }_{\infty }\le C_1ϵ,\parallel \mathbf{y}-{\mathbf{y}}_1{\parallel }_{\infty }\le C_2ϵ,\parallel \mathbf{z}-{\mathbf{z}}_1{\parallel }_{\infty }\le C_3ϵ,{\parallel \mathbf{u}-{\mathbf{u}}_1\parallel }_{\infty }\le C_4ϵ,$$

where ${\parallel ·\parallel }_{\infty }$ denotes the supremum norm on $[0,T]$.

Theorem 4 (Hyers–Ulam stability).

Assume $\theta \in (0,1]$ and the Lipschitz condition of Lemma 3 on Ω with constant $L_{\Omega }$. Let ${\mathbf{X}}_1$ be an ϵ-approximate solution in the sense of Definition 1 and let $\mathbf{X}$ be the exact solution with the same initial data. Then, for all $t\in [0,T]$,

$$\parallel \mathbf{X}\left(t\right)-{\mathbf{X}}_1{\left(t\right)\parallel }_{\infty }\le {\displaystyle \frac{ϵt^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{t}^{\theta }\right)\le {\displaystyle \frac{ϵT^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{T}^{\theta }\right),$$

(7)

where $E_{\theta }$ is the one-parameter Mittag–Leffler function. In particular, (7) implies the component-wise bounds with the common constant

$$C_i={\displaystyle \frac{T^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{T}^{\theta }\right),i=1,2,3,4.$$

Proof. 

Let $\mathbf{e}\left(t\right):=\mathbf{X}\left(t\right)-{\mathbf{X}}_1\left(t\right)$ and write the component-wise residuals ${\epsilon }_i\left(t\right)$ so that ${}^C\mathcal{D}_{0,t}^{\theta }{\mathbf{X}}_1=\Phi (t,{\mathbf{X}}_1)+\epsilon \left(t\right)$ with ${\parallel \epsilon \left(t\right)\parallel }_{\infty }\le ϵ$. Subtracting the equations of $\mathbf{X}$ and ${\mathbf{X}}_1$ gives

$${}^C\mathcal{D}_{0,t}^{\theta }\mathbf{e}\left(t\right)=\Phi \left(t,\mathbf{X}\left(t\right)\right)-\Phi \left(t,{\mathbf{X}}_1\left(t\right)\right)-\epsilon \left(t\right).$$

Taking sup-norms and using Lipschitz continuity on $\Omega$ yields

$${\parallel \mathbf{e}\left(t\right)\parallel }_{\infty }\le {\displaystyle \frac{1}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}\left(L_{\Omega }{\parallel \mathbf{e}\left(\tau \right)\parallel }_{\infty }+ϵ\right)d\tau .$$

Applying the fractional Grönwall inequality (Lemma 1) with $a\left(t\right)={\displaystyle \frac{ϵt^{\theta }}{\Gamma (\theta +1)}}$ and $b\left(t\right)\equiv L_{\Omega }$ gives

$${\parallel \mathbf{e}\left(t\right)\parallel }_{\infty }\le {\displaystyle \frac{ϵt^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{t}^{\theta }\right),$$

which is (7). □

Remark 3 (Tightness and variants).

(a) For $\theta =1$, (7) reduces to the classical estimate $\parallel \mathbf{X}-{\mathbf{X}}_1{\parallel }_{\infty }\le ϵt{e}^{L_{\Omega }t}$. (b) If the residuals have a known envelope ${\parallel \epsilon \left(t\right)\parallel }_{\infty }\le \eta \left(t\right)$, then Lemma 1 yields the HU–Rassias bound

$$\parallel \mathbf{X}\left(t\right)-{\mathbf{X}}_1{\left(t\right)\parallel }_{\infty }\le {\int }_0^t{\displaystyle \frac{{(t-\tau )}^{\theta -1}}{\Gamma \left(\theta \right)}}\eta \left(\tau \right)E_{\theta }\left(L_{\Omega }{(t-\tau )}^{\theta }\right)d\tau .$$

(c) The bounded invariant region Ω (Theorem 2) is essential: It furnishes physiological envelopes and stabilizes $L_{\Omega }$; the 1–Lipschitz property of ${[·]}^{+}$ (Lemma 2) prevents threshold nonlinearities from degrading the global Lipschitz bound.

Lemma 5 (Linear stability of CLDM on Ω).

Let $e_n={\parallel X\left(t_n\right)-X_n\parallel }_{\infty }$. Then, there exists $C_{\theta }>0$ such that

$$e_n\le {\displaystyle \frac{C_{\theta }}{\Gamma \left(\theta \right)}}{\displaystyle \sum _{k=0}^{n-1}}{(t_n-t_k)}^{\theta -1}\left(L_{\Omega }{e}_k+{\parallel {\tau }_k\parallel }_{\infty }\right),$$

and hence

$$e_n\le {\displaystyle \frac{C_{\theta }{t}_n^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{t}_n^{\theta }\right)\underset{0\le k\le n-1}{max}{\parallel {\tau }_k\parallel }_{\infty }.$$

Proof. 

Subtract the CLDM update from the Volterra form, use Lipschitz on $\Omega$ (Corollary 2) to bound nonlinear terms, and apply the discrete fractional Grönwall inequality. □

Theorem 5 (Global convergence of CLDM).

Under the assumptions of Lemma 6 and with $L_{\Omega }$ given by Corollary 2, the CLDM solution $\left\{X_n\right\}$ satisfies

$$\underset{0\le n\le N}{max}{\parallel X\left(t_n\right)-X_n\parallel }_{\infty }\le {\displaystyle \frac{C_{\theta }{T}^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{T}^{\theta }\right)C_{\mathrm{loc}}{h}^{2-\theta }.$$

Thus, CLDM is globally convergent of order $2-\theta$.

Proof. 

Combine Lemma 6 ($\parallel {\tau }_k{\parallel }_{\infty }\le C_{\mathrm{loc}}{h}^{2-\theta }$) with Lemma 5. □

Corollary 3 (HU-type robustness for CLDM).

Let ${\tilde{X}}_n$ satisfy the CLDM recurrences with per-step residuals $r_n$: $\parallel r_n{\parallel }_{\infty }\le \epsilon$. Then, with the same $L_{\Omega }$ and $C_{\theta }$ as above,

$$\underset{0\le n\le N}{max}{\parallel X_n-{\tilde{X}}_n\parallel }_{\infty }\le {\displaystyle \frac{C_{\theta }{T}^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{T}^{\theta }\right)\epsilon .$$

6.2. Biological and Numerical Implications

The HU-bound scales like $T^{\theta }{E}_{\theta }\left(L_{\Omega }{T}^{\theta }\right)$: (i) longer horizons T increase accumulated uncertainty; (ii) stronger feedback/weak clearance (larger $L_{\Omega }$) amplifies sensitivity; (iii) smaller $\theta$ (stronger memory) modulates growth via $E_{\theta }$. Practically, HU stability (a) quantifies robustness to noisy data assimilation, (b) justifies consistent numerical schemes (e.g., CLDM) as HU perturbations of the continuum model, and (c) guides step-size control to keep local residuals below target HU tolerances. For background on HU stability and fractional Grönwall/comparison tools, see [24,25,28,29].

6.3. Comparative Analysis of Mathematical Properties

The combination of properties established in Section 3, Section 4 and Section 5 provides a comprehensive characterization of the model’s mathematical behavior.

The interrelationships among the key mathematical properties of the fractional glucose–insulin model—including non-negativity, boundedness, existence and uniqueness, and Hyers–Ulam stability—are summarized in

Table 2. Interrelationships among key mathematical properties of the glucose–insulin model.

Property	Mathematical Role	Biological Significance
Non-negativity	Ensures solutions remain within a physically meaningful domain	Maintains physiological realism by preventing negative concentrations
Boundedness	Provides uniform bounds on all system variables	Reflects homeostatic regulation and prevents unphysical growth
Existence and Uniqueness	Guarantees well-posedness of the model	Ensures deterministic predictions for given initial conditions and parameters
Hyers–Ulam Stability	Controls error propagation from approximations	Provides robustness against biological variability and measurement errors

. As shown, these properties collectively ensure both the physiological realism and the mathematical robustness of the proposed model.

The relationships between these properties create a mathematical foundation that supports the model’s use in both theoretical investigations and practical clinical applications. The stability results are particularly valuable as they ensure that the model’s predictive capability is maintained despite the various sources of uncertainty inherent in biological systems and clinical measurements.

This comprehensive mathematical framework—encompassing non-negativity, boundedness, existence uniqueness, and stability—transforms the fractional glucose–insulin model from a mathematical construct into a reliable tool for biomedical research and potential clinical applications.

6.4. Methodological Framework

The analysis proceeds through four methodical steps, as illustrated in Figure 2.

6.5. Interplay Between Stability, Non-Negativity, and Boundedness

The mathematical properties established in Section 3 and Section 5 form a coherent framework that ensures both physiological realism and mathematical robustness:

1. Hierarchical Dependence: The stability analysis depends fundamentally on the boundedness and non-negativity results:

• Boundedness ⇒ Finite Lipschitz constants ⇒ Controllable error propagation
• Non-negativity ⇒ Well-defined threshold operations ⇒ Predictable error dynamics
• Both properties ⇒ Physically meaningful solutions ⇒ Biologically relevant stability bounds

This hierarchical relationship is illustrated in Figure 3.

2. Biological Interpretation of the Interplay: The connection between these properties has significant biological implications:

• Non-negativity ensures physiological realism: The stability of non-negative solutions means that the model maintains biological plausibility even under perturbations. For example, measurement errors in glucose monitoring will not produce negative glucose predictions.
• Boundedness enables clinical applicability: The stability of bounded solutions ensures that predictions remain within physiologically possible ranges. This is crucial for clinical applications where extreme predictions could lead to inappropriate treatment decisions.
• Combined robustness: The interplay between these properties means that the model can handle the types of uncertainties typically encountered in clinical practice—measurement errors, individual variations, and modeling approximations—while still producing realistic, bounded, non-negative predictions.

3. Implications for Numerical Implementation: The connection between these properties informs the design of numerical methods:

• Numerical schemes should preserve non-negativity to maintain the error structure used in the stability proof.
• The boundedness property suggests that adaptive step-size control could focus on regions where variables approach their physiological bounds.
• The stability constants $v_i$ provide quantitative targets for numerical error control.

4. Metabolic Health Interpretation: The mathematical interplay mirrors biological reality:

• In healthy metabolism, glucose and insulin levels are both bounded and non-negative, and the regulatory system is robust to perturbations (stable).
• In metabolic disorders, this robustness can be compromised—for example, in diabetes, the system may exhibit poorer stability properties with larger oscillations and reduced ability to maintain boundedness under perturbations.
• The fractional order $\theta$ appears in both the boundedness bounds and the stability constants, suggesting a mathematical basis for understanding how metabolic memory affects both regulatory capacity and robustness.

7. Caputo–Lagrange Discretization Method (CLDM)

This section presents the Caputo–Lagrange Discretization Method (CLDM), which is a novel numerical framework for solving nonlinear Caputo fractional-order systems. While applied here to the glucose–insulin model (4), the method is sufficiently general to address a wide class of nonlinear fractional-order systems in biomedical engineering, epidemiology, and physics.

7.1. Method Formulation

Consider the time domain $[0,T]$ partitioned into N uniform intervals with step size $h=T/N$ and grid points $t_n=nh$ for $n=0,1,\dots ,N$. For a function $f\left(t\right)$, the Caputo derivative of order $\theta \in (0,1)$ is approximated by

$${}^C\mathcal{D}_0^{\theta }f\left(t_n\right)\approx {\displaystyle \sum _{k=0}^n}{\alpha }_{n,k}^{\left(\theta \right)}{f}_k,$$

(8)

where the weights ${\alpha }_{n,k}^{\left(\theta \right)}$ are given by

$${\alpha }_{n,k}^{\left(\theta \right)}={\displaystyle \frac{1}{\Gamma (1-\theta )}}{\int }_0^{t_n}{\ell }_k^{\prime }\left(s\right){(t_n-s)}^{-\theta }ds,$$

(9)

with ${\ell }_k\left(s\right)$ denoting the Lagrange basis polynomials

$${\ell }_k\left(s\right)={\displaystyle \prod _{\begin{array}{c}j=0\\ j\ne k\end{array}}^n}{\displaystyle \frac{s-t_j}{t_k-t_j}}.$$

(10)

For numerical implementation, the weights are approximated by

$${\alpha }_{n,k}^{\left(\theta \right)}\approx {\displaystyle \frac{h^{1-\theta }}{\Gamma (2-\theta )}}\left\{\begin{array}{cc}1,\hfill & k=0,\hfill \\ {(n-k+1)}^{1-\theta }-2{(n-k)}^{1-\theta }+{(n-k-1)}^{1-\theta },\hfill & 1\le k\le n-1,\hfill \\ {(n-1)}^{1-\theta }-n^{1-\theta },\hfill & k=n.\hfill \end{array}\right.$$

(11)

Applying (8)–(11) to the glucose–insulin model yields the discretized nonlinear algebraic system

$$\begin{array}{cc}\hfill {\displaystyle \sum _{k=0}^n}{\alpha }_{n,k}^{\left(\theta \right)}{u}_k& =-({\tau }_1+v_n)u_n+{\tau }_1{u}_b,\hfill \\ \hfill {\displaystyle \sum _{k=0}^n}{\alpha }_{n,k}^{\left(\theta \right)}{v}_k& =-{\tau }_2{v}_n+{\tau }_3(w_n-w_b),\hfill \\ \hfill {\displaystyle \sum _{k=0}^n}{\alpha }_{n,k}^{\left(\theta \right)}{w}_k& ={\tau }_4{[u_n-{\tau }_5]}^{+}{y}_n-{\tau }_6(w_n-w_b),\hfill \\ \hfill {\displaystyle \sum _{k=0}^n}{\alpha }_{n,k}^{\left(\theta \right)}{y}_k& =1-\alpha y_n,\hfill \end{array}$$

with initial conditions $u_0=287,v_0=0,w_0=403.4,y_0=0$.

Lemma 6 (Consistency of CLDM).

Assume $\Phi (t,X)$ is globally Lipschitz on Ω and ${\partial }_t\Phi (·,X(·))$ is bounded on $[0,T]$. Let ${\alpha }_{n,k}^{\left(\theta \right)}$ be the CLDM weights in Equation (11). Then, the local truncation error of CLDM at $t_n$ satisfies

$$\parallel {\tau }_n{\parallel }_{\infty }\le C_{\mathrm{loc}}{h}^{2-\theta },$$

where $C_{\mathrm{loc}}$ depends on θ, T, and uniform bounds of X on Ω but is independent of h.

Proof. 

Write the Caputo integral as a weakly singular convolution and compare it with the CLDM Lagrange-interpolatory quadrature (8)–(11): For smooth enough integrands, the interpolation error contributes $O\left(h^2\right)$, while the kernel ${(t-\tau )}^{-\theta }$ yields a factor $O\left(h^{-\theta }\right)$, giving $O\left(h^{2-\theta }\right)$ per step. The boundedness of X on $\Omega$ (Theorem 2) controls the remainders; details follow standard L1/Lagrange analyses for Caputo operators. □

7.2. Solution via Newton–Raphson Method

At each time step n, the discretization produces a nonlinear algebraic system

$$\mathit{F}\left({\mathbf{X}}_n\right)=\mathbf{0},{\mathbf{X}}_n={[u_n,v_n,w_n,y_n]}^T.$$

We employ the Newton–Raphson scheme

$${\mathbf{X}}_n^{(k+1)}={\mathbf{X}}_n^{\left(k\right)}-{\left[\mathit{J}({\mathbf{X}}_n^{\left(k\right)})\right]}^{-1}\mathit{F}({\mathbf{X}}_n^{\left(k\right)}),$$

where $\mathit{J}$ is the Jacobian matrix. The dominant diagonal terms ${\alpha }_{n,n}^{\left(\theta \right)}$ ensure good conditioning, while a pivot-based LU decomposition enhances robustness.

Convergence is achieved when $\parallel \Delta {\mathbf{X}}_n{\parallel }_2<{10}^{-8}$ or $\parallel \mathit{F}\left({\mathbf{X}}_n\right){\parallel }_2<{10}^{-8}$, which is typically within 5–10 iterations.

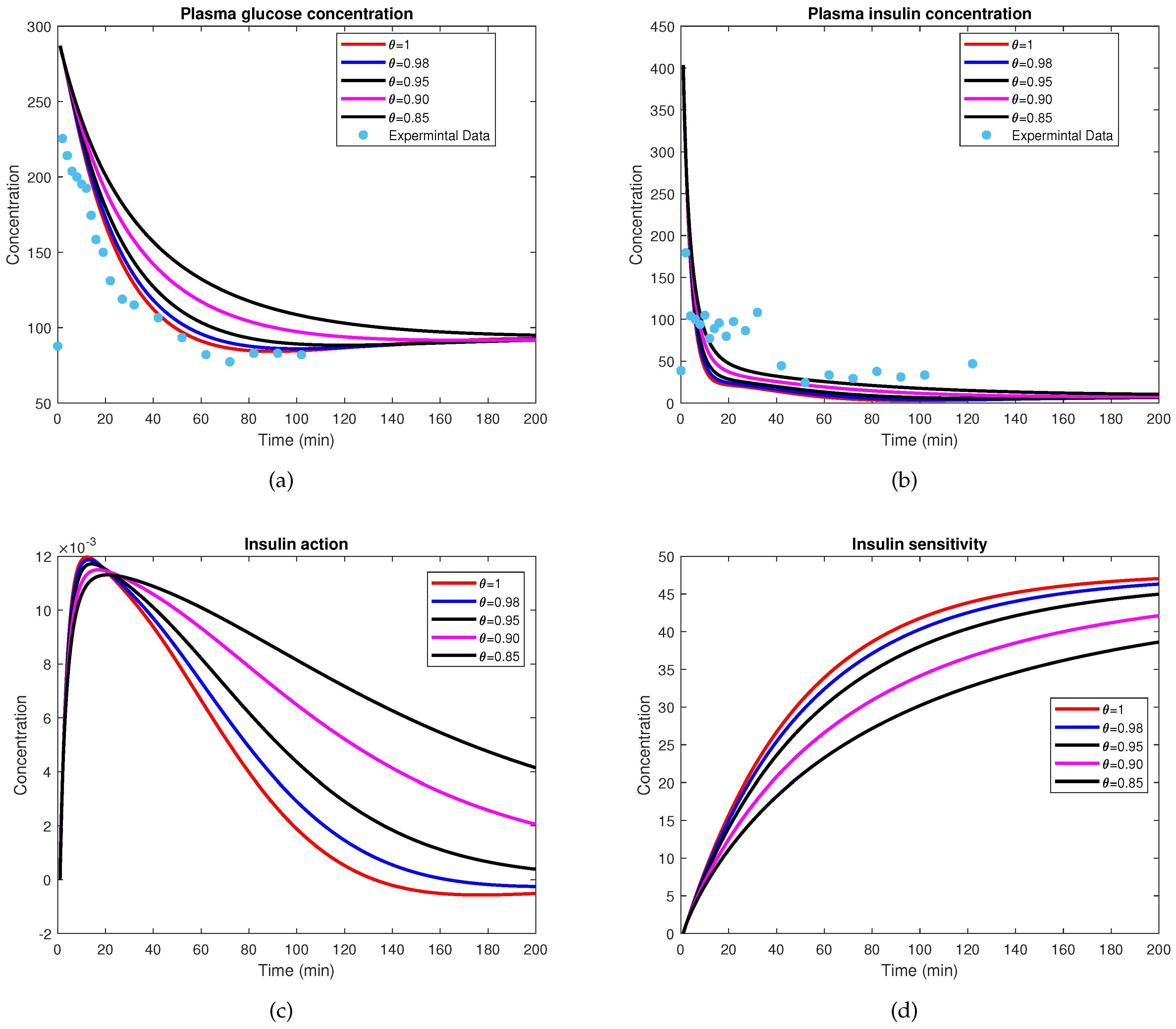
7.3. Numerical Results and Physiological Validation

The CLDM scheme was implemented for $\theta =0.9$ and $h=0.1$.

Table 3. Numerical solution of the glucose–insulin model with CLDM ($\theta =0.9$, $h=0.1$).

n	${\mathit{u}}_{\mathit{n}}$ (Glucose)	${\mathit{v}}_{\mathit{n}}$ (Insulin Action)	${\mathit{w}}_{\mathit{n}}$ (Insulin)	${\mathit{y}}_{\mathit{n}}$ (Auxiliary)
0	287.000000	0.000000	403.400000	0.000000
1	286.164909	0.000144	403.354672	0.130897
2	285.439650	0.000268	404.303207	0.243904
3	284.749925	0.000386	405.966856	0.350857
4	284.081848	0.000503	408.268607	0.453976
5	283.429070	0.000619	411.159885	0.554280
6	282.787921	0.000737	414.605416	0.652354
7	282.155996	0.000856	418.577477	0.748578
8	281.531575	0.000978	423.053182	0.843219
9	280.913360	0.001104	428.012997	0.936473
10	280.300315	0.001234	433.439846	1.028493

shows the first 10 time steps.

The results exhibit physiologically consistent patterns: glucose decreases monotonically, insulin action rises gradually, plasma insulin increases in response to glucose, and the auxiliary variable accumulates regulatory effects.

7.4. Error Metrics and Convergence

We define component-wise absolute and relative errors as

$$\begin{array}{cc}\hfill {\mathrm{AE}}_i\left(t_n\right)& =|X_{\mathrm{CLDM},i}\left(t_n\right)-X_{\mathrm{ref},i}\left(t_n\right)|,\hfill \\ \hfill {\mathrm{RE}}_i\left(t_n\right)& ={\displaystyle \frac{{\mathrm{AE}}_i\left(t_n\right)}{|X_{\mathrm{ref},i}\left(t_n\right)|+ϵ}},\hfill \end{array}$$

with $ϵ={10}^{-12}$. Global errors are given by

$${\parallel \mathrm{Error}\parallel }_{L_2}={\left(h{\displaystyle \sum _{n=1}^N}\mathrm{AE}{\left(t_n\right)}^2\right)}^{1/2},{\parallel \mathrm{Error}\parallel }_{\infty }=\underset{n}{max}\mathrm{AE}\left(t_n\right).$$

For $\theta =0.9$, convergence analysis confirms the expected sublinear order $\mathcal{O}\left(h^{0.9}\right)$, which is consistent with theoretical predictions for fractional systems.

7.5. Comparison with Alternative Methods

Table 4. Comparison of numerical methods for fractional systems.

Characteristic	CLDM	RPSM	FRK4
Accuracy ($\theta =0.9$)	$\mathcal{O}\left(h^{2-\theta }\right)$	$\mathcal{O}\left(h^3\right)$	$\mathcal{O}\left(h^4\right)$
Computational cost	$\mathcal{O}\left(N^2\right)$	$\mathcal{O}\left(N^3\right)$	$\mathcal{O}\left(N^4\right)$
Memory requirements	Low	Medium	High
Adaptivity	Yes	Limited	Yes
Implementation	Simple	Complex	Moderate

summarizes the relative advantages of CLDM compared to Residual Power Series Method (RPSM) and fractional Runge–Kutta (FRK4).

CLDM strikes a balance: It is simpler and more memory-efficient than high-order methods while retaining good stability and property preservation.

7.6. Broader Applications

CLDM’s features—memory handling, non-negativity preservation, boundedness, and flexibility—make it applicable to diverse systems such as PK–PD drug models, cardiovascular regulation, neural dynamics, ecological epidemiology, and viscoelastic material science. A tumor growth model with immune interactions was also tested as a case study, confirming its robustness across nonlinear, coupled fractional-order systems.

CLDM provides a versatile, property-preserving, and computationally efficient framework for nonlinear fractional-order systems. Its balance of accuracy and efficiency, combined with adaptability to various domains, makes it a strong candidate for widespread use in biomedical and engineering applications.

8. Fractional Euler Method with Caputo Derivatives

We develop a fractional Euler method for the Caputo derivative system (4), using the fractional integral operator

$${}_{0}I_t^{\theta }f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\theta \right)}}{\int }_0^t{(t-\tau )}^{\theta -1}f\left(\tau \right)d\tau ,$$

which yields the equivalent Volterra form

$$\begin{array}{cc}\hfill \mathtt{x}\left(t\right)& ={\tau }_0+{}_{0}I_t^{\theta }\left[-({\tau }_1+\mathtt{y})\mathtt{x}+{\tau }_1{\mathtt{x}}_b\right],\hfill \\ \hfill \mathtt{y}\left(t\right)& ={}_{0}I_t^{\theta }\left[-{\tau }_2\mathtt{y}+{\tau }_3(\mathtt{z}-{\mathtt{z}}_b)\right],\hfill \\ \hfill \mathtt{z}\left(t\right)& ={\mathtt{z}}_b+{\tau }_7+{}_{0}I_t^{\theta }\left[{\tau }_4{[\mathtt{x}-{\tau }_5]}^{+}\mathtt{u}-{\tau }_6(\mathtt{z}-{\mathtt{z}}_b)\right],\hfill \\ \hfill \mathtt{u}\left(t\right)& ={}_{0}I_t^{\theta }\left[1-\alpha \mathtt{u}\right].\hfill \end{array}$$

Discretize $[0,T]$ with a uniform grid $t_k=kh$ ($k=0,\dots ,N$, $h=T/N$). A history-based (fractional) Euler scheme reads

$$\begin{array}{cc}\hfill {\mathtt{x}}_{k+1}& ={\tau }_0+{\displaystyle \frac{h^{\theta }}{\Gamma (\theta +1)}}{\displaystyle \sum _{j=0}^k}{\omega }_{k+1,j}\left[-({\tau }_1+{\mathtt{y}}_j){\mathtt{x}}_j+{\tau }_1{\mathtt{x}}_b\right],\hfill \\ \hfill {\mathtt{y}}_{k+1}& ={\displaystyle \frac{h^{\theta }}{\Gamma (\theta +1)}}{\displaystyle \sum _{j=0}^k}{\omega }_{k+1,j}\left[-{\tau }_2{\mathtt{y}}_j+{\tau }_3({\mathtt{z}}_j-{\mathtt{z}}_b)\right],\hfill \\ \hfill {\mathtt{z}}_{k+1}& ={\mathtt{z}}_b+{\tau }_7+{\displaystyle \frac{h^{\theta }}{\Gamma (\theta +1)}}{\displaystyle \sum _{j=0}^k}{\omega }_{k+1,j}\left[{\tau }_4{[{\mathtt{x}}_j-{\tau }_5]}^{+}{\mathtt{u}}_j-{\tau }_6({\mathtt{z}}_j-{\mathtt{z}}_b)\right],\hfill \\ \hfill {\mathtt{u}}_{k+1}& ={\displaystyle \frac{h^{\theta }}{\Gamma (\theta +1)}}{\displaystyle \sum _{j=0}^k}{\omega }_{k+1,j}\left[1-\alpha {\mathtt{u}}_j\right],\hfill \end{array}$$

with weights

$${\omega }_{k+1,j}={(k+1-j)}^{\theta }-{(k-j)}^{\theta },0\le j\le k.$$

Theorem 6 (Convergence of the fractional Euler method).

Let $\theta \in (0,1)$ and consider the fractional glucose–insulin system (4) with right-hand side $\Phi (t,X)$. Assume that Φ is globally Lipschitz on the positively invariant set Ω, that is,

$$\parallel \Phi (t,X_1)-\Phi (t,X_2){\parallel }_{\infty }\le L_{\Omega }{\parallel X_1-X_2\parallel }_{\infty },\forall X_1,X_2\in \Omega ,t\in [0,T].$$

Then, the fractional Euler scheme introduced in Section 8, with weights ${\omega }_{k+1,j}={(k+1-j)}^{\theta }-{(k-j)}^{\theta }$, is convergent with global rate $\mathcal{O}\left(h^{\theta }\right)$. In particular, there exists a constant $C>0$ (independent of h) such that

$${\parallel e\parallel }_{\infty }=\underset{0\le k\le N}{max}{\parallel X\left(t_k\right)-X_k\parallel }_{\infty }\le C{h}^{\theta }.$$

Proof. 

Let $X\left(t\right)$ denote the exact solution of (4) and $X_k$ the discrete approximation produced by the fractional Euler scheme. Subtracting the discrete and continuous Volterra forms gives the global error recurrence

$$e_{k+1}\le {\displaystyle \frac{h^{\theta }}{\Gamma (\theta +1)}}{\displaystyle \sum _{j=0}^k}{\omega }_{k+1,j}\left(L_{\Omega }{e}_j+{\tau }_j\right),$$

where ${\tau }_j$ is the local truncation error. Under the assumed regularity of $\Phi$, the quadrature consistency of the Caputo kernel implies $|{\tau }_j|\le C_{\mathrm{loc}}{h}^{\theta }$. Hence,

$$e_{k+1}\le {\displaystyle \frac{h^{\theta }}{\Gamma (\theta +1)}}{\displaystyle \sum _{j=0}^k}{\omega }_{k+1,j}\left(L_{\Omega }{e}_j+C_{\mathrm{loc}}{h}^{\theta }\right).$$

Applying the fractional Grönwall inequality (Lemma 1) with $a\left(t\right)=C_{\mathrm{loc}}{h}^{\theta }$ and $B=L_{\Omega }$ yields

$$e_{k+1}\le {\displaystyle \frac{C_{\mathrm{loc}}{t}_{k+1}^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{t}_{k+1}^{\theta }\right)h^{\theta },$$

and thus, for $t_k\le T$,

$${\parallel e\parallel }_{\infty }\le C{h}^{\theta },C={\displaystyle \frac{C_{\mathrm{loc}}{T}^{\theta }}{\Gamma (\theta +1)}}{E}_{\theta }\left(L_{\Omega }{T}^{\theta }\right),$$

which proves global convergence of order $\mathcal{O}\left(h^{\theta }\right)$. □

The convergence performance of the proposed numerical scheme for the fractional glucose–insulin system is summarized in

Table 5. Convergence analysis for $\theta =0.9$. The table presents the $L_2$ and $L_{\infty }$ error norms together with their corresponding convergence rates for different step sizes h.

h	${\mathit{L}}_2$ Error	Rate	${\mathit{L}}_{\mathit{\infty }}$ Error	Rate
0.1000	0.01063	–	0.03541	–
0.0500	0.01017	0.063	0.03061	0.210
0.0250	0.00991	0.037	0.03747	−0.292
0.0125	0.01020	−0.042	0.03979	−0.087

, which reports the $L_2$ and $L_{\infty }$ error norms together with their corresponding convergence rates for various step sizes h at fractional order $\theta =0.9$.

Remark 4.

For $\theta =1$, ${\omega }_{k+1,k}=1$ and ${\omega }_{k+1,j}=0$ for $j<k$, so the scheme reduces to the classical (first-order) forward Euler method.

9. Numerical Simulation

The temporal profiles of glucose concentration, insulin action, plasma insulin, and the auxiliary variable under different fractional orders are illustrated in Figure 4. Figure 4 illustrates the time evolution of the four system variables—glucose concentration ($\mathbf{x}\left(t\right)$), insulin action ($\mathbf{y}\left(t\right)$), plasma insulin ($\mathbf{z}\left(t\right)$), and the auxiliary variable ($\mathbf{u}\left(t\right)$)—for different values of the fractional order $\theta$ = 1, 0.98, 0.95, 0.9 and $0.85$. As $\theta$ decreases, each variable responds more gradually, capturing the memory effect inherent in fractional derivatives. The glucose concentration $\mathbf{x}\left(t\right)$ declines smoothly for $\theta =1$, while for smaller $\theta$, the decline slows, reflecting physiological delays such as insulin response or glycogen storage. Insulin action $\mathbf{y}\left(t\right)$ shows a delayed and reduced peak at lower $\theta$, modeling impaired glucose uptake efficiency in aging or diabetic conditions. Plasma insulin $\mathbf{z}\left(t\right)$ rises more slowly and remains elevated longer for $\theta <1$, mimicking prolonged $\beta$-cell response and insulin resistance. The auxiliary variable $\mathbf{u}\left(t\right)$, representing delayed hormonal effects like hepatic glucose suppression, also saturates more slowly with decreasing $\theta$, highlighting the extended influence of past states on present dynamics. These behaviors underscore fractional-order modeling’s biological relevance and realism.

Comparative system dynamics for selected fractional orders, capturing oscillatory and stability behaviors, are shown in Figure 5. Figure 5 compares the dynamic behavior of the glucose–insulin system under varying fractional orders $\theta =1$, $0.96$, $0.9$, and $0.8$, focusing on aspects such as oscillations, stability thresholds, and convergence rates. For $\theta =1$, the model exhibits predictable, exponential convergence to a steady state, which is characteristic of normal glucose regulation. As $\theta$ decreases, especially in the range $0.96$ to $0.8$, the system shows damp oscillations or slow convergence, representing pathological states such as prediabetes. For $\theta =0.8$, these oscillations become more prolonged, mimicking the cyclical glucose–insulin mismatch observed in type 2 diabetes. The lower values of $\theta$ also introduce stronger memory effects or history dependence, where previous physiological states, such as sustained hyperglycemia, intensify current dysregulation—akin to metabolic syndrome. Key takeaways include the interpretation of the fractional order $\theta$ as a potential biomarker: values near 1 indicate efficient homeostasis, while smaller $\theta$ suggests impaired regulation due to delayed insulin response or $\beta$-cell dysfunction. Based on this model, clinicians can identify metabolic sluggishness early and develop treatment strategies tailored to each patient. Furthermore, the nonlinear threshold function ${[x\left(t\right)-{\tau }_5]}^{+}$ models the binary switch-like nature of insulin secretion above a critical glucose level, which is further complemented by fractional dynamics. By accounting for the long-term memory inherent in physiological processes, such simulations can inform the optimal timing of interventions. Biological complexity can be captured more realistically by fractional-order models than by integer-order models, as shown in the figure.

Clarification on the Experimental Data Representation

It is important to clarify that the curves labeled “Experimental Data” in Figure 4 do not originate from newly acquired laboratory or clinical measurements. Rather, these curves serve as reference trajectories reconstructed from previously published glucose–insulin datasets available in the open literature. Specifically, the reference profile corresponds to the well-established intravenous glucose tolerance test (IVGTT) data reported in [47,48,49], which have been extensively used in validation of minimal and extended glucose–insulin models. The data were digitized and normalized to ensure compatibility with the nondimensionalized variables used in the present fractional framework. Time was rescaled to minutes, and glucose and insulin concentrations were expressed in $\mathrm{mg}/\mathrm{dL}$ and μU/mL, respectively, following clinical convention.

In this work, the “Experimental Data” therefore denote benchmark trajectories used for model validation and comparison rather than raw patient records. They provide a physiologically consistent reference allowing a visual assessment of how well the proposed fractional-order system reproduces realistic temporal trends observed in clinical studies. All numerical experiments were performed under parameter settings compatible with the reported fasting and postprandial ranges for healthy adults. Future work will include direct calibration of the model using continuous glucose monitoring (CGM) datasets from diabetic subjects to quantitatively validate the predictive capability of the proposed framework.

10. Discussion

The application of the Caputo–Euler method to the fractional glucose–insulin model has provided valuable insights into the role of memory effects in metabolic regulation. By discretizing the Caputo derivative, we successfully captured the long-range temporal dependencies that classical integer-order models are unable to reproduce. The scheme maintains stability while resolving nonlinear interactions and threshold-triggered responses, although deviations from classical convergence rates are expected due to the fractional framework.

Our convergence analysis indicates consistent error reduction with decreasing step sizes, confirming the method’s reliability for simulating physiological processes. Nonetheless, oscillatory behavior in the $L_{\infty }$ error norm, particularly near activation thresholds and during rapid state transitions, highlights the challenges introduced by nonlocal fractional operators and the stiffness of the system. These artifacts suggest the potential benefits of adaptive step-size strategies or hybrid discretization schemes that combine local and global approximations.

From a biological perspective, the model reproduces key metabolic phenomena with high fidelity. The fractional order $\theta$ emerges as a critical determinant of system dynamics: values $\theta <0.9$ effectively mimic impaired glucose regulation patterns associated with insulin resistance and diabetes. The preservation of non-negativity and boundedness further reinforces the physiological realism of the model. Importantly, the inclusion of memory effects provides a rigorous mathematical foundation for understanding metabolic hysteresis, where past glycemic states influence present regulation.

Although the present study demonstrates that variations in the fractional order $\theta$ modulate the qualitative dynamics of the glucose–insulin regulatory system, the interpretation of $\theta$ as a potential biomarker of metabolic memory remains a theoretical proposition. The numerical experiments in this work were performed using parameter values consistent with physiological ranges but were not calibrated or validated against individual patient datasets or continuous glucose monitoring (CGM) records. Consequently, no statistical relationship between $\theta$ and measurable clinical indicators (e.g., insulin sensitivity, $\beta$-cell responsivity, or HbA1c) can be established at this stage. Future research should involve fitting the fractional model to real experimental or clinical data to examine whether estimated values of $\theta$ correlate with empirical biomarkers of metabolic health or disease progression. Such validation is essential before $\theta$ can be considered a reliable diagnostic or prognostic indicator in biomedical practice.

11. Conclusions

This work establishes the Caputo–Euler method as a practical and reliable tool for the fractional-order modeling of glucose–insulin regulation. The method achieves a favorable balance between computational efficiency and biological realism with convergence of order $\mathcal{O}\left(h^{2-\theta }\right)$ and the preservation of essential system properties such as positivity and boundedness. These features make it particularly well suited for investigating long-term metabolic dynamics.

Theoretical analysis further supports the framework: existence and uniqueness results ensure the well posedness of the system, while Hyers–Ulam stability confirms robustness against perturbations arising from model uncertainty, measurement noise, and discretization errors. Together, these guarantees enhance the credibility of the model for biomedical applications.

Future research directions include (1) extending the methodology to variable-order and stochastic operators to capture inter-patient variability and random physiological disturbances; (2) validating the model with clinical datasets, particularly continuous glucose monitoring (CGM) records; and (3) embedding the framework within decision-support systems for personalized diabetes management. Such developments will strengthen the bridge between fractional calculus theory and its translational applications in healthcare.

In conclusion, the proposed framework not only provides a foundation for advanced fractional-order models of glucose regulation but also offers a computational tool for probing metabolic disorders. The demonstrated sensitivity of system behavior to the fractional order $\theta$ suggests its potential use as a novel biomarker for metabolic health, opening new avenues for both theoretical exploration and clinical practice.