Diversity Constraint and Adaptive Graph Multi-View Functional Matrix Completion
Abstract
1. Introduction
2. Related Work
2.1. Curve Fitting of Multi-View Functional Data
2.2. Multi-View Functional Matrix Completion
3. Methodology
3.1. DCAGMFMC
3.2. Optimization Algorithm
3.3. Convergence Analysis
| Algorithm 1. DCAGMFMC |
| Input: Multi-view data matrix , parameters , iteration count Output: and . 1. Generate random values for and , then initialize according to Equation (25); 2. Fixing and , update according to Equation (16); 3. Fixing and , update according to Equation (19); 4. Fixing and , update according to Equation (25); 5. Repeat the aforementioned optimization steps (steps 2–4) until is achieved. |
3.4. Time Complexity Analysis
4. Experiments
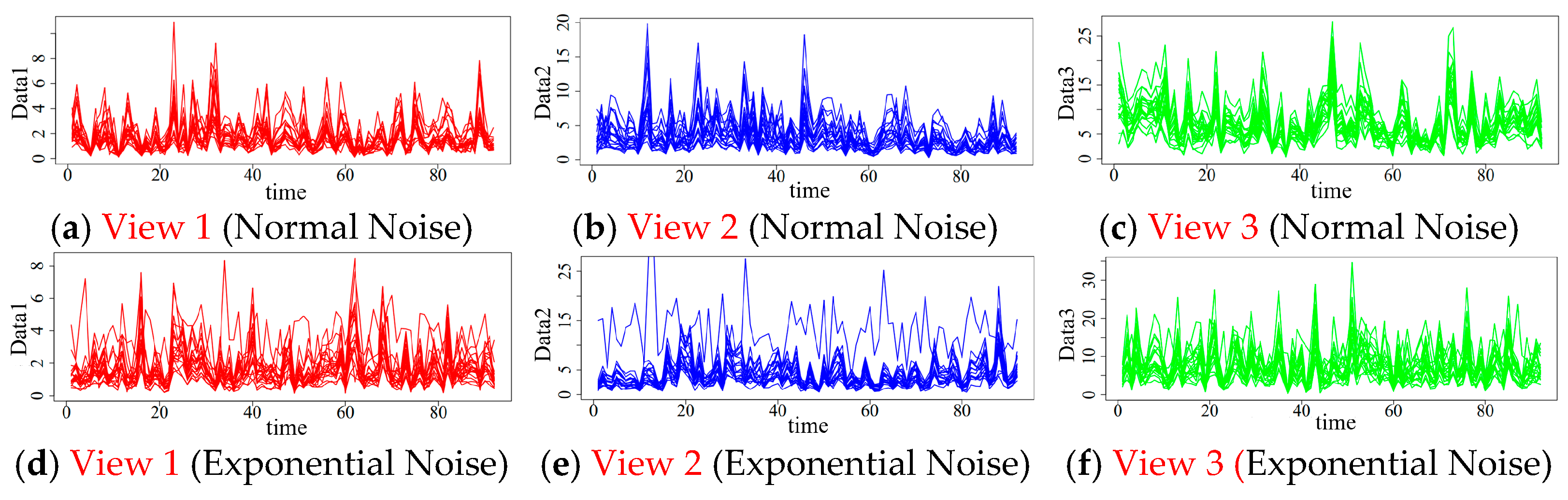
4.1. Simulation Data Generation
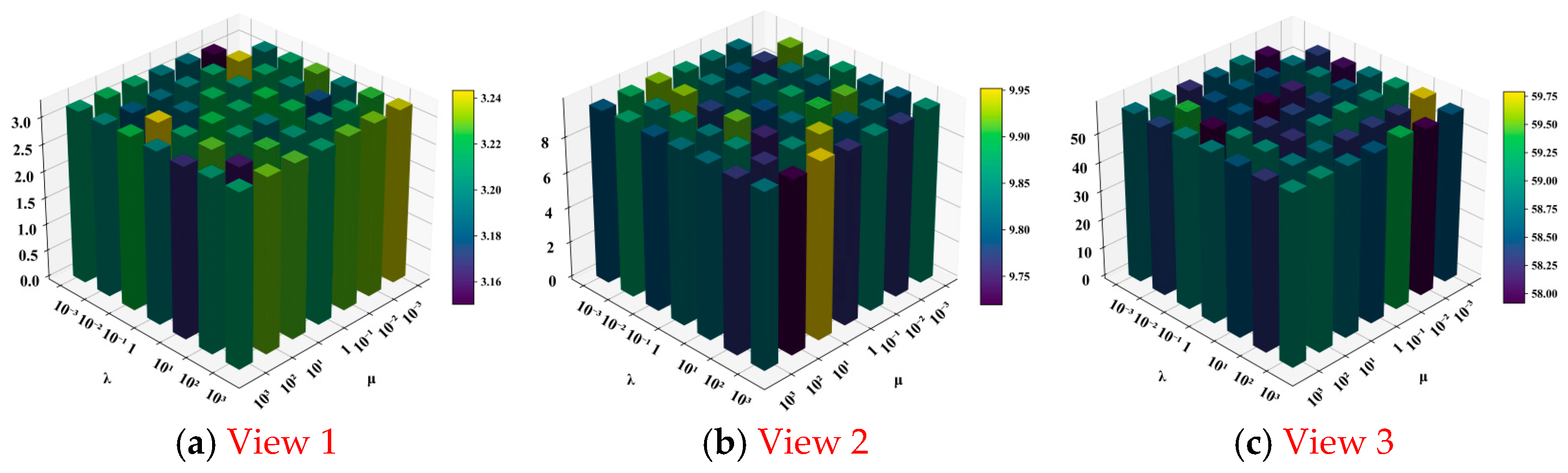
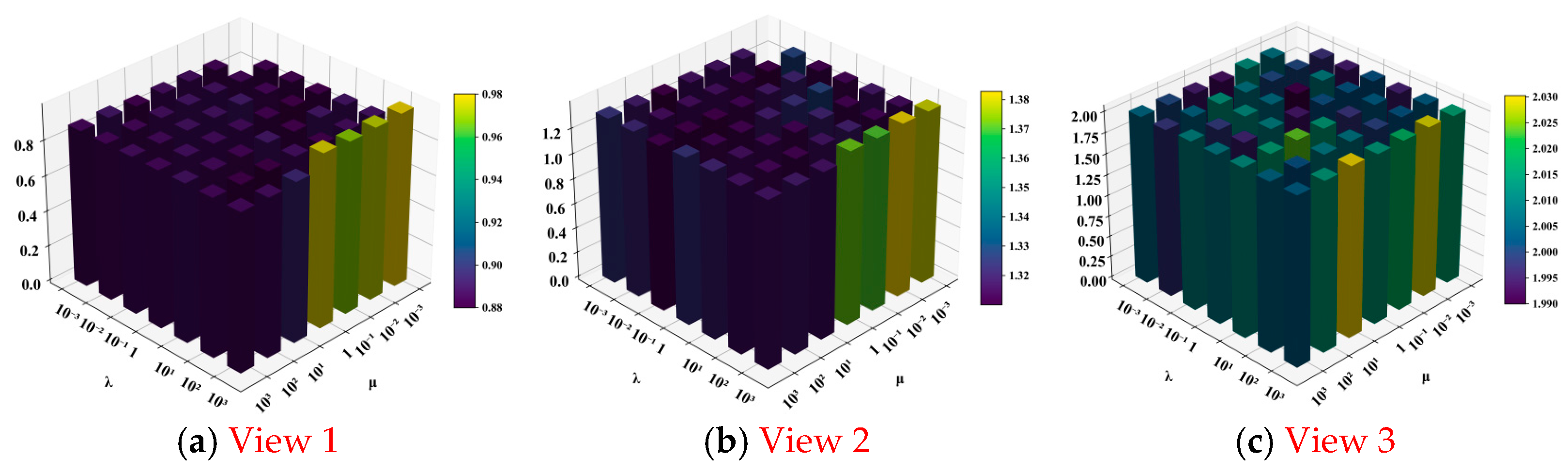
4.2. Experimental Results and Analysis
5. Example Application
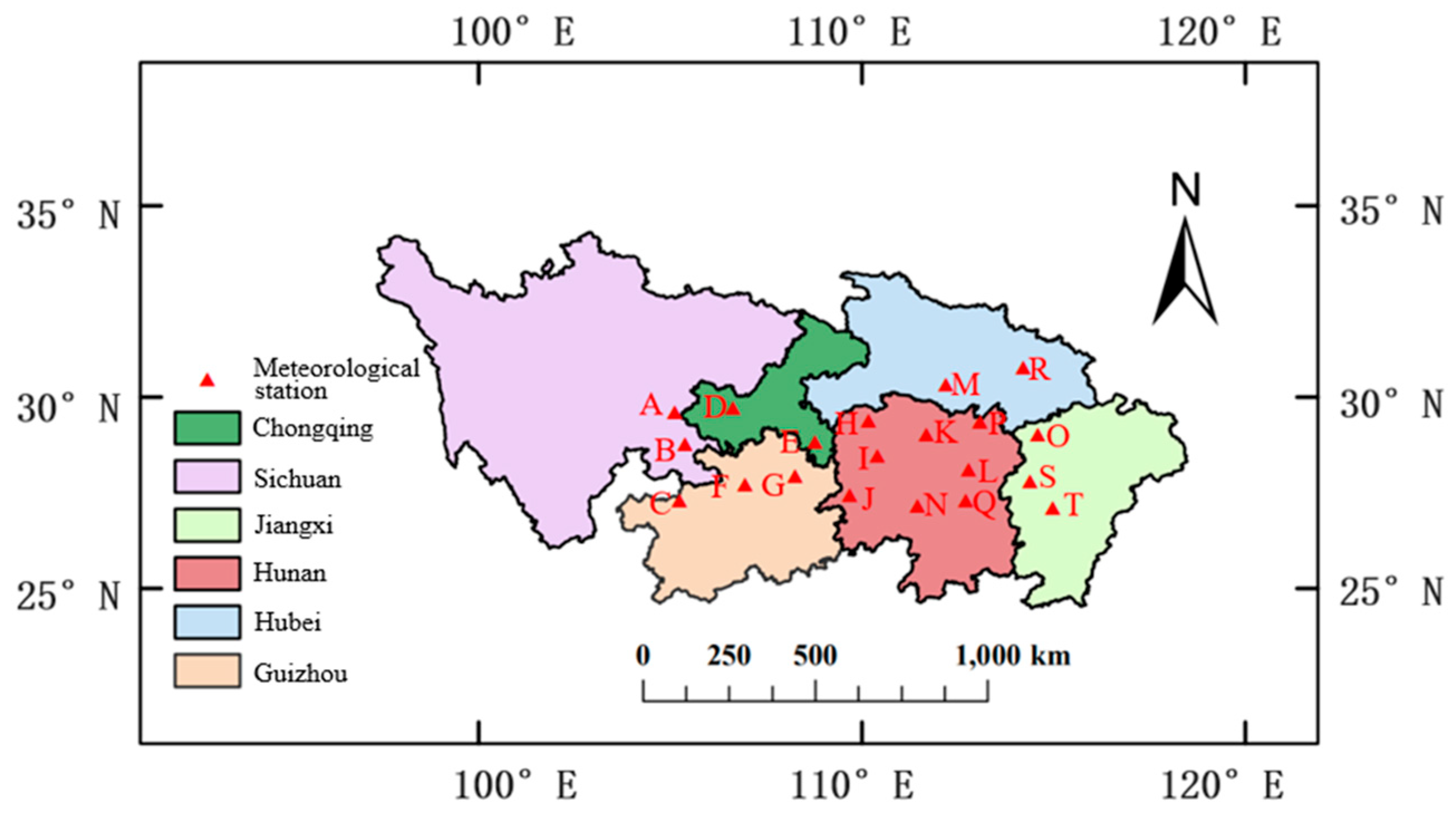
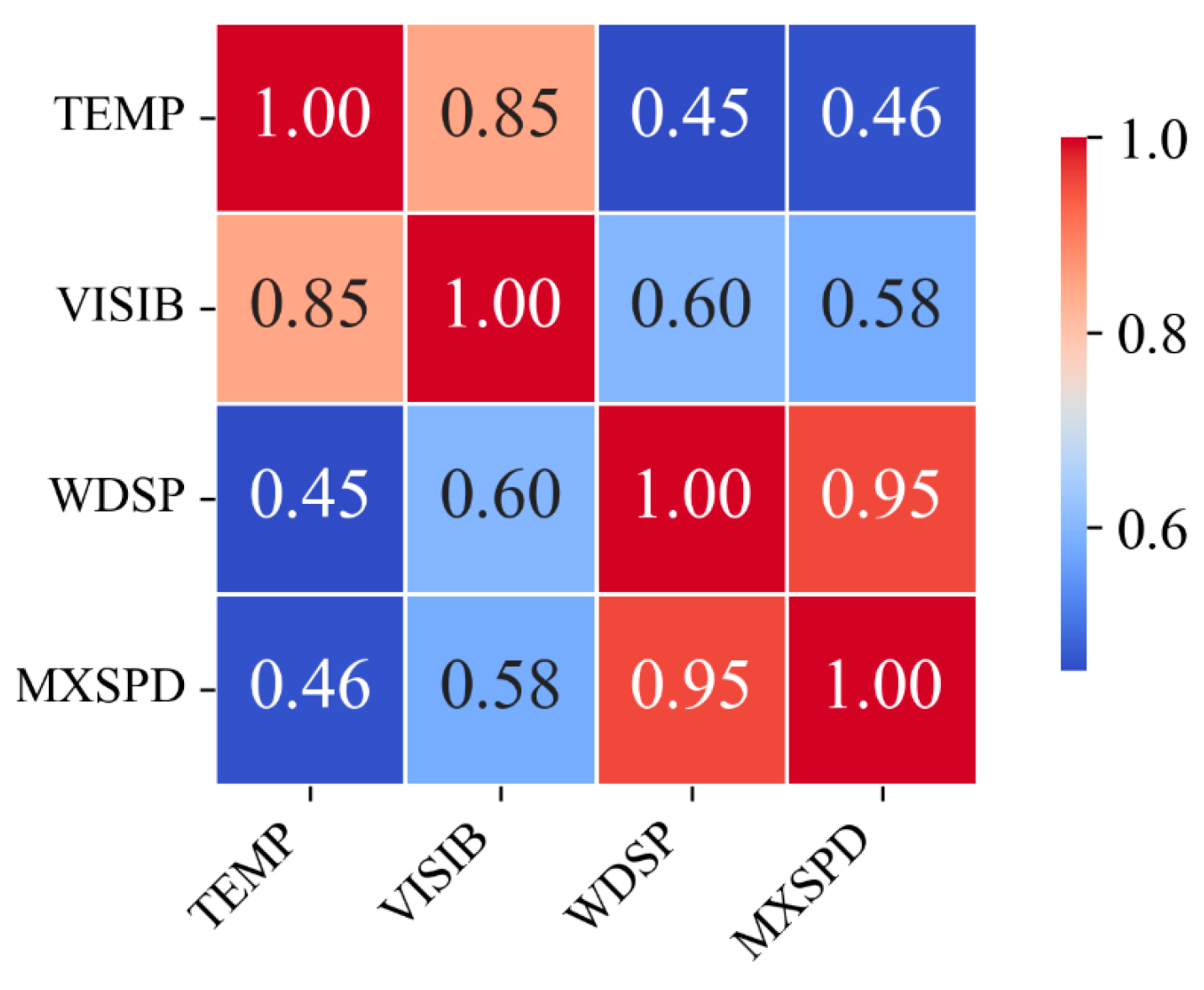
5.1. Meteorological Experiment Data
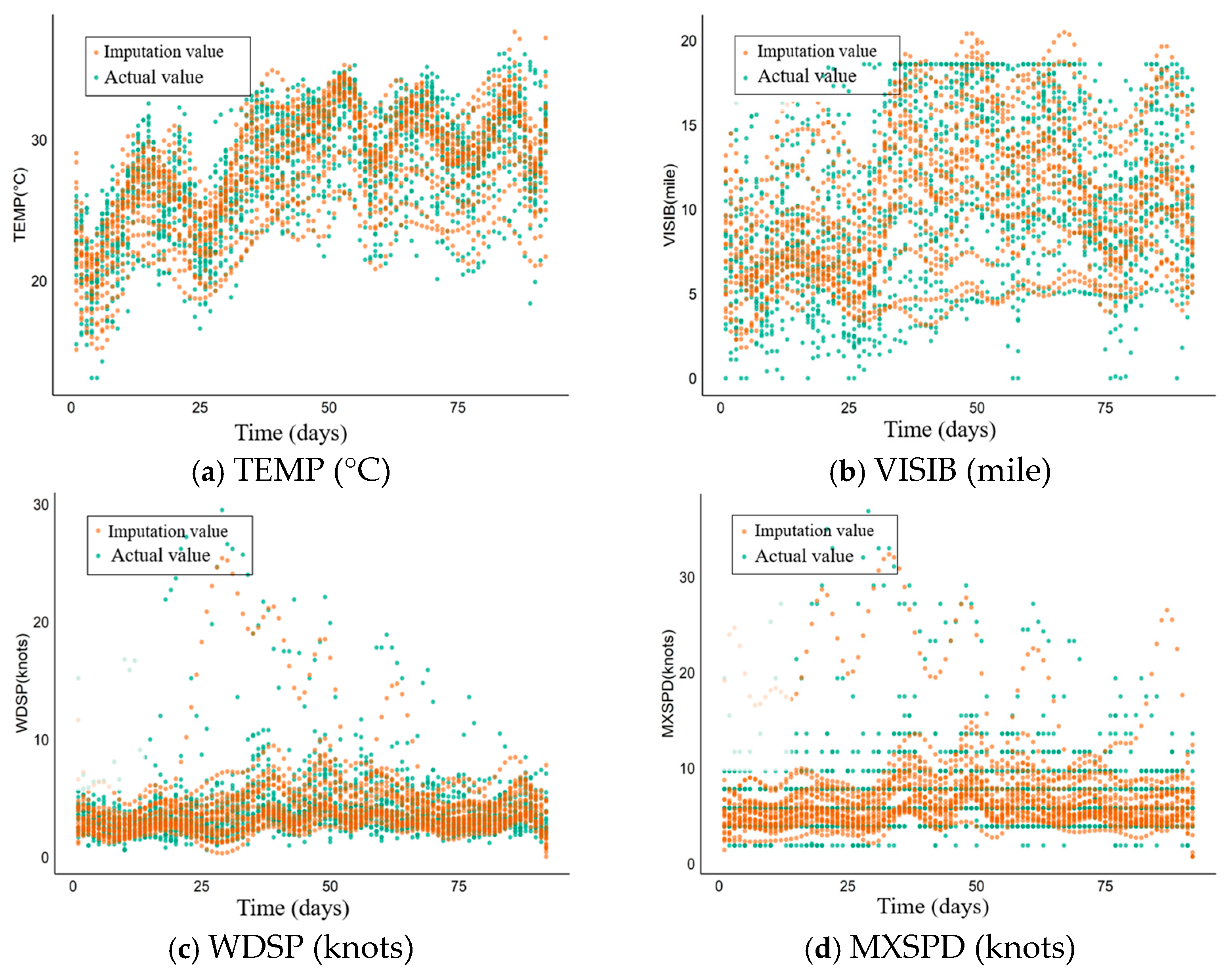
5.2. Ablation Experiment
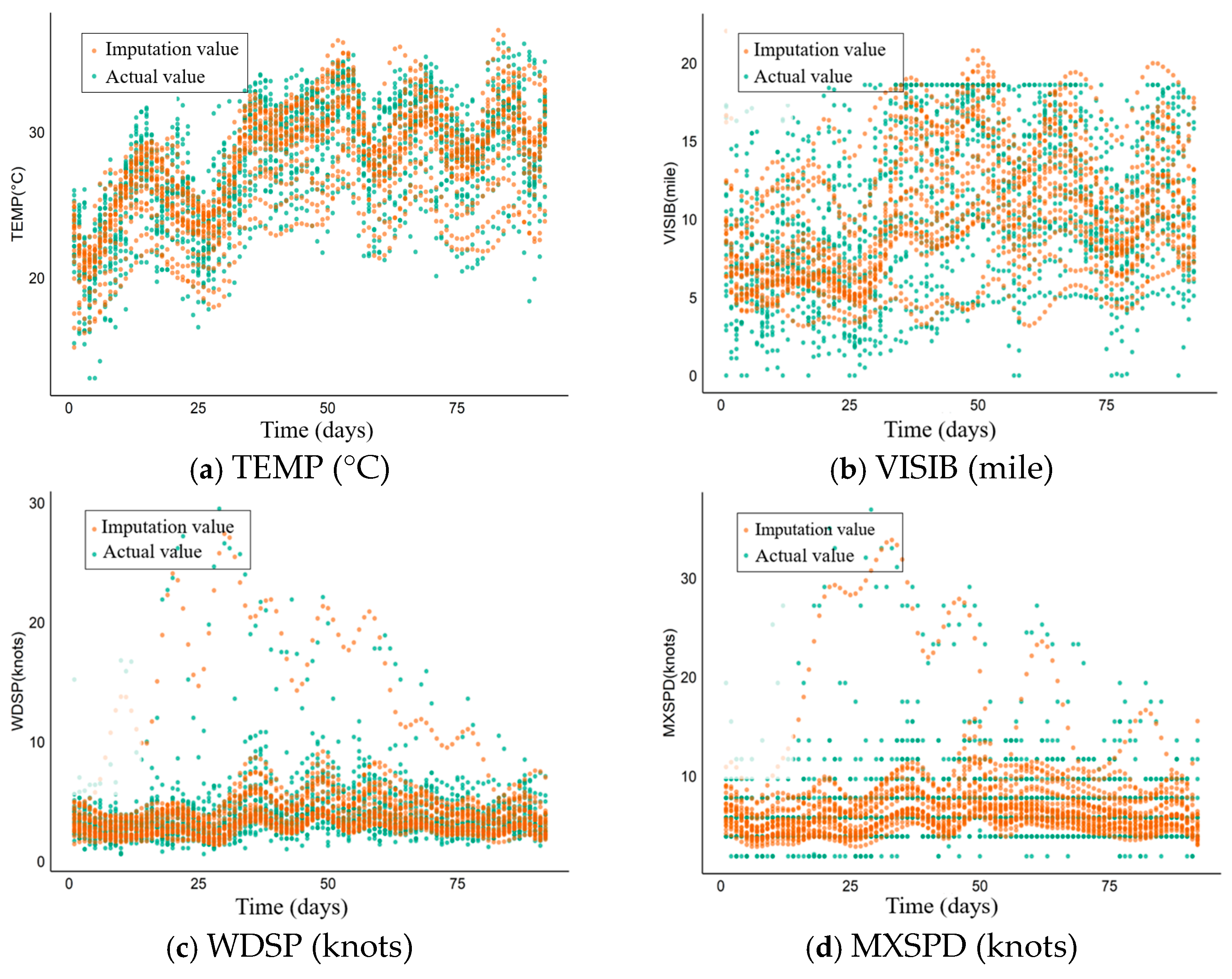
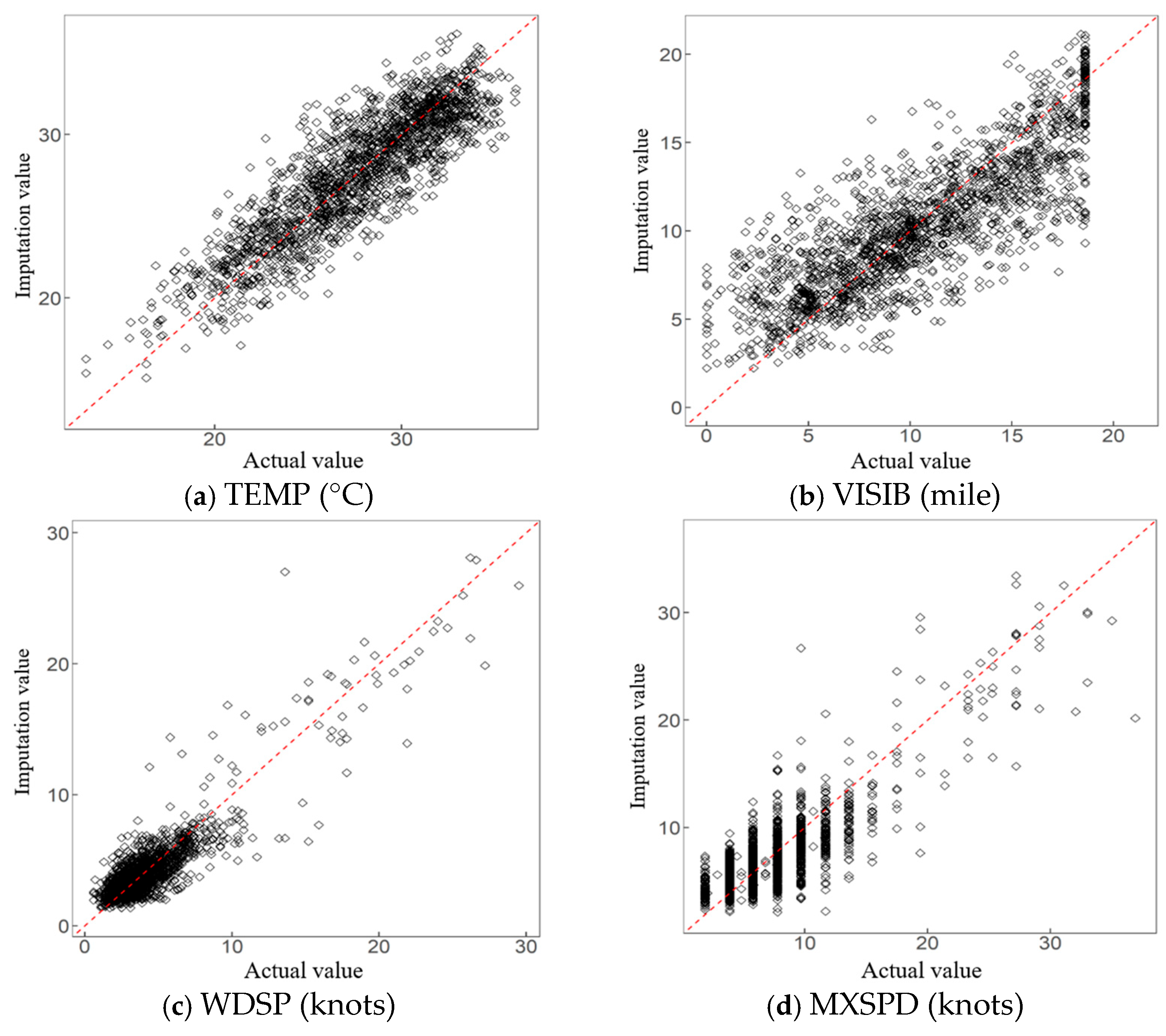
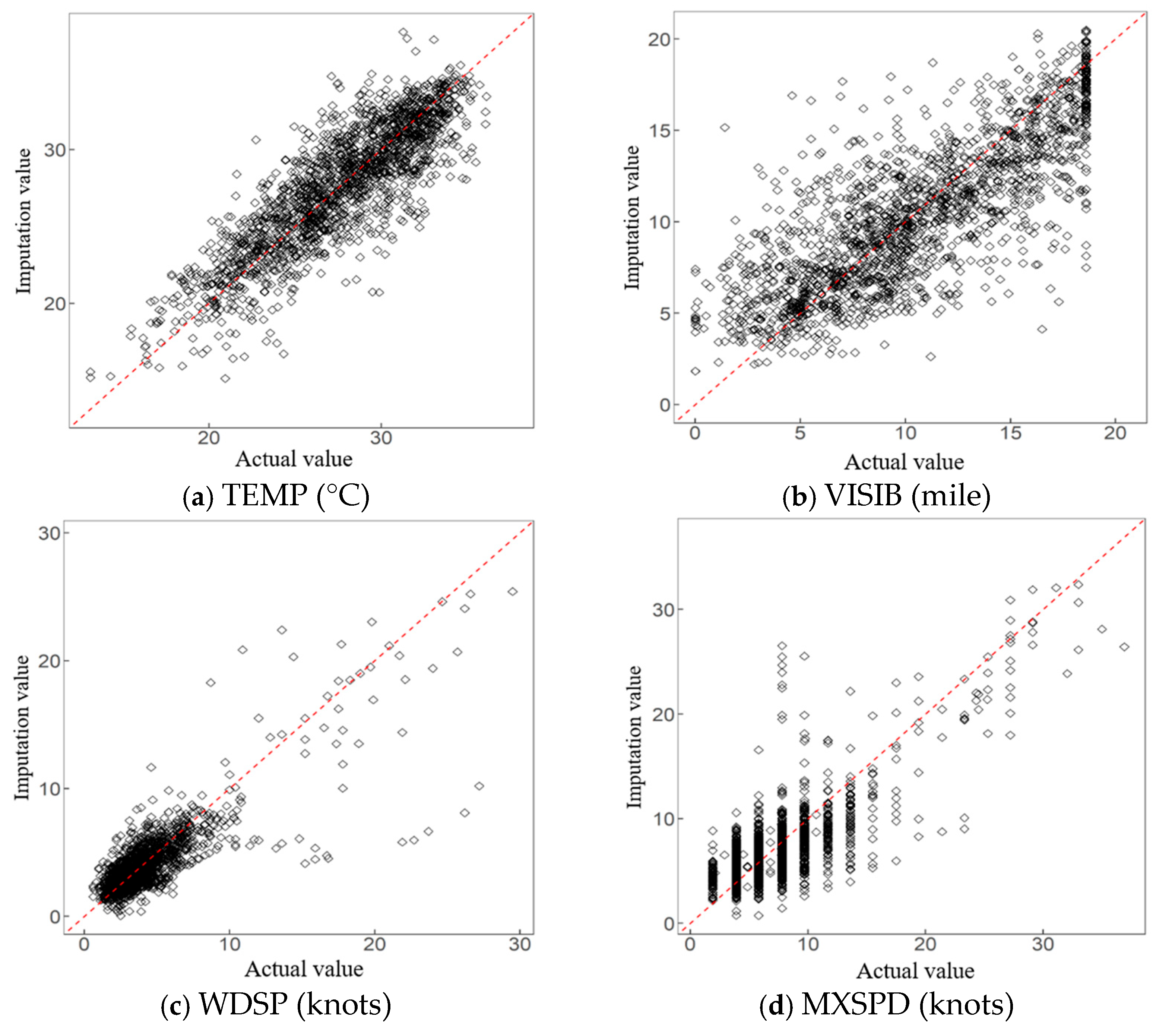
5.3. Application Effect and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PACE | Principal Components Analysis through Conditional Expectation |
| MICE | Multiple Imputation by Chained Equations |
| fregMICE | Functional Regression MICE |
| IDW | Inverse Distance Weighting |
| SFI | Soft Functional Impute |
| HFI | Hard Functional Impute |
| KNN | k-Nearest Neighbors |
| EM | Expectation Maximization |
| MF | Matrix Factorization |
| TRMF | Temporal Regularized Matrix Factorization |
| NCAD | Neural Contextual Anomaly Detection |
| FDA | Functional Data Analysis |
| MVL | Multi-view Learning |
| MVNFMC | Multi-view Non-negative Functional Matrix Completion |
| GRMFMC | Graph-Regularized Multi-view Functional Matrix Completion |
| DCAGMFMC | Diversity Constraint and Adaptive Graph Multi-view Functional Matrix Completion |
| PM | Pointwise Missing |
| IM | Interval Missing |
References
- Miao, X.; Wu, Y.; Chen, L.; Gao, Y.; Yin, J. An experimental survey of missing data Imputation algorithms. IEEE Trans. Knowl. Data Eng. 2022, 35, 6630–6650. [Google Scholar] [CrossRef]
- Kong, X.; Zhou, W.; Shen, G.; Zhang, W.; Liu, N.; Yang, Y. Dynamic graph convolutional recurrent imputation network for spatiotemporal traffic missing data. Knowl.-Based Syst. 2023, 261, 110188. [Google Scholar] [CrossRef]
- Gao, H.Y.; Li, W.X. Function-based multiple imputation method based on cross-sectional and longitudinal information. Tongji Yu Juece/Stat. Decis. 2025, 41, 37–42. [Google Scholar] [CrossRef]
- Bertsimas, D.; Pawlowski, C.; Zhuo, Y.D. From predictive methods to missing data imputation: An optimization approach. J. Mach. Learn. Res. 2018, 18, 1–39. Available online: https://jmlr.org/papers/v18/17-073.html (accessed on 15 October 2024).
- Yao, F.; Müller, H.G.; Wang, J.L. Functional data analysis for sparse longitudinal data. J. Am. Stat. Assoc. 2005, 100, 577–590. [Google Scholar] [CrossRef]
- Royston, P.; White, I.R. Multiple Imputation by Chained Equations (MICE): Implementation in Stata. J. Stat. Softw. 2011, 45, 1–20. [Google Scholar] [CrossRef]
- He, Y.; Yucel, R.; Raghunathan, T.E. A functional multiple imputation approach to incomplete longitudinal Data. Stat. Med. 2011, 30, 1137–1156. [Google Scholar] [CrossRef]
- Ciarleglio, A.; Petkova, E.; Harel, O. Elucidating age and sex-dependent association between frontal EEG asymmetry and depression: An application of multiple imputation in functional regression. J. Am. Stat. Assoc. 2022, 117, 12–26. [Google Scholar] [CrossRef]
- Rao, A.R.; Reimherr, M. Modern multiple imputation with functional data. Stat 2021, 10, e331. [Google Scholar] [CrossRef]
- Li, J.W.; Sun, Y.H.; Wang, S.; Zhang, Z.W.; Wang, Y. Ultra-short-term load forecasting considering missing data in abnormal situations. Autom. Electr. Power Syst. 2025, 49, 133–143. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.P.; Liu, F.Q.; Kong, X.F.; Ma, R. Research progress on abnormal and missing data processing methods in marine environmental monitoring. J. Appl. Oceanogr. 2025, 44, 388–401. [Google Scholar] [CrossRef]
- Liang, Y.P.; Li, X.Y.; Li, Q.G.; Mao, S.R.; Zhen, M.H.; Li, J.B. Research on intelligent prediction of gas concentration in working face based on CS-LSTM. J. Mine Saf. Environ. Prot. 2022, 49, 80–86. [Google Scholar] [CrossRef]
- Wu, Y.H.; Wang, Y.S.; Xu, H.; Chen, Z.; Zhang, Z.; Guan, S.J. Review on wind power output prediction technology. Comput. Sci. Explor. 2022, 16, 2653–2677. [Google Scholar] [CrossRef]
- Kidzinski, Ł.; Hastie, T. Longitudinal data analysis using matrix completion. Stat 2018, 1050, 24. [Google Scholar] [CrossRef]
- Xue, J.; Fu, D.Y.; Han, H.B.; Gao, H.Y. A non-negative functional matrix completion algorithm based on multi-view learning. Stat. Decis. 2022, 38, 5–11. [Google Scholar] [CrossRef]
- Kramer, O. K-nearest neighbors. In Dimensionality Reduction with Unsupervised Nearest Neighbors; Springer: Berlin/Heidelberg, Germany, 2013; pp. 13–23. [Google Scholar] [CrossRef]
- Gao, H.Y.; Liu, C.; Ma, W.J. Comparison and application of time series data imputation methods for surface water quality monitoring. Hydrology 2024, 44, 63–69. [Google Scholar] [CrossRef]
- Nelwamondo, F.V.; Mohamed, S.; Marwala, T. Missing data: A comparison of neural network and expectation maximization techniques. Curr. Sci. 2007, 93, 1514–1521. Available online: https://www.jstor.org/stable/24099079 (accessed on 15 October 2024).
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Yu, H.F.; Rao, N.; Dhillon, I.S. Temporal regularized matrix factorization for high-dimensional time series prediction. Adv. Neural Inf. Process. Syst. 2016, 29. Available online: https://proceedings.neurips.cc/paper_files/paper/2016/hash/85422afb467e9456013a2a51d4dff702-Abstract.html (accessed on 24 October 2025).
- He, J.; Lai, Z.; Shi, K. Time series imputation method based on joint tensor completion and recurrent neural network. Data Acquis. Process. 2024, 39, 598–608. [Google Scholar] [CrossRef]
- Cao, W.; Wang, D.; Li, J.; Zhou, H.; Li, L.; Li, Y. BRITS: Bidirectional recurrent imputation for time series. Adv. Neural Inf. Process. Syst. 2018, 31. Available online: https://proceedings.neurips.cc/paper_files/paper/2018/hash/734e6bfcd358e25ac1db0a4241b95651-Abstract.html (accessed on 24 October 2025).
- Carmona, C.U.; Aubet, F.X.; Flunkert, V.; Gasthaus, J. Neural contextual anomaly detection for time series. arXiv 2021, arXiv:2107.07702. [Google Scholar] [CrossRef]
- Yoon, J.S.; Jordon, J.; Schaar, M. GAIN: Missing data imputation using generative adversarial nets. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar] [CrossRef]
- Wang, J.L.; Chiou, J.M.; Müller, H.G. Functional data analysis. Annu. Rev. Stat. Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef]
- Ullah, S.; Finch, C.F. Applications of functional data analysis: A systematic review. BMC Med. Res. Methodol. 2013, 13, 43. [Google Scholar] [CrossRef]
- Yao, X.H. Research on Several Multivariate Functional Clustering Methods Based on Multi-View Learning. Ph.D. Thesis, Lanzhou University of Finance and Economics, Lanzhou, China, 2022. Available online: https://library.lzufe.edu.cn/asset/detail/0/20471970033 (accessed on 24 October 2025).
- Descary, M.H.; Panaretos, V.M. Functional data analysis by matrix completion. Ann. Stat. 2019, 47, 1–38. [Google Scholar] [CrossRef]
- Kong, S.; Wang, X.; Wang, D.; Wu, F. Multiple feature fusion for face recognition. In Proceedings of the 2013 10th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG), Shanghai, China, 22–26 April 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.; Xia, W.; Gao, Q.; Gao, X. Low-rank tensor constrained co-regularized multi-view spectral clustering. Neural Netw. 2020, 132, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Xiao, Y.S.; Liu, B. Multi-view semi-supervised marked distribution learning. Comput. Appl. Res. 2025, 42, 1–8. Available online: https://www.arocmag.cn/abs/2025.04.0114 (accessed on 24 October 2025).
- Gao, H.Y.; Ma, W.J. Air quality data restoration based on graph regularization and multi-view function matrix completion. China Environ. Sci. 2024, 44, 5357–5370. [Google Scholar] [CrossRef]
- Li, C.; Che, H.; Leung, M.F.; Liu, C.; Yan, Z. Robust multi-view non-negative matrix factorization with adaptive graph and diversity constraints. Inf. Sci. 2023, 634, 587–607. [Google Scholar] [CrossRef]
- Wang, J.; Tian, F.; Yu, H.; Liu, C.H.; Zhan, K.; Wang, X. Diverse non-negative matrix factorization for multiview data representation. IEEE Trans. Cybern. 2017, 48, 2620–2632. [Google Scholar] [CrossRef] [PubMed]
- Liang, N.; Yang, Z.; Li, Z.; Sun, W.; Xie, S. Multi-view clustering by non-negative matrix factorization with co-orthogonal constraints. Knowl.-Based Syst. 2020, 194, 105582. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhou, G.; Qiu, Y.; Wang, Y.; Zhang, Y.; Xie, S. Deep graph regularized non-negative matrix factorization for multi-view clustering. Neurocomputing 2020, 390, 108–116. [Google Scholar] [CrossRef]
- Yang, X.; Che, H.; Leung, M.F.; Liu, C. Adaptive graph nonnegative matrix factorization with the self-paced regularization. Appl. Intell. 2023, 53, 15818–15835. [Google Scholar] [CrossRef]
- Luo, P.; Peng, J.; Guan, Z.; Fan, J. Dual regularized multi-view non-negative matrix factorization for clustering. Neurocomputing 2018, 294, 1–11. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Zhang, R.; Liu, Y.; Nie, F. Generalized uncorrelated regression with adaptive graph for unsupervised feature selection. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1587–1595. [Google Scholar] [CrossRef]
- Hunter, D.R.; Lange, K. A tutorial on MM algorithms. Am. Stat. 2004, 58, 30–37. [Google Scholar] [CrossRef]
- Tseng, P. Convergence of a block coordinate descent method for nondifferentiable minimization. J. Optim. Theory Appl. 2001, 109, 475–494. [Google Scholar] [CrossRef]
- Mucherino, A.; Papajorgji, P.J.; Pardalos, P.M. K-nearest neighbor classification. In Data Mining in Agriculture; Springer: New York, NY, USA, 2009; pp. 83–106. [Google Scholar] [CrossRef]
- Jacques, J.; Preda, C. Model-based clustering for multivariate functional data. Comput. Stat. Data Anal. 2014, 71, 92–106. [Google Scholar] [CrossRef]
- Boor, C.D. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar] [CrossRef]
- Chiou, J.M.; Zhang, Y.C.; Chen, W.H.; Chang, C.W. A functional data approach to missing value imputation and outlier detection for traffic flow data. Transp. B Transp. Dyn. 2014, 2, 106–129. [Google Scholar] [CrossRef]
- NOAA National Centers for Environmental Information. Global Summary of the Day—Weather Data. 2024. Available online: https://www.ncei.noaa.gov/data/global-summary-of-the-day/archive (accessed on 1 October 2024).






| Imputation Methods | Normal Noise | Exponential Noise | |||||
|---|---|---|---|---|---|---|---|
| View 1 | View 2 | View 3 | View1 | View 2 | View 3 | ||
| Case a | KNN | 6.32 ± 0.37 | 25.56 ± 1.46 | 159.17 ± 15.53 | 6.60 ± 0.41 | 27.56 ± 1.91 | 174.85 ± 17.66 |
| SFI | 2.65 ± 0.00 | 18.40 ± 0.00 | 121.78 ± 0.00 | 2.81 ± 0.00 | 20.56 ± 0.00 | 136.37 ± 0.00 | |
| HFI | 2.64 ± 0.00 | 18.36 ± 0.00 | 122.48 ± 0.00 | 2.80 ± 0.00 | 20.62 ± 0.01 | 136.88 ± 0.00 | |
| MVNFMC | 8.41 ± 0.04 | 14.25 ± 0.09 | 64.95 ± 0.59 | 8.46 ± 0.04 | 15.01 ± 0.09 | 71.45 ± 0.55 | |
| GRMFMC | 16.60 ± 0.82 | 23.99 ± 1.02 | 88.90 ± 3.02 | 15.83 ± 1.30 | 25.06 ± 1.93 | 95.59 ± 1.64 | |
| DCAGMFMC | 3.18 ± 0.10 | 9.82 ± 0.09 | 58.39 ± 0.57 | 3.27 ± 0.11 | 10.92 ± 0.09 | 66.91 ± 0.75 | |
| Case b | KNN | 0.61 ± 0.05 | 1.01 ± 0.08 | 1.60 ± 0.11 | 0.98 ± 0.09 | 1.51 ± 0.11 | 2.63 ± 0.18 |
| SFI | 0.95 ± 0.00 | 1.69 ± 0.00 | 2.76 ± 0.00 | 1.79 ± 0.00 | 2.92 ± 0.00 | 4.24 ± 0.00 | |
| HFI | 0.94 ± 0.00 | 1.67 ± 0.00 | 2.75 ± 0.00 | 1.78 ± 0.00 | 2.91 ± 0.00 | 4.21 ± 0.00 | |
| MVNFMC | 0.52 ± 0.00 | 0.87 ± 0.00 | 1.46 ± 0.00 | 1.01 ± 0.00 | 1.57 ± 0.00 | 2.39 ± 0.01 | |
| GRMFMC | 0.82 ± 0.05 | 1.23 ± 0.07 | 1.95 ± 0.13 | 1.33 ± 0.05 | 1.99 ± 0.14 | 3.13 ± 0.27 | |
| DCAGMFMC | 0.47 ± 0.00 | 0.78 ± 0.00 | 1.22 ± 0.00 | 0.88 ± 0.00 | 1.32 ± 0.00 | 2.01 ± 0.01 | |
| Variable | Mean | SD | Max | Min | 25th %Percentile | Median | 75th %Percentile | Number |
|---|---|---|---|---|---|---|---|---|
| TEMP (°F) | 55.12 | 2.47 | 60.11 | 49.10 | 53.55 | 55.36 | 57.15 | 1840 |
| VISIB (mile) | 16.72 | 2.16 | 18.60 | 8.60 | 15.80 | 17.30 | 18.60 | 1840 |
| WDSP (knots) | 4.50 | 0.55 | 6.06 | 3.50 | 4.09 | 4.43 | 4.76 | 1840 |
| MXSPD (knots) | 8.59 | 1.11 | 11.99 | 6.34 | 7.98 | 8.49 | 9.05 | 1840 |
| Missing Rate (%) | Imputation Methods | Evaluation Metric | TEMP (°C) | VISIB (Mile) | WDSP (Knots) | MXSPD (Knots) |
|---|---|---|---|---|---|---|
| 20 | DCAGMFMC | RMSE | 1.55 ± 0.0283 | 1.47 ± 0.0224 | 0.70 ± 0.0214 | 1.16 ± 0.0232 |
| MAE | 0.63 ± 0.0104 | 0.56 ± 0.0105 | 0.25 ± 0.0061 | 0.44 ± 0.0058 | ||
| DCAGMFMC1 | RMSE | 2.06 ± 0.0254 | 1.58 ± 0.0233 | 0.73 ± 0.0161 | 1.24 ± 0.0232 | |
| MAE | 0.89 ± 0.0080 | 0.61 ± 0.0112 | 0.26 ± 0.0048 | 0.47 ± 0.0070 | ||
| DCAGMFMC2 | RMSE | 2.08 ± 0.0262 | 1.57 ± 0.0261 | 0.74 ± 0.0147 | 1.25 ± 0.0208 | |
| MAE | 0.90 ± 0.0078 | 0.61 ± 0.0121 | 0.26 ± 0.0051 | 0.47 ± 0.0053 | ||
| 30 | DCAGMFMC | RMSE | 1.28 ± 0.0287 | 1.21 ± 0.0229 | 0.57 ± 0.0170 | 0.97 ± 0.0187 |
| MAE | 0.43 ± 0.0092 | 0.38 ± 0.0085 | 0.16 ± 0.0042 | 0.30 ± 0.0041 | ||
| DCAGMFMC1 | RMSE | 1.70 ± 0.0234 | 1.27 ± 0.0186 | 0.62 ± 0.0175 | 1.01 ± 0.0151 | |
| MAE | 0.60 ± 0.0057 | 0.40 ± 0.0071 | 0.18 ± 0.0039 | 0.31 ± 0.0038 | ||
| DCAGMFMC2 | RMSE | 1.71 ± 0.0218 | 1.29 ± 0.0202 | 0.60 ± 0.0109 | 1.01 ± 0.0156 | |
| MAE | 0.61 ± 0.0058 | 0.41 ± 0.0069 | 0.17 ± 0.0031 | 0.31 ± 0.0038 | ||
| 40 | DCAGMFMC | RMSE | 1.12 ± 0.0261 | 1.05 ± 0.0187 | 0.52 ± 0.0093 | 0.86 ± 0.0200 |
| MAE | 0.32 ± 0.0068 | 0.28 ± 0.0055 | 0.13 ± 0.0022 | 0.22 ± 0.0038 | ||
| DCAGMFMC1 | RMSE | 1.47 ± 0.0190 | 1.14 ± 0.0200 | 0.57 ± 0.0148 | 0.89 ± 0.0186 | |
| MAE | 0.45 ± 0.0045 | 0.31 ± 0.0065 | 0.13 ± 0.0025 | 0.24 ± 0.0032 | ||
| DCAGMFMC2 | RMSE | 1.48 ± 0.0221 | 1.14 ± 0.0157 | 0.54 ± 0.0128 | 0.88 ± 0.0145 | |
| MAE | 0.45 ± 0.0052 | 0.31 ± 0.0050 | 0.13 ± 0.0030 | 0.23 ± 0.0032 | ||
| 50 | DCAGMFMC | RMSE | 0.99 ± 0.0256 | 0.94 ± 0.0162 | 0.46 ± 0.0104 | 0.77 ± 0.0185 |
| MAE | 0.26 ± 0.0059 | 0.23 ± 0.0043 | 0.10 ± 0.0021 | 0.18 ± 0.0028 | ||
| DCAGMFMC1 | RMSE | 1.35 ± 0.0197 | 1.02 ± 0.0196 | 0.49 ± 0.0136 | 0.80 ± 0.0132 | |
| MAE | 0.37 ± 0.0044 | 0.25 ± 0.0042 | 0.11 ± 0.0021 | 0.19 ± 0.0024 | ||
| DCAGMFMC2 | RMSE | 1.31 ± 0.0209 | 1.03 ± 0.0183 | 0.49 ± 0.0141 | 0.80 ± 0.0146 | |
| MAE | 0.36 ± 0.0040 | 0.25 ± 0.0051 | 0.11 ± 0.0022 | 0.19 ± 0.0023 |
| Missing Rate (%) | Imputation Methods | TEMP (°C) | VISIB (Mile) | WDSP (Knots) | MXSPD (Knots) |
|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | RMSE | ||
| 20 | KNN | 2.09 ± 0.1072 | 3.22 ± 0.1709 | 2.04 ± 0.2539 | 3.12 ± 0.2267 |
| HFI | 2.13 ± 0.0015 | 2.93 ± 0.0019 | 1.49 ± 0.0026 | 2.41 ± 0.0012 | |
| SFI | 2.14 ± 0.0011 | 2.92 ± 0.0008 | 1.49 ± 0.0019 | 2.43 ± 0.0022 | |
| MVNFMC | 3.63 ± 0.0155 | 1.99 ± 0.0237 | 0.90 ± 0.0134 | 1.47 ± 0.0245 | |
| GRMFMC | 5.89 ± 0.3016 | 2.73 ± 0.2030 | 1.55 ± 0.0704 | 2.37 ± 0.2344 | |
| DCAGMFMC | 1.55 ± 0.0283 | 1.47 ± 0.0224 | 0.70 ± 0.0214 | 1.16 ± 0.0232 | |
| 30 | KNN | 2.37 ± 0.1349 | 3.42 ± 0.1474 | 2.10 ± 0.2538 | 3.26 ± 0.1969 |
| HFI | 2.14 ± 0.0042 | 2.94 ± 0.0025 | 1.52 ± 0.0045 | 2.42 ± 0.0046 | |
| SFI | 2.14 ± 0.0026 | 2.94 ± 0.0009 | 1.51 ± 0.0030 | 2.43 ± 0.0038 | |
| MVNFMC | 2.98 ± 0.0145 | 1.64 ± 0.0178 | 0.77 ± 0.0138 | 1.22 ± 0.0205 | |
| GRMFMC | 4.31 ± 0.3372 | 2.34 ± 0.2533 | 1.29 ± 0.0660 | 1.81 ± 0.0898 | |
| DCAGMFMC | 1.28 ± 0.0287 | 1.21 ± 0.0229 | 0.57 ± 0.0170 | 0.97 ± 0.0187 | |
| 40 | KNN | 2.68 ± 0.1373 | 3.63 ± 0.1162 | 2.24 ± 0.1837 | 3.40 ± 0.1933 |
| HFI | 2.17 ± 0.0038 | 3.01 ± 0.0305 | 1.51 ± 0.0040 | 2.46 ± 0.0083 | |
| SFI | 2.18 ± 0.0060 | 2.97 ± 0.0079 | 1.52 ± 0.0030 | 2.43 ± 0.0040 | |
| MVNFMC | 2.56 ± 0.0171 | 1.39 ± 0.0158 | 0.65 ± 0.0072 | 1.08 ± 0.0156 | |
| GRMFMC | 3.15 ± 1.7703 | 1.51 ± 0.8450 | 0.83 ± 0.4679 | 1.22 ± 0.6879 | |
| DCAGMFMC | 1.12 ± 0.0261 | 1.05 ± 0.0187 | 0.52 ± 0.0093 | 0.86 ± 0.0200 | |
| 50 | KNN | 3.02 ± 0.1289 | 3.84 ± 0.1447 | 2.27 ± 0.1432 | 3.40 ± 0.129 |
| HFI | 2.23 ± 0.0192 | 3.03 ± 0.0272 | 1.53 ± 0.0089 | 2.47 ± 0.0100 | |
| SFI | 2.26 ± 0.0210 | 3.12 ± 0.0336 | 1.52 ± 0.0026 | 2.45 ± 0.0077 | |
| MVNFMC | 2.31 ± 0.0194 | 1.25 ± 0.0134 | 0.60 ± 0.0081 | 0.97 ± 0.0180 | |
| GRMFMC | 2.07 ± 1.8918 | 1.01 ± 0.9279 | 0.59 ± 0.5377 | 0.83 ± 0.7606 | |
| DCAGMFMC | 0.99 ± 0.0256 | 0.94 ± 0.0162 | 0.46 ± 0.0104 | 0.77 ± 0.0185 |
| Missing Rate (%) | Imputation Methods | TEMP (°C) | VISIB (Mile) | WDSP (Knots) | MXSPD (Knots) |
|---|---|---|---|---|---|
| MAE | MAE | MAE | MAE | ||
| 20 | KNN | 1.55 ± 0.0742 | 2.28 ± 0.1188 | 1.18 ± 0.0916 | 2.04 ± 0.1235 |
| HFI | 1.71 ± 0.0015 | 2.19 ± 0.0041 | 0.96 ± 0.0019 | 1.71 ± 0.0006 | |
| SFI | 1.71 ± 0.0019 | 2.17 ± 0.0029 | 0.95 ± 0.0024 | 1.72 ± 0.0008 | |
| MVNFMC | 1.70 ± 0.0067 | 0.80 ± 0.0087 | 0.33 ± 0.0035 | 0.58 ± 0.0064 | |
| GRMFMC | 2.53 ± 0.1387 | 1.09 ± 0.0865 | 0.54 ± 0.0258 | 0.83 ± 0.0833 | |
| DCAGMFMC | 0.63 ± 0.0104 | 0.56 ± 0.0105 | 0.25 ± 0.0061 | 0.44 ± 0.0058 | |
| 30 | KNN | 1.76 ± 0.0910 | 2.45 ± 0.1085 | 1.23 ± 0.0812 | 2.12 ± 0.0963 |
| HFI | 1.71 ± 0.0014 | 2.18 ± 0.0035 | 0.96 ± 0.0023 | 1.72 ± 0.0013 | |
| SFI | 1.71 ± 0.0017 | 2.20 ± 0.0037 | 0.96 ± 0.0013 | 1.73 ± 0.0020 | |
| MVNFMC | 1.14 ± 0.0048 | 0.54 ± 0.0047 | 0.22 ± 0.0028 | 0.38 ± 0.0043 | |
| GRMFMC | 1.47 ± 0.1213 | 0.76 ± 0.0823 | 0.36 ± 0.0201 | 0.53 ± 0.0329 | |
| DCAGMFMC | 0.43 ± 0.0092 | 0.38 ± 0.0085 | 0.16 ± 0.0042 | 0.30 ± 0.0041 | |
| 40 | KNN | 1.99 ± 0.0930 | 2.62 ± 0.0820 | 1.30 ± 0.0601 | 2.21 ± 0.0881 |
| HFI | 1.75 ± 0.0013 | 2.23 ± 0.0093 | 0.97 ± 0.0030 | 1.76 ± 0.0069 | |
| SFI | 1.73 ± 0.0013 | 2.18 ± 0.0031 | 0.97 ± 0.0029 | 1.73 ± 0.0011 | |
| MVNFMC | 0.84 ± 0.0050 | 0.40 ± 0.0037 | 0.17 ± 0.0016 | 0.29 ± 0.0028 | |
| GRMFMC | 0.93 ± 0.5280 | 0.42 ± 0.2368 | 0.20 ± 0.1144 | 0.32 ± 0.1770 | |
| DCAGMFMC | 0.32 ± 0.0068 | 0.28 ± 0.0055 | 0.13 ± 0.0022 | 0.22 ± 0.0038 | |
| 50 | KNN | 2.24 ± 0.0984 | 2.78 ± 0.1089 | 1.34 ± 0.0489 | 2.24 ± 0.0642 |
| HFI | 1.75 ± 0.0083 | 2.24 ± 0.0016 | 0.98 ± 0.0038 | 1.76 ± 0.0047 | |
| SFI | 1.78 ± 0.0067 | 2.22 ± 0.0068 | 0.98 ± 0.0023 | 1.76 ± 0.0031 | |
| MVNFMC | 0.68 ± 0.0054 | 0.32 ± 0.0031 | 0.13 ± 0.0016 | 0.24 ± 0.0029 | |
| GRMFMC | 0.55 ± 0.5017 | 0.25 ± 0.2330 | 0.13 ± 0.1204 | 0.19 ± 0.1737 | |
| DCAGMFMC | 0.26 ± 0.0059 | 0.23 ± 0.0043 | 0.10 ± 0.0021 | 0.18 ± 0.0028 |
| Missing Rate (%) | Imputation Methods | TEMP (°C) | VISIB (Mile) | WDSP (Knots) | MXSPD (Knots) |
|---|---|---|---|---|---|
| NRMSE | NRMSE | NRMSE | NRMSE | ||
| 20 | KNN | 0.50 ± 0.0258 | 0.67 ± 0.0355 | 0.68 ± 0.0845 | 0.73 ± 0.0530 |
| HFI | 0.09 ± 0.0001 | 0.16 ± 0.0001 | 0.05 ± 0.0001 | 0.07 ± 0.0000 | |
| SFI | 0.09 ± 0.0000 | 0.16 ± 0.0000 | 0.05 ± 0.0001 | 0.07 ± 0.0001 | |
| MVNFMC | 0.16 ± 0.0007 | 0.11 ± 0.0013 | 0.03 ± 0.0005 | 0.04 ± 0.0007 | |
| GRMFMC | 0.26 ± 0.0131 | 0.15 ± 0.0109 | 0.05 ± 0.0024 | 0.07 ± 0.0067 | |
| DCAGMFMC | 0.08 ± 0.0012 | 0.08 ± 0.0012 | 0.02 ± 0.0007 | 0.03 ± 0.0007 | |
| 30 | KNN | 0.57 ± 0.0325 | 0.71 ± 0.0306 | 0.70 ± 0.0844 | 0.76 ± 0.0460 |
| HFI | 0.09 ± 0.0002 | 0.16 ± 0.0001 | 0.05 ± 0.0002 | 0.07 ± 0.0001 | |
| SFI | 0.09 ± 0.0001 | 0.16 ± 0.0000 | 0.05 ± 0.0001 | 0.07 ± 0.0001 | |
| MVNFMC | 0.13 ± 0.0006 | 0.09 ± 0.0010 | 0.03 ± 0.0005 | 0.03 ± 0.0006 | |
| GRMFMC | 0.19 ± 0.0147 | 0.13 ± 0.0136 | 0.04 ± 0.0023 | 0.05 ± 0.0026 | |
| DCAGMFMC | 0.06 ± 0.0012 | 0.07 ± 0.0012 | 0.02 ± 0.0006 | 0.03 ± 0.0005 | |
| 40 | KNN | 0.65 ± 0.0331 | 0.75 ± 0.0241 | 0.75 ± 0.0611 | 0.79 ± 0.0452 |
| HFI | 0.09 ± 0.0002 | 0.16 ± 0.0016 | 0.05 ± 0.0001 | 0.07 ± 0.0002 | |
| SFI | 0.09 ± 0.0003 | 0.16 ± 0.0004 | 0.05 ± 0.0001 | 0.07 ± 0.0001 | |
| MVNFMC | 0.11 ± 0.0007 | 0.07 ± 0.0009 | 0.02 ± 0.0002 | 0.03 ± 0.0004 | |
| GRMFMC | 0.14 ± 0.0770 | 0.08 ± 0.0454 | 0.03 ± 0.0162 | 0.03 ± 0.0197 | |
| DCAGMFMC | 0.05 ± 0.0011 | 0.06 ± 0.0010 | 0.02 ± 0.0003 | 0.02 ± 0.0006 | |
| 50 | KNN | 0.73 ± 0.0311 | 0.80 ± 0.0300 | 0.76 ± 0.0476 | 0.79 ± 0.0301 |
| HFI | 0.10 ± 0.0014 | 0.16 ± 0.0007 | 0.05 ± 0.0001 | 0.07 ± 0.0002 | |
| SFI | 0.10 ± 0.0009 | 0.17 ± 0.0018 | 0.05 ± 0.0001 | 0.07 ± 0.0002 | |
| MVNFMC | 0.10 ± 0.0008 | 0.07 ± 0.0007 | 0.02 ± 0.0003 | 0.03 ± 0.0005 | |
| GRMFMC | 0.09 ± 0.0823 | 0.05 ± 0.0499 | 0.02 ± 0.0186 | 0.02 ± 0.0217 | |
| DCAGMFMC | 0.04 ± 0.0011 | 0.05 ± 0.0009 | 0.02 ± 0.0004 | 0.02 ± 0.0005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Bian, Y. Diversity Constraint and Adaptive Graph Multi-View Functional Matrix Completion. Axioms 2025, 14, 793. https://doi.org/10.3390/axioms14110793
Gao H, Bian Y. Diversity Constraint and Adaptive Graph Multi-View Functional Matrix Completion. Axioms. 2025; 14(11):793. https://doi.org/10.3390/axioms14110793
Chicago/Turabian StyleGao, Haiyan, and Youdi Bian. 2025. "Diversity Constraint and Adaptive Graph Multi-View Functional Matrix Completion" Axioms 14, no. 11: 793. https://doi.org/10.3390/axioms14110793
APA StyleGao, H., & Bian, Y. (2025). Diversity Constraint and Adaptive Graph Multi-View Functional Matrix Completion. Axioms, 14(11), 793. https://doi.org/10.3390/axioms14110793






