Fractional Solitons for Controlling Wave Dynamics in Fluids and Plasmas
Abstract
1. Introduction
2. Preliminaries of Local Fractional Calculus and Methodology
2.1. Local Fractional Continuity of a Function
2.2. Local Fractional Derivative
3. Summary of New Mapping Method
4. Fractional (2+1)-Dimensional Davey–Stewartson Equation and Methodology
4.1. Fractional (2+1)-Dimensional Davey–Stewartson Equation
4.2. Solutions to Fractional (2+1)-Dimensional Davey-Stewartson Equation Using NMM
- coeff.:
- coeff.:
- coeff.:
- coeff.:
- coeff.:
- coeff.:
- coeff.:
- coeff.:
- coeff.:
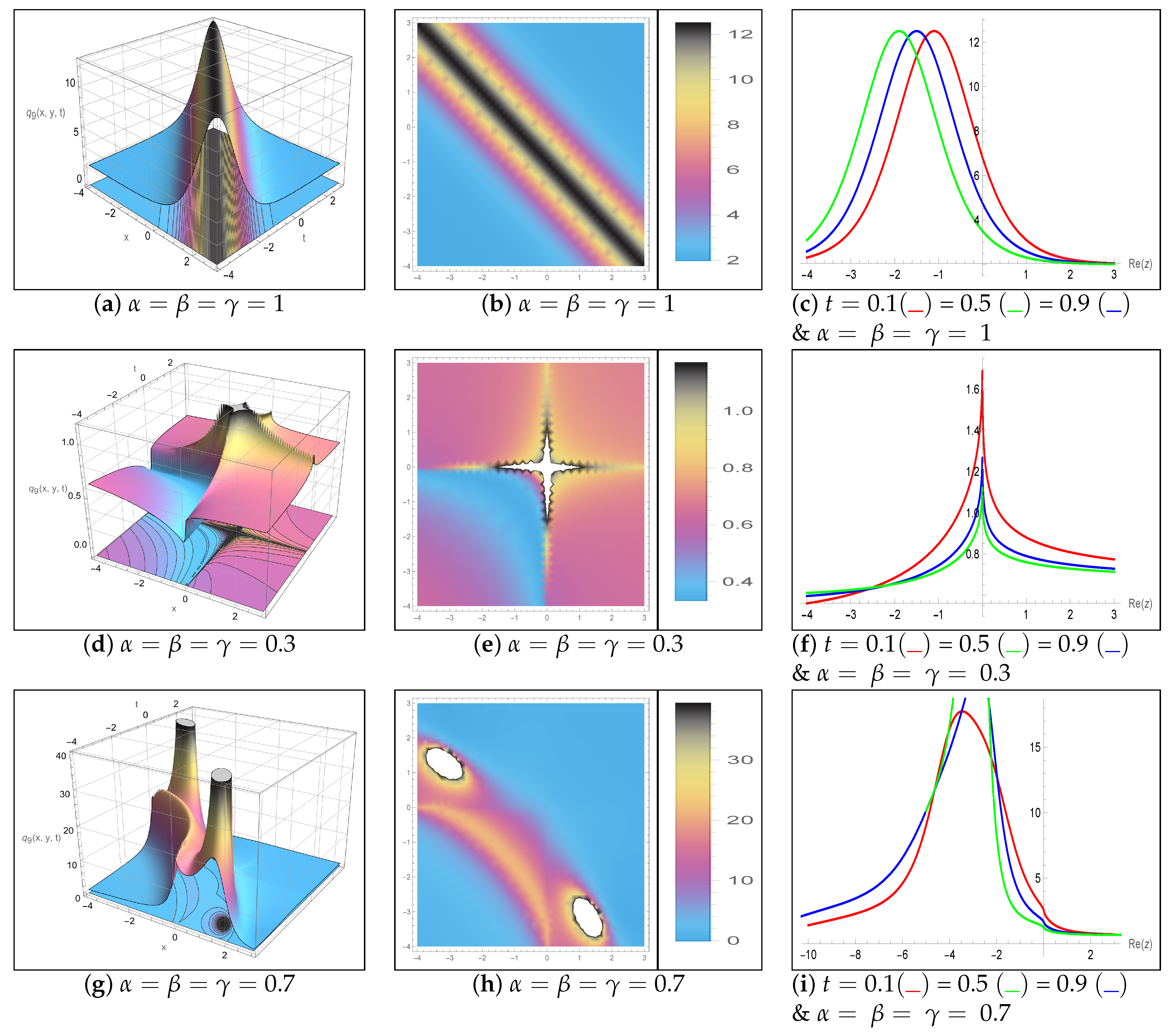
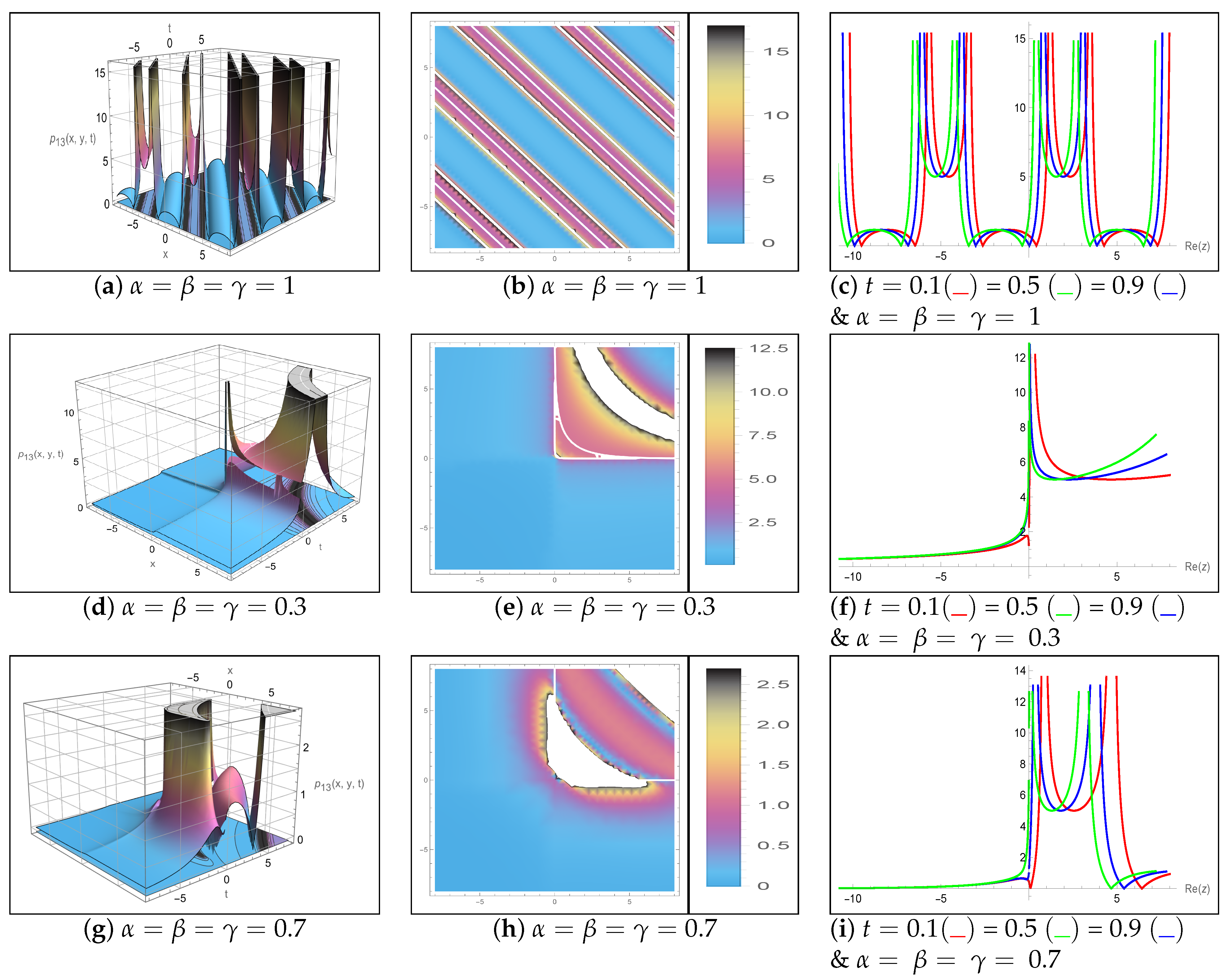
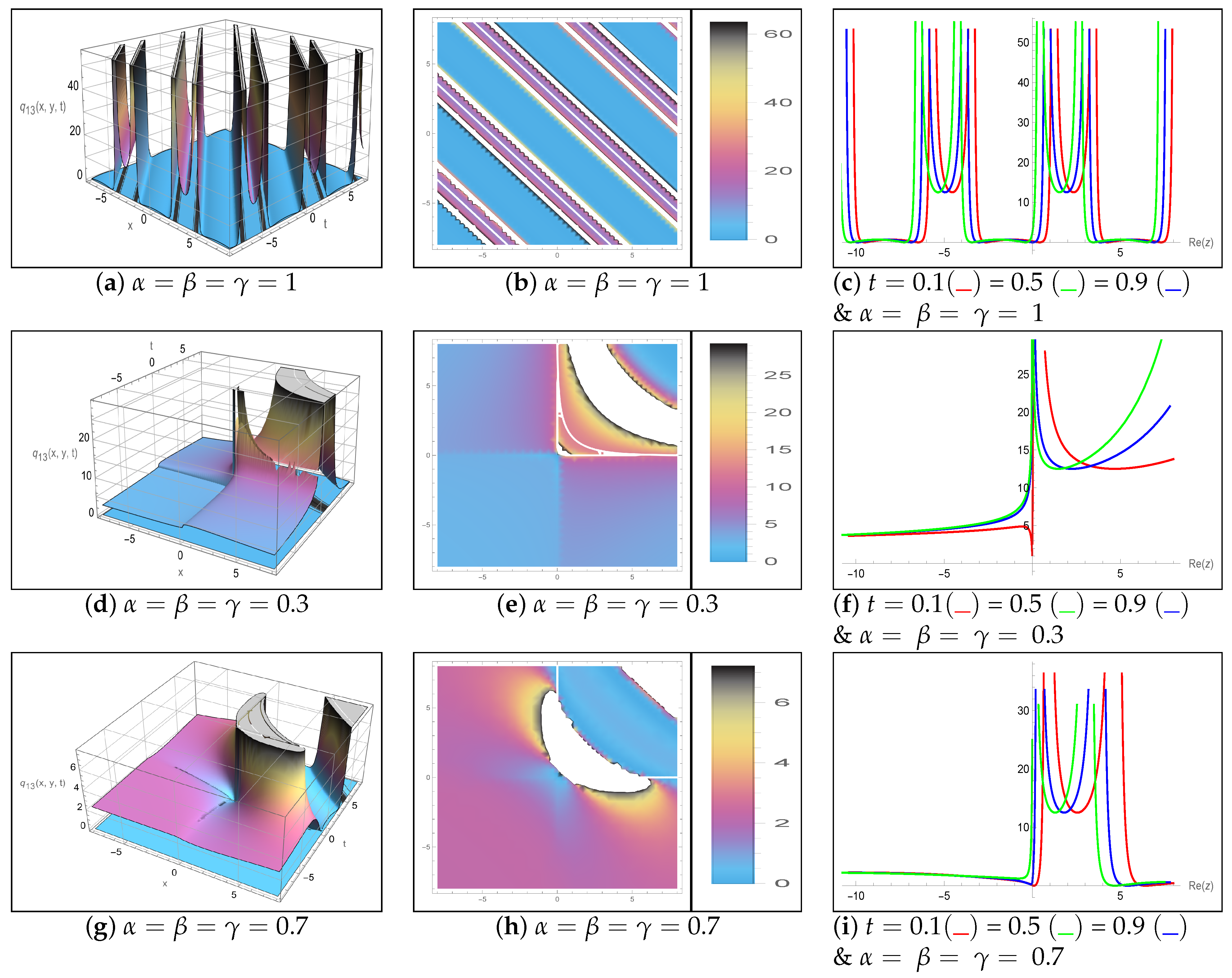
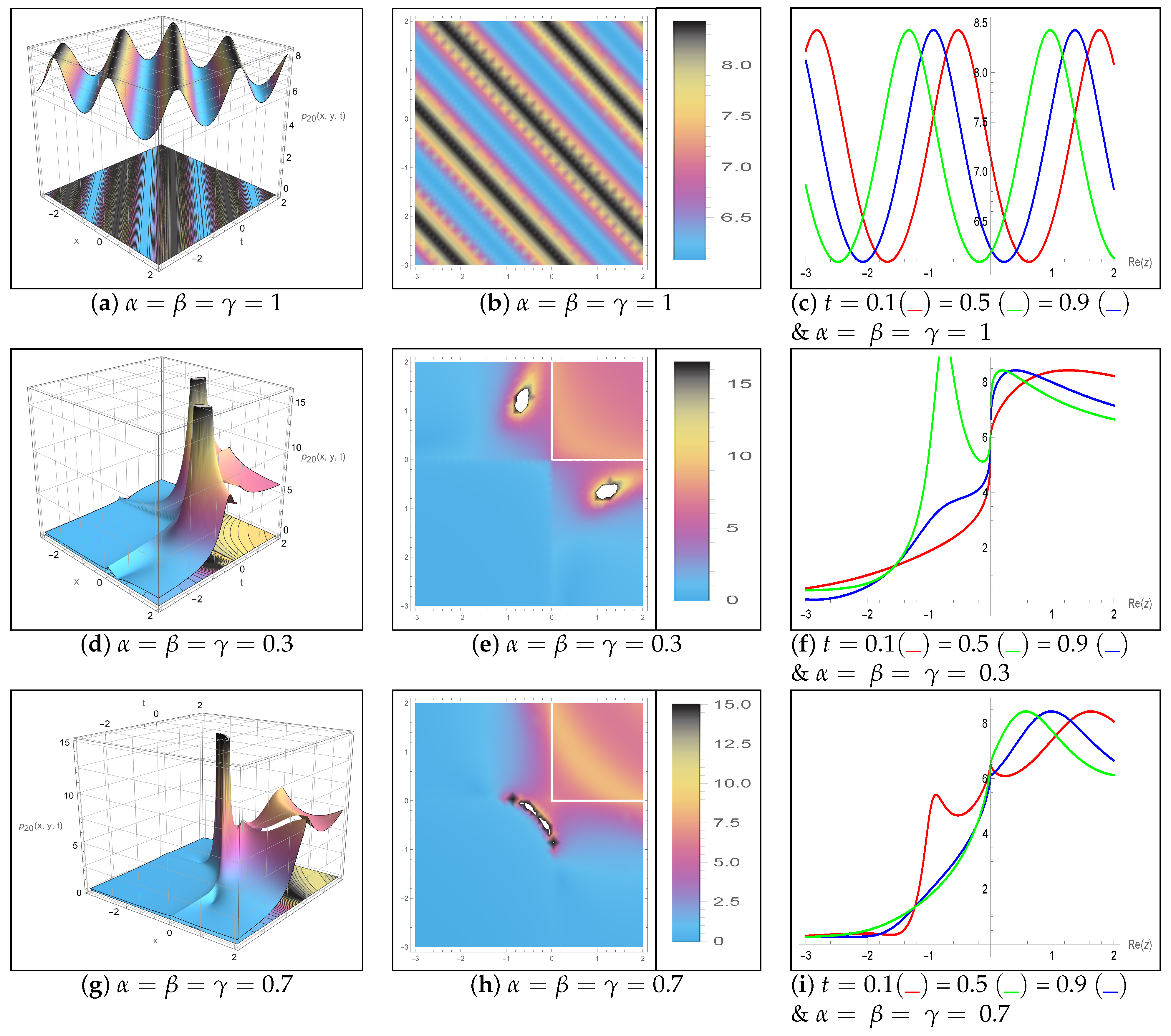
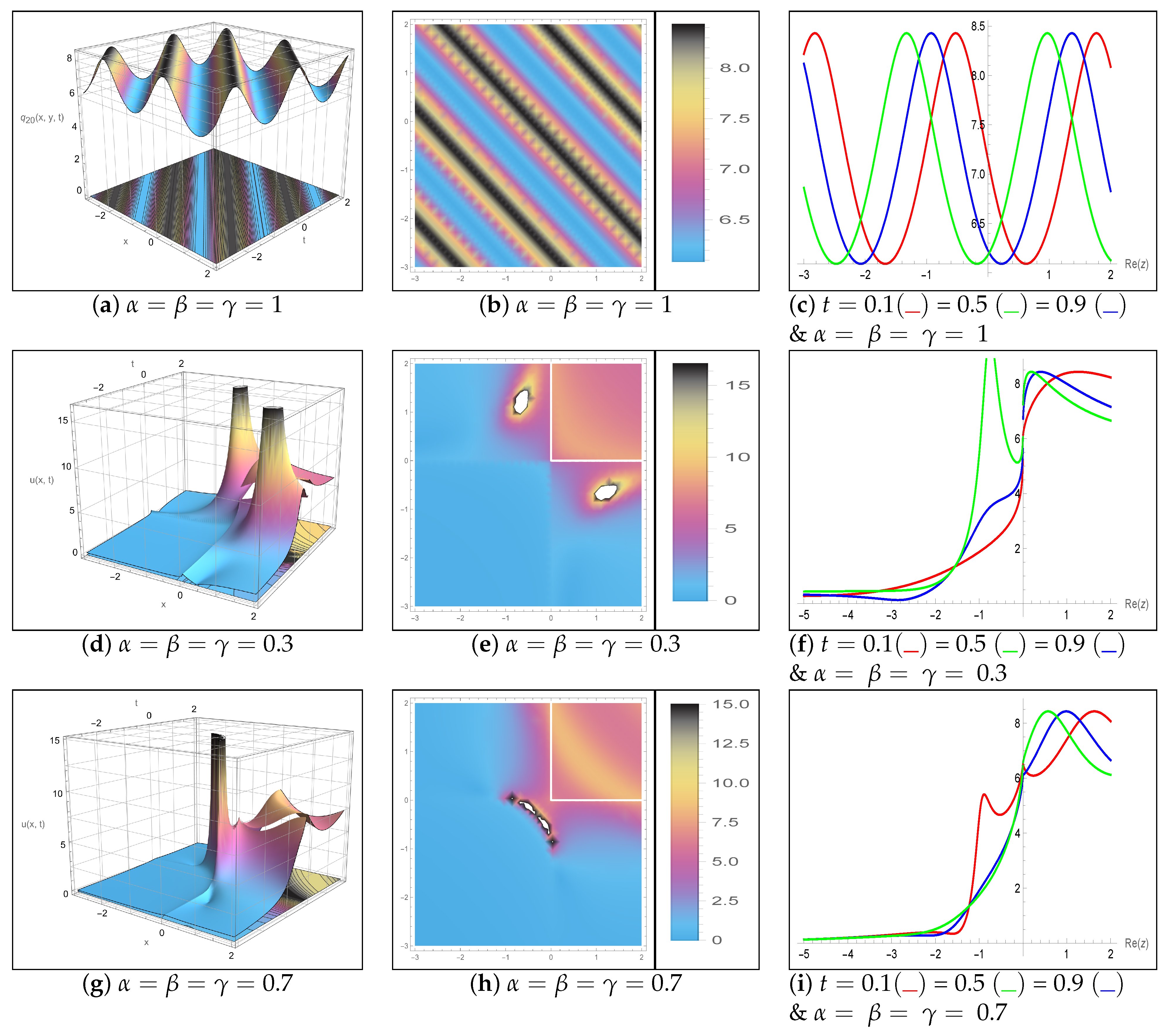
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bullough, R.K.; Caudrey, P.J. The soliton and its history. In Solitons; Springer: Berlin/Heidelberg, Germany, 1980; pp. 1–64. [Google Scholar]
- Chen, Z.; Segev, M.; Christodoulides, D.N. Optical spatial solitons: Historical overview and recent advances. Rep. Prog. Phys. 2012, 75, 086401. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, A. An historical review of application of optical solitons for high speed communications. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 475–485. [Google Scholar] [CrossRef]
- Stegeman, G.I.; Christodoulides, D.N.; Segev, M. Optical spatial solitons: Historical perspectives. IEEE J. Sel. Top. Quantum Electron. 2002, 6, 1419–1427. [Google Scholar] [CrossRef]
- Rehman, H.U.; Tehseen, M.; Ashraf, H.; Awan, A.U.; Ali, M.R. Unveiling dynamic solitons in the (2+1)-dimensional Kadomtsev–Petviashvili equation: Insights from fluids and plasma. Partial. Differ. Equ. Appl. Math. 2004, 9, 100633. [Google Scholar] [CrossRef]
- Bai, C.L.; Zhao, H. Complex-Hyperbolic-Funct. Method Its Appl. Nonlinear Equations. Phys. Lett. A 2006, 355, 32–38. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding optical solitons of generalized nonlinear Schrödinger equations. Optik 2022, 261, 169163. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati–Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 2015, 117. [Google Scholar] [CrossRef]
- Yang, Z.; Hon, B.Y. An improved modified extended tanh-function method. Z. Naturforschung A 2006, 61, 103–115. [Google Scholar] [CrossRef]
- Ozdemir, N. Optical solitons for the Biswas–Milovic equation with anti-cubic law nonlinearity in the presence of spatio-temporal dispersion. Phys. Scr. 2023, 98, 085229. [Google Scholar] [CrossRef]
- Aljahdaly, N.H. Some applications of the modified (G′/G2)-expansion method in mathematical physics. Results Phys. 2019, 13, 102272. [Google Scholar] [CrossRef]
- Manafian, J.; Lakestani, M. Application of tan (Φ/2)-expansion method for solving the Biswas–Milovic equation for Kerr law nonlinearity. Optik 2016, 127, 2040–2054. [Google Scholar] [CrossRef]
- Vitanov, N.K. On modified method of simplest equation for obtaining exact and approximate solutions of nonlinear PDEs: The role of the simplest equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4215–4231. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method–a kind of non-linear analytical technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Akcagil, S.; Aydemir, T. A new application of the unified method. New Trends Math. Sci. 2018, 6, 185–199. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Soukharev, M.B. Popular Ansatz methods and Solitary wave solutions of the Kuramoto-Sivashinsky equation. Regul. Chaotic Dyn. 2009, 14, 407–419. [Google Scholar] [CrossRef]
- Bittanti, S.; Colaneri, P.; De Nicolao, G. The periodic Riccati equation. In The Riccati Equation; Springer: Berlin/Heidelberg, Germany, 1991; pp. 127–162. [Google Scholar]
- Rezazadeh, H.; Korkmaz, A.; Eslami, M.; Mirhosseini-Alizamini, S.M. A large family of optical solutions to Kundu–Eckhaus model by a new auxiliary equation method. Opt. Quantum Electron. 2019, 51, 84. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Ilie, M.; Gómez-Aguilar, J.F. Biswas–Arshed equation with the beta time derivative: Optical solitons and other solutions. Optik 2020, 217, 164801. [Google Scholar] [CrossRef]
- Ullah, N.; Rehman, H.U.; Asjad, M.I.; Riaz, M.B.; Muhammad, T. Wave analysis in generalized fractional Tzitzéica-type nonlinear PDEs: Contributions to nonlinear sciences. Alex. Eng. J. 2024, 92, 102–116. [Google Scholar] [CrossRef]
- Zulfiqar, H.; Aashiq, A.; Tariq, K.U.; Ahmad, H.; Almohsen, B.; Aslam, M.; Rehman, H.U. On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise. Optik 2023, 289, 171250. [Google Scholar] [CrossRef]
- Rehman, H.U.; Ullah, N.; Imran, M.A.; Akgül, A. Optical solitons of two non-linear models in birefringent fibres using extended direct algebraic method. Int. J. Appl. Comput. Math. 2021, 7, 227. [Google Scholar] [CrossRef]
- Cevikel, A.C.; Aksoy, E. Soliton solutions of nonlinear fractional differential equations with their applications in mathematical physics. Rev. Mex. Física 2021, 67, 422–428. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A. Bright and dark soliton solutions for some nonlinear fractional differential equations. Chin. Phys. B 2016, 25, 030203. [Google Scholar] [CrossRef]
- Özkan, E.M.; Özkan, A. The soliton solutions for some nonlinear fractional differential equations with Beta-derivative. Axioms 2021, 10, 203. [Google Scholar] [CrossRef]
- Akram, G.; Arshed, S.; Sadaf, M. Soliton solutions of generalized time-fractional Boussinesq-like equation via three techniques. Chaos Solitons Fractals 2023, 173, 113653. [Google Scholar] [CrossRef]
- Akram, G.; Sadaf, M.; Mariyam, H. A comparative study of the optical solitons for the fractional complex Ginzburg–Landau equation using different fractional differential operators. Optik 2022, 256, 168626. [Google Scholar] [CrossRef]
- Wang, B.H.; Wang, Y.Y.; Dai, C.Q.; Chen, Y.X. Dynamical characteristic of analytical fractional solitons for the space-time fractional Fokas-Lenells equation. Alex. Eng. J. 2020, 59, 4699–4707. [Google Scholar] [CrossRef]
- Malomed, B.A. Optical solitons and vortices in fractional media: A mini-review of recent results. Photonics 2021, 8, 353. [Google Scholar] [CrossRef]
- Ullah, N.; Asjad, M.I.; Awrejcewicz, J.; Muhammad, T.; Baleanu, D. On soliton solutions of fractional-order nonlinear model appears in physical sciences. AIMS Math. 2022, 7, 7421–7440. [Google Scholar] [CrossRef]
- Ahmad, J.; Mustafa, Z. Analysis of soliton solutions with different wave configurations to the fractional coupled nonlinear Schrödinger equations and applications. Opt. Quantum Electron. 2023, 55, 1228. [Google Scholar] [CrossRef]
- Saha Ray, S. New exact solutions of fractional Davey-Stewartson equation with power-law nonlinearity and new integrable Davey-Stewartson-type equation. Eur. Phys. J. Plus 2016, 131, 1–11. [Google Scholar] [CrossRef]
- Alngar, M.E.; Alamri, A.M.; AlQahtani, S.A.; Shohib, R.M.; Pathak, P. Exploring optical soliton solutions in highly dispersive couplers with parabolic law nonlinear refractive index using the extended auxiliary equation method. Mod. Phys. Lett. B 2024, 38, 2450350. [Google Scholar] [CrossRef]
- Rehman, H.U.; Awan, A.U.; Tag-ElDin, E.M.; Alhazmi, S.E.; Yassen, M.F.; Haider, R. Extended hyperbolic function method for the (2+1)-dimensional nonlinear soliton equation. Results Phys. 2022, 40, 105802. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alurrfi, K.A.; Alshbear, R.A. On application of the new mapping method to magneto-optic waveguides having Kudryashov’s law of refractive index. Optik 2023, 287, 171072. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh method and the sine–cosine method for solving the KP-MEW equation. Int. J. Comput. Math. 2005, 82, 235–246. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Modelling 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Davey, A.; Stewartson, K. On three-dimensional packets of surface waves. Proc. R. Soc. London Ser. A 1974, 338, 101–110. [Google Scholar]
- Benney, D.J.; Roskes, G.J. Wave instabilities. Stud. Appl. Math. 1969, 48, 377–385. [Google Scholar] [CrossRef]
- Fokas, A.S. Inverse scattering of first-order systems in the plane related to nonlinear multidimensional equations. Phys. Rev. Lett. 1983, 51, 3. [Google Scholar] [CrossRef]
- Ghidaglia, J.M.; Saut, J.C. On the initial value problem for the Davey--Stewartson systems. Nonlinearity 1990, 3, 475. [Google Scholar] [CrossRef]
- Sugimoto, M.; Wang, B.; Zhang, R. Local well-posedness for the Davey–Stewartson equation in a generalized Feichtinger algebra. J. Fourier Anal. Appl. 2015, 21, 1105–1129. [Google Scholar] [CrossRef]
- Gurefe, Y.; Misirli, E.; Pandir, Y.; Abdullah, S.; Mehmet, E. New exact solutions of the Davey–Stewartson equation with power-law nonlinearity. Bull. Malays. Math. Sci. Soc. 2015, 38, 1223–1234. [Google Scholar] [CrossRef]
- Zhang, B.; Xiong, M.; Chen, L. Many new exact solutions for generalized Davey-Stewartson equation with arbitrary power nonlinearities using novel. J. Adv. Appl. Math. 2019, 4, 11. [Google Scholar] [CrossRef]
- Selima, E.S.; Seadawy, A.R.; Yao, X. The nonlinear dispersive Davey--Stewartson system for surface waves propagation in shallow water and its stability. Eur. Phys. J. Plus 2016, 131, 425. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, K.; Chang, J.; Yue, L.; Chen, H.; Huang, R.; Chao, Y. Experimental investigation of shock-wave–streamwise-vortex interaction. AIAA J. 2025, 63, 3079–3106. [Google Scholar] [CrossRef]
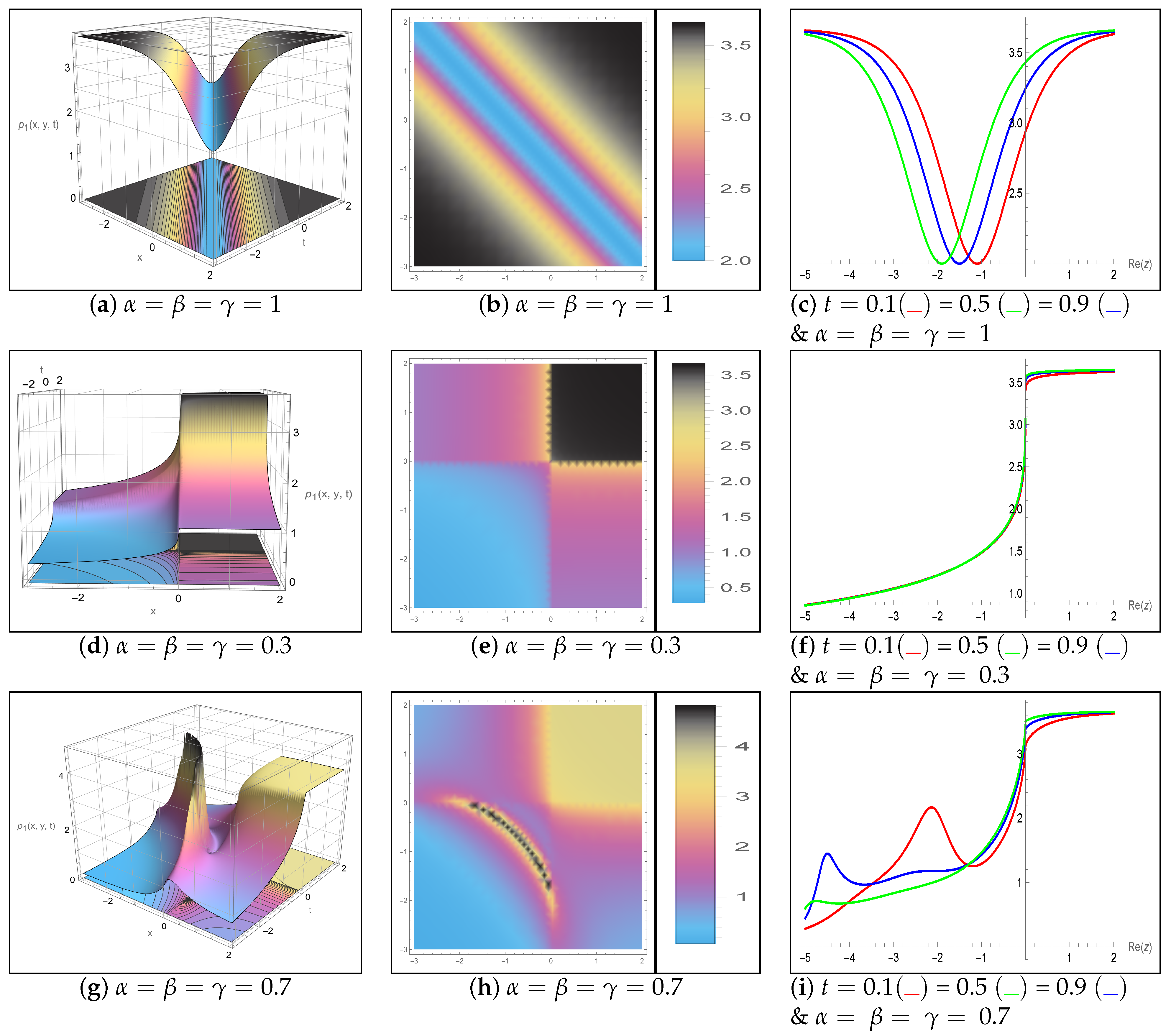
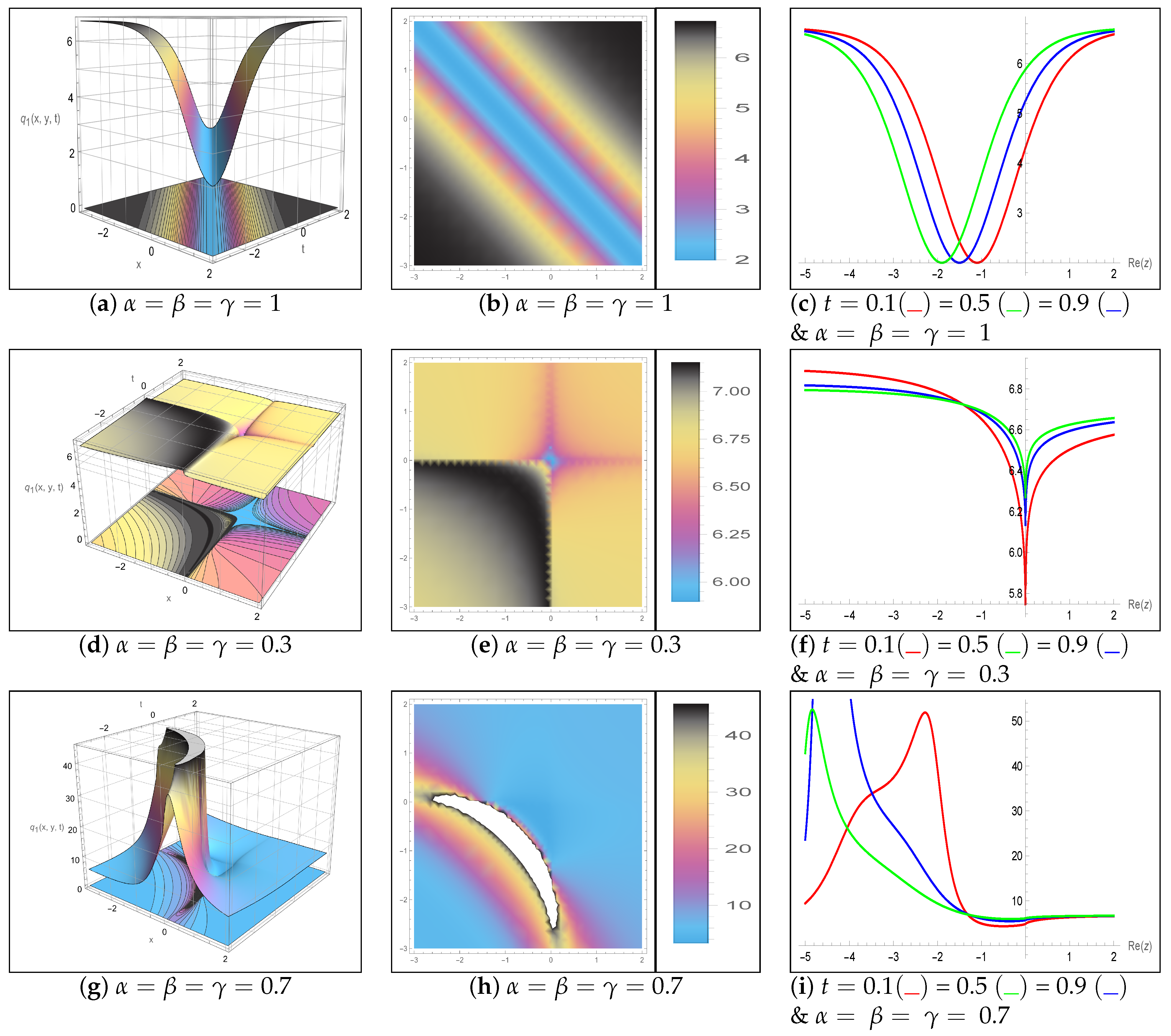
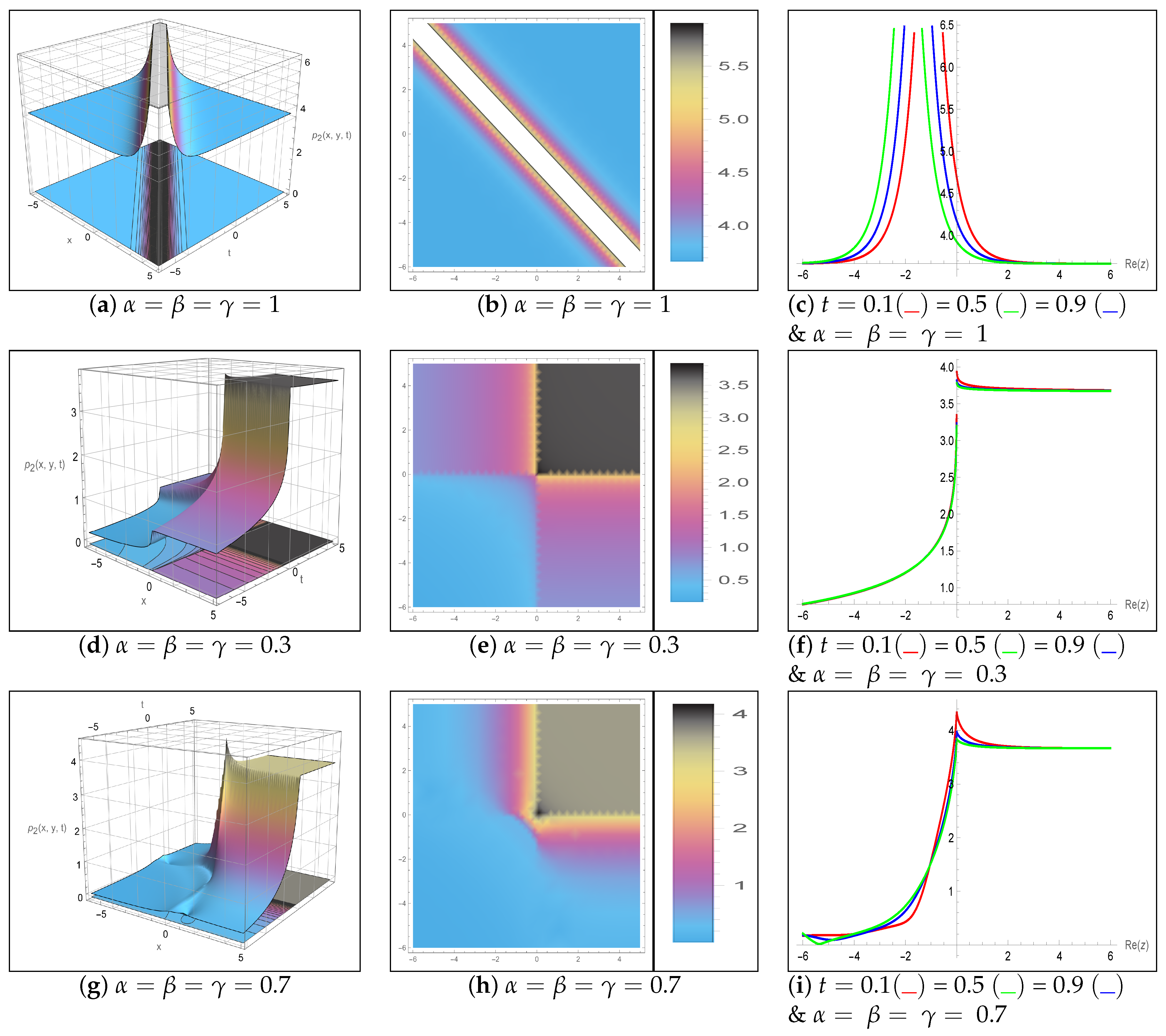
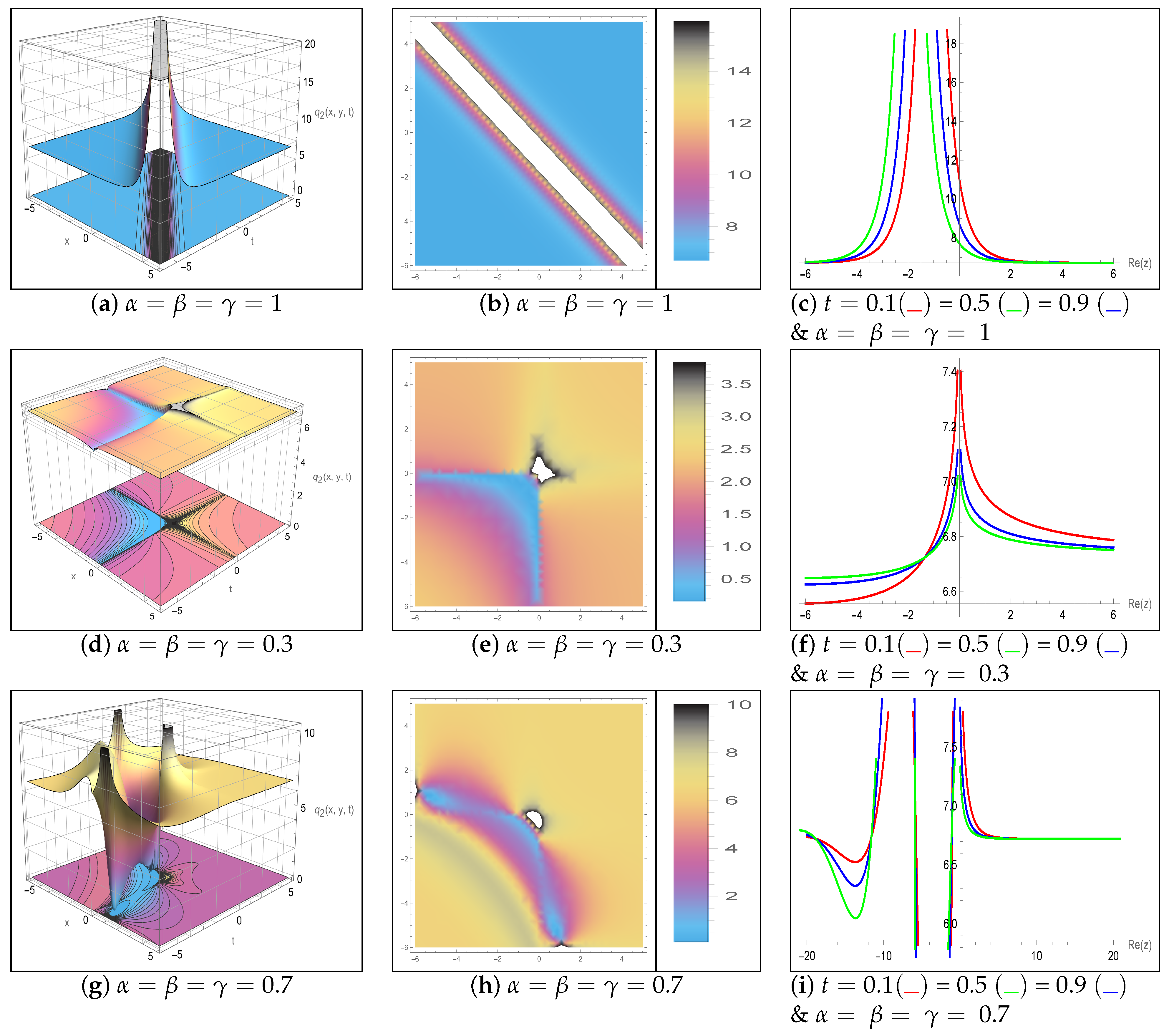

| Aspect | Previous Studies on DS System | Present Work (Novelty and Applications) |
|---|---|---|
| Origin of DS System | Davey and Stewartson [38] derived the DS system in two spatial dimensions using a perturbation expansion to describe the evolution of weakly nonlinear wave packets in finite-depth water. | Builds on this classical DS framework but extends it into the fractional-order domain using conformable derivatives. |
| Relation to Other Models | Shown to be a special case of the Benney–Roskes system [39]. | Establishes the DS system’s fractional generalization, broadening applicability to nonlocal and memory-dependent processes. |
| Integrability | Integrability studied through the inverse scattering transform (IST) in Ref. [40]. | Rather than focusing on integrability, this work applies the new mapping method (NMM) to systematically construct exact soliton solutions. |
| Well-posedness | Investigated in Refs. [41,42] using functional analysis and PDE techniques. | Complements these results by supplying explicit soliton families, illustrating stable/unstable behaviors under fractional effects. |
| Symmetry and Algebraic Studies | Champagne & Winternitz studied the Lie symmetry algebra of the DS system. | Goes beyond algebraic structure to provide constructive analytical soliton solutions in fractional settings. |
| Solution Methods | Applies the fractional complex transform with NMM to generate a richer family of solutions (bright, dark, singular, bright–dark, periodic). This provides a unified approach under fractional-order dynamics. | |
| Applications | Mostly focused on mathematical solution construction and theoretical aspects. | Provides physical interpretation of fractional parameters for controlling soliton amplitude, width, and stability. Potential applications include fluid dynamics, plasma physics, and nonlinear optics (e.g., communication systems, energy transport, photonic device design). |
| No. | Solution Name | Constraint Conditions | Stability |
|---|---|---|---|
| 1 | Stable | ||
| 2 | , | Stable | |
| 3 | , , , , | Stable | |
| 4 | Stable | ||
| 5 | Stable | ||
| 6 | Stable | ||
| 7 | Stable | ||
| 8 | , , | Stable | |
| 9 | , | , | Stable |
| 10 | , , , | , | Stable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tehseen, M.; Jaradat, E.K.; Abo-Dahab, E.M.; Rehman, H.U. Fractional Solitons for Controlling Wave Dynamics in Fluids and Plasmas. Axioms 2025, 14, 772. https://doi.org/10.3390/axioms14100772
Tehseen M, Jaradat EK, Abo-Dahab EM, Rehman HU. Fractional Solitons for Controlling Wave Dynamics in Fluids and Plasmas. Axioms. 2025; 14(10):772. https://doi.org/10.3390/axioms14100772
Chicago/Turabian StyleTehseen, Muhammad, Emad K. Jaradat, Elsayed M. Abo-Dahab, and Hamood Ur Rehman. 2025. "Fractional Solitons for Controlling Wave Dynamics in Fluids and Plasmas" Axioms 14, no. 10: 772. https://doi.org/10.3390/axioms14100772
APA StyleTehseen, M., Jaradat, E. K., Abo-Dahab, E. M., & Rehman, H. U. (2025). Fractional Solitons for Controlling Wave Dynamics in Fluids and Plasmas. Axioms, 14(10), 772. https://doi.org/10.3390/axioms14100772







