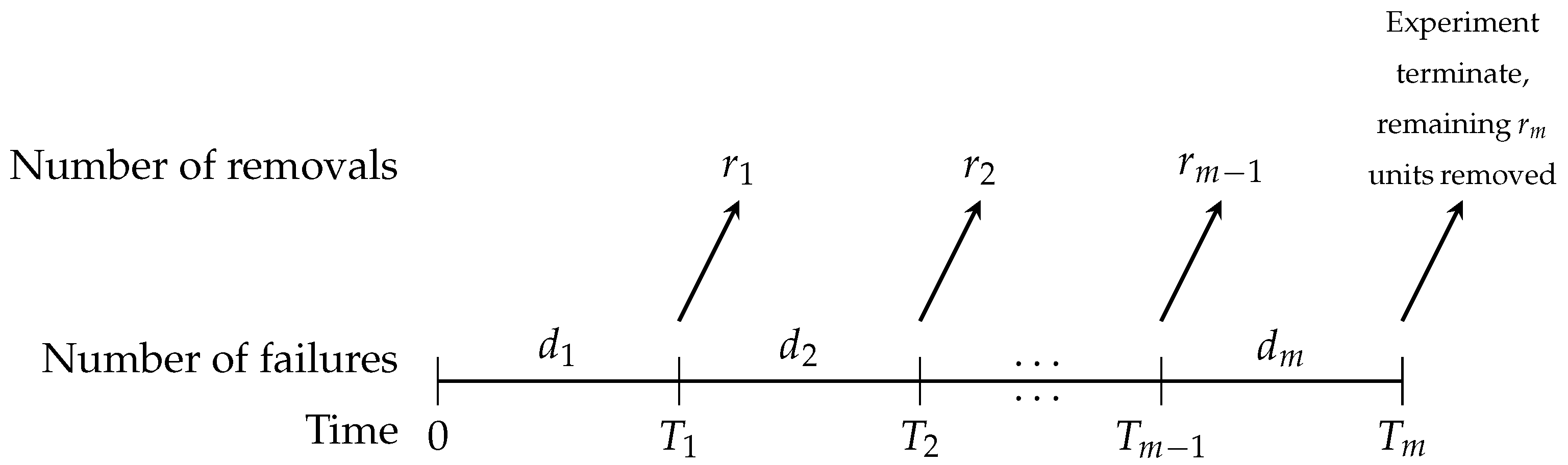Inferences for the GKME Distribution Under Progressive Type-I Interval Censoring with Random Removals and Its Application to Survival Data

Abstract

The analysis of lifetime data under censoring schemes plays a vital role in reliability studies and survival analysis, where complete information is often difficult to obtain. This work focuses on the estimation of the parameters of the recently proposed generalized Kavya–Manoharan exponential (GKME) distribution under progressive Type-I interval censoring, a censoring scheme that frequently arises in medical and industrial life-testing experiments. Estimation procedures are developed under both classical and Bayesian paradigms, providing a comprehensive framework for inference. In the Bayesian setting, parameter estimation is carried out using Markov Chain Monte Carlo (MCMC) techniques under two distinct loss functions: the squared error loss function (SELF) and the general entropy loss function (GELF). For interval estimation, asymptotic confidence intervals as well as highest posterior density (HPD) credible intervals are constructed. The performance of the proposed estimators is systematically evaluated through a Monte Carlo simulation study in terms of mean squared error (MSE) and the average lengths of the interval estimates. The practical usefulness of the developed methodology is further demonstrated through the analysis of a real dataset on survival times of guinea pigs exposed to virulent tubercle bacilli. The findings indicate that the proposed methods provide flexible and efficient tools for analyzing progressively interval-censored lifetime data.

1. Introduction

In reliability and survival analysis, selecting an appropriate statistical model is crucial for accurately describing lifetime data. For the data of increasing and decreasing nature of hazards, we have various lifetime distributions existing in the literature like Weibull, exponentiated exponential, gamma, and others. In a recent contribution, Verma et al. [1] proposed a new two-parameter generalized Kavya–Manoharan exponential (GKME) distribution. This distribution was applied to model the survival times of guinea pigs, life of fatigue fracture of Kevlar 373/epoxy, and time of successive failures of the air conditioning system of jet air-planes. The GKME distribution exhibited a better fit compared to several sound models, including the Weibull, exponentiated exponential, gamma, and the alpha power transformed Weibull distribution. Despite its flexibility and superiority over other models, no further methodological development or inferential work has been carried out for the GKME distribution. Verma et al. [1] explored several statistical properties of the GKME distribution and conducted parameter estimation within the classical framework using the method of maximum likelihood. However, their analysis was limited to complete data scenarios. In practical applications, particularly in reliability and survival studies, the available data are often subject to censoring. Recognizing this limitation, the present study seeks to bridge this gap by developing a comprehensive inferential framework for the GKME distribution under censored data.

The nature and structure of censoring depend on the experimental protocol and data collection procedures. For example, in many practical scenarios, experiments may be terminated before the failure of all test units due to time constraints, budgetary limitations, or other logistical challenges. This has led to the development of various censoring mechanisms. Among the most frequently used are the classical Type-I and Type-II censoring schemes (see, Sirvanci and Yang [2]; Basu et al. [3]; Singh et al. [4]). Another important consideration in life-testing arises when the exact failure times of units are not directly observable. In many experimental settings, continuous monitoring of all units is infeasible due to limited manpower or technical constraints. Instead, the experiment is structured around periodic inspections, during which only the number of failures occurring within each time interval is recorded. This scenario gives rise to interval censoring, wherein failure times are only known to fall within certain intervals. Interval-censored data are frequently encountered in biomedical studies, especially in longitudinal trials and clinical follow-ups (Finkelstein [5]). As noted by Jianguo [6], such data structures are also prevalent in demography, epidemiology, sociology, finance, and engineering disciplines. In their work, Guure et al. [7] investigated Bayesian inference for survival data subject to interval censoring under the log-logistic model. Later, Sharma et al. [8] utilized Lindley’s approximation for Bayesian estimation of interval-censored lifetime data based on the Lindley distribution.

However, these approaches generally do not permit the withdrawal of experimental units before the study reaches completion. In real-world applications, maintaining all units under observation until the end is often impractical or even undesirable. Factors such as cost, time, ethical concerns, or logistical limitations may necessitate the withdrawal of units during the course of the experiment. To address this, Balakrishnan and Aggarwala [9] have developed a progressive censoring scheme that provides a structured yet flexible way to remove subjects partway through the study. Under this approach, the withdrawal of units is planned in advance and carried out systematically, either immediately following certain observed failures or at specified points in time.

Taking this limitation into account, Aggarwala [10] proposed a hybrid censoring scheme, known as progressive Type-I interval (PITI) censoring, which integrates the features of Type-I interval censoring with those of progressive censoring. This approach has been widely applied, particularly in clinical trial settings. Consider longitudinal study involving n bladder cancer patients, where the objective is to track the duration of remission. Rather than observing each patient continuously, medical evaluations are conducted at predetermined time points $T_1,T_2,\dots ,T_m$. At the first check-up (time $T_1$), only $n-r_1$ individuals attend the visit, implying that $r_1$ participants have exited the study within the interval $(0,T_1]$. Of the $n-r_1$ patients examined at this stage, the recurrence of cancer is confirmed in $d_1$ cases. However, the precise time of recurrence for these individuals is not known, but only that the event occurred within the given time interval. Subsequently, at time $T_2$, the remaining cohort $n-r_1-d_1$ is considered, and once again a portion, say $r_2$, departs during the interval $(T_1,T_2]$. The remaining patients, $n-r_1-d_1-r_2$, are evaluated, and $d_2$ cases of recurrence are detected. This process continues through m successive inspection times, and at the final visit ($T_m$), all surviving patients who have not dropped out or shown recurrence are removed from the trial, effectively concluding the experiment. In prior work, Chen and Lio [11] proposed an approach for parameter estimation under the considered censoring scheme using the generalized exponential distribution. Their method assumes that the proportions $p_1,p_2,\dots ,p_m$ of dropouts at each interval are fixed in advance. More precisely, they set $r_i=\lfloor n_i{p}_i\rfloor$, where $n_i$ denotes the number of subjects at risk at the beginning of the i-th interval. While mathematically tractable, this deterministic assumption about dropouts may not reflect the inherent unpredictability of clinical trials. Patients often withdraw from treatment due to unforeseen events such as death from unrelated causes, side effects, personal preferences, or dissatisfaction with medical care, all of which lie outside the experimenter’s control. Recognizing these practical challenges, several researchers have advocated modeling the number of removals as random variables. For example, Tse et al. [12], introduced censoring schemes with binomially distributed removals. Ashour and Afify [13] extended this framework by applying PITI censoring with binomial removal under the assumption that the exact lifetime durations are observable. In the present study, however, we consider a more realistic scenario where exact failure times are unobservable. Instead, only the number of failures occurring within specified intervals is available. We adopt a binomial model for the dropout mechanism, wherein the number of removals at the i-th stage, denoted $r_i$, follows a binomial distribution with parameters that depend on the remaining number of patients and a dropout probability $p_i$. Under this more flexible framework, we aim to develop statistical estimators for the unknown shape and scale parameters of the underlying distribution, assuming a progressively Type-I interval censored structure with binomially distributed random removals and unobserved exact failure times. Several studies have extended its use to different lifetime models. For instance, Kaushik et al. [14,15] discussed Bayesian and classical estimation procedures under PITI censoring using generalized exponential and Weibull distribution. Lodhi and Tripathi [16] investigated inference for the truncated normal distribution in the presence of PITI censoring, while Alotaibi et al. [17] examined Bayesian estimation for the Dagum distribution. More recently, Roy et al. [18] studied the inverse Gaussian distribution under PITI censoring using the method of moments, maximum likelihood estimation, and Bayesian methods, and also proposed optimal censoring designs. Hasan et al. [19] considered four strategies for determining inspection times—predefined, equally spaced, optimally spaced, and equal probability—and derived optimal censoring plans by evaluating expected removals or their proportions. Building on these contributions, the present work aims to develop inferential procedures for the GKME distribution under the PITI censoring scheme.

Let X be a non-negative continuous random variable that follows the generalized Kavya–Manoharan exponential (GKME) distribution. Adopting the same notations as used in Verma et al. [1], the cumulative distribution function (CDF) of the GKME distribution is defined as

$$F\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\lambda }{\lambda -1}}[1-{\lambda }^{-(1-e^{-\beta x})}]\hfill & \mathrm{if}\lambda >0,\lambda \ne 1\hfill \\ 1-e^{-\beta x}\hfill & \mathrm{if}\lambda =1\hfill \end{array}\right.$$

(1)

where $\lambda$ and $\beta$ are shape and rate parameters, respectively. Henceforth, the GKME distribution with parameters $\lambda$ and $\beta$ is denoted by GKME $(\lambda ,\beta )$. The probability density function (PDF) and hazard function of the GKME distribution are, respectively,

$$f\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\lambda log\lambda }{\lambda -1}}\beta e^{-\beta x}{\lambda }^{-(1-e^{-\beta x})}\hfill & \mathrm{if}\lambda >0,\lambda \ne 1\hfill \\ \beta e^{-\beta x}\hfill & \mathrm{if}\lambda =1\hfill \end{array}\right.$$

(2)

and

$$h\left(x\right)=\left\{\begin{array}{cc}ln\lambda {\displaystyle \frac{{\lambda }^{-G\left(x\right)+1}}{{\lambda }^{-G\left(x\right)+1}-1}}g\left(x\right)\hfill & \mathrm{if}\lambda >0,\lambda \ne 1\hfill \\ {\displaystyle \frac{g\left(x\right)}{1-G\left(x\right)}}\hfill & \mathrm{if}\lambda =1.\hfill \end{array}\right.$$

(3)

Figure 1 displays the PDF and hazard function of the GKME distribution for various parameter settings. When $\lambda <1$, the PDF takes a unimodal form, and the peak of the curve becomes progressively flatter as $\beta$ increases. In contrast, for $\lambda >1$, the PDF resembles an exponential distribution. The behavior of the hazard function also depends on $\lambda$: it increases monotonically when $\lambda <1$, whereas it decreases monotonically when $\lambda >1$.

The remainder of this article is organized as follows. Section 2 provides a detailed description of the PITI scheme with binomial removals and presents the observed likelihood function under this censoring scheme. Section 3 focuses on the estimation of model parameters based on PITI-censored data using the ML method. Bayesian estimation using informative priors under SELF and GELF is discussed in Section 4. A Monte Carlo simulation is conducted in Section 5 to evaluate how various estimators perform when data are subject to PITI censoring. In Section 6, to illustrate the applicability of the proposed method, a real-world dataset involving survival times of guinea pigs is examined. Finally, conclusions are given in Section 7.

2. Censoring Scheme and Likelihood Function

To better understand the mechanism of PITI censoring scheme, let us suppose that a total of n units are placed under observation at the initial time $T_0=0$. The experiment proceeds through a series of pre-specified inspection intervals $(T_{i-1},T_i]$, for $i=1,2,\dots ,m$, during which the experimenter records two pieces of information: the number of failures $D_i={(d_1,d_2,\dots ,d_i)}^{\prime }$ and the number of removals (or dropouts) $R_i={(r_1,r_2,\dots ,r_i)}^{\prime }$. These observations are made on the cohort of units still active at the beginning of each interval, in accordance with the progressive Type-I interval censoring scheme described previously. It is important to emphasize that the dropouts occurring during the i-th interval, $(T_{i-1},T_i]$, are assumed to be randomly determined and occur independently across units. The likelihood of a unit dropping out in this interval is governed by a dropout probability $p_i$, where $0<p_i<1$. Consequently, the number of dropouts at the first inspection point, $r_1$, has a binomial distribution with parameters $(n,p_1)$, i.e., $r_1\sim \mathrm{Binomial}(n,p_1)$. For the subsequent intervals ($i=2,3,\dots ,m$), the number of units at risk at the start of the i-th interval is given by $n-{\sum }_{j=1}^{i-1}(d_j+r_j)$. Therefore, the number of removals $r_i$ at the i-th interval is governed by binomial distribution with the form $r_i\sim \mathrm{Binomial}\left(n-{\sum }_{j=1}^{i-1}(d_j+r_j),p_i\right),\mathrm{for}i=2,3,\dots ,m.$ Thus, for given p,

$$\begin{array}{cc}\hfill P(r_1\mid D_1,p_1)& =\left({\displaystyle \genfrac{}{}{0pt}{}{n-d_1}{r_1}}\right)p_1^{r_1}{(1-p_1)}^{n-d_1-r_1}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill P(r_2\mid R_1,D_2,p_2)& =\left({\displaystyle \genfrac{}{}{0pt}{}{n-d_1-d_2-r_1}{r_2}}\right)p_2^{r_2}{(1-p_2)}^{n-d_1-d_2-r_1-r_2}\hfill \end{array}$$

(5)

$$P(r_i\mid R_{i-1},D_i,p_i)=\left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}$$

(6)

for $i=1,2,\dots ,m$ and $r_m=n-{\sum }_{j=1}^m{d}_j-{\sum }_{j=1}^{m-1}{r}_j$. This Figure 2 illustrates the process involved in this type of censored data. Now the likelihood function for the observed data can be written as

$$\begin{array}{cc}\hfill L(\lambda ,\beta |R,D,T)\propto & \prod _{i=1}^m{\left[F\left(T_i\right)-F\left(T_{i-1}\right)\right]}^{d_i}{\left[1-F\left(T_i\right)\right]}^{r_i}\hfill \\ \hfill & P(r_i\mid R_{i-1},D_i,p_i)\hfill \end{array}$$

(7)

3. Maximum Likelihood Estimation

For estimating the parameters $\lambda$ and $\beta$ using ML estimation, the above likelihood function for GKME distribution is written as

$$\begin{array}{cc}\hfill L(\lambda ,\beta |R,D,T)=& \prod _{i=1}^m{\left[{\displaystyle \frac{\lambda }{\lambda -1}}\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]}^{d_i}{\left[{\displaystyle \frac{\lambda }{\lambda -1}}{\lambda }^{-(1-e^{-\beta T_i})}\right]}^{r_i}\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}\hfill \end{array}$$

(8)

The above expression can be decomposed as

$$L(\lambda ,\beta |R,D,T)=L_1(\lambda ,\beta |R,D,T)L_2\left(P\right|R,D,T)$$

(9)

where

$$L_1(\lambda ,\beta |R,D,T)=\prod _{i=1}^m{\left[F\left(T_i\right)-F\left(T_{i-1}\right)\right]}^{d_i}·{\left[1-F\left(T_i\right)\right]}^{r_i}$$

(10)

It can be observed that $L_2(.)$ does not involve the parameters $\lambda$ and $\beta$. Therefore, for the purpose of obtaining the ML estimates of $\lambda$ and $\beta$, it suffices to consider only the component $L_1(.)$. The associated log-likelihood function is then given by:

$$\begin{array}{cc}\hfill log{L}_1=& \sum _{i=1}^m{d}_i\left[log\left({\displaystyle \frac{\lambda }{\lambda -1}}\right)+log\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]\hfill \\ \hfill & +\sum _{i=1}^m{r}_i\left[log\left({\displaystyle \frac{\lambda }{\lambda -1}}\right)-(1-e^{-\beta T_i})log\lambda \right]\hfill \end{array}$$

(11)

Hence, the ML estimators of the parameters $\widehat{\lambda }$ and $\widehat{\beta }$ are determined by jointly solving the following pair of nonlinear equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial log{L}_1}{\partial \lambda }}=& \sum _{i=1}^m{d}_i\left[-{\displaystyle \frac{1}{\lambda (\lambda -1)}}+{\displaystyle \frac{(1-e^{-\beta T_i}){\lambda }^{-(2-e^{-\beta T_i})}-(1-e^{-\beta T_{i-1}}){\lambda }^{-(2-e^{-\beta T_{i-1}})}}{{\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}}}\right]\hfill \\ \hfill & +\sum _{i=1}^m{r}_i\left[-{\displaystyle \frac{1}{\lambda (\lambda -1)}}-{\displaystyle \frac{1}{\lambda }}(1-e^{-\beta T_i})\right]=0.\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial log{L}_1}{\partial \beta }}=& \sum _{i=1}^m{d}_i\left[{\displaystyle \frac{T_i{e}^{-\beta T_i}{\lambda }^{-(1-e^{-\beta T_i})}log\lambda -T_{i-1}{e}^{-\beta T_{i-1}}{\lambda }^{-(1-e^{-\beta T_{i-1}})}log\lambda }{{\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}}}\right]\hfill \\ \hfill & -\sum _{i=1}^m{r}_i\left[T_i{e}^{-\beta T_i}log\lambda \right]=0.\hfill \end{array}$$

(13)

From the above equations, the probability distributions of the estimators $\widehat{\lambda }$ and $\widehat{\beta }$ are analytically intractable. Therefore, it is impractical to derive the exact confidence intervals for these parameters. To address this, we utilize the asymptotic normality property of ML estimators to construct $100(1-\gamma )\%$ ACIs for $\lambda$ and $\beta$. These intervals are derived using the asymptotic variance-covariance matrix associated with their MLEs. The joint asymptotic distribution of ${(\lambda ,\beta )}^{\prime }$ follows a bivariate normal (BN) distribution: ${(\lambda ,\beta )}^{\prime }\sim BN({(\widehat{\lambda },\widehat{\beta })}^{\prime },{\mathcal{I}}^{-1}(\widehat{\lambda },\widehat{\beta }))$ where $\mathcal{I}(\widehat{\lambda },\widehat{\beta })$ represents the observed Fisher information matrix, given by

$$\mathcal{I}(\widehat{\lambda },\widehat{\beta })={\left[\begin{array}{cc}-{\displaystyle \frac{{\partial }^{2}logL}{\partial {\lambda }^2}}& -{\displaystyle \frac{{\partial }^{2}logL}{\partial \lambda \partial \beta }}\\ -{\displaystyle \frac{{\partial }^{2}logL}{\partial \beta \partial \lambda }}& -{\displaystyle \frac{{\partial }^{2}logL}{\partial {\beta }^2}}\end{array}\right]}_{[\lambda =\widehat{\lambda },\beta =\widehat{\beta }]}$$

The components of the Fisher information matrix are given by

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}log{L}_1}{\partial {\lambda }^2}}=& {\displaystyle \frac{n(2\lambda -1)}{{\lambda }^2{(\lambda -1)}^2}}+\sum _{i=1}^m{d}_i\left[{\displaystyle \frac{A_1{A}_{2_{\lambda }}-A_2{A}_{1_{\lambda }}}{A_1^2}}\right]+{\displaystyle \frac{1}{{\lambda }^2}}\sum _{i=1}^m{r}_i(1-e^{-\beta T_i})\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}log{L}_1}{\partial {\beta }^2}}=& \sum _{i=1}^m{d}_i\left[{\displaystyle \frac{A_1{A}_{1_{\beta \beta }}-A_{1_{\beta }}^2}{A_1^2}}\right]+log\lambda \sum _{i=1}^m{r}_i{T}_i^2{e}^{-\beta T_i}.\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}log{L}_1}{\partial \lambda \beta }}=& \sum _{i=1}^m{d}_i\left[{\displaystyle \frac{A_1{A}_{2_{\beta }}-A_2{A}_{1_{\beta }}}{A_1^2}}\right]-{\displaystyle \frac{1}{\lambda }}\sum _{i=1}^m{r}_i{T}_i{e}^{-\beta T_i}.\hfill \end{array}$$

(16)

where

• $A_1=({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})})$
• $A_2=(1-e^{-\beta T_i}){\lambda }^{-(2-e^{-\beta T_i})}-(1-e^{-\beta T_{i-1}}){\lambda }^{-(2-e^{-\beta T_{i-1}})}$
• $A_{1_{\lambda }}=(1-e^{-\beta T_i}){\lambda }^{-(2-e^{-\beta T_i})}-(1-e^{-\beta T_{i-1}}){\lambda }^{-(2-e^{-\beta T_{i-1}})}$
• $A_{1_{\beta }}=T_i{e}^{-\beta T_i}{\lambda }^{-(1-e^{-\beta T_i})}log\lambda -T_{i-1}{e}^{-\beta T_{i-1}}{\lambda }^{-(1-e^{-\beta T_{i-1}})}log\lambda$
• $A_{1_{\beta \beta }}=T_{i-1}^2{\lambda }^{-(1-e^{-\beta T_{i-1}})}{e}^{-\beta T_{i-1}}log\lambda (1+e^{-\beta T_{i-1}}log\lambda )-T_i^2{\lambda }^{-(1-e^{-\beta T_i})}{e}^{-\beta T_i}log\lambda (1+e^{-\beta T_i}log\lambda )$
• $A_{2_{\lambda }}=(1-e^{-\beta T_{i-1}})(2-e^{-\beta T_{i-1}}){\lambda }^{-(3-e^{-\beta T_{i-1}})}-(1-e^{-\beta T_i})(2-e^{-\beta T_i}){\lambda }^{-(3-e^{-\beta T_i})}$
• $A_{2_{\beta }}=T_i{\lambda }^{-(2-e^{-\beta T_i})}{e}^{-\beta T_i}\left(1-(1-e^{-\beta T_i})log\lambda \right)-T_{i-1}{\lambda }^{-(2-e^{-\beta T_{i-1}})}{e}^{-\beta T_{i-1}}\left(1-(1-e^{-\beta T_{i-1}})log\lambda \right).$

Based on the observed Fisher information matrix, the two-sided symmetric $100(1-\gamma )\%$ ACIs for $\lambda$ and $\beta$ are obtained as

$$\left(\widehat{\lambda }\mp z_{\gamma /2}\sqrt{\mathrm{var}\left(\widehat{\lambda }\right)}\right)\mathrm{and}\left(\widehat{\beta }\mp z_{\gamma /2}\sqrt{\mathrm{var}\left(\widehat{\beta }\right)}\right)$$

where $z_{\gamma /2}$ denotes the upper $\gamma /2$ percentile of the standard normal distribution, and $\mathrm{var}\left(\widehat{\lambda }\right)$ and $\mathrm{var}\left(\widehat{\beta }\right)$ correspond to the estimated variances of $\widehat{\lambda }$ and $\widehat{\beta }$, extracted from the principal diagonal of the asymptotic variance–covariance matrix, which is the inverse of the observed Fisher information matrix, $\mathcal{I}(\widehat{\lambda },\widehat{\beta })$.

4. Bayesian Estimation

In this section, we present the Bayes estimation of the unknown parameters $\alpha$ and $\beta$ using the MITI sample. Unlike classical estimation methods that rely only on the likelihood function, the Bayesian paradigm combines prior information about the parameters with the observed data through Bayes’ theorem. This results in the posterior distribution, which serves as the basis for inference. The Bayes estimator of a parameter is then obtained as a functional (such as the mean, median, or mode) of its posterior distribution, depending on the choice of loss function.

The loss function plays a crucial role, as it quantifies the penalty for the difference between the estimated and true values of the parameter. Different loss functions lead to different forms of Bayes estimators. In this study, we consider three widely used loss functions: SELF, LLF, and GELF. The SELF is symmetric and treats overestimation and underestimation equally. On the other hand, the LLF and GELF are asymmetric, making them more realistic for situations where the consequences of overestimation and underestimation are not the same.

SELF: In keeping with its name, SELF assigns a value equal to the square of the estimation error. Now, if the estimator estimates the true state $\nu$ by $\widehat{\nu }$ then the estimation error is to be $(\nu -\widehat{\nu })$, and accordingly, the incurred loss is

$$L(\nu ,\widehat{\nu })={(\nu -\widehat{\nu })}^2$$

(17)

From (17), it is clear that the higher the divergence from the true state, the heavier the penalization. It is needless to mention that the Bayes estimator under the SELF is the posterior mean, i.e., ${\widehat{\nu }}_{SELF}=E\left(\nu \right)$. GELF: The GELF proposed by Calabria and Pulcini [20] can be written as

$$L(\nu ,\widehat{\nu })\propto {\left({\displaystyle \frac{\widehat{\nu }}{\nu }}\right)}^w-wlog\left({\displaystyle \frac{\widehat{\nu }}{\nu }}\right)-1$$

(18)

The Bayes estimator corresponding to GELF is ${\left[E\left({\nu }^{-w}\right)\right]}^{-1/w}$. The sign of loss parameter w signifies the direction of asymmetry, while its size characterizes the intensity of asymmetry.

Prior Distribution and Posterior Analysis

In Bayesian analysis, prior distributions play a central role by incorporating existing knowledge or assumptions about the parameters before observing the data. The choice of an appropriate prior is crucial, as it can influence both the posterior distribution and the resulting inferences. However, there is no universally accepted methodology for selecting “optimal” priors, particularly when dealing with newly developed distributions. For the GKME distribution, determining a joint conjugate prior is analytically challenging due to the presence of two unknown parameters, which complicates the derivation of closed-form posterior distributions. To address this, it is common in Bayesian practice to adopt flexible and computationally convenient families of priors. In this study, we consider independent gamma priors for both parameters. The gamma distribution is a natural choice because it is defined on the positive real line, aligns well with the support of the parameters, and allows straightforward computation within the MCMC framework. This choice strikes a balance between flexibility and tractability, enabling us to obtain reliable posterior estimates while keeping the computational burden manageable. The gamma densities for $\lambda$ and $\beta$ with hyperparameters $(b_1,c_1)$ and $(b_2,c_2)$ are

$${\pi }_1\left(\lambda \right)\propto {\lambda }^{b_1-1}{e}^{-c_1\lambda };\lambda >0,b_1>0,c_1>0$$

(19)

and

$${\pi }_2\left(\beta \right)\propto {\beta }^{b_2-1}{e}^{-c_2\beta };\beta >0,b_2>0,c_2>0$$

(20)

Sometimes, we do not have enough prior information about the phenomenon; in such cases, we use non-informative priors. Here, we have used uniform prior as a non-informative prior. The joint prior density of parameters ($\lambda$,$\beta$) is given by

$$\pi (\lambda ,\beta )\propto {\lambda }^{b_1-1}{\beta }^{b_2-1}{e}^{-(c_1\lambda +c_2\beta )}$$

(21)

The joint posterior density of ($\lambda$, $\beta$) based on the likelihood function will be

$$\begin{array}{cc}\hfill {\pi }^{*}(\lambda ,\beta \mid x)=& K^{-1}{\lambda }^{b_1-1}{\beta }^{b_2-1}{e}^{-(c_1\lambda +c_2\beta )}\prod _{i=1}^m{\left[{\displaystyle \frac{\lambda }{\lambda -1}}\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]}^{d_i}{\left[{\displaystyle \frac{\lambda }{\lambda -1}}{\lambda }^{-(1-e^{-\beta T_i})}\right]}^{r_i}\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}\hfill \end{array}$$

(22)

where

$$\begin{array}{cc}\hfill K=& {\int }_0^{\infty }{\int }_0^{\infty }{\lambda }^{b_1-1}{\beta }^{b_2-1}{e}^{-(c_1\lambda +c_2\beta )}\prod _{i=1}^m{\left[{\displaystyle \frac{\lambda }{\lambda -1}}\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]}^{d_i}{\left[{\displaystyle \frac{\lambda }{\lambda -1}}{\lambda }^{-(1-e^{-\beta T_{i-1}})}\right]}^{r_i}\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}d\lambda d\beta \hfill \end{array}$$

The Bayes estimate of any function $\varphi (\lambda ,\beta )$ under SELF and GELF can be written as

$$\begin{array}{cc}\hfill {\widehat{\varphi }}_{SL}=& K^{-1}{\int }_0^{\infty }{\int }_0^{\infty }\varphi (\lambda ,\beta ){\lambda }^{b_1-1}{\beta }^{b_2-1}{e}^{-(c_1\lambda +c_2\beta )}\prod _{i=1}^m{\left[{\displaystyle \frac{\lambda }{\lambda -1}}\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]}^{d_i}\hfill \\ \hfill & {\left[{\displaystyle \frac{\lambda }{\lambda -1}}{\lambda }^{-(1-e^{-\beta T_i})}\right]}^{r_i}\left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}d\lambda d\beta \hfill \end{array}$$

(23)

and

$$\begin{array}{cc}\hfill {\widehat{\varphi }}_{GL}=& (K^{-1}{\int }_0^{\infty }{\int }_0^{\infty }\varphi {(\lambda ,\beta )}^{-w_2}{\lambda }^{b_1-1}{\beta }^{b_2-1}{e}^{-(c_1\lambda +c_2\beta )}\prod _{i=1}^m{\left[{\displaystyle \frac{\lambda }{\lambda -1}}\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]}^{d_i}\hfill \\ \hfill & {\left[{\displaystyle \frac{\lambda }{\lambda -1}}{\lambda }^{-(1-e^{-\beta T_i})}\right]}^{r_i}\left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}d\lambda d\beta {)}^{-1/w_2}\hfill \end{array}$$

(24)

The Bayes estimates of parameters $\lambda$ and $\beta$ are obtained by substituting $\lambda$ and $\beta$ in place of general function $\varphi (\lambda ,\beta )$. The double integral involved in (23) and (24) are analytically intractable. Thus, we compute the Bayes estimates $\lambda$ and $\beta$ via the MCMC approach. MCMC methods serve as essential tools for Bayesian computation. Notably, the Metropolis–Hastings (M-H) algorithm and Gibbs sampling (Hastings, [21]; Smith and Roberts [22]) are among the most commonly employed techniques for generating MCMC samples. For the implementation of the Gibbs sampling algorithm, it is necessary to derive the full conditional posterior densities of $\lambda$ and $\beta$, which are given by:

$$\begin{array}{cc}\hfill {\pi }^{*}(\lambda \mid \beta ,\underset{\sim }{x})=& {\lambda }^{b_1-1}{e}^{-c_1\lambda }\prod _{i=1}^m{\left[{\displaystyle \frac{\lambda }{\lambda -1}}\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]}^{d_i}{\left[{\displaystyle \frac{\lambda }{\lambda -1}}{\lambda }^{-(1-e^{-\beta T_i})}\right]}^{r_i}\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\pi }^{*}(\beta \mid \lambda ,\underset{\sim }{x})=& {\beta }^{b_2-1}{e}^{-c_2\beta }\prod _{i=1}^m{\left[{\displaystyle \frac{\lambda }{\lambda -1}}\left({\lambda }^{-(1-e^{-\beta T_{i-1}})}-{\lambda }^{-(1-e^{-\beta T_i})}\right)\right]}^{d_i}{\left[{\displaystyle \frac{\lambda }{\lambda -1}}{\lambda }^{-(1-e^{-\beta T_i})}\right]}^{r_i}\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^{i-1}{r}_j}{r_i}}\right)p_i^{r_i}{(1-p_i)}^{n-{\sum }_{j=1}^i{d}_j+{\sum }_{j=1}^i{r}_j}\hfill \end{array}$$

(26)

The detailed algorithm to generate posterior samples and to calculate Bayes estimates is given below in Algorithm 1:

Algorithm 1 MCMC algorithm for Bayesian estimation of $\lambda$ and $\beta$.

1: Initialize ${\lambda }^0=\widehat{\lambda }$ and ${\beta }^0=\widehat{\beta }$ 2: for $t=1$ to M do 3:       Generate ${\lambda }^t$ from ${\pi }_1(\lambda \mid {\beta }^{t-1},x)$ using M-H:     Generate candidate ${\lambda }^{*}\sim N({\lambda }^{t-1},1)$ and $U_1\sim U(0,1)$.     Compute acceptance probability $${\rho }_1({\lambda }^{t-1},{\lambda }^{*})=min\left\{1,{\displaystyle \frac{{\pi }^{*}({\lambda }^{*}\mid {\beta }^{t-1},x)}{{\pi }^{*}({\lambda }^{t-1}\mid {\beta }^{t-1},x)}}\right\}.$$     If ${\rho }_1\ge U_1$, set ${\lambda }^t={\lambda }^{*}$; else ${\lambda }^t={\lambda }^{t-1}$. 4:       Generate ${\beta }^t$ from ${\pi }_2(\beta \mid {\lambda }^t,x)$ using M-H:     Generate candidate ${\beta }^{*}\sim N({\beta }^{t-1},1)$ and $U_2\sim U(0,1)$.     Compute acceptance probability $${\rho }_2({\beta }^{t-1},{\beta }^{*})=min\left\{1,{\displaystyle \frac{{\pi }^{*}({\beta }^{*}\mid {\lambda }^t,x)}{{\pi }^{*}({\beta }^{t-1}\mid {\lambda }^t,x)}}\right\}.$$     If ${\rho }_2\ge U_2$, set ${\beta }^t={\beta }^{*}$; else ${\beta }^t={\beta }^{t-1}$. 5: end for 6: Discard the first $M_0$ samples (burn-in). 7: Bayes Estimates: $${\widehat{\lambda }}_{SL}={\displaystyle \frac{1}{M-M_0}}\sum _{t=M_0+1}^M{\lambda }^t,{\widehat{\beta }}_{SL}={\displaystyle \frac{1}{M-M_0}}\sum _{t=M_0+1}^M{\beta }^t$$ $${\widehat{\lambda }}_{GL}={\left[{\displaystyle \frac{1}{M-M_0}}\sum _{t=M_0+1}^M{\left({\lambda }^t\right)}^{-w_2}\right]}^{-1/w_2},{\widehat{\beta }}_{GL}={\left[{\displaystyle \frac{1}{M-M_0}}\sum _{t=M_0+1}^M{\left({\beta }^t\right)}^{-w_2}\right]}^{-1/w_2}$$ 8: Credible Intervals: 9: Order the post burn-in samples as $({\lambda }^{\left(1\right)},\dots ,{\lambda }^{(M-M_0)})$ and $({\beta }^{\left(1\right)},\dots ,{\beta }^{(M-M_0)})$. Then the $100(1-\gamma )\%$ symmetric credible intervals are $$\left({\lambda }^{[(M-M_0)\gamma /2]},{\lambda }^{\left[(M-M_0)(1-\gamma /2)\right]}\right),\left({\beta }^{[(M-M_0)\gamma /2]},{\beta }^{\left[(M-M_0)(1-\gamma /2)\right]}\right)$$ The intervals with the shortest length are taken as the HPD intervals.

5. Simulation Study

This section presents a comprehensive Monte Carlo simulation designed to evaluate the performance of the proposed estimators under the PITI censoring framework. The assessment involves both point and interval estimation criteria, measured using the MSE of the estimators and average width (AW) and coverage probability (CP) of the confidence and credible intervals. For generating PITI censored samples from a given distribution, we adopted Algorithm 2 as suggested by Balakrishnan and Cramer [23]. Data samples of size $n=20,30,40$, and 50 were generated from the GKME distribution with two different parameter combinations. To explore the effect of censoring time $T_m$, five variations of $T_m=3,4,5,6$ and 7 are considered and for censoring intervals, m, three different values of m are considered, i.e., $m=5,8$, and, 10. For observing the behavior of removal scheme, we have considered four random removal schemes, the first scheme considers no withdrawal of units or say, the risk of dropping at all the intermediate stages to be zero i.e., probability or removing the units p is zero at all the stages before final termination. The second scheme assumes an equal and non-zero probability of removal at each intermediate stage before termination, particularly, we have taken $p=0.2$. The third scheme assigns a higher probability p of removal at the beginning, which then decreases as the process advances. This situation can be seen in the fitness programs where many participants register initially but drop out early if they lose interest; those who persist beyond early stages are more likely to complete the program. Conversely, in the fourth scheme, probability of removal p is small in the initial stages and gradually increases in the later stages. This removal scheme can be seen in clinical trials where patients rarely drop out early because they are motivated or monitored closely at the beginning. As the trial progresses, fatigue, side effects, hospital services, or long follow-up may cause higher dropout rates in later stages. In particular, removal schemes are taken as $R1=(0^{m-1},1)$; $R2=(0.2^{m-1},1)$, $R3=(0.2^{\left[m/2\right]},0.2^{\left[\right(m-1)/2]},1)$, and $R4=(0.1^{\left[m/2\right]},0.2^{\left[\right(m-1)/2]},1)$, where $0^4=(0,0,0,0)$ and [.] denotes the greatest integer number. Under each configuration, ML estimates and Bayes estimates are computed alongside their MSEs. Confidence intervals for $95\%$ level of significance were derived using ACI methods, are their corresponding AW and CP are also reported. Bayes estimates of the parameters $\lambda$ and $\beta$ are calculated for informative prior, under SELF and GELF. The weight parameters used in GELF were $w=-1.5$ and $1.5$. For IP, we propose the use of independent gamma priors for $\lambda$ and $\beta$. The hyper-parameters of prior distribution are selected using the method of moments as outlined in Singh et al. [4] and Yadav et al. [24]. For NIP, we have used uniform prior. The MSEs of Bayes estimators is calculated along with AW and CP of $95\%$ highest posterior density credible intervals (HDIs) under both prior settings are also calculated. All analyses are conducted using R software (https://www.r-project.org/) along with relevant additional packages and computational tools required for estimation, simulation, and plotting.

Results from the simulation are summarized in

Table 1. Average estimates and MSEs (in parentheses) for various combinations of $(\lambda ,\beta )$ for fixed $m=5,T_m=5$ and $n=30$.

$\mathit{\lambda }$	$\mathit{\beta }$	${\widehat{\mathit{\lambda }}}_{\mathit{ML}}$	${\widehat{\mathit{\lambda }}}_{\mathit{SELF}}$	${\widehat{\mathit{\lambda }}}_{\mathit{GELF}}$		${\widehat{\mathit{\beta }}}_{\mathit{ML}}$	${\widehat{\mathit{\beta }}}_{\mathit{SELF}}$	${\widehat{\mathit{\beta }}}_{\mathit{GELF}}$
				$\mathit{w}=-\mathbf{1.5}$	$\mathit{w}=+\mathbf{1.5}$			$\mathit{w}=-\mathbf{1.5}$	$\mathit{w}=+\mathbf{1.5}$
0.50	0.50	0.716	0.7077	0.6988	0.7089	0.6713	0.6378	0.6506	0.6666
		(0.9483)	(0.7437)	(0.7405)	(0.7359)	(0.1831)	(0.1704)	(0.1678)	(0.1641)
	0.75	0.7006	0.6562	0.6967	0.6252	0.8839	0.8092	1.8979	1.7666
		(0.9336)	(0.7247)	(0.7309)	(0.7275)	(0.1997)	(0.1864)	(0.1792)	(0.1792)
	1.00	0.6017	0.5807	0.571	0.5344	1.2998	1.2808	1.2711	1.2844
		(0.9265)	(0.7184)	(0.729)	(0.717)	(0.2226)	(0.2034)	(0.2087)	(0.209)
	1.50	0.6044	0.52	0.5475	0.5531	1.5548	1.5545	1.5453	1.5593
		(0.922)	(0.7109)	(0.7206)	(0.7124)	(0.2484)	(0.2321)	(0.2334)	(0.2319)
	2.5	0.603	0.5169	0.5144	0.5478	2.8344	2.8189	2.8096	2.8272
		(0.9166)	(0.7152)	(0.7121)	(0.7121)	(0.2824)	(0.2698)	(0.2695)	(0.2695)
0.75	0.50	0.9741	0.9673	0.9658	0.9751	0.7582	0.7387	0.733	0.7456
		(0.9714)	(0.8639)	(0.8647)	(0.8644)	(0.2205)	(0.1761)	(0.173)	(0.1733)
	0.75	0.961	0.9627	0.9565	0.9664	1.0284	1.012	1.0105	1.0161
		(0.9499)	(0.8419)	(0.8497)	(0.8455)	(0.2414)	(0.1943)	(0.1948)	(0.1935)
	1.00	0.9514	0.957	0.9473	0.9561	1.2918	1.2741	1.2707	1.2794
		(0.9355)	(0.8281)	(0.8351)	(0.8303)	(0.2653)	(0.2166)	(0.2219)	(0.2198)
	1.50	0.9525	0.9565	0.946	0.9615	1.8594	1.7553	1.848	1.5618
		(0.9299)	(0.8191)	(0.8214)	(0.816)	(0.2935)	(0.246)	(0.2502)	(0.2469)
	2.50	0.951	0.9546	0.9449	0.9609	2.8285	2.8201	2.8093	2.82
		(0.9245)	(0.813)	(0.8218)	(0.821)	(0.326)	(0.2754)	(0.2839)	(0.2822)
1.50	0.50	1.6186	1.693	1.608	1.7154	0.7623	0.7555	0.7453	0.7545
		(1.3109)	(1.0013)	(1.003)	(1.0013)	(0.2503)	(0.1916)	(0.1958)	(0.1983)
	0.75	1.4877	1.6992	1.6802	1.7295	1.0305	1.0284	1.0169	1.0345
		(1.275)	(0.971)	(0.9683)	(0.975)	(0.2758)	(0.2178)	(0.2159)	(0.2187)
	1.00	1.4706	1.6631	1.6531	1.7462	1.3148	1.3047	1.3011	1.3043
		(1.2522)	(0.9516)	(0.9529)	(0.9454)	(0.3077)	(0.2497)	(0.2567)	(0.2549)
	1.50	1.4756	1.6651	1.6555	1.7367	1.6566	1.7559	1.7726	1.6591
		(1.2436)	(0.9377)	(0.9384)	(0.9411)	(0.2896)	(0.2804)	(0.2815)	(0.2789)
	2.50	1.4706	1.6621	1.6613	1.7377	2.8202	2.812	2.8091	2.8178
		(1.2334)	(0.9286)	(0.9325)	(0.9335)	(0.2753)	(0.3191)	(0.3192)	(0.3199)
2	0.50	2.2411	2.1313	2.2301	2.1402	0.5631	0.5595	0.5559	0.5599
		(2.1918)	(1.3874)	(1.3884)	(1.3881)	(0.282)	(0.2038)	(0.2527)	(0.2427)
	0.75	2.2222	2.1154	2.2085	2.113	0.8395	0.8361	0.8319	0.8324
		(2.1254)	(1.3213)	(1.3155)	(1.3208)	(0.3179)	(0.2622)	(0.2675)	(0.2673)
	1.00	2.2124	2.1051	2.0002	2.1074	1.1005	1.0952	1.0897	1.0958
		(2.0934)	(1.2842)	(1.295)	(1.2908)	(0.3538)	(0.2968)	(0.2937)	(0.2954)
	1.50	2.2096	2.2063	1.9941	2.1155	1.4642	1.4828	1.5278	1.4707
		(2.0656)	(1.2608)	(1.2649)	(1.2614)	(0.396)	(0.3421)	(0.3433)	(0.3402)
	2.50	2.0201	2.0187	2.009	2.0233	2.6357	2.6304	2.6286	2.6329
		(2.0509)	(1.2422)	(1.2504)	(1.2391)	(0.4462)	(0.3879)	(0.391)	(0.3862)
2.50	0.50	2.6935	2.6863	2.4813	2.5917	0.5838	0.5819	0.5728	0.5857
		(4.4482)	(2.5288)	(2.5247)	(2.4389)	(0.3117)	(0.2765)	(0.2717)	(0.273)
	0.75	2.6876	2.6256	2.5255	2.5306	0.851	0.8502	0.841	0.8571
		(4.187)	(2.1803)	(2.1786)	(2.1867)	(0.3495)	(0.2983)	(0.3009)	(0.302)
	1.00	2.6769	2.5352	2.5342	2.539	1.1106	1.1078	1.0993	1.1095
		(4.1387)	(2.1315)	(2.134)	(2.1352)	(0.3975)	(0.3599)	(0.3632)	(0.3637)
	1.50	2.6384	2.5352	2.5254	2.5357	1.4781	1.4866	1.4675	1.4481
		(4.1061)	(2.1047)	(2.1032)	(2.0957)	(0.4545)	(0.42)	(0.4138)	(0.4135)
	2.50	2.6397	2.5353	2.532	2.5384	2.6422	2.631	2.6303	2.6391
		(4.0908)	(2.0859)	(2.0912)	(2.0891)	(0.5204)	(0.4898)	(0.4909)	(0.4887)

,

Table 2. Average estimates and their MSEs (in parentheses) for varying n, R and fixed $m=5$, $T_m=5$ for $\lambda =0.5$ and $\beta =0.5$ and removal scheme $R2$.

n	R	${\widehat{\mathit{\lambda }}}_{\mathit{ML}}$	${\widehat{\mathit{\lambda }}}_{\mathit{SELF}}$	${\widehat{\mathit{\lambda }}}_{\mathit{GELF}}$		${\widehat{\mathit{\beta }}}_{\mathit{ML}}$	${\widehat{\mathit{\beta }}}_{\mathit{SELF}}$	${\widehat{\mathit{\beta }}}_{\mathit{GELF}}$
				$\mathit{w}=-\mathbf{1.5}$	$\mathit{w}=+\mathbf{1.5}$			$\mathit{w}=-\mathbf{1.5}$	$\mathit{w}=+\mathbf{1.5}$
20	$R1$	0.5715	0.5542	0.5503	0.5241	0.5604	0.5505	0.5499	0.5249
		(0.6705)	(0.4135)	(0.5143)	(0.2602)	(0.2705)	(0.2135)	(0.2043)	(0.1902)
	$R2$	0.5782	0.5524	0.5526	0.5321	0.5683	0.5621	0.5654	0.5418
		(0.8600)	(0.5421)	(0.6747)	(0.3372)	(0.3092)	(0.2510)	(0.2435)	(0.2226)
	$R3$	0.5722	0.5479	0.5597	0.5306	0.5717	0.5479	0.5693	0.5407
		(0.8053)	(0.4960)	(0.6209)	(0.3277)	(0.3553)	(0.2960)	(0.2909)	(0.2476)
	$R4$	0.5749	0.5447	0.5543	0.5265	0.5638	0.5592	0.5597	0.5276
		(0.7392)	(0.4610)	(0.5635)	(0.3026)	(0.4100)	(0.3421)	(0.34478)	(0.2772)
30	$R1$	0.5592	0.5268	0.5329	0.5261	0.5408	0.5267	0.5326	0.5164
		(0.4517)	(0.2793)	(0.3632)	(0.1926)	(0.2017)	(0.1593)	(0.1532)	(0.1626)
	$R2$	0.5626	0.5350	0.5438	0.5316	0.5511	0.5346	0.5426	0.5218
		(0.5893)	(0.3729)	(0.4470)	(0.2327)	(0.2384)	(0.2081)	(0.1872)	(0.1837)
	$R3$	0.5572	0.5323	0.5398	0.5398	0.5479	0.5319	0.5400	0.5204
		(0.5453)	(0.3304)	(0.4171)	(0.2229)	(0.2953)	(0.2304)	(0.2171)	(0.2029)
	$R4$	0.5538	0.5313	0.5372	0.5272	0.5448	0.5286	0.5369	0.5178
		(0.4884)	(0.3181)	(0.3872)	(0.2037)	(0.3393)	(0.2729)	(0.2570)	(0.2227)
40	$R1$	0.5397	0.5238	0.5243	0.5129	0.5317	0.5196	0.5249	0.5126
		(0.3399)	(0.2251)	(0.2622)	(0.1452)	(0.1399)	(0.1251)	(0.1022)	(0.1452)
	$R2$	0.5399	0.5262	0.5318	0.5172	0.5399	0.5259	0.5319	0.5166
		(0.4467)	(0.2814)	(0.3395)	(0.1923)	(0.1830)	(0.1554)	(0.1423)	(0.1554)
	$R3$	0.5354	0.5234	0.5309	0.5157	0.5362	0.5232	0.5292	0.5157
		(0.4131)	(0.2591)	(0.3146)	(0.1798)	(0.2331)	(0.1791)	(0.1746)	(0.1698)
	$R4$	0.5323	0.5214	0.5275	0.5141	0.5336	0.5225	0.5283	0.5143
		(0.3830)	(0.2454)	(0.3023)	(0.1554)	(0.2767)	(0.2014)	(0.2095)	(0.1823)
50	$R1$	0.5232	0.5264	0.5196	0.5208	0.5249	0.5359	0.5286	0.5261
		(0.2747)	(0.1824)	(0.2286)	(0.1213)	(0.0947)	(0.0924)	(0.0686)	(0.1313)
	$R2$	0.5321	0.5203	0.5259	0.513	0.5303	0.5254	0.5257	0.5329
		(0.3560)	(0.2194)	(0.2789)	(0.1479)	(0.1319)	(0.1104)	(0.0974)	(0.1418)
	$R3$	0.5378	0.5364	0.5247	0.5111	0.5287	0.5185	0.5243	0.5128
		(0.3291)	(0.2044)	(0.2617)	(0.1462)	(0.1791)	(0.1344)	(0.1217)	(0.1562)
	$R4$	0.5267	0.5374	0.5219	0.5107	0.526	0.5177	0.5223	0.512
		(0.3019)	(0.1904)	(0.2374)	(0.1318)	(0.2160)	(0.1594)	(0.1489)	(0.1679)

,

Table 3. ACI and HDI with their AW (in parentheses) and CP for varing n, R and fixed $m=5$, $T_m=5$ for $\lambda =0.5$ and $\beta =0.5$.

		$\mathit{\lambda }$		$\mathit{\beta }$
$\mathit{n}$	$\mathit{R}$	ACI	HDI	ACI	HDI
20	$R1$	(0.158, 0.92903)	(0.22748, 0.77724)	(0.23006, 0.82585)	(0.3652, 0.68335)
		(0.77103) 0.947	(0.54976) 0.987	(0.59579) 0.939	(0.31815) 0.988
	$R2$	(0.15659, 0.93573)	(0.22013, 0.77645)	(0.22941, 0.83262)	(0.37457, 0.69132)
		(0.77914) 0.951	(0.55632) 0.99	(0.60321) 0.957	(0.31675) 0.992
	$R3$	(0.15776, 0.92973)	(0.22685, 0.77757)	(0.23213, 0.83059)	(0.37152, 0.6867)
		(0.77197) 0.951	(0.55072) 0.987	(0.59846) 0.953	(0.31518) 0.991
	$R4$	(0.15793, 0.92917)	(0.22754, 0.77773)	(0.22968, 0.82611)	(0.36141, 0.6781)
		(0.77124) 0.947	(0.55019) 0.989	(0.59643) 0.947	(0.31669) 0.99
30	$R1$	(0.19023, 0.84791)	(0.30951, 0.71002)	(0.24322, 0.78554)	(0.39303, 0.61598)
		(0.65768) 0.949	(0.40051) 0.989	(0.54232) 0.948	(0.22295) 0.989
	$R2$	(0.19013, 0.85235)	(0.3044, 0.70963)	(0.23304, 0.77827)	(0.39348, 0.62119)
		(0.66222) 0.95	(0.40523) 0.99	(0.54523) 0.955	(0.22771) 0.991
	$R3$	(0.18998, 0.84813)	(0.30898, 0.71)	(0.24416, 0.78855)	(0.39456, 0.61857)
		(0.65815) 0.951	(0.40102) 0.99	(0.54439) 0.954	(0.22401) 0.99
	$R4$	(0.19037, 0.84807)	(0.30976, 0.71048)	(0.23133, 0.77657)	(0.39861, 0.61969)
		(0.6577) 0.952	(0.40072) 0.99	(0.54524) 0.952	(0.22108) 0.989
40	$R1$	(0.2074, 0.81914)	(0.33743, 0.66583)	(0.25406, 0.76284)	(0.41769, 0.60364)
		(0.61174) 0.947	(0.3284) 0.987	(0.50878) 0.942	(0.18595) 0.987
	$R2$	(0.20738, 0.82272)	(0.33263, 0.66467)	(0.24954, 0.7655)	(0.41346, 0.59651)
		(0.61534) 0.948	(0.33204) 0.991	(0.51596) 0.95	(0.18305) 0.99
	$R3$	(0.20762, 0.82)	(0.33649, 0.66511)	(0.25336, 0.76672)	(0.41524, 0.60369)
		(0.61238) 0.947	(0.32862) 0.99	(0.51336) 0.946	(0.18845) 0.989
	$R4$	(0.20721, 0.81894)	(0.33744, 0.66594)	(0.25357, 0.76285)	(0.41692, 0.60408)
		(0.61173) 0.947	(0.3285) 0.99	(0.50928) 0.95	(0.18716) 0.99
50	$R1$	(0.23963, 0.73802)	(0.41946, 0.59861)	(0.26722, 0.72253)	(0.44552, 0.53627)
		(0.49839) 0.946	(0.17915) 0.986	(0.45531) 0.946	(0.09075) 0.986
	$R2$	(0.24092, 0.73934)	(0.4169, 0.59785)	(0.25317, 0.71115)	(0.43237, 0.52638)
		(0.49842) 0.955	(0.18095) 0.99	(0.45798) 0.952	(0.09401) 0.986
	$R3$	(0.23984, 0.7384)	(0.41862, 0.59754)	(0.26539, 0.72468)	(0.43828, 0.53556)
		(0.49856) 0.949	(0.17892) 0.988	(0.45929) 0.95	(0.09728) 0.985
	$R4$	(0.23965, 0.73784)	(0.41966, 0.59869)	(0.25522, 0.71331)	(0.45412, 0.54567)
		(0.49819) 0.946	(0.17903) 0.97	(0.45809) 0.95	(0.09155) 0.987

and

Table 4. Average estimates and their MSEs (in parentheses) for varing m, $T_m$ for $\lambda =0.5$, $\beta =0.5$ and $n=30$ and removal scheme $R2$.

m	${\mathit{T}}_{\mathit{m}}$	${\widehat{\mathit{\lambda }}}_{\mathit{ML}}$	${\widehat{\mathit{\lambda }}}_{\mathit{SELF}}$	${\widehat{\mathit{\lambda }}}_{\mathit{GELF}}$		${\widehat{\mathit{\beta }}}_{\mathit{ML}}$	${\widehat{\mathit{\beta }}}_{\mathit{SELF}}$	${\widehat{\mathit{\beta }}}_{\mathit{GELF}}$
				$\mathit{w}=-\mathbf{1.5}$	$\mathit{w}=+\mathbf{1.5}$			$\mathit{w}=-\mathbf{1.5}$	$\mathit{w}=+\mathbf{1.5}$
5	3	0.6284	0.6122	0.6209	0.5783	0.5346	0.5204	0.5363	0.5191
		(0.9793)	(0.7747)	(0.7715)	(0.7669)	(0.1964)	(0.1858)	(0.1811)	(0.1774)
	4	0.6201	0.6005	0.6172	0.5674	0.5191	0.5123	0.5435	0.508
		(0.9657)	(0.7611)	(0.7579)	(0.7533)	(0.1885)	(0.1753)	(0.1732)	(0.1695)
	5	0.5958	0.5702	0.5967	0.5534	0.5174	0.507	0.5091	0.5021
		(0.9483)	(0.7437)	(0.7405)	(0.7359)	(0.1831)	(0.1704)	(0.1678)	(0.1641)
	6	0.5878	0.5743	0.582	0.5698	0.5152	0.494	0.5148	0.4923
		(0.9314)	(0.7268)	(0.7236)	(0.719)	(0.1795)	(0.1686)	(0.1642)	(0.1605)
	7	0.5727	0.5627	0.5836	0.5315	0.5108	0.5019	0.5126	0.5017
		(0.9185)	(0.7139)	(0.7107)	(0.7061)	(0.1671)	(0.1524)	(0.1518)	(0.1481)
8	3	0.6377	0.5976	0.6129	0.5762	0.5453	0.5355	0.543	0.5316
		(0.9888)	(0.7856)	(0.7843)	(0.7782)	(0.2172)	(0.2083)	(0.2009)	(0.2009)
	4	0.608	0.5873	0.6044	0.5807	0.527	0.5212	0.5363	0.5189
		(0.9618)	(0.7586)	(0.7573)	(0.7512)	(0.1933)	(0.1844)	(0.1791)	(0.177)
	5	0.5789	0.5827	0.569	0.5301	0.5101	0.5045	0.5262	0.5037
		(0.9497)	(0.7465)	(0.7452)	(0.7391)	(0.1845)	(0.1756)	(0.1703)	(0.1682)
	6	0.5729	0.5825	0.5837	0.5608	0.5121	0.5077	0.5175	0.5066
		(0.9354)	(0.7322)	(0.7309)	(0.7248)	(0.1771)	(0.1682)	(0.1629)	(0.1608)
	7	0.5593	0.5584	0.5927	0.5732	0.5078	0.4997	0.5006	0.4957
		(0.9286)	(0.7254)	(0.7241)	(0.718)	(0.1688)	(0.1599)	(0.1546)	(0.1525)
10	3	0.6336	0.6165	0.6402	0.6053	0.6177	0.5708	0.5519	0.5165
		(0.9895)	(0.7863)	(0.7857)	(0.7789)	(0.2112)	(0.2016)	(0.1963)	(0.1937)
	4	0.6109	0.5926	0.613	0.5551	0.5278	0.5172	0.5211	0.5159
		(0.9739)	(0.7707)	(0.7701)	(0.7633)	(0.1961)	(0.1865)	(0.1812)	(0.1786)
	5	0.6075	0.5961	0.6077	0.5899	0.5168	0.496	0.5093	0.4946
		(0.9526)	(0.7494)	(0.7488)	(0.742)	(0.1868)	(0.1772)	(0.1719)	(0.1693)
	6	0.6002	0.5904	0.5986	0.559	0.5163	0.4944	0.5186	0.4916
		(0.9447)	(0.7415)	(0.7409)	(0.7341)	(0.1772)	(0.1676)	(0.1623)	(0.1501)
	7	0.5854	0.5899	0.6063	0.5852	0.5141	0.5008	0.5193	0.4994
		(0.9371)	(0.7339)	(0.7333)	(0.7265)	(0.1628)	(0.1532)	(0.1479)	(0.1453)

. From these tables, the following conclusions can be drawn:

1.

Table 1 represents the average estimates and MSEs for various combinations of $(\lambda ,\beta )$ for fixed $m=5,T_m=5$ and $n=30$ for a fixed removal scheme. It is observed that the MSE of $\widehat{\lambda }$ decreases as $\widehat{\beta }$ increases, suggesting that higher scale parameter values lead to more precise estimation of $\lambda$. Conversely, the MSE of $\widehat{\lambda }$ increases as $\lambda$ increases, indicating that shape parameter variation introduces more estimation variability. For $\widehat{\beta }$, the MSE increases with both $\lambda$ and $\beta$, implying that higher parameter values make shape estimation relatively more difficult.

2.

Bayes estimators under GELF for loss parameter $w=+1.5$ exhibit the lowest MSE across all the parameter combinations. This indicates that Bayesian inference with asymmetric loss functions can effectively reduce estimation error.

3.

Table 2 represents the average estimate and MSE for varying n, removal schemes, R and keeping $m=5$, $T_m=5$, $\lambda =0.5$ and $\beta =0.5$ fixed. From Table 2, the MSE of the estimators $\widehat{\lambda }$ and $\widehat{\beta }$ is the least for removal scheme 1 followed by 4, 3 and 2 for a fixed n. And the MSE of estimators decreases as the sample size increases.

4.

Table 3 represents the ACI and HDI with their AW and CP for varying n, R and fixed $m=5$, $T_m=5$. The AW of HDI is lower than ACI for both $\lambda$ and $\beta$, meaning Bayesian HDIs provide narrower intervals, reflecting greater precision. CP associated with HDI is higher than that of ACI, showing that HDI not only gives narrower intervals but also maintains better coverage.

5.

AW corresponding to removal scheme $R1$ is lowest, followed by the AW corresponding to removal schemes $R4$, $R3$ and $R2$ in most of the cases. CP is also highest for removal scheme 2 in most cases.

6.

Table 4 represents the average estimates and their MSEs (in parentheses) for varying m, $T_m$ for $\lambda =0.5$, $\beta =0.5$ and $n=30$. MSE decreases as censoring time $T_m$ increases, because extending the study period allows more failures to be observed, leading to improved estimation. Conversely, MSE increases as the number of intervals m increases, because more intervals mean more chances of incomplete information due to multiple censoring points.

7.

The Bayes estimators can be seen to have a smaller MSEs than the classical estimators for all the considered cases.

Algorithm 2 Simulation of Progressive Interval Type-I Censored Sample

1: Specify the value of $n,m,(T_1,T_2,\dots ,T_m)$; model parameters $\lambda ,\beta$. 2: $$ 3: Set $i\leftarrow 0$, $dsum\leftarrow 0$, $rsum\leftarrow 0$. 4: $$ 5: Set $i\leftarrow i+1$. If $i=m+1$, exit the algorithm. 6: $$ 7: Generate $d_i\sim \mathrm{Bin}\left(n-dsum-rsum,{\displaystyle \frac{F\left(T_i\right)-F\left(T_{i-1}\right)}{1-F\left(T_{i-1}\right)}}\right)$. 8: Update $dsum\leftarrow dsum+d_i$. 9: if $i<m$  then 10: $$ 11:      Generate $r_i\sim \mathrm{Bin}(n-dsum-rsum,p_i)$. 12: $$ 13: else 14:       Set $r_i\leftarrow n-dsum-rsum$. 15: $$ 16: end if 17: Update $rsum\leftarrow rsum+r_i$ and go to Step 3.

6. Real Data Analysis

In this section, we analyze a real-life dataset concerning the survival times of patients diagnosed with plasma cell myeloma, originally reported by Carbone et al. [25]. The study investigated the association between clinical symptoms, the type of abnormal protein, and survival outcomes, as well as the response to therapy, for 112 individuals treated at the National Cancer Institute. The data are given in

Table 5. Survival times for patients with plasma cell myeloma.

Interval	Number of Failures	Number of Withdrawn
(Months)	(d)	(r)
$[0,5.5)$	18	1
$[5.5,10.5)$	16	1
$[10.5,15.5)$	18	3
$[15.5,20.5)$	10	0
$[20.5,25.5)$	11	0
$[25.5,30.5)$	8	1
$[30.5,40.5)$	13	2
$[40.5,50.5)$	4	3
$[50.5,60.5)$	1	2
$[60.5,\infty )$	0	0

.

For the analysis, we assume that the survival times follow a GKME distribution. The ML estimates of the parameters were obtained using the numerical routine method. Given the absence of prior knowledge about the dataset, a non-informative prior is used to obtain the Bayes estimates under SELF and GELF. Also, $95\%$ approximate CIs and HPD intervals corresponding to ML and Bayes estimates are constructed. The resulting point and interval estimates for $\lambda$ and $\beta$ are reported in

Table 6. ML estimates (standard error) and Bayes estimates of $\lambda$ and $\beta$ along with $95\%$ approximate confidence/HPD intervals for real dataset.

	ML	SELF	GELF
			$\mathit{w}=-\mathbf{1.5}$	$\mathit{w}=+\mathbf{1.5}$
$\widehat{\lambda }$	0.2151 (0.1330)	0.3002	0.3348	0.1785
	(0.0705, 0.6562)	(0.0657, 0.3846)
$\widehat{\beta }$	0.0649 (0.0093)	0.0634	0.0612	0.0631
	(0.0492, 0.0858)	(0.0436, 0.0705)

. The trace plots and posterior densities of the parameters $\lambda$ and $\beta$, based on the generated MCMC samples, are displayed in Figure 3 and Figure 4, which illustrate their distributional behavior.

7. Conclusions

In this article, we develop comprehensive inferential procedures under both classical and Bayesian paradigms for the GKME distribution in the presence of PITI censoring. The work includes the derivation of point estimators as well as the construction of interval estimates for the unknown parameters, providing a complete framework for statistical inference in such censoring scenarios. Under the classical inference framework, ML estimators are computed through an iterative numerical procedure, and their corresponding ACIs are constructed at the $95\%$ confidence level, relying on the asymptotic normality property of the MLEs. For the Bayesian analysis, the M-H algorithm is implemented to generate MCMC samples, which are then utilized to obtain Bayes estimates under both SELF and GELF. From these posterior samples, $95\%$ HDIs are also derived to quantify parameter uncertainty. To evaluate the performance of the proposed estimators, an extensive Monte Carlo simulation study is conducted, and the findings indicate that the estimators perform satisfactorily across various scenarios. Finally, the practical applicability of the proposed methodology is demonstrated through the analysis of a real dataset involving the survival times of guinea pigs under multiple removal schemes within the PITI censoring framework.