An Extended Complex Method to Solve the Predator–Prey Model

Abstract

Through transformation and utilizing a novel extended complex method combining with the Weierstrass factorization theorem, Wiman–Valiron theory and the Painlevé test, new non-constant meromorphic solutions were constructed for the predator–prey model. These meromorphic solutions contain the rational solutions, exponential solutions, elliptic solutions, and transcendental entire function solutions of infinite order in the complex plane. The exact solutions contribute to understanding the predator–prey model from the perspective of complex differential equations. In fact, the presented synthesis method provides a new technology for studying some systems of partial differential equations.

1. Introduction

In what follows, the notation $\mathit{W}$ stands for a class of meromorphic functions in the complex plane that consists of elliptic functions, rational functions, and rational functions of $exp\left(\alpha z\right)(\alpha \in \mathbf{C})$ [1]. In 2013, based on the results of Eremenko [2], Eremenko et al. [3], and using the Nevanlinna theory and elliptic function theory, Yuan et al. posed the complex method [4]. We can use the complex method to construct meromorphic solutions for complex differential equations and traveling wave solutions to partial differential equations, especially for Briot–Bouquet type differential equations. In article [4], the authors employ the complex method to obtain all meromorphic solutions of an auxiliary ordinary differential equation and then find all meromorphic exact solutions of the classical Korteweg–de Vries equation, Boussinesq equation, (3+1)-dimensional Jimbo–Miwa equation, and Benjamin–Bona–Mahony equation. In the later years, some studies used the complex method and its variants, combining with the Nevanlinna theory, the Painlevé test, a technique for comparing Laurent series [5], and the Weierstrass factorization theorem to obtain meromorphic solutions or exact solutions to some higher dimensional and higher-order differential equations, and Fermat-type differential equations such as [6,7,8,9,10]. Unfortunately, the complex method has not been applied to systems of differential equations.

The motivation of this article is to build a new extended complex method to solve the predator–prey model

$$\left\{\begin{array}{c}{x}^{\prime }=\alpha x-\beta xy\hfill \\ y^{\prime }=\delta xy-\theta y,\hfill \end{array}\right.$$

(1)

where $\alpha ,\beta ,\delta ,\theta$ are positive constants.

The predator–prey model, also known as the Lotka–Volterra equations, is a pair of first-order nonlinear differential equations frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. It was first introduced in ecological and chemical systems [11,12]. $x=x\left(t\right)$ is the number of prey (for example, rabbits), $y=y\left(t\right)$ is the number of some predators (for example, foxes), and t represents time. The populations change through time according to the pair of equations. Explicit expressions of convergent trigonometric solutions of Equation (1) were given [13]. Analytic solutions of a second-order form of the Lotka–Volterra equation were presented using a new variable transformation [14]. The periods of the predator–prey system have also been considered [15]. Some approximate solutions for a class of predator–prey systems with the Beddington–DeAngelis and Nicholson–Bailey functional responses were obtained by the nonstandard finite difference methods [16]. Many variations in the predator–prey models were investigated in recent years [17,18,19,20,21,22,23], even in fractional forms [24,25,26]. Recently, a generalized Lotka–Volterra systems was proposed in an arbitrary dimension, such as [27]

$$x_i^{\prime }=x_i\left(c_{i0}+\sum _{j=1}^n{c}_{ij}{x}_j\right),i=1,\cdots ,n.$$

(2)

A very comprehensive literature review can be referred to article [27], which contains some important properties such as the Allee effect [28], fear effect [29,30,31], cannibalism [32], and immigration [33,34].

The Lotka–Volterra systems have been applied in many research areas of natural sciences, such as chemical reactions [35], plasma physics [36], even social sciences or economics [37]. In ecology, a functional response is the intake rate of a predator as a function of food density. There are three main types of functional responses classified by C. S. Holling. The type I functional response assumes that the consuming and hunting rates are linear up to a maximum, where they become constant. The type II functional response assumes that that the consumption rate is decelerated with increased population and is described by $r\left(x\right)=\alpha x/(\alpha px+1)$, where x denotes the food or prey density, $\alpha$ is the rate at which the predator encounters food items per unit of food density, and p is the average time spent on processing a food item. The type III functional response assumes that the consumption rate is more than linear at low levels of resource and is described by $r\left(x\right)=n{x}^p/(x^p+{\alpha }^p)$, where $\alpha$ and n are positive and $p>1$ is an integer [27].

After skim reading the recent literature mentioned above on the predator–prey models and references [38,39,40,41,42,43,44], we found that there are very few results on the study of exact solutions for Equation (1). For example, Varma gave an exponential function solution under the assumption of ${\alpha }_1={\alpha }_2$ [39]. Although there are many methods and algorithms for building exact and explicit solutions of ordinary or partial differential equations, such as the Bäcklund transformation method, the inverse scattering method, the Darboux transformation method, the modified simple equation method, and the Homotopy analysis method. Unfortunately, there is no general way to deal with all forms of differential equations. Unlike the previous studies aforementioned, the present study is motivated by the consideration of meromorphic solutions of the predator–prey model in the complex plane. Therefore, the current paper first attempts to explore solutions to Equation (1) using an extended complex method combining other analysis tools. To construct non-constant meromorphic solutions on the complex plane, we need to assume $t=z,x=x\left(z\right),y=y\left(z\right),\alpha ,\beta ,\delta ,\theta$ are complex numbers, and rewrite the complex predator–prey model as follows:

$$\left\{\begin{array}{c}{x}^{\prime }\left(z\right)=\alpha x\left(z\right)-\beta x\left(z\right)y\left(z\right)\hfill \\ y^{\prime }\left(z\right)=\delta x\left(z\right)y\left(z\right)-\theta y\left(z\right).\hfill \end{array}\right.$$

(3)

The article is organized as follows: Section 2 involves the basic definitions, lemmas, and methodology of the extended complex method; Section 3 demonstrates the main results of this study; Section 4 presents the proof of Theorem 1; Section 5 shows the discussion and limitations; and Section 6 gives the conclusions and possible future research directions.

2. Preliminaries

Definition 1.

([45]) Let w be a meromorphic solution of a mth order algebraic differential equation $E(z,w)=0$. We call the involved term of $E(z,w)=0$, which determines the multiplicity q in w as the dominant term. The dominant part of $E(z,w)=0$ consists of all dominant terms and is denoted by $\widehat{E}=\widehat{E}(z,w)$. The multiplicity of a pole of each term in $\widehat{E}(z,w\left(z\right))$ is the same integer denoted by $D\left(q\right)$. The multiplicity of pole of each monomial $M_r\left[z\right]$ in $E(z,w)-\widehat{E}(z,w)$ is denoted by $D_r\left(q\right)$.

Definition 2.

([46]) For any meromorphic function v, the derivative operator of the dominant part $\widehat{E}(z,w\left(z\right))$ with respect to w is defined by

$${\widehat{E}}^{\prime }(z,w)v:=\underset{\lambda \to 0}{lim}{\displaystyle \frac{\widehat{E}(z,w+\lambda v)-\widehat{E}(z,w)}{\lambda }}.$$

(4)

The root of the following equation

$$P\left(i\right)=\underset{\chi \to 0}{lim}{\chi }^{-i+D\left(q\right)}{\widehat{E}}^{\prime }(\chi ,c_{-q}{\chi }^{-q}){\chi }^{i-q}=0$$

(5)

is called the Fuchs index of the equation $E(z,w)=0$.

We investigate the solutions to the complex ordinary differential equation

$$P(w,w^{\prime },\cdots ,w^{\left(m\right)})=0,$$

(6)

which w can be expressed by a Laurent series

$$w\left(z\right)=\sum _{k=-q}^{\infty }{c}_k{z}^k.$$

(7)

After plugging the formal Laurent series (7) in Equation (6), if there are exactly p different formal Laurent series that satisfy Equation (6), we say Equation (6) satisfies the $\langle p,q\rangle$ condition. If we only determine p different principle parts $w\left(z\right)={\sum }_{k=-q}^{-1}{c}_k{z}^k(q>0,c_{-q}\ne 0)$, we say Equation (6) satisfies the weak $\langle p,q\rangle$ condition. If Equation (6) satisfies the $\langle p,q\rangle$ condition, we say Equation (6) satisfies the finiteness property: it has only finitely many formal Laurent series with finite principal part admitting the equation, see [1].

Rewriting Equation (6) as the following form

$$P(w,w^{\prime },\cdots ,w^{\left(m\right)})=b{w}^n+c.$$

(8)

Lemma 1.

([47] [Theorem 1.4], [48] [Theorem 1]) Let $p,l,m,n\in \mathbf{N}$. If $degP(w,w^{\prime },\dots ,w^{\left(m\right))})<n$ and Equation (8) satisfies $\langle p,q\rangle$ condition, then all non-constant meromorphic solutions $w\in \mathit{W}$ and must be one of the following three forms:

(i) Each elliptic solution with a pole at $z=0$ can be written as

$$\begin{array}{cc}\hfill w\left(z\right)=& {\displaystyle \sum _{i=1}^{l-1}\sum _{j=2}^q\frac{{(-1)}^j{c}_{-ij}}{(j-1)!}\frac{d^{j-2}}{d{z}^{j-2}}\left(\frac{1}{4}{\left[\frac{{\wp }^{\prime }\left(z\right)+B_i}{\wp \left(z\right)-A_i}\right]}^2-\wp \left(z\right)\right)}\hfill \\ \hfill & {\displaystyle +\sum _{i=1}^{l-1}\frac{c_{-i1}}{2}\frac{{\wp }^{\prime }\left(z\right)+B_i}{\wp \left(z\right)-A_i}+\sum _{j=2}^q\frac{{(-1)}^j{c}_{-lj}}{(j-1)!}\frac{d^{j-2}}{d{z}^{j-2}}\wp \left(z\right)+c_0,}\hfill \end{array}$$

(9)

where $c_{-ij}$ are given by Equation (7), $B_i^2=4A_i^3-g_2{A}_i-g_3$ and ${\displaystyle \sum _{i=1}^l{c}_{-i1}=0.}$

(ii) Each rational function solution $w:=R\left(z\right)$ is of the form

$$R\left(z\right)=\sum _{i=1}^l\sum _{j=1}^q{\displaystyle \frac{c_{ij}}{{(z-z_i)}^j}}+c_0,$$

(10)

with $l(\le p)$ different poles of multiplicity q.

(iii) Each simply periodic solution is a rational function $R\left(\xi \right)$ of $\xi =exp\left(\alpha z\right)(\alpha \in \mathbf{C})$. $R\left(\xi \right)$ has $l(\le p)$ different poles of multiplicity q, and is of the form

$$R\left(\xi \right)=\sum _{i=1}^l\sum _{j=1}^q{\displaystyle \frac{c_{ij}}{{(\xi -{\xi }_i)}^j}}+c_0.$$

(11)

Lemma 2.

([49] [Corollary], [50] [Theorem 2.2.3]) A meromorphic function f is a rational function iff $T(r,f)=O(logr)$.

Lemma 3.

(Clunie’s lemma [50] [Lemma 2.4.2]) Let f be a transcendental meromorphic solution of the equation

$$f^{n}P(z,f,f^{\prime },\dots )=Q(z,f,f^{\prime },\dots ),$$

(12)

where n is a non-zero positive integer, and P and Q are polynomials in f and its derivatives with meromorphic coefficients $\left\{a_{\lambda }\right|\lambda \in I\}$, such that for each $\lambda \in I$, $m(r,a_{\lambda })=S(r,f),$ where I is an index set. If the total degree of Q as a polynomial in $f,f^{\prime },f^{″},\dots$ is at most n, then

$$m(r,P(z,f,f^{\prime },\dots )=S(r,f).$$

(13)

For a mth order complex differential equation $P(w,w^{\prime },\cdots ,w^{\left(m\right)})=b{w}^n+c$, where $degP(w,w^{\prime },\dots ,w^{\left(m\right))})<n$ and satisfies the $\langle p,q\rangle$ condition, then, all non-constant meromorphic solutions belong to the class $\mathit{W}$ by the virtue of Lemma 1.

A natural question is how to obtain meromorphic solutions of more general differential equations if we remove the constraints in Lemma 2 in [4] and Lemma 1 such as $degP(w,w^{\left(m\right)})<n$ or $degP(w,w^{\prime },\dots ,w^{\left(m\right))})<n$. In this direction, the author studied the thin-film equation [6] and the Fermat-type functional equation [10]. Nevertheless, up to now, we have not found any research that uses the complex method to solve the system of differential equations.

Based on the extended complex method [8], we would like to pose the following steps to solve systems of partial differential equations as follows:

Step 1. Using the transform $T:u(x,t)=u\left(z\right),w(x,t)=w\left(z\right),(x,t)\to z$ to reduce a given system of partial differential equations to the following system of ordinary differential equations

$$\left\{\begin{array}{c}P(u,u^{\prime },\cdots ,u^{\left(m\right)},w,w^{\prime },\cdots ,w^{\left(s\right)})=0\hfill \\ Q(u,u^{\prime },\cdots ,u^{\left(m\right)},w,w^{\prime },\cdots ,w^{\left(s\right)})=0.\hfill \end{array}\right.$$

(14)

Then reduce the system of ordinary differential equation, Equation (14), to a certain ordinary differential equation, Equation (8).

Step 2. Determine whether all meromorphic solutions $u\left(z\right)$ and $w\left(z\right)$ of Equation (8) belong to the class $\mathit{W}$ by using Nevanlinna’s value distribution theory and Painlevé test.

Step 3. Substituting (7) into Equation (8) to determine that the (weak) $\langle p,q\rangle$ condition holds by using the Painlevé test.

Step 4. Build the non-constant polynomial and transcendental entire function solutions to Equation (14) using their forms to be determined. By indeterminant relations (9)–(11), building the elliptic, rational and simply periodic solutions $u\left(z\right),w\left(z\right)$ of Equation (14) with pole at $z=0$, respectively.

Step 5. By Lemma 1 mainly, obtaining all meromorphic solutions $w(z-z_0)$.

Step 6. Substituting the inverse transform $T^{-1}$ into these meromorphic solutions $u(z-z_0),w(z-z_0)$, then obtain exact solutions $u,w$ of the original systems of differential equation, Equation (14).

3. Main Results

By using the extended complex method, combining with the Weierstrass factorization theorem, Wiman–Valiron theory, and the Painlevé test, we obtain the following theorem:

Theorem 1.

If $\beta \delta \ne 0$, Equation (3) has the following forms of non-constant meromorphic solutions provided that $\theta =-\alpha$:

(1) Rational solution:

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{1}{\delta (z-z_0)}}\hfill \\ y\left(z\right)={\displaystyle \frac{1}{\beta (z-z_0)}},\hfill \end{array}\right.$$

(15)

provided that $\alpha =0$, where $z_0\in \mathbf{C}$ is arbitrary.

(2) Exponential function solutions:

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{\alpha exp\left(\alpha (z-z_0)\right)}{\delta \left(exp\left(\alpha (z-z_0)\right)-\xi \right)}}\hfill \\ y\left(z\right)={\displaystyle \frac{\alpha exp(\alpha (z-z_0))}{\beta \left(exp\left(\alpha (z-z_0)\right)-\xi \right)}},\hfill \end{array}\right.$$

(16)

where $z_0,\xi (\ne 0)\in \mathbf{C}$ is arbitrary, $\alpha \ne 0$.

(3) Elliptic solutions:

$$\left\{\begin{array}{cc}x\left(z\right)\hfill & ={\displaystyle \frac{{\wp }^{\prime }\left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)}{2\delta \left(\wp \left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)-\frac{{\alpha }^2}{12}\right)}}-{\displaystyle \frac{\alpha }{2\delta }}\hfill \\ y\left(z\right)\hfill & =-{\displaystyle \frac{{\wp }^{\prime }\left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)}{2\beta \left(\wp \left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)-\frac{{\alpha }^2}{12}\right)}}+{\displaystyle \frac{\alpha }{2\beta }},\hfill \end{array}\right.$$

(17)

where $z_0\in \mathbf{C}$ is arbitrary, $\alpha \ne 0$.

If $\beta =\delta =0,\alpha \ne 0,\theta \ne 0$, Equation (3) has the following forms of entire solutions:

$$\left\{\begin{array}{c}x\left(z\right)=c_{1}exp\left(\alpha (z-z_0)\right)\hfill \\ y\left(z\right)=c_{2}exp\left(-\theta (z-z_0)\right),\hfill \end{array}\right.$$

(18)

where $c_1,c_2,z_0$ are arbitrary complex numbers.

If $\beta =0,\delta \ne 0$, $\alpha \ne 0$, Equation (3) has the following forms of meromorphic solution:

$$\left\{\begin{array}{c}x\left(z\right)=c_{1}exp\left(\alpha z\right)\hfill \\ y\left(z\right)=c_{2}exp\left({\displaystyle \frac{\delta c_{1}exp\left(\alpha z\right)}{\alpha }}-\theta z\right),\hfill \end{array}\right.$$

(19)

where $c_1,c_2$ are arbitrary complex numbers.

If $\beta \ne 0,\delta =0$, $\theta \ne 0$, Equation (3) has the following forms of meromorphic solution:

$$\left\{\begin{array}{c}x\left(z\right)=c_{1}exp\left(\alpha z+{\displaystyle \frac{\beta c_{2}exp\left(-\theta z\right)}{\theta }}\right)\hfill \\ y\left(z\right)=c_{2}exp\left(-\theta z\right),\hfill \end{array}\right.$$

(20)

where $c_1,c_2$ are arbitrary complex numbers.

4. Proof of Theorem 1

4.1. Painlevé Test and Fuchs Indexes

Eliminating $x\left(z\right)$ and $x^{\prime }\left(z\right)$ in Equation (3), we have

$$-\beta y^{\prime }{y}^2+\alpha \theta y^2+\alpha y{y}^{\prime }+{\left(y^{\prime }\right)}^2-y{y}^{″}=\beta \theta y^3.$$

(21)

Assuming that there is a meromorphic solution $y\left(z\right)$ satisfies Equation (21), and if $y\left(z\right)$ has a movable pole at $z=z_0$, then in a neighborhood of $z_0$, the Laurent series of y is of the form of ${\sum }_{k=-q}^{\infty }{c}_k{(z-z_0)}^k(q>0,c_{-q}\ne 0)$. Substituting this Laurent series into Equation (21), we have $p=2,q=1$, and

$$y\left(z\right)={\displaystyle \frac{1}{\beta }}{\displaystyle \frac{1}{z-z_0}}+{\displaystyle \frac{(1\pm \sqrt{2})\theta }{\beta }}+\cdots .$$

(22)

From Equation (21), we know $\widehat{E}=\widehat{E}(z,y)={\left(y^{\prime }\right)}^2-\beta y^{\prime }{y}^2-y{y}^{″}$, hence,

$$\begin{array}{cc}\hfill & {\widehat{E}}^{\prime }(z,y)v\hfill \\ \hfill & =\underset{\lambda \to 0}{lim}{\displaystyle \frac{\left({(y+\lambda v)}^{\prime 2}-\beta {(y+\lambda v)}^{\prime }{(y+\lambda v)}^2-(y+\lambda v){(y+\lambda v)}^{″}\right)-\left(y^{\prime 2}-\beta y^{\prime }{y}^2-y{y}^{″}\right)}{\lambda }}\hfill \\ \hfill & =(-y^{″}-2\beta y^{\prime }y)v+(2y^{\prime }-\beta y^2)v^{\prime }-y{v}^{″}\hfill \\ \hfill & =\left((-y^{″}-2\beta y^{\prime }y)+(2y^{\prime }-\beta y^2){\displaystyle \frac{\partial }{\partial z}}-y{\displaystyle \frac{{\partial }^2}{\partial z^2}}\right)v.\hfill \end{array}$$

(23)

Therefore, the Fuchs index equation of Equation (21) reads

$$P\left(i\right)=\underset{\chi \to 0}{lim}{\chi }^{-i+D\left(q\right)}{\widehat{E}}^{\prime }(\chi ,c_{-q}{\chi }^{-q}){\chi }^{i-q}=0,$$

(24)

where $q=1,D\left(q\right)=4$. Setting $y=c_{-1}{\chi }^{-1}={\displaystyle \frac{1}{\beta }}{\chi }^{-1},v={\chi }^{i-1}$, we have

$$\begin{array}{cc}\hfill P\left(i\right)& =\underset{\chi \to 0}{lim}{\chi }^{-i+4}{\widehat{E}}^{\prime }(\chi ,{\displaystyle \frac{1}{\beta }}{\chi }^{-1}){\chi }^{i-1}\hfill \\ \hfill & =\underset{\chi \to 0}{lim}{\chi }^{-i+4}\left((-y^{″}-2\beta y^{\prime }y)+(2y^{\prime }-\beta y^2){\displaystyle \frac{\partial }{\partial z}}-y{\displaystyle \frac{{\partial }^2}{\partial z^2}}\right){\chi }^{i-1}\hfill \\ \hfill & =-{\displaystyle \frac{1}{\beta }}(i+1)(i-1)=0.\hfill \end{array}$$

(25)

Therefore, Equation (21) has a non-negative integer Fuchs index $i=1$. This follows that there exists a coefficient $c_k(k>0)$ that is an arbitrary number in the Laurent series (22) [46], and Equation (21) satisfies the weak $\langle p,q\rangle =\langle 1,1\rangle$ condition. Further, $deg\left(-\beta y^{\prime }{y}^2+\alpha \theta y^2+\alpha y{y}^{\prime }+{\left(y^{\prime }\right)}^2-y{y}^{″}\right)=deg\left(\beta \theta y^3\right)=3$. Therefore, Equation (21) does not satisfy the constraint of the degree in Lemma 1. However, the explicit representation of the meromorphic solutions with at least one pole of Equation (21) is compatible with Lemma 1.

Remark 1.

If y is a rational solution of Equation (21), then $y\in \mathit{W}$. Now we assume that y is a transcendental meromorphic function with at least one pole.

If y is a transcendental meromorphic function with finite many poles. We rewrite Equation (21) into the following form

$$\begin{array}{c}\hfill y^2\left(\beta \theta y+\beta y^{\prime }\right)=\alpha \theta y^2+\alpha y{y}^{\prime }+{\left(y^{\prime }\right)}^2-y{y}^{″}.\end{array}$$

(26)

According to Clunie’s Lemma 3, we have $n=2,P=\beta \theta y+\beta y^{\prime },Q=\alpha \theta y^2+\alpha y{y}^{\prime }+{\left(y^{\prime }\right)}^2-y{y}^{″}$. Therefore, $degQ=2$, then $m(r,P)=m\left(r,\beta \theta y+\beta y^{\prime }\right)=S(r,y)$. Hence, $T\left(r,\beta \theta y+\beta y^{\prime }\right)-N\left(r,\beta \theta y+\beta y^{\prime }\right)$ = $m\left(r,\beta \theta y+\beta y^{\prime }\right)=S(r,y)$. From the assumption, $N\left(r,\beta \theta y+\beta y^{\prime }\right)=O(logr)=o\left(T\left(r,\beta \theta y+\beta y^{\prime }\right)\right)$. Therefore, $(1-o\left(1\right))T\left(r,\beta \theta y+\beta y^{\prime }\right)=S(r,y)$, by Lemma 2, f must be a rational function, which is a contradiction. Therefore, f must be a transcendental function with infinitely many poles. Because there is an arbitrary coefficient in the formal Laurent series, therefore, Equation (21) does not satisfy the finiteness property. Therefore, it fails to determine whether all meromorphic solutions of Equation (21) belong to class $\mathit{W}$. This discussion also holds for the solution x.

4.2. Entire Function Solutions

4.2.1. $\beta \delta \ne 0$

It is easy to check that Equation (3) has no non-constant polynomial solution $\left(x\right(z),y(z\left)\right)$. Because if we assume ${\displaystyle (x\left(z\right),y\left(z\right))=(\sum _{i=1}^n{a}_i{z}^i,\sum _{j=1}^m{b}_j{z}^j}$), and put it into Equation (3), the degree of $x^{\prime }\left(z\right)$ cannot equal to the degree of $\alpha x\left(z\right)-\beta x\left(z\right)y\left(z\right)$.

Then, we claim that Equation (3) has no transcendental entire function solution $\left(x\right(z),y(z\left)\right)$, where $\left(x\right(z),y(z\left)\right)$ have the same order under the condition of $\beta \delta \ne 0$. By the Weierstrass factorization theorem and Wiman–Valiron theory (see [51]), we know Equation (3) does not have any transcendental entire solution in the form of

$$(x\left(z\right),y\left(z\right))=(exp\left(g_1\left(z\right)\right)z^{m_1}\prod _{i=1}^{\infty }{E}_i({\displaystyle \frac{z}{z_i}}),exp\left(g_2\left(z\right)\right)z^{m_2}\prod _{j=1}^{\infty }{E}_j({\displaystyle \frac{z}{z_j}})),$$

(27)

where $x\left(z\right),y\left(z\right)$ have the same order, $g_1\left(z\right),g_2\left(z\right)$ are entire functions, and $E_i,E_j$ are canonical factors. Because there is only one top-degree term

$$exp\left(g_1\left(z\right)\right)z^{m_1}\prod _{i=1}^{\infty }{E}_i\left({\displaystyle \frac{z}{z_i}}\right)exp\left(g_2\left(z\right)\right)z^{m_2}\prod _{j=1}^{\infty }{E}_j\left({\displaystyle \frac{z}{z_j}}\right)$$

(28)

in each equation of Equation (3), and cannot vanish to zero, unless $\beta =\delta =0$.

Equation (3) does not have solutions of the form of $\left(x\right(z),y(z\left)\right)$, where $x\left(z\right)$ is a non-constant polynomial and $y\left(z\right)$ is a transcendental entire function, or $y\left(z\right)$ is a non-constant polynomial and $x\left(z\right)$ is a transcendental entire function.

Further, according to the relationship of the multiplicity of the poles, Equation (3) does not have solutions of the form of $\left(x\right(z),y(z\left)\right)$, where $x\left(z\right)$ is a non-constant polynomial and $y\left(z\right)$ is a meromorphic function with at least one pole, and conversely. Obviously, for a similar reason, Equation (3) does not have solutions of the form of $\left(x\right(z),y(z\left)\right)$, where $x\left(z\right)$ is a transcendental entire function and $y\left(z\right)$ is a meromorphic function with at least one pole, and vice versa.

4.2.2. $\beta =\delta =0$

When $\beta =\delta =0$, Equation (3) will reduce to the equation

$$\left\{\begin{array}{c}{x}^{\prime }\left(z\right)=\alpha x\left(z\right)\hfill \\ y^{\prime }\left(z\right)=-\theta y\left(z\right).\hfill \end{array}\right.$$

(29)

Then, we have

$$\left\{\begin{array}{c}x\left(z\right)=c_{1}exp\left(\alpha z\right)\hfill \\ y\left(z\right)=c_{2}exp\left(-\theta z\right),\hfill \end{array}\right.$$

(30)

where $c_1,c_2$ are arbitrary complex numbers, $\alpha \theta \ne 0$.

4.2.3. $\beta =0,\delta \ne 0$

When $\beta =0,\delta \ne 0$, Equation (3) will reduce to the equation

$$\left\{\begin{array}{c}{x}^{\prime }\left(z\right)=\alpha x\left(z\right)\hfill \\ y^{\prime }\left(z\right)=\delta xy-\theta y\left(z\right).\hfill \end{array}\right.$$

(31)

Then, we have

$$\left\{\begin{array}{c}x\left(z\right)=c_{1}exp\left(\alpha z\right)\hfill \\ y\left(z\right)=c_{2}exp\left({\displaystyle \frac{\delta c_{1}exp\left(\alpha z\right)}{\alpha }}-\theta z\right),\hfill \end{array}\right.$$

(32)

where $c_1,c_2$ are arbitrary complex numbers, $\alpha \ne 0$.

4.2.4. $\beta \ne 0,\delta =0$

When $\beta \ne 0,\delta =0$, Equation (3) will reduce to the equation

$$\left\{\begin{array}{c}{x}^{\prime }\left(z\right)=\alpha x\left(z\right)-\beta x\left(z\right)y\left(z\right)\hfill \\ y^{\prime }\left(z\right)=-\theta y\left(z\right).\hfill \end{array}\right.$$

(33)

Then, we have

$$\left\{\begin{array}{c}x\left(z\right)=c_{1}exp\left(\alpha z+{\displaystyle \frac{\beta c_{2}exp\left(-\theta z\right)}{\theta }}\right)\hfill \\ y\left(z\right)=c_{2}exp\left(-\theta z\right),\hfill \end{array}\right.$$

(34)

where $c_1,c_2$ are arbitrary complex numbers, $\theta \ne 0$.

In fact, two infinite order transcendental entire function solutions $y\left(z\right)$ in (32) and $x\left(z\right)$ in (34) have been found out, which cannot be written in the form of rational functions of $exp\left(\alpha z\right)(\alpha \in \mathbf{C})$. It means that we find out two new meromorphic solutions which are out of the class $\mathit{W}$. The existence of the two new solutions also illustrates the fact that there exist some Fuchs indexes ($i=1$) that are non-negative integers, and not all the solutions belong to the class $\mathit{W}$. The phenomenon also explains the facts that are in Remark 1.

Therefore, we need to further consider solutions in the form of $\left(x\right(z),y(z\left)\right)$, where $x,y$ are non-constant rational functions, or simply periodic function solutions, or elliptic function solutions where they have at least one pole.

4.3. Meromorphic Solutions with Poles

If $\beta \delta =0$, from the results in Section 4.2, we know Equation (3) does not have any non-constant meromorphic solutions $x\left(z\right)$ with at least one pole and $y\left(z\right)$ with at least one pole.

Therefore, in this subsection, we assume that $\beta \delta \ne 0$.

4.3.1. Building the Laurent Series and the Check the Weak $\langle p,q\rangle$ Condition

Assuming that $w\left(z\right)$ is a meromorphic solution of Equation (3), with a movable pole at $z=0$, then in a neighborhood of $z=0$, the Laurent series of $x\left(z\right)$ is the form of ${\sum }_{k=-q}^{\infty }{c}_k{z}^k(q>0,c_{-q}\ne 0)$, and the Laurent series of $y\left(z\right)$ is the form of ${\sum }_{k=-q}^{\infty }{d}_k{z}^k(q>0,d_{-q}\ne 0)$. The degree of the pole $z=0$ and the coefficients $c_{-q},d_{-q}$ can be uniquely determined by Equation (3). Substituting ${\sum }_{k=-q}^{\infty }{c}_k{z}^k$ and ${\sum }_{k=-q}^{\infty }{d}_k{z}^k$ into Equation (3), we have $p=1,q=1$, and

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill c_{-1}& =-{\displaystyle \frac{1}{\delta }},\hfill \\ \hfill d_{-1}& ={\displaystyle \frac{1}{\beta }},\hfill \\ \hfill c_0& =-{\displaystyle \frac{-\beta d_0+\alpha }{\delta }},\hfill \\ \hfill d_0& \mathrm{is}\mathrm{arbirary},\hfill \\ \hfill c_1& =-{\displaystyle \frac{\beta \left(\beta d_0^2-2d_1\right)}{\delta }},\hfill \\ \hfill d_1& =-{\displaystyle \frac{-{\beta }^2{d}_0^2-2\alpha \beta d_0+{\alpha }^2}{3\beta }},\hfill \\ \hfill c_2& =-{\displaystyle \frac{2\left(2\alpha {\beta }^2{d}_0^2-3{\alpha }^2\beta d_0+{\alpha }^3+\frac{\left(-4{\beta }^2{d}_0^2+{\alpha }^2\right)\alpha }{8}\right)}{3\delta }},\hfill \\ \hfill d_2& =-{\displaystyle \frac{\alpha \left(-4{\beta }^2{d}_0^2+{\alpha }^2\right)}{8\beta }}.\hfill \end{array}\hfill \end{array}\right.$$

(35)

Hence, we obtain the following form of the Laurent series

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{1}{\delta z}}+{\displaystyle \frac{\beta d_0}{\delta }}-{\displaystyle \frac{\alpha }{\delta }}+\left(-{\displaystyle \frac{{\beta }^2{d}_0^2}{3\delta }}+{\displaystyle \frac{4\alpha \beta d_0}{3\delta }}-{\displaystyle \frac{2{\alpha }^2}{3\delta }}\right)z+\cdots \hfill \\ y\left(z\right)={\displaystyle \frac{1}{\beta z}}+d_0+\left(-{\displaystyle \frac{{\alpha }^2}{3\beta }}+{\displaystyle \frac{2d_0\alpha }{3}}+{\displaystyle \frac{\beta d_0^2}{3}}\right)z+\cdots .\hfill \end{array}\right.$$

(36)

4.3.2. Rational Solutions

By (10), we infer that the indeterminant of the rational solution with pole $z=0$ is

$$\left\{\begin{array}{c}x\left(z\right)={\displaystyle \frac{c_{-1}}{z}}+c_0=-{\displaystyle \frac{1}{\delta z}}+{\displaystyle \frac{\beta d_0}{\delta }}-{\displaystyle \frac{\alpha }{\delta }}\hfill \\ y\left(z\right)={\displaystyle \frac{d_{-1}}{z}}+d_0={\displaystyle \frac{1}{\beta z}}+d_0,\hfill \end{array}\right.$$

(37)

where $d_0$ is arbitrary.

Substituting (37) into Equation (3), eliminating the coefficients, we have

$$\left\{\begin{array}{c}-{\displaystyle \frac{2\alpha \beta d_0}{\delta }}+{\displaystyle \frac{{\alpha }^2}{\delta }}+{\displaystyle \frac{{\beta }^2{d}_0^2}{\delta }}=0\hfill \\ -\beta d_0^2+\alpha d_0+\theta d_0+{\displaystyle \frac{\frac{\alpha }{\beta }+\frac{\theta }{\beta }}{z}}=0,\hfill \end{array}\right.$$

(38)

Therefore,

$$\left\{\begin{array}{c}\alpha +\theta =0\hfill \\ d_0=0\hfill \\ \alpha =0.\hfill \end{array}\right.$$

(39)

Therefore, Equation (3) has the following rational solution:

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{1}{\delta (z-z_0)}}\hfill \\ y\left(z\right)={\displaystyle \frac{1}{\beta (z-z_0)}},\hfill \end{array}\right.$$

(40)

where $\theta =-\alpha =0$, and $z_0\in \mathbf{C}$ is arbitrary.

Remark 2.

If we substitute (37) in Equation (21) directly, we can also obtain the rational solution (40).

4.3.3. Exponential Function Solutions

By (11), we infer that the indeterminant of the simply periodic solution with pole $z=0$ is

$$\left\{\begin{array}{c}x\left(z\right)={\displaystyle \frac{c_{-1}}{exp\left(\mu z\right)-\xi }}+c_0\hfill \\ y\left(z\right)={\displaystyle \frac{d_{-1}}{exp\left(\mu z\right)-\xi }}+d_0,\hfill \end{array}\right.$$

(41)

where $\xi \ne 0\in C$ is arbitrary, substituting (41) into Equation (3), we have

$$\left\{\begin{array}{c}-{\displaystyle \frac{c_{-\mathtt{1}}\mu {\mathrm{e}}^{\mu z}}{{\left({\mathrm{e}}^{\mu z}-\xi \right)}^2}}-{\displaystyle \frac{\alpha c_{-\mathtt{1}}}{{\mathrm{e}}^{\mu z}-\xi }}-\alpha c_0+{\displaystyle \frac{\beta c_{-\mathtt{1}}{d}_{-\mathtt{1}}}{{\left({\mathrm{e}}^{\mu z}-\xi \right)}^2}}+{\displaystyle \frac{\beta c_{-\mathtt{1}}{d}_0}{{\mathrm{e}}^{\mu z}-\xi }}+{\displaystyle \frac{\beta c_0{d}_{-\mathtt{1}}}{{\mathrm{e}}^{\mu z}-\xi }}+\beta c_0{d}_0=0\hfill \\ -{\displaystyle \frac{d_{-\mathtt{1}}\mu {\mathrm{e}}^{\mu z}}{{\left({\mathrm{e}}^{\mu z}-\xi \right)}^2}}-{\displaystyle \frac{\delta c_{-\mathtt{1}}{d}_{-\mathtt{1}}}{{\left({\mathrm{e}}^{\mu z}-\xi \right)}^2}}-{\displaystyle \frac{\delta c_{-\mathtt{1}}{d}_0}{{\mathrm{e}}^{\mu z}-\xi }}-{\displaystyle \frac{\delta c_0{d}_{-\mathtt{1}}}{{\mathrm{e}}^{\mu z}-\xi }}-\delta c_0{d}_0+{\displaystyle \frac{\theta d_{-\mathtt{1}}}{{\mathrm{e}}^{\mu z}-\xi }}+\theta d_0=0,\hfill \end{array}\right.$$

(42)

then, collecting similar terms, we must have

$$\left\{\begin{array}{c}-{\displaystyle \frac{c_{-\mathtt{1}}\mu exp\left(\mu z\right)}{{\left(exp\left(\mu z\right)-\xi \right)}^2}}+{\displaystyle \frac{\beta c_{-\mathtt{1}}{d}_{-\mathtt{1}}}{{\left(exp\left(\mu z\right)-\xi \right)}^2}}=0\hfill \\ -{\displaystyle \frac{d_{-\mathtt{1}}\mu exp\left(\mu z\right)}{{\left(exp\left(\mu z\right)-\xi \right)}^2}}-{\displaystyle \frac{\delta c_{-\mathtt{1}}{d}_{-\mathtt{1}}}{{\left(exp\left(\mu z\right)-\xi \right)}^2}}=0.\hfill \end{array}\right.$$

(43)

Then we have

$$\left\{\begin{array}{c}{c}_{-\mathtt{1}}=-{\displaystyle \frac{\mu exp\left(\mu z\right)}{\delta }}\hfill \\ d_{-\mathtt{1}}={\displaystyle \frac{\mu exp\left(\mu z\right)}{\beta }}.\hfill \end{array}\right.$$

(44)

Then we put

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{\mu exp\left(\mu z\right)}{\delta \left(exp\left(\mu z\right)-\xi \right)}}+c_0\hfill \\ y\left(z\right)={\displaystyle \frac{\mu exp\left(\mu z\right)}{\beta \left(exp\left(\mu z\right)-\xi \right)}}+d_0\hfill \end{array}\right.$$

(45)

into Equation (3), we have

$$\left\{\begin{array}{c}-{\displaystyle \frac{{\mu }^2{\mathrm{e}}^{\mu z}}{\delta \left({\mathrm{e}}^{\mu z}-\xi \right)}}+{\displaystyle \frac{\alpha \mu {\mathrm{e}}^{\mu z}}{\delta \left({\mathrm{e}}^{\mu z}-\xi \right)}}-\alpha c_0-{\displaystyle \frac{\beta \mu {\mathrm{e}}^{\mu z}{d}_0}{\delta \left({\mathrm{e}}^{\mu z}-\xi \right)}}+{\displaystyle \frac{c_0\mu {\mathrm{e}}^{\mu z}}{{\mathrm{e}}^{\mu z}-\xi }}+\beta c_0{d}_0=0\hfill \\ {\displaystyle \frac{{\mu }^2{\mathrm{e}}^{\mu z}}{\beta \left({\mathrm{e}}^{\mu z}-\xi \right)}}+{\displaystyle \frac{\mu {\mathrm{e}}^{\mu z}{d}_0}{{\mathrm{e}}^{\mu z}-\xi }}-{\displaystyle \frac{\delta c_0\mu {\mathrm{e}}^{\mu z}}{\beta \left({\mathrm{e}}^{\mu z}-\xi \right)}}-\delta c_0{d}_0+{\displaystyle \frac{\theta \mu {\mathrm{e}}^{\mu z}}{\beta \left({\mathrm{e}}^{\mu z}-\xi \right)}}+\theta d_0=0.\hfill \end{array}\right.$$

(46)

Then, collecting similar terms, we have

$$\left\{\begin{array}{c}{\displaystyle \frac{exp\left(\mu z\right)\mu \left(-\beta d_0+\delta c_0+\alpha -\mu \right)}{\delta \left(exp\left(\mu z\right)-\xi \right)}}=0\hfill \\ {\displaystyle \frac{exp\left(\mu z\right)\mu \left(\beta d_0-\delta c_0+\mu +\theta \right)}{\beta \left(exp\left(\mu z\right)-\xi \right)}}=0\hfill \\ -\alpha c_0+\beta c_0{d}_0=0\hfill \\ -\delta c_0{d}_0+\theta d_0=0.\hfill \end{array}\right.$$

(47)

Then

$$\left\{\begin{array}{c}{c}_0=0\hfill \\ d_0=0\hfill \\ \mu =\alpha \hfill \\ \theta =-\alpha .\hfill \end{array}\right.$$

(48)

Hence, we know Equation (3) has the following solution

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{\alpha exp\left(\alpha (z-z_0)\right)}{\delta \left(exp\left(\alpha (z-z_0)\right)-\xi \right)}}\hfill \\ y\left(z\right)={\displaystyle \frac{\alpha exp\left(\alpha (z-z_0)\right)}{\beta \left(exp\left(\alpha (z-z_0)\right)-\xi \right)}},\hfill \end{array}\right.$$

(49)

where $\theta =-\alpha$, and $z_0,\xi (\ne 0)\in \mathbf{C}$ is arbitrary.

Remark 3.

If we substitute $y\left(z\right)={\displaystyle \frac{d_{-1}}{exp\left(\mu z\right)-\xi }}+d_0$ in Equation (21) directly, we can also obtain the following solution

$$y\left(z\right)={\displaystyle \frac{\alpha exp\left(\alpha (z-z_0)\right)}{\beta \left(exp\left(\alpha (z-z_0)\right)-\xi \right)}},$$

(50)

where $\theta =-\alpha$, and $z_0,\xi (\ne 0)\in \mathbf{C}$ is arbitrary. Then by Equation (3), $x\left(z\right)$ will be directly derived.

4.3.4. Hyperbolic Function Solution

Solution (49) can be changed to the following solution

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{\alpha \left(cosh\left(\alpha (z-z_0)\right)+sinh\left(\alpha (z-z_0)\right)\right)}{\delta \left(cosh\left(\alpha (z-z_0)\right)+sinh\left(\alpha (z-z_0)\right)-\xi \right)}}\hfill \\ y\left(z\right)={\displaystyle \frac{\alpha \left(cosh\left(\alpha (z-z_0)\right)+sinh\left(\alpha (z-z_0)\right)\right)}{\beta \left(cosh\left(\alpha (z-z_0)\right)+sinh\left(\alpha (z-z_0)\right)-\xi \right)}},\hfill \end{array}\right.$$

(51)

where $\theta =-\alpha$, and $z_0,\xi (\ne 0)\in \mathbf{C}$ is arbitrary.

4.3.5. Elliptic Function Solutions

By (9), we infer that the indeterminant of the elliptic solution with pole $z=0$ is

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{c_{-1}}{2}}{\displaystyle \frac{{\wp }^{\prime }(z,g_2,g_3)+B}{\wp (z,g_2,g_3)-A}}+c_0\hfill \\ y\left(z\right)=-{\displaystyle \frac{d_{-1}}{2}}{\displaystyle \frac{{\wp }^{\prime }(z,g_2,g_3)+D}{\wp (z,g_2,g_3)-C}}+d_0.\hfill \end{array}\right.$$

(52)

By (36), we have

$$\left\{\begin{array}{c}x\left(z\right)=-{\displaystyle \frac{-\frac{1}{\delta }}{2}}{\displaystyle \frac{{\wp }^{\prime }(z,g_2,g_3)+B}{\wp (z,g_2,g_3)-A}}-{\displaystyle \frac{-\beta d_0+\alpha }{\delta }}\hfill \\ y\left(z\right)=-{\displaystyle \frac{\frac{1}{\beta }}{2}}{\displaystyle \frac{{\wp }^{\prime }(z,g_2,g_3)+D}{\wp (z,g_2,g_3)-C}}+d_0.\hfill \end{array}\right.$$

(53)

Comparing the Laurent series of Equations (53) and (36), with substituting (53) into each side of Equation (3), and collecting similar terms, we have

$$\left\{\begin{array}{cc}A\hfill & ={\displaystyle \frac{1}{3}}{\beta }^2{d}_0^2-{\displaystyle \frac{4}{3}}\alpha \beta d_0+{\displaystyle \frac{2}{3}}{\alpha }^2\hfill \\ C\hfill & ={\displaystyle \frac{1}{3}}{\beta }^2{d}_0^2+{\displaystyle \frac{2}{3}}\alpha \beta d_0-{\displaystyle \frac{1}{3}}{\alpha }^2\hfill \\ B\hfill & =-{\displaystyle \frac{\alpha \left(4{\beta }^2{d}_0^2-8\alpha \beta d_0+3{\alpha }^2\right)}{4}}\hfill \\ D\hfill & ={\displaystyle \frac{\alpha \left(-4{\beta }^2{d}_0^2+{\alpha }^2\right)}{4}}\hfill \\ \theta \hfill & =-\alpha .\hfill \end{array}\right.$$

(54)

Then substituting (53) with (54) into each side of Equation (3), we have

$$\left\{\begin{array}{cc}{d}_0\hfill & ={\displaystyle \frac{\alpha }{2\beta }}\hfill \\ g_2\hfill & ={\displaystyle \frac{4}{3}}{\beta }^4{d}_0^4-{\displaystyle \frac{20}{3}}\alpha {\beta }^3{d}_0^3+{\displaystyle \frac{44}{3}}{\alpha }^2{\beta }^2{d}_0^2-{\displaystyle \frac{31}{3}}{\alpha }^3\beta d_0+{\displaystyle \frac{7}{3}}{\alpha }^4={\displaystyle \frac{{\alpha }^4}{12}}\hfill \\ g_3\hfill & =-{\displaystyle \frac{8}{27}}{\beta }^6{d}_0^6+{\displaystyle \frac{20}{9}}\alpha {\beta }^5{d}_0^5-5{\alpha }^2{\beta }^4{d}_0^4+{\displaystyle \frac{149}{27}}{\alpha }^3{\beta }^3{d}_0^3-{\displaystyle \frac{5}{2}}{\alpha }^4{\beta }^2{d}_0^2+{\displaystyle \frac{2}{9}}{\alpha }^5\beta d_0+{\displaystyle \frac{29}{432}}{\alpha }^6=-{\displaystyle \frac{{\alpha }^6}{216}}.\hfill \end{array}\right.$$

(55)

Therefore, we obtain the following elliptic function solution:

$$\left\{\begin{array}{cc}x\left(z\right)\hfill & ={\displaystyle \frac{{\wp }^{\prime }\left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)}{2\delta \left(\wp \left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)-\frac{{\alpha }^2}{12}\right)}}-{\displaystyle \frac{\alpha }{2\delta }}\hfill \\ y\left(z\right)\hfill & =-{\displaystyle \frac{{\wp }^{\prime }\left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)}{2\beta \left(\wp \left(z-z_0,\frac{{\alpha }^4}{12},-\frac{{\alpha }^6}{216}\right)-\frac{{\alpha }^2}{12}\right)}}+{\displaystyle \frac{\alpha }{2\beta }},\hfill \end{array}\right.$$

(56)

where $\theta =-\alpha$, and $z_0\in \mathbf{C}$ is arbitrary. If $\alpha =0$, (56) will degenerate to rational solution (40).

Remark 4.

If we substitute $y\left(z\right)=-{\displaystyle \frac{d_{-1}}{2}}{\displaystyle \frac{{\wp }^{\prime }(z,g_2,g_3)+D}{\wp (z,g_2,g_3)-C}}+d_0$ in Equation (21) directly, we can also obtain the elliptic solution (56).

Hence, the proof of Theorem 1 is complete.

5. Discussion and Limitations

5.1. Discussion

The proof of Theorem 1 is explained as follows:

(1)

One needs to transform the system of differential equation Equation (3) into a single complex ordinary differential equation; see Equation (21).

(2)

Taking the Painlevé test to compute the Fuchs indexes, the results show that Equation (21) has a non-negative integer Fuchs index $i=1$. This phenomenon causes Equation (21) not to meet the $\langle p,q\rangle$ condition. Therefore, we cannot be sure whether all non-constant meromorphic solutions of Equation (21) belong to class W. In Remark 1, we found that Equation (21) may have rational function solutions and transcendental meromorphic function solutions with infinitely many poles, but definitely does not have transcendental meromorphic function solutions with finite many poles because Equation (21) does not satisfy the finiteness property due to Equation (21) having a non-negative integer Fuchs index $i=1$. In conclusion, it fails to judge whether all meromorphic solutions of Equation (21) belong to class $\mathit{W}$. This characteristic is determined by Equation (21) itself.

(3)

From (2), we know that Equation (21) does not satisfy the conditions of Lemma 1. Another reason is $deg\left(-\beta y^{\prime }{y}^2+\alpha \theta y^2+\alpha y{y}^{\prime }+{\left(y^{\prime }\right)}^2-y{y}^{″}\right)=deg\left(\beta \theta y^3\right)$. But we can still find out the solutions of Equation (21) through the forms of elliptic functions, rational functions, and rational functions of $exp\left(\alpha z\right)$ in Lemma 1; see Section 4.3.

(4)

In Section 4.2, we prove that if $\beta \delta \ne 0$, Equation (3) does not have non-constant solutions $\left(x\right(z),y(z\left)\right)$ where $x\left(z\right),y\left(z\right)$ are both polynomials, or both transcendental entire functions with the same order, or one is a non-constant polynomial and another is a transcendental entire function, or one is a ploynomial and another is a transcendental meromorphic functions with at least one pole, or one is a transcendental entire function and another is a transcendental meromorphic functions with at least one pole. Nevertheless, if $\beta \delta =0$, two infinite order transcendental entire function solutions $y\left(z\right)$ in (32) and $x\left(z\right)$ in (34) have been found. The two solutions respond to the fact that Equation (21) has a non-negative integer Fuchs index $i=1$ and not all the solutions of Equation (21) belong to class $\mathit{W}$. Further, if $\beta \delta =0$, from Section 4.2.2, Section 4.2.3 and Section 4.2.4, we know Equation (3) does not have any non-constant solutions $\left(x\right(z),y(z\left)\right)$ where $x\left(z\right),y\left(z\right)$ are both transcendental meromorphic functions with at least one pole.

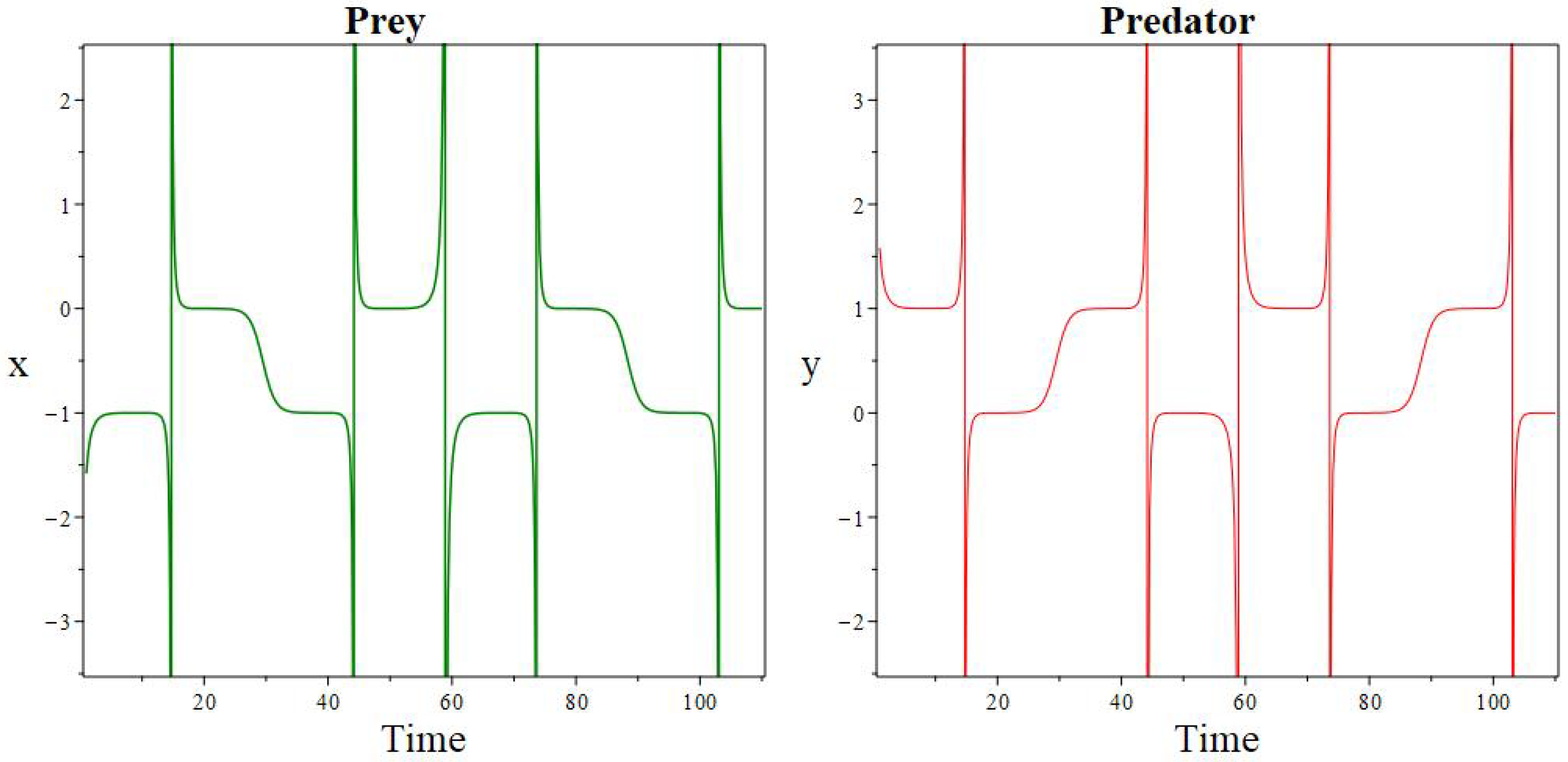
5.1.1. Plots

The plots of solution (56) with $\alpha =1,\delta =1,\beta =1$ was described in Figure 1.

5.1.2. Comparing

In [39], Varma gave an exponential function solution to the predator–prey model under the assumption of ${\alpha }_1={\alpha }_2$ as follows

$$\left\{\begin{array}{cc}\hfill & n_1={\displaystyle \frac{cexp\left(\alpha t\right)}{{\beta }_2+{\beta }_{1}exp\left[\frac{1}{\alpha }\{cexp\left(\alpha t\right)-k\}\right]}}\hfill \\ \hfill & n_2={\displaystyle \frac{cexp\left(\alpha t\right)}{{\beta }_1+{\beta }_{2}exp\left[-\frac{1}{\alpha }\{cexp\left(\alpha t\right)-k\}\right]}}.\hfill \end{array}\right.$$

(57)

Therefore, the exponential function solutions (30), (32), (34), (49) obtained in the current study is different from (57).

Consider the comparison of the method applied in article [44] and the extended complex method used in this article, we think that they both transform one system of differential equations into a single ordinary differential equation, and then carry out the Painlevé test. Both methods use the coefficient balance method. The main differences between the two articles are the following: article [44] does not consider the existence of transcendental entire function solutions to the Lotka–Volterra competition system with diffusion, and does not show the infinite order transcendental entire function solutions. In the current article, we find out the infinite order transcendental entire function solutions, which seem to be new compared to the opening literature we have read.

5.2. Limitations

Although there are many methods and algorithms for solving ordinary or partial differential equations, there is no unified approach to deal with all forms of differential equations. Therefore, the extended complex method must have its limitations. For example, (1) if $degP(w,w^{\prime },\dots ,w^{\left(m\right))})\ge n$ or Equation (8) does not satisfy the $\langle p,q\rangle$ condition, there is no guarantee that all non-constant meromorphic solutions of the ordinary differential equation belongs to class $\mathit{W}$; (2) it is difficult to use the indeterminant formula in Lemma 1 to obtain the infinite order transcendental entire function solutions directly; (3) the extended complex method has not been used in seeking exact solutions for other types of differential equations. Nevertheless, compared with the previous complex method [8], the extended complex method given in this article is more general because it can deal with differential equations such as the predator–prey model.

6. Conclusions and Future Research Directions

The extended complex method has been applied to investigate the meromorphic solutions to the predator–prey model. All the solutions mentioned in the theorem are verified using computational software. First, in the proof of Theorem 1, we rewrite the predator–prey model into one complex ordinary differential Equation (21), then apply the Painlevé analysis to obtain that there is a positive Fuchs index, and confirm that there exists a coefficient in the Laurent series (22) that is arbitrary. It indicated that Equation (21) (or Equation (3)) may have other types of solutions which are not included in the class $\mathit{W}$, such as the infinite order transcendental entire function solutions (32) and (34). Second, as far as we know, some of the constructed solutions seem to be new compared to the related open literature, such as the infinite order transcendental entire function solutions (32) and (34). These solutions potentially contribute to the understanding of the predator–prey models from the perspective of complex differential equations.

Inspired by the open problems posed in [27], we would like to pose the following problems for potential readers:

Problem 1.

Suppose that the positive integer $n\ge 2$. Study meromorphic solutions to the generalized higher-order predator–prey model:

$$\left\{\begin{array}{c}{x}^{\left(n\right)}\left(z\right)=\alpha x\left(z\right)-\beta x{\left(z\right)}^{(n-1)}y\left(z\right)\hfill \\ y^{\left(n\right)}\left(z\right)=\delta x\left(z\right)y{\left(z\right)}^{(n-1)}-\theta y\left(z\right),\hfill \end{array}\right.$$

(58)

where $\alpha ,\beta ,\delta ,\theta$ are positive constants, and the superscript $\left(n\right)$ indicates the n-th derivative.

Problem 2.

Study predator–prey models which is equipped with related influencing factors such as the Allee effect, fear effect, cannibalism, and immigration using the extended complex method.