A One-Phase Fractional Spatial Stefan Problem with Convective Specification at the Fixed Boundary
Abstract
1. Introduction
2. The Non-Fourier Caputo Model
2.1. Governing Equations
2.2. The Convective-Type Condition
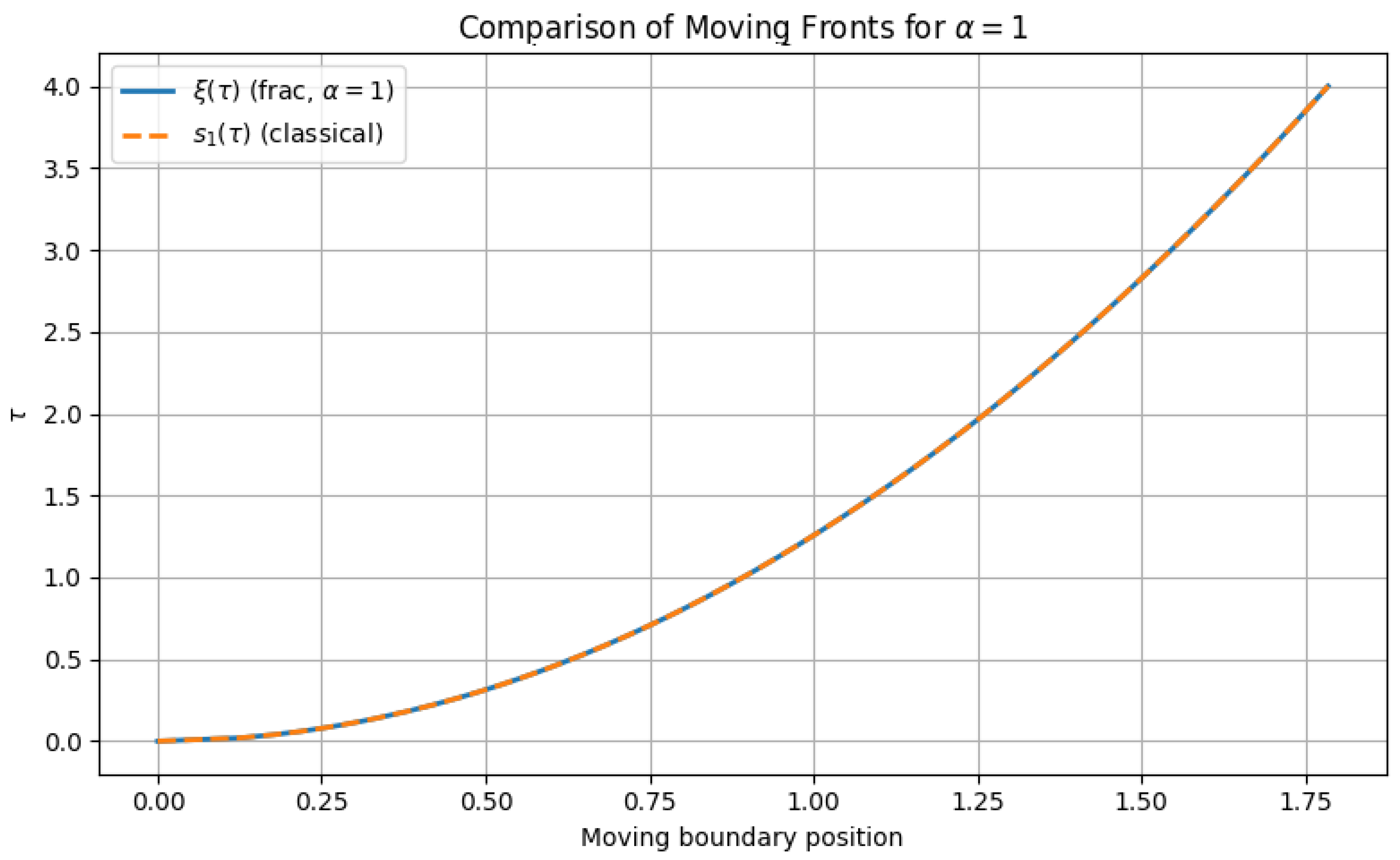
3. A Self-Similar Solution
4. Numerical Solutions and Computational Experiments
4.1. Dimensionless Form
4.2. Numerical Method
4.3. Model Analysis via Numerical Experiments
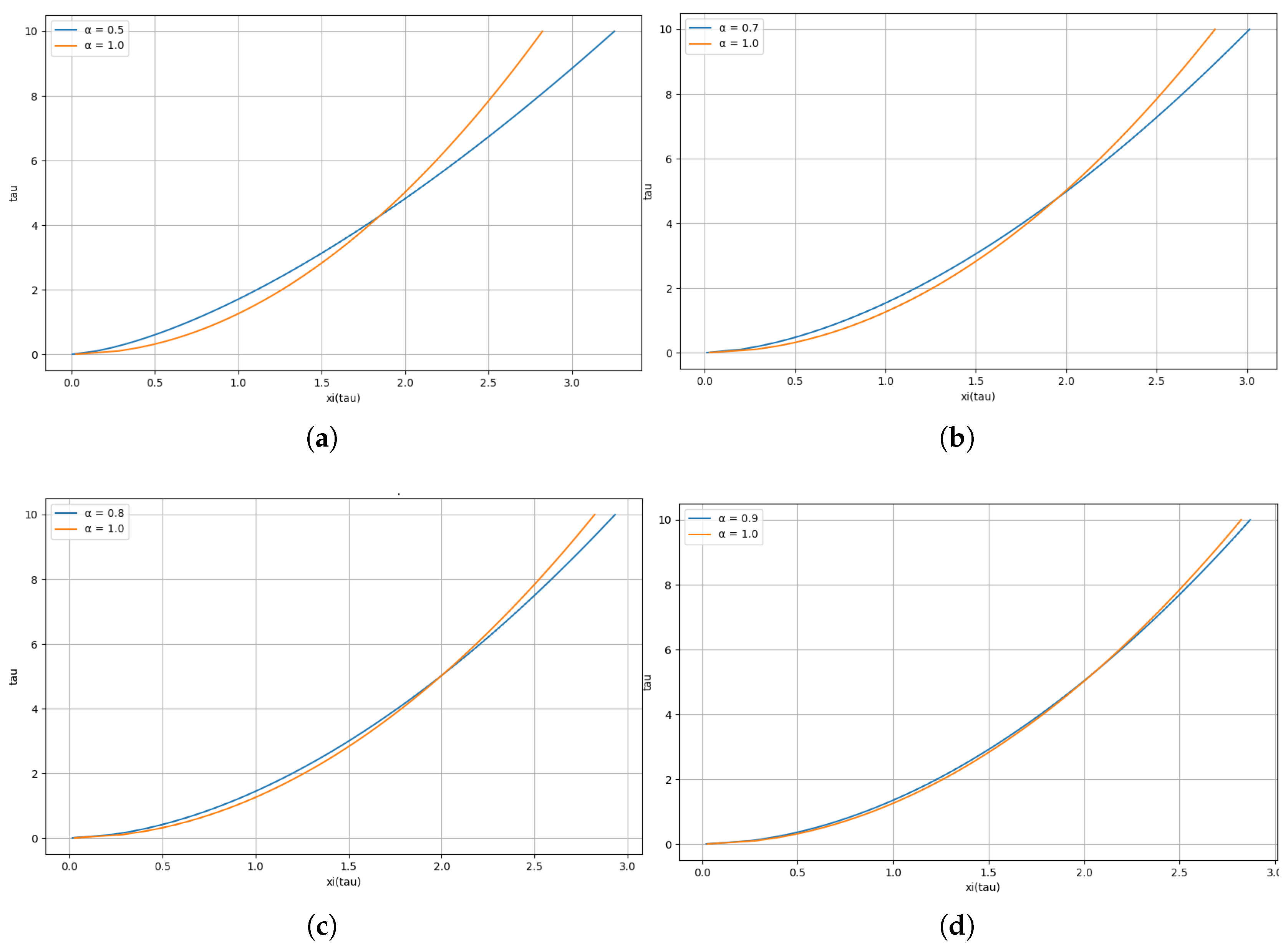
4.3.1. Variation in the Fractional Order
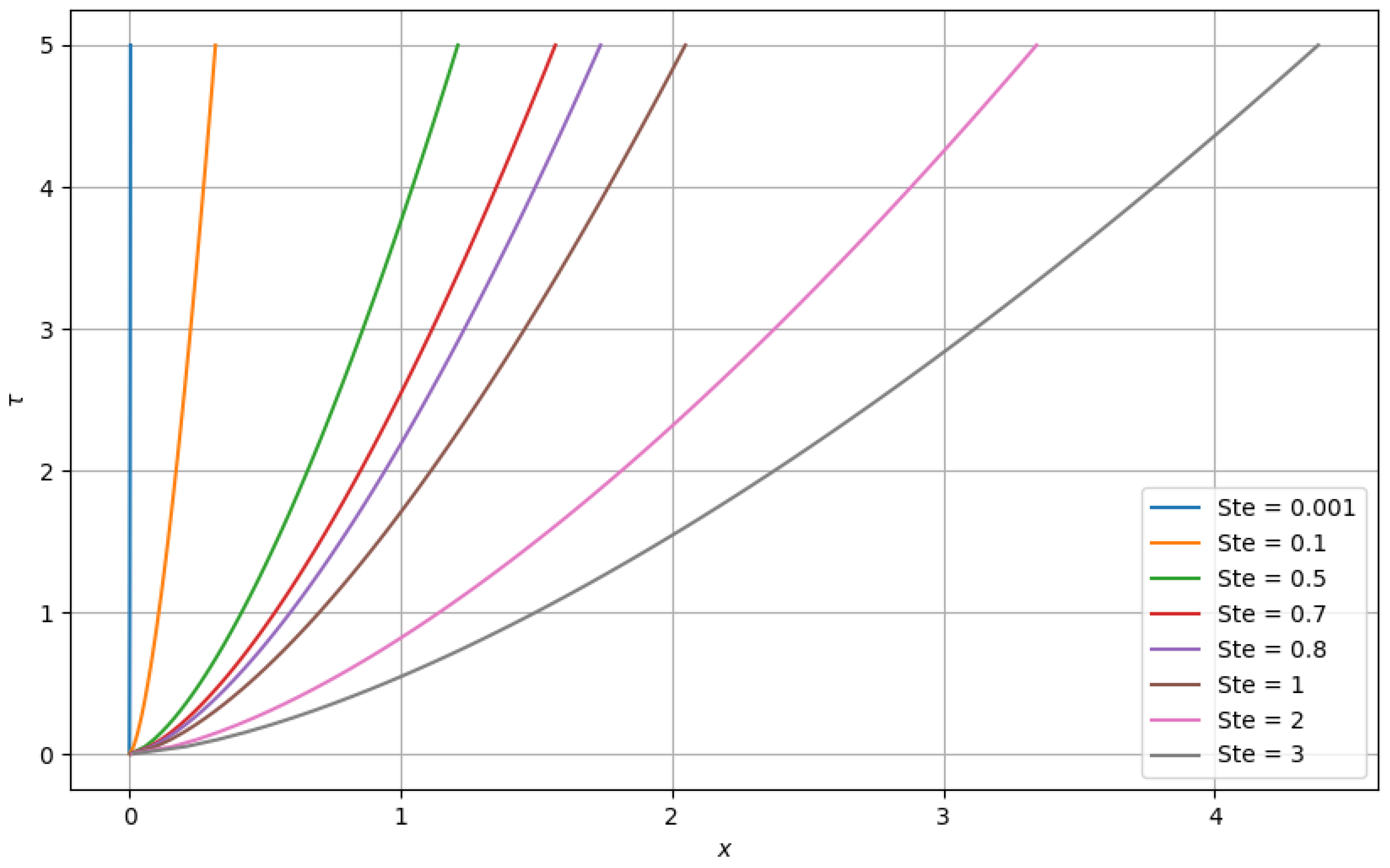
4.3.2. Variation in the Stefan Number
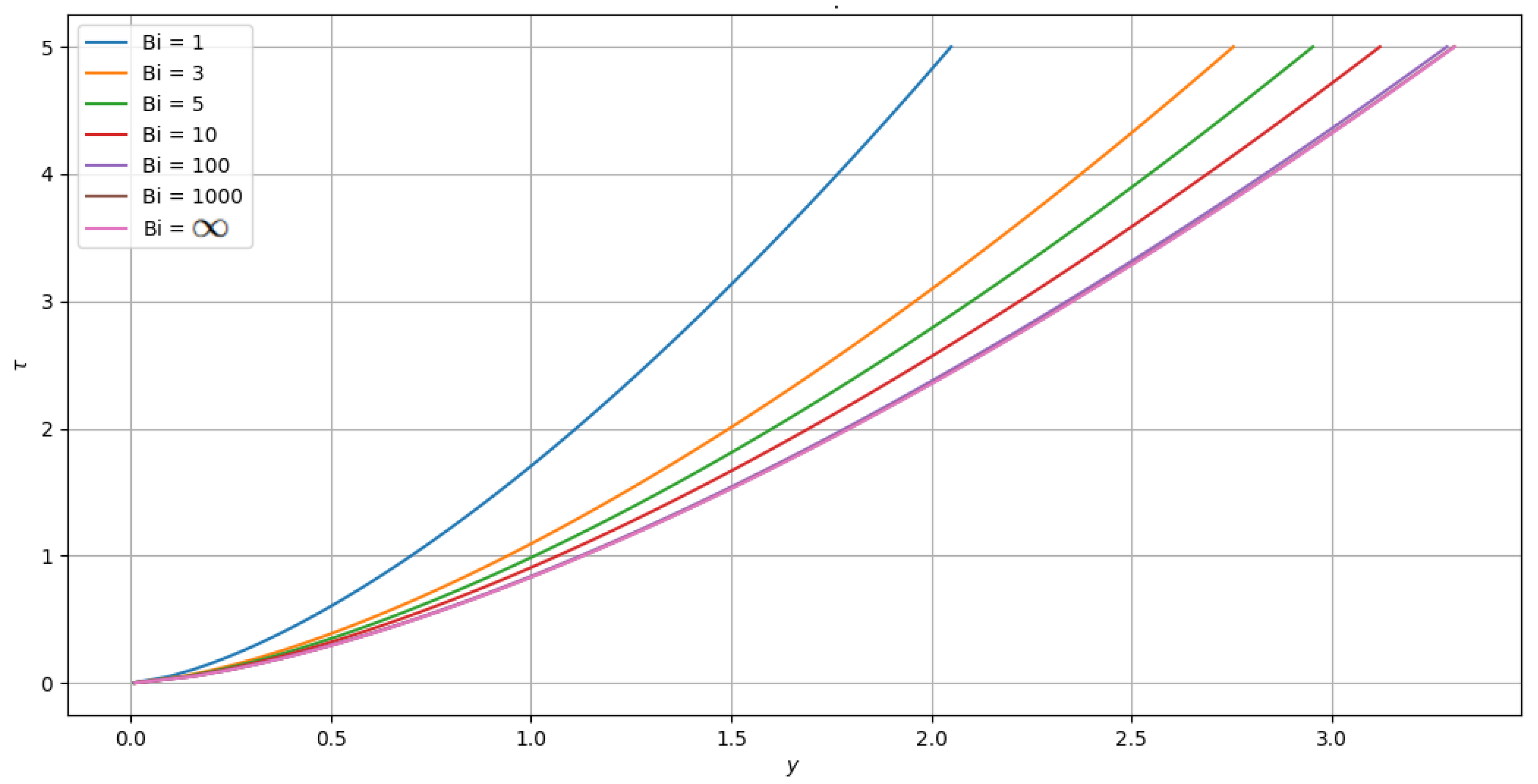
4.3.3. Variation in the Biot Number
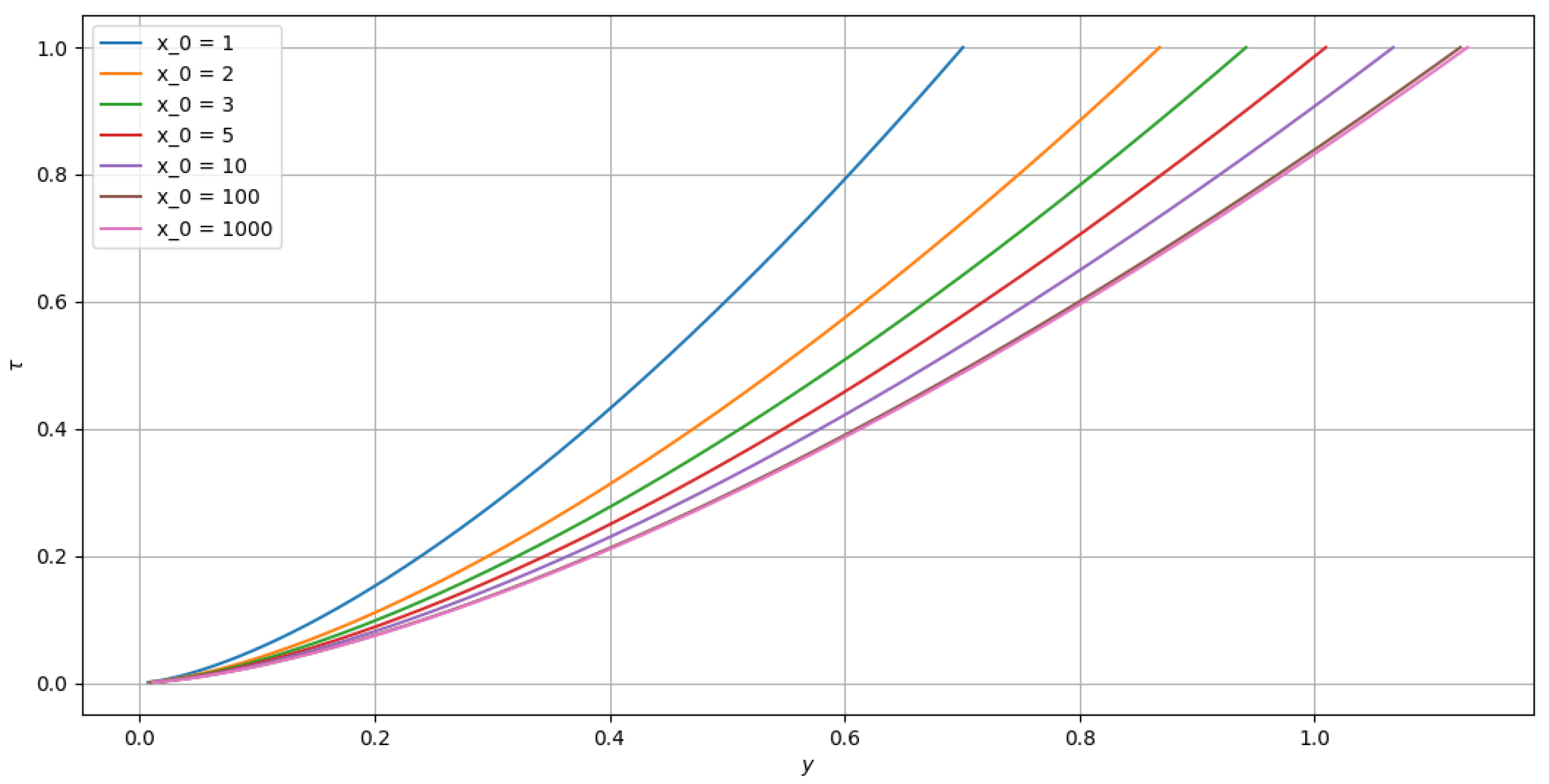
4.3.4. Some Comments on the Variation of the Characteristic Length
4.3.5. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- del Teso, F.; Endal, J.; Vázquez, J.L. The one-phase fractional Stefan problem. Math. Models Methods Appl. Sci. 2021, 31, 83–131. [Google Scholar]
- Voller, V.R. Fractional Stefan problems. Int. J. Heat Mass Transf. 2014, 74, 269–277. [Google Scholar] [CrossRef]
- Chugunov, V.; Fomin, S. Application of Fractional Differential Equations for Modeling Bacteria Migration in Porous Medium. Mathematics 2024, 12, 685. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Company: Singapore, 2000. [Google Scholar]
- Liu, F.; Yang, G.C. Rapid solidification of highly undercooled bulk liquid superalloy: Recent developments, future directions. Int. Mater. Rev. 2006, 51, 145–170. [Google Scholar] [CrossRef]
- Mainardi, F. Why the Mittag-Leffler Function Can Be Considered the Queen Function of the Fractional Calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef]
- Suzuki, A.; Fomin, S.; Chugunov, V.; Hashida, T. Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations. Water 2018, 10, 123. [Google Scholar] [CrossRef]
- Vázquez, L.; Trujillo, J.; Velasco, M. Fractional heat equation and the second law of thermodynamics. Fract. Calc. Appl. Anal. JCR 2011, 14, 334–342. [Google Scholar]
- Voller, V.R. Chapter Six-Anomalous Heat Transfer: Examples, Fundamentals, and Fractional Calculus Models. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2018; Volume 50, pp. 333–380. [Google Scholar] [CrossRef]
- Juric, D.; Tryggvason, G. A Front-Tracking Method for Dendritic Solidification. J. Comput. Phys. 1996, 123, 127–148. [Google Scholar] [CrossRef]
- Gruber, C.; Vogl, C.; Miksis, M.; Davis, S. Anomalous diffusion models in the presence of a moving interface. Interfaces Free. Boundaries 2013, 15, 181–202. [Google Scholar] [CrossRef]
- Voller, V.R. On a fractional derivative form of the Green–Ampt infiltration model. Adv. Water Resour. 2011, 34, 257–262. [Google Scholar] [CrossRef]
- Roscani, S.; Bollati, J.; Tarzia, D. A New Mathematical Formulation for a Phase Change Problem with a Memory Flux. Chaos Solitons Fractals 2018, 116, 340–347. [Google Scholar]
- Kubica, A.; Ryszewska, K. A self-similar solution to time-fractional Stefan problem. Math. Methods Appl. Sci. 2021, 44, 4245–4275. [Google Scholar] [CrossRef]
- Roscani, S.D.; Tarzia, D.A.; Venturato, L.D. The similarity method and explicit solutions for the fractional space one-phase Stefan problems. Fract. Calc. Appl. Anal. 2022, 25, 995–20220. [Google Scholar] [CrossRef]
- Guevara, D.; Venturato, L. Fractional Stefan Problem with Convective Boundary Condition: Python Implementation. 2025. Available online: https://zenodo.org/records/16373258 (accessed on 4 October 2025).
- Tarzia, D.A. Relationship Between Neumann Solutions for Two-Phase Lame-Clapeyron-Stefan with convective and temperature boundary conditions. Therm. Sci. 2017, 21, 187–197. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier Science Inc.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Kilbas, A.A.; Saigo, M. On Mittag-Leffler type function, fractional calculus operators and solutions of integral equations. Integral Transform. Spec. Funct. 1996, 4, 355–370. [Google Scholar] [CrossRef]
- Namba, T.; Rybka, P.; Sato, S. Special solutions to the space fractional diffusion problem. Fract. Calc. Appl. Anal. 2022, 25, 2139–2165. [Google Scholar] [CrossRef]
- Roscani, S.; Ryszewska, K.; Venturato, L. A One-Phase Space-Fractional Stefan Problem With No Liquid Initial Domain. SIAM J. Math. Anal. 2022, 54, 5489–5523. [Google Scholar] [CrossRef]
- Ryszewska, K. A space-fractional Stefan problem. Nonlinear Anal. 2020, 199, 112027. [Google Scholar] [CrossRef]
- Caruso, N.; Roscani, S.; Venturato, L.; Voller, V. On the Computation of the Prefactor of the Free Boundary in One Dimensional One-Phase Fractional Stefan Problems. Fractal Fract. 2025, 9, 397. [Google Scholar] [CrossRef]
- Gautschi, W. Some Elementary Inequalities Relating to the Gamma and Incomplete Gamma Function. J. Math. Phys. 1959, 38, 77–81. [Google Scholar] [CrossRef]
- Ziegler, F. The multiple meanings of the Stefan-number (and relatives) in refrigeration. Int. J. Refrig. 2010, 33, 1343–1349. [Google Scholar] [CrossRef]
- Solomon, A.D.; Alexiades, V.; Wilson, D.G. The Stefan problem with a convective boundary condition. Q. Appl. Math. 1982, 40, 203–217. [Google Scholar] [CrossRef][Green Version]

| Symbol | Definition | Dimension |
|---|---|---|
| u | Temperature | |
| x | Spatial position | |
| t | Time | |
| k | Thermal conductivity | |
| Mass density | ||
| c | Specific heat | |
| Diffusion coefficient | ||
| ℓ | Latent heat per unit mass | |
| h | Heat transfer coefficient | |
| Temporal constant for dimensional consistency | ||
| Spatial constant for dimensional consistency | ||
| Phase change temperature | ||
| Ambient temperature | ||
| Stefan number | ||
| Biot number |
| 0.5000 | 0.6000 | 0.7000 | 0.7500 | 0.8000 | 0.8500 | 0.9000 | 0.9500 | 1.0000 | |
| 0.700843 | 0.739294 | 0.777577 | 0.796692 | 0.815805 | 0.834926 | 0.854061 | 0.873218 | 0.892402 |
| 0.001 | 0.1 | 0.5 | 0.7 | 0.8 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|---|
| 0.50 | 0.00144 | 0.10853 | 0.41407 | 0.53696 | 0.59394 | 0.70084 | 1.14361 | 1.49870 |
| 0.60 | 0.00156 | 0.12075 | 0.44770 | 0.57424 | 0.63208 | 0.73929 | 1.16738 | 1.49522 |
| 0.70 | 0.00168 | 0.13302 | 0.48163 | 0.61163 | 0.67023 | 0.77758 | 1.19109 | 1.49332 |
| 0.80 | 0.00179 | 0.14530 | 0.51585 | 0.64916 | 0.70845 | 0.81581 | 1.21525 | 1.49392 |
| 0.90 | 0.00189 | 0.15757 | 0.55035 | 0.68684 | 0.74676 | 0.85406 | 1.24024 | 1.49767 |
| 1.00 | 0.00200 | 0.16980 | 0.58512 | 0.72468 | 0.78519 | 0.89240 | 1.26628 | 1.50492 |
| 0.001 | 0.1 | 0.5 | 0.7 | |
|---|---|---|---|---|
| 0.50 | 0.00144 | 0.10839 | 0.40752 | 0.52325 |
| 0.60 | 0.00156 | 0.12063 | 0.44117 | 0.56048 |
| 0.70 | 0.00168 | 0.13291 | 0.47527 | 0.59817 |
| 0.80 | 0.00179 | 0.14522 | 0.50978 | 0.63623 |
| 0.90 | 0.00189 | 0.15750 | 0.54464 | 0.67461 |
| 1.00 | 0.00200 | 0.16975 | 0.57980 | 0.71324 |
| 1 | 3 | 5 | 10 | 100 | 300 | 500 | 1000 | 10,000 | 100,000 | ∞ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.50 | 0.70084 | 0.94198 | 1.00988 | 1.06722 | 1.12443 | 1.12890 | 1.12980 | 1.13047 | 1.13108 | 1.13114 | 1.13115 |
| 0.60 | 0.73929 | 0.97453 | 1.03861 | 1.09201 | 1.14465 | 1.14874 | 1.14956 | 1.15018 | 1.15074 | 1.15079 | 1.15080 |
| 0.70 | 0.77758 | 1.00671 | 1.06719 | 1.11696 | 1.16547 | 1.16922 | 1.16997 | 1.17053 | 1.17104 | 1.17109 | 1.17110 |
| 0.80 | 0.81581 | 1.03892 | 1.09607 | 1.14256 | 1.18741 | 1.19085 | 1.19154 | 1.19206 | 1.19253 | 1.19257 | 1.19258 |
| 0.90 | 0.85406 | 1.07142 | 1.12555 | 1.16913 | 1.21077 | 1.21395 | 1.21459 | 1.21507 | 1.21550 | 1.21554 | 1.21555 |
| 1.00 | 0.89240 | 1.10438 | 1.15582 | 1.19683 | 1.23569 | 1.23864 | 1.23924 | 1.23968 | 1.24008 | 1.24012 | 1.24013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guevara, D.E.; Roscani, S.D.; Tarzia, D.A.; Venturato, L.D. A One-Phase Fractional Spatial Stefan Problem with Convective Specification at the Fixed Boundary. Axioms 2025, 14, 757. https://doi.org/10.3390/axioms14100757
Guevara DE, Roscani SD, Tarzia DA, Venturato LD. A One-Phase Fractional Spatial Stefan Problem with Convective Specification at the Fixed Boundary. Axioms. 2025; 14(10):757. https://doi.org/10.3390/axioms14100757
Chicago/Turabian StyleGuevara, Diego E., Sabrina D. Roscani, Domingo A. Tarzia, and Lucas D. Venturato. 2025. "A One-Phase Fractional Spatial Stefan Problem with Convective Specification at the Fixed Boundary" Axioms 14, no. 10: 757. https://doi.org/10.3390/axioms14100757
APA StyleGuevara, D. E., Roscani, S. D., Tarzia, D. A., & Venturato, L. D. (2025). A One-Phase Fractional Spatial Stefan Problem with Convective Specification at the Fixed Boundary. Axioms, 14(10), 757. https://doi.org/10.3390/axioms14100757






