Integrating Proper Orthogonal Decomposition with the Crank–Nicolson Finite Element Method for Efficient Solutions of the Schrödinger Equation

Abstract

This study proposes a dimensionality reduction method based on proper orthogonal decomposition (POD) for numerically solving the Schrödinger equation by optimizing the coefficient vectors of the Crank–Nicolson finite element (CNFE) solution. The fully discrete CNFE scheme is derived from the Schrödinger equation, with the stability and convergence of the CNFE solution rigorously established. Utilizing the POD technology, POD basis functions are constructed and a reduced-dimension model is formulated. The uniqueness and unconditional stability are proved, and the error estimate of the reduced-dimension solution is derived. With a $100\times 100$ spatial grid, the reduced-dimension CNFE (RDCNFE) method employing POD technology reduces the degrees of freedom each time step from ${101}^2$ to 6. Numerical results show that for each additional second of simulation time, the CPU runtime of the standard CNFE method increases by several seconds, while the RDCNFE method increase remains below one second. This demonstrates that the reduced-dimension method significantly enhances computational efficiency for the Schrödinger equation while preserving numerical accuracy.

1. Introduction

This paper develops the Crank–Nicolson finite element and its POD-based reduced-dimension methods for solving the linear Schrödinger equation, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle \mathit{i}\frac{\partial u}{\partial t}-\Delta u(\mathit{x},t)+u(\mathit{x},t)=f(\mathit{x},t),}\hfill & (\mathit{x},t)\in \Omega \times J,\hfill \\ u(\mathit{x},t)=0,\hfill & (\mathit{x},t)\in \partial \Omega \times \overline{J},\hfill \\ u(\mathit{x},0)=u_0\left(\mathit{x}\right),\hfill & \mathit{x}\in \Omega .\hfill \end{array}\right.\end{array}$$

(1)

Here, $\mathit{i}=\sqrt{-1}$ denotes the imaginary unit. $\Omega \subset {\mathbb{R}}^d(d=1,2,3)$ represents a bounded convex polygonal domain. Its boundary is denoted by $\partial \Omega$. The temporal domain is $J=(0,T]$$(0<T<\infty )$, $f(\mathit{x},t)$ is a given source term, and $u_0\left(\mathit{x}\right)$ is known initial function.

By taking the inner products of Equation (1) with u and ${\displaystyle \frac{\partial u}{\partial t}}$, and subsequently extracting the imaginary and real parts, the two conservation laws are established, as outlined:

$$\begin{array}{c}Q\left(t\right)=\parallel u(:,t)\parallel =\parallel u_0\parallel =Q\left(0\right),\\ E\left(t\right)={\parallel u(:,t)\parallel }_{H^1}={\parallel u_0\parallel }_{H^1}=E\left(0\right).\end{array}$$

(2)

The Schrödinger equation, as a special form of the parabolic partial differential equation, strictly governs the spatiotemporal evolution law of the wave function of microscopic particles by introducing the imaginary unit i. This equation originated from the fundamental theory of quantum mechanics and was widely used in theoretical physics, nuclear physics, plasma physics, electromagnetic wave theory, quantum chemistry, optoelectronics, and seismology.

In recent years, the numerical research of the Schrödinger equation has made remarkable progress. In [1], Liu et al. extended the $H^1$-Galerkin mixed finite element model to the one-dimensional Schrödinger equation, yielding optimal-order convergence analyses for both discrete schemes. In [2], in order to study the nonlinear Schrödinger problem, Henning and Peterseim successfully applied the implicit Crank–Nicolson finite element scheme, deriving a corresponding error estimate. Notably, their approach eliminates the need for a mesh ratio condition. Employing bilinear finite element method, Shi et al. [3,4] analyzed the nonlinear Schrödinger equation, obtaining superapproximation property and proving superconvergence results for Crank–Nicolson fully-discrete formulations. Subsequently, Shi et al. [5] proposed a novel and stable mixed finite element format $(P1+P0\times P0)$. The optimal error estimates were obtained for the original variables in the $L^2$ and $H^1$ norm and for the flux variables in the $L^2$ norm. In [6], the 2D nonlinear Schrödinger equation was solved by employing the two-grid finite element technique. This approach utilized coarse-grid solutions as initial approximations, and the fully discrete system was linearized through single-step Newton iterations applied at the fine grid. The rigorous error analysis for the scheme was provided. Theoretical research showed that the spatial grid size relationship $H=O(h^{{\displaystyle \frac{1}{2}}})$ in the two-grid scheme is satisfied, and asymptotic optimal approximation can be achieved without losing accuracy. In [7], Hu further developed an enhanced two-grid numerical method, eliminating time-step restrictions and the mesh size ratio. This framework derived optimal $L^p$ and $H^1$ error estimates for the two-grid solutions. Hu et al. [8] devised an error analysis framework, integrating Newton iterations with Crank–Nicolson finite element discretization to study the nonlinear Schrödinger equation. The results showed that the Newton iterative solutions can uniformly converge to the implicit Crank–Nicolson solutions at a double exponential rate (relative to the number of iterations) at all time grids, and the theoretical optimal convergence orders were achieved in both the spatial and temporal dimensions. For the 2D time-dependent Schröinger problem, Tian et al. [9,10,11] proposed the two-grid mixed finite element semi- and fully- discrete methods. They established the convergence properties, and further derived error estimates for the two-grid solutions under these two distinct discrete schemes.

In this paper, the Schrödinger Equation (1) is solved by employing the Crank–Nicolson finite element fully discrete scheme. However, in traditional finite element schemes, high degrees of freedom reduce computational efficiency. We introduce the proper orthogonal decomposition (POD) technique, showing that the reduced-dimension model building significantly reduces the dimensions of the system and maintains accuracy at the same time, effectively improves computational efficiency, and reduces the accumulation of round-off error.

At present, there are mainly two methods based on the POD finite element dimension reduction model. The first method is to reduce the dimensions of the finite element space by constructing a reduced-dimension optimization model. The POD bases are generated using snapshot, then the full-order finite element space is replaced with the reduced-order POD space. This method is applied to the parabolic equations [12], the Sobolev equations [13], the Burgers equations [14], and so on. In 2020, Luo et al. [15,16] developed a novel method for dimensionality reduction in the finite element solution coefficient vectors. This method uses the POD-based solution vectors to replace the original solution vectors. The basis functions are unchanged throughout this process. The dimensionality reduction technique based on POD demonstrates remarkable efficiency in minimizing the computational complexity of finite element analysis through substantial reduction of degrees of freedom. Luo et al. applied this method to solve various PDEs, including parabolic equations [15,17,18], hyperbolic equations [16], and fractional Tricomi equations [19]. Based on this framework, they employed POD techniques to construct a dimensionality reduction model for the mixed finite element solution coefficient vectors. This model was subsequently employed to study diverse mathematical problems, such as the nonlinear Rosenau equations [20], the unsteady Stokes equations [21], and unsaturated flow problems [22]. Furthermore, Luo and Yang extended this method by integrating the reduced-dimension technology with the space-time finite element format, enabling the study of unsteady incompressible Navier–Stokes equations [23].

At present, the research on numerically solving the Schrödinger equation using the reduced-order model is still relatively limited. In the existing work, Li et al. [24] applied POD to construct a reduced-order finite difference scheme for a 1D Schrödinger equation. They derived the error estimates and conducted numerical experiments to compare it with the standard finite difference method. It has been confirmed that it has the superiority of maintaining numerical accuracy while reducing the computational cost. However, a critical limition exists in the development of efficient and rigorously analyzed reduced-order models for multi-dimensional quantum systems, particularly those leveraging high-order spatial discretizations like the finite element method. Furthermore, the extensive work on intrusive POD-Galerkin methods for parabolic and hyperbolic PDEs [12,13,14,15,16,17,18,19,20,21,22,23] has not been adequately explored in the context of the Schrödinger equation. This paper proposes a novel numerical framework for the Schrödinger equation by integrating the CNFE scheme with the POD technique applied to the solution coefficient vectors, which is a powerful method originally developed by Luo et al. [15,16,17,18,19,20,21,22,23] for other PDEs. To the best of our knowledge, this study represents the first application and rigorous analysis of this specific technique to the Schrödinger equation. The complex-valued nature and conservation properties of the Schrödinger equation present distinct challenges that are thoroughly addressed in this work. Numerical experiments demonstrate that the proposed method achieves a significant reduction in CPU runtime, by nearly an order of magnitude in long-time simulations, while maintaining accuracy comparable to the full-order CNFE method. This approach provides an efficient and reliable reduced-order model that is especially promising for long-term numerical simulations of quantum systems.

Sections are arranged as follows. Section 2 provides the necessary preliminaries for this paper. Section 3 establishes the CNFE fully discrete scheme, analyzes the stability of the CNFE solution, and obtains the error estimate of the optimal convergence order under the $L^2$ norm. In Section 4, the snapshot matrix is constructed using the CNFE solution coefficient vectors, POD bases are generated, and the reduced-dimension discrete scheme is constructed. The uniqueness and stability are proved, and the error estimate of reduced-dimension solution is derived. Section 5 compares the computational efficiency and accuracy before and after dimensionality reduction through numerical experiments. Section 6 provides conclusions, limitations, and prospects.

2. Preliminaries

This section presents commonly used Sobolev spaces and norm definitions, Green formulas and Gronwall lemmas [25,26], and the basic theory of POD [27].

2.1. Sobolev Spaces and Required Lemmas

Definition 1.

Let m be an integer and $1⩽p⩽+\infty$ be a real number, then the Sobolev space $W^{m,p}(\Omega )$ is defined as

$$W^{m,p}(\Omega )=\{u\in L^p(\Omega );\left|\alpha \right|⩽m,D^{\alpha }u\in L^p(\Omega )\}.$$

Here, $L^p(\Omega )=\{u;{\int }_{\Omega }{\left|u\right|}^{p}dx<+\infty \}$. The corresponding norm is defined as

$${\parallel u\parallel }_{L^p}={\parallel u\parallel }_{p,\Omega }=({\int }_{\Omega }{\left|u\right|}^{p}dx{)}^{{\displaystyle \frac{1}{p}}}.$$

In particular, when $p=2$, we denote ${\parallel u\parallel }_{2,\Omega }=\parallel u\parallel$, and when $m=0$, we have $W^{0,p}(\Omega )=L^p(\Omega )$.

Definition 2.

The norm on the space $W^{m,p}(\Omega )$ is defined as follows.

• (1) When $1\le p<+\infty$,

  $${\parallel u\parallel }_{m,p,\Omega }={\left(\sum _{\left|\alpha \right|\le m}{\int }_{\Omega }{\left|D^{\alpha }u\right|}^{p}dx\right)}^{{\displaystyle \frac{1}{p}}}.$$

When $p=2$, the space $W^{m,2}(\Omega )$ is denoted as $H^m(\Omega )$, and the corresponding norm is written as ${\parallel u\parallel }_{m,2,\Omega }={\parallel u\parallel }_m$. In particular, when $m=0$ and $p=2$, the space $H^0(\Omega )=L^2(\Omega )$, and the corresponding norm is ${\parallel u\parallel }_{0,2,\Omega }={\parallel u\parallel }_0=\parallel u\parallel$.

• (2) When $p=+\infty$,

  $${\parallel u\parallel }_{m,\infty ,\Omega }=\underset{\left|\alpha \right|\le m}{sup}\underset{x\in \Omega }{ess\; sup}\left|D^{\alpha }u\right|.$$

When $m=0$, we denote ${\parallel u\parallel }_{0,\infty ,\Omega }={\parallel u\parallel }_{\infty }$.

Lemma 1.

Green’s Formula: For $u\in H^2(\Omega )$ and $v\in H^1(\Omega )$, the following identity holds:

$${\int }_{\Omega }v\Delta ud\mathit{x}=-{\int }_{\Omega }\nabla u·\nabla vd\mathit{x}+{\int }_{\partial \Omega }v{\displaystyle \frac{\partial u}{\partial \overrightarrow{n}}}ds,$$

where $\overrightarrow{n}$ is the unit outward normal vector on $\partial \Omega$, $\nabla u$ denotes the gradient of u, and ${\displaystyle \Delta =\sum _{i=1}^n\frac{{\partial }^2}{\partial {\mathit{x}}_i^2}}$.

Lemma 2.

Discrete Gronwall Inequality: Let $\left\{{\varphi }_n\right\}$ and $\left\{a_n\right\}$ be nonnegative sequences, with $\left\{a_n\right\}$ being non-decreasing. Suppose

$${\varphi }_n\le a_0,{\varphi }_n\le a_n+\sum _{j=0}^{n-1}{\omega }_j{\varphi }_j,n\ge 1,$$

where ${\omega }_j\ge 0$. Then,

$${\displaystyle {\varphi }_n\le e^{{\sum }_{j=0}^{n-1}{\omega }_j}{a}_n,n\ge 1.}$$

2.2. The Basic Theory of POD

First, the coefficient vectors of the CNFE solution for the first Q time steps, denoted by ${\mathit{\omega }}^n$$(n=1,2,\dots ,Q)$, are taken as snapshots to construct the snapshot matrix:

$$\mathit{A}={\left(\begin{array}{cccc}{\omega }_1^1& {\omega }_1^2& \dots & {\omega }_1^Q\\ {\omega }_2^1& {\omega }_2^2& \dots & {\omega }_2^Q\\ ⋮& ⋮& \ddots & ⋮\\ {\omega }_M^1& {\omega }_M^2& \dots & {\omega }_M^Q\end{array}\right)}_{M\times Q}.$$

(3)

Let $l=\mathrm{rank}\left(\mathit{A}\right)$. Performing the singular value decomposition, the snapshot matrix $\mathit{A}$ is factorized as follows:

$$\mathit{A}=\mathit{U}\left(\begin{array}{cc}\sum _{l\times l}& {\mathit{O}}_{l\times (Q-l)}\\ {\mathit{O}}_{(M-l)\times l}& {\mathit{O}}_{(M-l)\times (Q-l)}\end{array}\right){\mathit{V}}^T.$$

(4)

Here, the diagonal matrix ${\Sigma }_{l\times l}=\mathrm{diag}\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_l\}$ consists of the singular values of matrix $\mathit{A}$ arranged in descending order ${\sigma }_1⩾{\sigma }_2⩾\dots ⩾{\sigma }_l>0$. The matrix $\mathit{U}=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_M)$ is an $M\times M$ orthogonal matrix composed of the orthogonal eigenvectors of ${\mathbf{AA}}^T$. The matrix $\mathit{V}=({\mathit{\psi }}_1,{\mathit{\psi }}_2,\dots ,{\mathit{\psi }}_Q)$ is a $Q\times Q$ orthogonal matrix formed by the orthogonal eigenvectors of ${\mathit{A}}^T\mathit{A}$. $\mathit{O}$ denotes a zero matrix.

Let

$${\mathit{A}}_q=\mathit{U}\left(\begin{array}{cc}\sum _{q\times q}& {\mathit{O}}_{q\times (Q-q)}\\ {\mathit{O}}_{(M-q)\times q}& {\mathit{O}}_{(M-q)\times (Q-q)}\end{array}\right){\mathit{V}}^T.$$

(5)

Here, ${\Sigma }_{q\times q}=\mathrm{diag}\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_q\}$ is a diagonal matrix composed of the first q positive singular values from the diagonal matrix ${\Sigma }_{l\times l}$ of $\mathit{A}$.

The following lemma is required in this paper, and its detailed proof can be found in references [27].

Lemma 3.

Let $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_q)$, which consists of the first q eigenvectors of $\mathit{U}=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_M)$, then

$${\mathit{A}}_{\mathbf{q}}=\sum _{i=1}^q{\sigma }_i{\mathit{\phi }}_i{\mathit{\psi }}_i^T=\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{A}.$$

(6)

For the matrix $\mathit{A}$, the following matrix norms are defined.

Definition 3.

The norm ${\parallel ·\parallel }_2$ of the matrix $\mathbf{A}$ induced by the norm ${\displaystyle {\parallel \mathit{u}\parallel }_2=\sqrt{\sum _{i=1}^M{\left|u_i\right|}^2}}$ for the vector $\mathit{u}={(u_1,u_2,\dots ,u_M)}^T$ is defined as follows

$${\parallel \mathbf{A}\parallel }_2=\underset{\mathit{u}\in {\mathbb{R}}^M}{sup}{\displaystyle \frac{{\parallel \mathit{Au}\parallel }_2}{{\parallel \mathit{u}\parallel }_2}}.$$

From the relationship between the matrix norm and its spectral radius, it is straightforward to obtain that

$$\begin{array}{c}\hfill \underset{\mathrm{rank}\left(\mathit{B}\right)⩽q}{min}{∥\mathit{A}-\mathit{B}∥}_2={∥\mathit{A}-{\mathit{A}}_q∥}_2={∥\mathit{A}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{A}∥}_2=\sqrt{{\mu }_{q+1}},\end{array}$$

(7)

where $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_q)$ consists of the first q eigenvectors of $\mathit{U}=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_M)$, and $\sqrt{{\mu }_{q+1}}={\sigma }_{q+1}$. If the Q column vectors of $\mathit{A}$ are represented by ${\mathit{\omega }}^n={({\omega }_1^n,{\omega }_2^n,\dots ,{\omega }_M^n)}^T$$(n=1,2,\dots ,Q)$, we obtain

$$\begin{array}{c}∥{\mathit{\omega }}^n-{\mathit{\omega }}_q^n∥={∥(\mathit{A}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{A}){\mathit{e}}^n∥}_2⩽∥\mathit{A}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{A}∥∥{\mathit{e}}^n∥=\sqrt{{\mu }_{q+1}},n=1,2,\dots ,Q,\hfill \end{array}$$

(8)

where ${\displaystyle {\mathit{\omega }}_q^n=\sum _{j=1}^q({\mathit{\phi }}_j,{\mathit{\omega }}^n){\mathit{\phi }}_j}$ represents the projection of ${\mathit{\omega }}^n$ onto $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_q)$, $({\mathit{\phi }}_j,{\mathit{\omega }}^n)$ denotes the inner product of ${\mathit{\phi }}_j$ and ${\mathit{\omega }}^n$, and ${\mathit{e}}^n$ denotes the unit vector with the n-th component equal to 1. Inequality (8) indicates that ${\mathit{\omega }}_q^n$ is the optimal approximation of ${\mathit{\omega }}^n$, with an error bounded by $\sqrt{{\mu }_{q+1}}$.

3. The Crank–Nicolson Finite Element Method of the Schrödinger Equation

This section details the numerical solution of the Schrödinger equation via the Crank–Nicolson finite element method. We first establish the weak formulation and CNFE full discrete scheme. Subsequently, we rigorously analyze the stability and convergence of the scheme. Finally, we derive the matrix formulation of the finite element system. This formulation facilitates computational implementation and serves as the basis for constructing the reduced-dimension model.

3.1. The CNFE Scheme

We use the Sobolev spaces and norms under the standard definition [25]. For the complex-valued function $v=v_1+\mathit{i}{v}_2$, let

$$\begin{array}{c}{\parallel v\parallel }_{m,p}=(\parallel v_1{\parallel }_{m,p}^p+\parallel v_2{{\parallel }_{m,p}^p)}^{{\displaystyle \frac{1}{p}}},\\ {\parallel v\parallel }_{m,\infty }=\parallel v_1{\parallel }_{m,\infty }+{\parallel v_2\parallel }_{m,\infty }.\end{array}$$

(9)

Let $V=H_0^1(\Omega )$. The weak formulation of (1) can be derived using Green’s formula.

Problem 1.

Find $u\in V$ that satisfies

$${\displaystyle \mathit{i}(\frac{\partial u}{\partial t},\chi )+(\nabla u,\nabla \chi )+(u,\chi )=(f,\chi ),\forall \chi \in V.}$$

(10)

Let ${\Im }_h$ represent the quasi-uniform rectangular subdivision on $\overline{\Omega }$, with each division unit denoted as $\mathbb{K}$ and division diameter denoted as $h_{\mathbb{K}}$. $h=\underset{\mathbb{K}\in {\Im }_h}{max}{h}_{\mathbb{K}}$. The following FE subspace $V_h$ is constructed from the orthonormal basis ${\left\{{\zeta }_j\left(x\right)\right\}}_{j=1}^M$ in $L^2(\Omega )$ inner product space:

$$\begin{array}{c}{V}_h=\{v_h\in V\cap C(\Omega );v_h{\mid }_{\mathbb{K}}\in P_{M-1}\left(\mathbb{K}\right),\mathbb{K}\in \Im \}=\mathrm{span}\{{\zeta }_j\left(\mathit{x}\right):1⩽j⩽M\}.\hfill \end{array}$$

(11)

Here, $P_{M-1}\left(\mathbb{K}\right)$ is the space of $(M-1)$th degree polynomial functions on $\mathbb{K}\in {\Im }_h$.

For an integer $N>0$, define $\Delta t=T/N$, ${\mathit{\psi }}^n=\mathit{\psi }\left(t_n\right)$, ${\overline{\partial }}_t{\mathit{\psi }}^n=({\mathit{\psi }}^n-{\mathit{\psi }}^{n-1})/\Delta t$ and ${\mathit{\psi }}^{n-{\displaystyle \frac{1}{2}}}=({\mathit{\psi }}^n+{\mathit{\psi }}^{n-1})/2$. Let $u_h^n$ be the CNFE approximation of the weak solution u at $t_n=n\Delta t$ for Problem 1. Consequently, the CNFE scheme for this problem can be established.

Problem 2.

Find $u_h^n\in V_h(1⩽n⩽N)$ that satisfies

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \mathit{i}({\overline{\partial }}_t{u}_h^n,{\chi }_h)+(\nabla u_h^{n-\frac{1}{2}},\nabla {\chi }_h)+(u_h^{n-\frac{1}{2}},{\chi }_h)=(f^{n-\frac{1}{2}},{\chi }_h),\forall {\chi }_h\in V_h,}\hfill \\ u_h(\mathit{x},0)=u_h^0\left(\mathit{x}\right),\mathit{x}\in \Omega .\hfill \end{array}\right.\end{array}$$

(12)

3.2. The Stability and Convergence of the CNFE Solution

Theorem 1.

Let $N>1$, $u_h^n\in V_h(1⩽n⩽N)$ be any solution to the full discrete CNFE scheme:

$$(u_h^n-u_h^{n-1},{\chi }_h)-\Delta t\mathit{i}(\nabla u_h^{n-{\displaystyle \frac{1}{2}}},\nabla {\chi }_h)-\Delta t\mathit{i}(u_h^{n-{\displaystyle \frac{1}{2}}},{\chi }_h)=-\Delta t\mathit{i}(f^{n-{\displaystyle \frac{1}{2}}},{\chi }_h),\forall {\chi }_h\in V_h.$$

(13)

Then, there exist $\Delta t<\Delta t_0$ such that the CNFE scheme (12) has a unique solution, and the solution remains uniformly bounded in $L^2(\Omega )$ with

$$\parallel u_h^N{\parallel }_{L^2(\Omega )}^2⩽e^4\left(\parallel u_h^0{\parallel }_{L^2(\Omega )}^2+T\sum _{n=1}^N\Delta t{\parallel f^{n-{\displaystyle \frac{1}{2}}}\parallel }_{L^2(\Omega )}^2\right).$$

(14)

Proof of Theorem 1.

Let $u_{1,h}$ and $u_{2,h}$ be any two solutions satisfying (12); then, there is

$${\displaystyle \mathit{i}({\overline{\partial }}_t(u_{1,h}^n-u_{2,h}^n),{\chi }_h)+(\nabla (u_{1,h}^{n-\frac{1}{2}}-u_{2,h}^{n-\frac{1}{2}}),\nabla {\chi }_h)+((u_{1,h}^{n-\frac{1}{2}}-u_{2,h}^{n-\frac{1}{2}}),{\chi }_h)=0.}$$

(15)

Let $e_h=u_{1,h}-u_{2,h}$, set ${\chi }_h=e_h^{n-{\displaystyle \frac{1}{2}}}$ in (15) and take its imaginary part to obtain

$${\displaystyle \frac{\parallel e_h^n{\parallel }^2-{\parallel e_h^{n-1}\parallel }^2}{2\Delta t}}=0,$$

(16)

so

$$\parallel e_h^n{\parallel }^2=\parallel e_h^{n-1}{\parallel }^2=\dots ={\parallel e_h^0\parallel }^2=0.$$

(17)

In (15), let ${\chi }_h={\overline{\partial }}_t{e}_h^n$, and take the real part to obtain

$${\displaystyle \frac{\parallel \nabla e_h^n{\parallel }^2-{\parallel \nabla e_h^{n-1}\parallel }^2}{2\Delta t}}+{\displaystyle \frac{\parallel e_h^n{\parallel }^2-{\parallel e_h^{n-1}\parallel }^2}{2\Delta t}}=0,$$

(18)

so we have

$$\parallel e_h^n{\parallel }_1^2=\parallel e_h^{n-1}{\parallel }_1^2=\dots ={\parallel e_h^0\parallel }_1^2=0.$$

(19)

From (17) and (19), it can be obtained that $e_h=u_{1,h}-u_{2,h}=0$. Therefore, (12) has a unique solution.

Testing (13) with ${\chi }_h=u_h^{n-{\displaystyle \frac{1}{2}}}$ and taking the real part, we obtain

$$\begin{array}{cc}\parallel u_h^n{\parallel }^2-{\parallel u_h^{n-1}\parallel }^2\hfill & =-\Delta tIm(f^{n-{\displaystyle \frac{1}{2}}},u_h^n+u_h^{n-1})\hfill \\ \hfill & {\displaystyle ⩽\frac{T}{2}\Delta t\parallel f^{n-\frac{1}{2}}{\parallel }^2+\frac{\Delta t}{T}\parallel u_h^n{\parallel }^2+\frac{\Delta t}{T}{\parallel u_h^{n-1}\parallel }^2.}\hfill \end{array}$$

(20)

Hence,

$$\begin{array}{cc}\parallel u_h^n{\parallel }^2\hfill & {\displaystyle ⩽\left(1+\frac{2\Delta t}{T-\Delta t}\right)\parallel u_h^{n-1}{\parallel }^2+\frac{1}{2}\frac{\Delta t}{T-\Delta t}{T}^2{\parallel f^{n-\frac{1}{2}}\parallel }^2}\hfill \\ \hfill & {\displaystyle ⩽\dots ⩽\left(1+\frac{2\Delta t}{T-\Delta t}\right)\parallel u_h^0{\parallel }^2+\frac{1}{2}\frac{\Delta t}{T-\Delta t}{T}^2\sum _{i=1}^n{\parallel f^{i-\frac{1}{2}}\parallel }^2.}\hfill \end{array}$$

(21)

Applying this iteratively yields

$$\begin{array}{cc}\parallel u_h^N{\parallel }^2\hfill & {\displaystyle ⩽e^{{\sum }_{n=1}^N\frac{2\Delta t}{T-\Delta t}}\left(\parallel u_h^0{\parallel }^2+\frac{1}{2}\frac{\Delta t}{T-\Delta t}{T}^2\sum _{n=1}^N{\parallel f^{n-\frac{1}{2}}\parallel }^2\right)}\hfill \\ \hfill & {\displaystyle ⩽e^4\left(\parallel u_h^0{\parallel }^2+T\sum _{n=1}^N\Delta t{\parallel f^{n-\frac{1}{2}}\parallel }^2\right).}\hfill \end{array}$$

(22)

□

Lemma 4.

The solution $u_h^n$ of Problem 2 is consistent with the following conservation laws:

$$\begin{array}{c}{Q}^n=\parallel u_h^n\parallel =\parallel u_h^{n-1}\parallel =\dots =\parallel u_h^0\parallel ,\hfill \\ E^n=\parallel u_h^n{\parallel }_1^2=\parallel u_h^{n-1}{\parallel }_1^2=\dots ={\parallel u_h^0\parallel }_1^2.\hfill \end{array}$$

(23)

Proof of Lemma 4.

We compute the inner product of (12) with $u_h^{n-{\displaystyle \frac{1}{2}}}$, set $f=0$, and then take the imaginary part to obtain

$$({\overline{\partial }}_t{u}_h^n,u_h^{n-{\displaystyle \frac{1}{2}}})={\displaystyle \frac{\parallel u_h^n{\parallel }^2-{\parallel u_h^{n-1}\parallel }^2}{2\Delta t}}=0.$$

(24)

So, we have $Q^n=\parallel u_h^n\parallel =\parallel u_h^{n-1}\parallel =\dots =\parallel u_h^0\parallel$.

We compute the inner product of (12) with ${\overline{\partial }}_t{u}_h^n$, set $f=0$, and then take the real part to obtain

$$Re(\nabla u_h^{n-{\displaystyle \frac{1}{2}}},\nabla {\overline{\partial }}_t{u}_h^n)+Re(u_h^{n-{\displaystyle \frac{1}{2}}},{\overline{\partial }}_t{u}_h^n)=0,$$

(25)

that is,

$${\displaystyle \frac{\parallel \nabla u_h^n{\parallel }^2-{\parallel \nabla u_h^{n-1}\parallel }^2}{2\Delta t}}+{\displaystyle \frac{\parallel u_h^n{\parallel }^2-{\parallel u_h^{n-1}\parallel }^2}{2\Delta t}}=0.$$

(26)

Letting

$$E^n=\parallel \nabla u_h^n{\parallel }^2+\parallel u_h^n{\parallel }^2={\parallel u_h^n\parallel }_1^2,$$

(27)

we can obtain

$$E^n=\parallel u_h^n{\parallel }_1^2=\parallel u_h^{n-1}{\parallel }_1^2=\dots ={\parallel u_h^0\parallel }_1^2.$$

(28)

□

Convergence analysis of the CNFE scheme requires defining the projection operator $P_h$.

Lemma 5.

[2] The projection operator $P_h:V\to V_h$ is defined as

$$(\nabla (u-P_{h}u),\nabla {\chi }_h)=0,\forall {\chi }_h\in V_h,$$

(29)

with the following error estimates:

$$\parallel u-P_h{u\parallel }_{L^2(\Omega )}+h\parallel \nabla (u-P_{h}u){\parallel }_{L^2(\Omega )}⩽C{h}^2{\parallel u\parallel }_{H^2(\Omega )},$$

(30)

$$\parallel {\displaystyle \frac{\partial (u-P_{h}u)}{\partial t}}{\parallel }_{L^2(\Omega )}+h\parallel \nabla {\displaystyle \frac{\partial (u-P_{h}u)}{\partial t}}{\parallel }_{L^2(\Omega )}⩽C{h}^2\parallel {\displaystyle \frac{\partial u}{\partial t}}{\parallel }_{H^2(\Omega )},$$

(31)

$$\parallel {\displaystyle \frac{{\partial }^2(u-P_{h}u)}{\partial t^2}}{\parallel }_{L^2(\Omega )}⩽C{h}^2\parallel {\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}{\parallel }_{H^2(\Omega )}.$$

(32)

Theorem 2.

With $u_h^0=P_h{u}^0$, if the CNFE solution $u_h^n$ of the Problem 2 satisfies the regularity condition $u\in H^2(\Omega )$, ${\displaystyle \frac{\partial u}{\partial t}\in L^2(0,T;H^2(\Omega ))}$ and ${\displaystyle \frac{{\partial }^{3}u}{\partial t^3}\in L^2(0,T;L^2(\Omega ))}$; then, for $1⩽J⩽N$,

$$\begin{array}{c}\parallel u\left(t_J\right)-u_h^J\parallel ⩽C(h^2+{(\Delta t)}^2),\hfill \end{array}$$

(33)

with $C>0$ independent of h and $\Delta t$.

Proof of Theorem 2.

Subtracting (12) from (10) by taking $t=t^{n-{\displaystyle \frac{1}{2}}}$, and then using (29), the error equation is derived as

$$\mathit{i}\left({\displaystyle \frac{\partial u^{n-\frac{1}{2}}}{\partial t}}-{\overline{\partial }}_t{u}_h^n,{\chi }_h\right)+(\nabla (P_h{u}^{n-{\displaystyle \frac{1}{2}}}-u_h^{n-{\displaystyle \frac{1}{2}}}),\nabla {\chi }_h)+(u^{n-{\displaystyle \frac{1}{2}}}-u_h^{n-{\displaystyle \frac{1}{2}}},{\chi }_h)=0.$$

(34)

Letting $u^n-u_h^n=u^n-P_h{u}^n+P_h{u}^n-u_h^n={\eta }^n+{\rho }^n$, we rewrite (34) as

$${\displaystyle \mathit{i}({\overline{\partial }}_t{\rho }^n,{\chi }_h)+(\nabla {\rho }^{n-\frac{1}{2}},\nabla {\chi }_h)+({\rho }^{n-\frac{1}{2}},{\chi }_h)=-\mathit{i}\left(\frac{\partial u^{n-\frac{1}{2}}}{\partial t}-{\overline{\partial }}_t{u}^n,{\chi }_h\right)-\mathit{i}({\overline{\partial }}_t{\eta }^n,{\chi }_h)-({\eta }^{n-\frac{1}{2}},{\chi }_h).}$$

(35)

Choosing ${\chi }_h={\rho }^{n-{\displaystyle \frac{1}{2}}}$ in (35) and extracting the imaginary part, we have

$${\displaystyle \frac{{\parallel \rho \parallel }^n-{\parallel \rho \parallel }^{n-1}}{2\Delta t}}=(F1+F2+F3,{\rho }^{n-{\displaystyle \frac{1}{2}}}).$$

(36)

For the right-hand side of (36), each term can be bounded, as follows:

$$|(F1,{\rho }^{n-{\displaystyle \frac{1}{2}}})|=Re\left({\displaystyle \frac{\partial u^{n-\frac{1}{2}}}{\partial t}}-{\overline{\partial }}_t{u}^n,{\rho }^{n-{\displaystyle \frac{1}{2}}}\right)⩽C{(\Delta t)}^3{\int }_{t_{n-1}}^{t_n}\parallel {\displaystyle \frac{{\partial }^{3}u}{\partial t^3}}{\parallel }^{2}ds+{\parallel {\rho }^{n-{\displaystyle \frac{1}{2}}}\parallel }^2,$$

(37)

$${\displaystyle |(F2,{\rho }^{n-\frac{1}{2}})|=Re({\overline{\partial }}_t{\eta }^n,{\rho }^{n-\frac{1}{2}})=Re\left(\frac{{\eta }^n-{\eta }^{n-1}}{\Delta t},{\rho }^{n-\frac{1}{2}}\right)⩽C\frac{1}{\Delta t}{\int }_{t_{n-1}}^{t_n}\parallel \frac{\partial \eta }{\partial t}{\parallel }^{2}ds+{\parallel {\rho }^{n-\frac{1}{2}}\parallel }^2,}$$

(38)

$$|(F3,{\rho }^{n-{\displaystyle \frac{1}{2}}})|=Im({\eta }^{n-{\displaystyle \frac{1}{2}}},{\rho }^{n-{\displaystyle \frac{1}{2}}})⩽C\parallel {\eta }^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+\parallel {\rho }^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2⩽C{h}^4{\parallel u\parallel }_{H^2(\Omega )}^2+{\parallel {\rho }^{n-{\displaystyle \frac{1}{2}}}\parallel }^2.$$

(39)

Then, from (37)–(39), we have

$$\begin{array}{cc}{\displaystyle \frac{\parallel {\rho }^n{\parallel }^2-{\parallel {\rho }^{n-1}\parallel }^2}{2\Delta t}⩽}\hfill & {\displaystyle C({(\Delta t)}^3\parallel \frac{{\partial }^{3}u}{\partial t^3}{\parallel }_{L^2(t_{n-1},t_n;L^2(\Omega ))}^2+\frac{1}{\Delta t}{h}^4\parallel \frac{\partial u}{\partial t}{\parallel }_{L^2(t_{n-1},t_n;H^2(\Omega ))}^2}\hfill \\ \hfill & {\displaystyle +h^4{\parallel u\parallel }_{H^2(\Omega )}^2+\parallel {\rho }^n{\parallel }^2+{\parallel {\rho }^{n-1}\parallel }^2).}\hfill \end{array}$$

(40)

Multiplying by $2\Delta t$ on both sides of (40) and summing over $n=1,\dots ,J$, while considering that ${\rho }^0=P_h{u}^0-u_h^0=0$ yields

$$\parallel {\rho }^J{\parallel }^2⩽C\left({(\Delta t)}^4\parallel {\displaystyle \frac{{\partial }^{3}u}{\partial t^3}}{\parallel }_{L^2(0,T;L^2(\Omega ))}^2+h^4\parallel {\displaystyle \frac{\partial u}{\partial t}}{\parallel }_{L^2(0,T;H^2(\Omega ))}^2+h^4{\parallel u\parallel }_{H^2(\Omega )}^2\right)+C\Delta t\sum _{n=1}^J{\parallel {\rho }^n\parallel }^2.$$

(41)

Applying Gronwall’s inequality for sufficiently small $\Delta t$ yields

$$\parallel {\rho }^J{\parallel }^2⩽C(h^4+{(\Delta t)}^4).$$

(42)

Integrating Lemma 5 with (42) and employing the triangle inequality, we have

$$\parallel u\left(t_J\right)-u_h^J\parallel =\parallel {\eta }^J+{\rho }^J\parallel ⩽C(h^2+{(\Delta t)}^2).$$

(43)

Similar to (35), we obtain

$$\begin{array}{cc}\hfill & \mathit{i}({\overline{\partial }}_t{\rho }^{n+1},{\chi }_h)+(\nabla {\rho }^{n+{\displaystyle \frac{1}{2}}},\nabla {\chi }_h)+({\rho }^{n+{\displaystyle \frac{1}{2}}},{\chi }_h)\hfill \\ =\hfill & {\displaystyle -\mathit{i}\left(\frac{\partial u^{n+\frac{1}{2}}}{\partial t}-{\overline{\partial }}_t{u}^{n+1},{\chi }_h\right)-\mathit{i}({\overline{\partial }}_t{\eta }^{n+1},{\chi }_h)-({\eta }^{n+\frac{1}{2}},{\chi }_h).}\hfill \end{array}$$

(44)

Subtracting (35) from (44), then dividing by $\Delta t$, and letting $z^n={\overline{\partial }}_t{\rho }^n$, we have

$$\begin{array}{cc}\hfill & \mathit{i}({\overline{\partial }}_t{z}^{n+1},{\chi }_h)+(\nabla z^{n+{\displaystyle \frac{1}{2}}},\nabla {\chi }_h)+(z^{n+{\displaystyle \frac{1}{2}}},{\chi }_h)\hfill \\ =\hfill & {\displaystyle -\mathit{i}\frac{1}{\Delta t}\left(\left(\frac{\partial u^{n+\frac{1}{2}}}{\partial t}-{\overline{\partial }}_t{u}^{n+1},{\chi }_h\right)-\left(\frac{\partial u^{n-\frac{1}{2}}}{\partial t}-{\overline{\partial }}_t{u}^n,{\chi }_h\right)\right)-\mathit{i}({\overline{\partial }}_t^2{\eta }^n,{\chi }_h)-({\overline{\partial }}_t{\eta }^{n+\frac{1}{2}},{\chi }_h).}\hfill \end{array}$$

(45)

Letting ${\chi }_h=z^{n+{\displaystyle \frac{1}{2}}}$ in (45), and taking the imaginary part, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\parallel z^{n+1}{\parallel }^2-{\parallel z^n\parallel }^2}{2\Delta t}}\hfill \\ ⩽\hfill & {\displaystyle C({(\Delta t)}^3{\int }_{t_n}^{t_{n+1}}\parallel \frac{{\partial }^{3}u}{\partial t^3}{\parallel }^{2}ds+{(\Delta t)}^3{\int }_{t_{n-1}}^{t_n}\parallel \frac{{\partial }^{3}u}{\partial t^3}{\parallel }^{2}ds+\frac{1}{\Delta t}{\int }_{t_{n-1}}^{t_{n+1}}\parallel \frac{{\partial }^2\eta }{\partial t^2}{\parallel }^{2}ds}\hfill \\ \hfill & {\displaystyle +\frac{1}{\Delta t}{\int }_{t_{n-\frac{1}{2}}}^{t_{n+\frac{1}{2}}}\parallel \frac{\partial \eta }{\partial t}{\parallel }^{2}ds+\parallel z^{n+1}{\parallel }^2+{\parallel z^n\parallel }^2).}\hfill \end{array}$$

(46)

Multiplying by $2\Delta t$ on both sides of (46) and summing over $n=1,\dots ,J$, we obtain

$${\displaystyle \parallel z^{J+1}{\parallel }^2⩽\parallel z^1{\parallel }^2+C\left({(\Delta t)}^4\parallel \frac{{\partial }^{3}u}{\partial t^3}{\parallel }_{L^2(0,T;L^2(\Omega ))}^2+\parallel \frac{{\partial }^2\eta }{\partial t^2}{\parallel }_{L^2(0,T;L^2(\Omega ))}^2+\parallel \frac{\partial \eta }{\partial t}{\parallel }_{L^2(0,T;L^2(\Omega ))}^2\right)+C\Delta t\sum _{n=1}^{J+1}{\parallel z^n\parallel }^2.}$$

(47)

Using the Gronwall’s inequality, we have

$${\displaystyle \parallel {\overline{\partial }}_t{\rho }^n\parallel =\parallel z^n\parallel ⩽C\left({(\Delta t)}^2\parallel \frac{{\partial }^{3}u}{\partial t^3}{\parallel }_{L^2(0,T;L^2(\Omega ))}^2+h^2\left(\parallel \frac{{\partial }^{2}u}{\partial t^2}{\parallel }_{L^2(0,T;H^2(\Omega ))}^2+\parallel \frac{\partial u}{\partial t}{\parallel }_{L^2(0,T;H^2(\Omega ))}^2\right)\right)⩽C({(\Delta t)}^2+h^2).}$$

(48)

Choosing ${\chi }_h={\overline{\partial }}_t{\rho }^n$ and taking the real part for (35), we obtain

$${\displaystyle \frac{\parallel \nabla {\rho }^n{\parallel }^2-{\parallel \nabla {\rho }^{n-1}\parallel }^2}{2\Delta t}}+{\displaystyle \frac{\parallel {\rho }^n{\parallel }^2-{\parallel {\rho }^{n-1}\parallel }^2}{2\Delta t}}=(N_1+N_2+N_3,{\overline{\partial }}_t{\rho }^n).$$

(49)

For the right-hand side of (49), we bound each term as follows:

$$|(N1,{\overline{\partial }}_t{\rho }^n)|=Im\left({\displaystyle \frac{\partial u^{n-\frac{1}{2}}}{\partial t}}-{\overline{\partial }}_t{u}^n,{\overline{\partial }}_t{\rho }^n\right)⩽C{(\Delta t)}^3{\int }_{t_{n-1}}^{t_n}\parallel {\displaystyle \frac{{\partial }^{3}u}{\partial t^3}}{\parallel }^{2}ds+{\parallel {\overline{\partial }}_t{\rho }^n\parallel }^2,$$

(50)

$$|(N2,{\overline{\partial }}_t{\rho }^n)|=Im({\overline{\partial }}_t{\eta }^n,{\overline{\partial }}_t{\rho }^n)⩽C{\displaystyle \frac{1}{\Delta t}}{\int }_{t_{n-1}}^{t_n}\parallel {\displaystyle \frac{\partial \eta }{\partial t}}{\parallel }^{2}ds+{\parallel {\overline{\partial }}_t{\rho }^n\parallel }^2,$$

(51)

$$|(N3,{\overline{\partial }}_t{\rho }^n)|=Re({\eta }^{n-{\displaystyle \frac{1}{2}}},{\overline{\partial }}_t{\rho }^n)⩽C\parallel {\eta }^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+\parallel {\overline{\partial }}_t{\rho }^n{\parallel }^2⩽C{h}^4{\parallel u\parallel }_{H^2(\Omega )}^2+{\parallel {\overline{\partial }}_t{\rho }^n\parallel }^2.$$

(52)

Then, from (49)–(52), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\parallel \nabla {\rho }^n{\parallel }^2-{\parallel \nabla {\rho }^{n-1}\parallel }^2}{2\Delta t}+\frac{\parallel {\rho }^n{\parallel }^2-{\parallel {\rho }^{n-1}\parallel }^2}{2\Delta t}}\hfill \\ ⩽\hfill & {\displaystyle C{(\Delta t)}^3{\int }_{t_{n-1}}^{t_n}\parallel \frac{{\partial }^{3}u}{\partial t^3}{\parallel }^{2}ds+C\frac{1}{\Delta t}{\int }_{t_{n-1}}^{t_n}\parallel \frac{\partial \eta }{\partial t}{\parallel }^{2}ds+C{h}^4{\parallel u\parallel }_{H^2(\Omega )}^2+{\parallel {\overline{\partial }}_t{\rho }^n\parallel }^2.}\hfill \end{array}$$

(53)

Multiplying by $2\Delta t$ on both sides of (53) and summing over $n=1,\dots ,J$, we obtain

$$\parallel \nabla {\rho }^J{\parallel }^2+{\parallel {\rho }^J\parallel }^2⩽C(h^4+{(\Delta t)}^4).$$

(54)

From (43) and (54), we obtain (33).

□

The CNFE solution $u_h^n$ to Problem 2 can be represented employing the basis functions of $V_h$, as follows:

$$\begin{array}{c}{\displaystyle u_h^n=\sum _{j=1}^M{U}_{hj}^n{\zeta }_j=\mathit{\zeta }·{\mathit{U}}_h^n,}\hfill \end{array}$$

(55)

where basis vector $\mathit{\zeta }=({\zeta }_1,{\zeta }_2,\dots ,{\zeta }_M)$ is orthonormal, satisfying

$$({\zeta }_i,{\zeta }_j)={\delta }_{ij},i,j=1,2,\dots ,M.$$

${\mathit{U}}_h^n={(U_{h1}^n,U_{h2}^n,\dots ,U_{hM}^n)}^T$ is the unknown coefficient vectors of CNFE solution.

Based on the FE solution $u_h^n$ expressed from (55), we can reformulate Problem 2 as the matrix form equivalently.

Problem 3.

Find ${\mathit{U}}_h^n\in {\mathbb{R}}^M$ and $u_h^n\in V_h(1⩽n⩽N)$ satisfying

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \mathit{i}{\overline{\partial }}_t{\mathit{U}}_h^n+\mathit{B}{\mathit{U}}_h^{n-\frac{1}{2}}+{\mathit{U}}_h^{n-\frac{1}{2}}={\mathit{F}}^{n-\frac{1}{2}},}\hfill \\ {\displaystyle u_h^n=\sum _{j=1}^M{U}_{hj}^n{\zeta }_j={\mathit{U}}_h^n·\zeta ,}\hfill \end{array}\right.\end{array}$$

(56)

where

$$\mathit{B}={\left(b_{ij}\right)}_{1⩽i,j⩽M},b_{ij}=(\nabla {\zeta }_j,\nabla {\zeta }_i),$$

and

$${\displaystyle {\mathit{F}}^{n-\frac{1}{2}}={((f^{n-\frac{1}{2}},{\zeta }_1),(f^{n-\frac{1}{2}},{\zeta }_2),\dots ,(f^{n-\frac{1}{2}},{\zeta }_M))}^T.}$$

4. The Reduced-Dimension Crank–Nicolson Finite Element Method of the Schrödinger Equation

This section presents a reduced-dimension modeling framework using POD for the Schrödinger equation. First, the snapshot matrix generated by solving the CNFE scheme is used to generate the POD basis. The basis is then employed to construct a reduced-dimension model. Finally, we rigorously analyze the uniqueness, stability, and error estimates of the reduced-order solution to establish its theoretical reliability.

4.1. Constructing POD Bases

Firstly, a $M\times Q$ snapshot matrix $\mathit{A}=({\mathit{U}}_h^1,{\mathit{U}}_h^2,\dots ,{\mathit{U}}_h^Q)$ is generated by solving Problem 3 and obtaining the first Q-step CNFE solution vectors ${\mathit{U}}_h^n$$(n=1,2,\dots ,Q)$. Next, the positive eigenvalues of $\mathit{A}{\mathit{A}}^T$ are computed, arranging them in descending order as ${\mu }_1⩾{\mu }_2⩾\dots ⩾{\mu }_r>0$ , where $r=\mathrm{rank}\left(\mathit{A}\right)$. The associated eigenvectors are then used to form the matrix $\tilde{\mathbf{\Phi }}=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_r)\in {\mathbb{R}}^{M\times r}$. Subsequently, we construct the POD bases $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_q)$$(q⩽r)$ by selecting the first q columns of $\tilde{\mathbf{\Phi }}$. These bases satisfy the equality as follows:

$$\parallel \mathit{A}-\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{A}\parallel }_2=\sqrt{{\mu }_{q+1}},$$

(57)

where ${\displaystyle {\parallel \mathit{A}\parallel }_2=\underset{\mathit{v}\in {\mathbb{R}}^M}{\sup }\frac{\parallel \mathit{A}\mathit{v}\parallel }{\parallel \mathit{v}\parallel }}$, and ${\displaystyle \parallel \mathit{v}\parallel =\sqrt{\sum _{i=1}^M{\left|v_i\right|}^2}}$ represents the norm of the vector $\mathit{v}={(v_1,v_2,\dots ,v_M)}^T$.

For $n=1,2,\dots ,Q$, it satisfies that

$$\parallel {\mathit{U}}_h^n-\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}_h^n\parallel =\parallel (\mathit{A}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{A}){\mathit{e}}^n\parallel ⩽\parallel (\mathit{A}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{A}){\parallel }_2\parallel {\mathit{e}}^n\parallel ⩽\sqrt{{\mu }_{q+1}}.$$

(58)

Here, ${\mathit{e}}^n(1⩽n⩽Q)$ denotes the unit vectors. Therefore, $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_q)$$(q⩽r)$ is an optimal set of POD bases.

Remark 1.

Given that the dimension $M\times M$ of $\mathit{A}{\mathit{A}}^T$ drastically exceeds the dimension $Q\times Q$ of ${\mathit{A}}^T\mathit{A}$, and considering both matrices share identical non-zero eigenvalues, we initially compute the first q eigenvalues ${\mu }_j(1⩽j⩽q)$ of matrix ${\mathit{A}}^T\mathit{A}$ and eigenvectors ${\mathit{\varphi }}_j(1⩽j⩽q)$. The POD bases $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_q)(q⩽r)$ are then generated using the relation ${\mathit{\phi }}_j=\mathit{A}{\mathit{\varphi }}_j/\sqrt{{\mu }_j}(1⩽j⩽q)$.

Remark 2.

The number of snapshots is a critical parameter in constructing the POD bases, as it must sufficiently capture the dominant dynamics of the system. If too few snapshots are used, the POD bases may be incomplete, thereby reducing the accuracy of the reduced-dimension model. Conversely, an excessive number of snapshots may introduce redundant information, increasing offline computational costs without significantly improving model accuracy. Therefore, in the numerical experiments of this study, we set the number of snapshots to $Q=20$ to balance computational efficiency and model accuracy.

4.2. Formulating the RDCNFE Scheme

First, setting ${\mathit{\alpha }}_q^n={({\alpha }_1^n,{\alpha }_2^n,\dots ,{\alpha }_q^n)}^T$, and ${\mathit{U}}_q^n={(U_{q1}^n,U_{q2}^n,\dots ,U_{qM}^n)}^T$ denotes the coefficient vector of RDCNFE solution. Next, directly compute the first Q RDCNFE solution vector by the relation ${\mathit{U}}_q^n=\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}_h^n=:\mathbf{\Phi }{\mathit{\alpha }}_q^n(1⩽n⩽Q)$ from Section 4.1. Finally, the following matrix-based RDCNFE scheme is established by substituting ${\mathit{U}}_h^n$ of Problem 3 with ${\mathit{U}}_q^n=\mathbf{\Phi }{\mathit{\alpha }}_q^n(Q+1⩽n⩽N)$.

Problem 4.

Find ${\mathit{U}}_q^n\in {\mathbb{R}}^M$ and $u_q^n\in V_h(1⩽n⩽N)$ that satisfy

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & {\mathit{\alpha }}_q^n={\mathbf{\Phi }}^T{\mathit{U}}_h^n,1⩽n⩽Q,\hfill \\ \hfill & \mathit{i}\mathbf{\Phi }{\overline{\partial }}_t{\mathit{\alpha }}_q^n+\mathit{B}\mathbf{\Phi }{\mathit{\alpha }}_q^{n-{\displaystyle \frac{1}{2}}}+\mathbf{\Phi }{\mathit{\alpha }}_q^{n-{\displaystyle \frac{1}{2}}}={\mathbf{F}}^{n-{\displaystyle \frac{1}{2}}},Q+1⩽n⩽N,\hfill \\ \hfill & {\displaystyle u_q^n=\sum _{j=1}^M{U}_{qj}^n{\zeta }_j={\mathit{U}}_q^n·\mathit{\zeta }=\mathbf{\Phi }{\mathit{\alpha }}_q^n·\mathit{\zeta },1⩽n⩽N.}\hfill \end{array}\hfill \end{array}\right.$$

(59)

Here, ${\mathit{U}}_h^n(n=1,2,\dots ,Q)$ are the first Q-step CNFE solution vectors of Problem 3, while $\mathit{B}$, $\mathit{F}$, and $\mathit{\zeta }=({\zeta }_1\left(x\right),{\zeta }_2\left(x\right),\dots ,{\zeta }_M\left(x\right))$ are defined in Section 3.2.

4.3. Establishing the Uniqueness, Stability, and Convergence of the RDCNFE Solution

Before discussing the properties of the RDCNFE solution, we first present the following conservation law of the RDCNFE solution.

Lemma 6.

The solution $u_q^n$ of Problem 4 is consistent with the following conservation laws:

$$\begin{array}{c}{Q}^n=\parallel u_q^n\parallel =\parallel u_q^{n-1}\parallel =\dots =\parallel u_q^0\parallel ,\hfill \\ E^n=\parallel u_q^n{\parallel }_1^2=\parallel u_q^{n-1}{\parallel }_1^2=\dots ={\parallel u_q^0\parallel }_1^2.\hfill \end{array}$$

(60)

Proof of Lemma 6.

By employing ${\mathit{U}}_q^n=\mathbf{\Phi }{\mathit{\alpha }}_q^n$, the second equation of Problem 4 can be written as

$$\begin{array}{c}\hfill \mathit{i}{\overline{\partial }}_t{\mathit{U}}_q^n+\mathit{B}{\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}}+{\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}}={\mathit{F}}^{n-{\displaystyle \frac{1}{2}}},Q+1⩽n⩽N.\end{array}$$

(61)

Let $f=0$, then ${\mathit{F}}^{n-{\displaystyle \frac{1}{2}}}=0$.

For $1⩽n⩽Q$, Lemma 4 ensures that the CNFE solution $u_h^n$ of Problem 3 satisfies the conservation laws. Consequently, derived from the first and third equations of Problem 4, the RDCNFE solution $u_q^n$ must also satisfy the conservation laws.

For $Q+1⩽n⩽N$, we compute the inner product of (61) with ${\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}}$, and then take the imaginary part to get

$$({\overline{\partial }}_t{\mathit{U}}_q^n,{\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}})={\displaystyle \frac{\parallel {\mathit{U}}_q^n{\parallel }^2-{\parallel {\mathit{U}}_q^{n-1}\parallel }^2}{2\Delta t}}=0.$$

(62)

So, we have $\parallel {\mathit{U}}_q^n\parallel =\parallel {\mathit{U}}_q^{n-1}\parallel =\dots =\parallel {\mathit{U}}_q^0\parallel$. Since $u_q^n={\mathit{U}}_q^n·\mathit{\zeta }$, it can be obtained that $Q^n=\parallel u_q^n\parallel =\parallel u_q^{n-1}\parallel =\dots =\parallel u_q^0\parallel$. We compute the inner product of (61) with ${\overline{\partial }}_t{\mathit{U}}_q^n$, set $f=0$, and then take the real part to obtain

$$Re(\mathit{B}{\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}},{\overline{\partial }}_t{\mathit{U}}_q^n)+Re({\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}},{\overline{\partial }}_t{\mathit{U}}_q^n)=0,$$

(63)

that is

$${\displaystyle \frac{\parallel {\mathit{B}}^{\frac{1}{2}}{\mathit{U}}_q^n{\parallel }^2-{\parallel {\mathit{B}}^{\frac{1}{2}}{\mathit{U}}_q^{n-1}\parallel }^2}{2\Delta t}}+{\displaystyle \frac{\parallel {\mathit{U}}_q^n{\parallel }^2-{\parallel {\mathit{U}}_q^{n-1}\parallel }^2}{2\Delta t}}=0.$$

(64)

So we have

$$\parallel {\mathit{B}}^{{\displaystyle \frac{1}{2}}}{\mathit{U}}_q^n{\parallel }^2+\parallel {\mathit{U}}_q^n{\parallel }^2=\parallel {\mathit{B}}^{{\displaystyle \frac{1}{2}}}{\mathit{U}}_q^{n-1}{\parallel }^2+{\parallel {\mathit{U}}_q^{n-1}\parallel }^2.$$

(65)

Since $\mathit{\zeta }$ is orthonormal and based on the definition of $\mathit{B}$, so we have $\parallel {\mathit{B}}^{{\displaystyle \frac{1}{2}}}{\mathit{U}}_q^n{\parallel }^2+\parallel {\mathit{U}}_q^n{\parallel }^2={\parallel {\mathit{U}}_q^n\parallel }_1^2$, so

$$\parallel {\mathit{U}}_q^n{\parallel }_1^2=\parallel {\mathit{U}}_q^{n-1}{\parallel }_1^2=\dots ={\parallel {\mathit{U}}_q^0\parallel }_1^2.$$

(66)

Further, it can be obtained

$$E^n=\parallel u_q^n{\parallel }_1^2=\parallel u_q^{n-1}{\parallel }_1^2=\dots ={\parallel u_q^0\parallel }_1^2.$$

(67)

□

Theorem 3.

Given the same hypothesis as Theorem 2, for the solution $u^n\in V$ of Problem 1 and the RDCNFE solution $u_q^n\in V_h$ of Problem 4, the RDCNFE solution exhibits uniqueness and unconditional stability for $1⩽n⩽N$, with the following error estimate:

$$\begin{array}{c}\hfill \parallel u^n-u_q^n\parallel ⩽C(h^2+{(\Delta t)}^2+\sqrt{{\mu }_{q+1}}).\end{array}$$

(68)

Proof of Theorem 3.

• Proving the uniqueness of the RDCNFE solution.
  When $1⩽n⩽Q$, Theorem 1 ensures that the CNFE solution $u_h^n$ of Problem 3 is unique. Consequently, derived from the first and third equations of Problem 4, the RDCNFE solution $u_q^n$ must also exhibit uniqueness.
  When $Q+1⩽n⩽N$, the RDCNFE scheme is also given by

  $$i{\mathbf{\Phi }}^T\mathbf{\Phi }{\overline{\partial }}_t{\mathit{\alpha }}_q^n+({\mathbf{\Phi }}^T\mathit{B}\mathbf{\Phi }+{\mathbf{\Phi }}^T\mathbf{\Phi }){\mathit{\alpha }}_q^{n-{\displaystyle \frac{1}{2}}}={\mathbf{\Phi }}^T{\mathit{F}}^{n-{\displaystyle \frac{1}{2}}}.$$

  (69)
  Since the POD basis vectors ${\left\{{\mathit{\phi }}_j\right\}}_{j=1}^q$ are orthonormal, the matrix ${\mathbf{\Phi }}^T\mathbf{\Phi }$ is the identity matrix. The matrix $\mathit{B}$ is symmetric and positive definite, so ${\mathbf{\Phi }}^T\mathit{B}\mathbf{\Phi }$ is also a symmetric positive definite matrix.
  Therefore, the coefficient matrix of the linear system (69) remains symmetric and positive definite. Consequently, the coefficient matrix is invertible, which ensures that there exists a unique solution $u_q^n\in V_h$ to problem 4.
• Demonstrating the stability of the RDCNFE solution.
  When $1⩽n⩽Q$, based on the orthonormal property of vectors in $\mathbf{\Phi }$ and Theorem 1, imply that

  $$\begin{array}{c}\parallel u_q^n\parallel =\parallel {\mathit{U}}_q^n·\mathit{\zeta }\parallel =\parallel \mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}_h^n·\mathit{\zeta }\parallel ⩽C\parallel u_h^n\parallel ⩽C,1⩽n⩽Q.\hfill \end{array}$$

  (70)
  When $Q+1⩽n⩽N$, by employing ${\mathit{U}}_q^n={\mathbf{\Phi }}_1{\mathit{\alpha }}_q^n$, we can transform the final two equations of Problem 4 into

  $$\begin{array}{cc}\hfill & i{\overline{\partial }}_t{\mathit{U}}_q^n+\mathit{B}{\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}}+{\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}}={\mathit{F}}^{n-{\displaystyle \frac{1}{2}}},Q+1⩽n⩽N,\hfill \end{array}$$

  (71)

  $$\begin{array}{cc}\hfill & {\displaystyle u_q^n=\sum _{j=1}^M{U}_{qj}^n{\zeta }_j={\mathit{U}}_q^n·\mathit{\zeta },Q+1⩽n⩽N.}\hfill \end{array}$$

  (72)
  Taking the inner product of (71) and ${\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}}$, and taking the imaginary part, we obtain

  $$\begin{array}{cc}\parallel {\mathit{U}}_q^n{\parallel }^2-{\parallel {\mathit{U}}_q^{n-1}\parallel }^2\hfill & =\Delta t\mathrm{Im}({\mathit{F}}^{n-{\displaystyle \frac{1}{2}}},{\mathit{U}}_q^{n-{\displaystyle \frac{1}{2}}})\hfill \\ \hfill & ⩽C\Delta t(\parallel {\mathit{F}}^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+\parallel {\mathit{U}}_q^n{\parallel }^2+\parallel {\mathit{U}}_q^{n-1}{\parallel }^2),Q+1⩽n⩽N.\hfill \end{array}$$

  (73)
  Summing from $Q+1$ to n for (73), we obtain

  $${\displaystyle \parallel {\mathit{U}}_q^n{\parallel }^2⩽\parallel {\mathit{U}}_q^Q{\parallel }^2+C\Delta t\sum _{i=Q+1}^n\parallel {\mathit{F}}^{i-\frac{1}{2}}{\parallel }^2+C\Delta t\sum _{i=Q}^n{\parallel {\mathit{U}}_q^i\parallel }^2,Q+1⩽n⩽N.}$$

  (74)
  Employing Gronwall’s inequality yields

  $$\begin{array}{cc}{\displaystyle \parallel {\mathit{U}}_q^n{\parallel }^2}\hfill & {\displaystyle ⩽C\left(\parallel {\mathit{U}}_q^Q{\parallel }^2+\Delta t\sum _{i=Q+1}^n{\parallel {\mathit{F}}^{i-\frac{1}{2}}\parallel }^2\right)e^{C(n-Q)\Delta t}}\hfill \\ \hfill & {\displaystyle ⩽C\left(\parallel {\mathit{U}}_q^Q{\parallel }^2+\Delta t\sum _{i=Q+1}^n{\parallel {\mathit{F}}^{i-\frac{1}{2}}\parallel }^2\right)}\hfill \\ \hfill & {\displaystyle ⩽C\left(\parallel {\mathit{U}}_h^Q{\parallel }^2+\Delta t\sum _{i=Q+1}^n{\parallel {\mathit{F}}^{i-\frac{1}{2}}\parallel }^2\right)}\hfill \\ \hfill & ⩽C,Q+1⩽n⩽N.\hfill \end{array}$$

  (75)
  Given that $\parallel \mathit{\zeta }\parallel ⩽C$, we obtain

  $$\parallel u_q^n\parallel =\parallel {\mathit{U}}_q^n·\mathit{\zeta }\parallel ⩽C\parallel {\mathit{U}}_q^n\parallel ·\parallel \mathit{\zeta }\parallel ⩽C,Q+1⩽n⩽N.$$

  (76)
  From (76), the RDCNFE solution $u_q^n(1⩽n⩽N)$ has stability.
• Analyzing the convergence of the RDCNFE solution.
  For $1⩽n⩽Q$, given that $\parallel \mathit{\zeta }\parallel ⩽C$ and from (58), we have

  $$\begin{array}{c}\parallel u_h^n-u_q^n\parallel ⩽\parallel {\mathit{U}}_h^n-{\mathit{U}}_q^n{\parallel }_{\infty }\parallel \mathit{\zeta }\parallel ⩽C\parallel {\mathit{U}}_h^n-\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}_h^n\parallel ⩽C\sqrt{{\mu }_{q+1}},1⩽n⩽Q.\hfill \end{array}$$

  (77)
  For $Q+1⩽n⩽N$, setting ${\mathit{\delta }}^n={\mathit{U}}_h^n-{\mathit{U}}_q^n$, and combining (56) and (71), we obtain

  $$i{\overline{\partial }}_t{\mathit{\delta }}^n+\mathit{B}{\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}}+{\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}}=0,Q+1⩽n⩽N.$$

  (78)
  Computing the inner product of (78) and ${\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}}$ yields

  $$i({\overline{\partial }}_t{\mathit{\delta }}^n,{\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}})+(\mathit{B}{\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}},{\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}})+{\parallel {\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}}\parallel }^2=0,Q+1⩽n⩽N.$$

  (79)
  Extracting the imaginary part, we have

  $${\displaystyle \frac{\parallel {\mathit{\delta }}^n{\parallel }^2-{\parallel {\mathit{\delta }}^{n-1}\parallel }^2}{2\Delta t}}=0,Q+1⩽n⩽N,$$

  (80)

  that is

  $$\parallel {\mathit{\delta }}^n{\parallel }^2=\parallel {\mathit{\delta }}^{n-1}{\parallel }^2=\dots ={\parallel {\mathit{\delta }}^Q\parallel }^2⩽C{\mu }_{q+1},Q+1⩽n⩽N.$$

  (81)
  Computing the inner product of (78) and ${\overline{\partial }}_t{\mathit{\delta }}^n$ yields

  $$i({\overline{\partial }}_t{\mathit{\delta }}^n,{\overline{\partial }}_t{\mathit{\delta }}^n)+(\mathit{B}{\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}},{\overline{\partial }}_t{\mathit{\delta }}^n)+({\mathit{\delta }}^{n-{\displaystyle \frac{1}{2}}},{\overline{\partial }}_t{\mathit{\delta }}^n)=0,Q+1⩽n⩽N.$$

  (82)
  Extracting the real part, it follows that

  $${\displaystyle \frac{\parallel {\mathit{B}}^{\frac{1}{2}}{\mathit{\delta }}^n{\parallel }^2-{\parallel {\mathit{B}}^{\frac{1}{2}}{\mathit{\delta }}^{n-1}\parallel }^2}{2\Delta t}}+{\displaystyle \frac{\parallel {\mathit{\delta }}^n{\parallel }^2-{\parallel {\mathit{\delta }}^{n-1}\parallel }^2}{2\Delta t}}=0,Q+1⩽n⩽N,$$

  (83)

  that is

  $$(\parallel {\mathit{B}}^{{\displaystyle \frac{1}{2}}}{\parallel }^2+1)\parallel {\mathit{\delta }}^n{\parallel }^2=(\parallel {\mathit{B}}^{{\displaystyle \frac{1}{2}}}{\parallel }^2+1)\parallel {\mathit{\delta }}^{n-1}{\parallel }^2=0,Q+1⩽n⩽N,$$

  (84)

  so

  $$\parallel {\mathit{\delta }}^n{\parallel }^2=\parallel {\mathit{\delta }}^{n-1}{\parallel }^2=\dots ={\parallel {\mathit{\delta }}^Q\parallel }^2⩽C{\mu }_{q+1},Q+1⩽n⩽N.$$

  (85)
  Further, given that $\parallel \mathit{\zeta }\parallel ⩽C$, we have

  $$\begin{array}{c}\parallel u_h^n-u_q^n\parallel ⩽\parallel {\mathit{U}}_h^n-{\mathit{U}}_q^n{\parallel }_{\infty }·\parallel \mathit{\zeta }\parallel ⩽\parallel {\mathit{U}}_h^n-{\mathit{U}}_q^n\parallel ·\parallel \mathit{\zeta }\parallel ⩽C\sqrt{{\mu }_{q+1}},Q+1⩽n⩽N.\hfill \end{array}$$

  (86)
  Employing the triangle inequality, and based on Theorem 2, (77) and (86), we obtain

  $$\begin{array}{c}\parallel u^n-u_q^n\parallel ⩽\parallel u^n-u_h^n\parallel +\parallel u_h^n-u_q^n\parallel ⩽C(h^2+{(\Delta t)}^2+\sqrt{{\mu }_{q+1}}),1⩽n⩽N.\hfill \end{array}$$

  (87)

□

Remark 3.

According to the error estimate given in Theorem 3, $\parallel u^n-u_q^n\parallel \le C(h^2+{(\Delta t)}^2+\sqrt{{\mu }_{q+1}})$, in order for the proposed RDCNFE method to maintain the same convergence order as the standard CNFE method, it is necessary to ensure that the POD projection error term $\sqrt{{\mu }_{q+1}}$ does not exceed the discretization error terms $h^2+{(\Delta t)}^2$. That is, the inequality

$$\sqrt{{\mu }_{q+1}}⩽h^2+{(\Delta t)}^2,$$

must be satisfied. In practical computations, the number of POD basis vectors q can be adjusted to meet this condition, thereby achieving an optimal balance between computational efficiency and accuracy.

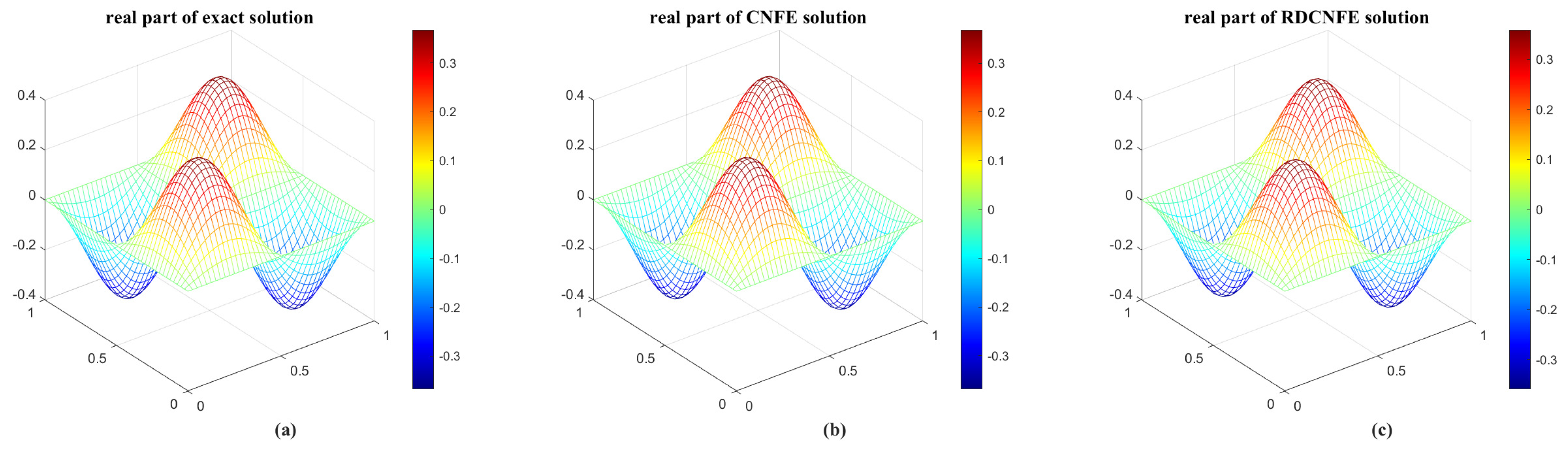
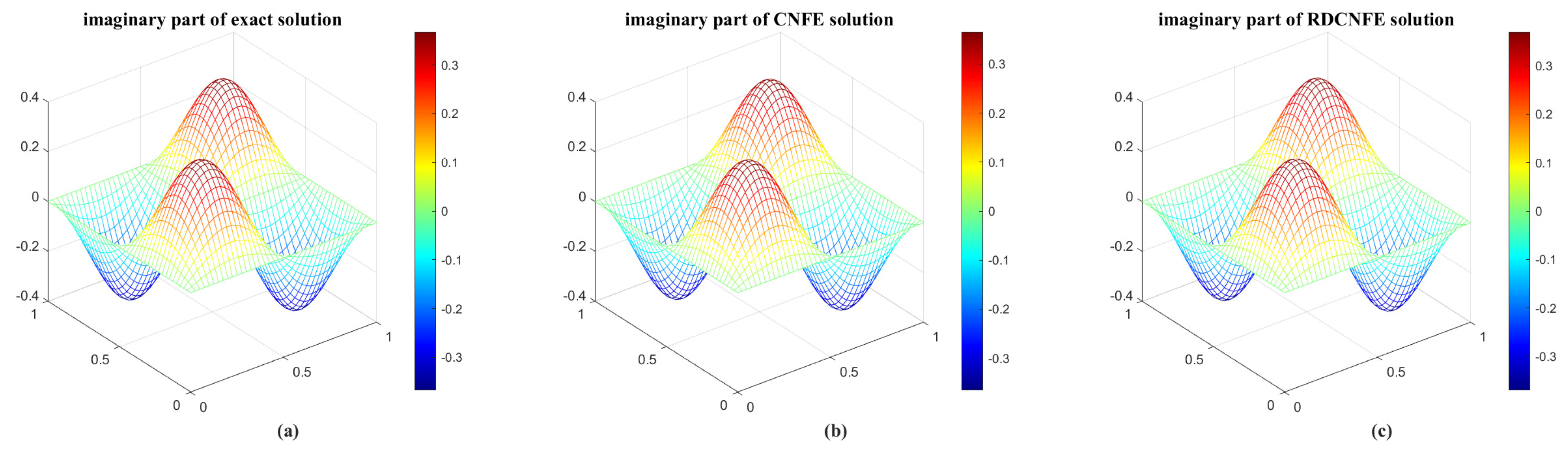
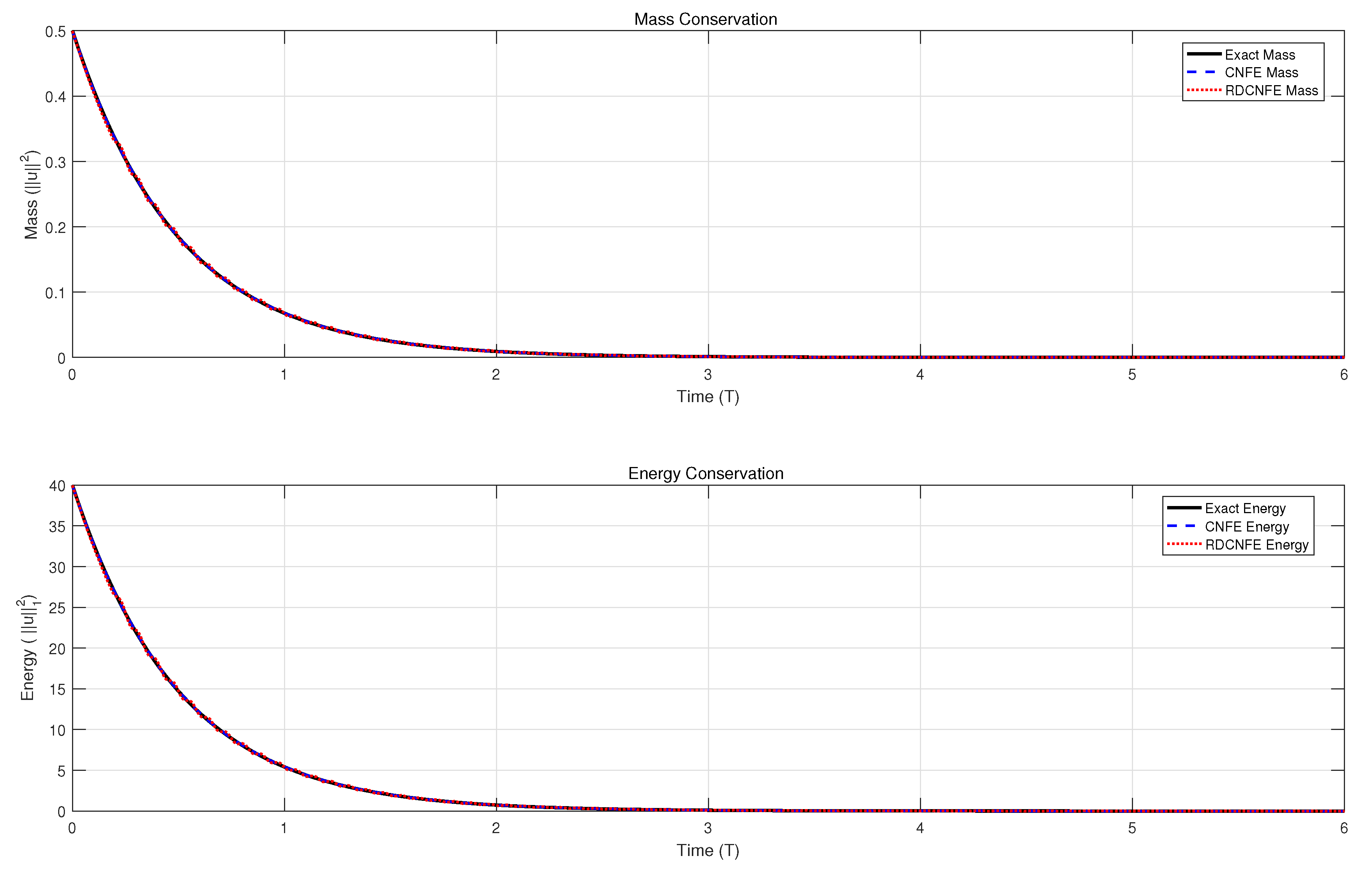
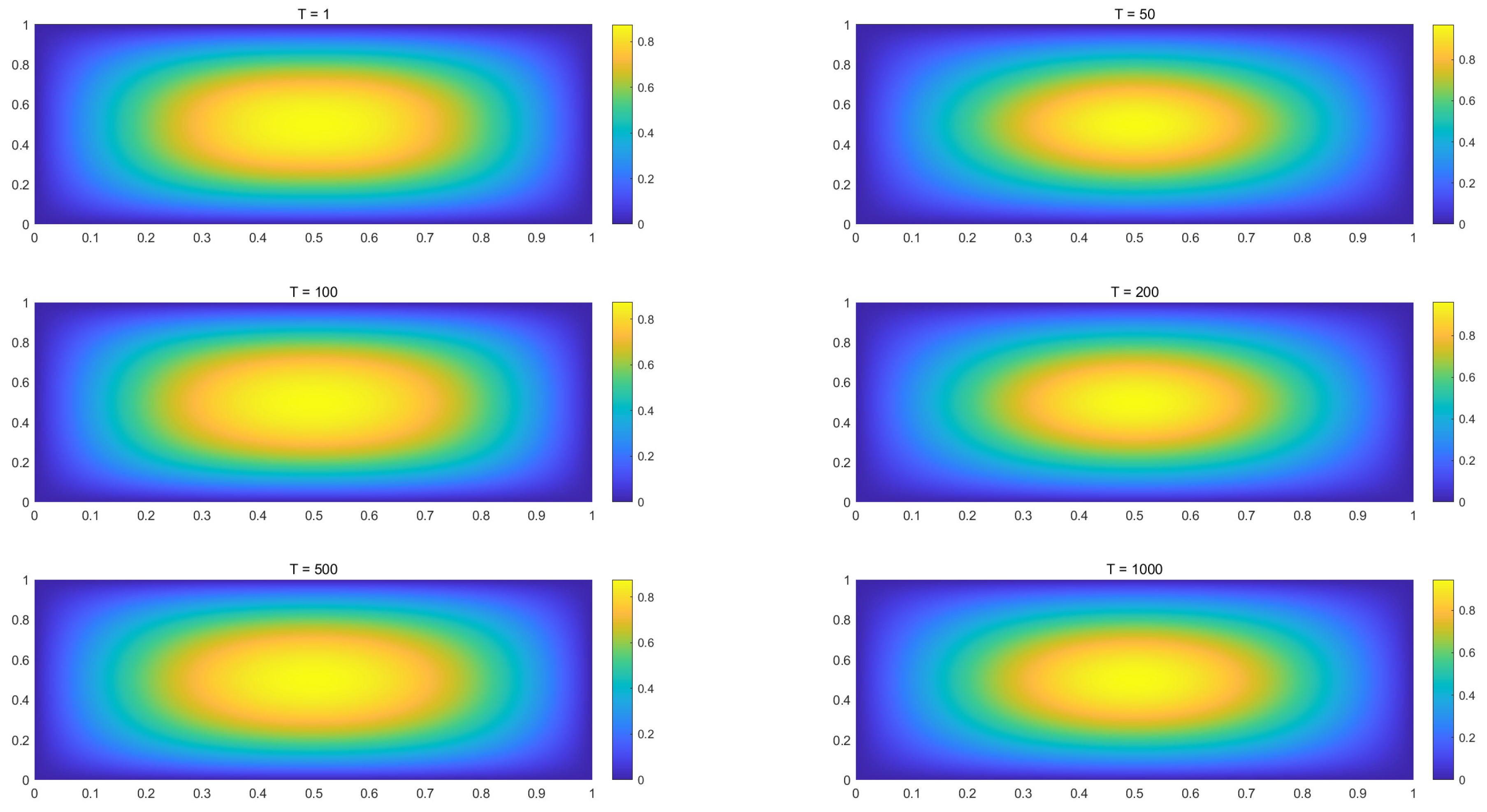
5. Conducting the Numerical Experiments for the Schrödinger Equations

In this section, the Schrödinger equation is numerically simulated using CNFE and POD-based reduced-dimension methods. Firstly, the effectiveness of the CNFE and RDCNFE methods can be assessed by comparing their solution accuracy, convergence rates, and computational efficiency at specific time nodes. Subsequently, a more complex problem without an analytical solution is investigated to further demonstrate the effectiveness of both methods.

For this purpose, we conduct numerical experiments on the two-dimensional Schrödinger equation specified below.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle \mathit{i}{u}_t(x,y,t)-\Delta u(x,y,t)+u(x,y,t)=f(x,y,t),}\hfill & (x,y,t)\in \Omega \times (0,T],\hfill \\ u(x,y,t)=\Delta u(x,y,t)=0,\hfill & (x,y,t)\in \partial \Omega \times [0,T],\hfill \\ u(x,y,0)=u_0(x,y),\hfill & (x,y)\in \Omega .\hfill \end{array}\right.\end{array}$$

(88)

The standard CNFE solution $u_h^n$ can be obtained by solving the Problem 3. In order to construct the corresponding RDCNFE solution $u_q^n$, the following four steps need to be performed in sequence.

• By addressing Problem 3, the first $Q=20$ CNFE solution vectors ${\mathit{U}}_h^n(n=1,2,\dots ,20)$ are derived to establish the snapshot matrix $\mathit{A}=({\mathit{U}}_h^1,{\mathit{U}}_h^2,\dots ,{\mathit{U}}_h^{20})$.
• Compute the positive eigenvalues ${\mu }_j(j=1,2,\dots ,20)$ of the matrix ${\mathit{A}}^T\mathit{A}$ and arrange them in descending order, along with their corresponding eigenvectors ${\mathit{\varphi }}_j(j=1,2,\dots ,20)$.
• By estimation, it is observed that $\sqrt{{\mu }_7}⩽h^2+{(\Delta t)}^2$. Consequently, the first six eigenvectors ${\mathit{\varphi }}_j(j=1,2,\dots ,6)$ of ${\mathit{A}}^T\mathit{A}$ can be selected to generate POD bases $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_6)$ using the formula ${\mathit{\phi }}_j=\mathit{A}{\mathit{\varphi }}_j/\sqrt{{\mu }_j}$.
• Insert the provided data into Problem 4 and compute the RDCNFE solution $u_q^n$ of (88) using the framework gived in Problem 4.

Example 1.

The 2D Schrödinger model (88) is analyzed, with the exact solution

$$u(x,y,t)={\mathrm{e}}^{-t}(1+\mathit{i})\sin \left(2\pi x\right)\sin \left(2\pi y\right),(x_1,x_2)\in {[0,1]}^2,t\in [0,T],$$

(89)

and the source term

$$f(x,y,t)={\mathrm{e}}^{-t}\left[8{\pi }^2(\mathit{i}+1)+2\right]\sin \left(2\pi x\right)\sin \left(2\pi y\right).$$

(90)

At $T=1$ with $h=\sqrt{2}/40$ and $\Delta t=1/100$, standard CNFE and POD-based RDCNFE solutions are computed and compared against the exact solution. Figure 1, Figure 2 and Figure 3 demonstrate that both methods yield highly accurate approximations.

Figure 4 presents the temporal evolution of mass $(\parallel u{\parallel }^2)$ and energy $(\parallel u{\parallel }_1^2)$. It is important to note that due to the presence of the source term $f(\mathit{x},t)$, the exact solution itself is not conservative. It can be observed that as time goes by, the mass and energy gradually decay as expected physically. The key observation is that the numerical results obtained by both the CNFE and RDCNFE methods coincide perfectly with the exact solution. This excellent agreement demonstrates that our numerical methods accurately capture the true dynamics of the system, including the non-conservative effects introduced by the source term. The performance of the RDCNFE method is virtually identical to that of the full-order CNFE method in this regard.

When $T=1$ and $\Delta t=1/100$, for comparison, the $L^2$ errors and convergence orders of u are calculated by the standard CNFE method and RDCNFE method, respectively, and the results are listed in

Table 1. $L^2$ errors and convergence orders of the CNFE, RDCNFE, and exact solutions when T = 1 and $\Delta t$ = 1/100.

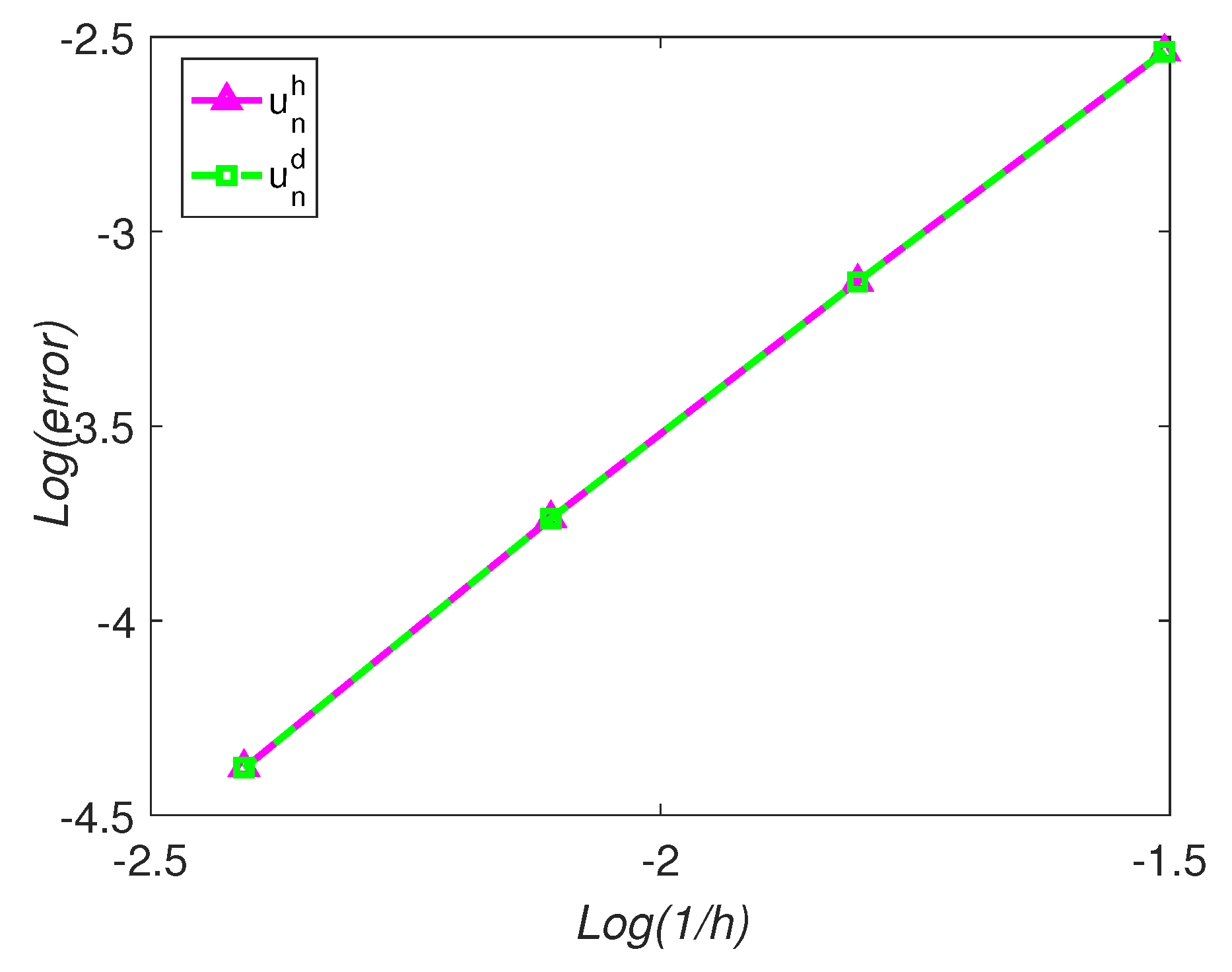
	CNFE Method		RDCNFE Method
Grid	$\left|\right|{\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\left|\right|$	Order	$\left|\right|{\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{q}}^{\mathit{n}}\left|\right|$	Order
$32\times 32$	2.9018 × ${10}^{-3}$		2.9018 × ${10}^{-3}$
$64\times 64$	7.4470 × ${10}^{-4}$	1.9622	7.4470 × ${10}^{-4}$	1.9622
$128\times 128$	1.8326 × ${10}^{-4}$	2.0228	1.8326 × ${10}^{-4}$	2.0228
$256\times 256$	4.1776 × ${10}^{-5}$	2.1332	4.1776 × ${10}^{-5}$	2.1332

. The tabulated results demonstrate consistent $L^2$ errors and convergence rates between RDCNFE and standard CNFE methods, validating the theoretical analysis.

Based on the error results presented in Table 1, the convergence curves are plotted in Figure 5. It can be observed that the $L^2$ errors for both methods decrease as the mesh is refined, demonstrating the convergence of both the standard CNFE method and the RDCNFE method. Furthermore, the two curves are perfectly aligned, indicating that the precision achieved by the dimension-reduction method is nearly identical to that of the CNFE method.

With T ranging from $1.0$ to $9.0$, and with fixed parameters $h=\sqrt{2}/100$ and $\Delta t=1/1000$, a comparative validation is performed between the standard CNFE method and RDCNFE method. From the data in the

Table 2. $L^2$ errors and CPU runtimes of the CNFE, RDCNFE, and exact solutions when $h=\sqrt{2}/100$ and $\Delta t$ = 1/1000.

	CNFE Method		RDCNFE Method
Real Time	$\left|\right|{\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\left|\right|$	CPU Runtime	$\left|\right|{\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{q}}^{\mathit{n}}\left|\right|$	CPU Runtime
$T=1.0$	2.2825 × ${10}^{-4}$	4.259 s	2.2825 × ${10}^{-4}$	1.182 s
$T=2.0$	2.0730 × ${10}^{-4}$	8.183 s	2.0730 × ${10}^{-4}$	2.006 s
$T=3.0$	2.4137 × ${10}^{-4}$	11.578 s	2.4137 × ${10}^{-4}$	2.826 s
$T=4.0$	2.3860 × ${10}^{-4}$	14.815 s	2.3860 × ${10}^{-4}$	3.715 s
$T=5.0$	2.3419 × ${10}^{-4}$	19.868 s	2.3419 × ${10}^{-4}$	4.728 s
$T=6.0$	2.3509 × ${10}^{-4}$	22.819 s	2.3509 × ${10}^{-4}$	5.606 s
$T=7.0$	2.3558 × ${10}^{-4}$	27.952 s	2.3558 × ${10}^{-4}$	6.260 s
$T=8.0$	2.3539 × ${10}^{-4}$	30.962 s	2.3539 × ${10}^{-4}$	7.241 s
$T=9.0$	2.3535 × ${10}^{-4}$	34.373 s	2.3535 × ${10}^{-4}$	8.050 s

, the $L^2$ error accuracy of the two methods is identical. Notably, for every additional second of simulation time, the CPU runtime of the standard CNFE method increases by several seconds. In contrast, benefiting from the advantages of the reduced-dimension model, the increase in CPU time for the RDCNFE method is consistently kept below one second. This comparative result clearly demonstrates the significant advantage of the POD reduced-dimension technique in enhancing computational efficiency.

Example 2.

Let the source term $f=0$, and consider the model (88) with the following initial values in $\Omega ={[0,1]}^2\subset {\mathbb{R}}^2$.

$$u_0(x,y)=e^{-[{(x-0.5)}^2+{(y-0.5)}^2]}\sin \left(\pi x\right)\sin \left(\pi y\right).$$

(91)

Given that $h=\sqrt{2}/100$ and $\Delta t=T/100$, Figure 6 and Figure 7 present the standard CNFE and POD-based RDCNFE solutions at time levels $T=1,50,100,200,500,1000$, respectively. The results demonstrate that as T increases, the numerical solutions obtained by both methods remain stable. Furthermore, the diffusion processes simulated by the two methods exhibit a high degree of consistency in both morphology and distribution characteristics.

6. Conclusions, Limitations, and Prospects

6.1. Conclusions

This paper developed a POD-based reduced-dimension algorithm for the CNFE discretization of the 2D Schrödinger equation. Firstly, the fully discrete CNFE scheme was formulated, with rigorous proofs establishing solution uniqueness, stability, and optimal-order error estimates. The scheme was then transformed into matrix form using the finite element basis function expansion. Secondly, the POD method is employed to construct the RDCNFE scheme. The uniqueness and stability of the RDCNFE solution were analyzed, and its convergence was proven. Finally, the advantages of both methods are quantitatively evidenced through numerical experiments. Numerical experiments demonstrated that, while maintaining computational accuracy equivalent to the standard CNFE scheme, the reduced-dimension model significantly decreased the computational cost. By reducing the number of degrees of freedom, the increase in CPU runtime was reduced from several seconds to less than 1 s. For cases lacking a known exact solution, the numerical solutions obtained by both methods remain stable, and the simulated physical processes exhibit close morphological agreement. This POD-based framework provides a reliable and efficient computational method for simulating the Schrödinger equation.

6.2. Limitations

While the proposed RDCNFE method demonstrates significant efficiency gains and theoretical robustness, this study is subject to several limitations that outline the scope of our current findings and provide directions for future research. First, the numerical experiments and theoretical analysis are conducted on a simple square domain. The performance and accuracy of the method on more complex, non-convex, or three-dimensional geometries remain unverified, which is a necessary step to demonstrate its broad applicability in practical scientific and engineering simulations. Second, our analysis is currently restricted to the Schrödinger equation with homogeneous Dirichlet boundary conditions. The extension of the theoretical framework to accommodate more general boundary conditions, such as Neumann or Robin types, which are prevalent in physical applications, constitutes an important area for future development. Third, the stability and error estimates derived in this work assume the use of exact integration in the finite element formulation. The impact of numerical quadrature errors on both the full-order and reduced-order models is not accounted for, which is a crucial consideration for practical implementations. Addressing these limitations will be the focus of our subsequent research efforts.

6.3. Future Works

The present study serves as a foundational step, and its identified limitations naturally chart the course for future research. The immediate extension of this work will involve applying the proposed RDCNFE framework to problems defined on complex non-convex and three-dimensional domains to rigorously assess its robustness and practical applicability. Concurrently, efforts will be made to generalize the theoretical analysis to encompass Neumann and Robin boundary conditions, which are essential for modeling a wider array of physical scenarios. Furthermore, to complete the theoretical foundation, a critical analysis of the impact of numerical quadrature errors on both the full-order and reduced-order models will be indispensable for practical implementations.

From the current research scope, this POD-based reduced-dimension technology can also explore more complex systems. A promising direction is to apply it to nonlinear and fractional Schrödinger equations, as well as coupled Schrödinger equations, to solve increasingly complex quantum mechanics problems. Finally, by combining POD with other advanced numerical techniques, such as the two-grid and spectral methods, powerful hybrid algorithms can be developed. Future research work also includes exploratory efforts to compare the established POD methods with emerging data-driven model reduced-order techniques, such as deep neural networks and tensor decomposition, in order to discover new possibilities for computational efficiency.