Stability of the Split-Step θ-Method for Stochastic Pantograph Systems with Markovian Switching and Jumps

Abstract

This study focuses on analyzing the almost sure exponential stability of the split-step $\theta$-method ($SS\theta$-method) when applied to stochastic pantograph differential equations characterized by Markovian switching and jump processes. Initially, we establish the almost sure exponential stability of the system’s trivial solution. Subsequently, under an additional sufficient condition, it is demonstrated that the discrete solutions generated by the $SS\theta$-method also exhibit this stability property. Finally, a computational experiment is conducted to support the theoretical results.

1. Introduction

In practice, many stochastic systems exhibit dependence not only on their present conditions but also on historical dynamics. To effectively characterize such behavior, stochastic delay differential equations (SDDEs) are widely utilized (see, for instance, [1,2,3,4,5,6]). When these systems experience sudden shifts in configuration or parameter values, it becomes appropriate to employ SDDEs incorporating Markovian switching, as discussed in the comprehensive work [7]. Mao et al. [8] studied the exponential stability of SDDEs with Markovian switching. Song and Zhu [9] examined the asymptotic stability in mean square, stochastic stability, and exponential stability in mean square of linear SDDEs with infinite Markovian switchings. Subsequently, Zhang and Chen [10] investigated the stability of SDDEs with Markovian switching. While Brownian motion is a well-known model for continuous stochastic processes, it may not adequately capture random discontinuities caused by events like mechanical breakdowns, seismic activity, or extreme weather. In these cases, modeling with jump processes provides a more suitable representation. Accordingly, SDDEs that integrate both Markovian switching and jump disturbances have become an area of active research, with detailed investigations reported in [11,12] and numerous references therein.

Pantograph equations, a distinctive subclass of delay differential systems, were originally introduced in the context of modeling electric locomotives, as documented in [13]. With the integration of stochastic analysis, stochastic pantograph differential equations (SPDEs) have emerged as essential tools in disciplines such as mechanics, biology, engineering, and financial mathematics [14]. Fan et al. showed sufficient conditions of existence and uniqueness of the solutions for SPDEs in [15] and studied the stability in [16]. Jang et al. [17] conducted further research into the asymptotic stability of SPDEs with Markovian switching. Milošević [18] discussed the existence, uniqueness and almost sure polynomial stability of solutions to a class of highly nonlinear SPDEs, as well as the corresponding Euler–Maruyama approximation. For these above-mentioned foundational results regarding the existence, uniqueness, and stability of solutions to SPDEs, readers can further refer to other relevant literature. The work of You et al. [19] addresses the almost sure exponential stability of SPDEs influenced by Markovian switching mechanisms. Furthermore, Mao and collaborators [20] extended the analysis to neutral SPDEs, examining their almost sure exponential stability under general decay conditions in the presence of Markovian switching.

However, most of SPDEs cannot be solved explicitly. Especially, explicit solutions can rarely be obtained for nonlinear SPDEs. As a result, numerical approximation techniques have become essential tools for their analysis (see, e.g., [21,22]). Notably, Zhou and Hu [23] examined the almost sure exponential stability of the backward Euler–Maruyama scheme when applied to SPDEs governed by Markovian switching. In another study, Guo and Li [24] evaluated both the Euler–Maruyama and the backward Euler–Maruyama methods, demonstrating the almost sure exponential stability of their numerical solutions. In [25], Cheng et al. focused on the strong convergence and stability of the balanced Euler scheme for SPDEs with regime-switching behavior. A notable development in numerical schemes for stochastic differential equations was put forward by Ding et al. [26], who proposed the so-called $SS\theta$-scheme. This method has since attracted significant scholarly attention. For instance, Huang [27] studied the mean-square stability properties of the $SS\theta$-scheme in the context of SDDEs. Similarly, the work in [28] established conditions under which the $SS\theta$-scheme guarantees mean-square stability for SDDEs under mild assumptions. Mo et al. [29] demonstrated that the $SS\theta$-scheme ensures mean-square exponential stability of the zero solution in neutral SDDEs affected by jump processes. In [30], Yuan et al. verified the asymptotic mean-square stability for the same class of equations. Moreover, Xiao et al. [31] investigated how adaptive time-stepping strategies influence the mean-square stability of the $SS\theta$-scheme when applied to SPDEs. Guo and Li [32] further explored the almost sure exponential stability of two variants of theta-type numerical schemes tailored for SPDEs.

Despite the significant advancements in the study of $SS\theta$-methods, existing research has yet to explore their almost sure stability when applied to SPDEs featuring both Markovian switching and jump disturbances (SPDEwMJs). Consequently, it becomes essential to examine the stability characteristics of such systems using the $SS\theta$-framework. This work initially demonstrates the almost sure exponential stability of the zero solution to a representative SPDEwMJ. Following this, we establish that the proposed $SS\theta$-based numerical scheme maintains this stability under an additional, suitably chosen condition.

The rest of the present article is structured in the following manner. Section 2 outlines the foundational conceptions and notation required for the subsequent analysis. Section 3 focuses on establishing the almost sure exponential stability of both the exact solution and the numerical approximation derived via the $SS\theta$-method. Section 4 presents a concrete example for illustrating and validating the theoretical findings. Lastly, this work concludes by presenting a concise summary of its key findings.

2. Preliminaries

Throughout the present article, the following notations are adopted. Denote $\mathbb{R}=(-\infty ,+\infty )$ and ${\mathbb{R}}^{+}=[0,+\infty )$. For all $x\in \mathbb{R}$, $\lfloor x\rfloor$ stands for the greatest integer not exceeding x. The space ${\mathbb{R}}^n$ is referred to as the n-dimensional Euclidean space, where $|x|$ denotes the Euclidean norm for any vector $x\in {\mathbb{R}}^n$. Let $(\mathrm{\Omega },\mathcal{F},\mathrm{P})$ be a complete probability space, accompanied by a filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ satisfying the usual conditions (i.e., right-continuity and completeness). We consider a right-continuous Markov chain ${\left\{r\left(t\right)\right\}}_{t\ge 0}$ defined on $(\mathrm{\Omega },\mathcal{F},\mathrm{P})$, taking values in a finite set $S=\{1,2,\dots ,N\}$. The infinitesimal generator of this Markov process is denoted by the matrix $\mathrm{\Gamma }={\left({\gamma }_{ij}\right)}_{N\times N}$ with

$$P\{r(t+\Delta )=j|r\left(t\right)=i\}=\left\{\begin{array}{cc}{\gamma }_{ij}\Delta +o(\Delta ),\hfill & \mathrm{if}i\ne j,\hfill \\ 1+{\gamma }_{ii}\Delta +o(\Delta ),\hfill & \mathrm{if}i=j,\hfill \end{array}\right.$$

where $\Delta >0$, with $\underset{\Delta \to 0}{lim}{\displaystyle \frac{o(\Delta )}{\Delta }}=0$; for $i\ne j$, ${\gamma }_{ij}\ge 0$ denotes the transition rate from state i to state j, whereas ${\gamma }_{ii}=-\sum _{j\ne i}{\gamma }_{ij}$. For the properties of $r\left(t\right)$, reference may be made to [7].

Consider the following SPDEwMJ, which takes the form

$$\begin{array}{cc}\hfill dx\left(t\right)=& f\left(x\right(t),x(qt),r(t),t)dt+g\left(x\right(t),x(qt),r(t),t)d\omega \left(t\right)\hfill \\ \hfill & +h\left(x\right(t),x(qt),r(t),t)dN\left(t\right),t\ge 0\hfill \end{array}$$

(1)

with initial conditions $x\left(0\right)=x_0$ and $r\left(0\right)=i_0\in S$; here, $0<q<1$, the functions $f,g,h$ are defined as mappings from ${\mathbb{R}}^n\times {\mathbb{R}}^n\times S\times {\mathbb{R}}^{+}$ to ${\mathbb{R}}^n$. It is assumed that $x_0$ is a bounded, ${\mathcal{F}}_0$-measurable random variable. Let $\omega \left(t\right)$ denote a one-dimensional standard Brownian motion, and let $N\left(t\right)$ be a scalar Poisson process with intensity $\lambda >0$. The compensated Poisson process is defined by $\tilde{N}\left(t\right)=N\left(t\right)-\lambda t$. Furthermore, the processes $\omega \left(t\right)$, $N\left(t\right)$, and $r\left(t\right)$ are mutually independent. To support the stability analysis, we impose the assumption that $f(0,0,i,t)=g(0,0,i,t)=h(0,0,i,t)=0,forall(i,t)\in S\times {\mathbb{R}}^{+},$ which guarantees that Equation (1) admits the trivial solution.

Throughout the paper, the following hypotheses are assumed to be satisfied:

Hypothesis 1 (H1).

For any integer $\alpha \ge 1$, there exists a constant $L_{\alpha }>0$ with the property that for all $x_1,x_2,y_1,y_2\in {\mathbb{R}}^n$, $i\in S$, and $t\in {\mathbb{R}}^{+}$, the following inequality holds

$$\begin{array}{cc}\hfill & max\{|f(x_1,y_1,i,t)-f(x_2,y_2,i,t){|}^2,{|g(x_1,y_1,i,t)-g(x_2,y_2,i,t)|}^2,\hfill \\ \hfill & |h(x_1,y_1,i,t)-h(x_2,y_2,i,t){|}^2\}\le L_{\alpha }\left(|x_1-x_2{|}^2+{|y_1-y_2|}^2\right).\hfill \end{array}$$

(2)

for any $i\in S$, $t\in {\mathbb{R}}^{+}$ and $x_j,y_j\in {\mathbb{R}}^n$ with $|x_j|\vee |y_j|\le \alpha$ (j = 1, 2).

Hypothesis 2 (H2).

There exist constants ${\lambda }_1>0$ and ${\lambda }_2>0$ with the property that for all $x,y\in {\mathbb{R}}^n$, $i\in S$, and $t\in {\mathbb{R}}^{+}$, the following inequality is satisfied:

$${|h(x,y,i,t)|}^2\le {\lambda }_1{|x|}^2+{\lambda }_{2}q{e}^{-(1-q)t}{|y|}^2.$$

(3)

To prove the existence and uniqueness of solutions to Equation (1), we introduce the following notation. Let $C^{2,1}({\mathbb{R}}^n\times {\mathbb{R}}^{+};{\mathbb{R}}^{+})$ denote the class of real-valued functions $V(x,t):{\mathbb{R}}^n\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ that are twice continuously differentiable with respect to x and once with respect to t. For any $V\in C^{2,1}({\mathbb{R}}^n\times {\mathbb{R}}^{+};{\mathbb{R}}^{+})$, define the associated operator $LV:{\mathbb{R}}^n\times {\mathbb{R}}^n\times S\times {\mathbb{R}}^{+}\to \mathbb{R}$ as

$$\begin{array}{cc}\hfill LV(x,y,i,t)=& V_t(x,t)+V_x(x,t)f(x,y,i,t)+{\displaystyle \frac{1}{2}}trace\left[g^{\top }(x,y,i,t)V_{xx}(x,t)g(x,y,i,t)\right]\hfill \\ \hfill & +\lambda \left[V(x+h(x,y,i,t),t)-V(x,t)\right]+\sum _{j=1}^N{\gamma }_{ij}V(x,t).\hfill \end{array}$$

where $V_t(x,t)={\displaystyle \frac{\partial V(x,t)}{\partial t}},V_x(x,t)={\left({\displaystyle \frac{\partial V(x,t)}{\partial x_i}}\right)}_{1\times n},V_{xx}(x,t)={\left({\displaystyle \frac{{\partial }^{2}V(x,t)}{\partial x_i\partial x_j}}\right)}_{n\times n}.$

Theorem 1. 

Suppose that assumptions (H1) and (H2) are satisfied. Further, assume there exist positive constants ${\lambda }_3$ and ${\lambda }_4$ such that the following inequality is valid for all $x,y\in {\mathbb{R}}^n$ and $(i,t)\in S\times {\mathbb{R}}^{+}$:

$$2x^{T}f(x,y,i,t)+{|g(x,y,i,t)|}^2\le -{\lambda }_3{|x|}^2+{\lambda }_{4}q{e}^{-(1-q)t}{|y|}^2.$$

(4)

If, in addition, the inequality ${\lambda }_3>{\lambda }_4+\lambda (1+2{\lambda }_1+2{\lambda }_2)$ is satisfied, then for any initial data $x_0\in {\mathbb{R}}^n$ and $i_0\in S$, Equation (1) admits a unique global solution $x\left(t\right)$ defined on the entire interval $t\in {\mathbb{R}}^{+}$.

Proof. 

Let $V(x\left(t\right),t)={|x\left(t\right)|}^2$. Applying Itô’s formula to ${|x\left(t\right)|}^2$, it can be derived that for any $i\in S$ and $t\ge 0$,

$$\begin{array}{cc}\hfill & LV(x,y,i,t)\hfill \\ \hfill & =2x^{T}f(x,y,i,t)+{|g(x,y,i,t)|}^2+{\lambda [|h(x,y,i,t)|}^2+2x^{T}h(x,y,i,t)]\hfill \\ \hfill & \le 2x^{T}f(x,y,i,t)+{|g(x,y,i,t)|}^2+{\lambda [|x|}^2+{2|h(x,y,i,t)|}^2].\hfill \end{array}$$

It can be inferred from Equations (3) and (4) that one gains

$$LV(x,y,i,t)\le -[{\lambda }_3-\lambda (1+2{\lambda }_1)]{|x|}^2+({\lambda }_4+2\lambda {\lambda }_2)q{e}^{-(1-q)t}{|y|}^2.$$

(5)

By combining Inequality (4) with the condition ${\lambda }_3>{\lambda }_4+\lambda (1+2{\lambda }_1+2{\lambda }_2)$, and applying reasoning similar to that used in the proof of Theorem 2.3 (1) in You et al. [19], it follows that Equation (1) is endowed with a unique global solution $x\left(t\right)$ for all $t\ge 0$. □

Next, the $SS\theta$-method applied to Equation (1) will be discussed. Before discussing it, we invoke the following lemma:

Lemma 1 

([7] (p. 112)). Let $\Delta >0$, and define $r_k^{\Delta }=r(k\Delta )$ for all integers $k\ge 0$. Then the sequence $\{r_k^{\Delta },k=0,1,2,\dots \}$ forms a discrete-time Markov chain whose one-step transition probability matrix is given by

$$p(\Delta )={\left(p_{ij}(\Delta )\right)}_{N\times N}=e^{\Delta \mathrm{\Gamma }}.$$

(6)

Given a fixed step size $\Delta >0$, the discrete Markov chain ${\left\{r_k^{\Delta }\right\}}_{k=0}^{\infty }$ can be generated using the following simulation procedure: First, compute the transition probability matrix using Equation (6). Set the initial value $r_0^{\Delta }=i_0$, and generate a uniform random variable ${\xi }_1\sim \mathcal{U}(0,1)$. Then define

$$r_1^{\Delta }=\left\{\begin{array}{cc}{i}_1,\hfill & \mathrm{if}{i}_1\in S\setminus \left\{N\right\}\mathrm{satisfies}\sum _{j=1}^{i_1-1}{p}_{i_0,j}(\Delta )\le {\xi }_1<\sum _{j=1}^{i_1}{p}_{i_0,j}(\Delta ),\hfill \\ N,\hfill & \mathrm{if}\sum _{j=1}^{N-1}{p}_{i_0,j}(\Delta )\le {\xi }_1,\hfill \end{array}\right.$$

with the convention ${\sum }_{j=1}^0{p}_{i_0,j}(\Delta )=0$. Repeat the process by generating another independent uniform random number ${\xi }_2\sim \mathcal{U}(0,1)$, and define

$$r_2^{\Delta }=\left\{\begin{array}{cc}{i}_2,\hfill & \mathrm{if}{i}_2\in S\setminus \left\{N\right\}\mathrm{satisfies}\sum _{j=1}^{i_2-1}{p}_{r_1^{\Delta },j}(\Delta )\le {\xi }_2<\sum _{j=1}^{i_2}{p}_{r_1^{\Delta },j}(\Delta ),\hfill \\ N,\hfill & \mathrm{if}\sum _{j=1}^{N-1}{p}_{r_1^{\Delta },j}(\Delta )\le {\xi }_2.\hfill \end{array}\right.$$

By iterating this process, one obtains a complete trajectory ${\left\{r_k^{\Delta }\right\}}_{k=0}^{\infty }$, and independent realizations can be generated as needed for simulation purposes.

With the discrete Markov chain construction established, we now introduce the $SS\theta$-method for numerically solving Equation (1). Let $t_k=k\Delta$ for $k\in Z^{+}$ and select a parameter $\theta \in [0,1]$. Starting from initial values $(y_0,r_0^{\Delta })=(x_0,i_0)$, the numerical scheme is defined as follows:

$$\left\{\begin{array}{cc}\hfill u_k& =y_k+\theta f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta ,\hfill \\ \hfill y_{k+1}& =y_k+f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta +g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k\hfill \\ \hfill & +h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta N_k,\hfill \end{array}\right.$$

(7)

where $y_k$ and $u_k$ are numerical approximations to the solution $x\left(t_k\right)$, $\Delta {\omega }_k=\omega \left(t_{k+1}\right)-\omega \left(t_k\right)$, $\Delta N_k=N\left(t_{k+1}\right)-N\left(t_k\right)$, and $r_k^{\Delta }=r\left(t_k\right)$ as previously defined.

When $\theta =0$, Scheme (7) reduces to the classical Euler–Maruyama method, whereas $\theta =1$ yields the split-step backward Euler variant.

At the end of this section, we formulate the almost sure exponential stability for both the trivial solution $x\left(t\right)$ and the approximate solution $y_k$ of Equation (1).

Definition 1. 

Let the initial condition $x_0$ be bounded and $i_0\in S$.

(1) 

The trivial solution of Equation (1) is referred to as almost surely exponentially stable in the sense that there exists a constant $\epsilon >0$ satisfying

$$\underset{t\to \infty }{lim\; sup}{\displaystyle \frac{log|x(t)|}{t}}\le -\epsilon a.s.$$

(8)

(2) 

The numerical approximation$y_k$, generated by Scheme (7), is referred to as almost surely exponentially stable when there exists a constant $\eta >0$ satisfying

$$\underset{k\to \infty }{lim\; sup}{\displaystyle \frac{log|y_k|}{k\Delta }}\le -\eta a.s.$$

(9)

3. Almost Sure Exponential Stability of the Trivial Solution and the $\mathit{SS}\mathit{\theta }$-Method

This section aims to establish the almost sure exponential stability of both the trivial solution and its corresponding numerical approximation via the $SS\theta$-method for Equation (1).

The following theorem provides a rigorous statement regarding the almost sure exponential stability of the trivial solution $x\left(t\right)$.

Theorem 2. 

Presuming that (H1)–(H2) and Inequality (4) are valid. If ${\lambda }_3>{\lambda }_4+\lambda (1+2{\lambda }_1+2{\lambda }_2)$ holds, then the trivial solution $x\left(t\right)$ to Equation (1), starting from any bounded initial value $x_0\in {\mathbb{R}}^n$ and $i_0\in S$, satisfies

$$\underset{t\to \infty }{lim\; sup}{\displaystyle \frac{log|x(t)|}{t}}\le -{\displaystyle \frac{\epsilon }{2}}a.s.,$$

(10)

where $\epsilon =1\wedge \left\{{\lambda }_3-{\lambda }_4-\lambda (1+2{\lambda }_1+2{\lambda }_2)\right\}.$

Proof. 

Using the Itô’s formula to $e^{\epsilon t}{|x\left(t\right)|}^2$ yields

$$\begin{array}{cc}\hfill d\left(e^{\epsilon t}{|x\left(t\right)|}^2\right)=& \epsilon e^{\epsilon t}{|x\left(t\right)|}^{2}dt+e^{\epsilon t}\left[2x^{\top }\left(t\right)f(x\left(t\right),x\left(qt\right),r\left(t\right),t)+{|g(x\left(t\right),x\left(qt\right),r\left(t\right),t)|}^2\right]dt\hfill \\ \hfill & +2e^{\epsilon t}{x}^{\top }\left(t\right)g(x\left(t\right),x\left(qt\right),r\left(t\right),t)d\omega \left(t\right)\hfill \\ \hfill & +e^{\epsilon t}\left({|x\left(t\right)+h(x\left(t\right),x\left(qt\right),r\left(t\right),t)|}^2-{|x\left(t\right)|}^2\right)dN\left(t\right).\hfill \end{array}$$

(11)

Using the decomposition $N\left(t\right)=\tilde{N}\left(t\right)+\lambda t$, one integrates both sides to obtain

$$\begin{array}{cc}\hfill e^{\epsilon t}{|x\left(t\right)|}^2=& |x_0{|}^2+\epsilon {\int }_0^t{e}^{\epsilon s}{|x\left(s\right)|}^{2}ds\hfill \\ \hfill & +{\int }_0^t{e}^{\epsilon s}\left[2x^{\top }\left(s\right)f(x\left(s\right),x\left(qs\right),r\left(s\right),s)+{|g(x\left(s\right),x\left(qs\right),r\left(s\right),s)|}^2\right]ds\hfill \\ \hfill & +\lambda {\int }_0^t{e}^{\epsilon s}\left({|x\left(s\right)+h(x\left(s\right),x\left(qs\right),r\left(s\right),s)|}^2-{|x\left(s\right)|}^2\right)ds\hfill \\ \hfill & +2{\int }_0^t{e}^{\epsilon s}{x}^{\top }\left(s\right)g(x\left(s\right),x\left(qs\right),r\left(s\right),s)d\omega \left(s\right)\hfill \\ \hfill & +{\int }_0^t{e}^{\epsilon s}\left({|x\left(s\right)+h(x\left(s\right),x\left(qs\right),r\left(s\right),s)|}^2-{|x\left(s\right)|}^2\right)d\tilde{N}\left(s\right).\hfill \end{array}$$

(12)

Define the local martingale $M\left(t\right)$ by

$$\begin{array}{cc}\hfill M\left(t\right)=& 2{\int }_0^t{e}^{\epsilon s}{x}^{\top }\left(s\right)g(x\left(s\right),x\left(qs\right),r\left(s\right),s)d\omega \left(s\right)\hfill \\ \hfill & +{\int }_0^t{e}^{\epsilon s}\left({|x\left(s\right)+h(x\left(s\right),x\left(qs\right),r\left(s\right),s)|}^2-{|x\left(s\right)|}^2\right)d\tilde{N}\left(s\right)\hfill \end{array}$$

with $M\left(0\right)=0$. Invoking inequalities in Equations (3) and (4) and the elementary estimate $2x^{\top }\left(s\right)h(·)\le {|x\left(s\right)|}^2+{|h(·)|}^2$, one deduces

$$\begin{array}{cc}\hfill e^{\epsilon t}{|x\left(t\right)|}^2\le & |x_0{|}^2+{\int }_0^t{e}^{\epsilon s}\left[\epsilon -{\lambda }_3+\lambda (1+2{\lambda }_1)\right]{|x\left(s\right)|}^{2}ds\hfill \\ \hfill & +q{\int }_0^t{e}^{\epsilon s}\left({\lambda }_4+2\lambda {\lambda }_2\right)e^{-(1-q)s}{|x\left(qs\right)|}^{2}ds+M\left(t\right).\hfill \end{array}$$

By performing a change of variable in the delay term and bounding ${|x\left(qs\right)|}^2$ in terms of ${|x\left(s\right)|}^2$, one can further write

$$\begin{array}{cc}\hfill e^{\epsilon t}{|x\left(t\right)|}^2\le & |x_0{|}^2+{\int }_0^t{e}^{\epsilon s}\left[\epsilon -{\lambda }_3+\lambda (1+2{\lambda }_1)\right]{|x\left(s\right)|}^{2}ds\hfill \\ \hfill & +{\int }_0^t{e}^{(\epsilon -1+q)s/q}\left({\lambda }_4+2\lambda {\lambda }_2\right){|x\left(s\right)|}^{2}ds+M\left(t\right).\hfill \end{array}$$

It follows from $\epsilon =1\wedge \{{\lambda }_3-{\lambda }_4-\lambda (1+2{\lambda }_1+2{\lambda }_2)\}$ that one derives $\epsilon \le 1$, thus $e^{(\epsilon -1+q)s/q}\le e^{\epsilon s}$. Then,

$$\begin{array}{cc}\hfill e^{\epsilon t}{|x\left(t\right)|}^2& \le |x_0{|}^2+{\int }_0^t{e}^{\epsilon s}[\epsilon -{\lambda }_3+{\lambda }_4+\lambda (1+2{\lambda }_1+2{\lambda }_2)]{|x\left(s\right)|}^{2}ds+M\left(t\right)\hfill \\ \hfill & \le |x_0{|}^2+M\left(t\right).\hfill \end{array}$$

(13)

Thanks to the non-negative semi-martingale convergence theorem [7] (Theorem 1.1.10), it follows that

$$\underset{t\to \infty }{lim\; sup}{e}^{\epsilon t}{|x\left(t\right)|}^2<\infty .$$

Denote $\rho ={lim\; sup}_{t\to \infty }{e}^{\epsilon t}{|x\left(t\right)|}^2<\infty$. Then, for any fixed $\widetilde{ϵ}>0$, there exists a time $T(\widetilde{ϵ},\rho )>0$ such that for all $t>T(\widetilde{ϵ},\rho )$, one has $e^{\epsilon t}{|x\left(t\right)|}^2<\rho +\widetilde{ϵ}.$ Taking logarithms yields $\epsilon t+2log|x\left(t\right)|\le log(\rho +\widetilde{ϵ}),$ which implies Equation (10). The proof is complete. □

We now turn our attention to analyzing the almost sure exponential stability of the numerical solution $y_k$.

Theorem 3. 

Given that all the conditions outlined in Theorem 2 are fulfilled. Additionally, for all $(x,y,i,t)\in {\mathbb{R}}^n\times {\mathbb{R}}^n\times S\times {\mathbb{R}}^{+}$, suppose the function $f(x,y,i,t)$ satisfies

$${|f(x,y,i,t)|}^2\le {\lambda }_5{|x|}^2+{\lambda }_{6}q{e}^{-(1-q)t}{|y|}^2,$$

(14)

where ${\lambda }_5,{\lambda }_6>0$. Define

$$\epsilon =min\left\{1,{\lambda }_3-2\lambda {\lambda }_1-\lambda -q\left(⌊{\displaystyle \frac{1}{q}}⌋+1\right)({\lambda }_4+2\lambda {\lambda }_2)\right\},$$

(15)

with ${\lambda }_3>2\lambda {\lambda }_1+\lambda +q\left(⌊{\displaystyle \frac{1}{q}}⌋+1\right)({\lambda }_4+2\lambda {\lambda }_2).$ Consequently, for any given $\delta \in (0,\epsilon /2)$, there is a positive constant $\overline{\Delta }$ such that for all step sizes $\Delta \in (0,\overline{\Delta }]$ and any $x_0$ that is bounded and ${\mathcal{F}}_0$-measurable, the numerical solution $y_k$ produced by Scheme (7) satisfies

$$\underset{k\to \infty }{lim\; sup}{\displaystyle \frac{log|y_k|}{k\Delta }}\le -{\displaystyle \frac{\epsilon }{2}}+\delta a.s.$$

(16)

That is, the $SS\theta$-method preserves the almost sure exponential stability of Equation (1).

Proof. 

It follows from Equation (7) that yields

$$\begin{array}{cc}\hfill |y_{k+1}{|}^2=& |y_k+f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta \hfill \\ \hfill & +g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k+h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta N_k{|}^2\hfill \\ \hfill =& |y_k{|}^2+|f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2{\Delta }^2+|g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2{|\Delta {\omega }_k|}^2\hfill \\ \hfill & +|h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2{|\Delta N_k|}^2\hfill \\ \hfill & +2\langle y_k,f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\rangle \Delta \hfill \\ \hfill & +2\langle y_k+f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta ,h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta N_k\rangle \hfill \\ \hfill & +2\langle y_k+f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta ,g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k\rangle \hfill \\ \hfill & +2\langle g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k,h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta N_k\rangle .\hfill \end{array}$$

(17)

Note that

$$\begin{array}{cc}\hfill & |g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2{|\Delta {\omega }_k|}^2\hfill \\ \hfill & =|g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2(|\Delta {\omega }_k{|}^2-\Delta )+|g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2\Delta ,\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill & |h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2{|\Delta N_k|}^2\hfill \\ \hfill & =|h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2(|\Delta N_k{|}^2-\lambda \Delta (1+\lambda \Delta ))\hfill \\ \hfill & +\lambda \Delta (1+\lambda \Delta )|h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2.\hfill \end{array}$$

(19)

According to Equation (7) that one derives

$$\begin{array}{cc}\hfill & 2\langle y_k,f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta \rangle \hfill \\ \hfill & =2\langle u_k,f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta \rangle -2\theta {\Delta }^2{|f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)|}^2,\hfill \\ \hfill & 2\langle y_k+f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta ,h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta N_k\rangle \hfill \\ \hfill & =2\langle u_k+(1-\theta )\Delta f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k),h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\tilde{N}}_k\rangle \hfill \\ \hfill & +2\lambda \Delta \langle u_k,h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\rangle \hfill \\ \hfill & +2\lambda {\Delta }^2(1-\theta )\langle f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k),h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\rangle ,\hfill \\ \hfill & \le 2\langle u_k+(1-\theta )\Delta f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k),h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\tilde{N}}_k\rangle \hfill \\ \hfill & +\lambda \Delta |u_k{|}^2+[\lambda \Delta +(1-\theta )\lambda {\Delta }^2]{|h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)|}^2\hfill \\ \hfill & +(1-\theta )\lambda {\Delta }^2{|f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)|}^2,\hfill \end{array}$$

(20)

and

$$\begin{array}{cc}\hfill & 2\langle y_k+f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta ,g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k\rangle \hfill \\ \hfill & =2\langle u_k+(1-\theta )f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta ,g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k\rangle .\hfill \end{array}$$

(21)

Therefore, substituting Equations (18)–(21) into Equation (17) yields

$$\begin{array}{cc}\hfill |y_{k+1}{|}^2\le & |y_k{|}^2+\lambda \Delta |u_k{|}^2+[(1-2\theta )+\lambda (1-\theta )]{\Delta }^2{|f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)|}^2\hfill \\ \hfill & +\Delta [2u_k^{T}f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)+|g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2]\hfill \\ \hfill & +[\lambda \Delta (2+\lambda \Delta )+\lambda {\Delta }^2(1-\theta )]{|h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)|}^2\hfill \\ \hfill & +l_k^{\prime }+m_k^{\prime }+n_k^{\prime }+p_k^{\prime }+q_k^{\prime },\hfill \end{array}$$

(22)

where

$$\begin{array}{cc}\hfill & l_k^{\prime }=|g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2(|\Delta {\omega }_k{|}^2-\Delta ),\hfill \\ \hfill & m_k^{\prime }=|h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2(|\Delta N_k{|}^2-\lambda \Delta (1+\lambda \Delta )),\hfill \\ \hfill & n_k^{\prime }=2\langle u_k+(1-\theta )f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta ,g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k\rangle ,\hfill \\ \hfill & p_k^{\prime }=2\langle g(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\omega }_k,h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta N_k\rangle ,\hfill \\ \hfill & q_k^{\prime }=2\langle u_k+(1-\theta )\Delta f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k),h(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)\Delta {\tilde{N}}_k\rangle .\hfill \end{array}$$

(i):

For $\theta \in [0,{\displaystyle \frac{1}{2}})$, it follows from Equations (3) and (4) and Equation (14) has

$$\begin{array}{cc}\hfill & |y_{k+1}{|}^2\hfill \\ \hfill & \le |y_k{|}^2+[(1-2\theta )+\lambda (1-\theta )]{\Delta }^2[{\lambda }_5|u_k{|}^2+{\lambda }_{6}q{e}^{-(1-q)k\Delta }|u_{\lfloor qk\rfloor }{|}^2]\hfill \\ \hfill & +\Delta [-{\lambda }_3|u_k{|}^2+{\lambda }_{4}q{e}^{-(1-q)k\Delta }|u_{\lfloor qk\rfloor }{|}^2]+\lambda \Delta |u_k{|}^2\hfill \\ \hfill & +[\lambda \Delta (2+\lambda \Delta )+\lambda {\Delta }^2(1-\theta )]({\lambda }_1|u_k{|}^2+{\lambda }_{2}q{e}^{-(1-q)k\Delta }|u_{\lfloor qk\rfloor }{|}^2)\hfill \\ \hfill & +l_k^{\prime }+m_k^{\prime }+n_k^{\prime }+p_k^{\prime }+q_k^{\prime },\hfill \end{array}$$

(23)

that is,

$$\begin{array}{cc}\hfill & |y_{k+1}{|}^2-{|y_k|}^2\hfill \\ \hfill & \le \{{\lambda }_5[(1-2\theta )+\lambda (1-\theta )]{\Delta }^2-{\lambda }_3\Delta +{\lambda }_1[\lambda \Delta (2+\lambda \Delta )+\lambda {\Delta }^2(1-\theta )]+\lambda \Delta \}\hfill \\ \hfill & \times |u_k{|}^2+\left\{{\lambda }_6[(1-2\theta )+\lambda (1-\theta )]{\Delta }^2+{\lambda }_4\Delta +{\lambda }_2[\lambda \Delta (2+\lambda \Delta )\right.\hfill \\ \hfill & \left.+\lambda {\Delta }^2(1-\theta )]\right\}q{e}^{-(1-q)k\Delta }{|u_{\lfloor qk\rfloor }|}^2+l_k^{\prime }+m_k^{\prime }+n_k^{\prime }+p_k^{\prime }+q_k^{\prime }.\hfill \end{array}$$

(24)

For any constant $C\ge 1$, note that $1-C^{-\Delta }=1-e^{-\Delta logC}\le (logC)\Delta$, one gets

$$\begin{array}{cc}\hfill & C^{(k+1)\Delta }|y_{k+1}{|}^2-C^{k\Delta }{|y_k|}^2\hfill \\ \hfill & =C^{(k+1)\Delta }(|y_{k+1}{|}^2-|y_k{|}^2)+C^{(k+1)\Delta }(1-C^{-\Delta }){|y_k|}^2\hfill \\ \hfill & \le C^{(k+1)\Delta }\left\{{\lambda }_5[(1-2\theta )+\lambda (1-\theta )]{\Delta }^2-{\lambda }_3\Delta +{\lambda }_1[\lambda \Delta (2+\lambda \Delta )+\lambda {\Delta }^2(1-\theta )]\right.\hfill \\ \hfill & \left.+\lambda \Delta \right\}{|u_k|}^2+C^{(k+1)\Delta }\left\{{\lambda }_6[(1-2\theta )+\lambda (1-\theta )]{\Delta }^2+{\lambda }_4\Delta +{\lambda }_2\left[\lambda \Delta (2+\lambda \Delta )\right.\right.\hfill \\ \hfill & \left.\left.+\lambda {\Delta }^2(1-\theta )\right]\right\}q{e}^{-(1-q)k\Delta }{|u_{\lfloor qk\rfloor }|}^2+C^{(k+1)\Delta }{M}_k^{\prime }\hfill \\ \hfill & +C^{(k+1)\Delta }(logC)\Delta {|y_k|}^2,\hfill \end{array}$$

(25)

where $M_k^{\prime }=l_k^{\prime }+m_k^{\prime }+n_k^{\prime }+p_k^{\prime }+q_k^{\prime }$, and $M_k^{\prime }$ is a local martingale. Since for any $|y_k{|}^2={|u_k-\theta \Delta f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)|}^2$, then by Equation (14) that one gains

$$\begin{array}{cc}\hfill |y_k{|}^2=& |u_k-\theta \Delta f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k){|}^2\hfill \\ \hfill \le & (1+\theta \Delta )|u_k{|}^2+\theta \Delta (1+\theta \Delta ){|f(u_k,u_{\lfloor qk\rfloor },r_k^{\Delta },t_k)|}^2\hfill \\ \hfill \le & (1+\theta \Delta )(1+{\lambda }_5\theta \Delta )|u_k{|}^2+{\lambda }_6\theta \Delta (1+\theta \Delta )q{e}^{-(1-q)k\Delta }{|u_{\lfloor qk\rfloor }|}^2.\hfill \end{array}$$

(26)

Substituting Equation (26) into Equation (25) that one derives

$$\begin{array}{cc}\hfill & C^{(k+1)\Delta }|y_{k+1}{|}^2-C^{k\Delta }{|y_k|}^2\hfill \\ \hfill & \le C^{(k+1)\Delta }\{{\lambda }_5[(1-2\theta )+\lambda (1-\theta )]\Delta -{\lambda }_3+{\lambda }_1[\lambda (2+\lambda \Delta )+\lambda \Delta (1-\theta )]\hfill \\ \hfill & +\lambda +(1+\theta \Delta )(logC)(1+{\lambda }_5\theta \Delta )\}\Delta |u_k{|}^2\hfill \\ \hfill & +C^{(k+1)\Delta }\{{\lambda }_6[(1-2\theta )+\lambda (1-\theta )]\Delta +{\lambda }_4+{\lambda }_2[\lambda (2+\lambda \Delta )+\lambda \Delta (1-\theta )]\hfill \\ \hfill & +{\lambda }_6\theta \Delta (1+\theta \Delta )logC\}q\Delta e^{(-(1-q)k\Delta }{|u_{\lfloor qk\rfloor }|}^2+C^{(k+1)\Delta }{M}_k^{\prime }\hfill \\ \hfill & =b_1(C,\Delta )C^{(k+1)\Delta }\Delta |u_k{|}^2+b_2(C,\Delta )q{C}^{(k+1)\Delta }\Delta e^{-(1-q)k\Delta }{|u_{\lfloor qk\rfloor }|}^2\hfill \\ \hfill & +C^{(k+1)\Delta }{M}_k^{\prime },\hfill \end{array}$$

(27)

where

$$\begin{array}{cc}\hfill b_1(C,\Delta )=& {\lambda }_5[(1-2\theta )+\lambda (1-\theta )]\Delta -{\lambda }_3+{\lambda }_1[\lambda (2+\lambda \Delta )+\lambda \Delta (1-\theta )]\hfill \\ \hfill & +\lambda +(1+\theta \Delta )(logC)(1+{\lambda }_5\theta \Delta ),\hfill \\ \hfill b_2(C,\Delta )=& {\lambda }_6[(1-2\theta )+\lambda (1-\theta )]\Delta +{\lambda }_4+{\lambda }_2[\lambda (2+\lambda \Delta )+\lambda \Delta (1-\theta )]\hfill \\ \hfill & +{\lambda }_6\theta \Delta (1+\theta \Delta )logC.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill C^{k\Delta }{|y_k|}^2\le & |x_0{|}^2+b_1(C,\Delta )\Delta \sum _{i=0}^{k-1}{C}^{(i+1)\Delta }{|u_i|}^2+\sum _{i=0}^{k-1}{C}^{(i+1)\Delta }{M}_i^{\prime }\hfill \\ \hfill & +b_2(C,\Delta )q\Delta \sum _{i=0}^{k-1}{C}^{(i+1)\Delta }{e}^{-(1-q)i\Delta }{|u_{\lfloor qi\rfloor }|}^2.\hfill \end{array}$$

(28)

Similar to the estimation of the inequality (54) in [18], one can get

$$\begin{array}{cc}\hfill & \sum _{i=0}^{k-1}exp(-(1-q)i\Delta )C^{(i+1)\Delta }{|u_{\lfloor qi\rfloor }|}^2\hfill \\ \hfill & \le (\lfloor 1/q\rfloor +1)\sum _{j=0}^{\lfloor q(k-1)\rfloor }{e}^{\left(-{\displaystyle \frac{1-q}{q}}j\Delta \right)}{C}^{\left(\right(j+1)/q+1)\Delta }{|u_j|}^2\hfill \\ \hfill & =(\lfloor 1/q\rfloor +1)\sum _{j=0}^{k-1}{e}^{\left(-{\displaystyle \frac{1-q}{q}}j\Delta \right)}{C}^{\left(\right(j+1)/q+1)\Delta }{|u_j|}^2\hfill \\ \hfill & -(\lfloor 1/q\rfloor +1)\sum _{j=\lfloor q(k-1)\rfloor +1}^{k-1}{e}^{\left(-{\displaystyle \frac{1-q}{q}}j\Delta \right)}{C}^{\left(\right(j+1)/q+1)\Delta }{|u_j|}^2\hfill \\ \hfill & \le (\lfloor 1/q\rfloor +1)\sum _{j=0}^{k-1}{e}^{\left(-{\displaystyle \frac{1-q}{q}}j\Delta \right)}{C}^{\left(\right(j+1)/q+1)\Delta }{|u_j|}^2.\hfill \end{array}$$

(29)

Substituting Equation (29) into Equation (28) that one gains

$$\begin{array}{cc}\hfill C^{k\Delta }{|y_k|}^2& \le |x_0{|}^2+b_1(C,\Delta )\Delta \sum _{i=0}^{k-1}{C}^{(i+1)\Delta }{|u_i|}^2+\sum _{i=0}^{k-1}{C}^{(i+1)\Delta }{M}_i^{\prime }\hfill \\ \hfill & +q(\lfloor 1/q\rfloor +1)b_2(C,\Delta )\Delta \sum _{i=0}^{k-1}{C}^{\left(\right(i+1)/q+1)\Delta }{e}^{\left(-{\displaystyle \frac{1-q}{q}}i\Delta \right)}{|u_i|}^2.\hfill \end{array}$$

(30)

Denote

$$\begin{array}{c}\hfill h(C,\Delta )=b_1(C,\Delta )+q(\lfloor 1/q\rfloor +1)C^{\Delta /q}{b}_2(C,\Delta ).\end{array}$$

Then for $q\in (0,1)$ and $\theta \in [0,1/2)$, one further derives

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial h(C,\Delta )}{\partial C}}=& {\displaystyle \frac{1}{C}}(1+\theta \Delta )(1+{\lambda }_5\theta \Delta )+(\lfloor 1/q\rfloor +1)\Delta C^{\Delta /q-1}{b}_2(C,\Delta )\hfill \\ \hfill & +q(\lfloor 1/q\rfloor +1)C^{\Delta /q-1}{\lambda }_6\theta \Delta (1+\theta \Delta )>0.\hfill \end{array}$$

Let

$${\Delta }_1={\displaystyle \frac{{\lambda }_3-\lambda (1+2{\lambda }_1)-q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)}{[(1-2\theta )+\lambda (1-\theta )][{\lambda }_5+{\lambda }_{6}q(\lfloor 1/q\rfloor +1)]+\lambda (\lambda +1-\theta )[{\lambda }_1+{\lambda }_{2}q(\lfloor 1/q\rfloor +1)]}}.$$

It follows from ${\lambda }_3>\lambda +2\lambda {\lambda }_1+q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)$ that for any $\Delta \in (0,{\Delta }_1)$ one yields

$$\begin{array}{c}\hfill h(1,\Delta )=b_1(1,\Delta )+q(\lfloor 1/q\rfloor +1)b_2(1,\Delta )<0.\end{array}$$

As a result, one can deduce the existence of a unique constant ${\tilde{C}}_{\Delta }>1$ such that the relation $h({\tilde{C}}_{\Delta },\Delta )=0$ holds. If ${\tilde{C}}_{\Delta }>e$, then $h(e,\Delta )<0$. Set $C=e$, it follows from Equation (30) that one gains

$$\begin{array}{cc}\hfill e^{k\Delta }{|y_k|}^2\le & |x_0{|}^2+b_1(e,\Delta )\Delta \sum _{i=0}^{k-1}{e}^{(i+1)\Delta }{|u_i|}^2+\sum _{i=0}^{k-1}{e}^{(i+1)\Delta }{M}_i^{\prime }\hfill \\ \hfill & +q(\lfloor 1/q\rfloor +1)b_2(e,\Delta )e^{\Delta /q}\Delta \sum _{i=0}^{k-1}{e}^{(i+1)\Delta }{|u_i|}^2\hfill \\ \hfill =& |x_0{|}^2+h(e,\Delta )\Delta \sum _{i=0}^{k-1}{e}^{(i+1)\Delta }{|u_i|}^2+\sum _{i=0}^{k-1}{e}^{(i+1)\Delta }{M}_i^{\prime }\hfill \\ \hfill \le & |x_0{|}^2+\sum _{i=0}^{k-1}{e}^{(i+1)\Delta }{M}_i^{\prime }.\hfill \end{array}$$

(31)

By invoking the discrete semi-martingale convergence theorem [18] (Lemma 2), one obtains $\underset{k\to \infty }{lim\; sup}{e}^{k\Delta }{|y_k|}^2<\infty \mathrm{a}.\mathrm{s}.$ Consequently, there exists a finite and positive random variable $\eta$ such that $\underset{k\to \infty }{lim\; sup}{e}^{k\Delta }{|y_k|}^2<\eta .$ For

$$\begin{array}{c}\hfill \underset{\Delta \to 0}{lim}h(e,\Delta )=-{\lambda }_3+2\lambda {\lambda }_1+\lambda +1+q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)<0.\end{array}$$

then ${\lambda }_3-2\lambda {\lambda }_1-\lambda -q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)>1$. It follows from (15) that one can get $\epsilon =1$. For any $\Delta \in (0,{\Delta }_1)$, one gains

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim\; sup}{\displaystyle \frac{log|y_k|}{k\Delta }}\le \underset{k\to \infty }{lim\; sup}{\displaystyle \frac{log\eta }{2k\Delta }}-{\displaystyle \frac{1}{2}}=-{\displaystyle \frac{1}{2}}.\end{array}$$

(32)

Else if ${\tilde{C}}_{\Delta }\le e$, then $e^{\left(-{\displaystyle \frac{1-q}{q}}i\Delta \right)}\le {\tilde{C}}_{\Delta }^{\left(-{\displaystyle \frac{1-q}{q}}i\Delta \right)}$. Set $C={\tilde{C}}_{\Delta }$. According to Equation (30), that one gains

$$\begin{array}{cc}\hfill {\tilde{C}}_{\Delta }^{k\Delta }{|y_k|}^2\le & |x_0{|}^2+b_1({\tilde{C}}_{\Delta },\Delta )\Delta \sum _{i=0}^{k-1}{\tilde{C}}_{\Delta }^{(i+1)\Delta }{|u_i|}^2+\sum _{i=0}^{k-1}{\tilde{C}}_{\Delta }^{(i+1)\Delta }{M}_i^{\prime }\hfill \\ \hfill & +q(\lfloor 1/q\rfloor +1)b_2({\tilde{C}}_{\Delta },\Delta ){\tilde{C}}_{\Delta }^{\Delta /q}\Delta \sum _{i=0}^{k-1}{\tilde{C}}_{\Delta }^{(i+1)\Delta }{|u_i|}^2\hfill \\ \hfill =& |x_0{|}^2+h({\tilde{C}}_{\Delta },\Delta )\Delta \sum _{i=0}^{k-1}{\tilde{C}}_{\Delta }^{(i+1)\Delta }{|u_i|}^2+\sum _{i=0}^{k-1}{\tilde{C}}_{\Delta }^{(i+1)\Delta }{M}_i^{\prime }\hfill \\ \hfill =& |x_0{|}^2+\sum _{i=0}^{k-1}{\tilde{C}}_{\Delta }^{(i+1)\Delta }{M}_i^{\prime }.\hfill \end{array}$$

(33)

According to the discrete semi-martingale convergence theorem, there exists a finite and positive random variable ${\eta }_1$ such that $\underset{k\to \infty }{lim\; sup}{\left({\tilde{C}}_{\Delta }\right)}^{k\Delta }{|y_k|}^2<{\eta }_1$. Moreover, when $\Delta \in (0,{\Delta }_1)$ and the function $h({\tilde{C}}_{\Delta },\Delta )=0$, it follows that

$$\begin{array}{c}\hfill \underset{\Delta \to 0}{lim}h({\tilde{C}}_{\Delta },\Delta )=-{\lambda }_3+2\lambda {\lambda }_1+\lambda +\underset{\Delta \to 0}{lim}log{\tilde{C}}_{\Delta }+q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)=0.\end{array}$$

So ${\lambda }_3-2\lambda {\lambda }_1-\lambda -q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)=\underset{\Delta \to 0}{lim}log{\tilde{C}}_{\Delta }\le 1.$ One can obtain $\epsilon ={\lambda }_3-2\lambda {\lambda }_1-\lambda -q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2),$ $\underset{\Delta \to 0}{lim}log{\tilde{C}}_{\Delta }=\epsilon$. So, for any $\delta \in (0,\epsilon /2)$, there exists ${\Delta }_2>0$ such that $log{\tilde{C}}_{\Delta }>\epsilon -2\delta$. Therefore, for any $\Delta \in (0,{\Delta }_1\wedge {\Delta }_2)$, one has

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim\; sup}{\displaystyle \frac{log|y_k|}{k\Delta }}\le \underset{k\to \infty }{lim\; sup}{\displaystyle \frac{log{\eta }_1}{2k\Delta }}-{\displaystyle \frac{log{\tilde{C}}_{\Delta }}{2}}=-\epsilon /2+\delta <0.\end{array}$$

(34)

In summary, when $\theta \in [0,1/2)$, the $SS\theta$-method applied to Equation (1) is almost surely exponentially stable.

(ii):

For $\theta \in [{\displaystyle \frac{1}{2}},1]$, Equation (23) becomes

$$\begin{array}{cc}\hfill |y_{k+1}{|}^2& \le |y_k{|}^2+\lambda (1-\theta ){\Delta }^2[{\lambda }_5|u_k{|}^2+{\lambda }_{6}q{e}^{-(1-q)k\Delta }|u_{\lfloor qk\rfloor }{|}^2]\hfill \\ \hfill & +\Delta [-{\lambda }_3|u_k{|}^2+{\lambda }_{4}q{e}^{-(1-q)k\Delta }|u_{\lfloor qk\rfloor }{|}^2]+\lambda \Delta |u_k{|}^2\hfill \\ \hfill & +[\lambda \Delta (2+\lambda \Delta )+\lambda {\Delta }^2(1-\theta )]({\lambda }_1|u_k{|}^2+{\lambda }_2{e}^{-(1-q)k\Delta }|u_{\lfloor qk\rfloor }{|}^2)\hfill \\ \hfill & +l_k^{\prime }+m_k^{\prime }+n_k^{\prime }+p_k^{\prime }+q_k^{\prime }.\hfill \end{array}$$

(35)

Similarly, one gains

$$\begin{array}{cc}\hfill C^{k\Delta }{|y_k|}^2& \le |x_0{|}^2+b_1^{\prime }(C,\Delta )\Delta \sum _{i=0}^{k-1}{C}^{(i+1)\Delta }{|u_i|}^2+\sum _{i=0}^{k-1}{C}^{(i+1)\Delta }{M}_i^{\prime }\hfill \\ \hfill & +q(\lfloor 1/q\rfloor +1)b_2^{\prime }(C,\Delta )\Delta \sum _{i=0}^{k-1}{C}^{\left(\right(i+1)/q+1)\Delta }{e}^{\left(-{\displaystyle \frac{1-q}{q}}i\Delta \right)}{|u_i|}^2.\hfill \end{array}$$

(36)

where

$$\begin{array}{cc}\hfill b_1^{\prime }(C,\Delta )=& {\lambda }_5\lambda (1-\theta )\Delta -{\lambda }_3+{\lambda }_1[\lambda (2+\lambda \Delta )+\lambda \Delta (1-\theta )]\hfill \\ \hfill & +\lambda +(1+\theta \Delta )(logC)(1+{\lambda }_5\theta \Delta ),\hfill \\ \hfill b_2^{\prime }(C,\Delta )=& {\lambda }_6\lambda (1-\theta )\Delta +{\lambda }_4+{\lambda }_2[\lambda (2+\lambda \Delta )+\lambda \Delta (1-\theta )]\hfill \\ \hfill & +{\lambda }_6\theta \Delta (1+\theta \Delta )logC.\hfill \end{array}$$

Denote

$$\begin{array}{c}\hfill h_1(C,\Delta )=b_1^{\prime }(C,\Delta )+q(\lfloor 1/q\rfloor +1)C^{\Delta /q}{b}_2^{\prime }(C,\Delta ).\end{array}$$

Then for $q\in (0,1)$ and $\theta \in [1/2,1]$,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial h_1(C,\Delta )}{\partial C}}=& {\displaystyle \frac{1}{C}}(1+\theta \Delta )(1+{\lambda }_5\theta \Delta )+\Delta C^{\Delta /q-1}(\lfloor 1/q\rfloor +1)b_2^{\prime }(C,\Delta )\hfill \\ \hfill & +q(\lfloor 1/q\rfloor +1)C^{\Delta /q-1}{\lambda }_6\theta \Delta (1+\theta \Delta )>0.\hfill \end{array}$$

Set

$${\Delta }_3={\displaystyle \frac{{\lambda }_3-\lambda (1+2{\lambda }_1)-q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)}{\lambda (1-\theta )[{\lambda }_5+{\lambda }_{6}q(\lfloor 1/q\rfloor +1)]+\lambda (\lambda +1-\theta )[{\lambda }_1+{\lambda }_{2}q(\lfloor 1/q\rfloor +1)]}}.$$

It follows from ${\lambda }_3>\lambda +2\lambda {\lambda }_1+q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)$ that for any $\Delta \in (0,{\Delta }_3)$ one yields

$$\begin{array}{c}\hfill h_1(1,\Delta )=b_1^{\prime }(1,\Delta )+q(\lfloor 1/q\rfloor +1)b_2^{\prime }(1,\Delta )<0.\end{array}$$

In the remaining derivation, the reasoning is analogous to that for the proof of $\theta \in [0,1/2)$; it can be deduced that the $SS\theta$-method applied to Equation (1) also exhibits almost sure exponential stability when $\theta \in [1/2,1]$. This completes the proof. □

Remark 1. 

When $\theta =0$, numerical Scheme (7) reduces to the classical Euler–Maruyama method, and the scheme is equivalent to the split-step backward Euler method if $\theta =1$; thus, the classical Euler–Maruyama method and the split-step backward Euler method are involved in numerical Scheme (7). In addition, the studied equations in [14,15,16,18,20,21,23,24,25,32] are either SPDEs or SPDEs with Markov switching, authors did not take Poisson jumps into consideration. This paper examines SPDEs incorporating Markov switching and Poisson jumps, which renders the results herein more general.

4. A Numerical Experiment

This section offers a numerical example to demonstrate the theoretical results established in the preceding sections. Let $\omega \left(t\right)$ be a scalar Brownian motion, and let $N\left(t\right)$ denote a Poisson process with constant intensity $\lambda =1$. Consider the Markov chain $r\left(t\right)$, taking values in the state space $S=\{1,2\}$, with generator matrix

$$\mathrm{\Gamma }={\left({\gamma }_{ij}\right)}_{2\times 2}=\left[\begin{array}{cc}-1& 1\\ 2& -2\end{array}\right].$$

It is assumed that $\omega \left(t\right)$, $r\left(t\right)$, and $N\left(t\right)$ are mutually independent.

Without loss of generality, we fix $q=1/2$ and consider the following SPDEwMJ:

$$\begin{array}{cc}\hfill dx\left(t\right)=& f\left(x\right(t),x(qt),r(t),t)dt+g\left(x\right(t),x(qt),r(t),t)d\omega \left(t\right)\hfill \\ \hfill & +h\left(x\right(t),x(qt),r(t),t)dN\left(t\right),t\ge 0,\hfill \end{array}$$

(37)

subject to the initial condition $x_0=1$, where

$$f(x,y,i,t)=\left\{\begin{array}{cc}-4x+exp(-(1-q)t/2)siny,\hfill & \mathrm{if}i=1,\hfill \\ -3x+1/2exp(-(1-q)t/2)y,\hfill & \mathrm{if}i=2.\hfill \end{array}\right.$$

$$g(x,y,i,t)=\left\{\begin{array}{cc}1/2exp(-(1-q)t/2){\left(xy\right)}^{1/2},\hfill & \mathrm{if}i=1,\hfill \\ 1/2x+1/2exp(-(1-q)t/2)y,\hfill & \mathrm{if}i=2.\hfill \end{array}\right.$$

$$h(x,y,i,t)=\left\{\begin{array}{cc}-(1/4x+1/16yexp(-(1-q)t/2\left)\right),\hfill & \mathrm{if}i=1,\hfill \\ -(1/5x+1/8yexp(-(1-q)t/2\left)\right),\hfill & \mathrm{if}i=2.\hfill \end{array}\right.$$

Obviously, $f(0,0,i,t)=g(0,0,i,t)=h(0,0,i,t)=0$ for any $i\in S$ and $t\ge 0$. Now we check that conditions (H1), (H2), Equations (4) and (14) are satisfied with ${\lambda }_1=1/8$, ${\lambda }_2=1/16$ ${\lambda }_3=5$, ${\lambda }_4=2.25$, ${\lambda }_5=32$ and ${\lambda }_6=4$. Thus, one obtains

$$5={\lambda }_3>{\lambda }_4+\lambda (1+2{\lambda }_1+2{\lambda }_2)=3.625,$$

and

$$5={\lambda }_3>2\lambda {\lambda }_1+\lambda +q(\lfloor 1/q\rfloor +1)({\lambda }_4+2\lambda {\lambda }_2)=4.8125.$$

It follows directly from Theorems 2 and 3 that both the trivial solution of Equation (37) and its numerical approximation via the $SS\theta$-method defined in Equation (7) are almost surely exponentially stable. Furthermore, the corresponding Lyapunov exponents are no greater than $-0.5$ for the exact solution, and $-0.09375+\delta$ for the $SS\theta$-method, where $\delta \in (0,0.09375)$.

To validate these theoretical findings, we simulate the numerical solution of Equation (37) using the $SS\theta$-method described in Equation (7), with initial conditions $x_0=1$ and $r_0=1$. Following the simulation framework outlined in [33] (Chapter 4), the zero-one jump process is approximated via the acceptance-rejection method, under the assumption of a sufficiently small temporal step $\Delta$. Here, we choose $\Delta =0.001$ and examine the method’s behavior for $\theta \in [0,1]$ in increments of 0.1 to comprehensively evaluate the performance of the $SS\theta$-method. Additionally, to estimate the Lyapunov exponent numerically, we employ a Monte Carlo approach, generating 500 independent sample trajectories for each value of $\theta$. Among them, five representative sample paths are randomly selected and used for visualization purposes. The Lyapunov exponents computed at final time $T=100$ along these five individual sample paths are reported in

Table 1. Lyapunov exponents at $T=100$ using SS$\theta$-method in Equation (7) to Equation (37).

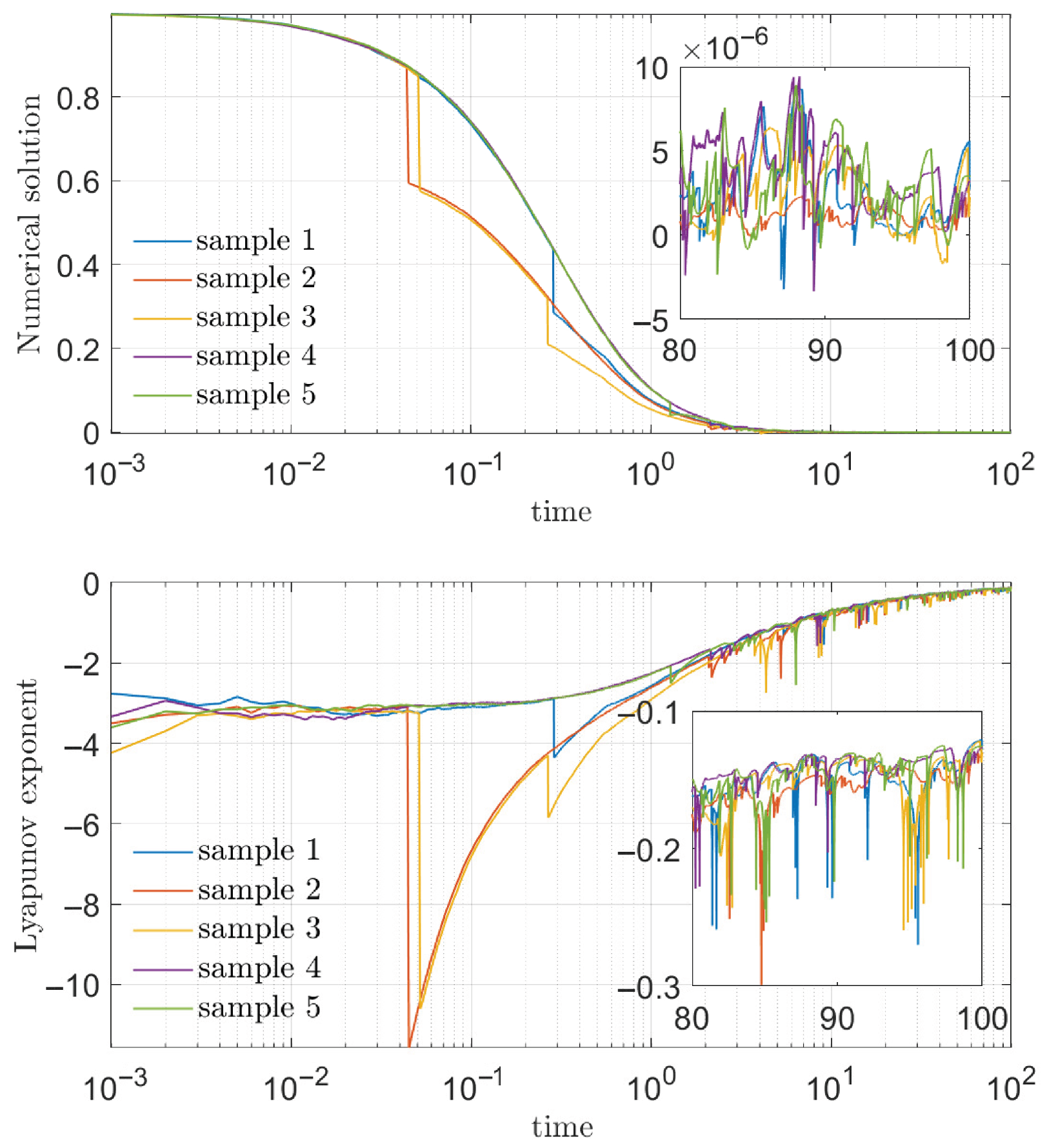
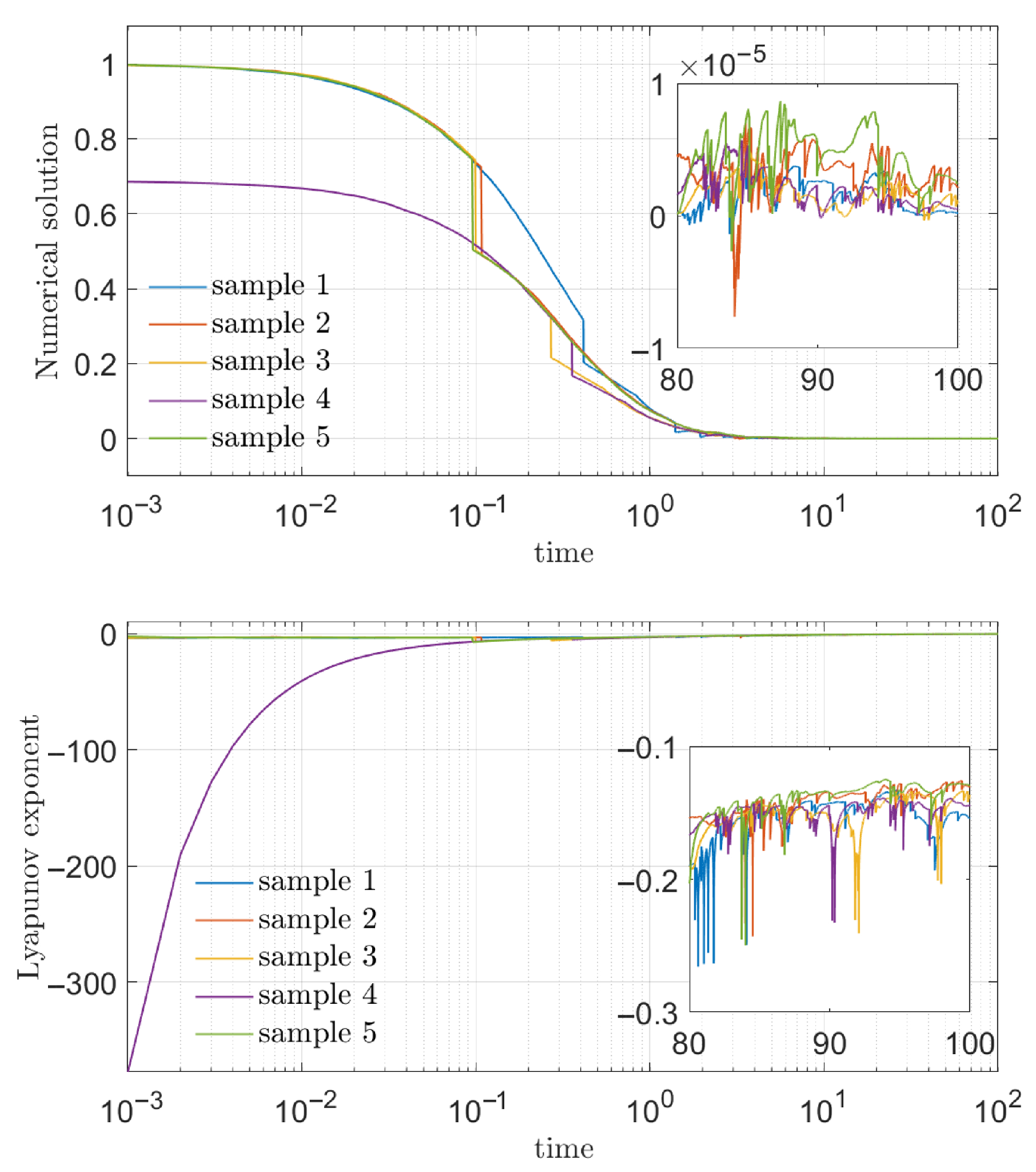
$\mathit{\theta }$	Sample 1	Sample 2	Sample 3	Sample 4	Sample 5
0.0	−0.13672	−0.13897	−0.13034	−0.18784	−0.12176
0.1	−0.12984	−0.13489	−0.12816	−0.13406	−0.12738
0.2	−0.14278	−0.14453	−0.14883	−0.15272	−0.14469
0.3	−0.1361	−0.15363	−0.16493	−0.16144	−0.1369
0.4	−0.12721	−0.13012	−0.12988	−0.12638	−0.12565
0.5	−0.13342	−0.12176	−0.12739	−0.13461	−0.14543
0.6	−0.15233	−0.13627	−0.13078	−0.14636	−0.14031
0.7	−0.12412	−0.12947	−0.1177	−0.12865	−0.12469
0.8	−0.15403	−0.13062	−0.13635	−0.14418	−0.12927
0.9	−0.12944	−0.13174	−0.12968	−0.14019	−0.13093
1.0	−0.13241	−0.12314	−0.12265	−0.12548	−0.14104

.

The numerical solutions and Lyapunov exponents with respect to time over 500 discredited sample paths along 5 individual paths are shown in Figure 1 and Figure 2. By virtue of Figure 1 and Figure 2, it can be seen that the numerical scheme via the $SS\theta$-method defined in Equation (7) is almost surely exponentially stable.

5. Conclusions

In this study, we propose a class of $SS\theta$-methods for analyzing the stability of stochastic pantograph differential equations with Markovian switching and jump perturbations. While the literature has extensively addressed the stability of such systems, relatively few results are available concerning the stability properties of their numerical approximations. This work aims to bridge this gap by contributing new insights into the almost sure exponential stability concerning both the exact and numerical solutions. We first establish the almost sure exponential stability of the trivial solution to the underlying system. Under an additional assumption that the drift term satisfies a linear growth condition, we further demonstrate that the numerical solutions obtained using the proposed $SS\theta$-method also retain this stability property. Finally, we support the theoretical analysis with numerical simulations, illustrating the effectiveness and consistency of the developed method.