On Trees with a Given Number of Vertices of Fixed Degree and Their Two Bond Incident Degree Indices
Abstract
1. Introduction
2. Extremal Values of and for Trees Containing no Vertex of Even Degree
- (i)
- Minimum value;
- (ii)
- Minimum value either for or for ;
- (iii)
- Maximum value for .
- (i)
- Minimum value;
- (ii)
- Minimum value either for or for ;
- (iii)
- Maximum value for .
3. Extremal Values of and for Trees with Even Degree Vertices
- (i)
- Minimum value;
- (ii)
- Minimum value either for or for ;
- (iii)
- Maximum value for .
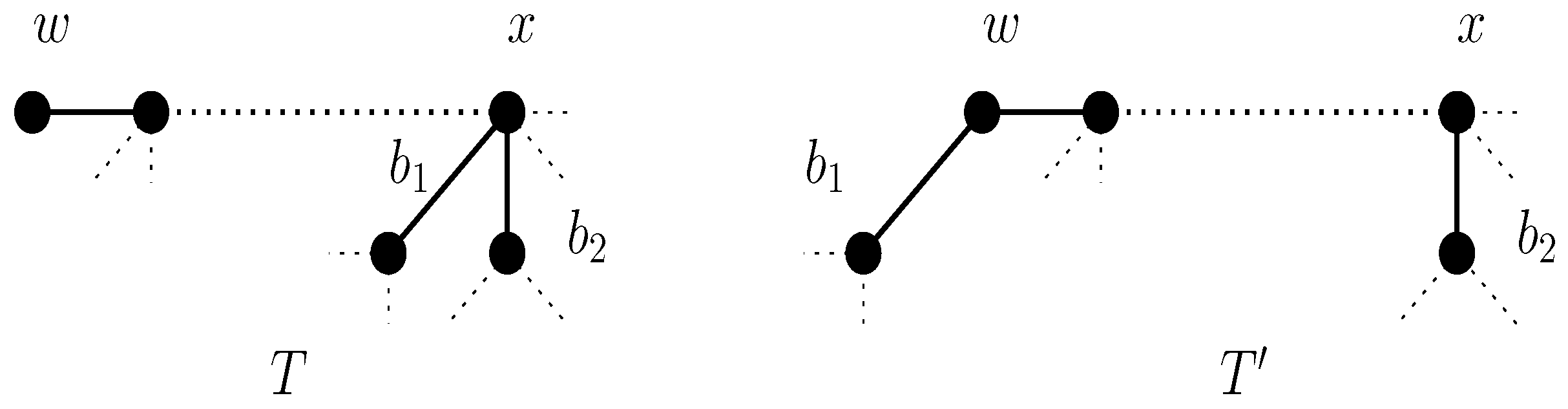
- (i)
- Minimizing
- (ii)
- Minimizing either for or for
- (iii)
- Maximizing for .
- (i)
- Maximum value;
- (ii)
- Maximum value either for or for ;
- (iii)
- Minimum value for .
- (i)
- Maximizing ;
- (ii)
- Maximizing either for or for ;
- (iii)
- Minimizing for .
4. Extremal Values of and for Trees with Vertices of Maximum Degree
- (i)
- Minimum value;
- (ii)
- Minimum value either for or for ;
- (iii)
- Maximum value for .
- (i)
- Minimum value;
- (ii)
- Minimum value either for or for ;
- (iii)
- Maximum value for .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Estrada, E.; Bonchev, D. Section 13.1. Chemical Graph Theory. In Handbook of Graph Theory; Gross, J.L., Yellen, J., Zhang, P., Eds.; CRC Press: Boca Raton, FL, USA, 2013; pp. 1538–1558. [Google Scholar]
- Waterbeemd, H.V.D.; Carter, R.E.; Grassy, G.; Kubiny, H.; Martin, Y.C.; Tutte, M.S.; Willet, P. Glossary of terms used in computational drug design. Pure Appl. Chem. 1997, 69, 1137–1152. [Google Scholar] [CrossRef]
- Akram, S.; Javaid, M.; Jamal, M. Bounds on F-index of tricyclic graphs with fixed pendent vertices. Open Math. 2020, 18, 150–161. [Google Scholar] [CrossRef]
- Koam, A.N.A.; Ahmad, A.; Qummer, A.A. On the Study of Reverse Degree-Based Topological Properties for the Third Type of p th Chain Hex-Derived Network. J. Math. 2021, 2021, 4540276. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar]
- Diudea, M.V. (Ed.) QSPR/QSAR Studies by Molecular Descriptors; Nova: Hungtinton, CA, USA, 2001. [Google Scholar]
- Mueller, L.A.; Kugler, K.G.; Netzer, M.; Graber, A.; Dehmer, M. A network-base approach to classify the three domains of life. Biol. Direct. 2011, 6, 140–141. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. III. Total π-electron energy of alternant hydrocarbons. Chem. Phys. 1972, 17, 535–538. [Google Scholar]
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.; Shi, Y.; Xu, T.; Gutman, I. On molecular graphs with smallest and greatest zeroth order general Randić index. MATCH Commun. Math. Comput. Chem. 2005, 54, 425–434. [Google Scholar]
- Miličević, A.; Nikolić, S. On variable Zagreb indices. Croat. Chem. Acta 2004, 77, 97–101. [Google Scholar]
- Li, X.; Zheng, J. A unified approach to the extremal trees for different indices. MATCH Commun. Math. Comput. Chem. 2005, 54, 195–208. [Google Scholar]
- Kier, L.B.; Hall, L.H. The nature of structure-activity relationships and their relation to molecular connectivity. Eur. J. Med. Chem. 1977, 12, 307–312. [Google Scholar]
- Li, X.; Zhao, H. Trees with the first three smallest and largest generalized topological indices. MATCH Commun. Math. Comput. Chem. 2004, 50, 57–62. [Google Scholar]
- Zhang, H.; Zhang, S. Unicyclic graphs with the first three smallest and largest first general Zagreb index. MATCH Commun. Math. Comput. Chem. 2006, 55, 427–438. [Google Scholar]
- Zhang, S.; Wang, W.; Cheng, T.C.E. Bicyclic graphs with the first three smallest and largest values of the first general Zagreb index. MATCH Commun. Math. Comput. Chem. 2006, 56, 579–592. [Google Scholar]
- Hu, Y.; Li, X.; Shi, Y.; Xu, T. Connected (n,m)-graphs with minimum and maximum Zeroth-order general Randić index. Discrete Appl. Math. 2007, 155, 1044–1054. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y. (n,m)-Graphs with maximum Zeroth-order general Randić index for α∈(-1,0). MATCH Commun. Math. Comput. Chem. 2009, 62, 163–170. [Google Scholar]
- Cheng, T.C.E.; Guo, Y.; Zhang, S.; Du, Y. Extreme values of the sum of squares of degrees of bipartite graphs. Discrete Math. 2009, 309, 1557–1564. [Google Scholar] [CrossRef]
- Su, G.; Xiong, L.; Su, X.; Li, G. Maximally edge-connected graphs and Zeroth-order general Randić index for α<-1. J. Comb. Optim. 2016, 31, 182–195. [Google Scholar]
- Dankelmann, P.; Hellwig, A.; Volkmann, L. Inverse degree and edge connectivity. Discrete Math. 2009, 309, 2943–2947. [Google Scholar] [CrossRef]
- Pan, X.F.; Liu, H.; Liu, M. Sharp bounds on the zeroth-order general Randic index of unicyclic graphs with given diameter. Appl. Math. Lett. 2011, 24, 687–691. [Google Scholar] [CrossRef][Green Version]
- Vukičević, D. Bond additive modelling 4. QSPR and QSAR studies of the variable Adriatic indices. Croat. Chem. Acta 2011, 41, 87–91. [Google Scholar] [CrossRef]
- Yarahmadi, Z.; Ashrafi, A.R. The exdeg polynomial of some graph operations and applications in nanoscience. J. Comput. Teoret. Nanosci. 2015, 12, 45–51. [Google Scholar] [CrossRef]
- Rizwan, M.; Bhatti, A.A.; Javaid, M.; Jarad, F. Some bounds on bond incident degree indices with some parameters. Math. Prob. Engin. 2021, 2021, 8417486. [Google Scholar] [CrossRef]
- Rizwan, M.; Bhatti, A.A.; Javaid, M.; Shang, Y. Conjugated tricyclic graphs with maximum variable sum exdeg index. Heliyon 2023, 9, e15706. [Google Scholar] [CrossRef]
- Du, J.; Sun, X. On the graph connectivity and the variable sum exdeg index. AIMS Math. 2021, 6, 607–622. [Google Scholar] [CrossRef]
- Vukičević, D. Bond additive modelling 5. Mathematical properties of the variable sum exdeg index. Croat. Chem. Acta 2011, 84, 93–101. [Google Scholar] [CrossRef]
- Ali, A.; Dimitrov, D. On the extremal graphs with respect to bond incident degree indices. Discrete Appl. Math. 2018, 238, 32–40. [Google Scholar] [CrossRef]
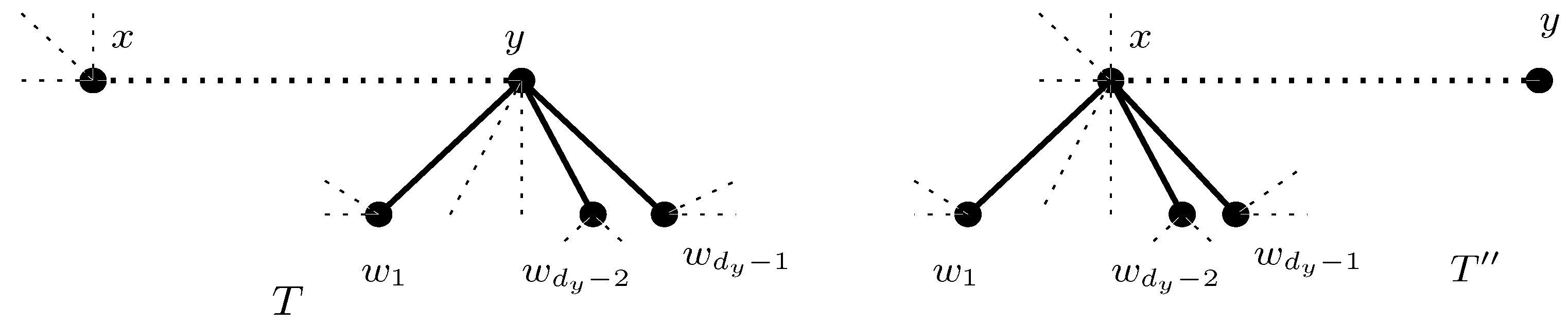
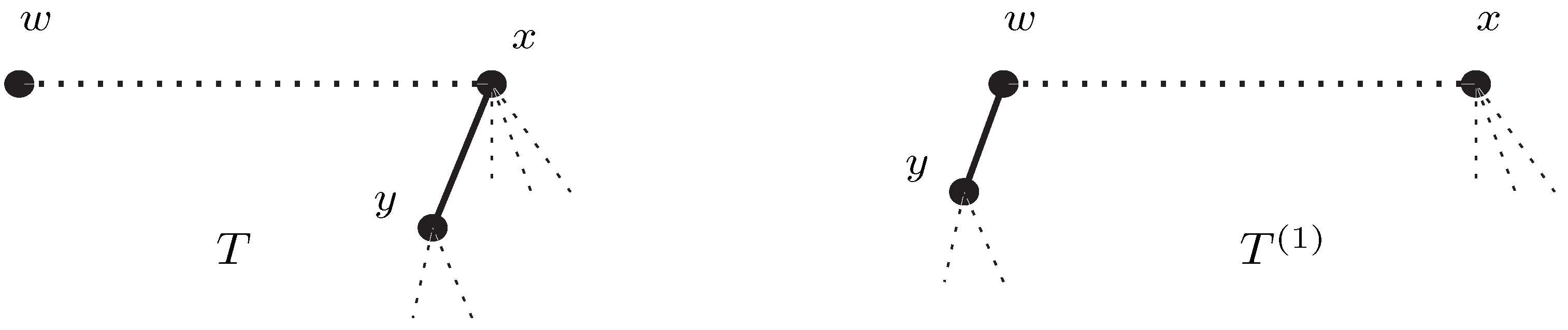
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albalahi, A.M.; Rizwan, M.; Bhatti, A.A.; Gutman, I.; Ali, A.; Alraqad, T.; Saber, H. On Trees with a Given Number of Vertices of Fixed Degree and Their Two Bond Incident Degree Indices. Axioms 2025, 14, 23. https://doi.org/10.3390/axioms14010023
Albalahi AM, Rizwan M, Bhatti AA, Gutman I, Ali A, Alraqad T, Saber H. On Trees with a Given Number of Vertices of Fixed Degree and Their Two Bond Incident Degree Indices. Axioms. 2025; 14(1):23. https://doi.org/10.3390/axioms14010023
Chicago/Turabian StyleAlbalahi, Abeer M., Muhammad Rizwan, Akhlaq A. Bhatti, Ivan Gutman, Akbar Ali, Tariq Alraqad, and Hicham Saber. 2025. "On Trees with a Given Number of Vertices of Fixed Degree and Their Two Bond Incident Degree Indices" Axioms 14, no. 1: 23. https://doi.org/10.3390/axioms14010023
APA StyleAlbalahi, A. M., Rizwan, M., Bhatti, A. A., Gutman, I., Ali, A., Alraqad, T., & Saber, H. (2025). On Trees with a Given Number of Vertices of Fixed Degree and Their Two Bond Incident Degree Indices. Axioms, 14(1), 23. https://doi.org/10.3390/axioms14010023







