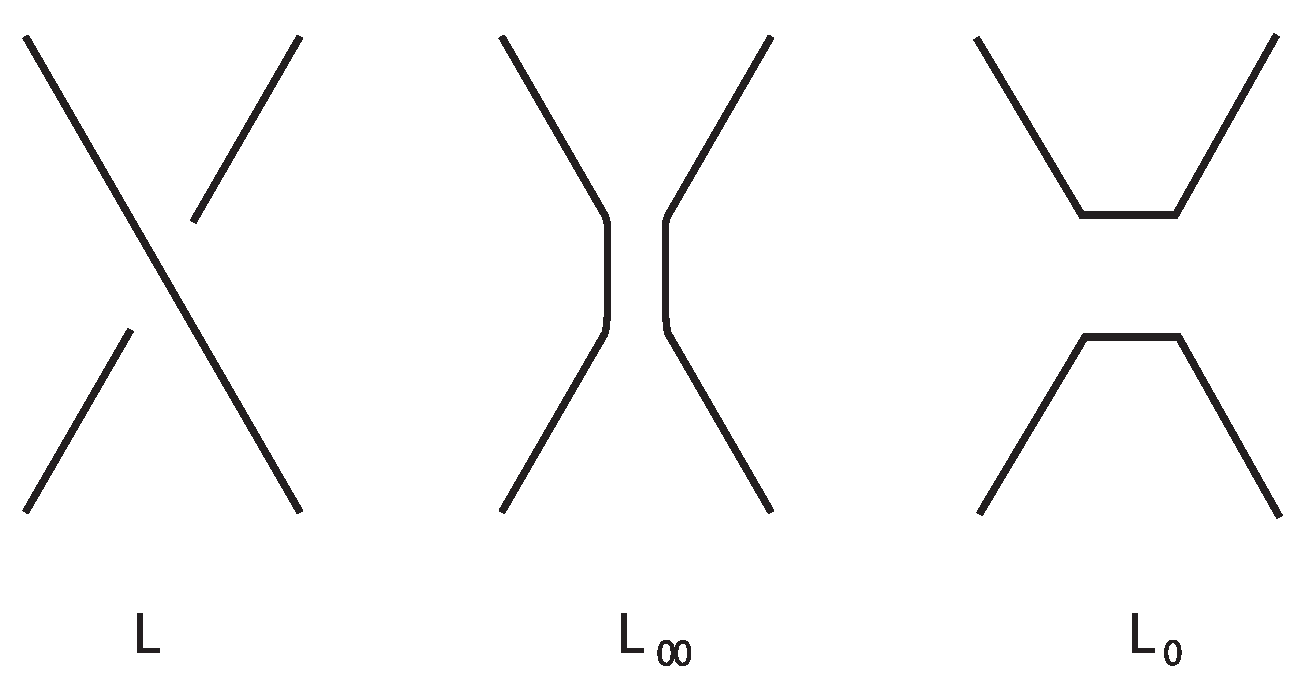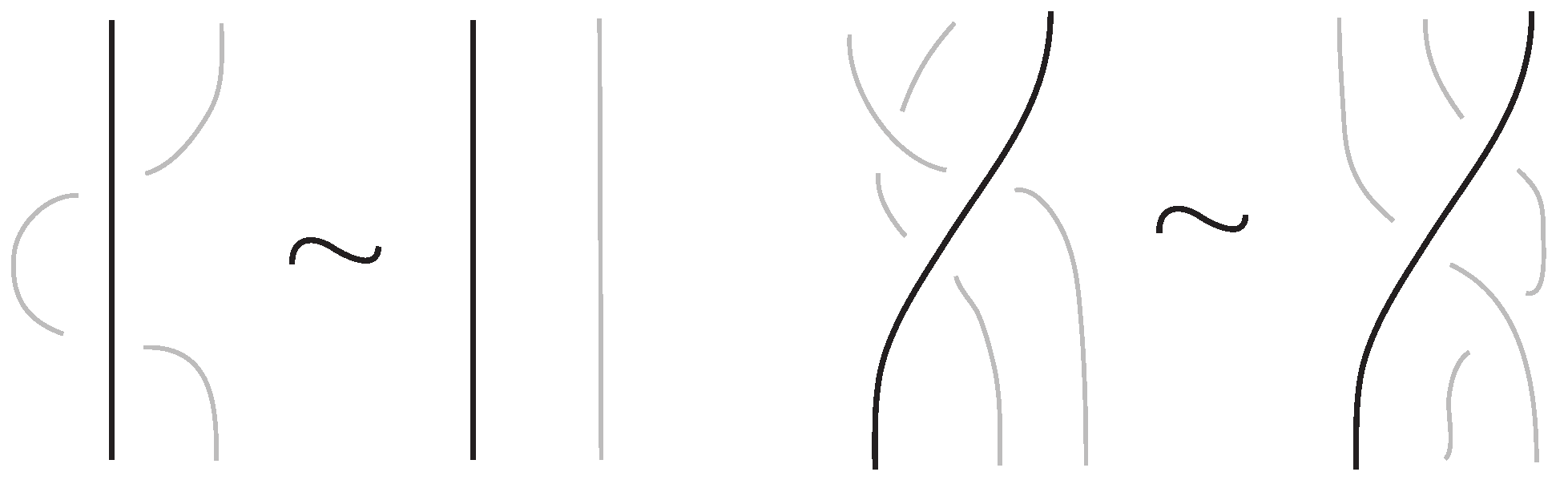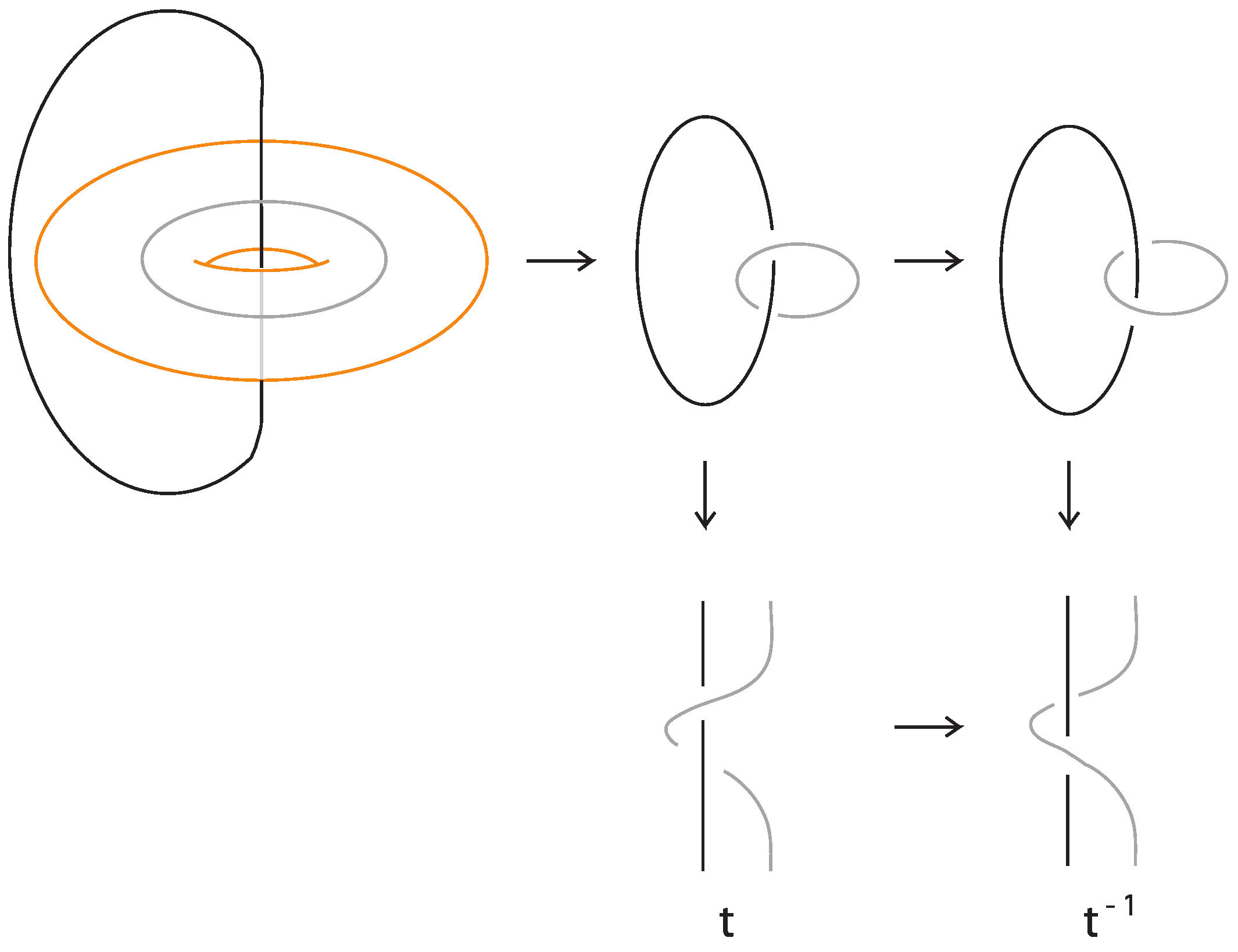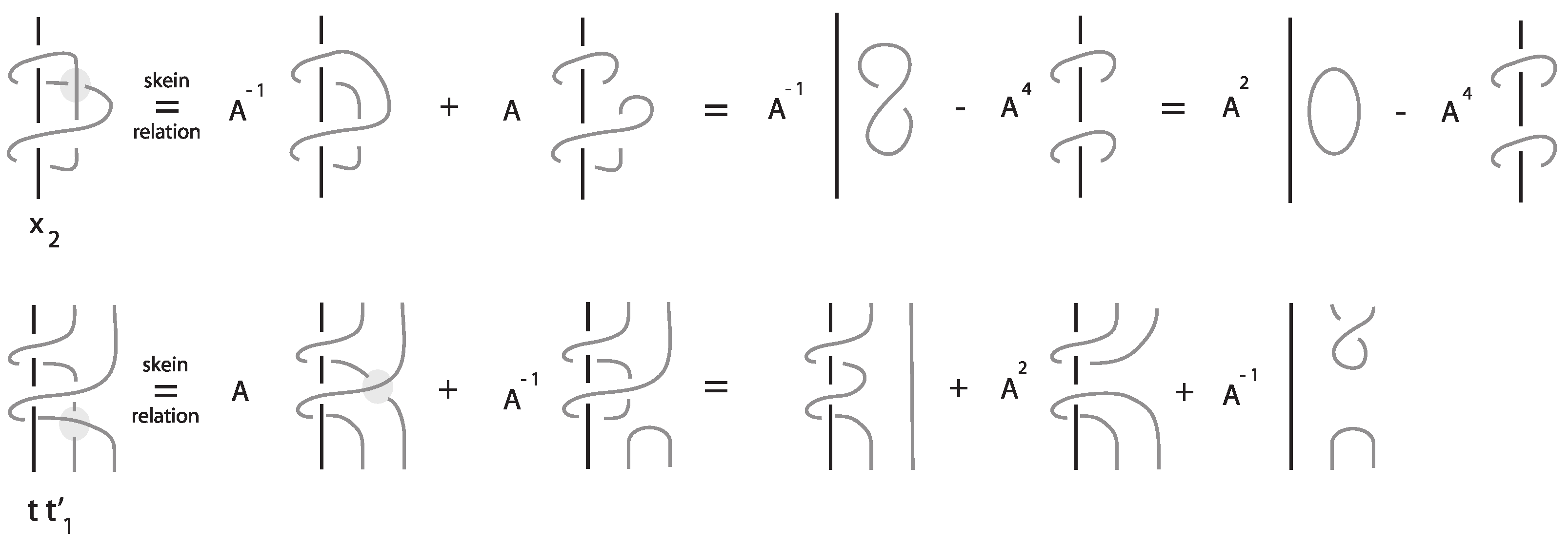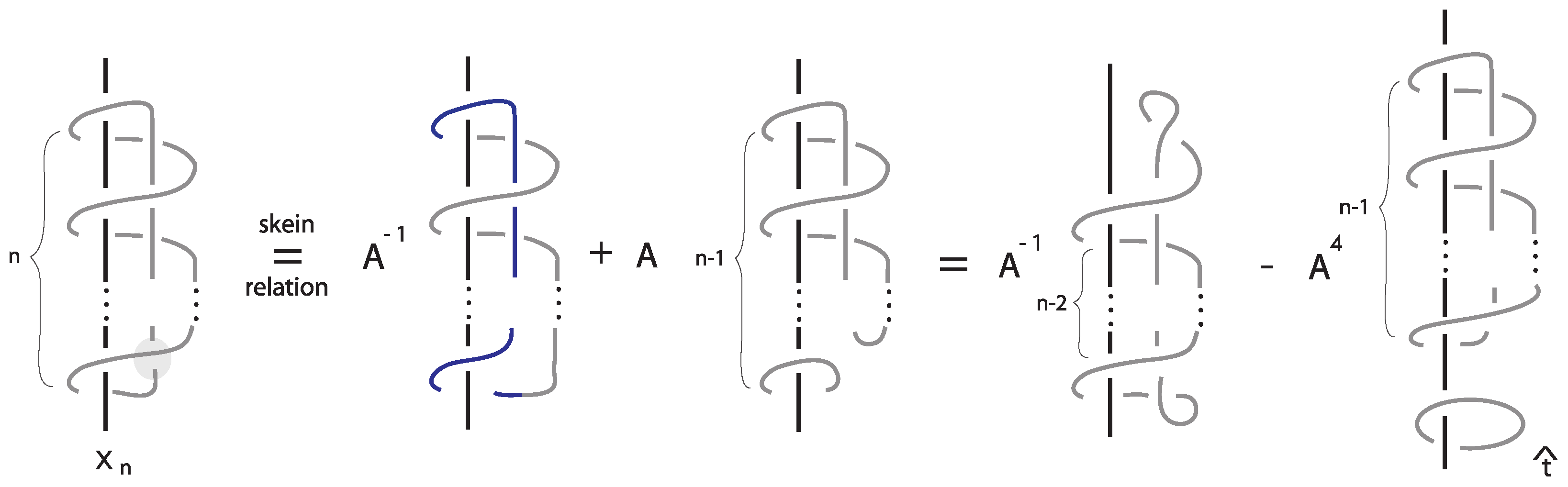The Kauffman Bracket Skein Module of S¹ × S² via Braids

Abstract

In this paper, we present two different ways for computing the Kauffman bracket skein module of $S^1\times S^2$, $\mathrm{KBSM}\left(S^1\times S^2\right)$, via braids. We first extend the universal Kauffman bracket type invariant V for knots and links in the Solid Torus ST, which is obtained via a unique Markov trace constructed on the generalized Temperley–Lieb algebra of type B, to an invariant for knots and links in $S^1\times S^2$. We do that by imposing on V relations coming from the braid band moves. These moves reflect isotopy in $S^1\times S^2$ and they are similar to the second Kirby move. We obtain an infinite system of equations, a solution of which is equivalent to computing $\mathrm{KBSM}\left(S^1\times S^2\right)$. We show that $\mathrm{KBSM}\left(S^1\times S^2\right)$ is not torsion free and that its free part is generated by the unknot (or the empty knot). We then present a diagrammatic method for computing $\mathrm{KBSM}\left(S^1\times S^2\right)$ via braids. Using this diagrammatic method, we also obtain a closed formula for the torsion part of $\mathrm{KBSM}\left(S^1\times S^2\right)$.

1. Introduction and Overview

Skein modules of 3-manifolds are generalizations of link invariants in $S^3$ to link invariants in arbitrary 3-manifolds. They were introduced by Turaev [1] and Przytycki [2] and they have become very important algebraic tools in the study of 3-manifolds, since their properties reflect geometric and topological information about them. Skein modules of 3-manifolds are modules composed of linear combinations of links in the 3-manifolds, modulo some properly chosen (local) skein relations. In this paper, we compute the Kauffman bracket skein module of $S^1\times S^2$, KBSM ($S^1\times S^2$), namely, the skein module based on the Kauffman bracket skein relation

$$L_{+}-A{L}_0-A^{-1}{L}_{\infty }$$

where $L_{\infty }$ and $L_0$ are represented schematically by the illustrations in Figure 1.

The computation of KBSM ($S^1\times S^2$) is equivalent to constructing all possible analogues of the Jones polynomial for knots and links in $S^1\times S^2$, since the linear dimension of KBSM ($S^1\times S^2$) means the number of independent Kauffman bracket-type invariants defined on knots and links in $S^1\times S^2$. In other words, KBSM ($S^1\times S^2$) yields all possible isotopy invariants of knots which satisfy the Kauffman bracket skein relation.

The precise definition of KBSM is as follows:

Definition 1.

Let M be an oriented 3-manifold and ${\mathcal{L}}_{\mathrm{fr}}$ be the set of isotopy classes of unoriented framed links in M. Let $R=\mathbb{Z}\left[A^{\pm 1}\right]$ be the Laurent polynomials in A and let $R{\mathcal{L}}_{\mathrm{fr}}$ be the free R-module generated by ${\mathcal{L}}_{\mathrm{fr}}$. Let $\mathcal{S}$ be the ideal generated by the skein expressions $L_{+}-A{L}_0-A^{-1}{L}_{\infty }$ and $L⨆\mathrm{O}-(-A^2-A^{-2})L$. Note that blackboard framing is assumed and that $L⨆\mathrm{O}$ stands for the union of a link L and the trivially framed unknot in a ball disjoint from L.

Then, the Kauffman bracket skein module of M, KBSM $\left(M\right)$, is defined to be:

$$\mathrm{KBSM}\left(M\right)=R{\mathcal{L}}_{\mathrm{fr}}/\phantom{R{\mathcal{L}}_{\mathrm{fr}}\mathcal{S}}S.$$

The importance of the Kauffman bracket skein module of a 3-manifold M lies in the fact that it detects the presence of non-separating 2-spheres and tori embedded in M. On the level of Kauffman bracket skein modules, a non-separating 2-sphere in M is detected by the existence of torsion in KBSM (M). For more details, the reader is referred to [2].

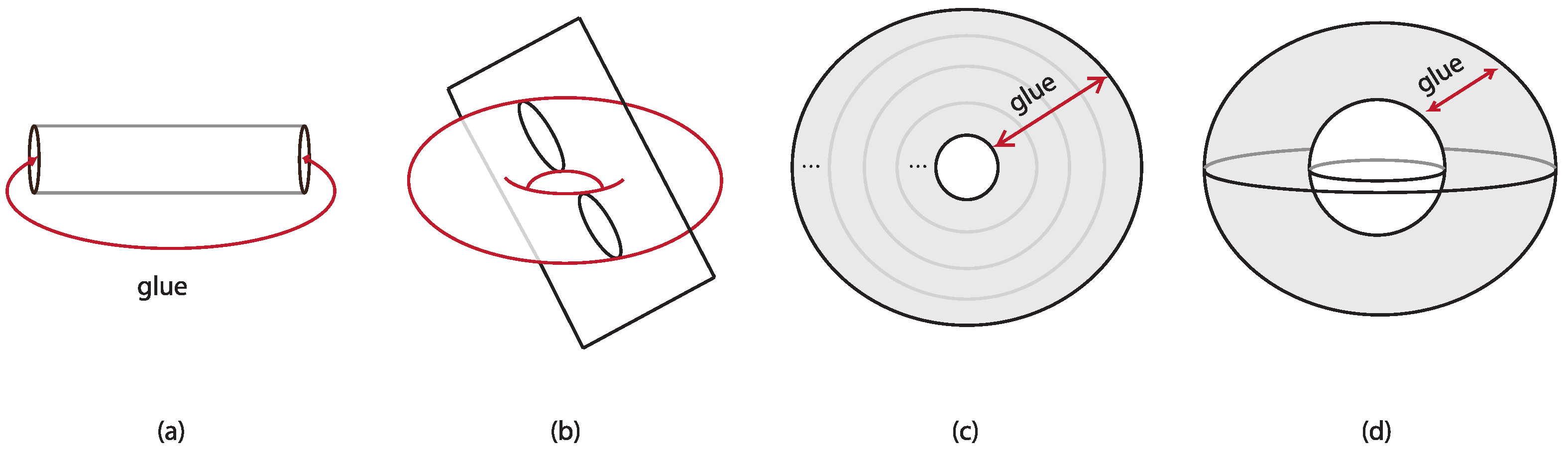
We consider $S^1\times S^2$ as being obtained from $S^3$ by integral surgery along the unknot with coefficient zero, that is, $S^1\times S^2$ is a special type of lens spaces $L(p,q)$ for $p=0$ and $q=1$ ($L(0,1)\cong S^1\times S^2$). In [3], the Kauffman bracket skein module of the lens spaces $L(p,q),p>0$ is computed via the ‘braid technique’, and a basis of KBSM ($L(p,q)$) is obtained that is different from the basis presented in [4]. In this paper, we apply the ‘braid technique’ to exhaust the computation of the Kauffman bracket skein module of the family of lens spaces. More precisely, the integral surgery model of $S^1\times S^2$ allows us to ‘push’ every knot and link in $S^1\times S^2$ to the solid torus, and thus, a basis of KBSM (ST) spans KBSM ($S^1\times S^2$). Following the pioneering work of V.F.R. Jones ([5,6]), in [3], we consider the generalized Temperley–Lieb algebra of type B, $T{L}_{1,n}$, together with a Markov trace constructed on $T{L}_{1,n}$ and the universal invariant V of the Kauffman bracket type for knots and links in ST defined in [3]. This invariant gives distinct values to distinct elements of any basis of KBSM (ST), and thus, it recovers KBSM (ST). Hence, in order to compute KBSM ($S^1\times S^2$), one needs to extend the invariant V for knots and links in ST to an invariant of knots and links in $S^1\times S^2$, by imposing relations coming from the extra isotopy moves of $S^1\times S^2$, that we call (braid) band moves, abbreviated $bm$ (or $bbm$). In other words, the following infinite system of equations is obtained:

$$V_a=V_{bm\left(a\right)},\mathrm{for}\mathrm{every}a\mathrm{in}\mathrm{a}\mathrm{basis}\mathrm{of}\mathrm{KBSM}\left(\mathrm{ST}\right).$$

(1)

By construction, a solution to the infinite system of Equation (1) corresponds to the computation of the Kauffman bracket skein module of $S^1\times S^2$. These equations are simplified with the use of a new basis of KBSM (ST), $B_{\mathrm{ST}}$, presented in [3,7,8], that arises naturally on the level of braids. Using the basis $B_{\mathrm{ST}}$ of KBSM (ST), we show that the free part of the Kauffman bracket skein module of $S^1\times S^2$ is generated by the unknot (or the empty knot) and we also show how torsion is captured in the solution of the infinite system. It is worth mentioning that $S^1\times S^2$ is the first 3-manifold, where torsion on its Kauffman bracket skein module is detected via the ‘braid technique’. Finally, we compute KBSM ($S^1\times S^2$) via a different diagrammatic method based on braids following [9,10]. In this way, we obtain a closed formula for the torsion part of the module and our result agrees with that of Hoste and Przytycki [11]. The diagrammatic method via braids has been successfully applied in [10] for the case of the Kauffman bracket skein module of the complement of $(2,2p+1)$-torus knots and in [3] for the case of the lens spaces $L(p,q)$, $p\ne 0$. The importance of the braid approach lies in the fact that it can shed light to the problem of computing (various) skein modules of arbitrary closed, connected, oriented (abbreviated to c.c.o.) 3-manifolds (see also [12] for the case of the HOMFLYPT skein module of the lens spaces $L(p,1)$). For a survey on skein modules, see [13] and for the braid approach, see [14]. Finally, it is worth mentioning that in [15], the authors introduce the Mixed Hecke algebra on two fixed strands and they present a spanning set and potential basis for this algebra. This is the first step towards a polynomial invariant for knots and links in the complement of the two-component unlink and in the handlebody of genus two via braids and knot algebras. Our intention is to compute the HOMFLYPT skein module of the connected sum of lens spaces by solving the infinite system of equations obtained from band moves on the two fixed strands.

The paper is organized as follows. In Section 2, we recall the topological setting and the essential techniques and results from [16,17]. We first present different models for $S^1\times S^2$, which demonstrate the difference between the knot theory of this 3-manifold to the knot theory of $S^3$. We then explain how knots and links in $S^1\times S^2$ can be viewed as mixed links in $S^3$. Mixed links are closely related to Kirby diagrams of links in $S^3$, that is, link diagrams in $S^3$ that involve the surgery description of $S^1\times S^2$. We present isotopy moves for mixed links in $S^3$ that correspond to isotopy moves for knots and links in $S^1\times S^2$, and using the analogue of the Alexander theorem for knots and links in ST, we pass on the level of mixed braids. We then translate isotopy in $S^1\times S^2$ to braid equivalence (the analogue of the Markov theorem for braid equivalence in $S^1\times S^2$). In Section 3, we present results from [3,7,18,19]. More precisely, we start by recalling results on the generalized Hecke algebra of type B, $H_{1,n}$, and we present the universal invariant of the HOMFLYPT type for knots in ST via a unique Markov trace, $tr$, defined on $H_{1,n}$. This invariant captures the HOMFLYPT skein module of ST. We then pass to the generalized Temperley–Lieb algebra of type B, defined as a quotient algebra of $H_{1,n}$ over an appropriate chosen ideal (see relations (3)), and we obtain the universal invariant V for knots and links in ST of the Kauffman bracket type, that captures KBSM (ST). We also present the basis $B_{\mathrm{ST}}$ of KBSM (ST) that describes naturally the isotopy moves for knots and links in $S^1\times S^2$, and that simplifies the infinite system of Equation (1). In Section 4, we solve the infinite system of Equation (1) and we prove that the free part of KBSM ($S^1\times S^2$) is generated by the unknot (or the empty knot). We also show how torsion is detected in the solution of this system. Finally, in Section 5, we demonstrate the diagrammatic approach based on braids for computing KBSM ($S^1\times S^2$).

2. Topological Set Up

2.1. Models of $S^1\times S^2$

$S^1\times S^2$ can be realized as a thickened torus in 4-dimensions, such that the cross-sections are two copies of the 2-sphere $S^2$. To better perceive this, we consider the analogue construction of $S^1\times S^1$ in dimension three: we consider copies of $S^1$ and we ‘glue’ them together to obtain a cylinder. Finally, we glue the first and the last $S^1$ to obtain a torus (see Figure 2a,b). This construction is equivalent to ‘gluing’ the inner and outer $S^1$s from an infinitum of concentric $S^1$s (see Figure 2c). Analogously, $S^1\times S^2$ may be visualized as a three ball $B^3$ with a concentric and of smaller radius $S^2$ being hollowed out, and where the boundary of $B^3$ is glued to the inner $S^2$, as illustrated in Figure 2d.

The model of $S^1\times S^2$, as illustrated in Figure 2d, can be used to highlight the difference between the knot theory of $S^1\times S^2$ and the knot theory of $S^3$. Consider, for example, the knot in Figure 3 and notice that using isotopy, we may unknot this knot with the use of the non-separating 2-sphere. This method is known as the Dirac trick.

A different way to visualize $S^1\times S^2$ is by ‘gluing’ two solid tori via some homeomorphism h on their boundaries, such that h takes a meridian curve $m_1$ on the first solid torus ${\mathrm{ST}}_1$, to the corresponding meridian curve $m_2$ of the second solid torus ${\mathrm{ST}}_2$. We may choose h to be the identity $i:\partial {\mathrm{ST}}_1\to \partial {\mathrm{ST}}_2$. Since now $ST=S^1\times D^2$, where $D^2$ denotes a disc, and since the gluing of two discs results in a 2-sphere $S^2$, the resulting 3-manifold can be considered as a family of 2-spheres parametrized by a circle (for an illustration, see Figure 4).

The above construction of $S^1\times S^2$ coincides with the Dehn surgery method for obtaining $S^1\times S^2$. This is a method for obtaining any 3-manifold by removing finitely many disjoint solid tori from $S^3$ and then sewing them back in a different way. Recall now that by Alexander’s trick, the 3-sphere $S^3$ is the union of two solid tori via a homeomorphism h on their boundaries that maps a meridian curve on the first solid torus to a longitude curve on the second. Hence, $S^1\times S^2$ may be obtained by first removing a solid torus ${\mathrm{ST}}_1$ from $S^3$, and since $S^3={\mathrm{ST}}_1{\displaystyle \bigcup _h}{\mathrm{ST}}_2$, what remains is another solid torus ${\mathrm{ST}}_2$. We finally glue ${\mathrm{ST}}_1$ to ${\mathrm{ST}}_2$ via $h:m_1\mapsto m_2$, where $m_1$ is a meridian on ${\mathrm{ST}}_1$ and $m_2$ is a meridian on ${\mathrm{ST}}_2$. Let us present the above results in a more rigorous format. Consider the tubular neighborhood of the unknot in $S^3$. This is obviously a solid torus, say ${\mathrm{ST}}_1$. Then, this solid torus is to be “drilled away” from $S^3$ and then sewed back via h. h can be fully determined by a coefficient that instructs how ${\mathrm{ST}}_1$ is to be sewed back. In the case of $S^1\times S^2$, the meridian of ${\mathrm{ST}}_1$ is to be glued to a meridian of ${\mathrm{ST}}_2$, that is, a $(0,1)$ curve on the boundary of ${\mathrm{ST}}_2$. Thus, we say that $S^1\times S^2$ is obtained from $S^3$ by surgery along the unknot with coefficient zero, i.e., $S^1\times S^2\cong {\mathrm{O}}^0$. It is worth mentioning that $S^1\times S^2$ may be considered as a special type of lens spaces $L(p,q)$, where $p=0$ and $q=1$.

2.2. Knots and Braids in $S^1\times S^2$

In this subsection, we recall results from [16,17,20]. As mentioned before, we shall consider ST to be the complement of another solid torus in $S^3$ and an oriented link L in ST can be represented by an oriented mixed link in $S^3$. A mixed link is a link in $S^3$, consisting of the unknotted fixed part $\widehat{I}$ representing the complementary solid torus in $S^3$ and the moving part L that links with $\widehat{I}$. A mixed link diagram is a diagram $\widehat{I}\cup \tilde{L}$ of $\widehat{I}\cup L$ on the plane of $\widehat{I}$, where this plane is equipped with the top-to-bottom direction of I (for an illustration, see Figure 5).

Isotopy of oriented links in ST consists in isotopy in $S^3$ for the moving part of the mixed link, together with the mixed Reidemeister moves that involve both the fixed and the moving part of the mixed link (see Figure 6).

As mentioned above, $S^1\times S^2$ can be obtained from $S^3$ by surgery on the unknot with surgery coefficient zero. In other words, $S^1\times S^2$ can be obtained by “killing” the meridian m, that is, by mirroring $D\times S^1$ along its boundary. Knots and links in $S^1\times S^2$ may be then visualized in $S^3$ as mixed links, together with the surgery coefficient on their fixed component (“Kirby” like diagrams). It follows that isotopy in $S^1\times S^2$ can be then viewed as isotopy in ST together with the band moves, which reflect the surgery description of the manifold and that are similar to the second Kirby move. It is worth mentioning that there are two types of band moves, according to the orientation of the component of the knot and that of the surgery curve (see Figure 7 for the two types of band moves for the case of $S^1\times S^2$). In the β-type moves, the orientation of the arc is initially opposite to the orientation of the surgery curve, but after the performance of the move their orientations agree. In the α-type, the orientations initially agree, but disagree after the performance of the move.

In [16], it is shown that in order to describe isotopy for knots and links in a c.c.o. 3-manifold, it suffices to consider only one type of band moves (cf. [Theorem 6] of [16]) and thus, isotopy between oriented links in $S^1\times S^2$ is reflected in $S^3$ by means of the following theorem:

Theorem 1

(The analogue of Reidemeister’s theorem). Two oriented links in $S^1\times S^2$ are isotopic if and only if two corresponding mixed link diagrams of theirs differ by isotopy in ST together with a finite sequence of one type of band moves.

As shown in [18], every mixed link is isotopic to the closure of a mixed braid. A mixed braid in $S^3$ is a standard braid where, without loss of generality, its first strand represents $\widehat{I}$, the fixed part, and the other strands, β, represent the moving part. We shall call the subbraid β the moving part of $I\cup \beta$ (see bottom left illustration of Figure 8).

We now recall the analogue of the Alexander theorem for knots and links in ST (cf. [Theorem 1] of [19]):

Theorem 2

(The analogue of Alexander’s theorem). A mixed link diagram $\widehat{I}\cup \tilde{L}$ of $\widehat{I}\cup L$ may be turned into a mixed braid $I\cup \beta$ with isotopic closure.

Hence, a link in $S^1\times S^2$, which is visualized as a mixed link in $S^3$, may be turned to a mixed braid in $S^3$. We now translate isotopy in $S^1\times S^2$ on the level of mixed braids. We define a braid band move (abbreviated to bbm) to be a move between mixed braids, which is a β-type band move between their closures. It starts with a little band oriented downward, which, before sliding along a surgery strand, gets one twist positive or negative (see middle part of Figure 8). Note that in [20], it was shown that the choice of the position of connecting the two components after the performance of a bbm is arbitrary.

The sets of braids related to ST form groups, which are in fact the Artin braid groups of type B, denoted $B_{1,n}$, with presentation:

$$B_{1,n}=〈\begin{array}{cc}\begin{array}{c}t,{\sigma }_1,\dots ,{\sigma }_{n-1}\hfill \end{array}\hfill & \left|\begin{array}{c}{\sigma }_{1}t{\sigma }_{1}t=t{\sigma }_{1}t{\sigma }_1\hfill \\ t{\sigma }_i={\sigma }_{i}t,i>1\hfill \\ {\sigma }_i{\sigma }_{i+1}{\sigma }_i={\sigma }_{i+1}{\sigma }_i{\sigma }_{i+1},1\le i\le n-2\hfill \\ {\sigma }_i{\sigma }_j={\sigma }_j{\sigma }_i,|i-j|>1\hfill \end{array}\right.\hfill \end{array}〉,$$

where the generators ${\sigma }_i$ and t are illustrated in Figure 9i. Notice that the mixed braid group $B_{1,n}$ can be considered as a subgroup of the classical braid group on $(n+1)$ strands, $B_{n+1}$, involving elements whose first strand is fixed.

Let $\mathcal{L}$ denote the set of oriented knots and links in $S^1\times S^2$. Isotopy in $S^1\times S^2$ is then translated on the level of mixed braids by means of the following theorem (see also [Theorem 5] of [20] and [Theorem 9] of [16]):

Theorem 3.

Let $L_1,L_2$ be two oriented links in $S^1\times S^2$ and let $I\cup {\beta }_1,I\cup {\beta }_2$ be two corresponding mixed braids in $S^3$. Then, $L_1$ is isotopic to $L_2$ in $S^1\times S^2$ if and only if $I\cup {\beta }_1$ is equivalent to $I\cup {\beta }_2$ in $\mathcal{B}$ by the following moves:

$$\begin{array}{cccc}\left(i\right)& Conjugation:\hfill & \alpha \sim {\beta }^{-1}\alpha \beta ,\hfill & \mathrm{if}\alpha ,\beta \in B_{1,n}.\hfill \\ \left(ii\right)& Stabilizationmoves:\hfill & \alpha \sim \alpha {\sigma }_n^{\pm 1}\in B_{1,n+1},\hfill & \mathrm{if}\alpha \in B_{1,n}.\hfill \\ \left(iii\right)& Loopconjugation:\hfill & \alpha \sim t^{\pm 1}\alpha t^{\mp 1},\hfill & \mathrm{if}\alpha \in B_{1,n}.\hfill \\ \left(iv\right)& Braidbandmoves:\hfill & \alpha \sim {\alpha }_{+}{\sigma }_1^{\pm 1},\hfill & a_{+}\in B_{1,n+1},\hfill \end{array}$$

where ${\alpha }_{+}$ is the word α with all indices shifted by +1. Note that moves (i), (ii), and (iii) correspond to link isotopy in ST.

Notation 1.

We denote a braid band move by bbm and, specifically, the result of a positive (cor. negative) braid band move performed on a mixed braid β by $bb{m}_{+}\left(\beta \right)$ (cor. $bb{m}_{-}\left(\beta \right)$).

3. Algebraic Tools

In this section, we recall results from [3] that are crucial for the computation of KBSM ($S^1\times S^2$). More precisely, we first recall results on the generalized Temperley–Lieb algebra of type B, $T{L}_{1,n}$, that are related to the knot theory of ST, and through $T{L}_{1,n}$, we obtain the universal invariant for knots and links in ST of the Kauffman bracket type. We also present different bases of KBSM (ST) via braids.

3.1. Knot Algebras Related to ST and $S^1\times S^2$

It is well understood that the generalized Hecke algebra of type B is related to the knot theory of the solid torus [19]. This algebra is defined as a quotient of the mixed braid group algebra $\mathbb{Z}\left[q^{\pm 1}\right]B_{1,n}$ over the ideal generated by the quadratic relations ${\sigma }_i^2=(q-1){\sigma }_i+q$. Namely:

$$H_{1,n}\left(q\right)={\displaystyle \frac{\mathbb{Z}\left[q^{\pm 1}\right]B_{1,n}}{\langle {\sigma }_i^2-\left(q-1\right){\sigma }_i-q\rangle }}.$$

As shown in [19], $H_{1,n}$ admits a unique Markov trace, $tr$. This Markov trace gives rise to the most generic analogue of the HOMFLYPT polynomial, X, for links in the solid torus ST. The construction of $tr$ was possible with the use of appropriate inductive bases on $\mathcal{H}:={\bigcup }_{n=1}^{\infty }{H}_{1,n}$. Namely:

Theorem 4

(Proposition 1 and Theorem 1 of [19]). The following sets form linear bases for ${\mathrm{H}}_{1,n}\left(q\right)$:

$$\begin{array}{cccc}\left(i\right)\hfill & {\Sigma }_n\hfill & =\hfill & \{t_{i_1}^{k_1}\dots t_{i_r}^{k_r}·\sigma \},\mathrm{where}0\le i_1<\dots <i_r\le n-1,\hfill \\ \left(ii\right)\hfill & {\Sigma }_n^{\prime }\hfill & =\hfill & \{{t_{i_1}^{\prime }}^{k_1}\dots {t_{i_r}^{\prime }}^{k_r}·\sigma \},\mathrm{where}0\le i_1<\dots <i_r\le n-1,\hfill \end{array}$$

(2)

where $k_1,\dots ,k_r\in \mathbb{Z}$, $t_0^{\prime }=t_0:=t,t_i^{\prime }=g_i\dots g_{1}t{g}_1^{-1}\dots g_i^{-1}$, and $t_i=g_i\dots g_{1}t{g}_1\dots g_i$ are the ‘looping elements’ in ${\mathrm{H}}_{1,n}\left(q\right)$ (see Figure 9ii) and σ is a basic element in the Iwahori–Hecke algebra of type A, ${\mathrm{H}}_n\left(q\right)$.

Note that a basic element in ${\mathrm{H}}_n\left(q\right)$ is of the form of elements in the following set [5]:

$$S_n=\left\{(g_{i_1}{g}_{i_1-1}\dots g_{i_1-k_1})(g_{i_2}{g}_{i_2-1}\dots g_{i_2-k_2})\dots (g_{i_p}{g}_{i_p-1}\dots g_{i_p-k_p})\right\},$$

for $1\le i_1<\dots <i_p\le n-1$.

Theorem 5

(Theorem 6 and Definition 1 of [19]). Given $z,s_k$ with $k\in \mathbb{Z}$ specified elements in $R=\mathbb{Z}\left[q^{\pm 1}\right]$, there exists a unique linear Markov trace function on $\mathcal{H}$:

$$\mathrm{tr}:\mathcal{H}\to R\left(z,s_k\right),k\in \mathbb{Z}$$

determined by the rules:

$$\begin{array}{ccccc}\left(1\right)\hfill & \mathrm{tr}\left(ab\right)\hfill & =\hfill & \mathrm{tr}\left(ba\right)\hfill & \mathrm{for}a,b\in {\mathrm{H}}_{1,n}\left(q\right)\hfill \\ \left(2\right)\hfill & \mathrm{tr}\left(1\right)\hfill & =\hfill & 1\hfill & \mathrm{for}\mathrm{all}{\mathrm{H}}_{1,n}\left(q\right)\hfill \\ \left(3\right)\hfill & \mathrm{tr}\left(a{g}_n\right)\hfill & =\hfill & z\mathrm{tr}\left(a\right)\hfill & \mathrm{for}a\in {\mathrm{H}}_{1,n}\left(q\right)\hfill \\ \left(4\right)\hfill & \mathrm{tr}\left(a{t_n^{\prime }}^k\right)\hfill & =\hfill & s_k\mathrm{tr}\left(a\right)\hfill & \mathrm{for}a\in {\mathrm{H}}_{1,n}\left(q\right),k\in \mathbb{Z}\hfill \end{array}$$

Then, the function $X:\mathcal{L}$$\to R(z,s_k)$

$$X_{\widehat{\alpha }}={\Delta }^{n-1}·{\left(\sqrt{\lambda }\right)}^e\mathrm{tr}\left(\pi \left(\alpha \right)\right),$$

is an invariant of oriented links in ST , where $\Delta :=-{\displaystyle \frac{1-\lambda q}{\sqrt{\lambda }\left(1-q\right)}}$, $\lambda :={\displaystyle \frac{z+1-q}{qz}}$, $\alpha \in B_{1,n}$ is a word in the ${\sigma }_i$s and $t_i^{\prime }$s, $\widehat{\alpha }$ is the closure of α, e is the exponent sum of the ${\sigma }_i$s in α, and π is the canonical map of $B_{1,n}$ to ${\mathrm{H}}_{1,n}\left(q\right)$, such that $t\mapsto t$ and ${\sigma }_i\mapsto g_i$.

Remark 1.

As shown in [19,21], the invariant X recovers the HOMFLYPT skein module of ST (see also [12] for a survey on the HOMFLYPT skein module of the lens spaces $L(p,1)$ via braids).

The algebraic counterpart construction of the Kauffman bracket is the Temperley–Lieb algebra together with a unique Markov trace constructed by V.F.R. Jones (see [5] and references therein). It is therefore natural to consider the generalized Temperley–Lieb algebra of type B, defined as a quotient of $H_{1,n}\left(q\right)$, in order to obtain a universal invariant of the Kauffman bracket type for knots and links in ST. We have the following definition ([Definition 2] of [3]):

Definition 2.

The generalized Temperley–Lieb algebra of type B, $T{L}_{1,n}$, is defined as the quotient of the generalized Hecke algebra of type B, $H_{1,n}\left(q\right)$, over the ideal generated by expressions of the form:

$$\begin{array}{ccc}{\sigma }_{i,i+1}\hfill & :=& 1+u({\sigma }_i+{\sigma }_{i+1})+u^2({\sigma }_i{\sigma }_{i+1}+{\sigma }_{i+1}{\sigma }_i)+u^3{\sigma }_i{\sigma }_{i+1}{\sigma }_i.\hfill \end{array}$$

(3)

Remark 2.

For the rest of the paper, we will adapt a different presentation for $H_{1,n}$ that involves the parameter u and the quadratic relations:

$${\sigma }_i^2=(u-u^{-1}){\sigma }_i+1.$$

(4)

In [3], it is shown that for $z=-{\displaystyle \frac{1}{u(1+u^2)}}$, the Markov trace constructed in $H_{1,n}$ factors through to ${TL}_{1,n}$ (see also [22]). This leads to the universal invariant of the Kauffman bracket type for knots and links in ST. More precisely, we have the following theorem:

Theorem 6.

The invariant

$$V_{\widehat{\alpha }}\left(u\right):={\left(-{\displaystyle \frac{1+u^2}{u}}\right)}^{n-1}{\left(u\right)}^{2e}\mathrm{tr}\left(\overline{\pi }\left(\alpha \right)\right),$$

where $\alpha \in B_{1,n}$ is a word in the ${\sigma }_i$s and $t_i^{\prime }$s, $\widehat{\alpha }$ is the closure of α, e is the exponent sum of the ${\sigma }_i$s in α, $\overline{\pi }$ the canonical map of $B_{1,n}$ to ${\mathrm{TL}}_{1,n}$, such that $t\mapsto t$ and ${\sigma }_i\mapsto g_i$, and is the universal invariant for knots and links in ST of the Kauffman bracket type.

The invariant V recovers the Kauffman bracket skein module of ST and, as shown in [3], it can be extended to an invariant for knots and links in $L(p,q)$ by considering the effect of the braid band moves on elements in some basis of KBSM (ST) (see also [2]). Equivalently, and since $S^1\times S^2\cong L(0,1)$, in order to compute KBSM ($S^1\times S^2$), it suffices to consider elements in some basis of KBSM (ST), impose on V relations coming from the band moves, and solve the resulting infinite system of equations.

3.2. The Kauffman Bracket Skein Module of ST via Braids

From the discussion in Section 2, it is clear that the knot theory of ST is of fundamental importance for studying knot theory in other c.c.o. 3-manifolds. In [23], the Kauffman bracket skein module of the solid torus is computed using diagrammatic methods by means of the following theorem:

Theorem 7

([2]). The Kauffman bracket skein module of ST, KBSM (ST), is freely generated by an infinite set of generators ${\left\{x^n\right\}}_{n=0}^{\infty }$, where $x^n$ denotes a parallel copy of n longitudes of ST and $x^0$ is the affine unknot (see Figure 10).

In the braid setting, elements in the standard basis of KBSM (ST) correspond bijectively to the elements of the following set (for an illustration, see Figure 11):

$${\mathcal{B}}_{\mathrm{ST}}^{\prime }=\{t{t}_1^{\prime }\dots t_n^{\prime },n\in \mathbb{N}\}.$$

(5)

In other words, the set ${\mathcal{B}}_{\mathrm{ST}}^{\prime }$ forms a basis for KBSM (ST) in terms of braids.

Remark 3.

i. 

The basis ${\mathcal{B}}_{\mathrm{ST}}^{\prime }$ is a subset of $\mathcal{H}$ and, in particular, ${\mathcal{B}}_{\mathrm{ST}}^{\prime }$ is a subset of ${\Sigma }^{\prime }={\bigcup }_n{\Sigma }_n^{\prime }$. Moreover, and in contrast to elements in ${\Sigma }^{\prime }$, the elements in ${\mathcal{B}}_{\mathrm{ST}}^{\prime }$ have no ‘gaps’ in the indices, the exponents are all equal to one, and there are no ‘braiding tails’, i.e., there is no brading word σ after the monomial in the $t_i^{\prime }$s.

ii. 

The invariant V defined in Theorem 6 recovers KBSM (ST), since it gives distinct values to distinct elements of ${\mathcal{B}}_{\mathrm{ST}}^{\prime }$. Indeed, we have that $\mathrm{tr}(t{t}_1^{\prime }\dots t_n^{\prime })=s_1^{n+1}$.

It follows from Remark 3(ii) that in order to compute the Kauffman bracket skein module of $S^1\times S^2$, it suffices to extend the (most generic) invariant V for knots and links in ST, following the ideas in [12,21]. That is, it suffices to solve the infinite system of Equation (1), $V_{\widehat{\alpha }}=V_{\widehat{bb{m}_{\pm }\left(\alpha \right)}}$, for all α in a basis of KBSM (ST). Note that the above agree with the relation between KBSM ($S^1\times S^2$) and KBSM (ST) that is presented in [2]. Thus, we conclude that:

$$\mathrm{KBSM}(S^1\times S^2)={\displaystyle \frac{\mathrm{KBSM}\left(\mathrm{ST}\right)}{<a-bb{m}_{\pm }\left(a\right)>}}\iff V_{\widehat{a}}=V_{\widehat{bb{m}_{\pm }\left(a\right)}},\forall a\mathrm{in}\mathrm{a}\mathrm{basis}\mathrm{of}\mathrm{KBSM}\left(\mathrm{ST}\right).$$

These equations have very complicated formulations with the use of the standard basis ${\mathcal{B}}_{\mathrm{ST}}^{\prime }$. To simplify the infinite system of equations, in [3], a new basis $B_{\mathrm{ST}}$ for the Kauffman bracket skein module of ST is presented, using the looping generator t (see also [8]). For an illustration of elements in this basis, see Figure 12. More precisely, we have the following:

Theorem 8.

The following set is a basis for KBSM (ST):

$$B_{\mathrm{ST}}=\{t^n,n\in \mathbb{N}\}.$$

(6)

Remark 4.

Note that elements in the basis $B_{\mathrm{ST}}$ have no crossings on the braid level, and thus, they are more “natural” compared to the standard basis $B_{\mathrm{ST}}^{\prime }$ (recall Equation (5)), and appropriate for our purpose.

From Theorem 3, we observe that the equations $V_{\widehat{a}}=V_{\widehat{bb{m}_{\pm }\left(a\right)}}$ have particularly simple formulations with the use of the new basis $B_{\mathrm{ST}}$. Indeed, we have that $t^n\stackrel{bb{m}_{\pm }}{\to }{t}_1^n{\sigma }_1^{\pm 1}$. In Figure 13b, we illustrate a bbm applied on $t{t}_1^2\in B_{\mathrm{ST}}$ and we also demonstrate the performance of a bbm on $t{t_1^{\prime }}^2\in {\mathcal{B}}_{\mathrm{ST}}^{\prime }$.

4. The Kauffman Bracket Skein Module of ${\mathit{S}}^{\mathbf{1}}\times {\mathit{S}}^{\mathbf{2}}$ via ${\mathit{T}\mathit{L}}_{\mathbf{1},\mathit{n}}$

In this section, we solve the infinite system of Equation (1), which is equivalent to computing the Kauffman bracket skein module of the lens spaces $S^1\times S^2$. Recall that this infinite system of equations is obtained by performing braid band moves on elements in the basis $B_{\mathrm{ST}}$ of KBSM (ST) and by imposing to the generic invariant V for knots and links in ST relations of the form $V_{\widehat{t^n}}=V_{\widehat{bbm\left(t^n\right)}}$, for all $n\in \mathbb{N}$, where $bbm\left(t^n\right)=t_1^n{\sigma }_1^{\pm 1}$. Recall also that the unknowns in the system are the $s_i$s, coming from the fourth rule of the trace function in Theorem 5, that is, $tr\left(t^n\right)=s_n$, for all $n\in \mathbb{Z}$.

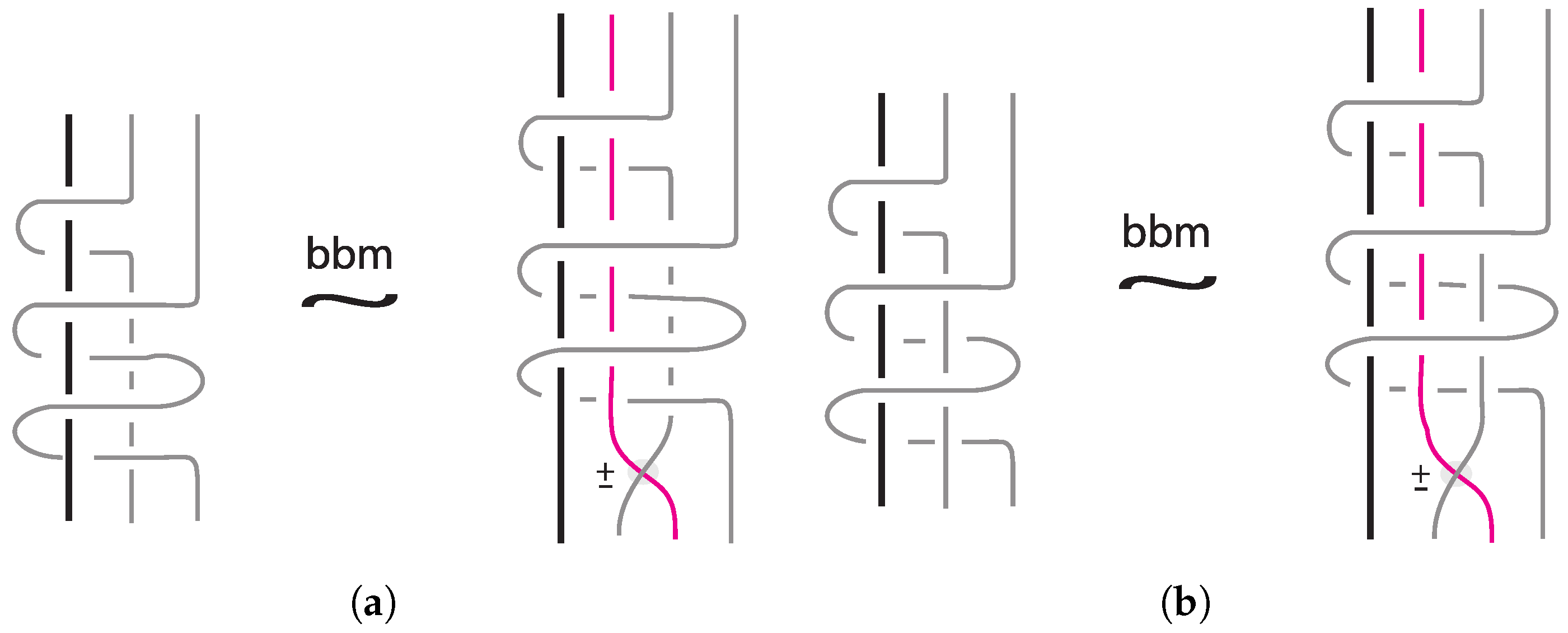
We first observe that the equations obtained by applying the two types of bbms on an element in $B_{\mathrm{ST}}$ other than the unknot, are different, and thus, both bbms are needed in order to compute KBSM ($S^1\times S^2$). In other words, we have that:

For $n\in \mathbb{N}\backslash \left\{0\right\}$, the equations $V_{\widehat{t^n}}=V_{\widehat{t_1^n{\sigma }_1}}$ and $V_{\widehat{t^n}}=V_{\widehat{t_1^n{\sigma }_1^{-1}}}$ are not equivalent.

Consider $t^n\in B_{\mathrm{ST}}$, where $n\ge 1$. Then, the equations obtained by performing bbms on $t^n$ are:

$$\begin{array}{ccc}{V}_{\widehat{t^n}}=V_{\widehat{t_1^n{\sigma }_1^{\pm 1}}}\hfill & \stackrel{(+)-bbm}{\underset{(-)-bbm}{\iff }}& \left\{\begin{array}{cc}{s}_n\hfill & =\left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{4n+2}tr\left(t_1^n{\sigma }_1\right)\hfill \\ s_n\hfill & =\left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{4n-2}tr\left(t_1^n{\sigma }_1^{-1}\right)\hfill \end{array}\right.\hfill \end{array}$$

We now deal with the equation obtained from a negative bbm and we underline expressions which are crucial for the next step.

$$\begin{array}{cccc}{s}_n\hfill & =& \left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{4n-2}tr\left(t_1^n\underline{{\sigma }_1^{-1}}\right)\hfill & \stackrel{{\sigma }_1^{-1}={\sigma }_1-(u-u^{-1})}{\iff }\\ & & & \\ s_n\hfill & =& \left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{4n-2}\left[tr\left(t_1^n{\sigma }_1\right)-(u-u^{-1})tr\left(t_1^n\right)\right]\hfill & \iff \\ & & & \\ s_n\hfill & =& \underline{\left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{4n+2}tr\left(t_1^n{\sigma }_1\right)}{u}^{-4}+\left({\displaystyle \frac{1+u^2}{u}}\right)u^{4n-2}(u-u^{-1})tr\left(t_1^n\right)\hfill & \stackrel{(+)-bbm}{\iff }\\ & & & \\ s_n\hfill & =& u^{-4}{s}_n+\left({\displaystyle \frac{1+u^2}{u}}\right)u^{4n-2}(u-u^{-1})tr\left(t_1^n\right)\hfill & \end{array}$$

Hence, for $n\in \mathbb{N}\backslash \left\{0\right\}$, we have that the equations obtained from the performance of the two types of bbms are equivalent if and only if:

$${\displaystyle \frac{u^4-1}{u^4}}·\left[s_n-u^{4n}tr\left(t_1^n\right)\right]=0$$

(7)

We now evaluate $tr\left(t_1^n\right)$ for $n=1$ and we have:

$$\begin{array}{ccccc}tr\left(t_1\right)\hfill & =& tr\left(\underline{{\sigma }_1}t{\sigma }_1\right)=tr\left(t\underline{{\sigma }_1^2}\right)\hfill & =& (u-u^{-1})tr\left(t{\sigma }_1\right)+tr\left(t\right)=\hfill \\ & & & & \\ & =& (u-u^{-1})\underline{z}·s_1+s_1\hfill & \stackrel{z={\displaystyle \frac{-1}{u(1+u^2)}}}{=}& {\displaystyle \frac{u^4+1}{u^2(1+u^2)}}·s_1,\hfill \end{array}$$

while by substituting $n=1$ in Equation (7), we obtain that $tr\left(t_1\right)={\displaystyle \frac{1}{u^4}}·s_1$. Therefore, we have a contradiction and we conclude that in order to compute KBSM ($S^1\times S^2$), we need to consider the effect of both types of bbms on elements in $B_{\mathrm{ST}}$.

4.1. Useful Lemmata

In this subsection, we present a series of results toward the solution of the infinite system (1), by studying the effect of the braid band moves on the elements in the basis $B_{\mathrm{ST}}$. We recall first an ordering relation defined in [21]. For that, we shall need the notion of the index of a word w, denoted $ind\left(w\right)$.

Definition 3

(Definition 1 of [21]). Let w be a word in Σ or in ${\Sigma }^{\prime }$. Then, the index of w, $ind\left(w\right)$, is defined to be the highest index of the $t_i$s ($t_i^{\prime }$s, respectively) in w, by ignoring possible gaps in the indices of the looping generators and by ignoring the braiding parts. Moreover, the index of a monomial in ${\sigma }_i$s is equal to 0.

Definition 4

(Definition 2 of [21]). Let $w={t_{i_1}^{\prime }}^{k_1}\dots {t_{i_{\mu }}^{\prime }}^{k_{\mu }}·{\beta }_1$ and $u={t_{j_1}^{\prime }}^{{\lambda }_1}\dots {t_{j_{\nu }}^{\prime }}^{{\lambda }_{\nu }}·{\beta }_2$ in ${\Sigma }^{\prime }$, where $k_t,{\lambda }_s\in \mathbb{Z}$ for all $t,s$ and ${\beta }_1,{\beta }_2\in H_n\left(q\right)$. Then, we define the following ordering in ${\Sigma }^{\prime }$:

(a) 

If ${\sum }_{i=0}^{\mu }{k}_i<{\sum }_{i=0}^{\nu }{\lambda }_i$, then $w<u$.

(b) 

If ${\sum }_{i=0}^{\mu }{k}_i={\sum }_{i=0}^{\nu }{\lambda }_i$, then:

(i) 

if $ind\left(w\right)<ind\left(u\right)$, then $w<u$,

(ii) 

if $ind\left(w\right)=ind\left(u\right)$, then:

(α) 

if $i_1=j_1,\dots ,i_{s-1}=j_{s-1},i_s<j_s$, then $w>u$,

(β) 

if $i_t=j_t$ for all t and $k_{\mu }={\lambda }_{\mu },k_{\mu -1}={\lambda }_{\mu -1},\dots ,k_{i+1}={\lambda }_{i+1},|k_i| < |{\lambda }_i|$, then $w<u$,

(γ) 

if $i_t=j_t$ for all t and $k_{\mu }={\lambda }_{\mu },k_{\mu -1}={\lambda }_{\mu -1},\dots ,k_{i+1}={\lambda }_{i+1},|k_i| = |{\lambda }_i|$ and $k_i>{\lambda }_i$, then $w<u$,

(δ) 

if $i_t=j_t\forall t$ and $k_i={\lambda }_i$, $\forall i$, then $w=u$.

The ordering in the set Σ is defined as in ${\Sigma }^{\prime }$, where $t_i^{\prime }$s are replaced by $t_i$s.

Our goal is to express $bbm\left(t^n\right)=t_1^n{\sigma }_1^{-1}\widehat{\cong }t{t}_1^{n-1}{\sigma }_1$ for $n\in \mathbb{N}$, to sums of elements in $B_{\mathrm{ST}}$.

Lemma 1.

For $n\in \mathbb{N}\backslash \left\{0\right\}$, the following holds in $T{L}_{1,n}$:

$$\begin{array}{cccc}\mathrm{i}.\hfill & t_1^n{\sigma }_1\hfill & \widehat{\cong }& t^n{\sigma }_1+{\displaystyle \sum _{i=0}^{n-1}}(u-u^{-1})t^i{t_1}^{n-i}\hfill \\ & & & \\ \mathrm{ii}.\hfill & t_1^n{\sigma }_1^{-1}\hfill & \widehat{\cong }& t^n{\sigma }_1+{\displaystyle \sum _{i=1}^{n-1}}(u-u^{-1})t^i{t_1}^{n-i}\hfill \end{array}$$

Proof. 

We prove Lemma 1(i) by induction on $n\in \mathbb{N}$. The base of induction is $t_1{\sigma }_1\widehat{\cong }(u-u^{-1})t_1+t{\sigma }_1$, which holds. Assume now that the relations hold for n. Then, for $n+1$, we have that:

$$\begin{array}{ccc}{t}_1^{n+1}{\sigma }_1\hfill & =& t_1^n\underline{t_1{\sigma }_1}\widehat{\cong }(u-u^{-1})t_1^{n+1}+t\underline{t_1^n{\sigma }_1}\stackrel{ind.}{\underset{step}{=}}\hfill \\ & & \\ & =& (u-u^{-1})t_1^{n+1}+t^{n+1}{\sigma }_1+{\displaystyle \sum _{i=0}^{n-1}}(u-u^{-1})t^{i+1}{t_1}^{n-i}=\hfill \\ & & \\ & =& t^{n+1}{\sigma }_1+{\displaystyle \sum _{i=0}^n}(u-u^{-1})t^i{t_1}^{n+1-i}\hfill \end{array}$$

□

We now express monomials of the form $t^m{t}_1^n\in \Sigma$, where $m,n\in \mathbb{N}$ in sums of elements of the form $t^m{t_1^{\prime }}^n\in {\Sigma }^{\prime }$. In [21], a method for expressing monomials in Σ to sums of monomials in ${\Sigma }^{\prime }$ (and vice-versa) is presented on the level of the generalized Hecke algebra of type B, $H_{1,n}$. This was achieved with the use of the ordering relation defined on the basic sets of $H_{1,n}$ (Definition 4). More precisely, in [21], it is shown that a monomial τ in Σ can be written as a sum of elements in the set $\{{t_0^{\prime }}^{k_0}{t_1^{\prime }}^{k_1}\dots {t_m^{\prime }}^{k_m}|k_i\ge k_{i+1},k_i\in \mathbb{Z}\backslash \left\{0\right\},\forall i\}$, such that the term ${\tau }^{\prime }$, which is obtained from τ by changing $t_i$ into $t_i^{\prime }$ for all i, is the highest order term in the sum. Recall now that the generalized Temperley–Lieb algebra of type B, $T{L}_{1,n}$, is a quotient of $H_{1,n}$ over the ideal generated by elements in Equation (3) that only involves the σs, and since the only braiding generator in the monomials $bbm\left(t^n\right)$ is ${\sigma }_1^{\pm 1}$, it follows that the results presented in [21] are also true in $T{L}_{1,n}$ for the monomials $bbm\left(t^n\right)=t_1^n{\sigma }_1^{\pm 1}$. In particular, we have that for $n\in \mathbb{N}\backslash \left\{0\right\}$, the following holds in $T{L}_{1,n}$:

$$\begin{array}{ccccccc}{t}_1^n{\sigma }_1\hfill & \widehat{\cong }& {\displaystyle \sum _{i=0}^n}{a}_i{t}^i{t_1^{\prime }}^{n-i}\hfill & \mathrm{and}& t_1^n{\sigma }_1^{-1}\hfill & \widehat{\cong }& {\displaystyle \sum _{i=1}^n}{a}_i^{\prime }{t}^i{t_1^{\prime }}^{n-i}.\hfill \end{array}$$

where $a_i$ and $a_i^{\prime }$ are coefficients for all i.

We now deal with elements of the form $t^k{t_1^{\prime }}^m$, such that $k,m\in \mathbb{N}$ and $k\ge m>0$.

Lemma 2.

For $k,m\in \mathbb{N}$ and $k\ge m>0$, the following relation holds in $T{L}_{1,n}$:

$$t^k{t_1^{\prime }}^m\widehat{\cong }-A^{-2}{t}^{k+m}-A^3{t}^{k+m-2}-A{t}^{k-1}{t_1^{\prime }}^{m-1}$$

Proof. 

We consider $t^k{t_1^{\prime }}^m$ and we apply the Kauffman bracket skein relation as demonstrated in Figure 14. Applying the skein relations and conjugation, we may express these elements in terms of elements in the basis $B_{\mathrm{ST}}$, together with elements of the form $t^{k-i}{t_1^{\prime }}^{m-i},i>0$, of lower order than $t^k{t_1^{\prime }}^m$. The process is repeated until we are left with elements in $B_{\mathrm{ST}}$.  □

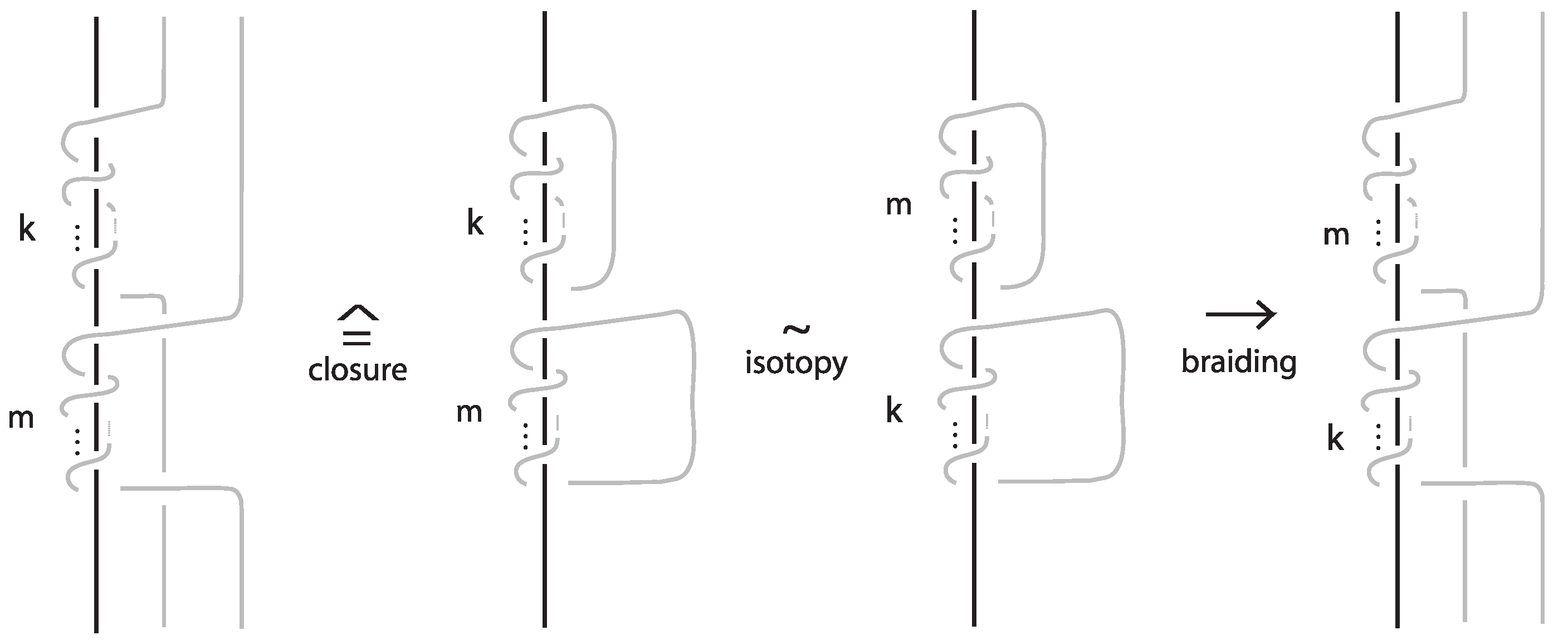
Remark 5.

In Lemma 2, we considered elements of the form $t^k{t_1^{\prime }}^m$, where $k\ge m>0$. If $k<m$, then we consider the closure operation on the mixed braids and we order the exponents, since the $t_i^{\prime }$s are conjugates, i.e., $t^k{t_1^{\prime }}^m\widehat{=}{t}^m{t_1^{\prime }}^k$. Then, we braid the resulting loops again (see Figure 15).

Corollary 1.

For $k,m\in \mathbb{N}$ and $k\ge m>0$, the following relation holds in $T{L}_{1,n}$:

$$t^k{t_1^{\prime }}^m\widehat{\cong }-A^{-2}{t}^{k+m}+\underset{i=0}{\sum ^{\lfloor {\displaystyle \frac{k+m-2}{2}}\rfloor }}{a}_i{t}^{2i},$$

where $a_i$ are coefficients.

4.2. The Infinite System

By general position arguments, for computing the Kauffman bracket skein module of $S^1\times S^2$, we may first consider the effect of negative bbms on elements in $B_{\mathrm{ST}}$, obtain a spanning set for $B_{-}^{S^1\times S^2}:={\displaystyle \frac{B_{\mathrm{ST}}}{<a-bb{m}_{-}\left(a\right)>}}$, and then study the effect of positive bbms on elements in $B_{-}^{S^1\times S^2}$. With a slight abuse of notation, we denote the above as follows:

$$\mathrm{KBSM}\left(S^1\times S^2\right)={\displaystyle \frac{{\mathrm{B}}_{ST}}{<a-bb{m}_{\pm }\left(a\right)>}}={\displaystyle \frac{{\mathrm{B}}_{ST}/<a-bb{m}_{-}\left(a\right)>}{<a-bb{m}_{+}\left(a\right)>}}={\displaystyle \frac{B_{-}^{S^1\times S^2}}{<a-bb{m}_{+}\left(a\right)>}}.$$

Hence, we consider elements in $B_{ST}$ and perform negative braid band moves, obtaining an infinite system of equations, the solution of which corresponds to a basis for $B_{S^1\times S^2}^{-}$. We have the following:

Theorem 9.

$B_{-}^{S^1\times S^2}$ is generated by the unknot $t^0$ and t.

Proof. 

We consider the infinite system of equations $V_{\widehat{t^n}}=V_{\widehat{t_1^n{\sigma }_1^{-1}}}$, for $n\in \mathbb{N}$. We have that:

$$\begin{array}{cccccc}\mathrm{For}n=0:\hfill & \hfill 1\stackrel{bb{m}_{-}}{\to }{\sigma }_1^{-1}& \Rightarrow & \hfill V_{\widehat{1}}=V_{\widehat{{\sigma }_1^{-1}}}& \Rightarrow & 1=\left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{-2}tr\left({\sigma }_1^{-1}\right)\Rightarrow \hfill \\ & & & & & \\ & & & \hfill 1& =& -{\displaystyle \frac{1+u^2}{u^3}}\left(z-(u-u^{-1})\right)\stackrel{z=-{\displaystyle \frac{1}{u(1+u^2)}}}{\Rightarrow }\hfill \\ & & & & & \\ & & & \hfill 1& =& 1\hfill \\ & & & & & \\ \mathrm{For}n=1:\hfill & \hfill t\stackrel{bb{m}_{-}}{\to }{t}_1{\sigma }_1^{-1}& \Rightarrow & \hfill V_{\widehat{t}}=V_{\widehat{t_1{\sigma }_1^{-1}}}& \Rightarrow & s_1=\left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{2}tr\left(t_1{\sigma }_1^{-1}\right)\Rightarrow \hfill \\ & & & & & \\ & & & \hfill s_1& =& --{\displaystyle \frac{1+u^2}{u}}{u}^{2}z{s}_1\Rightarrow \hfill \\ & & & & & \\ & & & \hfill s_1& =& s_1\hfill \end{array}$$

Hence, $t^0$, which corresponds to the unknot, and t are free in $B_{S^1\times S^2}^{-}$.

Consider now $n\in \mathbb{N}$ such that $n\ge 2$. Then:

$$t^n\stackrel{bb{m}_{-}}{⟶}{t}_1^n{\sigma }_1^{-1}\widehat{\cong }t{t}_1^{n-1}{\sigma }_1\widehat{\underset{\left[13\right]}{\cong }}\underset{i=1}{\sum ^n}{a}_i{t}^i{t_1^{\prime }}^{n-i}\underset{\mathrm{Cor}.1}{\widehat{\cong }}{a}_n{t}^n+\underset{i=0}{\sum ^{\lfloor {\displaystyle \frac{n-2}{2}}\rfloor }}{a}_i{t}^{2i}$$

where $a_i$ are coefficients for all i.

Hence, $tr\left(t_1^n{\sigma }_1^{-1}\right)=a_n{s}_n+{\displaystyle \sum _{i=1}^{\lfloor {\displaystyle \frac{n}{2}}\rfloor }}{b}_i{s}_{n-2i}$, for all $n\in \mathbb{N}$. Thus, by ignoring the coefficients, we have the following:

$$\begin{array}{ccc}{V}_{\widehat{t^n}}=V_{\widehat{t_1^n{\sigma }_1^{-1}}}\hfill & \Rightarrow & s_n=\left\{\begin{array}{cc}{\displaystyle \sum _{i=0}^{(n-2)/2}}{s}_{2i}\hfill & ,\mathrm{for}neven\hfill \\ {\displaystyle \sum _{i=0}^{(n-3)/2}}{s}_{2i+1}\hfill & ,\mathrm{for}nodd\hfill \end{array}\right.\Rightarrow \end{array}$$

$$\begin{array}{cc}\underline{\mathrm{n}-\mathrm{even}}& \underline{\mathrm{n}-\mathrm{odd}}\\ & \\ s_2=s_0& s_3=s_1\\ & \\ s_4=s_0+s_2& s_5=s_1+s_3\\ & \\ ⋮& ⋮\\ & \\ s_{2k}={\displaystyle \sum _{i=0}^{k-1}}{s}_{2i}& s_{2k+1}={\displaystyle \sum _{i=0}^{k-1}}{s}_{2i+1}\\ & \\ \Downarrow & \Downarrow \\ s_{2k}\sim a·s_0& s_{2k+1}\sim b·s_1,\end{array}$$

where $a,b$ are coefficients.

Recall now that $tr\left(t\right)=s_1$ and $tr\left(t^0\right)=s_0$. The result follows.  □

Corollary 2.

The set $\{t^0,t\}$ forms a basis for $B_{-}^{S^1\times S^2}$.

We now consider the effect of positive braid band moves on the elements $t^0$ and t. We have the following result:

Theorem 10.

The free part of KBSM $\left(S^1\times S^2\right)$ is generated by the unknot and the torsion part is generated by t.

Proof. 

We consider the elements in the basis of $B_{S^1\times S^2}^{-}$ and we study the effect of a positive braid band move on them. We have that:

$$\begin{array}{cccccc}\mathrm{For}n=0:\hfill & \hfill 1\stackrel{bb{m}_{+}}{\to }{\sigma }_1& \Rightarrow & \hfill V_{\widehat{1}}=V_{\widehat{{\sigma }_1}}& \Rightarrow & 1=\left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{-2}tr\left({\sigma }_1\right)\Rightarrow \hfill \\ & & & & & \\ & & & \hfill 1& =& -(1+u^2)uz\stackrel{z=-{\displaystyle \frac{1}{u(1+u^2)}}}{\Rightarrow }\hfill \\ & & & & & \\ & & & \hfill 1& =& 1\left(\mathrm{free}\mathrm{part}\right)\hfill \\ & & & & & \\ \mathrm{For}n=1:\hfill & \hfill t\stackrel{bb{m}_{+}}{\to }{t}_1{\sigma }_1& \Rightarrow & \hfill V_{\widehat{t}}=V_{\widehat{t_1{\sigma }_1}}& \Rightarrow & s_1=\left(-{\displaystyle \frac{1+u^2}{u}}\right)u^{6}tr\left(t_1{\sigma }_1\right)\hfill \end{array}$$

We evaluate $tr\left(t_1{\sigma }_1\right)$:

$$\begin{array}{ccccc}tr\left(t_1{\sigma }_1\right)\hfill & =& (u-u^{-1})tr\left(t_1\right)+tr\left({\sigma }_{1}t\right)\hfill & =& {(u-u^{-1})}^{2}tr\left(t{\sigma }_1\right)+(u-u^{-1})tr\left(t\right)+z{s}_1\hfill \\ & & & & \\ & & & =& (u^2-1+u^{-2})z{s}_1+(u-u^{-1})s_1\hfill \end{array}$$

Substituting $tr\left(t_1{\sigma }_1\right)$ in the equation above, we obtain the following:

$$V_{\widehat{t}}=V_{\widehat{t_1{\sigma }_1}}\iff (1-u^6)(1-u^2)s_1=0.$$

(8)

From Equation (8) and Theorem 9, we have that $s_1=tr\left(t\right)$ generates the torsion part of KBSM ($S^1\times S^2$). The free part of KBSM ($S^1\times S^2$) is generated by the unknot (or the empty knot).  □

Although we do not obtain a closed formula for the torsion part of KBSM ($S^1\times S^2$), Theorem 10 implies the following:

Corollary 3.

If π denotes the natural projection

$$\pi :\mathrm{KBSM}\left(S^1\times S^2\right)\to \mathrm{KBSM}\left(S^1\times S^2\right)/Tor,$$

then:

$$\pi \left(t^{2n+1}\right)=0,\forall n\in \mathbb{N}\mathrm{and}\mathrm{KBSM}\left(S^1\times S^2\right)/Tor=\mathbb{Z}\left[A^{\pm 1}\right].$$

5. A Diagrammatic Approach via Braids

In this section, we present the diagrammatic approach for computing KBSM ($S^1\times S^2$) via braids. Note that during the process that we will describe below, the braids “lose” their natural top-to-bottom orientation, giving rise to what we call unoriented braids. Unoriented braids were defined in [3] as standard braids by ignoring the natural top-to-bottom orientation (for an illustration, see Figure 16). These tools seem promising in computing Kauffman bracket skein modules of arbitrary 3-manifolds (see, for example, [9,10]).

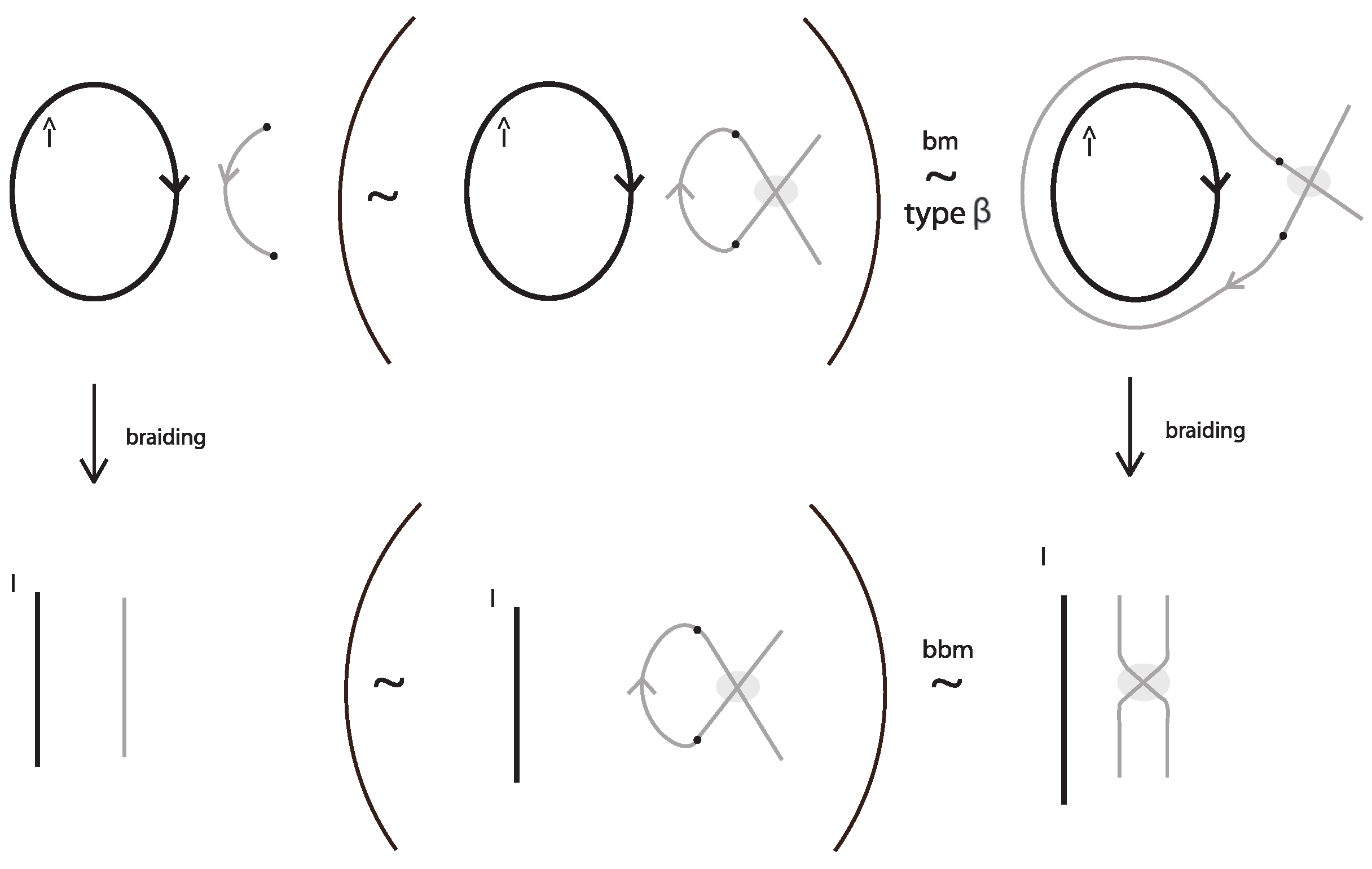
In [16], it is shown that in order to describe isotopy for knots and links in a c.c.o. 3-manifold, it suffices to consider only one type of band moves (recall the discussion in Section 3). In the algebraic approach, we only considered the type β-band moves that correspond to the braid band moves, and in the diagrammatic approach, we will be using the α-type band moves (recall Figure 7). Our starting point again is the following:

$$\mathrm{KBSM}(S^1\times S^2)=\mathrm{KBSM}\left(\mathrm{ST}\right)/<\alpha -\mathrm{type}\mathrm{band}\mathrm{moves}>=B_{\mathrm{ST}}/<\alpha -\mathrm{type}\mathrm{band}\mathrm{moves}>,$$

(9)

that is, we study the effect of the α-type band moves on elements in the $B_{\mathrm{ST}}$ basis of KBSM (ST). We denote the effect of α-type band moves on $t^n\in B_{\mathrm{ST}}$ as $bm\left(t^n\right)=A^6{x}_n$, where $x_n$ is illustrated in Figure 17. Obviously, $x_1=\widehat{t}$.

We now return to the infinite system of Equation (9) and we have the following:

$$t\stackrel{\mathrm{band}}{\underset{\mathrm{move}}{⟶}}{A}^6{x}_1\iff (1-A^6)t=0.$$

(10)

Hence, t produces torsion in KBSM ($S^1\times S^2$).

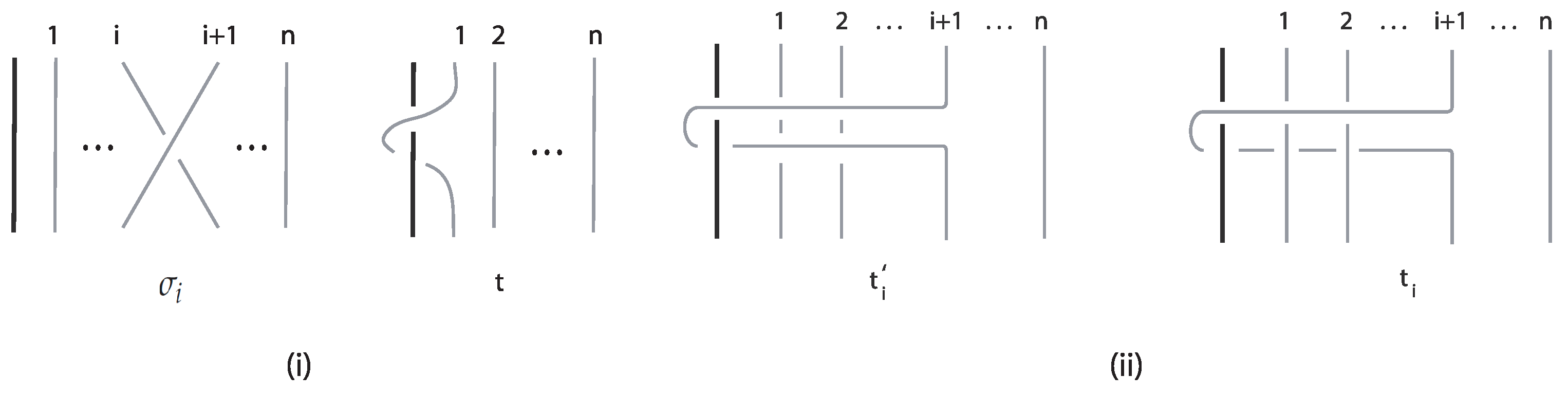
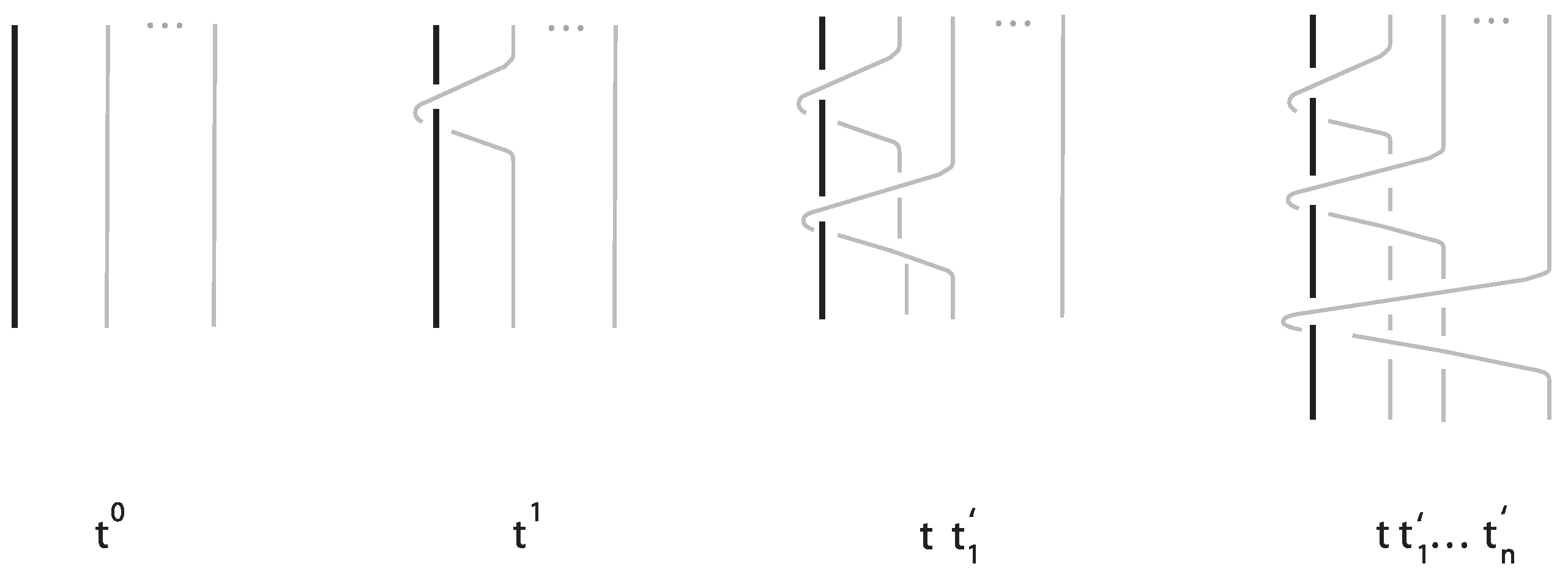
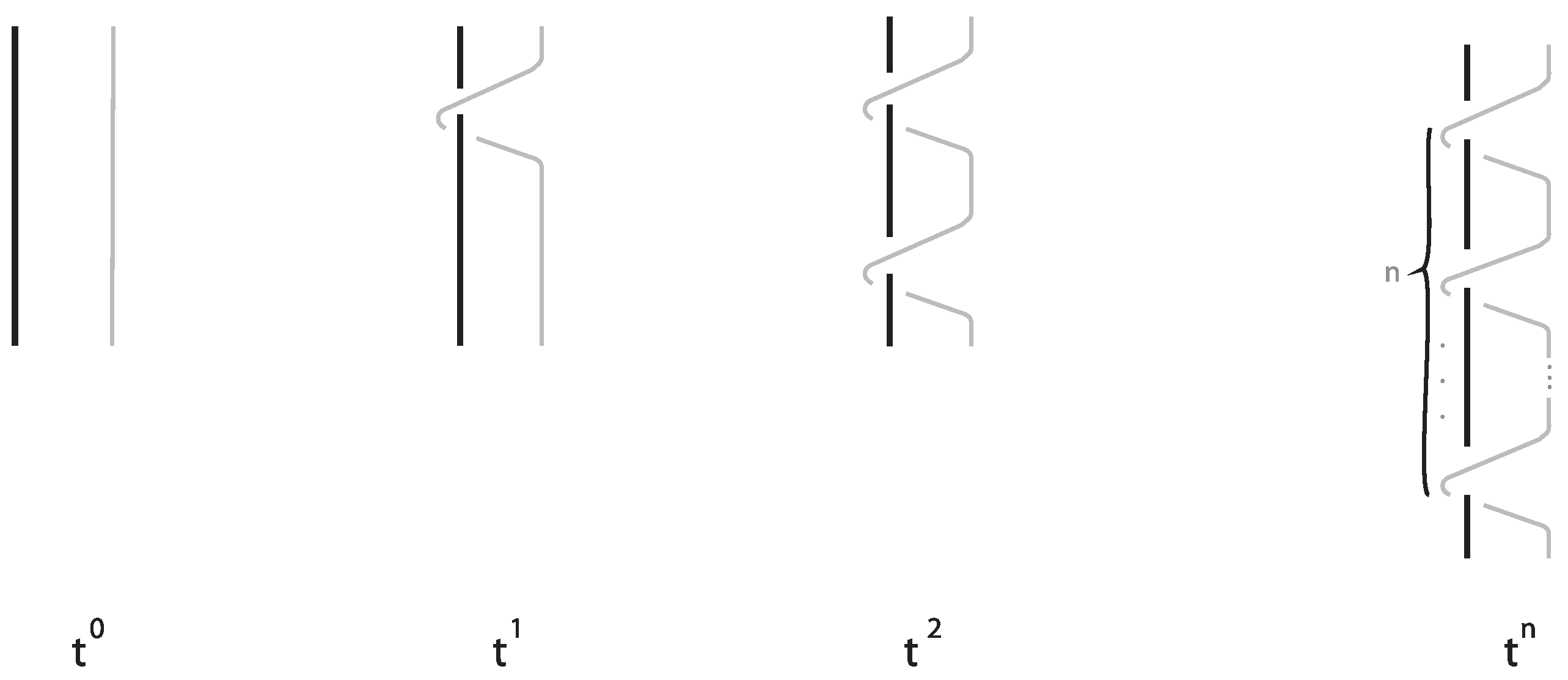
Notation 2.

We denote by $\widehat{t}$ the closure of the looping generator t and by ${\widehat{t}}^m$ the closure of m-looping generators in ST. Moreover, $x_n{\widehat{t}}^m$, $n,m\in \mathbb{N}$, denotes $x_n$ followed by m copies of $\widehat{t}$. For an illustration, see Figure 18.

In order to clarify the steps needed toward the computation of KBSM (ST) using the diagrammatic method via braids, we also demonstrate how we obtain the equation for $t^2$. After the performance of the band move on $t^2$, we apply the Kauffman bracket skein relation on the resulting $A^6{x}_2$ and we write $x_2$ in terms of $\widehat{t}$s. Applying the skein relation then again to the $\widehat{t}$s, we express them in terms of the $t_i$s, obtaining the equation of the infinite system. For an illustration, see Figure 19. Indeed, we have that:

$$\begin{array}{ccccc}\hfill t^2& \to & bm\left(t^2\right)=A^6{x}_2& \widehat{\cong }& -A^{10}{\widehat{t}}^2-A^8\hfill \\ & & & & \\ \hfill {\widehat{t}}^2& \stackrel{\mathrm{braiding}}{\to }& t{t}_1^{\prime }& \widehat{\cong }& -A^{-2}{t}^2-A^2\hfill \end{array}$$

Hence, we obtain the following equation:

$$(1-A^8)t^2=-A^8(1-A^4).$$

We observe that, in order to obtain the equations of the infinite system, a recursive formula for $x_n$ is needed. We have the following:

Lemma 3.

For $n\in \mathbb{N}$, such that $n\ge 2$, the following relations hold in KBSM ($S^1\times S^2$):

$$x_n\sim -A^8{x}_{n-2}-A^4{x}_{n-1}\widehat{t}.$$

Note now that $\widehat{t}$ will not affect the process illustrated in Figure 20 for $x_{n-1}\widehat{t}$. Indeed, we have that

$$x_{n-1}\widehat{t}\sim -A^8{x}_{n-3}\widehat{t}-A^4{x}_{n-2}{\left(\widehat{t}\right)}^2.$$

Moreover, for $n=2$, we have that $x_2\sim -A^4{\widehat{t}}^2-A^2$.

We now present an ordering relation for elements in the set $D:={\left\{x_n{\widehat{t}}^m\right\}}_{n,m\in \mathbb{N}}$.

Definition 5.

Let $\alpha =x_n{\widehat{t}}^m$ and $\beta =x_k{\widehat{t}}^l$. Then:

i. 

If $n+m<k+l$, then $\alpha <\beta$.

ii. 

If $n+m=k+l$, then:

a. 

If $n<k$, then $\alpha <\beta$.

b. 

If $n=k$, then $\alpha =\beta$.

Proposition 1.

The set $D:={\left\{x_n{\widehat{t}}^m\right\}}_{n,m\in \mathbb{N}}$, equipped with the ordering relation given in Definition 5, is a totally ordered and a well-ordered set.

Proof. 

In order to show that the set D is a totally ordered set when equipped with the ordering given in Definition 5, we need to show that the ordering relation is antisymmetric, transitive, and total. We only show that the ordering relation is transitive. The antisymmetric property follows similarly and totality follows from Definition 5, since all possible cases have been considered.

Let $\alpha =x_n{\widehat{t}}^m,\beta =x_k{\widehat{t}}^l,\gamma =x_p{\widehat{t}}^q$, such that $\alpha <\beta$ and $\beta <\gamma$. We prove that $\alpha <\gamma$. Since $\beta <\gamma$, we have that:

(a.)

either $n+m<k+l$, and since $\beta <\gamma$, we have that $k+l\le p+q\Rightarrow n+m<p+q\Rightarrow \alpha <\gamma$,

(b.)

or $n+m=k+l$ such that $n<k$. Then, since $\beta <\gamma$, we have that:

(i.)

either $k+l<p+q$, the same as in case (a.),

(ii.)

or $k+l=p+q$, such that $k<p$. Then, $n<k<p\Rightarrow \alpha <\gamma$.

We conclude that the ordering relation is transitive. The minimum element in D is $x_0{\widehat{t}}^0$, i.e., the unknot, and hence D is a well-ordered set.  □

The next step is to convert the $x_n$s to elements in the $B_{\mathrm{ST}}$ basis of KBSM (ST) for all $n\in \mathbb{N}$. For that, we need the following lemmas:

Lemma 4.

For $n\in \mathbb{N}$, such that $n\ge 2$, the following relations hold in KBSM ($S^1\times S^2$):

$$x_n={(-1)}^{n-1}{A}^{4n-4}{\widehat{t}}^n+\left\{\begin{array}{cc}{\displaystyle \sum _{i=0}^{{\displaystyle \frac{n-2}{2}}}}{a}_i{\widehat{t}}^{2i}\hfill & ,\mathrm{for}n\mathrm{even}\hfill \\ & \\ {\displaystyle \sum _{i=0}^{\lfloor {\displaystyle \frac{n-2}{2}}\rfloor }}{b}_i{\widehat{t}}^{2i+1}\hfill & ,\mathrm{for}n\mathrm{odd}\hfill \end{array}\right.$$

(11)

Proof. 

We prove Lemma 4 by strong induction on n. The case $n=2$ is the base of induction and we have that $x_2\widehat{\cong }-A^4{\widehat{t}}^2-A^2$. Hence, relation (11) holds for $n=2$. Assume that relations (11) hold for all $n\in \mathbb{N},n>2$ up to $k\in \mathbb{N}$. Then, for $k+1$ we have:

$$\begin{array}{cccc}{x}_{k+1}\hfill & \stackrel{L.3}{=}& -A^8\underline{x_{k-1}}-A^4\underline{x_k}\widehat{t}\hfill & \stackrel{ind.}{\underset{step}{=}}\\ & & & \\ & =& -A^8\left({(-1)}^{k-1}{A}^{4(k-1)-4}{\widehat{t}}^{k-1}+\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\right)\hfill & +\\ & & & \\ & +& -A^4\left({(-1)}^{k-1}{A}^{-4k+4}{\widehat{t}}^{k+1}+\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\right)\hfill & =\\ & & & \\ & =& {(-1)}^k{A}^{-4k}{\widehat{t}}^{k-1}+{(-1)}^{k+2}{A}^{-4k}{\widehat{t}}^{k+1}+\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\hfill & =\\ & & & \\ & =& {(-1)}^{k+2}{A}^{-4(k+1)+4}{\widehat{t}}^{k+1}+\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\hfill \end{array}$$

where “l.o.t.” stands for lower ordered terms.  □

Note that $\widehat{t^k}$ corresponds to the monomial $t{t}_1^{\prime }\dots t_{k-1}^{\prime }={\tau }_{0,k-1}^{\prime }$, namely, a monomial in the ${\mathcal{B}}_{\mathrm{ST}}^{\prime }$ basis of KBSM (ST). We now convert these monomials to elements in the $B_{\mathrm{ST}}$ basis. We also note that this is performed in ([Section 3] of [3]) via the ordering relation of Definition 4.

Lemma 5.

The following relations hold in KBSM (ST), and hence in KBSM ($S^1\times S^2$), for $k,m\in \mathbb{N}$ such that $k,m\ge 2$:

$$\beta {t_i^{\prime }}^k{t_{i+1}^{\prime }}^m\widehat{\cong }-A^{-2}\beta {t_i^{\prime }}^{k+m}-A^3\beta {t_i^{\prime }}^{k+m-2}-A\beta {t_i^{\prime }}^{k-1}{t_{i+1}^{\prime }}^{m-1}$$

where β is a monomial of $t_i^{\prime }$s with index at most $i-1$.

Proof. 

The proof of Lemma 5 is an immediate result of Lemma 2 (recall also Figure 14).  □

Lemma 5 implies the following:

Proposition 2.

For $n\in \mathbb{N}$, such that $n>0$, the following relations hold:

$${\widehat{t}}^n\widehat{\underset{\mathrm{skein}}{\cong }}{\left(-A^{-2}\right)}^n{t}^{n+1}+\underset{i=0}{\sum ^n}{a}_i{t}^i,$$

where the $a_i$s are coefficients.

Proof. 

Consider the monomial ${\widehat{t}}^n:=t{t}_1^{\prime }\dots t_{n-1}^{\prime }$ and apply Lemma 5 on each pair of loop generators with consecutive indices. Each time Lemma 5 is applied, the coefficient $-A^{-2}$ will appear on the highest order term of the resulting sum. In total, there are $n-1$ pairs of $t_i^{\prime }$s where Lemma 5 is to be applied. The result follows.  □

We are now ready to present the main theorem of this section.

Theorem 11.

The following relations hold in KBSM ($S^1\times S^2$):

$$\left(1-A^{2n+4}\right)t^n=\left\{\begin{array}{cc}{\displaystyle \sum _{i=0}^{(n-2)/2}}{a}_i{t}^{2i}\hfill & ,\mathrm{for}n\mathrm{even}\hfill \\ & \\ {\displaystyle \sum _{i=0}^{(n-3)/2}}{b}_i{t}^{2i+1}\hfill & ,\mathrm{for}n\mathrm{odd}\hfill \end{array}\right.$$

Proof. 

$$\begin{array}{cccccc}{t}^n& \stackrel{bm}{\to }& A^6\underline{x_n}\hfill & \stackrel{L.4}{=}& A^6\left[{(-1)}^{n-1}{A}^{4n-4}\underline{{\widehat{t}}^n}+\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\right]\hfill & \widehat{\underset{\mathrm{Prop}.2}{\cong }}\\ & & & & & \\ & & & \widehat{\underset{\mathrm{skein}}{\cong }}& {(-1)}^{n-1}{A}^{4n+2}{\left(-A^{-2}\right)}^{n-1}\left(t^n+{\displaystyle \sum _{i=0}^{n-2}}{a}_i{t}^i\right)+\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\hfill & =\\ & & & & & \\ & & & =& {(-1)}^{2n-2}{A}^{4n+2-2n+2}{t}^n++\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\hfill & =\\ & & & & & \\ & & & =& A^{2n+4}{t}^n++\sum \mathrm{l}.\mathrm{o}.\mathrm{t}.\hfill & \end{array}$$

where “l.o.t.” stands for lower ordered terms than $t^n$.  □

Considering now the result of Theorem 11 on the infinite system of Equation (9), a solution of which corresponds to computing KBSM ($S^1\times S^2$), we have that the elements of the form $t^{2n+1}$ for $n\in \mathbb{N}$, correspond to the torsion part of KBSM ($S^1\times S^2$), since these elements can be written as $a·t$ and t produces torsion in $S^1\times S^2$ (recall relation (10)). Moreover, we have that the free part of KBSM ($S^1\times S^2$) is generated by the unknot. In other words, we have shown that:

Theorem 12.

$$\mathrm{KBSM}\left(S^1\times S^2\right)=\mathbb{Z}\left[A^{\pm 1}\right]\oplus \underset{i=0}{\stackrel{\infty }{⨁}}{\displaystyle \frac{\mathbb{Z}[A^{\pm 1]}}{(1-A^{2i+4})}}$$

Our results agree with that on [11], where KBSM ($S^1\times S^2$) is computed with the use of an appropriate basis of Chebyshev polynomials presented in [24].

6. Conclusions

In this paper, we compute the Kauffman bracket skein module of $S^1\times S^2$ using two different methods: the algebraic method based on the generalized Temperley–Lieb algebra of type B, and the diagrammatic method via braids. The algebraic approach was first implemented for the computation of HOMFLYPT skein modules of 3-manifolds via the generalized Hecke algebras of type B (see for example [12]). It was then extended for the computation of Kauffman bracket skein modules of 3-manifolds via the generalized Temperley–Lieb algebra of type B (see [3]). The diagrammatic method for computing Kauffman bracket skein modules has been successfully implemented for the case of the handlebody of genus two (see [9] and also [25] for the classical case), for the complement of $(2,2p+1)$-torus knots ([10]) and for the case of the lens spaces $L(p,q)$ ([3]). It is also worth mentioning that these techniques have been applied toward the computation of various skein modules of different families of ‘knotted objects’ in (various) 3-manifolds. In [26], for example, the notion of skein modules is extended for knotoids in the solid torus.