Maximizing the Index of Signed Complete Graphs Containing a Spanning Tree with k Pendant Vertices

Abstract

A signed graph $\Sigma =(G,\sigma )$ consists of an underlying graph $G=(V,E)$ with a sign function $\sigma :E\to \{-1,1\}$. Let $A(\Sigma )$ be the adjacency matrix of $\Sigma$ and ${\lambda }_1(\Sigma )$ denote the largest eigenvalue (index) of $\Sigma$. Define $(K_n,H^{-})$ as a signed complete graph whose negative edges induce a subgraph H. In this paper, we focus on the following question: which spanning tree T with a given number of pendant vertices makes the ${\lambda }_1\left(A(\Sigma )\right)$ of the unbalanced $(K_n,T^{-})$ as large as possible? To answer the question, we characterize the extremal signed graph with maximum ${\lambda }_1\left(A(\Sigma )\right)$ among graphs of type $(K_n,T^{-})$.

1. Introduction

Throughout this paper, unless stated otherwise, all the underlying graphs are considered as simple and connected. A signed graph $\Sigma =(G,\sigma )$ consists of an underlying graph $G=(V,E)$ with a sign function $\sigma :E\to \{-1,1\}$. The (unsigned) graph G is said to be the underlying graph of $\Sigma$, and the function $\sigma$ is called the signature of $\Sigma$. Two distinct adjacent vertices are neighbors. The set of neighbors of a vertices v in a graph G is denoted by $N_G\left(v\right)$ and let $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$. The degree of a vertex v in a graph G, denoted by $d_G\left(v\right)$, is the number of neighbors of v in G. We denote the minimum and maximum degrees of the vertices of G by $\delta \left(G\right)$ and $\Delta \left(G\right)$. Specifically, a vertex of degree one is called a pendant vertex. A complete graph of order n, denoted by $K_n$, is a simple graph in which any two vertices are adjacent. In signed graphs, edge signs are usually interpreted as $\pm 1$. An edge e is positive (resp. negative) if $\sigma \left(e\right)=+1$ (resp. $\sigma \left(e\right)=-1$). The sign of a signed cycle C is given by $\sigma \left(C\right)={\prod }_{e\in C}\sigma \left(e\right)$. A cycle C is positive (resp. negative) if its sign is + (resp. −); alternatively, we can say that a signed cycle is positive (resp. negative) if it contains an even (resp. odd) number of negatives edges. A signed graph is balanced if there are no negative cycles; otherwise, it is unbalanced. Note that unsigned graphs are treated as (balanced) signed graphs whose edges are all assigned positive signs, that is, the all-positive signature.

The adjacency matrix of $\Sigma$ is defined as $A(\Sigma )=\left(a_{ij}^{\sigma }\right)$, where $a_{ij}^{\sigma }=\sigma \left(v_i{v}_j\right)$ if $v_i\sim v_j$, and 0 otherwise. Note that $A(\Sigma )$ is a real symmetric matrix. Let $P\left(\lambda \right)=det(\lambda I-A(\Sigma \left)\right)$ be the characteristic polynomial of $A(\Sigma )$, where I is the identity matrix. The spectrum of $\Sigma$ is by definition the spectrum of the adjacency matrix $A(\Sigma )$, that is, its set of eigenvalues together with their multiplicities. As usual, we use ${\lambda }_1(\Sigma )\ge {\lambda }_2(\Sigma )\ge \cdots \ge {\lambda }_n(\Sigma )$ to denote the spectrum of $\Sigma$, where ${\lambda }_n(\Sigma )$ is the least eigenvalue and ${\lambda }_1(\Sigma )$ is the largest eigenvalue that is often called the index of $\Sigma$. The spectral radius of $\Sigma$, denoted by $\rho \left(A\right(\Sigma \left)\right)$, is the largest absolute value of the eigenvalues of $A(\Sigma )$, i.e., $\rho \left(A(\Sigma )\right)=max\{{\lambda }_1\left(A(\Sigma )\right),-{\lambda }_n\left(A(\Sigma )\right)\}$.

At the very beginning, signed graphs were studied in the context of social psychology, where the vertices are considered as individuals, and the positive and negative edges represent friendships and enmities between them, respectively. The concept of balance was first introduced in works of Harary [1] and Cartwright and Harary [2]. And the matroids of graphs were extended to matroids of signed graphs by Zaslavsky [3]. Chaiken [4] and Zaslavsky [3] obtained the matrix tree theorem for signed graphs independently. In fact, the theory of signed graphs is a special case of that of gain graphs and biased graphs [5]. A detailed reference of materials on signed graphs is the dynamic survey of Zaslavsky [6].

Extremal graph theory deals with the problem of determining extremal values and extremal graphs for a given graph invariant in a given set of graphs. In [7], Wu, Xiao, and Hong determined the unique tree of order n with k pendant vertices which achieved the maximal spectral radius. They showed that the maximal spectral radius was obtained uniquely at $T_{n,k}$, where $T_{n,k}$ was a tree of order n obtained from a star $K_{1,k}$ and k paths of almost equal lengths by joining each pendant vertex of $K_{1,k}$ to an end vertex of one path. Guo [8] determined the graphs with the largest spectral radius among all the unicyclic and bicyclic graphs with n vertices and k pendant vertices, respectively. Petrović and Borovićanin [9] then determined the unique graph with the largest spectral radius among all tricyclic graphs with n vertices and k pendant vertices. A graph G is called a cactus if any two of its cycles have at most one common vertex. In [10], Wu, Deng, and Jiang identified the graphs with the largest spectral radius among all the cacti with n vertices and k pendant vertices. Apart from these, there are also some research results on the least eigenvalues of graphs with given pendant vertices, which can be seen in [11,12,13]. In addition, since the Perron–Frobenius theorem (see [Theorem 2.2.1] of [14]) does not hold in general for signed graphs, the results and tools about the extremal spectral theory of signed graphs are limited. It is significant and meaningful to seek and develop new methods. To study the extremal spectral radius problem of signed graphs, it is necessary to study how to distribute the negative edges of signed graphs so that the largest or the least eigenvalues can reach the maximum or the minimum. Thus, the relations between the index or the least eigenvalue and a given graph invariant in a given set of signed graphs have been studied. Some recent research can be found in [15,16,17,18]. For some other extremal spectral theory of signed graphs, see [19,20,21] for details.

In this paper, we deal with signed graphs with extremal eigenvalues. It is worth noting that Koledin and Stanić [22] studied the connected signed graphs of fixed order, size, and the number of negative edges with maximum index. They conjectured that if $\Sigma$ is a signed complete graph of order n with k negative edges, $k<n-1$ and $\Sigma$ has maximum index, then the negative edges induce the signed star $K_{1,k}$, which was proved by Akbari, Dalvandi, Heydari, and Maghasedi [23] for signed complete graphs whose negative edges form a tree. And the conjecture in [22] was then completely confirmed by Ghorbani and Majidi [24]. Motivated by these, we have characterized the extremal signed graph with maximum ${\lambda }_1\left(A(\Sigma )\right)$ and minimum ${\lambda }_n\left(A(\Sigma )\right)$ among graphs of type $(K_n,T^{-})$, respectively, in [25]. In this article, we continue the line of work in [22,24] on identifying the complete signed graphs with maximal index comprising n vertices and m negative edges. There have also been some good results on this issue. Kafai, Heydari, Rad, and Maghasedi [26] showed that among all signed complete graphs of order $n>5$ whose negative edges induce a unicyclic graph of order k and maximizes the index, the negative edges induce a triangle with all remaining vertices being pendant at the same vertex of the triangle. In [27], Ghorbani and Majidi identified the unique signed graph with maximal index among complete signed graphs whose negative edges induced a tree of diameter of at least d for any given d. They also gave the smallest minimum eigenvalue of complete signed graphs with n vertices whose negative edges induced a tree. We then developed an idea that takes some other given parameters into consideration.

Let $K_n$ and $(K_n,H^{-})$ denote the complete graph of order n and a signed complete graph whose negative edges induce a subgraph H, respectively. Let T be a spanning tree of $K_n$. In this paper, we mainly focus on the question: which spanning tree T with a given number of pendant vertices makes the ${\lambda }_1\left(A(\Sigma )\right)$ of the unbalanced $(K_n,T^{-})$ as large as possible? Let $P_n$ be the path of order n. Then we have the following result.

Theorem 1.

Let T be a spanning tree with k pendant vertices of $K_n$ and $n\ge 6$. If $\Sigma =(K_n,T^{-})$ is an unbalanced signed complete graph with the maximum index, then $T\cong T^{*}$, where $T^{*}$ is a tree obtained by attaching $k-1$ pendant vertices to one of the end vertices of $P_{n-k+1}$ as shown in Figure 1.

Figure 1. The spanning trees ${\displaystyle T^{*}}$, ${\displaystyle T_1^{*}}$, ${\displaystyle T_2^{*}}$, and ${\displaystyle T_3^{*}}$.

The outline of the paper is as follows. We give the necessary preliminaries in Section 2. The proof of Theorem 1 and the characterization of signed graphs $(K_n,T^{-})$ with maximum index are presented in Section 3. In Section 4, we summarize the main result of the paper and suggest directions for future research.

2. Preliminaries

In this section, we will introduce some significant tools. Let $T_{a,b}$ denote the double star obtained by adding a pendant vertices to one end vertex of $P_2$ and b pendant vertices to the other. Throughout the discussion in [25], we have the following remark.

Remark 1.

Let $\Sigma =(K_n,T_{s,t}^{-})$ be a signed complete graph and $n=s+t+2$. Then ${\lambda }_1\left(A\left((K_n,T_{s,t}^{-})\right)\right)<{\lambda }_1\left(A\left((K_n,T_{s-1,t+1}^{-})\right)\right)<{\lambda }_1\left(A\left((K_n,T_{1,n-3}^{-})\right)\right)$ for $s\ge 2$.

Lemma 1

([22] (Lemma 5.1)). Let $r,s,t$, and u be distinct vertices of a signed graph  Σ and $X={(x_1,x_2,\dots ,x_n)}^T$ be an eigenvector corresponding to ${\lambda }_1\left(A(\Sigma )\right)$. Then

(i)

let ${\Sigma }^{\prime }$ be obtained from Σ by reversing the sign of the positive edge $rs$ and the negative edge $rt$. If

$$\left\{\begin{array}{c}{x}_r\ge 0,x_t\ge x_{s}or\hfill \\ x_r\le 0,x_t\le x_s,\hfill \end{array}\right.$$

then ${\lambda }_1\left(A(\Sigma )\right)\le {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. If at least one inequality for the entries of X is strict, then ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$;

(ii)

let ${\Sigma }^{\prime }$ be obtained from Σ by reversing the sign of the positive edge $rs$ and the negative edge $tu$. If $x_r{x}_s\le x_t{x}_u$, then ${\lambda }_1\left(A(\Sigma )\right)\le {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. If at least one of the entries $x_r,x_s,x_t,x_u$ is distinct from zero, then ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$.

3. Proof of the Main Result

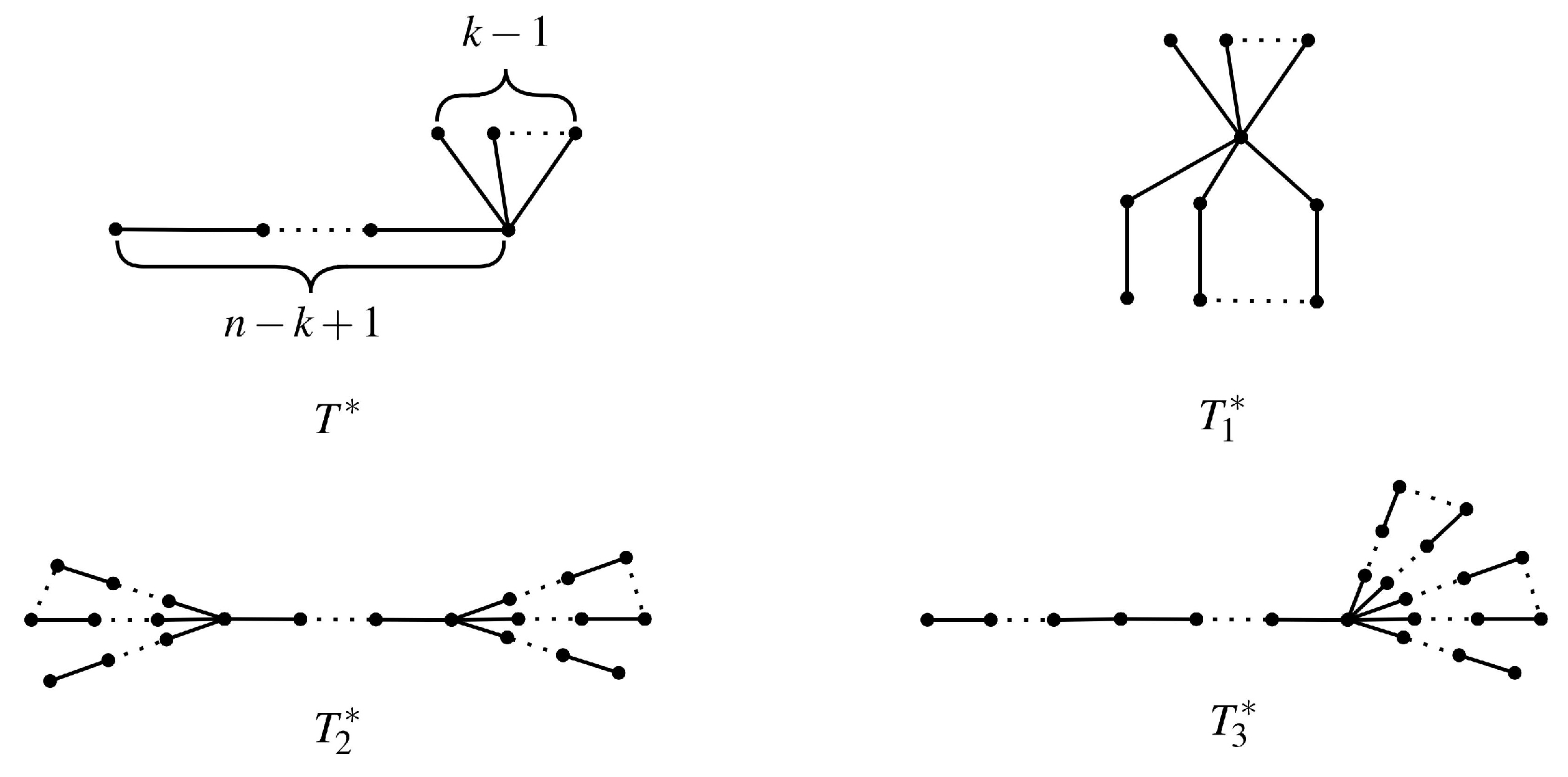
In this section, we will give the proof of Theorem 1.

Proof of Theorem 1.

If $k=n-1$, then $T\cong K_{1,n-1}$. If $k=n-2$, then $T\cong T_{s,t}$, and ${\lambda }_1\left(A\left((K_n,T_{s,t}^{-})\right)\right)\le {\lambda }_1\left(A\left((K_n,T_{1,n-3}^{-})\right)\right)$ with equality if and only if $T_{s,t}^{-}\cong T_{1,n-3}^{-}$ by Remark 1. If $k=2$, then $T\cong P_n$. Thus, we only need to consider $3\le k\le n-3$. Obviously, $(K_n,T^{-})$ is unbalanced since the only balanced $(K_n,T^{-})$ is the one with $T\cong K_{1,n-1}$. And $3\le \Delta \left(T\right)\le k$. Let $X={(x_1,x_2,\dots ,x_n)}^T$ be a unit eigenvector corresponding to ${\lambda }_1\left(A(\Sigma )\right)$. By arranging the vertices of $\Sigma$ appropriately, we can assume that $V(\Sigma )=\{v_1,v_2,\dots ,v_n\}$ such that $x_1\le x_2\le \cdots \le x_n$, where $x_i$ corresponds to the vertex $v_i$ for $1\le i\le n$. Note that $-X$ must be an eigenvector of $\Sigma$ if X is an eigenvector. Then we divide the proof into the following two cases.

Case 1.

There exists a nonnegative eigenvector. Obviously, $x_n>0$ since $X\ne \mathbf{0}$.

Claim 1.

Up to replacing $v_1$ with another vertex $v_i$ such that $x_i=x_1$, we have $d_T\left(v_1\right)=\Delta \left(T\right)$.

It is trivial when $d_T\left(v_1\right)=\Delta \left(T\right)$. If $d_T\left(v_1\right)<\Delta \left(T\right)$, then there is a vertex $v_t\in V\left(T\right)$ such that $d_T\left(v_t\right)=\Delta \left(T\right)$. Let P be the unique path in T between $v_1$ and $v_t$. Then we assert that $x_t=x_1$. Otherwise, we will divide into the following two cases. If $d_T\left(v_1\right)=1$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $v_{1}w$ and the negative edges $v_{t}w$ whose negative edges also form a spanning tree with k pendant vertices, where $w\in N_T\left(v_t\right)\setminus V\left(P\right)$. Thus,

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in N_T\left(v_t\right)\setminus V\left(P\right)}{x}_w(x_t-x_1)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)x_w-{\lambda }_1\left(A(\Sigma )\right)x_w=2(x_t-x_1)>0$$

for any $w\in N_T\left(v_t\right)\setminus V\left(P\right)$, a contradiction. If $d_T\left(v_1\right)\ge 2$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_{1}w$ and the negative edge $v_{t}w$ for any $w\in N_T\left(v_t\right)\setminus V\left(P\right)$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. Thus, $x_t=x_1$. And then we just need to exchange the subscripts $v_t$ and $v_1$, as desired.

Claim 1 means that $3\le d_T\left(v_1\right)=\Delta \left(T\right)\le k$. Note that there are at least two vertices of T with degree greater than three if $\Delta \left(T\right)\le k-1$. Next, we will show that $d_T\left(v_1\right)=\Delta \left(T\right)=k$.

Claim 2.

$\Delta \left(T\right)=k$.

Otherwise, there is a positive integer $t>1$ such that $d_T\left(v_t\right)\ge 3$. Let P be the path from $v_1$ to $v_t$ in T. Since $d_T\left(v_t\right)\ge 3$, there is a vertex $v_s$ such that $v_s\notin V\left(P\right)$ and $v_s{v}_t\in E\left(T\right)$. Then we first assert that $x_t=x_1$. Otherwise, we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_1{v}_s$ and the negative edge $v_t{v}_s$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. Let $N_1=N_T\left(v_1\right)\setminus V\left(P\right)$ and $N_t=N_T\left(v_t\right)\setminus V\left(P\right)$. Then $x_u=0$ for any $u\in N_1\cup N_t$ and $x_1=x_t=0$. Next, we will divide into the following three cases. If $v_1{v}_t\in E\left(T\right)$, then

$$0={\lambda }_1\left(A(\Sigma )\right)x_1=\sum _{u\in V\left(G\right)\setminus N_1\cup N_t\cup \{v_1,v_t\}}{x}_u,$$

which implies $x_u=0$ for any $u\in V\left(G\right)\setminus N_1\cup N_t\cup \{v_1,v_t\}$, and then $X=\mathbf{0}$, a contradiction. If $N_T\left(v_1\right)\cap N_T\left(v_t\right)=\left\{v_r\right\}$, i.e., $d_T(v_1,v_t)=2$, then we claim that $d_T\left(v_r\right)=2$. Otherwise, let $u\in N_r=N_T\left(v_r\right)\setminus \{v_1,v_t\}$. If $x_r>0$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u{v}_1$ and the negative edge $u{v}_r$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. So, $x_r=0$. However,

$$0={\lambda }_1\left(A(\Sigma )\right)x_1=\sum _{u\in V\left(G\right)\setminus (N_T\left[v_1\right]\cup N_T\left[v_t\right])}{x}_u,$$

which implies $x_u=0$ for any $u\in V\left(G\right)\setminus N_1\cup N_t\cup \{v_1,v_t\}$, and then $X=\mathbf{0}$, a contradiction. Thus, by the characteristic equation we obtain

$$\left\{\begin{array}{c}{\lambda }_1\left(A(\Sigma )\right)x_r=\sum _{u\in V\left(G\right)\setminus (N_T\left[v_1\right]\cup N_T\left[v_t\right])}{x}_u,\hfill \\ {\lambda }_1\left(A(\Sigma )\right)x_1=-x_r+\sum _{u\in V\left(G\right)\setminus (N_T\left[v_1\right]\cup N_T\left[v_t\right])}{x}_u.\hfill \end{array}\right.$$

It shows that $({\lambda }_1\left(A(\Sigma )\right)-1)x_r=0$. And then ${\sum }_{u\in V\left(G\right)\setminus (N_T\left[v_1\right]\cup N_T\left[v_t\right])}{x}_u=x_r=0$ since ${\lambda }_1\left(A(\Sigma )\right)>1$. So $X=\mathbf{0}$, a contradiction. Now, we assume that $N_T\left(v_1\right)\cap N_T\left(v_t\right)=\varnothing$, i.e., $d_T(v_1,v_t)\ge 3$. Let $P=v_1{v}_f\cdots v_h{v}_t$. By a similar discussion, we have $d_T\left(u\right)=2$ for any $u\in V\left(P\right)\setminus \{v_1,v_t\}$. By the characteristic equation we obtain

$$\left\{\begin{array}{c}{\lambda }_1\left(A(\Sigma )\right)x_1=-x_f+x_h+\sum _{u\in V\left(G\right)\setminus (N_T\left[v_1\right]\cup N_T\left[v_t\right])}{x}_u,\hfill \\ {\lambda }_1\left(A(\Sigma )\right)x_t=x_f-x_h+\sum _{u\in V\left(G\right)\setminus (N_T\left[v_1\right]\cup N_T\left[v_t\right])}{x}_u.\hfill \end{array}\right.$$

Thus, $x_f=x_h$ and ${\sum }_{u\in V\left(G\right)\setminus (N_T\left[v_1\right]\cup N_T\left[v_t\right])}{x}_u=0$. And then $x_f=x_h=0$. So $X=\mathbf{0}$, a contradiction.

By Claim 2, $d_T\left(v_i\right)\le 2$ for any positive integer $i\in [2,n]$. Let p and q be the minimum and maximum subscripts such that $\{v_p,v_q\}\subset N_T\left(v_1\right)$, respectively. It is obvious that $x_p={\min }_{w\in N_T\left(v_1\right)}{x}_w$ and $x_q={max}_{w\in N_T\left(v_1\right)}{x}_w$.

Claim 3.

Up to replacing $v_p$ with another vertex $v_i$ such that $x_i=x_p$, we have $d_T\left(v_p\right)=2$.

It is trivial when $d_T\left(v_p\right)=2$. Now, we consider $d_T\left(v_p\right)=1$. Note that $\mid V\left(T\right)\setminus N_T\left[v_1\right]\mid \ge 2$ since $k\le n-3$, i.e., $n\ge k+1+2$. Let $v_s\in N_T\left(v_1\right)\setminus \left\{v_p\right\}$, $v_t\in V\left(T\right)\setminus N_T\left[v_1\right]$, and $v_s{v}_t\in E\left(T\right)$. Then we assert that $x_s=x_p$. Otherwise, we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_p{v}_t$ and the negative edge $v_s{v}_t$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. Thus, we just need to exchange the subscripts $v_s$ and $v_p$, as desired.

Claim 4.

$x_p>0$.

Otherwise, $x_1=x_p=0$. Let $v_t{v}_p\in E\left(T\right)$ by Claim 3$,S_1={\sum }_{v\in N_T\left(v_1\right)\setminus \left\{v_p\right\}}{x}_v$, and $S_2={\sum }_{v\in V\left(T\right)}{x}_v-S_1-x_1-x_p-x_t$. By the characteristic equation we obtain

$$\left\{\begin{array}{c}0={\lambda }_1\left(A(\Sigma )\right)x_1=-S_1+S_2+x_t,\hfill \\ 0={\lambda }_1\left(A(\Sigma )\right)x_p=S_1+S_2-x_t.\hfill \end{array}\right.$$

Then $S_2=0$ and $x_t=S_1$. And $({\lambda }_1\left(A(\Sigma )\right)-1)x_t=0$ by ${\lambda }_1\left(A(\Sigma )\right)x_t=S_1=x_t$. So, $x_t=S_1=0$ since ${\lambda }_1\left(A(\Sigma )\right)>1$. Thus, $X=\mathbf{0}$, a contradiction.

If $d_T\left(v\right)=1$ for any vertex $v\in N_T\left(v_1\right)\setminus \left\{v_p\right\}$, then $T=T^{*}$ (see Figure 1). Next, assume that there is a positive integer $r\in (p,q]$ such that $v_r\in N_T\left(v_1\right)$ and $d_T\left(v_r\right)=2$. Let $P_1$ be the unique path in T which contains $v_1$ and $v_p$, and let $P_2$ be the unique path in T which contains $v_1$ and $v_r$. Suppose that $N_T\left(v_p\right)\setminus \left\{v_1\right\}=\left\{v_{p^{\prime }}\right\}$ and $v_s\in V\left(P_2\right)$ such that $d_T\left(v_s\right)=1$. If $x_p>x_s$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_s{v}_{p^{\prime }}$ and the negative edge $v_p{v}_{p^{\prime }}$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. Let $v_{s^{\prime }}{v}_s\in E\left(P_2\right)$. If $x_p\le x_s$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $v_1{v}_s$ and $v_{s^{\prime }}{v}_p$ and the negative edges $v_1{v}_p$ and $v_{s^{\prime }}{v}_s$ whose negative edges also form a spanning tree with k pendant vertices, and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(x_1-x_{s^{\prime }})(x_p-x_s)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also the unit eigenvector corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ and

$$\left\{\begin{array}{c}0=({\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right))x_1=2(x_p-x_s),\hfill \\ 0=({\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right))x_p=2(x_1-x_{s^{\prime }}),\hfill \end{array}\right.$$

that is, $x_p=x_s$ and $x_1=x_{s^{\prime }}$. Let $N=\{v_1,v_p,v_{p^{\prime }},v_s,v_{s^{\prime }}\}$ and $M={\sum }_{v\in V\left(T\right)\setminus N}{x}_v$. Since

$$\left\{\begin{array}{c}{\lambda }_1\left(A(\Sigma )\right)x_p=-x_1-x_{p^{\prime }}+x_s+x_{s^{\prime }}+M,\hfill \\ {\lambda }_1\left(A(\Sigma )\right)x_s=x_1+x_{p^{\prime }}+x_p-x_{s^{\prime }}+M,\hfill \end{array}\right.$$

we have

$$\left\{\begin{array}{cc}{x}_1=x_{s^{\prime }}=x_{p^{\prime }}=0,\hfill & \hfill \left(1\right)\\ ({\lambda }_1\left(A(\Sigma )\right)-1)x_p=({\lambda }_1\left(A(\Sigma )\right)-1)x_s=M.\hfill & \hfill \left(2\right)\end{array}\right.$$

We assert that $v_r\ne v_{s^{\prime }}$. Otherwise, $x_1=x_p=x_r=x_{p^{\prime }}=x_s=0$, which implies that $X=\mathbf{0}$, a contradiction. If $d_T\left(v_q\right)=1$, then

$${\lambda }_1\left(A(\Sigma )\right)x_q=-x_1+x_p+x_{p^{\prime }}+x_s+x_{s^{\prime }}+M-x_q=2x_p+({\lambda }_1\left(A(\Sigma )\right)-1)x_p-x_q$$

by (1) and (2), that is, $x_p=x_q>0$. If $d_T\left(v_q\right)=2$, let $N_T\left(v_q\right)\setminus \left\{v_1\right\}=v_{q^{\prime }}$, then

$$({\lambda }_1\left(A(\Sigma )\right)+1)x_q=-x_1-x_{q^{\prime }}+x_p+x_{p^{\prime }}+x_s+x_{s^{\prime }}+M-x_{q^{\prime }}=-2x_{q^{\prime }}+({\lambda }_1\left(A(\Sigma )\right)+1)x_p,$$

that is, $2x_{q^{\prime }}=({\lambda }_1\left(A(\Sigma )\right)+1)(x_p-x_q)\le 0$. Thus, $x_{q^{\prime }}=0$ and $x_p=x_q>0.$ So,

$$0={\lambda }_1\left(A(\Sigma )\right)x_1=-k{x}_p+x_{p^{\prime }}+x_s+x_{s^{\prime }}+M-(k-1)x_p=({\lambda }_1\left(A(\Sigma )\right)-1-2(k-1))x_p,$$

which means that ${\lambda }_1\left(A(\Sigma )\right)=2k-1$. Next, we will consider that following two cases.

Subcase 1.1.

$v_r{v}_{s^{\prime }}\in E\left(T\right)$, i.e., $P_2=v_1{v}_r{v}_{s^{\prime }}{v}_s$. Note that

$$0={\lambda }_1\left(A(\Sigma )\right)x_{s^{\prime }}=x_1+x_p+x_{p^{\prime }}-x_s-x_r+M-x_r=({\lambda }_1\left(A(\Sigma )\right)-1)x_p-2x_p.$$

We have ${\lambda }_1\left(A(\Sigma )\right)=3$, and then $k=2$, a contradiction.

Subcase 1.2.

$v_r{v}_{s^{\prime }}\notin E\left(T\right)$. Let $\{v_s,v_{s^{\prime \prime }}\}\subset N_T\left(v_{s^{\prime }}\right)\cap V\left(P_2\right)$, i.e., $P_2=v_1{v}_r\cdots v_{s^{\prime \prime }}{v}_{s^{\prime }}{v}_s$. Since

$$0={\lambda }_1\left(A(\Sigma )\right)x_{s^{\prime }}=-x_{s^{\prime \prime }}-x_s+x_1+x_p+x_{p^{\prime }}+M-x_{s^{\prime \prime }}=-2x_{s^{\prime \prime }}+({\lambda }_1\left(A(\Sigma )\right)-1)x_p,$$

we have $x_{s^{″}}=(k-1)x_p$. This leads to $x_v=0$ for any $v\in V\left(T\right)\setminus (N_T\left(v_1\right)\cup \{x_s,x_{s^{\prime \prime }}\})$. So, $0={\lambda }_1\left(A(\Sigma )\right)x_{p^{\prime }}=(2k-2)x_p$, which means that $k=1$, a contradiction.

Case 2.

There are no nonnegative eigenvectors. For a fixed eigenvector $X={(x_1,x_2,\dots ,x_n)}^T$, let $V_{+}=\left\{v_i\right|x_{v_i}\ge 0\}$ and $V_{-}=\left\{v_i\right|x_{v_i}<0\}$. Clearly, $V_{+}\ne \varnothing$, $V_{-}\ne \varnothing$ and there must exist a vertex v such that $x_v>0$. Let $\mid V_{+}\mid =a$, $\mid V_{-}\mid =b$ and $x_1\le \cdots \le x_b<0\le x_{b+1}\le \cdots \le x_n$. Note that $a+b=n$. For convenience, set $u_i=v_{n-(i-1)}$ and $y_i=x_{n-(i-1)}$ for $1\le i\le a$, then $x_1\le \cdots \le x_b<0\le y_a\le \cdots \le y_1$ and $y_1>0$. Obviously, $u_i\in V_{+}$ for $1\le i\le a$.

Subcase 2.1.

$a=1$ or $b=1$. By symmetry, we just consider $a=1$.

Claim 5.

$d_T\left(u_1\right)=\Delta \left(T\right)$.

It is trivial when $d_T\left(u_1\right)=\Delta \left(T\right)$. If $d_T\left(u_1\right)<\Delta \left(T\right)$, then there is a vertex $v_t\in V\left(T\right)$ such that $d_T\left(v_t\right)=\Delta \left(T\right)$. Let P be the unique path in T between $u_1$ and $v_t$. If $d_T\left(u_1\right)=1$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_{1}w$ and the negative edges $v_{t}w$ whose negative edges also form a spanning tree with k pendant vertices, where $w\in N_T\left(v_t\right)\setminus V\left(P\right)$. Thus,

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in N_T\left(v_t\right)\setminus V\left(P\right)}{x}_w(x_t-y_1)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)x_w-{\lambda }_1\left(A(\Sigma )\right)x_w=2(x_t-y_1)<0$$

for any $w\in N_T\left(v_t\right)\setminus V\left(P\right)$, a contradiction. If $d_T\left(u_1\right)\ge 2$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{1}w$ and the negative edge $v_{t}w$ for any $w\in N_T\left(v_t\right)\setminus V\left(P\right)$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

Claim 5 means that $3\le d_T\left(u_1\right)=\Delta \left(T\right)\le k$. Note that there are at least two vertices of T with degree greater than three if $\Delta \left(T\right)\le k-1$. Next, we will show that $d_T\left(u_1\right)=\Delta \left(T\right)=k$.

Claim 6.

$\Delta \left(T\right)=k$.

Otherwise, there is a vertex $v_t\in V_{-}$ such that $d_T\left(v_t\right)\ge 3$. Let P be the path from $u_1$ to $v_t$ in T. Since $d_T\left(v_t\right)\ge 3$, there is a vertex $v_s\in V_{-}\setminus V\left(P\right)$ such that $v_s{v}_t\in E\left(T\right)$. We can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_1{v}_s$ and the negative edge $v_t{v}_s$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

By Claim 6, $d_T\left(v_i\right)\le 2$ for any $v_i\in V_{-}$. Let q be the maximum subscripts such that $v_q\in N_T\left(u_1\right)$. Evidently, $x_q={max}_{w\in N_T\left(u_1\right)}{x}_w$.

Claim 7.

For any vertex $v_i$ with $x_i<x_q$, we have $v_i\in N_T\left(u_1\right)$.

Otherwise, there is a positive integer t ($t<q$) such that $x_t<x_q$ and $u_1{v}_t\notin E\left(T\right)$. Let P be the path between $u_1$ and $v_t$ in T. If $v_q\notin V\left(P\right)$, then there must be a vertex $v_s$ such that $v_s\in N_P\left(v_t\right)$ and we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_t$, $v_s{v}_q$ and the negative edges $u_1{v}_q$, $v_t{v}_s$ whose negative edges also form a spanning tree with k pendant vertices. Thus,

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-x_s)(x_q-x_t)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. If $v_q\in V\left(P\right)$ and $d_T\left(v_t\right)=1$, then $P=u_1{v}_q\cdots v_t$ and we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_1{v}_t$ and the negative edge $u_1{v}_q$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. If $v_q\in V\left(P\right)$ and $d_T\left(v_t\right)=2$, then there must be a vertex $v_s\notin V\left(P\right)$ such that $v_s{v}_t\in E\left(T\right)$. We can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_t$, $v_q{v}_s$ and the negative edges $u_1{v}_q$, $v_t{v}_s$ whose negative edges also form a spanning tree with k pendant vertices, then

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-x_s)(x_q-x_t)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction.

Let p be the minimum subscript such that $v_p\notin N_T\left(u_1\right)$. If $p>q$, then the subscripts of vertices of $N_T\left(v_1\right)$ are consecutive. If $1\le p<q$, then $x_p=x_q$ by Claim 7. Let r ($p<r\le q$) be the minimum subscript such that $v_r\in N_T\left(u_1\right)$. Then $x_r=x_p$ and we exchange the subscripts of $v_r$ and $v_p$. We continue this procedure until the subscripts of vertices of $N_T\left(u_1\right)$ are consecutive. Without loss of generality, it is not restrictive to assume that $N_T\left(u_1\right)=\{v_1,v_2,\cdots ,v_k\}$ by Claims 5–7.

Claim 8.

$d_T\left(v_k\right)=2.$

Otherwise, $d_T\left(v_k\right)=1.$ Recall that $3\le \Delta \left(T\right)\le k$; thus, there must exist vertices $v_i$ and $v_j$ such that $v_i{v}_j\in E\left(T\right)$, where $1\le i\le k-1$ and $j\ge k+1$. Note that $x_i\le x_k\le x_j<0$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_k{v}_j$ and the negative edge $v_i{v}_j$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

By Claim 8, let $v_s\in N_T\left(v_k\right)\setminus \left\{u_1\right\}$. Then the following claim holds.

Claim 9.

$x_s=x_{n-1}$.

Otherwise, $x_s<x_{n-1}$. Let P be the path between $v_k$ and $v_{n-1}$ in T. If $v_s\notin V\left(P\right)$, then there is a vertex $v_t\in N_T\left(v_{n-1}\right)$ such that $v_t{v}_{n-1}\in E\left(P\right)$. Note that $x_t\le x_k\le x_s<x_{n-1}<0$. If $u_1{v}_t\in E\left(T\right)$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $v_k{v}_{n-1}$, $v_s{v}_t$ and the negative edges $v_k{v}_s$, $v_t{v}_{n-1}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4[x_s(x_k-x_{n-1})+x_{n-1}(x_t-x_k)]\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. If $u_1{v}_t\notin E\left(T\right)$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_k{v}_{n-1}$ and the negative edge $v_k{v}_s$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(x_k-x_t)(x_s-x_{n-1})\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)x_k-{\lambda }_1\left(A(\Sigma )\right)x_k=2(x_s-x_{n-1})<0,$$

a contradiction. Next, we assume that $v_s\in V\left(P\right)$. Note that $x_k\le x_s<x_{n-1}<0$. If $d_T\left(v_{n-1}\right)=1$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_k{v}_{n-1}$ and the negative edge $v_k{v}_s$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. If $d_T\left(v_{n-1}\right)=2$, let $v_t\in N_T\left(v_{n-1}\right)$ such that $v_t{v}_{n-1}\in E\left(T\right)\setminus E\left(P\right)$. Thus, $x_k\le x_t$ and we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $v_k{v}_{n-1}$, $v_s{v}_t$ and the negative edges $v_k{v}_s$, $v_t{v}_{n-1}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(x_k-x_t)(x_s-x_{n-1})\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)x_k-{\lambda }_1\left(A(\Sigma )\right)x_k=2(x_s-x_{n-1})<0,$$

a contradiction.

If $s=n-1$, then $v_k{v}_{n-1}\in E\left(T\right)$. If $s<n-1$, then we just need to exchange the subscripts of $v_s$ and $v_{n-1}$ by Claim 9. Without loss of generality, it is not restrictive to assume that $N_T\left(v_k\right)=\{u_1,v_{n-1}\}$.

Claim 10.

$d_T\left(v_i\right)=1$ for $1\le i\le k-1$.

Suppose by way of contradiction that there exist positive integers $t\in [1,k-1]$ and $s\in [k+1,n-2]$ such that $v_t{v}_s\in E\left(T\right)$. Let P be the path which contains $u_1$ and $v_k$ in T, and $v_r\in V\left(P\right)$ such that $d_T\left(v_r\right)=1$. Obviously, $x_t\le x_r$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_s{v}_r$ and the negative edge $v_s{v}_t$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

By Claims 5–10, we can immediately obtain that $T\cong T^{*}$ depicted in Figure 1.

Subcase 2.2.

$a\ge 2$ and $b\ge 2$. Recall that $-X$ must be an eigenvector of $\Sigma$ if X is an eigenvector. So, without loss of generality, assume that $u_r\in V_{+}$ is the vertex such that $d_T\left(u_r\right)=\Delta \left(T\right)$. Let $N_r^{+}=N_T\left(u_r\right)\cap V_{+}$ and $N_r^{-}=N_T\left(u_r\right)\cap V_{-}$.

Claim 11.

If $N_r^{+}\ne \varnothing$, then $N_r^{-}\ne \varnothing$.

Assume to the contrary that $N_r^{-}=\varnothing$. Then there is a vertex $u_t\in N_r^{+}$ such that $P=u_r{u}_t\cdots v_1$ is the unique path between $u_r$ and $v_1$ in T. Since $3\le \Delta \left(T\right)\le k$, $\mid N_r^{+}\setminus \left\{u_t\right\}\mid \ne \varnothing$. If $d_T\left(v_1\right)=1$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_{1}w$ and the negative edge $u_{r}w$ for all $w\in N_r^{+}\setminus \left\{u_t\right\}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in N_r^{+}\setminus \left\{u_t\right\}}{y}_w(y_r-x_1)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However, for any $w\in N_r^{+}\setminus \left\{u_t\right\}$, we have

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_w-{\lambda }_1\left(A(\Sigma )\right)y_w=2(y_r-x_1)>0,$$

a contradiction. If $d_T\left(v_1\right)\ge 2$, let $w\in N_r^{+}\setminus \left\{u_t\right\}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_{1}w$ and the negative edge $u_{r}w$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

By Claim 11, we divide the proof into the following two cases.

Subcase 2.2.1.

$N_r^{+}\ne \varnothing$. Note that $N_r^{-}\ne \varnothing$ by Claim 11.

Claim 12.

$d_T\left(u\right)=1$ for any $u\in N_r^{-}$.

Otherwise, suppose that $v_i\in N_r^{-}$ such that $d_T\left(v_i\right)\ge 2$. We assert that $\mid N_r^{-}\mid \ge 2$. Otherwise, let $w\in N_r^{+}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_{i}w$ and the negative edge $u_{r}w$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. Now, we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v_{i}w$ and the negative edge $u_{r}w$ for all $w\in N_r^{+}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in N_r^{+}}{y}_w(y_r-x_i)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However, for any $w\in N_r^{+}$, we have

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_w-{\lambda }_1\left(A(\Sigma )\right)y_w=2(y_r-x_i)>0,$$

a contradiction.

Claim 13.

$y_r\ge y_i$ for any $u_i\in N_r^{+}$.

Assume to the contrary that there is a vertex $u_s\in N_r^{+}$ such that $y_r<y_s$. If $d_T\left(u_s\right)=1$, then by the characteristic equation we obtain

$$\left\{\begin{array}{c}({\lambda }_1+1)(y_r+y_s)=2{\displaystyle \sum _{w\in (V\left(T\right)\setminus N_T\left[u_r\right])}}{x}_w,\hfill \\ ({\lambda }_1-1)(y_s-y_r)=2{\displaystyle \sum _{w\in (N_T\left(u_r\right)\setminus \left\{u_s\right\})}}{x}_w.\hfill \end{array}\right.$$

These mean that ${\displaystyle \sum _{w\in (V\left(T\right)\setminus N_T\left[u_r\right])}}{x}_w\ge 0$ and ${\displaystyle \sum _{w\in (N_T\left(u_r\right)\setminus \left\{u_s\right\})}}{x}_w>0$. By Claim 12, for any vertex $v_i\in N_r^{-}$, we have

$$({\lambda }_1+1)x_i+y_r-y_s-{\displaystyle \sum _{w\in (N_T\left(u_r\right)\setminus \left\{u_s\right\})}}{x}_w={\displaystyle \sum _{w\in (V\left(T\right)\setminus N_T\left[u_r\right])}}{x}_w,$$

which means that ${\displaystyle \sum _{w\in (V\left(T\right)\setminus N_T\left[u_r\right])}}{x}_w<0$, a contradiction. Now, we assume that $d_T\left(u_s\right)\ge 2$. Recall that $N_r^{-}\ne \varnothing$ and let $u\in N_r^{-}$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{s}u$ and the negative edge $u_{r}u$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

Claim 14.

$y_r=y_1$.

Otherwise, $y_r<y_1$. We first assume that $d_T\left(u_1\right)=1$ and $u_1{u}_r\in E\left(T\right)$. Then there is a vertex $u_s\in N_r^{+}$ such that $d_T\left(u_s\right)\ge 2$ since $T\ne K_{1,n-1}$. And we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{s}w$ and the negative edge $u_{r}w$ for all $w\in N_r^{+}\setminus \left\{u_s\right\}$ and reversing the sign of the positive edge $u_{1}v$ and the negative edge $u_{r}v$ for all $v\in N_r^{-}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in N_r^{+}\setminus \left\{u_s\right\}}{y}_w(y_r-y_s)+4\sum _{v\in N_r^{-}}{x}_v(y_r-y_1)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. Now we assume that $d_T\left(u_1\right)=1$ and $u_1{u}_r\notin E\left(T\right)$. Let $P=u_1\cdots u_t{u}_r$ be the path between $u_1$ and $u_r$ in T. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{t}w$ and the negative edge $u_{r}w$ for all $w\in N_r^{+}\setminus \left\{u_t\right\}$ and reversing the sign of the positive edge $u_{1}v$ and the negative edge $u_{r}v$ for all $v\in N_r^{-}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in N_r^{+}\setminus \left\{u_t\right\}}{y}_w(y_r-y_s)+4\sum _{v\in N_r^{-}}{x}_v(y_r-y_1)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. Finally, let $d_T\left(u_1\right)\ge 2$ and $v\in N_r^{-}$. Note that $d_T\left(u_r\right)=\Delta \left(T\right)\ge 3$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{1}v$ and the negative edge $u_{r}v$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

It is not restrictive to assume that $d_T\left(u_1\right)=\Delta \left(T\right)\ge 3$ by Claim 14. Let $x_p={\min }_{w\in N_1^{-}}{x}_w$.

Claim 15.

$x_p=x_1$.

If $p=1$, then the result obviously holds. Now, we assume that $p\ge 2$. Assume to the contrary that $x_p>x_1$. By Claim 12, there is a vertex $u_t\in N_r^{+}$ such that $P=v_1\cdots u_t{u}_1{v}_p$ is the path between $v_1$ and $v_p$ in T. If $v_1{u}_t\in E\left(T\right)$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_1$, $u_t{v}_p$ and the negative edges $u_1{v}_p$, $u_t{v}_1$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-y_t)(x_p-x_1)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_1-{\lambda }_1\left(A(\Sigma )\right)y_1=2(x_p-x_1)>0,$$

a contradiction. If $v_1{u}_t\notin E\left(T\right)$, then there exists a vertex $w\in N_T\left(v_1\right)\cap E\left(P\right)$. If $w\in V_{+}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_1$, $w{v}_p$ and the negative edges $u_1{v}_p$, $w{v}_1$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-y_w)(x_p-x_1)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_1-{\lambda }_1\left(A(\Sigma )\right)y_1=2(x_p-x_1)>0,$$

a contradiction. If $w\in V_{-}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_1$, $w{v}_p$ and the negative edges $u_1{v}_p$, $w{v}_1$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-x_w)(x_p-x_1)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction.

Claim 16.

$d_T\left(u_1\right)=\Delta \left(T\right)=k$.

Otherwise, $d_T\left(u_1\right)=\Delta \left(T\right)<k$. Then there is a vertex $w\in V\setminus \left\{u_1\right\}$ such that $d_T\left(w\right)\ge 3$. Let P be the path from $u_1$ to w in T. Assume that $w\in V_{+}$ at first. We assert that $N_T\left(w\right)\cap V_{-}=\varnothing$. Otherwise, let $v\in N_T\left(w\right)\cap V_{-}$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{1}v$ and the negative edge $wv$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. Since $d_T\left(w\right)\ge 3$, $N_T\left(w\right)\setminus V\left(P\right)\ne \varnothing$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edge $u{v}_1$ and the negative edges $uw$ for all $u\in N_T\left(w\right)\setminus V\left(P\right)$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_w-x_1)\sum _{u\in N_T\left(w\right)\setminus V\left(P\right)}{y}_u\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_u-{\lambda }_1\left(A(\Sigma )\right)y_u=2(y_w-x_1)>0$$

for any $u\in N_T\left(w\right)\setminus V\left(P\right)$, a contradiction. Now, we assume that $w\in V_{-}$. Note that at least one of $(N_T\left(w\right)\setminus V\left(P\right))\cap V_{+}\ne \varnothing$ and $(N_T\left(w\right)\setminus V\left(P\right))\cap V_{-}\ne \varnothing$ holds since $d_T\left(w\right)\ge 3$. If $(N_T\left(w\right)\setminus V\left(P\right))\cap V_{-}\ne \varnothing$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $v{v}_1$, $u{u}_1$ and the negative edges $vw$, $uw$ for all $u\in (N_T\left(w\right)\setminus V\left(P\right))\cap V_{-}$ and $v\in (N_T\left(w\right)\setminus V\left(P\right))\cap V_{+}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(x_w-x_1)\sum _{v\in (N_T\left(w\right)\setminus V\left(P\right))\cap V_{+}}{y}_v+4(x_w-y_1)\sum _{u\in (N_T\left(w\right)\setminus V\left(P\right))\cap V_{-}}{x}_u\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. If $(N_T\left(w\right)\setminus V\left(P\right))\cap V_{-}=\varnothing$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_t{v}_1$, $v{v}_1$ and the negative edges $u_t{u}_1$, $vw$ for all $v\in (N_T\left(w\right)\setminus V\left(P\right))\cap V_{+}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4[y_t(y_1-x_1)+(x_w-x_1)\sum _{v\in (N_T\left(w\right)\setminus V\left(P\right))\cap V_{+}}{y}_v]\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_t-{\lambda }_1\left(A(\Sigma )\right)y_t=2(y_1-x_1)>0,$$

a contradiction.

Claim 16 shows that $d_T\left(u\right)\le 2$ for any $u\in V\setminus \left\{u_1\right\}$, which means that T must be a starlike tree. Since $T\ne K_{1,n-1}$, there is a vertex $u_s\in N_T\left(u_1\right)\cap V_{+}$ such that $d_T\left(u_s\right)=2$. Let $w\in N_T\left(u_s\right)\setminus \left\{u_1\right\}$. We assert that $w\in V_{+}$. Otherwise, we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_{1}w$, $v_1{u}_s$ and the negative edges $u_1{u}_s$, $u_{s}w$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4[y_1(y_s-x_w)+y_s(x_w-x_1)]\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. If $d_T\left(w\right)=2$, set $v\in N_T\left(w\right)\setminus \left\{u_s\right\}$, then either $v\in V_{-}$ or $v\in V_{+}$. If $v\in V_{-}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_{1}w$, $v_1{u}_s$, $u_{s}v$ and the negative edges $u_1{u}_s$, $u_{s}w$, $wv$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4[(y_1-x_v)(y_s-x_w)+y_s(x_w-x_1)]\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. If $v\in V_{+}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_{1}w$, $v_1{u}_s$, $u_{s}v$ and the negative edges $u_1{u}_s$, $u_{s}w$, $wv$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4[(y_1-y_v)(y_s-x_w)+y_s(x_w-x_1)]\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_1-{\lambda }_1\left(A(\Sigma )\right)y_1=2(y_s-x_w)>0,$$

a contradiction. These show that $d_T\left(w\right)=1$ and $T\cong T_1^{*}$, where $T_1^{*}$ is the spanning tree shown in Figure 1. Let $\{u_s,u_t,u_p,u_q\}\subset V_{+}$ such that $\{u_1{u}_s,u_1{u}_t,u_s{u}_p,u_t{u}_q\}\subset E\left(T\right)$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_p{u}_t$ and the negative edge $u_1{u}_t$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1. As we continue the above procedure inductively, we obtain that ${\lambda }_1\left(A\left((\Sigma ,T_1^{*})\right)\right)<{\lambda }_1\left(A\left(({\Sigma }^{\prime },T^{*})\right)\right)$.

Subcase 2.2.2.

$N_r^{+}=\varnothing$. Note that $\mid N_r^{-}\mid \ge 3$ since $d_T\left(u_r\right)=\Delta \left(T\right)\ge 3$.

Claim 17.

$y_r=y_1$.

Otherwise, $y_r<y_1$. Let $P=u_1\cdots v_s{u}_r$ be the unique path between $u_1$ and $u_r$ in T, where $v_s\in N_r^{-}$. If $d_T\left(u_1\right)=1$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{1}w$ and the negative edge $u_{r}w$ for all $w\in N_r^{-}\setminus \left\{v_s\right\}$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in N_r^{-}\setminus \left\{v_s\right\}}{x}_w(y_r-y_1)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. Now we assume that $d_T\left(u_1\right)\ge 2$ and $w\in N_r^{-}\setminus \left\{v_s\right\}$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{1}w$ and the negative edge $u_{r}w$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction.

Let $x_p={min}_{w\in N_1^{-}}{x}_w$.

Claim 18.

$x_p=x_1$.

If $p=1$, then the result obviously holds. Now assume that $p\ge 2$. Assume to the contrary that $x_p>x_1$. There is a vertex $v_t\in N_1^{-}$ such that $P=v_1\cdots v_t{u}_1{v}_p$ or $P=v_1\cdots v_p{u}_1{v}_t$ is the path containing $v_1$, $v_p$ and $u_1$ in T. We first consider the case of $P=v_1\cdots v_t{u}_1{v}_p$. If $v_1{v}_t\in E\left(T\right)$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_1,v_t{v}_p$ and the negative edges $u_1{v}_p,v_t{v}_1$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-x_t)(x_p-x_1)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. If $v_1{v}_t\notin E\left(T\right)$, then there exists a vertex $w\in N_T\left(v_1\right)\cap E\left(P\right)$. If $w\in V_{+}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_1,w{v}_p$ and the negative edges $u_1{v}_p,w{v}_1$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-y_w)(x_p-x_1)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)y_1-{\lambda }_1\left(A(\Sigma )\right)y_1=2(x_p-x_1)>0,$$

a contradiction. If $w\in V_{-}$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $u_1{v}_1,w{v}_p$ and the negative edges $u_1{v}_p,w{v}_1$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4(y_1-x_w)(x_p-x_1)\hfill \\ \hfill & >0,\hfill \end{array}$$

a contradiction. Then we consider the case of $P=v_1\cdots v_p{u}_1{v}_t$. Similar to the above, we can obtain the contradiction.

It is not restrictive to assume that $d_T\left(u_1\right)=\Delta \left(T\right)\ge 3$ by Claim 17. Let $D_3=\{v\mid d_T\left(v\right)\ge 3\}$. If $D_3\setminus \left\{u_1\right\}=\varnothing$, then T is a starlike tree. Now, we consider $D_3\setminus \left\{u_1\right\}\ne \varnothing$ and $w\in D_3\setminus \left\{u_1\right\}$. Let $P_1=u_1{v}_r\cdots w$ be the unique path between $u_1$ and w in T. If $w\in V_{+}$, then we assert that $x_v<0$ for any $v\in N_T\left(w\right)\setminus V\left(P_1\right)$. Assume to the contrary that $x_v\ge 0$ and $v\in N_T\left(w\right)\setminus V\left(P_1\right)$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $v{v}_r$ and the negative edge $vw$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. Similarly, we can obtain that $x_v>0$ for any $v\in N_T\left(w\right)\setminus V\left(P_1\right)$ if $w\in V_{-}$. And either $D_3\cap V_{-}=\varnothing$ or $D_3\cap (V_{+}\setminus \left\{u_1\right\})=\varnothing$. We first consider $D_3\cap V_{-}\ne \varnothing$ and $D_3\cap (V_{+}\setminus \left\{u_1\right\})=\varnothing$. Let $v_s\in D_3\cap V_{-}$. If $u_1{v}_s\notin E\left(T\right)$, let $P_2=u_1{v}_r\cdots v{v}_s$ be the unique path between $u_1$ and $v_s$ in T. Note that $v_r$ and v may be the same vertex. Let $S=N_T\left(v_s\right)\setminus \left\{v\right\}$. If $d_T\left(v_1\right)=2$, then for any $w\in S$, we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edge $v_{1}w$ and the negative edge $v_{s}w$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. If $d_T\left(v_1\right)=1$, then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the signs of the positive edges $w{v}_1$ and the negative edges $w{v}_s$ for all $w\in S$ whose negative edges also form a spanning tree with k pendant vertices and

$$\begin{array}{cc}\hfill {\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)-{\lambda }_1\left(A(\Sigma )\right)& \ge X^T(A\left({\Sigma }^{\prime }\right)-A(\Sigma ))X\hfill \\ \hfill & =4\sum _{w\in S}{y}_w(x_s-x_1)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

If ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)={\lambda }_1\left(A(\Sigma )\right)$, then X is also an eigenvector of $A\left({\Sigma }^{\prime }\right)$ corresponding to ${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$. However,

$${\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)x_1-{\lambda }_1\left(A(\Sigma )\right)x_1=-2{\Sigma }_{w\in S}{y}_w<0,$$

a contradiction. If $u_1{v}_s\in E\left(T\right)$, we can similarly obtain the contradiction. Thus, $D_3\cap V_{-}=\varnothing$. So, we only need to consider $D_3\cap (V_{+}\setminus \left\{u_1\right\})\ne \varnothing$. Similarly, we can obtain that $\mid D_3\cap (V_{+}\setminus \left\{u_1\right\})\mid =1$. Then $T\cong T_2^{*}$, where $T_2^{*}$ is the spanning tree shown in Figure 1.

Let $D_3\cap (V_{+}\setminus \left\{u_1\right\})=\left\{u_s\right\}$. Then $y_s\le y_1$. For any $w\in N_T\left(u_s\right)$, we have $x_w<0$. Then we can construct a new unbalanced signed graph ${\Sigma }^{\prime }$ by reversing the sign of the positive edge $u_{1}w$ and the negative edge $u_{s}w$ whose negative edges also form a spanning tree with k pendant vertices such that ${\lambda }_1\left(A(\Sigma )\right)<{\lambda }_1\left(A\left({\Sigma }^{\prime }\right)\right)$ by Lemma 1, a contradiction. As we continue the above procedure inductively, we obtain that ${\lambda }_1\left(A\left((\Sigma ,T_2^{*})\right)\right)<{\lambda }_1\left(A\left(({\Sigma }^{\prime },T_3^{*})\right)\right)$, where $T_3^{*}$ is depicted in Figure 1. One can easily observe that $\Delta \left(T_3^{*}\right)=k$. In this case, we have ${\lambda }_1\left(A\left(({\Sigma }^{\prime },T_3^{*})\right)\right)\le {\lambda }_1\left(A\left(({\Sigma }^{\prime },T^{*})\right)\right)$. Therefore, ${\lambda }_1\left(A\left((\Sigma ,T_2^{*})\right)\right)<{\lambda }_1\left(A\left(({\Sigma }^{\prime },T^{*})\right)\right)$. This completes the proof.□

4. Conclusions

This study investigates the largest eigenvalues of unbalanced signed complete graphs whose spanning trees have k pendant vertices. We determine the extremal signed graph which attains the maximum index among signed graphs of this type. However, there are still some parameters that can be taken into account. It is challenging to consider the index or the least eigenvalue of such unbalanced signed graphs with fixed different parameters.