An Exploration of Ideals and Filters in Triangle Algebras
Abstract
1. Introduction
- Lattices: Here, ideals are examples of convex sublattices, and many conditions on elements and ideals of lattices amount to weakened forms of distributivity [1];
- Rings: The set of all ideals of a ring is a common example of a residuated lattice, and ideals are in a one-to-one correspondence with congruence relations. Furthermore, the kernel of any homomorphism is an ideal and reciprocally any ideal is the kernel of a homomorphism. Moreover, the set of all ideals of a ring was used to study some subclasses of the variety of rings; these researches aimed to investigate the properties of some subclasses of rings whose residuated lattices of ideals belong to a specific subvariety of residuated lattices (see [2,3]). For example, Belluce et al. [2] studied those rings whose semiring of ideals, under an ideal sum and ideal product, can be equipped with the structure of a Heyting algebra.
- Residuated lattices: Ideals have crystallized researchers’ attention in MV-algebras [4,5], whereas in general residuated lattices, it is filters (shown to be equivalent to deductive systems) that focus researchers’ attention. In MV-algebras, filters and ideals are dual notions (see [6]), but this is no longer the case in the general framework of residuated lattices (see [7]). Some authors have claimed that the notion of ideals is missing in BL-algebras; to fill this gap, Lele and Nganou [4] introduced the notions of ideal, prime ideal and Boolean ideal in BL-algebras and derived some of their characterizations. They used their notion of ideals to characterize BL-algebras.
2. Preliminaries
2.1. Residuated Lattices
- (RL1)
- is a bounded lattice;
- (RL2)
- is a commutative monoid;
- (RL3)
- for every , , where ⩽ is the lattice order induced by the lattice operations ∧ and ∨.
- (r1)
- ;
- (r2)
- ;
- (r3)
- ;
- (r4)
- ;
- (r5)
- ;
- (r6)
- ;
- (r7)
- and ;
- (r8)
- ;
- (r9)
- ;
- (r10)
- ;
- (r11)
- ;
- (r12)
- ;
- (r13)
- ;
- (r14)
- ;
- (r15)
- ;
- (r16)
- ;
- (r17)
- ;
- (r18)
- ;
- (r19)
- .
- (F1)
- and ;
- (F2)
- and ).
- (I1)
- and ;
- (I′1)
- ;
- (I2)
- and ;
- (I3)
- and ;
- (I4)
- and );
- (I5)
- and );
- (I6)
- .
2.2. Triangle Algebras
| (T1) | (T′1) ; |
| (T2) ; | (T′2) ; |
| (T3) ; | (T′3) ; |
| (T4) ; | (T′4) ; |
| (T5) ; | (T′5) ; |
| (T6) ; | (T′6) ; |
| (T7) ; | |
| (T8) ; | |
| (T9) . |
| x | x | ⊙ | 0 | u | 1 | → | 0 | u | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||
| u | 0 | u | 1 | u | 0 | u | u | u | 0 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | 1 | 0 | u | 1 | 1 | 0 | u | 1 |
- (p1)
- ;
- (p2)
- ;
- (p3)
- ;
- (p4)
- ;
- (p5)
- , , and ;
- (p6)
- , , and ;
- (p7)
- , ;
- (p8)
- , ;
- (p9)
- .
- (F1)
- and ;
- (F2)
- and ;
- (FT)
- .
3. Ideals in Triangle Algebras
3.1. Definition and Characterizations of the Notion of Ideal
- (I1)
- and ;
- (I2)
- and ;
- (IT)
- .
- 1.
- and ;
- 2.
- and ;
- 3.
- and (triangle inequalities).
- Since (T1), we have , thus ((T′3) and ).Since , we have by ( and ).
- Hence, we have .By replacing x and y in the above by and , respectively, and using and , we have .
- Since and , we have . Therefore, .Furthermore,
- (I1)
- and ;
- (I3)
- and ;
- (IT)
- .
- (I′1)
- ;
- (I4)
- and ;
- (IT)
- .
- (I′1)
- ;
- (I5)
- and ;
- (IT)
- .
- (N1)
- ;
- (N2)
- ;
- (N3)
- ;
- (N4)
- ;
- (N5)
- .
3.2. Pseudo-Duality
- Let , then there exists such that . Since , we have . Hence, L; .
- Let such that there exists , , then . Hence, .
- (i)
- ;
- (ii)
- .
- (i)
- Let , then . Putting , we have , .Reciprocally, let , then there exists such that , which implies . Since , we have , by (I6), thus , by (I1), i.e., .
- (ii)
- Let , then . Since , we have , with .Reciprocally, let , then there exists such that , which implies . Since , we have , i.e., .
- For (F1),
- let such that and , we have to show that .It holds that implies , thus . Since , there exists such that , so by transitivity, , thus .
- For (F2),
- let , we have to show that .Since , there exists such that .Since , there exists such that . Then, by , , thus , i.e., .Since and I is an ideal, and we have by [4] , we obtainIt follows that , thus .
- For (FT),
- let . We have to show that . Since , there exists such that . Since , , we have , thus
- Let such that . Since , we have , for .
- Let . Hence, there exists such that , which implies . Since , by (I6), , so , by (I1).
- For (I1),
- let such that and . We have that and imply . Hence, , because F is a filter. Thus .
- For (I3),
- let . Then, and . Hence, .Furthermore,Therefore, . From the triangle inequality , we have . Hence, . Thus, .
- For (IT),
- it holds because .
- Let , we have to find such that .Since , we have . Because , we have , with .
- Let . We have to find such that . Since , there exists such that . Hence, . Because , we have , which implies , by (F1). Since and , we have . Thus, , with .
- Let us prove that . Let . Then, there exists such that . Therefore, . Hence, . Because , we have , by (FT). Since , we have , and then , by (F1). Thus, .
- Let , then , which implies by (FT) . Since , we have . Thus .
- Let , then , i.e., , by . Since , we have , by . Thus .
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
- (1)
- (2)
- Let .
- (3)
- Let . Then, , and since , we have , which implies . Thus .
- (4)
- Since is an ideal, then , by Proposition 12 (1).
| ⇒ | 0 | v | a | b | 1 | ∗ | 0 | v | a | b | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| v | 0 | 1 | 1 | 1 | 1 | v | 0 | v | v | v | v | |
| a | 0 | b | 1 | b | 1 | a | 0 | v | a | v | 1 | |
| b | 0 | a | a | 1 | 1 | b | 0 | v | v | b | b | |
| 1 | 0 | v | a | b | 1 | 1 | 0 | v | a | b | 1 |
- (i)
- are filters and I is an ideal;
- (ii)
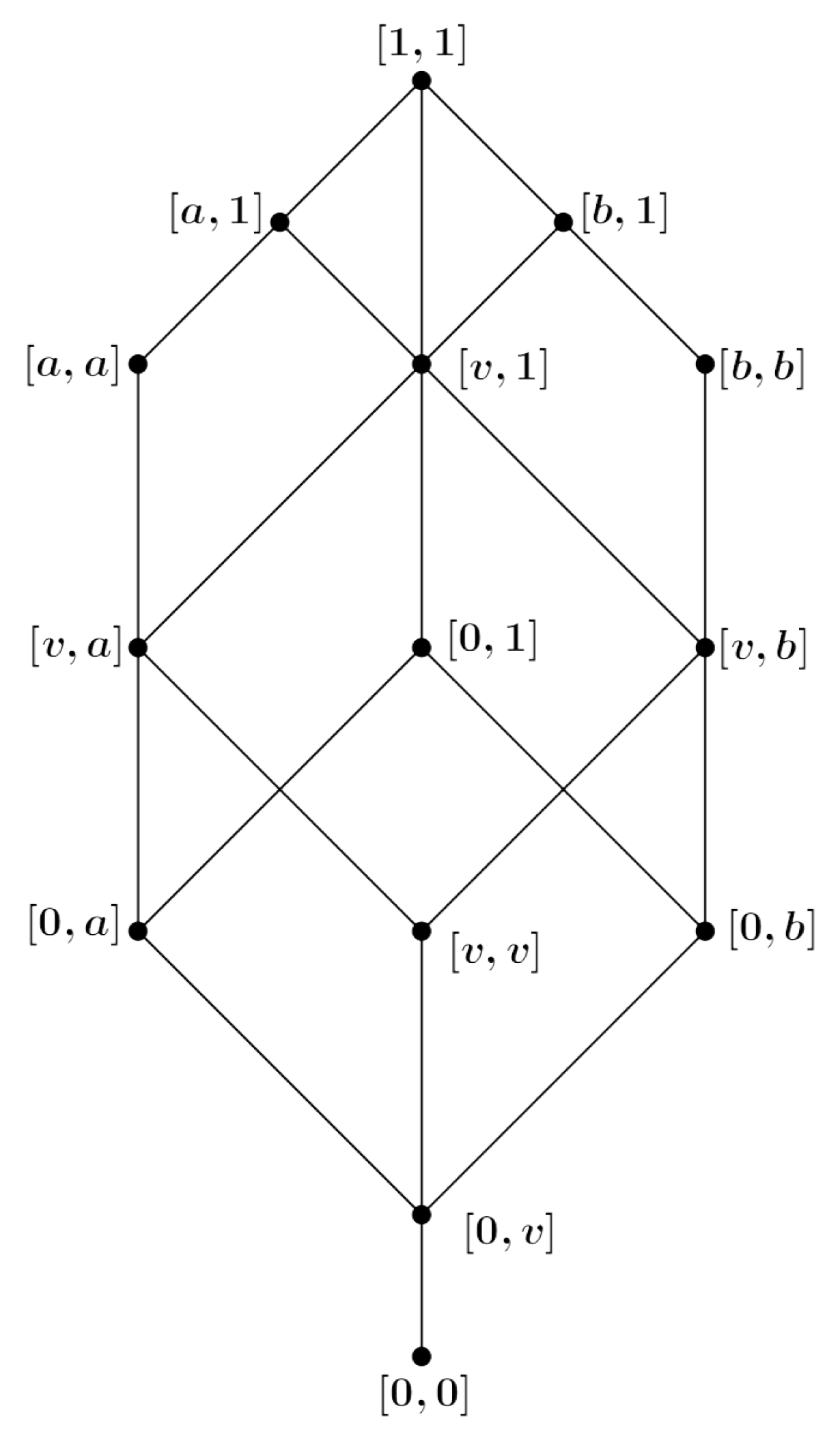
- , , , , and . We have , but and , so .
3.3. Ideals and Congruences
- is an equivalence relation.
- Reflexivity: Let , we have
- Symmetry: is symmetric by definition.
- Transitivity: Let such that and , we have to show that .Since , we have and ;since , we have and ;since , then by (T3) and , by residuation . Furthermore, , then by transitivity . Hence, . Since , we haveSince , we have ; then, . Furthermore, and , which implies , by Proposition 3.Likewise, we can show that .
- is compatible with the operations ofLet , such that , that is and .
- We have to show that .We have , then , since is increasing. Consequently, . Hence, , since . Likewise, we show that . Thus .
- We have to show that .We have by , then . Consequently . Hence, , since . Likewise, we show that . Thus .
- We have to show that .We have by , then . Hence, , then , since . Likewise, we show that . Thus .
- We have to show that .We have by and residuation. Hence, , then Therefore , since . Likewise, we show that . Thus .
- We have to show that .We have by and residuation. Hence, , then It follows , since . Likewise, we show that . Thus .
- We have to show that .We have by (T7). Then , hence . We have , since , . Likewise, we show that . Thus .
- We have to show that .We have by . Therefore, by . Hence, , and .Likewise, we show that . Thus .
- Let , then , by Proposition 4.Moreover, . Hence, , and consequently .
- Since I is an ideal, it holds that .Let , then , which implies , by Proposition 4.
- For (I1),
- let such that and . Since , then , which implies , because ∼ is a congruence. Therefore, , because . Hence, .
- For (I3),
- let . Since , then . Consequently, . Similarly, . Hence, , therefore , i.e., . Thus, .
- For (IT),
- let . Since , then thus , which implies .
- Let , such that and .Since , we have . Hence, . Because f is a homomorphism, we have . Then .Since , we have . Therefore, . Hence, .
- Let . Then and . Furthermore, because f is a homomorphism, we have . Thus, .
- Let . We have . Therefore, .
3.4. Ideals Generated by a Subset
- 1.
- For , S is a filter of the residuated lattice , but S is not a filter of the triangle algebra (see Example 2). Using the fact that is the smallest filter of containing S, we have ; however, using the characterization above given in [16], we have . Hence, .
- 2.
- For . Since , we have , . Therefore, , . Hence, . Thus, .
- First, we show that B is a filter.
- For (F1),
- let such that and . Therefore, there exists , such that . Since , then . Thus, .
- For (F2),
- let . Then, there exists , such that and there exists , such that . By , we have . Thus .
- For (FT),
- let . Therefore, there exists , such that . Hence, by (T3), we have which implies, by and : . Thus, .
- Next, we show that .Let . Since , we have .
- Let F be a filter of containing S. Let , then there exists , , such that . Let , then , thus , so by (FT) . Because this is true for all , we have, by (F2): . Since , we have, by (F1): .
- Let , then (FT), , so .
- Let , then there exists , , such that . Since (by (F1)), it holds that .
- We first show that I is an ideal.
- For (I1),
- this is obvious.
- For (I3),
- let . Therefore, , with , and , with . Hence, . Thus .
- For (IT),
- let . Then, we have , with . Hence,Thus, .
- Let . Since , (T′1), we have . Thus, .
- Let J be an ideal of containing S. Let , we have , with . Let , then . Because J is an ideal of , (IT), for all . Hence, by (I3), and by (I1), . Thus .
- Idempotence: ;
- Symmetry: ;
- Associativity: . Moreover,Since , and , we have , thus , i.e., . Moreover, , thus , consequently, , i.e., .We show likewise , therefore, .
- Absorption laws: ; .
- Bounds: Let a be non-empty family of elements of . For this family, the infimum is given by and the supremum .
- Let us show first that is a residuated lattice.
- For RL1,
- is a bounded lattice.
- For RL2,
- is a commutative ordered monoid.
- For RL3,
- let . We will prove that .
- ∗
- Assume that and let .Let , then and . Hence, . Therefore, , i.e., . Thus .
- ∗
- Assume that .Let , then and . Then , since . Hence, . Thus .
- Since is a residuated lattice and the product and the conjunction coincide, it holds that is a Heyting algebra.
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gratzer, G. Lattice Theory: First Concepts and Distributive Lattices; Dover Books on Mathematics Series; Dover Publications: Mineola, NY, USA, 2009. [Google Scholar]
- Belluce, L.P.; Di Nola, A. Commutative rings whose ideals form an MV-algebra. Math. Log. Q. 2009, 55, 468–486. [Google Scholar]
- Heubo-Kwegna, O.A.; Lele, C.; Ndjeya, S.; Nganou, J.B. BL-rings. Log. J. IGPL 2018, 26, 290–299. [Google Scholar]
- Lele, C.; Nganou, J.B. MV-algebras derived from ideals in BL-algebras. Fuzzy Sets Syst. 2013, 218, 103–113. [Google Scholar]
- Liu, Y.; Qin, Y.; Qin, X.; Xu, Y. Ideals and fuzzy ideals on residuated lattices. Int. J. Mach. Learn. Cybern. 2017, 8, 239–253. [Google Scholar]
- Piciu, D. Algebras of Fuzzy Logic; Editura Universitaria; University of Craiova: Craiova, Romania, 2007. [Google Scholar]
- Yongwei, Y.; Xiaolong, X. On characterizations of BL-algebras via implicative ideals. Ital. J. Pure Appl. Math. 2017, 37, 493–506. [Google Scholar]
- Tchoua, Y.F.; Koguep, N.B.B.; Temgoua, A.E.R.; Lele, C. N-fold boolean, implicative and integral ideals on bounded commutative residuated lattices. New Math. Nat. Comput. 2019, 15, 427–445. [Google Scholar]
- Tchoua, Y.F.; Koguep, N.B.B.; Lele, C.; Temgoua, A.E.R. Ideals and N-Involutive filters on residuated lattices. Kybernetika, 2024; submitted. [Google Scholar]
- Pal, A.; Pal, M. Some Results on Interval-Valued Fuzzy Matrices. In 1st International Conference on E-Business Intelligence (ICEBI 2010); Advances in Intelligent Systems Research; Atlantis Press: Amsterdam, The Netherlands, 2010; pp. 554–559. [Google Scholar]
- Van Gasse, B.; Cornelis, C.; Deschrijver, G.; Kerre, E.E. Triangle Algebras: Towards an Axiomatization of Interval-Valued Residuated Lattices. In International Conference on Rough Sets and Current Trends in Computing (RSCTC 2006); Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 117–126. [Google Scholar]
- Van Gasse, B.; Deschrijver, G.; Cornelis, C.; Kerre, E.E. Triangle algebras: A formal logic approach to interval-valued residuated lattices. Fuzzy Sets Syst. 2008, 159, 1042–1060. [Google Scholar]
- Van Gasse, B.; Deschrijver, G.; Cornelis, C.; Kerre, E.E. The pseudo-linear semantics of interval-valued fuzzy logics. Inf. Sci. 2009, 179, 717–728. [Google Scholar]
- Van Gasse, B.; Deschrijver, G.; Cornelis, C.; Kerre, E.E. Filters in residuated lattice and triangle algebras. Inf. Sci. 2010, 180, 3006–3020. [Google Scholar]
- Zahiri, S.; Saeid, A.B.; Eslami, E. On maximal filters in triangle algebras. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2016, 30, 1181–1193. [Google Scholar]
- Zahiri, S.; Borum, S.A.; Eslami, E. A new approach to filters in triangle algebras. Mathematics 2017, 101, 267–283. [Google Scholar]
- Zahiri, S.; Borum, S.A.; Eslami, E. An Investigation on the Co-annihilators in Triangle Algebras. Iran. J. Fuzzy Syst. 2018, 15, 91–102. [Google Scholar]
- Zhang, X.; Liang, R. Interval-Valued General Residuated Lattice-Ordered Groupoids and Expanded Triangle Algebras. Axioms 2022, 12, 42. [Google Scholar] [CrossRef]
- Buşneag, D.; Piciu, D.; Dina, A.M. Ideals in residuated lattices. Carpanthian J. Math. 2021, 37, 53–63. [Google Scholar]
- Holdon, L.C. On ideals in De Morgan residuated lattices. Kybernetika 2018, 54, 443–475. [Google Scholar]
- Ward, M.; Dilworth, R. Residuated lattices. Trans. Am. Math. Soc. 1939, 45, 335–354. [Google Scholar]
- Tallee, K.A.G.; Koguep, N.B.B.; Lele, C.; Strüngmann, L. Relative annihilator in bounded commutative residuated lattices. Ind. J. Pure Appl. Math. 2023, 54, 359–374. [Google Scholar]
- Zahiri, S.; Borum, S.A. Kerman An Investigation On THE n-Fold IVRL-Filters In Triangle Algebras. Math. Bohem. 2020, 1, 75–91. [Google Scholar]
- Zahiri, S.; Borum, S.A.; Turunen, E. On local triangle algebras. Fuzzy Sets Syst. 2021, 418, 126–138. [Google Scholar]
- Oner, T.; Senturk, I.; Oner, G. An Independent Set of Axioms of MV-Algebras and Solutions to the Set-Theoretical Yang-Baxter Equation. Axioms 2017, 6, 17. [Google Scholar] [CrossRef]
- Senturk, I.; Oner, T.; Borum, S.A. Theoretical Solutions for the Yang-Baxter Equation in Triangle Algebras. Discuss. Math. Gen. Algebra Appl. 2024, 44, 15–42. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noumen, E.; Tchoua Yinga, F.; Koguep Njionou, B.B.; Cornelis, C. An Exploration of Ideals and Filters in Triangle Algebras. Axioms 2024, 13, 566. https://doi.org/10.3390/axioms13080566
Noumen E, Tchoua Yinga F, Koguep Njionou BB, Cornelis C. An Exploration of Ideals and Filters in Triangle Algebras. Axioms. 2024; 13(8):566. https://doi.org/10.3390/axioms13080566
Chicago/Turabian StyleNoumen, Euclide, Fabrice Tchoua Yinga, Blaise Blériot Koguep Njionou, and Chris Cornelis. 2024. "An Exploration of Ideals and Filters in Triangle Algebras" Axioms 13, no. 8: 566. https://doi.org/10.3390/axioms13080566
APA StyleNoumen, E., Tchoua Yinga, F., Koguep Njionou, B. B., & Cornelis, C. (2024). An Exploration of Ideals and Filters in Triangle Algebras. Axioms, 13(8), 566. https://doi.org/10.3390/axioms13080566






