Modeling and Analysis of Monkeypox Outbreak Using a New Time Series Ensemble Technique

Abstract

The coronavirus pandemic has raised concerns about the emergence of other viral infections, such as monkeypox, which has become a significant hazard to public health. Thus, this work proposes a novel time series ensemble technique for analyzing and forecasting the spread of monkeypox in the four highly infected countries with the monkeypox virus. This approach involved processing the first cumulative confirmed case time series to address variance stabilization, normalization, stationarity, and a nonlinear secular trend component. After that, five single time series models and three proposed ensemble models are used to estimate the filtered confirmed case time series. The accuracy of the models is evaluated using typical accuracy mean errors, graphical evaluation, and an equal forecasting accuracy statistical test. Based on the results, it is found that the proposed time series ensemble forecasting approach is an efficient and accurate way to forecast the cumulative confirmed cases for the top four countries in the world and the entire world. Using the best ensemble model, a forecast is made for the next 28 days (four weeks), which will help understand the spread of the disease and the associated risks. This information can prevent further spread and enable timely and effective treatment. Furthermore, the developed novel time series ensemble approach can be used to forecast other diseases in the future.

1. Introduction

Monkeypox (Mpox) is a contagious zoonotic disease that has experienced significant spread worldwide, with symptoms such as fever, fatigue, and rash as key indicators [1]. This disease has raised concern in Latin America and Chicago due to endemic transmission and low vaccination coverage, highlighting the importance of accessible vaccination strategies and ongoing surveillance to control the disease [2,3]. Consequently, there has been notable interest in recent years due to outbreaks occurring in various regions, leading to hundreds of research studies [4,5]. Therefore, developing and developed countries have had to prepare response plans and continuously monitor Mpox disease since it has significantly impacted international territories since 2022 [6,7,8]. However, it was necessary to emphasize the importance of genomic surveillance to understand and control the spread of emerging infectious diseases, emphasizing the need for a rapid and coordinated response at national and international levels [9,10]. Similarly, the need to highlight the importance of reliable information sources to understand and address this disease effectively was evident [11,12]. Additionally, it was relevant to highlight the assessment of fear associated with Mpox to design customized education and prevention programs, with more significant implications for the development of strategies considering psychosocial factors, such as epistemic credulity and media perception [13,14,15], as well as the critical need to improve awareness strategies and preventive measures to mitigate the risk of Mpox transmission and other potential public health threats to empower individuals in making informed decisions about their well-being [16,17]. Therefore, a rapid and collaborative international response was necessary to control and prevent the spread of the virus to develop effective detection strategies, emergency management, and advancements in antiviral drugs and vaccines to address this public health threat [18,19].

Short-term forecasts of its trajectory at various geographic levels can assist in developing policy and intervention measures for any fast-spreading new illness. However, there are few opportunities to evaluate predicting performance and improve models during a public health crisis [20]. Fortunately, as of September 2022, instances were rapidly declining globally, with non-endemic nations reporting a total of 90,574 cases and 170 fatalities as of 27 December 2023 [21]. Given the diverse effects of the epidemic on different geographical scales and the dramatic drop in Mpox cases, it is critical to retroactively review forecasting approaches to better prepare for future public health catastrophes [22]. In response to this concern, research began to understand the outbreak of Mpox. One study indicated that since May 2022, 108 countries with Mpox outbreaks have been identified, with the disease primarily affecting homosexual and bisexual men [23]. It was suggested that risk factors for contracting Mpox include being a young man, having sex with other men, having unprotected sex, being HIV positive, and having a history of sexually transmitted infections [24]. Furthermore, in November 2022, over 850,000 English tweets using the keyword “Monkeypox” were analyzed, revealing initially negative emotions towards a new global outbreak. It was observed that tweets helped disseminate information such as vaccination locations, global case quantification, symptoms, and prevention methods. However, they were also prone to providing misinformation [25]. On the other hand, the evolution of Mpox entails a significant risk of severe outcomes in terms of hospitalization, with significant differences between the recent outbreak and historical ones, suggesting a possible variation in disease severity at different periods [26].

Various researchers in the year 2022 studied the behavior of Mpox, proposing statistical models that could predict cases of contagion and death with different levels of success. In some cases, they suggested linear regression models for forecasting Mpox outbreaks [27]. In contrast, in another case, they proposed a convolutional neural network model to detect and predict Mpox contagion cases [28]. In 2023, a hybrid technique for predicting Mpox infection and death yielded notable results. In this regard, time series have emerged as a valuable tool for predicting the spread of infectious diseases and improving response capacity to outbreaks. The use of predictive statistical models in the healthcare domain has experienced a significant increase in recent times. These models serve as a crucial link between statistics and medical practice, offering valuable support in decision-making and facilitating the creation of various systems and tools to mitigate uncertainties, improve performance, and establish effective control measures to combat diseases [29].

Other studies addressed the growing threat of Mpox in a post-COVID-19 context, using neural networks to predict its spread in the USA, Germany, the UK, France, and Canada, showing high accuracy in outbreak prediction. The effectiveness of the artificial neural network (ANN) model compared to other methods such as LSTM and GRU was highlighted, emphasizing the importance of deep learning in predicting and controlling emerging diseases like Mpox [30]. Furthermore, classification systems based on neural networks and explainable AI tools were proposed, trained using a dataset of images and achieving over 98 percent accuracy [31]. Challenges such as data availability and quality, biases in datasets, and interpretability in this field were identified, emphasizing the importance of periodically updating the dataset with new images of infected patients for future research [32]. Similarly, time series models, such as ARIMA, have been used to understand the dynamics of infectious disease outbreaks and predict their spread, focusing on developing an effective prediction model to understand short-term behavior [33]. Likewise, a decrease in nucleotide mutation rates was observed, maintaining a balance between bidirectional rates through time series analysis by predicting Mpox virus mutation using deep learning models such as LSTM [34]. Other approaches, such as the innovative filtering and combination technique, accurately forecasted cumulative daily confirmed cases of Mpox using time series and machine learning models, demonstrating the forecasting system’s efficiency and accuracy [35]. Similarly, machine learning techniques and time series analysis allowed for identifying key patterns and trends in disease spread, showing that convolutional neural networks perform better in analysis [36,37]. Likewise, the effectiveness of the stacked ensemble learning approach in predicting transmission rates, especially in Europe, where the pandemic was severe, was evidenced [38]. Furthermore, other studies highlighted the superiority of machine learning approaches over traditional time series models for predicting Mpox, showing that the multilayer perceptron model outperformed ARIMA with lower mean squared error, recommending the application of methods such as extreme learning machine and support vector machine for better future adaptation [39].

Short-term forecasting of infectious diseases has become vital for health policy-making and improving the population’s standards in specific or general localities. In this regard, new contributions should be encouraged by proposing different forecasting tools to provide an extensive range of forecasting models that can be applied to specific or general areas for analysis and study. Hence, the main aim of this research work is two-fold: first, propose a new ensemble time series technique, and second, apply the proposed method to attain precise and efficient short-term Mpox infectious disease forecasting for the world’s four most influential countries (Brazil, France, Spain, and the USA) and the world. Therefore, this approach involved processing the first cumulative confirmed case time series to address variance stabilization, normalization, stationarity, and a nonlinear secular trend component. After that, five single time series models including autoregressive, simple exponential smoothing, autoregressive integrated moving averages, nonlinear autoregressive, and the Theta model, were used to ensure the cleaning (i.e., free from variance stabilization, normalization, stationarity, and seasonality issues), and three proposed ensemble models were used to estimate the filtered confirmed case time series. The proposed ensemble models are based on the weighting technique, such as equal weight to single models, in-sample-based weighing (training), and out-of-sample (validation). However, four different accuracy average errors, such as the mean absolute error, the mean absolute percent error, the root mean squared error, and the root mean log squared error, and a statistical equal forecast test, the Diebold–Marino test, are determined to check the performance of the proposed novel time series ensemble forecasting technique. Furthermore, the developed novel time series ensemble approach can be used to forecast other diseases in the future.

The remainder of this manuscript is structured as follows: Section 2 outlines the general framework of the proposed time series ensemble approach. In Section 3, the proposed time series forecasting approach is applied to the daily cumulative confirmed cases series from the four countries: Brazil, the USA, Spain, and France, as well as the total cases worldwide. Using the best ensemble model within the proposed forecasting approach in this paper, a projection has been made for the next twenty-eight days, equivalent to four weeks. To understand the spread of the disease and associated risks in the four countries with the highest number of infections, as well as the total cases worldwide, a comprehensive discussion is presented in Section 4. Lastly, Section 5 concludes by discussing the study’s limitations and proposing directions for future research.

2. The Proposed Ensemble Approach for Time Series

This section explains the proposed time series ensemble technique for short-term Mpox infectious disease forecasting for the four most influential countries in the world. In the proposed time series ensemble technique, the cumulative time series of confirmed cases is first preprocessed by variance stabilization, trend seasonality, and stationarity concerns. Then, five base models are employed: the autoregressive, the simple exponential smoothing, the autoregressive moving average, the nonlinear autoregressive, and the Theta model. These are utilized to implement the three proposed ensemble models, resulting in a filtered cumulative time series of confirmed cases. Further information about these steps is provided in the subsequent subsections.

2.1. Preparation of Data

This study aims to attain precise and efficient short-term Mpox infectious disease forecasting for the world’s four most influential countries (Brazil, France, Spain, and the USA) and the world. To accomplish this objective, this work employed a novel methodology to model and forecast the cumulative Mpox-confirmed cases. The intent is to discern intricate features inherent in the cumulative Mpox-confirmed case dynamics over time. The anticipated features include a nonlinear secular long-run trend component, high variance and standard deviation, non-normality, and non-stationarity. First, let the time series of the cumulative confirmed new cases of Mpox be donated by $C_d^k$; the super subscript k (k $=1,2,\dots ,5$) shows the country series, while d shows the dth day data point; and take the natural logarithm (log($C_d^k$)) for all the series to normalize and stabilize the variance and standard deviation. The dynamics of the log daily cumulative confirmed times series, log($C_d^k$), may be described as:

$$\log \left(C_d^k\right)={\tau }_d^k+c_d^k$$

(1)

That is, the log($C_d^k$) is divided into two major components: a nonlinear secular trend component (${\tau }_d^k$) and a residual component ($c_d^k$). The (${\tau }_d^k$) component is a function of the series ($1,2,3,\dots ,d$) and is estimated by the cubic regression splines method, and the regression coefficients are estimated by the ordinary least square method. Hence, the final estimated equation may be written in the following manner:

$${\widehat{\tau }}_d^k={\widehat{\alpha }}_1\left({\tau }_{d-1}^k\right)+{\widehat{\alpha }}_2\left({\tau }_{d-2}^k\right)+{\widehat{\alpha }}_3\left({\tau }_{d-3}^k\right)+c_d^k$$

(2)

It is worth mentioning that many authors in the literature capture the nonlinear trend in a time series using regression splines [40,41,42]. On the other hand, $c_d^k$ is a residual component that describes the random series and is obtained as

$$c_d^k=log\left(C_d^k\right)-{\widehat{\tau }}_d^k$$

(3)

Thus, once the cumulative confirmed series are preprocessed (normalize and stabilize the variance and standard deviation; long-run trend component), the next step is to model the remaining residual $c_d^k$ series; the current work considers five single-time series models and three proposed ensemble models. Hence, all forecasting models are described in the coming subsection.

2.1.1. Autoregressive Model

The autoregressive (AR) model is a time series framework that evidences the interdependence between a given observation and multiple lagged observations (preceding time steps) for predictive purposes. Within an AR model, the forthcoming value of a variable is articulated as a linear combination of its past values, where the model determines the coefficients associated with these past values. The order of an AR model, denoted as ’p’, specifies the count of preceding values considered in predicting the subsequent value. For instance, an AR (1) model utilizes the antecedent value of the variable to forecast its future value, while an AR (2) model integrates the two preceding values into its predictive equation.

$$C_d={\varphi }_1{C}_{d-1}+{\varphi }_2{C}_{d-2}+\dots +{\varphi }_p{C}_{d-p}+{\epsilon }_d$$

(4)

where:

$$\begin{array}{cc}\hfill {\varphi }_1& :\mathrm{Coefficient}\mathrm{for}{C}_{d-1}\hfill \\ \hfill {\varphi }_2& :\mathrm{Coefficient}\mathrm{for}{C}_{d-2}\hfill \\ \hfill {\varphi }_p& :\mathrm{Coefficient}\mathrm{for}{C}_{d-p}\hfill \\ \hfill C_d& :\mathrm{Current}\mathrm{value}\mathrm{at}\mathrm{time}d\hfill \\ \hfill C_{d-1}& :\mathrm{Value}\mathrm{at}\mathrm{time}d-1\hfill \\ \hfill C_{d-2}& :\mathrm{Value}\mathrm{at}\mathrm{time}d-2\hfill \\ \hfill C_{d-p}& :\mathrm{Value}\mathrm{at}\mathrm{time}d-p\hfill \end{array}$$

The current work used an AR(3) model for the Brazil, France, and Spain cases, while an AR(4) model was used for the USA and the World cases.

2.1.2. Exponential Smoothing Model

The Exponential Smoothing Model (ESM) encompasses a repertoire of forecasting models characterized by exponentially diminishing weights allocated to antecedent observations. Functioning as a dedicated time series forecasting model, it employs a weighted average of historical observations to prognosticate the forthcoming value of a variable. The foundational premise of the ESM model lies in positing that the future value of a variable is intricately tied to its historical values, with a discernibly higher weighting accorded to more recent observations relative to their older counterparts. The ES model can be formally expressed as follows:

$$C_{d+1}=\alpha ·C_d+(1-\alpha )·C_{d-1}$$

(5)

where:

$$\begin{array}{cc}\hfill C_{d+1}& :\mathrm{predicted}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{at}\mathrm{time}d+1\hfill \\ \hfill C_d& :\mathrm{observed}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{at}\mathrm{time}d\hfill \\ \hfill C_{d-1}& :\mathrm{observed}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{at}\mathrm{time}d-1\hfill \\ \hfill \alpha & :\mathrm{smoothing}\mathrm{parameter}\mathrm{that}\mathrm{determines}\mathrm{the}\mathrm{weight}\mathrm{assigned}\hfill \\ \hfill & \mathrm{to}\mathrm{the}\mathrm{most}\mathrm{recent}\mathrm{observation}\hfill \end{array}$$

2.1.3. Autoregressive Moving Average Model

The ARMA model integrates autoregressive and moving average components, drawing upon past observations and antecedent forecast errors to project forthcoming values. This model is parameterized by two variables, p, and q, wherein p denotes the order of the AR model, and q signifies the order of the Moving Average (MA) model. The AR component of the model captures the linear relationship between the current variable value and its antecedent values. In contrast, the MA component captures the linear association between the present variable value and its preceding errors. In formal terms, the ARMA model is expressed as follows:

$$\begin{array}{c}\hfill C_d=c+{\varphi }_1{C}_{d-1}+{\varphi }_2{C}_{d-2}+\dots +{\varphi }_p{C}_{d-p}+\\ \hfill {\epsilon }_t+{\theta }_1{\epsilon }_{d-1}+{\theta }_2{\epsilon }_{d-2}+\dots +{\theta }_q{\epsilon }_{d-q}\end{array}$$

(6)

where:

$$\begin{array}{cc}\hfill C_t& :\mathrm{Current}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\hfill \\ \hfill c& :\mathrm{Constant}\hfill \\ \hfill {\varphi }_1& :\mathrm{AR}\mathrm{coefficient}\mathrm{for}{C}_{d-1}\hfill \\ \hfill {\varphi }_p& :\mathrm{AR}\mathrm{coefficient}\mathrm{for}{C}_{d-p}\hfill \\ \hfill C_{d-1}& :\mathrm{Past}\mathrm{values}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{up}\mathrm{to}\mathrm{order}p\hfill \\ \hfill {\epsilon }_t& :\mathrm{Error}\mathrm{term}\mathrm{at}\mathrm{time}d\hfill \\ \hfill {\theta }_1,{\theta }_q& :\mathrm{MA}\mathrm{coefficients}\hfill \end{array}$$

In our case, for the selection of the model, we used the auto.arima function using an R-package, version 2023.09.1 forecast.

2.1.4. Nonparametric Autoregressive Model

The nonparametric autoregressive model (NAR) presents an alternative to conventional parametric models, departing from the latter’s reliance on specific mathematical equations to elucidate the relationship between past and future values. In contrast, NAR models employ flexible and adaptive techniques, such as kernel regression or spline functions, to capture dynamic patterns in the data without explicit parameter estimation. These models are distinguished by their flexibility, absence of predefined parameters, emphasis on local relationships, and reliance on data-driven structures to address intricate and nonlinear dependencies within time series data. In this model, the association between $C_d$ and its previous terms lacks a specific parametric form, allowing for potential nonlinearities. This relationship is expressed as:

$$C_d=q_1\left(C_{d-1}\right)+q_2\left(C_{d-2}\right)+\dots +q_n\left(C_{d-n}\right)+{\epsilon }_d$$

(7)

Here, $q_j$ ($j=1,2,\dots ,n$) denotes smoothing functions describing the association between $C_d$ and its previous values. In this specific study, cubic regression splines represent the functions $q_i$, and lags 1, 2, and 3 are employed for NPAR modeling.

2.1.5. Theta Model

The Theta model is a forecasting methodology employed to predict future values by analyzing the average change discerned within the time series data. This methodology encompasses the computation of the mean alteration between successive time points, subsequently extrapolating these findings into future periods. The mathematical representation of the Theta model is the following:

$$C_{d+1}={\displaystyle \frac{1}{d}}\left(C_d+C_{d-1}+\dots +C_{d-m+1}\right)$$

(8)

where:

$$\begin{array}{cc}\hfill C_{d+1}& :\mathrm{Predicted}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{at}\mathrm{time}d+1\hfill \\ \hfill m& :\mathrm{Number}\mathrm{of}\mathrm{past}\mathrm{values}\mathrm{used}\mathrm{in}\mathrm{the}\mathrm{average}\hfill \\ \hfill C_d& :\mathrm{Past}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{at}\mathrm{time}d\hfill \\ \hfill C_{d-1}& :\mathrm{Past}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{at}\mathrm{time}d-1\hfill \\ \hfill C_{d-m+1}& :\mathrm{Past}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{variable}\mathrm{at}\mathrm{time}d-(m-1)\hfill \end{array}$$

The Theta model, characterized by its simplicity and user-friendly attributes, is an apt methodology for short-term forecasting within the domain of stationary time series devoid of discernible trends or seasonality.

2.1.6. The Proposed Ensemble Models

At its core, an ensemble technique integrates outcomes from various models, each meticulously calibrated before unity. This approach capitalizes on the inherent strengths of individual models while compensating for their inherent limitations. Within the scope of this study, ensemble techniques are initially employed to compute weights for the results derived from individual models. Consequently, the proposed ensemble encompasses three distinct weighting strategies: (a) equitable distribution of weight among all single models, denoted as EnsE; (b) weight assignment based on training average accuracy errors (

Table 1. Evaluation average errors.

S.No	Error	Formula
1	MAE	${\displaystyle \frac{1}{D}}{\displaystyle \sum _{d=1}^D}|C_d-{\widehat{C}}_d|$
2	MAPE	${\displaystyle \frac{1}{D}}{\displaystyle \sum _{d=1}^D}\left|{\displaystyle \frac{C_d-{\widehat{C}}_d}{C_d}}\right|$
3	RMSE	${\left[{\displaystyle \sum _{d=1}^D}\left[{\displaystyle \frac{{(C_m-{\widehat{C}}_d)}^2}{D}}\right]\right]}^{0.5}$
4	RMSLE	${\left({\displaystyle \frac{1}{D}}{\displaystyle \sum _{d=1}^D}{[log(C_m+1)-log({\widehat{C}}_d+1)]}^2\right)}^{0.5}$

), designated as EnsT; and (c) weight assignment based on validation mean accuracy measures, denoted as EnsV. The model allocates greater weight to the ensemble model for training and validation datasets with lower mean accuracy errors, while models exhibiting higher mean accuracy errors contribute comparatively less weight to the ensemble. Notably, the model weights assume small positive values, and their accumulation equates to one, signifying the percentage of reliance or anticipated performance from each model.

After estimating the nonlinear curve trend component using the regression spline method discussed above, the next step is forecasting the remaining part (c) using five single and three proposed ensemble models. Once this is performed, we can obtain the daily cumulative confirmed cases of Mpox for the next day as follows:

$${\widehat{C}}_d^k=exp({\widehat{\tau }}_d^k+{\widehat{c}}_d^k)$$

(9)

2.2. Evaluation Criteria

This study examines two evaluation criteria for the proposed time series ensemble forecasting technique: accuracy average errors and an equal forecast accuracy test. Primarily, Table 1 presents the accuracy average errors, outlining the formulas for computing each metric. The metrics encompass the mean absolute error (MAE), the mean absolute percent error (MAPE), the root mean squared error (RMSE), and the root mean log squared error (RMSLE).

In the given formulations, $C_d$ denotes observed values, while ${\widehat{C}}_d$ represents forecasted daily cumulative confirmed cases for the dth observation ($d=1,2,\dots ,126=D$). Consequently, diminishing values for MAE, MAPE, RMSE, and RMSLE generally signify heightened predictive accuracy of the model.

Second, a statistically equal forecast test, the Diebold–Marino (DM) test [43], is performed to evaluate the forecasting ensemble time series proposed approach. In the literature on forecasting models, the DM test was mostly used to evaluate time series forecasting models, determining whether the forecast errors from one model are statistically different from those from another model [44,45,46]. To perform the DM test, the forecast errors of each model are calculated using a loss function. Then, a statistical value is computed by comparing the errors of each model. The test statistic is based on the difference between the mean squared errors of the two models. Suppose the test statistic is above a certain threshold and the p-value is below a significance level ($\alpha =0.05$). In that case, the forecasts from one model are significantly better than the other model. For instance, calculate the forecast errors for both models. Forecast errors ($e_t=C_t-{\widehat{C}}_t$) are the differences between the observed values ($C_t$) and the forecast values (${\widehat{C}}_t$). Compute the mean difference ($\overline{d}$) of the forecast errors: $\overline{d}={\displaystyle \frac{1}{T}}{\sum }_{t=1}^T(e_{1t}-e_{2t})$. Where: $e_{1t}$ and $e_{2t}$ are the forecast errors from Model 1 and Model 2 at time t, respectively, and T is the number of observations. Next, calculate the variance of the differences, such as ${\sigma }_d^2={\displaystyle \frac{1}{T}}{\sum }_{t=1}^T{(e_{1t}-e_{2t}-\overline{d})}^2$. Thus, the Diebold–Mariano test statistic DM = ${\displaystyle \frac{\overline{d}}{\sqrt{{\sigma }_d^2}}}$. Finally, the null and alternative hypotheses are generally stated as ${\mathrm{H}}_0$: There is no difference in forecast accuracy between the two models (H₀: $\overline{d}$ = 0) vs. H_A: The two models differ in forecast accuracy (H_A: $\overline{d}\ne 0$). Hence, the null hypothesis implies that there was not a statistically significant difference in forecast accuracy between the models. In contrast, the alternative hypothesis suggests a significant difference in forecast accuracy between the two models.

To conclude this section, the main steps, including the proposed time series ensemble forecasting technique, are listed in bullet points below, and the flowchart is presented in Figure 1.

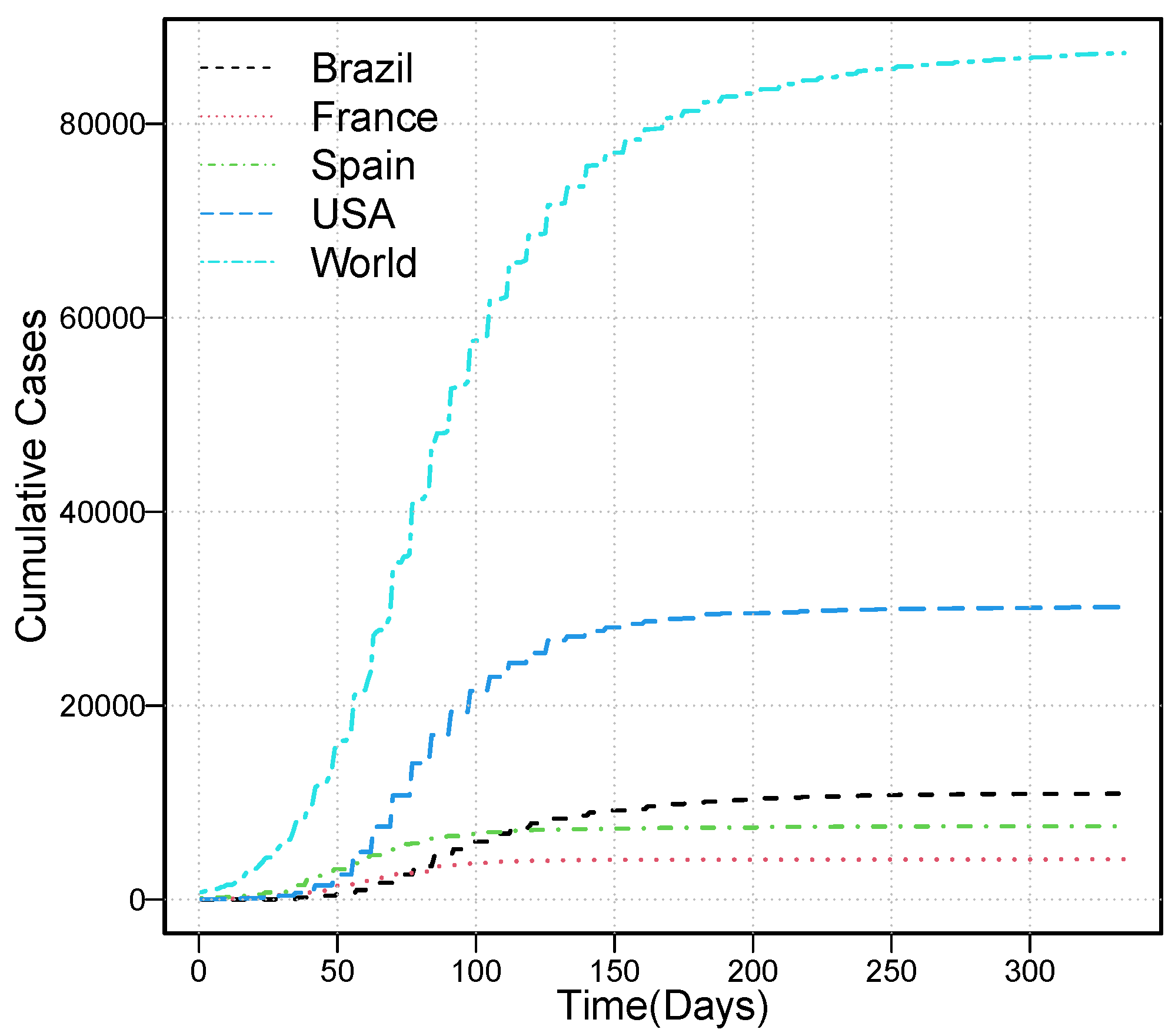
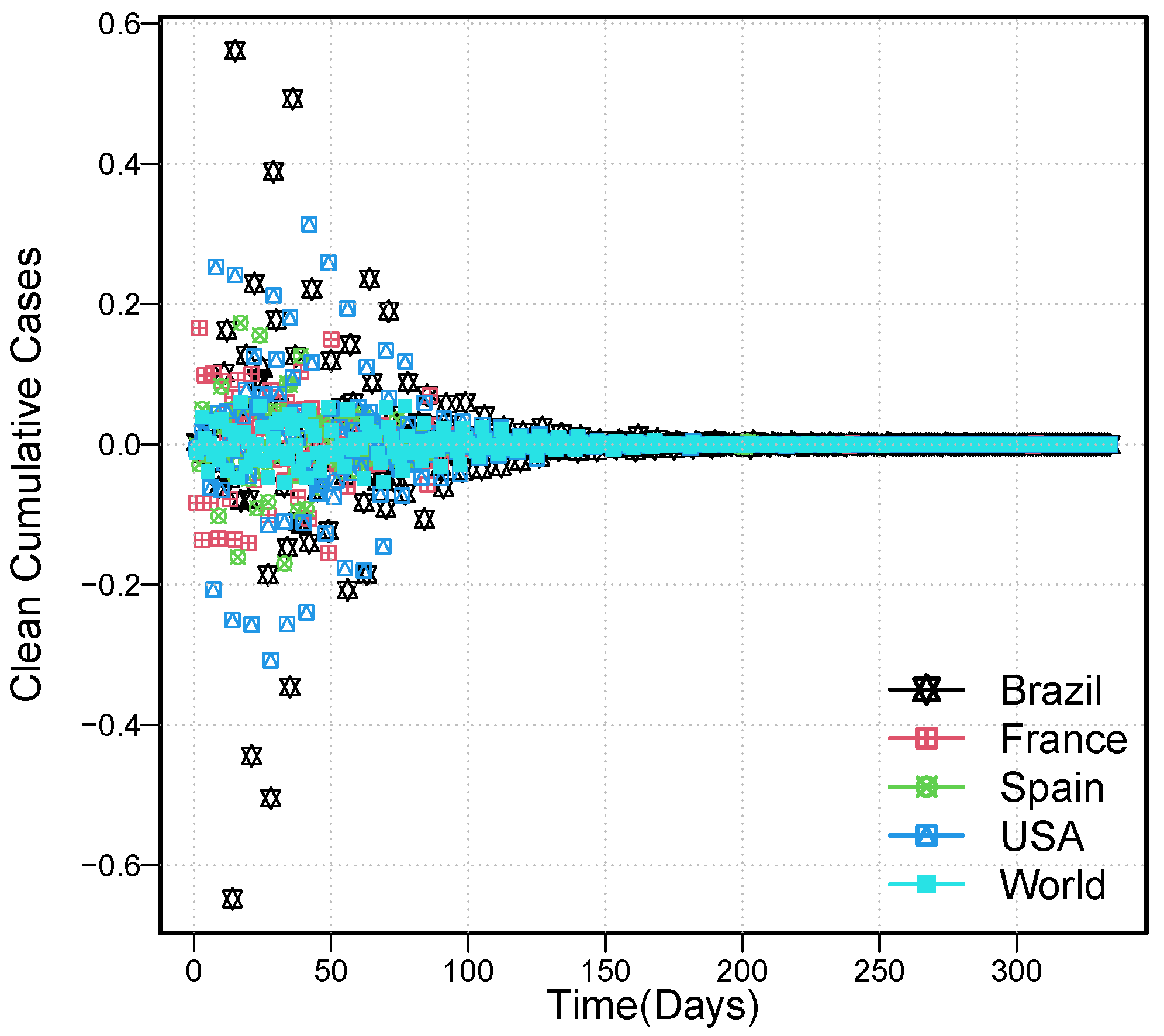
• In the first step, the cumulative Mpox-confirmed cases time series ($C_m$) is preprocessed (to address the issue of stabilizing the variance and standard deviation and remove the nonlinear long-run trend component), discussed in detail in Section 2.1.
• In the second step, we divide the stochastic (short-run dynamic) residual component ($c_n$) into three parts: training, validation, and testing datasets. Let $\{c_n,n=1,2,...,N\left(507\right)\}$ represent the residual series of the cumulative Mpox-confirmed cases time series. Then, training dataset: $\{c_w,w=1,2,...,W\left(254\right)\}$; validation dataset: $\{c_v,v=1,2,...,V\left(127\right)\}$; testing dataset: $\{c_d,d=1,2,...,D\left(126\right)\}$; where $N(N=W+V+D)$ is the total number of data points.
• In the third step, model the train data using single models, i.e., AR, ARMA, ESM, NAR, and Theta models.
• In the fourth step, calculate the one-day-ahead forecast using the expanding window technique. The forecast values, ${\widehat{c}}_{N-(W+V+d)}^j$ for j = 1, 2, 3, 4, 5, are obtained by the models listed in step 3.
• In the fifth step, the output of a basic ensemble method is mathematically described by Equation (10).

  $${\widehat{c}}_{N-(W+V)+d}^l=\sum _{l=1}^5{\mathsf{\Omega }}_l{\widehat{c}}_{N-(W+V)+d}^l$$

  (10)

  where ${\mathsf{\Omega }}_l$, $l=1,2,\dots ,5$ are obtained by three weighting strategies: (a) Equal weight to all single models and denoted by the EnsE; (b) Weight assigned based on training, mean accuracy measures (MAE, MAPE, RMSE, and RMSLE), and denoted by (EnsT); (c) Weight assigned based on validation mean accuracy measures and denoted by (EnsV). The lower accuracy means the error model assigns more weight to the ensemble model in training and validation datasets. In contrast, the highest accuracy means the error model has less weight than the ensemble model. However, the model weights are small, positive values, and the sum of all weights equals one, indicating the percentage of trust or expected performance from each model.
• In the sixth step, obtain the one-day-ahead forecast values using equations for the EnsE, the EnsT, and the EnsV models.
• In the last step, evaluate the model based on accuracy and average errors (see Table 1).

3. Case Study Results

This work aims to provide a short-term forecast of the cumulatively infected cases of Mpox using the four most influential countries (Brazil, France, Spain, and the USA) worldwide and for the whole world. The Mpox datasets (daily cumulative confirmed cases) were taken from the official website of “Our World in Data” from 1 June 2022 to 30 April 2023. The graphical presentation and the descriptive statistics of cumulative confirmed cases for all countries and the world can be seen in Figure 2 and

Table 2. Descriptive statistics.

Estimator	Minimum	25%	50%	Mean	75%	Maximum	Variance	Standard Deviation	Skewness	Kurtosis
Brazil	1.00	3705.50	9606.00	7418.42	10,758.00	10,915.00	17,131,328.25	4139.00	−0.86	2.06
France	17.00	2889.00	4102.00	3329.43	4128.00	4144.00	1,848,070.37	1359.44	−1.49	3.59
Spain	142.00	6284.00	7392.00	6155.19	7531.75	7549.00	5,487,833.98	2342.61	−1.64	4.13
USA	25.00	16,965.00	28,809.00	22,030.52	29,933.00	30,154.00	125,647,213.44	11,209.25	−1.11	2.52
World	756.00	47,108.75	80,054.50	63,284.54	85,658.75	87,294.00	894,676,742.03	29,911.15	−1.06	2.53
log (Brazil)	0.00	8.21	9.17	8.05	9.28	9.30	5.67	2.38	−2.25	7.10
log (France)	2.83	7.97	8.32	7.84	8.33	8.33	1.13	1.06	−2.52	8.73
log (Spain)	4.96	8.75	8.91	8.50	8.93	8.93	0.85	0.92	−2.44	7.89
log (USA)	3.22	9.74	10.27	9.37	10.31	10.31	3.34	1.83	−2.11	6.24
log (World)	6.63	10.76	11.29	10.72	11.36	11.38	1.29	1.14	−2.03	6.12

. Figure 2 shows the cumulative Mpox-confirmed cases and an increasing nonlinear curve in all cases. However, this figure shows that the world has the most confirmed Mpox cases, while the USA shows the highest confirmed cases among the most affected countries. On the other hand, Spain had the most confirmed counts at the start, but after September 2022, Brazil obtained the second-highest number of confirmed cases of Mpox, and Spain had the third-highest number of confirmed cases. In the same way, France had higher infected cases at the start, but after August 2022, there were more confirmed new cases than in Spain and Brazil. The current situation is that amongst all countries, the USA has the most new confirmed counts, while Brazil and Spain are in the second and third positions, and France is the fourth most affected country among all countries until 30 April 2023.

In contrast to the graphic presentation, the descriptive statistics, such as minimum, 25% (first quartile), 50% (second quartile or median), 75% (third quartile), arithmetic mean, variance, standard deviation, skewness, kurtosis, and maximum statistics for Brazil, France, Spain, the USA, and the entire world, using original and natural logarithm cumulative confirmed cases time series, are tabulated in Table 1. It is clearly confirmed from this table that the natural logarithm effect on all considered cumulative time series stabilizes the variance and standard deviation as well. Due to this effect, this work will proceed with a log series for all cases for further analysis. Therefore, the complete datasets for all considered countries and the entire world of the daily cumulative confirmed cases covering 334 days were divided into three parts as follows: 1 June to 20 January 2023 (234 days) was used for model estimation (training part), 21 January 2023 to 11 March 2023 (50 days) was used for model validation (hold-out sample), and 12 March 2023 to 30 April 2023 (50 days) was used for model testing (out-of-sample) the one-day-ahead cumulative confirmed cases forecasts.

As confirmed by the previous discussion, all series have an increasing nonlinear trend component. This work extracts the nonlinear curve trend component using the regression spine method to achieve this. The graphical representation of the nonlinear curve trend component along with the original log confirmed cumulative series is shown in Figure 3. Clearly, it can be seen that in all cases, such as sky blue (the whole world), blue (the USA), green (Spain), black (Brazil), and red (France), the nonlinear curve trend component is extracted very well. Once the nonlinear curve trend component is removed, this work moves ahead with further modeling and forecasting with clean cumulative confirmed case time series. The remaining filtered series (clean cumulative confirmed case time series) for the four most affected countries and the entire world case are shown in Figure 4.

Before modeling and forecasting time series data, it is essential to check the stationarity property of the dataset. To do this, this work performed the augmented Dickey–Fuller test and reported the results (statistics and p-values) for the original and clean (taking the natural logarithm and removing the trend component) cumulative confirmed cases time series for all considered countries and the entire world case in

Table 3. Nonstationary outcomes: ADF test statistic and p-values for all considered series.

Test	Nonstatinay Outcomes
Series	Statistic	p-value
Brazil	1.3999	−0.9900
France	−13.3770	−0.0086
Spain	−1.7358	−0.6881
USA	−15.9970	−0.0061
World	−2.2683	−0.4635
log (Brazil)	−17.6770	−0.0041
log (France)	0.3030	−0.9910
log (Spain)	−14.6470	−0.0049
log (USA)	0.1666	−0.9919
log (World)	−19.83	−0.0056

. This table indicates the original cumulative established case time series of the four most affected countries and the world as a whole, all nonstationary. In contrast, the clean cumulative confirmed cases time series (with natural logarithm and removing the trend component) for all considered countries have a higher negative statistic value. They are mostly minuscule (less than 0.05), indicating that the series is stationary at a 5% significance level. Once the dataset has been preprocessed, confirmed cumulative case series are modeled and forecast. To this end, this work uses five single time series models, including the autoregressive model, the exponential smoothing model, the autoregressive moving averages model, the nonlinear autoregressive model, and the Theta model, and the three proposed ensemble models (the EnsE, the EnsT, and the EnsV). Therefore, in the proposed time series ensemble forecasting approach, compare nine total models within the two contexts, such as comparing single model performance, the proposed ensemble models, and single verse ensemble models.

Hence, for all nine models for the four most affected countries and the world case, one-day-ahead out-of-sample forecast outcomes (MAP, MAE, RMSE, and RMLSE) are listed in

Table 4. Accuracy mean errors.

Brazil
Model	MAPE	MAE	RMLSE	RMSE
AR	0.000037	0.4055247	0.0001216	1.332314
ARIMA	0.00041	4.4930502	0.0005071	5.557751
ESM	0.0000798	0.874099	0.0001807	1.98015
NPAR	0.0002975	3.2604158	0.0003833	4.199699
Theta	0.0000156	0.1711713	0.0001092	1.196843
EnsE	0.00016798	1.8408522	0.00026038	2.8533514
EnsT	0.0000121	0.1708917	0.0001002	1.18923
EnsV	0.0000111	0.1681917	0.0000992	1.1861
France
Model	MAPE	MAE	RMLSE	RMSE
AR	0.00002361	0.00031809	0.00000107	0.00086441
ARIMA	0.00000025	0.00000309	0.00000216	0.00000649
ESM	0.00001608	0.06575863	0.00002243	0.09174509
NPAR	0.00040145	1.64194309	0.00040924	1.67457669
Theta	0.00000034	0.00137947	0.00000262	0.01071651
EnsE	0.000088326	0.341923274	0.000087104	0.355713038
EnsT	0.00000023	0.00000219	0.00000201	0.00000581
EnsV	0.00000019	0.00000199	0.00000191	0.00000553
Spain
Model	MAPE	MAE	RMLSE	RMSE
AR	0.00006945	0.5258639	0.00026101	1.977389
ARIMA	0.00007903	0.5984467	0.00025369	1.921771
ESM	0.00004015	0.3040281	0.00020946	1.586085
NPAR	0.00011278	0.8540059	0.00031197	2.362472
Theta	0.00005783	0.4378565	0.00021667	1.640763
EnsE	0.000071848	0.54404022	0.00025056	1.897696
EnsT	0.00003758	0.2845781	0.00020426	1.546656
EnsV	0.00003314	0.2417941	0.00019113	1.498126
USA
Model	MAPE	MAE	RMLSE	RMSE
AR	0.00022263	6.778124	0.00045471	13.8483
ARIMA	0.00033699	10.259437	0.00047854	14.57806
ESM	0.00064046	19.507443	0.00085277	26.00396
NPAR	0.0026346	20.142995	0.00093493	33.12454
Theta	0.00010858	3.306309	0.00042027	12.79745
EnsE	0.000788652	11.9988616	0.000628244	20.070462
EnsT	0.00010219	3.100101	0.00040191	12.12132
EnsV	0.00010156	2.996107	0.00039027	11.99131
World
Model	MAPE	MAE	RMLSE	RMSE
AR	0.00039134	34.98612	0.00085887	76.997
ARIMA	0.0009302	83.32306	0.00161852	145.44294
ESM	0.00026482	23.63597	0.00080848	72.37218
NPAR	0.00188915	168.46651	0.0024785	221.42033
Theta	0.00045734	40.91939	0.0009391	84.17509
EnsE	0.00078657	70.26621	0.001340694	120.081508
EnsT	0.00025961	23.17451	0.00080099	71.71362
EnsV	0.00021311	21.92421	0.00079817	70.9131

. From Table 4, it is concluded that the EnsV produced the best forecasting results compared to all nine forecasting models within the proposed time series ensemble forecasting approach in all four most affected countries and the entire world case. For instance, the average accuracy errors for these locations are the following: Brazil (MAPE = 0.0000111, MAE = 0.1681917, RMSLE = 0.0000992, RMSE = 1.1861); France (MAPE = 0.00000019, MAE = 0.00000199, RMSLE = 0.00000191, RMSE = 0.00000553); Spain (MAPE = 0.00003314, MAE = 0.2417941, RMSLE = 0.00019113, RMSE = 1.498126); the USA (MAPE = 0.00010156, MAE = 2.996107, RMSLE = 0.00039027, RMSE = 11.99131); and the entire world (MAPE = 0.00021311, MAE = 0.00079817, RMSLE = 21.92421, RMSE = 70.9131). However, the EnsT model shows the second-best forecasting results among all nine forecasting models in all four most affected countries and the entire world, while the third-best forecasting accuracy average error results are given in the following manner: Brazil (the Theta model; MAPE = 0.0000156, MAE = 0.1711713, RMSLE = 0.0001092, RMSE = 1.196843); France (the ARMA model; MAPE = 0.00000025, MAE = 0.00000309, RMSLE = 0.00000216, RMSE = 0.00000649); Spain (the ESM model; MPAE = 0.00004015, MAE = 0.3040281, RMSLE = 0.00020946, RMSE = 1.586085); and the entire world case (the Theta model; MAPE = 0.00010858, MAE = 3.306309, RMSLE = 0.00042027, RMSE = 12.79745). Therefore, it is seen that within all nine forecasting models, the proposed ensemble models (the EnsT and the EnsV models) generally perform better than single models; however, within the single models, different countries have different single best models, as mentioned previously. Note that the best model is an EnsV or equivalent model for all four countries most affected by Mpox and the world. Also, using the proposed ensemble learning leads to a marked reduction in extreme errors (see Table 1). The proposed ensemble learning approach, thus, proves to be particularly effective in forecasting new cumulative confirmed cases of Mpox diseases.

Table 5. The DM test outcomes (p values) for all considered models.

Brazil
Model	AR	ARIMA	ESM	NPAR	Theta	EnsE	EnsT	EnsV
AR	0	0.9038	0.86576	0.90261	0.11822	0.89295	0.1206	0.02124
ARIMA	0.0962	0	0.095	0.09497	0.09634	0.09441	0.09635	0.04636
ESM	0.13424	0.905	0	0.90497	0.13173	0.90073	0.13206	0.03214
NPAR	0.09739	0.90503	0.09503	0	0.09765	0.09371	0.09769	0.0377
Theta	0.88178	0.90366	0.86827	0.90235	0	0.89248	0.19405	0.08491
EnsE	0.10705	0.90559	0.09927	0.90629	0.10752	0	0.10764	0.0767
EnsT	0.8794	0.90365	0.86794	0.90231	0.80595	0.89236	0	0.16451
EnsV	0.87876	0.90364	0.86786	0.9023	0.81509	0.89233	0.83549	0
France
Model	AR	ARIMA	ESM	NPAR	Theta	EnsE	EnsT	EnsV
AR	0	0.1528	0.89355	0.90909	0.8088	0.90891	0.16157	0.05157
ARIMA	0.8472	0	0.89355	0.90909	0.80892	0.90891	0.16814	0.05214
ESM	0.10645	0.10645	0	0.9091	0.1059	0.90906	0.10645	0.04645
NPAR	0.09091	0.09091	0.0909	0	0.09091	0.0909	0.09091	0.02091
Theta	0.1912	0.19108	0.8941	0.90909	0	0.90891	0.19098	0.01098
EnsE	0.09109	0.09109	0.09094	0.9091	0.09109	0	0.09109	0.0109
EnsT	0.83843	0.83186	0.89355	0.90909	0.80902	0.90891	0	0.10876
EnsV	0.83843	0.83186	0.89355	0.90909	0.80902	0.90891	0.89124	0
Spain
Model	AR	ARIMA	ESM	NPAR	Theta	EnsE	EnsT	EnsV
AR	0	0.31686	0.16252	0.86438	0.17723	0.21356	0.16323	0.05276
ARIMA	0.68314	0	0.1435	0.85099	0.15514	0.09668	0.14585	0.04703
ESM	0.83748	0.8565	0	0.85315	0.89717	0.8492	0.17161	0.04404
NPAR	0.13562	0.14901	0.14685	0	0.15109	0.14476	0.14771	0.04814
Theta	0.82277	0.84486	0.10283	0.84891	0	0.83356	0.12132	0.03136
EnsE	0.78644	0.90332	0.1508	0.85524	0.16644	0	0.15276	0.0332
EnsT	0.83677	0.85415	0.82839	0.85229	0.87868	0.84724	0	0.15806
EnsV	0.83724	0.85297	0.83596	0.85186	0.86864	0.84668	0.84194	0
USA
Model	AR	ARIMA	ESM	NPAR	Theta	EnsE	EnsT	EnsV
AR	0	0.87614	0.90392	0.88212	0.0928	0.88923	0.09259	0.0135
ARIMA	0.12386	0	0.89914	0.87477	0.10621	0.85232	0.09628	0.02522
ESM	0.09608	0.10086	0	0.82032	0.09496	0.09167	0.09569	0.03581
NPAR	0.11788	0.12523	0.17968	0	0.11499	0.12034	0.11566	0.04574
Theta	0.9072	0.89379	0.90504	0.88501	0	0.89675	0.17506	0.04038
EnsE	0.11077	0.14768	0.90833	0.87966	0.10325	0	0.10556	0.04586
EnsT	0.90741	0.90372	0.90431	0.88434	0.82494	0.89444	0	0.14791
EnsV	0.9065	0.90478	0.90419	0.88426	0.82962	0.89414	0.85209	0
World
Model	AR	ARIMA	ESM	NPAR	Theta	EnsE	EnsT	EnsV
AR	0	0.87949	0.0909	0.90117	0.88117	0.88653	0.09156	0.0228
ARIMA	0.12051	0	0.11744	0.90647	0.12065	0.13134	0.11756	0.01748
ESM	0.9091	0.88256	0	0.90144	0.89973	0.89038	0.14314	0.02083
NPAR	0.09883	0.09353	0.09856	0	0.09849	0.09662	0.09861	0.04863
Theta	0.11883	0.87935	0.10027	0.90151	0	0.88731	0.10136	0.00168
EnsE	0.11347	0.86866	0.10962	0.90338	0.11269	0	0.10985	0.00983
EnsT	0.90844	0.88244	0.85686	0.90139	0.89864	0.89015	0	0.08811
EnsV	0.90772	0.88252	0.87917	0.90137	0.89832	0.89017	0.89189	0

gives the p-values for the hypothesis of equal forecast accuracy according to the Diebold and Mariano (DM) test. The DM test has been applied to the series obtained by joining the 50 one-day-ahead forecast errors for each country and each pair of forecasts. Each element of the table is the p-value of a hypothesis system, assuming no difference in the accuracy of the forecasters in the row or column compared to the alternative that the model in the row is more accurate than the model in the queue. Focusing on the EnsV model, in all considered countries and the entire world case, it is statistically significant in terms of accuracy average errors (MAPE, MAE, RMSLE, and RMSE; see Table 4) and statistically not different in terms of the DM test (see Table 5). On the other hand, if we restrict ourselves to single models for all considered countries and the entire world, the best model varies from country to country. Therefore, to conclude this section, from the accuracy average errors (MAPE, MAE, RMSLE, and RMSE) and an equal forecast statistical test (the DM test), we can conclude that the proposed time series ensemble learning forecasting approach is highly efficient and accurate for one day ahead of confirmed cumulative new cases of Mpox for the four most affected countries as well as for the entire world case. In addition, within the proposed time series ensemble learning approach, the proposed EnsV model produces more precise forecasts when compared with the alternative ensemble models and single time series models.

4. Discussion

Once the best models were assessed through average accuracy errors (MAPE, MAE, RMSLE, and RMSE) and an equal forecast statistical test (the DM test), this work proceeded to future forecasting with the superior model (the EnsV). The current work used the ENMV for the confirmed cases of Mpox and forecast from 1 June to 28 June 2023 (four weeks) for the cumulative confirmed cases. The predicted and actual values of the Mpox cumulative confirmed cases are tabulated in Table 5. As seen from this table, the cumulative confirmed cases gradually increased throughout the forecasted span in the case of Brazil. However, in France’s case, only the first two days increased in the cumulative confirmed cases and then became constant, which means there was no evidence of the spread of Mpox within 26 days. In the case of Spain, the same as in the case of France, the first two days increased in the cumulative confirmed cases and then were constant, which means no evidence of the spread of Mpox within 26 days. On the other hand, in the USA case, the cumulative combined cases gradually increased from 30,156 to 30,228. In the same way, in the entire world case, the Mpox increased in confirmed cumulative cases from 87,320 to 87,748. Thus, it is concluded that from this analysis, the spread of Mpox in Brazil, the US, and the entire world has been an increasing trend, while on the other hand, from France and Spain’s points of view, there is no evidence of an increase in the virus.

Finally, to demonstrate the superiority of the proposed final best (EnsV) model forecasting ability, we compared the cumulative infected cases of Mpox to the predicted cases by the suggested best (EnsV) model. To achieve this, we computed the percentage forecast error (PFE), defined as PEF = (|forecasted value - actual value|/|real value|)×100. The PFE values are presented in the final column of

Table 6. Monkeypox virus dataset: the forecasted and actual daily cumulative confirmed cases of the Mpox virus using the best proposed model over four weeks.

Area	Brazil			France			Spain			USA			World
Date	Actual	Forecasted	PFE	Actual	Forecasted	PFE	Actual	Forecasted	PFE	Actual	Forecasted	PFE	Actual	Forecasted	PFE
1 May 2023	10,915	10,918	0.02290	4144	4145	0.02413	7549	7550	0.01325	30,154	30,156	0.00663	87,305	87,320	0.01718
2 May 2023	10,915	10,918	0.02749	4146	4146	0.00000	7551	7552	0.01324	30,154	30,157	0.00995	87,367	87,275	0.10530
3 May 2023	10,920	10,922	0.01832	4146	4147	0.02412	7551	7554	0.03973	30,154	30,158	0.01327	87,373	87,296	0.08813
4 May 2023	10,920	10,924	0.03663	4146	4148	0.04824	7551	7554	0.03973	30,154	30,158	0.01327	87,425	87,419	0.00686
5 May 2023	10,920	10,924	0.03663	4146	4149	0.07236	7551	7554	0.03973	30,154	30,158	0.01327	87,425	87,428	0.00343
6 May 2023	10,920	10,924	0.03663	4146	4149	0.07236	7551	7554	0.03973	30,154	30,158	0.01327	87,431	87,439	0.00915
7 May 2023	10,920	10,924	0.03663	4146	4149	0.07236	7551	7554	0.03973	30,154	30,158	0.01327	87,431	87,448	0.01944
8 May 2023	10,920	10,925	0.04579	4146	4149	0.07236	7551	7554	0.03973	30,154	30,158	0.01327	87,438	87,452	0.01601
9 May 2023	10,920	10,925	0.04579	4146	4149	0.07236	7551	7554	0.03973	30,188	30,160	0.09275	87,509	87,472	0.04228
10 May 2023	10,929	10,930	0.00915	4146	4149	0.07236	7551	7554	0.03973	30,188	30,169	0.06294	87,510	87,489	0.02400
11 May 2023	10,929	10,930	0.00915	4146	4149	0.07236	7551	7554	0.03973	30,188	30,176	0.03975	87,556	87,524	0.03655
12 May 2023	10,929	10,930	0.00915	4146	4149	0.07236	7551	7554	0.03973	30,188	30,181	0.02319	87,557	87,550	0.00799
13 May 2023	10,929	10,931	0.01830	4146	4149	0.07236	7551	7554	0.03973	30,188	30,189	0.00331	87,571	87,559	0.01370
14 May 2023	10,929	10,931	0.01830	4146	4149	0.07236	7551	7554	0.03973	30,188	31,092	2.99457	87,576	87,568	0.00913
15 May 2023	10,929	10,931	0.01830	4146	4149	0.07236	7551	7554	0.03973	30,188	30,194	0.01988	87,576	87,579	0.00343
16 May 2023	10,929	10,932	0.02745	4146	4149	0.07236	7551	7554	0.03973	30,194	30,196	0.00662	87,615	87,599	0.01826
17 May 2023	10,941	10,938	0.02742	4146	4149	0.07236	7551	7554	0.03973	30,194	30,200	0.01987	87,615	87,612	0.00342
18 May 2023	10,941	10,938	0.02742	4146	4149	0.07236	7551	7554	0.03973	30,194	30,204	0.03312	87,637	87,622	0.01712
19 May 2023	10,941	10,942	0.00914	4146	4149	0.07236	7551	7554	0.03973	30,194	30,206	0.03974	87,642	87,639	0.00342
20 May 2023	10,941	10,942	0.00914	4146	4149	0.07236	7551	7554	0.03973	30,194	30,208	0.04637	87,642	87,650	0.00913
21 May 2023	10,941	10,943	0.01828	4146	4149	0.07236	7551	7554	0.03973	30,194	30,208	0.04637	87,642	87,661	0.02168
22 May 2023	10,941	10,944	0.02742	4146	4149	0.07236	7551	7554	0.03973	30,194	30,210	0.05299	87,667	87,672	0.00570
23 May 2023	10,941	10,945	0.03656	4146	4149	0.07236	7551	7554	0.03973	30,225	30,215	0.03309	87,710	87,689	0.02394
24 May 2023	10,941	10,945	0.03656	4146	4149	0.07236	7551	7554	0.03973	30,225	30,219	0.01985	87,711	87,704	0.00798
25 May 2023	10,941	10,945	0.03656	4146	4149	0.07236	7551	7554	0.03973	30,225	30,213	0.03970	87,733	87,725	0.00912
26 May 2023	10,941	10,945	0.03656	4146	4149	0.07236	7551	7554	0.03973	30,225	30,218	0.02316	87,733	87,739	0.00684
27 May 2023	10,941	10,945	0.03656	4146	4149	0.07236	7551	7554	0.03973	30,225	30,223	0.00662	87,733	87,741	0.00912
28 May 2023	10,941	10,945	0.03656	4146	4149	0.07236	7551	7554	0.03973	30,225	30,228	0.00993	87,733	87,748	0.01710

. This column demonstrates that the anticipated values were reasonably close to the actual values regarding low PFE. As a result, our findings provide policy-makers with useful information for guiding future resource allocation and informing mitigation actions. Furthermore, the forecasting exercise will aid in understanding the spread and risk, which may be used to avoid future spread and provide prompt and effective treatment.

5. Conclusions

This work mainly aimed to forecast the short-term transmission rate of the Mpox infection disease in the most infected countries, such as the USA, Brazil, France, Spain, and the world. To this end, this work proposes a unique time series ensemble approach to analyze and predict the spread of Mpox in the top four countries with high infection rates. This approach involved processing the first cumulative confirmed case time series to address variance stabilization, normalization, stationarity, and a nonlinear secular trend component. After that, five single-time series models and three of their proposed ensemble models were used to forecast the clean, confirmed-case time series. The accuracy of the models is evaluated using average accuracy errors (MAE, MAPE, RMSE, and RMSLE) and an equal forecasting accuracy statistical test (the DM test). Based on the results, it is found that the proposed time ensemble forecasting approach is an efficient and accurate way to forecast the cumulative confirmed cases for the top four countries on the globe and the entire world. In addition, using the best ensemble model, a forecast is made for the next 28 days (four weeks), which will help understand the spread of the disease and the associated risks. This information can prevent further spread and enable timely and effective treatment. Furthermore, the developed novel time series ensemble approach can be used to forecast other diseases in the future.

The study only used a cumulative Mpox dataset from the four most affected countries and the whole world. Still, it could be expanded to include other variables, such as the number of new daily cases and daily and cumulative death counts. This would help evaluate the effectiveness of the proposed time series ensemble forecasting approach. Furthermore, it could forecast short-term daily and cumulative COVID-19 confirmed cases, death counts, and recovered cases. However, the proposed forecasting methods only employed single-time series models. In the future, machine learning models such as random forest, support vector regression, Xboost gradient algorithm, etc., will be integrated to enhance the forecasting technique.