1. Introduction
The notion of the mean first-passage time (MFPT) is crucial in understanding the dynamics of cell migration in various biological phenomena including embryonic development, immune responses, and cancer metastasis. In very simple terms, we pose the following: how long does it take for a cell to reach the boundary of the domain Ω in which the former moves? The media in which cells migrate support many and very complex biological processes difficult to describe quantitatively, which do influence the dynamics of a generic cell. Subject to such indeterminations, the possibilities to describe the motion of the cell in a deterministic way (say, through deterministic equations) confront enormous difficulties. Then, it appears to be preferable to invoke probabilistic (say, stochastic) approaches. The latter include parameters amounting to average the effects of many complex processes. So the above question is recast as follows: what is the mean (or average) time until the cell hits the boundary from a given starting point? This is called the MFPT.
So, more specifically, the MFPT represents the average time it takes for a migrating cell to reach a specific location or target within its environment for the first time so that is used for quantifying the efficiency and characteristics of cell mobility in heterogeneous and complex biological landscapes. In the last decades, the MFPT has been used to model the migratory behavior of cells, particularly the migration of cancer cells from the initial tumor environment into the surrounding tissues and the blood or lymphatic vessels (tumor-induced angiogenesis and lymph angiogenesis); see [
1,
2,
3,
4,
5,
6].
In theoretical and computational models, the calculation of MFPT is often approached through random walk theory, stochastic differential equations, or agent-based models, each incorporating various aspects of cell behavior and environmental interactions. Studies of the MFPT from different standpoints can be seen in [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18].
The starting point of our approach will be based upon diffusion equations. The diffusion equation is a fundamental partial differential equation used to describe the distribution of cells over time as they move randomly through a medium. Particularly, it models how cells spread out from regions of high concentration to regions of low concentration due to random motility. We may consider both isotropic (no drift) and biased diffusions (including drift or advection). The isotropic diffusion equation for the concentration (probability density) of a cell at a point
x in the domain at time
, starting initially at the point
y in Ω, is
where the positive constant
D is the diffusion coefficient of the randomly moving cell within a specific tissue at rest, and
is the Laplacian in two or three spatial dimensions with respect to variable
x. Most of this feature paper will deal with the MFPT implied by the above diffusion equation in three-dimensional domains.
In another situation, one may also consider that the cell is subject to both diffusive and drift motions. For this biased diffusion, the medium in which the cell moves has a global drift motion with small velocity
. Thus, the probability density (cell concentration) of a cell being at
x at time
t, being originated at
y inside the domain at time
, is supposed to be the solution
of the advection–diffusion equation
where
is the gradient with respect to variable
x. The advection–diffusion equation describes the spatiotemporal behavior of cells undergoing both diffusion (random motion) and advection (directed motion) due to external factors within the corresponding domain. The dimensionless Péclet number
(where
L is a length scale typical of the domain in which the cell moves) characterizes the relative importance of diffusion and convection in biased diffusion. Typically,
can vary between, say, 0 and 5. Therefore, the advection–diffusion equation is more comprehensive than the pure diffusion equation, as it accounts for both random motility and directed movement due to external forces or signals. By incorporating appropriate boundary conditions, the advection–diffusion equation can be tailored to specific experimental or biological scenarios, allowing for more precise and relevant modeling of cell migration dynamics.
According to the physical nature of the domain boundaries, we may categorize three types: absorbing, reflective and transmissible. When we consider an absorbing boundary, we assume that the cell will reach it and leave the domain without returning. Under this assumption, the boundary effectively absorbs the cell, that is, the cell concentration will be zero at the boundary. This behavior is usually expressed by a homogeneous Dirichlet boundary condition. On the other hand, a reflective boundary prevents cells from leaving the domain by reflecting them back into the interior. Reflective boundaries are used to model scenarios where cells are confined within a certain region and cannot escape, such as within a tissue or a bounded experimental apparatus. Thus, a cell that moves towards a reflective boundary will bounce back into the domain, which is represented by setting the normal derivative of the cell concentration to zero at the boundary. The reflective boundary behavior is described by the so-called Neumann boundary condition. The transmissible boundary allows cells to pass through it in a regulated or controlled manner, which is crucial when modeling the movement of cells in environments where the domain boundaries are not entirely impermeable but instead permit some degree of cell migration across them. Unlike reflective or absorbing boundaries, the transmissible boundary is partially permeable, which means that some fraction of the migrating cells can cross the boundary, while others might be reflected back into the domain. In this way, at a transmissible boundary, the flux of cells (or the rate at which cells move across the boundary) is continuous. The so-called Robin boundary condition describes the transmissible boundary behavior and ensures that the number of cells entering and/or leaving the domain through the boundary is correctly accounted for in the diffusion equation. Transmissible boundaries are relevant in biological contexts where cells can migrate through semi-permeable membranes, pores, or channels, and might encounter boundaries that allow selective passage.
In this feature article, we overview the characterization of the MFPT of moving cells, starting from the inhomogeneous Poisson-type adjoint diffusion equation (associated to the diffusion equation) inside two- and three-dimensional domains bounded by closed curves or surfaces, respectively, with very disparate geometries, possibly driven by different factors, and subject to various boundary conditions of the Dirichlet, Neumann, Robin, or mixed types. Our approach to the adjoint diffusion equation associated to the MFPT, subject to those boundary conditions, will exploit and extend an existing mathematical theory (named potential theory), historically associated to electrostatics; see [
19,
20,
21]. We shall reduce the determination of that adjoint diffusion equation and of the MFPT to solving inhomogeneous linear integral equations for certain density functions on the boundary. For certain shapes of the boundary, the linear integral equations can be solved compactly, and the resulting MFPT agrees with those obtained though other procedures. For more general shapes of the boundary, not differing much from the solvable geometries, the integral equations provide the basis for studies and approximate solutions for the MFPT function. In particular, the method also allows to deal with mixed boundary conditions, which constitute a genuine long-standing and open problem. The approach will be presented in an outline, omitting computations.
The main novelty of this paper is the presentation and discussion of several plots representing the MFPT behavior of cells moving inside domains with different boundary surfaces and subject to different boundary conditions. Let us describe the novel contents of each section.
Section 2 will deal with three-dimensional domains subject to the Dirichlet and Neumann boundary conditions, and without advection, so that, in general, the MFPT function will be characterized through an inhomogeneous linear integral equation.
Section 2 will focus on explicitly solvable domains, too. Specifically, in
Section 2.1, a sphere is assumed to have a absorbing boundary so that a cell moves from inside the sphere into its boundary and, at some moment, will leave the sphere. In this case, the MFPT function is plotted in subfigure b of the first figure. In
Section 2.2, a spherical annulus is analyzed in three different situations: with inner reflective and outer absorbing boundary conditions in subfigure b of the second figure; with inner absorbing and outer reflective boundary conditions in subfigure a of the third figure; and with both inner and outer absorbing boundary conditions in subfigure b of the third figure. In
Section 2.3, the non-explicitly solvable case of one closed boundary surface with mixed Dirichlet and Neumann boundary conditions on complementary parts of the boundary surface is treated. This section summarizes developments in [
22]. Notice that all figures presented in this manuscript are novel and bring some light to understand the MFPT function behavior.
Section 3 will outline the characterization of the MFPT function in an annulus, like subfigure a of the fourth figure, with advection, firstly subject to Dirichlet and Robin boundary conditions (see subfigure b of the fourth figure) and secondly subject to a particular case of Dirichlet and Neumann boundary conditions, see the sixth figure.
Section 4 will focus on the pure diffusion equation, without advection, on an annular cylinder, like the seventh figure, subject also to Dirichlet and Robin boundary conditions, and will present also the non-explicitly solvable characterization of the MFPT function in a slightly distorted annular cylinder.
Section 3 and
Section 4 summarize some results in [
23]. Finally, conclusions and discussion are mentioned in the last section, as well as future research directions.
2. The Diffusion Equation with Dirichlet, Neumann and Mixed Boundary Conditions: Application to Spherical Surfaces
In this section, we start by considering a three-dimensional simply connected domain Ω bounded by a smooth closed surface
S. Later on, the domain Ω will be well defined according to its boundary conditions. Let
x and
y be any points in Ω. We define the probability density (or concentration) of a migrating cell to be at
x at time
, being originated at
at time
as the solution
of the diffusion equation
as discussed in the Introduction. Moreover, we assume the initial condition, for
and any
x and
y in Ω,
where
is the Dirac delta function, and the absorption condition
where
stands for the total probability at time
t for the migrating cell, which was in
y at the initial time. In this way, the mean first-passage time (MFPT) function
T in
y is defined as the time average of such a probability by means of
Now, we may consider different boundary conditions on the surface of our domain Ω. Namely, if we suppose a Dirichlet boundary condition of the type
for any
on the surface
S, then the MFPT function
T defined in (
4) can be shown to be a solution of the inhomogeneous adjoint Poisson equation
in Ω, subject to the Dirichlet boundary condition
for any
on the boundary
S. One may also consider the fulfillment, at the end of a given computation, of the finiteness condition
in Ω.
2.1. One Surface Subject to a Dirichlet Boundary Condition
For a general three-dimensional simply connected domain Ω bounded by the surface
S, the characterization of the MFPT function
T, assuming the Dirichlet boundary condition (
7) on the boundary
S, is obtained as the sum of a particular solution
of the inhomogeneous adjoint Poisson Equation (
6), defined in the whole
, plus a general solution of the homogeneous Poisson equation
Specifically, the MFPT function
T is given by
for every
, where the functions
and
are given by
and the density
at
z on
S is shown to fulfill
in [
22] (Theorem 3.1). The proof used the results in [
19,
24].
As a particularly illustrative example, let us consider the special case where our domain Ω is a sphere of radius
R, subject to a Dirichlet boundary condition, inside a blood vessel. The cell migrates from a point
y inside the sphere Ω towards its surface
S and leaves it. Then, the exact MFPT function, denoted by
in this example, is shown to be
by solving directly the inhomogeneous Poisson Equation (
6). On the other hand, by solving the integral Equation (
9) for
, with
z on
S, one finds that
which leads consistently to
If we take into account the real scenario of a motionless (negligible drift motion) sphere inside a blood vessel, we may assume that the radius
R = 10 μm and the cell diffusion coefficient
D = 6.6 × 10
−4 μm
2 s
−1, according to the data in [
25,
26].
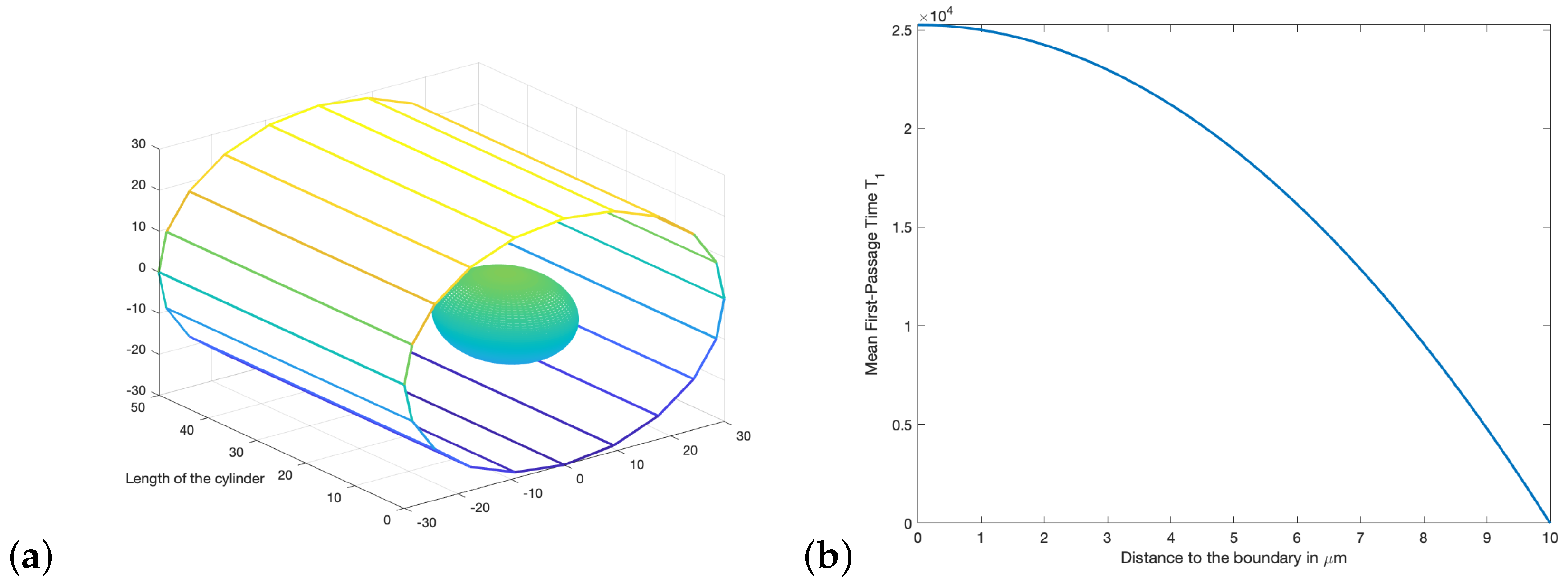
Figure 1a represents our spherical domain Ω of radius 10 μm inside a cylinder of radius 30 μm.
Figure 1b represents the MFPT of a cell moving from the center of the sphere towards its absorbing boundary surface so that, at some moment, it will leave the sphere into the cylinder.
2.2. Two Disjoint Surfaces, with Dirichlet and Neumann Boundary Conditions
Now, we focus on the case when the three-dimensional domain Ω (non-simply connected) is bounded by two simply connected surfaces
and
so that the surface
is entirely contained inside the volume enclosed by
, and the intersection of both surfaces is an empty set. The surface
is assumed to verify a Dirichlet boundary condition so that the cell will be absorbed and disappear through
, and the surface
is subject to a Neumann boundary condition. In this way, the probability density
of a migrating cell being at
x at time
t, starting initially in
y, has to satisfy both of the following conditions: for any
on the surface
, it holds the absorbing condition
and for any
on the surface
, it holds the Neumann condition
According to [
22] (Theorem 4.1), it follows that the MFPT function
is characterized by
for every
, where again
,
and
The densities
and
defined in
and
, respectively, fulfill the system
Notice that the representation of the densities
and
in (
12) and (
13), respectively, constitutes a generalization of the previous density
in (
9) (except for an overall change in the sign of
, for convenience).
The method based upon the inhomogeneous linear integral equations has been also applied to the special situation where the domain Ω is bounded by two concentric spherical surfaces and , with radii and , respectively, where , and is subject to different boundaries conditions. Firstly, the outer spherical surface is assumed to satisfy a Dirichlet boundary condition, and the inner spherical surface is subject to a Neumann boundary condition. Secondly, we commute the boundary conditions, i.e., suppose that the outer surface satisfies a Neumann boundary condition while the inner surface is absorbing. Finally, both outer and inner boundary surfaces and , respectively, are supposed to be absorbing.
So, in the special situation where
and
are two concentric spherical surfaces such that the surface
is subject to a Dirichlet boundary condition, while
is subject to a Neumann boundary condition, cells are inside the domain Ω and will disappear through the outer spherical surface
while they are reflected by the inner one
. By solving the coupled integral Equations (
12) and (
13) for the densities
and
, the exact MFPT function, denoted by
, is shown to be given, using the radial coordinate
r, by
for every
. One has
The MFPT function
in (
14) can be shown to coincide consistently with the direct solution of the inhomogeneous adjoint Poisson Equation (
6).
In the case where we exchange the boundary conditions on the surfaces
and
, namely, when we assume that the outer boundary satisfies a Neumann boundary condition and the inner surface
satisfies a Dirichlet boundary condition, one finds that the corresponding MFPT function, denoted by
, is given by
for every
In this situation, cells are reflected from the outer boundary surface towards the inner one and, at the end, will leave the domain through the inner boundary surface.
Finally, when both surfaces
and
are subject to Dirichlet boundary conditions, i.e., cells are absorbed by both boundary surfaces, then the MFPT function, denoted by
in this case, is shown to be
for every
All functions
and
are shown to coincide with the direct solutions of the corresponding inhomogeneous adjoint Poisson equation.
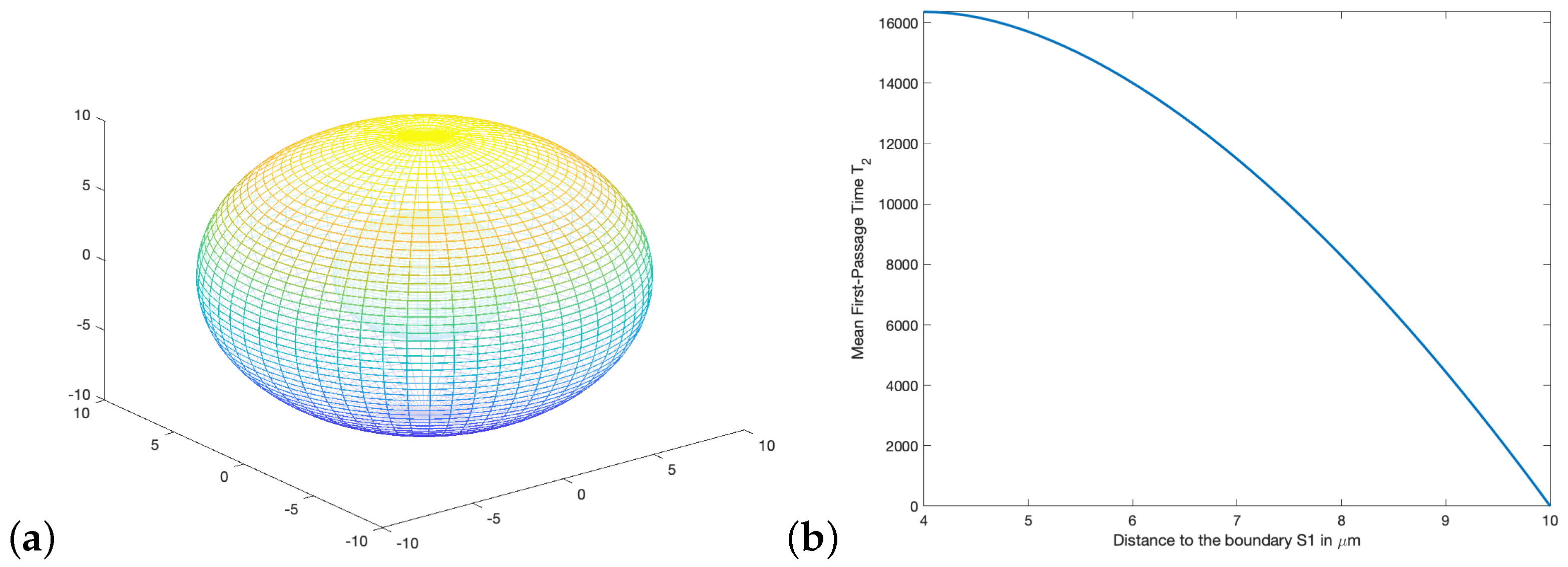
In order to better understand the behavior of the MFPT function inside a spherical annulus subject to Dirichlet and/or Neumann boundary conditions, let us focus on a particular example. Consider the spherical annulus Ω given in
Figure 2a, where the outer sphere has radius
= 10 μm and the inner sphere has radius
= 4 μm. The cell is moving inside Ω, and its behavior is determined by the boundary conditions we have assumed on Ω. Precisely, when the outer sphere is absorbing and the inner sphere is reflective, the cell moves from the interior of the spherical annulus into the outer sphere and, at some moment, will leave the domain through it. In this situation,
Figure 2b plots the MFPT function
defined in (
14).
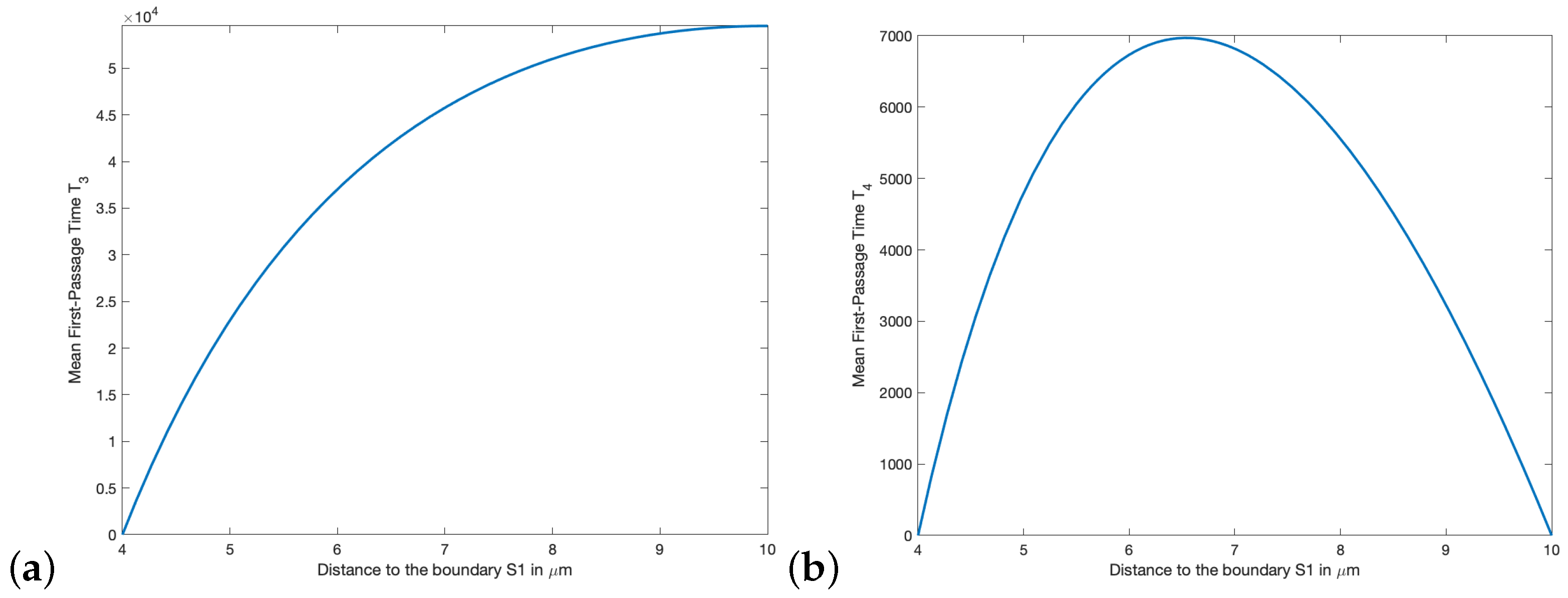
On the other hand, if the outer sphere is reflective and the inner sphere is absorbing, then the cell moves from the outer boundary into the inner one and, at some point, will leave the spherical annulus through the inner sphere. In this case,
Figure 3a below plots the MFPT function
defined in (
15). Comparing both scenarios plotted in
Figure 2b above and
Figure 3a below, the first one performs better. In the situation where both the outer and inner spheres are absorbing,
Figure 3b below plots the MFPT function
given in (
16). Clearly, the scenario where both surfaces satisfy a Dirichlet boundary condition has better performance.
2.3. One Surface Subject to Mixed Dirichlet–Neumann Condition
In this subsection, we consider a three-dimensional simply connected domain Ω bounded by a smooth closed surface
S, under the following assumptions.
S contains entirely a closed simply connected curve
C that divides
S into two disjoint adjacent open surfaces
and
, i.e.,
and
. Here, we assume that
is subject to the Dirichlet boundary condition and
to the Neumann one. Therefore, according to [
22] (Theorem 5.1), the corresponding MFPT function
T is characterized by
for every
, where, again,
, and the densities
and
are given in
and
, respectively, by
and
This case does not seem to be exactly solvable, so no compact exact solution seems to exist, in general. The case where
S is a spherical surface has been investigated,
being a small surface compared to
.The above coupled linear integral Equations (
18) and (
19) have been employed to generate, by iterations, an approximate solution to the first order in the area of
divided by that of
, regarded as a small parameter. We choose
to be the small open surface, and write each point
on
in spherical coordinates so that
with
and
, with small and fixed
. We shall omit some direct computations involved. Taking into account
, we may approximate the MFPT function by
where
is a small correction given by
with constants
defined by
where
stands for the standard Legendre polynomial of order
l.
3. The Advection–Diffusion Equation with Dirichlet and Robin Boundary Conditions in an Annulus
Here, let us assume that the domain Ω is an annulus enclosed by two concentric circles
and
, with radii
and
, respectively, so that
. Suppose that a cell moves, subject to advection, inside the annulus towards the absorbing outer boundary
and the transmissible inner boundary
. The probability density (cell concentration) of a cell being at
x at time
, being originated at
y inside the annulus at time
, is assumed to be the solution
of the advection–diffusion equation
mentioned in the Introduction, subject to the initial condition (
2) and the absorption condition (
3). Additionally, let us assume that the outer circle
satisfies the Dirichlet boundary condition (
5), while the inner circle
satisfies the Robin boundary condition of type
Let us suppose
, with
being the radial coordinate, so there is a radial drift on the cell directed towards the center. The MFPT function defined in (
4) solves the adjoint Poisson equation
in the annulus, subject to the Dirichlet boundary condition (
7) on the outer circle
, and the Robin boundary condition
on the inner circle
.
Solving the Poisson Equation (
23) in the annulus, it follows that the MFPT function, denoted by
, is given by
for every
, where
In order to better understand the behavior of the MFPT function
inside an annulus subject to Dirichlet and Robin boundary conditions, let us focus on a particular example of an annulus bounded by an outer circle of radius
= 10 μm and an inner circle of radius
= 4 μm, as in
Figure 4a. Again, we assume that the cell diffusion coefficient
D = 6.6 × 10
−4 μm
2 s
−1. The cell is moving inside Ω between the inner transmissible boundary, subject to Robin boundary condition (
24), and the outer absorbing boundary, subject to Dirichlet boundary condition (
7). Moreover, since we are in the advection–diffusion scenario, we assume that the medium in which the cell moves has a global drift motion with small velocity
. In this case,
Figure 4b plots the MFPT function
defined in (
25).
We may compare the MFPT behavior taking into account different velocities
. Precisely,
Figure 5 below represents the MFPT function
considering also
and
.
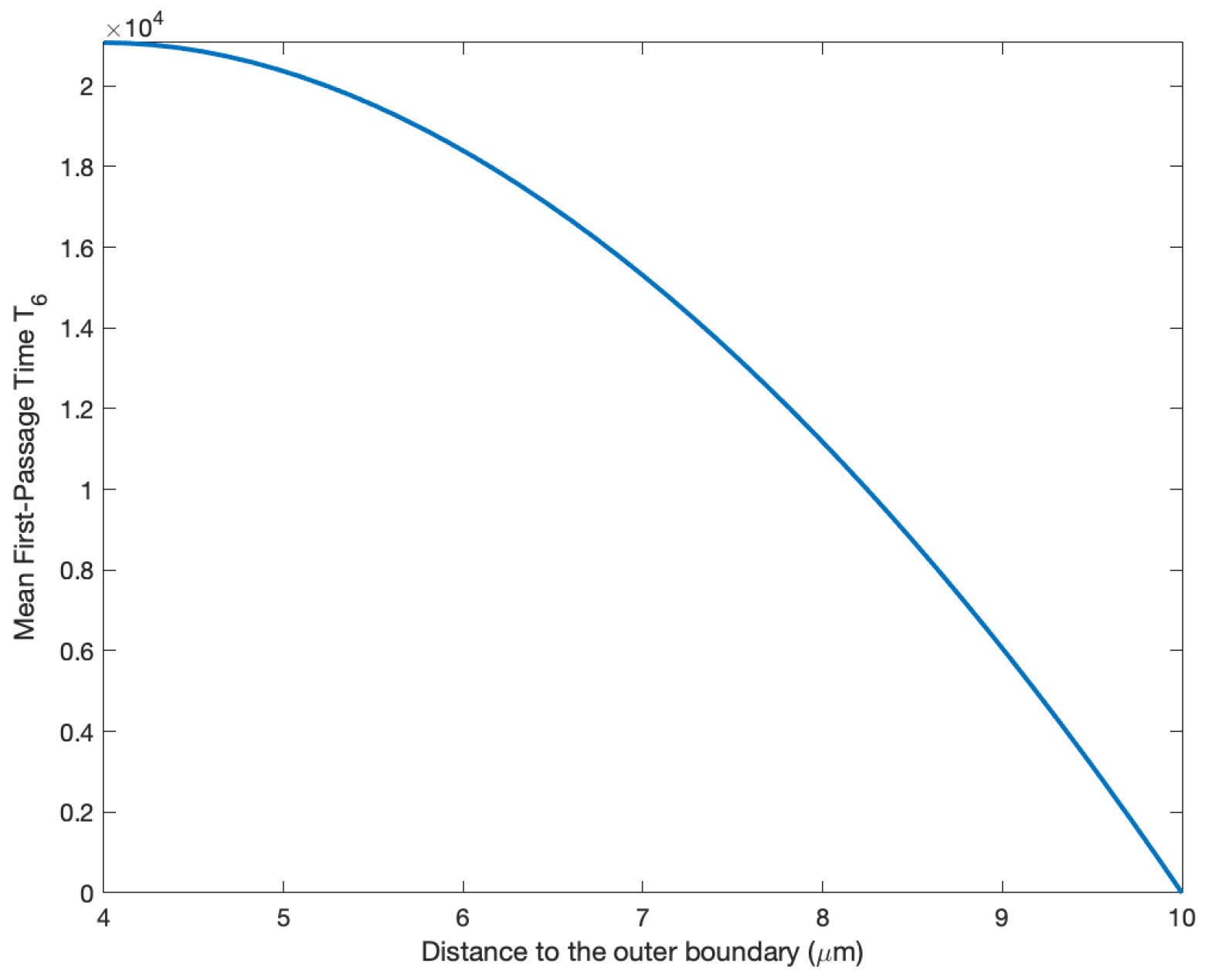
In the special case, when the inner transmissible boundary is replaced by a reflective one, then the MFPT behavior is again similar to previous cases in
Section 2 as shown in
Figure 6. Namely, when we replace the Robin boundary condition (
24) by the Neumann boundary condition
on the inner circle
, then the MFPT function, denoted by
, the solution of the Poisson problem (
23) is given by
for every
.
4. The Three-Dimensional Diffusion Equation with Dirichlet and Robin Boundary Conditions: Application to Perfect and Distorted Annular Cylinders
In this section, let us consider firstly an annular cylinder with length
h as shown in
Figure 7 below, bounded by an outer cylindrical surface with radius
and an inner one with radius
, which may be an extension to three dimensions of the previous annulus in
Figure 4a. Moreover, assume that the MFPT function defined in (
4) satisfies the Dirichlet boundary condition (
7) on the outer cylindrical surface as well as the following Robin boundary condition
for any
z on the inner boundary surface and on the two lids with real constants
and
b.
Thus, solving the adjoint Poisson Equation (
6), without advection, in the annular cylinder, applying well-known procedures based on the three-dimensional Green functions, it follows that the MFPT function, denoted by
, is represented, using cylindrical coordinates
, by
where
and
are defined through the standard regular and irregular Bessel functions of the
ith order,
and
, respectively,
. See [
27]. Constants
are determined by the Dirichlet boundary condition (
7) on the outer surface, and the Robin boundary condition (
28) on the inner one. For proof and details, see [
23] (Proposition 2). For general results regarding Green’s functions, see [
20].
Now, let us turn to a deformation of the annular cylinder considered previously, i.e., a domain bounded by small deformations of the perfect shaped cylindrical surfaces and without the two lids so that the new domain is actually bounded by two distorted cylindrical surfaces extended along the z-axes from
to
. Again, we assume the Dirichlet boundary condition (
7) on the outer boundary surface and the Robin boundary condition (
28) on the inner one and no advection.
In this way, according to [
23] (Theorem 2), the MFPT function solution of the adjoint Poisson problem (
23) subject to the mentioned Dirichlet and Robin boundary conditions is denoted by
and defined by expressing
as the sum of a particular solution
, given below, plus a solution of the homogeneous equation
inside the annular cylinder, expressed in turn as the sum of two cylindrical surface integrals, containing the standard three-dimensional Green function
solution of
in the whole space, i.e.,
and the densities
and
.
The function
is chosen as the solution of the advection-free adjoint diffusion equation inside the two-dimensional annulus
, with Dirichlet and Robin boundary conditions at
and
, respectively. Therefore,
for constants
The densities
and
are shown to solve the inhomogeneous system of linear integral equations
and
Notice that
and that the functions
and
employed in this section differ by a factor of
from those used in
Section 2. No compact solution seems to exist for the above coupled integral equations for
and
. On the other hand, as the infinite cylinder is slightly deformed, the above inhomogeneous linear integral equations provide the basis for approximate solutions.
5. Conclusions and Discussion
We have presented and discussed previous theoretical results, based upon the adjoint diffusion equation with various boundary conditions for the MFPT function, and the resulting inhomogeneous linear integral equation. We have taken into account different geometries of the domains as well as distinct boundary conditions, yielding (exactly in a few cases and approximately in more general cases) the MFPT function and its interpretation. One main conclusion is that the inhomogeneous linear integral equation associated to the adjoint diffusion equation provides a basis for approximate studies of the MFPT. New plots, figures, and analyses based on various results reported in this feature paper have been included for a better understanding.
Our study starts in
Section 2 with three-dimensional cases, with no advection. First, the basics of the approach yielding the adjoint diffusion equation associated to the MFPT are discussed. Then, for one closed surface, the adjoint diffusion equation is reduced to an inhomogeneous linear integral equation for a certain density function on the boundary, with the Dirichlet boundary condition, in
Section 2.1. For one spherical surface, the inhomogeneous linear integral equation is solved in
Section 2.1 as well. The solutions of the inhomogeneous linear integral equations corresponding to two concentric spherical surfaces with various boundary conditions (Dirichlet and Neumann) are discussed succinctly in
Section 2.2. For one closed boundary surface with Dirichlet and Neumann boundary conditions on complementary parts of it (i.e., mixed boundary conditions), which stands as a problem lacking a compact solution, the inhomogeneous linear integral equations for the solution of the adjoint diffusion equation are formulated and discussed succinctly in
Section 2.3. Several figures and plots are presented and discussed in
Section 2.
In two dimensions, including advection, the solution of the adjoint diffusion equation subject to Dirichlet and Robin boundary conditions is given in
Section 3. Moreover, the MFPT is plotted according to the assumed boundary conditions. Based upon the latter but restricted to vanishing advection, in three dimensions, the adjoint diffusion equation is solved inside a perfect annular cylinder as well as inside a slightly distorted infinite cylinder by using inhomogeneous linear integral equations.
Finally, in three dimensions without advection, the MFPT is treated in
Section 4, where the domain is a perfect or distorted annular cylinder subject to a Dirichlet boundary condition on the outer cylinder surface and a Robin boundary condition on the inner one.
In the framework of cell migration, an interesting scenario to have in mind in future research is to study the MFPT in a sphere traversed by a thin cylinder which models a blood vessel surrounded by cells that may move from the sphere to the thin cylinder inside it. It will be interesting to consider the case where the cylinder surface, inside the sphere, satisfies a transmissible or an absorbing boundary condition. A better understanding of the recipe (that is, the addition of the surface integrals) in a more general setting constitutes an open problem, so far. It would require further study and understanding, in connection with the framework in [
21]. A further open problem, among others, is the inclusion of advection (drift) in the diffusive migration of the cell.