Abstract
Sharing confidential information is a critical concern in today’s world. Secret sharing schemes facilitate the sharing of secrets in a way that ensures only authorized participants (shareholders) can access the secret using their allocated shares. Hierarchical secret sharing schemes (HSSSs) build upon Shamir’s scheme by organizing participants into different levels based on priority. Within HSSS, participants at each level can reconstruct the secret if a specified number, denoted as the threshold value (t), or more of them are present. Each level has a predetermined threshold value. If the number of participants falls below the threshold at any level, higher-level participants must be involved in reconstructing the secret at lower levels. Our paper proposes schemes that implement hierarchical access structures and enable the sharing of multiple secrets. Additionally, our proposed scheme includes share verification. We have analyzed potential attacks and demonstrated the scheme’s resistance against them. Through security analysis and comparison with existing schemes, we highlight the novelty and superiority of our proposed approach, contributing to advancements in secure information-sharing practices.
MSC:
94A62; 94A60; 94A17
1. Introduction
Information such as encryption keys, missile launch codes, and numbered bank accounts must be highly confidential. Exposure to such sensitive information could be dangerous. Secret sharing schemes provide an efficient way of storing such sensitive and vital information and prevent unauthorized access. Apart from core cryptography, researchers have been using secret-sharing concepts in various applications such as the cloud and IoT. Recently, Gutte and Paraser [1] have used secret sharing for visual cryptography and suggested a weed optimization algorithm for image sharing. Similarly, Wang et al. [2], and Ren et al. [3] have worked on low latency cloud-based indoor localization systems and secure, anonymous data aggregation schemes, respectively. Considerable work has been conducted on this topic in the last few years (cf. [4,5,6,7,8,9,10,11,12], where further references can be found).
Initially, some core concepts of algebra were used by authors to design secret-sharing schemes. Shamir [13] used polynomials, Blakley [14] used hyperplane geometry and Simmons [15] as well as Asmuth and Bloom [16] used Chinese remainder theorem. In secret sharing schemes, secret S is distributed among n shareholders in such a way that t shareholders or more than t shareholders can reconstruct the secret but less than t shareholders know nothing about the secret. Such a scheme is known as the -threshold scheme. Schemes given by [13,14,16] have several common drawbacks as follows:
- These are single secret sharing schemes.
- For every new secret, a new share has to be generated for every participant after the reconstruction of the previous secret
- Private channels are essential for the communication between dealers and participants and among the participants.
- These schemes are not capable of identifying the cheater.
To solve the first and the second problem, “multi secret sharing schemes” have been introduced [17,18,19]. Instead of having a single secret, multiple secrets are shared among the participants in a multi-secret sharing scheme. To include verification and cheater detection, a “Verifiable secret sharing scheme” was proposed in [20,21]. In [22,23], Harn et al. proposed the protected secret sharing scheme to avoid a separate communication channel while exchanging shares among different shareholders. The application of Shamir’s scheme is ideal for the condition where all participants (shareholders) play the same role and there is no distribution of shares based on priority or any unique properties. However, employees are categorized based on their work responsibilities in organizations such as multinational companies and educational institutions. Among several structures, the Hierarchical structure is trendy in which every participant has some weight according to his/her role. Shares are distributed or assigned according to their weight. Hierarchical secret sharing schemes are proposed in the literature [15,24,25,26,27].
In hierarchical secret sharing schemes, all the participants are divided into m disjoint sets called levels say . The ith level consists of participants with threshold. In the reconstruction of the secret, there may be two situations: In the first situation, the particular level has or more participants on the same level while in the other situation, the number of participants in level is less than . In the second situation, the involvement of the higher level participant is needed.
Let us assume that at a particular level, participants are less in number say , than the . So, remaining participants are needed from the upper level to reconstruct the secret. In this paper, the level is higher than the level .
In 2004, Yang et al. [28] proposed a unique multi-secret sharing scheme using a single polynomial, known as the YCH scheme. Low computation and fewer public values are required in the YCH scheme. In the YCH scheme, a single polynomial is used for multiple secrets instead of using separate polynomials for individual secrets. We have included a YCH scheme for each level in our work, making the scheme efficient. We have used two variable one-way functions for verifiability, which verify the dealer and other participants. The following summary highlights the key innovations and benefits of your proposed hierarchical secret-sharing scheme in a concise and structured manner
- Efficiency through YCH Scheme Integration: Our proposed hierarchical secret sharing scheme leverages the YCH scheme at each level, optimizing computational resources and reducing the number of public values required.
- Enhanced Security with Cheater Detection: We introduce mechanisms to swiftly identify both malicious dealers and dishonest participants, ensuring the integrity of the secret-sharing process.
- Dual Functionality of Participant Shares: Participants’ shares in our scheme serve dual purposes: facilitating secret reconstruction and enabling verification processes, enhancing overall scheme flexibility.
- Secure Communication Independent Verification: Utilizing two-variable one-way functions, our scheme eliminates the dependency on secure channels for share transmission, ensuring robustness against interception.
The remainder of the paper is structured as follows: Section 2, reviews relevant literature. Section 3, introduces preliminaries pertinent to our proposed scheme. Section 4, addresses identified problems and motivations. Our proposed scheme is detailed in Section 5. Section 6, covers the security and performance analysis of the scheme. Section 7, provides a comparison with existing schemes. Finally, Section 8, concludes with future research directions.
2. Related Work
The Shamir [13] and Blakley [14] threshold secret sharing schemes are two particular examples of hierarchical secret sharing (HSS) in which all participants have the same privileges. In order to improve the applicability of hierarchical secret sharing, many researchers have focused on specific families of access structures. Blundo et al. [29] have focused on graph-based access structure, Pardo et al. [30] explained the bipartite access structure and Tentu et al. [31] include multipartite access structure, compartmented access structure, and hierarchical access structure.
In 1979, the weighted threshold secret sharing mechanism was suggested by Shamir [13]. However, this approach is inefficient since it assigns multiple shares to each participant equal to its integral weight. Simmons [15] then proposed a multipartite access structure in 1988, defining the compartmented access structure and the hierarchical access structure. Following Simmons, Brickell [32] proposed a strategy for constructing an optimal secret-sharing scheme that takes into account multilevel and compartmented access arrangements. However, the approach is inefficient since nonsingular matrices require exponential operations. The multipartite access structure is defined as the split of all members of a group into subsets, with members of the same subset having the same rights. The compartmented access structure and the hierarchical access structure are two types of multipartite access structures. The conjunctive hierarchical access structure and the disjunctive hierarchical access structure belong to the hierarchical access structure family. In 2009, Lin et al. [33] incorporated some modifications into Shamir’s scheme [13] and explained the hierarchical secret sharing (HTSS) scheme with two types of variations. “Multilevel threshold secret sharing (MTSS), and compartmented threshold secret sharing (CTSS)”.
Verification of shares is also one of the major concerns in secret sharing schemes. In [20,21] authors have specifically explained the verification of shares in a secret sharing scheme. In 2015, Chanu et al. [34] used Two variable one-way functions to verify the correctness of the received share. Further, in 2017, Basit et al. [35] used Shamir’s scheme with the successive application of a one-way function and shifted and key technique to propose Multi-stage Multi-secret sharing for hierarchical Access Structure.
Apart from the above-mentioned papers, the Hierarchical secret sharing (HSSS) scheme is discussed in [22,33,34,35,36,37,38], but their schemes lack fairness. In 2018, Banerjee et al. [36] proposed Cheating detection and cheater Identification for hierarchical structure but lacks correctness. In 2021, Bisht and Deshmukh [39] proposed work on multi-level secret sharing but lacks fairness and perfectness. Similarly, Yuan et al. [38] used homogenous recurrence relation to propose a new efficient scheme that deals with the multi-secret hierarchical scheme.
This scheme has been proposed to overcome the shortcomings of the above-discussed schemes and incorporate the features in the following ways:
- It supports the hierarchical access structures as discussed in the first paragraph of the current section. It improves and enhances the applicability of the hierarchical access structure.
- It supports weighted threshold secret sharing as discussed in the second paragraph without any exponential operation and extra burden.
- It supports secret sharing with multi-stage, multi-level properties with verification of shares lacking in schemes discussed in the third and fourth paragraphs.
- In the last paragraph of this section, novel schemes are discussed. These schemes do not explain security features such as correctness and forward/backward secrecy.
The proposed schemes offer crucial security features like fairness and correctness, with significantly lower computational and storage costs. All the previously discussed related works have been summarized in Table 1, for the reader’s clarity and ease of observation.

Table 1.
Related Work Comparison.
3. Preliminaries/Foundations
This section describes some of the preliminaries required to design our scheme.
3.1. Polynomial Interpolation
The use of polynomials in designing secret-sharing protocols is one of the easiest and most popular methods [40,41,42]. The following two points are very common regarding polynomials:
- Polynomial can be utilized to plot a curve using the points that satisfy the same polynomial.
- We can determine polynomials of a fixed degree by knowing the points that satisfy the polynomials. The number of such points must be at least one greater than the degree of polynomial.
There are various interpolation techniques in the literature such as Linear Interpolation, Polynomial Interpolation (Lagrange and Newton), Spline Interpolation (Natural Cubic Spline, Clamped Cubic Spline,), Piecewise Linear Interpolation, Inverse Distance Weighting (IDW) and Kriging [43,44,45]. Lagrange Interpolation is one of the techniques and it is used in Shamir’s secret sharing scheme [46,47,48].
3.2. Shamir’s () Secret Sharing Scheme
In secret sharing, the principle objective is to partition the secret S into n pieces such that:
- Learning of t or more pieces makes S uniquely determined.
- Learning of any or fewer pieces leaves S totally unpredictable.
This scheme depends on polynomial interpolation. The fundamental idea of Adi Shamir’s threshold scheme can be understood by a simple example:
- At least 2 points are necessary to draw a line. (i.e., one point is not sufficient)
- At least 3 points are necessary to draw a parabola (i.e., less than 3 points are not sufficient)
- Similarly, it takes at least ‘t’ points to draw a polynomial of degree ‘’ (i.e., less than t points are not sufficient).
Following are the main phases of threshold scheme, where n is the total number of shareholders and t is the minimum number of shareholders necessary to reconstruct the secret S.
Distribution phase:
- Select a prime number Q
- Randomly select a function
- Compute (i, g(i)) corresponding to the ith shareholder,
- These points (i, g(i)) are distributed securely to n shareholders/participants
Reconstruction phase:
- Compute Lagrange’s interpolating polynomial using t shares
- In this way, we obtain the polynomial in the formwhere = S is the secret.
3.3. Hierarchical Access Structure
Access Structure () Recovery of secrets is authorized for some groups of people and it is unauthorized for another group of people. Those sets that are authorized are known as access structures. Adversary Structure () The set of all non-authorized sets that do not have any information related to the secret is said to be an adversary structure.
In threshold access structure any set of t or more participants out of n is said to be an authorized set and any set less than t in number is said to be a non-authorized set. Let be the set of n participants. In Set builder form a threshold access structure and the corresponding adversary structures are as follows:
and
respectively.
In 2006, Herranz et al. [49] explained importance of multipartite structure. According to Herranz “In multipartite structure the set of players is divided into K disjoint classes, and all players in each class play exactly the same role within the access structure. These access structures can make a lot of sense in real life applications, where persons or machines are divided into different groups according to their position in a company, their responsibilities, their computational resources or their probability of being corrupted by an attacker ”.
A multipartite access structure splits the set of participants in into m disjoint sets called levels and all participants in each level play exactly the same role inside the particular access structure.
3.4. Overview of YCH Scheme
Initialization phase
In this scheme following notations are used:
- -scheme, where t is for the threshold and n is for the number of participants.
- denotes the k secrets to be shared.
- n secret shadows are randomly chosen by the dealer and distributed to the participants through a secure channel.
- A random value ‘r’ is chosen.
- A 2-variable 1-way function h(r,), . is chosen.
Construction phase
- (Number of secrets is less than the threshold)
- (a)
- A prime number ‘Q’ is chosen by the dealer.
- (b)
- The dealer choose a polynomial mod Q. Degree of polynomial is where,
- (c)
- are the secrets to be shared and are random numbers.
- (d)
- (e)
- For every ith participant the dealer computes mod Q
- (f)
- Publish .
- (Number of secrets is greater than the threshold)
- (a)
- A prime number Q and a polynomial are chosen by the dealer. The degree of the polynomial is . Where are the secrets.
- (b)
- For i = 1 to n. is computed.
- (c)
- For . is computed
- (d)
- calculated values like are publicly published.
- (e)
- are also published in public.
Recovery phase
In order to recover the secrets
- Each participant uses his/her share to compute (for i = 1 to t)
- The polynomial is determined as follows:
- (Number of secrets is less than the threshold)
- For (Number of secrets is greater than the threshold)
- From the above equations, we get the secrets
3.5. 2-Variable 1-Way Function
Definition: A 2-variable, 1-way function is a function that maps a random value r and a share s onto a bit string of fixed length.
Properties: It contains the following properties:
- when r and s are given is easily computable. But for a given s and , it is very difficult to compute r.
- It is hard to compute when there is no knowledge of s.
- For the given s, it is hard to find two different values and that satisfy the situation .
- It is tough to compute s, for the given r and .
- If we have pairs of r and , it is difficult to find for which .
4. Identification of Problem and Motivation
In all the existing schemes, a separate polynomial is taken corresponding to each secret which results in overhead of public values and calculations. Verification in a hierarchical system is included in papers like [36] with some limitations. In the present work, we try to reduce the limitations in the verification phase.
Contribution
In our study, we propose a “multi-secret sharing scheme for hierarchical access structures” utilizing the YCH scheme. This approach offers several advantages:
- Efficient Parallel Reconstruction: The YCH scheme allows for parallel reconstruction of multiple secrets, enhancing efficiency in scenarios requiring simultaneous access to different shared secrets.
- Dynamic Distribution of Secrets: Our scheme supports dynamic determination of the number of secrets to be distributed, providing flexibility in managing shared information.
- Optimized Resource Utilization: It minimizes storage requirements and computing time by utilizing fewer public values, making it more efficient compared to traditional schemes.
Additionally, employing a two-variable one-way function provides the following benefits:
- Cheater Identification: Any participant can identify dishonest behavior, whether from the dealer or other participants, ensuring the integrity of the sharing process.
- Secure Communication Elimination: There is no dependency on secure channels between the dealer and participants for share transmission, simplifying implementation and reducing overhead.
- Invalid Share Detection: The scheme includes mechanisms to detect and reject invalid shares, enhancing overall security against fraudulent activities.
This comprehensive approach not only enhances the efficiency and flexibility of hierarchical secret sharing but also strengthens security measures, making it suitable for diverse applications requiring robust information protection and sharing capabilities
5. Proposed Scheme
5.1. Overview
All participants are classified into m levels. Each level has a fixed () pair where t is the threshold out of n participants. The dealer chooses pseudo share for the ith participant at level l. Pseudo-share is distributed through a secure channel. are the secrets. Using the YCH scheme, the dealer computes the actual share () for each participant. public share () is calculated on the addition of actual shares in the one-way function.
In the Reconstruction phase, the actual share of the participants is calculated by subtracting the one-way function from the public share. This actual share is used in the Lagrange interpolation polynomial and generates the polynomial having coefficients as secrets. If the share’s number at a particular level is less than its threshold value, then the upper-level shareholder provides his share to reconstruct the secret.
5.2. Initialization
- Number of participants is n.
- The number of levels is m. They are .
- Each level is associated with a , access structure.
- Dealer chooses n shares , , .
5.3. Distribution
At each level l there may be two situations:
- The number of secrets k is less than the threshold
- A number of secrets k is more than the threshold.
- (number of secret is less than or equal to )
- (a)
- A prime number Q is chosen by the dealer.
- (b)
- The dealer constructs polynomial mod Q. The degree of the polynomial is (). Let,where are the secrets,
- (c)
- , are randomly chosen numbers.
- (d)
- For the ith participant the dealer computes , .
- (e)
- Publish .
- (Number of secrets is greater than ).
- (a)
- A prime number Q is chosen.
- (b)
- Dealer constructs a polynomial of degree . Letwhere are the secrets.
- (c)
- For . is Computed.
- (d)
- For . is Computed
- (e)
- calculated values like are made public
- (f)
- are published in public.
For both cases, the dealer performs the following calculations:
- Calculate actual share () and pseudo share () for the ith participant of level l using the following formulas:where g is a one-way function in which denotes the share of th participant of level l
- Calculate the actual share () and pseudo share () of the ith participant of upper level u using the formula:where is the identifier for ith element of uth level.
- and (if needed) are distributed to each participant using a secure channel.
- All , r values are published.
5.4. Reconstruction
Each participant computes the actual share of other participants involved in the reconstruction by using the formula
and then the following two cases are considered.
Case 1
A particular level has a sufficient number of participants, i.e., greater or equal to the threshold, then participants of the same level exchange their pseudo share and use the following formula:
- for
- for
Case 2
Particular levels have an insufficient number of thresholds, then the share of the upper-level participant for this level is used in the above formula. Thus, we obtain the secret .
5.5. Verification
The following steps are involved in the verification phase:
- 1.
- Pseudo share is distributed to participants securely by the dealer.
- 2.
- Each ith participant uses his actual share () in a two-variable one-way function with random variable r. Let that two-way variable function be .
- 3.
- Calculated values made public.
- 4.
- Public share is also published.
Now at the time of the exchange of shares:
- 5.
- Each participant computes the actual share of each participant
- 6.
- Using that actual share, is calculated for participant.
- 7.
- If is equal to the already public value of then the participant share is valid; otherwise, the actual share of the participant is not valid.
- 8.
- In a similar way, an individual participant will be able to check the legitimacy of his/her share given by the dealer.
5.6. Example
We can understand the proposed scheme more clearly by following examples with small parameters.
Let us consider the hierarchical system with two levels and . The upper level is and the lower is . The dealer has two secrets, i.e., and . Identifiers , , for the level and , , for the level .
The dealer chooses shares , , for the level-1 and , , for the level-2.
5.6.1. Distribution
For the sake of easiness, we perform calculations on the second level.
calculate actual share for the ith participants for the level-2 by using formula:
= h() are
The actual share of the ith participants of the upper level for the level-2
Similarly, we obtain = 1 and = 1.
Choose one-way function mod 23.
Compute the pseudo share of the ith participants of the level R.
Therefore, we obtain = 13, = 10, = 19.
Similarly, the pseudo share of the participants of the upper level for level 2 are
Publish all pseudo share and distribute to every participant through a secure channel.
5.6.2. Reconstruction
In the reconstruction phase, each participant has a pseudosphere and the share for the particular level actual share is computed by using
Hence, we have
Similarly, the actual share of the upper-level participants for level 2 is as follows:
Now, there is the possibility of two cases:
- A particular level (here level 2) has a sufficient number of participants.
- A particular level has fewer participants than the upper-level participant and takes part in the reconstruction of the secret.
Case-1
That is,
Case-2
The participants in level 2 are one less than the threshold. Therefore, one of the upper-level participants takes part in the reconstruction. Hence, the pair of (ID, actual share) are: (4, 9) (5, 2) (1, 9) applying the same formula as in Case 1.
Therefore, . Hence, the secrets are 2 and 3.
6. Security and Performance Analysis
While choosing a scheme, we must be clear about the capabilities of the adversary, along with an explanation of the security properties it supports. There must be a strong analysis of the computational and communication costs. In this section, we have explained all these concepts in detail.
6.1. Adversary Model
There must be an adversary model against which the scheme is safe. The most common adversarial model for analyzing security protocols was presented by Dolev and Yao [50] in 1983. Apart from this, we have considered two types of adversaries:
- Insider Adversary, these are legitimate shareholders who acquired shares from the dealer.
- Outsider Adversary, the external adversary is an attacker who does not own any of the dealer’s shares but may try to gain unauthorized access.
In general, a dealer is considered as trustworthy as in [36], but here we have considered the worst situation that the dealer is committing fraud by providing fake shares to the participants.
6.2. Security Analysis
Any scheme must pass through formal and informal analysis to verify its applicability in the current scenario. In the proposed scheme, we have used the Random Oracle Modal (RoM) for formal analysis. In informal analysis, we have proved our scheme safe from several attacks.
6.2.1. Formal Security Analysis (Random Oracle Model)
A cryptographic hash function H is treated as a really random function by the random-oracle model. The random-oracle model more particularly hypothesizes the existence of a public, random function H that can only be evaluated by “querying” an oracle, which can be thought of as a “black box”, that returns when given input x. A formal approach that can be used to create and verify cryptographic methods is provided by the random-oracle model. In 2014, Herranz et al. [51] provided the formal definition of security for MSS in the random oracle model. Moreover, they proposed an MSS formally proved its computational security in ROM. As far as we know, that is an MSS’s first formal security analysis. Security analysis of the multi-secret sharing scheme has been performed by [52]. In this section, we prove the computational security of the proposed scheme assuming that the hash function H behaves as a random oracle.
Before we proceed with the proof, the following are the assumptions:
- We assume the proposed scheme as the set of tuples, where Int stands for the initialization/setup phase, dist stands for distribution and Rec is for the recovery phase.
- PP (Public parameters) =
- p: prime number p > n such that p is at least bits long
- H: a hash function,
- : Set of participants
- t: Threshold
- There is an adversary containing a set of participants and threshold value t.
Theorem 1.
For an adversary λ, we have
here adversary makes at most queries to the random oracle for H against the GMS and Ω.
Proof.
For the proof we follow the following steps:
Step 1 We act as the challenger of the security game described in [52].
Step 2 We pass public parameters to the initialization algorithm and send the result to the adversary.
Step 3 broadcast , we choose ,
Step 4 After masking hash query x to the random oracle H, if then abort the game, otherwise proceed for the next step.
Step 5 A random value is is chosen and sent to the adversary. At the same time, is saved in the table.
Step 6 Two global secrets
are broadcast by adversary .
Step 7 We choose a random value such that for and the adversary does not query to the random oracle H.
Step 8 A random polynomial is chosen where, and compute and and again store in the hash table. Similarly, choose l no. of random values and store in the hash table.
Step 9 Choose a random bit and compute and give shares of corrupted players . along with this public output which are also shared.
Step 10 after continuous query to , adversary , outputs a bit which is defined in the following equation
From the above steps, we conclude that is not allowed to query such that and . □
6.2.2. Informal Security Analysis
Any proposed protocol must be passed through the following goals:
- Correctness: In the verification phase, each participant computes the actual share of other participants using that actual share, is calculated for th participant. If is equal to the already public value of then the participant share is valid otherwise the actual share of the participant is not valid.
- Forward secrecy: keys like can only be computed or stored by members of the closed communication group; if a member leaves the group, the departing member will be unable to access the content of future conversations.
- Perfectness: We use Shamir’s (t, n) secret sharing scheme for share distribution at each level in the proposed scheme. It is well known that fewer than t participants in Shamir’s (t, n) secret-sharing scheme cannot reconstruct the secret. Hence, our scheme is also perfect.
- Fairness of secret sharing One desirable quality in secret sharing is Fairness, which indicates that if one member obtains the secret, the other participants are not harmed. Halpern and Teague [53] were the first to offer rational cryptographic protocols in 2004. They pointed out that any method for reassembling secrets with a well-known upper constraint on the running duration is unstable and that parties will not submit anything in the final round since they have no reason to do so because the other participant does. Regrettably, earlier secret-sharing systems necessitated numerous rounds with high overheads. Zhang et al. [26,27] explain the scheme. Fairness but leave out the access mechanism. To summarize, existing fairness schemes necessitate a trusted third party or many rounds of communication. The proposed scheme provides Fairness without the dependency on a third party and extra overheads in communication.
- Freshness of keys: In the proposed scheme, all the exchangeable values depend upon the random bi-variate polynomial. It makes pseudo-share, and shares are always fresh. Hence, it is impossible to impersonate a member by recording a previously used key.
- Eavesdropping attack In the proposed scheme, each ith participant uses his actual share () in a two-variable one-way function with random variable r which makes it independent of public parameters. Therefore, an adversary will not be able to know any secret information from communication parameters. So, the proposed scheme is safe from eavesdropping activities.
- Cheating identification In the proposed scheme, an individual participant can check the legitimacy of his/her share given by the dealer. Thus, the proposed scheme provides cheating identification.
- Verifiability In the reconstruction phase, participants can verify shares received from other participants and dealers. On the other hand, a dealer can also verify the participant’s shares. Thus, the proposed scheme provides verifiability.
- Unconditional security While exploring the security analysis, both types of adversaries are considered with their capacity to the full extent.
Recently, Li et al. [54] have used secret sharing with blockchain for the Internet of Medical Things (IoMT) and proposed a more energy-efficient protocol that lacks a hierarchy.
6.3. Performance Analysis
6.3.1. Evaluation of Stealth Share
In this subsection, we analyze the time required for the entire process from share generation to secret reconstruction, examining how share size and the number of participants influence it. Figure 1, provides two types of analysis based on participant count and share size. Part (a) illustrates the relationship between the number of clients (t) and the time (in seconds) taken for secret creation and reconstruction. Initially, with a small number of clients, the time remains just above 0 s, indicating minimal impact. However, as the number of clients increases, the time escalates in a step-like manner, approaching just below 1 s with seven clients. Conversely, part (b) explores the impact of share size (in bits) on the time required for creation and reconstruction. Here, the time remains consistently close to zero, suggesting that a share size of up to 40 bits does not significantly affect the process. We have used a Python library along with resources available at [55] for the evaluation of our proposed scheme as well as existing schemes. We perform the proposed scheme and other similar schemes on a Windows 10 laptop with AMD Ryzen 7, 3.0 GHz and 16 GB RAM. Furthermore, mathematically we see that each participant stores a univariate polynomial of , resulting in a storage requirement of bits per participant. This polynomial-based modulus is notably smaller than the moduli used in public-key systems [56]. The threshold here is t. To ensure collusion-free authentication, each participant must concurrently manage t + 1 univariate polynomials. Consequently, the overall storage cost is considerably lower compared to symmetric key-based schemes.
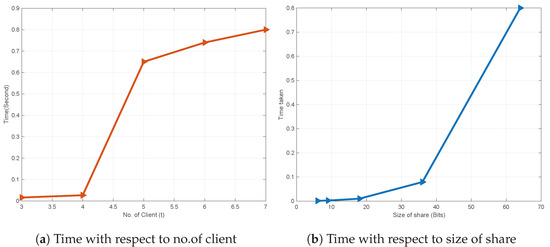
Figure 1.
Time in stealth share with respect to no.of client and size of share.
6.3.2. Computational Cost
In the proposed scheme, each member must compute pairwise shared keys with others in the verification phase. According to Horner’s rule [57], t and h computations are required for each univariate polynomial of and degree. In the proposed protocol, calculation reduces to Shamir’s secret sharing scheme. According to [58] computational time for eight people is 0.0039 s. There is a slight change in computation time as we increase the number of people; Basit et al. [35] use an extra polynomial, and Tentu et al. [31] use modular exponentiation, which increases computational cost. The computational cost for the same no. of persons is 0.2439 s and 80.003 s of [35] and [31], respectively. Similarly, the computational cost for eight people in [27] is 0.23 s. We conclude that the computation cost is meager compared to the other existing schemes. For more clarity, we have presented a graphical comparison of schemes in terms of computational time and security features it supports in Figure 2.
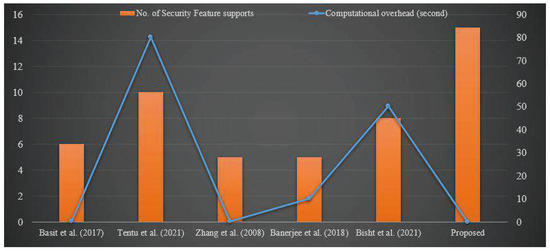
Figure 2.
Comparison of computational cost and security features supported by Basit et al. [35], Tentu et al. [31], Zhang et al. [27], Banerjee et al. [36], Bisht et al. [39] and Propose protocol.
7. Comparison with Existing Schemes
The proposed scheme uses the YCH scheme, while all other schemes for hierarchical access structures use simply Shamir’s scheme. In the proposed scheme “Multiple-secrets” are shared among a group of people for different levels. Our scheme provides a mechanism for verifying the shares, which is also new for hierarchical access structures. This is more efficient than other schemes. Basit et al. [35] used Shamir’s scheme with the successive application of one-way function and shift key technique to propose Multi-stage, Multi-secret sharing for hierarchical Access Structure. Apart from the above papers, the Hierarchical secret sharing (HSSS) scheme is discussed in [33,36,39] but their schemes lack fairness. Banerjee et al. [36] proposed Cheating detection and cheater Identification for hierarchical structure but lacks correctness. Bisht and Deshmukh [39] proposed work on multi-level secret sharing but lacks fairness and perfectness. Similarly, Yuan et al. [28] used homogenous recurrence relation to propose a new efficient scheme that deals with a multi-secret hierarchical scheme. It is a novel work but lacks an explanation about correctness and forward/backward secrecy. Our scheme also avoids the problem of Chen et al. scheme’s [59] which requires checking the non-singularity of multiple matrices. Furthermore, during the entire scheme, each participant keeps only one share, which is as long as the secret, indicating that our method is optimum. Furthermore, despite requiring more public value, our scheme can simultaneously disclose many secrets. In Table 1, we can see the importance of the present scheme in comparison with other schemes.
In our proposed scheme, we have used a one-way function, which restricts the outsider Adversary from stealing or breaching information about the secret. To deal with the situation of Case-1 and Case-2, two-variable one-way functions are used. Using a two-variable one-way function, every participant can verify the share received from the dealer and other participants. Our scheme also satisfies the security goals like correctness and secrecy. In Table 2, we have compared the recent scheme for multi-secret sharing. From there, we conclude that our scheme can provide many security properties in the case of IoT authentication. Furthermore, in Figure 2, we can see that computational overhead (0.23 s) is significantly less than others and security features (almost 20) are more in numbers supported by the proposed scheme.

Table 2.
Comparison in tabular form.
8. Conclusions
In the present work, we categorized participants into different levels with varying thresholds, aligning with a hierarchical structure. Subsequently, we proposed a hierarchical multi-secret sharing scheme based on the YCH scheme. The YCH scheme is highly efficient, and the inclusion of a one-way function enhances its security, making it unconditionally secure. The reusability of shares eliminates the need for frequent refreshment of shares for future communication. In addition to being reusable, multi-secret, and hierarchical, our scheme includes a valuable feature: the verification of shares. Specific participants can verify the shares they receive from other participants or the dealer. This verification feature makes our proposed scheme particularly useful for robust security solutions. Comparisons with existing schemes demonstrate its superiority in preserving security. Our scheme not only improves operational efficiency but also provides a scalable solution adaptable to various access structures. Future work could explore further optimizations and applications in complex, multi-stage security environments.
Author Contributions
I.A. conceptualized the study, developed the methodology, conducted validation, performed formal analysis, participated in investigation, curated data, and contributed to visualization. A.S.A. contributed to methodology development, software implementation, validation, formal analysis, investigation, data curation, and visualization. S.A., as the corresponding author, contributed to conceptualization, methodology development, software implementation, validation, formal analysis, investigation, data curation, and provided supervision throughout the study. M.S.M.A. contributed to methodology development, validation, investigation, and data curation. Together, they ensured comprehensive coverage of the research process from conception to final analysis and presentation of results. All authors have read and agreed to the published version of the manuscript.
Funding
This study was carried out with financial support from Princess Nourah Bint Abdulrahman University (PNU), Riyadh, Saudi Arabia. The authors extend their appreciation to Princess Nourah Bint Abdulrahman University (PNU), Riyadh, Saudi Arabia for funding this research under Researchers Supporting Project Number (PNURSP2024R231).
Data Availability Statement
Data sharing is not applicable as no datasets were generated or analyzed during the current study.
Acknowledgments
The authors are very thankful to the anonymous referees for their valuable comments and suggestions which have improved the manuscript immensely. Moreover, we are very thankful to the “SageMath” open source community. This paper has been executed utilizing free open source arithmetic programming in SageMath [60]. The authors extend their appreciation to Princess Nourah Bint Abdulrahman University (PNU), Riyadh, Saudi Arabia for funding this research under Researchers Supporting Project Number (PNURSP2024R231).
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Gutte, V.S.; Parasar, D. Sailfish invasive weed optimization algorithm for multiple image sharing in cloud computing. Int. J. Intell. Syst. 2022, 37, 4190–4213. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Zu, C.; Yang, Z.; Bian, G.; Zhang, Y.; Ruan, W.; Wu, B.; Wu, X.; Yuan, L. An accurate cloud-based indoor localization system with low latency. Int. J. Intell. Syst. 2022, 37, 4794–4809. [Google Scholar] [CrossRef]
- Ren, P.; Li, F.; Wang, Y.; Zhou, H.; Liu, P. Ipsadas: Identity-privacy-aware secure and anonymous data aggregation scheme. Int. J. Intell. Syst. 2022, 37, 5290–5324. [Google Scholar] [CrossRef]
- Bufalo, M.; Bufalo, D.; Orlando, G. Some properties of the computation of the modular inverse with applications in cryptography. Computation 2023, 11, 70. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Wu, Z.-Y.; Chen, T.-L.; Huang, Y.-M.; Liu, C.-H. Security privacy and policy for cryptographic based electronic medical information system. Sensors 2021, 21, 713. [Google Scholar] [CrossRef]
- Hazzazi, M.M.; Attuluri, S.; Bassfar, Z.; Joshi, K. A novel cipher-based data encryption with galois field theory. Sensors 2023, 23, 3287. [Google Scholar] [CrossRef]
- Hernández-Álvarez, L.; Bullón, Pérez, J.J.; Batista, F.K.; Queiruga-Dios, A. Security threats and cryptographic protocols for medical wearables. Mathematics 2022, 10, 886. [Google Scholar] [CrossRef]
- Jara-Vera, V.; Sánchez-Ávila, C. Some notes on a formal algebraic structure of cryptology. Mathematics 2021, 9, 2183. [Google Scholar] [CrossRef]
- Masood, F.; Ahmad, J.; Shah, S.A.; Jamal, S.S.; Hussain, I. A novel hybrid secure image encryption based on julia set of fractals and 3d lorenz chaotic map. Entropy 2020, 22, 274. [Google Scholar] [CrossRef]
- Rauf, A.; Wang, Z.; Sajid, H.; Ali Tahir, M. Secure route-obfuscation mechanism with information-theoretic security for internet of things. Sensors 2020, 20, 4221. [Google Scholar] [CrossRef]
- Richter, M.; Bertram, M.; Seidensticker, J.; Tschache, A. A mathematical perspective on post-quantum cryptography. Mathematics 2022, 10, 2579. [Google Scholar] [CrossRef]
- Tito-Corrioso, O.; Borges-Quintana, M.; Borges-Trenard, M.A.; Rojas, O.; Sosa-Gómez, G. On the fitness functions involved in genetic algorithms and the cryptanalysis of block ciphers. Entropy 2023, 25, 261. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the 1979 International Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, 4–7 June 1979; IEEE Computer Society: New York, NY, USA, 1979; pp. 313–318. [Google Scholar]
- Simmons, G.J. How to (really) share a secret. In Conference on the Theory and Application of Cryptography; Springer: New York, NY, USA, 1988; pp. 390–448. [Google Scholar]
- Asmuth, C.; Bloom, J. A modular approach to key safeguarding. IEEE Trans. Inf. Theory 1983, 29, 208–210. [Google Scholar] [CrossRef]
- He, J.; Dawson, E. Multistage secret sharing based on one-way function. Electron. Lett. 1994, 30, 1591–1592. [Google Scholar] [CrossRef]
- He, J.; Dawson, E. Multisecret-sharing scheme based on one-way function. Electron. Lett. 1995, 31, 93–95. [Google Scholar] [CrossRef]
- Chien, H.Y.; Jan, J.K.; Tseng, Y.M. A practical (t, n) multi-secret sharing scheme. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2000, 83, 2762–2765. [Google Scholar]
- Choc, B.; Goldwasser, S.; Micali, S.; Awerbuch, B. Verifiable secret sharing and achieving simultaneity in the presence of faults. In Annual Symposium on Foundations of Computer Science (Proceedings); Elsevier: Amsterdam, The Netherlands, 1985; pp. 383–395. [Google Scholar]
- Tompa, M.; Woll, H. How to share a secret with cheaters. J. Cryptol. 1989, 1, 133–138. [Google Scholar] [CrossRef]
- Harn, L.; Hsu, C.-F. (t, n) Multi-secret sharing scheme based on bivariate polynomial. Wirel. Pers. Commun. 2017, 95, 1495–1504. [Google Scholar] [CrossRef]
- Harn, L.; Hsu, C.-F.; Xia, Z.; Zhou, J. How to share secret efficiently over networks. Secur. Commun. Netw. 2017, 2017, 5437403. [Google Scholar] [CrossRef]
- Ballico1, E.; Boato, G.; Fontanari, C.; Granelli, F. Hierarchical secret sharing in ad hoc networks through birkhoff interpolation. In Advances in Computer, Information, and Systems Sciences, and Engineering: Proceedings of IETA 2005, TeNe 2005, EIAE 2005; Springer: Dordrecht, The Netherlands, 2006; pp. 157–164. [Google Scholar]
- Ma, C.; Cheng, R. Key management based on hierarchical secret sharing in ad-hoc networks. In Information Security and Cryptology: Third SKLOIS Conference, Inscrypt 2007, Xining, China, August 31–September 5, 2007, Revised Selected Papers 3; Springer: Berlin/Heidelberg, Germany, 2008; pp. 182–191. [Google Scholar]
- Zhang, E.; Li, M.; Yiu, S.-M.; Du, J.; Zhu, J.-Z.; Jin, G.-G. Fair hierarchical secret sharing scheme based on smart contract. Inf. Sci. 2021, 546, 166–176. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Huang, G. Sure interpolation and its application to hierarchical threshold secret sharing scheme. In Proceedings of the 2008 International Symposium on Computer Science and Computational Technology, Shanghai, China, 20–22 December 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 1, pp. 447–450. [Google Scholar]
- Yang, C.-C.; Chang, T.-Y.; Hwang, M.-S. A (t, n) multi-secret sharing scheme. Appl. Math. Comput. 2004, 151, 483–490. [Google Scholar] [CrossRef]
- Blundo, C.; De Santis, A.; Stinson, D.R.; Vaccaro, U. Graph decompositions and secret sharing schemes. J. Cryptol. 1995, 8, 39–64. [Google Scholar] [CrossRef]
- Padró, C.; Sáez, G. Secret sharing schemes with bipartite access structure. IEEE Trans. Inf. Theory 2000, 46, 2596–2604. [Google Scholar]
- Tentu, A.N.; Bhavani, K.; Basit, A.; Venkaiah, V.C. Sequential (t, n) multi secret sharing scheme for level-ordered access structure. Int. J. Inf. Technol. 2021, 13, 2265–2275. [Google Scholar] [CrossRef]
- Brickell, E.F. Some ideal secret sharing schemes. In Workshop on the Theory and Application of of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1989; pp. 468–475. [Google Scholar]
- Lin, C.; Harn, L.; Yea, D. Ideal hierarchical (t, n) secret sharing schemes. In Proceedings of the Fifth International Conference on Information Assurance and Security (IAS09), Xi’an, China, 18–20 August 2009; Citeseer: Princeton, NJ, USA, 2009. [Google Scholar]
- Chanu, O.B.; Tentu, A.N.; Venkaiah, V.C. Multi-stage multi-secret sharing schemes based on chinese remainder theorem. In Proceedings of the 2015 International Conference on Advanced Research in Computer Science Engineering & Technology (ICARCSET 2015), Unnao, India, 6–7 March 2015; pp. 1–6. [Google Scholar]
- Basit, A.; Kumar, N.C.; Venkaiah, V.C.; Moiz, S.A.; Tentu, A.N.; Naik, W. Multi-stage multi-secret sharing scheme for hierarchical access structure. In Proceedings of the 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 557–563. [Google Scholar]
- Banerjee, S.; Gupta, D.S.; Biswas, G. Hierarchy-based cheating detection and cheater identification in secret sharing schemes. In Proceedings of the 2018 4th International Conference on Recent Advances in Information Technology (RAIT), Dhanbad, India, 15–17 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Liu, Y.; Zhang, F.; Zhang, J. Attacks to some verifiable multi-secret sharing schemes and two improved schemes. Inf. Sci. 2016, 329, 524–539. [Google Scholar] [CrossRef]
- Yuan, J.; Yang, J.; Wang, C.; Jia, X.; Fu, F.-W.; Xu, G. A new efficient hierarchical multi-secret sharing scheme based on linear homogeneous recurrence relations. Inf. Sci. 2022, 592, 36–49. [Google Scholar] [CrossRef]
- Bisht, K.; Deshmukh, M. A novel approach for multilevel multi-secret image sharing scheme. J. Supercomput. 2021, 77, 12157–12191. [Google Scholar] [CrossRef]
- Prashanti, G.; Bhat, M.N. Cheating identifiable polynomial based secret sharing scheme for audio and image. Multimed. Tools Appl. 2024, 83, 403–423. [Google Scholar] [CrossRef]
- Chattopadhyay, A.K.; Saha, S.; Nag, A.; Nandi, S. Secret sharing: A comprehensive survey, taxonomy and applications. Comput. Sci. Rev. 2024, 51, 100608. [Google Scholar] [CrossRef]
- Kamal, A.A.A.M.; Iwamura, K. Privacy preserving multi-party multiplication of polynomials based on (k, n) threshold secret sharing. ICT Express 2023, 9, 875–881. [Google Scholar] [CrossRef]
- Liu, C.; Min, S.; Pang, Y.; Chai, Y. The meshfree radial point interpolation method (RPIM) for wave propagation dynamics in non-homogeneous media. Mathematics 2023, 11, 523. [Google Scholar] [CrossRef]
- Chen, C.S.; Noorizadegan, A.; Young, D.L.; Chen, C.S. On the selection of a better radial basis function and its shape parameter in interpolation problems. Appl. Math. Comput. 2023, 442, 127713. [Google Scholar] [CrossRef]
- Dupac, M. Mathematical modeling and simulation of the inverse kinematic of a redundant robotic manipulator using azimuthal angles and spherical polar piecewise interpolation. Math. Comput. Simul. 2023, 209, 282–298. [Google Scholar] [CrossRef]
- Sauer, T.; Xu, Y. On multivariate Lagrange interpolation. Math. Comput. 1995, 64, 1147–1170. [Google Scholar] [CrossRef]
- Nevai, P. Mean convergence of Lagrange interpolation. III. Trans. Am. Math. Soc. 1984, 282, 669–698. [Google Scholar] [CrossRef]
- Gautschi, W. On mean convergence of extended Lagrange interpolation. J. Comput. Appl. Math. 1992, 43, 19–35. [Google Scholar] [CrossRef]
- Herranz, J.; Sáez, G. New results on multipartite access structures. IEE Proc.-Inf. Secur. 2006, 153, 153–162. [Google Scholar] [CrossRef]
- Dolev, D.; Yao, A. On the security of public key protocols. IEEE Trans. Inf. Theory 1983, 29, 198–208. [Google Scholar] [CrossRef]
- Herranz, J.; Ruiz, A.; Sáez, G. New results and applications for multi-secret sharing schemes. Des. Codes Cryptogr. 2014, 73, 841–864. [Google Scholar] [CrossRef]
- Mashhadi, S. Toward a formal proof for multi-secret sharing in the random oracle model. Inf. Secur. J. A Glob. Perspect. 2020, 29, 244–249. [Google Scholar] [CrossRef]
- Halpern, J.; Teague, V. Rational secret sharing and multiparty computation. In Proceedings of the Thirtysixth Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 13–16 June 2004; pp. 623–632. [Google Scholar]
- Li, C.; Dong, M.; Xin, X.; Li, J.; Chen, X.B.; Ota, K. Efficient privacy-preserving in IoMT with blockchain and lightweight secret sharing. IEEE Internet Things J. 2023, 10, 22051–22064. [Google Scholar] [CrossRef]
- Buchanan, W.J. Shamir Secret Sharing (SSS). Asecuritysite.com. 2024. Available online: https://asecuritysite.com/shares (accessed on 30 April 2024).
- Wu, S.; Hsu, C.; Xia, Z.; Zhang, J.; Wu, D. Symmetric-bivariate-polynomial-based lightweight authenticated group key agreement for industrial internet of things. J. Internet Technol. 2020, 21, 1969–1979. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming; Pearson Education: London, UK, 2005. [Google Scholar]
- Security and So Many Things—Asecuritysite.com. Available online: https://asecuritysite.com/ (accessed on 30 April 2024).
- Chen, Q.; Tang, C.; Lin, Z. Efficient explicit constructions of multipartite secret sharing schemes. IEEE Trans. Inf. Theory 2021, 68, 601–631. [Google Scholar] [CrossRef]
- SageMath. Use SageMath Online—Cocalc.com. Available online: https://cocalc.com/features/sage (accessed on 30 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).