A New Methodology for the Development of Efficient Multistep Methods for First-Order Initial Value Problems with Oscillating Solutions: III the Role of the Derivative of the Phase Lag and the Derivative of the Amplification Factor
Abstract
1. Introduction
- In Section 2, we mention the theory for the derivatives of the phase lag and the derivative of the amplification factor of the multistep methods for first-order IVPs.
- In Section 3, we present methodologies for the vanishing of the following:
- -
- The derivative of the phase lag;
- -
- The derivative of the amplification factor;
- -
- The derivative of the phase lag and derivative of the amplification factor.
- In Section 10, we study the stability of the newly obtained algorithms.
- In Section 11, we present the numerical results and a conclusion on the role of the derivative of the phase lag and the derivative of the amplification factor.
2. The Theory
- We differentiate using v the formulae produced in the previous step.
- We request the formulae of the derivatives of the phase lag and the amplification factor, produced in the previous steps, to be equal to zero.
3. Vanishing of the Derivatives of the Phase Lag and the Amplification Factor
- The vanishing of the derivative of the phase lag;
- The vanishing of the derivative of the amplification factor;
- The vanishing of the derivative of the phase lag and the amplification factor.
4. Phase-Fitted and Amplification-Fitted Adams–Bashforth Fourth-Order Method with the Vanished First Derivative of the Phase Lag
- We calculate the first derivative of the above formula, i.e., .
- We request the formula of the previous step to be equal to zero, i.e., .
5. Phase-Fitted and Amplification-Fitted Adams–Bashforth Fourth-Order Method with the Vanished First Derivative of the Amplification Factor
- We calculate the first derivative of the above formula, i.e., .
- The request the formula of the previous step to be equal to zero, i.e., .
6. Phase-Fitted and Amplification-Fitted Adams–Bashforth Fifth-Order Method
7. Phase-Fitted and Amplification-Fitted Adams–Bashforth Fourth-Order Method with the Vanished First Derivative of the Phase Lag
8. Phase-Fitted and Amplification-Fitted Adams–Bashforth Fifth-Order Method with the Vanished First Derivative of the Amplification Factor
9. Phase-Fitted and Amplification-Fitted Adams–Bashforth Fifth-Order Method with the Vanished First Derivative of the Phase Lag and the First Derivative of the Amplification Factor
10. Stability Analysis
10.1. Five-Step Adams–Bashforth Methods
10.2. Six-Step Adams–Bashforth Methods
11. Numerical Results
11.1. Problem of Stiefel and Bettis
- The classical Adams–Bashforth method of the fourth order, which is mentioned as Numeric. Proced. I;
- The classical Adams–Bashforth method of the fifth order, which is mentioned as Numeric. Proced. II;
- The classical Adams–Bashforth method of the sixth order, which is mentioned as Numeric. Proced. III;
- The Runge–Kutta Dormand and Prince fourth-order method [16], which is mentioned as Numeric. Proced. IV;
- The Runge–Kutta Dormand and Prince fifth order method [16], which is mentioned as Numeric. Proced. V
- The Runge–Kutta Fehlberg fourth-order method [33], which is mentioned as Numeric. Proced. VI;
- The Runge–Kutta Fehlberg fifth-order method [33], which is mentioned as Numeric. Proced. VII;
- The Runge–Kutta Cash and Karp fifth-order method [34], which is mentioned as Numeric. Proced. VIII;
- The phase-fitted and amplification-fitted Adams–Bashforth fourth-order method with the vanished first derivative of the phase lag which is developed in Section 4, which is mentioned as Numeric. Proced. X;
- The phase-fitted and amplification-fitted Adams–Bashforth fourth-order method with the vanished first derivative of the amplification factor, which is developed in Section 5, which is mentioned as Numeric. Proced. XI;
- The phase-fitted and amplification-fitted Adams–Bashforth fifth-order method which is developed in Section 6, which is mentioned as Numeric. Proced. XII;
- The phase-fitted and amplification-fitted Adams–Bashforth fifth-order method with the vanished first derivative of the phase lag which is developed in Section 7, which is mentioned as Numeric. Proced. XIII;
- The phase-fitted and amplification-fitted Adams–Bashforth fifth-order method with the vanished first derivative of the amplification factor which is developed in Section 8, which is mentioned as Numeric. Proced. XIV;
- The phase-fitted and amplification-fitted Adams–Bashforth fifth-order method with vanished the first derivative of the phase lag and the vanished first derivative of the amplification factor which is developed in Section 9, which is mentioned as Numeric. Proced. XV.
- Numeric. Proced. I is more efficient than Numeric. Proced. V;
- Numeric. Proced. I and Numeric. Proced. VIII give approximately the same accuracy;
- Numeric. Proced. VI is more efficient than Numeric. Proced. I;
- Numeric. Proced. IV is more efficient than Numeric. Proced. VI;
- Numeric. Proced. IV and Numeric. Proced. VII give approximately the same accuracy;
- Numeric. Proced. II is more efficient than Numeric. Proced. IV;
- Numeric. Proced. III is more efficient than Numeric. Proced. II;
- Numeric. Proced. IX gives mixed results. For big step sizes, it is more efficient than Numeric. Proced. III. For small step sizes, it is less efficient than Numeric. Proced. III;
- Numeric. Proced. XIII is more efficient than Numeric. Proced. IX;
- Numeric. Proced. X is more efficient than Numeric. Proced. XIII;
- Numeric. Proced. XIV is more efficient than Numeric. Proced. X;
- Numeric. Proced. XII and Numeric. Proced. XIV give approximately the same accuracy;
- Numeric. Proced. XI is more efficient than Numeric. Proced. XIV;
- Finally, Numeric. Proced. XV is the most efficient one.
11.2. Problem of Franco and Palacios [35]
- Numeric. Proced. II is more efficient than Numeric. Proced. I;
- Numeric. Proced. IV is more efficient than Numeric. Proced. II;
- Numeric. Proced. IV and Numeric. Proced. VI give approximately the same accuracy;
- Numeric. Proced. III is more efficient than Numeric. Proced. IV;
- Numeric. Proced. VIII gives mixed results. For big step sizes, it is more efficient than Numeric. Proced. III. For small step sizes, it is less efficient than Numeric. Proced. III;
- Numeric. Proced. VII is more efficient than Numeric. Proced. III and Numeric. Proced. VIII;
- Numeric. Proced. XIII is more efficient than Numeric. Proced. VII;
- Numeric. Proced. IX gives mixed results. For big step sizes, it is more efficient than Numeric. Proced. VII. For small step sizes, it is less efficient than Numeric. Proced. VII;
- Numeric. Proced. V is more efficient than Numeric. Proced. IX;
- Numeric. Proced. XI is more efficient than Numeric. Proced. V;
- Numeric. Proced. X is more efficient than Numeric. Proced. XI;
- Numeric. Proced. XIV is more efficient than Numeric. Proced. X;
- Numeric. Proced. XII and Numeric. Proced. XIV give approximately the same accuracy;
- Finally, Numeric. Proced. XV is the most efficient one.
11.3. Nonlinear Problem of Petzold [36]
- Numeric. Proced. I, Numeric. Proced. V and Numeric. Proced. VI give approximately the same accuracy;
- Numeric. Proced. VIII is more efficient than Numeric. Proced. VI;
- Numeric. Proced. VII is more efficient than Numeric. Proced. VIII;
- Numeric. Proced. II, Numeric. Proced. IV, and Numeric. Proced. VII give approximately the same accuracy;
- Numeric. Proced. III is more efficient than Numeric. Proced. II;
- Numeric. Proced. IX is more efficient than Numeric. Proced. III;
- Numeric. Proced. XIII is more efficient than Numeric. Proced. IX;
- Numeric. Proced. X is more efficient than Numeric. Proced. XIII;
- Numeric. Proced. XII is more efficient than Numeric. Proced. X;
- Numeric. Proced. XII and Numeric. Proced. XIV give approximately the same accuracy;
- Numeric. Proced. XI is more efficient than Numeric. Proced. XIV;
- Finally, Numeric. Proced. XV is the most efficient one.
11.4. A Nonlinear Orbital Problem [37]
- Numeric. Proced. I, Numeric. Proced. II, and Numeric. Proced. III are divergent for the data of the specific problem;
- Numeric. Proced. VI gives the same accuracy as Numeric. Proced. IV in the one point of its convergence;
- Numeric. Proced. VIII is more efficient than Numeric. Proced. IV;
- Numeric. Proced. VII is more efficient than Numeric. Proced. VIII;
- Numeric. Proced. V is more efficient than Numeric. Proced. VII;
- Numeric. Proced. XIV is more efficient than Numeric. Proced. V;
- Numeric. Proced. XI is more efficient than Numeric. Proced. XIV;
- Numeric. Proced. XIII is more efficient than Numeric. Proced. XI;
- Numeric. Proced. IX is more efficient than Numeric. Proced. XIII;
- Numeric. Proced. X is more efficient than Numeric. Proced. IX;
- Numeric. Proced. XV and Numeric. Proced. XII give approximately the same accuracy;
- Finally, Numeric. Proced. XV and Numeric. Proced. XII are the most efficient.
11.5. Problem of Franco and Gómez [38]
- Numeric. Proced. I and Numeric. Proced. II are divergent in the data of the specific problem;
- Numeric. Proced. IV is more efficient than Numeric. Proced. III;
- Numeric. Proced. VI is more efficient than Numeric. Proced. IV;
- Numeric. Proced. VIII is more efficient than Numeric. Proced. VI;
- Numeric. Proced. VIII, Numeric. Proced. X, and Numeric. Proced. XI give approximately the same accuracy;
- Numeric. Proced. IX is more efficient than Numeric. Proced. XI;
- Numeric. Proced. XIII is more efficient than Numeric. Proced. IX;
- Numeric. Proced. VII is more efficient than Numeric. Proced. XIII;
- Numeric. Proced. V is more efficient than Numeric. Proced. VII;
- Numeric. Proced. XIV is more efficient than Numeric. Proced. V;
- Numeric. Proced. XV is more efficient than Numeric. Proced. XIV;
- Numeric. Proced. XII and Numeric. Proced. XV give approximately the same accuracy, and they are the most efficient.
11.6. Two-Body Gravitational Problem
- Numeric. Proced. I, Numeric. Proced. II, Numeric. Proced. IV, Numeric. Proced. V, Numeric. Proced. VI, Numeric. Proced. VII, and Numeric. Proced. VIII are divergent in the data of the specific problem.
- Numeric. Proced. III is convergent but gives one result of low accuracy.
- Numeric. Proced. IX, Numeric. Proced. X, Numeric. Proced. XI, Numeric. Proced. XII, Numeric. Proced. XIII, Numeric. Proced. XIV, and Numeric. Proced. XV give approximately the same accuracy for small step sizes. The accuracy given by the above methods is high.
- For large step sizes, we have the following remarks:
- -
- Numeric. Proced. IX and Numeric. Proced. X are more efficient than Numeric. Proced. XIV;
- -
- Numeric. Proced. XI is more efficient than Numeric. Proced. IX and Numeric. Proced. X;
- -
- Numeric. Proced. XIII is more efficient than Numeric. Proced. XI;
- -
- Numeric. Proced. XV is more efficient than Numeric. Proced. XIII;
- -
- Numeric. Proced. XII is more efficient than Numeric. Proced. XV.
- Based on the above, Numeric. Proced. IX, Numeric. Proced. X, Numeric. Proced. XI, Numeric. Proced. XII, Numeric. Proced. XIII, Numeric. Proced. XIV, and Numeric. Proced. XV are the most efficient for small step sizes. For large step sizes Numeric. Proced. XII is the most efficient.
11.7. Perturbed Two–Body Gravitational Problem-Case
- Numeric. Proced. I, Numeric. Proced. II, Numeric. Proced. IV, Numeric. Proced. V, Numeric. Proced. VI, Numeric. Proced. VII, and Numeric. Proced. VIII are divergent for the data of the specific problem;
- Numeric. Proced. III is convergent, but the given results are of low accuracy;
- Numeric. Proced. IX, Numeric. Proced. X, Numeric. Proced. XI, Numeric. Proced. XII, Numeric. Proced. XIII, Numeric. Proced. XIV, and Numeric. Proced. XV give approximately the same accuracy. The accuracy given by the above methods is high, even for large step sizes.
- For large step sizes, we have the following remarks:
- -
- Numeric. Proced. XI is more efficient than Numeric. Proced. XIV;
- -
- Numeric. Proced. IX is more efficient than Numeric. Proced. XI;
- -
- Numeric. Proced. X is more efficient than Numeric. Proced. IX;
- -
- Numeric. Proced. XIII and Numeric. Proced. X give approximately the same accuracy;
- -
- Numeric. Proced. XII is more efficient than Numeric. Proced. XIII;
- -
- Numeric. Proced. XV is more efficient than Numeric. Proced. XII.
- Based on the above, Numeric. Proced. IX, Numeric. Proced. X, Numeric. Proced. XI, Numeric. Proced. XII, Numeric. Proced. XIII, Numeric. Proced. XIV, and Numeric. Proced. XV are the most efficient for small step sizes. For large step sizes, Numeric. Proced. XV is the most efficient.
- The methodology which is laid out in Section 9 that focuses on the vanishing of phase lag and amplification factor, as well as the eradication of their first derivatives.
- The methodology which is laid out in Section 6 that focuses on the vanishing of phase lag and amplification factor (the phase-fitted and amplification-fitted method).
- The methodology which is laid out in Section 7 that focuses on the vanishing of phase lag and amplification factor (the phase-fitted and amplification-fitted method) as well as the eradication of the first derivative of the phase lag.
- The methodology which is laid out in Section 8 that focuses on the vanishing of phase lag and amplification factor (the phase-fitted and amplification-fitted method) as well as the eradication of the first derivative of the amplification factor.
11.8. High-Order Ordinary Differential Equations and Partial Differential Equations
12. Conclusions
- Methodology which includes the elimination of the derivatives of the phase lag;
- Methodology which includes the elimination of the derivatives of the amplification factor;
- Methodology which includes the elimination of the derivatives of the phase lag and the derivatives of the amplification factor.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Direct Formulae for the Calculation of the Derivatives of the Phase Lag and the Amplification Factor
Appendix A.1. Direct Formula for the Derivative of the Phase Lag
Appendix A.2. Direct Formula for the Derivative of the Amplification Factor
Appendix B. Formula
Appendix C. Formulae , , and
Appendix D. Formula
Appendix E. Formulae , , and
Appendix F. Formula
Appendix G. Formulae , , , and
References
- Landau, L.D.; Lifshitz, F.M. Quantum Mechanics; Pergamon: New York, NY, USA, 1965. [Google Scholar]
- Prigogine, I.; Rice, S.A. (Eds.) Advances in Chemical Physics Vol. 93: New Methods in Computational Quantum Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Simos, T.E. Numerical Solution of Ordinary Differential Equations with Periodical Solution. Ph.D. Dissertation, National Technical University of Athens, Athens, Greece, 1990. (In Greek). [Google Scholar]
- Ixaru, L.G. Numerical Methods for Differential Equations and Applications; Book Series: Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 1984; ISBN 978-90-277-1597-5. [Google Scholar]
- Quinlan, G.D.; Tremaine, S. Symmetric multistep methods for the numerical integration of planetary orbits. Astron. J. 1990, 100, 1694–1700. [Google Scholar] [CrossRef]
- Lyche, T. Chebyshevian multistep methods for ordinary differential equations. Numer. Math. 1972, 10, 65–75. [Google Scholar] [CrossRef]
- Konguetsof, A.; Simos, T.E. On the construction of Exponentially-Fitted Methods for the Numerical Solution of the Schrödinger Equation. J. Comput. Meth. Sci. Eng. 2001, 1, 143–165. [Google Scholar] [CrossRef]
- Simos, T.E. Atomic Structure Computations in Chemical Modelling: Applications and Theory; Hinchliffe, A., UMIST, Eds.; The Royal Society of Chemistry: Washington, DC, USA, 2000; pp. 38–142. [Google Scholar]
- Simos, T.E.; Vigo-Aguiar, J. On the construction of efficient methods for second order IVPs with oscillating solution. Int. J. Mod. Phys. C 2001, 10, 1453–1476. [Google Scholar] [CrossRef]
- Dormand, J.R.; El-Mikkawy, M.E.A.; Prince, P.J. Families of Runge-Kutta-Nyström formulae. IMA J. Numer. Anal. 1987, 7, 235–250. [Google Scholar] [CrossRef]
- Franco, J.M.; Gomez, I. Some procedures for the construction of high-order exponentially fitted Runge-Kutta-Nyström Methods of explicit type. Comput. Phys. Commun. 2013, 184, 1310–1321. [Google Scholar] [CrossRef]
- Franco, J.M.; Gomez, I. Accuracy and linear Stability of RKN Methods for solving second-order stiff problems. Appl. Numer. Math. 2009, 59, 959–975. [Google Scholar] [CrossRef]
- Chien, L.K.; Senu, N.; Ahmadian, A.; Ibrahim, S.N.I. Efficient Frequency-Dependent Coefficients of Explicit Improved Two-Derivative Runge-Kutta Type Methods for Solving Third- Order IVPs. Pertanika J. Sci. Technol. 2023, 31, 843–873. [Google Scholar] [CrossRef]
- Zhai, W.J.; Fu, S.H.; Zhou, T.C.; Xiu, C. Exponentially-fitted and trigonometrically-fitted implicit RKN methods for solving y"=f(t,y). J. Appl. Math. Comput. 2022, 68, 1449–1466. [Google Scholar] [CrossRef]
- Fang, Y.L.; Yang, Y.P.; You, X. An explicit trigonometrically fitted Runge-Kutta method for stiff and oscillatory problems with two frequencies. Int. J. Comput. Math. 2020, 97, 85–94. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Kalogiratou, Z.; Monovasilis, T.; Psihoyios, G.; Simos, T.E. Runge–Kutta type methods with special properties for the numerical integration of ordinary differential equations. Phys. Rep. 2014, 536, 75–146. [Google Scholar] [CrossRef]
- Anastassi, Z.A.; Simos, T.E. Numerical multistep methods for the efficient solution of quantum mechanics and related problems. Phys. Rep. 2009, 482–483, 1–240. [Google Scholar] [CrossRef]
- Chawla, M.M.; Rao, P.S. A Noumerov-Type Method with Minimal Phase-Lag for the Integration of 2nd Order Periodic Initial-Value Problems. J. Comput. Appl. Math. 1984, 11, 277–281. [Google Scholar] [CrossRef]
- Gr, L. Ixaru and M. Rizea, A Numerov-like scheme for the numerical solution of the Schrödinger equation in the deep continuum spectrum of energies. Comput. Phys. Commun. 1980, 19, 23–27. [Google Scholar]
- Raptis, A.D.; Allison, A.C. Exponential-fitting Methods for the numerical solution of the Schrödinger equation. Comput. Phys. Commun. 1978, 14, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, D.; Dai, Y.; Wu, D. An improved trigonometrically fitted P-stable Obrechkoff Method for periodic initial-value problems. Proc. R. Soc.-Math. Phys. Eng. Sci. 2005, 461, 1639–1658. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z. A P-stable eighteenth-order six-Step Method for periodic initial value problems. Int. J. Mod. Phys. C 2007, 18, 419–431. [Google Scholar] [CrossRef]
- Shokri, A.; Khalsaraei, M.M. A new family of explicit linear two-step singularly P-stable Obrechkoff methods for the numerical solution of second-order IVPs. Appl. Math. Comput. 2020, 376, 125116. [Google Scholar] [CrossRef]
- Abdulganiy, R.I.; Ramos, H.; Okunuga, S.A.; Majid, Z.A. A trigonometrically fitted intra-step block Falkner method for the direct integration of second-order delay differential equations with oscillatory solutions. Afr. Mat. 2023, 34, 36. [Google Scholar] [CrossRef]
- Lee, K.C.; Senu, N.; Ahmadian, A.; Ibrahim, S.N.I. High-order exponentially fitted and trigonometrically fitted explicit two-derivative Runge-Kutta-type methods for solving third-order oscillatory problems. Math. Sci. 2022, 16, 281–297. [Google Scholar] [CrossRef]
- Fang, Y.L.; Huang, T.; You, X.; Zheng, J.; Wang, B. Two-frequency trigonometrically-fitted and symmetric linear multi-step methods for second-order oscillators. J. Comput. Appl. Math. 2021, 392, 113312. [Google Scholar] [CrossRef]
- Chun, C.; Neta, B. Trigonometrically-Fitted Methods: A Review. Mathematics 2019, 7, 1197. [Google Scholar] [CrossRef]
- Simos, T.E. A New Methodology for the Development of Efficient Multistep Methods for First–Order IVPs with Oscillating Solutions. Mathematics 2024, 12, 504. [Google Scholar] [CrossRef]
- Simos, T.E. Efficient Multistep Algorithms for First–Order IVPs with Oscillating Solutions: II Implicit and Predictor—Corrector Algorithms. Symmetry 2024, 16, 508. [Google Scholar] [CrossRef]
- Saadat, H.; Kiyadeh, S.H.H.; Karim, R.G.; Safaie, A. Family of phase fitted 3-step second-order BDF methods for solving periodic and orbital quantum chemistry problems. J. Math. Chem. 2024, 62, 1223–1250. [Google Scholar] [CrossRef]
- Stiefel, E.; Bettis, D.G. Stabilization of Cowell’s method. Numer. Math. 1969, 13, 154–175. [Google Scholar] [CrossRef]
- Fehlberg, E. Classical Fifth-, Sixth-, Seventh-, and Eighth-order Runge-Kutta Formulas with Stepsize Control. NASA Technical Report 287 (1968). Available online: https://ntrs.nasa.gov/api/citations/19680027281/downloads/19680027281.pdf (accessed on 12 December 2022).
- Cash, J.R.; Karp, A.H. A variable order Runge–Kutta method for initial value problems with rapidly varying right-hand sides. ACM Trans. Math. Softw. 1990, 16, 201–222. [Google Scholar] [CrossRef]
- Franco, J.M.; Palacios, M. High-order P-stable multistep methods. J. Comput. Appl. Math. 1990, 30, 1–10. [Google Scholar] [CrossRef]
- Petzold, L.R. An efficient numerical method for highly oscillatory ordinary differential equations. SIAM J. Numer. Anal. 1981, 18, 455–479. [Google Scholar] [CrossRef]
- Simos, T.E. New Open Modified Newton Cotes Type Formulae as Multilayer Symplectic Integrators. Appl. Math. Model. 2013, 37, 1983–1991. [Google Scholar] [CrossRef]
- Franco, J.; Gómez, I. Trigonometrically–fitted nonuliear two–step methods for solving second order oscillatory IVPs. Appl. Math. Comput. 2014, 232, 643–657. [Google Scholar]
- Ramos, H.; Vigo-Aguiar, J. On the frequency choice in trigonometrically fitted methods. Appl. Math. Lett. 2010, 23, 1378–1381. [Google Scholar] [CrossRef]
- Ixaru, L.G.; Berghe, G.V.; De Meyer, H. Frequency evaluation in exponential fitting multistep algorithms for ODEs. J. Comput. Appl. Math. 2002, 140, 423–434. [Google Scholar] [CrossRef]
- Boyce, W.E.; DiPrima, R.C.; Meade, D.B. Elementary Differential Equations and Boundary Value Problems, 11th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; NJ07030-5774. [Google Scholar]
- Evans, L.C. Partial Differential Equations, 2nd ed.; American Mathematical Society: Providence, RI, USA, 2010; Chapter 3; pp. 91–135. [Google Scholar]
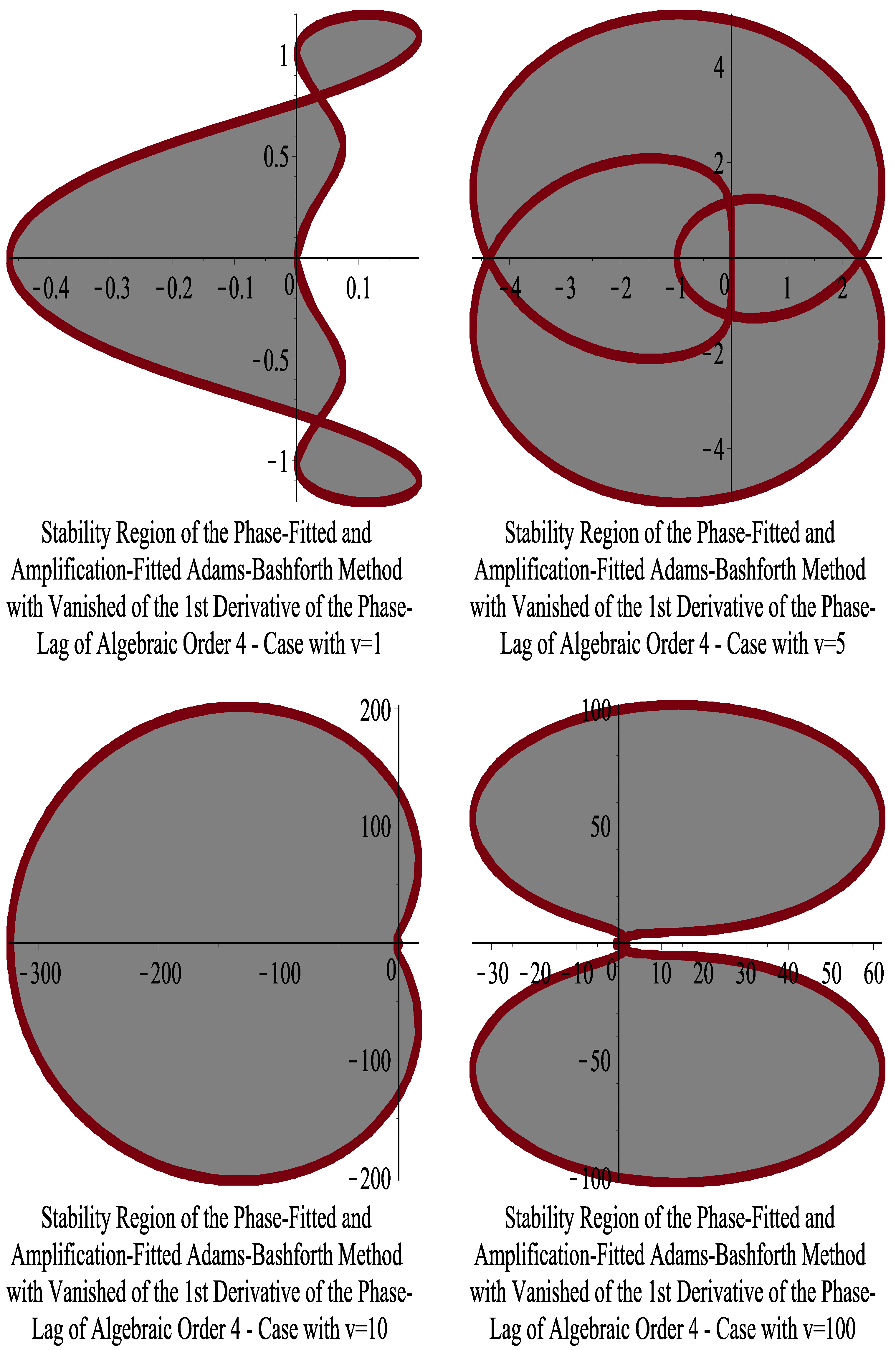













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simos, T.E. A New Methodology for the Development of Efficient Multistep Methods for First-Order Initial Value Problems with Oscillating Solutions: III the Role of the Derivative of the Phase Lag and the Derivative of the Amplification Factor. Axioms 2024, 13, 514. https://doi.org/10.3390/axioms13080514
Simos TE. A New Methodology for the Development of Efficient Multistep Methods for First-Order Initial Value Problems with Oscillating Solutions: III the Role of the Derivative of the Phase Lag and the Derivative of the Amplification Factor. Axioms. 2024; 13(8):514. https://doi.org/10.3390/axioms13080514
Chicago/Turabian StyleSimos, Theodore E. 2024. "A New Methodology for the Development of Efficient Multistep Methods for First-Order Initial Value Problems with Oscillating Solutions: III the Role of the Derivative of the Phase Lag and the Derivative of the Amplification Factor" Axioms 13, no. 8: 514. https://doi.org/10.3390/axioms13080514
APA StyleSimos, T. E. (2024). A New Methodology for the Development of Efficient Multistep Methods for First-Order Initial Value Problems with Oscillating Solutions: III the Role of the Derivative of the Phase Lag and the Derivative of the Amplification Factor. Axioms, 13(8), 514. https://doi.org/10.3390/axioms13080514





