A Conservative Difference Scheme for Solving the Coupled Fractional Schrödinger–Boussinesq System
Abstract
1. Introduction
2. Construction of Conservative Difference Scheme
2.1. Notations and Lemmas
2.2. Derivation of the Conservative Difference Scheme
3. Theoretical Analysis
3.1. The Conservative Property
3.2. A Priori Bound
3.3. Solvability
3.4. Convergence
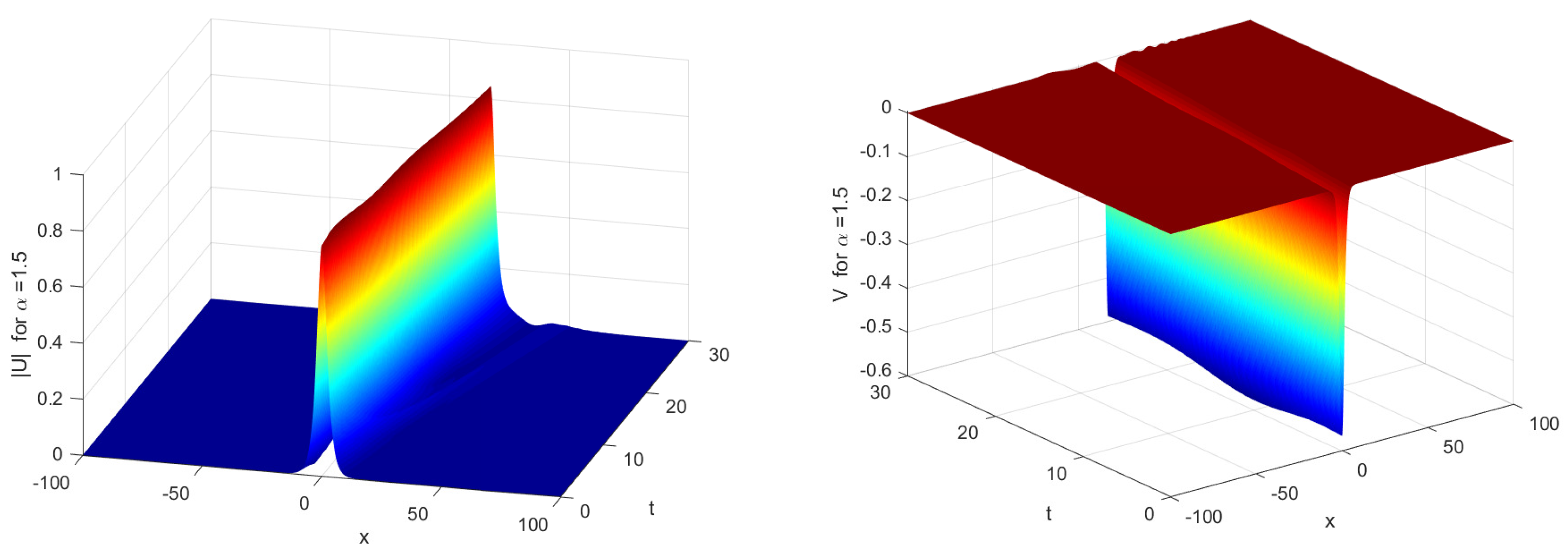
4. Numerical Experiments
| Algorithm 1: The conservative scheme (26)–(30) of the FCSBS |
1 Given: , and . 2 Step 1: Solve and from (27) and (28). 3 Step 2: Solve from (26). |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, B. The global solution of the system of equations for complex Schrödinger field coupled with Boussinesq type self-consistent field. Acta Math. Sin. 1983, 26, 295–306. (In Chinese) [Google Scholar] [CrossRef]
- Guo, B. Initial boundary value problem for one class of system of multidimensional nonlinear Schrödinger–Boussinesq type equations. J. Math. Res. Expo. 1988, 8, 61–71. [Google Scholar]
- Banquet, C.; Ferreira, C.F.; Villamizar-Roa, E.J. On the Schrödinger–Boussinesq system with singular initial data. J. Math. Anal. Appl. 2013, 400, 487–496. [Google Scholar] [CrossRef]
- Esfahani, A.; Pastor, A. Well-posedness and orbital stability of traveling waves for the Schrödinger–Boussinesq system. Nonlinear Anal. Real 2015, 22, 206–218. [Google Scholar] [CrossRef]
- Liu, T. Porosity reconstruction based on biot elastic model of porous media by homotopy perturbation method. Chaos Soliton. Fract. 2022, 158, 112007. [Google Scholar] [CrossRef]
- Liu, T. Parameter estimation with the multigrid-homotopy method for a nonlinear diffusion equation. J. Comput. Appl. Math. 2022, 413, 114393. [Google Scholar] [CrossRef]
- Yao, R.; Li, Z. Exact explicit solutions of the nonlinear Schrödinger equation coupled to the Boussinesq equation. Acta Math. Sci. 2003, 23B, 453–460. [Google Scholar] [CrossRef]
- Kumar, D.; Kaplan, M. Application of the modified Kudryashov method to the generalized Schrödinger–Boussinesq equations. Opt. Quant. Electron. 2018, 50, 329. [Google Scholar] [CrossRef]
- Bilige, S.; Chaolu, T.; Wang, X. Application of the extended simplest equation method to the coupled Schrödinger–Boussinesq equation. Appl. Math. Comput. 2013, 224, 517–523. [Google Scholar] [CrossRef]
- Deng, X. Exact solitary and periodic wave solutions for the coupled Schrödinger–Boussinesq equation. Optik 2017, 136, 312–318. [Google Scholar] [CrossRef]
- Huang, L.; Jiao, Y.; Liang, D. Multi-symplectic scheme for the coupled Schrödinger–Boussinesq equations. Chin. Phys. B 2013, 22, 070201. [Google Scholar] [CrossRef]
- Liao, F.; Zhang, L.; Wang, S. Numerical analysis of cubic orthogonal spline collocation methods for the coupled Schrödinger–Boussinesq equtions. Appl. Numer. Math. 2017, 119, 194–212. [Google Scholar] [CrossRef]
- Oruç, Ö. A local radial basis function-finite difference (RBF-FD) method for solving 1D and 2D coupled Schrödinger–Boussinesq (SBq) equations. Eng. Anal. Bound Elem. 2021, 129, 56–66. [Google Scholar] [CrossRef]
- Li, M. Cut-off error splitting technique for conservative nonconforming VEM for N-coupled nonlinear Schrödinger–Boussinesq equations. J. Sci. Comput. 2022, 93, 86. [Google Scholar] [CrossRef]
- He, Y.; Chen, H. Efficient and conservative compact difference scheme for the coupled Schrödinger–Boussinesq equations. Appl. Numer. Math. 2022, 182, 285–307. [Google Scholar] [CrossRef]
- Yan, J.; Zheng, L.; Lu, F.; Zhang, Q. Efficient energy-preserving methods for the Schrödinger–Boussinesq equation. Math. Meth. Appl. Sci. 2022. early view. [Google Scholar] [CrossRef]
- Tian, J.; Sun, Z.; Liu, Y.; Li, H. TT-M finite element algorithm for the coupled Schrödinger–Boussinesq equations. Axioms 2022, 11, 314. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, Z.; Liu, Y.; Li, H. Structure-preserving BDF2 FE method for the coupled Schrödinger–Boussinesq equations. Numer. Algorithms 2023, 93, 1243–1267. [Google Scholar] [CrossRef]
- Almushaira, M. Efficient eighth-order accurate energy-preserving compact difference schemes for the coupled Schrödinger–Boussinesq equations. Math. Methods Appl. Sci. 2023, 46, 17199–17225. [Google Scholar] [CrossRef]
- Laskin, N. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 2000, 268, 298–305. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E.; Hendy, A.S.; De Staelen, R.H. A compact fourth-order in space energy-preserving method for Riesz space-fractional nonlinear wave equations. Appl. Math. Comput. 2018, 325, 1–14. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C. An energy conservative difference scheme for the nonlinear fractional Schrödinger equation. J. Comput. Phys. 2015, 293, 238–251. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C. An implicit midpoint difference scheme for the fractional Ginzburg-Landau equation. J. Comput. Phys. 2016, 312, 31–49. [Google Scholar] [CrossRef]
- Han, L.; Zhang, J.; Guo, B. Global well-posedness for the fractional Schrödinger–Boussinesq system. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 2644–2652. [Google Scholar] [CrossRef]
- Alzahrani, A.B.M. Numerical analysis of nonlinear coupled Schrödinger-KdV system with fractional derivative. Symmetry 2023, 15, 1666. [Google Scholar] [CrossRef]
- Alzahrani, A.B.M.; Alhawael, G. Novel computations of the time-fractional coupled Korteweg-de Vries equations via non-singular kernel operators in terms of the natural transform. Symmetry 2023, 15, 2010. [Google Scholar] [CrossRef]
- Noor, S.; Alotaibi, B.M.; Shah, R.; Ismaeel, S.M.E.; El-Tantawy, S.A. On the solitary waves and nonlinear oscillations to the fractional Schrödinger-KdV equation in the framework of the Caputo operator. Symmetry 2023, 15, 1616. [Google Scholar] [CrossRef]
- Noor, S.; Hammad, M.A.; Shah, R.; Alrowaily, A.W.; El-Tantawy, S.A. Numerical investigation of fractional-order Fornberg-Whitham equations in the framework of Aboodh transformation. Symmetry 2023, 15, 1353. [Google Scholar] [CrossRef]
- Liu, T.; Shateyi, S. Efficient fourth-order weights in Kernel-Type methods without increasing the stencil size with an application in a time-dependent fractional PDE problem. Mathematics 2024, 12, 1121. [Google Scholar] [CrossRef]
- Shi, Y.; Ma, Q.; Ding, X. Dynamical behaviors in a discrete fractional-order predator-prey system. Filomat 2018, 32, 5857–5874. [Google Scholar] [CrossRef]
- Shi, Y.; Ma, Q.; Ding, X. A New Energy-Preserving Scheme for the Fractional Klein-Gordon-Schrödinger Equations. Adv. Appl. Math. Mech. 2019, 11, 1219–1247. [Google Scholar]
- Shi, Y.; Ma, Q.; Ding, X. Conservative difference scheme for fractional Zakharov system and convergence analysis. Int. J. Comput. Math. 2021, 98, 1474–1494. [Google Scholar] [CrossRef]
- Shao, J.; Guo, B. The Cauchy problem for Schrödinger-damped Boussinesq system. J. Math. Anal. Appl. 2021, 494, 124639. [Google Scholar] [CrossRef]
- Ray, S. A novel approach with time-splitting spectral technique for the coupled Schrödinger–Boussinesq equations involving Riesz fractional derivative. Commun. Theor. Phys. 2017, 68, 301–308. [Google Scholar]
- Liao, F.; Zhang, L.; Hu, X. Conservative finite difference methods for fractional Schrödinger–Boussinesq equations and convergence analysis. Numer. Methods Partial Differ. Equ. 2019, 35, 1305–1325. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Riesz potential operators and inverses via fractional centred derivatives. Int. J. Math. Math. Sci. 2006, 2006, 048391. [Google Scholar] [CrossRef]
- Sun, Z.Z. On the compact difference schemes for heat equation with Neumann boundary conditions. Numer. Methods Partial Differ. Equ. 2009, 25, 1320–1341. [Google Scholar] [CrossRef]
- Kirkpatrick, K.; Lenzmann, E.; Staffilani, G. On the continuum limit for discrete NLS with long-range lattice interactions. Commun. Math. Phys. 2013, 317, 563–591. [Google Scholar] [CrossRef]
- Hardy, G.; Littlewood, J.; Polya, G. Inequalities; Cambridge University Press: London, UK, 1952. [Google Scholar]
- Sun, Z.; Gao, G. A Finite Difference Method for Fractional Differential Equations; Science Press: Beijing, China, 2015. [Google Scholar]
- Sun, Z. Numerical Methods of the Partial Differential Equation, 3rd ed.; Science Press: Beijing, China, 2022. [Google Scholar]
- Zhou, Y.L. Application of Discrete Functional Analysis to the Finite Difference Method; International Academic Publishers: Beijing, China, 1991. [Google Scholar]


| 0.2 | 1.9023 | - | 3.0730 | - |
| 0.1 | 4.6269 | 2.0397 | 7.8856 | 1.9624 |
| 0.05 | 1.1443 | 2.0156 | 1.9945 | 1.9832 |
| 0.025 | 2.8480 | 2.0064 | 5.0138 | 1.9920 |
| h | ||||
|---|---|---|---|---|
| 0.8 | 1.3701 | - | 2.4057 | - |
| 0.4 | 8.3255 | 4.0406 | 1.1953 | 4.3310 |
| 0.2 | 5.1080 | 4.0267 | 7.5222 | 3.9901 |
| 0.1 | 3.2168 | 3.9891 | 4.7002 | 4.0004 |
| 0.4 | 1.0515 | - | 1.4519 | - | |
| 0.2 | 2.6501 | 1.9883 | 3.8539 | 1.9135 | |
| 0.1 | 6.6320 | 1.9985 | 9.9573 | 1.9525 | |
| 0.05 | 1.6427 | 2.0134 | 2.4988 | 1.9945 | |
| 0.4 | 1.0853 | - | 1.8775 | - | |
| 0.2 | 2.7038 | 2.0051 | 5.0057 | 1.9072 | |
| 0.1 | 6.5112 | 2.0540 | 1.2739 | 1.9744 | |
| 0.05 | 1.5851 | 2.0384 | 3.1749 | 2.0044 | |
| 0.4 | 8.4791 | - | 2.1617 | - | |
| 0.2 | 1.8849 | 2.1694 | 5.5049 | 1.9734 | |
| 0.1 | 4.5930 | 2.0370 | 1.3870 | 1.9888 | |
| 0.05 | 1.1236 | 2.0313 | 3.4447 | 2.0095 |
| h | |||||
|---|---|---|---|---|---|
| 0.8 | 6.7973 | 2.7931 | |||
| 0.4 | 3.5251 | 4.2692 | 1.4894 | 4.2291 | |
| 0.2 | 2.3469 | 3.9088 | 9.1033 | 4.0322 | |
| 0.8 | 4.4944 | 2.7949 | |||
| 0.4 | 2.2684 | 4.3084 | 1.5832 | 4.1419 | |
| 0.2 | 1.4070 | 4.0109 | 9.6993 | 4.0288 | |
| 0.8 | 1.9728 | 2.6786 | |||
| 0.4 | 1.2055 | 4.0326 | 1.5358 | 4.1244 | |
| 0.2 | 7.4847 | 4.0095 | 9.4378 | 4.0244 |
| 2.554995107627433 | 2.554995107627433 | 2.554995107627433 | |
| 2.554995107626755 | 2.554995107629729 | 2.554995107640402 | |
| 2.554995107626069 | 2.554995107632120 | 2.554995107656555 | |
| 2.554995107625393 | 2.554995107634486 | 2.554995107675087 | |
| 2.554995107624756 | 2.554995107636796 | 2.554995107695591 | |
| 2.554995107624175 | 2.554995107639026 | 2.554995107716158 |
| −2.129162589689532 | −2.129162589689532 | −2.129162589689532 | |
| −2.129162589689426 | −2.129162589689919 | −2.129162589705912 | |
| −2.129162589689318 | −2.129162589694141 | −2.129162589842022 | |
| −2.129162589689236 | −2.129162589706523 | −2.129162590245636 | |
| −2.129162589689183 | −2.129162589730667 | −2.129162591086285 | |
| −2.129162589689132 | −2.129162589768579 | −2.129162592542394 |
| 0.709988640473137 | 0.736137911989638 | 0.760042303573453 | |
| 0.709988638543045 | 0.736137992708215 | 0.760042445633956 | |
| 0.709988636400984 | 0.736137952537480 | 0.760042483756246 | |
| 0.709988634397767 | 0.736137815839193 | 0.760042226275524 | |
| 0.709988632497735 | 0.736137699207129 | 0.760041902905055 | |
| 0.709988630697259 | 0.736137652809705 | 0.760041732381828 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Yan, R.; Liu, T. A Conservative Difference Scheme for Solving the Coupled Fractional Schrödinger–Boussinesq System. Axioms 2024, 13, 400. https://doi.org/10.3390/axioms13060400
Shi Y, Yan R, Liu T. A Conservative Difference Scheme for Solving the Coupled Fractional Schrödinger–Boussinesq System. Axioms. 2024; 13(6):400. https://doi.org/10.3390/axioms13060400
Chicago/Turabian StyleShi, Yao, Rian Yan, and Tao Liu. 2024. "A Conservative Difference Scheme for Solving the Coupled Fractional Schrödinger–Boussinesq System" Axioms 13, no. 6: 400. https://doi.org/10.3390/axioms13060400
APA StyleShi, Y., Yan, R., & Liu, T. (2024). A Conservative Difference Scheme for Solving the Coupled Fractional Schrödinger–Boussinesq System. Axioms, 13(6), 400. https://doi.org/10.3390/axioms13060400







