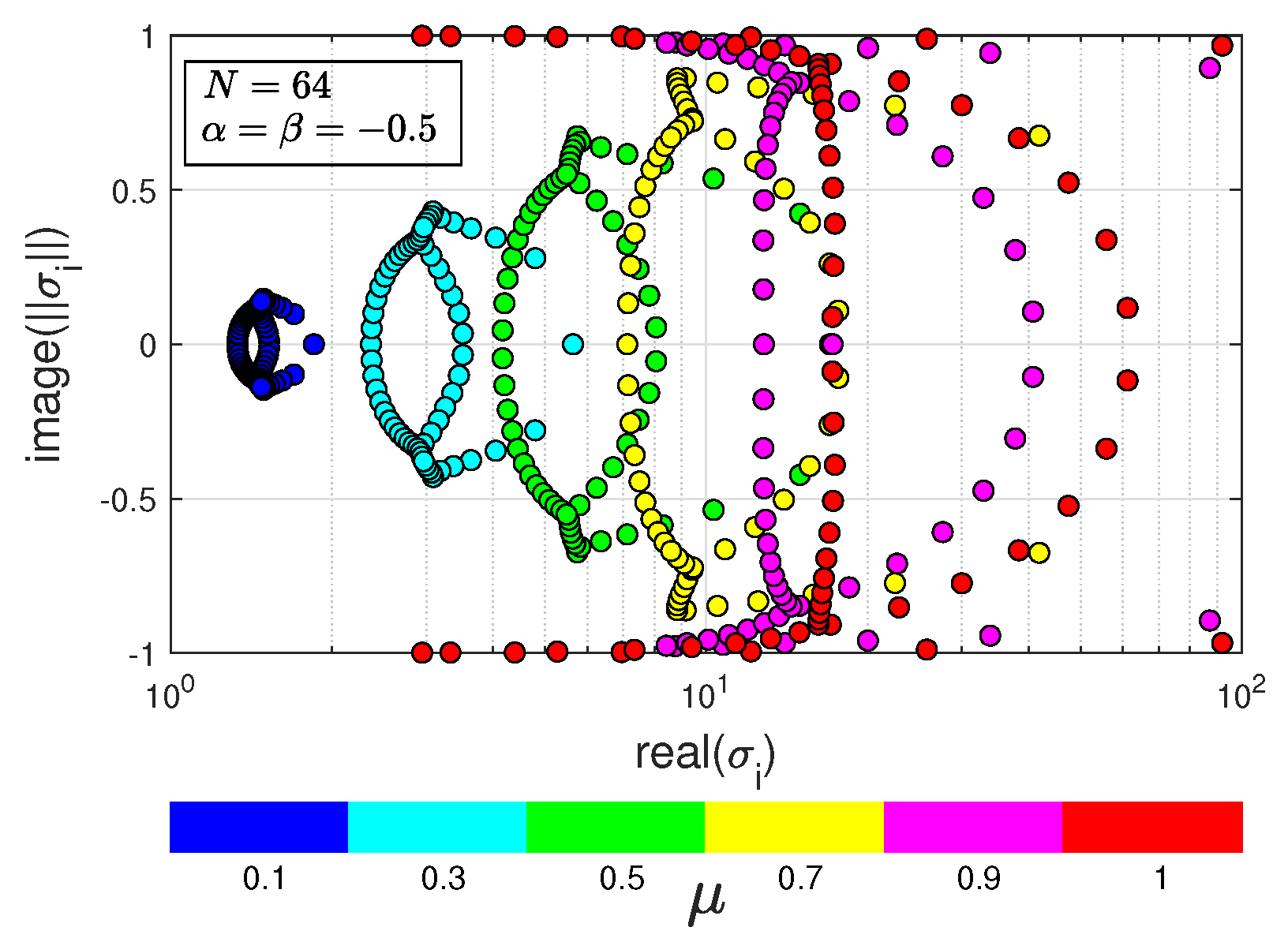
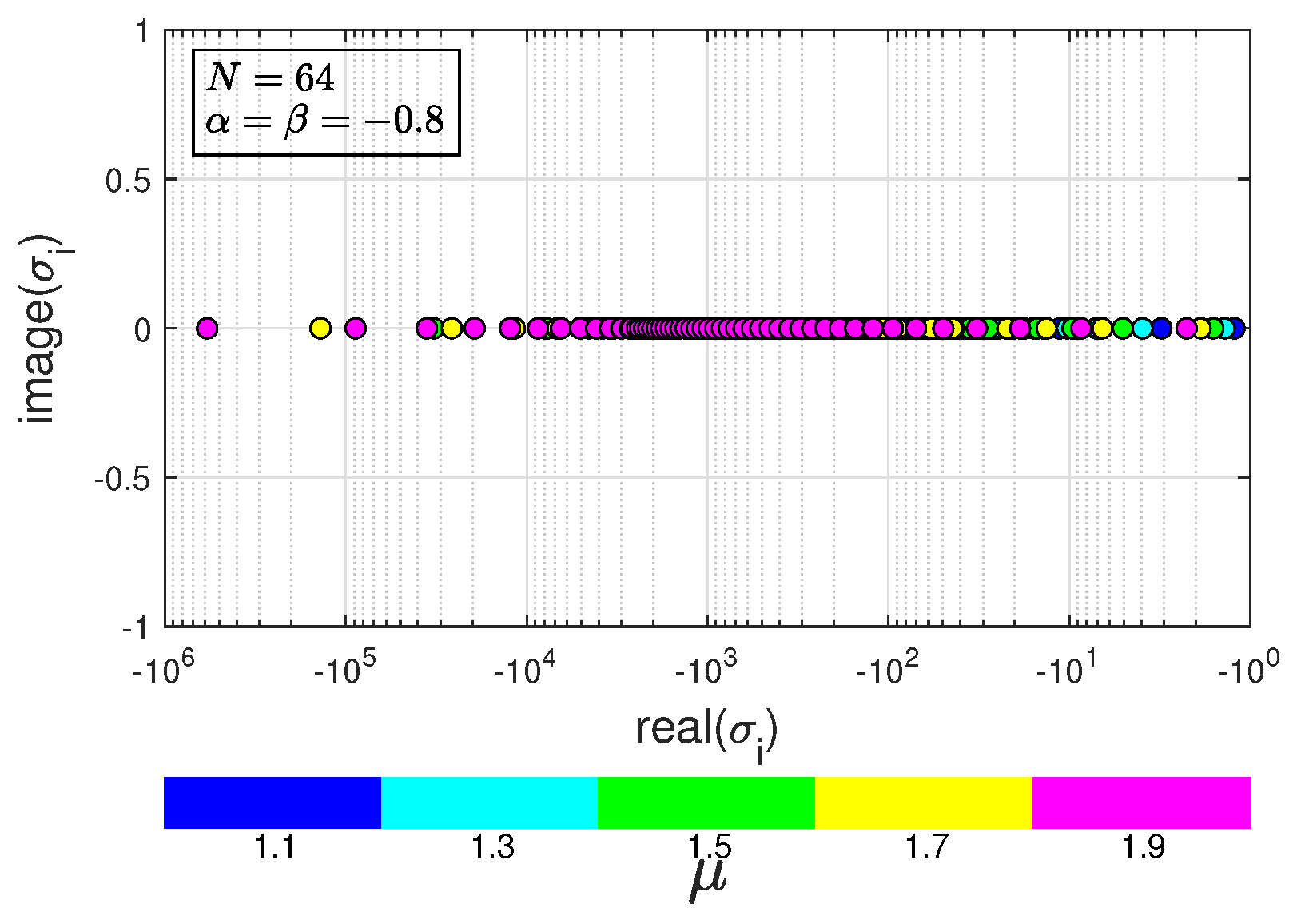
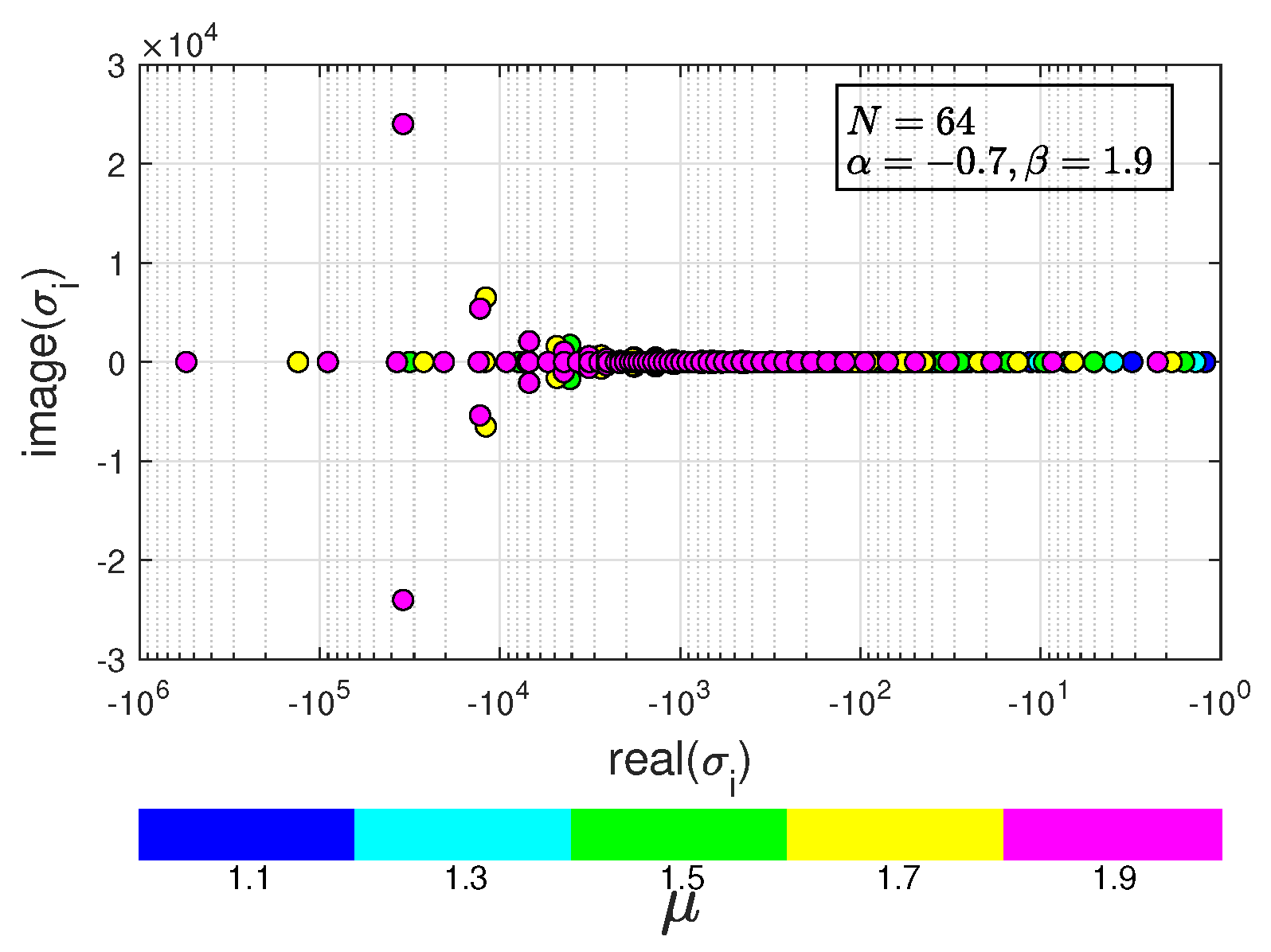
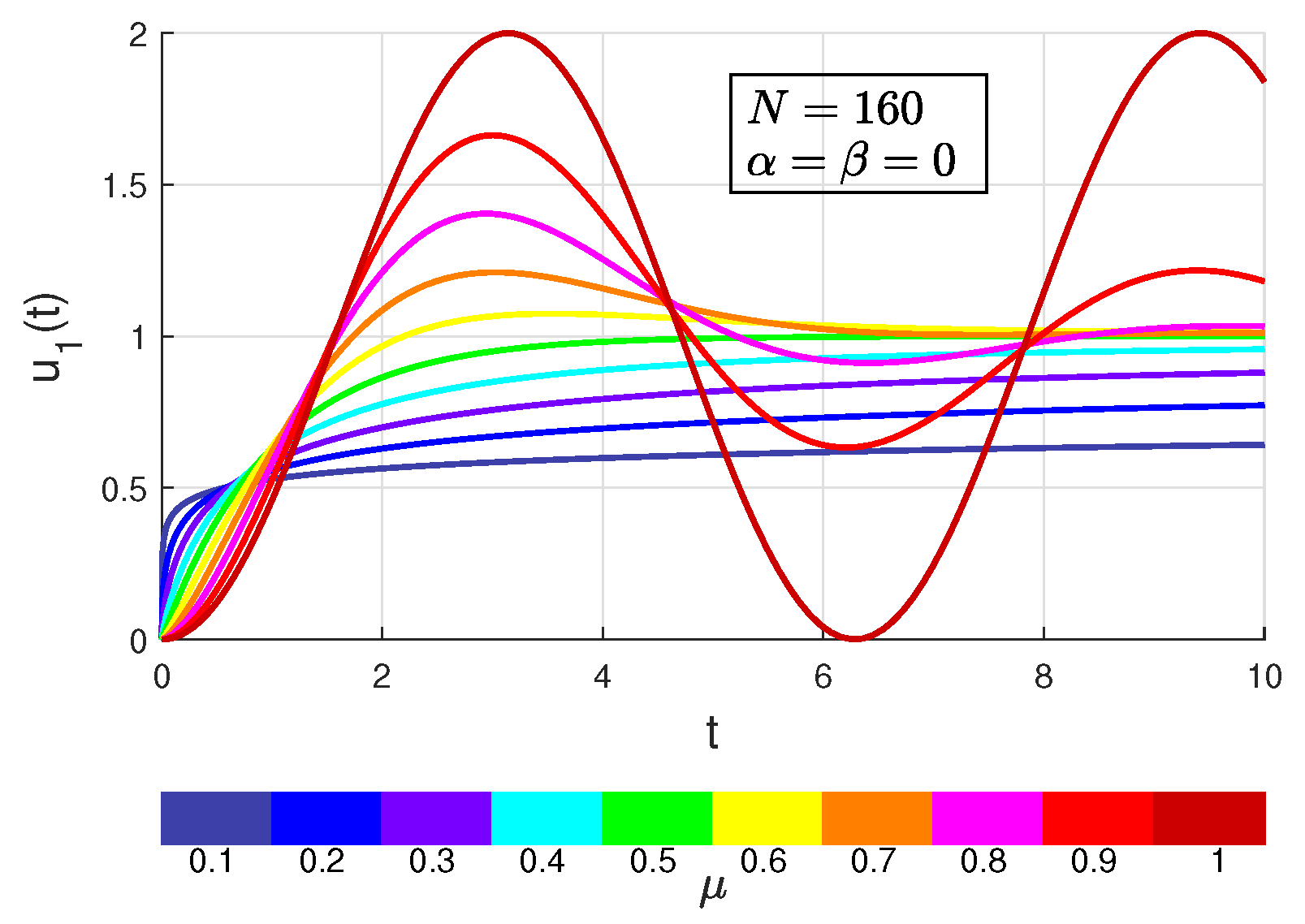
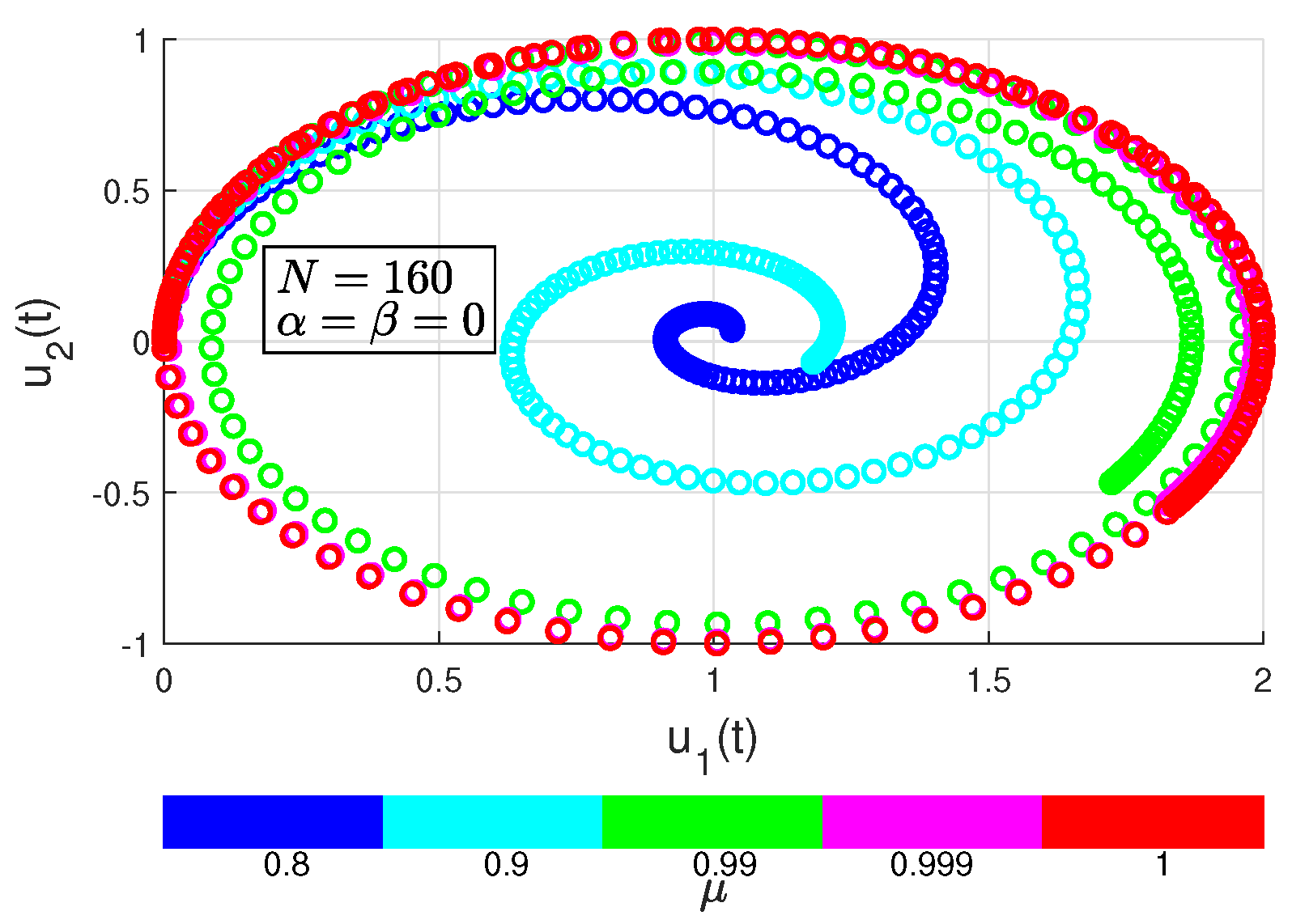
Figure 1.
Eigenvalues of : .
Figure 1.
Eigenvalues of : .
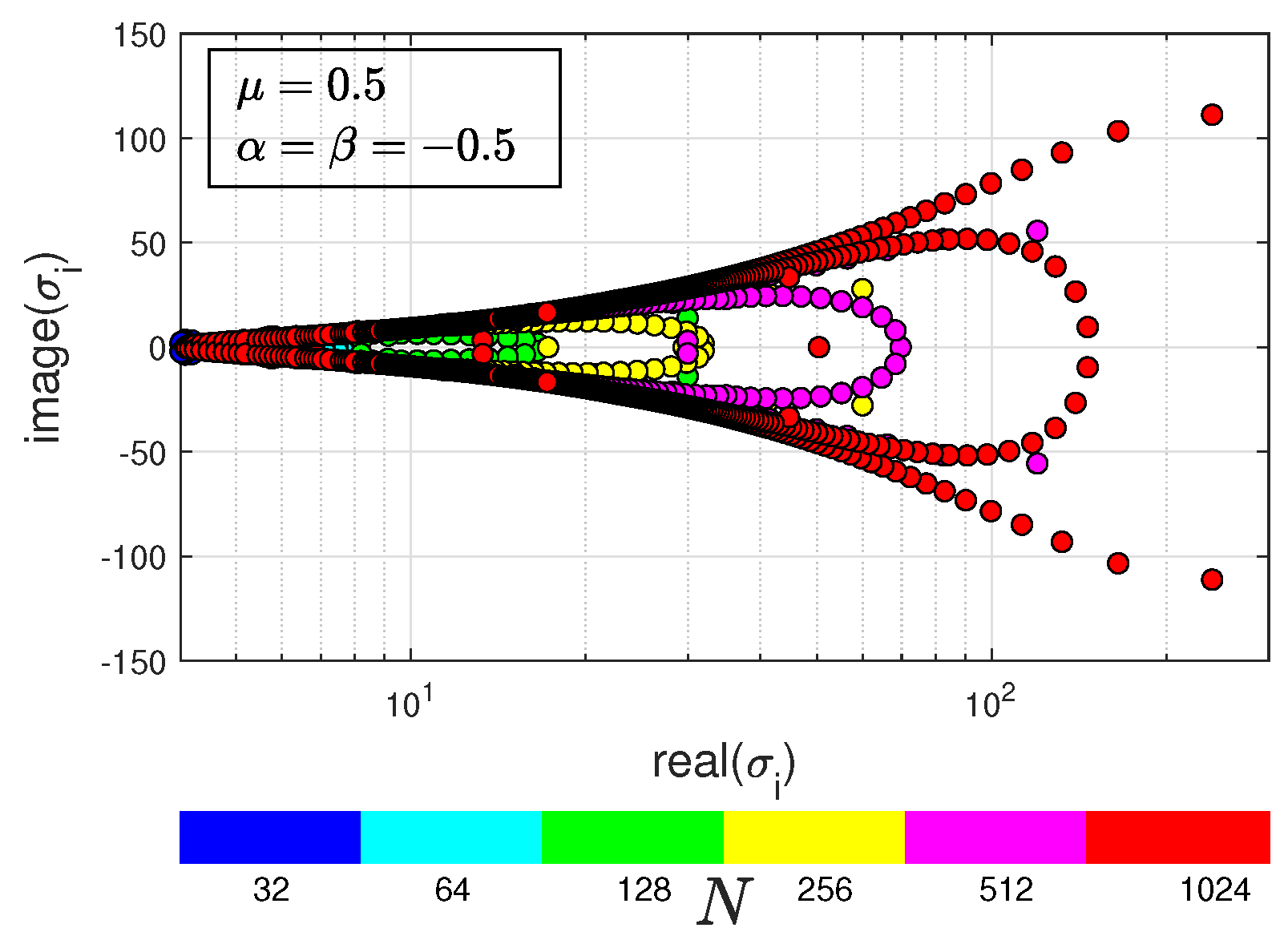
Figure 2.
Eigenvalues of : .
Figure 2.
Eigenvalues of : .
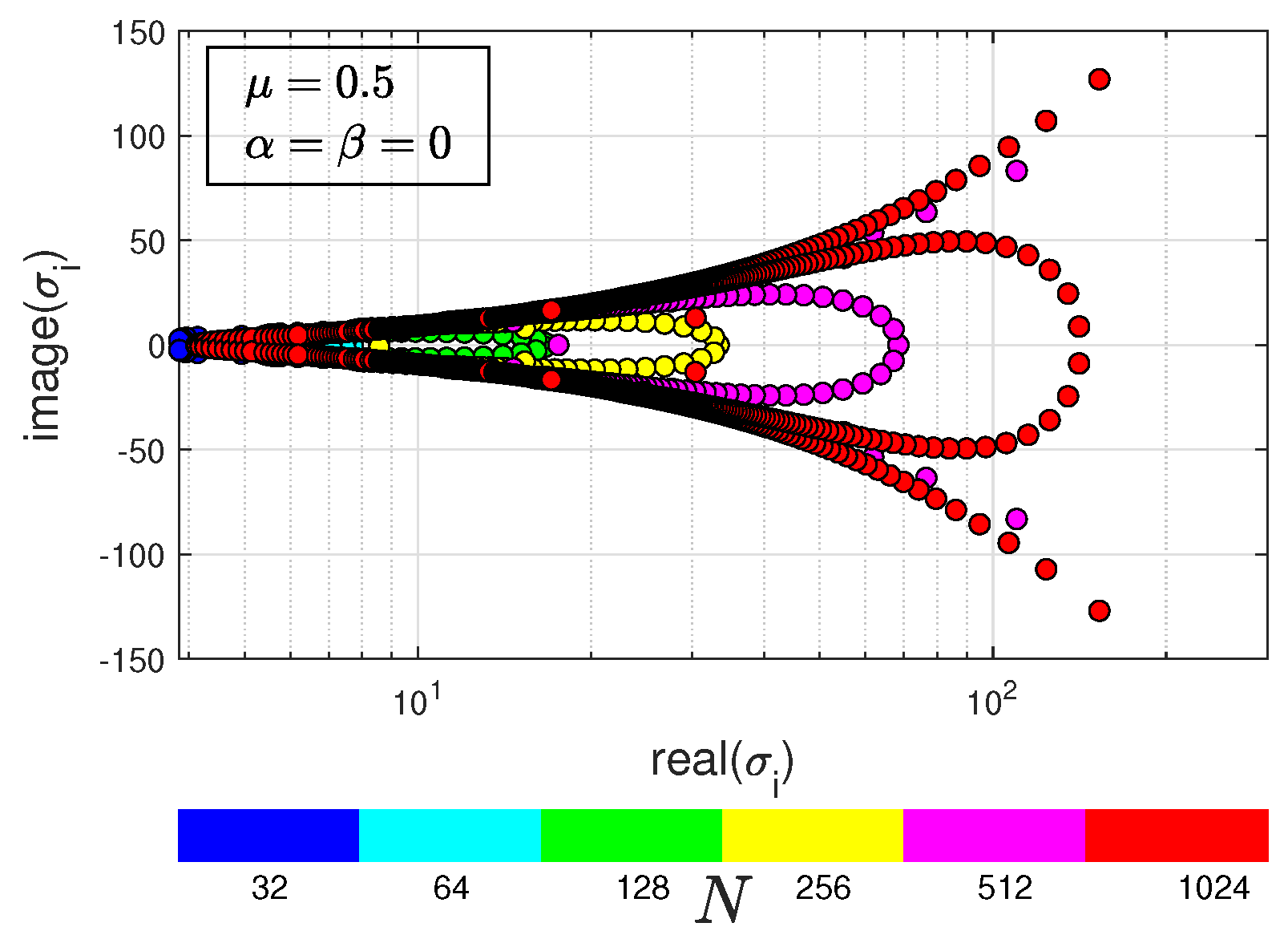
Figure 3.
Eigenvalues of : .
Figure 3.
Eigenvalues of : .
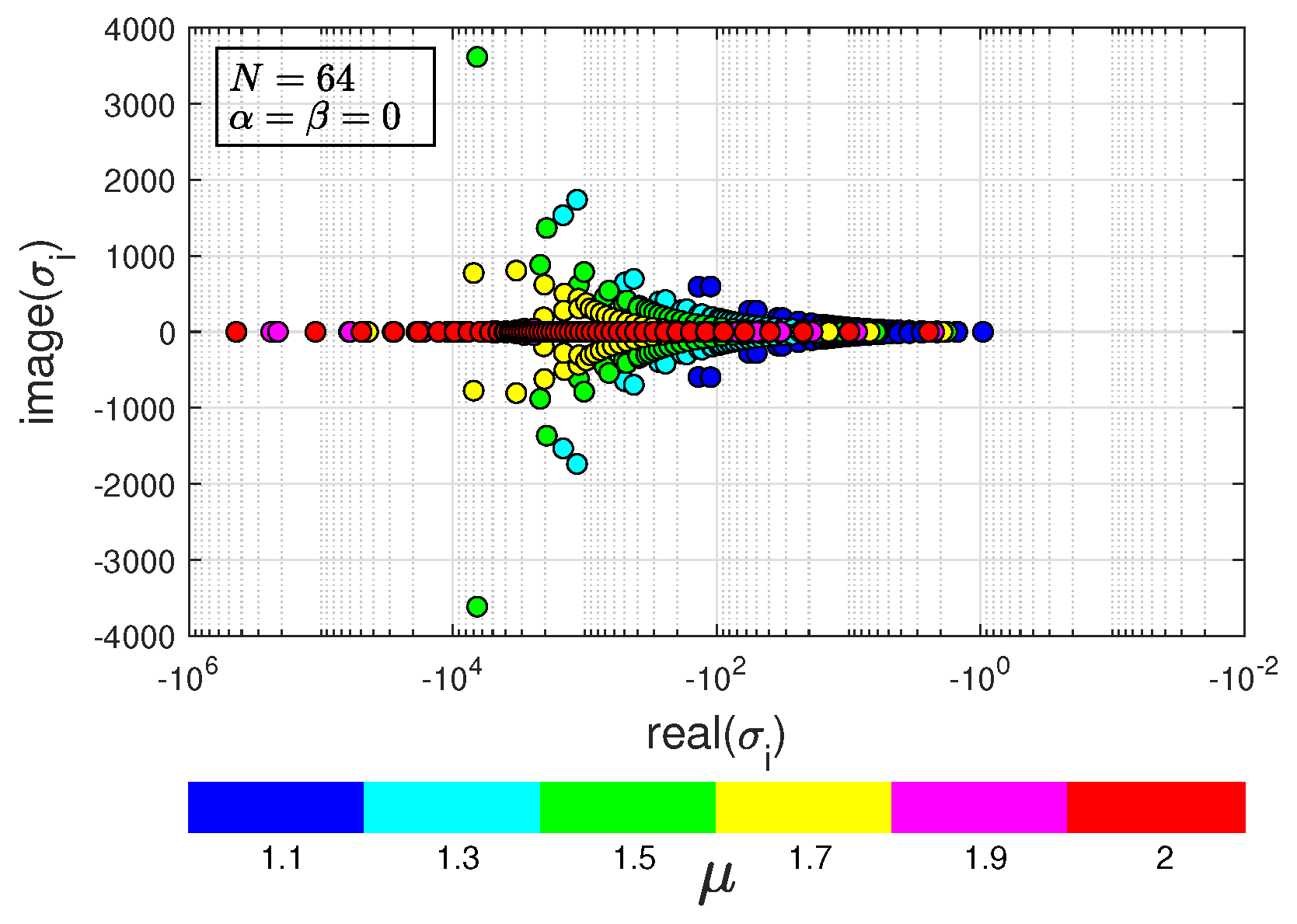
Figure 4.
Eigenvalues of : .
Figure 4.
Eigenvalues of : .
Figure 5.
Eigenvalues of : .
Figure 5.
Eigenvalues of : .
Figure 6.
Eigenvalues of : .
Figure 6.
Eigenvalues of : .
Figure 7.
Eigenvalues of : .
Figure 7.
Eigenvalues of : .
Figure 8.
Eigenvalues of : .
Figure 8.
Eigenvalues of : .
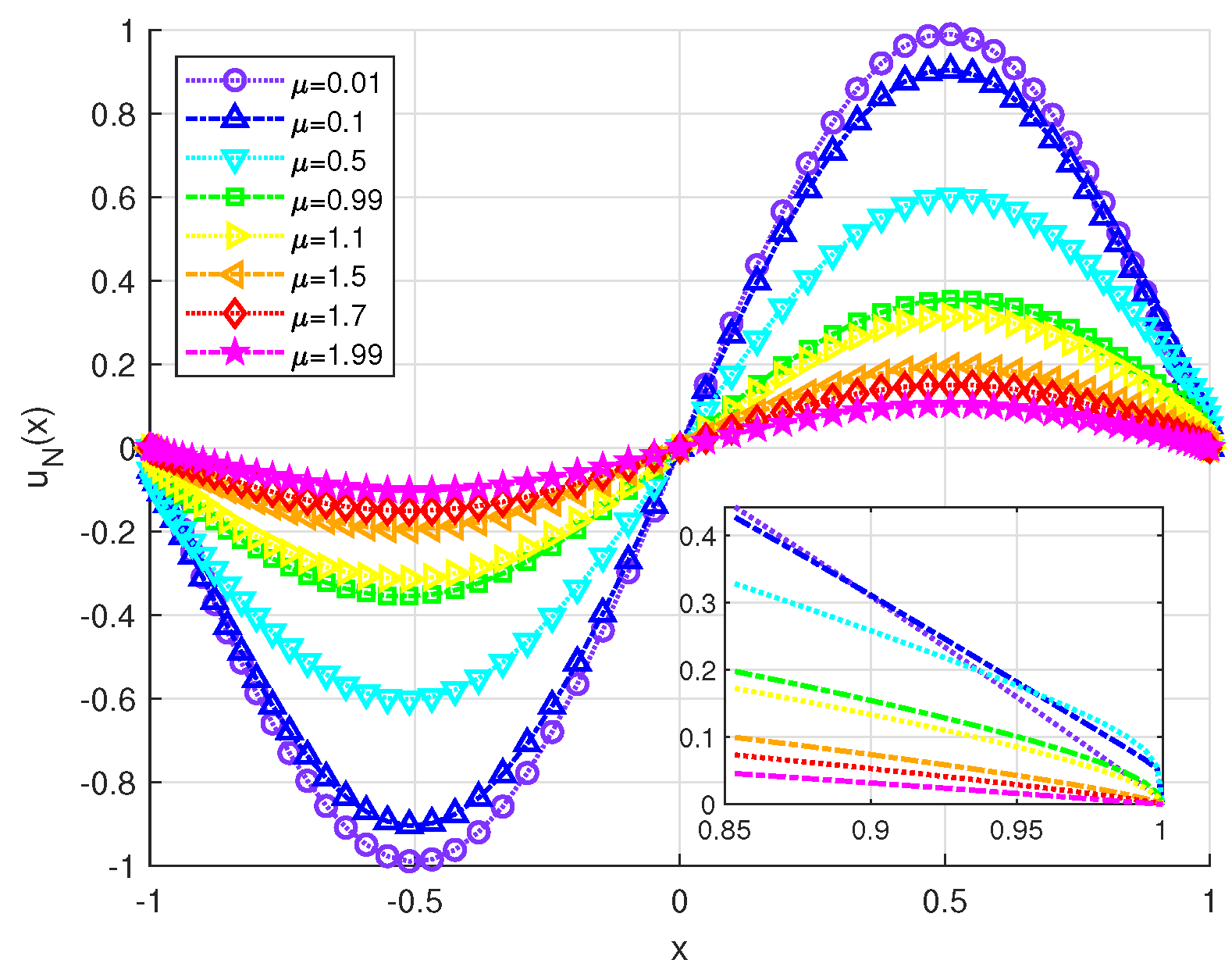
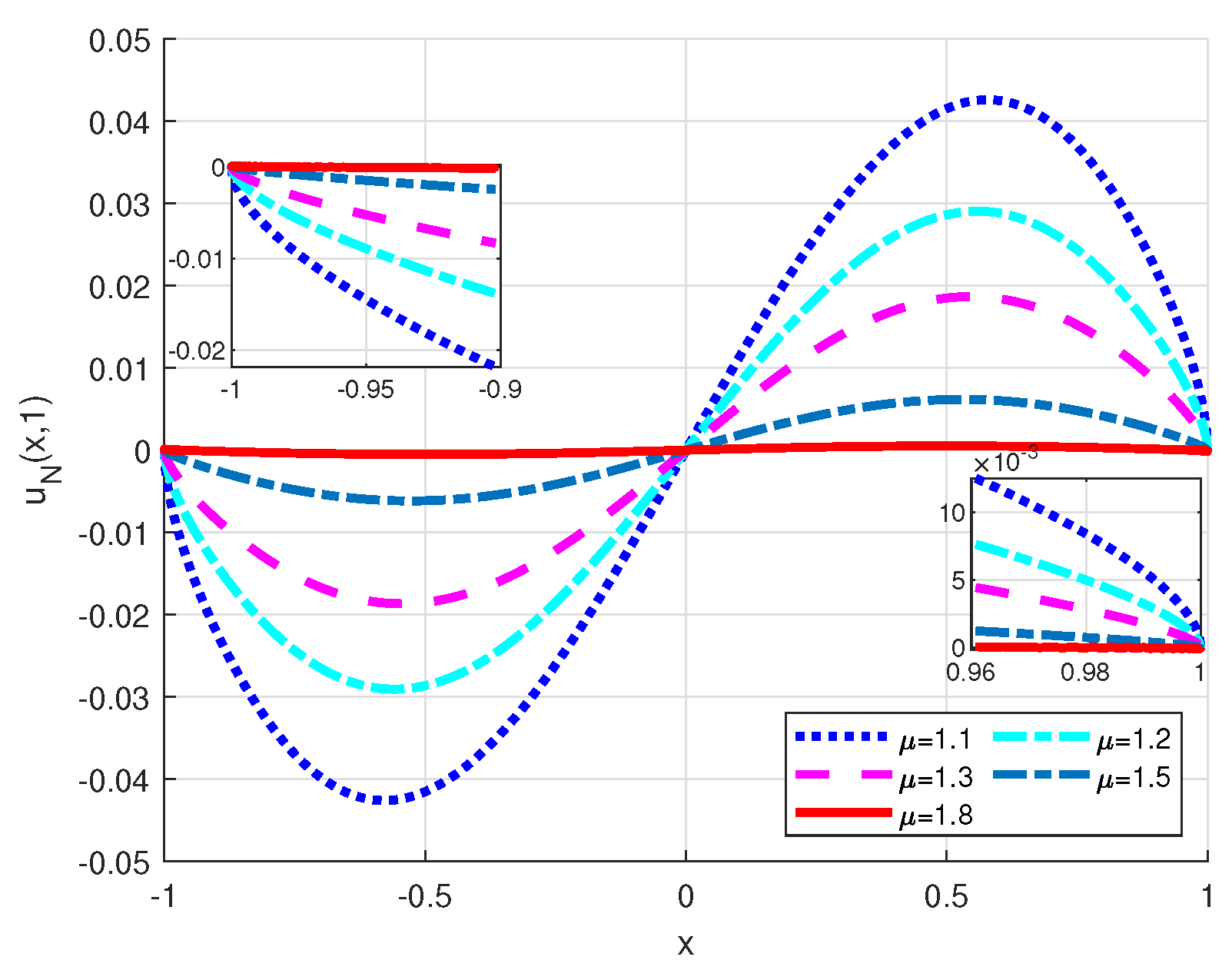
Figure 9.
Curves of numerical solution of Example 4.
Figure 9.
Curves of numerical solution of Example 4.
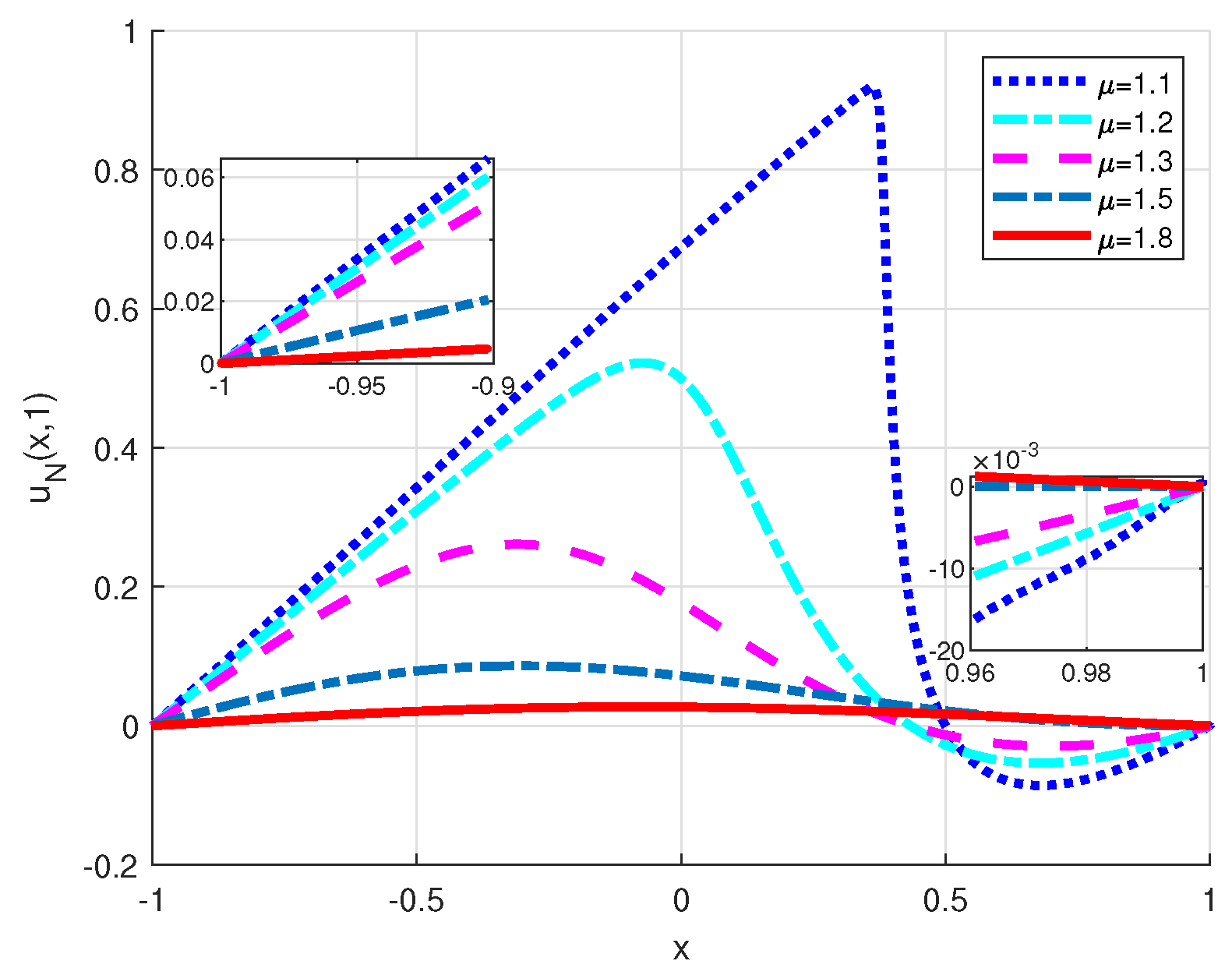
Figure 10.
Portrait of phase plane and of Example 4.
Figure 10.
Portrait of phase plane and of Example 4.
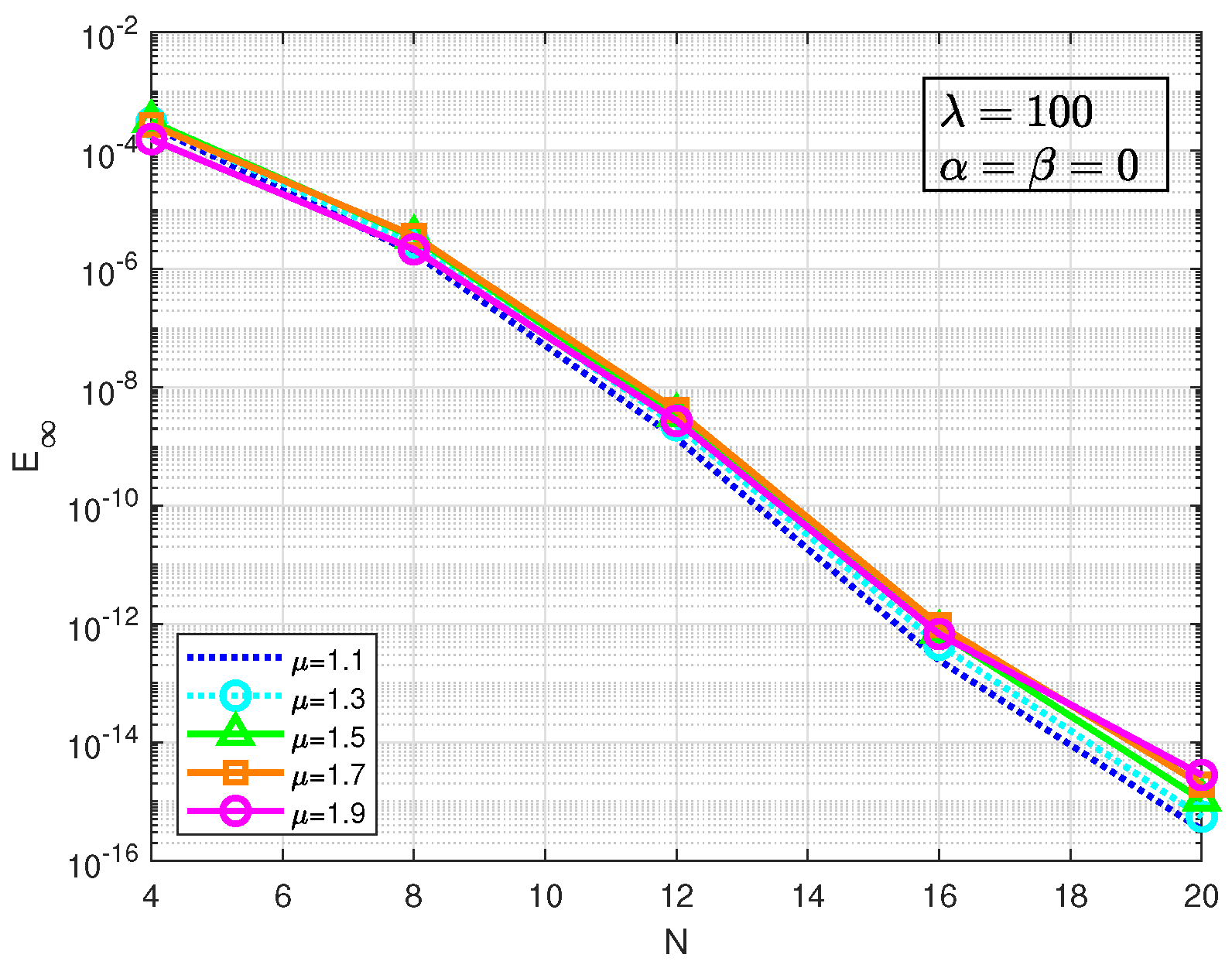
Figure 11.
Errors of C21 of Example 5.
Figure 11.
Errors of C21 of Example 5.
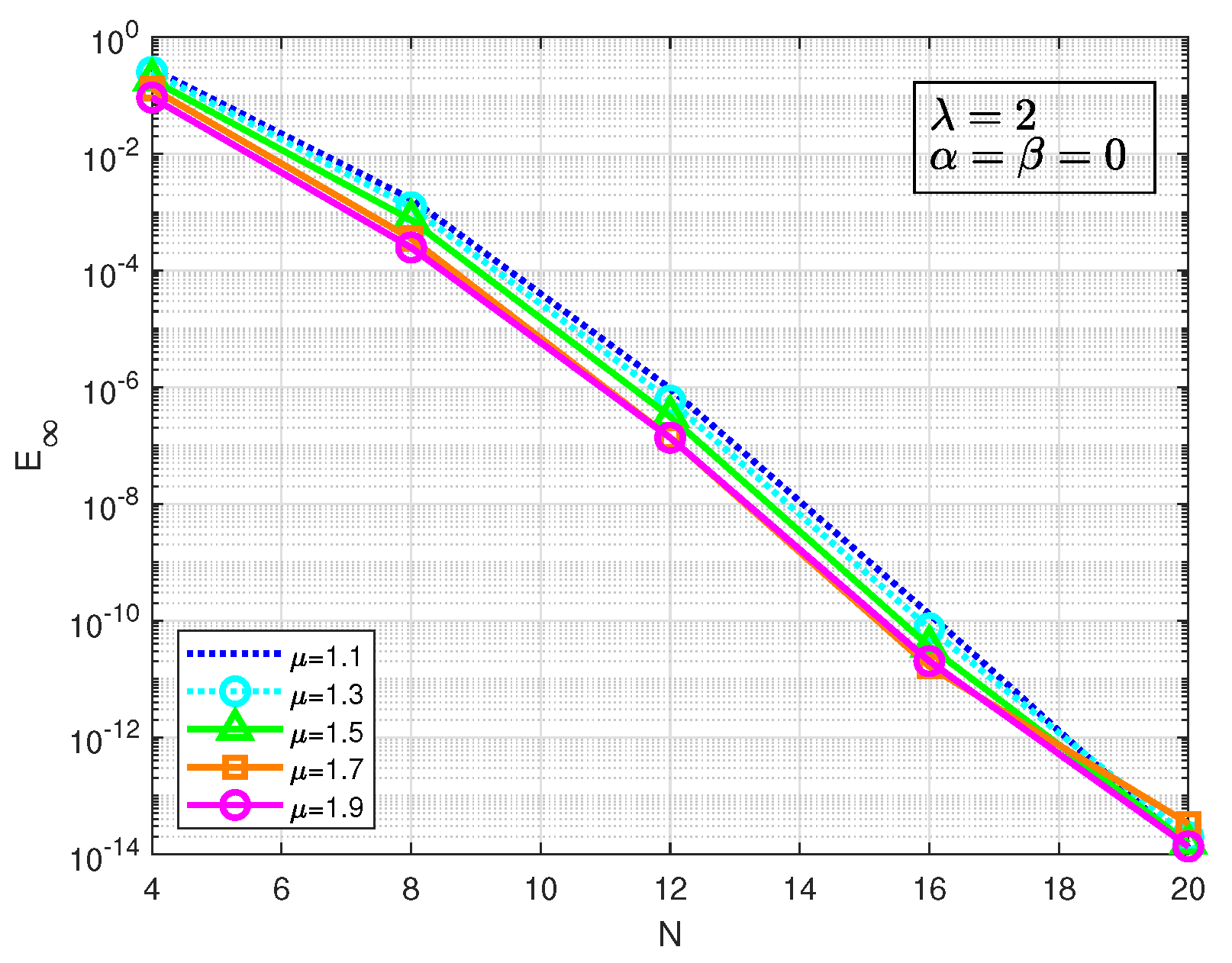
Figure 12.
Errors of C21 of Example 5.
Figure 12.
Errors of C21 of Example 5.
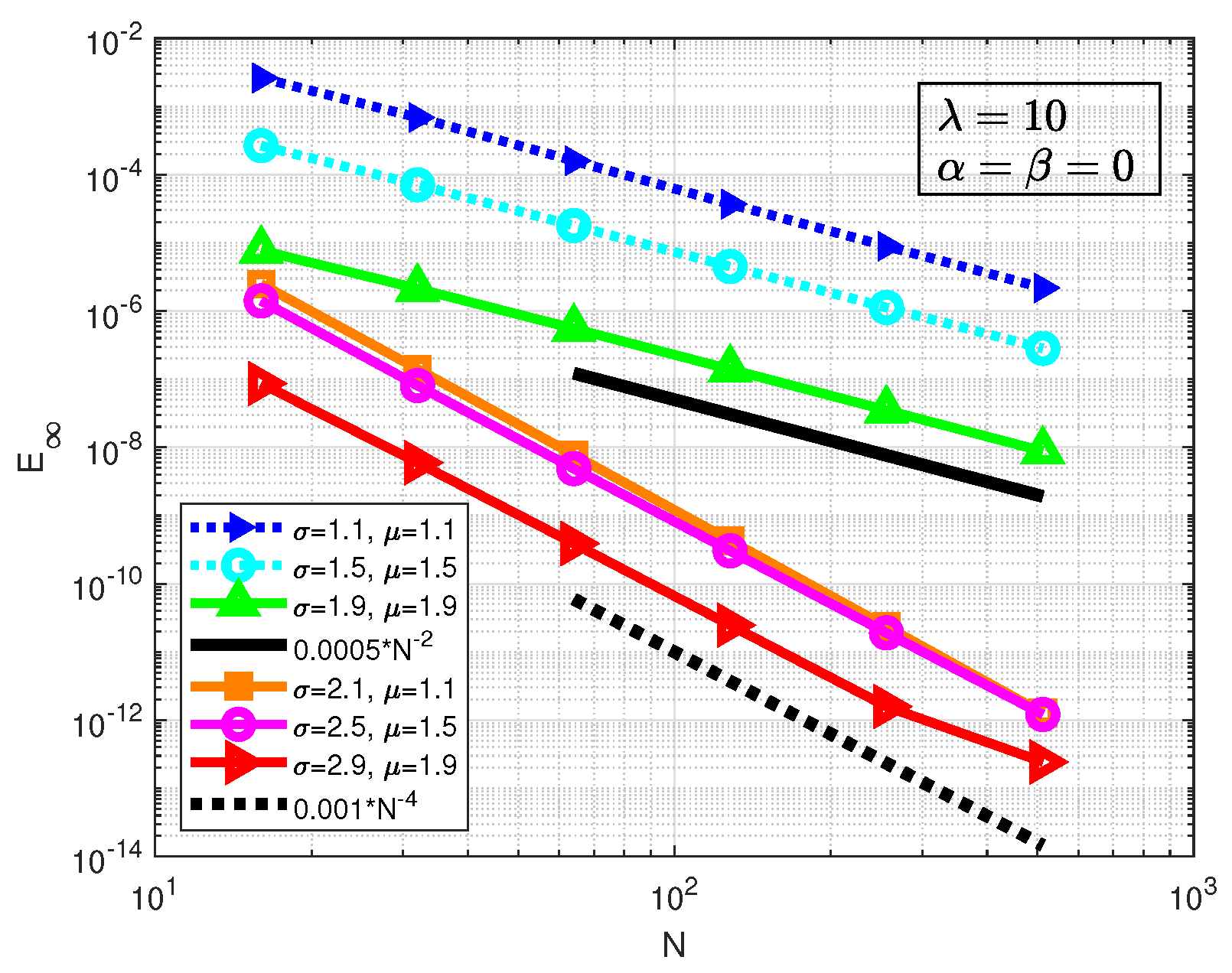
Figure 13.
Errors of C22 of Example 5.
Figure 13.
Errors of C22 of Example 5.
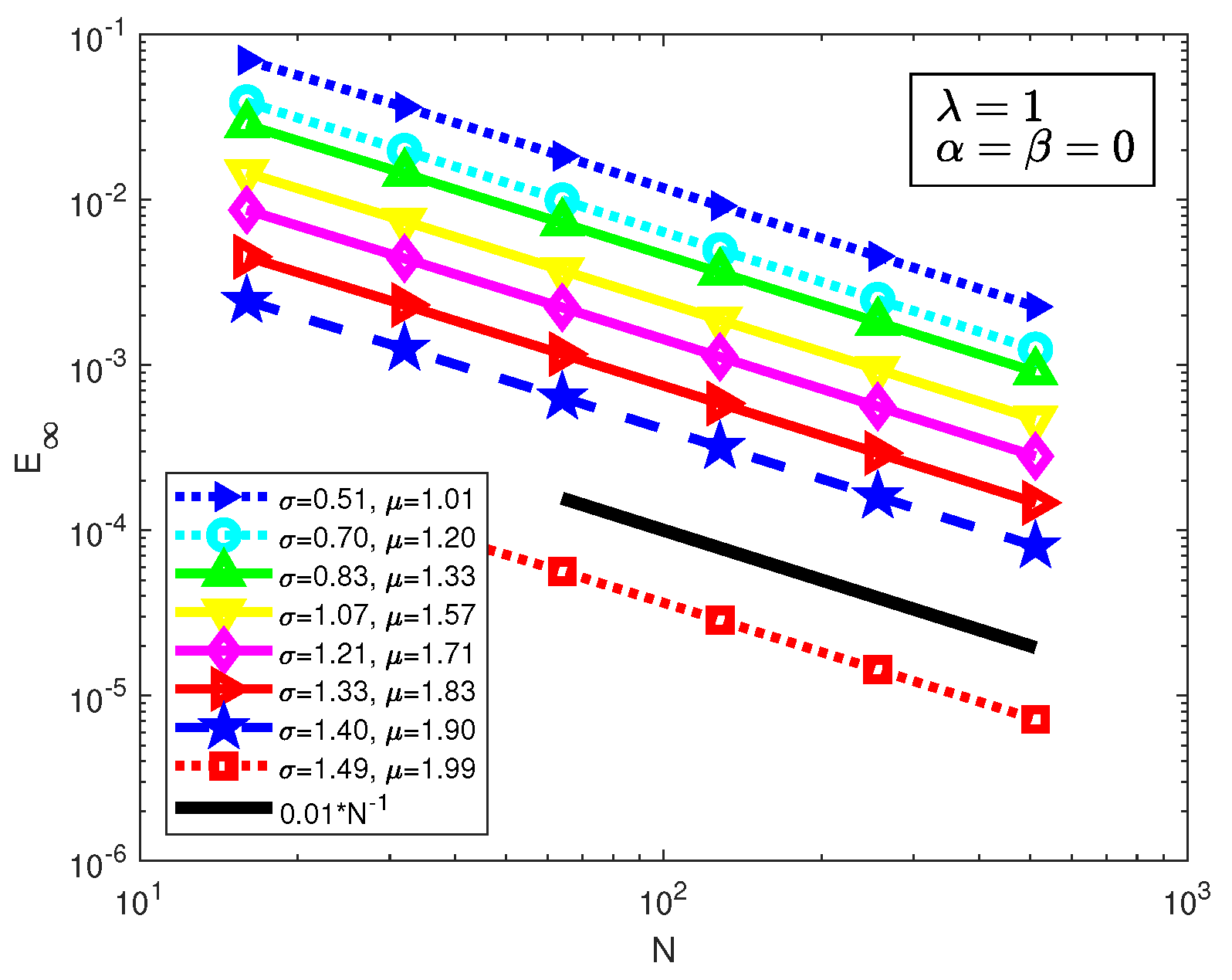
Figure 14.
Errors of C22 of Example 5.
Figure 14.
Errors of C22 of Example 5.
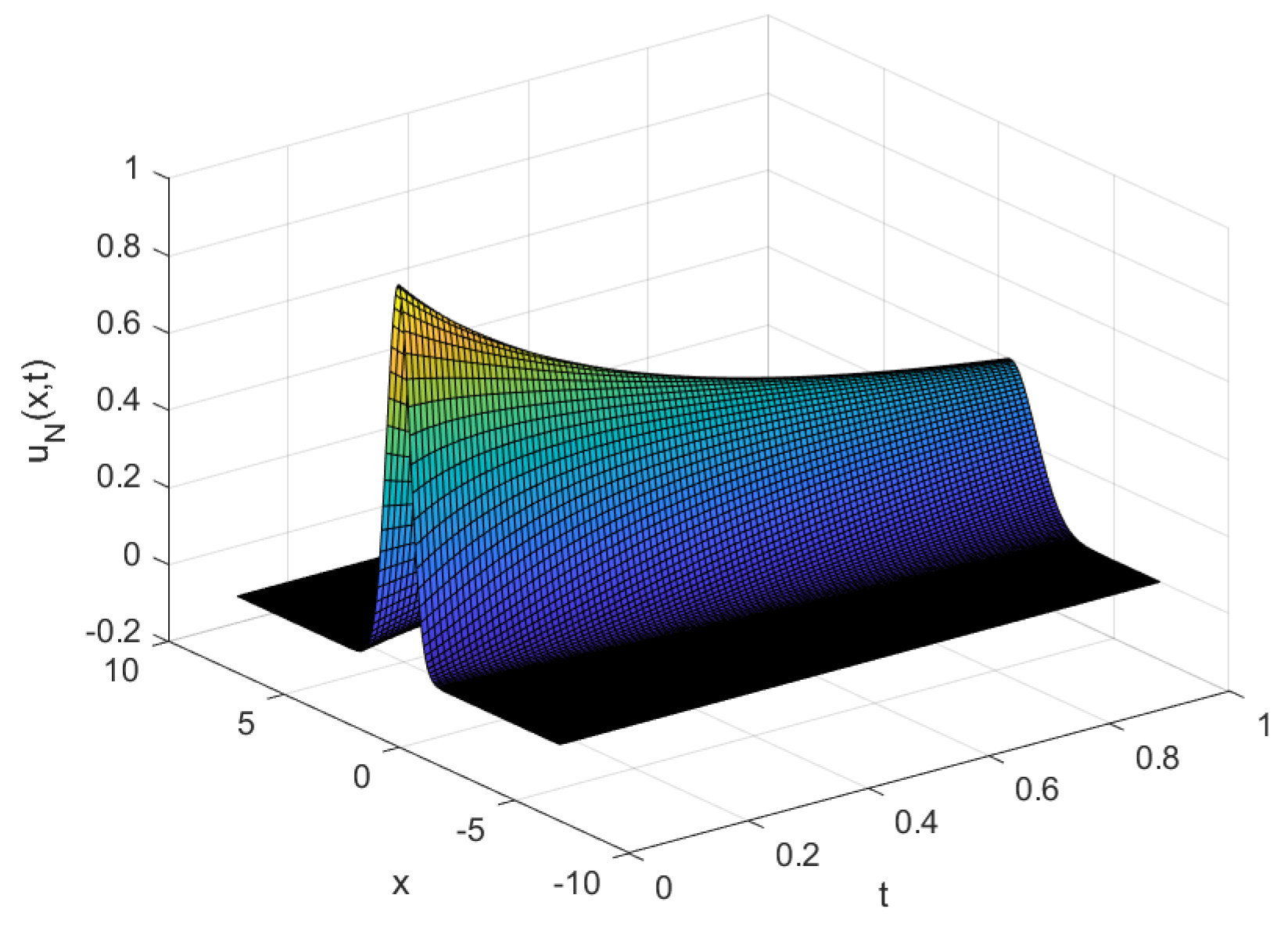
Figure 15.
Numerical solution of C31 of Example 6 with .
Figure 15.
Numerical solution of C31 of Example 6 with .
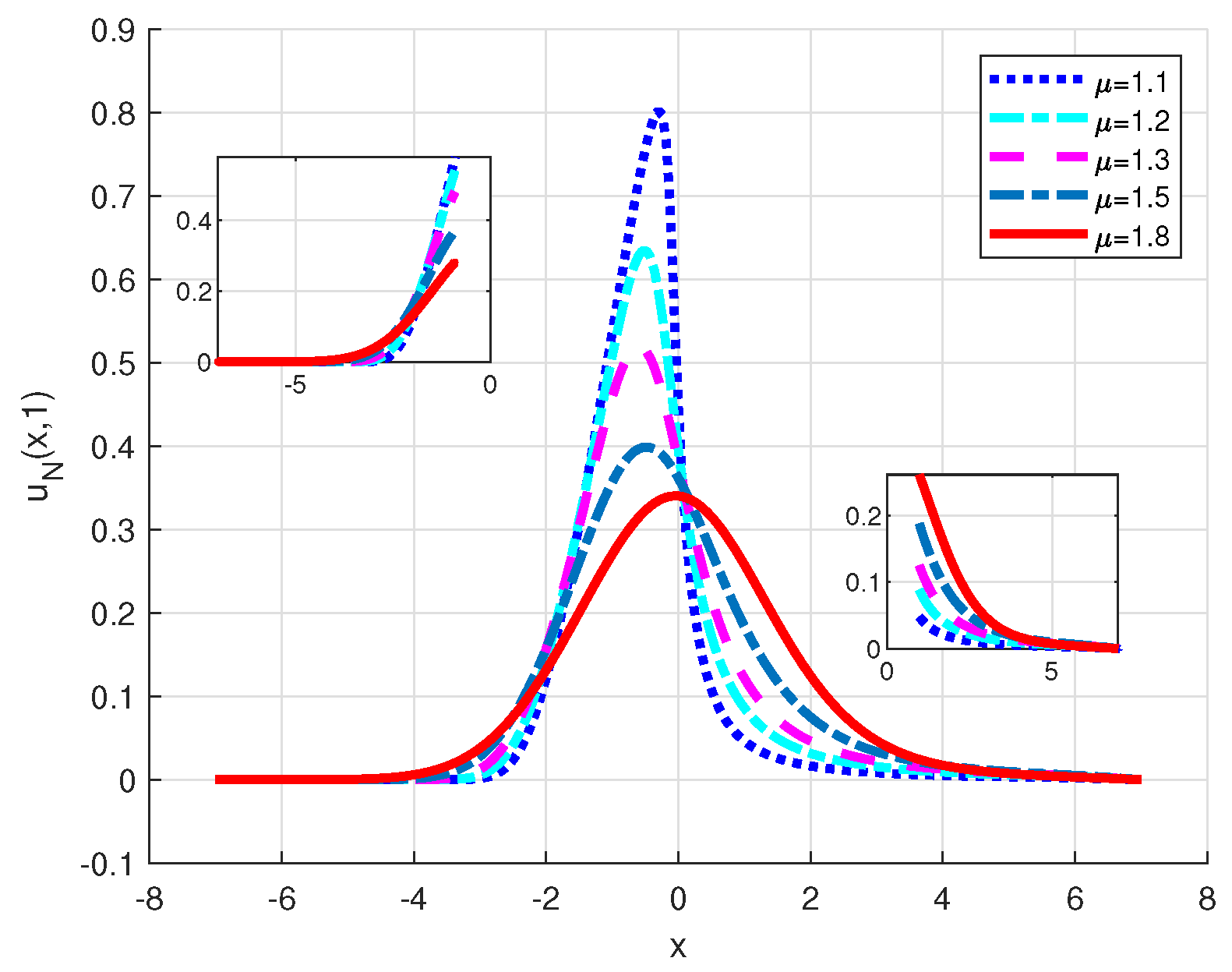
Figure 16.
Numerical solution of C32 of Example 6 with .
Figure 16.
Numerical solution of C32 of Example 6 with .
Figure 17.
Numerical solution of C41 of Example 7 with .
Figure 17.
Numerical solution of C41 of Example 7 with .
Figure 18.
Numerical solution of C41 of Example 7 with .
Figure 18.
Numerical solution of C41 of Example 7 with .
Figure 19.
Numerical solution of C42 of Example 7 with .
Figure 19.
Numerical solution of C42 of Example 7 with .
Figure 20.
Numerical solution of C42 of Example 7 with .
Figure 20.
Numerical solution of C42 of Example 7 with .
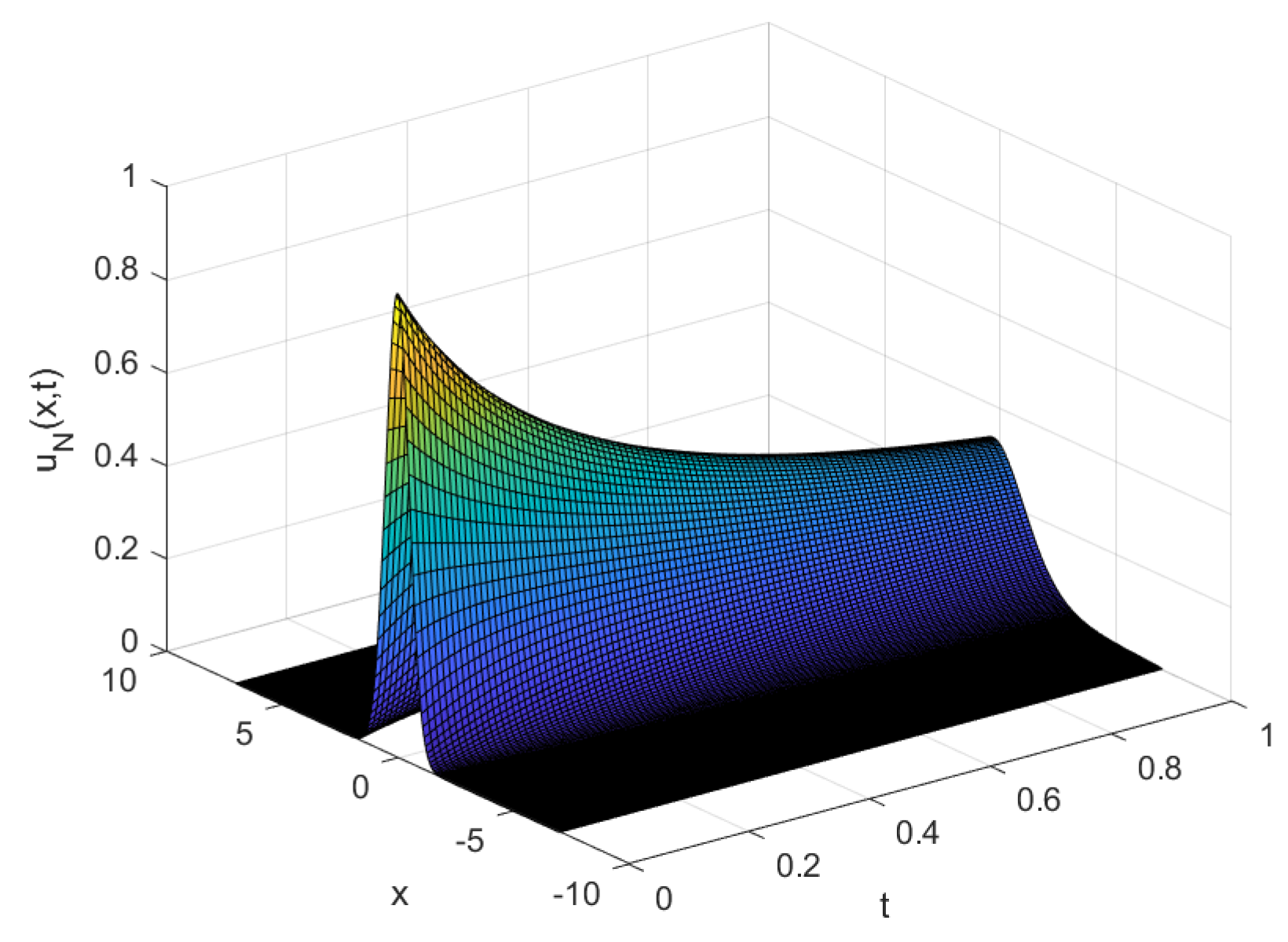
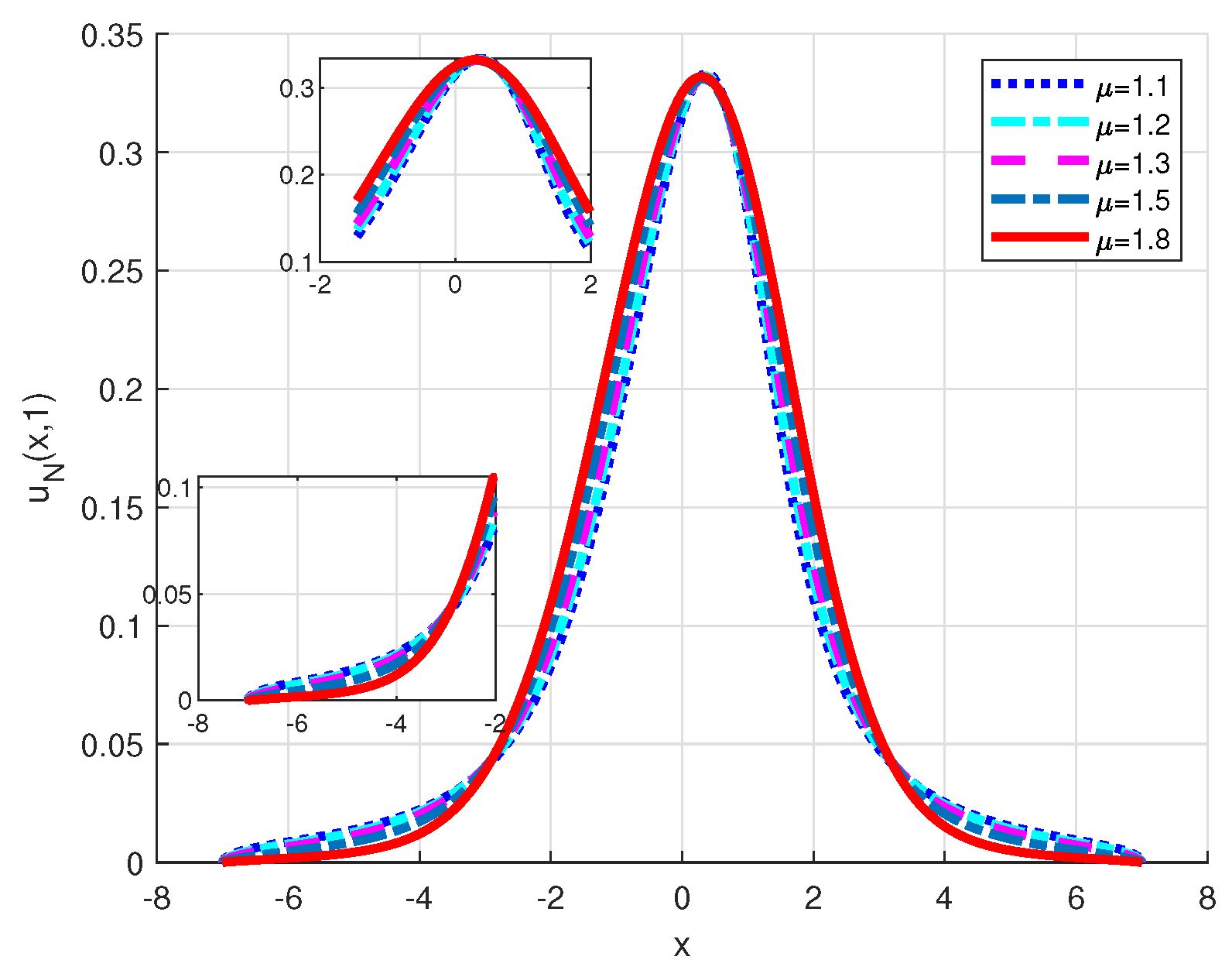
Figure 21.
Numerical solution of Example 8 with .
Figure 21.
Numerical solution of Example 8 with .
Figure 22.
Numerical solution of Example 8 with .
Figure 22.
Numerical solution of Example 8 with .
Figure 23.
Numerical solution of Example 8 with .
Figure 23.
Numerical solution of Example 8 with .
Figure 24.
Numerical solution of Example 8 with .
Figure 24.
Numerical solution of Example 8 with .
Table 1.
The first nine eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
Table 1.
The first nine eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
| Our Method | [40] | [38] | [39] | [37] |
|---|
| 9.45685689126 | 9.4568568891 | 9.4568568892 | 9.4997 | 9.4569 |
| 28.47687912479 | 28.4768791170 | 28.4768791186 | 28.5116 | 28.4769 |
| 62.20037779983 | 62.2003777331 | 62.2003777529 | 62.3239 | 62.2004 |
| 97.06323747284 | 97.0632373708 | 97.0632377552 | 97.0896 | 97.0632 |
| 155.45013805266 | 155.4501373840 | 155.4499080962 | 155.6972 | - |
| 196.59593024267 | 196.5959302453 | 196.5986985127 | 196.5152 | - |
| 301.52706976868 | - | - | 304.19 + 3.00i | - |
| 306.72685026127 | - | - | 304.19 + 3.00i | - |
| 461.179 + 43.050i | - | - | 461.24 + 43.29i | - |
Table 2.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
Table 2.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
| Our Method | [40] | [38] | [37] |
|---|
| 13.420474051 | 13.42047399 | 13.4204739885 | 13.4205 |
| 14.645442473 | 14.64544252 | 14.6454425351 | 14.6454 |
| 47.292859 + 18.850956i | 47.292858 + 18.850956i | - | - |
| 91.705190 + 43.625498i | 91.705189 + 43.625496i | - | - |
| 145.569415 + 75.805031i | 145.569416 + 75.805025i | - | - |
| 207.859129 + 114.486222i | 207.859147 + 114.486204i | - | - |
Table 3.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
Table 3.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
| | | | | Error |
|---|
| 9.8691292203 | 9.8695568729 | 9.8695996482 | 9.86960440108 | 1.073 |
| 39.4719645919 | 39.4777722446 | 39.4783530678 | 39.47841760434 | 1.995 |
| 88.8081881526 | 88.8246142309 | 88.8262570696 | 88.82643960980 | 7.148 |
| 157.8754859530 | 157.9098514892 | 157.9132885198 | 157.91367041743 | 8.527 |
| 246.6748284659 | 246.7335809315 | 246.7394571083 | 246.74011002723 | 1.336 |
| 355.2042026720 | 355.2956013900 | 355.3047427196 | 355.30575843924 | 2.035 |
Table 4.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with different and .
Table 4.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with different and .
| | [40] | | [39] |
|---|
| 9.5141431295 | 9.5141431288 | 9.8648626632 | 9.8648 |
| 33.5956714125 | 33.5956714089 | 39.4139459491 | 39.4139 |
| 73.0390172335 | 73.0390172163 | 88.6441581077 | 88.6442 |
| 124.4185311384 | 124.4185311250 | 157.5323069955 | 157.5325 |
| 191.1460514291 | 191.1460515330 | 246.0882332022 | 246.0886 |
| 267.9451997398 | 267.9452006460 | 354.2916713396 | 354.2922 |
Table 5.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
Table 5.
The first six eigenvalues of Example 1, computed with the Chebyshev collocation method () with and .
| | | |
|---|
| 1.3531852 + 7.2497408i | 5.4727766 + 8.2732647i | 11.1466676 + 6.1222836i |
| 2.8098353 + 15.7308531i | 13.3926574 + 21.8112244i | 33.3136683 + 23.1298984i |
| 4.3033960 + 24.6907235i | 22.3712536 + 37.9533918i | 61.1959645 + 46.6510167i |
| 5.8291184 + 33.9686708i | 32.1686781 + 55.9626406i | 93.8181576 + 75.3667762i |
| 7.3824934 + 43.4883769i | 42.6472214 + 75.4712271i | 130.5448587 + 108.4998614i |
| 8.9599335 + 53.2043853i | 53.7149929 + 96.2501648i | 170.9467051 + 145.5427194i |
Table 6.
The first five eigenvalues of Example 2, computed with the Legendre collocation method () with and .
Table 6.
The first five eigenvalues of Example 2, computed with the Legendre collocation method () with and .
| | | | |
|---|
| Our Method | [36] | Our Method | [36] |
|---|
| 1.297024021884 | 1.296995777 | 1.483262055566 | 1.4832334320 |
| 3.486806460504 | 3.486730536 | 4.458260013435 | 4.4581739838 |
| 5.911808693986 | 5.911679975 | 8.150874006594 | 8.1507167266 |
| 8.534627231336 | 8.534441423 | 12.424593370123 | 12.424353637 |
| 11.292675855564 | 11.29243001 | 17.162678802344 | 17.162347657 |
Table 7.
The first five eigenvalues of Example 2, computed with the Legendre collocation method () with and .
Table 7.
The first five eigenvalues of Example 2, computed with the Legendre collocation method () with and .
| | | | |
|---|
| Our Method | [36] | Our Method | [36] |
|---|
| 1.728321890005 | 1.72829595710 | 2.048752746738 | 2.04873498313 |
| 5.756434650807 | 5.75634828003 | 7.503181981160 | 7.50311692608 |
| 11.312063027525 | 11.3118933010 | 15.800031154322 | 15.7998941633 |
| 18.177615608424 | 18.1773428791 | 26.724474991011 | 26.7242432849 |
| 26.187596954514 | 26.1872040516 | 40.114581604547 | 40.1142338051 |
Table 8.
The error and convergence order of C11 in Example 3, computed with the Chebyshev collocation method () for .
Table 8.
The error and convergence order of C11 in Example 3, computed with the Chebyshev collocation method () for .
| N | | | | | | | | |
|---|
| E∞ | CO | E∞ | CO | E∞ | CO | E∞ | CO |
|---|
| 12 | 6.434 | - | 1.329 | - | 2.627 | - | 5.384 | - |
| 20 | 2.356 | 6.47 | 5.692 | 6.17 | 1.109 | 6.20 | 1.968 | 6.48 |
| 28 | 4.373 | 5.01 | 1.055 | 5.01 | 2.055 | 5.01 | 3.648 | 5.01 |
| 36 | 1.244 | 5.00 | 2.998 | 5.01 | 5.840 | 5.01 | 1.037 | 5.01 |
| 44 | 4.559 | 5.00 | 1.099 | 5.00 | 2.140 | 5.00 | 3.800 | 5.00 |
| 52 | 1.977 | 5.00 | 4.764 | 5.00 | 9.280 | 5.00 | 1.648 | 5.00 |
| 60 | 9.664 | 5.00 | 2.328 | 5.00 | 4.536 | 5.00 | 8.054 | 5.00 |
| 68 | 5.168 | 5.00 | 1.245 | 5.00 | 2.426 | 5.00 | 4.307 | 5.00 |
Table 9.
The error and convergence order of C11 in Example 3, computed with the Chebyshev collocation method () for .
Table 9.
The error and convergence order of C11 in Example 3, computed with the Chebyshev collocation method () for .
| N | | | | | | | | |
|---|
| E∞ | CO | E∞ | CO | E∞ | CO | E∞ | CO |
|---|
| 8 | 4.044 | - | 1.236 | - | 1.263 | - | 7.994 | - |
| 16 | 2.036 | 0.99 | 2.410 | 2.36 | 1.811 | 6.12 | 4.055 | 14.27 |
| 24 | 1.359 | 1.00 | 9.146 | 2.39 | 4.193 | 3.61 | 6.775 | 4.41 |
| 32 | 1.020 | 1.00 | 4.591 | 2.40 | 1.487 | 3.60 | 1.908 | 4.41 |
| 40 | 8.158 | 1.00 | 2.689 | 2.40 | 6.658 | 3.60 | 7.143 | 4.40 |
| 48 | 6.799 | 1.00 | 1.737 | 2.40 | 3.453 | 3.60 | 3.201 | 4.40 |
| 56 | 5.828 | 1.00 | 1.200 | 2.40 | 1.982 | 3.60 | 1.624 | 4.40 |
| 64 | 5.100 | 1.00 | 8.708 | 2.40 | 1.226 | 3.60 | 9.024 | 4.40 |
Table 10.
The error of C11 in Example 3, computed with the Chebyshev collocation method ().
Table 10.
The error of C11 in Example 3, computed with the Chebyshev collocation method ().
| | | | | | |
|---|
| 5(1) | 1.776 | 1.599 | 1.954 | 1.776 | 2.309 | 1.599 |
| 10(2) | 2.387 | 2.132 | 2.103 | 2.558 | 2.217 | 2.103 |
| 15(3) | 5.912 | 2.728 | 2.819 | 6.003 | 2.728 | 3.547 |
Table 11.
The error of C12 in Example 3, computed with the Chebyshev collocation method ().
Table 11.
The error of C12 in Example 3, computed with the Chebyshev collocation method ().
| N | | | | | | |
|---|
| 6 | 9.557 | 2.978 | 5.208 | 8.299 | 1.377 | 1.931 |
| 10 | 7.758 | 2.475 | 4.212 | 6.440 | 1.072 | 1.626 |
| 14 | 1.522 | 4.709 | 8.159 | 1.212 | 2.043 | 3.113 |
| 18 | 2.749 | 5.519 | 5.405 | 1.002 | 1.333 | 2.055 |
| 22 | 2.398 | 5.959 | 3.545 | 1.024 | 1.420 | 1.631 |
Table 12.
The error and convergence order of C13 in Example 3, computed with the Chebyshev collocation method ().
Table 12.
The error and convergence order of C13 in Example 3, computed with the Chebyshev collocation method ().
| N | | | | | | | | |
|---|
| E∞ | CO | E∞ | CO | E∞ | CO | E∞ | CO |
|---|
| 4 | 6.129 | - | 8.253 | - | 1.039 | - | 1.028 | - |
| 8 | 5.106 | 0.26 | 6.075 | 0.44 | 5.514 | 0.91 | 4.442 | 1.21 |
| 16 | 4.185 | 0.29 | 4.324 | 0.49 | 2.803 | 0.98 | 1.894 | 1.23 |
| 32 | 3.379 | 0.31 | 3.002 | 0.53 | 1.408 | 0.99 | 8.145 | 1.22 |
| 64 | 2.693 | 0.33 | 2.049 | 0.55 | 7.047 | 1.00 | 3.525 | 1.21 |
| 128 | 2.123 | 0.34 | 1.383 | 0.57 | 3.524 | 1.00 | 1.530 | 1.20 |
| 256 | 1.659 | 0.36 | 9.261 | 0.58 | 1.762 | 1.00 | 6.653 | 1.20 |
| 512 | 1.288 | 0.37 | 6.170 | 0.59 | 8.812 | 1.00 | 2.895 | 1.20 |
Table 13.
The error and convergence order of C13 in Example 3, computed with the Chebyshev collocation method ().
Table 13.
The error and convergence order of C13 in Example 3, computed with the Chebyshev collocation method ().
| N | | | | | | | | |
|---|
| E∞ | CO | E∞ | CO | E∞ | CO | E∞ | CO |
|---|
| 4 | 9.283 | - | 7.376 | - | 4.563 | - | 1.312 | - |
| 8 | 3.180 | 1.55 | 1.939 | 1.93 | 8.566 | 2.41 | 7.498 | 4.13 |
| 16 | 1.144 | 1.47 | 5.948 | 1.70 | 2.268 | 1.92 | 1.754 | 2.10 |
| 32 | 4.247 | 1.43 | 1.918 | 1.63 | 6.379 | 1.83 | 4.370 | 2.01 |
| 64 | 1.597 | 1.41 | 6.280 | 1.61 | 1.821 | 1.81 | 1.103 | 1.99 |
| 128 | 6.032 | 1.40 | 2.066 | 1.60 | 5.221 | 1.80 | 2.793 | 1.98 |
| 256 | 2.283 | 1.40 | 6.811 | 1.60 | 1.499 | 1.80 | 7.077 | 1.98 |
| 512 | 8.647 | 1.40 | 2.246 | 1.60 | 4.303 | 1.80 | 1.794 | 1.98 |