Bidiagonal Factorizations of Filbert and Lilbert Matrices

Abstract

Extensions of Filbert and Lilbert matrices are addressed in this work. They are reciprocal Hankel matrices based on Fibonacci and Lucas numbers, respectively, and both are related to Hilbert matrices. The Neville elimination is applied to provide explicit expressions for their bidiagonal factorization. As a byproduct, formulae for the determinants of these matrices are obtained. Finally, numerical experiments show that several algebraic problems involving these matrices can be solved with outstanding accuracy, in contrast with traditional approaches.

1. Introduction

Many efforts have been devoted in the last decades to the study of Hankel and Toeplitz matrices. Their applications extend through many areas, such as signal processing and system identification. In particular, the singular value decomposition of a Hankel matrix plays a crucial role in state-space realization and hidden Markov models (see [1,2,3,4,5]).

An interesting case is the so-called reciprocal Hankel matrix, defined by Richardson in [6]. Given an integer sequence ${\left\{a_k\right\}}_{k\in \mathbb{N}}$, these matrices $R=\left(R_{i,j}\right)$ are defined as $R_{i,j}=1/a_{i+j-1}$. An appealing case appears when considering the famous Fibonacci sequence, defined by:

$$F_0:=0,F_1:=1,F_i=F_{i-1}+F_{i-2},i\in \mathbb{N},i\ge 2,$$

for which the corresponding reciprocal Hankel matrix is called a Filbert matrix because of its similarities with the well-known Hilbert matrix, its entries being given by

$$F^{\left(n\right)}={(1/F_{i+j-1})}_{1\le i,j\le n+1}.$$

Fibonacci numbers, omnipresent in nature, come into play in diverse scientific areas, e.g., image encryption algorithms [7] or thermal engineering [8], and they have proved to also be relevant in signal processing [9].

Filbert matrices are also deeply related with q-Hilbert matrices, for $q=(1-\sqrt{5})/(1+\sqrt{5})$ (cf. [10]), which in turn were recently studied by some authors [11]. These are defined by

$$H_n^{(\alpha ,q)}:={\left({\displaystyle \frac{{\left[\alpha \right]}_q}{{[i+j+\alpha -2]}_q}}\right)}_{1\le i,j\le n+1},$$

where ${\left[\alpha \right]}_q$ is the q-integer defined as ${\left[\alpha \right]}_q:=1+q+\cdots +q^{\alpha -1}$.

A generalization of Filbert matrices $F_n^{\left(\alpha \right)}={(1/F_{i+j+\alpha })}_{1\le i,j\le n+1}$, for $\alpha \ge -1$ being an integer parameter, was studied in [12].

We can also consider the Lucas sequence,

$$L_0:=2,L_1:=1,L_i=L_{i-1}+L_{i-2},i\in \mathbb{N},i\ge 2,$$

to obtain the Lilbert matrices $L_n={(1/L_{i+j-1})}_{1\le i,j\le n+1}$, defined in [13]. As with Filbert matrices, Lilbert matrices can be generalized analogously. In the mentioned papers, an explicit formula for the $LU$-decomposition, the Cholesky factorization and the inverse has been obtained for Filbert, Lilbert matrices and some extensions [12,13].

The condition number of Vandermonde and Hilbert matrices grows dramatically with their dimensions [14,15,16]. Unfortunately, specific information about the condition number of the Filbert and Lilbert matrices is not widely documented. However, we can expect these matrices to be ill-conditioned due to its similar structure to Hilbert matrices. In Section 5, devoted to numerical experiments, it is shown that the two-norm condition number of the Filbert and Lilbert matrices grows significantly as the size of the matrices increases. For instance, the condition number of a $5\times 5$ Filbert matrix is approximately ${10}^5$. As a consequence, conventional routines applying the best algorithms for solving algebraic problems such as computing the inverse of a matrix, its singular values or the resolution of a linear system, fail to provide any accuracy in the obtained results.

At this point, it should be mentioned that any Hankel matrix can be transformed into a Toeplitz matrix with no cost by means of a permutation—the one given by the anti-identity matrix. In principle, when solving algebraic problems such as the resolution of linear systems, this would allow us to apply several well-established numerical methods, including the so-called fast direct Toeplitz solvers [17,18], with a computational cost of $O\left(n{log}^{2}n\right)$, and the iterative procedures based on the gradient conjugate algorithm with a suitable preconditioner, which can improve the cost to $O(nlogn)$ [19]. However, these direct algorithms guarantee only weak stability [20], i.e., that for well-conditioned problems, the computed and the exact solution are close. The same can be said about preconditioned conjugate gradient methods, since the speed of convergence and its stability heavily depend on the condition number of the given matrix.

In this work, the generalized versions of Filbert and Lilbert matrices are addressed by means of a Neville elimination process, giving explicit expressions for its multipliers and pivots. Following [21], this allows us to determine a bidiagonal factorization of the considered matrices. As a byproduct, formulae for the determinants of both classes of matrices are derived. Moreover, numerical experiments for the above-mentioned algebraic problems—which are heavily ill-conditioned—have been performed, showing results that they exhibit machine-order accuracy, in stark contrast with traditional numerical methods.

The paper is organized as follows: to keep this paper as self-contained as possible, Section 2 recalls basic concepts and results related to Neville elimination and bidiagonal factorizations of nonsingular matrices. Filbert and Lilbert matrices are considered in Section 3 and Section 4, respectively, where the pivots and multipliers of their Neville elimination are obtained, and a remarkable analogy with those of quantum Hilbert matrices is illustrated. As seen later, the obtained bidiagonal factorizations have experimentally shown an impressive level of performance, attaining machine-order errors while classical numerical methods fail to deliver the correct solution by orders of magnitude. Finally, Section 5 presents a series of numerical experiments.

2. Notations and Auxiliary Results

As advanced in the Introduction, the main result of this paper, gathered in the following sections, consists in the computation of the bidiagonal factorization of Filbert and Lilbert matrices, which is possible by following a Neville elimination process. This being the case, let us begin by recalling some basic results concerning the Neville elimination (NE). First of all, it is an algorithm that, given a $(n+1)\times (n+1)$ real-valued matrix A, obtains an upper-triangular matrix U after n iterations. More specifically, intermediate steps, labeled by $A^{(k+1)}$ for $k=1,\cdots ,n$, are obtained from the previous iteration $A^{\left(k\right)}$, making zeros below the diagonal in the kth column. To do so, the initial step is by definition $A^{\left(1\right)}:=A$, whereas the entries of $A^{(k+1)}$ for every $k=1,\cdots ,n$ are obtained through the subsequent recursion formula

$$a_{i,j}^{(k+1)}:=\left\{\begin{array}{cc}{a}_{i,j}^{\left(k\right)},\hfill & \mathrm{if}1\le i\le k,\hfill \\ a_{i,j}^{\left(k\right)}-\frac{a_{i,k}^{\left(k\right)}}{a_{i-1,k}^{\left(k\right)}}{a}_{i-1,j}^{\left(k\right)},\hfill & \mathrm{if}k+1\le i,j\le n+1,\mathrm{and}{a}_{i-1,j}^{\left(k\right)}\ne 0,\hfill \\ a_{i,j}^{\left(k\right)},\hfill & \mathrm{if}k+1\le i\le n+1,\mathrm{and}{a}_{i-1,k}^{\left(k\right)}=0.\hfill \end{array}\right.$$

(1)

In the last iteration of this process, the matrix $U:=A^{(n+1)}$ is obtained, which, as mentioned before, is upper-triangular. In this process, the entries corresponding to the jth column at the $j-1$ step, i.e.,

$$p_{i,j}:=a_{i,j}^{\left(j\right)},1\le j\le i\le n+1,$$

(2)

are called the $(i,j)$ pivots (or ith diagonal pivots in the $i=j$ case) of the NE process. The following quotient is also of relevance:

$$m_{i,j}:=\left\{\begin{array}{cc}{a}_{i,j}^{\left(j\right)}/a_{i-1,j}^{\left(j\right)}=p_{i,j}/p_{i-1,j},\hfill & \mathrm{if}{a}_{i-1,j}^{\left(j\right)}\ne 0,\hfill \\ 0,\hfill & \mathrm{if}{a}_{i-1,j}^{\left(j\right)}=0,\hfill \end{array}\right.$$

(3)

and is known as the $(i,j)$ multiplier.

By applying a second Neville elimination to $U^T$, a diagonal matrix is obtained; this process is known as a complete Neville elimination. When in this process, there is no need to perform any row exchanges, the matrix A is said to verify the WRC condition (see, e.g., [21]). In Theorem 2.2 of [21], it is proved that a $(n+1)\times (n+1)$ real-valued nonsingular matrix A verifies the WRC condition if and only if it can be expressed in a unique way as the following product,

$$A=F_n{F}_{n-1}\cdots F_{1}D{G}_1{G}_2\cdots G_n,$$

(4)

where $F_i,G_i\in {\mathbb{R}}^{(n+1)\times (n+1)}$ are the lower- and upper-, respectively, triangular bidiagonal matrices given by

$$F_i=\left(\begin{array}{c}1\\ & \ddots \\ & & 1\\ & & m_{i+1,1}& 1\\ & & & \ddots & \ddots \\ & & & & m_{n+1,n+1-i}& 1\end{array}\right),G_i^T=\left(\begin{array}{c}1\\ & \ddots \\ & & 1\\ & & {\tilde{m}}_{i+1,1}& 1\\ & & & \ddots & \ddots \\ & & & & {\tilde{m}}_{n+1,n+1-i}& 1\end{array}\right),$$

(5)

while the entries of the diagonal matrix D are the diagonal pivots $p_{i,i}$ obtained in the NE of A. In fact, the NE processes of A and $A^T$ also give the nondiagonal entries of $F_i$ and $G_i$, since the values $m_{i,j},{\tilde{m}}_{i,j}$ appearing in (5) are precisely the multipliers of these algorithms as defined in (3).

Another interesting result is provided by Theorem 2.2 of [22]. Taking advantage of the diagonal pivots and multipliers obtained in the NE of A, it is possible to formulate the inverse $A^{-1}$ as

$$A^{-1}={\widehat{G}}_1{\widehat{G}}_2\cdots {\widehat{G}}_n{D}^{-1}{\widehat{F}}_n{\widehat{F}}_{n-1}\cdots {\widehat{F}}_1,$$

(6)

where the matrices ${\widehat{F}}_i$ and ${\widehat{G}}_i$ are very much like their counterparts $F_i$ and $G_i$, but with a different arrangement of the multipliers, being defined as

$${\widehat{F}}_i=\left(\begin{array}{c}1\\ & \ddots \\ & & 1\\ & & -m_{i+1,i}& 1\\ & & & \ddots & \ddots \\ & & & & -m_{n+1,i}& 1\end{array}\right),{\widehat{G}}_i^T=\left(\begin{array}{c}1\\ & \ddots \\ & & 1\\ & & -{\tilde{m}}_{i+1,i}& 1\\ & & & \ddots & \ddots \\ & & & & -{\tilde{m}}_{n+1,i}& 1\end{array}\right).$$

It is worth noting that more general classes of matrices can be factorized as in (4), see [23].

Hereafter, the convention adopted by Koev in [24] to store the coefficients of the bidiagonal decomposition (4) of A in a $(n+1)\times (n+1)$ matrix $BD\left(A\right)$ is followed. The entries of this matrix form are given by

$$BD{\left(A\right)}_{i,j}:=\left\{\begin{array}{cc}{m}_{i,j},\hfill & \mathrm{if}i>j,\hfill \\ p_{i,i},\hfill & \mathrm{if}i=j,\hfill \\ {\tilde{m}}_{j,i},\hfill & \mathrm{if}i<j.\hfill \end{array}\right.$$

(7)

Remark 1.

Provided that the bidiagonal factorization of a nonsingular matrix $A\in {\mathbb{R}}^{(n+1)\times (n+1)}$ exists, then, using the factorization (4), it follows that

$$A^T=G_n^T{G}_{n-1}^T\cdots G_1^{T}D{F}_1^T{F}_2^T\cdots F_n^T.$$

Furthermore, in the case of A being symmetric, we have that $G_i=F_i^T$ for $i=1,\cdots ,n$ and, as a consequence,

$$A=F_n{F}_{n-1}\cdots F_{1}D{F}_1^T{F}_2^T\cdots F_n^T.$$

(8)

It is worth noting that thanks to the structure of the factors in the bidiagonal decomposition (4) of a nonsingular matrix A, in order to compute its determinant, it suffices to perform the product of the diagonal pivots obtained in the NE of A, since the determinant of each of the factors $F_i$ and $G_i$ is trivially one. This result will be used later in the manuscript to obtain the determinants of generalized Filbert and Lilbert matrices and is summarized in the following lemma.

Lemma 1.

Consider a nonsingular matrix $A\in {\mathbb{R}}^{(n+1)\times (n+1)}$. If the bidiagonal decomposition of A exists, then

$$detA=\prod _{i=1}^{n+1}{p}_{i,i},$$

(9)

where $p_{i,i}$ are the diagonal pivots of the Neville elimination of A given by (2).

3. Bidiagonal Factorization of Filbert Matrices

Let us recall that the sequence of Fibonacci numbers: ${\left(F_n\right)}_{n\in \mathbb{N}}$ is given by

$$F_0:=0,F_1:=1,$$

with the recursion formula

$$F_{n+1}=F_n+F_{n-1},n\ge 1.$$

(10)

Filbert matrices are defined in terms of the Fibonacci sequence as

$$F_{i,j}=\frac{1}{F_{i+j-1}},1\le i,j\le n+1,$$

(11)

and they have the property—shared with Hilbert matrices—of having an inverse with integer entries [6]. In fact, an explicit formula for the entries of the inverse matrices is proved using computer algebra. This formula shows a remarkable analogy with the corresponding formula for the elements of the inverse of Hilbert matrices in the sense that it can be obtained by replacing some binomial coefficients $\left(\genfrac{}{}{0pt}{}{n}{k}\right)$ by the analogous Fibonomial coefficients introduced in [25] as follows

$${\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_F:=\prod _{i=1}^k\frac{F_{n-i+1}}{F_i},0\le k\le n,$$

(12)

with the usual convention that empty products are defined as one. Let us observe that by defining

$${\left[0\right]}_F!:=1,{\left[n\right]}_F!:=\prod _{k=1}^n{F}_k,$$

we can also write

$${\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_F=\frac{{\left[n\right]}_F!}{{\left[k\right]}_F!{[n-k]}_F!},0\le k\le n.$$

(13)

The following identities for Fibonomial coefficients hold

$${\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_F=1,0\le k\le n\le 2,$$

(14)

and taking into account the following recursion formula

$${\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_F=F_{k-1}{\left(\genfrac{}{}{0pt}{}{n-1}{k}\right)}_F+F_{n-k+1}{\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)}_F,1\le k<n,$$

(15)

(see [25]), it can be clearly seen that the Fibonomial coefficients are integers. It can also be checked that Fibonomial coefficients satisfy the following useful identities:

$$\begin{array}{cc}\hfill & \left(\mathrm{a}\right)\frac{F_{\alpha }}{F_n}{\left(\genfrac{}{}{0pt}{}{\alpha -1}{n-1}\right)}_F={\left(\genfrac{}{}{0pt}{}{\alpha }{n}\right)}_F,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \left(\mathrm{b}\right)\frac{F_{\alpha -n}}{F_n}{\left(\genfrac{}{}{0pt}{}{\alpha -1}{n-1}\right)}_F={\left(\genfrac{}{}{0pt}{}{\alpha -1}{n}\right)}_F,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \left(\mathrm{c}\right)\frac{F_{\alpha }}{F_{\alpha -n+1}}{\left(\genfrac{}{}{0pt}{}{\alpha -1}{n-1}\right)}_F={\left(\genfrac{}{}{0pt}{}{\alpha }{n-1}\right)}_F.\hfill \end{array}$$

(18)

Now, we consider the following generalization of the Filbert matrix $F^{\left(n\right)}$ described in (11). Given $\alpha \in \mathbb{N}$, let $F_n^{\left(\alpha \right)}:={\left(F_{i,j}^{\left(\alpha \right)}\right)}_{1\le i,j\le n+1}$ with

$$F_{i,j}^{\left(\alpha \right)}=\frac{1}{F_{i+j+\alpha -2}},1\le i,j\le n+1.$$

(19)

Clearly, for $\alpha =1$, $F^{(n,1)}$ coincides with the Filbert matrix (11).

There are many nice equalities relating the Fibonacci numbers with each other. In this paper we use the following identity:

$$F_{n+p}{F}_{n+q}-F_n{F}_{n+p+q}={(-1)}^n{F}_p{F}_q,p,q,n\in \mathbb{N},$$

(20)

which is known as Vajda’s identity. On the other hand, it is well known that Fibonacci numbers $F_n$, $n\in \mathbb{N}$, satisfy the following property:

$$\underset{n\to \infty }{lim}\frac{F_{n+1}}{F_n}=\phi ,$$

where $\phi :=(1+\sqrt{5})/2$ is the “golden ratio”. Moreover, using the Binet form of Fibonacci numbers, we can write

$$F_n=\frac{{\phi }^n-{(1-\phi )}^n}{\sqrt{5}}={\phi }^{n-1}\frac{1-q^n}{1-q}={\phi }^{n-1}{\left[n\right]}_q,\mathrm{for}q=\frac{1-\sqrt{5}}{1+\sqrt{5}}.$$

The previous equalities illustrate a clear relation between q-Hilbert and Filbert matrices that is going to be reflected in the obtained expression for the pivots and multipliers of the Neville elimination and, consequently, their bidiagonal factorization (4) (cf. [11]).

Theorem 1.

Given $\alpha \in \mathbb{N}$, let $F_n^{\left(\alpha \right)}\in {\mathbb{R}}^{(n+1)\times (n+1)}$ be the Filbert matrix given by (19). The multipliers $m_{i,j}$ of the Neville elimination of $F_n^{\left(\alpha \right)}$ are given by

$$m_{i,j}={\tilde{m}}_{i,j}:={(-1)}^{j-1}\frac{F_{i+\alpha -2}^2}{F_{i+j+\alpha -2}{F}_{i+j+\alpha -3}},1\le j<i\le n+1.$$

(21)

Moreover, the diagonal pivots $p_{i,i}$ of the Neville elimination of $F_n^{\left(\alpha \right)}$ are given by

$$p_{i,i}={(-1)}^{(i-1)(i+\alpha -2)}\frac{1}{F_{2i+\alpha -2}{\left(\genfrac{}{}{0pt}{}{2i+\alpha -3}{i-1}\right)}_F^2},1\le i\le n+1,$$

(22)

and can be computed as follows:

$$p_{1,1}=1/F_{\alpha },p_{i+1,i+1}={(-1)}^{\alpha -2}\frac{F_i^2{F}_{i+\alpha -1}^2}{F_{2i+\alpha }{F}_{2i+\alpha -1}^2{F}_{2i+\alpha -2}}{p}_{i,i},1\le i\le n.$$

(23)

Proof. 

Let $F^{\left(k\right)}:={\left(f_{i,j}^{\left(k\right)}\right)}_{1\le i,j\le n+1}$, $k=1,\dots ,n+1$, be the matrices obtained after $k-1$ steps of the Neville elimination procedure for $F_n^{\left(\alpha \right)}$. Now, by induction on $k=2,\dots ,n+1$, we see that

$$f_{i,j}^{\left(k\right)}={(-1)}^{(k-1)(i+\alpha -2)}\frac{{\left(\genfrac{}{}{0pt}{}{j-1}{k-1}\right)}_F}{F_k{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k}\right)}_F},k\le j,i\le n+1.$$

(24)

It can be easily checked that $f_{i,1}/f_{i-1,1}=F_{i+\alpha -2}/F_{i+\alpha -1}$; thus, using the Vajda identity (20) with $n:=i+\alpha -2$, $p:=1$ and $q:=j-1$, we can write

$$\begin{array}{cc}\hfill f_{i,j}^{\left(2\right)}& =\frac{1}{F_{i+j+\alpha -2}}-\frac{F_{i+\alpha -2}}{F_{i+\alpha -1}}\frac{1}{F_{i+j+\alpha -3}}=\frac{F_{i+\alpha -1}{F}_{i+j+\alpha -3}-F_{i+\alpha -2}{F}_{i+j+\alpha -2}}{F_{i+\alpha -1}{F}_{i+j-1}{F}_{i+j+\alpha -3}}\hfill \\ \hfill & ={(-1)}^{i+\alpha -2}\frac{F_{j-1}}{F_{i+\alpha -1}{F}_{i+j+\alpha -2}{F}_{i+j+\alpha -3}},\hfill \end{array}$$

and (24) follows for $k=2$. If (24) holds for some $k\in \{2,\dots ,n\}$, we have

$$\frac{f_{i,k}^{\left(k\right)}}{f_{i-1,k}^{\left(k\right)}}={(-1)}^{k-1}\frac{{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -4}{k-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k}\right)}_F}{{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -2}{k}\right)}_F}={(-1)}^{k-1}\frac{F_{i+\alpha -2}^2}{F_{i+k+\alpha -2}{F}_{i+k+\alpha -3}},$$

for $i=k+1,\dots ,n+1$. Taking into account that by (1), $f_{i,j}^{(k+1)}=f_{i,j}^{\left(k\right)}-f_{i,k}^{\left(k\right)}{f}_{i-1,j}^{\left(k\right)}/f_{i-1,k}^{\left(k\right)}$ and the following identity, obtained from (18),

$$\frac{F_{i+k+\alpha -3}}{F_{i+\alpha -2}}{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -4}{k-1}\right)}_F={\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F,$$

we can write

$$f_{i,j}^{(k+1)}={(-1)}^{(k-1)(i+\alpha -2)}\frac{{\left(\genfrac{}{}{0pt}{}{j-1}{k-1}\right)}_F}{F_k{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F}{\tilde{C}}_{i,j}^{\left(k\right)}$$

(25)

with

$${\tilde{C}}_{i,j}^{\left(k\right)}:=\frac{1}{{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k}\right)}_F}-\frac{F_{i+\alpha -2}}{F_{i+k+\alpha -2}}\frac{1}{{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -3}{k}\right)}_F},$$

for $k+1\le j,i\le n+1$. Taking into account (17) and (16), respectively, we have

$$\begin{array}{ccc}\hfill {\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k}\right)}_F& =& \frac{F_{k+1}}{F_{i+j+\alpha -k-2}}{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k+1}\right)}_F,\hfill \\ \hfill {\left(\genfrac{}{}{0pt}{}{i+j+\alpha -3}{k}\right)}_F& =& \frac{F_{k+1}}{F_{i+j+\alpha -2}}{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k+1}\right)}_F,\hfill \end{array}$$

and from (25), we derive

$$f_{i,j}^{(k+1)}=\frac{{(-1)}^{(k-1)(i+\alpha -2)}{\left(\genfrac{}{}{0pt}{}{j-1}{k-1}\right)}_F}{F_{k+1}{F}_k{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k+1}\right)}_F}\left(F_{i+j-k+\alpha -2}-\frac{F_{i+\alpha -2}}{F_{i+k+\alpha -2}}{F}_{i+j+\alpha -2}\right).$$

(26)

On the other hand, by considering the Vajda identity in (20) with $p:=j-k$, $n:=i+\alpha -2$ and $q:=k$, it can be checked that

$$F_{i+j-k+\alpha -2}{F}_{i+k+\alpha -2}-F_{i+\alpha -2}{F}_{i+j+\alpha -2}={(-1)}^{i+\alpha -2}{F}_{j-k}{F}_k,$$

and then, from (26), we can write

$$\begin{array}{ccc}\hfill f_{i,j}^{(k+1)}& =& \frac{{(-1)}^{(k-1)(i+\alpha -2)}{\left(\genfrac{}{}{0pt}{}{j-1}{k-1}\right)}_F}{F_k{F}_{k+1}{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k+1}\right)}_F}\frac{F_{i+j-k+\alpha -2}{F}_{i+k+\alpha -2}-F_{i+\alpha -2}{F}_{i+j+\alpha -2}}{F_{i+k+\alpha -2}}\hfill \\ & =& {(-1)}^{k(i+\alpha -2)}\frac{{\left(\genfrac{}{}{0pt}{}{j-1}{k-1}\right)}_F{F}_{j-k}}{F_{k+1}{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k+1}\right)}_F{F}_{i+k+\alpha -2}},\hfill \end{array}$$

for $k+1\le j,i\le n+1$. Finally, taking into account (17) and (16), respectively, we can write

$${\left(\genfrac{}{}{0pt}{}{j-1}{k-1}\right)}_F=\frac{F_k}{F_{j-k}}{\left(\genfrac{}{}{0pt}{}{j-1}{k}\right)}_F,{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right)}_F=\frac{F_k}{F_{i+k+\alpha -2}}{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -2}{k}\right)}_F,$$

and conclude that

$$f_{i,j}^{(k+1)}={(-1)}^{k(i+\alpha -2)}\frac{{\left(\genfrac{}{}{0pt}{}{j-1}{k}\right)}_F}{F_{k+1}{\left(\genfrac{}{}{0pt}{}{i+k+\alpha -2}{k}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k+1}\right)}_F},k+1\le j,i\le n+1,$$

and (24) holds for $k+1$.

Now, by (2) and (24), the pivots of the Neville elimination of H satisfy

$$\begin{array}{cc}\hfill p_{i,j}& =f_{i,j}^{\left(j\right)}={(-1)}^{(j-1)(i+\alpha -2)}\frac{1}{F_j{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -3}{j-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{i+j+\alpha -2}{j}\right)}_F},1\le j<i\le n+1.\hfill \end{array}$$

For the particular case $i=j$, we obtain

$$p_{i,i}=\frac{{(-1)}^{(i-1)(i+\alpha -2)}}{F_i{\left(\genfrac{}{}{0pt}{}{2i+\alpha -3}{i-1}\right)}_F{\left(\genfrac{}{}{0pt}{}{2i+\alpha -2}{i}\right)}_F}=\frac{{(-1)}^{(i-1)(i+\alpha -2)}}{F_{2i+\alpha -2}{\left(\genfrac{}{}{0pt}{}{2i+\alpha -3}{i-1}\right)}_F^2},$$

(27)

and (22) follows. It can be easily checked that $p_{1,1}=1/F_{\alpha }$ and

$$\frac{p_{i+1,i+1}}{p_{i,i}}={(-1)}^{2i+\alpha -2}\frac{F_i^2{F}_{i+\alpha -1}^2}{F_{2i+\alpha }{F}_{2i+\alpha -1}^2{F}_{2i+\alpha -2}},$$

confirming Formula (23).

Let us observe that since the pivots of the Neville elimination of $F_n^{\left(\alpha \right)}$ are nonzero, this elimination can be performed without row exchanges.

Finally, using (3) and (24), the multipliers $m_{i,j}$ can be described as:

$$\begin{array}{cc}\hfill m_{i,j}& =\frac{p_{i,j}}{p_{i-1,j}}={(-1)}^{j-1}\frac{F_{i+\alpha -2}^2}{F_{i+j+\alpha -2}{F}_{i+j+\alpha -3}},1\le j<i\le n+1.\hfill \end{array}$$

(28)

Since $F_n^{\left(\alpha \right)}$ is symmetric, using Remark 1, we deduce that ${\tilde{m}}_{i,j}=m_{i,j}$.    □

Taking into account Theorem 1, the decomposition (4) of $F_n^{\left(\alpha \right)}$ and (6) of ${\left(F_n^{\left(\alpha \right)}\right)}^{-1}$ can be stored by means of $BD\left(F_n^{\left(\alpha \right)}\right)={\left(BD{\left(F_n^{\left(\alpha \right)}\right)}_{i,j}\right)}_{1\le i,j\le n+1}$ with

$$BD{\left(F_n^{\left(\alpha \right)}\right)}_{i,j}:=\left\{\begin{array}{cc}{(-1)}^{j-1}\frac{F_{i+\alpha -2}^2}{F_{i+j+\alpha -2}{F}_{i+j+\alpha -3}},\hfill & \mathrm{if}i>j,\hfill \\ {(-1)}^{(i-1)(i+\alpha -2)}\frac{1}{F_{2i+\alpha -2}{\left(\genfrac{}{}{0pt}{}{2i+\alpha -3}{i-1}\right)}_F^2},\hfill & \mathrm{if}i=j,\hfill \\ {(-1)}^{i-1}\frac{F_{j+\alpha -2}^2}{F_{i+j+\alpha -2}{F}_{i+j+\alpha -3}},\hfill & \mathrm{if}i<j.\hfill \end{array}\right.$$

(29)

On the other hand, using Lemma 1 and Formula (22) for the diagonal pivots, the determinant of Filbert matrices $F_n^{\left(\alpha \right)}$ can be expressed as follows:

$$det{F}_n^{\left(\alpha \right)}={(-1)}^{\frac{1}{6}n(n+1)(2n+3\alpha -2)}\frac{1}{F_{\alpha }}\prod _{k=1}^n{\left(F_{2k+\alpha }{\left(\genfrac{}{}{0pt}{}{2k+\alpha -1}{k}\right)}_F^2\right)}^{-1},$$

which is an equivalent formula to that obtained in Theorem 5 of [12].

4. Bidiagonal Factorization of Lilbert Matrices

Let us recall that Lucas numbers are defined recursively is a similar way to Fibonacci numbers, just changing the value of the initial element of the sequence,

$$L_0:=2,L_1:=1,L_{n+1}=L_n+L_{n-1},n\ge 1.$$

(30)

The analogous Lilbonomial coefficients are

$${\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_L:=\prod _{i=1}^k\frac{L_{n-i+1}}{L_i}=\frac{{\left[n\right]}_L!}{{\left[k\right]}_L!{[n-k]}_L!},0\le k\le n,$$

(31)

with the usual convention that empty products are defined as one and

$${\left[0\right]}_L!:=1,{\left[n\right]}_L!:=\prod _{k=1}^n{L}_k.$$

Let us observe that using the Binet form of Lucas numbers, we can write

$$L_n={\phi }^n+(1-{\phi }^n)={\phi }^n(1+q^n),$$

for $q=(1-\sqrt{5})/(1+\sqrt{5})$ and $\phi =(1+\sqrt{5})/2$. Moreover, as for Fibonacci numbers, in the literature, one can find many interesting equalities relating the Lucas numbers with each other, as well as Lucas and Fibonacci numbers. In this section, we use the following Vajda-type equality

$$L_n{L}_{n+p+q}-L_{n+p}{L}_{n+q}=5{(-1)}^n{F}_p{F}_q,p,q,n\in \mathbb{N},$$

(32)

proved in Theorem 5 of [26] to derive the bidiagonal factorization of the Lucas matrix $L_n^{\left(\alpha \right)}:={\left(L_{i,j}\right)}_{1\le i,j\le n+1}$ with

$$L_{i,j}^{\left(\alpha \right)}=\frac{1}{L_{i+j+\alpha -2}},1\le i,j\le n+1.$$

(33)

Theorem 2.

Given $\alpha \in \mathbb{N}$, let $L_n^{\left(\alpha \right)}\in {\mathbb{R}}^{(n+1)\times (n+1)}$ be the Lilbert matrix given by (33). The multipliers $m_{i,j}$ of the Neville elimination of $L_n^{\left(\alpha \right)}$ are given by

$$m_{i,j}={\tilde{m}}_{i,j}:={(-1)}^{j-1}\frac{L_{i+\alpha -2}^2}{L_{i+j+\alpha -2}{L}_{i+j+\alpha -3}},1\le j<i\le n+1.$$

(34)

Moreover, the diagonal pivots $p_{i,i}$ of the Neville elimination of $L_n^{\left(\alpha \right)}$ are

$$p_{i,i}={(-1)}^{(i-1)(i+\alpha -1)}{5}^{i-1}\frac{{[i-1]}_F{!}^2}{{[i-1]}_L{!}^2}\frac{1}{L_{2i+\alpha -2}{\left(\genfrac{}{}{0pt}{}{2i+\alpha -3}{i-1}\right)}_L^2},1\le i\le n+1,$$

(35)

and can be computed as follows

$$p_{1,1}=1/L_{\alpha },p_{i+1,i+1}=5{(-1)}^{\alpha -1}\frac{F_i^2{L}_{i+\alpha -1}^2}{L_{2i+\alpha }{L}_{2i+\alpha -1}^2{L}_{2i+\alpha -2}}{p}_{i,i},1\le i\le n.$$

(36)

Proof. 

The proof is analogous to that of Theorem 1 for the computation of the pivots and multipliers of the Neville elimination of Filbert matrices and, for this reason, we only provide a sketch. Let $L^{\left(k\right)}:={\left({\ell }_{i,j}^{\left(k\right)}\right)}_{1\le i,j\le n+1}$, $k=1,\dots ,n+1$, be the matrices obtained after $k-1$ steps of the Neville elimination procedure for $L_n^{\left(\alpha \right)}$. Using an inductive reasoning, similar to that of Theorem 1, the Vajda-type equality (32) and the definition (31) of Lilbonomial coefficients, the entries of the intermediate matrices of the Neville elimination can be written as follows:

$${\ell }_{i,j}^{\left(k\right)}={(-1)}^{(k-1)(i+\alpha -2)}{(-5)}^{(k-1)}\frac{{({[k-1]}_F!)}^2}{{({[k-1]}_L!)}^2}\frac{{\left[\genfrac{}{}{0pt}{}{j-1}{k-1}\right]}_F}{L_k{\left[\genfrac{}{}{0pt}{}{i+j+\alpha -2}{k}\right]}_L{\left[\genfrac{}{}{0pt}{}{i+k+\alpha -3}{k-1}\right]}_L},$$

(37)

for $k\le j,i\le n+1$, and then the pivots of the Neville elimination are

$$p_{i,j}={\ell }_{i,j}^{\left(j\right)}={(-1)}^{(j-1)(i+\alpha -2)}{(-5)}^{(j-1)}\frac{{({[j-1]}_F!)}^2}{{({[j-1]}_L!)}^2}\frac{1}{L_j{\left[\genfrac{}{}{0pt}{}{i+j+\alpha -2}{j}\right]}_L{\left[\genfrac{}{}{0pt}{}{i+j+\alpha -3}{j-1}\right]}_L}.$$

(38)

Identities (35) and (36) are deduced by considering $i=j$ in (38). Moreover, Formula (34) for the multipliers $m_{i,j}={\tilde{m}}_{i,j}$ are derived by taking into account that $m_{i,j}=p_{i,j}/p_{i-1,j}$ (see (3)).    □

Taking into account Theorem 2, the decomposition (4) of $L_n^{\left(\alpha \right)}$ and (6) of ${\left(L_n^{\left(\alpha \right)}\right)}^{-1}$, can be stored by means of $BD\left(L_n^{\left(\alpha \right)}\right)={\left(BD{\left(L_n^{\left(\alpha \right)}\right)}_{i,j}\right)}_{1\le i,j\le n+1}$ with   

$$BD{\left(L_n^{\left(\alpha \right)}\right)}_{i,j}:=\left\{\begin{array}{cc}{(-1)}^{j-1}\frac{L_{i+\alpha -2}^2}{L_{i+j+\alpha -2}{L}_{i+j+\alpha -3}},\hfill & \mathrm{if}i>j,\hfill \\ {(-1)}^{(i-1)(i+\alpha -1)}{5}^{i-1}\frac{{[i-1]}_F{!}^2}{{[i-1]}_L{!}^2}\frac{1}{L_{2i+\alpha -2}{\left(\genfrac{}{}{0pt}{}{2i+\alpha -3}{i-1}\right)}_L^2},\hfill & \mathrm{if}i=j,\hfill \\ {(-1)}^{i-1}\frac{L_{j+\alpha -2}^2}{L_{i+j+\alpha -2}{L}_{i+j+\alpha -3}},\hfill & \mathrm{if}i<j.\hfill \end{array}\right.$$

(39)

Using Lemma 1 and Formula (35) for the diagonal pivots, the determinant of Lilbert matrices $L_n^{\left(\alpha \right)}$ can be expressed as follows

$$det{L}_n^{\left(\alpha \right)}={(-1)}^{\frac{1}{6}n(n+1)(2n+3\alpha +1)}{5}^{\frac{1}{2}n(n+1)}\prod _{k=1}^n\frac{{\left[i\right]}_F!}{{\left[i\right]}_L!}{\left(L_{2k+\alpha }{\left(\genfrac{}{}{0pt}{}{2k+\alpha -1}{k}\right)}_L^2\right)}^{-1},$$

which is an equivalent formula to that obtained in Theorem 1.17 of [13].

5. Numerical Experiments

In this section, a collection of numerical experiments is presented, comparing the algorithms that take advantage of the bidiagonal decompositions presented in this work with the best standard routines. It should be noted that the cost of computing the matrix form (7) of the bidiagonal decomposition (4) is $O\left(n^2\right)$ for both Filbert matrices $F_n^{\left(\alpha \right)}$ (see (29)) and for Lilbert matrices $L_n^{\left(\alpha \right)}$ (see (39)).

We considered several Filbert matrices $F_n^{\left(\alpha \right)}$, for $\alpha =1$ and $\alpha =2$, as well as Lilbert matrices $L_n^{\left(\alpha \right)}$, for $\alpha =1$ and $\alpha =3$, with dimension $n+1=5,\dots ,15$. To keep the notation as contained as possible, in what follows, Filbert and Lilbert matrices are denoted as F and L, respectively, and their bidiagonal decompositions by $BD\left(F\right)$ and $BD\left(L\right)$.

The two-norm condition number of all considered matrices was computed in Mathematica. As can be easily seen in Figure 1, the condition number grows dramatically with the size of the matrix. As mentioned at the beginning of the paper, this bad conditioning prevents standard routines from giving accurate solutions to any algebraic problem, even for relatively small-sized problems.

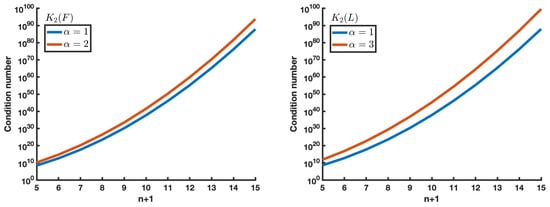
Figure 1. The 2-norm conditioning of Filbert matrices F and Lilbert matrices L.

To analyze the behavior of the bidiagonal approach and confront it with standard direct methods, several numerical experiments were performed, concerning both Filbert and Lilbert matrices. The factorizations obtained in Section 3 and Section 4 were used as an input argument of the Matlab functions of the TNTool package, made available in [27]. In particular, the following functions were used, each corresponding to an algebraic problem:

• TNInverseExpand$\left(BD\right(A\left)\right)$ provides $A^{-1}$, with an $O\left(n^2\right)$ computational cost (see [22]).
• TNSolve$\left(BD\right(A),d)$ solves the system $Ax=b$, with an $O\left(n^2\right)$ cost.
• TNSingularValues$\left(BD\right(A\left)\right)$ obtains the singular values of A, with an $O\left(n^3\right)$ cost.

For each problem, the approximated solution obtained by the TNTool subroutine was compared with the classical method provided by Matlab $R2022b$. Relative errors in both cases were computed by comparing with the exact solution given by Mathematica $13.1$, which makes use of 100-digit arithmetic.

Computation of inverses. In this experiment, we compared the accuracy in determining the inverse of each considered matrix with two methods: the bidiagonal factorization as an input to the TNInverseExpand routine and the standard Matlab command inv. It is clear from Figure 2 that our procedure obtained great accuracy in every analyzed case, whereas the results obtained with Matlab failed dramatically for moderate sizes of the matrices.

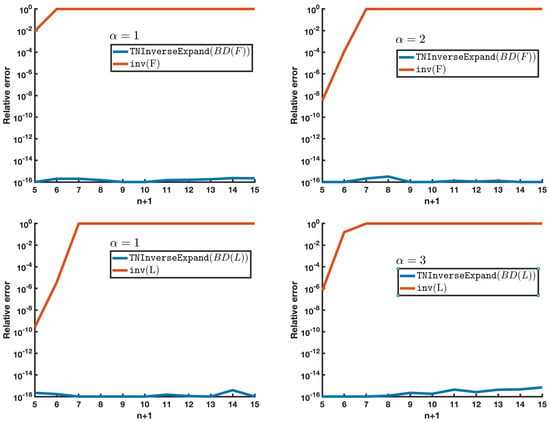
Figure 2. Relative error of the approximations to the inverse of Filbert and Lilbert matrices, $F^{-1}$ and $L^{-1}$, respectively.

Resolution of linear systems. For each of the matrices considered, in this experiment, the solution of the linear systems $Fx=d$ and $Lx=d$ was computed, where $d={\left({(-1)}^{i+1}{d}_i\right)}_{1\le i\le n+1}$ and $d_i$, $i=1,\dots ,n+1$, are random nonnegative integer values. This was again performed in two ways: by using the proposed bidiagonal factorization as an input of the TNSolve routine and by the standard ∖ Matlab command. As before, the standard Matlab routine could not overcome the ill-conditioned nature of the analyzed matrices, in contrast with the machine precision-order errors achieved by the bidiagonal approach, as is depicted in Figure 3.

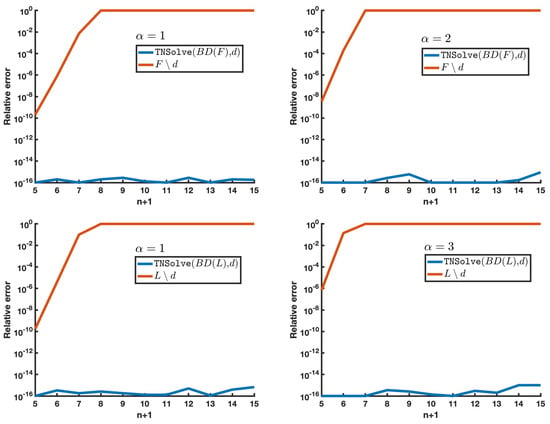
Figure 3. Relative error of the approximations to the solution of the linear systems $Fc=d$ and $Lc=d$, where $d={\left({(-1)}^{i+1}{d}_i\right)}_{1\le i\le n+1}$ and $d_i$, $i=1,\dots ,n+1$, are random nonnegative integer values.

Computation of singular values. The relative errors in determining the smallest singular value of both Filbert and Lilbert matrices are illustrated in this experiment. These were computed with both the standard Matlab command svd and by providing as an input argument to TNSingularValues the corresponding bidiagonal decomposition. It follows from Figure 4 that our method determined accurately the lowest singular value for every studied case, while the standard Matlab command svd results were very far from the exact solution even for small sizes of the considered matrices.

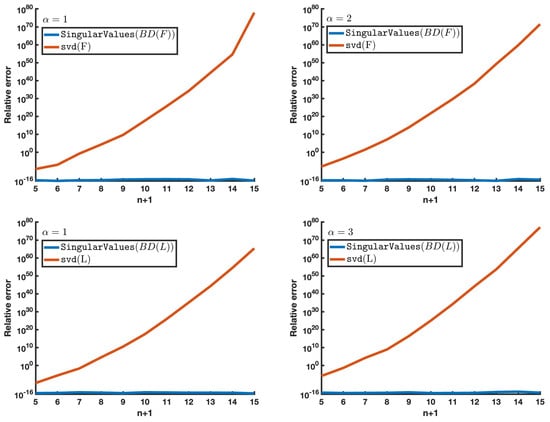
Figure 4. Relative error of the approximations to the lowest singular value of Filbert matrices F and Lilbert matrices L.

6. Conclusions

The paper analyzed the generalized versions of Filbert and Lilbert matrices $F_n^{\left(\alpha \right)}$ and $L_n^{\left(\alpha \right)}$, based on Fibonacci and Lucas numbers, respectively. Leaning on the Neville elimination, their bidiagonal factorizations were obtained explicitly, which also led to formulae for the corresponding determinants. Numerical experiments were provided, exhibiting a great level of accuracy in the case of the routines that took as an input the bidiagonal decomposition of the matrices, even for notably ill-conditioned cases, while the results of standard procedures were wrong by orders of magnitude. Future prospects include the study of the condition number of these matrices, which could offer some insight about the excellent experimental results obtained.