Pricing Chinese Convertible Bonds with Learning-Based Monte Carlo Simulation Model
Abstract
1. Introduction
2. Literature Review
2.1. Brief History for Pricing Convertible Bonds
2.2. Research on Pricing Chinese Convertible Bonds
2.3. Machine Learning Method for Pricing Convertible Bonds
2.4. Motivation and Overview
3. Methods
3.1. Fundamental Framework for Pricing Convertible Bonds via Regression-Based Monte Carlo Approaches
3.2. The Standard Procedure of Basic LSM with OLS
- (1)
- Define a complete probability space within the bounded time horizon . is the whole set containing all possible outcomes ω of the state variable and is an equivalent martingale measure under the assumption of no arbitrage opportunities. Divide into a set of finite number of stopping times . Considering a series of cash flows from a convertible bond along the path at discrete time point , with risk-neutral pricing measure , the continuation value at a given time can be expressed as the expectation of the future cash flows discounted by risk-free interest rate,
- (2)
- Facing the difficulty of the computation of the above conditional expectation Formula (1), Longstaff and Schwartz (2001) proposed an approach of a least squares regression on some basis functions of the state variables to make the estimation. Usually, the first few Laguerre polynomials are chosen to be the basis functions. The estimated conditional expectation value would be derived in the form of a linear combination of the state variable :
- (3)
- For each path, when is greater than the conversion value , a rational investor would continue holding the convertible bond, so the optimal stopping value remains unchanged. Otherwise, the optimal stopping time point and stopping time value are updated.
- (4)
- By Monte Carlo simulation, stock price paths are generated based on the Heston model. Once the optimal exercise decisions and corresponding payoffs are determined for each path, the time-0 price of the convertible bond is calculated by averaging the discounted each back to the time over all simulated paths.
- (5)
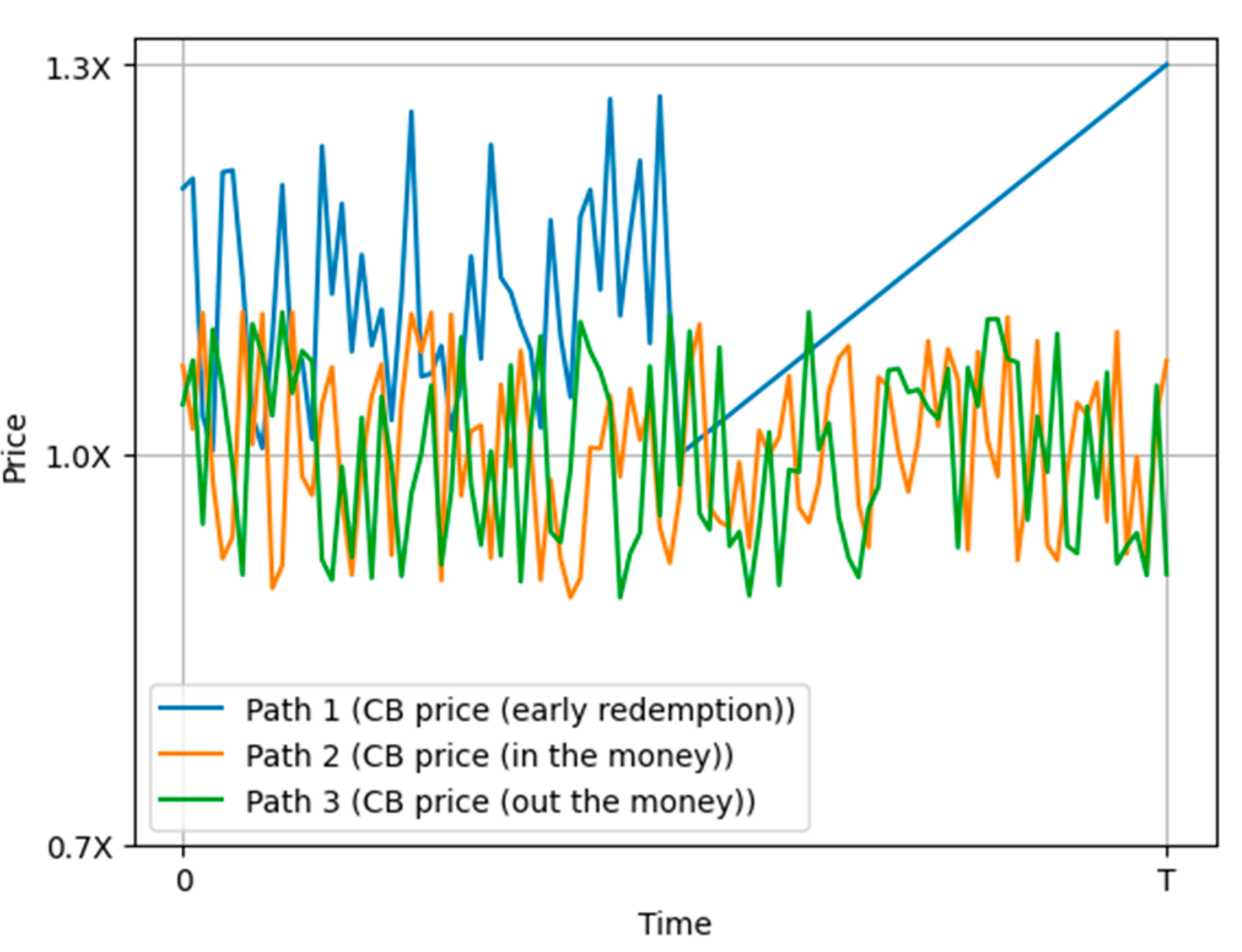
- To provide a more intuitive illustration of the pricing process in the LSM model, Figure 1 depicts the simulated price paths in different scenarios. Path 1 represents the path of the convertible bond when early redemption is triggered. Path 2 and Path 3 represent the paths of the convertible bond in the money and out of the money, respectively.
3.3. Foundations of Convertible Bond Valuation through Machine Learning Methodology
3.3.1. Support Vector Regression
3.3.2. Random Forest
3.3.3. Bayesian Optimization
4. Empirical Studies
4.1. Data Description
4.2. Model Description
4.3. Simulated Data Study
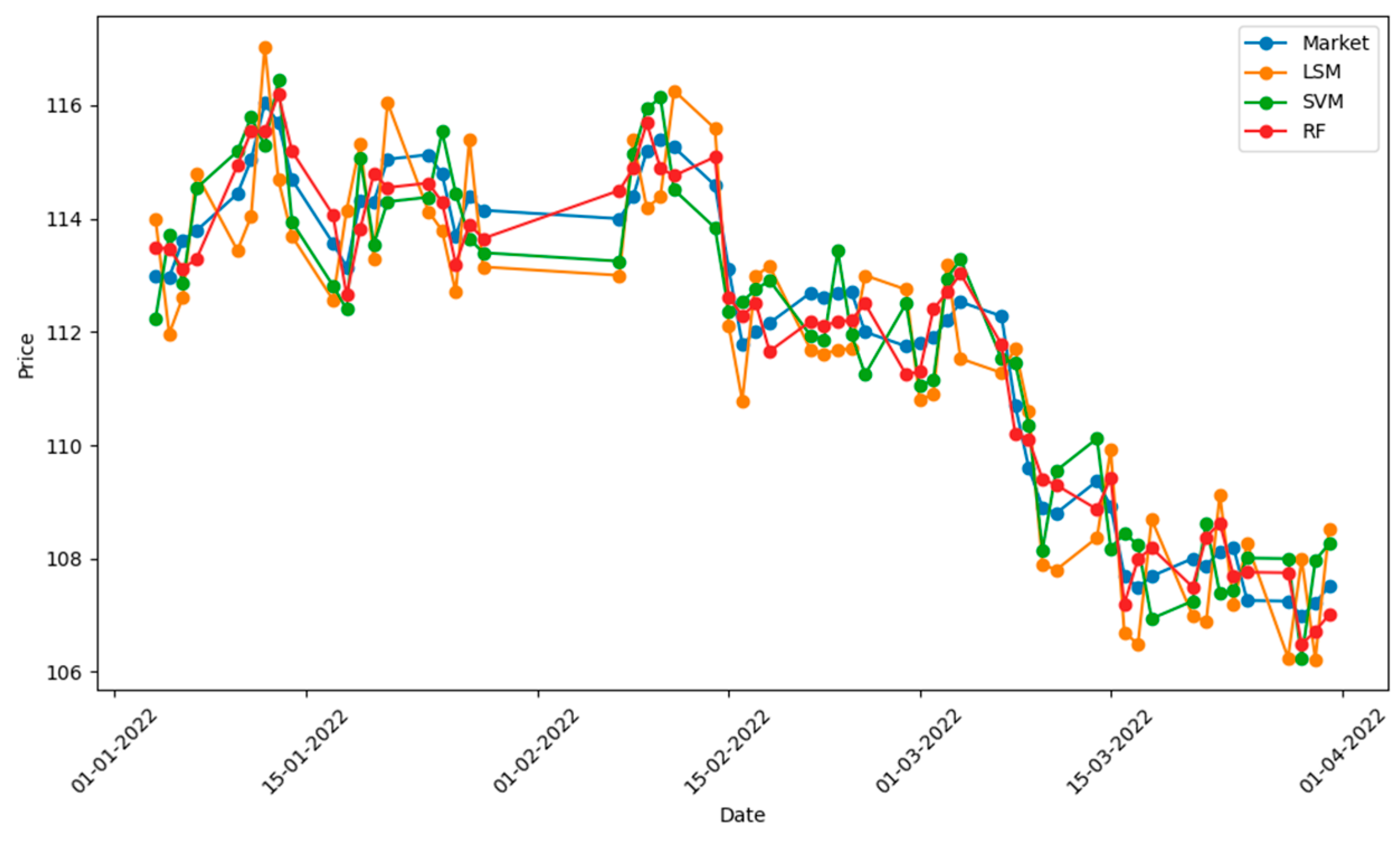
4.4. A Case Study of CEB Convertible Bond
5. Conclusions and Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Longstaff, F.; Schwartz, E. Valuing American options by simulation: A simple least-squares approach. Rev. Financ. Stud. 2001, 14, 113–147. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, J. Pricing Chinese Convertible Bonds with Default Intensity by Monte Carlo Method. Discret. Dyn. Nat. Soc. 2019, 2019, 8610126. [Google Scholar] [CrossRef]
- Li, P.; Song, J. Pricing Chinese Convertible Bonds with Dynamic Credit Risk. Discret. Dyn. Nat. Soc. 2014, 2014, 492134. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Yan, L.; Ma, C. Valuing Convertible Bonds Based on LSRQM Method. Discret. Dyn. Nat. Soc. 2014, 2014, 301282. [Google Scholar] [CrossRef]
- Nazemi, A.; Rauch, J.; Fabozzi, F.J. Interpretable Machine Learning for Creditor Recovery Rates. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of Rational Option Pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141. [Google Scholar] [CrossRef]
- Merton, R.C. On the pricing of corporate debt: The risk structure of interest rates. J. Financ. 1974, 29, 449–470. [Google Scholar]
- Ingersoll, J.E. A contingent-claims valuation of convertible securities. J. Financ. Econ. 1977, 4, 289–321. [Google Scholar] [CrossRef]
- Brennan, M.J.; Schwartz, E.S. Convertible bonds: Valuation and optimal strategies for call and conversion. J. Financ. 1977, 32, 1699–1715. [Google Scholar] [CrossRef]
- Brennan, M.J.; Schwartz, E.S. Analyzing convertible bonds. J. Financ. Quant. Anal. 1980, 15, 907–929. [Google Scholar] [CrossRef]
- McConnell, J.J.; Schwartz, E.S. LYON taming. J. Financ. 1986, 41, 561–576. [Google Scholar] [CrossRef]
- Hull, J.; White, A. The Use of the Control Variate Technique in Option Pricing. J. Financ. Quant. Anal. 1988, 23, 237–251. [Google Scholar] [CrossRef]
- Kalotay, A.J.; Williams, G.O.; Fabozzi, F.J. A Model for Valuing Bonds and Embedded Options. Financ. Anal. J. 1993, 49, 35–46. [Google Scholar] [CrossRef]
- Duan, J.-C. The GARCH Option Pricing Model. Math. Financ. 1995, 1, 13–32. [Google Scholar] [CrossRef]
- Cox, J.C.; Ross, S.A.; Rubinstein, M. Option pricing: A simplified approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Hung, M.-W.; Wang, Y., Jr. Pricing Convertible Bonds Subject to Default Risk. Derivations 2002, 10, 75–87. [Google Scholar] [CrossRef]
- Das, S.R.; Sundaram, R.K. An Integrated Model for Hybrid Securities. Manag. Sci. 2007, 53, 1439–1451. [Google Scholar] [CrossRef][Green Version]
- Fu, M.C.; Laprise, S.B.; Madan, D.B.; Su, Y.; Wu, R. Pricing American options: A comparison of Monte Carlo simulation approaches. J. Comput. Financ. 2001, 4, 39–88. [Google Scholar] [CrossRef]
- Cortazar, G.; Gravet, M.; Urzua, J. The valuation of multidimensional American real options using the LSM simulation method. Comput. Oper. Res. 2008, 35, 113–129. [Google Scholar] [CrossRef]
- Nadarajah, S.; Margot, F.; Secomandi, N. Comparison of least squares Monte Carlo methods with applications to energy real options. Eur. J. Oper. Res. 2017, 256, 196–204. [Google Scholar] [CrossRef]
- Cecconi, F.; Khodabakhshian, A.; Rampini, L. Data-driven decision support system for building stocks energy retrofit policy. J. Build. Eng. 2022, 54, 104633. [Google Scholar] [CrossRef]
- Batten, J.A.; Khaw KL, H.; Young, M.R. Pricing convertible bonds. J. Bank. Financ. 2018, 92, 216–236. [Google Scholar] [CrossRef]
- Zheng, Z.; Lin, H. Research on the Pricing of Convertible Bonds in China. J. Xiamen Univ. (Philos. Soc. Sci. Ed.) 2004, 162, 93–99. [Google Scholar]
- Yang, J.; Choi, Y.; Li, S.; Yu, J. A note on “Monte Carlo analysis of convertible bonds with reset clause”. Eur. J. Oper. Res. 2010, 200, 924–925. [Google Scholar] [CrossRef]
- Feng, J.; Zhou, X.; Duan, M. Design and Impact Analysis of Convertible Bond Option Terms. Manag. Rev. 2018, 30, 58–68. [Google Scholar]
- Xie, Y. Research on Pricing of Convertible Bonds Based on Black-Scholes Model—Taking Oupai Convertible Bonds as an Example. China Price 2021, 11, 53–55. [Google Scholar]
- Yang, X.; Yu, J.; Xu, M.; Fan, W. Convertible bond pricing with partial integro-differential equation model. Math. Comput. Simul. 2018, 152, 35–50. [Google Scholar] [CrossRef]
- Chang, J.; Wang, Y. Pricing of Convertible Bonds Based on Tsallis Entropy Distribution under Stochastic Interest Rate Model. Oper. Res. Manag. 2020, 29, 189–197, 231. [Google Scholar]
- Takahashi, S.; Chen, Y.; Tanaka-Ishii, K. Modeling financial time-series with generative adversarial networks. Phys. A Stat. Mech. Appl. 2019, 527, 121261. [Google Scholar] [CrossRef]
- Dogariu, M.; Ştefan, L.-D.; Boteanu, B.A.; Lamba, C.; Ionescu, B. Towards Realistic Financial Time Series Generation via Generative Adversarial Learning. In Proceedings of the 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 23–27 August 2021. [Google Scholar]
- Zhou, W.; Yang, M.; Han, L. A Nonparametric Approach to Pricing Convertible Bond via Neural Network. In Proceedings of the Eighth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing (SNPD 2007), Qingdao, China, 30 July–1 August 2007; Volume 2, pp. 564–569. [Google Scholar]
- Niu, X.; Ba, X. Pricing and Empirical Analysis of Convertible Bonds Based on Machine Learning. J. Party Sch. Guizhou Prov. 2021, 5, 58–71. [Google Scholar]
- Ren, G.; Meng, T. Research on Pricing Methods of Convertible Bonds Based on Deep Learning GAN Models. Int. J. Financ. Stud. 2024, 11, 145. [Google Scholar] [CrossRef]
- Fabozzi, F.J.; Paletta, T.; Tunaru, R. An improved least squares Monte Carlo valuation method based on heteroscedasticity. Eur. J. Oper. Res. 2017, 263, 698–706. [Google Scholar] [CrossRef]
- Jang, H.; Kim, S.; Han, J.; Lee, S.; Ban, J.; Han, H.; Lee, C.; Jeong, D.; Kim, J. Fast Monte Carlo Simulation for Pricing Equity-Linked Securities. Comput. Econ. 2019, 56, 865–882. [Google Scholar] [CrossRef]
- Andreasson, J.; Shevchenko, P.V. A bias-corrected Least-Squares Monte Carlo for solving multi-period utility models. Soc. Sci. Res. Netw. 2021. [Google Scholar] [CrossRef]
- Boire, F.M.; Reesor, R.M.; Stentoft, L. Bias Correction in the Least-Squares Monte Carlo Algorithm. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Lin, J.; Almeida, C. American option pricing with machine learning: An extension of the Longstaff-Schwartz method. Braz. Rev. Financ. 2021, 19, 85–109. [Google Scholar] [CrossRef]
- Tompaidis, S.; Yang, C. Pricing American-style options by Monte Carlo simulation: Alternatives to ordinary least squares. J. Comput. Financ. 2014, 18, 121–143. [Google Scholar] [CrossRef]
- Mu, G.; Godina, T.; Maffia, A.; Sun, Y.C. Supervised machine learning with control variates for American option pricing. Found. Comput. Decis. Sci. 2018, 43, 207–217. [Google Scholar] [CrossRef]
- Goudenège, L.; Molent, A.; Zanette, A. Machine learning for pricing American options in high-dimensional Markovian and non-Markovian models. Quant. Financ. 2020, 20, 573–591. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ech-Chafiq, Z.E.F.; Labordère, P.H.; Lelong, J. Pricing Bermudan Options Using Regression Trees/Random Forests. SIAM J. Financ. Math. 2023, 14, 1113–1139. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Guo, J.; Zan, X.; Wang, L.; Lei, L.; Ou, C.; Bai, S. A random forest regression with Bayesian optimization-based method for fatigue strength prediction of ferrous alloys. Eng. Fract. Mech. 2023, 293, 109714. [Google Scholar] [CrossRef]
| Name | Meaning |
|---|---|
| The conversion value equals the payoff in terms of the corresponding number of shares | |
| The conversion ratio | |
| The underlying stock price at time t | |
| The final redemption value of the convertible bond |
| Payoff | Condition | Decision |
|---|---|---|
| Forced conversion | ||
| Voluntary conversion | ||
| F | Redemption at maturity | |
| 0 | Otherwise | Continuation |
| Name | Value Range | Optimum Value (Simulation) | Optimum Value (Real Case) |
|---|---|---|---|
| max_depth | (5,20) | 17.807 | 16.305 |
| max_features | (0,20) | 17 | 16 |
| n_estimators | (10,150) | 103.516 | 101.498 |
| min_samples_split | (1,5) | 3 | 2 |
| min_samples_leaf | (1,5) | 2 | 1 |
| Name | Mean | Median | Max | Min |
|---|---|---|---|---|
| CEB | 107.09 | 105.61 | 115.95 | 104.358 |
| CB Price | STD | Q1 | Q2 | Q3 |
| 2.18 | 105.04 | 105.61 | 106.82 |
| Simulated data | 100.00 | 0.2672 | 0.03158 |
| CEB | 112.97 | 0.2672 | 0.03158 |
| Moneyness | Total | ITM | ATM | OTM |
|---|---|---|---|---|
| Bys-RF | 0.4922 | 0.6001 | 0.6122 | 0.3673 |
| SVR | 0.5324 | 0.6326 | 0.6426 | 0.3987 |
| LSM | 0.7295 | 0.9355 | 0.8126 | 0.6532 |
| Number of Paths | Moneyness | Bys-RF | SVR | LSM |
|---|---|---|---|---|
| 500 | Total | 0.6345 | 0.6789 | 1.0224 |
| ITM | 0.7536 | 0.7452 | 1.324 | |
| ATM | 0.6948 | 0.6879 | 1.0321 | |
| OTM | 0.4927 | 0.4523 | 0.7987 | |
| 1000 | Total | 0.5011 | 0.5324 | 0.7295 |
| ITM | 0.6012 | 0.6326 | 0.9355 | |
| ATM | 0.6023 | 0.6426 | 0.8126 | |
| OTM | 0.3751 | 0.3987 | 0.6532 | |
| 1500 | Total | 0.4029 | 0.5221 | 0.6254 |
| ITM | 0.5012 | 0.6178 | 0.7659 | |
| ATM | 0.4564 | 0.5748 | 0.6588 | |
| OTM | 0.2918 | 0.3889 | 0.5114 |
| Number of Time Steps | Moneyness | Bys-RF | SVR | LSM |
|---|---|---|---|---|
| 500 | Total | 0.5901 | 0.6144 | 0.6378 |
| ITM | 0.6984 | 0.7865 | 0.8569 | |
| ATM | 0.6512 | 0.6978 | 0.7894 | |
| OT | 0.4325 | 0.4556 | 0.5985 | |
| 1000 | Total | 0.4897 | 0.5324 | 0.7295 |
| ITM | 0.6012 | 0.6326 | 0.9355 | |
| ATM | 0.6215 | 0.6426 | 0.8126 | |
| OTM | 0.3698 | 0.3987 | 0.6532 | |
| 1500 | Total | 0.4215 | 0.5978 | 0.7015 |
| ITM | 0.5078 | 0.7145 | 0.8123 | |
| ATM | 0.4598 | 0.6878 | 0.7564 | |
| OTM | 0.3021 | 0.4589 | 0.6545 |
| Issue Date | 2017.3.31 |
|---|---|
| Time horizon | 6 |
| Face value | 100 |
| Coupon (%) | 0.2, 0.5, 1.0, 1.5, 1.8, 2.0 |
| Call value till maturity | 105 |
| The first conversion price | 4.36 |
| Change of conversion price | 2017.7.5, adjusted to 4.26 |
| Reset clause | In 30 consecutive trading days, the closing stock price is lower than 80% of the conversion price in 15 trading days |
| Call on condition | In 30 consecutive trading days, the closing stock price is not less than 130% of the conversion price in 15 trading days |
| Call value | Face value plus the accrued interest |
| Put on condition | When the use of the capital is changed |
| Put value | Face value plus the accrued interest |
| The long-term mean volatility of the underlying stock before the issuing date | |
| r | The 6-year risk-free interest rate at the issuing date |
| Moneyness | Total | ITM | ATM | OTM |
|---|---|---|---|---|
| RF | 0.6589 | 0.7748 | 0.6897 | 0.5987 |
| SVR | 0.8945 | 1.0586 | 0.9465 | 0.7946 |
| LSM | 0.7365 | 1.0568 | 0.8654 | 0.7145 |
| Moneyness | Bys-RF | SVR | LSM | |
|---|---|---|---|---|
| With hyperparameter Tuning | Total | 0.5233 | 0.7 | 0.7643 |
| ITM | 0.5931 | 0.8235 | 0.8878 | |
| ATM | 0.5278 | 0.7978 | 0.8235 | |
| OTM | 0.4363 | 0.6912 | 0.6945 | |
| Without hyperparameter tuning | Total | 0.6183 | 0.8141 | 0.7765 |
| ITM | 0.7238 | 1.0186 | 0.9568 | |
| ATM | 0.6497 | 0.8451 | 0.8654 | |
| OTM | 0.5895 | 0.7546 | 0.7145 |
| Algorithm | Computational Cost Estimate | Estimated Computation Time | Reason for Difference |
|---|---|---|---|
| Traditional LSM | Moderate | About 10 min | Simple regression model fitting, relatively low computational complexity. |
| SVR replacing LSM | High | 15–20 min | Support vector regression (SVR) involves solving a quadratic programming problem, which can be computationally intensive, especially for large datasets. It also requires tuning hyperparameters which may require additional computation. |
| RF replacing LSM | High | About 30 min | Random forest (RF) involves building multiple decision trees, each of which requires training on subsets of the data. For large datasets or a large number of trees, this can lead to significantly higher computational costs compared to simple regression. Additionally, tuning the RF hyperparameters adds to the computation time. |
| Bys-RF replacing LSM | Very high | 30–40 min | Bayesian optimization iteratively explores the hyperparameter space of the random forest model to find optimal settings. While it can improve model performance, this iterative process requires additional computation, resulting in higher computational costs compared to standard random forest fitting. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Wen, C.; Li, R. Pricing Chinese Convertible Bonds with Learning-Based Monte Carlo Simulation Model. Axioms 2024, 13, 218. https://doi.org/10.3390/axioms13040218
Zhu J, Wen C, Li R. Pricing Chinese Convertible Bonds with Learning-Based Monte Carlo Simulation Model. Axioms. 2024; 13(4):218. https://doi.org/10.3390/axioms13040218
Chicago/Turabian StyleZhu, Jiangshan, Conghua Wen, and Rong Li. 2024. "Pricing Chinese Convertible Bonds with Learning-Based Monte Carlo Simulation Model" Axioms 13, no. 4: 218. https://doi.org/10.3390/axioms13040218
APA StyleZhu, J., Wen, C., & Li, R. (2024). Pricing Chinese Convertible Bonds with Learning-Based Monte Carlo Simulation Model. Axioms, 13(4), 218. https://doi.org/10.3390/axioms13040218








